Self-Assembling Purine and Pteridine Quartets: How Do π-Conjugation Patterns Affect Resonance-Assisted Hydrogen Bonding?

Abstract

Computed association strengths for 43 purine and pteridine quartets (38 to 100 kcal/mol) show excellent linear correlation with π-conjugation gain in the assembled monomers (r² = 0.965). Even quartets having the same secondary electrostatic interactions can display very different association strengths depending on the π-conjugation patterns of the monomeric units.

Davies et al.’s 1962 paper unveiled the first X-ray structure of a guanine (G) quartet (G•G•G•G), showing that four guanines could self-assemble into a planar, cyclic, arrangement through four pairs of hydrogen bonds.¹ G-quartets sandwiching monovalent ions can form higher order nucleic acid structures called G-quadruplexes, and these secondary structures are often found in the guanine-rich telomeric regions of DNA.^2–5 Because of its occurrence at biologically relevant sites, robust assembly, and gel-like supramoleuclar property, G-quartets are potential therapeutic targets and find useful applications in nanotechnology, for example, as ion channels, ionophores, and biosensors.^4,6

Is the G-quartet structure special? Among related assemblies, the G-quartet was found to be especially robust. The two base lesion products of guanine: xanthine (X) and 8-oxoguanine (O), also could form quartets through four pairs of hydrogen bonding interactions, but the resulting X•X•X•X, G•G•X•O, and X•O•X•O assemblies (Figure 1), were found to have weaker association strengths.^7–9 It was suggested that hydrogen bonding interactions in the G-quartet displayed cooperativity,^10,11 i.e., the computed association strengths of four guanines in a cyclic arrangement was greater than four times that of the guanine dimer. No cooperative effects were found for the X-quartet. Otero et al.¹⁰ attributed the special cooperativity in G-quartet to resonance-assisted hydrogen bonding (RAHB)^12,13 (i.e., π-conjugation gain in the assembled guanines). But Guerra et al. pointed out that the X-quartet also has a π-system capable of RAHB.¹⁴ These authors suggested instead that differences in covalency were responsible for the strong hydrogen bonds in G-quartet.¹⁴

Figure 1.

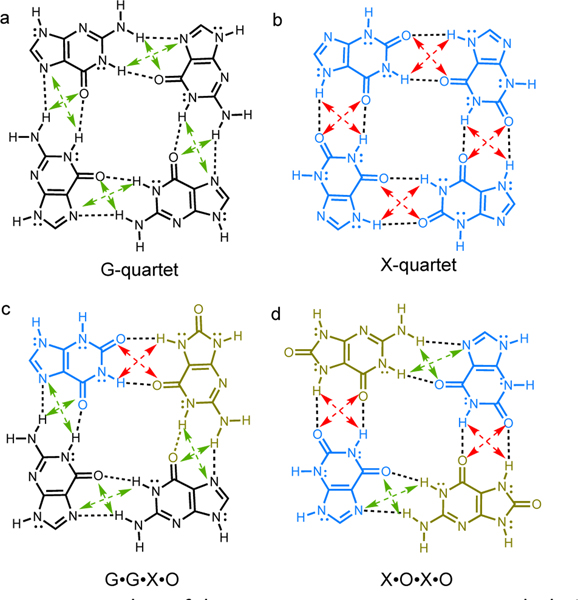
Examples of known quartet structures, and their secondary electrostatic interaction (SEI) patterns. AA-DD interactions (attractive) are indicated in green dashed lines, AD-DA interactions (repulsive) are indicated in red dashed lines.

We now examine these viewpoints by investigating the effect of RAHB in 43 purine and pteridine quartets. We recently showed that the energetic effects of RAHB can vary depending on the π-conjugation patterns of the interacting fragments.^15–1 Hydrogen bonding interactions that enhance cyclic [4n+2] π-electron delocalizations in compounds (i.e., increase aromatic character) show strong resonance-assistance. Interactions with little to no effect on ring π-aromaticity, show weak resonance-assistance.

Here, we show that differences in the π-conjugation patterns of monomers can explain the association trends of quartets. Note that cyclic [4n+2] π-electron delocalization in the six membered ring of guanine is breached by only one C=O group, but by two in xanthine (Figure 1). In the G-quartet, hydrogen bonding polarizes the π-electrons of the monomers (C=O groups are polarized to C⁺–O^–), and the resulting resonance forms for all four guanine units show cyclic [4n+2] π-electron delocalizations (Figure 2). In the X-quartet, hydrogen bonding polarizes the π-electrons of the xanthines, but the effect of aromatization is less prominent, due to two C=O groups interrupting cyclic π-electron delocalization in the six membered rings.

Figure 2.

Resonance form for G-quartet, showing increased aromaticity in the six membered rings, due to RAHB.

Comparisons of the optimized geometries of guanine, xanthine, G-quartet, and X-quartet are instructive. In the G-quartet, all four of the hydrogen bonding C=O groups are lengthened by 0.015 Å (C=O length: 1.223 Å) when compared to the monomer (C=O length: 1.208 Å), suggesting notable π-electron polarization. In the X-quartet, the four C=O groups are lengthened only by 0.007Å (C=O length: 1.219 Å) compared to the monomer (C=O length: 1.212 Å), suggesting a lesser degree of π-electron polarization.

Guanine and xanthine quartets also differ in the types of secondary electrostatic interactions (SEI)¹⁸ present. According to the SEI model, complexes with all proton acceptors (A) on one fragment and all proton donors (D) on the other fragment are the most robust, since the diagonal pairs of electrostatic interactions would be attractive (see Figure 1, green dashed arrows). Hydrogen bonding fragments have alternating A and D sites are expected to have weaker association strengths, since the diagonal pairs of electrostatic interactions would be repulsive (see Figure 1, red dashed lines).

In the G-quartet, all four pairs of hydrogen bonds are of the AA-DD type; quartet assembly involves two hydrogen bond donors from the Watson-Crick face and two hydrogen bond acceptors from the Hoogsteen face. In the X-quartet, all four pairs of hydrogen bonds are of the AD-DA type, contributing to a weaker association. Of the quartets considered in our study, 13 complexes have four pairs of AA-DD hydrogen bonding motifs (i.e., [AA-DD]₄, e.g., the G-quartet), 24 complexes have four pairs of AD-DA hydrogen bonding motifs(i.e., [AD-DA]₄, e.g, the X-quartet), and six complexes have mixed AA-DD and AD-DA motifs (e.g., X•O•X•O and G•G•X•O).

Computed gas-phase association energies (∆E) for the quartet complexes range from 38.2 kcal/mol to 100.7 kcal/mol, indicating a wide span of hydrogen bond strengths (4.7 to 12.6 kcal/mol per interaction). Following the SEI model, the [AA-DD]₄ quartets (four sets of AA-DD hydrogen bonds) have higher ∆E values (73.3 to 100.7 kcal/mol) compared to quartets with mixed hydrogen bonding motifs (60.3 to 67.6 kcal/mol), and the [AD-DA]₄ quartets (38.2 to 69.7 kcal/mol) can have even weaker association strengths (see Figure 3). Figure 3 suggests that there is a relationship between RAHB and SEI for the quartets systems. But this is not a general relationship. Note that some of the quartets with [AD-DA]₄ patterns (blue circles, Figure 3) have stronger associations strengths compared to those with mixed SEI patterns (green triangles, Figure 3). Recent works from our group reported similar findings for triply hydrogen bonded arrays; AAA-DDD arrays were found to have weaker computed gas-phase association energies and weaker RAHB effects than AAD-DDA and ADA-DAD arrays in general, despite having the most favourable SEI arrangement.¹⁶

Figure 3.

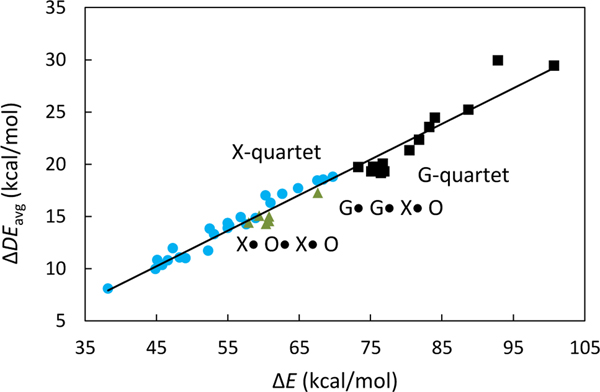
Plot of ∆E vs. ∆DE_avg for 43 quartets. [AA-DD]₄ quartets are in black squares, quartets with mixed SEI patterns are in olive triangles, and [AD-DA]₄ quartets are in blue circles.

Notably, quartets with the same SEI patterns can display quite different ∆E values (~30 kcal/mol difference, see Figure 1). Computed block-localized wavefunction (BLW)^19,20 analyses suggest that these variations arise due to differences in the π-conjugation patterns of assembling monomers. Even though all of the quartets studied have π-conjugated monomers, and can benefit from resonance-assistance, some quartets display greater RAHB effects than others. Quartets that display strong π-conjugation gain upon hydrogen bond assembly have higher association strengths. Excellent linear correlation between computed gas-phase association energy (∆E) vs. π-conjugation gain (∆DE_avg) in assembled monomers was found for all 43 quartets (r² = 0.965, see Figure 3). Analyses based on natural bond orbital (NBO) deletion²¹ computations show the same trend (see SI).

π-Electron delocalization energies (DE_π) were computed for the quartet complexes (DE_complex) and for the individual monomers (DE_monomers) comprising each quartet, and the difference (∆DE_π) provided a measure of increased π-conjugation in the quartet upon self-assembly of the monomers. When divided by four, the resulting ∆DE_avg values (∆DE_avg = ∆DE_π/4) provide an estimate of the average π-conjugation increase in monomers for a given quartet structure; an averaged value was used since some quartets contain different monomeric units.

When cations are complexed to G-quartet, the effect of RAHB is even greater since the ring π-electrons are polarized even more, as indicated by resonance gain and increased bond length alternation in the quartet structure (see Figure 4, note longer double bonds when G-quartet is complexed to one and two cations). Optimized structures of the G-quartet with zero (C=O length: 1.223 Å), one (C=O length: 1.241 Å), and two (C=O length: 1.258 Å) K⁺ ions show lengthened C=O bond lengths, suggesting increased π-electron polarization in ion complexed quartets. Computed ∆DE_avg values for the G-quartet indicate that resonance gain in the assembled guanine units (∆DE_avg = 19.3 kcal/mol) increase significantly as one (∆DE_avg = 30.4kcal/mol) and two (∆DE_avg = 40.2 kcal/mol) K⁺ ions are complexed to opposite faces of the quartet.

Figure 4.

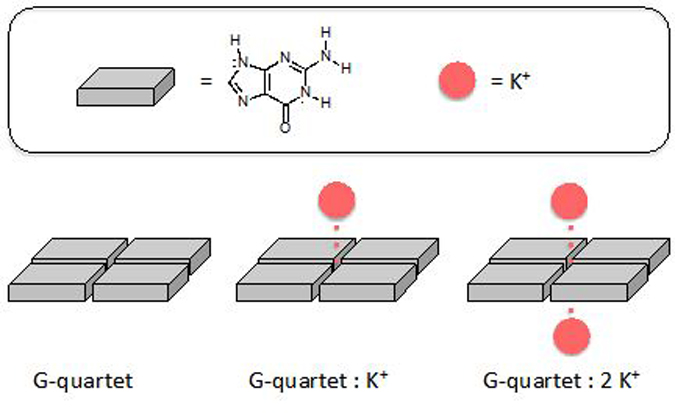
Schematic illustration of G-quartet complexed to zero, one, and two K⁺ cations.

Conclusions

The concept of resonance-assisted hydrogen bonding (RAHB) was originally conceived by Gilli et al.^12,13 to explain the occurrence of strong hydrogen bonding interactions, when hydrogen bond donors and acceptors are connected through a common π-conjugated framework (e.g., malonaldehyde and other intramolecular hydrogen-bonded systems, the secondary structures of proteins, and DNA base pairs). While we agree with past theoretical evidence¹⁴ showing that orbital interactions (which capture the effects of RAHB) are not the principal component of a hydrogen bond, we show that perturbations in orbital interactions are important factors that influence the trends of hydrogen bonding interactions when several hydrogen bonding systems are compared with each other. Among structurally related hydrogen-bonded complexes (e.g., quartets), the energetic effects of RAHB can vary significantly depending on the π-conjugation patterns of the interacting fragments. This relationship explains why quartet structures that assemble through the same SEI patterns, numbers, and types of hydrogen bonds can have very different association strengths.

Computational Methods

Geometries of all quartets and monomers were optimized at ωB97X-D/6–311+G(d,p), using an ultrafine grid, employing Gaussian09.²² Hydrogen bonding interaction energies (∆E) were computed at the same level, and evaluated based on the total electronic energies of the individual monomers comprising a quartet minus the total electronic energy of the quartet complex. All ∆E values include zero-point vibrational energy (ZPVE) corrections. Vibrational frequency analyses verified the nature of the stationary points. All monomers were optimized with C_s constraint and all quartets were optimized at their highest possible planar geometry (C_4h, C_2h, or C_s, depending on the types and orientation of the monomeric units, see details in the Supporting Information, SI). All of the quartet structures had imaginary frequencies lower than 50i cm^–1. Five monomers had imaginary frequencies higher than 50i cm^–1, and their computed planarization energies (all lower than 1 kcal/mol) are included in Table S4.

All block localized wavefunction (BLW) computations were performed at the B3LYP/6–31G(d) level employing GAMESS.²³ BLW analyses^19,20 quantified the effects of π-conjugation increase in the self-assembled quartets. For all complexes and monomers, DE_π values were computed based on the energy difference between the fully electron delocalized wavefunction (ψ_deloc) and a π-electron localized wavefunction (ψ_loc) of the complex or monomer considered, in which the expansion of molecular orbitals over basis functions were restricted to a selected π-block in the molecule considered; DE_π = E(ψ_loc) – E(ψ_deloc). Each π-block included two π-electrons (i.e., from a π-bond or a π lone pair) and the p_z, d_xz, and d_yz basis functions belonging to the heavy atoms in the blocks. The computed DE_π [E(ψ_loc) – E(ψ_deloc)] values of the quartets were compared to those of the monomers comprising the quartet and divided by four, and the resulting ∆DE_avg value provides a measure of the π-conjugation gain in quartets upon hydrogen bonding.