Predicting Tubular Reabsorption with a Human Kidney Proximal Tubule Tissue-on-a-Chip and Physiologically-Based Modeling

Abstract

Kidney is a major route of xenobiotic excretion, but the accuracy of preclinical data for predicting in vivo clearance is limited by species differences and non-physiologic 2D culture conditions. Microphysiological systems can potentially increase predictive accuracy due to their more realistic 3D environment and incorporation of dynamic flow. We used a renal proximal tubule microphysiological device to predict renal reabsorption of five compounds: creatinine (negative control), perfluorooctanoic acid (positive control), cisplatin, gentamicin, and cadmium. We perfused compound-containing media to determine renal uptake/reabsorption, adjusted for non-specific binding. A physiologically-based parallel tube model was used to model reabsorption kinetics and make predictions of overall in vivo renal clearance. For all compounds tested, the kidney tubule chip combined with physiologically-based modeling reproduces qualitatively and quantitatively in vivo tubular reabsorption and clearance. However, because the in vitro device lacks filtration and tubular secretion components, additional information on protein binding and the importance of secretory transport is needed in order to make accurate predictions. These and other limitations, such as the presence of non-physiological compounds such as antibiotics and bovine serum albumin in media and the need to better characterize degree of expression of important transporters, highlight some of the challenges with using microphysiological devices to predict in vivo pharmacokinetics.

1. Introduction

Microphysiological systems, also known as “Tissue-on-a-Chip” systems, are considered a promising biomedical technology to replicate human biology in vitro, with a goal of augmenting, and in some cases replacing, animal tests (Cavero et al., 2019; Low and Tagle, 2017; Marx et al., 2016; Rezaei Kolahchi et al., 2016). While most of the excitement about Tissue-on-a-Chip systems is due to the promise of improving testing of drug efficacy and safety, such systems also have to the potential to increase understanding of xenobiotic pharmacokinetics (Esch et al., 2011; Kanamori et al., 2018). Species differences present a major challenge in extrapolating pharmacokinetics from animals to humans (Kimura et al., 2018; Medinsky, 1995), and in vitro testing in 2D culture does not necessarily accurately recapitulate in vivo pharmacokinetics (Ishida, 2018). While in vitro assays for hepatic clearance and plasma protein binding are well-established (Wetmore, 2015), less attention has been paid to studies of renal clearance beyond glomerular filtration. Moreover, most in vitro studies of pharmacokinetics in the kidney use human renal subcellular fractions and recombinant enzyme expression systems, not renal proximal tubule cells (RPTECs) or more complex systems (Scotcher et al., 2016b).

The limitations of traditional RPTEC cultures include limited availability of high quality human kidney tissues, decline of expression of key drug-metabolizing enzymes with time in culture, and inter-individual/-experimental variability (Scotcher et al., 2016b). In addition, the key functions of the kidney are filtration, excretion, and secretion in the context of the flow of the urine through the tubules, all of these elements are difficult to recapitulate in a traditional 2D experiment. The promise of the microfluidic models, that are collectively known as kidney-on-a-chip, is that they can potentially mimic the structural, mechanical, transport, absorptive, and physiological properties of the human kidney (Sakolish et al., 2016).

The proximal tubule is the primary functional site for transport- mediated reabsorption and secretion of xenobiotics. Active transport of xenobiotics is achieved given the polarized configuration of the proximal tubule’s epithelial cells and involves transporters found on the brush- border containing apical side and the basolateral side (Chang et al., 2016b). Therefore, several microphysiological devices have been developed to model the proximal tubule (Chang et al., 2016b; Sakolish et al., 2016). An early kidney bioreactor design demonstrated the seeding and culture of canine (MacKay et al., 1998) and porcine (Humes et al., 1999) renal tubule cells into a hollow polysulferone filament suspended in an “extracapillary space” which aimed to mimic the vascular component of the tubule. These studies demonstrated the clearance of inulin, as well as fluid transport across this barrier tissue. Additionally, they demonstrated realistic enzymatic and metabolic activity, laying the groundwork for future human cell-based tissue chip devices. Recently, one such device has been developed (Chang et al., 2017; Weber et al., 2016) which is a 3-dimensional flow-directed human kidney proximal tubule model that replicates the polarity of the proximal tubule, expresses appropriate marker proteins, and exhibits biochemical and synthetic activities, as well as secretory and reabsorptive processes associated with proximal tubule function in vivo. This device has been shown to effectively model basolateral solute transport, apical solute uptake, and intracellular enzymatic function (Weber et al., 2016), as well as drug-induced nephrotoxicity (Chang et al., 2017). This model was recently validated in an independent laboratory and used to extend its utility to testing of nephrotoxic compounds focusing on biological relevance such as long-term viability, baseline protein and gene expression, ammoniagenesis, and vitamin D metabolism, as well as toxicity biomarkers (Sakolish et al., 2018). However, this system has yet to be tested for its ability to evaluate renal clearance.

Therefore, to demonstrate the utility of this tissue-on-a-chip model for studies of pharmacokinetics, we carried out our studies with five representative compounds. As a negative control, we used creatinine, which should undergo no reabsorption. As a positive control, we used perfluorooctanoic acid, which is reabsorbed in the human proximal tubule via active transport (Worley and Fisher, 2015; Yang et al., 2010). Additionally, we tested cisplatin, gentamicin, and cadmium, which are well characterized nephrotoxic agents. Moreover, cadmium was considered an ideal test compound for this system, which lacks a “vascular” channel, because it is both reabsorbed by active transport as well as accumulated in the kidney to a high degree. The proximal tubule microphysiological device (Sakolish et al., 2018; Weber et al., 2016), hereafter referred to as the “kidney tubule chip” (Figure 1A), was used to characterize the renal reabsorption of these five test compounds. The kidney tubule chip results for reabsorption were combined with a physiologically-based “parallel tube model” (Janku, 1993) that was used to model overall renal clearance kinetics in humans in vivo (Figure 1B). Predictions for in vivo renal clearance based on the kidney tubule chip data were then compared to reported in vivo renal clearance. Overall, we found the kidney tubule chip, when combined with a physiologically-based kinetic model, to both qualitatively and quantitatively recapitulate in vivo kinetics in the kidney.

Figure 1.

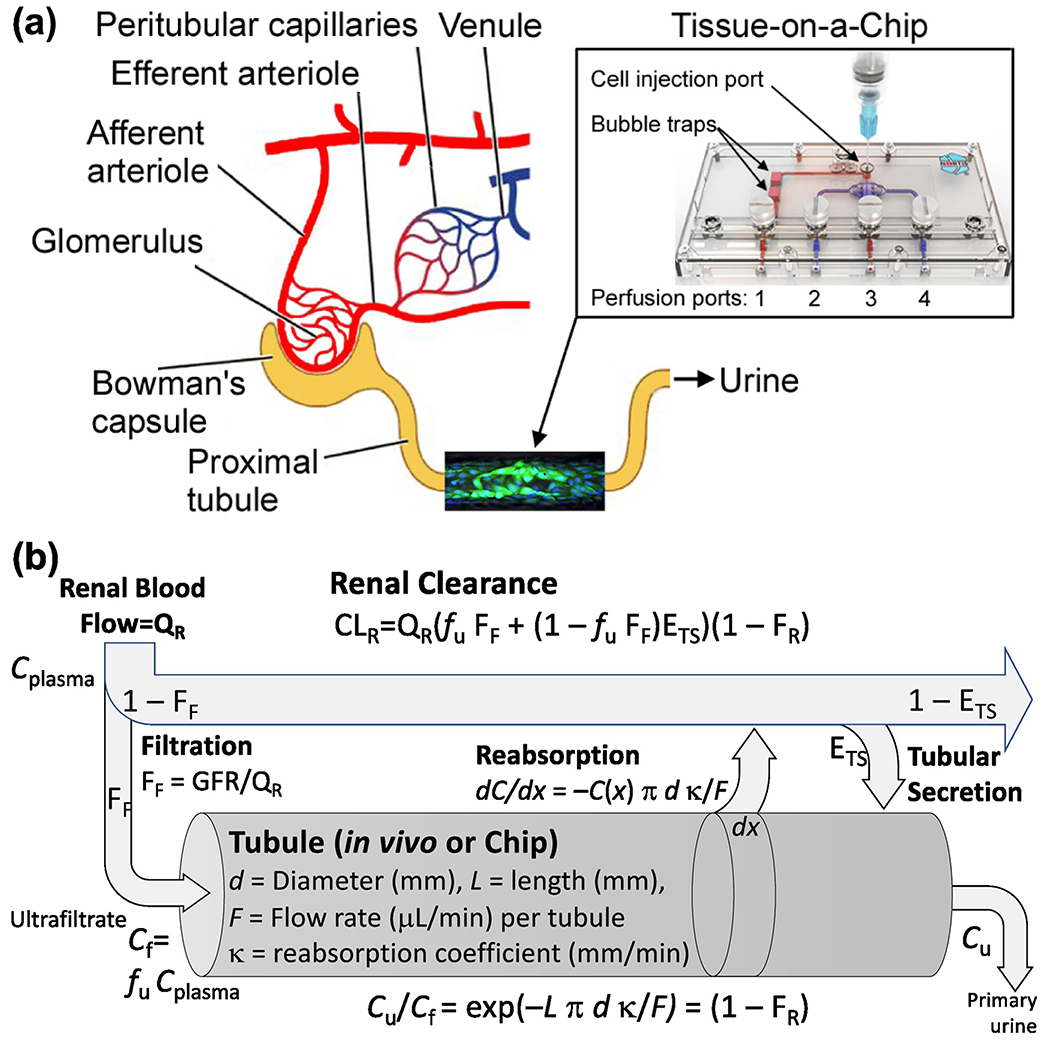
Human kidney proximal tubule Tissue-on-a-Chip model: (a) Schematic representation of the nephron and where the kidney tubule chip fits. Perfusion and injection ports are shown and referenced to in Materials and Methods. Each chip represents a segment of a single proximal tubule, with the extrapolation between them conducted using the physiologically-based model in (b). (b) Physiologically-based model for renal clearance including a physical tubular reabsorption model. The “tubule” portion of this model corresponds to either the in vivo tubule or the portion of the “chip” where an in vitro tubule is formed. The remainder of the model is only applicable in vivo. Physical dimensions and other parameters for the human proximal tubule and the kidney tubule chip are described in the text.

2. Materials and Methods

Human Proximal Kidney Tubule Tissue-on-a-chip Model.

The microfluidic platform used in these studies was from Nortis Bio (Seattle, WA). For the purpose of this tissue-on-a-chip model, this polydimethylsiloxane (PDMS) and glass device was used to create a single fluidic channel aimed to resemble a segment of a single proximal kidney tubule with physical dimensions that are close to those reported for the proximal portion of the renal tubule in the human kidney (i.e., 7 mm long and 120 μm thick for tissue-on-a-chip, as compared with 14 mm long and 30 μm thick in vivo (Lote, 2000)). The device holds approximately 5,000 cells (Weber et al., 2016). The device preparation and cell seeding protocols were as previously described (Sakolish et al., 2018; Van Ness et al., 2017). In order to maintain comparability with previously published results, we employed the same cells and media as used previously by the chip developers (Weber et al., 2016). This goal of standardization and increased reproducibility outweighed some of limitations of this protocol, including the inclusion of gentamicin in the media to prevent bacterial growth from contamination. Briefly, the growth area of the chip (Figure 1A) was filled with collagen type I (6 mg/mL; Ibidi, Martinsried, Germany) through ports 2 and 4, and the matrix was allowed to polymerize around the microfiber filament for 24 hrs. After polymerization, the filament was carefully removed from port 3 to form a suspended luminal channel within the gelled extracellular matrix, connected to the fluidic channel that is perfusable through ports 1 and 3. This channel was then coated with collagen type IV (5 μg/mL; Corning, Corning, NY) for 30 min at 37°C and unsupplemented renal epithelial growth medium (REGM, Lonza, Basel, Switzerland) was flushed through the system to remove excess collagen IV at a rate of 2 μL/min for 1 hour.

Kidney Tubule Chip Experiments.

Primary human renal proximal tubule epithelial cells (RPTECs, Lonza, CC-2553, Lot #0000581945) were added and cultured at 37°C with 5% CO₂ in REGM medium (Lonza) that was supplemented with fetal bovine serum (0.5%), human transferrin (10 mg/mL), hydrocortisone (0.5 mg/mL), insulin (5 mg/mL), triiodothyronine (5×10⁻¹² M), epinephrine (0.5 mg/mL), epidermal growth factor (10 mg/mL), and antibiotics (30 μg/mL gentamicin and 15 ng/mL amphotericin B). Cells between passages 4-6 were used for kidney tubule chip experiments. Cell pellets were resuspended to a concentration of 20×10⁶ cells/mL, and 3.5 μL of this suspension was injected into the lumen of each device through an injection port (Figure 1A). Cells were allowed to adhere for 24 hrs prior to the introduction of physiologic fluid flow at 0.5 μL/min with corresponding media. This flow rate resulted in cells being exposed to ~0.25 dyne/cm based on the equation for fluid shear stress, τ=6Qμ/bh2 (where τ is the shear stress at the surface of the cells [dyne/cm²], Q was the flow rate [8.3×10⁻⁶ cm³/s], μ was the viscosity of the culture media [8.9×10⁻³ dyne*s/cm²], b was the width of the channel [0.012 cm], and h was the height [0.012 cm]). Devices were maintained under constant flow for up to 24 days. Chemical treatments (influent) were performed on cells that were grown in devices (0.5 μL/min flow rate) for up to 22 days. Additionally, to study non-specific device binding with the materials of the devices (ECM, syringes, and tubing), “blank” kidney tubule chips were prepared using the same collagen coatings and treatments, but were not seeded with RPTECs. These devices were perfused with the same compound-treated media as in the cell-based experiments, effluent samples were collected over a period of 1 week, and % recovery from stock solutions was determined daily as detailed below. Culture media containing cisplatin (6.4 and 64 μM; Sigma-Aldrich, St. Louis, MO), cadmium chloride (0.05 and 0.5 μM; Sigma-Aldrich), gentamicin (200 and 600 μM; Hospira UK, Hurley, UK), perfluorooctanoic acid (PFOA; 10 and 1000 nM; Sigma-Aldrich), or creatinine (0.1 and 10 mM; Sigma-Aldrich) was continuously perfused through the tubules. These concentrations were selected based on reported human C_max values. For cisplatin, reported range of C_max is 1.4-13.9 μM (Verschraagen et al., 2003). For cadmium, reported human occupational C_max was ~1 μM and the general population C_max was ~0.1 μM in Nigeria (Alli, 2015). The Agency for Toxic Substances and Disease Registry reports the geometric blood level of cadmium in the general population (≥1 year of age) in the USA as ~0.002 μM. Gentamicin, a component of the formulation of the cell culture media at near human C_max levels (reported average human C_max is ~50 μM (Boisson et al., 2018; Cobussen et al., 2019; Inparajah et al., 2010)), was tested at higher concentrations. For PFOA, serum concentrations in the general population range between 5 and 50 nM and occupationally exposed subjects has blood levels as high as 24.2 μM (ATSDR, 2018).

Analytical Methods.

Creatinine concentrations were measured through the use of a commercial colorimetric assay kit (Abcam, Cambridge, MA) following manufacturer’s protocols.

Perfluorooctanoic acid (PFOA) analysis was performed on 100 μL effluent samples of kidney tubule chip-derived perfused media. Extraction standard (final concentration: 5ng/mL) was spiked before the sample extraction and was used to correct for recoveries after the extraction process. Protein in the samples were precipitated by adding 300 μL of acetonitrile. The samples were vortexed for three minutes. Then the samples were centrifuged at 10,000xg for 5 minutes. The supernatant was taken and evaporated to near dryness. The samples were then reconstituted in 96% (w/w) methanol. Internal standard (final concentration: 5ng/mL) was spiked before sample injections and was used to monitor for instrument stability. PFOA samples were analyzed with triple quadrupole mass spectrometry (Agilent 6470, Santa Clara, CA) coupled to high performance liquid chromatography (HPLC QqQ MS; Agilent 6470 MS 1290 Infinity II HPLC), which was equipped with Agilent Zorbax C18 guard and analytical columns (guard: 1.8μm 5 x 2.1 mm; analytical: 1.8 μm,80Å 50 x 2.1 mm). The solvent gradient was based on the published method (Kautiainen et al., 2000). Briefly, the column compartment was held at 50 °C. Ten microliters of sample was injected. The mobile phase flow rate was set to 0.4 mL/min. Mobile phases were A: 5 mM ammonium acetate in water B:5 mM ammonium acetate in 95% Methanol (v/v). The gradient was 90% A held for 0.5 min, 90 to 70% A from 0.5 – 2 min, 70 – 5 %A from 2 – 14 min, 5 to 0% A from 14 – 14.5 min, and 0% A from 14.5 – 16.5 min, followed by a 6 minutes post run to stabilize the column pressure and flow condition. Isotopically labeled PFOA was used as an extraction (M8) and internal (M2) standard. Data were acquired in negative electrospray ionization mode. Calibration standards were prepared on the day of analysis from a standard mixture purchased from Wellington Laboratories. Calibration concentrations ranged from 0.04 to 10 ng/mL. Blanks containing the media (100 μl) were analyzed with each analysis sequence. Continuing calibration standard checks were performed after every 20 samples followed by a blank analyses. Sample concentrations were then determined based on the calibration curve taking into account the sample dilution factor (1:4).

Gentamicin samples were analyzed with triple quadrupole mass spectrometry coupled to high performance liquid chromatography (Agilent 6470 MS 1290 Infinity II HPLC) using SeQuant® ZIC®-cHILIC guard and analytical columns (guard: 5μm 20 x 2.1 mm; analytical: 3 μm, 100Å 100 x 2.1 mm). The column compartment was held at 50 °C during sample analyses. Ten microliters of sample was injected. The mobile phase flow rate was set to 0.4 mL/min. Mobile phases were A: acetonitrile with 1 % (w/w) formic acid and B: 100 mM ammonium acetate with 3% (w/w) formic acid. The gradient was 50 to 95% B from 0-7 min, 95% B from 7-8 min, and then 95-50% B from 8-16 min for column equilibration. Amikacin was used as an internal standard according to Kumar et al. (2012). Data were acquired in positive electrospray ionization mode.

Cadmium (Cd) and cisplatin (Pt) analyses were performed on 100 μL effluent samples of kidney tubule chip-derived perfused media. The samples were digested by adding 2.4 ml of 1% Nitric acid (Omnitrace Ultra Nitric acid). The samples were shaken with loose covering to allow any gases to escape. Then the samples were allowed to stand overnight to ensure complete digestion. Calibration standards were freshly prepared daily from certified standards in cell culture media to adjust for any matrix effects. Calibration concentrations ranged from 0.04 to 80 ng/ml for cadmium, and 0 to 640 μM for cisplatin. Blanks containing the media (100 μl) and acid (2.4 ml) were analyzed with each sample batch. Continuing calibration standard checks were performed after every 15 samples followed by a blank analyses. Samples and calibration standards were analyzed on an ICP-Mass Spectrophotometer NexIon 300 (Perkin Elmer, Waltham, MA). Concentrations were determined as Cd (114) or Pt (195), the most abundant isotopes, to provide the best sensitivity and were based on a linear calibration curve (r² greater than 0.99) using indium as the internal standard for cadmium, or bismuth for cisplatin. Sample concentrations were then determined based on the calibration curve taking into account the sample dilution factor (1:25). To avoid carryover, 2% nitric acid was used as a wash between sample analyses.

The ratio of effluent to influent concentrations, adjusted for non-specific device binding, is calculated as follows: C(out)/C(in)=(C(out)_cells/C(in)_cells)/(C(out)_blank/C(in)_blank), where “out” and “in” refer to effluent and influent, and “cells” and “blank” refer to measurements from devices seeded with cells and measurements from blank devices, as described above.

Protein Binding Assays.

To confirm bioavailability, medium protein binding were evaluated for each drug utilizing rapid equilibrium dialysis (RED) as described elsewhere (Waters et al., 2008). The RED assay was conducted using single use RED inserts (Pierce Biotechnology, Rockford, IL) according to instructions, with protocol modification to incorporate “no protein” equilibrium controls. For tissue-on-a-chip protein binding experiments, proteins and concentrations matched those used in RPTEC culture (detailed above). Equilibrium controls comprising of PBS buffer in both sample and buffer chambers were used to ensure drugs are fully equilibrated within the device in the absence of proteins. All RED assays were completed in triplicate. Mass spectrometry conditions for detection were as detailed above.

Chip-to-Human Extrapolation Model.

As shown schematically in Figure 1A, the kidney tubule chip models the proximal tubule from ultrafiltrate to primary urine. However, because of the lack of a vascular channel, only renal reabsorption and not tubular secretion is included. To place the chip in an in vivo physiological context, we use the “parallel tube model” (Janku, 1993) for in vivo renal kinetics. This sub-model for renal kinetics, shown schematically in Figure 1B, contrasts with the standard “well-stirred” kidney sub-model that is typically used in PBPK models (Scotcher et al., 2016a). Specifically, instead of lumping the different renal processes together into a single clearance parameter, the parallel tube model separately accounts for the processes of protein binding, filtration, reabsorption, and secretion while maintaining the constraints related to renal blood flow and filtrate flow. This physiological basis also provides a means to appropriately scale clearance from the in vitro chip to the whole kidney in vivo accounting for differences in flow rates and surface areas.

The equation relating the in vivo processes of protein binding, filtration, reabsorption, and secretion in this model is as follows (Janku, 1993):

$${\text{CL}}_{\text{R}}{=\text{Q}}_{\text{R}}\left(f_{\text{u}}{\text{F}}_{\text{F}}+\left(1-f_{\text{u}}{\text{F}}_{\text{F}}\right){\text{E}}_{\text{TS}}\right)\left(1-{\text{F}}_{\text{R}}\right).$$ (1a)

Here Q_R is the renal blood flow, f_u is the unbound fraction (taken from the literature for each compound), F_F is the filtration fraction =GFR/Q_R (around 20% for healthy adults), E_TS is extraction ratio for tubular secretion, and F_R is the fraction re-absorbed. Dividing by GFR, the ratio of renal clearance to glomerular filtration is therefore

$${\text{CL}}_{\text{R}}/\text{GFR}=\left(f_{\text{u}}\text{+}\left(1/{\text{F}}_{\text{F}}-f_{\text{u}}\right){\text{E}}_{\text{TS}}\right)\left(1-{\text{F}}_{\text{R}}\right).$$ (1b)

The quantity (1 − F_R) represents the contribution to renal clearance by the chip, and is equal to the ratio between the concentration in primary urine (u) to the concentration in ultrafiltrate (f):

$$\left(1-{\text{F}}_{\text{R}}\right)={\text{C}}_{\text{u}}/{\text{C}}_{\text{f}}.$$ (1c)

In order to extrapolate this urine-filtrate concentration ratio from chip to humans, we derive a simple physical model for tubular reabsorption, also shown in Figure 1B. Each tubule (chip or in vivo) has length L (mm), surface area per unit length ξ (mm²/mm) = πd for a lumen diameter d, and flow rate F (ml/min). Assuming linear kinetics, the reabsorption flux at any point is proportional to the compound concentration C (mg/ml) at that point in the tubule with an absorption constant κ (mm/min). Therefore, at each point x along the tubule, the change in concentration C(x) per unit length of the tubule is dC/dx = −C(x) ξ κ /F = −C(x) π d κ / F, giving an exponential decline along the length of the tubule C(x) = C(0)exp(−x π d κ / F). Identifying C(0) as the ultrafiltrate concentration and C(L) as the primary urine concentration gives

$${\text{C}}_{\text{u}}/{\text{C}}_{\text{f}}=\text{exp}(-L\pi d\text{κ}/F).$$ (2)

Applying equation (2) separately for human (h) and chip (c) parameters and re-arranging algebraically gives the following relationship for the urine/filtrate ratio:

$${({\text{C}}_{\text{u}}/{\text{C}}_{\text{f}})}_{\text{h}}={{({\text{C}}_{\text{u}}/{\text{C}}_{\text{f}})}_{\text{c}}}^{\text{α}},$$ (3a)

$$\text{α}=({\text{L}}_{\text{h}}/{\text{L}}_{\text{c}})\times (d_{\text{h}}/d_{\text{c}})\times ({\text{κ}}_{\text{h}}/{\text{κ}}_{\text{c}})÷({\text{F}}_{\text{h}}/{\text{F}}_{\text{c}}).$$ (3b)

Combining equation (3a) with equations (1b) and (1c) leads to the relationship:

$${\text{CL}}_{\text{R}}/{\text{GFR}}_{\text{pred}}=(f_{\text{u}}+(1/{\text{F}}_{\text{F}}-f_{\text{u}}\left){\text{E}}_{\text{TS}}\right)\times {{({\text{C}}_{\text{u}}/{\text{C}}_{\text{f}})}_{\text{c}}}^{\text{α}}.$$ (4)

The absorption constants κ are the only chemical-specific parameters, the others being physical dimensions or flows. The parameters for the chip were measured as follows: length of the tubule, L_c=7mm; flow rate, F_c=0.5μL/min; lumen diameter d_c=120 μm=0.12 mm. The parameters for human in vivo proximal tubules were taken from the literature: L_h=14mm (Lote, 2000); d_h=30 μm=0.03 mm (mean diameter measured by optical coherence tomography (Li et al., 2009)), and F_h=0.07μL/min (based on 125 ml/min=mean of healthy male (n=347) and female (141) inulin-based GFR measurements (Wesson, 1969), divided by the reported average of 896,711 nephrons per kidney across 5 racial groups (Bertram et al., 2011), divided by 2 kidneys). Plugging these numbers into equation (3b) gives α = (14/7) × (0.03/0.12) × (κ_h/κ_c) ÷ (0.07/0.5) = 3.6 × (κ_h/κ_c). We evaluated the predictive performance of the chip by assuming κ_h=κ_c (i.e., that the reabsorption coefficient in the chip is the same as in vivo), and the prediction simply scales the chip results to humans based only on different physical dimensions and flows. These predictions are then compared using one-way ANOVA and Tukey post-hoc test (p<0.05 considered significant) to in vivo data for each drug. These, and other statistical calculations (e.g., mean and SE), were conducted in GraphPad Prizm v.8.

Creatinine renal kinetics.

Creatinine is unbound to protein and is passively cleared by glomerular filtration with no tubular secretion (Perrone et al., 1992). Therefore, f_u was set to 1, E_TS was set to 0, and CL_R/GFR set to 1. Mean urinary creatinine levels are around 130 mg/dL, or around 12 mM.

PFOA renal kinetics.

PFOA is both highly bound to plasma proteins, as well as highly reabsorbed via active transport by the proximal tubule. Estimates of plasma protein binding in humans are consistently ≥90%, with more recent results indicating ≥99% depending on concentration (Han et al., 2003; Kerstner-Wood et al., 2003). Therefore, we set f_u to 0.01, while recognizing uncertainty in this value. While some nonhuman species appear to possess active secretory mechanisms, in humans, the net effect of secretion and reabsorption of PFOA in humans is imbalanced in favor of reabsorption (Han et al., 2012), so E_TS was set to 0. Overall renal clearance rates in vivo have been reported over a wide range, from 0.03 mL/d/kg to 0.2 mL/d/kg (Fujii et al., 2015; Harada et al., 2005; Zhang et al., 2013), corresponding to CL_R/GFR ratios of about 0.001-0.01. Mean serum concentrations in these studies ranged from 3 - 14 ng/mL, or about 0.007 – 0.03 μM.

Cisplatin renal kinetics.

Although total clearance of cisplatin is slowed by extensive protein binding, free cisplatin is rapidly excreted through the kidneys in vivo, with free cisplatin renal clearance exceeding creatinine clearance, thus indicating that cisplatin is actively secreted (Daley-Yates and McBrien, 1982; Reece et al., 1985). Biokinetic modeling of an in vitro proximal tubule system by Wilmes et al. (2015) at sub-cytotoxic concentrations (0.5 and 2 μM) estimated transport on the basolateral side to be virtually unidirectional into the cells, with both entry and exit on the apical side, suggesting that re-absorption into the blood-stream is negligible. Consistent with secretion being dominant, Wilmes et al. (2015) also reported a net increase in cisplatin in the apical medium. At higher concentrations, Reece et al. (1985) reported non-linearity in renal clearance of free cisplatin as evidenced by prolonged plasma levels, and suggested that tubular re-absorption may also be involved, but recent evidence suggests that extensive tissue binding may also contribute to non-linearity (Chang et al., 2016a). To separate the contributions of renal clearance versus tissue and plasma distribution, we used clearance estimates for free cisplatin, specifically the in vivo measurement for the renal clearance to creatinine clearance ratio, CL_R/GFR, equal to the mean±s.d. of 4.1±2.5 (n=7) reported in Reece et al. (1985). Because this study measured clearance of free cisplatin, f_u was set to 1. Additionally, because of the high degree of tubular secretion, we set E_TS=1. The C_max in this study was between 200 and 800 ng/ml platinum, or 1 to 4 μM.

Gentamicin renal kinetics.

Contrepois et al. (1985) reported measurements of renal disposition of a constant infusion of gentamicin in 33 male subjects. They reported no serum protein binding so f_u was set to 1, and no evidence of tubular secretion so E_TS was set to 0. The reported ratio between renal clearance and GFR was CL_R/GFR=0.79±0.06. The serum concentrations in this study were reported to be 5.3±1.3 μg/mL, or about 11 μM.

Cadmium renal kinetics.

For cadmium (Cd) we used the human PBPK model published first by Nordberg and Kjellstrom (1979) and its updates (Fransson et al., 2014; Ruiz et al., 2010), shown in Figure 2. This model represents the most widely used cadmium PBPK model, and is linear multi-compartment model that includes the oral and inhalation routes of exposure, absorption through the gastrointestinal tract, distribution to major accumulating tissues, and ultimately fecal or renal excretion. Cadmium is not metabolized, so not biotransformation is included in any tissues. However, a key feature of this model its accounting for binding to plasma components, accumulation in erythrocytes, and binding specifically to metallothionein. This model has been validated with several human data sets (ATSDR, 2012). Because this model employs a “lumped” kidney compartment in its depiction of renal clearance, we used ratio of urine to plasma concentrations to estimate the human value of CL_R/GFR. To most closely match the chip experiments, this ratio was calculated using simulations of dietary intake that led to plasma concentrations at age of 45 in humans equal to the free concentrations administered to the chip. The model urine predictions are in units of μg Cd/g Cr, which were converted to μM using the Cd molecular weight and the NHANES mean urinary Cr level of 124.6 mg/dL for the age range 40-49 (Barr et al., 2005). The model was coded in Berkeley Madonna software, and model codes and parameter values were from Ruiz et al. (2010).

Figure 2.

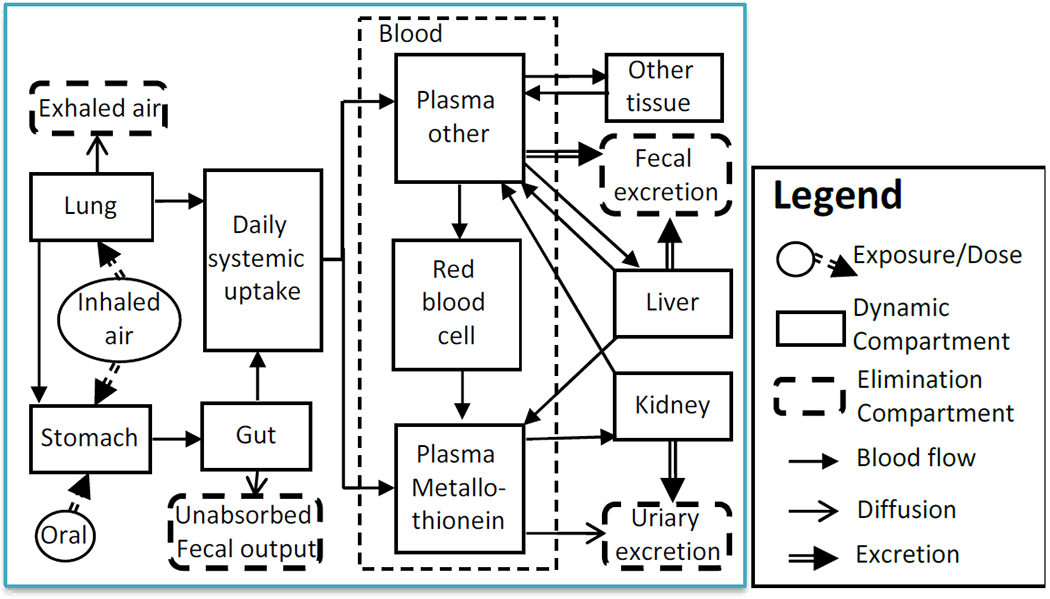
A diagram of the cadmium PBPK model describing Cd kinetics from systemic uptake to excretion in humans. The concentration of Cd in total plasma is calculated as f_plasma×(C_{Plasma other}+C_{Plasma metallothionein}), where f_plasma is mass fraction whole blood that is plasma.

3. Results

3.1. Media Protein Binding

The binding of creatinine, PFOA, cisplatin, gentamicin, and cadmium within serum-supplemented media was determined through the use of rapid equilibrium dialysis. Creatinine, PFOA, cisplatin and gentamicin showed minimal protein binding in the culture media, but the free fraction of cadmium in the culture media was as low as 29% (Table 1, Figure 3), indicating a large percentage of cadmium being bound to the serum proteins in the supplemented media.

Table 1.

Binding and uptake reference compounds in cell culture media and Tissue-on-a-Chip devices at end of each experiment.

Compound and logKow	Concentration tested (μM)	Free fraction in cell culture media1,3 (%)	Device only loss3 (%)	Device+cells loss3 (%)	Cells only C(out)/C(in)3 (%)
Cisplatin	6.4	99.7 ± 0.2	−1.2 ± 1.6	−2.4 ± 0.6	101.2 ± 0.6
logKow= −2.19	64	99.9 ± 2.3	−1.0 ± 2.4	4.1 ± 1.2	94.9 ± 1.1
Gentamicin	200	89.7 ± 0.5	-2	−0.5 ± 2.6	100.5 ± 2.6
logKow= −1.88	600	89.4 ± 3.5	-2	0.4 ± 6.6	99.6 ± 6.6
Cadmium	0.05	28.9 ± 3.6	1.4 ± 4.9	43.6 ± 7.2	57.2 ± 7.3
logKow= 0.21	0.5	41.8 ± 2.6	3.7 ± 0.8	27.1 ± 10.3	75.6 ± 10.7
PFOA	0.01	141.8 ± 22.0	10.8 ± 21.8	13.2 ± 5.8	97.3 ± 6.6
logKow= 4.90	1	98.6 ± 14.9	32.1 ± 4.4	40.9 ± 0.2	87.1 ± 0.2
Creatinine	100	93.4 ± 6.0	8.6 ± 2.3	6.7 ± 6.6	100.5 ± 2.5
losKow= −1.76	10,000	100.8 ± 3.5	15.1 ± 7.6	15.1	104.7

¹Determined through the use of the rapid equilibrium dialysis method.

²No loss of gentamicin was observed in tests with cells; therefore, blank devices were not tested.

³Data is reported here as Mean ± SD (n=3).

Figure 3.

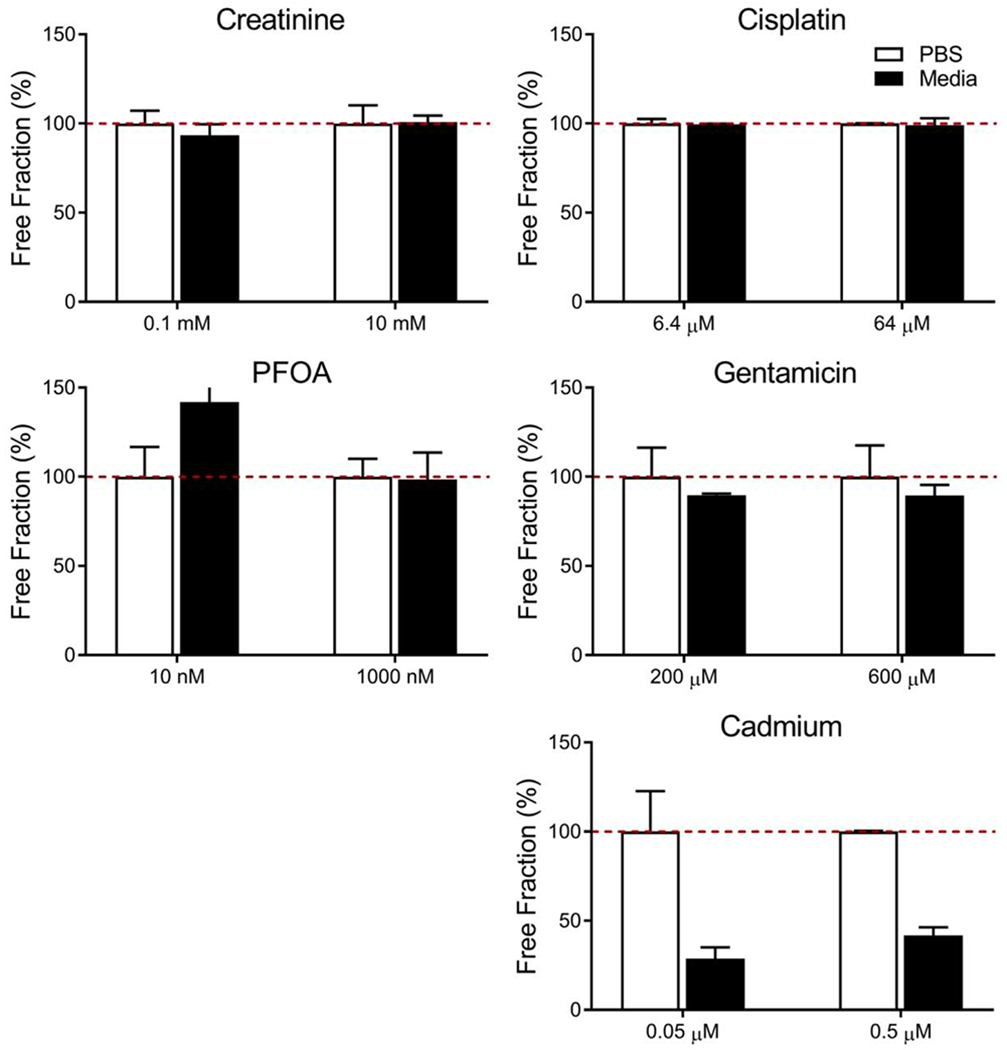
Free fraction of testing compounds in buffer and cell culture media. Samples were tested in either PBS buffer solution (white bars), or serum containing culture media (black bars) to determine free fraction within the proximal tubule chip. Results are reported as mean ± SD (n=3).

3.2. Kidney tubule chip experiments

Cellular and molecular parameters of this microphysiological system, as well as toxicity studies of cadmium, cisplatin and gentamicin were reported in (Sakolish et al., 2018). We have showed that RPTECs grown in 3D under shear stress self-organized, elongated, and aligned in a monolayer in the direction of fluid flow. These cells were viable and maintained kidney-like gene expression over 24 days in culture. Also, the utility of this model for studies of drug and chemical safety in the kidney was demonstrated.

For pharmacokinetic analysis, chemical concentration in effluent samples were collected and compared against stock solutions. We observed little uptake within the kidney tubule chip for creatinine, cisplatin and gentamicin, but uptake for PFOA and cadmium (Table 1, Figure 4). Specifically, cisplatin and gentamicin concentrations quickly reached equilibrium within the chip, leading to nearly 100% recovery from effluent samples. For PFOA, losses were observed throughout the 7 days of exposure. For cadmium, even after 22 days of exposure, effluent cadmium concentrations continued to be lower than infused solutions, indicating cadmium was being sequestered in the chip. For all test compounds except PFOA, the results from blank devices indicated minimal non-specific binding, with equilibrium reached after about 48 hours of perfusion (Table 1, Figure 5). Adjusting the measured losses from the kidney tubule chip for the minimal loss due to non-specific binding in the absence of cells, the remaining losses are attributed to cell-drug interactions/tubular uptake by RPTECs. These adjusted values of C_out/C_in showed that creatinine, cisplatin, and gentamicin undergo little reabsorption (0-5% loss), PFOA showed moderate reabsorption (3-13% loss), while cadmium showed the most substantial reabsorption (24-43% loss) (Table 1).

Figure 4.

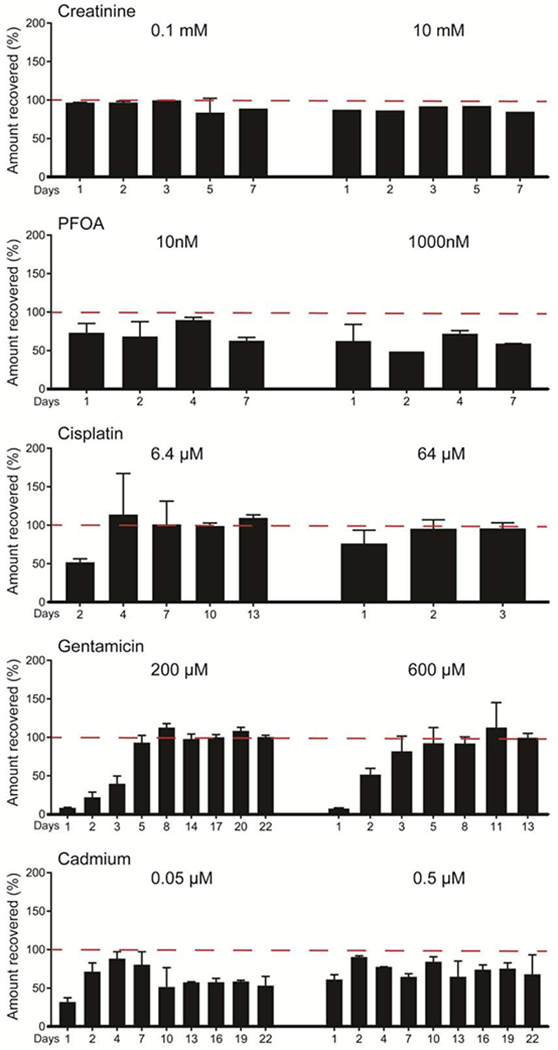
Recovery from proximal tubule devices seeded with RPTECs. Effluent samples were collected from cell-seeded chips after perfusion, and compound concentrations were compared against stock solutions to determine % recovery for each condition. Results are reported as mean ± SD (10 mM creatinine, n=1; 0.1 mM creatinine and PFOA, n=2; all others, n=3).

Figure 5.

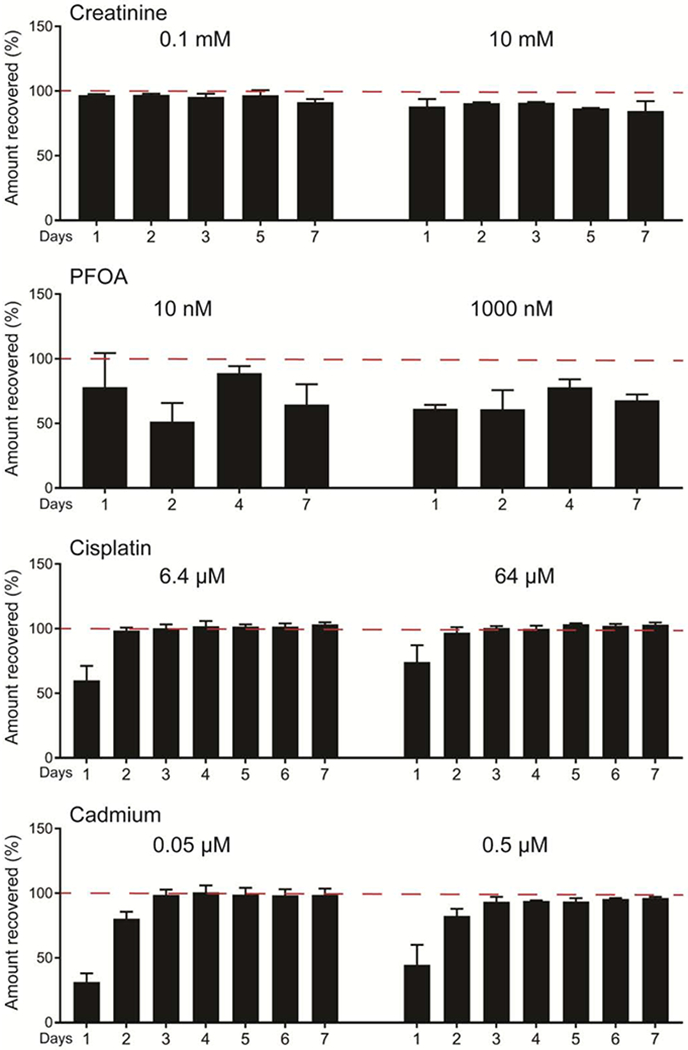
Recovery from blank tissue chips. Effluent samples were collected from blank chips after perfusion, and compound concentrations were compared against stock solutions to determine % recovery for each condition. Minimal device binding is observed over the first 2 days of perfusion, however equilibrium is quickly achieved. Results are reported as mean ± SD (creatinine and PFOA, n=2; all others, n=5).

3.3. Chip-to-human model predictions of renal clearance

Predictions for human in vivo renal clearance were made for each drug combining the measured reabsorption in the chip with the physiological model shown in Figure 1B. For creatinine, the data from the kidney chip suggested no reabsorption component (Table 1), consistent with expectations that creatinine excretion reflects GFR (Figure 6).

Figure 6.

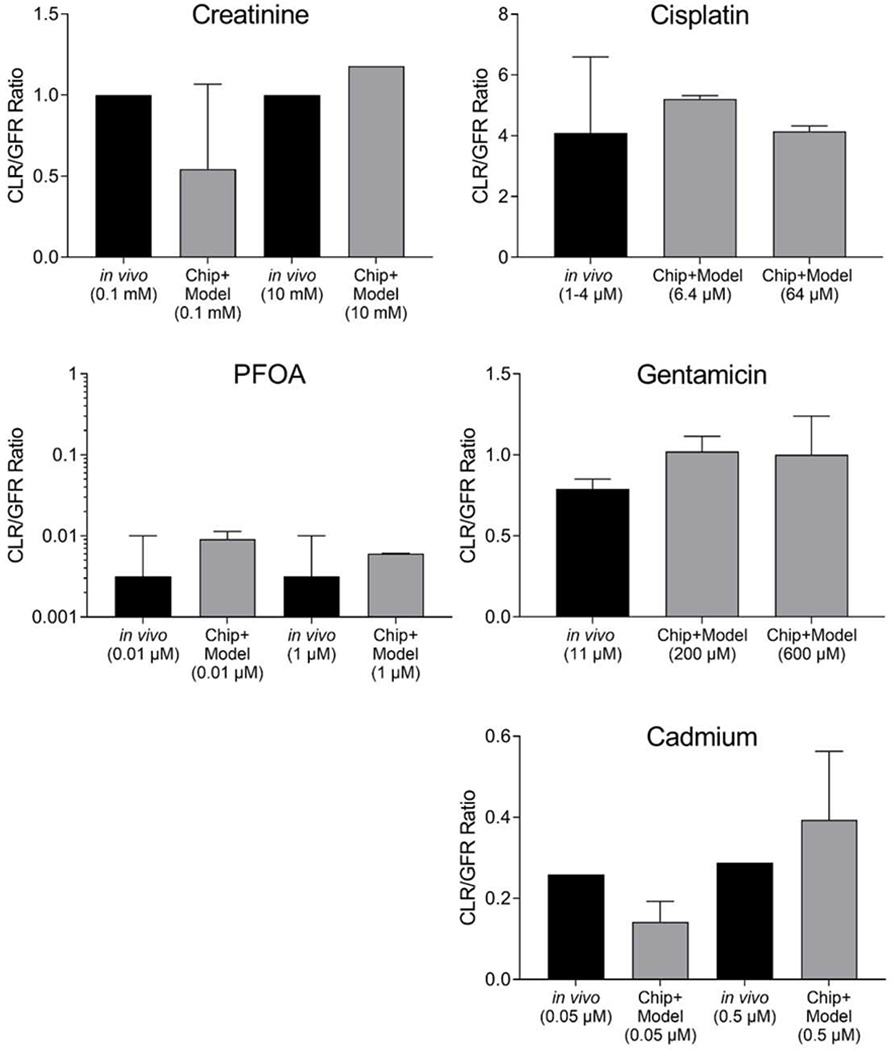
Renal clearance in vivo and predicted from the kidney tubule chip for the 2 control compounds creatinine and PFOA, and 3 reference compounds tested: cisplatin, gentamicin, and cadmium. Ratio of renal clearance to GFR in vivo (black bars) or as predicted from kidney tubule chip data and the physiological model (gray bars), with 1SD error bars (creatinine, n=2 for 0.1, and n=1 for 10uM; cisplatin, n=3; PFOA, n=2; gentamicin, n=4; cadmium, n=8). In vivo data were obtained from Reece et al. (1985) for cisplatin and Contrepois et al. (1985) for gentamicin; in vivo data for cadmium were from the human cadmium PBPK model of Ruiz et al. (2010). For cisplatin, the model assumed efficient tubular secretion (E_TS=1 in Figure 1B), whereas for the other compounds, tubular secretion was assumed to be negligible (E_TS=0). Additionally, for PFOA, 99% protein binding was assumed (f_u=0.01), based on reports in the literature (Han et al., 2003; Wu et al., 2009). None of the comparisons between in vivo data and Chip+Model predictions were statistically significant indicating the fidelity of the in vitro model to recapitulate in vivo kinetics.

For PFOA, the predicted renal clearance is qualitatively consistent with what is known about its slow excretion in humans, though there is still uncertainty of about an order of magnitude in the precise clearance value. Because of the high degree of protein binding in vivo, a 1% unbound fraction was assumed based on measurements in the literature (Han et al., 2003; Wu et al., 2009), and the renal clearance prediction is driven by this value. Nonetheless, the data from the kidney chip do suggest a measurable amount of renal re-absorption which further decreases the clearance prediction. Overall, the combined kidney chip and model prediction is consistent the available in vivo data, with none of the comparisons being statistically significantly different (Figure 6).

For cisplatin, the predicted renal clearance was well within the range observed by Reece et al. (1985) in vivo (Figure 6). Specifically, the data from the chip suggested at most a small (up to 5%) reabsorption component (Table 1), so the prediction in our model is driven by the inclusion of efficient tubular secretion (see Methods). Because there is no parallel vascular channel in the chip tested, it was not possible to directly evaluate tubular secretion. Our predictions assumed E_TS=1, but smaller values are possible. Back-calculating κ_h from the in vivo mean CLR/GFR ratio of 4.1, allowing E_TS to range from 0 to 1, and then using these values for κ_h in the chip, leads to a back-calculated C_u/C_f in the chip of 95%-100%, which is consistent with the measured values in the chip (Table 1). It appears that the chip correctly predicted that reabsorption plays a small role quantitatively in cisplatin renal clearance, consistent with previous biokinetic modeling of in vitro proximal tubule transport (Wilmes et al., 2015).

In the case of gentamicin (Figure 6), the in vivo renal clearance data (Contrepois et al., 1985) indicate around 20% re-absorption, while within the tissue chip, we observed minimal net uptake by the RPTECs (<0.5% on average). However, there was some variability, particularly at the higher tested concentration, and the predicted renal clearance at the 600 μM concentration was within 1 standard deviation of the in vivo observation. Back-calculating κ_h from the in vivo mean CLR/GFR ratio of 0.79, and then using this value for κ_h in the chip, leads to a back-calculated C_u/C_f in the chip of 94%, about 6% lower than the values in Table 1. However, the chip was tested at higher concentrations (200 and 600 μM) than the in vivo study (11 μM), which may have led to saturation of reabsorption capacity in the chip. An additional confounding factor is that RPTECs were conditioned in their commercial media, which already contains approximately 60 μM gentamicin as an antibiotic, which may have also contributed to saturation. Use of an antibiotic is needed due to frequent changes of media-containing syringes where accidental contamination risk is high. Moreover, the need to increase transferability and standardization across laboratories, a major issue for tissue chips, outweighed the option of choosing a different antibiotic for use in the media.

For cadmium, the high uptake into cells (Table 1) is qualitatively consistent with what is known about cadmium renal accumulation and its slow excretion in humans. Due to a lack of human experimental data on cadmium kinetics, a human PBPK model (Ruiz et al., 2010), calibrated to NHANES biomonitoring data, was utilized to predict in vivo cadmium blood and urine steady state concentrations (Figure 2). The human PBPK model was implemented with dietary cadmium intakes of 15 μg/day and 215 μg/day in order to match plasma concentrations at age 45 to the free concentrations administered to the chip (0.0145 μM and 0.209 μM, respectively). The resulting predicted renal clearance/GFR ratios were 0.26 and 0.29, respectively. These values are within 1 or 2 standard deviations of the predicted values from the chip of 0.14±0.05 and 0.39±0.17, with comparisons between in vivo and Chip+Model predictions at the same concentration not statistically different (Figure 6). Back-calculating μ_h from the in vivo modeled CLR/GFR ratios, and then using this value for μ_h in the chip, leads to a back-calculated C_u/C_f in the chip of 68% and 71%, similar to the values in Table 1.

Because for cadmium, the PBPK model simulates plasma as having the same concentration as the chip influent, it is also possible to directly compare the observed and predicted “urine” concentrations. As shown in Figure 7, the urine concentration predictions based on combining chip data with the physiological model were more consistent than using the measured chip effluent concentrations alone, suggesting the importance of the model to adjust for differences in physical dimensions and flows. The comparisons differed by 5% or less when in vivo plasma concentrations were matched to total rather than free influent concentrations (results not shown).

Figure 7.

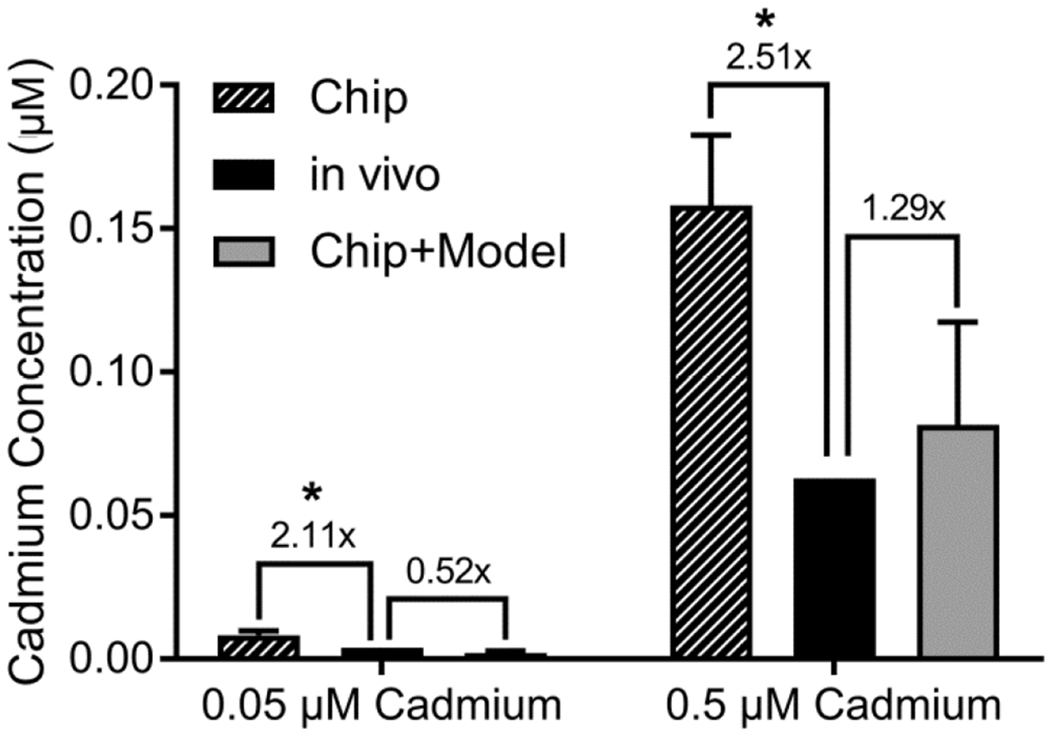
Measured and predicted cadmium concentrations in chip effluent and urine. In each panel, comparison is made between the cadmium concentrations measured in chip effluent (solid bars), cadmium concentrations in urine calculated using the PBPK model of Ruiz et al. (2010) (open bars), and cadmium concentration in urine predicted from chip data combined with the physiologically-based model for renal clearance in Figure 1. Data is reported as mean ± SD (n=8). The comparison between Chip and in vivo predictions were statistically significant (*), but the comparison between Chip+Model and in vivo predictions were not significant.

4. Discussion

It has been argued that tissue chips are superior to the traditional in vitro cell culture models and may even replace laboratory animals in toxicology (Marx et al., 2016). Indeed, there have been many advances in material science and bio-medical engineering that produced exciting new tissue chips for in vitro studies using single and multi-organ systems, work that will allow us to better understand the mechanisms of how cells deal with chemicals and drugs (Jennings, 2015). However, to advance the utilization of this knowledge and these tools for regulatory purposes, they need to be combined with biokinetics. Therefore, in this study, we proposed that combining a 3D microphysiological in vitro model of the human proximal tubule with in silico model to extrapolate assay results to in vivo clearance represents a sensible approach to improving prediction of renal clearance. Using a physiologically-based model of renal clearance and tubular reabsorption, we were able to demonstrate the physiological relevance of the kidney tubule chip to studies of human in vivo pharmacokinetics for five representative compounds.

For creatinine, the “negative” control compound, the chip data was consistent with negligible re-absorption, so that renal clearance is predicted to be similar to GFR, as expected based on in vivo data (Ciarimboli et al., 2012; Miller, 2008). Similar results have been found with other cylindrical tubule models. In their bioreactor model, MacKay et al (MacKay et al., 1998) demonstrated ≥98.9% recovery of inulin in luminal effluent, compared to ≤7.4% in blank devices, highlighting the need for a confluent monolayer of cells.

As a “positive” control to demonstrate total re-uptake by the tubule, glucose was initially considered, being a major transport target of the tubule (Rahmoune et al., 2005). However, due to the presence of glucose in the cell-conditioning media, and the likely conditioning of cells in the presence of glucose, it was decided that PFOA would be a more suitable positive control due to its well-known reabsorption in human tubules. For PFOA, the chip data indicated a measurable amount of re-absorption, consistent with what is known about transporter-mediated renal kinetics of PFOA (Worley and Fisher, 2015; Yang et al., 2010). While we a priori expected more re-absorption than was observed in these experiments, we note that this could be explained by one or more of the following factors. First, based on the parallel tube model, the high degree of protein binding of PFOA in vivo actually is the primary driver of slow renal clearance as long as f_u ≤ 0.01, with reabsorption contributing to a lesser degree. Second, the lack of a vascular channel may limit the reabsorption capacity in the tissue chip. Third, qualitatively, we observed that basal OAT4 expression in the RPTECs used in the PFOA experiments was relatively low based on immunohistochemistry (Sakolish et al., 2018).

For cisplatin and gentamicin, the expected reabsorption by the chip was small – on the order of 5%. Little or no reabsorption was indeed observed in the chip, though measuring such small concentration differences can be difficult given the small amounts of effluent produced in this model. Additionally, for cisplatin, a large amount of tubular secretion is expected, and this process was not modeled in the chip and had to be assumed as part of the physiologically-based modeling. Moreover, because the chip lacked a vascular channel, reabsorption could not be disentangled from metabolism, though for both cisplatin and gentamicin, the total amount of renal metabolism relative to clearance is expected to be small. Additionally, cisplatin appears to have the ability to accumulate in renal proximal tubule cells (Wilmes et al., 2015), but this process is likely saturated in our experiments due to the relatively high concentrations and the length of time of treatment. The lack of a vascular channel also implies that reabsorption via passive diffusion will not be fully recapitulated by this device, though recent progress has been made in modeling-based prediction of passive reabsorption (Huang and Isoherranen, 2018; Scotcher et al., 2016c) that could be incorporated in the future. Transporter-mediated pathways remain a challenge to predict either in silico or in vitro (Mathialagan et al., 2017), but can be recapitulated by the chip device at levels below saturation. However, the lack of a vascular channel in the current device leaves open the possibility that any active reabsorption may become physically saturated due to a lack of a “sink” for reabsorbed compounds other than the RPTECs themselves. Thus, while our results are consistent with in vivo pharmacokinetics, some residual uncertainty remains as to generalizability of the predictions of reabsorption kinetics to other compounds that behave like cisplatin or gentamicin. Other tissue chip devices have aimed to include both reabsorption and secretion (Jang et al., 2013; van Duinen et al., 2015), but quantitative comparisons of the data that could be obtained in those models with in vivo pharmacokinetics are yet to be made. Therefore, for a new compound, renal clearance predictions using kidney tubule chip will only be accurate if tubular secretion is assumed to be negligible and active reabsorption is not saturated.

For cadmium, whose renal kinetics are known to involve active transporter proteins as well as accumulation (Yang and Shu, 2015), the kidney tubule chip reproduced qualitatively the tendency of the kidney to retain cadmium. Even more impressive is the quantitative similarity between the in vivo renal clearance of cadmium derived from biomonitoring data and the clearance predicted based on the data from the kidney tubule chip used in this study. Based on the measured uptake (Figure 4), we estimated the total amount of cadmium that is assumed to have accumulated in RPTECs after 22 days to be 3.2 μg/g at 0.05 μM and 16.5 μg/g at 0.5 μM. These values appear to be well within the capacity of the kidney to accumulate cadmium. For instance, Akerstrom et al. (2013) reported concentrations in human kidney biopsies ranging from 1.6 to 55.4 μg/g in a general population, while Ellis et al. (1981) reported concentrations up to about 400 μg/g in smelter workers. Therefore, given the known ability of the kidney to accumulate cadmium, along with the lack of binding demonstrated by blank devices (without cells), the observed uptake is consistent with accumulation of cadmium in RPTECs and in human kidney.

An additional concern is that a large fraction of cadmium was binding to the serum proteins in the culture media (up to 71% was protein-bound). In vivo, compounds that are bound to serum are effectively blocked from entering the tubule by the size-exclusive glomerular barrier (Rodewald and Karnovsky, 1974). We accounted for this in the model by assuming that only unbound cadmium was available for uptake, matching the in vivo simulations to only free cadmium concentrations. However, because the proximal tubule is greatly involved in the reabsorption of serum proteins that pass by the glomerular barrier into the tubule (Gekle, 2005), it is possible that RPTECs in the tissue chip are actively uptaking the serum-bound cadmium. This can occur through the megalin-cubilin transport pathways (Zhai et al., 2000) in addition to the Ca²⁺, Fe²⁺, and Zn²⁺ ion channels (Bridges and Zalups, 2005; He et al., 2009), metal-ion transporters (Bannon et al., 2003), and organic cation transporters (Soodvilai et al., 2011), which are the typical pathways for tubular cadmium transport. However, similar results were obtained by assuming all cadmium was available for uptake (not shown), suggesting that the presence of serum proteins in media does not influence the predictions.

Recent reviews have identified a number of gaps and uncertainties in current methods for predicting renal clearance (Scotcher et al., 2016a; Scotcher et al., 2016b). Renal clearance appears to correlate with some physio-chemical properties, leading to development of some predictive computational models (Dave and Morris, 2015; Varma et al., 2009). For instance, lipophilicity inversely correlates with clearance (Varma et al., 2009), a trend that is reproduced by our results (e.g., cisplatin/PFOA has the highest/lowest predicted clearance, along with the lowest/highest logK_ow). On the other hand, polar descriptors generally positively correlate with clearance (Varma et al., 2009), but this trend was not apparent in our dataset (gentamicin is the most polar, and cadmium the least). While some published computational models appear to be quite accurate in predicting renal clearance (Dave and Morris, 2015), they have been trained and tested with drugs, which have a narrower range of chemical properties that may not include compounds such as cadmium and PFOA. Beyond in silico approaches, simpler in vitro approaches such as permeability assays and other 2D cultures are also an option for predicting renal clearance. However, in general no “consensus” or “gold standard” has been agreed upon in the community (Scotcher et al., 2016b), and the available assays are mostly aimed at pharmaceuticals and thus may not be applicable to the broader range of chemicals in the environment.

5. Conclusions

Tissue chips have great potential to assist in predictive pharmacokinetics, allowing for more realistic predictions of drug efficacy, toxicity, and organ/tissue interactions (Jennings, 2015). This study demonstrated that the proximal tubule chip provides reasonably accurate predictions for tubular reabsorption, both qualitatively and quantitatively, when combined with a physiological model for overall renal clearance and a physical model for the tubule that accounts for the in vivo-to-chip differences in physical dimensions and flows. Because of the lack of a vascular channel, this device is most appropriate for predicting kinetics of non-secreted compounds that are both actively reabsorbed and accumulated in the kidney, such as cadmium. In this way, tissue chip model has a similar limitation to current static culture-based in vitro systems such as permeability assays and kidney slices, none of which can fully integrate all processes of filtration, reabsorption, and secretion. The tissue chip model does have an advantage in accounting for 3D structure and shear stresses caused by flow, as well as having a clear physiological basis for extrapolating from in vitro to in vivo.

Nonetheless, while clearly the kidney chip provides a better mechanistic understanding of renal injury and its dynamic effects on transport and clearance (Sakolish et al., 2019), its utility for predicting renal clearance may still be limited without supplementation with additional data and there are several limitation of this model. Specifically, because the in vitro device lacks filtration and tubular secretion components, additional information on protein binding and the importance of secretory transport is needed in order to make accurate predictions. It is also very important to select appropriate cell types and culture conditions to match the conditions of the organ or tissue of focus. The cell culture media is frequently supplemented with antibiotics (such as gentamicin and amphotericin B) that are proximal tubule toxins, and as such their utilization in toxicity experiments in this model is not recommended. An additional challenge to replicating complex in vitro experiments arises from the need to use bovine-derived serum supplements to the media, material that may introduce additional variability due to its undefined composition. Furthermore, the degree of expression of individual transporters in commercially available RPTECs need to be better characterized in order to ensure quantitative and reproducible in vitro-in vivo concordance. Finally, in order to be more broadly applicable, tissue chips will need to recapitulate more complex structures and cell types, specifically in the case of the kidney chip, a basolateral chamber to mimic the bloodstream. Addressing these and other limitations when designing and applying tissue chip technologies in the future will be necessary in order for these models to fulfill their promise and offer sufficient benefits in terms of accuracy and precision in order to justify their additional cost and complexity as compared to existing in vitro and in silico approaches.

Highlights.

• The kidney plays an essential role in removing toxic compounds from the body

• “Kidney on a chip” devices can help to be understand these processes

• Adding a mathematical model improves chip-based prediction of kidney reabsorption

• Limitations of this model include lack of filtration and secretion