Variance estimates are similar using pedigree or genomic relationships with or without the use of metafounders or the algorithm for proven and young animals

Abstract

With an increase in the number of animals genotyped there has been a shift from using pedigree relationship matrices (A) to genomic ones. As the use of genomic relationship matrices (G) has increased, new methods to build or approximate G have developed. We investigated whether the way variance components are estimated should reflect these changes. We estimated variance components for maternal sow traits by solving with restricted maximum likelihood, with four methods of calculating the inverse of the relationship matrix. These methods included using just the inverse of A (${\mathbf{A}}^{-1}$), combining ${\mathbf{A}}^{-1}$ and the direct inverse of G (${\mathbf{H}}_{\mathbf{D}\mathbf{I}\mathbf{R}\mathbf{E}\mathbf{C}\mathbf{T}}^{-1}$), including metafounders (${\mathbf{H}}_{\mathbf{M}\mathbf{E}\mathbf{T}\mathbf{A}}^{-1}$), or combining ${\mathbf{A}}^{-1}$ with an approximated inverse of G using the algorithm for proven and young animals (${\mathbf{H}}_{\mathbf{A}\mathbf{P}\mathbf{Y}}^{-1}$). There was a tendency for higher additive genetic variances and lower permanent environmental variances estimated with ${\mathbf{A}}^{-1}$ compared with the three ${\mathbf{H}}^{-1}$ methods, which supports that ${\mathbf{G}}^{-1}$ is better than ${\mathbf{A}}^{-1}$ at separating genetic and permanent environmental components, due to a better definition of the actual relationships between animals. There were limited or no differences in variance estimates between ${\mathbf{H}}_{\mathbf{D}\mathbf{I}\mathbf{R}\mathbf{E}\mathbf{C}\mathbf{T}}^{-1}$, ${\mathbf{H}}_{\mathbf{M}\mathbf{E}\mathbf{T}\mathbf{A}}^{-1}$, and ${\mathbf{H}}_{\mathbf{A}\mathbf{P}\mathbf{Y}}^{-1}$. Importantly, there was limited differences in variance components, repeatability or heritability estimates between methods. Heritabilities ranged between <0.01 to 0.04 for stayability after second cycle, and farrowing rate, between 0.08 and 0.15 for litter weight variation, maximum cycle number, total number born, total number still born, and prolonged interval between weaning and first insemination, and between 0.39 and 0.44 for litter birth weight and gestation length. The limited differences in heritabilities suggest that there would be very limited changes to estimated breeding values or ranking of animals across models using the different sets of variance components. It is suggested that variance estimates continue to be made using ${\mathbf{A}}^{-1}$, however including ${\mathbf{G}}^{-1}$ is possibly more appropriate if refining the model, for traits that fit a permanent environmental effect.

Introduction

Variance estimates are needed for single-step genomic best linear unbiased prediction (ssGBLUP). Traditionally variance estimates were calculated using a pedigree based relationship matrix (A). The effect of using a genomic based relationship matrix (G) during solving of variance estimates, has shown a tendency for higher genetic variances estimated with ${\mathbf{A}}^{-1}$ (Legarra, 2016). The full information of ${\mathbf{A}}^{-1}$ and ${\mathbf{G}}^{-1}$ can be combined in the ${\mathbf{H}}^{-1}$ matrix (${\mathbf{H}}_{\mathbf{D}\mathbf{I}\mathbf{R}\mathbf{E}\mathbf{C}\mathbf{T}}^{-1}$), described by Aguilar et al. (2010) and Christensen and Lund (2010). In the past unknown sires and dams in the base generation have been treated as unrelated, in reality they have some unknown relationship. One way of accounting for this, is to estimate relationships between and within metafounders, computed based on genotypes and pedigree of descendants (Legarra et al., 2015). These relationships can be included in ${\mathbf{A}}_{\mathbf{M}\mathbf{E}\mathbf{T}\mathbf{A}}^{-1}$ and combined with ${\mathbf{G}}_{\mathbf{M}\mathbf{E}\mathbf{T}\mathbf{A}}^{-1}$ (${\mathbf{H}}_{\mathbf{M}\mathbf{E}\mathbf{T}\mathbf{A}}^{-1}$). The number of genotyped animals is constantly increasing, and there is a need for more computational efficient methods of building ${\mathbf{G}}^{-1}$. The algorithm for proven and young animals (APY) is one such method (Misztal et al., 2014; Fragomeni et al., 2015). It is an approximation of ${\mathbf{G}}^{-1}$ (${\mathbf{G}}_{\mathbf{A}\mathbf{P}\mathbf{Y}}^{-1}$), requiring inversion of a genomic relationship matrix computed for a subset of genotyped animals (that are a good representation of the population diversity), which can then be combined with ${\mathbf{A}}^{-1}$ (${\mathbf{H}}_{\mathbf{A}\mathbf{P}\mathbf{Y}}^{-1}$). It should be noted that different relationship matrices may require different variance components. It was hypothesized that genetic variances estimated with ${\mathbf{A}}^{-1}$ would be higher compared with ${\mathbf{H}}_{\mathbf{D}\mathbf{I}\mathbf{R}\mathbf{E}\mathbf{C}\mathbf{T}}^{-1}$, but differences would be limited. Since the relationships of metafounders are based on genotypes of descendants, and ${\mathbf{H}}_{\mathbf{A}\mathbf{P}\mathbf{Y}}^{-1}$ uses an approximation of ${\mathbf{G}}^{-1}$, it is hypothesized that the three ${\mathbf{H}}^{-1}$ methods will have similar variance estimates. Therefore, our objective is to compare variance estimates using ${\mathbf{A}}^{-1}$, ${\mathbf{H}}_{\mathbf{D}\mathbf{I}\mathbf{R}\mathbf{E}\mathbf{C}\mathbf{T}}^{-1}$, ${\mathbf{H}}_{\mathbf{M}\mathbf{E}\mathbf{T}\mathbf{A}}^{-1}$, and ${\mathbf{H}}_{\mathbf{A}\mathbf{P}\mathbf{Y}}^{-1}$, based on empirical pig data for different maternal traits.

Materials and methods

The data used for this study was collected as part of routine data recording in a commercial breeding program. Samples collected for DNA extraction were only used for routine diagnostic purposes of the breeding program. Data recording and sample collection were conducted strictly in line with the Dutch law on the protection of animals (Gezondheids- en welzijnswet voor dieren).

Dataset

Data were provided by Topigs Norsvin on a breeding large white maternal sow line. There were 10 traits for which variance components were to be estimated: mean litter birth weight (LBW), litter variation defined as the within litter standard deviation of birth weight (LVAR), stayability after second cycle defined as a binary trait for animals that reach second parity or not (STAY), maximum cycle number (MAX) was defined as the maximum number of parities with large parities (more than five) treated as equal to five, total number born (TNB), number still born (STB) which was expressed as log₁₀(STB + 1), litter mortality (LMO), prolonged interval between weaning and first insemination (PIWI) defined as a binary trait, where prolonged is defined as 0 if insemination is 6 d or fewer after weaning or 1 if insemination is 7 d or more after weaning, gestation length (GLE), and farrowing rate (FRT).

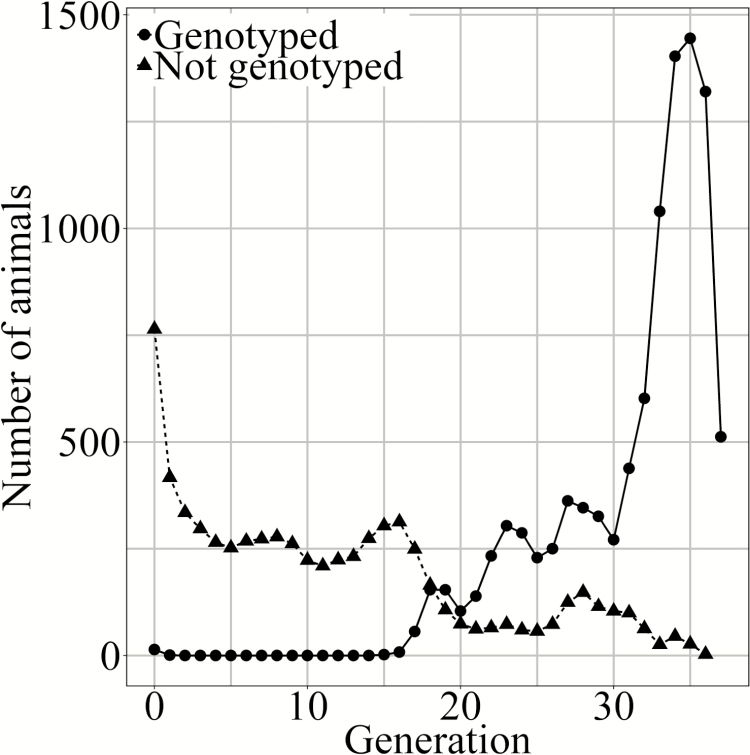
The phenotype data from the maternal line analyzed (originally 293,619 animals with at least one record, from 39 generations), was to be limited to genotyped animals (42,112 records from 10,860 genotyped animals with at least one record). Data filtering removed records where levels of categorical fixed effects had fewer than five records. After filtering based on fixed effects 34,441 records from 9,695 genotyped animals remained (Table 1). There were also genotyped sires (498) and dams (2,585) of remaining phenotyped animals. These sires and dams had no own records. Due to software limitations for the variance components estimated using ${\mathbf{H}}_{\mathbf{D}\mathbf{I}\mathbf{R}\mathbf{E}\mathbf{C}\mathbf{T}}^{-1}$, the number of genotypes to be included in the analysis was limited to 10,000, by selecting animals as explained further on (see analysis using genomic relationships approximated with APY, for details on selected animals). The pedigree was then limited to these 10,000 animals and their ancestors with a total of 16,932 animals and 36 generations. The number of genotyped and ungenotyped animals per generation in the pedigree is illustrated in Figure 1.

Table 1.

Summary of data used for the estimation of variance components after filtering

Trait1	Total number of				Mean	SD
	Records	Animals	Sires	Dams
LBW, g	33,974	9,465	625	3,442	1246.18	213.77
LVAR, g	33,955	9,462	626	3,441	262.28	77.34
STAY, %	7,782	7,782	508	2,648	0.92	0.27
MAX, number	5,910	5,910	397	2,085	3.96	1.31
TNB, number	33,974	9,465	626	3,442	16.03	3.77
STB, number	33,970	9,465	626	3,442	2.512	1.916
LMO, %	32,754	9,039	621	3,284	14.38	15.21
PIWI, %	7,797	7,797	530	2,877	13.80	34.49
GLE, days	33,274	9,182	625	3,338	115.09	1.54
FRT, %	33,974	9,465	626	3,442	94.76	22.28

1LBW, litter birth weight; LVAR, litter variation; STAY, stayability after second cycle; MAX, maximum cycle number; TNB, total number born; STB, total number stillborn (no log-transformation for summary); LMO, litter mortality; PIWI, prolonged interval between weaning and first insemination; GLE, gestation length; FRT, farrowing rate. Sires and dams are the number of sires and dams of progeny with at least one record for that trait.

Figure 1.

Number of genotyped and ungenotyped animals per generation in the pedigree.

Animal Models

All variance components were estimated with a univariate animal model with restricted maximum likelihood (REML). For the traits STAY, MAX, and PIWI, the model can be summarized in matrix notation as:

$${\displaystyle \begin{array}{l}{\displaystyle \mathbf{y}=\mathbf{X}\mathbf{b}+\mathbf{Z}\mathbf{a}+\mathbf{e}}\end{array}}$$

where y is a vector of the trait observations, the matrices X and Z, are incidence matrices associated with the vector of fixed effects b, and the vector of random additive genetic effects $\mathbf{a}\sim (\mathbf{0},\mathbf{K}{\sigma }_A^2)$, respectively, and $\mathbf{e}\sim (\mathbf{0},\mathbf{I}{\sigma }_e^2)$ is a vector of residuals. The term ${\sigma }_A^2$ and ${\sigma }_e^2$ is for additive genetic and residual variances, respectively. The matrices K is the relationship matrix (either A, ${\mathbf{A}}_{\mathbf{M}\mathbf{E}\mathbf{T}\mathbf{A}}$, ${\mathbf{H}}_{\mathbf{D}\mathbf{I}\mathbf{R}\mathbf{E}\mathbf{C}\mathbf{T}}$, ${\mathbf{H}}_{\mathbf{M}\mathbf{E}\mathbf{T}\mathbf{A}}$, ${\mathbf{H}}_{\mathbf{A}\mathbf{P}\mathbf{Y}}$), and I is an identity matrix, respectively. For each of the methods (${\mathbf{A}}^{-1}$, ${\mathbf{A}}_{\mathbf{M}\mathbf{E}\mathbf{T}\mathbf{A}}^{-1}$, ${\mathbf{H}}_{\mathbf{D}\mathbf{I}\mathbf{R}\mathbf{E}\mathbf{C}\mathbf{T}}^{-1}$, ${\mathbf{H}}_{\mathbf{M}\mathbf{E}\mathbf{T}\mathbf{A}}^{-1}$, and ${\mathbf{H}}_{\mathbf{A}\mathbf{P}\mathbf{Y}}^{-1}$) the same fixed and random effects were used (Table 2). Details on the computation of the different relationship matrices will be given below.

Table 2.

Summary of random and fixed effects fitted for each trait

Effect1	Traits
	STAY	MAX	PIWI	LBW	LVAR	LMO	TNB	STB	GLE	FRT
Random effects
Animal	●	●	●	●	●	●	●	●	●	●
PE				●	●	●	●	●	●	●
Sire							●	●	●	●
Fixed effects
Parity				●	●	●		●
HYSF			●	●	●	●	●	●	●
HYSI1	●	●
HYSI										●
I2							●	●	●
CIWP							●	●
CTNB				●					●
LP			●
LP2			●
NW			●
PBCB						●	●	●	●

1Sire, service sire; PE, permanent environment; HYSF, herd-year-season at farrowing; HYSI1, herd-year-season at first insemination; HYSI, herd-year-season at insemination; I2, second insemination; CIWP, class interval between weaning a pregnancy; CTNB, class of total number born; LP, lactation period; LP2, LP × LP; NW, number weaned; PBCB, purebred or crossbred litter; LBW, litter birth weight; LVAR, litter variation; STAY, stayability after second cycle; MAX, maximum cycle number; TNB, total number born; STB, total number stillborn; LMO, litter mortality; PIWI, prolonged interval between weaning and first insemination; GLE, gestation length; FRT, farrowing rate.

When appropriate random permanent environment and service sire effects were fitted (Table 2). For the traits LBW, LVAR, and LMO, a permanent environmental effect was fitted, and the associated model can be summarized as:

$${\displaystyle \begin{array}{l}{\displaystyle \mathbf{y}=\mathbf{X}\mathbf{b}+\mathbf{Z}\mathbf{a}+\mathbf{W}\mathbf{c}+\mathbf{e}}\end{array}}$$

where W is an incidence matrix associated with the vector of random permanent environmental effects $\mathbf{c}\sim (\mathbf{0},\mathbf{I}{\sigma }_{\mathrm{p}\mathrm{e}}^2)$. The term ${\sigma }_{\mathrm{p}\mathrm{e}}^2$ is for permanent environmental variance.

For the traits TNB, STB, GLE, and FRT, the associated model included both a permanent environmental and a nongenetic service sire effect, and can be summarized as:

$${\displaystyle \begin{array}{l}{\displaystyle \mathbf{y}=\mathbf{X}\mathbf{b}+\mathbf{Z}\mathbf{a}+\mathbf{W}\mathbf{c}+\mathbf{V}\mathbf{s}+\mathbf{e}}\end{array}}$$

where V is an incidence matrix associated with a vector of service sire effects $\mathbf{s}\sim (\mathbf{0},\mathbf{I}{\sigma }_{\mathrm{s}\mathrm{i}\mathrm{r}\mathrm{e}}^2)$. The term ${\sigma }_{\mathrm{s}\mathrm{i}\mathrm{r}\mathrm{e}}^2$, is for service sire variances.

Analysis Using Pedigree Relationships

Variance components were estimated using AIREMLF90 (Misztal et al., 2002). All methods used the same pedigree so that additive genetic variance estimates are comparable with the same base (Legarra, 2016). The pedigree was provided to AIREMLF90, which for solving built the ${\mathbf{A}}^{-1}$ internally including inbreeding. The variance estimates calculated with ${\mathbf{A}}^{-1}$ were used as starting values for each of the following methods.

Analysis Using Genomic Relationships

The AIREMLF90 software implements ${\mathbf{A}}^{-1}$ by default. For solving with ${\mathbf{H}}_{\mathbf{D}\mathbf{I}\mathbf{R}\mathbf{E}\mathbf{C}\mathbf{T}}^{-1}$, the pedigree and genotypes were provided to PREGSF90 which built ${\mathbf{A}}^{-1}$ and ${\mathbf{G}}^{-1}$ internally with the default options. The ${\mathbf{G}}_{\mathbf{D}\mathbf{I}\mathbf{R}\mathbf{E}\mathbf{C}\mathbf{T}}$ matrix needed was computed with PREGSF90 as follows:

$${\displaystyle \begin{array}{l}{\displaystyle {\mathbf{G}}_{\mathbf{D}\mathbf{I}\mathbf{R}\mathbf{E}\mathbf{C}\mathbf{T}}=\alpha (a\times {\mathbf{G}}_{\mathbf{r}\mathbf{a}\mathbf{w}}+\mathbf{J}\times b)+\beta \mathbf{A}}\end{array}}$$

where a and b (0.933 and 0.134) were computed following Powell et al. (2010) to scale inbreeding in ${\mathbf{G}}_{\mathbf{r}\mathbf{a}\mathbf{w}}$ to the same level as in A, $\alpha =0.95$ and $\beta =0.05$, J was a matrix of ones, and ${\mathbf{G}}_{\mathbf{r}\mathbf{a}\mathbf{w}}$ was computed following the first method of VanRaden (2008):

$${\displaystyle \begin{array}{l}{\displaystyle {\mathbf{G}}_{\mathbf{r}\mathbf{a}\mathbf{w}}=\frac{\mathbf{Z}{\mathbf{Z}}^{\prime }}{k}}\end{array}}$$

where $k=2\times \mathrm{\Sigma }[p\times (1-p)]$, and the allele frequencies (p) were estimated from the genotyped population.

PREGSF90 then created ${\mathbf{G}}_{\mathbf{D}\mathbf{I}\mathbf{R}\mathbf{E}\mathbf{C}\mathbf{T}}^{-1}-{\mathbf{A}}_{22}^{-1}$ in a binary format, where ${\mathbf{A}}_{22}^{-1}$ is the inverse of the relationship matrix for genotyped animals. AIREMLF90 built ${\mathbf{H}}_{\mathbf{D}\mathbf{I}\mathbf{R}\mathbf{E}\mathbf{C}\mathbf{T}}^{-1}$ internally by using ${\mathbf{G}}_{\mathbf{D}\mathbf{I}\mathbf{R}\mathbf{E}\mathbf{C}\mathbf{T}}^{-1}-{\mathbf{A}}_{22}^{-1}$ as follows (Aguilar et al., 2010; Christensen and Lund, 2010):

$${\displaystyle \begin{array}{l}{\displaystyle {\mathbf{H}}_{\mathbf{D}\mathbf{I}\mathbf{R}\mathbf{E}\mathbf{C}\mathbf{T}}^{-1}={\mathbf{A}}^{-1}+\left[\begin{array}{l}\mathbf{0}{\displaystyle \mathbf{0}}\\ \mathbf{0}{\displaystyle {\mathbf{G}}_{\mathbf{D}\mathbf{I}\mathbf{R}\mathbf{E}\mathbf{C}\mathbf{T}}^{-1}-{\mathbf{A}}_{22}^{-1}}\end{array}\right]}\end{array}}$$

Analysis Using Metafounders

The data used in the analysis was from a single purebred line, and a single metafounder was defined and added as a pseudo-individual to the pedigree to reflect a single founding group (Christensen, 2012). The pedigree relationship matrix was built with this extended pedigree (${\mathbf{A}}_{\mathbf{M}\mathbf{E}\mathbf{T}\mathbf{A}}^{-1}$), using Calc_grm (Calus and Vandenplas, 2016). The self-relationship of the metafounder (γ) was estimated using the method of moments based on summary statistics of Legarra et al. (2015). The estimated self-relationship was equal to 0.364. The ${\mathbf{H}}_{\mathbf{M}\mathbf{E}\mathbf{T}\mathbf{A}}^{-1}$ was built using Calc_grm (Calus and Vandenplas, 2016) as:

$${\displaystyle \begin{array}{l}{\displaystyle {\mathbf{H}}_{\mathbf{M}\mathbf{E}\mathbf{T}\mathbf{A}}^{-1}={\mathbf{A}}_{\mathbf{M}\mathbf{E}\mathbf{T}\mathbf{A}}^{-1}+\left[\begin{array}{l}\mathbf{0}{\displaystyle \mathbf{0}}\\ \mathbf{0}{\displaystyle {\mathbf{G}}_{\mathbf{M}\mathbf{E}\mathbf{T}\mathbf{A}}^{-1}-{\mathbf{A}}_{22}^{-1}}\end{array}\right]}\end{array}}$$

where ${\mathbf{A}}_{22}^{-1}$ is the inverse of the pedigree relationship matrix among genotyped animals, and ${\mathbf{G}}_{\mathbf{M}\mathbf{E}\mathbf{T}\mathbf{A}}^{-1}$ is computed with allele frequencies of 0.5 following Legarra et al. (2015).

The ${\mathbf{A}}_{\mathbf{M}\mathbf{E}\mathbf{T}\mathbf{A}}^{-1}$ and ${\mathbf{H}}_{\mathbf{M}\mathbf{E}\mathbf{T}\mathbf{A}}^{-1}$ were then provided to AIREMLF90 directly for solving. By adding the metafounder to ${\mathbf{A}}_{\mathbf{M}\mathbf{E}\mathbf{T}\mathbf{A}}^{-1}$ and ${\mathbf{H}}_{\mathbf{M}\mathbf{E}\mathbf{T}\mathbf{A}}^{-1}$, the additive genetic variances (and its standard error) were no longer on the same scale as the ones obtained with ${\mathbf{A}}^{-1}$ or ${\mathbf{H}}_{\mathbf{D}\mathbf{I}\mathbf{R}\mathbf{E}\mathbf{C}\mathbf{T}}^{-1}$. The additive genetic variances (and its standard error) expressed on the metafounder base were thus rescaled after estimation, by multiplying the variance with a function of the self-relationship $1-(\gamma /2)$ (Legarra et al., 2015).

Analysis Using Genomic Relationships Approximated with APY

The approximation of ${\mathbf{G}}^{-1}$ with APY was done following the method of Misztal et al. (2014) with Calc_grm (Calus and Vandenplas, 2016). To ensure the relationships in ${\mathbf{G}}_{\mathbf{A}\mathbf{P}\mathbf{Y}}$ were relative to the same base as A, scaling was based on the method of Powell et al. (2010) as used above for ${\mathbf{G}}_{\mathbf{D}\mathbf{I}\mathbf{R}\mathbf{E}\mathbf{C}\mathbf{T}}$. The ${\mathbf{G}}_{\mathbf{A}\mathbf{P}\mathbf{Y}}^{-1}-{\mathbf{A}}_{22}^{-1}$ was translated into a binary format and provided as an external matrix to AIREMLF90, which then built ${\mathbf{H}}_{\mathbf{A}\mathbf{P}\mathbf{Y}}^{-1}$.

To determine the number of animals to be included as core animals recommendations by Bradford et al. (2017) were followed. First the ${\mathbf{G}}_{\mathbf{D}\mathbf{I}\mathbf{R}\mathbf{E}\mathbf{C}\mathbf{T}}$ was built in Calc_grm and a principal components analysis was used to identify that 98% of variation was explained by 5,136 individuals. Core animals were selected based on the amount of information available for an individual. The number of records for LBW was used as an indicator, whereas the other traits with repeated records would provide similar animals to the core as LBW, while the traits with a single observation provide too many core animals. In total 4,764 core animals were selected which included those with four or more LBW phenotype records (4,229), and genotyped sires (498) and dams (37) that were not phenotyped but had progeny with both genotypes and phenotypes. The genotyped animals with three or fewer LBW records (5,466) were selected as non-core animals, and 230 animals were randomly removed from this group to limit the number of genotyped animals to 10,000 to meet software limitations as mentioned previously.

Estimating Repeatability and Heritability

All models converged for each of the methods and trait combinations. Convergence was achieved when the squared relative difference between the variances estimated in two consecutive runs was lower than $1.0\times {10}^{-10}$. The variances estimated with AIREMLF90 were used to calculate repeatability (r) and heritability ($h^2$). Repeatability was calculated as $r=({\sigma }_a^2+{\sigma }_{\mathrm{s}\mathrm{i}\mathrm{r}\mathrm{e}}^2+{\sigma }_{\mathrm{p}\mathrm{e}}^2)/({\sigma }_a^2+{\sigma }_{\mathrm{s}\mathrm{i}\mathrm{r}\mathrm{e}}^2+{\sigma }_{\mathrm{p}\mathrm{e}}^2+{\sigma }_e^2)$, and heritability was calculated as $h^2=({\sigma }_a^2)/({\sigma }_a^2+{\sigma }_{\mathrm{s}\mathrm{i}\mathrm{r}\mathrm{e}}^2+{\sigma }_{\mathrm{p}\mathrm{e}}^2+{\sigma }_e^2)$. Note that variances for service sire (${\sigma }_{\mathrm{s}\mathrm{i}\mathrm{r}\mathrm{e}}^2$) and permanent environment (${\sigma }_{\mathrm{p}\mathrm{e}}^2$) were only included for traits which fit those effects in the model, while the additive (${\sigma }_a^2$) and residual (${\sigma }_e^2$) variances were estimated for all traits. Standard errors for repeatability and heritability were estimated with Monte Carlo sampling as described by Houle and Meyer (2015), and implemented in AIREMLF90, which were then used to determine significant differences between models, based on a Z-test with a significance of 0.05.

Results

The models based on ${\mathbf{A}}^{-1}$ tended to have higher estimates for additive genetic effects and lower estimates for the permanent environment compared with the models based on ${\mathbf{H}}_{\mathbf{D}\mathbf{I}\mathbf{R}\mathbf{E}\mathbf{C}\mathbf{T}}^{-1}$ (8 of the 10 traits). Variance estimates using the ${\mathbf{H}}_{\mathbf{D}\mathbf{I}\mathbf{R}\mathbf{E}\mathbf{C}\mathbf{T}}^{-1}$, ${\mathbf{H}}_{\mathbf{M}\mathbf{E}\mathbf{T}\mathbf{A}}^{-1}$ (variances rescaled to be expressed on the same base as the other methods), and ${\mathbf{H}}_{\mathbf{A}\mathbf{P}\mathbf{Y}}^{-1}$ were all very similar when compared with each other. For most traits, the variances estimated with ${\mathbf{A}}_{\mathbf{M}\mathbf{E}\mathbf{T}\mathbf{A}}^{-1}$ were the same as when estimated with ${\mathbf{A}}^{-1}$, the additive genetic variance for traits LBW and GLE (also sire variance for GLE) had a maximum deviation of less than 1%, with no differences for other variance estimates. Therefore these results are not reported below, or discussed. To make the comparison between the methods, the traits have been separated into four categories, based on the difference in additive genetic variance estimated with ${\mathbf{A}}^{-1}$ or ${\mathbf{H}}_{\mathbf{D}\mathbf{I}\mathbf{R}\mathbf{E}\mathbf{C}\mathbf{T}}^{-1}$. These include: additive genetic variances estimated with ${\mathbf{A}}^{-1}$ that are significantly higher than with ${\mathbf{H}}_{\mathbf{D}\mathbf{I}\mathbf{R}\mathbf{E}\mathbf{C}\mathbf{T}}^{-1}$ (TNB and PIWI; Table 3), additive genetic variances estimated with ${\mathbf{A}}^{-1}$ are higher than with ${\mathbf{H}}_{\mathbf{D}\mathbf{I}\mathbf{R}\mathbf{E}\mathbf{C}\mathbf{T}}^{-1}$ by at least 10% but the difference is not significant (MAX, LMO, FRT; Table 4), additive genetic variances estimated with ${\mathbf{A}}^{-1}$ and ${\mathbf{H}}_{\mathbf{D}\mathbf{I}\mathbf{R}\mathbf{E}\mathbf{C}\mathbf{T}}^{-1}$ have less than a 10% difference and are not significantly different (LVAR, STAY, STB, GLE; Table 5), and additive genetic variances estimated with ${\mathbf{A}}^{-1}$ are lower but not significantly different to ${\mathbf{H}}_{\mathbf{D}\mathbf{I}\mathbf{R}\mathbf{E}\mathbf{C}\mathbf{T}}^{-1}$ (LBW; Table 6). Note that there were no traits where the additive genetic variances estimated with ${\mathbf{A}}^{-1}$ were significantly lower than with ${\mathbf{H}}_{\mathbf{D}\mathbf{I}\mathbf{R}\mathbf{E}\mathbf{C}\mathbf{T}}^{-1}$.

Table 3.

Genetic parameters for maternal sow traits where additive genetic variances (${\sigma }_a^2$) estimated with ${\mathbf{A}}^{-1}$ are significantly greater than with ${\mathbf{H}}_{\mathbf{D}\mathbf{I}\mathbf{R}\mathbf{E}\mathbf{C}\mathbf{T}}^{-1}$, with permanent environmental variance (${\sigma }_{\mathrm{p}\mathrm{e}}^2$), sire variance (${\sigma }_{\mathrm{s}\mathrm{i}\mathrm{r}\mathrm{e}}^2$), and residual variance (${\sigma }_e^2$) estimates included for the calculation of repeatability (r) and heritability ($h^2$), with standard errors (± SE)1

Trait	Method	${\sigma }_a^2$	${\sigma }_{\mathrm{p}\mathrm{e}}^2$	${\sigma }_{\mathrm{s}\mathrm{i}\mathrm{r}\mathrm{e}}^2$	${\sigma }_e^2$	r	$h^2$	−2LogL difference*
TNB	${\mathbf{A}}^{-1}$	1.893 ± 0.158	1.124 ± 0.109	0.435 ± 0.040	8.971 ± 0.083	0.28 ± 0.01	0.15 ± 0.01	6,119
	${\mathbf{H}}_{\mathbf{D}\mathbf{I}\mathbf{R}\mathbf{E}\mathbf{C}\mathbf{T}}^{-1}$	1.540 ± 0.120	1.426 ± 0.081	0.429 ± 0.040	9.000 ± 0.083	0.27 ± 0.01	0.12 ± 0.01	5,911
	${\mathbf{H}}_{\mathbf{M}\mathbf{E}\mathbf{T}\mathbf{A}}^{-1}$	1.488 ± 0.117	1.546 ± 0.077	0.430 ± 0.040	9.003 ± 0.083	0.28 ± 0.01	0.12 ± 0.01	5,881
	${\mathbf{H}}_{\mathbf{A}\mathbf{P}\mathbf{Y}}^{-1}$	1.512 ± 0.120	1.534 ± 0.077	0.430 ± 0.040	9.002 ± 0.083	0.28 ± 0.01	0.12 ± 0.01	0
PIWI	${\mathbf{A}}^{-1}$	177.5 ± 25.46	—	—	976.8 ± 23.49	0.15 ± 0.02	0.15 ± 0.02	17
	${\mathbf{H}}_{\mathbf{D}\mathbf{I}\mathbf{R}\mathbf{E}\mathbf{C}\mathbf{T}}^{-1}$	115.1 ± 15.94	—	—	1030.9 ± 18.95	0.10 ± 0.01	0.10 ± 0.01	17
	${\mathbf{H}}_{\mathbf{M}\mathbf{E}\mathbf{T}\mathbf{A}}^{-1}$	118.4 ± 15.95	—	—	1037.6 ± 18.42	0.10 ± 0.02	0.10 ± 0.02	0
	${\mathbf{H}}_{\mathbf{A}\mathbf{P}\mathbf{Y}}^{-1}$	117.0 ± 15.96	—	—	1038.8 ± 18.47	0.10 ± 0.01	0.10 ± 0.01	5

1TNB, total number born; PIWI, prolonged interval between weaning and first insemination; ${\mathbf{A}}^{-1}$, inverted pedigree relationship matrix; ${\mathbf{H}}_{\mathbf{D}\mathbf{I}\mathbf{R}\mathbf{E}\mathbf{C}\mathbf{T}}^{-1}$, ${\mathbf{G}}^{-1}$ inverted from the full genomic relationship matrix (G); ${\mathbf{H}}_{\mathbf{M}\mathbf{E}\mathbf{T}\mathbf{A}}^{-1}$, ${\mathbf{G}}^{-1}$ inverted from the full G with metafounder included in ${\mathbf{A}}^{-1}$; ${\mathbf{H}}_{\mathbf{A}\mathbf{P}\mathbf{Y}}^{-1}$, ${\mathbf{G}}^{-1}$ approximation based on recursion of core animals in G.

*Difference between maximum likelihood function of the model fitted and the lowest value obtained for the trait (TNB: 169,900; PIWI: 76,119), where a smaller value indicates a better fit.

Table 4.

Genetic parameters for maternal sow traits where additive genetic variances (${\sigma }_a^2$) estimated with ${\mathbf{A}}^{-1}$ are greater but not significantly than with ${\mathbf{H}}_{\mathbf{D}\mathbf{I}\mathbf{R}\mathbf{E}\mathbf{C}\mathbf{T}}^{-1}$, with permanent environmental variance (${\sigma }_{\mathrm{p}\mathrm{e}}^2$), sire variance (${\sigma }_{\mathrm{s}\mathrm{i}\mathrm{r}\mathrm{e}}^2$), and residual variance (${\sigma }_e^2$) estimates included for the calculation of repeatability (r) and heritability ($h^2$), with standard errors (± SE)1

Trait	Method	${\sigma }_a^2$	${\sigma }_{\mathrm{p}\mathrm{e}}^2$	${\sigma }_{\mathrm{s}\mathrm{i}\mathrm{r}\mathrm{e}}^2$	${\sigma }_e^2$	r	$h^2$	-2LogL difference*
MAX	${\mathbf{A}}^{-1}$	0.151 ± 0.034	—	—	1.285 ± 0.034	0.11 ± 0.02	0.11 ± 0.02	0
	${\mathbf{H}}_{\mathbf{D}\mathbf{I}\mathbf{R}\mathbf{E}\mathbf{C}\mathbf{T}}^{-1}$	0.117 ± 0.025	—	—	1.316 ± 0.029	0.08 ± 0.02	0.08 ± 0.02	1
	${\mathbf{H}}_{\mathbf{M}\mathbf{E}\mathbf{T}\mathbf{A}}^{-1}$	0.143 ± 0.028	—	—	1.307 ± 0.028	0.10 ± 0.02	0.10 ± 0.02	35
	${\mathbf{H}}_{\mathbf{A}\mathbf{P}\mathbf{Y}}^{-1}$	0.119 ± 0.024	—	—	1.326 ± 0.028	0.08 ± 0.02	0.08 ± 0.02	1
LMO	${\mathbf{A}}^{-1}$	16.06 ± 1.99	17.32 ± 1.82	—	195.00 ± 1.80	0.15 ± 0.01	0.07 ± 0.01	23
	${\mathbf{H}}_{\mathbf{D}\mathbf{I}\mathbf{R}\mathbf{E}\mathbf{C}\mathbf{T}}^{-1}$	13.45 ± 1.44	18.75 ± 1.49	—	195.71 ± 1.82	0.14 ± 0.01	0.06 ± 0.01	20
	${\mathbf{H}}_{\mathbf{M}\mathbf{E}\mathbf{T}\mathbf{A}}^{-1}$	13.78 ± 1.43	19.34 ± 1.44	—	195.80 ± 1.82	0.15 ± 0.01	0.06 ± 0.01	0
	${\mathbf{H}}_{\mathbf{A}\mathbf{P}\mathbf{Y}}^{-1}$	13.62 ± 1.43	19.34 ± 1.45	—	195.82 ± 1.82	0.14 ± 0.01	0.06 ± 0.01	3
FRT	${\mathbf{A}}^{-1}$	5.31 ± 1.59	3.89 ± 2.47	11.95 ± 1.42	466.06 ± 4.24	0.043 ± 0.001	0.011 ± 0.001	1
	${\mathbf{H}}_{\mathbf{D}\mathbf{I}\mathbf{R}\mathbf{E}\mathbf{C}\mathbf{T}}^{-1}$	3.36 ± 1.59	5.41 ± 2.29	11.91 ± 1.41	466.22 ± 4.24	0.043 ± 0.006	0.007 ± 0.002	0
	${\mathbf{H}}_{\mathbf{M}\mathbf{E}\mathbf{T}\mathbf{A}}^{-1}$	3.05 ± 0.97	5.95 ± 2.28	11.90 ± 1.41	466.22 ± 4.24	0.043 ± 0.006	0.006 ± 0.002	4
	${\mathbf{H}}_{\mathbf{A}\mathbf{P}\mathbf{Y}}^{-1}$	2.92 ± 0.93	6.05 ± 2.28	11.89 ± 1.41	466.22 ± 4.24	0.043 ± 0.005	0.006 ± 0.002	5

1MAX, maximum cycle number; LMO, litter mortality; FRT, farrowing rate; ${\mathbf{A}}^{-1}$, inverted pedigree relationship matrix; ${\mathbf{H}}_{\mathbf{D}\mathbf{I}\mathbf{R}\mathbf{E}\mathbf{C}\mathbf{T}}^{-1}$, ${\mathbf{G}}^{-1}$ inverted from the full genomic relationship matrix (G); ${\mathbf{H}}_{\mathbf{M}\mathbf{E}\mathbf{T}\mathbf{A}}^{-1}$, ${\mathbf{G}}^{-1}$ inverted from the full G with metafounder included in ${\mathbf{A}}^{-1}$; ${\mathbf{H}}_{\mathbf{A}\mathbf{P}\mathbf{Y}}^{-1}$, ${\mathbf{G}}^{-1}$ approximation based on recursion of core animals in G.

*Difference between maximum likelihood function of the model fitted and the lowest value obtained for the trait (MAX: 18,619; LMO: 265,007; FRT: 300,766), where a smaller value indicates a better fit.

Table 5.

Genetic parameters for maternal sow traits where additive genetic variances (${\sigma }_a^2$) estimated with ${\mathbf{A}}^{-1}$ are not different than with ${\mathbf{H}}_{\mathbf{D}\mathbf{I}\mathbf{R}\mathbf{E}\mathbf{C}\mathbf{T}}^{-1}$, with permanent environmental variance (${\sigma }_{\mathrm{p}\mathrm{e}}^2$), sire variance (${\sigma }_{\mathrm{s}\mathrm{i}\mathrm{r}\mathrm{e}}^2$), and residual variance (${\sigma }_e^2$) estimates included for the calculation of repeatability (r) and heritability ($h^2$), with standard errors (± SE)1

Trait	Method	${\sigma }_a^2$	${\sigma }_{\mathrm{p}\mathrm{e}}^2$	${\sigma }_{\mathrm{s}\mathrm{i}\mathrm{r}\mathrm{e}}^2$	${\sigma }_e^2$	r	$h^2$	-2LogL difference*
LVAR	${\mathbf{A}}^{-1}$	640 ± 55	256 ± 39	—	4,201 ± 37	0.18 ± 0.01	0.13 ± 0.02	401
	${\mathbf{H}}_{\mathbf{D}\mathbf{I}\mathbf{R}\mathbf{E}\mathbf{C}\mathbf{T}}^{-1}$	637 ± 46	286 ± 28	—	4,205 ± 37	0.18 ± 0.01	0.12 ± 0.01	51
	${\mathbf{H}}_{\mathbf{M}\mathbf{E}\mathbf{T}\mathbf{A}}^{-1}$	673 ± 49	316 ± 27	—	4,206 ± 38	0.19 ± 0.01	0.13 ± 0.01	900
	${\mathbf{H}}_{\mathbf{A}\mathbf{P}\mathbf{Y}}^{-1}$	676 ± 49	312 ± 27	—	4,206 ± 37	0.19 ± 0.01	0.13 ± 0.01	0
STAY	${\mathbf{A}}^{-1}$	0.003 ± 0.001	—	—	0.068 ± 0.001	0.044 ± 0.014	0.044 ± 0.014	104
	${\mathbf{H}}_{\mathbf{D}\mathbf{I}\mathbf{R}\mathbf{E}\mathbf{C}\mathbf{T}}^{-1}$	0.002 ± 0.001	—	—	0.069 ± 0.001	0.029 ± 0.009	0.029 ± 0.009	80
	${\mathbf{H}}_{\mathbf{M}\mathbf{E}\mathbf{T}\mathbf{A}}^{-1}$	0.002 ± 0.001	—	—	0.069 ± 0.001	0.029 ± 0.011	0.029 ± 0.011	12
	${\mathbf{H}}_{\mathbf{A}\mathbf{P}\mathbf{Y}}^{-1}$	0.001 ± 0.001	—	—	0.069 ± 0.001	0.015 ± 0.008	0.015 ± 0.008	0
STB	${\mathbf{A}}^{-1}$	0.048 ± 0.004	0.027 ± 0.003	0.006 ± 0.001	0.299 ± 0.003	0.21 ± 0.01	0.13 ± 0.01	464
	${\mathbf{H}}_{\mathbf{D}\mathbf{I}\mathbf{R}\mathbf{E}\mathbf{C}\mathbf{T}}^{-1}$	0.052 ± 0.004	0.027 ± 0.002	0.006 ± 0.001	0.299 ± 0.003	0.22 ± 0.01	0.14 ± 0.01	96
	${\mathbf{H}}_{\mathbf{M}\mathbf{E}\mathbf{T}\mathbf{A}}^{-1}$	0.051 ± 0.004	0.030 ± 0.002	0.006 ± 0.001	0.299 ± 0.002	0.23 ± 0.01	0.13 ± 0.01	0
	${\mathbf{H}}_{\mathbf{A}\mathbf{P}\mathbf{Y}}^{-1}$	0.052 ± 0.004	0.029 ± 0.004	0.006 ± 0.001	0.299 ± 0.003	0.23 ± 0.01	0.14 ± 0.01	238
GLE	${\mathbf{A}}^{-1}$	0.950 ± 0.045	0.149 ± 0.003	0.227 ± 0.001	0.888 ± 0.003	0.60 ± 0.02	0.43 ± 0.01	1,409
	${\mathbf{H}}_{\mathbf{D}\mathbf{I}\mathbf{R}\mathbf{E}\mathbf{C}\mathbf{T}}^{-1}$	0.905 ± 0.040	0.226 ± 0.002	0.231 ± 0.001	0.892 ± 0.003	0.60 ± 0.01	0.40 ± 0.01	96
	${\mathbf{H}}_{\mathbf{M}\mathbf{E}\mathbf{T}\mathbf{A}}^{-1}$	0.911 ± 0.043	0.286 ± 0.002	0.231 ± 0.001	0.892 ± 0.002	0.62 ± 0.01	0.39 ± 0.01	0
	${\mathbf{H}}_{\mathbf{A}\mathbf{P}\mathbf{Y}}^{-1}$	0.914 ± 0.044	0.283 ± 0.004	0.231 ± 0.001	0.892 ± 0.003	0.61 ± 0.01	0.39 ± 0.01	38

1LVAR, litter variation; STAY, stayability after second cycle; STB, total number stillborn; GLE, gestation length; ${\mathbf{A}}^{-1}$, inverted pedigree relationship matrix; ${\mathbf{H}}_{\mathbf{D}\mathbf{I}\mathbf{R}\mathbf{E}\mathbf{C}\mathbf{T}}^{-1}$, ${\mathbf{G}}^{-1}$ inverted from the full genomic relationship matrix (G); ${\mathbf{H}}_{\mathbf{M}\mathbf{E}\mathbf{T}\mathbf{A}}^{-1}$, ${\mathbf{G}}^{-1}$ inverted from the full G with metafounder included in ${\mathbf{A}}^{-1}$; ${\mathbf{H}}_{\mathbf{A}\mathbf{P}\mathbf{Y}}^{-1}$, ${\mathbf{G}}^{-1}$ approximation based on recursion of core animals in G.

*Difference between maximum likelihood function of the model fitted and the lowest value obtained for the trait (LVAR: 376,393; STAY: 2,215; STB: 61,502; GLE: 102,987), where a smaller value indicates a better fit.

Table 6.

Genetic parameters for maternal sow traits where additive genetic variances (${\sigma }_a^2$) estimated with ${\mathbf{A}}^{-1}$ are lower but not significantly than with ${\mathbf{H}}_{\mathbf{D}\mathbf{I}\mathbf{R}\mathbf{E}\mathbf{C}\mathbf{T}}^{-1}$, with permanent environmental variance (${\sigma }_{\mathrm{p}\mathrm{e}}^2$), sire variance (${\sigma }_{\mathrm{s}\mathrm{i}\mathrm{r}\mathrm{e}}^2$), and residual variance (${\sigma }_e^2$) estimates included for the calculation of repeatability (r) and heritability ($h^2$), with standard errors (± SE)1.

Trait	Method	${\sigma }_a^2$	${\sigma }_{\mathrm{p}\mathrm{e}}^2$	${\sigma }_{\mathrm{s}\mathrm{i}\mathrm{r}\mathrm{e}}^2$	${\sigma }_e^2$	r	$h^2$	-2LogL difference*
LBW	${\mathbf{A}}^{-1}$	13,535 ± 688	3,552 ± 361	—	14,172 ± 129	0.55 ± 0.01	0.43 ± 0.02	1,201
	${\mathbf{H}}_{\mathbf{D}\mathbf{I}\mathbf{R}\mathbf{E}\mathbf{C}\mathbf{T}}^{-1}$	14,284 ± 647	4,247 ± 210	—	14,268 ± 130	0.57 ± 0.01	0.44 ± 0.01	120
	${\mathbf{H}}_{\mathbf{M}\mathbf{E}\mathbf{T}\mathbf{A}}^{-1}$	14,428 ± 699	5,176 ± 194	—	14,281 ± 130	0.58 ± 0.01	0.43 ± 0.01	0
	${\mathbf{H}}_{\mathbf{A}\mathbf{P}\mathbf{Y}}^{-1}$	14,140 ± 695	5,195 ± 199	—	14,278 ± 130	0.58 ± 0.01	0.42 ± 0.01	32

1LBW, litter birth weight; ${\mathbf{A}}^{-1}$, inverted pedigree relationship matrix; ${\mathbf{H}}_{\mathbf{D}\mathbf{I}\mathbf{R}\mathbf{E}\mathbf{C}\mathbf{T}}^{-1}$, ${\mathbf{G}}^{-1}$ inverted from the full genomic relationship matrix (G); ${\mathbf{H}}_{\mathbf{M}\mathbf{E}\mathbf{T}\mathbf{A}}^{-1}$, ${\mathbf{G}}^{-1}$ inverted from the full G with metafounder included in ${\mathbf{A}}^{-1}$; ${\mathbf{H}}_{\mathbf{A}\mathbf{P}\mathbf{Y}}^{-1}$, ${\mathbf{G}}^{-1}$ approximation based on recursion of core animals in G.

*Difference between maximum likelihood function of the model fitted and the lowest value obtained for the trait (LBW: 423,684), where a smaller value indicates a better fit.

The decision to present the results within these four categories was because there was no observed patterns based on trait heritability. Whether the trait was lowly or highly heritable did not appear to relate to differences in estimated heritability between methods. Nor was there consistency based on whether the trait was lowly to highly heritable when comparing differences in variance estimates.

The additive genetic effect for TNB was significantly higher for ${\mathbf{A}}^{-1}$ (1.893) compared with ${\mathbf{H}}_{\mathbf{D}\mathbf{I}\mathbf{R}\mathbf{E}\mathbf{C}\mathbf{T}}^{-1}$ (1.540). The lower additive genetic variance for ${\mathbf{H}}_{\mathbf{D}\mathbf{I}\mathbf{R}\mathbf{E}\mathbf{C}\mathbf{T}}^{-1}$ is countered by a higher estimate for the permanent environmental component (1.426), which is lower for ${\mathbf{A}}^{-1}$ (1.124). For PIWI which did not fit a permanent environmental or service sire effect, the higher variance for the additive genetic component in ${\mathbf{A}}^{-1}$ (177.53 compared with 115.08) was moved to the residual with ${\mathbf{H}}_{\mathbf{D}\mathbf{I}\mathbf{R}\mathbf{E}\mathbf{C}\mathbf{T}}^{-1}$ (967.81 compared with 1038.80). For both traits (TNB and PIWI), there was no significant difference in additive genetic variance estimated with ${\mathbf{H}}_{\mathbf{M}\mathbf{E}\mathbf{T}\mathbf{A}}^{-1}$ or ${\mathbf{H}}_{\mathbf{A}\mathbf{P}\mathbf{Y}}^{-1}$ compared with the ${\mathbf{H}}_{\mathbf{D}\mathbf{I}\mathbf{R}\mathbf{E}\mathbf{C}\mathbf{T}}^{-1}$, nor was there any significant difference for the other variance components, repeatability, or heritability (Table 3).

The additive variance estimates were higher with ${\mathbf{A}}^{-1}$ compared with ${\mathbf{H}}_{\mathbf{D}\mathbf{I}\mathbf{R}\mathbf{E}\mathbf{C}\mathbf{T}}^{-1}$ for the traits MAX (0.151 and 0.117), LMO (16.06 and 13.45), and FRT (5.31 and 3.36), but these differences were not significant (Table 4). For MAX using the ${\mathbf{H}}_{\mathbf{D}\mathbf{I}\mathbf{R}\mathbf{E}\mathbf{C}\mathbf{T}}^{-1}$ and ${\mathbf{H}}_{\mathbf{A}\mathbf{P}\mathbf{Y}}^{-1}$ methods, the variance removed from the additive genetic component (compared with ${\mathbf{A}}^{-1}$) was moved to the residual. It was also the only trait where the additive genetic variance estimated with ${\mathbf{H}}_{\mathbf{M}\mathbf{E}\mathbf{T}\mathbf{A}}^{-1}$ (0.143) was significantly different to both ${\mathbf{H}}_{\mathbf{D}\mathbf{I}\mathbf{R}\mathbf{E}\mathbf{C}\mathbf{T}}^{-1}$ and ${\mathbf{H}}_{\mathbf{A}\mathbf{P}\mathbf{Y}}^{-1}$ (0.119). The heritability of MAX for each of the methods was low (between 0.08 and 0.11). For both LMO and FRT, the lower variance estimate for the additive genetic component corresponded with a larger estimate for the permanent environmental component. The repeatability between the four methods for both LMO and FRT were not different, nor was the heritability of LMO (between 0.06 and 0.07), however the heritability of FRT was slightly lower for the ${\mathbf{H}}_{\mathbf{D}\mathbf{I}\mathbf{R}\mathbf{E}\mathbf{C}\mathbf{T}}^{-1}$, ${\mathbf{H}}_{\mathbf{M}\mathbf{E}\mathbf{T}\mathbf{A}}^{-1}$, and ${\mathbf{H}}_{\mathbf{A}\mathbf{P}\mathbf{Y}}^{-1}$ methods compared with ${\mathbf{A}}^{-1}$ but all were very low (0.006 to 0.011).

The differences in variance estimates between ${\mathbf{A}}^{-1}$ and the three ${\mathbf{H}}^{-1}$ methods were similar for LVAR, STAY, STB, and GLE (Table 5). Any differences were insignificant and less than 10% relatively. There was still a tendency for ${\mathbf{A}}^{-1}$ to have a larger additive genetic variance and lower permanent environmental variance compared with ${\mathbf{H}}_{\mathbf{D}\mathbf{I}\mathbf{R}\mathbf{E}\mathbf{C}\mathbf{T}}^{-1}$. This was true for LVAR, STAY and GLE. The additive genetic variance for LVAR estimated with ${\mathbf{H}}_{\mathbf{M}\mathbf{E}\mathbf{T}\mathbf{A}}^{-1}$ (673) and ${\mathbf{H}}_{\mathbf{A}\mathbf{P}\mathbf{Y}}^{-1}$ (676) were higher than with ${\mathbf{A}}^{-1}$ (640) and ${\mathbf{H}}_{\mathbf{D}\mathbf{I}\mathbf{R}\mathbf{E}\mathbf{C}\mathbf{T}}^{-1}$ (637). However, this had limited impact on the repeatability (between 0.18 and 0.19) and heritability (0.12 to 0.13). The additive genetic variances estimated for STAY with ${\mathbf{A}}^{-1}$ and the three ${\mathbf{H}}^{-1}$ methods were all low, between 0.001 and 0.003, and with residual variances of between 0.068 and 0.069. There was a difference in heritability for STAY, between ${\mathbf{A}}^{-1}$ (0.044) and ${\mathbf{H}}_{\mathbf{A}\mathbf{P}\mathbf{Y}}^{-1}$ (0.015), however they were both very low and not significantly different. There was however no significant difference between ${\mathbf{H}}_{\mathbf{D}\mathbf{I}\mathbf{R}\mathbf{E}\mathbf{C}\mathbf{T}}^{-1}$, ${\mathbf{H}}_{\mathbf{M}\mathbf{E}\mathbf{T}\mathbf{A}}^{-1}$, and ${\mathbf{H}}_{\mathbf{A}\mathbf{P}\mathbf{Y}}^{-1}$. For STB, the additive genetic variances (between 0.048 and 0.052) and residual variances (0.299) were also very low across all methods. Variance estimates for the permanent environmental component (0.027 to 0.030) and service sire component (0.006) were also very low for STB, however unlike for STAY there was no significant difference in heritability between methods (0.13 to 0.14).

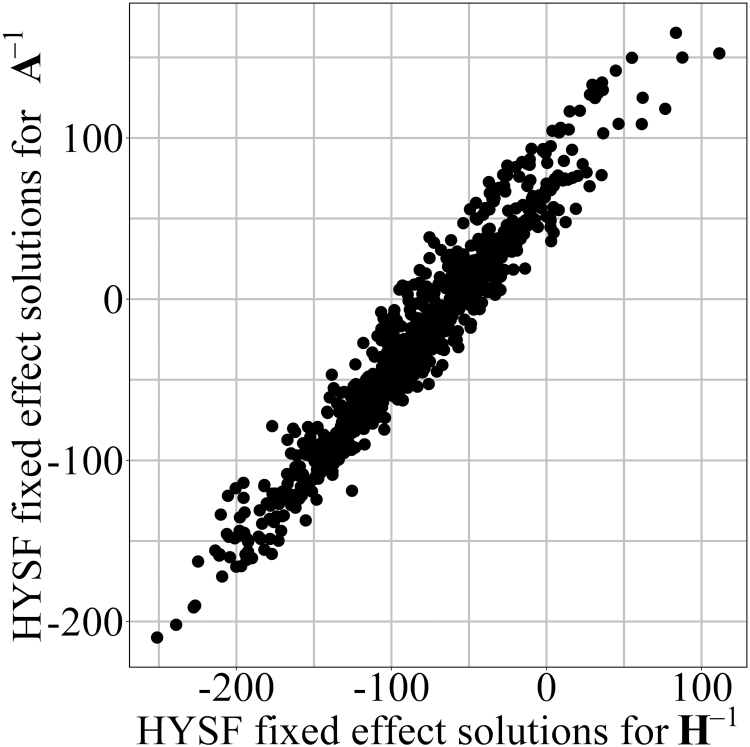
The trait LBW was the only trait to have an observably lower additive genetic variance with ${\mathbf{A}}^{-1}$ (13,535) compared with ${\mathbf{H}}_{\mathbf{D}\mathbf{I}\mathbf{R}\mathbf{E}\mathbf{C}\mathbf{T}}^{-1}$ (14,284) (Table 6). However, this difference was not significant. The permanent environmental variance estimated with ${\mathbf{A}}^{-1}$ (3,552) was also lower compared with ${\mathbf{H}}_{\mathbf{D}\mathbf{I}\mathbf{R}\mathbf{E}\mathbf{C}\mathbf{T}}^{-1}$ (4,247), this difference was significant. The difference was even greater for ${\mathbf{H}}_{\mathbf{M}\mathbf{E}\mathbf{T}\mathbf{A}}^{-1}$ (5,176) and ${\mathbf{H}}_{\mathbf{A}\mathbf{P}\mathbf{Y}}^{-1}$ (5,195). To investigate this difference further, the solutions for each of the fixed effects were plotted for the ${\mathbf{A}}^{-1}$ and ${\mathbf{H}}_{\mathbf{D}\mathbf{I}\mathbf{R}\mathbf{E}\mathbf{C}\mathbf{T}}^{-1}$. For each of the fixed effects, there was a linear relationship and a correlation approaching one, except for herd-year-season at farrowing (Figure 2). Similar results were found for ${\mathbf{H}}_{\mathbf{M}\mathbf{E}\mathbf{T}\mathbf{A}}^{-1}$ and ${\mathbf{H}}_{\mathbf{A}\mathbf{P}\mathbf{Y}}^{-1}$ when compared with ${\mathbf{A}}^{-1}$.

Figure 2.

Solutions for herd-year-season at farrowing (HYSF) when solving with either ${\mathbf{A}}^{-1}$ (inverted pedigree relationship matrix) or ${\mathbf{H}}_{\mathbf{D}\mathbf{I}\mathbf{R}\mathbf{E}\mathbf{C}\mathbf{T}}^{-1}$ (inverted relationship matrix that combines pedigree and the full genomic information).

The log-likelihood multiplied by negative two was included as an indication of model fit. The differences between the methods were very small. However, there was a limited tendency for the ${\mathbf{A}}^{-1}$ to have the poorest fit with a larger value for 7 of the 10 traits (STAY, LMO, STB, TNB, PIWI, GLE, and LBW). While the ${\mathbf{H}}_{\mathbf{M}\mathbf{E}\mathbf{T}\mathbf{A}}^{-1}$ tended to have the best fit with lowest value for 6 of the 10 traits (LMO, STB, PIWI, GLE, and LBW). There appeared to be no pattern between the heritability of the trait, or differences in variance estimates, with which method provided the best fit.

Discussion

We hypothesized that there would be limited differences in variances estimated with ${\mathbf{A}}^{-1}$ and ${\mathbf{H}}_{\mathbf{D}\mathbf{I}\mathbf{R}\mathbf{E}\mathbf{C}\mathbf{T}}^{-1}$. There was a tendency for ${\mathbf{A}}^{-1}$ to have a larger estimate for the additive genetic effect, and for ${\mathbf{H}}_{\mathbf{D}\mathbf{I}\mathbf{R}\mathbf{E}\mathbf{C}\mathbf{T}}^{-1}$ to have a larger estimate for the permanent environmental component, but these differences were small and support the first hypothesis. Our second hypothesis was that there would be no difference in variance estimates between ${\mathbf{H}}_{\mathbf{D}\mathbf{I}\mathbf{R}\mathbf{E}\mathbf{C}\mathbf{T}}^{-1}$, ${\mathbf{H}}_{\mathbf{M}\mathbf{E}\mathbf{T}\mathbf{A}}^{-1}$, and ${\mathbf{H}}_{\mathbf{A}\mathbf{P}\mathbf{Y}}^{-1}$. The second hypothesis was also supported, as there were limited but not significant differences between ${\mathbf{H}}_{\mathbf{D}\mathbf{I}\mathbf{R}\mathbf{E}\mathbf{C}\mathbf{T}}^{-1}$, ${\mathbf{H}}_{\mathbf{M}\mathbf{E}\mathbf{T}\mathbf{A}}^{-1}$, and ${\mathbf{H}}_{\mathbf{A}\mathbf{P}\mathbf{Y}}^{-1}$. The differences in heritability and repeatability are so small across the four methods, for each of the traits, that there should be limited impact on estimated breeding values from ssGBLUP (Henderson, 1984), but some minor re-ranking of animals for traits that fit a permanent environmental effect or have data structure issues are probable when moving from ${\mathbf{A}}^{-1}$ to ${\mathbf{H}}^{-1}$ methods. We also investigated if any of the methods provided a better model fit. When considering the maximum likelihood function (−2 × LogL) a value closer to zero is considered a better fit. Across the 10 traits, there was a tendency that the ${\mathbf{A}}^{-1}$ method had the poorest, and ${\mathbf{H}}_{\mathbf{M}\mathbf{E}\mathbf{T}\mathbf{A}}^{-1}$the best fit. Differences in maximum likelihood were, however, generally small, and therefore not conclusive.

Heritability

The variance component estimates for this study were similar to previous estimates published in the literature for maternal sow traits. There were some small differences between variance estimates in this study and previous estimates, which can be explained by different datasets, numbers of animals and records, breeds and lines used, and fixed effects fitted. We have compared the heritabilities calculated from the variance estimates and found the majority of the traits, including LBW, MAX, TNB, STB, and FRT, all had heritabilities within the range of previously published estimates (Roehe, 1999; Hanenberg et al., 2001; Knol et al., 2002; van Grevenhof et al., 2015; Sevillano et al., 2016). The heritability for STAY (0.04) was the only estimate to have a lower heritability compared with previous estimates (0.11 ± 0.01; van Grevenhof et al., 2015). Heritability for both LVAR (0.13) and PIWI (0.15) was higher but not significantly different to previous published estimates (0.00 to 0.08 and 0.07 to 0.14, respectively) (Hanenberg et al., 2001; Damgaard et al., 2003; Bergsma et al., 2008). While heritability of GLE (0.43) was the only trait to have a significantly higher estimate compared with previous estimates (0.25 to 0.33) (Hanenberg et al., 2001; Rydhmer et al., 2008).

Variance Estimates with Full G

The standard errors for variance components estimated with ${\mathbf{H}}_{\mathbf{D}\mathbf{I}\mathbf{R}\mathbf{E}\mathbf{C}\mathbf{T}}^{-1}$ were lower compared with ${\mathbf{A}}^{-1}$, an indication that ${\mathbf{H}}_{\mathbf{D}\mathbf{I}\mathbf{R}\mathbf{E}\mathbf{C}\mathbf{T}}^{-1}$ is a more informative matrix. The variances estimated with ${\mathbf{H}}_{\mathbf{D}\mathbf{I}\mathbf{R}\mathbf{E}\mathbf{C}\mathbf{T}}^{-1}$ tended to have lower additive genetic and high permanent environmental variances, compared with the ${\mathbf{A}}^{-1}$. This is likely due to the fact that ${\mathbf{H}}_{\mathbf{D}\mathbf{I}\mathbf{R}\mathbf{E}\mathbf{C}\mathbf{T}}^{-1}$ is a more accurate definition of the relationship between individuals due to the additional information of ${\mathbf{G}}_{\mathbf{D}\mathbf{I}\mathbf{R}\mathbf{E}\mathbf{C}\mathbf{T}}^{-1}$ (Legarra, 2016), therefore, ${\mathbf{H}}_{\mathbf{D}\mathbf{I}\mathbf{R}\mathbf{E}\mathbf{C}\mathbf{T}}^{-1}$ is likely to be better at separating the additive genetic and permanent environmental effects. Assuming that the genomic based variance component estimates are more correct, this could mean that additive genetic variances with ${\mathbf{A}}^{-1}$ may be overestimated in some cases, but these differences were limited.

Variance Estimates with Metafounders

We did not expect there to be significant differences in estimated variances between ${\mathbf{H}}_{\mathbf{D}\mathbf{I}\mathbf{R}\mathbf{E}\mathbf{C}\mathbf{T}}^{-1}$ and ${\mathbf{H}}_{\mathbf{M}\mathbf{E}\mathbf{T}\mathbf{A}}^{-1}$ methods after scaling, and this was verified for most traits. The reason for this expectation was that we already expected limited differences between ${\mathbf{A}}^{-1}$ and ${\mathbf{G}}^{-1}$ (Legarra, 2016), including metafounders should make the pedigree relationships and genomic relationships more compatible, so estimates using metafounders should be similar to ${\mathbf{A}}^{-1}$, ${\mathbf{H}}_{\mathbf{D}\mathbf{I}\mathbf{R}\mathbf{E}\mathbf{C}\mathbf{T}}^{-1}$, or both methods of defining the relationships. Increasing the number of metafounders could be beneficial for more complex data structures, over longer periods of time. In this case all unknown parents were from a single line and were considered as one metafounder. However, even by only including a single metafounder, pedigree and genomic relationship matrices are more compatible (Christensen, 2012), which improves the ability to estimate variances. The inclusion of a single metafounder in simulations has been shown to be beneficial, with more accurate EBVs (Meyer et al., 2018). However, this was not observed with additional metafounders (van Grevenhof et al., 2018), but could be used to refine ${\mathbf{H}}_{\mathbf{M}\mathbf{E}\mathbf{T}\mathbf{A}}^{-1}$ as scaling variance components becomes more difficult with more metafounders. Adding a metafounder to ${\mathbf{A}}^{-1}$ yielded the same variances, after rescaling the genetic variance. This confirms that the scaling factor as proposed by (Legarra et al., 2015) indeed is correct. It also shows that adding metafounders to ${\mathbf{A}}^{-1}$ for analyses based on pedigree only has no practical benefit, simply because there are no genomic relationships that need to be made compatible with pedigree relationships.

Variance Estimates with APY

It has already been shown that the ${\mathbf{G}}_{\mathbf{A}\mathbf{P}\mathbf{Y}}^{-1}$ is an accurate approximation of the ${\mathbf{G}}_{\mathbf{D}\mathbf{I}\mathbf{R}\mathbf{E}\mathbf{C}\mathbf{T}}^{-1}$ (Misztal et al., 2014, 2016; Bradford et al., 2017). Therefore, variances estimated with ${\mathbf{H}}_{\mathbf{A}\mathbf{P}\mathbf{Y}}^{-1}$ and ${\mathbf{H}}_{\mathbf{D}\mathbf{I}\mathbf{R}\mathbf{E}\mathbf{C}\mathbf{T}}^{-1}$ were expected to be similar. The results in this study support this, with there being no traits that had a significantly different additive genetic variance, and only LBW having a significantly different permanent environmental variance. The number of core animals selected (4,764) was based on the principal components analysis of ${\mathbf{G}}_{\mathbf{D}\mathbf{I}\mathbf{R}\mathbf{E}\mathbf{C}\mathbf{T}}^{-1}$. The similar results between ${\mathbf{H}}_{\mathbf{D}\mathbf{I}\mathbf{R}\mathbf{E}\mathbf{C}\mathbf{T}}^{-1}$ and ${\mathbf{H}}_{\mathbf{A}\mathbf{P}\mathbf{Y}}^{-1}$ observed here, confirmed that the number of allocated core animals was sufficient.

The main benefit of using ${\mathbf{H}}_{\mathbf{A}\mathbf{P}\mathbf{Y}}^{-1}$ compared with ${\mathbf{H}}_{\mathbf{D}\mathbf{I}\mathbf{R}\mathbf{E}\mathbf{C}\mathbf{T}}^{-1}$ was the reduced computational requirement of building ${\mathbf{G}}_{\mathbf{A}\mathbf{P}\mathbf{Y}}^{-1}$ compared with ${\mathbf{G}}_{\mathbf{D}\mathbf{I}\mathbf{R}\mathbf{E}\mathbf{C}\mathbf{T}}^{-1}$. For variance component estimation with REML, there was no benefit to using ${\mathbf{H}}_{\mathbf{A}\mathbf{P}\mathbf{Y}}^{-1}$ as the potential advantage of the sparse ${\mathbf{G}}_{\mathbf{A}\mathbf{P}\mathbf{Y}}^{-1}$, was canceled by the ${\mathbf{A}}_{22}^{-1}$ being dense. To utilize the sparsity of ${\mathbf{G}}_{\mathbf{A}\mathbf{P}\mathbf{Y}}^{-1}$ and improve the efficiency of variance component estimation, adapted software could be used that avoids the inversion of the left hand side such as Gibbs sampling (Misztal et al., 2002), or by using a sparse approximation of ${\mathbf{A}}_{22}^{-1}$ (Faux and Gengler, 2015), to preserve the sparsity of ${\mathbf{G}}_{\mathbf{A}\mathbf{P}\mathbf{Y}}^{-1}$.

Variance Estimates for LBW

The only trait to have a lower additive genetic variance with ${\mathbf{A}}^{-1}$ compared with each of the ${\mathbf{H}}^{-1}$ methods was LBW. We hypothesized that the additive genetic and permanent environmental variances both being higher with ${\mathbf{H}}^{-1}$ could be due to confounding between some genetic component and a fixed effect. All animals phenotyped were also genotyped, and there was a consistent lower fixed effect for herd-year-season at farrowing with ${\mathbf{H}}^{-1}$ methods. There is likely some confounding between some genetic component not captured by the pedigree and herd-year-season at farrowing. The other traits that fit this fixed effect (PIWI, LVAR, LMO, TNB, STB, and GLE) tended to have lower estimates for permanent environmental variance between ${\mathbf{A}}^{-1}$ and any of the ${\mathbf{H}}^{-1}$ matrices, but unlike LBW the additive genetic variance was either not significantly different or greater with ${\mathbf{A}}^{-1}$ compared with and any of the ${\mathbf{H}}^{-1}$ matrices. An alternative explanation is LBW is treated as a trait of the sow, and by not fitting the genetic effect for piglet (assuming the genetic correlation between the sow and piglet trait is positive) may lead to inflation of the genetic variance for the sow trait (Roehe, 1999). It is unlikely that the ${\mathbf{H}}^{-1}$ can better account for this as it would be expected to correspond with a decrease in either additive genetic or permanent environmental variances. Instead there is no difference in residual variance with ${\mathbf{H}}^{-1}$, with a larger permanent environmental variance with ${\mathbf{H}}_{\mathbf{D}\mathbf{I}\mathbf{R}\mathbf{E}\mathbf{C}\mathbf{T}}^{-1}$ and even higher with ${\mathbf{H}}_{\mathbf{M}\mathbf{E}\mathbf{T}\mathbf{A}}^{-1}$ and ${\mathbf{H}}_{\mathbf{A}\mathbf{P}\mathbf{Y}}^{-1}$. This leaves confounding between some genetic component and a fixed effect as the best explanation for the difference between ${\mathbf{A}}^{-1}$ and ${\mathbf{H}}_{\mathbf{D}\mathbf{I}\mathbf{R}\mathbf{E}\mathbf{C}\mathbf{T}}^{-1}$, which is exacerbated by ${\mathbf{H}}_{\mathbf{M}\mathbf{E}\mathbf{T}\mathbf{A}}^{-1}$ and ${\mathbf{H}}_{\mathbf{A}\mathbf{P}\mathbf{Y}}^{-1}$. With the differences in variance estimates for LBW, there is limited impact on the repeatability or heritability, suggesting limited impact on EBVs (Henderson, 1984).

Possible Reasons for Different Variance Estimates

It is likely that some of the differences in variance estimates observed are due to the estimation process and also to factors not investigated in this study. The animals selected for genotyping were unlikely random, with a bias for animals in recent generations being genotyped (Figure 1). If within generations predominantly the better animals are genotyped, then this would break the assumption of random Mendelian sampling and bias the results from ${\mathbf{A}}^{-1}$ (Patry and Ducrocq, 2011; VanRaden, 2012; Masuda et al., 2018). The too low variance of observed Mendelian Sampling terms is expected to lead to decreased, and thus underestimated, genetic variances with ${\mathbf{A}}^{-1}$ (Gao et al., 2019), while use of genomic information provides a handle on the Mendelian Sampling terms and thus is expected to lead to less biased estimates as a result from nonrandom genotyping. Across the traits analyzed here, there was a tendency that with ${\mathbf{A}}^{-1}$ higher rather than lower genetic variances were estimated, which suggests that any differences observed here in estimated genetic variances between models is unlikely due to the genotyping strategy. Furthermore, there were no animals with only phenotypes and pedigree information, as the data were limited to animals with genotypes and their ancestors. Finally, the differences observed with ${\mathbf{H}}_{\mathbf{M}\mathbf{E}\mathbf{T}\mathbf{A}}^{-1}$ could be due to the approximation of the self-relationship of the metafounder (Garcia-Baccino et al., 2017).

Application and Recommendations

Variance component estimations may continue to be estimated with ${\mathbf{A}}^{-1}$, as there is limited differences between methods and it remains the easiest method to implement. For some traits, it could be appropriate to investigate variance component estimation with one of the ${\mathbf{H}}^{-1}$ methods. Complex traits, traits with large datasets that need sub-setting, and traits that fit a permanent environmental effect, could benefit from variance component estimation using ${\mathbf{H}}^{-1}$. Further investigation and application to such traits could help to understand the differences between ${\mathbf{A}}^{-1}$ and ${\mathbf{G}}^{-1}$, and to better define the models used for calculating EBVs of these traits. To the authors knowledge, this is the only study to compare variance estimates between the four methods of defining the relationship matrix (${\mathbf{A}}^{-1}$,${\mathbf{H}}_{\mathbf{D}\mathbf{I}\mathbf{R}\mathbf{E}\mathbf{C}\mathbf{T}}^{-1}$,${\mathbf{H}}_{\mathbf{M}\mathbf{E}\mathbf{T}\mathbf{A}}^{-1}$, and ${\mathbf{H}}_{\mathbf{A}\mathbf{P}\mathbf{Y}}^{-1}$), and with the use of industry data. In this study, a single maternal large white sow line was used, and the number of animals genotyped was limited to 10,000. However, we have no reason to believe that these results and recommendations are not applicable to other lines, breeds, species, or a larger number of genotyped animals.

Conflict of interest statement

The authors declare that there is no conflict of interest.