The Development of Bimanual Coordination Across Toddlerhood

Abstract

As one of the hallmarks of human activity and cultural achievement, bimanual coordination has been the focus of research efforts in multiple fields of inquiry. Since the seminal work of Cohen (1971) and Kelso and colleagues (Haken, Kelso, & Bunz, 1985; Kelso, Southard, & Goodman, 1979), bimanual action has served as a model system used to investigate the role of cortical, perceptual, cognitive, and situational underpinnings of coordinated movement sequences (e.g., Bingham, 2004; Oliveira & Ivry, 2008). This work has been guided primarily by dynamical systems theory in general, and by the formal Haken-Kelso-Bunz (HKB; 1985) model of bimanual coordination, in particular. The HKB model describes the self-organizing relationship between a coordinated movement pattern and the underlying parameters that support that pattern, and can also be used to conceptualize and test predictions of how changes in coordination occur.

Much of the work investigating bimanual control under the HKB model has been conducted with adults who are acting over time periods of a few seconds to a few days However, there are also changes in bimanual control that occur over far longer time spans, including those that emerge across childhood and into adolescence (e.g. Wolff, Kotwica, & Obregon, 1998). Using the formal HKB model as a starting point, we analyzed the ontogenetic emergence of a particular pattern of bimanual coordination, specifically, the anti-phase (or inverse oscillatory motion) coordination pattern between the upper limbs in toddlers who are performing a drumming task (see Brakke, Fragaszy, Simpson, Hoy & Cummins-Sebree, 2007).

This study represents a first attempt to document the emergence of the anti-phase pattern by examining both microgenetic and ontogenetic patterns of change in bimanual activity. We report the results of a longitudinal study in which seven toddlers engaged monthly in a bimanual drumming task from 15 to 27 months of age. On some trials, an adult modeled in-phase or anti-phase action; on other trials, no action was modeled. We documented the motion dynamics accompanying the emergence of the anti-phase bimanual coordination pattern by assessing bout-to-bout and month-to-month changes in several movement parameters—oscillation frequency, amplitude ratio of the drumsticks, initial position of the limbs to begin bouts, and primary arm-joint involvement. These parameters provided a good starting point to understand how toddlers explore movement space in order to perform the anti-phase coordination pattern more stably.

Trained research assistants used Motus software to isolate each bout of drumming and to digitize the movement of the two drumstick heads relative to the stationary drum surface. Because we were primarily interested in the vertical movement of the drumsticks that were held in the child’s hands, we relied on 2-dimensional analyses and analyzed data that were tracked by a single camera. We used Linear Mixed Effects analyses as well as qualitative analyses for each participant to help elucidate the emergence and stability of the child’s use of anti-phase coordination. This approach facilitated descriptions of individual pathways of behavior that are possible only with longitudinal designs such as the one used here.

Our analyses indicated that toddlers who were learning to produce anti-phase motion in this context employed a variety of strategies to adjust the topography of their action. Specifically, as we hypothesized, toddlers differentially exploited oscillation frequency and movement amplitude to support change to anti-phase action, which briefly appeared as early as 15 months of age but did not become relatively stable until approximately 20 months of age. We found evidence that many toddlers reduced oscillation frequency before transitioning from in-phase to anti-phase drumming. Toddlers also used different means of momentarily modulating the amplitude ratio between limbs to allow a change in coordination from in-phase to anti-phase. Nevertheless, these oscillation-frequency and amplitude-ratio strategies were interspersed by periods of non-systematic exploration both within and between bouts of practice. We also observed that toddlers sometimes changed their initial limb positions to start a bout or altered which primary arm joints they used when drumming. When they enacted these changes, the toddlers increased performance of the anti-phase coordination pattern in their drumming. However, we found no evidence of systematic exploration with these changes in limb position and joint employment, suggesting that the toddlers did not intentionally employ these strategies to improve their performance on the task.

Although bimanual drumming represents a highly specific behavior, our examination of the mechanisms underlying emergence of the anti-phase coordination pattern in this context is one of the missing pieces needed to understand the development of motor coordination more broadly. Our results document that the anti-phase coordination pattern emerges and stabilizes through modulation of the dynamics of the movement and change of the attractor landscape (i.e., the motor repertoire). Consistent with literatures in motor control, motor learning, and skill development, our results suggest that the acquisition of movements in ontogenetic development can be thought as exploration of the emergent dynamics of perception and action. This conclusion is commensurate with a systemic approach to motor development in which functional dynamics, rather than specific structures, provide the basis for understanding developmental changes in skill. Based on our results as well as the relevant previous empirical literature, we present a conceptual model that incorporates developmental dynamics into the HKB model. This conceptual model calls for new investigations using a dynamical systems approach which allows direct control of movement parameters, and which builds on the methods and phenomena that we have described in the current work.

1. Why Study the Early Development of Rhythmic Bimanual Coordination?

How does motor development happen? How do young children explore emerging forms of coordination? What are the mechanisms that toddlers use to change their behavior? And how do we capture different timescales of change when we address these questions? In this monograph, we seek to understand the development of motor coordination early in life. Reporting the findings of a detailed longitudinal study, we describe the emergence of a specific bimanual coordination pattern in toddlers assessed each month from 15 to 27 months of age and examine the means through which toddlers explore movement possibilities to facilitate performance of this pattern.

Why should we be concerned with this phenomenon and address it in the way that we did? In this chapter we establish the challenges and value of motor development research with toddlers. We then argue that bimanual coordination, as the basis of a wealth of daily activities, provides a good means of understanding organization at a systems level. By understanding the exploratory process underlying emergence of a bimanual coordination pattern, we can understand more general processes of change observed in development.

1.1. Facing the challenges of early skill development

Scientists who study childhood motor development have documented a wealth of behavioral changes that occur during the first few years of life as new skills emerge and are honed. Investigators have also established a number of the contexts in which these changes occur and the correlates, perhaps even causes, of development. Where research has been less thorough is in exploring how new skill patterns emerge – the mechanisms by which skill development occurs and the agentic actions that young children employ to explore new action possibilities.

There are good reasons for this gap. Early childhood development can be messy – no two children develop in exactly the same way with exactly the same timing in exactly the same context. And emergence of a new skill within a particular child’s repertoire may not be neat and linear; rather, it may rely on irregular bouts of exploratory activity encompassing a range of movements in different contexts. Added to the inherent challenges of asking young children – for example, toddlers -- to perform particular movements in particular ways, this set of circumstances makes unraveling the mechanisms of skill development in a laboratory research setting a complex task.

Note, however, that these challenges should not serve as excuses to stop researchers from studying this stage of life. The irregularities of toddler behavior represent parts of the developmental process rather than problems per se. The human body demonstrates a rich set of important changes in all areas of development at this age range. Thus, we must find tools that encompass, rather than exclude, a variety of behavioral processes. The study of these phenomena is necessary if one wants to understand the human motor system and the variety of complex factors that interact to produce change in this system.

Fortunately, behavioral scientists are adept at developing theoretical and analytical tools for addressing complex challenges. One of the frameworks for addressing such problems that has been applied over recent decades in a wide range of disciplines, including human development, is provided by Dynamical Systems Theory (DST; see Thelen & Smith, 1994), which views the developing human body as a self-organizing system in which behavior emerges from the cooperative interaction of a number of subsystems and contextual factors. DST-based approaches focus on the process of change within complex systems and embrace the individual differences and nonlinear processes that characterize much of ontogeny. In this monograph, we apply a DST framework to the early development of a motor skill that children typically enjoy and that lends itself well to this approach. This skill is bimanual drumming. In selecting this behavior, we also provide an ontogenetic test of a model that is widely used in studies of short-term bimanual coordination with older children and adults. The rationale for our research approach and hypotheses is grounded in part in this work, so we provide an introduction to the theoretical framework here. We incorporate relevant findings from past developmental studies in Chapter 2 and research leading to our specific hypotheses in Chapter 3.

1.2. The coupled oscillator model of cyclic bimanual coordination

Much of human activity and achievement relies on coordinated manual activity; it is essential for using many tools, creating music and art, and interacting with the physical world. Unless one has an injury or is involved in learning a new skill, someone engaging in manual activity may give little thought to the unique adaptability that human beings, as a species, have via the ability to flexibly coordinate the actions of the two hands.

A class of actions within bimanual coordination that has received substantial research attention includes rhythmic, or periodic, bimanual actions such as finger-tapping or pendulum-swinging. This class of behaviors has become a model system in the perception-action-based study of motor control and development (Bingham, 2004). Such periodic behaviors support a variety of analyses focused on stability and change because they can be performed continuously and with great precision, yet can be perturbed, or disrupted, if one experimentally alters the conditions under which the action is performed. Additionally, bimanual periodic movements provide windows into intrinsic coupling, or linking of the two limbs through reciprocal neural and perceptual feedback between muscle groups when they move together. As we will discuss, these characteristics allowed investigators to develop formal models that are in line with long-established principles and concepts from physics. These models provide predictions that guide behavioral experiments.

One of the strengths of the bimanual action model as studied from a DST approach is that it gives insights on how the system coordinates many degrees of freedom to accomplish a task goal. That is, a rhythmic bimanual coordination task requiring that both limbs oscillate at a particular frequency demands the cooperation of multiple neural, muscular, cognitive, and motivational systems within a particular set of contextual constraints.

In these tasks, we often observe that the limbs are not independent of each other; rather, they demonstrate coupling, a bidirectional influence of motion from one limb to the other. This interdependence allows scientists to mathematically model the bilateral limbs or digits as coupled oscillators. This means that, as the limbs simultaneously move within a repeating cycle of behavior, they reciprocally provide feedback to each other and entrain their respective movements into a coordinated pattern – in other words, the behaviors of the two bodily systems are linked together to produce a single larger behavioral system. It is through examination of the oscillation patterns that emerge that researchers can, then, have access to the many levels of cooperation at work. Several research programs have focused on exploring questions of motor learning and control by investigating different parameters associated with rhythmic bimanual activity (see, e.g., Beek, Peper, & Daffertshofer, 2002, Kostrubiec, Zanone, Fuchs, & Kelso, 2012).

For the reader who may be less familiar with this area of inquiry, we introduce an exercise that illustrates the oscillator model and simulates the challenge faced by the toddler participants in the research we report in this monograph. Our demonstration characterizes the upper limbs as a pair of biomechanical oscillators that are most comfortable moving in synchrony. To illustrate this, one can simultaneously draw circles in the air in front one’s chest (The reader is encouraged to try this action.) Here, the oscillations take a circular form. Chances are, when performing this action, one’s arms move in synchrony; that is, homologous muscle groups are activated so that the two hands move in mirror-image to one another. The arms are, in effect, coupled because the movement of each arm informs the movement of the other, and they act as oscillators because the limbs are repeating the same cycle of movement and returning to relatively fixed points in space within that cycle. One can perform this action for an indefinite time, and the coordination pattern will likely remain stable even as there are variations in the speed and magnitude of the air-circles.

In contrast to the mirror-image movements described above, if one breaks synchrony by starting one hand at the top of the circle and the other at the bottom, so that one hand is moving up while the other is moving down, what happens? Chances are that, even though each limb is creating the same motion as it did before, this is a more difficult coordination pattern to maintain. The limbs may be moving more slowly, or drawing sloppier circles, and one may feel the need to pay more attention to the action to maintain the coordination pattern. In fact, if the actor tries to speed up or stop paying attention, the hands may back into the mirror-image synchronous pattern after just a few seconds. Similarly, we expect that moving the hands with a faster pace in the inverse circular pattern will yield more variability in performance. The decreased level of stability leads to difficulty in maintaining the inverse, or anti-phase, pattern for long periods. Thus, modifying some parameters of the task, such as attentional focus or the pace of circle drawing, will facilitate or hinder individuals’ performance of the task. To better perform inverse circle-drawing, then, one must perceive how parameters of the movement relate to the dynamics and stability of the movement itself.

This exercise illustrates the existing coordination tendencies, or intrinsic dynamics, that support particular stable actions in the human motor repertoire. Biomechanical and attentional systems, for example, easily cooperate when one moves the hands in phase with each other. Our demonstration also highlights the importance that learning has in motor-skill acquisition. Adults with years of experience are generally capable of producing a wide variety of coordinated actions with two hands. Yet, the same adults may find it challenging to keep both hands moving in the relatively simple pattern required by the new air-circle task. Note, however, that use of the term ‘intrinsic’ within DST does not mean that the existing dynamics of an individual’s motor system are deterministic or inflexible. Rather, intrinsic coordination tendencies denote the complex interaction of the various subsystems that self-organize to support stable performance of a particular action given the demands of the task at hand and surrounding contextual factors. Although the intrinsic dynamics that exist at a particular point of time may direct movement toward an action that is already stable in one’s repertoire, the organization of these dynamics can be modified with exposure to new behavior patterns. Thus, in our demonstration the more difficult inverse-circling pattern might become easier with practice and a return to the synchronous pattern would occur less quickly as the new anti-phase coordination pattern becomes more stable.

Drumming presents a similar challenge as the air-circle task to toddlers between one and two years of age. For older children and adults, both mirror-image and inverse-motion percussive movements represent relatively stable action patterns – in fact, people of these ages may find it difficult to resist the temptation to beat out a simple tattoo when stick-like objects are placed in their hands. Toddlers, however, are still exploring how to use their arms and hands flexibly to execute efficient coordinated actions even within an action context as simple as two-handed drumming. How they might do so in this context over time is the focus of the research we report in this monograph.

In line with the proposition that the study of bimanual control can provide insights about underlying subsystems at work in developmental change, we analyzed and report the emergence of the anti-phase (or inverse oscillatory motion) coordination pattern between the upper limbs of toddlers who are performing a drumming task. We examine, specifically, how toddlers explore different mechanisms of enacting a shift from in-phase to anti-phase activity over short or long timeframes. Just as adults must perceive the dynamics of making circles in the air in order to change or stabilize their behavior in the exercise above, we believe toddlers should perceive the dynamics of their movement in a drumming task and modulate its parameters accordingly. There are many potential ways in which toddlers might do this, and different toddlers may use different means of exploration. Our research questions and hypotheses derive from the following considerations, which will be further explored in the next two chapters of this monograph.

In order to test a model with specific hypotheses, we needed to identify potential parameters that toddlers might use to modify their action and then determine which of these to analyze. Successful bimanual drumming requires controlling the position, movement speed, and amplitude of the upper limbs, with coordinated motion of the shoulder, elbow, and wrist joints along with postural support from the lower body and torso. In addition, behaviors reflecting cognitive processes such as visual attention and, perhaps, deferred imitation likely play a role in how the behavior is performed. All these factors interact with the child’s motivation for performing the action – is it to master something new, to make noise, or to play a game with the model?

We based our choice of parameters on the dynamical systems approach to motor behavior. As highlighted earlier, rhythmic bimanual coordination has been formalized in a number of models allowing direct predictions (see Chapter 3). In this study, we were guided by the most recognized model of couple oscillators in human control: the HKB model (Haken, et al., 1985; discussed more fully in Chapter 3). This model allows us to predict which parameters toddlers would explore in order to perceive the dynamics of the movement and, then, perform the non-stable anti-phase pattern. Thus, from this model and related literature, we examined whether toddlers explored oscillation frequency, amplitude ratio between limbs, initial positional conditions of the limbs, and joint motion, in order to perform the anti-phase pattern. The rationales for why each of these parameters was chosen and how these parameters relate to the dynamics of the movement are presented in Chapter 3.

1.3. The role of variability in the exploration of movement

An important question that is tied to the discussion of developmental change is how such change occurs. Theories of learning and development, as well as work in applied areas, rely on knowledge of the principles and mechanisms of change in order to properly form hypotheses assess outcomes, and create interventions. We believe that, as discussed, relevant knowledge is still lacking because past literature provides only limited empirical examination of how changes occur in this early age.

Thus, a question that is directly related to how change is enacted and tied to our thinking on exploration of parameters is whether children’s exploration of the relevant movement space is systematic, or whether it essentially represents random or noisy exploration. Variability is a cornerstone of behavioral change within dynamical systems theory. Some authors have assigned initial unsystematic variability a substantive role in the later selection of preferred movement patterns (see Hadders-Algra, Brogren, & Forssberg, 1996). Exploiting this variability may yield interesting or efficient new forms of behavior within particular contexts, which quickly become preferred and explored more systematically (Kahrs, Jung, & Lockman, 2013; Thelen & Ulrich, 1991).

According to Thelen and colleagues (Thelen, Corbetta, Kamm, Spencer, Schneider, & Zernicke, 1993) and others (Fitzpatrick, Schmidt, & Lockman, 1996; Forrester & Whitall, 2000), skilled action is characterized by stable coupling, whereas unskilled action represents subsystems that are more loosely assembled. The latter allows greater variability and instability, which facilitates the exploration necessary for a behavioral transition (in our case, a phase shift) to occur. In other words, instabilities are associated with transitions, and skill development is often characterized by alternating periods of stability and instability (Forrester & Whitall, 2000). Note, however, that instability of performance does not require random exploration of underlying parameters; rather, such instability may result from systematic exploration of parameters. We hypothesized that toddlers would engage in systematic exploration of different parameters that lead to instabilities in the coupling between hands which, in turn, would facilitate exploration and practice of the inverse, or anti-phase, coordination pattern.

1.4. Contributions of this Monograph

We present here a piece of work that goes beyond common investigation of developmental phenomena. We explore different timescales of change supporting toddlers’ perception of movement dynamics through action exploration. Exploration of movement parameters can occur within or between trials performed close in time, and it can also occur through actions performed across different months as well. Our analyses allow us to observe not only general (group-based) but also individual-based aspects of change. We examine how the group of developing toddlers, as a whole, relies on exploration of specific movement parameters and how each individual takes advantage of the explored parameters. Finally, we use our empirical work as a substantive domain in which to consider the more general question of how exploration is entailed in development.

Although earlier motor development literature has provided evidence of exploration and search in terms of movement parameters directed toward achieving a given task goal (Angulo-Kinzler, 2001; Fitzpatrick, et al., 1996; Goldfield, 1995; Thelen et al., 1993), we hypothesized specific patterns of change that go beyond processes that have previously been investigated (see Chapter 3). Our enhanced analyses, although not in themselves always definitive, provide a clearer picture of how relevant experiences during motor development are constrained and lead to increased complexity in motor behavior at both individual and group levels. Our findings also suggest the importance of a new generation of motor-development research that is focused on mechanisms of change through the course of skill development.

Anticipating a diverse readership for this volume, in Chapter 2 we begin by offering a brief review of the developmental research on bimanual actions that informs our investigation and in Chapter 3 we include an introduction to dynamical systems theory as applied to the study of motor coordination. Also in Chapter 3, we present the foundational model for rhythmic bimanual coordination and propose a conceptual model that guides our hypotheses and analyses. In Chapters 4 through 9, we empirically address our conceptual model with a series of analyses focusing on different movement parameters. In Chapter 10 we provide a summary of our findings, discuss the limitations of the project as an initial developmental test of this model, and point the way toward future research initiatives that can address remaining questions relevant to toddlers’ emerging coordination in this context.

2. What We Know About Early Development of Bimanual Coordination

2.1. Motor Skills as Problems of Development

Infancy and toddlerhood are of particular interest in the study of motor development because of the dramatic and relatively rapid changes in motor skills that emerge over the first few years of life. One of the challenges in applying adult-based theories of motor control to young children derives from the dramatically greater within- and between-child variability in movement exhibited during development in childhood than during adulthood (Maruyama, Dineva, Spencer, & Schӧner, 2014; Newell, Liu, & Mayer-Kress, 2001). The dynamical systems approach to motor behavior has facilitated investigation of developmental processes in children by focusing on the individual process of change over different timescales (Molenaar, Lerner, & Newell, 2013; Newell et al., 2001). According to a dynamical systems view, the performance of a coordinated action such as inverse, or anti-phase, drumming results from interactions among the experience and characteristics of the individual, the environment in which the movement is performed, and the requirements of the task to which the movement is directed (Kelso, 1995; Newell, 1986; Schöner & Kelso, 1988; Thelen & Smith, 1994).

2.2. Understanding the Emergence of Behaviors through Practice and Maturation

Throughout toddlerhood, individuals are growing considerably and undergoing many changes in their cognitive, perceptual, and motoric abilities. Understanding processes that lead to changes in the performance of specific behaviors throughout the life-span is a primary goal of inquiry in the field of motor development (Clark & Whitall, 1989; Newell, Liu, & Mayer-Kress, 2003). Through many years of life, individuals practice new skills while maturation and growth processes are occurring in the body. In a demonstration of this point, Adolph et al. (2012) longitudinally recorded toddlers taking thousands of steps, and dozens of falls, each day between the ages of 12 and 19 months. Cole, Robinson, and Adolph (2016) found that these steps were distributed across nearly two hundred bouts of walking per day, on average. A similar record of activity would, we believe, likely be found in children’s manual activity. Young children are, indeed, active explorers of their world and have ample opportunity to practice the different skills they need to effectively interact with it.

Practice may be considered a search for a solution to a given problem, as posited in multiple subdisciplines of motor behavior, from control (Bernstein, 1967), to learning (Newell, Kugler, Van Emmerik, & Mcdonald, 1989) and development (Connolly, 1977; Thelen et al., 1993). It is imperative, therefore, to understand how such practice contributes to the solution, or resulting behaviors within and across time-scales. Integrated longitudinal analyses that incorporate both microgenetic and ontogenetic change processes in behavior reflect the practice that individuals usually apply on their own when exploring new movement possibilities (e.g. Thelen et al., 1993). Observations of toddlers in a variety of environments, such as those made by Adolph et al. (2012) support the validity of interpretations that arise from such work. Longitudinal designs illuminate trajectories of development within individuals and, through aggregation, provide portraits of the varying developmental pathways that children experience over time. Such longitudinal study can capture variables that may influence the skill of interest along multiple, nested, timescales of development (Newell et al., 2003), from moment-to-moment (microgenetic) to month-to-month (ontogenetic). Examining behavior across these nested timescales allows investigators to exploit the benefits of longitudinal study while capturing the phenomena associated with practice in the moment.

As an additional benefit, longitudinal observation of practice can elucidate the underlying cognitive, perceptual, and motoric abilities (from now on, organismic constraints) that are at play at the moment the individual performs a task within a particular context. Conversely, a novel task that is presented just once to different children of different ages (i.e., in a cross-sectional design) might reveal only how children in a given age group initially perform a behavior when confronted with a new action context. By allowing repeated practice to occur within a research design, one can examine how individuals employ iterative problem-solving procedures to gain expertise with the task, becoming more efficient and/or more flexible. The detailed level of observation that we use in our work allows us to learn how individuals, across time, solve movement problems related to a particular task goal. We can thereby learn how children explore the problem space and identify the solutions that emerge from their exploration processes.

A few investigators, including Esther Thelen and colleagues, have longitudinally examined kinematic development of different motor skills from a dynamical systems perspective. For example, Thelen (Thelen & Ulrich, 1991; also see Thelen & Smith, 1994) examined infants’ stepping movements and identified flexor dominance as a parameter that was modulated to allow emergence of stable alternating steps, which in turn supported later locomotor skills. Also, Thelen et al. (1993) demonstrated that the emergence of reaching and grasping during the third or fourth month of life occurs as a process of modifying an infant’s existing movement tendencies to the newly required coordinated movement of reaching for a toy. For some of Thelen et al.’s infants, this meant adding additional energy to the system to generate arm extensions large enough to reach the toy. For others, a successful reach involved stiffening the arms to damp down the magnitude of their oscillatory arm movements to find the appropriate trajectory to reach the toy. Thelen and colleagues emphasized the variability of movement trajectories, both between and within infants, that allowed each of their infants to generate solutions to the reaching problem and also resulted in those solutions being unique to individual infants.

Missing from past research on early motor skill development, however, is longitudinal study of the rhythmic bimanual coordination tasks—tasks that have been a staple of adult motor control and learning research (see Adolph & Franchack, 2017 for a review). Within the literature on school-aged children, there has been some focus on bimanual coordination using a variety of cyclic tasks (de Boer, Peper, & Beek, 2012; Fitzpatrick, et al., 1996; Lantero & Ringenbach, 2007; Mori, Iteya, & Gabbard, 2007; Njiokiktjien, De Sonneville, Hessels, Kurgansky, Vildavsky & Vranken, 1997; Ringenbach & Amazeen, 2005; Robertson, 2001; Wolff et al., 1998). However, although many of these projects have adopted a dynamical systems approach, they have used cross-sectional designs that do not integrate multiple timescales in their analyses in the ways offered in the infant development work discussed above.

Thus, even after many years of research on rhythmic bimanual coordination, important questions remain that touch directly on central themes of development. We still do not understand, for example, why the anti-phase coordination pattern is the first, and often only, additional pattern that is stable throughout life besides the in-phase motion. Also, we know little about the developmental process of the coordination pattern itself. That is, how do toddlers break the intrinsic tendency to perform the in-phase pattern within a particular context to perform the anti-phase pattern? This question can be generalized to a large range of coordination patterns.

Although there have been studies focused on the acquisition of new patterns of bimanual coordination in adults (e.g., Kennedy, Wang, Panzer, & Shea, 2016; Kovacs, Buchanan & Shea, 2009; Zanone & Kelso, 1992), these have been focused on only initial and final states of individuals’ coordination patterns over short time periods, and have not identified what underlying processes allow those individuals to break intrinsic coupling tendencies and learn something new. In contrast, it is our contention that studies of motor development must consider the extant initial tendencies of the system that have emerged from an individual’s maturational and experiential background, the properties of the task and how these properties constrain the opportunities for action, and the perceptual variables that afford and channel behavior. For these goals, it is necessary to have a conceptual model that goes beyond observation of initial and end states of coordination and addresses the exploration of dynamics. We present such a model in Chapter 3.

With our work we aim to examine the early emergence of a bimanual skill—anti-phase drumming—as a function of experience and growth. In keeping with the theoretical considerations discussed so far, we investigated the strategies that toddlers employ to practice and increase stability in a rhythmic bimanual coordination pattern (i.e., the anti-phase pattern) between 15 and 27 months of age. We studied the emergence of the anti-phase drumming pattern through microgenetic motion-capture and analyses during monthly sessions that occurred over the months during which we observed the toddlers. This procedure allowed us to investigate changes in behavior from moment to moment during a bout of action, across action bouts (or trials) within each assessment session, and over the course of months as children mature. Incorporating these nested time scales in which children grow and behave is critical to understanding the emergence and stabilization of new skills (Adolph & Berger, 2006; Newell, et al., 2003; Thelen & Smith, 1994).

When adapting a formal theoretical model (the HKB model – see Chapter 3 for a full discussion) to a developmental framework, it is important to capture the emergence of a behavior at the appropriate time and also to assess a task context that is appropriate to the paradigm. The same principles that have been supported during short-term motor control should apply over longer timeframes of development (Newell et al. 2001, 2003; Thelen & Smith, 1994). In bringing together literatures focused on short-term motor control and longer-term emergence of motor skill, we thus face the challenges of selecting a task and age range that will allow the necessary analyses. Participating in a study of bimanual control typically requires that participants have the abilities to follow precise directions, regulate attention, and engage fine- motor dexterity – none of which are attributes common among children in their formative toddler years. We have, however, considered toddlers’ repertoires and identified a behavior—drumming—that fulfills the requirements of the HKB model and allows us to examine the role of key movement parameters in effecting changes in coordination patterns within and across monthly assessment sessions. We now explore relevant research on toddlers’ bimanual skill and provide the rationale for our age range and task context.

2.3. Early Development of Bimanual Coordination: Overview

The bimanual testing paradigms developed with adults, particularly those employing drawing tasks, have been extended for work with children as young as 3 years of age (e.g., de Boer et al., 2012; Fagard, Hardy-Leger, Kervella, & Marks, 2001; Fitzpatrick et al., 1996; Lanterno & Ringenbach, 2007; Mori et al., 2007; Otte & van Mier, 2006; Pellegrini, Andrade, & Teixeira, 2004; Ringenbach & Amazeen, 2005; Robertson, 2001; Serrien, Sovijärvi-Spapé, & Rana, 2014; Wolff et al., 1998). Findings from this body of research with children indicate that development of coordinated bimanual behaviors continues for years, reflecting experience along with maturation of critical brain areas such as the corpus callosum, which supports interhemispheric transfer of information necessary for bilateral coordination (DeBoer et al., 2012; Fagard et al., 2001; Gooijers & Swinnen, 2014; Jeeves, Silver, & Milne, 1988; Marion, Killan, Naramor, & Brown, 2003), and other areas such as the cerebellum and premotor cortext (Debaere, Wenderoth, Sunaert, Van Hecke, & Swinnen, 2004; Diamond, 2000).

Interestingly, though, the capacity to maintain a given coordination pattern between limbs moving simultaneously (i.e., coupling strength) does not appear to undergo a single linear pathway of change throughout childhood. Rather, depending on the task context, experience, and age range being observed, coupling strength can increase, decrease, or fluctuate over time. These changes can occur over the course of years or months, or even between days or trials.

For example, in rhythmic tasks that employ in-phase actions that build upon the system’s intrinsic tendencies, coupling strength appears to increase with maturation and practice as children mature from 3- to 4-years to around age 11 (Fitzgerald et al., 1996; Forrester & Whitall, 2000; Ringenbach & Amazeen 2005). This increase in coupling is reflected in coordinated bimanual activity that is temporally and spatially more stable than that produced by young children. However, in task contexts requiring children to simultaneously move the limbs in a pattern that counters the intrinsic mirror-image movement, interlimb coupling tendencies appear to compete with the intended action pattern. The existing coupling tendencies exert strong influence on young children’s performance. As children get older, again around 9- to 11-years, they seem to exhibit reduced coupling strength in precision-task contexts, as evidenced by their stronger performance in non-symmetrical actions that counter intrinsic coupling tendencies (Fagard, 1987; Fagard & Pezé, 1997; Otte & van Mier, 2006; Steese-Seda, Brown, & Caetano, 1995; Wolff et al., 1998). Although younger children are able to perform tasks requiring non-symmetrical coordination, they typically do so more slowly, less precisely, and with larger amplitudes than do adults (Kuhtz-Buschbeck, Boczek-Funcke, Illert, Joehnk, & Stolze, 1999; Ringenbach & Amazeen, 2005; Robertson, 2001).

Importantly, children also demonstrate greater variability in their repetitive actions than do adults, particularly with their non-dominant hands (Fitzpatrick et al., 1996; Kuhtz-Buschbeck et al, 1999; Njiokiktjien et al, 1997; Wolff et al., 1998). Although this variability can be interpreted as immature or unskilled behavior as noted in the previous paragraph, this developmental difference is meaningful when one considers that intra-bout variability here may reflect instability of the behavioral system (Schöner, Haken, & Kelso, 1986; Ringenbach & Amazeen, 2005; Thelen & Smith, 1994), instability which is necessary for new behaviors to emerge. Nevertheless, attending specifically to the performance of the non-dominant hand can improve children’s coordination during such tasks (Pellegrini, et al., 2004), as can synchronizing activity with an older, more experienced partner (Kirschner & Tomasello, 2009).

The rhythmic bimanual tasks experimentally used with youth and adults typically require fine-motor dexterity and a level of attention to instructions that are difficult for children under three years of age. Fortunately, however, there are other oscillatory tasks that fulfill the requirements for study under the theoretical framework that guides this work. For example, 1- to 4-year-old children often respond well to drumming tasks, allowing bimanual coordination to be assessed in this age range (Brakke, Fragaszy, Simpson, Hoy & Cummins-Sebree, 2007; Kirschner & Tomasello, 2009). Drumming represents a gross-motor analog of cyclic finger-tapping that does not require precise distal fine-motor control or dexterity, appears to be of intrinsic interest to many young children, and is amenable to experimental interventions, including those involving adult modeling or other dyadic contexts (Kirschner & Tomasello, 2009; Kleinspehn-Ammerlahn, Riediger, Schmiedek, von Oertzen, Li, & Lindenberger, 2011). Thus, we were confident that bimanual drumming would provide an appropriate task paradigm for our test of the HKB theory.

2.4. Establishing Toddlers’ Readiness for Phase Exploration

Bimanual drumming can be characterized by the relative positions, or phase relationships, of the two hands as they move through the oscillatory actions associated with this behavior. Because we were interested in the ontogenetic emergence of a new phase relationship within the drumming context, it was important to select the appropriate age range to document the onset and improvement in consistency of the anti-phase coordination pattern without placing excess burden on families who volunteered to attend monthly assessment sessions at our laboratory. To identify appropriate ages, we examined past literature that had documented the emergence of bimanual coordination while drumming. Because upper-limb coupling, and the ability to counteract such coupling, are critical to the toddlers’ performance, we examined evidence in the literature of manual performance and role-differentiation to help guide our target age range in the following subsections of 2.4.

2.4.1. Coupling and differentiation.

Motor coupling in the upper limbs may play a role in human behavior even in the earliest days of life. Investigations of neonatal spontaneous movements suggest that an initial tendency to move bilateral homologous muscles together exists (von Hofsten & Rönnqvist, 1993), with some strengthening of coupling over the first six months of life (Piek & Carman, 1994). These coupling tendencies appear to be expressed primarily through in-phase movement in the arms but anti-phase movement also appears (von Hofsten & Rönnqvist, 1993). Such anti-phase coupling is important to note, as it demonstrates that spontaneous movement need not entail only mirror-image movements; other intrinsic patterns are available to infants as well. These spontaneous movements, as well as other oscillatory movements such as arm waves that are present in early infancy (Kawai, Savelsbergh, & Wimmers, 1999; Piek & Carman, 1994; Robertson, 1993), appear to serve as foundations upon which more complex coordinated behaviors are built. Kahrs et al. (2013), for example, specifically identify development of efficient repetitive banging between 6–15 months of age as a motor substrate to later tool use. It may be the case that early spontaneous anti-phase movements provide some sort of foundation for later anti-phase stability in contexts such as ours, although it seems clear that in-phase coupling provides a more robust intrinsic tendency that substantively influences behavior during the first few years of life.

Research on bimanual hand use later in infancy has focused on fluctuations in infants’ use of two-handed activity during the first year. Coupling fluctuations have been examined primarily in the context of the development of reaching and grasping in children under one year of age (Babik, Campbell, & Michel, 2014; Corbetta & Bojczyk, 2002; Fagard, 1991; Fagard & Pezé, 1997; Goldfield & Michel, 1986), although a few other actions such as midline block-banging are represented in the literature as well (Ramsay, 1985).

Infants’ earliest controlled reaches occur around three to four months of age (Clifton, Muir, Ashmead, & Clarkson, 1993; von Hofsten, 1991). Corbetta and Thelen (1996) have examined the coordinative tendencies of infant reaching throughout the first year of life and found that the tendencies to use one or both hands fluctuate throughout the year, starting with the earliest reaching actions (see also Fagard & Pezé, 1997; Goldfield & Michel, 1986; Ramsay, 1985). The research on infant bimanual action has also suggested that the fluctuating use of one or two hands during the first year appears to be linked to fluctuations in the strength of neural coupling (Corbetta, Friedman, & Bell, 2014; Fargard & Pezé, 1997), often accompanying the emergence of new behaviors in other domains such as reduplicated babbling (Ramsay, 1985) or walking (Corbetta & Bojczyk, 2002).

Within object-manipulation contexts, multiple research teams (Babik & Michel, 2016b; Fagard & Jacquet, 1989. Kimmerle, Ferre, Kotwika, & Michel, 2010; Kimmerle, Mick, & Michel, 1995; Potier, Meguerditchian, & Fagard, 2013) have demonstrated that infants change from an early undifferentiated use of the hands to relatively stable and flexible role- differentiation over the first two years of life. As infants near their first birthday, they typically begin to gain volitional control over their intrinsic coupling tendencies, and start to exhibit differentiated hand use and coordination in simple tasks such as holding an object stable with one hand while exploring it with the other (Babik & Michel, 2016b; Fagard & Jacquet, 1989; Kimmerle et al., 1995). Such differentiation is highly task-dependent, however, and many actions in which the hands act in complementary roles emerge early in the second year (Bruner, 1970; Kimmerle et al., 1995; Kimmerle et al., 2010; Potier et al., 2013; Ramsay & Weber, 1986) or even later (Brakke et al., 2007; Connolly & Dalgleish, 1989; Fagard & Jacquet, 1989). Kimmerle et al. (1995) have suggested that this shift in infants’ approach to manipulation represents a transition in neural control of the hands, perhaps related to the fluctuations in coordination tendencies that Corbetta et al. (2014) observed and related to the onset of walking.

Most of the studies cited above investigated role-differentiated bimanual manipulation, in which one hand often serves a stable supporting role while the other engages in active manipulation of the object. The requirements for such types of coordination are different than those needed to engage in the continuous rhythmic action patterns used to test models of coordination in older children and adults. In the discrete reaching movements that are more commonly studied with infants, data are often limited to single iterations of timing and spatial measures as the movement is performed. Periodic actions offer the advantage of measuring microgenetic changes and regularities across continuous iterations (Babik & Michel, 2016a; de Campos, Cerra, Silva, & Rocha, 2014; Corbetta & Thelen, 1996; Fagard & Jacquet, 1996; Kimmerle, et al., 2010; Thelen, et al., 1993; von Hofsten, 1991).

An earlier study conducted by Brakke et al. (2007) addressed coordination in a rhythmic bimanual task context very similar to the one we report in this monograph. Examining a cross-sectional sample of 12-, 18-, and 24-month-old toddlers, Brakke and colleagues found that the same principles that guide coordination in older individuals, also appear to guide the emergence of first in-phase, then anti-phase, drumming across toddlerhood. Specifically, while 12-month-olds typically relied solely on unimanual drumming, in-phase activity served as a relatively stable attractor state at both 18- and 24-months of age and accounted for approximately half of the recorded drumming bouts during each of these two time periods. The two age groups differed in their performance of non-symmetrical bouts, however. At 18 months, many bouts exhibited high instability in phase relationships over time, resulting particularly from variability in movement-timing and spatial motion of the non-dominant hand. This variability suggests that these children may have been experiencing a transition point of de-coupling their two limbs while drumming. By 24 months, however, children exhibited much more stable anti-phase activity characterized by less variability in the action of the nondominant limb and in the resulting phase relationships.

The Brakke et al. (2007) study suggests that children undergo a transition between 12 and 24 months in their control of bimanual action and in the emergence of the anti-phase coordination pattern in particular. These findings, however, were based on cross-sectional data. Thus, although the earlier work demonstrated the emergence of new behavioral patterns, it did so without addressing how initial coordination tendencies are overcome. Furthermore, earlier research on ontogenetic acquisition of bimanual movements has not, to our knowledge, explained the microgenetic changes that occur within or between individual bouts of action when learning a new coordination pattern. In the next section we consider how longitudinal investigations of toddlers’ drumming may be used to illuminate individual ontogenetic trajectories of bimanual control.

2.4.2. Exploring movement parameters.

In order to perform new coordination patterns within a particular context, a child must explore a range of different movement parameters that yield a variety of potential behaviors. As mentioned previously, when learning new motor behaviors, the movements required to execute the to-be-learned action must compete with the child’s current coordination tendencies to yield a new behavioral pattern. In this vein, infants and toddlers must spend a great deal of time exploring the dynamics and outcomes of potential behaviors as they play and develop skill mastery. These explorations reveal to the child potential coordination patterns that are relatively stable to perform. After resolving the initial competition between old and new action patterns, such explorations also allow more effective and efficient performance as the movement systems begin to cooperate.

Evidence suggests that infants indeed undergo a period of coordination instability and exploration prior to selecting a biomechanically-efficient movement pattern that fulfills the relevant goals (Angulo-Kinzler, 2001; Clark & Phillips, 1993; Holt, Saltzman, Ho, Kubo, & Ulrich, 2006; Kahrs et al., 2013). This trajectory illustrates the competition that occurs with the intrinsic tendencies when individuals are attempting a new coordination pattern. For example, as young as three months of age, infants learn through exploration to coordinate their leg kicks to activate an attached mobile in response to different reinforcement contingencies that are dependent on their movements (Angulo-Kinzler, 2001).

Freedland and Bertenthal (1994) reported a similar pattern of change in their study of new crawlers. In particular, these authors found that all the infants they assessed came to use a diagonally-alternating pattern of moving hands and feet after a period of practice in a hands-and-knees support posture. The emergence of the efficient crawling pattern in all 6 infants tested co-occurred with systematic changes in parameters of stance phase and cadence. Other investigators (Clark & Phillips, 1993; Holt et al., 2006) have studied children during their early months of independent walking. They, too, have documented that infants first explore different kinematic solutions to moving their leg segments with a high degree of instability. After a few months of practice, they locate the attractor states that are energy-efficient and adult-like in their form (Holt et al., 2006).

Early in life individuals appear to perceive movement dynamics and alter the related parameters to successfully perform upper limb tasks as well. Thelen et al. (1993), for example, directly examined parameters that contribute to infants’ reaching movements over the course of the first year of life and observed an influential role of movement velocity modulation to achieve stable reaching. These studies and others suggest that ontogenetic emergence of new behavioral patterns during early life do indeed follow the principles of the dynamical systems approach (e.g., Clark & Phillips, 2003; Corbetta & Thelen, 1996; Volman & Geuze, 2000; see also Thelen & Smith, 1994). Equally importantly, all of these studies demonstrated that infants exploit exploratory behavioral patterns in order to achieve new task goals.

2.4.3. Perception of patterns.

Learning and exploration of coordination patterns can be facilitated by observation of similar patterns (Carroll & Bandura, 1982, 1985, 1987). In our work, we provided an adult model during some drumming bouts to demonstrate the anti-phase pattern for the toddler. A wealth of prior research supports the expectation that a demonstration models have the potential to facilitate toddlers’ exploration of anti-phase coordination. For example, toddlers in our participants’ age range have been shown to be inveterate imitators, particularly when the modeled actions are intentional (Carpenter, Akhtar, & Tomasello, 1998; Gergely, 2003) or familiar (Gampe, Keitel, & Daum, 2015). Because the cyclic limb movement involved in drumming is quite similar to actions such as hammering or banging, that are frequently employed by infants (Gampe et al., 2015; Kahrs, Jung, & Lockman, 2014), we expected our toddlers to have the requisite observational learning skills to attempt to imitate the anti-phase actions that they saw modeled.

The evidence for imitation of precise manual movements in infants over one year of age is also supported by cortical recordings of infants as they observe and perform manual actions. Cortical hemodynamic mapping suggests that as young as five months of age, infants are able to differentiate manual movements from other biological movements originating from the mouth or eye (Lloyd-Fox, Blasi, Everdell, Elwell, & Johnson, 2011). By twelve months, EEG desynchronization data indicate that perceptual processing of action performed by others can predict the infant’s own grasping skill – suggesting “an emerging neural system that supports the coupling of action and perception with infants’ emerging motor competence in the first year of life” (Yoo, Cannon, Thorpe, & Fox, 2015, p. 24.). Thus, we expected the neural architecture to support the toddlers’ capacity to perceive and act in response to the adult model’s actions to be well in place by 15 months of age, consistent with behavioral observations of imitation.

2.4.4. Limb coordination: Support for bimanual oscillation.

An additional prerequisite of learning anti-phase movement in a drumming context is the presence of oscillatory movement in the upper limbs. Similar movements are part of neonates’ spontaneous motor repertoire (e.g., Robertson, 1993; van der Meer, van der Weel, & Lee, 1995; von Hofsten & Rönnqvist, 1993). It is typically not until several months later, however, that infants incorporate objects as tools in oscillatory action. Ramsay (1985) documented fluctuating periods of midline oscillatory block-banging in infants starting at about 5 or 6 months. Fragaszy, Simpson, Cummins-Sebree, and Brakke (2016) and Kahrs et al. (2014) assessed changes in hammering movements between 12–24 and 19–35 months of age, respectively. In both of these studies, children of all ages readily engaged in the continuous rhythmic activity required for hammering and demonstrated improvements in efficiency and accuracy across months following changes, typically proximal to distal, in the arm joints responsible for the movement. Similarly, Brakke et al. (2007) found that 12-, 18-, and 24-month toddlers consistently produced drumming movements, but at the youngest of these ages most drumming was unimanual. Taken together, the developmental findings on bimanual coordination reviewed above support our decision to collect longitudinal data on toddlers’ bimanual drumming beginning when they were about 15 months and ending when they were about 27 months.

2.5. Putting the Skills Together: The Bimanual Drumming Task

In the research we report in this manuscript, we studied children’s search strategies for finding stable modes of continuous bimanual coordination, in particular in the context of mastering anti-phase drumming coordination. The toddlers performed in-phase and anti-phase drumming patterns with an adult serving as a demonstration model in front of them during some bouts. The children could attend or respond to different aspects of the task such as the phase relationship, amplitude, or speed of movement. Based on our conceptual model and on earlier DST research findings with adults and older children (see, for instance, Beek et al., 2002; Kelso, 1995; Peper, Ridderikhoff, Daffertshofer, & Beck, 2004; de Poel, Peper, & Beek, 2009; to be discussed in the following chapter), we hypothesized that a number of parameters would be explored as the toddlers’ performance of anti-phase drumming emerged. These parameters included the model’s phase relation of the arms (i.e., movement pattern), the frequency of oscillation, the amplitude ratio between arms, initial condition of the limbs in performance, and joint actively participating in the movement.

Briefly, these parameters modulate how a given movement pattern, in this case anti-phase, can be maintained over time as an indicator of the movement’s stability. Thus, in line with a perception and action approach to motor control, our primary hypothesis is that toddlers will perceive how these variables relate to their performance on the anti-phase pattern and, because of this, they will systematically modulate the parameters in order to perform the anti-phase pattern more stably. Such modulation would be evidenced through clear systematic changes on these parameters over time. We expected particularly that such perception and modulation would be more apparent when the anti-phase movements made by the adult model are salient. A review of how these parameters relate to the stability of the anti-phase pattern is presented in the next chapter.

Notice that we are not implying a direct relation, or even a single causal relation, between these variables, given that many factors may support or disrupt the stability of coordinated movement patterns. However, examination of these movement parameters provides useful suggestions about toddlers’ strategies for facilitating stable performance of the anti-phase coordination pattern. Our work alone does not permit us to draw definitive conclusions about the causal role of toddlers’ strategies to change coordination patterns. The research we report does, however, suggest fruitful areas for future investigations that can provide additional insight into how the underlying perceptual, motor and cognitive abilities, or organismal constraints, change with time and experience over the course of skill development.

3. Anti-Phase Acquisition from a Dynamical Systems Approach

We have set an ambitious analytic agenda to investigate change relative to different movement parameters along multiple timescales. Our empirical work is guided by theoretical frameworks that include dynamical systems in general, and the HKB model in particular. For readers who are not already expert in this area of inquiry, we have provided brief reviews of these approaches in Chapter 3. We turn to the methods and analyses of our empirical work in Chapter 4.

Rejecting an initial scientific dichotomy on emphasizing the central or peripheral control of actions (Reed, 1982; Turvey, 1977), researchers influenced by Bernstein (1967) and Gibson (1966) proposed that the perceptual-motor system is self-organized and adapted to directly interact with its surrounding environment (e.g., Kugler, Kelso, & Turvey, 1980; 1982). The synthesis of an ecological view of psychology (Gibson, 1986; Shaw, Turvey, & Mace, 1982) with the framework of nonlinear dynamics (see Kugler et al., 1980, 1982) allowed investigators to identify core concepts for understanding human motor organization as a complex system.

This dynamical systems approach harnesses the variability that occurs with behavior and identifies it as a key phenomenon in the process of change. Instead of being interpreted as noise, variability becomes a means of analysis as a measure of instability within an existing or emerging behavioral system (e.g., Thelen & Smith, 1994). In addition, this approach recognizes the presence of individual differences in the structure and timing of organizational pathways and uses these differences to identify the parameters that interact to form a common collective variable or behavior. In our case, the collective variable is coordinated upper limb oscillation (measured through relative phase; discussed in Chapter 4). Further, the theory’s tenet of self-organization means that the system does not need a central or external controller that prescribes the system’s processes or outcome; rather, order emerges from the interactions of all its components. The components of complex systems such as those underlying motor coordination have non-linear interactions that give rise to specific self-organized attractor states of behavior that provide points of stability for the system. These attractor states are said to be emergent in the sense that they are not prescribed by any single component but arise organically from the environment-organism system. In motor coordination, for example, a highly recognizable attractor state occurs with the precisely coordinated alternating leg swings that characterize walking (Clark & Phillips, 1993; Thelen & Ulrich, 1991).

This systems view of behavior can be linked conceptually to Waddington’s (1957) well-known epigenetic landscape as presented for behavioral development by Thelen (e.g., Muchisky, Gershkoff-Stowe, Cole, & Thelen, 1996; see also Newell et al., 2003), in which behavior (or a biological trait, in Waddington’s original theoretical model) over time is likened to a ball rolling down a hilly landscape. Depending on the magnitude of the hills and valleys along different trajectories as well as the intrinsic properties of the ball and its movement, the ball (representing behavior) may travel along a number of paths as it moves through time but will ultimately land in a valley, or canal, of sufficient depth to constrain the ball’s movement and resist perturbations. This canalization of behavior supports the stable behavioral states, or attractors, of dynamical systems. As mentioned, walking represents one such highly-canalized attractor state. In our earlier example with circular arm movements, the homologous, mirror-image movement of the limbs represents a stable attractor for the system within that movement context.

A complex motor system might show a number of attractor states. The proximity of the initial behavioral state to each attractor determines whether the system will converge to one or the other of these. The attractor states are stable in the sense that perturbations to the system, if not extreme, will be damped and the system will return to the attractor state. If a perturbation is large enough, it is possible that the system will deviate so much from its original attractor that it will find another one, resulting in a new behavioral pattern. The probability of finding a new attractor depends on the attractor layout, or the number and distribution of attractors relative to the extant behavior. An example of such an attractor layout – and one that we discuss later – is illustrated in Figure 3.1.

Figure 3.1.

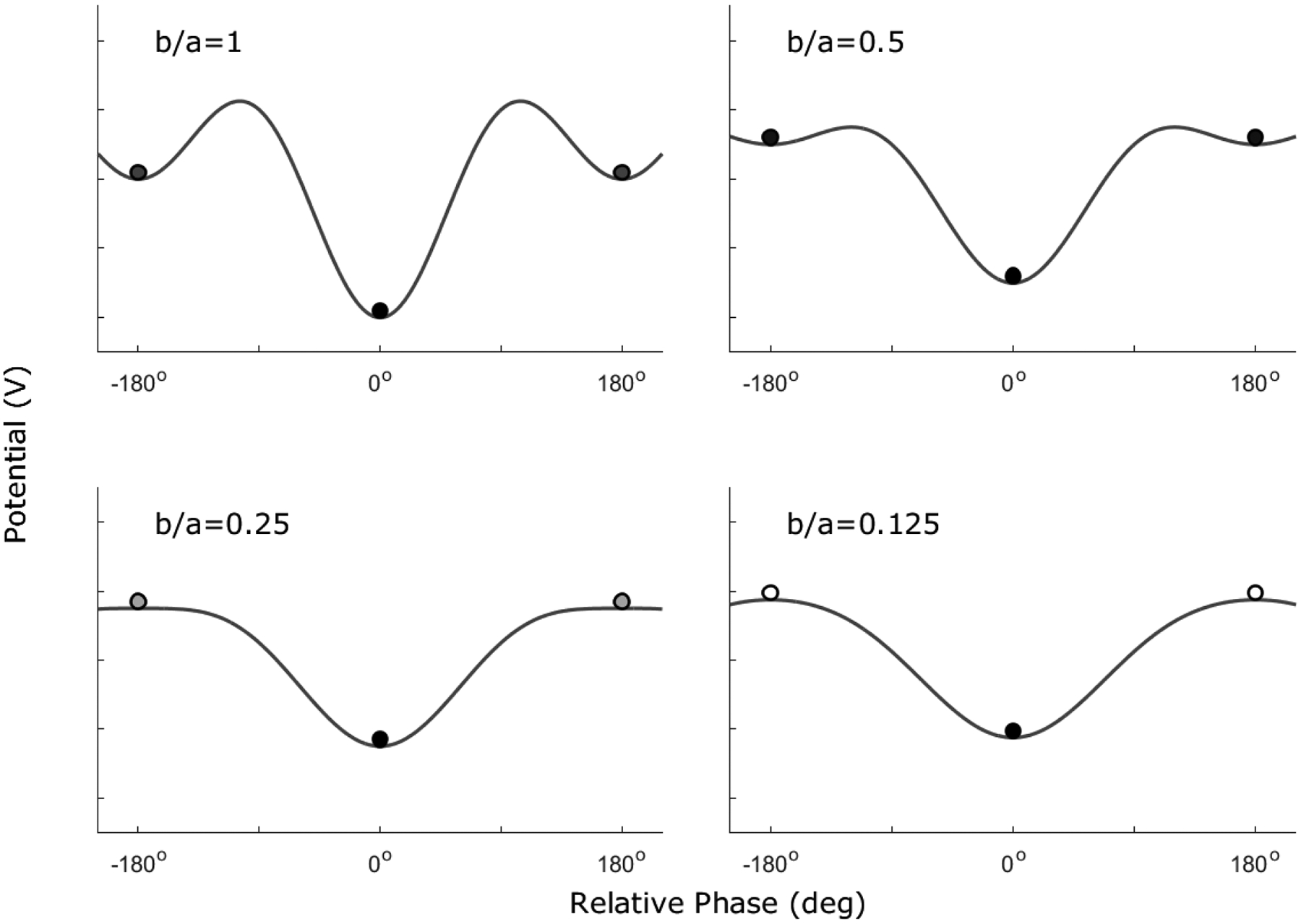
The HKB model plotted in its potential function version, $V\left(d\varphi /dt\right)=-a\text{ cos}\left(\varphi \right)-b\text{ cos}\left(2\varphi \right)$, for different values of b/a. The potential function describes the HKB model as valleys that represent regions in which behaviors are stable, as represented by the plotted circles. The black-filled circles are placed on stable regions characterized by concave troughs, which gives these behaviorial states, such as in-phase coordination, resistance to perturbation. The gray-filled circles are in neutral regions with flat surfaces (the −180° and 180° regions when b/a = 0.25). Any change in behavior after a small perturbation in these regions is proportional to the perturbation. The white-filled circles are in unstable regions with the convex surfaces. Here, if no perturbation occurs, the system is maintained at that point. Any small perturbation, however, makes the circle (representing behavior) move to find other more stable regions. This shift may occur with the anti-phase coordination pattern, but never for the in-phase.

A behavioral system such as bimanual coordination is comprised of several interacting subsystems, which may be biomechanical, physiological, psychological, or ecological (Thelen & Smith, 1994). Although each of the interactive subsystems on which the system’s organization depends exhibits its own intrinsic tendencies, the subsystems may get entrained to each other to different degrees and facilitate a new cooperative and coherent organization of the overall collective system. The way in which the subsystems interact gives rise to the level of behavioral stability observed. If there is a gradual change in some value underlying the behavior (the parameter of movement velocity, for example), the way these subsystems interact may abruptly change. Some attractors might lose stability and other attractors emerge; imagine, for example, the transition from walking to jogging as velocity increases. This process, known as a bifurcation, changes the attractor layout of the system and provides the foundation for behavioral development.

3.1. The HKB Model: Dynamical Systems in Bimanual Coordination

The adaptation of the dynamical systems theoretical approach and analytical tools to human behavior has prompted a wave of interest in bimanual coordination and other motor systems by providing a framework that not only allows description of coordinated action, but experimental control and manipulation of potentially important variables.

Following Cohen’s (1971) pioneering observations of the oscillatory nature of rhythmic bimanual action, Kelso (1984) initiated the investigation of bimanual coordination under the dynamical systems approach. In looking for an experimental paradigm that could support the emerging view of dynamical systems, Kelso observed that coordinated motion of fingers of the same or different hands could reproduce the qualitative phase changes observed in earlier studies of gait (e.g., Hoyt & Taylor, 1981; see Kelso, 1995 for the full story). That is, as the frequency of oscillation of two fingers (e.g., one on each hand) increased, the relation between the two would reliably change from inverse to mirror-like (or from anti-phase to in-phase). With the help of Hermann Haken (the proponent of synergetics; see Haken, 1977), Kelso formalized the experimental results in a formal model (Haken et al., 1985), providing a testable characterization of nonlinearity and behavioral emergence in the field of motor behavior.

The HKB model, as it has become known, is formalized through the equation $d\varphi /dt=-a\text{ sin}\left(\varphi \right)-2b\text{sin}\left(2\varphi \right)$, where ϕ represents the relative phase between the two oscillators (the limbs), dϕ/dt is the first derivative of relative phase on time, and a and b are the parameters of the function. Figure 3.1 shows the attractor layout that arises from this function. This attractor layout is a transformation of the equation that shows valleys in which the behavior would be stable (the bottom of the valley) or not (the peaks of the function). In the figure, the fixed points – behavioral states that are maintained if no perturbation occurs (the first derivative is zero, dϕ/dt = 0) – are depicted by circles. The stable fixed points, or attractors, are depicted by filled circles. The attractors are stable because the first derivative is positive for any value lower than the attractor value and is negative for any value higher than the attractor value. This means that if ϕ has a lower value than the attractor, it will increase up to the moment it reaches the fixed point, and if ϕ has a larger value than the attractor, it will decrease until the moment it reaches the fixed point. Note that two different layouts emerge if the values of a and b are changed. Following Haken et al. (1985), the parameter that qualitatively modulates the layout – called the control parameter – is b/a (see Figure 3.1).

In behavioral terms, the attractor states for the phase relationship between the limbs occur at 0° and 180°, representing, respectively, in-phase and anti-phase relative motion. However, a bifurcation occurs when b/a crosses the critical value of 0.25. When this occurs, the 180° attractor – or anti-phase pattern – loses stability and becomes a repellor (the opposite of an attractor – any point close to it diverges from the fixed point). If this occurs, the system, with its embedded noise, drifts away from the 180° fixed point and moves to the 0° value of ϕ (i.e., the in-phase pattern). Thus, anti-phase movement is considered a less stable attractor than in-phase movement even in adults. This imbalance can be demonstrated by waving or tapping one’s index fingers very quickly in anti-phase mode. The stability of this motion is likely to erode and transform to in-phase movement as the action continues.

These dynamics reflect the tendencies of the individual’s underlying sub-systems (biomechanical, attentional, and so on) to coordinate in some specific ways. Across many studies (e.g., Beek et al., 2002; Kelso, 1984; Zanone & Kelso, 1992), the motor preference for coupled movements has been seen in the tendency for people to perform movements that involve mirror-like, in-phase patterns more stably and consistently than they perform other coordination patterns. In other words, an attractor such as in-phase action tends to reflect the coupling strength of a coordinated system to the degree that it evidences stability and resists change when subjected to different perturbations (Fitzpatrick et al., 1996). When the action involves non-mirror-like patterns, movement is more variable; if the pace is increased the variability within and between movements also increases, perhaps transitioning to simultaneous, mirror-like movement (e.g., Kelso, 1984).

Stability of coordination is typically defined in terms of the relative spatio-temporal motion of the limbs: the mirrored trajectory of both limbs (i.e., in-phase, 0° relative phase) is more stable than the contrary trajectory of the limbs (i.e., anti-phase, 180° relative phase). Any other phase relation between rhythmic movements (e.g., 60° or 90°) is unstable and rarely persists unless specific practice is provided (Kennedy, et al., 2016; Kovacs et al., 2009; Smethurst & Carson, 2001; Zanone & Kelso, 1992). This instability has been observed in both “open-chain” or “free-motion” action systems (e.g., finger-waving, wrist pronation) and for “anchored” action systems (e.g., circle-drawing, pendulum-swinging, and finger-tapping) (Forrester & Whitall, 2000). The stability and consistency of the movement patterns have been shown to be influenced by instructions or other contextual factors that involve the interplay of the musculoskeletal system with neurocognitive and external constraints or perceptual variables (Bingham, 2004; Forrester & Whitall, 2000; Pellecchia & Turvey, 2001; Ridderikhoff, Peper, & Beek, 2005; Sisti et al., 2011; Smethurst & Carson, 2003; Srinivasan, Martin, & Reed, 2013) and thus are truly emergent from the interplay of a constellation of factors.

3.2. Emergence of Anti-Phase Coordination as a Developmental Process

In skill development, a young child’s coordination tendencies change as maturation and experience interact over time. The study of cyclic bimanual coordination in motor control and learning, however, has focused on relatively short-term stability of movement patterns under optimal and disrupted conditions, rather than on the developmental dynamics that accompany the emergence of behaviors over ontogenetic time. Within skill development processes, when a task reflects a well-established movement pattern, intrinsic and task dynamics are aligned and cooperate to produce a stable behavioral outcome (Schöner, 1989; Schöner, Zanone, & Kelso, 1992). When a different movement pattern is performed, however, the initial intrinsic dynamics compete with the novel task requirements until the new pattern becomes part of the learner’s stable behavioral repertoire. The stabilization of the new pattern in the repertoire in turn entails an alteration of the extant intrinsic dynamics. These competitive and cooperative processes have been demonstrated in terms of their influence on motor skill in brief timescales of minutes or days (e.g., Kostrubiec, Tallet, & Zanone, 2006; Wenderoth, Bock, & Krohn, 2002; Zanone & Kelso, 1994). In contrast, little is known about how young children might employ strategies to cope with this dynamic competition supporting new task requirements through ontogenetic scales of development (but see Thelen et al., 1993 and Fitzpatrick et al., 1996, for similar approaches in other motor contexts).

For our purposes, we will provide a conceptual model that explains strategies that toddlers can employ to counter their intrinsic tendencies that support in-phase motion of the limbs and establish a new bimanual coordination pattern within the drumming context. This conceptual model, based in the HKB model and literature on bimanual coordination, provides a rationale for the acquisition of the anti-phase pattern before any other bimanual coordination pattern. After describing our conceptual model, we explore the propositions included within it, addressing the hypothesized parameters that toddlers would explore to perform the emergent anti-phase coordination pattern.

3.3. Exploring Movement Parameters

Having provided an overview of Dynamical Systems Theory and the HKB model, we now turn to commenting on parameters that toddlers may use to explore the dynamics of bimanual coordination as they practice the anti-phase pattern. The conceptual model presented here is not a formal mathematical model but it does build upon existing formal models of bimanual coordination. We also incorporate empirical results of research with many similar rhythmic bimanual coordination tasks to inform our expectations (e.g., Beek et al., 2002; de Boer et al., 2013; Forrester & Whitall, 2000; Kennedy et al., 2016; Njiokiktjien et al., 1997; Ringenbach & Amazeen, 2005; Schmidt, Shaw, & Turvey, 1993; Smethurst & Carson, 2001).

In the remainder of this chapter, we introduce a slightly modified version of the foundational HKB model of bimanual coordination that starts with the assumption that in-phase coordination represents a strong intrinsic tendency present in the toddlers’ repertoire whereas the anti-phase pattern requires practice to be reliably performed. We then explain the concept of two oscillators representing the hands’ motion and describe empirical results relevant to the parameters that might be modified in these oscillators to change the state of the system.

3.3.1. Adapting the HKB model to Ontogeny.

Haken et al. (1985) initially formulated the HKB model to accommodate the results presented in Kelso’s (1981, 1984) seminal investigations of bimanual coordination. Later (e.g., Schöner et al., 1986; Schöner et al., 1992) the model became an influential formal descriptor of the intrinsic dynamics of the bimanual coordination system. The intrinsic dynamics represent the current tendencies of the system when it performs a general task – in this case, bimanual rhythmic oscillation. These tendencies influence how an individual learns a new coordination pattern – or in terms of the theory, how the system creates a new attractor in the attractor layout (Zanone & Kelso, 1992; Kostrubiec et al., 2012). This additional attractor can be considered a newly-learned behavior within a specific action context, and learning something new requires that one perform in a way that competes with the existing intrinsic dynamics. While the intrinsic dynamics are “pushing” behavior towards an extant attractor state, the individual must actively compete with these dynamics to yield a new stable behavior. This competition arises in practice and may have learning, or emergent cooperation of new and existing movement dynamics, as its outcome.

In studies of motor development, then, one must identify the intrinsic dynamics of the system. In older children and adults who are practiced and skilled in the use of their two hands, the intrinsic dynamics are represented by the HKB model with both in- and anti-phase patterns as stable fixed points (Haken et al., 1985; although some individuals present other stable patterns, see Zanone & Kelso, 1997). In our case with young toddlers, however, the anti-phase pattern is not yet stable. How does the attractor layout look during this time? Here, the in-phase pattern is the only reliable fixed point in the entire attractor layout, aligning with Brakke et al.’s (2007) observation that in-phase coordination represented the only stable pattern that could be continuously produced by 12- and 18-month-old infants in a drumming task similar to the one used in the research reported in this monograph. We believe that the HKB model with low values of b/a (see Figure 3.1) captures this situation.

3.3.2. Anti-Phase as an Emergent Coordination Pattern.

Let us consider the HKB equation as representing the emergent configuration of the human motor system’s tendencies for action. Recall that b/a represents the control parameter in the equation. We observed in Figure 3.1 that, even in considering low values of b/a, with an unstable 180° phase relation, the anti-phase coordination pattern represents the point of the landscape in which there is no tendency to act as in-phase. That is, there is no tendency for the white circle represented in Figure 3.1 (b/a = 0.125)to “fall” into the in-phase coordination pattern. Even in the area around the 180° region, the influence of the in-phase pattern is weaker that in other portions of the action space. Thus, the region of the anti-phase coordination pattern represents the region in which the system gravitates least to the in-phase pattern. This would make that region the easiest in which to acquire a new stable pattern given that it is there that the competition between intrinsic in-phase tendencies and new task requirements would be the lowest.

A more difficult question is why the 180° region would be the area with lowest influence of intrinsic in-phase coupling in the first place. A different mathematical model (with different functions) than the HKB equation could provide other regions with lowest competition. A tentative answer is provided by Bingham’s (2004) theoretical model, in which the author proposes that it is through the perception of the motion of the limbs that stability in motor coordination emerges. The main point in this argument is that under this perception-action derived model, learning would occur as individuals come to perceptually differentiate new patterns of coordination, allowing for performance of these patterns to occur. In line with this idea, Wilson, Snapp-Childs, and Bingham (2010) tested whether individuals who had specific perceptual training with a 90°-phase task would subsequently be able to perform it. The results were positive and corroborated the idea that individuals learn by perceptually discriminating coordination patterns (see also Gibson & Gibson, 1955). This effect of pattern discrimination is consistent with Wenderoth et al. (2002), who demonstrated that to-be-learned coordination patterns closer to 0° were easier to learn than those closer to 180°. This is because the in-phase pattern is better distinguished from other phase relationships than is the anti-phase pattern.

In this sense, then, provided that one can clearly differentiate 180° from 0°, the performance of the anti-phase pattern is less influenced than any other phase in the spectrum of movement pattern possibilities in that it is maximally different from in-phase. Clearly, one still needs to explain how this process of differentiation interacts with other systems in terms of increasing stability with age, and it may be that other processes are involved in behavioral acquisition. Nevertheless, we have reason to believe that, first, we can conceptualize the HKB model in infancy as a low b/a version of the model and that, second, that the first additional coordination pattern to stably emerge in our drumming context is the anti-phase pattern given the topology of this model.

3.4. Exploring the HKB Model: Changing Dynamics to Acquire the Anti-Phase Pattern

Having provided the groundwork for addressing acquisition of anti-phase action within the context of a drumming task, we turn to address how toddlers might respond to the competition between the intrinsic dynamics identified in our adapted HKB model and the emerging anti-phase pattern. This topic of how an individual competes with its own intrinsic tendencies, although widely discussed in the original studies of motor learning, has never been fully addressed. Following Goldfield, Kay, and Warren (1993; see also Berthouze & Goldfield, 2008) and Newell et al. (1989), we believe that toddlers will explore the movement parameters that allow the discovery and creation of new stable regions in the attractor layout. In the case of bimanual coordination, toddlers can explore parameters related to their limbs’ phase relationships and decrease the influence of the intrinsic dynamics with practice.

To decrease the influence of the intrinsic dynamics, one must be able to change the a and b parameters described in the HKB model in a way that the attraction to the in-phase pattern is decreased, allowing practice of different coordination patterns. Note, however, that a and b parameters in the HKB model have no physical meaning. That is, they are just variables that change the configuration of the results of a differential equation. The question becomes what the physical variables are that relate to b/a in the way that promotes change in the attractor layout. To understand the possible parameters, we now need to consider both the oscillator aspect of the HKB model as well as relevant empirical observations from the literature.

3.4.1. Frequency of oscillation.

The HKB model was constructed to address the findings of Kelso (1981, 1984). In Kelso’s studies, individuals were asked to repetitively move the index fingers or wrist of each limb in a mirrored (using homologous muscles, in-phase) or inverse (non-homologous muscles, anti-phase) direction along a single dimension (for example, flexion/extension or tapping) following the pace of a metronome. When the metronome pace was increased, if the condition started as in-phase, the oscillation pace was increased with only a slight increase in variability. If, however, the pace was increased during an anti-phase trial, movement variability would increase until the individual experienced a phase shift and ended up performing the in-phase pattern. Thus, a spontaneous shift in relative phase toward the more stable attractor would occur.

In dynamical systems terms, the relative phase is the order parameter, an outcome variable that captures the collective organization of the system. The frequency of oscillation is the control parameter, a variable whose modulation can easily change the emergent pattern, although it does not code nor prescribe any particular organization (Kelso, 1995). As we have established, in the HKB mathematical model, the control parameter is represented by the ratio b/a. A simple way to relate the behavioral and mathematical representations of the HKB model is to state that oscillation frequency covaries with b/a. Indeed Haken et al. (1985) suggested that frequency of oscillation related to a and b in this way. The relation between frequency and stability in the HKB model is indirect, nevertheless. (For a full explanation of the HKB model details see Beek et al., 2002; see also the discussion on the amplitude ratio presented later in this chapter).

Thus, because we are looking for a variable that children can modulate to facilitate the engagement of the anti-phase coordination pattern and test here, frequency of oscillation is an obvious candidate. Many investigators studying adults and older children have manipulated the frequency of oscillation upward to show a shift from anti-phase to in-phase (e.g., Kelso, 1984; Robertson, 2001; Scholz & Kelso, 1990). The possibility of decreasing frequency of oscillation to improve anti-phase stability, however, has not been as thoroughly explored. If the oscillation frequency is decreased during in-phase movement, the possibility of performing the anti-phase pattern is increased because the constraints of the intrinsic dynamics are weakened. Indeed, developmental studies employing in- and anti-phase coordination tasks with typically developing children have shown that the anti-phase pattern is performed in a lower frequency of oscillation than is the in-phase pattern (Harbst, Lazarus, & Whitall, 2000; Isenhower, Marsh, Richardson, Helt, Schmidt, & Fein, 2012; Wolff, 1998). These theoretical and empirical foundations lead us to predict that toddlers will use the frequency of oscillation as a means of decreasing competition between intrinsic dynamics and the emergent pattern, thereby increasing the stabilization of the anti-phase pattern.

Specifically, we hypothesize a path of change that starts with the already-stable pattern of in-phase. As the experimenter incites the children to perform the anti-phase movement pattern, the toddlers will decrease frequency of oscillation and then shift to the anti-phase pattern, in this order. We report our tests of this strategy along different time scales in Chapter 6.

3.4.2. Amplitude ratio.

Because our model characterizes the limbs as a pair of oscillators, we can exploit the properties of oscillators to identify an additional parameter that children may exploit when exploring anti-phase movement. Amplitude represents a measure of displacement magnitude along an axis. In other words, in our case, amplitude measures how high the drumsticks that the toddler is holding are being lifted above a base point in each movement cycle. Two coupled oscillators would show similar frequency and amplitude under continuous, stable oscillation. As discussed above, we proposed that when both oscillators change their cycle frequency, a behavioral transition would be more likely to occur that represents a qualitative change in the attractor layout. Accordingly, we tested the relation between oscillation frequency and phase relation in the developing behavior of our toddlers, and report our findings in Chapter 6 of this monograph.

According to the HKB model, the actual variable that leads to the phase transition in oscillatory movement is the amplitude (see Beek et al., 2002; Peper, et al., 2004). It is through an interaction between frequency of oscillation and amplitude that frequency can cause the phase transition to occur. Thus, amplitude seems to be a meaningful variable to examine in toddlers’ development as well. In reality, however, the role of amplitude is not well understood. Ryu and Buchanan (2004) showed that scaling the amplitude in a bimanual circle-drawing task resulted in the same shift from in-phase to anti-phase as observed when frequency was scaled. However, the phase shift occurred with both increasing and decreasing amplitude, which is different than the findings relative to frequency manipulation.

Peper and Beek (1998a, 1998b) demonstrated in a series of studies that the prediction of both versions of the HKB coupled-oscillators model fail on the basis of experiments which showed that the expected amplitude effects did not show transitions at the expected values or did not show transitions at all. Results reported by Ryu and Buchanan (2004), however, suggest that amplitude changes as a whole do not help individuals perform relative phases other than in-phase. In all of Ryu and Buchanan’s cases, the modulation of amplitude led to a shift to in-phase action, independent of whether the individual was increasing or decreasing the amplitude. Thus, at first glance, modulation of amplitude seems to be counter-productive when trying to learn a new coordination pattern.

Given these discrepant results, how might toddlers modulate amplitude to deal with the competition between intrinsic dynamics and a new coordination pattern? In early studies of discrete bimanual coordination, Kelso and colleagues (Kelso, Putnam, & Goodman, 1983; Kelso, Southard & Goodman, 1979) demonstrated that individuals tend to show relatively homologous movements of the two limbs even when reaching for targets with different requirements such as target width, amplitude, or movement time. That is, the spatio-temporal characteristics of each limb correlated with each other, suggesting that motor coupling may be at play. However, this unitary behavior disappears when the disparity between the requirements of each hand crosses a critical value (see Marteniuk, MacKenzie, & Baba, 1984; Schӧner, 1990). Thus, if individuals must perform highly dissimilar movements with each hand to meet the target requirements, the tendency for coupling disappears. Indeed, for bimanual rhythmic movements, the ratio between movement amplitudes of the involved limbs is critical to the stability of the movement pattern. Peper, de Boer, de Poel & Beek (2008), for instance, showed that when adults performed limb oscillations with an amplitude ratio of 2:1 between limbs, the variability in the relative phase increased (see also de Boer et al., 2013; de Poel et al., 2009). It is reasonable to expect, then, that another route that toddlers could use to counter the in-phase movement pattern could be to change the amplitude of one or both hands, which would decrease the stability of the relative phase and allow an intentional change to the anti-phase pattern. We tested this possibility and report our results in Chapter 7.

3.4.3. Initial Conditions.

Another parameter that can be modulated to facilitate practice of the different movement patterns is the initial condition of the system, which represents the phase between the limbs at the beginning of a bout. The rationale is simple and follows directly from observation of Figure 3.1. If individuals start a drumming bout in the in-phase mode, then they must leave that region of the attractor landscape to perform the anti-phase pattern. This, as we are arguing, can occur by modulating frequency of oscillation and/or amplitude ratio. Note, however, that if the individual starts at the anti-phase region of the attractor layout, no further modifications during the trial are necessary. Thus, being able to start the bout in the correct movement pattern may lead to increased practice in that pattern. Our hypothesis is that, as toddlers start to increase stability in the anti-phase pattern, they will, through their own choice, increase the number of bouts initiated in the anti-phase pattern, facilitating practice and performance of this coordination pattern.

It is interesting that past investigators have rarely addressed such situations in learning. To our knowledge, the only group that has directly assessed (and found) the influence of initial conditions is Liu, Mayer-Kress and Newell (2010) who studied adults’ learning to maintain the rotation of a roller-ball. Note that the capacity to start the movement in a given movement pattern is indicative of the current state of the system and, thus, was investigated here. We report these findings in Chapter 8.

3.4.4. Joint coordination.

A finding briefly discussed in Chapter 2 was that toddlers demonstrate a proximal-to-distal change in the joints being primarily employed in the development of banging (Fragraszy et al., 2016; Kahrs et al., 2014). Both of the cited studies demonstrated such change around the same developmental period (toddlerhood) investigated in the present study. Kahrs et al., (2014) in particular related observed joint changes to increased accuracy in banging, with motion at the wrist being the major predictor of precision.

Although the proximo-distal change in development is specific not only to banging (see Berthier, Clifton, McCall, & Robin, 1999), one could posit that specific joint changes would occur given the task requirements. The findings from the Kahrs et al. (2014) study are consistent with the argument that change in joint participation is tightly linked to the accuracy requirements of the task. This conclusion would corroborate findings in the literature on motor control in adults as well. For example, Buchanan, Kelso, de Guzman, and Ding (1997) showed that to maintain the hand-trajectory curvature required in an oscillatory task, adults changed the participating joints accordingly.

In the current task, one could predict that maintaining the motion of the limbs at the shoulder level would induce a mechanical interference between limbs given that motion of the arms involves motion of the trunk. This coupling means that the anti-phase pattern could be performed only with considerable effort. Thus, toddlers who change their movement pattern from proximal to more distal joints (e.g., the elbow or wrist) would facilitate anti-phase performance by decreasing mechanical interference. Thus, we expected to see proximo-distal changes over time with associated changes in anti-phase performance. We tested this prediction and present the relevant findings in Chapter 9.

3.5. Summarizing the Motivations for Our Investigation and Plan for This Monograph

Behavioral research within the dynamical systems framework is characterized by a number of steps, as outlined by Thelen and Ulrich (1991). Specifically, these steps include identifying a collective outcome variable that represents the form of the coordinated behavior; identifying and describing one or more attractor states within the state space of the collective variable; documenting periods of stability, instability, and bifurcation (phase shifts) across time; and, finally, identifying and, if possible, experimentally manipulating possible control parameters that allow the collective variable to organize into different coordination patterns. These steps, with the exception of the experimental manipulation of parameters for our toddler participants, have guided the development of our model and conduct of our research. In the work reported in this monograph, our collective variable is the phase relationship between the two limbs, with in-phase and anti-phase attractor states and potential parameters of movement frequency, movement amplitude ratio, the toddler’s spontaneous initial condition of limb positions, and joint recruitment. We hypothesize that these parameters will be modulated to effect phase shifts from in-phase to anti-phase, shifts that we expect to observe across both within- and between-month timeframes. We expect, however, that different children will employ different means and paths to enact these changes. This expectation is rooted in our belief in the individual nature of change. This expectation likewise has led us to select analytic tools that can document and interrogate such individual variations.

In Chapter 4 we present the overall methods of the paper and in Chapter 5 we present the analyses of anti-phase performance over time. In Chapters 6, 7, 8 and 9 we directly address whether frequency of oscillation, amplitude ratio, initial condition of the limbs, and joint recruitment were modulated to support anti-phase practice and acquisition. In Chapter 10 we discuss the results in light of our conceptual model, connect the findings to the possible underlying mechanisms at play, and call for further study to confirm and elucidate some of the relations that our work suggests.

4. Methods and General Analytic Plan

4.1. Participants

Families with children approaching 15 months of age were recruited through flyers placed at local childcare facilities serving a variety of family socioeconomic and racial/ethnic demographics as well as through personal networks of research personnel. Mindful of the time we were asking families to commit to the project, we asked families to, if willing, attend through 24 months of age. This was the age that, in the previous study, children had produced relatively stable anti-phase activity and demonstrated a high level of control of their drumming activity. At 24 months, families were given the option of continuing up to 27 months; some decided to continue and some did not. We used age-based rather than criterion-based termination points because, given how little we knew about the ontogenetic emergence of anti-phase activity and the recognition that such activity would likely not be fully mastered in early childhood and would be subject to substantial individual differences, it would be difficult to identify a clear criterion for ending participation.

Twelve families with a child of appropriate age volunteered to participate in the study and attended at least three monthly assessment sessions beginning when the child was 15 or 16 months of age. The sample of children included five males and seven females with no diagnosed disabilities or developmental delay. Based parental report, participant families varied in their socioeconomic backgrounds, with parental education levels ranging from high school only (2 families) through baccalaureate education (3 families) and graduate-level degrees (7 families). All of the toddlers had at least one employed parent; two of the toddlers lived in single-parent homes at the time of assessment. Nine parents identified their children as Black or African American, with one toddler identified as White and two as multiracial. One toddler was of Hispanic ethnicity. Eight of the toddlers were firstborn, two had at least one older sibling, and two were of unknown birth order.

Participant families were compensated $20 for each monthly visit between child ages 15 and 24 months. Eight families extended their participation through additional months, up to child age 27 months. Three children were withdrawn from the study prior to 24 months of age. One of these moved out of the area and two experienced continued scheduling conflicts. Data from two additional toddlers were removed from analyses; one because four consecutive sessions were missed during a temporary move to a summer home before sessions resumed, and one because she refused to engage in the task until 19 months of age, and at that point she engaged very little with the task unless a family member served as a model. Thus, the final data set represents the activity corpus of seven (3 girls, 4 boys) children who provided data between 15 or 16 and 24 (or more) months of age. All of these participants were full-term except for P4, whose parent indicated after the project began that P4 had been born approximately five weeks prematurely. This participant engaged fully with the task and produced data comparable to that of the other toddlers at the same ages. As evident from the data we collected to characterize the toddlers’ manual activity (see Section 4.5 – Characterization of the Sample), all of the toddlers were capable of grasping and releasing objects and attending to objects presented by the experimenter All participants exhibited right-hand preference throughout most assessments except for P7, who was consistently left-handed, and P5, whose hand preference appeared to fluctuate from month to month. All were walking independently at the beginning of the study period and no developmental atypicalities were reported by parents. Parents reported that children had had the usual previous experience with toys and other objects; toddlers may have had some experience with banging or drumming on objects during play but parents reported no systematic exposure to drumming practice outside of the laboratory.

Even among the families within the final dataset, most were unable to attend the assessment session every month over the course of the year. Reasons for missing sessions included vacations, illness, and scheduling conflicts. In addition, some children attended but produced no usable data during particular months. During these sessions, toddlers may have declined to interact with any of the objects presented or they may have specifically chosen not to engage in drumming. Often, however, the toddlers eagerly anticipated the object interactions and would even select the appropriate sets of toys in turn or arrange the drums and sticks themselves.

All sessions were held in a laboratory room on the college campus. Sessions were typically scheduled on Saturday mornings, and to the extent possible were scheduled at consistent times across months when children would be well-rested and fed prior to arrival. Each session lasted approximately twenty minutes, with short breaks as needed if children became restless during task administration. Because we were interested in eliciting as many bouts as possible to provide data sequences for analysis, we did not limit the number of trials to a particular number. Sessions ended when the child behaviorally indicated that she or he was finished with the drumming task by putting the drumsticks down or handing them to the Experimenter.

4.2. Apparatus/Materials

The child sat in a chair-and-table apparatus that was arranged by placing two chair cubes (Childgarden.com product CF910–008) in close proximity (Figure 4.1). These cubes can be placed so that the flat surface faces up, forming a 35.6 cm square table, or so that the flat surface is vertical and forms the back of a chair, with the child sitting on a plastic connecting platform at either a height of 15.25 or 25.4 cm above the floor. This apparatus worked well because the chair height could be adjusted so that it was accessible and comfortable for children and placed them at the appropriate height for the table.

Figure 4.1.

Child with drumsticks. Reflective tape on the ends of the drum sticks provided the points for motion tracking. (Image used with permission of parent)

Drumming was performed using plastic drumsticks, with the head of each drumstick covered with reflective tape. We decided to use sticks, rather than asking children to drum with their hands alone, because children in this age range had responded well to stick-drumming in the past, suggesting that the incorporation of the objects made the task an appropriate and interesting one for children in this age range (Brakke et al., 2007). Because we had also found in pilot testing that toddlers’ interest in the task could be revived by presenting new drumsticks, two sets of plastic children’s drumsticks were available for use. Those of the primary set were black, 18 cm long with handle diameters of 1.3 cm and spheroid heads that were 2.5 cm in diameter. The secondary set consisted of red plastic sticks, 25 cm long with handle diameters of 1.5 cm and no defined heads. We recognize that the use of two sets of sticks slightly alters the kinematics of action between trials. Nevertheless, our analyses did not rely on arm and stick length. Instead, our analyses rely on changes among a set of variables, such as relative phase and amplitude ratio, that relate one hand to the other over time and how these changes influence anti-phase performance. Our choice of analyses avoids the requirement for controlling the precise site of grasping each drumstick, which also varied when toddlers adjusted their grasps or held the sticks closer to the midpoints rather than the usual proximal tips. These variations in length and arm placement may have introduced occasional bias in measurement of displacement values, but these effects are alleviated when change, not the values per se, is analyzed. We plan a future analysis to examine the dynamics of stick dimension and grasping preferences. We expect this analysis will add tremendously to the understanding of how toddlers modify their actions to accommodate new task constraints. For now, we acknowledge the limitation and include explicit warnings in the manuscript when discussing findings from analyses that do not permit us to determine the impact of either stick length or unconstrained grasping positions.

Because commercially available toy drums were too large for children of this age, we used a Rubbermaid 4.2 cup Stain Shield clear plastic container with lid (19.5 cm diameter × 6.0 cm high; flat drumming surface of 15.5 cm diameter), covered in black contact paper, as the drum. This drum provided a target that was at a comfortable height for the child when sitting at the table, and produced a clearly audible thump when struck with a drumstick. A 2.5 cm square piece of reflective tape was attached to the center of the drum surface. A second set of drumsticks and identical drum was used by the model who sat across the table from the child. A Seiko SQ50-V metronome provided a beat of 160 bpm (2.67 Hz) for applicable bouts.

A custom-made calibration frame was constructed to fit the small calibration area. This frame, made with 10 wooden dowels inserted vertically into a pegboard and plywood base, created a cubic calibrated area of 62 cm along each dimension. All surfaces were painted black. The origin marker was placed at the front left corner of the base, and narrow (.1 cm) bands of reflective tape were placed on each vertical rod at heights of 10 cm, 30 cm, and 50 cm. Precise measurements were taken so that the exact location of each marker was identified from every camera view, allowing reliable calibration to be established before the start of each assessment session. In order to present a clear view of the reflector tape on the drumsticks and drum, each child wore a custom-made long-sleeved black shirt with back closure during all filming sessions. Black cloth backdrops were hung behind and to the sides of the child. The cube used for the table was covered in black contact paper, while the cube used as the chair remained red, since it typically was not within visible range of the drumming action.

All sessions were filmed by four Panasonic PKG S55 cameras placed to the sides and front corners of the room, each approximately 1.5 m from the calibrated assessment area (Figure 4.2). Each camera was mounted on a tripod at an approximate height of 1.25 m, with an adjacent spotlight (Smith Victor 700 SG; 650W max.) focused on the assessment area. All sessions were recorded on 60-minute DV mini tapes (TDK) and copied onto backup DVDs. Bouts were isolated, digitized, and processed using Vicon/Peak Motus software v. 8 on a personal computer connected to a JVC SRDVM professional series player/recorder.

Figure 4.2.

Arrangement of the assessment room.

4.3. Procedures

All assessments were conducted at the campus laboratory that had been set up for the purposes of the infant drumming assessments. The initial appointment for assessment was made as close to child exact-age 15 months as possible, although a few initial appointments could not be scheduled until the child was 16 months old. Subsequent monthly sessions, all held on Saturdays to accommodate parents’ work schedules and lab availability, were scheduled as close to the day of the month that the child was born as possible.

Upon arrival, families were greeted and a few minutes were taken to acclimate the child as needed, help the child don the black shirt, and at the first session, complete informed consent procedures. The PI, who served as the Experimenter (E) and drumming model during all sessions, accompanied the parent and child to the assessment area, asking the child to sit in the cube chair and the parent to sit either behind the child or across the room. Parents were asked to encourage their children to attend and participate but not physically help with the drumming. One or two research assistants turned on the videorecorders, took notes, and assisted with preparing manipulanda for the assessments.

The study was designed as a structured observation rather than a tightly controlled experiment, given the challenges of working with children between one and two years of age (i.e., burgeoning willfulness along with difficulties following precise instructions for complex motor tasks). Before engaging in the drumming task, the researcher administered a brief hand preference assessment to the child, assessing which hand was used to grasp small toys and perform common functions such as using a spoon or hairbrush. The assessment also included a single role-differentiated bimanual task of opening a small container and removing a toy from within. Specific behaviors and data from this assessment are presented below in Section 4.5.

After the hand preference assessment, the researcher, sitting as the adult model across the table from the participant, introduced the drum and drumsticks to the child. In order to gauge spontaneous coordination patterns and tempo, the child was first encouraged to drum independently, with no model or metronome support, in order to gauge spontaneous behavior for that session. After the child did so for a few bouts, or refused to do so, the metronome was turned on to sound at 160 bpm (2.67 Hz), and the child again encouraged to produce a few bouts of independent drumming. Finally, the social modeling condition was introduced, with the adult model alternating between in-phase and anti-phase bouts in time with the beat of the metronome. If the participant spontaneously initiated one or more drumming bouts without a demonstration by the adult model, the toddler was allowed to do so and the alternating demonstrations resumed afterward.

The metronome value was derived from the average rate of spontaneous drumming exhibited by children 12–24 months of age in an earlier study, so that it would be a comfortable rate for children in this age range. The adult model kept pace with the metronome when demonstrating in-phase drumming. However, because anti-phase activity tends to be less stable than in-phase at faster velocities, anti-phase drumming was modeled with each limb at 80 bpm, or 1.33 Hz. Thus, there was a single drumstrike at each beat of the metronome. We selected these drumming rates to be a comfortable and manageable pace for children to follow. Our analyses in subsequent chapters explore whether the differential tempo of the model’s drumming under different conditions influenced the toddlers’ performance; in short, it appears not to have had a substantive effect.

Initiating this condition with an in-phase or anti-phase bout was counterbalanced between children and at different ages within each child. Because we aimed to elicit as much drumming behavior from each child as possible, bouts were not limited to a particular length but rather were determined by the dynamics of the dyadic interaction between toddler and adult model; the model monitored the toddler’s attention and engagement with the task in order to time initiation and termination of bouts. Most modeled bouts lasted between 10 and 20 cycles; child bouts varied widely depending on the toddler’s interest and responsiveness to the model. Drumming sessions continued as long as the child was interested; most children clearly indicated when they were finished with a session by putting the drumsticks down or leaving the chair. Children exhibited a wide range of engagement with the drumming task, differing across children as well as from month to month. Typically, children produced between 5 and 18 analyzable bouts; however, there were outliers on days during which the toddler was particularly enthusiastic (e.g., P3 at 19 months of age; P5 at 17 months) or reluctant to engage (e.g., P1 at 17 months; P6 at 23 months).

Later, trained research assistants used Motus software to establish the calibration space for each session, isolate each bout of drumming, and then digitize the movement of the two drumstick heads as well as the stationary drum surface. To be included in the digitized record, a bout had to be clearly visible and have had at least 3 strikes of the leading hand’s drumstick on the drum surface. Because we were primarily interested in the vertical movement of the drumsticks held in the toddler’s hands, and in keeping with standard practice in related research, we relied on 2-dimensional analyses and analyzed data from a single camera (typically the one looking over E’s right shoulder and facing the participant) rather than synchronizing and integrating multiple camera views.

4.4. Data Preparation and Analysis

Our primary outcome variable involved occurrence of relative phase, as defined in section 4.4.1 below. In later chapters, we report analyses using oscillation frequency, amplitude ratio of the arms, initial limb positions (or “initial conditions”), limb joint axis of primary movement, and initial attentional focus as predictor variables. We also include age in months and adult-model condition as predictors in analyses as appropriate. We define each of these measures more fully in the chapters reporting the respective analyses. Here, we outline some data preparation and analytic techniques common to all of these analyses.

The analyses reported in this monograph focus on movement of the drumsticks in the vertical direction, which represents the primary axis of interest. We made this decision for two reasons. First, the majority of the analyses were built upon the hypotheses resulting from the dynamical systems approach that primarily focus on the coordination between limbs along a single axis. When different axes have been analyzed (e.g., Buchanan, Kelso, DeGuzman, & Ding, 1997), each has been analyzed separately. Second, understanding variables that relate to the developmental organization of coordination of two time-series is a complex matter in itself. There are many relevant variables and, as we will show, not all relate to coordination at the same time within the same individuals. Given the goals of the present study, we therefore did not judge it advantageous to increase the complexity of analyses by adding a second movement dimension.

In order to ensure that each bout included enough data points to permit our analyses, bouts with fewer than 5 cycles of action by a single arm were not analyzed. To make sure that this criterion would not bias results in relation to phase-modeling conditions, and to test that children had no undue difficulty performing in the anti-phase adult-model condition, we performed a general linear mixed effects analysis (LME; described in section 4.4.2) to learn whether there was a tendency for short bouts to have occurred more in one or another condition. The results demonstrated that short bouts occurred more often under the No-model condition than with either an in-phase or anti-phase model. This appears to reflect the tendency for children to produce more trials in the No-model condition than in the modeled conditions. It is not surprising that bouts produced without a social partner (a stimulus of a kind) to model the action would be more variable in their duration.

Prior to all analyses reported below, all digitized data were filtered by a low-pass Butterworth filter at 10 Hz and a smoothing procedure (moving average of a span of 5 frames – smooth code from Matlab). The filtering frequency was decided on the basis of maintaining specific movement characteristics of this age range. Technically speaking, although frequencies faster than 5 Hz frequency band contributed relatively little to the frequency spectrum of the signal (less than 5%), we determined that a cut-off frequency under 10 Hz would create unrealistically smooth motion of the limbs, almost as if the toddlers were moving like adults.

4.4.1. Relative phase.

To discuss bimanual coordination patterns, researchers have frequently used the collective variable of relative phase, a measure of delay between two sinusoidal functions (Figure 4.3). When plotting a circle, one can identify the sine of a given vector that has as its origin the center of the circle and has the magnitude of the radius of the circle (Figure 4.3.a). If, understanding that the magnitude remains constant, the vector is changed over time by altering its angle (let us say θ), one can describe the sine changing in terms of this angle as it forms the sine wave. Plotting this over θ (Figure 4.3.b), this change nicely exhibits an oscillatory pattern that can be used to represent the oscillatory pattern that toddlers are required to perform in our task. The phase of a sinusoidal function is the angle that characterizes the sinusoidal wave at a particular moment in time. For instance, following Figure 4.3.a, if a sine-wave starts with a phase of 90°, the initial value is 1. In figure 4.3.b, the initial phase of the angle is 45°.

Figure 4.3.

Schematic of the relative phase derivation. Part (a) illustrates how the sine of an angle is derived from a vector (in any x and y coordinates, see the continuous and Hilbert transform relative phase measures in the text). In (b), the oscillation of the sine is shown in terms of changes in the angle θ. Part (c) depicts how the phase of each angle is considered in terms of the other. In the illustration, the phase relation is 45°, but see text for additional details.

The relative phase between two sinusoidal functions is the difference between these phases (in the case of Figure 4.3.c, the relative phase would be 45°). Note that using a single value to describe a phase relationship over time assumes that the sinusoidal functions maintain their properties over time (e.g., amplitude, frequency, phase). In efforts such as ours, this is not the case and the phase relationship might change over the course of a drumming bout. In these less-constrained settings, the relative phase is just the difference between the current angles at which two sinusoidal functions are evaluated at a particular moment in time. Thus, a single bout of action may be characterized by frequently-changing relative-phase values. Categorizing phase relationships into in-phase (close to 0°), anti-phase (close to 180°), and out-of-phase (values that are between in- and anti-phase) simplify these characterizations.

There are many ways to measure relative phase (see Kurz & Stergiou, 2004). In the present study we used the Hilbert Transformed Relative Phase. The Hilbert transform extends a single time series into the complex plane resulting in real and imaginary parts. This system allows for computation of the signal’s phase at a given instant using the vector composed of the real and imaginary parts of the signal (as illustrated in Figure 4.3.a) and comparing it to the signal produced by the contralateral limb – resulting in the relative phase. This method has been successfully implemented in studies of motor behavior (for instance, Lafe, Pacheco, & Newell, 2016) and is arguably better than alternative measures (see Lamb & Stöckl, 2014 for methodological comparisons).

4.4.2. Linear Mixed Effect Models (LME).

For all chapters, hierarchical linear mixed effects models (LME) analyses were used (see Singer & Willet, 2003 for a review). This technique allows analyzing nested data (data within individuals, in the present case) in a single analysis without violating the assumption of independence of data. Also, it provides means to measure the effect of the independent variables while respecting the individual differences among our participants. That is, unlike other approaches, this analysis allows estimation of random effects. These represent the variability that occurs around the usual fixed effects to measure how each nested set of data was different from the other set. This approach thus can show, for instance, how each individual differed over the course of months from the average group change along the same parameter.

Figure 4.4 illustrates the differences between the usual analysis of variance (ANOVA) and LME. Figure 4.4.a shows a performance change from pre- to posttest as presented in an ANOVA. This analysis presents the average of the group in the pre- and posttests (or the mean change under similar analyses) in explaining the data, with all the variance around this mean being considered as unexplained variance. Thus, a single-average beginning and end (or average change) is considered for all individuals of the group together. The LME extends the analysis from the general effect of the whole group (fixed effects) to a consideration of variability (random effects) that is particular to the individual level of analysis.

Figure 4.4.

(a) Example of the differences between an average approach to repeated measures; (b) example of differences in the intercept (same slope representing change); (c) example of differences in the slope; (d) example of differences in both intercept and slope.

Both effects are tested in the LME. That is, we can test whether all individuals differ only on the pretest, only on the change from the pre- to posttest, or in terms of both. These cases are illustrated in Figures 4.4.b, 4.4.c, and 4.4.d, respectively. The LME also provides a test of whether these variances are related. That is, it is possible that those individuals with high pretest performance do not increase performance as much as the ones who performed poorly in the pretest.

When implementing LME analyses, we used a backward method selection of variables in the model using the Bayesian Information Criterion (BIC: Schwarz, 1978) as a fitting measure. That is, we evaluated whether an independent variable was required in the model by using a measure that evaluates whether the model can explain relatively the same amount of data with or without the variable in question. The BIC is an evaluation measure that penalizes the model by the number of variables required to explain the variance.

Specifically, we fitted a model with all independent variables and noted the resultant BIC. From this, we collected the t-statistic of each variable and chose the lowest t-statistic variable to be excluded from the model. We then re-ran the model without the excluded variable and noted the new BIC. If the new BIC was lower than or equal to the first, we concluded that the model could maintain its explanatory power with the smaller number of predictors. We then repeated this procedure. If the new BIC was instead higher than in the previous run, we returned the excluded variable to the model. This procedure was followed by first taking out a variable with its fixed and random part at once using the Maximum Likelihood fitting method. Once the lowest BIC was reached, we tested only the random part of the effects using the Restricted Maximum Likelihood fitting method. The differences between the fitting methods come from their ability to test either fixed and random effects or only random effects.

Finally, some of our data did not follow a normal distribution. Although it can be argued that the LME is robust against small violations of the assumption of normality (Raudenbush & Bryk, 2002), we tested different transformations and distributions that the GLME (general linear mixed effect modeling) could handle if the data were non-normally distributed. Each performed transformation is described in the specific chapter in which the analysis was performed with the kind of transformation required.

4.4.3. Wavelet Analyses.

Two of the primary variables we hypothesized would contribute to the acquisition of the anti-phase movement pattern coordination are frequency of oscillation and amplitude ratio between drumsticks (representing extensions of the limbs or hands). General spectrum analyses provide the power (≈ amplitude) of all frequencies of oscillation of a given signal. Nevertheless, these analyses are associated with the assumption of a stationary time series, which is not an assumption that can be appropriate for the data under analyses here: learning and development are, by definition, about change in many properties of performance (variability, mean performance, etc.). A tool used to measure frequency of oscillation not assuming non-stationarity in recent research on motor control is the Wavelet analysis (see Torrence & Compo, 1998).

In general, wavelet analysis decomposes a continuous or discrete signal into a spectrum profile that represents the distribution of powers per frequency, per unit of time. That is, instead of having a single distribution of powers in terms of frequencies for the whole bout, the analysis provides the distribution of powers for each time point. To use this approach, we chose a prototype or “mother” function that represents the function into which the data will be decomposed. Like the Fourier transformation in spectrum analysis that decomposes the signal in terms of sine-waves, the wavelet analysis decomposes the signal in terms of the prototype function. We used a common prototype function: the Morlet function. Figure 4.5.a illustrates the prototype function.

Figure 4.5.

(a) Morlet function used for the wavelet analyses; (b) a simulated signal made of three different sine waves; (c) and the frequency vs. time plane of the wavelet analysis of the signal shown in b.

The prototype function, then, is scaled in amplitude and time to match the signal observed in terms of time windows of different sizes. In this way, one can know the required amplitude and frequency of the prototype function necessary to describe the signal in that time window. Figure 4.5.b shows a signal composed of different sine waves and Figure 4.5.c shows its decomposition in frequency and time. As can be observed, in the first third of the signal, there is a lower-amplitude (from −0.5 to 0.5) fast-frequency (0.4 Hz) oscillation: observed as a middle power (green) fast frequency in the figure. The second third of the signal includes a higher-amplitude, lower-frequency (0.1 Hz) signal. The last third of the signal is a combination of a small-amplitude-fast-frequency (0.4 Hz) signal with a large-amplitude-slow-frequency (0.04 Hz) signal (demonstrated by two colored areas in the Figure 4.5.c plot). The shaded area in 4.5.c is the cone of influence, which identifies an area in which part of the required procedure itself may have induced some spurious results. Note, however that the potentially spurious results are limited to frequencies considerably lower than the ones studied here.

For all analyses that concerned amplitude or frequency in the present study, the frequency and amplitude of the signal were determined through the wavelet analysis. That is, as we performed the wavelet analysis, we found the peak power (the most prevalent signal) for each time point. We then identified the related frequency for each time point, creating a time-series of frequencies. In addition, we noted the peak power for each individual time point, thereby creating a time-series of powers. The powers were treated as the amplitude of the given signal at that time point – the amplitude of oscillation.

4.5. Characterization of the Toddlers’ Manual Activity

We expected the toddlers to reach and grasp small objects efficiently, use the hands together to explore objects and perform simple role-differentiated coordinated actions, and interact with familiar objects or tools in appropriate, if not elegant, ways. To establish basic manual competence and laterality, we conducted a brief battery of object-manipulation tasks at the beginning of each monthly session. The assessment presented here concerns participants’ ability to grasp the objects involved in the tasks, success or failure in performing the task, and hand laterality in unimanual and bimanual tasks. We defined grasping as the child first securing the object with the fingers or palm(s) using one or both hands, and then controlling the movement of the object along the table’s surface or lifting it above the table.

The unimanual tasks asked children to 1) write or draw on a piece of paper, 2) throw a ball, 3) squeeze a small toy animal to make it squeak noise, 4) pick up a small object from the table, 5) brush their hair, 6) pretend to eat with an empty plastic spoon, and to 7) brush their teeth with a small dry toothbrush. The bimanual tasks involved 1) lifting a lid and retrieving a toy, 2) opening a toy flip-phone, and 3) pressing the numeric buttons on the flip-phone. Success was defined as correctly completing the requested action. Partial credit was given for responses that included some but not all components of the requested action. Behaviors given partial credit included actions that were motorically competent but failed to meet the specific request, for example, using the spoon to feed a toy rather than self. If children did not attempt a response to a given request on a given day, that item was treated as missing. The hand used to open the phone, lift the box lid, and press the phone buttons was scored each time the action was performed. The dominant hand for each task on a given day was categorized as Right, Left, or Mixed.

Figure 4.6.a shows the percentage of grasping for each month for each participant. Percentages were calculated on only those tasks with which the children engaged; sometimes toddlers refused to participate in one or two of the tasks; this occurred independently of age and task. As can be seen in the figure, all children were quite consistent in grasping successfully throughout the study.

Figure 4.6.

(a) Percentage of grasping in the unimanual/bimanual tests per month per participant; (b) number of successes, partial successes and failures per month per participant; and (c) number of right, left, bimanual, and alternating hand usage on the unimanual/bimanual tests per month per participant.

Figure 4.6.b show performance on all tasks for each month for each participant. Although some participants (P2, for instance) varied in the quantity of tasks that they engaged, success or partial success were the two most prevalent categories throughout the study. For most participants, failures occurred mainly during the first months (see P1, P2, P3 and P4) and usually involved squeezing a toy, eating with a spoon, or brushing teeth. The ratio of partial success to success did not seem to change with age or as a function of the task being unimanual or bimanual. Indeed, a LME analysis demonstrated that the ratio did not change over time or as a function of type of task (only the intercept remained in the model). This consistent ratio may reflect some toddlers’ tendency to perform the same actions with particular objects in the battery from month to month. They appeared to remember what they had done before and often insisted on repeating the actions in the same way, even if this yielded a partial success score. This occurred, in fact, with the majority of partial successes with the hairbrush, spoon, and toothbrush, for which children often acted on an adult, doll, or toy animal rather than performing the actions on themselves. These actions demonstrated motoric competency but were scored as partial because the children altered the targets of the action to ones they could see.

Finally, Figure 4.6.c illustrates the distribution of tasks performed with the right, left, or both hands. As can be observed, P1, P2, P3, P4, and P6 showed a higher prevalence of right-handed movements, with the left hand appearing most often in the lid-opening task. On the contrary, P5 and P7 showed higher usage of the left hand for the presented tasks, although P5 demonstrated higher variability in usage and thus appeared less lateralized than other participants.

5. Overview of Toddlers’ Performance: Phase Relationships and Production of Bouts

In the present chapter, we describe processes of change across months within a bimanual skill-development context. Our main goal is to describe the emergence of the anti-phase coordination pattern in drumming. Following the procedures used by Brakke et al. (2007), we first characterize the potential transition from unimanual to bimanual activity, and then explore the development of phase relations in bimanual drumming, characterizing the dynamics of such change in individual children.

5.1. Specific Analyses

The main outcome variable of interest for the bimanual analyses reported in this chapter is the relative phase between the drumsticks (see Chapter 4).

Our first analysis described the number of trials and cycles that participants performed per visit. This analysis reflects engagement with the task as well as the capacity to execute the oscillating behavior. We divided the trials into bimanual and unimanual trials, defined by vertical motion of one or both drumsticks during the bout. We employed three different linear mixed effects models. The first LME characterized the probability of occurrence of unimanual bouts per month. The probability was computed simply by the number of unimanual bouts divided by the total number of bouts during that month for each participant. The second LME characterized the change in number of bimanual bouts per month, and the third, the duration of each bout. All of these had the intercept and change per month as random effects being tested.

We then examined the time spent performing the anti-phase pattern per bout in terms of absolute time in seconds and percentage of total engagement. Given that the principal attractors observed in the literature for both children and adults are either in- (0°) or anti-phase (180°) (e.g., Cohen, 1971; Isenhower et al., 2012; Kelso, 1984), we defined the range of anti-phase motion to be above 135° and less than 225° (a range of 90°). Thus, if the relative phase was within this range, we characterized the phase as “anti-phase”. Note that this criterion is more conservative than the criterion adopted in other studies with children (for instance, 180° range in Volman & Geuze, 2000). In this initial analysis, we therefore included three categories of coding: in-phase (from −45° to 45°), anti-phase (from 135° to 225°) and out-of-phase (any phase relation not in the in- or anti-phase range). These categories allowed some range of flexibility in defining the phase relationships for the children as they were exploring the new task.

After categorizing the phase relation for each bout, we observed that there was a high degree of variability between bouts in terms of the number of seconds spent in anti-phase pattern, with many bouts showing no anti-phase time at all. This is reasonable considering that the in-phase pattern serves as a strong attractor state. However, assigning values of zero for non-performance of this coordination pattern would bias the mean values of anti-phase cycles and would not reflect individual toddlers’ capacity to perform the anti-phase pattern. Thus, as a summary measure, we used the maximum amount of time in anti-phase per bout instead of the average.

Although the overall time in anti-phase during each month provides an index of the capacity of each individual to perform the anti-phase pattern, the capacity to maintain the pattern over continuous periods longer than a single action cycle must also be addressed. In other words, we should consider the stability of the pattern. Bimanual drumming is considered a continuous task and thus the ability to maintain a stable mode of coordination across cycles directly relates to performance mastery. At younger ages, for example, toddlers may not maintain the anti-phase pattern for more than a few movement cycles because of the initial tendency to perform a coupled in-phase pattern, or because phase relations may be highly variable when the toddler is learning to engage the anti-phase pattern. For the purpose of assessing stability, then, we analyzed each bout in terms of the longest continuous time the toddler spent performing the anti-phase pattern. We used the same categorization of anti-phase cycles described for the previous analysis. We used the maximum time across all bouts in all social-model conditions per month as a summary statistic.

For both total time per month and the longest continuous time performing anti-phase (hereafter called longest time), we performed an LME analysis for each measure in terms of months and social-model conditions (In-phase, Anti-phase, and No-model condition). Intercept and change per month were also tested as random variables.

Finally, we explored the distribution of phase patterns per month over the whole spectrum of possible relationships from −90° to 270°. This allowed us to observe how the intrinsic dynamics of action (see Kelso, 1995) changed in terms of central tendency and range. This analysis was done by concatenating the relative phase of all trials per month and then depicting the distribution frequency in terms of different relative phases. To do this we fitted the distribution using kernel fitting (viz, the fitdist function of Matlab).

Given that the procedure we used involves an adult demonstrating anti-phase and in-phase drumming, an additional analysis is required to verify whether attention to the adult’s actions influenced results. Given that this is just a “control” analysis for the other measures, the details of the analyses and measures are provided in the online supplementary files S1 and S2; in this chapter we briefly summarize the results.

5.2. Results

5.2.1. Overview of Visual Attention.

In order to assess to which aspects of the task children were attending, we observationally coded targets of visual attention during each drumming bout. Toddlers’ initial eye gaze was coded as being directed at the drum(s) on the table, at the adult model’s face or body, at the parent, or at other targets in the room, for example, the camera, other parts of the room, or other research assistants. For this analysis we were interested in how attention at the start of each trial was directed, but not how attention was distributed over time. Thus, prolonged looks and quick glances were counted equally.

Two independent coders scored 81 trials representing sessions from all seven participants and obtained 95% agreement with a weighted Cohen’s Kappa value of .90, which is in the “Very Good” range. This analysis revealed that, throughout the study period, toddlers at the start of each trial looked attentively to the drums (67% of the trials) or the experimenter (23% of the trials). The remaining attention was shared across other targets. These values were maintained across the months of assessment, and patterns did not differ significantly over age or across social-model conditions (see the online supplementary files S1 and S2 for more detail on this analysis). We found, however that the toddlers performed the anti-phase pattern for longer periods when they had initially attended to the adult model when compared to the drums and other targets of visual attention, and better when they started by looking to the drums rather than at other targets that could be considered distractions from the task. These differences lessened as the toddlers got older; the effects on anti-phase stability of attending to the adult, drums or other targets decreased, but did not disappear, with age.

5.2.2. Unimanual Bouts.

For the probability of occurrence of unimanual bouts, we used the GLME for binomial distributions with each observation weighted by the number of bouts in that month. Figures 5.1.a and 5.1.b illustrate the data and the fitted model. Table 5.1 shows the results of the GLME analysis. The results suggest no general trend in terms of unimanual bouts (both intercept and change were non-significant) but the random effects were necessary to explain the model. That is, individuals varied in terms of how much they performed unimanual bouts initially and in terms of the change of unimanual bouts prevalence over time. Additionally, as can be seen in Figures 5.1.a and 5.1.b, those individuals who produced an initial high prevalence of unimanual bouts were also the ones showing a subsequent strong decrease in prevalence. In sum, those who engaged in unimanual bouts at the beginning of the study period decreased the probability of these bouts afterward, mirroring the developmental transition demonstrated in Brakke et al. (2007) for a similar age range.

Figure 5.1.

Data (a, c, and e) and fitted LME models (b, d, and f) on the probability of unimanual bouts (a and b), number of bimanual bouts (c and d), and time per bimanual bouts (e and f).

Table 5.1.

Results of the linear mixed effect analyses

Unimanual bouts (probability of occurrence)			R2 = 0.59
Fixed Effects
Name	Estimate (± SE)a	t-stat (df = 66)	p-value
Interceptb	−1.22 (± 0.97)	1.26	.212
Change (per month)	−0.24 (± 0.18)	1.35	.181

Random Effects
Name	Type	Estimate
Intercept	SD	2.44
Intercept x Change	R	−0.85
Change	SD	0.44
Residual		1.00

Bimanual bouts (count)			R2 = 0.33
Fixed Effects
Name	Estimate (± SE)c	t-stat (df. = 66)	p-value
Interceptb	2.34 (± 0.25)	9.31	< .001
Change (per month)	−0.02 (± 0.03)	0.56	.576

Random Effects
Name	Type	Estimate
Intercept	SD	0.63
Intercept x Change	r	−0.87
Change	SD	0.08
Residual		1.00

Time per bout (s)			R2 = 0.52
Fixed Effects
Name	Estimate (± SE)c	t-stat (df = 66)	p-value
Interceptb	1.48 (± 0.14)	10.66	<.001
Change (per month)	0.04 (± 0.01)	3.28	.002

Random Effects
Name	Type	Estimate
Intercept	SD	0.28
Change	SD	< .001
Residual		1.90

^aThese estimates are not the probabilities. These are the outcome from the GLME. The probabilities are derived by plugging these values into the logistic function;

^bThe intercept is considered at the 15^th month of age;

^cThese estimates are not the number of bouts or seconds. These are the outcome from the GLME. The real values are derived by plugging these values on the exponential function;

5.2.3. Bimanual Bouts and Time.

The number of bouts produced, and the time spent performing a bout per month, independent of phase, are presented in Table 5.2. Figures 5.1.c and 5.1.d illustrate the data and fitted statistical model for the number of bimanual bouts. To assess the number of bimanual bouts, we used the GLME with a Poisson distribution. Table 5.1 includes the results of the LME. Only the intercept remained in the fixed effects after using the backward fitting method. This suggests that, in general, the toddlers maintained a relatively consistent number of bouts (averaging 10.28) throughout the study period. Additionally, individuals demonstrated significant variability among the sample in terms of how many bouts they produced during the first months and how they changed the number of bouts per month. Importantly, the variance in intercept and change were negatively correlated, meaning that those who had a higher number of bouts at the beginning of the year decreased the number later and vice-versa.

Table 5.2.

Bimanual bouts and time per bouts per month for each participant

Bouts (count)
P	Age (months)
	15	16	17	18	19	20	21	22	23	24	25	26	27
1		5	2		3	7	8	8	22	9	7
2		13	5		1		5	9	13	14	5	10
3	27	8	13	22	42	24	17	9	12	16	8	18	9
4		1	7	3		14		7	12	23	7	8	6
5	24	2	37	16	17	10	13		1	17
6		15	8	5	9		4			2
7		18	12	9	8	7	8	1	7	6	9	3	27
Average time per bouts (s)
P	Age (months)
	15	16	17	18	19	20	21	22	23	24	25	26	27
1		5.6	9.3		12.3	11.6	16.5	7.4	9.9	8.0	11.4
2		3.1	3.5		1.6		8.3	8.1	7.3	7.0	7.7	8.4
3	4.2	4.5	2.7	3.8	3.2	4.8	6.2	4.5	5.6	7.1	5.2	5.0	7.0
4		10.6	5.9	2.7		6.4		3.2	3.6	3.9	6.5	4.9	6.6
5	4.1	2.1	3.4	4.7	5.4	3.4	2.2		5.7	6.6
6		3.8	3.0	5.3	4.7		4.3			9.2
7		3.4	3.7	3.6	3.5	3.6	3.6	2.5	5.5	4.3	5.4	6.0	5.4

For the time performing bouts, we used the GLME with a log transformation of data (similar to the Poisson distribution analyses with continuous data). Table 5.1 shows the results and Figures 5.1.e and 5.1.f illustrate the data and statistical fitted model. Both intercept and change per month were significant on the fixed effects. Thus, on average, toddlers started the data collection averaging 8.75 seconds per bout and increased by 1 second per month. Remember, however, that bouts with fewer than five complete cycles were omitted from analysis and are not reflected in these values. The intercept and change per month also varied between individuals but no correlation between these measures was observed.

5.2.4. Total and Longest Time in Anti-Phase.

Figure 5.2 shows the distribution of relative phases per individual for each social-model condition, combining all bouts across all ages. For all social-model conditions, the in-phase pattern of coordination is the most frequent pattern. Clearly, then, the in-phase pattern can be considered the toddlers’ preferred pattern from the start of the assessment period at 15 to 16 months of age. Across all ages, the toddlers had to counteract this in-phase tendency in order to perform the anti-phase pattern. The figure also shows a tendency for phase relationships to be more variable, including more anti-phase bouts, in the No-model and Anti-phase conditions compared to the In-phase condition.

Figure 5.2.

Polar histograms for each participant in each social-model condition, totaled across all ages. For better visualization, values were normalized according to the most frequent bin. Each bin contains 30° of phase range. In-phase cycles are represented on the right half of each plot (centering on 0°); anti-phase cycles are represented on the left.

The anti-phase coordination pattern occurred at least once in the group of participants at all ages under all conditions. Figure 5.3 shows the trend of anti-phase pattern performance over time for each condition. As the figure illustrates, there was high variability in anti-phase performance over time with a small apparent increase in the Anti-Phase demonstration condition over months.

Figure 5.3.

Total time performing the anti-phase pattern (upper panels) and longest time within a trial performing the anti-phase pattern (between 135° and 225°) within each month per participant per model condition.

For the total time within a bout performing the anti-phase pattern, we used the LME. Table 5.3 presents the results. The analysis showed that, on average, the amount of time performing the anti-phase pattern (1.81 s) was greater for the anti-phase model condition compared to the no-model and in-phase model conditions (−1 s and −1.42 s; in other words, bouts in these conditions were 1.0 and 1.42 seconds shorter, respectively, than in the anti-phase model condition). This time increased by 0.16 s per month. The random effects showed that the change per month varied between individuals.

Table 5.3.

LME results for the total time and longest time within a bout performing the anti-phase pattern per month and model condition.

Total Time
R2 = 0.30	df = 179
Fixed Effects
Name	Estimate (± SE)	t-stat	p-value
Intercepta	1.81 (± 0.26)	6.90	< .001
Change (per month)	0.16 (± 0.05)	3.40	< .001
No-Model	−1.00 (± 0.26)	3.83	< .001
In-Phase Model	−1.41 (± 0.26)	5.38	< .001

Random Effects
Name	Type	Estimate
Intercept	SD	0.001
Change (per month)	SD	0.09
Residual	SD	1.44

Longest Time
R2 = 0.10	df = 180
Fixed Effects
Name	Estimate (± SE)	t-stat	p-value
Intercepta	0.89 (± 0.07)	12.13	< .001
No-Model	−0.25 (± 0.10)	2.47	.014
In-Phase Model	−0.47 (± 0.10)	4.52	< .001

Random Effects
Name	Type	Estimate
Residual	SD	0.57

^aThe intercept refers to the estimate for the 15^th month of age; df: degrees of freedom; SE: Standard Error; SD: Standard Deviation.

For the analysis of longest time (i.e., the longest continuous time performing anti-phase), we again used the LME. Table 5.3 presents the results for this variable. The analysis indicated that, on average, individuals maintained the anti-phase coordination pattern for 0.86 s in the Anti-phase model condition compared to 0.42 s with an in-phase social model and 0.60 s in the No-model condition, with no significant change over time. This result is expected when we consider the variability illustrated in Figure 5.3 – individuals do not seem to exhibit a smooth linear trend in their performance of the anti-phase pattern.

To further demonstrate the developmental increase in capacity for performing the anti-phase coordination pattern, we present Figure 5.4 following van Geert and van Dijk (2002). This figure illustrates the longest, or most stable, anti-phase segment performed by each toddler up to that month. If the toddlers never improved in their potential for stable anti-phase performance, the slope of the lines in the figure would be flat. By contrast, we observe a sharp increase around 18 months in multiple toddlers (see P3, P5, P6, & P7), demonstrating substantive improvement in their capacity to stably produce anti-phase cycles.

Figure 5.4.

Longest time performing the anti-phase pattern ever performed to date for each month. Flat lines indicate that no sequences have occurred that are longer than in previous sessions.

5.2.5. Distribution of relative phases.

Figure 5.5 shows the distribution of relative phases performed by each child in each social-model condition. This analysis provides a qualitative characterization of how the phase relations of action changed in each condition as the toddlers developed.

Figure 5.5.

Distribution of relative phases performed per month for each individual in each condition. Younger ages appear behind older ages for each child. The X axis represents the relative phase in degrees for each measurement window, the Y axis indicates the frequency of measurement windows that fall within the different relative phases, and the Z axis depicts the toddler’s age at each assessment session.

Toddlers demonstrated individual patterns of change in phase distributions that appear to show similar general trends across participants. We begin with the individual characterizations. P1 exhibited a strong tendency to perform the in-phase pattern in both in-phase and no-model conditions. His attempts to break this strong attraction to in-phase are observed in the anti-phase model condition, in which a large dispersion throughout the range of possible phase relationships is observed. P2 demonstrated similar patterns in both in-phase and no-model conditions: he evidenced a strong tendency to perform in-phase during early months with later increased stability in both in- and anti-phase patterns. The Anti-phase condition, nevertheless, is where we observe P2’s initial instability (i.e., distribution over the whole spectrum of phases) with an increase of stability in the anti-phase pattern in later months. P3 showed a similar pathway of change as P2, but interestingly demonstrated more instability in the anti-phase pattern with an anti-phase social model and in the in-phase pattern with either an in-phase social model or no model at all.

P4 exhibited high variability in all conditions with a tendency to perform both the in-phase and anti-phase patterns more stably in later months, but only when the adult model was demonstrating the matching phase relationship. P5 demonstrated strong in-phase stability in the In-phase condition for the entire study period. In the Anti-phase condition, we see a pattern of initial high variability, then later stability in the anti-phase pattern. In the No-model condition, P5 demonstrated initial stable in-phase patterns early in the study period, and in later months also stably performed the anti-phase pattern. P6 exhibited a well-defined change pattern of sequential stability, instability, and stability under both In-phase and Anti-phase conditions. With the in-phase model, he demonstrated the change pattern starting and finishing with production of stable in-phase movement patterns while, with the anti-phase model, he exhibited the change pattern with initial in-phase stability and later anti-phase stability. In the No-model condition, similar to P5, P6 demonstrated stable anti-phase pattern performance in later months. Finally, P7 showed a progression from stability to instability and subsequent stability in the no-model condition while performing the in-phase pattern. In the Anti-phase and In-phase conditions, P7 demonstrated a similar increase in instability but also exhibited later increased capacity to perform the anti-phase pattern as demonstrated by less variance in the phase distribution.

In summary, although variability was expected between individuals, we observed a convergent pattern of change in stability of coordination among the toddlers. This started with a decrease in stability in the in-phase pattern, primarily observed in the No-model and Anti-phase conditions. After this decrease, there occurred an initial exploration in the anti-phase region. Finally, then, some toddlers exhibited later stable performance of both phase-relation patterns. The stability of the in-phase pattern in the In-phase condition was less likely to be perturbed than under the Anti-phase condition. However, even in the In-phase condition there were clear moments during which the toddlers preferred to perform the anti-phase pattern instead of the pattern demonstrated by the adult model – suggesting that this task was often one of exploration as much as one of imitation for these toddlers.

5.3. Discussion

The analyses reported in this chapter were designed to explore the emergence of the anti-phase coordination pattern in toddlers from 15 to 27 months of age. We observed that toddlers presented short periods of relative phases around the anti-phase pattern as early as 15–17 months of age; more stable patterns were more likely to occur later, around the 20th month of age. This developmental change accompanied an increase in the temporal length of continuous anti-phase pattern, primarily performed in the Anti-phase condition. Additionally, we found a possible pattern of change in the exploration of action from stable in-phase activity to subsequent unstable performance, followed again by stable performance of both anti- and in-phase coordination patterns. These empirical patterns are consistent with earlier research by Brakke et al. (2007) showing that there was in-phase stability and anti-phase instability in a small group of 18-month-olds, but stable performance of both in-phase and anti-phase coordination among 24-month-old toddlers

5.3.1. From single cycles to sequences.

Isolated demonstrations of anti-phase coordination occurred in early months of toddlers’ participation in our study, but this does not mean that a stable pattern, indicating some degree of mastery, emerged during this period. For this reason, we analyzed both the total time each toddler performed anti-phase movement in a given trial and the longest time that the toddler continuously performed anti-phase movement to examine how stability progressed over the study period.

A simple explanation of the early isolated runs of anti-phase activity is that toddlers--given their developing motor control and the active nature of their exploration during play-- may have briefly explored this movement pattern while watching the model engaged in anti-phase action. This possible explanation is consistent with Thelen’s account of early phase exploration (Thelen & Corbetta, 1994). Another possible explanation comes from application of the HKB model to syncopation tasks made by Kelso, DelColle, and Schöner, (1990). Under some conditions, as when oscillation frequency increases beyond a certain value, there is a way of acting known as meta-stability. This type of action, perhaps counter-intuitively, denotes the actor wandering through the entire spectrum of phase relations, with neither in- nor anti-phase patterns being stable. Nevertheless, as Kelso et al. (1990) demonstrated, in meta-stability, the actor’s wandering tends to focus around the attractor states of in- and anti-phase coordination modes. This means in our case that the toddlers’ actions will remain longer at phase relations near 0° and 180°.

Interestingly, in exploring the data, we could identify signs of this wandering for some participants and not others; such wandering also appeared to correlate with age. This phenomenon must be more fully explored in future research but the data currently in hand seem to point to a transition from meta-stability to stronger coupling but that still occurs within the realm of relative coordination (see Fitzpatrick et al., 1996; Kelso, 1995). Relative coordination represents softer coupling when compared to absolute coordination; it means that individuals demonstrate attraction to a particular phase relation, but they may experience phase slips here and there for one or two cycles. This observation is similar to a report made by Fitzpatrick et al. (1996) that, at the age of 3 years, children demonstrated relative coordination in clapping behavior and, by the age of about 7 years, had developed into absolute coordination characterized by strong coupling.

When we consider either single cycles or longest sequences of anti-phase coordination, we observe an effect of the adult model. Specifically, the Anti-phase condition resulted in longer sequences and more cycles of anti-phase action; this condition also led to the majority of improvements in performance. The toddlers’ more stable anti-phase performance under the Anti-phase condition is expected given the adult’s corresponding action, while in the other conditions either the adult is presenting a different action pattern or not presenting any drumming behavior at all. It is interesting, however, that toddlers also demonstrate consistent coordination patterns that do not match the adult’s actions during a particular bout, suggesting that other motivations may sometimes be at play.

The data shown in figure 5.4 suggest that large increases in stability occurred around 20 months of age for most of the toddlers. Again, this result is consistent with Brakke et al. (2007), who demonstrated that 18-month-old toddlers were able to engage in anti-phase coordination patterns, but were less likely to do so in a stable fashion that were 24-month-old toddler. It appears, then, that the anti-phase pattern might be first stably performed in most toddlers around the 20th month of life, although individual variation is of course present.

Recall that past research has suggested that stability of both in- and anti-phase patterns continues to improve up to approximately 11 years of age in different contexts, likely reflecting maturation of the corpus callosum and other structures (Volman & Geuze, 2000; Wolff et al., 1998). Thus, well-defined, precisely-timed extended drumming sequences were not expected to be seen in the toddlers we studied, and the stability identified here is low relative to what is observed in older individuals. Nevertheless, we found that some toddlers were able to perform either of the two target coordination patterns with a considerable degree of consistency by around two years of age (see, for example, Figure 5.5, P2 in the in-phase condition), suggesting that anti-phase activity was already gaining the status of an attractor state. This finding, too, is consistent with the performance of the 24-month-old toddlers reported by Brakke et al. (2007).

5.3.2. Pathway of stability-instability-stability.

Our observations point to a convergent pattern of toddlers initially demonstrating stability while performing the in-phase pattern, followed by more unstable performance characterized by engaging in a large range of frequent relative phases. For some children within this age range we studied, this unstable performance leads to a new repertoire of stable anti- and in-phase patterns. Although we cannot provide a direct quantitative measure of the path of stability-instability-stability, our interpretation of Figure 5.5 fits with the theorized pathway of change.

Figure 5.6 displays a hypothetical pathway in terms of phase relationship distribution that occurs over time for an idealized child. This hypothesized pathway aligns with findings of studies based on the dynamical systems approach to skill acquisition. Zanone and Kelso (1992) found that, when adult participants learned a new 90° relative-phase pattern between motion of two fingers, they experienced at the end of the practice a loss of stability when performing the more-familiar 180° pattern. Later, Lee, Swinnen, and Verschueren (1995) demonstrated that this loss of stability was only temporary. That is, although individuals’ well-established patterns become more variable during the acquisition of a new movement pattern, in the end of practice, the original patterns return to regular levels of stability. Thus, the emergence of a new skill can affect, at least temporarily, the stability of already-known coordination patterns. This trajectory of fluctuating stability is similar to the one we identify in our toddler participants during the emergence of anti-phase coordination.

Figure 5.6.

Hypothetical relative-phase distribution as individuals get older and acquire or stabilize the anti-phase relative phase pattern.

We note, however, that it will be important to conduct additional research on this hypothesized pathway, given that this progression we observed was primarily in the No-model and the Anti-phase conditions. Within the In-phase condition, two toddlers showed no loss of stability (P1 and P5) whereas the other toddlers exhibited stability for some months. In the Anti-phase condition, instability might be expected given that toddlers are attempting to perform a yet-unstable pattern that they are seeing demonstrated by an adult. Any instability observed in the in-phase pattern in the identical social-model condition, however, would occur only as a result of the competition between pre-existing stable patterns and the intention to perform a different behavior in the absence of direct perception of the novel pattern. In the No-model condition, the context is different, in that there is no coordination pattern being demonstrated by a social partner. Nevertheless, the No-model condition is informative because it allows for assessments of stability of the different coordination patterns without the prompt of a model, and therefore reflects the toddler’s independent exploration of action space.

The findings reported in this chapter allow us to conclude that toddlers--over the age range included in our study--show improvement in their capacity to perform the anti-phase pattern. In keeping with our primary goal for the research reported in this monograph, we next examine participants’ strategies for implementing this coordination pattern.

6. Anti-Phase Pattern Acquisition: The Role of Frequency of Oscillation

This chapter is the first of four that assesses how toddlers explore the dynamics of action to perform the anti-phase movement pattern. As explained in Chapter 3, the toddler can change movement parameters to modify the competition and cooperation between the emergent pattern, and the intrinsic dynamics that facilitate the practice. We start our investigation by studying the frequency-of-oscillation parameter. This control parameter is the most discussed and empirically studied in the literature (see Kelso, 1995 for a review). The primary hypothesis being assessed here is that the toddlers will explore a range of limb oscillation frequencies to facilitate performance of anti-phase movement oscillation while using drumsticks to beat on a plastic drum. Specifically, we hypothesized that toddlers would explore the action by using lower frequencies of in-phase movement thereby allowing later performance of the anti-phase pattern.

6.1. Specific Analyses

As highlighted in Chapter 3, oscillation frequency, or rate of oscillatory movement over time, is a control parameter that can be manipulated over longer or shorter time scales. First, we analyzed the effect of the drumming model and toddlers’ age (in months) on oscillation frequency. Precision of synchrony (i.e., the degree to which the toddler was matching the adult’s beat on the drum) was assessed by calculating the disparity between the adult’s beats and the closest beat of the toddler. The moment of the toddler’s drumbeat, or hit, was defined as the lowest drumstick position within a cycle, assuming this was below the mean position value for the entire bout. The hand in each trial with hits closest in time to the adult’s right-hand hits was used to calculate the disparity from 0 – perfectly synchronous – to 1 – totally asynchronous. Additionally, we analyzed frequency of oscillation as a function of social model condition and months.

We then followed a step-by-step procedure observing how oscillation frequency related to anti-phase performance within both longer (month-to-month) and shorter (within monthly sessions) time-scales. The first step of our analysis was to see whether there is a general relation between relative phase and frequency in the hypothesized direction. Thus, we aimed to find out whether toddlers, across all ages, performed the anti-phase pattern with lower frequencies than when they performed the in-phase pattern.

The second step in our analytic plan was to determine whether we could find the relation between oscillation frequency and month-to-month phase changes. This analysis aimed to identify a long-term pattern of change that corroborates our hypothesis. That is, we expected to see a trend that goes from in-phase high frequencies, to in-phase low frequencies, to anti-phase low frequencies. In this chapter, we first qualitatively address the relation for each toddler individually and then provide statistical analyses of the data. The qualitative observations and the majority of quantitative analyses have been framed in terms of the relative-phase/frequency plane for both month-to-month and within-months analyses. For the month-to-month analysis, we used the bivariate distribution on this plane, representing the frequency of occurrences in each quadrant of the plane.

Figure 6.1 illustrates two possible scenarios that would support our expectations. Figure 6.1 (a–c) shows a hypothetical progression across three months that represents the pattern we predicted. As illustrated in Figures 6.1.a and 6.1.b, change occurs first with a decrease in oscillation frequency. As shown by the difference between Figure 6.1.b and 6.1.c, only then does the toddler alter relative phase. This pattern of change occurs at a timescale of multiple months. Another possibility is presented in Figure 6.1.d, which shows the resultant distribution when a modulation of both oscillation frequency and relative phase occurs within a given month. Although this last figure (6.1.d) does not offer sequential evidence to support our hypothesis, neither does it refute it. Patterns of distributions that deviate from either of these two scenarios would, however, represent evidence counter to our hypothesis.

Figure 6.1.

Hypothetical data in the Relative Phase/Oscillation Frequency plane. Parts a, b, and c show the month-to-month hypothesized pathway of an initial frequency shift prior to a change in phase relationship. Part d shows a pathway that supports the expectation within a single session.

The third step of our analysis evaluates the relation of our frequency and phase variables that is established within months. From the relative-phase/frequency plane, we can use a single measure that identifies the region of the plane in which the individual’s movement position is located at each point for each trial. Using as reference the middle point of the plane (i.e., 90° relative phase and 2 Hz of frequency of oscillation) we can identify, in radians, the state of the individual in the plane at that given instant, and then represent these positions on a plot. This plot maps onto our the four regions of interest: from zero to π/2 (≈ 1.57) represents the anti-phase/high frequency region (AH); from π/2 to π (≈ 3.14) represents the in-phase/ high frequency region (IH); from π to 3π/2 (≈ 4.71) represents the in-phase/ low frequency region (IL); and 3π/2 to 2π (≈ 6.28) represents the anti-phase/ low frequency region (AL). Figures 6.2.a and 6.2.b show the relationship between the position in the plane and its translation to the accompanying plot. Figure 6.2.c shows a possible within-month pathway that would support our hypothesis; that is, the expected sequence from in-phase/high frequency to in-phase/low frequency to anti-phase/low frequency within a trial. Note that if the toddler changes the pattern by searching along high frequencies (in-phase/high-frequency, to anti-phase/high-frequency, then anti-phase/low-frequency) the curve would move downward in Figure 6.2.c.

Figure 6.2.

Hypothetical data illustrating the transformation from the Relative-Phase/Oscillation Frequency plane to polar coordinates (a and b), and the expected within-month pathway that would occur in terms of the new plot (c). Part (c) shows the expected pattern of moving from in-phase/high frequency (IH) to in-phase/low frequency (IL), and then to anti-phase/low frequency (IH).

One extra step for the within-months analyses was to normalize time. Each bout had a different length and the hypothesis here tested is time-independent. Thus, all moments within a given bout were treated in percentages of the full bout length.

The measures used here are the relative phase, frequency of oscillation during drumming bouts (see Chapter 4), and the relative-phase/ frequency plane measures required for the within-month analyses. For all steps, we performed LME analyses relevant to the main timescale of interest (see Results, section 6.2). For all times that an average or standard deviation was required from angle data sets, we used circular statistics (CircStat toolbox for Matlab – Berens, 2009).

6.2. Results

6.2.1. Synchrony and frequency between toddler and experimenter.

We have already established that the adult’s modeling of action influenced our toddlers’ performance of the anti-phase coordination pattern (see Chapter 5). In order to characterize a possible exploration of oscillation frequency to facilitate anti-phase coordination, we needed to investigate the influence of the adult’s actions on frequency directly. First, we observed whether toddlers were performing the beat of the drumstick in time with the beat demonstrated by the adult experimenter (measured through disparity, see Methods). The LME analysis provided good fitting of the equation to the data (R² = 0.63). Table 6.1 presents the results. In general, all toddlers performed in the Anti-phase condition in moderate synchrony with the adult model (disparity of 0.38) and the In-phase condition with a large disparity (0.72). Recall that perfect synchrony would be represented by a disparity score of 0, and perfect asynchrony by a score of 1.0. Individuals varied in terms of the disparity between their drumbeats and those of the adult.

Table 6.1.

LME results for the synchrony and frequency of oscillation per month and model condition.

Synchrony
R2 = 0.63	df = 118
Fixed Effects
Name	Estimate (± SE)	t-stat	p-value
Intercepta	0.37 (± 0.03)	13.43	< .001
In-Phase Model	0.35 (± 0.03)	13.56	< .001

Random Effects
Name	Type	Estimate
Intercept	SD	0.06
Residual	SD	0.14

Frequency of Oscillation
R2 = 0.16	df = 2.31*105
Fixed Effects
Name	Estimate (± SE)	t-stat	p-value
Intercepta	2.28 (± 0.15)	15.45	< .001
Change (per month)	−0.04 (± 0.02)	2.79	.005
No-Model	0.29 (± 0.006)	41.18	< .001
In-Phase Model	0.25 (± 0.007)	31.98	< .001
Change*No-Model	−0.007 (± 0.001)	6.73	< .001
Change*In-Phase Model	0.02 (± 0.001)	21.21	< .001

Random Effects
Name	Type	Estimate
Intercept	SD	0.39
Change (per month)	SD	0.04
Residual	SD	0.68

^aThe intercept refers to the estimate for the 15^th month of age.

Table 6.1 shows the results for oscillation frequency. In general, the toddlers maintained a higher frequency of oscillation than modeled in the Anti-phase condition (2.28 Hz vs. adult’s 1.33 Hz). For both in-phase (2.52 Hz vs. adult’s 2.67 Hz) and no-model (2.55 Hz) conditions, the frequency was slightly below the relevant value modeled by the adult. With practice over months, the toddlers decreased frequency of oscillation in the Anti-phase (−.04 Hz/mo) and No-model conditions (−.007 Hz/mo) and increased it under the In-phase condition by .02 Hz per month. The toddlers varied in terms of initial frequency of oscillation and change per month, which aligns with the synchrony analyses. Individuals starting with fast oscillations eventually came closer to the modeled beat, as occurred in the Anti-phase condition, with the opposite (i.e., increasing frequency of oscillation) occurring with those who started with slow oscillations in the In-phase condition.

Thus, toddlers did not seem to try to match the frequency of the adult model insofar as they did not hit the drum synchronously with the adult model (especially in the in-phase condition), nor was the toddlers’ oscillation frequency often matched with that of the adult. It seems rather that toddlers were more influenced by the pattern of motion of the adult, as shown in Chapter 5.

General relation between relative phase and frequency of oscillation.

This next analysis addresses the question of whether relative phase performance was related to specific frequencies of oscillation. Our expectation was that the in-phase movement pattern could be performed with higher oscillation frequencies when compared to the anti-phase pattern regardless of the frequency of the adult’s demonstration, because in-phase is a more stable attractor at higher frequencies. Table 6.2 shows the results for the LME analysis. In general, in the Anti-phase condition, toddlers performed higher relative phases on average (around 116.31°) with a decrease of −23.55 ° of phase per additional Hz increased in frequency of oscillation. This means that toddlers performed the higher relative-phases (closer to anti-phase or 180 °) with lower frequency of oscillation compared to lower relative-phases (e.g., in-phase pattern, around 0°) that were performed with higher frequency. Similar patterns were observed under the In-phase and No-model conditions; see Table 6.2. While the average phase in the Anti-phase condition increased with months, suggesting more anti-phase activity with age, the In-phase and No-model conditions became more in-phase with time as the average relative phase decreased. Thus, despite the fact that In-phase and Anti-phase conditions had different frequencies demonstrated by the adult model, the frequency and relative-phase relation was maintained for all conditions.

Table 6.2.

LME results for the relation between relative-phase (°) and frequency of oscillation (Hz) per month and model condition.

R2 = 0.08	df = 2.31*105
Fixed Effects
Name	Estimate (± SE)	t-stat	p-value
Intercepta	115.53 (± 7.20)	16.04	< .001
Change (per month)	4.07 (± 0.68)	5.97	< .001
Frequency	−23.14 (± 0.72)	32.20	< .001
Change*Frequency	−1.09 (± 0.11)	9.92	< .001
Change*No-Model	−4.99 (± 0.19)	26.26	< .001
Frequency*No-Model	−6.09 (± 0.40)	15.20	< .001
Change*In-Phase Model	−5.61 (± 0.23)	24.28	< .001
Frequency*In-Phase Model	−8.43 (± 0.46)	18.51	< .001
Change*Frequency*No-Model	2.66 (± 0.10)	25.76	< .001
Change*Frequency*In-Phase Model	2.47 (± 0.12)	21.17	< .001

Random Effects
Name	Type	Estimate
Intercept	SD	18.62
Change (per Month)	SD	1.70
Residual	SD	91.60

^aThe intercept refers to the estimate for the 15^th month of age.

Additionally, while the relation between frequency and relative phase became more pronounced in the Anti-phase condition with age, the opposite occurred for the In-phase and No-model conditions. In other words, toddlers did not modulate their oscillation frequency according to their relative phase in the No-model and In-phase conditions. This may have been related to the decrease in frequency of oscillation that we observed when children performed the anti-phase coordination pattern, with a higher proportion of anti-phase bouts occurring under the identical condition. The random effects demonstrated that individuals started and changed their average relative phase differently over the course of months; there was no correlation between their starting phase relationship and the changes in phase that subsequently occurred.

6.2.2. Developmental trend in the relation between phase and frequency.

Although we found a general relation between our frequency and phase variables, considering the high variability evident in the anti-phase pattern for these toddlers (see Chapter 5), we conducted individual analyses on their performance trajectories. We report these trajectories by plotting the relation between frequency and relative phase for each individual at each age assessed, discussing the resulting plots, and then presenting a summary of statistical results to support the description. Although condition interacted with the relation between frequency of oscillation and relative phase, the present description does not differentiate between conditions given that the general relation was maintained across all conditions; specifically, higher relative phases were related to slower frequencies.

6.2.2.1. Participant 1.

Figure 6.3 shows the occurrence of the anti-phase pattern for Participant 1 (P1) for all his months of participation. In his first month of practice at 16 months of age, this toddler showed a strong prevalence of in-phase coordination with some degree of variability along oscillation frequency, concentrating around 3 Hz. No phase relationship close to the anti-phase pattern is apparent at this age. However, in the second month (17th month of age), the toddler evidenced a high prevalence of the anti-phase pattern, with a low frequency of oscillation. This trajectory potentially corroborates our hypothesis because the exploration along frequency of oscillation occurred before the anti-phase pattern emerged the next month, and the anti-phase coordination pattern occurred with low frequency of oscillation. The plots of later months appear to repeat this pattern by showing a high prevalence of in-phase patterns in months 19 through 21 with increased action in the low-frequency region, then another contact with the anti-phase pattern in the low frequency region at 22 months of age. The occurrence of anti-phase action increased up to month 25 when two clear preferences appear to have emerged: in-phase at high frequencies and anti-phase at low frequencies.

Figure 6.3.

Participant 1 bivariate distribution of occurrences in the Relative Phase/Oscillation Frequency plane for each month.

6.2.2.2. Participant 2.

P2 showed a more variable pattern than P1 in his first two test sessions (age 16 and 17 months, see Figure 6.4), with attempts to achieve the anti-phase pattern through both high and low frequencies. There is little to see in month 19 given that P2 engaged in a single short bout at this session. During month 21, one can see a preference for the in-phase pattern and a brief exploration in the low frequencies of in-phase. From month 22 on, P2 exhibited a much higher probability of engaging in the anti-phase pattern, demonstrating consistent performances in the 24th and 25th months in the low-frequency region.

Figure 6.4.

Participant 2 bivariate distribution of occurrences in the Relative Phase/Oscillation Frequency plane for each month.

6.2.2.3. Participant 3.

P3 (Figure 6.5) exhibited two different patterns of exploration in the first three months (15, 16 and 17). When she was 15 months old, the exploration was based on different frequencies of in-phase with few occurrences of the anti-phase coordination pattern. Nevertheless, at 16 and 17 months of age, P3 attempted to move toward the anti-phase pattern by modulating only the relative phase and not the frequency, as evidenced by the broad horizontal bands at the top of the plots. In her 18th month, P3 produced a distribution that involved almost the whole relative phase vs. frequency plane. Over the next two months, the preferred mode of exploration favored high frequencies again. This preference was maintained up to 25 months of age, when there emerged a more defined preference for low frequencies with the anti-phase pattern and high frequencies with the in-phase pattern.

Figure 6.5.

Participant 3 bivariate distribution of occurrences in the Relative Phase/Oscillation Frequency plane for each month.

6.2.2.4. Participant 4.

P4 (Figure 6.6), showed a limited range of exploration in terms of frequency, performing only at low frequencies but moving across the full range of relative phases during her first month (16). Later in months 17 and 18, similar to P3, she tried to perform the anti-phase pattern while maintaining a high frequency of oscillation. From 20 months of age to the end of data collection at 27 months, this toddler showed variable patterns. When she was 20 months old, P4 produced the whole spectrum of movement possibilities, something that occurs again at 25 months of age. However, from 22 to 24 months of age, P4 again employed the strategy of maintaining high frequencies and increased the frequency of occurrence in the anti-phase pattern with especially high frequencies at 24 months. At 26 months of age, the patterns settled into the expected in-phase/high frequency and anti-phase/low frequency. At 27 months, she performed the whole spectrum of relative phases with lower frequencies.

Figure 6.6.

Participant 4 bivariate distribution of occurrences in the Relative Phase/Oscillation Frequency plane for each month.

6.2.2.5. Participant 5.

P5 (see Figure 6.7) produced a high level of in-phase activity with high frequencies during the initial month (15^th month of age). In the 17th month, this toddler found the anti-phase pattern using the high-frequency region and, up to 19 months of age, there occurred a frequency decrease in the anti-phase pattern as he got older. Accompanying the decrease in frequency, was an increase in stability of the anti-phase pattern, as illustrated by the spread of data along the relative-phase dimension. The following months exhibited a prevalence of either in-phase high frequency at months 20 and 21 or at lower frequency closer to anti-phase relationships at month 23. Finally, when 24 months old, P5 demonstrated the in-phase/high frequency and anti-phase/low frequency relation.

Figure 6.7.

Participant 5 bivariate distribution of occurrences in the Relative Phase/Oscillation Frequency plane for each month.

6.2.2.6. Participant 6.

P6 (see Figure 6.8) shows an initial distribution at Month 16 that is broad with a higher tendency to be in-phase at any frequency. Providing support for the expected pathway of exploration, in the next month (17), she exhibited more activity with the anti-phase pattern in low frequencies with a subsequent increase in stability during months 18, 19 and 21, and differentiation between in and anti-phase patterns at month 24.

Figure 6.8.

Participant 6 bivariate distribution of occurrences in the Relative Phase/Oscillation Frequency plane for each month.

6.2.2.7. Participant 7.

P7 (see Figure 6.9) produced distributions consistent with exploration along the in-phase pattern during months 16 and 17. From months 18 to 23, the distribution seems to be gradually shifting, in the anti-phase region, from low to high frequencies. Later, at 25 months of age, P7 demonstrates, although with some variability, the expected differentiation in relative phase and frequency. At 24, 26, and 27 months of age, however, the toddler demonstrates variable and inconsistent patterns.

Figure 6.9.

Participant 7 bivariate distribution of occurrences in the Relative Phase/Oscillation Frequency plane for each month.

In summary, we observed substantial variability between, as well as within, individuals. Not all of the toddlers showed a pattern that could be interpreted in terms of our hypothesized relationship. However, as our descriptions suggest, P1, P2, P6 and P7 demonstrated a pathway that reflects exploration of low-frequency performance of in-phase activity followed by later performance of the anti-phase pattern. To confirm our impressions from the plotted data, we must determine whether such a trajectory holds under analysis with inferential statistics.

6.2.3. Quantitative analyses of the month-to-month pathway.

To determine whether toddlers’ performance of a low-frequency in-phase pattern would provide a basis for performing an anti-phase pattern, we performed a GLME with a binomial distribution, using the proportion of anti-phase pattern as a function of the accumulated performance in the in-phase /low-frequency range. Additionally, we weighted the observations by the length of the bouts; because longer bouts provide a more reliable estimate of occurrence, the model weighed its estimation in terms of the length of the bout. Figure 6.10 shows data and the fitted results for each individual. Table 6.3 presents the results of the analyses. In general, the GLME indicated that individuals started with a relative occurrence of the anti-phase pattern at 26%. Interestingly, the statistical model included a significant increase of the anti-phase pattern’s relative occurrence associated with in-phase/low-frequency practice in the fixed effects. This demonstrates a general relation across all individuals of in-phase/low-frequency experience with a greater proportion of the anti-phase pattern. Clearly, as illustrated in Figure 6.10, the random effects demonstrated that individuals varied in terms of their starting proportion of the anti-phase pattern and how much they changed as a function of practice. This result provides strong support for our hypothesis and corroborate our interpretation of the phase/frequency plots.

Figure 6.10.

Frequency of occurrence of the anti-phase pattern as a function of the accumulated frequency in the in-phase/low frequency region. The left panel shows the real data for each participant relating the anti-phase occurrence with the cumulative in-phase/low-frequency performance. The right panel shows the fitted data from the LME analysis.

Table 6.3.

GLME results for the anti-phase frequency of occurrence as a function of accumulated in-phase/low-frequency performance.

R2 = 0.42	df = 66
Fixed Effects
Name	Estimate (± SE)a	t-stat	p-value
Interceptb	−1.01 (± 0.15)	6.89	< .001
Cumulative In-Phase	0.64 (± 0.22)	2.95	.004

Random Effects
Name	Type	Estimate
Intercept	SD	0.39
Cumulative In-Phase	SD	0.57
Residual	SD	1.00

^aThe estimates are not the frequency of occurrence per se. To derive the actual value, one needs to plug the estimates into the logistic function;

^bThe intercept refers to the estimate for the 15^th month of age.

6.2.4. Within-months analyses of the relation between frequency and relative phase.

Here, we assessed whether there was any systematic change within months that would provide evidence for the exploration of lower oscillation frequencies supporting emergence of the anti-phase coordination pattern. For the sake of space, we include the trial-to-trial modulation in terms of frequency/relative-phase plane in Supplementary File S2 for this monograph. We thus move to the quantitative assessment of change within trials taking into consideration how toddlers started the trial, how they changed within trial, their overall standard deviation, and how they finished the trial – all in terms of frequency and relative-phase.

6.2.4.1. Quantitative analyses of within-month relations between frequency and relative phase.

As explained in the methods section of this chapter, we transformed the data of the relative phase and oscillation frequency into an angle measure, indicating in which movement region (IL, IH, AL, AH; see Section 6.1) the individual was at a given moment in time. To provide a direct assessment of the exploration within trials, we normalized the data with the AL region having an angle of 0°. Consequently, IH became either −180° or 180°. Thus, if the toddlers explored through the hypothesized route (IH → IL → AL), their starting position would be negative and the change within a trial would be positive. If any other situation occurred, then our hypothesis would not be supported because another pathway would be indicated.

For this analysis, we included only trials from the anti-phase demonstration condition given that the several statistical interactions that the model could generate would make it difficult to generate reasonable interpretations with the additional variables of condition. The Anti-phase condition is the one most likely to produce anti-phase cycles, so is most amenable to this analysis. Table 6.4 shows the LME results. In summary, the results point out that individuals at first demonstrated a tendency to be within the in-phase/low-frequency range (represented as a negative value; see the previous paragraph). The change within trials was not significant in early months. Later, as the individuals got older, they approached the anti-phase region, indicated by a positive change per month. Also, they showed an increase in the change within trials, indicating that, with practice, they became more able to change from in-phase/low-frequency to anti-phase.

Table 6.4.

LME results for the position in the relative-phase vs. frequency of oscillation plane in terms of months and trial time (in percentage).

R2 = 0.04	df = 72577
Fixed Effects
Name	Estimate (± SE)	t-stat	p-value
Intercepta	−32.94 (± 5.47)	6.02	< .001
Change (per month)	0.51 (± 0.53)	0.97	.334
Change (%trial time)	−7.27 (± 10.77)	0.68	.499
Change (per month)* Change (%trial time)	1.55 (± 0.42)	3.64	< .001

Random Effects
Name	Type	Estimate
Intercept	SD	13.65
Change (per Month)	SD	1.21
Change (%trial time)	SD	27.30
Residual	SD	106.00

^aThe intercept refers to the estimate for the 15^th month of age.

Note that neither change within trial nor change across months was significant, but both terms remained in the model. This occurred because individual differences were large; some toddlers changed while others did not. But the interaction between change per month and within-trials change was significant indicating that toddlers, in later months of practice, were able to modulate their frequency of oscillation within a trial to perform the anti-phase pattern. Also, individuals varied in terms of which phase and frequency they started the trial, how they changed per month through modifying their phase and frequency exploration across months and how they changed within a trial by modifying the phase and oscillation frequency.

6.3. Discussion

The current chapter addressed whether the emergence of the anti-phase coordination pattern in toddlers occurred as an outcome of exploration of oscillation frequency, which would ultimately provide the basis for a more stable performance characterized by some degree of skill with this phase relationship. The dynamical systems approach to motor development emphasizes that emergent patterns are stabilized through finding an assembly that matches the task at hand (in our case, a coordination pattern) and adjusting the parameters of this movement to provide better performance and higher stability (e.g., Goldfield, 1995). Recognizing that intrinsic tendencies play a large role in the stability of the performed movement pattern and how learning occurs (Kostrubiec et al., 2012; Zanone & Kelso, 1994), we hypothesized that toddlers would explore the oscillation-frequency parameter space (see Goldfield et al., 1993) to decrease competition with intrinsic tendencies, allowing the to-be-learned pattern to be performed. Specifically, we believed that toddlers would decrease the frequency of in-phase oscillation in order to perform the anti-phase pattern.

We initially observed that toddlers performed the in-phase pattern with a higher oscillation frequency than the anti-phase pattern. This might occur for two different reasons. The first is that the anti-phase pattern is not as stable as the in-phase pattern. Previous literature has indicated that maintaining an anti-phase relation seems to be more difficult, especially at high frequencies, than the in-phase relation up to adulthood (Kelso, 1984). Thus, a longer period of practice is required for anti-phase movement to achieve a considerable degree of stability (cf. Volman & Geuze, 2000; Wolff et al., 1998). This leads to in-phase activity to be more often performed at higher frequencies than anti-phase activity (Isenhower et al., 2012).

The second possibility is that the differential oscillation frequencies occurred because the model who was performing the anti-phase pattern in front of the children was performing the anti-phase pattern at lower frequencies (2.67 Hz for In-Phase condition and 1.33 Hz for Anti-Phase condition so that the sound of the beat was constant and stable). These differences in frequencies may have influenced some bouts in which the child was trying to match the oscillation frequency of the adult. We acknowledge this as a potential limitation of our analyses. Nevertheless, our results demonstrated that the toddlers, in general, did not perform at the adult’s oscillation frequency either in terms of beat disparity (synchrony) or frequency. Furthermore, the relation between frequency and relative phase was also present under the No-model condition in which no demonstration was provided. Thus, we can at least conclude that the toddlers found a relation between relative phase and frequency that accords with the previous literature (e.g., Cohen, 1971; Isenhower et al., 2012) by modulating frequency of oscillation. Further work with young children that more systematically manipulates oscillation frequency should shed additional light on how this relationship progresses during development.

Assuming that toddlers indeed explored frequency of oscillation, we expected that toddlers would engage in systematic search that would yield, first, decreased frequency in the in-phase pattern and, second, modulated relative phase to perform the anti-phase pattern. The pattern of exploration we observed with multiple participants seemed to match our expectation at the month-to-month analysis. In the relative phase versus frequency of oscillation plane, we observed that the distribution of movement was varied and some, but not all, toddlers behaved in ways consistent with our hypothesis. Our observations were supported at the inferential level, with the statistical model demonstrating a general trend of individuals improving their performance as a function of in-phase/low-frequency performance.

It is clear, however, that the in-phase cumulative experience correlates with age to some degree and, thus, experience cannot be separated from age in our analyses. Indeed, an analysis using age rather than cumulative in-phase experience in the equation produced similar results. Note that this analytic uncertainty does not compromise our expectations. As stated by many developmental scholars over the decades (e.g., Adolph, Hoch, & Cole, 2018; Wohlwill, 1970), time is not, of itself, an explanatory variable for development; rather, time is usually a marker for correlated but unmeasured processes, or a temporary substitute for unknown processes. Here, we identified such a process, namely experiencing the dynamics through in-phase/low frequency performance, that could replace time in our analysis. The concern with age, nevertheless, is that other processes, including experiential as well as morphological ones, are also occurring and it may well be that these other processes have some influence in the emergence of the anti-phase pattern. Although additional research is needed to assess the role of such processes, our current data are, at minimum, consistent with the hypotheses proposed in our conceptual model.

When the toddlers’ actions were considered in a within-month basis, we found that, in general, the toddlers demonstrated the expected sequence. That is, within trials, they started at early ages in the in-phase range, usually with low frequency of oscillation. As they got older, the toddlers’ average relative phase increasingly moved toward the anti-phase pattern. Within individual bouts (see Supplementary File S2), we observed that children demonstrated high variability and, rarely, one would exhibit a smooth change from in-phase to anti-phase; this explains the low R² (see Table 6.3). In this sense, the toddlers tended to change consistently with our expectations but this occurred at the level of averages; that is, they showed high variability in their real-time behavior with an underlying systematic trend among the group.

In sum, we have general trends in the data that are meshed into a pool of large variability between and within individuals. In the end, what does this mean in terms of our predictions? First, although in some cases the explained variance was low, especially in the within-month analysis, the trend is nonetheless evident. This means that the hypothesized systematic trend cannot explain much of the change but it is present. A second point is that we could not expect, in light of the literature, that all of the variability in the development of a movement pattern would be explained by a single variable or process. Learning a coordinated rhythmic bimanual movement is a great challenge even for adults (see Zanone & Kelso, 1992). Finally, we see that individuals can achieve the same goal through different pathways, as illustrated with other coordinated actions by Thelen et al. (1993). The nature of motor development is to a large extent equifinal: it has multiple pathways that can lead to the same ultimate performance of a given behavior. This is exemplified in our multiple hypotheses that highlighted at least three different pathways by which individuals could modulate their movement to perform the anti-phase pattern (see Chapter 3 and the chapters subsequent to this one). Also, we observed that at least four toddlers of the seven were indeed demonstrating sequences on a month-to-month basis that match our expectations with regard to oscillation frequency.

We cannot dismiss the premise that variability, especially within bouts, is present and, thus, is part of the process of change. We interpret our stronger month-to-month findings with a large effect size, and more varied effects in the within-months analysis, as suggesting that although toddlers may perceive the dynamics (as demonstrated in the month-to-month trend), there is considerable variability in this perception. Previous investigators have already argued the potential role of variability in facilitating perception of action possibilities as well as the relation between movements and performance (Pacheco, Hsieh, & Newell, 2017, Schöllhorn, Mayer-Kress, Newell, & Michelbrink, 2009). In the current study, we posited that through perceiving the relation between frequency of oscillation and variability (or stability) of relative phase (see Chapter 3), toddlers would identify the appropriate way to alter their movements to accomplish the goal after some experience with the dynamics of bimanual movements. This prediction of the toddlers’ behavior aligns with our findings for some individuals who exhibited a broad range of movement exploration to only later accommodate to a lower-frequencies and anti-phase movement pattern (see Supplementary File S2 for a detailed demonstration of this).

This intertwined role between present variability and identification of the most appropriate pathway of change is in line with developmental theories that provide a selectionist view of change in development (Hadders-Algra, Brogen, & Forssberg, 1996; Rosengreen, Savelsbergh, & van der Kamp, 2003; see also Edelman, 1987). The general idea here is that through variation the individual can select the most appropriate behavior and, thus, improve performance. Some authors have argued for behavioral selection along different time-scales of change such as short-term motor learning (e.g., Morice, Siegler, Bardy & Warren, 2007; Sternad, 2018) or longer-term motor development (e.g., Angulo-Kinzler, 2001; Angulo-Kinzler, Ulrich, & Thelen, 2002). This variability that allows behavioral selection is somewhat similar to the proposition of motor babbling in motor development (see Fagard, Esseily, Jacquey, O’Regan, & Somogyi, 2018).

Note, however, that we are positing that this variation is not totally random but is guided by perception of the dynamics to allow further exploration (see the Supplementary File S2 – Figure S.2.2). That is, variation provides the pathway of change, not the final goal (see Pacheco et al., 2017). Only with perception of the movement dynamics (the relation between oscillation frequency and relative phase) would the toddlers find the best way to compete with their motor systems’ intrinsic dynamics and practice the anti-phase pattern. This would avoid the necessity of postulating a totally random search that, for some (Gelfand & Tsetlin, 1962), relies on a risky and time-consuming process.

Thus, we expect that a degree of organization is at hand during practice to explain the acquisition of a skill within a particular context– specifically, the emergence of the anti-phase pattern of drumming. The fact that we found for most of our individuals a developmental trend in frequency pattern that matched theoretical expectations along at least one timescale provides support for this position. To address the toddlers who did not show systematic developmental patterns with this parameter, we investigate the possibility of a few alternative routes using other available parameters in Chapters 7 and 8.

A final consideration comes from the fact that, as argued in Chapter 3, we could accept both within- and between-month sequences to support the proposed pattern exploration. In terms of motor development, it is unlikely that a single timescale will yield definitive boundaries of change. That is, there is no reason to believe that improvements in a given motor skill can only occur within a day, across a single month, or so on. Even changes believed to be slow and gradual can be measured in terms of small sudden jumps that occur from time to time (see Adolph, Robinson, Young and Gill-Alvarez [2008] for a discussion of change in development). Our results demonstrate changes on both between- (see Participants 1 and 2) and within-month bases (see Supplementary Files S2). Clearly, during this stage of life, individuals are continuously exploring possibilities of action as well as the interaction between parameters of movement and these possibilities. A month-to-month change might represent a period in which toddlers are learning to interact in new forms with the environment and these forms require slower velocities of motion and/or lower frequencies of oscillation. Nevertheless, the moment of discovery may occur within a single bout. This would result in subsequent, relatively immediate, changes in movement parameters.

In summary, we assessed the hypothesis that toddlers would explore oscillation frequency in order to practice and acquire stability in the anti-phase movement pattern. Both month-to-month and within-month time scales were assessed, taking care to analyze each individual separately. We found that our hypothesis is not exclusive of others in that only some toddlers supported it and the degree to which the hypothesized strategy was apparent in each child depended on the timescale assessed. As discussed, this is expected given the redundant nature of both control and pathways of skill acquisition. In the next chapters we address such redundancy and highlight other strategies of effecting change in coordination patterns.

7. Anti-Phase Pattern Acquisition: The Role of Amplitude Ratio

The interplay between a coordination pattern’s stability and relevant control parameters reflects the competition and cooperation among subsystems of task, environment, and organism (Kelso, 1995; Newell, 1986). The principal argument we present in this monograph is that toddlers explore these control parameters in ways to decrease the influence of the intrinsic dynamics supporting the primary existing pattern when trying to acquire the anti-phase movement pattern. In Chapter 6, we demonstrated that some toddlers explored frequency of oscillation in a way that is consistent with our proposed conceptual model. Additional task parameters such as amplitude ratio between hands can also change the coupling strength between limbs, thus increasing variability or decreasing stability in a given movement pattern. We now turn to investigation of whether our toddlers employed strategies that manipulated the relative amplitude of the two limbs in order to initiate anti-phase activity within our task context.

Although the study of amplitude in affecting movement coordination has been more limited than the literature focusing oscillation frequency, several researchers have addressed this parameter as well. As discussed in Chapter 3, although the absolute amplitude of the oscillation of both limbs was initially argued to be a control parameter in the coordination between limbs, the literature has demonstrated that this does not hold empirically (Beek et al., 2002; Peper & Beek, 1999; Peper et al., 2004). Instead, the difference of the amplitude between the limbs, or amplitude ratio, plays a major role in coupling (e.g., Peper et al., 2008). Changing the amplitude ratio increases instability in the performed movement pattern, allowing one to change from the current movement pattern to another easily and immediately. We thus assessed whether toddlers would explore amplitude ratio as a way to escape from the already-stable in-phase pattern and perform anti-phase coordination.

7.1. Specific Analysis

The specific hypothesis we are testing here is that toddlers would, when in the in-phase coordination mode, alter the amplitude ratio between limbs to destabilize the coordination pattern and allow search for the anti-phase pattern. This would occur only along brief time-scales within trials because such a change naturally produces an immediate alteration in phase relationship.

Given our hypothesis, the focus of this chapter is on the relation between relative phase and the amplitude ratio between the oscillating limbs, as represented by the drumsticks held in each hand. Thus, we mainly used the Hilbert-transformed relative-phase and the amplitude derived from the wavelet analysis (see Chapter 4). The amplitude ratio was estimated by taking the logarithm (base 2) of the amplitude of motion of one drumstick tip divided by the other and getting the absolute value resultant, thus always yielding a positive value. This measure is the absolute log of the amplitude ratio, or ALAR. The ALAR measure was used because if we simply divided the amplitude of one limb (as represented by the drumstick) by the other, we would risk having two different values that mean exactly the same thing. For example, if the right-limb motion has twice the amplitude of the left limb (and we are dividing right by left), we obtain the value of 2. If we divide left limb by right limb, however, the resulting value is 0.5. For our purposes, these two cases have the same meaning: one limb’s movement is twice as large as the other’s. Because we are not here interested in laterality, we do not care which limb has the larger amplitude of movement. Thus, we would like to avoid having different values reflecting essentially the same relationship. When we take the logarithm (base 2) of these two values (2.0 and 0.5), the former results in 1 and the latter in −1. The absolute value of each is now 1. This solves our problem. In this logarithmic measure, 0 means equal amplitude between the limbs, 1 indicates that one drumstick’s amplitude is twice the amplitude of the other drumstick, 2 means that one drumstick’s amplitude is four times the amplitude of the other’s, and so on.

To determine the relation between amplitude ratio as a strategy employed by the toddlers and relative phase, we performed four analyses. The first three are quantitative and involve inferential statistics while the last one is qualitative. The first analysis performed tested the prediction that the Anti-phase condition would show higher maximum ALAR values than the other two conditions. The rationale is that, recognizing that this condition has the experimenter directing attention to the anti-phase pattern through her drumming demonstration, more instances of toddlers switching from in- to anti-phase coordination pattern using ALAR would occur than in the other demonstration conditions. We performed an LME on ALAR as the dependent variable, month and conditions as independent variables with intercept and change per month as random effects.

The second analysis tested the expected relation between ALAR and relative phase variability. That is, we tested whether our findings would match the literature in predicting that higher ALAR leads to higher variability in the movement pattern being performed (e.g., de Poel et al. 2009). For this, we performed an LME with the relative phase’s standard deviation per trial as the dependent variable, months, model, ALAR and mean relative phase as independent variables and intercept, change per month, and ALAR with random effects.

Using the same measures, in the third analysis we then performed a more specific test of ALAR and relative-phase relations that correspond to our hypothesis that toddlers would modulate the amplitude ratio to change from in-phase to anti-phase. Thus, in this case we would observe a current increase in ALAR leading to a higher chance of relative phase becoming anti-phase. We calculated a moving average on both ALAR and relative-phase data within trials with a 500 ms delay in between ALAR and relative phase (equivalent to 30 frames); a 1 second delay was also tested and the results were similar. We then modified relative phase to be measured in terms of proximity to anti-phase, heretofore called proximity. These proximity values ranged from 0 to 1 with 1 being considered anti-phase and 0 being in-phase; 90°, for instance, would yield a value of 0.5.

We then tested whether the amplitude ratio (ALAR) would predict a change from in-phase to anti-phase. In terms of the mathematical, we tested whether ALAR would lead to values closer to anti-phase in the next 500 ms when the current values were closer to in-phase (i.e., not above 0.5). This was done by an LME having the proximity measure of relative-phase 500 ms ahead as dependent variable and month, conditions and current ALAR (0 ms ahead) as predictors. This LME analysis only used data that related to current states of the proximity measure below 0.5 because we were specifically interested in the switch from in-phase to anti-phase movement.

7.2. Results

7.2.1. Conditions and amplitude ratio.

To establish amplitude ratio as a strategy to implement the anti-phase pattern, we expected toddlers to exhibit higher amplitude ratios when they were actively trying to perform the anti-phase pattern. This motivation to produce anti-phase coordination is more likely to occur in the Anti-phase condition than with no adult model or an adult demonstrating in-phase action. Nevertheless, the LME analysis suggested no effect of condition. The maximum ALAR per month was around 1.90, independent of month, models or individual (no random effects). This implies that the presence of an anti-phase model did not lead to more exploration in terms of ALAR.

7.2.2. General relation between ALAR and relative phase.

In order to determine whether toddlers did explore ALAR, we must first make sure that ALAR indeed related to the variability of the relative phase, as expected. Table 7.1 presents the results of this LME analysis. Toddlers had an intercept of 25.23° standard deviation of relative phase, which increased 12.48° per ALAR unit and 0.04° per mean relative phase. This means that higher ALAR and relative phases far from in-phase increased the standard deviation of relative phase, as expected. Thus, the toddlers’ coordinated movement was more variable with larger differences between limb amplitudes as coordination approached anti-phase movement patterns. The detrimental effect of ALAR on standard deviation and mean relative-phase decreased with time, suggesting that toddlers were, in later months, more stable against perturbations caused by ALAR modification. Individuals varied in terms of intercept, change per month, and ALAR effect.

Table 7.1.

LME results for the relation between ALAR and standard deviation of relative phase.

R2 = 0.16	df = 2.10*105
Fixed Effects
Name	Estimate (± SE)	t-stat	p-value
Intercepta	25.22 (± 2.16)	11.69	< .001
Change (per month)	0.18 (± 0.21)	0.88	.378
ALAR	12.49 (± 0.95)	13.18	< .001
Mean RP	0.04 (± 0.001)	25.19	< .001
Change*ALAR	−0.12 (± 0.02)	4.73	< .001
Change*Mean RP	−0.001 (± 0.0002)	5.13	< .001
ALAR*Mean RP	−0.01 (± 0.001)	8.08	< .001
Change*ALAR*Mean RP	0.0008 (± 0.0002)	4.08	< .001

Random Effects
Name	Type	Estimate
Intercept	SD	5.69
Change (per Month)	SD	0.54
ALAR	SD	2.47
Residual	SD	17.82

^aThe intercept refers to the estimate for the 15^th month of age; RP: Relative Phase.

7.2.3. ALAR relation with relative phase.

As discussed in Section 7.1, we expected a modulation in ALAR that results in relative-phase changes from in-phase to anti-phase. Figure 7.1 shows a hypothetical trajectory that corresponds to our expectations. Figure 7.2 illustrates exemplar trials from each participant demonstrating the modulation of ALAR and subsequent change in relative phase. We located these sequences by observing whether the pattern demonstrated in a given trial matched the expected pattern of changing ALAR prior to a shift from in-phase to anti-phase coordination. Note that, in some cases, the anti-phase pattern was maintained for only a short period after the phase shift; this may have occurred because of the inherent variability of the anti-phase coordination pattern at this age. We use these exemplars as points of discussion, but we point out that they are not the only trials in which these phenomena were observed.

Figure 7.1.

Example of an expected movement pattern if amplitude ratio is modulated to achieve anti-phase coordination. The left panel shows a simulated hand motion in the vertical plane and the right panel shows the calculated amplitude ratio (ALAR) and Hilbert-transform relative-phase for this time series.

Figure 7.2.

Representative instances in which the amplitude ratio (ALAR) was modulated and led to a change in relative-phase (from in-phase to anti-phase). Left panel shows the right (black) and left (gray) hands oscillation. Right panel shows relative phase (black) and ALAR (gray).

As can be seen in the selected trials, P1, in his 23rd month of age, modulated amplitude ratio at time 1 s that led to a short period of anti-phase coordination (windows 4 to 10). P2 at 21 months of age twice modulated amplitude (around 1 s and around 4 s) with the last instance leading to short periods of anti-phase activity (around window 20). P3, in her 24th month of age, modulated amplitude ratio from time 2 s to 6 s and during this period exhibited anti-phase coordination (windows 11 to 16). P4 at 22 months of age maintained a consistent amplitude ratio (ALAR = 1) throughout the trial, showing a shift from around 90° to 180° at window 4. P5 at 19 months of age exhibited a bilateral modulation of amplitude followed by two instances of amplitude ratio modulation (2 s and 4.5 s – decrease and increase of left drumstick amplitude, respectively) with a subsequent appearance of the anti-phase pattern. P6, in her 17th month of age, showed an increase in amplitude ratio at time 2 s which led to an anti-phase pattern (window 10). Finally, P7 at 25 months of age demonstrated a change in amplitude ratio around 4 s to 5 s that led to a change in relative phase that was not maintained for long.

To assess whether our prediction here fit with the aggregate data, we then analyzed the relation between ALAR and relative phase in terms of proximity to a perfect anti-phase pattern. Table 7.2 presents the results of this analysis. The GLME analysis (with logit transformation of the dependent variable) showed that individuals demonstrated a proximity of 0.27 in the first month with an increase of proximity with ALAR to 0.32; recall that a value of 1.0 would indicate fully anti-phase behavior and 0, fully in-phase. This effect increased per month. That is, toddlers’ tendency to demonstrate the anti-phase pattern of coordination increased when they modified the ALAR, with this effect increasing as they got older. The effects were similar in the In-phase and No-model conditions. These conditions, however, reflected a decreased effect of ALAR over time. Individuals varied in terms of their intercept, change (per month) and ALAR. Figure 7.3 shows the fitted model of ALAR effect on relative-phase proximity per individual.

Table 7.2.

GLME results for the relation between ALAR (time t) and proximity to the anti-phase pattern (time t + 500 ms) when considering only t’s on which the proximity was below 0.5 (at least 90° far from the 180° pattern).

R2 = 0.11	df = 1.30*105
Fixed Effects
Name	Estimate (± SE)a	t-stat	p-value
Interceptb	−1.00 (± 0.13)	7.46	< .001
Change (per month)	0.01 (± 0.01)	1.06	.287
ALAR	0.24 (± 0.08)	3.04	.002
No-Model	−0.37 (± 0.02)	20.25	< .001
In-Phase Model	−0.42 (± 0.02)	19.44	< .001
Change*ALAR	0.01 (± 0.002)	6.91	< .001
Change*No-Model	0.02 (± 0.003)	5.90	< .001
ALAR*No-Model	0.10 (± 0.02)	5.57	< .001
Change*In-Phase Model	0.007 (± 0.003)	2.34	.019
ALAR*In-Phase Model	0.15 (± 0.02)	6.80	< .001
Change*ALAR*No-Model	−0.01 (± 0.003)	4.46	< .001
Change*ALAR*In-Phase Model	−0.03 (± 0.003)	8.97	< .001

Random Effects
Name	Type	Estimate
Intercept	SD	0.35
Change (per Month)	SD	0.02
ALAR	SD	0.21
Residual	SD	0.17

^aThe estimates are not the proximity variable directly. This can be obtained by plugging these estimates into the logistic function.

^bThe intercept refers to the estimate for the 15^th month of age.

Figure 7.3.

Fitted relation between proximity of the anti-phase pattern (at time t + 500 ms), for the anti-phase model condition, months of age and ALAR at time t for each participant.

As can be observed in this figure, all individuals increased the probability of going from in-phase to higher relative phases as they matured and practiced through subsequent months. The magnitude differed for each individual but the pattern seems to demonstrate that individuals utilized the strategy of modulating ALAR to perform anti-phase movement more as they got older.

7.3. Discussion

This chapter investigated whether toddlers might employ an amplitude-ratio strategy within a drumming bout to destabilize the inherent tendency of performing the in-phase pattern and consequently be able to perform the anti-phase pattern. As highlighted in Chapters 3 and 6, the exploitation of action dynamics to learn and adapt behavior is a feature that reflects the toddler’s level of control developed up to that age. As we similarly observed for oscillation frequency, we found sequences in the toddlers’ behavior, using inferential statistics and direct observation of the relevant limb-oscillation patterns, that support such exploitation of amplitude ratio to effect phase shifts.

7.3.1. Amplitude ratio as a control parameter modulated in learning.

In the literature on bimanual coordination, maintaining a strong relation between limbs (either in- or anti-phase) was initially considered in the literature in terms of the absolute, symmetrical, amplitude of both hands (Haken et al., 1985). That is, it was assumed that if the amplitude were smaller, the coupling strength would decrease. As discussed in Chapter 3, the existing relation between frequency and amplitude allowed frequency of oscillation (e.g., Kelso, 1984, 1995) to be accommodated in the model. Nevertheless, empirical tests of the amplitude relation to frequency and the effect of amplitude on relative-phase stability in adults, did not offer support for this assumption (e.g., Peper & Beek, 1999; also see Beek et al., 2002; Peper et al., 2004). That is, oscillation frequency and amplitude did not hold a consistent relation with each other, nor was smaller amplitude related to loss of coupling strength.

At the same time, the literature focusing on other tasks that are not derived from the HKB model (e.g., bimanual circle drawing or bimanual reaching) had shown consistent effects when movements of each limb were performed with different amplitudes by adults. The first effect was the assimilation effect in which the larger amplitude movement exhibited a bias to be smaller than required and the smaller amplitude movement would show a bias to be larger than required (Marteniuk et al., 1984). This effect showed a tendency for both limbs to interact, possibly because of neural crosstalk, even when they were not required to do so (Kelso et al., 1983). The second effect was that coupling strength would decrease if the movement requirements of each hand were more differentiated, for example if the required trajectory were different, or of even greater amplitude differences were introduced (Marteniuk et al., 1984; see also Schӧner, 1990).

These effects were later replicated in a number of experiments with limb oscillation (e.g., de Poel et al., 2009; Kovacs & Shea, 2011; Peper et al., 2008). Furthermore, the effect of change in amplitude ratio on coupling strength was demonstrated even when considering the effect of passive movements of one limb on active movements of the other limb when controlling for the effect of amplitude alone (de Boer et al., 2012). Amplitude ratio appears to serve as a control parameter, at least in adults, that can alter the stability of the coordination pattern being produced. This is corroborated in ontogenetic terms by the fact that, as stated, we observed a change in pattern from in- to anti-phase accompanying changes in amplitude ratio that was supported by detailed analysis of the data identifying instances of changes from anti-phase to in-phase when ALAR was modulated.

In our study we found that modulating the amplitude ratio at earlier ages did not necessarily lead to changes in phase (measured in terms of proximity to anti-phase) demonstrated later in the study period. That is, ALAR could be high but not necessarily used as a strategy to perform the anti-phase pattern. In Chapter 6, we argued that variation in behavior, or random exploration, could precede the selection of behavior. If we follow this line of reasoning, we would expect an initial moment at which variations occur and, only later would appropriate selection of behavior occur. That is, the relation between ALAR and instability of relative-phase would always be present; some variation--at first in ALAR--would lead to perception of the relation between ALAR and relative phase by the toddlers. That is, variation would elicit perception of dynamics. This perception would lead toddlers would actively modulate ALAR to effect the change in phase (see Chapter 10 for further discussion on the issue).

A further point relevant to amplitude ratio is that in past literature, this parameter interacted with other aspects of the task such as handedness, attention, and feedback. For instance, de Poel et al. (2009) demonstrated that increased stability in a given relative-phase movement pattern, previously attributed to attention being focused on one hand, actually resulted from the effect of attention on changing the amplitude ratio between hands. Kovacs and Shea (2011) and Buchanan and Ryu (2012) also found that assimilation effects were modulated by visual feedback and the stability of the relative phase depended on the hand for which the amplitude was larger or smaller. Thus, it could be that amplitude ratio modulation does not reflect the strategy of modulating amplitude ratio per se but rather the exploration of differential attentional focus on one limb or the other, for instance. Such differentiation would provide a better understanding of how toddlers actually explore movement dynamics and clarifying its role provides fertile ground for further investigation.

The relevance of our finding is not simply that it provides support for the role of amplitude ratio as a control parameter and enriches the literature on aspects of bimanual coordination that influence performance. Instead, the fact that toddlers can explore the relations between control and order parameters such as ALAR and relative phase, respectively, provides additional strong evidence supporting the perceptual and action exploration of movement dynamics (e.g., Goldfield et al., 1993; Thelen et al., 1993). The relation between amplitude ratio modulation and relative-phase is learned through practice and, as demonstrated in Figure 7.3, is exploited more as the toddler gains knowledge of how movement modulations affect the movement’s stability.

Nevertheless, one must be cautious when considering these results. As discussed in Chapter 4, toddlers performed the task with 2 distinct set of drumsticks (with different lengths) and we did not control for the hand placement on the drumstick. These factors might have influenced the way the toddlers moved their arms and definitely change the absolute amplitude of motion captured for the present analyses. In terms of the different drumsticks, the issue was probably resolved provided we did not use absolute amplitude as a measure but, instead, amplitude ratio – which cancels the differences of the drumstick length. Also, if the toddlers placed their hands similarly on both drumsticks, the amplitude ratio would resolve this issue as well. Nevertheless, drumstick length and hand placement might alter the limb motion dynamics. As this discussion is not definitive, future research should explore how the manipulation of drumsticks and exploration of hand placement by the toddlers modify performance in bimanual coordination.

Thus, as we also observed in Chapter 6, we found evidence here that toddlers perceive movement dynamics through exploration of movement parameters such as ALAR (in addition to oscillation frequency) and use such perception to allow practice of the to-be-acquired movement pattern of anti-phase coordination. Other parameters remain as candidates for exploration as toddlers learn to control phase relationships in this drumming task. In the next chapter, we explore whether toddlers modulated the initial limb positions (or initial conditions) when beginning a bout, which would alleviate the requirements to use oscillation frequency or amplitude ratio. In Chapter 9, we assess the primary joints employed in drumming, which represents an additional level of potential exploration in motor development.

8. Anti-Phase Pattern Acquisition: The Role of the Initial Condition

Oscillation frequency and amplitude ratio are parameters that toddlers modify after they begin a bout of drumming, in the midst of the stream of movement. However, anti-phase action could also be employed at the start of a bout. To begin a bout with an anti-phase coordination pattern, toddlers would need to position their arms at different vertical positions so that one limb makes the first drum strike while the other is raised above the drum’s surface. That is, our participants may have chosen to start an action bout with the anti-phase pattern, maintaining it or not as the trial developed. We refer to this starting position for each trial as the initial condition of the limbs.

In this chapter, we explore the possibility of modulating action through initial limb conditions further, given that it has consequences for our conceptual model and prior analyses.

When we recognize that the initial phase condition itself may be modulated, with toddlers starting a bout in a close-to-anti-phase mode, the requirement to modulate oscillation frequency or amplitude ratio is negated at least along the within-bout timeframe. Although lower oscillation frequencies would still benefit the maintenance of the anti-phase pattern once the trial is underway, no oscillation frequency change is required to initiate anti-phase coordination. Increasing amplitude ratio would only destabilize the ongoing anti-phase pattern.

We include this analysis also because understanding initial condition modulation and its dynamics provide some sense of the underlying processes that give rise to the acquisition of a movement pattern. For instance, in a number of studies, Zanone and colleagues (e.g., Zanone & Kostrubiec, 2004; Kostrubiec et al., 2006; Kostrubiec et al., 2012) have argued that accuracy and stability seem to reflect two different processes. They reported that individuals are able to be accurate while still being highly unstable in their performance. The lack of stability and accuracy together led these researchers to suggest that learners had not mastered performance of the new behavior (see Zanone & Kostrubiec, 2004). Along these lines, it is possible that toddlers who participated in our research were able to perceive and initiate a movement in the anti-phase mode through using initial limb positioning, but were unable to demonstrate stability through maintaining anti-phase movement after the trial began. If this occurred, it could indicate a degree of learning without mastery of the coordination pattern. .

The only study that has systematically varied initial conditions to understand their influence in learning was reported by Liu and colleagues (Liu et al., 2010). Using a roller-ball motor paradigm, these authors observed that there was a period in practice in which individuals exhibited one of two stable movement solutions for the task. If two attractor states are equally stable, as in such a case, the direction that individuals’ actions take may depend on their starting position in each trial. Liu et al. (2010) hypothesized that if an individual started in the attractor basin or well of one movement pattern, the system would gravitate towards that pattern instead of the other attractor state. Thus, the initial condition would control which movement pattern would be observed in practice.

The focus of this chapter is on the appearance of anti-phase coordination as a function of the initial phase condition of the upper limbs (as represented by the drumsticks), during each trial. We examined whether the initial condition appeared to influence the relative phase presented throughout the trial.

8.1. Specific Analysis

To identify the initial condition, we calculated the mean relative phase of the first 500 ms of the trial (30 frames); trial videos had been clipped so that they would begin with the toddler’s initial motion of at least one hand toward the drum to make the first strike. The percentage of time that the individual presented the anti-phase pattern (defined as any phase between 135° and 225°) was recorded for the remainder of the trial.

We performed two LME analyses. The first LME was to determine the influence of having an anti-phase initial condition on the percentage of anti-phase behavior demonstrated during a trial. The dependent variable was the percentage of anti-phase movement per trial, the independent variables were month, model and anti-phase initial condition and we tested intercept and change per month as random effects. If there were an influence of initial condition on the toddlers’ anti-phase performance, we expected to see toddlers adopt this positional strategy more over time. That is, we tested the initial condition of each trial as a function of age (months) and model condition in order to see whether these conditions were associated with differing proportions of anti-phase activity throughout trials at different ages.

8.2. Results

8.2.1. Relation between initial condition and anti-phase performance.

The first analysis tested the hypothesized relation between initial conditions and anti-phase performance on the rest of the trial. For this, we performed a GLME analysis with binomial distribution (with weighting on the length of the trial) between anti-phase percentage of occurrence and anti-phase initial condition, considering also condition and months.

Table 8.1 presents the results of this analysis. The individuals started the study period with 19% of first-month trials across all social-model conditions being anti-phase and, with subsequent months, they increased that value by 1% a month. Starting the trial with an anti-phase model increased this percentage by 14%. As expected, the percentages of anti-phase activity during the other conditions were lower. The effect of a toddler’s anti-phase initial condition was higher in the in-phase, and lower in the No-model condition, suggesting that if toddlers performed anti-phase in the In-phase condition, it was because they were actively performing that coordination pattern at the start of the trial. In the No-model condition, however, the starting position of the limbs did not correspond as strongly to later phase relations in a particular trial.

Table 8.1.

LME results for the relation between percentage of relative-phase performed per trial (not considering the initial condition) and anti-phase initial condition per month and model condition.

R2 = 0.30	df = 726
Fixed Effects
Name	Estimate (± SE)a	t-stat	p-value
Interceptb	−1.43 (± 0.17)	8.22	< .001
Change (per month)	0.04 (± 0.01)	3.10	.002
No-Model	−0.74 (± 0.03)	23.42	< .001
In-Phase Model	−1.23 (± 0.04)	28.65	< .001
Anti-Phase I.C.	0.74 (± 0.03)	25.54	< .001
Change*No-Model	0.04 (± 0.004)	8.19	< .001
Change*In-Phase Model	0.03 (± 0.005)	4.87	< .001
No-Model*Anti-Phase I.C.	−0.28 (± 0.07)	4.21	< .001
In-Phase Model*Anti-Phase I.C.	0.76 (± 0.08)	9.64	< .001
Change*No-Model*Anti-Phase I.C.	0.08 (± 0.008)	9.48	< .001
Change*In-Phase Model* Anti-Phase I.C.	0.02 (± 0.009)	2.13	.034

Random Effects
Name	Type	Estimate
Intercept	SD	0.45
Change (per Month)	SD	0.04
Residual	SD	1

^aThese estimates are not directly the percentage of relative-phase performed. To derive the estimate, one must plug the value into the logistic equation.

^bThe intercept refers to the estimate for the 15^th month of age; I. C.: Initial Condition.

8.2.2. Occurrences of anti-phase limb position as the initial condition.

After finding the predicted relation between initial phase condition and use of anti-phase action throughout a trial, the question we addressed was whether toddlers made use of the initial-condition strategy to increase their use of anti-phase movement over time. Figure 8.1 illustrates the relative occurrences (or percent of total trials) of the anti-phase coordination pattern as the initial condition per month and condition. As can be seen in the figure, the use of anti-phase initial condition occurred throughout the study period with no clear association with any particular condition. If we view the relative occurrence of initial anti-phase position as representing a preference for performing anti-phase movement as the initial condition, we see no change in this preference across development.

Figure 8.1.

Relative occurrences of anti-phase coordination mode as the initial limb condition per month and practice condition.

To analyze our observations quantitatively, we conducted a GLME analysis with a binomial distribution. As expected, the anti-phase pattern occurred as the initial condition on 11% of trials. This did not change over time as the change per month term was removed from the statistical model using the backward fitting method. Additionally, individuals did not vary in their likelihood of starting trials in the anti-phase initial condition. This suggests that toddlers did not change or differ in their use of this strategy, even though it was a successful one with respect to increasing anti-phase interaction.

8.3. Discussion

In this chapter, we investigated whether toddlers would modulate their initial condition, or starting coordination mode, to facilitate performance of the anti-phase coordination pattern throughout a trial. We also characterized whether such a strategy changed over time or depended on the phase condition that was modeled. We observed, consistent with the conceptual model we put forward, that changing the initial condition is associated with longer time performing the anti-phase pattern within individual trials. However, we found no evidence that toddlers employed this strategy more over time. We would expect, in a didactic developmental trend, to see difficulty initiating the movement bouts in the emerging pattern during early months and then, as this capacity improves with increasing age, more attempts at initiating trials in the Anti-phase condition. Neither phenomenon was observed.

One can also use initial limb conditions to make inferences about toddlers’ intentions. In particular, how toddlers position their limbs at the start of a trial may reflect the intention to perform a given coordination pattern. If this is the case, our results suggest that toddlers already know how to perform the anti-phase pattern, albeit with low stability, by 15 months of age. This is in line with our finding that short periods of anti-phase movement are observed at this age (Chapter 5) and indications elsewhere in the literature that spontaneous anti-phase movements appear early in infancy (e.g., Kawai, Savelsbergh, & Wimmers, 1999; Piek & Carman, 1994; Robertson, 1993; von Hofsten & Rönnqvist, 1993; see Chapter 2 for a review). Also, our findings suggest that toddlers did not change their intention regarding phase relation of performance throughout the months during which they were studied. In particular, no changes in the No-model condition, when toddlers were free of the perceptual influence of the adult model’s actions, were observed over time.

An alternative proposition to consider is that the measure we used of initial condition was simply reflecting the toddler’s tendency to start the trial by using one versus two hands. Here, the idea is that toddlers would start performing a unimanual oscillation, and only upon observing the adult model using two hands, initiate movement of the second hand and subsequent anti-phase coordination. Taking the results into account, this would mean that this tendency is independent of age or model. This does not seem intuitive as the study context would invite toddlers to perform bimanual rather than unimanual patterns, which would lead toddlers change their initial preference to be more bimanual (specifically in-phase in terms of our results). Although we observed a change from unimanual to bimanual oscillation of the arms as toddlers progressed through the study (see Chapter 5), a thorough analysis of the specific patterns used does not point to this interpretation. Thus, it seems that toddlers intended to initiate trials with the anti-phase pattern with the same frequency through the data collection.

If toddlers intended to perform anti-phase patterns from the first month of the study as we believe, this suggests that toddlers were recalling the movement pattern. Thus, they already present the anti-phase pattern their movement repertoire at young ages, albeit with low stability (see Schӧner [1989] for a formal treatment on recall under the dynamical systems perspective). This supports the differentiation between accuracy and stability as posited by Zanone and Kostrubiec (2004); one can be accurate on average but still be highly variable. Nevertheless, Zanone and Kostrubiec (2004) would consider this as evidence that the toddlers had not yet learned the pattern, which appears contrary to the fact that they could recall the pattern. Thus, from early ages, toddlers can start movements using the anti-phase pattern, but they cannot maintain it for longer periods. This is consistent with observations of role-differentiated patterns that require, for brief moments, uncoupled (different) movement between limbs.

In terms of the expectations in the current study, we observed that, contrary to our findings with frequency of oscillation and amplitude ratio between arms, toddlers did not explore the initial condition of the movement pattern to allow them to practice the anti-phase pattern, even when it was demonstrated for them.

9. Anti-Phase Pattern Acquisition: The Role of the Joint Motion

In this chapter, the last one focused specifically on data analyses, we introduce the toddlers’ upper-limb joint coordination into the examination of emerging anti-phase drumming performance. Following Bernstein (1967), we recognize that the emergence of the anti-phase coordination pattern occurs on top of a movement system with many degrees of freedom open to several levels of analysis. It has been shown elsewhere (e.g., Latash, Krishnamoorthy, Scholz, & Zatsiorsky, 2005) that biomechanical, physiological, neural and other levels of control underlying a particular motor system may adjust to facilitate learning a new task. Here our ontogenetic focus means that we must consider not only those modifications that occur as a result of experience with a particular task, but also those that occur as a consequence of children’s advancing control of limbs and muscles that occurs with maturation and accumulated experience.

In studies using similar tasks (i.e., banging) with children in the same age range, toddlers have evidenced developmental changes in whether the shoulder, elbow, or wrist joint is generally used, changes that follow a proximal-to-distal sequence (Fragaszy et al., 2016; Kahrs et al., 2014). This sequence is commonly reported in the literature of motor development (see Newell & van Emmerik, 1990 for a discussion of sequential trends). Note, however, that this sequence is not invariably observed (see, for instance, Kahrs et al.’s, 2014 description of the use of the left arm in banging). Irrespective of whether the proximal-to-distal sequence is universal, it is important to understand how a change in the involvement of different joints alters the way the anti-phase pattern is performed.

Note that although joint changes may not affect the coordination pattern at all, in light of arguments for possible compensatory mechanisms at the level of joints (see Latash, Scholz, & Schöner, 2002), joint changes might facilitate the performance of a task. The literature includes several examples of changes in limb coordination that facilitate performance with some task parameters. For instance, Bardy and colleagues (Bardy et al., 1999; Bardy et al., 2002; see also Buchanan & Horak, 1999; 2001) demonstrated that the postural system reorganizes the way ankle and hip joints coordinate as the visual display is varied. Similar phenomena have been observed in upper limb control. Buchanan et al., (1997) showed that the shoulder, elbow, and wrist joints changed their influence on the movement of the hand as the required trajectory of the hand was modified. These authors argued that the recruitment and suppression of joint movements occurred to facilitate task achievement.

In our work, we hypothesized that variations in the suppression and recruitment of specific joints would also affect anti-phase performance. Our prediction was guided by a possible mechanical influence from one arm to the other as a function of the primary joint involved in the drumming. If the arm moves primarily at the shoulder joint, we would expect the arm’s movement to influence the trunk’s motion unless the trunk compensates for all resultant forces of shoulder movement. This influence would in turn cause a mechanical interference between arms when performing anti-phase motion, but not when performing in-phase motion. Performing the anti-phase pattern would therefore be facilitated if more distal joints (elbow/ wrist) were used in the oscillation of the sticks during drumming.

Based on the rationale just provided, in this chapter, we report analyses concerning which joints were responsible for arm oscillation during drumming, how joint use changed over time, and the connection between joint use and toddlers’ performance of the anti-phase pattern.

9.1. Specific Analyses

To address the issues concerning joint use described above, the outcome measures used in the analyses described next were the percentage of time performing the anti-phase pattern per trial and the primary joint involved in drumming. For the latter variable, we observed each trial and coded which joint (shoulder, elbow, or wrist) of each arm was primarily involved in the drumming. When two joints participated in the bout, we noted both, but coded as “primary” the one that judged to be the principal driver of oscillation. We used an observational coding scheme rather than kinematic analyses given that our interest was in global joint use and we wanted to keep interpretation of the data as simple as possible. Two observers coded 68 trials from eight monthly sessions and obtained a weighted Cohen’s Kappa of .84 on primary and secondary joint involvement, which is in the Very Good range. Given that in 87% of cases, toddlers used the same primary joint of motion for their right and left arms, we decided to use only the right primary joint for our analyses. Although one child demonstrated left-hand dominance, because of the high concordance between left and right arms we decided to consistently record the joint involvement of the right limb.

We performed the first analysis to determine whether the chances of performing anti-phase movement increased when the distal joints of elbow or wrist were involved as primary joints of motion. Thus, for the GLME analyses the dependent variable was the percentage of time in the anti-phase region (from 135° to 225°) and the predictors were the primary joint, conditions, and toddlers’ age (in months). As in other chapters, we tested random effects on intercept and change per month.

Given the frequency of cases in which more than one joint was used for drumming, we also considered that toddlers could be releasing degrees of freedom (Bernstein, 1967) through taking advantage of the greater movement options afforded by use of multiple joints. This would demonstrate better control and, according to our hypothesis, decrease mechanical influence between limbs. Thus, we also performed the GLME using the percentage of time in the anti-phase region (from 135° to 225°) as the dependent variable, and using conditions, months, and joint number (i.e., whether the toddler used one vs. any two joints) as independent variables.

In determining the relation between anti-phase action and joints, we then analyzed whether there was a change in joint employment over months, and as a function of anti-phase performance and conditions. We performed a GLME for occurrence of each joint considered as primary when drumming: shoulder, elbow or wrist.

9.2. Results

9.2.1. Relation between anti-phase action and joints.

For the LME on the primary joint employed in each trial, we performed a GLME with binomial distribution, weighting on the number of frames per trial. Table 9.1 presents the results of this analysis. The LME indicated that during the 15^th month, when the primary joint was the shoulder, the initial percentage of movement performed as anti-phase was 12%. As we expected, this percentage increased by at least 50% when the primary joint was the elbow (22%) or the wrist (18%). When toddlers were observed at 27 months, the differences between joints dissipated: The percentages of anti-phase pattern per trial performed when the shoulder joint was primary was virtually identical to that performed when the elbow joint was primary, and the percentage when the wrist joint was primary was slightly lower (38%, 38% and 30%, respectively). Individuals differed in terms of their anti-phase percentages at the beginning of data collection. The other effects summarized in Table 9.1 show decreased probability of the anti-phase pattern in the In-phase and No-model conditions, regardless of the primary joint. These effects represent the toddlers’ tendency to not perform the anti-phase movement pattern in the In-phase and No-model conditions.

Table 9.1.

GLME results for the relation between percentage of relative-phase performed per trial and primary joint employed in drumming per month and model condition.

R2 = 0.25	df = 637
Fixed Effects
Name	Estimate (± SE)a	t-stat	p-value
Interceptb	−2.02 (± 0.19)	10.60	< .001
Change (per month)	0.13 (± 0.004)	30.01	< .001
No-Model	−0.31 (± 0.02)	14.45	< .001
In-Phase Model	−0.38 (± 0.05)	8.34	< .001
Elbow	0.80 (± 0.04)	20.36	< .001
Wrist	0.54 (± 0.04)	14.20	< .001
Change*In-Phase Model	−0.03 (± 0.005)	4.66	< .001
Change*Elbow	−0.07 (± 0.005)	13.01	< .001
No-Model*Elbow	−0.51 (± 0.03)	17.77	< .001
In-Phase Model*Elbow	−0.36 (± 0.07)	4.99	< .001
Change*Wrist	−0.07 (± 0.005)	15.17	< .001
Change*In-Phase Model*Elbow	−0.12 (± 0.01)	10.76	< .001

Random Effects
Name	Type	Estimate
Intercept	SD	0.50
Residual		1

^aThese estimates are not directly the percentage of relative-phase performed. To derive the estimate, one must plug the value into the logistic equation.

^bThe intercept refers to the estimate for the 15^th month of age.

To examine change in anti-phase performance as a function of altering the movement pattern from one to two joints, we performed a GLME with binomial distribution with weighting on the number of frames per trial. Table 9.2 presents the results of this analysis. The LME showed that the initial percentage of anti-phase performed was 16% when only a single joint was used to perform the drumming. When two joints participated, the percentage increased to 21%. After 12 months of practice, these values were 28% and 36%, respectively. This supports our prediction that toddlers could perform the anti-phase pattern more when they released degrees of freedom through involvement of multiple joints. Individuals differed in terms of their anti-phase percentages at the beginning of the data collection. The other effects demonstrate the toddlers’ tendency to perform less anti-phase coordination in the In-phase and No-model conditions – with the exception that the effect of releasing degrees of freedom on anti-phase percentage is also observed for the In-phase condition.

Table 9.2.

GLME results for the relation between percentage of relative-phase performed per trial and the usage of one or two joints in drumming per month and model condition.

R2 = 0.21	df = 727
Fixed Effects
Name	Estimate (± SE)a	t-stat	p-value
Interceptb	−1.65 (± 0.18)	9.04	< .001
Change (per month)	0.06 (± 0.003)	22.00	< .001
Two Joints	0.34 (± 0.02)	19.99	< .001
No-Model	−0.59 (± 0.03)	21.40	< .001
In-Phase Model	−1.02 (± 0.05)	21.09	< .001
Change*No-Model	0.05 (± 0.004)	12.76	< .001
Change*In-Phase Model	0.04 (± 0.006)	7.54	< .001
Two Joints*In-Phase Model	0.30 (± 0.06)	4.93	< .001
Change*Two Joints*No-Model	−0.06 (± 0.003)	16.98	< .001
Change*Two Joints*In-Phase Model	−0.07 (± 0.008)	9.47	< .001

Random Effects
Name	Type	Estimate
Intercept	SD	0.48
Residual		1

^aThese estimates are not directly the percentage of relative-phase performed. To derive the estimate, one must plug the value into the logistic equation.

^bThe intercept refers to the estimate for the 15^th month of age.

9.2.2. Change in joint motion across months and model.

Given that we found the expected relation between joint use and anti-phase performance, we tested whether toddlers modified their movement patterns over time to attend to the task demands. Figure 9.1 shows the mode of the primary joint per month, condition and children. As can be observed, some toddlers (i.e., P3, P5 and P7) modified their primary joint along a proximal-to-distal change in control that was associated with better performance, but this was not the case for all children. For instance, P4 seemed to demonstrate the opposite trend.

Figure 9.1.

Primary joint (mode) per month and hand for each child.

For all joints, we performed GLMEs with binomial distribution. The results showed that, for all joints, no change was observed. Also, the LME did not show any relation of primary joint used with the anti-phase percentage performed or condition. The shoulder was, on average, the primary joint for 23% of the trials, the elbow for 47%, and the wrist for 30% of the trials.

Figure 9.2 illustrates the modal number of joints employed in drumming. As can be observed, there does not appear to be a trend from one to two joints, or the opposite, in any of the toddlers. Some participants tended to prefer single-joint movements (P2, P3 and P4) and others two-joint movements (P1 and P5), with some variability for each month. Performing the GLME with binomial distribution, we found that, as expected from Figure 9.2, the number of joints employed was not a function of any of the independent variables. On average, 50% of the trials included substantive participation of two joints.

Figure 9.2.

Use of one or two joints per month and hand for each child.

9.3. Discussion

In this chapter, we evaluated the possibility that toddlers would alter their joint movements to facilitate performance of anti-phase coordination. We expected that distal joints and more degrees of freedom would be explored to favor longer bouts in anti-phase. Our results demonstrated that, when toddlers employed distal joints as the primary joint of oscillation or implemented more than one joint in the movement, longer bouts of anti-phase were observed. Nevertheless, we did not find a trend of increased use of distal joints or more joints over months or as a function of condition. This suggests that children did not explore movement at the level of the joints as a strategy to perform the anti-phase coordination pattern.

One should be careful with these findings as they are limited by the joint measures used. As explained in the methods of this chapter, joint motion analyses were made on a discrete scale (participated or not in the movement) which clearly undermine the precision of our outcomes. Indeed, results could improve or challenge our current interpretations if we had joint angle motion data. We invite researcher to further test the findings provided here. Nevertheless, our results provide an initial understanding on whether participation of specific joints in the movement affect stability of the anti-phase movement pattern – even in terms of just participation or not.

The fact that use of distal joints supported increased performance of the anti-phase coordination pattern aligns with our hypothesis regarding a mechanical influence. That is, moving the whole arm at the level of the shoulder joint would result in motion of the trunk and this would interfere with the motion of the other shoulder moving in a different phase. Thus, to perform anti-phase, moving distal joints would decrease such trunk influence and facilitate more efficient performance.

Note that the influence of joint use disappeared over time, which seems counterintuitive to our rationale. Two explanations are possible. We might be incorrect in assuming that the relation we found is mechanical in nature. It might instead reflect, for example, some differential neural requirements for commanding heavier segments of the arm (the whole arm in this case) which would lead to neural cross-talk (i.e., commanding larger segments of each arm would interfere with another). In this case, moving the elbow or wrist would favor anti-phase performance and the decrease in differences between joints would reflect decrease in neural cross-talk with development. Another possibility is that there is, indeed, a mechanical interference that leads to better performance with more distal joints. However, with development and release of degrees of freedom, the trunk starts moving through rotation or lateral flexion. Such movement would decrease the direct interference between arms when they are implementing a coordination pattern other than in-phase. Both possibilities require more detailed kinematic analyses, but in light of the evidence on recruitment of additional degrees of freedom (see next paragraph), we lean toward the latter explanation.

Our analyses also suggested that anti-phase performance was facilitated when two joints were employed in drumming. The literature includes several studies demonstrating changes in joint participation to accommodate task demands (e.g., Bardy et al., 2002; Buchanan & Horak, 1999; Buchanan et al., 1997). Note that the experimental tasks employed in these studies required some form of adaptation at the level of the joints to complete the target motion. For instance, Buchanan et al. (1997) manipulated the curvature of the trajectory that the hand needed to perform the target motion. More specifically, the manipulation required changing the hand’s trajectory from a straight line to an arc of the same length, thereby requiring the involvement of different joints.

In our case, however, in-phase and anti-phase activity could be performed by any of the joints, singly or in combination. Thus, we linked the changes in which primary joints were used to some level of improved control (see section 9.1). This analysis addresses Bernstein’s (1967) idea that improvement in performance of a skill reflects a release of degrees of freedom through participation of more joints in the movement assembly. This type of change in control is usually observed in the initial developmental stages of gross motor movements such as throwing or kicking (Robertson & Halverson, 1984). This path of releasing degrees of freedom in joint control, nevertheless, has been shown to be a function of the task being performed rather than a general rule in skill acquisition (see Newell et al., 2003). Given that the toddlers’ performance improved when more than a single joint performed the task, this recruitment of degrees of freedom appears beneficial.

Finally, although our discussion considered developmental changes such as proximal-to-distal trends and releasing of degrees of freedom, we did not observe change in these variables over time. As stated already, the toddlers did not demonstrate a growing tendency across development to involve more distal or additional joints when performing the task. As shown in Figures 9.1 and 9.2, over time there was some within-toddler variability with respect to which joint was primary, but there was greater consistency in the use of one versus two joints in drumming across months. The former finding implies some exploratory variability such as was discussed in Chapter 6 (see also Thelen & Corbetta, 1994). That is, variability in the joint used to perform the task may be beneficial for the toddlers to perceive the task dynamics by relating consistency in phase coordination to the joint primarily used to perform the movement. Here, however, we did not find a developmental stage where the variability gave rise to selection of more appropriate strategies or exploration. The use of one or two joints in drumming, nonetheless, was consistent within subjects and appeared to reflect individual preferences. Whether these individual profiles are related to previous experiences or intrinsic tendencies (as in Thelen et al., 1993) is beyond the scope of the present monograph. The role of the number of joints, however, did not appear to be a factor explored by the toddlers we studied.

10. General Discussion: The Emergence of a New Bimanual Coordination Pattern

Our goal in this monograph has been to describe, longitudinally, how toddlers stabilize an emerging coordination pattern within the particular context of anti-phase coordination while drumming. We framed our analyses within the dynamical systems approach to motor behavior which provided us the theoretical foundation to guide our predictions and assessments. Following the literature, we determined that observing a specific kind of coordination—rhythmic bimanual coordination—would be valuable for understanding the principles of movement acquisition, motor development, and dynamical systems theory. This monograph, as we summarize here, enriches the literature by describing emergent behavioral patterns and by providing insights into the intersections among these research areas. At the same time, as an initial exploration of the developmental dynamics of early rhythmic bimanual coordination, the work presented in this monograph identifies several questions that can be addressed only by additional investigations.

In the preceding chapters, we reported the results of our longitudinal assessment of bimanual drumming in children between 15 and 27 months of age. Drumming proved to be an age-appropriate task well-suited to examination within the dynamical systems framework, as it provided a means of measuring continuous cyclic movement in the context of two attractor states – specifically, in-phase and anti-phase coordination patterns. An extensive body of earlier research has employed cyclic bimanual movement tasks (e.g., finger-tapping) to study motor coordination and control in adults and older children Our work, however, has taken this paradigm in new directions to provide the first longitudinal test of the dominant theoretical model of bimanual coordination as applied to early human development. A particular strength of our work is that integrates microgenetic and ontogenetic timescales to identify mechanisms that underlie the emergence of skill in anti-phase drumming during toddlerhood. We identified several specific variables as potential drivers of change within the dynamical systems framework, and examined individual trajectories of development over multiple timescales (see Thelen & Ulrich, 1991, for a similar approach applied to locomotor development).

In this last chapter, we summarize the discussion of the several interrelated parameters that children can explore and exploit to effect change in their coordination patterns. We also expand our conceptual model from Chapter 3, highlighting possible routes for further study of the acquisition of new movement patterns.

10.1. Anti-Phase Emergence

In Chapter 3, we provided reasons, based on evaluation of the HKB model, why the anti-phase coordination pattern would be the first to emerge as a relatively stable alternative to in-phase action. As discussed there, it is not possible for us here to definitively address this question and exhaust all possible options. Nevertheless, we observed that most of our toddlers’ coordinated actions centered around the two primary relative-phase patterns of interest: in- and anti-phase.

In Chapter 5, we found that toddlers demonstrated unstable periods of anti-phase coordination during the initial testing session when toddlers were as young as 15 months of age. In Chapter 8, we similarly found that our participants could start drumming bouts in the anti-phase coordination pattern from their earliest assessment sessions. The appearance of anti-phase movement was expected in light of earlier observations that even at slightly younger ages, toddlers perform other activities that require uncoupling to differentiate the roles of the hands (e.g., Babik & Michel, 2016a; Kimmerle et al., 2010; Kimmerle et al., 1995). An important point, however, is that toddlers’ stable performance of the anti-phase pattern only occurred later, usually around 20 months (Chapter 5).

The early but initially unstable existence of the anti-phase pattern in our participants suggests that younger toddlers can perceive and enact the anti-phase pattern but they are not able to maintain it over time. This could mean that toddlers’ anti-phase actions can be accurate with performance around the required pattern, but not stable (i.e. highly variable and easily disturbed), as Zanone and Kostrubiec (2004; see also Kostrubiec et al., 2012) argue. These authors argue that stability is necessary to consider a new pattern as truly learned. It is apparent, however, that being able to start a bout in the anti-phase coordination pattern suggests that our participants already had incorporated the anti-phase pattern as a movement in their repertoire. Thus, we believe that our toddlers were accurate and minimally stable in the anti-phase coordination pattern when they started our data collection, which differentiates our state of affairs from that described in Zanone and Kostrubiec (2004).

We also reported in Chapter 5 and in subsequent chapters that the presence of an adult who was modeling anti-phase drumming influenced only some aspects of our toddlers’ behavior. For example, the presence of an adult model did facilitate production of a greater proportion of antiphase trials than in other conditions, especially when toddlers were attending to the drum and model. Also, stabilization of anti-phase sequences was greater in the presence of the anti-phase adult model, as was the tendency to start the bout with the limbs in anti-phase position. However, model condition did not appear to play a significant role in toddlers’ action strategies (e.g., amplitude ratio or joint involvement).

Toddlers are going through one of the fastest rates of change of the life span, with biomechanical, perceptual, and cognitive subsystems developing along complex time scales. It is likely that, with the interaction of all these changing subsystems that are responsible for the performance of the anti-phase pattern, the overall stability of any learned pattern will be, at first, quite small in degree. From an ecological developmental view, individuals first go through changes that facilitate the perception of action possibilities (or affordances; see Gibson, 2000), and their own resulting options for action increase. In addition, children learn to explore the appropriate movement parameters to accomplish a given task in a more efficient way. This is exemplified in several studies: for instance, in reaching (Thelen et al., 1993; Thelen et al., 1996), jumping (Goldfield et al., 1993), kicking (Angulo-Kinzler et al., 2002), and sitting (Hadders-Algra et al., 1996). The empirical chapters of this monograph addressed these processes in a paradigmatic bimanual task context by using the HKB model as a guide, and studying whether and how toddlers explored movements in such ways. This allowed us to understand how toddlers initially break the intrinsic tendency to act in the in-phase pattern to establish a new coordination pattern within this context.

10.2. Exploration Based on Perceived Dynamics

In Chapter 3, we described the literature that suggests that, to establish the anti-phase coordinative pattern, toddlers could explore different movement parameters to decrease the competing tendency to perform the already-stable in-phase pattern, allow practice of other patterns, and facilitate use of the anti-phase pattern. Note that, although it has not been common to assess the exploration of these parameters in bimanual coordination from the dynamical systems approach to motor behavior, a number of studies have reported how children find efficient ways to accomplish a particular task by tuning or parameterizing their movement patterns (e.g., Goldfield et al., 1993; Thelen et al., 1993).

To decrease competition with the intrinsic tendencies of the system and improve performance of the anti-phase coordination pattern, we expected that toddlers would explore movement dynamics in specific ways. In Chapter 3, we described our specific hypotheses of how toddlers would explore different aspects of the task—frequency of oscillation, amplitude ratio between limbs, initial conditions, and employed joints. Additionally, we posited that, given that these parameters provide specific ways to allow anti-phase performance, we would not find random exploration through the full range of possibilities; rather, the exploration would be finely tuned to the movement dynamics. We summarize our findings from the analyses of different parameters here.

10.2.1. Frequency of oscillation.

Frequency of oscillation, as proposed in Chapter 3, could be modulated to allow practice in two different time scales: over months (ontogenetic) or within trials (microgenetic). We hypothesized a pattern of change that would, theoretically, help toddlers act against the tendencies of the system and allow practice of anti-phase: decreasing frequency while in an in-phase mode, and then exploring and finding the anti-phase mode. Indeed, we found some instances of both ontogenetic modulation and microgenetic modulation, following the expected pattern. Although the aggregated pattern that occurred between months afforded a better visualization of the modulation occurring in some toddlers, the microgenetic analyses revealed that some of our toddlers exhibited the tendency to decrease initial oscillation frequency to allow anti-phase coordination to be performed (see Supplementary File S2).

10.2.2. Amplitude ratio.

For amplitude ratio, we hypothesized that toddlers would, when in the in-phase movement pattern, increase the amplitude of one of the limbs, decrease the amplitude of the other, or both; thus creating instability in coupling. This would allow the toddlers to escape from the in-phase pattern and perform the anti-phase pattern. We presented the systematic results from our analyses in Chapter 7. We found that, at first, toddlers did not relate amplitude ratio to phase transitions. However, with increasing age, they began to use this as a strategy. This is a clear example of learning movement dynamics. Thus, we found good support for the hypothesis that toddlers indeed tried to explore amplitude ratio to perform the anti-phase pattern. These results match the consistent findings in the literature regarding the relation between amplitude ratio and stability of coupling (de Boer et al., 2013; de Poel et al., 2009; Kovacs & Shea, 2011; Peper et al., 2008). Whereas the previous studies just found that in manipulating amplitude ratio, variability of relative phase increased as a byproduct, the current research offers the new finding that toddlers actively tried to use such a strategy to initiate change in their coordination pattern.

10.2.3. Initial positional condition of limbs.

Considering that the previous two parameters (frequency and amplitude ratio) must be modulated only when starting in the in-phase coordination pattern, we speculated that, with age, toddlers would also modify their initial movement pattern to allow practice in the anti-phase pattern. The initial condition in dynamical systems is an important parameter that can contribute to long-term behavioral expression (Liu et al., 2010, also see Schӧner, 1989). In accordance with the dynamical systems literature, we found that indeed, starting in a coordination pattern closer to anti-phase facilitated toddlers’ anti-phase performance later in the trial. However, we found that toddlers did not change their tendency to start the trials in a particular relative phase over the course of months.

In Chapter 8, the only interpretation we considered fruitful in terms of our data is that toddlers already had the anti-phase pattern in their repertoire, albeit minimally stable as discussed earlier. They initiated the bouts using anti-phase and in-phase patterns with no change in preference over time. The low percentage of initial anti-phase limb conditions correlates to the initial stability of the pattern. The lack of change in preference and the strong bias towards in-phase can be interpreted as a tendency to perform the task in the best way they could. That is, if we consider drumming as a general task, for toddlers the best way to perform it (faster frequency of oscillation, louder sound from hits of the stick, etc.) would result from in-phase patterns that take advantage of existing motor coupling tendencies. The longer periods in anti-phase and the desire to change to anti-phase seem to have occurred when toddlers were drumming with an adult model who behaviorally called for a different play activity such as trying a new movement or imitating the model.

10.2.4. Employment of joints.

Following others’ perspectives on sequential changes in recruitment of degrees of freedom (see, as a brief review, Newell & van Emmerik, 1990) and armed with evidence that the period of observation had the potential to demonstrate changes in the primary joints employed for the task (e.g., Fragaszy et al., 2016; Kahrs et al., 2014), we hypothesized that toddlers would explore at the joint level of analysis to improve their anti-phase coordination pattern performance. This hypothesis arose from a possible mechanical interference between limbs when the shoulders (and thus large masses) were the primary joints that were moving (see Chapter 9 for consideration of other explanations).

We observed that, indeed, there was a beneficial effect on the primary joint employed being more distal than the shoulder. Furthermore, going beyond our expectations, we found that utilizing more than a single joint facilitated performance of anti-phase. Toddlers did not, however, modify their primary joint or the number of joints to support anti-phase movement over time. As we discussed in Chapter 9, toddlers seemed to have maintained a single strategy in terms of number of joints and showed unsystematic variation in terms of primary joint. Our results call for the more detailed kinematic analyses in the future to illuminate the dynamics associated with this variable.

10.2.5. Systematic versus random exploration.

Finally, we expected that we would find systematic exploration of the previously mentioned parameters to facilitate anti-phase acquisition. The rationale was that, provided that toddlers could perceive the movement dynamics, they would modify parameters in terms of such dynamics to afford anti-phase coordination pattern practice and improvement. Also, we followed Gelfand and Tsetlin (1962), who argued that random search in such a high-dimensional space would be inefficient. In other words, exploring randomly through all possible instances of a movement would require more than 27 months for one to learn a particular movement pattern.

As we have discussed in relation to each parameter, such exploration occurred only for frequency of oscillation and amplitude ratio. Thus, at least with these two parameters, toddlers demonstrated perceiving the movement dynamics and acting accordingly. There is a caveat, nevertheless. With both of these parameters, we found either that a few children initially demonstrated broader exploration than expected and then settled into more stable forms of performance (as in oscillation frequency) or that the effect of the parameter occurred only later in life (as in amplitude ratio). This means that, in some cases, it took time for perception of the dynamics to occur relevant to these parameters for the systematic pattern to then emerge.

10.3. Limitations

The findings that we have reported advance understanding of the early emergence of movement coordination patterns through different time-scales, and through group and individual-based analyses motivated on strong theoretical grounds. Nevertheless, we must remind our readers that our analyses and measures cannot yet be considered entirely definitive, but will require future replication and expansion. Most notably, and as mentioned throughout the chapters of this monograph, we acknowledge that toddlers performed under conditions in which the adult model demonstrated in-phase and anti-phase actions with different oscillation frequencies. In addition, toddlers used two sets of drumsticks which differed in length, and were in control of precisely where and how they grasped the drumsticks. Additionally, the coding of joint motion in our research used discrete categories rather than continuous measures. With the exception of the last point, all these procedural decisions were made in recognition of the practical challenges of working with toddlers as participants. When possible, we conducted analyses designed to evaluate the importance of these procedural decisions. For example, we analyzed toddlers’ frequency/relative-phase relation independent of the demonstration (adult model) condition, and used an amplitude ratio measure that cancels out absolute differences in drumstick length and absolute amplitude motion. Although the findings from these analyses generated no cause for concern about our conclusions, we nevertheless recognize that our results must be treated cautiously, and anticipate that they will motivate future studies designed to clarify the patterns and explanations of our current results.

10.4. The Updated Conceptual Model

We started this investigation by putting forth an adapted version of the HKB model that would represent the status of toddlers’ intrinsic dynamics around 15 months of age. The model was the standard HKB model using low values of b/a. After our investigations, the conceptual model must be updated. Figure 10.1 provides our updates.

Figure 10.1.

Dynamics in the acquisition of the anti-phase coordination pattern. Using the potential form of the function the panels show both the intrinsic dynamics (filled dark gray line), intentional dynamics (dotted light gray line) and a possible initial condition (filled black circle). The upper left panel shows the model with no parameters being modulated and b/a = 0.5). The upper right panel shows the expected effect of decreased frequency or usage of distal joints, the lower left panel shows the expected effect of increasing the amplitude ratio and the lower right panel shows the effect (represented by the arrow) on changing the initial condition.

As we moved through the analyses discussed in our empirical chapters, we found that the toddlers presented an initial capacity to perform brief sequences of anti-phase coordination and even to start some trials performing this pattern. Thus, it is possible to say that the model should include a small ‘trough’ at the anti-phase region. This would represent a weakly stable attractor that is easily disturbed by any perturbation.

Considering our findings and the adaptations discussed in the literature for the HKB model (see de Poel et al., 2009, Equation 3), it becomes apparent that first, the model needs to include the fact that the frequency of oscillation alters the initial stability of in-phase in relation to anti-phase (which can be considered as changes only in the a term– to create the desired effect in the model). This is different than initially proposed in the HKB model but suits the findings that toddlers, by decreasing frequency of oscillation, can explore the relative-phase dimension with less competition of their intrinsic dynamics. Also we need to include the effect of amplitude ratio (which requires the introduction of ΔA) that destabilizes the current pattern being performed. Even knowing that toddlers did not explore primary joint employment and initial condition, we found that these parameters do change relative-phase stability. Similar to oscillation frequency, these parameters are represented as changes in a, and serve as ways to start action closer to the intended trough in the landscape. Thus, the model would follow the equation $d\varphi /dt=\Delta A-a*\text{sin}\left(\varphi \right)-2*b*\text{sin}\left(\varphi \right)$ (note that we are not including handedness as considered elsewhere – see Treffner & Turvey, 1995). Additionally, we need to add the intention to perform a new pattern that appears as a new dynamic in the equation. The interesting point that differentiates this replication of the model from previous ones is that we assume that toddlers are modulating these parameters along an ontogenetic time scale to allow performance of the emergent movement pattern rather than just testing how these different parameters affect the extant short-term dynamics, although both processes are related.

10.5. The Emergence of Anti-Phase Coordination: From Models to Development

The goal of this monograph was twofold: to provide a description of the emergence of anti-phase coordination and to study this phenomenon under a dynamical systems perspective in order to understand how toddlers explore the action dynamics to begin to stabilize a new movement pattern. To guide our analyses, we based our investigations on the HKB model and its extensions in the literature.

10.5.1. Many subsystems influence change.

In line with the dynamical systems approach, we treated phase-relation behavior as an a posteriori aspect of the organization of the system, or our collective variable. We assessed how toddlers explored the dynamics of this task in order to increase stability in anti-phase action. This approach is consistent with Kelso’s (1995) strategy of considering every potential influence on the collective variable in terms of its dynamics. That is, intention (Scholz & Kelso, 1990), task requirements (Schӧner et al., 1992), memory (Schӧner, 1989), and other relevant parameters are all considered in terms of the variables included in the HKB model (see Kelso, 1995 for a review).

A major question that remains is how to relate these findings to the underlying components of development. That is, how do motor and perceptual learning, neuronal maturation, biomechanics, and other factors participate in this process? Although separating out the unique influence of each subsystem and its associated level of analysis might be almost impossible (see Bingham, 1988), we can provide some initial conjectures based on our results and previous research.

As summarized in previous sections, we discovered that toddlers could already engage in a few cycles of the anti-phase pattern as early as 15 months of age and that toddlers could start the drumming bouts in the anti-phase pattern at this age. Following Schöner (1989), these results may represent a recall of the pattern from infancy. The lack of stability during our participants’ first months in the study suggests a memorized pattern with little behavioral stability. This possibility requires a deeper understanding of memory, in which recall and stability are separated. What we can say, at least, is that the anti-phase pattern initially was part of the motor repertoire, even with minimal stability.

Toddlers’ performance of more anti-phase cycles in the Anti-phase condition at the initial practice session demonstrates that they were able to perceive the differences between phases performed by others. In other words, they were able to differentiate anti-phase from other movement patterns. This would also imply perceptual differentiation without stability, which contradicts the position put forth by Bingham (2004). The fact that toddlers employed the amplitude ratio strategy in specific ways, as illustrated in Chapter 7 (Table 7.2), provides an even stronger argument for the toddlers’ capacity to perceive differences between their own movements and the adult model’s, and then find ways to modify their actions. We note, however, that the amplitude ratio modulation occurred later in our study period so does not speak directly to the toddlers’ initial perceptual abilities at 15 to 16 months of age.

Another finding is that anti-phase stability improved across age, at least during the period covered by this study. Several mechanisms may explain this improvement. A simple explanation would be that the continuous development of brain areas such as the corpus callosum (see Luders, Thompson, & Toga, 2010), plus the continuous practice in the anti-phase pattern that takes place as part of life experience, provides enough support for increased stability. A more thorough explanation would examine how practice may interact with maturational processes to facilitate the acquisition of a new behavioral pattern. In this monograph, we found that individuals perceive the movement dynamics and, based on their understanding of how to interact with these dynamics, they modulate specific movement parameters as they practice.

Toddlers’ exploration of oscillation frequency offered a possible way for them to cope with cross-talk at the neural level (e.g., de Oliveira, 2002; Oliveira & Ivry, 2008, Swinnen, 2002). That is, because of the interactions between neural command streams, interference between commands could occur, especially at high frequencies. These conditions would create the tendency for the system to change from two separate commands to a single and unique command which integrated both limbs (Swinnen, 2002). In our study, toddlers perceived the interaction between frequency of oscillation and phase stability and modulated it accordingly. They also perceived that by modulating amplitude ratio, changes between phases could be performed. That is, toddlers perceived how changing their movements facilitated or hampered their actions. This represents learning at the level of the perception-action coupling, that is, acting to perceive and perceiving to act.

A facilitator of relative anti-phase stability that may result from maturation is an increased tolerance for high oscillation frequencies. Volman and Geuze (2000) observed that the frequency that elicits transitions from anti- to in-phase coordination patterns increases in children between 7 and 11 years. Thus, even as toddlers learn to cope with instability, the system increases the range of frequencies allowed in performing anti-phase. This possibility suggests the value of additional research with children of the ages tested in the present study that experimentally manipulates target oscillation frequencies.

It is also possible that a decrease in oscillation frequency helps toddlers maintain the anti-phase coordination pattern in terms of the mechanics of the movement. As stated in Chapter 2, at younger ages toddlers primarily use the shoulder to perform oscillatory motions in related task contexts (Fragaszy et al., 2016; Kahrs et al., 2014). As argued in Chapters 3 and 9, this would reciprocally influence motions at the trunk that might interfere with the oscillation of the other arm. However, this possibility can be dismissed in the current study because, first, our toddlers primarily performed the task using their elbow as the main joint of motion (see Chapter 9) and, second, when attempting to find a relation between the performed joint and the frequency of oscillation, we found the opposite pattern. Specifically, toddlers had lower oscillation frequencies when performing with their wrists and elbows than with their shoulders, a contrast that occurred primarily in the anti-phase model condition. Again, further kinematic study is needed to understand how this parameter is related to the action dynamics in our particular task.

In fact, although we found a relation between the mechanics of the movement considered in terms of the primary joint employed in drumming and performance of the anti-phase pattern, toddlers did not modify their movements in accordance with this relation. Thus, in the period of the current study, we have no evidence of the joint-level dynamics influencing the stability of the pattern. An additional interesting step would be to investigate older children at different ages and experimentally manipulate the primary joint of motion to observe whether and when such influence can be captured.

10.5.2. Individuality in the emergence of anti-phase coordination.

We observed that toddlers indeed explored and varied their movements according to the dynamics of their movement in this task, and that the appropriate modulation of movements to cope with dynamics improved with age. Nevertheless, variability between individuals was pronounced in terms of establishing anti-phase movement and the parameters being modulated to allow performance of the anti-phase pattern. We have acknowledged that variability between individuals would be the norm rather than the exception in development. It is clear from the literature that individuals do not always follow the same path in motor development (Clark & Phillips, 1993; Thelen & Ulrich, 1991, Thelen et al., 1993). Furthermore, with the number of parameters being analyzed here, it is clear that toddlers could achieve high performance of the anti-phase coordination pattern through modulation of different parameters – that is, we acknowledged possible redundancy in trajectories to the same end (i.e., equifinality) in development.

If we integrate the findings from all chapters, we find that, indeed, many toddlers preferred different means to achieve the same end of anti-phase drumming. Still other toddlers may not have discovered a consistent means to do so. Examining toddlers individually allows us to see this variety in developmental trajectories. In early observational sessions, for example, P1 attempted to modulate oscillation frequency to perform the anti-phase pattern, but in later months neither his observed behaviors nor inferential analyses (Figure 6.10) revealed significant improvement in stability (Figure 5.5). The small improvement observed can be related to increased usage in amplitude ratio (using the elbow as the primary joint), and by employing two joints in the drumming action. Demonstrating a very different trend was P2, who exhibited a clear increase in stability in the anti-phase pattern, a systematic trend in terms of frequency of oscillation (Figure 6.4), an already-present use of amplitude ratio, and the use of the elbow as primary joint. Interestingly, P2 primarily employed a single joint to produce motion.

P3, P4, and P7 showed similar patterns of change over time (Figure 6.10). Demonstrating the redundant pathways of change, P3 and P4 seemed to have gained more advantage from the amplitude ratio strategy than the oscillation frequency, while the opposite occurred for P7. Also, although all of them preferred a single-joint strategy, each chose as the primary joint a different one: P3 showed high variability between primary joints; P4 showed a high tendency to use the shoulder as the primary joint, and P7 was clearly a wrist-mover.

P5 demonstrated an early increase in performance in the anti-phase pattern at 19 months (see Figure 5.4) which could have been facilitated by using the amplitude ratio strategy or by performing with more distal joints and by using a two-joint strategy most of the time. Note, however, that this toddler showed high instability in execution during some months – probably as an effect of attempting to reach anti-phase through high frequencies (see Supplementary File S2). Finally, another toddler who demonstrated great gains in anti-phase performance was P6 who, in contrast to P2, clearly based her improvement in oscillation frequency. In terms of joints, P6 showed high variability in her primary joint and used a single joint in most trials.

10.5.3. Variation and selection in development.

The observation that toddlers explored and varied movements within their constraints, and that these experiences provided pathways for selection of new movement patterns, aligns with selectionist explanations of development such as Edelman’s theory of neuronal group selection (Edelman, 1987). With regard to behavior, developmental scientists have provided support for such a view in that individuals exhibit variability and, through exploration and selection, better or more efficient behavioral forms emerge (e.g., Angulo-Kinzler, 2001; Angulo-Kinzler et al., 2002; Hadders-Algra et al., 1996; D’Souza, Cowie, Karmiloff-Smith, & Bremner, 2017; Thelen & Corbetta, 1994). As stated earlier, we expected systematic patterns of exploration, but we observed a mesh of variability within our regularity. This suggests that some variation must be present for systematic patterns to emerge in exploration – a point made clear by Thelen and her colleagues (e.g., Thelen et al., 1993; Thelen & Corbetta, 1994; Thelen & Ulrich, 1991). In other words, variability may be the means through which perception of dynamics first emerge. We hold a view, nevertheless, which is contrary to some authors’ expectations that at some point variability is random through all possible states (e.g., as implied by Morice et al., 2007). The patterns in our data suggest that variation is constrained to a limited region of the movement possibilities and does not necessarily lead directly to the best solution for a particular situation. Variability can, at most, indicate the best direction of change by revealing the dynamics of the movement (see Pacheco et al., 2017).

What we are proposing is that the individual constraints (morphological, neurological, motor, perceptual, and so on) channel the variability that is possible at the behavioral level. The expressed behavior in turn constrains the perception of the properties of movement and how this movement relates to the task at hand. The ongoing perception-action cycle then constrains the perception of new possibilities for potential movements. Following this line of reasoning, behavioral selection is presumed to occur as the movements interact more appropriately with the task and become more stable in the face of perturbations. This view explains the emergent change in movement patterns observed through development (see Sporns & Edelman, 1993, Rosengren, Savelsbergh, & van der Kamp et al., 2003).

An interesting point of discussion is that not all parameters were equally varied and explored by our toddler participants. Again, only data on the oscillation frequency and amplitude ratio supported our hypotheses. This implies that, across the ontogenetic period studied in our work, movement dynamics were not fully unraveled by the toddlers. For instance, we did not see an increasing prevalence of toddlers starting the movement matching the experimenter model by modulating initial phase condition. One could speculate that adults would likely modulate in this way in cases in which they lose track of the rhythm or pattern, and would restart the movement to adjust to the demonstrated phase relation. Nor did modulate the involvement of their joints to facilitate performance. In some respects, these findings are similar to those of Fitzpatrick et al. (2012) who reported that only the most relevant parameters of hammering were discriminated and modulated in 3- to 5-year-old children.

In light of our earlier discussion of variation and selection, it could be that initial limb position and joint employment, as we scored them, were not sufficiently varied during our assessments for perception of dynamics to occur. As stated by Michaels and Carello (1981), in an early discussion of perception and action, perception takes time. It could be that changes in the initial-condition and joint-employment parameters obey different timescales of change (cf. Newell et al., 2003) and, thus that observations across more extended timespans would be needed to provide some hint of when and how these parameters are modified to support performance in rhythmic bimanual coordination.

10.6. Conclusion

In this monograph, we delved into the rich and complex world of motor development focusing on the core skill of bimanual coordination to longitudinally investigate how humans solve the always-present problem of goal-directed coordination. We went beyond the description of toddlers becoming more stable performers of the anti-phase drumming task over the course of months. We wanted also to understand the means by which these toddlers, month after month and within each trial, searched the dynamics of movement to find solutions for performing this task.

At first glance, our analyses of the data generated by observing our toddlers may seem to confirm our introductory assertion that development can be messy. Each of our seven toddlers exhibited a unique behavioral trajectory from month to month and produced widely varying bouts of action even within months. However, in choosing to interpret messiness as variability of behavior, and exploiting this variability as the means by which toddlers explore possible actions, we have revealed some ordered (emergent) patterns of behavioral change. Using the HKB theory (or DST) and related evidence from past literature to guide innovative analyses that integrate multiple timescales of development, we have documented not just that drumming behavior changes over the course of toddlerhood, but how it does so. We have identified at least three mechanisms of change: oscillation frequency, amplitude ratio, and involvement of arm joints to effect the movement. Toddlers differed in the extent to which they exploited each of these strategies, but each of the three was apparent in multiple participants. Thus, we demonstrated how toddlers first understood their movement capacities and, then, learned how to master the appropriate action through perception and action.

The importance of our findings cannot be undermined. Motor development cannot be just a matter of learning a fixed movement pattern; the environment and organism are full of variations that potentially impose different constraints every single trial. Developmental processes must coordinate the self and environment in a way that leads one to the desired outcome. To help us understand the intricate and complex relation of environment and toddlers’ perception and action relative to drumming, we employed several analytic techniques new to most developmental specialists (e.g., wavelet analyses, Hilbert-transformed relative phase) and challenged ourselves with an exploratory longitudinal design.

In our semi-structured drumming task, manipulated and spontaneous variations of relevant movement parameters meshed to reveal meaningful systematic trends in behavior.

We found that toddlers engaged in their first cycles of anti-phase upper-limb coordination as early as 15 months of age. Nevertheless, only later (after 18–20 months of age) did they perform relatively stably a sequence of cycles using anti-phase coordination. Consistent with our theoretical predictions, we found that toddlers exhibited different pathways in the emergence of the anti-phase pattern through modulation of oscillation frequency and amplitude ratio.

We posit that the emergence and stabilization of the anti-phase coordination pattern point to a more intricate network of changes in many subsystems. Our results suggest possible developmental changes due to perceptual, memory, motor, and neural systems. We also refuted influence at other levels (i.e., biomechanics). Additionally, we put forth a conceptual model that helps to characterize ways that toddlers explore and maintain their movement patterns consistent with principles of dynamical systems and formal models of motor learning. We believe that this monograph has provided an initial description of the longitudinal changes that occur in rhythmic bimanual coordination – in particular the emergence and stabilization of the anti-phase pattern. We provided evidence that acquisition of a new behavioral pattern within a given context occurs as a function of exploration of different movement parameters, allowing intrinsic dynamics and task requirements to cooperate in support of the emerging movement pattern. In addition, we believe that the movement parameters and how they are explored seem to be related to how toddlers’ dynamic developmental affords their exploration. We hope that this work will inspire a new generation of longitudinal and experimental research that further elucidates the processes of change in early childhood motor development.

Table 7.3.

LME results for the relation between ALAR and standard deviation of relative phase.

R2 = 0.16	df = 2.10*105
Fixed Effects
Name	Estimate (± SE)	t-stat	p-value
Intercepta	25.22 (± 2.16)	11.69	< .001
Change (per month)	0.18 (± 0.21)	0.88	.378
ALAR	12.49 (± 0.95)	13.18	< .001
Mean RP	0.04 (± 0.001)	25.19	< .001
Change*ALAR	−0.12 (± 0.02)	4.73	< .001
Change*Mean RP	−0.001 (± 0.0002)	5.13	< .001
ALAR*Mean RP	−0.01 (± 0.001)	8.08	< .001
Change*ALAR*Mean RP	0.0008 (± 0.0002)	4.08	< .001

Random Effects
Name	Type	Estimate
Intercept	SD	5.69
Change (per Month)	SD	0.54
ALAR	SD	2.47
Residual	SD	17.82

^aThe intercept refers to the estimate for the 15^th month of age.