Abstract
Mitochondria play an essential role in bioenergetics and cellular Ca handling. The mitochondrial permeability transition pore (mPTP) is a non-specific channel located in the inner mitochondrial membrane. Long-lasting openings of the pore allow the rapid passage of ions and large molecules, which can result in cell death. The mPTP also exhibits transient, low conductance openings that contribute to Ca homeostasis. Although many regulators of the pore have been identified, none of them uniquely governs the passage between the two operating modes, which thus probably relies on a still unidentified network of interactions. By developing a core computational model for mPTP opening under the control of mitochondrial voltage and Ca, we uncovered the existence of a positive feedback loop leading to bistability. The characteristics of the two stable steady-states correspond to those of the two opening states. When inserted in a full model of Ca handling by mitochondria, our description of the pore reproduces observations in mitochondrial suspensions. Moreover, the model predicted the occurrence of hysteresis in the switching between the two modes, upon addition and removal of free Ca in the extra-mitochondrial medium. Stochastic simulations then confirmed that the pore can undergo transient openings resembling those observed in intact cells.
Subject terms: Calcium signalling, Computational models
Introduction
In most cell types, cytosolic Ca is a key ion that controls major intracellular processes in health and disease1. The signalling specificity of this ion largely relies on the spatio-temporal organisation of its stimulus-induced increases2. For example, oscillations and waves can occur due to the auto-catalytic Ca release from the endoplasmic reticulum (ER), which acts as the main Ca store. However, Ca exchanges with other organelles further extend the spatio-temporal diversity of Ca signals. Among these, exchanges between the cytosol and mitochondria play an important role. Entry of Ca into mitochondria is mediated by the mitochondrial Ca uniporter (MCU), while exit occurs via the Na-Ca and the H-Ca exchangers (NCLX and HCX), in non-excitable cells3. Ca uptake by mitochondria not only participates in the regulation of the cytosolic Ca concentration ([Ca]) but also stimulates mitochondrial respiration and ATP production4.
The mitochondrial permeability transition pore (mPTP) can also transport Ca. Indeed, in response to a metabolic stress or to an excessive accumulation of mitochondrial Ca, an increase in the permeability of the inner mitochondrial membrane (IMM) can be observed. First described in the 1970’s5–7, this phenomenon, called permeability transition, could rapidly be ascribed to a non-selective pore. Mitochondrial Ca overload and/or oxidative stress lead to a massive and unselective opening of the pore, which allows for the transit of molecules up to 1500 Da. This includes Ca, metabolic substrates and ATP. Consequently, opening of the mPTP in this mode induces the dissipation of the IMM voltage () and, finally, cellular death. However, the pore can also exhibit moderate and transient openings8. Indeed, the existence of smaller conductance sub-states of the mPTP has been demonstrated by experiments on mitochondrial suspensions9 and by electrophysiology10,11. This mode of reduced activity contributes to Ca homeostasis and thereby helps maintaining normal cellular functions8,12.
Well before its plausible molecular identification13,14, it was known that many factors, including reactive oxygen species (ROS), pH, inorganic phosphates or cyclophilin D regulate the permeability transition12. Importantly, the main drivers of mPTP opening are and mitochondrial Ca concentration ([Ca]). Opening requires a low voltage and a high Ca load. Once open, the mPTP allows for the passage of ions, including Ca itself, which leads to mitochondrial membrane depolarisation (Fig. 1). There is no evidence of any specific regulator that would drive the mPTP from a low- to a large opening state, and it can thus be anticipated that this passage results from a network of feedback regulations.
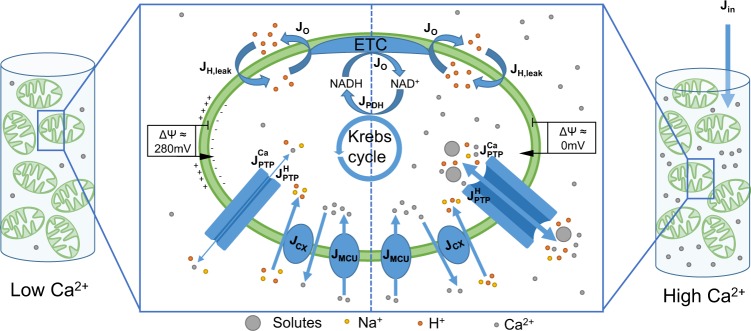
Figure 1.
Schematic representation of the model describing Ca dynamics and mPTP opening in mitochondrial suspensions. The model includes Ca exchanges between mitochondria and the extra-mitochondrial medium through the Mitochondrial Ca Uniporter (), the Ca exchangers (), and the mPTP (). The mPTP is potentially permeable to ions (H, Mg, K, ...) and small solutes. These fluxes are gathered in . Mitochondrial Ca triggers the reduction of NAD in NADH () that can be oxidised by the electron transport chain () to generate a proton gradient. A leakage of protons into the mitochondrial space is considered (). ATP synthesis is not included because the medium does not contain adenine nucleotides. The model reproduces a resting state (on the left) and a Ca-overloaded state (on the right). At rest, the Ca concentration in the suspension is low. Thus, the mPTP does not open fully, and the fluxes through this pore (, ) are low. In these conditions, a is maintained thanks to the extrusion of protons. Upon the addition of a massive amount of Ca in the medium (), the mPTP opens and becomes highly permeable to ions and solutes. This leads to the dissipation of the . See text, SI Appendix and Wacquier et al.22 for more details on the model.
In this study, we hypothesised that the two operating states of the mPTP rely on bistability. In such a scenario, two stable steady-states can coexist in a range of [Ca], which confers robustness to both states of channel opening. This assumption is based on the observation of a positive feedback loop that relies on the cross-inhibition between mPTP opening and mitochondrial voltage (): low voltage indeed opens the mPTP, which leads to further mitochondrial depolarisation (i.e. decrease in ). As mitochondrial Ca, known as the main mPTP regulator, directly controls , we anticipated that this positive feedback loop constitutes the core regulatory mechanism of mPTP opening. We first built a computational model formalising the mechanism just described. As assumed, the model can display bistability. We validated the model and parameter values using experiments in mitochondrial suspensions, which allow for controlled Ca exchanges between mitochondria and the extra-mitochondrial medium (em). The model then led us to rightly predict the conditions in which a hysteretic behaviour, which is a hallmark of bistability, can be observed. The robustness of bistability was assessed by a sensitivity analysis of the computational model. Finally, we showed that the model recapitulates the reversible, transient openings of the mPTP observed in intact cells. In conclusion, this work proposes a simple dynamical mechanism by which mitochondria can safely use the mPTP in two operating modes, which differ drastically by their conductances and by their physiological implications. Put in a cellular context, the proposed bistable behaviour not only provides robustness to the Ca transport properties of the mPTP, but also ensures that, once initiated, the mPTP-induced mitochondrial depolarisation is physiologically irreversible.
Model
The regulation of the mPTP by [Ca] and is schematised in Fig. 2A. Based on this scheme, a single differential equation is used to describe the evolution of the fraction of open mPTP in the mitochondrial pool, noted . A small value of thus corresponds to the transient, low conductance mode while a high value of this variable can be associated to the large, long-lasting opening mode. In the following, we refer to these states as the low and high conductance modes. It should be noted that these terms do not refer to the single channel activities measured by electrophysiology. As in previous models15,16, the evolution equation includes a highly non-linear term of opening of the mPTP, that is triggered when falls below a threshold17,18. In agreement with experimental data19,20, the value of the threshold is controlled by [Ca] ( in the model). The rate of mPTP closure is described by a linear function. Thus, the evolution of the fraction of open mPTP is given by :
| 1 |
where and are rate constants of mPTP opening and closing, respectively. and set the Ca and the voltage dependencies of mPTP opening. When the mPTP is open, Ca and protons leak through the pore. Each ion flux depends on the electrochemical gradient and on the opening state of the mPTP. We describe these fluxes by mathematical expressions based on a simplified version of the Goldman-Hodgkin-Katz formalism21. Fluxes of Ca and H are described by Eqs. 2 and 3, respectively.
| 2 |
| 3 |
where and are rate constants of Ca and H fluxes through the mPTP, and and are coefficients characterising the voltage dependencies of these ions fluxes through the mPTP. The concentration of H does not appear in Eq. 3 as it is not a variable of the model. It is therefore implicitly included in , and the flux only appears in the evolution equation for voltage (Eq. 4). Moreover, also includes other compounds leaking through the pore (ions and small solutes).
Figure 2.
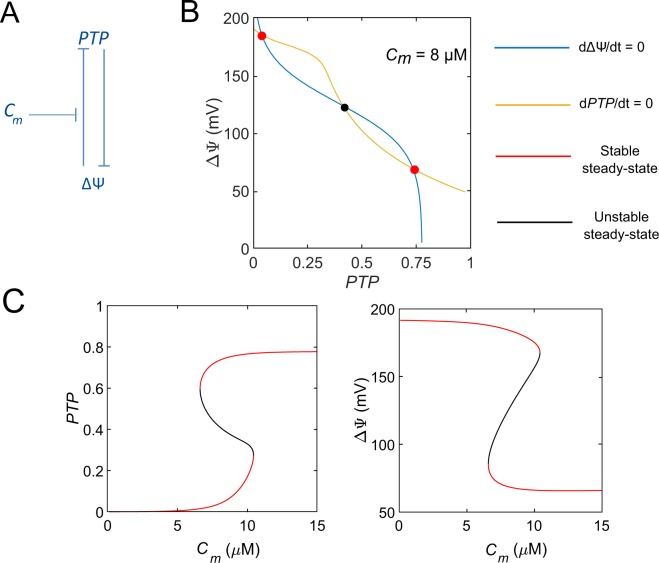
A two-variable model describing mPTP opening. (A) Scheme of the model. The positive feedback loop between the fraction of open mPTP () and mitochondrial voltage () underlies bistability. This loop results from cross-inhibition. modulates the threshold of inhibition by . (B) Phase space for . The yellow and blue curves represent and null-clines, respectively. was fixed at 0.5 and at 200 . In red: stable steady-state. In black : unstable steady-state. (C) Bifurcation diagrams of and as a function of .
Experimentally, the dynamics of mPTP opening are commonly investigated in suspensions of mitochondria. To model this experimental system, Eqs. 1–3 describing mPTP opening and closing, and the associated ion fluxes, are included in a previously-published model describing Ca dynamics in such a system (Fig. 1)22. This model describes 1) Ca exchanges between mitochondria and their medium via the MCU () and the NCLX/HCX () 2) The Ca-dependent synthesis of NADH by the Krebs cycle (), and its consumption by the electron transport chain (ETC, ) 3) The variations of voltage induced by Ca transporters, the ETC and proton leaks (). Eq. 1 is thus coupled with this model.
The mitochondrial voltage varies in time according to :
| 4 |
Positive voltage corresponds to an excess of positive charges in the extra-mitochondrial medium. scales molecular fluxes into voltage changes. It includes the membrane capacitance and the Faraday constant. scales NADH consumption into voltage variations.
For the time evolution of extra-mitochondrial Ca concentration (), we write
| 5 |
where is the Ca buffering capacity of the medium considering the rapid buffering approximation23. It corresponds to the ratio between free and total Ca concentrations in the extra-mitochondrial medium (em). is the volumic ratio between mitochondria and their medium (). allows to simulate the addition of Ca in the medium.
In a similar way, the time evolution of mitochondrial Ca concentration () is expressed by
| 6 |
where is the Ca buffering capacity of mitochondria.
Finally, NADH is produced by the Krebs cycle and consumed in the ETC, which is described by
| 7 |
The detailed kinetic expressions of the fluxes are exposed in the Supplementary Material. Parameters values are listed in Table S1 and, except for the mPTP opening description, are taken from our previous models that were validated against experimental data22,24.
Results
The mPTP acts as a bistable switch
Bistability often occurs in a system including a positive feedback loop25,26. As schematised in Fig. 2A, such a loop exists between the mPTP and , as a high prevents the opening of the pore, while is dissipated by an open mPTP due to ion leakage8. Because [Ca] controls the value at which starts inhibiting mPTP opening, Ca could play a key role in the switch. To study the possible existence of a Ca-controlled bistability in the mathematical description of the mPTP presented in the previous section, we first considered a minimal model that only considers the evolution of and (Eqs. 1 and 4) while , and are kept constant. We analysed the behaviour of this two-variable model on the basis of bifurcation diagrams where the steady-states of and are shown as a function of (Fig. 2C). For low (7 ), the system tends towards a resting state, i.e. a large and an almost closed mPTP (low value of variable ). For high (11 ), the system will always evolve towards a dissipated potential and a fully open mPTP. For intermediate concentrations, one can observe the coexistence between these two stable steady-states, separated by an unstable one. This scenario is also visible in the phase plane, where the null-clines intersect once at low or high value of , for low or high respectively (not shown), and three times for intermediate Ca concentrations (Fig. 2B). The two steady-states display the characteristics of the two operating modes of the mPTP described above. The first one occurs at low Ca, when a high is established across the IMM8. The other state is reminiscent of the behaviour of the mPTP reported at high mitochondrial Ca load: the mPTP largely opens, leading to the dissipation of . Interestingly, in suspensions, it is possible to come back from the high to the low conductance mode by adding a Ca chelator27. The model is possibly in agreement with this reversible bistability, as the ordinate axis does not intersect the bistable area26.
To validate the model, its behaviour must be compared to experiments. Successive additions of large amounts of Ca in a suspension of mitochondria isolated from hepatocytes can induce mPTP opening. In Fig. 3A, each arrow represents the addition of 5 M exogenous Ca. Changes in Ca concentration in the medium ([Ca]) are monitored by spectrophotometry22, allowing to follow Ca exchanges between mitochondria and the medium. Up to the first four additions of Ca in the medium, most of the Ca is sequestered by mitochondria via the MCU, and the mPTP has a limited effect22. However, after the fifth addition, one observes a brutal increase in the [Ca] (Fig. 3A). This important rise is attributed to the opening of the mPTP in its high conductance mode. This opening is accompanied by the release of Ca from mitochondria, which explains the fast and sudden elevation in the medium. To compare the behaviour of the model with these experimental observations, we took variations of Ca and NADH concentrations into account and simulated the whole dynamical system, defined by Eqs. 1 and 4–7 with the same values of parameters as in our previous study22. The model faithfully reproduces the experimentally observed behaviour (Fig. 3B): after a few pulses, increases all of a sudden (blue curve). This increase is associated with the opening of the mPTP (red curve), which triggers a Ca flux from mitochondria to the medium (via ) while is collapsing due to the important ion fluxes through the mPTP (yellow curve).
Figure 3.
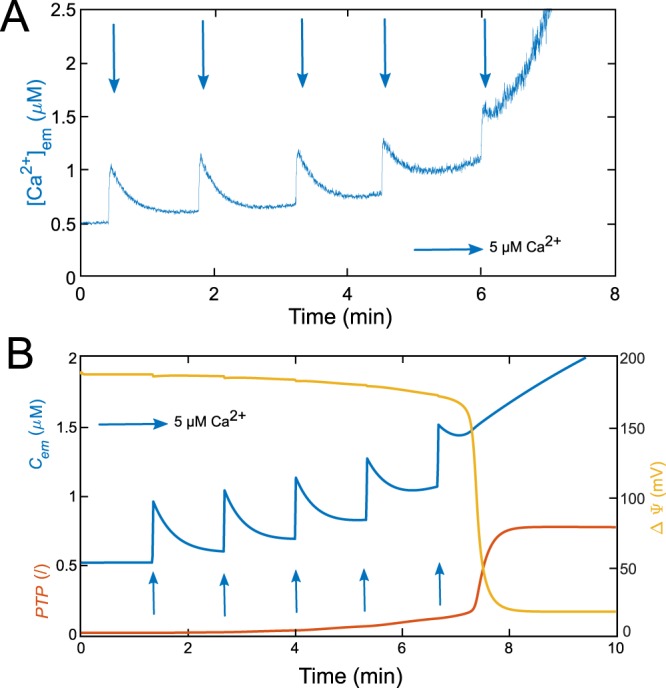
Successive additions of Ca leading to mPTP opening in experiments and in the model. (A) Experiment performed in a suspension of mitochondria extracted from rat hepatocytes. The [Ca] is monitored by fluorescence using 5 Fluo-4. Following the addition of five Ca pulses (blue arrows), the mPTP opens, as attested by the sudden rise in Ca concentration in the medium. (B) Simulations of the five-variable model (Eqs. 1 and 4–7). The model successfully reproduces the [Ca] behaviour (in blue), in response to the Ca pulses (implemented with ). The final increase in the is associated with a sudden increase in mPTP opening (variable , standing for the fraction of open PTP, in red) and a fall in (in yellow). See Table S1 for parameter values.
The switch-like behaviour shown in Fig. 3 is compatible with the existence of bistability, but might also rely on the existence of a sharp threshold. To investigate if the switch corresponds to a change of steady-state, we cannot draw bifurcation diagrams as a function of as in the two-variable model (Fig. 2C), since is a variable in the full model. We thus established pseudo bifurcation diagrams showing the values of and as a function of the amount of Ca added during the pulses (Figs. 4A,B and S1). The blue curve is drawn by performing a series of simulations where the steady-states of the model are sequentially computed after successive additions of 0.1 Ca. After a critical amount of added Ca, the system is driven towards a state with a large opening of the mPTP. This opening is, as expected, associated with a drop in and Ca efflux from mitochondria. From this state, we then simulated the removal of Ca from the medium (red curve corresponding to successive decreases of Ca of 0.1 M). Biologically, it would correspond to the addition of a Ca chelator. It is clear that the blue and red trajectories do not coincide and that bistability also occurs in the full model. The amount of Ca that has to be removed to bring the mPTP back in its low conductance mode exceeds the amount of Ca that was necessary to trigger the passage from the low to the high conductance mode. This hysteretic behaviour is typical of a bistable system26.
Figure 4.
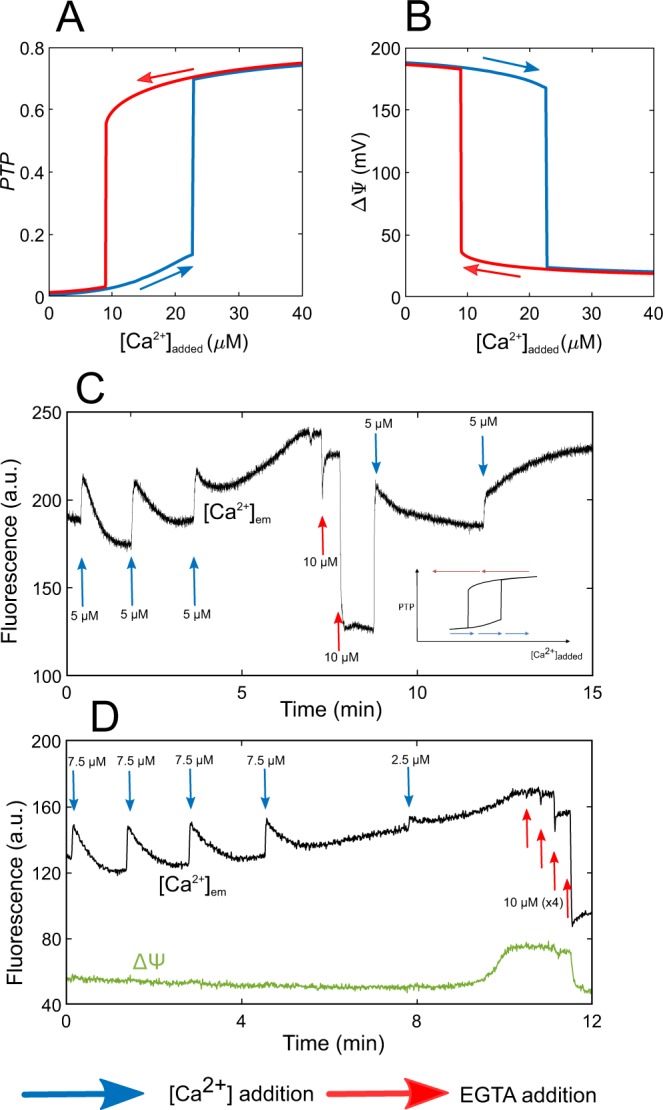
mPTP opening corresponds to a bistable switch. Numerical bifurcation diagrams of the fraction of open mPTP, (A) and (B) as a function of added Ca. Blue and red curves stand for trajectories following Ca additions (from left to right) or Ca removal (from right to left), respectively. The equivalent bifurcation diagrams of and as a function of added Ca are shown in Fig. S1. (C,D) Experimental evidence for bistability of the mPTP in a hepatocyte mitochondrial suspension. Ca is monitored in the medium with 5 Fluo-4 (C,D) and with 5 TMRM (SI Appendix) (D). In both cases, the concentration of EGTA necessary to close the mPTP is larger than the concentration of Ca that allowed its opening. This highlights the existence of hysteresis as schematised in the inset in Panel (C). Panels (C,D) are representative of 12 similar experiments.
Hysteresis in mPTP opening
We next wondered if experiments can validate the hysteresis predicted by the model. We first checked in a control experiment that in a medium devoid of mitochondria, the addition of a given amount of Ca is rapidly counterbalanced by the addition of the same amount of the high affinity Ca buffer EGTA (Fig. S2). This observation is in agreement with the 1 to 1 stoichiometry of Ca binding to EGTA and with the values of and (6 M s and 1 s, respectively28). Then, on the basis of the model prediction shown in Fig. 4, we submitted mitochondria in suspensions to successive additions of Ca, up to the opening of the mPTP. As soon as the mPTP opens, we rapidly added EGTA. We then compared the amount of EGTA necessary to close the mPTP to the amount of Ca that was necessary to open it. Following the addition of three Ca pulses of 5 M in a mitochondrial suspension, the mPTP opens and [Ca] starts to rise (Fig. 4C). Thus, between 10 and 15 M Ca were necessary to trigger opening. Accordingly, in the absence of hysteresis, the removal of 5 Ca should close the mPTP. Nevertheless, the addition of 10 M EGTA is not sufficient to close the mPTP: the [Ca] is still high, indicating that the mPTP is still open. By contrast, the Ca level decreases drastically after a second addition of 10 M EGTA. At this stage, the mPTP is closed or in a low conducting mode. As a control, upon Ca re-addition, we see a characteristic spike due to Ca entry in mitochondria. This would not be visible with an open mPTP, as mitochondria would not be able to sequester Ca. Finally, a further Ca addition allows to open the mPTP again.
The existence of hysteresis is also supported by the simultaneous measurement of and [Ca] during a similar experiment (Fig. 4D). After 32.5 of added Ca, the drop in potential associated to mPTP opening is observed through an increase in the fluorescence of the probe. Concomitantly, the opening of the pore is seen via the increase in the [Ca]. 40 EGTA are then required to bring the system back to its basal state, in agreement with the presence of a hysteresis loop.
Robustness of bistability
To be biologically relevant, bistability in mPTP dynamics must be robust with respect to cell-to-cell variations. It is thus important to check that the bistable behaviour predicted by the mathematical model occurs for a large range of values of the kinetic parameters. We first analysed the extent of the domain of bistability when changing the values of the parameters of the model (Fig. 5, in blue). It is visible that bistability occurs in a quite extended range of values of all parameters. The existence of bistability is sensitive to the kinetic parameters that control the opening of the pore ( and ). If the pore opens too slowly, or closes too fast, bistability is lost. Bistability is thus favoured by a given ratio between opening and closure rates (Fig. S3B). The most sensitive parameter is , that regulates the threshold of inhibition of the pore by (Fig. S3C). This parameter also alters the threshold of mPTP opening by Ca. Consequently, increasing this parameter shifts the whole bifurcation curve (Fig. 4A for example) to the left, until the bistable domain disappears from positive Ca concentrations. On the opposite, decreasing the parameter shifts the bistable area to the right. For high values, the system is thus bistable, but we consider this situation as biologically not relevant as it requires the addition of an unrealistically large amount of Ca. Interestingly, the existence of bistability is extremely robust with respect to changes in the parameters related to Ca fluxes (, and ). Changing these parameters mainly impacts on the rates at which Ca is exchanged between mitochondria and the medium. This relative insensitivity confirms that the relationship between and is the core mechanism leading to bistability, whereas Ca controls the transition between the two states. Finally, if the ion flux through the mPTP () is weak, bistability is also lost (Fig. S3D). Indeed, the loss of induced by mPTP opening is then much reduced, which weakens the positive feedback loop that generates bistability.
Figure 5.
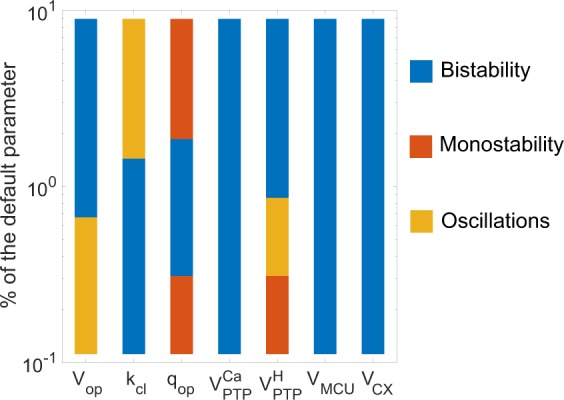
Range of bistability in the mPTP opening model. In blue: the system is bistable; in orange-coloured: the system has one stable steady-state; in yellow: the system oscillates at high values. Sensitivity analysis was performed by individually varying seven different parameters from 10 to 1000 % of their default values. See Fig. S3 for bistability conditions and notes on oscillatory behaviour.
Simulation of transient openings of the mPTP
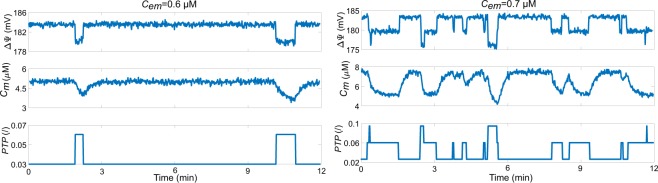
The level of opening of the mPTP in its low conductance mode is in average very small. The associated Ca fluxes are thus expected to be minimal. In intact cells, openings in this mode indeed take the form of short-lived, stochastic events as reported for permeabilised heart cells29 and astrocytes30. These random openings are associated with small-amplitude drops in and mitochondrial Ca and are localised to small areas of the cell.
We developed a stochastic version of the model to simulate transient mPTP openings (SI Appendix). As these openings remain highly localised, we simulated a small volume containing a single mitochondrion, and considered that the concentration of cytosolic Ca around this mitochondrion () remains constant. An increase in simulates an efflux from the ER, triggered by an external stimulus. At low , simulations predict a noisy but stationary state for and , associated with a mPTP that is nearly always closed. If we increase , small and rapid drops in , accompanied by some Ca efflux from the mitochondrion, can be observed (Fig. 6). These isolated events correspond to sudden, random and brief openings of the pore in its low conductance mode. For higher Ca concentrations, the number of events increases, as well as the mPTP open probability (Fig. S4). If the number of events becomes too large, changes in and are quite irregular, as observed in heart mitochondria in suspension31.
Figure 6.
Stochastic opening of the mPTP. Time series of the evolution of , and for different , obtained by simulations of a stochastic version of the model. The simulated system corresponds to the volume of a single mitochondrion exposed to a constant .
Discussion
We have provided a minimal description of the dynamics of the mPTP, in which we only considered the regulation of the pore by its main regulators, Ca and . It is clear, however, that mPTP opening is inhibited by a variety of compounds, which include Mg, adenine nucleotides, cyclosporin A, mitochondrial H, metabolic fluxes and environment, and stimulated by others, such as reactive oxygen species, organic phosphate or cyclophilin D12,15,20,32. Although the influence of most of these factors can partly be accounted for by their influence on or Ca, a more accurate description of the mPTP regulation would be useful to account for some experimental observations. Inhibition of mPTP opening by protons is sometimes proposed as a primary mechanism of mPTP regulation33. In the present model, protons influence mPTP opening through membrane voltage, but not directly (see Eq. 4). It is known that the mPTP is open at pH 7.3-7.5 and closed at pH 734,35. Because at rest, mitochondrial pH lies between 7.2 and 7.633,36, and because an increase in [Ca] leads to an increase in mitochondrial pH, direct H regulation of the mPTP cannot on its own account for the abrupt openings of the pore observed upon additions of Ca (Fig. 3).
Focussing on the core regulatory mechanism of mPTP opening by Ca and allowed us to uncover the occurrence of bistability in an intermediate range of [Ca]. This bistability underlies the well-established existence of two operating modes displaying widely different average conductances. The proposed mechanism moreover agrees with the recent observation of a common molecular nature of the two modes of the pore, which is formed from the FF ATP synthase, at the interface between monomers within dimers13.
The bistable scenario proposed in this study contrasts with the description of the passage between the low- and the high-conductance mode of the pore as a switch controlled by a single threshold governed, for example, by mitochondrial pH16,33,37,38, [Ca]39, [Ca]40 or mitochondrial volume41. In Bazil et al.15, the switch is imposed by , and the value of the threshold is controlled by [Ca], as in the present study. This 200-variable model is very detailed, as it includes regulation of the mPTP by a variety of factors as well as mitochondrial bioenergetics. It nicely reproduces experimental observations but is hardly usable for a bifurcation analysis. In a broader context, many processes governed by binary choices in cell biology have been described by bistability. This includes cell differentiation42, enzymatic reactions43, the cell cycle26,44, or bacterial communication45. One of the main advantages of bistability-controlled transitions is their robustness. In the case of the mPTP, this property plays a key role in relation to the very nature of the pore. Indeed, when the pore enters in a high conductance mode, it provokes a decrease in and [Ca]. If a threshold-associated switch was at play, this decrease would bring the channel back in a low conductance mode, provoking in turn an increase in and [Ca], hence the opening of the channel again. These unrealistic back and forths between a fully- and a partially-open pore do not occur in a bistable scenario, which ensures that, once initiated, the full opening of the channel is maintained up to a point where largely depolarised mitochondria lead to cell death.
Much remains to be done to assess the physiological relevance of the low conductance mode of the pore in intact cells. We have touched this question by performing stochastic simulations of the model in conditions corresponding to a single mitochondrion facing different levels of Ca in its surrounding cytosol. A stochastic approach is necessary because openings are transient and weak. The low level of mPTP opening computed in the deterministic bifurcation diagram (Fig. 4A) corresponds to an average over extended periods of time, during which the mPTP undergoes random, discrete openings (Fig. 6). In cells, such transient openings are thought to play an important role in releasing matrix Ca to maintain mitochondrial homeostasis46. In vivo, mitochondria are morphologically and functionally heterogenous47, which can explain the large variety of changes in [Ca] that have been reported experimentally22. Moroever, mitochondria are permanently rebuilt through fusion and fission that are promoted by mitochondrial movements48. The last two factors are expected to further increase the variability in mPTP openings, in addition to their inherent stochastic character, which again calls for a relatively noise-insensitive mode of switching between the two conductance modes.
The mPTP is involved in the pathophysiology of many diseases, ranging form ischemia/reperfusion injury to neurodegenerative disorders49. It would be useful to integrate the present description of the mPTP as a bistable molecular switch in comprehensive models of mitochondrial Ca and metabolism15,50,51 to provide a detailed computational support to the experimental investigation of such pathologies52.
Supplementary information
Acknowledgements
G.D. is Research Director at the Belgian FRS-FNRS. G.D. and B.W. benefit from a financial support from ULB. L.C., G.D. and B.W. benefit from a WBI-France exchange program (WBI, FRS, Ministère Français de l’Enseignement supérieur et de la Recherche dans le cadre des Partenariats Hubert Curien).
Author contributions
B.W., L.C. and G.D. conceived and designed the simulations and the experiments. L.C. and B.W. performed the experiments. B.W. performed the simulations. B.W., L.C. and G.D. analysed the data. B.W., L.C. and G.D. wrote the manuscript.
Competing interests
The authors declare no competing interests.
Footnotes
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
is available for this paper at 10.1038/s41598-020-60177-1.
References
- 1.Berridge MJ, Bootman MD, Lipp P. Calcium - a Life and Death signal. Nature. 1998;395:645–648. doi: 10.1038/27094. [DOI] [PubMed] [Google Scholar]
- 2.Dupont, G., Falcke, M., Kirk, V. & Sneyd, J. Models of Calcium Signalling, vol. 43 of Interdisciplinary Applied Mathematics (Springer International Publishing, 2016).
- 3.Jouaville Laurence S., Ichas François, Mazat Jean-Pierre. Bioenergetics of the Cell: Quantitative Aspects. Boston, MA: Springer US; 1998. Modulation of cell calcium signals by mitochondria; pp. 371–376. [PubMed] [Google Scholar]
- 4.Denton RM. Regulation of Mitochondrial Dehydrogenases by Calcium Ions. Biochimica et Biophysica Acta (BBA) - Bioenergetics. 2009;1787:1309–1316. doi: 10.1016/j.bbabio.2009.01.005. [DOI] [PubMed] [Google Scholar]
- 5.Hunter DR, Haworth RA. The Ca-Induced Membrane Transition in Mitochondria. III. Transitional Ca Release. Archives of Biochemistry and Biophysics. 1979;195:468–477. doi: 10.1016/0003-9861(79)90373-4. [DOI] [PubMed] [Google Scholar]
- 6.Haworth RA, Hunter DR. The Ca-Induced Membrane Transition in Mitochondria. II. Nature of the Ca Trigger Site. Archives of Biochemistry and Biophysics. 1979;195:460–467. doi: 10.1016/0003-9861(79)90372-2. [DOI] [PubMed] [Google Scholar]
- 7.Hunter DR, Haworth RA. The Ca-Induced Membrane Transition in Mitochondria. I. The Protective Mechanisms. Archives of Biochemistry and Biophysics. 1979;195:453–459. doi: 10.1016/0003-9861(79)90371-0. [DOI] [PubMed] [Google Scholar]
- 8.Brenner C, Moulin M. Physiological Roles of the Permeability Transition Pore. Circulation Research. 2012;111:1237–1247. doi: 10.1161/CIRCRESAHA.112.265942. [DOI] [PubMed] [Google Scholar]
- 9.Ichas F, Jouaville L, Mazat J-P. Mitochondria Are Excitable Organelles Capable of Generating and Conveying Electrical and Calcium Signals. Cell. 1997;89:1145–1153. doi: 10.1016/S0092-8674(00)80301-3. [DOI] [PubMed] [Google Scholar]
- 10.Szabò I, Zoratti M. The Giant Channel of the Inner Mitochondrial Membrane Is Inhibited by Cyclosporin A. The Journal of Biological Chemistry. 1991;266:3376–3379. [PubMed] [Google Scholar]
- 11.Kinnally KW, Campo ML, Tedeschi H. Mitochondrial Channel Activity Studied by Patch-clamping Mitoplasts. Journal of Bioenergetics and Biomembranes. 1989;21:497–506. doi: 10.1007/BF00762521. [DOI] [PubMed] [Google Scholar]
- 12.Hurst S, Hoek J, Sheu S-S. Mitochondrial Ca and Regulation of the Permeability Transition Pore. Journal of Bioenergetics and Biomembranes. 2017;49:27–47. doi: 10.1007/s10863-016-9672-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Giorgio V, et al. Dimers of Mitochondrial ATP Synthase Form the Permeability Transition Pore. Proceedings of the National Academy of Sciences. 2013;110:5887–5892. doi: 10.1073/pnas.1217823110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Carraro Michela, Checchetto Vanessa, Szabó Ildikó, Bernardi Paolo. F‐ ATP synthase and the permeability transition pore: fewer doubts, more certainties. FEBS Letters. 2019;593(13):1542–1553. doi: 10.1002/1873-3468.13485. [DOI] [PubMed] [Google Scholar]
- 15.Bazil JN, Buzzard GT, Rundell AE. A Bioenergetic Model of the Mitochondrial Population Undergoing Permeability Transition. Journal of Theoretical Biology. 2010;265:672–690. doi: 10.1016/j.jtbi.2010.06.001. [DOI] [PubMed] [Google Scholar]
- 16.Pokhilko AV, Ataullakhanov FI, Holmuhamedov EL. Mathematical Model of Mitochondrial Ionic Homeostasis: Three Modes of Ca Transport. Journal of Theoretical Biology. 2006;243:152–169. doi: 10.1016/j.jtbi.2006.05.025. [DOI] [PubMed] [Google Scholar]
- 17.Petronilli V, Cola C, Massari S, Colonna R, Bernardi P. Physiological Effectors Modify Voltage Sensing by the Cyclosporin A-sensitive Permeability Transition Pore of Mitochondria. Journal of Biological Chemistry. 1993;268:21939–21945. [PubMed] [Google Scholar]
- 18.Bernardi P, Veronese P, Petronilli V. Modulation of the Mitochondrial Cyclosporin A-sensitive Permeability Transition Pore I. Evidence for Two Separate Me Binding Sites with Opposing Effects on the Pore Open Probability. The Journal of Biological Chemistry. 1993;268:1005–1010. [PubMed] [Google Scholar]
- 19.Giorgio V, et al. Ca Binding to F-ATP Synthase Beta Subunit Triggers the Mitochondrial Permeability Transition. EMBO reports. 2017;18:1065–1076. doi: 10.15252/embr.201643354. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Giorgio V, Guo L, Bassot C, Petronilli V, Bernardi P. Calcium and Regulation of the Mitochondrial Permeability Transition. Cell Calcium. 2018;70:56–63. doi: 10.1016/j.ceca.2017.05.004. [DOI] [PubMed] [Google Scholar]
- 21.Bertram R, GramPedersen M, Luciani DS, Sherman A. A Simplified Model for Mitochondrial ATP Production. Journal of Theoretical Biology. 2006;243:575–586. doi: 10.1016/j.jtbi.2006.07.019. [DOI] [PubMed] [Google Scholar]
- 22.Wacquier B, RomeroCampos HE, González-Vélez V, Combettes L, Dupont G. Mitochondrial Ca Dynamics in Cells and Suspensions. The FEBS Journal. 2017;284:4128–4142. doi: 10.1111/febs.14296. [DOI] [PubMed] [Google Scholar]
- 23.Smith GD, Wagner J, Keizer J. Validity of the Rapid Buffering Approximation Near a Point Source of Calcium Ions. Biophysical Journal. 1996;70:2527–2539. doi: 10.1016/S0006-3495(96)79824-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Wacquier, B., Combettes, L., Tran Van Nhieu, G. & Dupont, G. Interplay Between Intracellular Ca Oscillations and Ca -stimulated Mitochondrial Metabolism. Scientific Reports6, 10.1038/srep19316 (2016). [DOI] [PMC free article] [PubMed]
- 25.Thomas R, Kaufman M. Multistationarity, the Basis of Cell Differentiation and Memory. I. Structural Conditions of Multistationarity and Other Nontrivial Behavior. Chaos: An Interdisciplinary Journal of Nonlinear Science. 2001;11:170. doi: 10.1063/1.1350439. [DOI] [PubMed] [Google Scholar]
- 26.Ferrell JE. Self-perpetuating States in Signal Transduction: Positive Feedback, Double-negative Feedback and Bistability. Current Opinion in Cell Biology. 2002;14:140–148. doi: 10.1016/S0955-0674(02)00314-9. [DOI] [PubMed] [Google Scholar]
- 27.Broekemeier KM, Klocek CK, Pfeiffer DR. Proton Selective Substate of the Mitochondrial Permeability Transition Pore: Regulation by the Redox State of the Electron Transport Chain. Biochemistry. 1998;37:13059–13065. doi: 10.1021/bi980820c. [DOI] [PubMed] [Google Scholar]
- 28.Dargan SL, Parker I. Buffer Kinetics Shape the Spatiotemporal Patterns of IP-Evoked Ca Signals. The Journal of Phisiology. 2003;553:775–788. doi: 10.1113/jphysiol.2003.054247. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Lu X, Kwong JQ, Molkentin JD, Bers DM. Individual Cardiac Mitochondria Undergo Rare Transient Permeability Transition Pore Openings. Novelty and Significance. Circulation research. 2016;118:834–841. doi: 10.1161/CIRCRESAHA.115.308093. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Agarwal A, et al. Transient Opening of the Mitochondrial Permeability Transition Pore Induces Microdomain Calcium Transients in Astrocyte Processes. Neuron. 2017;93:587–605.e7. doi: 10.1016/j.neuron.2016.12.034. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Hüser J, Rechenmacher CE, Blatter LA. Imaging the Permeability Pore Transition in Single Mitochondria. Biophysical Journal. 1998;74:2129–2137. doi: 10.1016/S0006-3495(98)77920-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Briston, T. et al. Mitochondrial Permeability Transition Pore: Sensitivity to Opening and Mechanistic Dependence on Substrate Availability. Scientific Reports7, 10.1038/s41598-017-10673-8 (2017). [DOI] [PMC free article] [PubMed]
- 33.Oster AM, Thomas B, Terman D, Fall CP. The Low Conductance Mitochondrial Permeability Transition Pore Confers Excitability and CICR Wave Propagation in a Computational Model. Journal of Theoretical Biology. 2011;273:216–231. doi: 10.1016/j.jtbi.2010.12.023. [DOI] [PubMed] [Google Scholar]
- 34.Zoratti M, Szabò I. The Mitochondrial Permeability Transition. Biochimica et Biophysica Acta. 1995;1241:139–176. doi: 10.1016/0304-4157(95)00003-A. [DOI] [PubMed] [Google Scholar]
- 35.Antoniel M, et al. The Unique Histidine in OSCP Subunit of F-ATP Synthase Mediates Inhibition of the Permeability Transition Pore by Acidic pH. EMBO reports. 2018;19:257–268. doi: 10.15252/embr.201744705. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Azarias G, Chatton J-Y. Selective Ion Changes during Spontaneous Mitochondrial Transients in Intact Astrocytes. Plos One. 2011;6:e28505. doi: 10.1371/journal.pone.0028505. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Selivanov V, et al. A Model of mitochondrial Ca -induced Ca Release Simulating the Ca Oscillations and Spikes Generated by Mitochondria. Biophysical chemistry. 1998;72:111–121. doi: 10.1016/S0301-4622(98)00127-6. [DOI] [PubMed] [Google Scholar]
- 38.Makarov V, Khmelinskii I, Javadov S. Computational Modeling of In Vitro Swelling of Mitochondria: A Biophysical Approach. Molecules. 2018;23:783. doi: 10.3390/molecules23040783. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Chapa-Dubocq X, Makarov V, Javadov S. Simple Kinetic Model of Mitochondrial Swelling in Cardiac Cells. Journal of Cellular Physiology. 2018;233:5310–5321. doi: 10.1002/jcp.26335. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Baranov SV, Stavrovskaya IG, Brown AM, Tyryshkin AM, Kristal BS. Kinetic Model for Ca -induced Permeability Transition in Energized Liver Mitochondria Discriminates between Inhibitor Mechanisms. Journal of Biological Chemistry. 2008;283:665–676. doi: 10.1074/jbc.M703484200. [DOI] [PubMed] [Google Scholar]
- 41.Eisenhofer, S. et al. A Mathematical Model of Mitochondrial Swelling. BMC Research Notes3, 10.1186/1756-0500-3-67 (2010). [DOI] [PMC free article] [PubMed]
- 42.Mojtahedi M, et al. Cell Fate Decision as High-Dimensional Critical State Transition. Plos Biology. 2016;14:e2000640. doi: 10.1371/journal.pbio.2000640. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Olsen LF, Hauser MJB, Kummer U. Mechanism of Protection of Peroxidase Activity by Oscillatory Dynamics. European Journal of Biochemistry. 2003;270:2796–2804. doi: 10.1046/j.1432-1033.2003.03655.x. [DOI] [PubMed] [Google Scholar]
- 44.Tyson JJ, Novak B. Control of Cell Growth, Division and Death: Information Processing in Living Cells. Interface Focus. 2014;4:20130070–20130070. doi: 10.1098/rsfs.2013.0070. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Martinez-Corral R, Liu J, Süel GM, Garcia-Ojalvo J. Bistable Emergence of Oscillations in Growing Bacillus subtilis Biofilms. Proceedings of the National Academy of Sciences. 2018;115:E8333–E8340. doi: 10.1073/pnas.1805004115. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Elrod JW, et al. Cyclophilin D Controls Mitochondrial Pore-dependent Ca Exchange, Metabolic Flexibility, and Propensity for Heart Failure in Mice. Journal of Clinical Investigation. 2010;120:3680–3687. doi: 10.1172/JCI43171. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Collins TJ. Mitochondria Are Morphologically and Functionally Heterogeneous within Cells. The EMBO Journal. 2002;21:1616–1627. doi: 10.1093/emboj/21.7.1616. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Liu X, Weaver D, Shirihai O, Hajnóczky G. Mitochondrial ‘Kiss-and-run’: Interplay Between Mitochondrial Motility and Fusion-fission Dynamics. The EMBO Journal. 2009;28:3074–3089. doi: 10.1038/emboj.2009.255. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Bhosale, G. & Duchen, M. R. Investigating the Mitochondrial Permeability Transition Pore in Disease Phenotypes and Drug Screening. Current Protocols in Pharmacology e59, 10.1002/cpph.59 (2019). [DOI] [PMC free article] [PubMed]
- 50.Magnus G, Keizer J. Minimal Model of beta-cell Mitochondrial Ca Handling. The American Physiology Society. 1997;273:C717–C733. doi: 10.1152/ajpcell.1997.273.2.C717. [DOI] [PubMed] [Google Scholar]
- 51.Cortassa S, Aon M, Marbán E, Winslow RL, O’Rourke B. An Integrated Model of Cardiac Mitochondrial Energy Metabolism and Calcium Dynamics. Biophysical Journal. 2003;84:2734–2755. doi: 10.1016/S0006-3495(03)75079-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Maldonado, E. M., Taha, F., Rahman, J. & Rahman, S. Systems Biology Approaches Toward Understanding Primary Mitochondrial Diseases. Frontiers in Genetics10, 10.3389/fgene.2019.00019 (2019). [DOI] [PMC free article] [PubMed]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.