Abstract
Ferroelectric materials have technological applications in information storage and electronic devices. The ferroelectric polar phase can be controlled with external fields, chemical substitution and size-effects in bulk and ultrathin film form, providing a platform for future technologies and for exploratory research. In this work, we integrate spin-polarized density functional theory (DFT) calculations, crystal structure databases, symmetry tools, workflow software, and a custom analysis toolkit to build a library of known, previously-proposed, and newly-proposed ferroelectric materials. With our automated workflow, we screen over 67,000 candidate materials from the Materials Project database to generate a dataset of 255 ferroelectric candidates, and propose 126 new ferroelectric materials. We benchmark our results against experimental data and previous first-principles results. The data provided includes atomic structures, output files, and DFT values of band gaps, energies, and the spontaneous polarization for each ferroelectric candidate. We contribute our workflow and analysis code to the open-source python packages atomate and pymatgen so others can conduct analogous symmetry driven searches for ferroelectrics and related phenomena.
Subject terms: Electronic structure, Ferroelectrics and multiferroics
| Measurement(s) | ferroelectrics • Workflow |
| Technology Type(s) | digital curation |
Machine-accessible metadata file describing the reported data: 10.6084/m9.figshare.11702073
Background & Summary
High-throughput screening of material databases integrated with first-principles calculations has been increasingly successful in the discovery of new functional materials1–4. While many of the individual components for performing high-throughput searches exist, the infrastructure needed to connect and automate all the necessary components is still under development. The identification of ferroelectrics through symmetry arguments has been an active area of research5–16. Moreover, lists of known ferroelectrics have been previously curated17–23. However, the identification of new ferroelectrics has yet to be automated in a manner readily applicable to emerging materials databases24–30. Automated high-throughput searches for ferroelectric candidates would provide a valuable guide for in-depth computational studies and experimental efforts.
Ferroelectrics have important technological applications, such as in tunable capacitors, non-volatile random access memory devices, and electro-optical data storage. In addition, ferroelectrics are capable of displaying couplings between their electronic degrees of freedom with magnetic or lattice degrees of freedom in multiferroic materials. Ferroelectricity often arises from a structural phase transition between a high-symmetry nonpolar structural phase to a low-symmetry polar structural phase with decreasing temperature, resulting in the emergence of a spontaneous polarization31–33. In this scenario, the atomic geometry of the nonpolar structure can continuously distort such that the new polar structure has a subset of the symmetries of the original structure, satisfying the requirements of a second-order phase transition; in these cases, the polar space group must be an isotropy subgroup of the nonpolar space group, which is a stronger requirement than they only share a simple group-subgroup relation34–36.
Thus, certain ferroelectrics can be systematically screened by searching for pairs of nonpolar and polar structures related by a small symmetry-breaking distortion. In the late 1980s, Abrahams performed some of the earliest searches for ferroelectrics in crystallographic databases using symmetry criteria5,6. More recently, automated searches for new ferroelectric candidates have used symmetry arguments to identify nonpolar reference structures for existing polar materials7–9. Other studies have used a combination of group theoretic and first-principles calculations to propose ferroelectric candidates10–12. Bennett and co-workers proposed using high-throughput calculations to perform chemical substitution into structures of known classes of ferroelectrics13–15. Recent work used high-throughput phonon calculations to identify ferroelectrics through polar soft phonon modes of nonpolar phases16.
Previous studies have focused on a limited number of compounds or families of compounds using a relatively narrow set of symmetry conditions. Current curated lists of ferroelectrics only include known ferroelectrics that have been experimentally verified. With shrinking computing costs, high-throughput material searches using first-principles methods provide an efficient strategy to discover and catalog materials. Ferroelectric databases and systematic screening of properties such as band gaps, polarizations, volume expansion, critical temperatures, and coupling to magnetic and/or topological degrees of freedom may lead to new functional materials and potentially new physical phenomena.
In this work, we integrate density functional theory (DFT), crystal structure databases, symmetry tools, workflow software, and a custom analysis toolkit to build a workflow capable of generating libraries of known, previously-proposed and newly-proposed ferroelectrics. This workflow is general and can be used with any crystal structure dataset. We present the results from performing this workflow on the Materials Project database of inorganic crystal structures24. We screen over 67,000 material structures using symmetry relations between nonpolar and polar structure pairs and calculating the polarization from first-principles calculations. We identify 255 ferroelectric candidates, 200 being classified as high-quality candidates by a stringent verification process. Within these high-quality candidates, 74 are known or previously proposed, and 126 are new ferroelectrics. With the workflow developed here, we construct the first automatically-curated first-principles dataset of diverse, multi-class known and new ferroelectrics calculated with a standardized method that permits straightforward comparison. This dataset can be used to develop new tools and criteria for studying ferroelectricity across diverse materials systems. In addition our code for conducting this search has been contributed to the open-source python packages atomate and pymatgen so others can conduct searches of their own and build directly on this work37,38.
Our automated workflow has three stages: symmetry analysis, first-principles calculations, and post-processing. Accordingly, the rest of the work is organized as follows: the description of the workflow, based in the concept of ferroelectric nonpolar-polar symmetry pair, is described in the Methods section. Technical aspects of our workflow and database are included in the section Data Records. Finally, we validate our workflow method against experimental databases of ferroelectrics and verify our workflow is comparable to previous first-principles results in the section Technical Validation.
Methods
Identifying ferroelectricity from first principles
Ferroelectrics are characterized by a polarization versus electric-field hysteresis loop. Experimentally, the spontaneous polarization can be determined as half of the change in polarization at zero external field31. The spontaneous polarization is not a direct observable; one measures the change in spontaneous polarization between two stable configurations of a material39.
In three dimensions, the only space groups compatible with a polarization, meaning they leave a vector invariant under its symmetry operations, are those with polar point groups. Out of the 32 crystallographic point groups, 10 are polar; these polar point groups can keep points along specific lines (point groups 2, 3, 4, 6, mm2, 4mm, 3m, 6mm), planes (point group m), or all points in three-dimensional space (point group 1) invariant40,41. All other point groups are nonpolar. We define polar structures as crystal structures with a polar space group, which is composed of a polar point group plus translations, likewise for nonpolar structures.
Following the modern theory of polarization39,42–47, the polarization, P, of a crystal is defined as,
| 1 |
where e is the charge of the electron, is an integer, Ri is a primitive lattice vector, and Ω is the unit cell volume (bold letters denote vectors). P0 includes electronic and ionic contributions. The second term on the right hand side of Eq. 1 is the quantum of polarization, , a consequence of translation symmetry. In the general case, P0 is defined up to any integer multiple of ; for nonmagnetic crystals containing elements from even columns of the Periodic Table, P0 is defined up to even integer multiples. Since we are screening many systems here, we use the more general definition in this work.
Only differences of the computed polarization on the “same branch” are physically meaningful, where different branches are related by integer multiples of the quantum of polarization. Equivalently, the evolution of the polarization along an adiabatic path between two states must be smooth. Nonpolar space groups can only host formal polarizations that are zero or one-half modulo the polarization quantum. We use a nonpolar reference structure to calculate the change in polarization due to a polar distortion. In general, paths between two opposite polar configurations are sufficient to compute the change in polarization; however, we choose to use a nonpolar reference structure in this work as is standard for calculating the polarization from first principles.
To recover a smooth polarization path, we ensure the nonpolar structure must be continuously deformable into the polar structure along a path that preserves the symmetry of the polar structure and for which the system remains insulating. We then perform calculations of multiple structures along the distortion path to compute the spontaneous polarization, which can be compared to experiment. Using this approach, the spontaneous polarization can be directly predicted using first-principles methods with good accuracy48.
Hence, for the purposes of this work, we only consider ferroelectrics for which a high-symmetry nonpolar reference structure can be readily identified in the database for a lower-symmetry polar structure that can support a polarization42. We automate a search for compounds supporting two such phases and then compute the polarization difference along the structural path connecting the two structures.
If a polar ferroelectric structure corresponds to a metastable state, and is higher in energy than a nearby non-polar ground state by a small amount, the system can be considered an antiferroelectric49,50. Antiferroelectrics exhibit double hysteresis loops in polarization versus electric-field measurements; the field-induced first-order phase transition originates with an energy barrier between the nonpolar ground state and the polar metastable phase. In an antiferroelectric, the nonpolar ground state phase is related by a nonpolar distortion to a distinct nonpolar reference structure; the ground state structure is generally characterized as “anti-polar” to distinguish it from the nonpolar reference structure. Symmetry conditions for antiferroelectrics are described in ref. 51. For completeness, we note that to identify antiferroelectrics using the workflow presented here, in addition to finding a reference nonpolar phase, the polar metastable ferroelectric phase and an antipolar ground state, the material would need to display a small energy difference between the polar and antipolar structures on the order of 1–10 meV52.
Workflow overview
We first describe the general workflow diagram comprising symmetry analysis, first-principles calculations, and post-processing. As shown in Fig. 1, the complete workflow involves the passing of data between many separate calculations. In developing our workflow, we automate the following tasks:
Identifying candidate materials possessing nonpolar-polar structure pairs related by a continuous distortion (an isotropy subgroup symmetry relation).
Performing spin-polarized DFT calculations of changes in total energy, band gap, and polarization for multiple structures along the nonpolar-polar distortion.
Post-processing calculation data to compute the spontaneous polarization of the polar ferroelectric phase.
Validating the calculation quality for each ferroelectric candidate.
Creating an interface for viewing the results for all candidates (see the section Graphical Interface).
Fig. 1.

Diagram of the automated ferroelectric search workflow developed here. Databases are shown as purple cylinders. Processes are shown as rectangles: blue designates processes used to identify and perform first-principles calculations, green designates post-processing and verification, and orange designates the web-interface. Arrow directions indicate the flow of information. For example, the Workflow Database provides information to the Computing Resources about which calculations to compute and the Workflow Database is updated as calculations complete or as errors occur on the Computing Resources.
We start by choosing a crystal structure database on which to perform the search (see Structure Selection Symmetry Analysis). We emphasize that any crystallographic database (e.g. any of the databases described in24–30) can be used to perform our workflow, as long as the atomic coordinates and lattice parameters of the structures are provided.
Within the chosen database, we perform a symmetry analysis to find candidate materials possessing nonpolar-polar structure pairs related by a continuous symmetry deformation. Any such pairs found to satisfy the symmetry deformation criteria are stored in the Distortion Database as being deformable by symmetry. This criteria includes the following conditions: (1) The polar structure belongs to a space group that is a subgroup of the space group of the nonpolar structure; and (2) There exists a transformation matrix between the high-symmetry setting of the nonpolar structure to the low-symmetry setting of the polar structure. The latter imposes that the distortion of the lattice parameters and atomic coordinates between the nonpolar and polar structures is continuous, meaning the polar structure belongs to an isotropy subgroup of the nonpolar structure.
We then carry out DFT calculations on the candidate pairs to extract the changes in the band gaps, total energies, and polarization along the nonpolar-polar distortion (see Computational Methods). These results are stored in a Workflow Database and then accessed by our Computing Resources to perform the calculations. Next, the information stored in the Distortion, Workflow, and Calculation Databases is used together to post-process quantities such as the computed spontaneous polarization and to validate ferroelectric candidates using experimental and previous first-principles results (see Post-processing and Spontaneous Polarization Values and Verification of Computational Methodology). The information needed to assess the quality and properties of the candidates is then added to the Candidate Database where it can be accessed by our web Interface for viewing the candidate materials in aggregate (see Graphical Interface). Finally, candidates are screened to ensure the polarization and energy profile across the nonpolar-polar distortion are smooth and continuous, i.e. all calculations ended correctly and provide reliable results.
In the sections below, we describe in detail the methods used for creating an automatically curated dataset of ferroelectrics from the Materials Project database24. The Materials Project database is largely based on structures from the Inorganic Crystal Structure Database (ICSD)27,28 and includes hypothetical structures created through stoichiometric substitution. We use the Materials Project database to test our workflow. Our results for the Materials Project are not intended as the most general curated list of ferroelectrics; however, as the first automatically obtained list of ferroelectrics, they uncover new candidates and provide a blueprint for further studies. More elaborately curated lists may be constructed by applying our workflow to additional databases in future studies. The results from applying our workflow are described below and summarized in Table 1. We note that our workflow is modular and open-source, so it can be readily adapted and applied by others to expand the search for ferroelectrics and related materials such as antiferroelectrics and multiferroics.
Table 1.
Results obtained by applying our workflow to the Materials Project database.
| Symmetry | Structures† | ∼67,000 |
| Polar structures† | ∼15,000 | |
| Distinct polar formula† | ∼10,000 | |
| Nonpolar-polar structure pairs | ∼17,000 | |
| Structure pairs with distinct chemical formulae | ∼1,600 | |
| Pairs with continuous transformation | 413 | |
| DFT | Pairs with metallic endpoints | 80 |
| Pairs with metallic interpolations | 59 | |
| Pairs with calculation errors | 19 | |
| Pairs that completed successfully | 255 | |
| Valid | High-quality ferroelectric candidates | 200 |
| Known ferroelectrics in high-quality candidates | 74 | |
| New ferroelectrics in high-quality candidates | 126 |
The symbol † indicates “in Materials Project database at time of search”. Boxes relate numbers by symmetry conditions (Symmetry), first-principles calculations (DFT), and validation processes (Valid.). “Nonpolar-polar structure pairs” satisfy simple group-subgroup relations while “pairs with continuous transformation” satisfy group-isotropy subgroup relations.
Structure selection
As motivated earlier, the input to our workflow is a collection of candidate materials possessing nonpolar-polar structure pairs. There are several methods that can be used to create candidate nonpolar-polar structure pairs. For example, one can apply a polar distortion to an existing nonpolar structure or create a hypothetical nonpolar reference structure for an existing polar structure. In this work, to classify a material as a ferroelectric candidate, we require both nonpolar and polar structures to be present in the database. As shown below, even this direct approach provides new candidate materials, previously overlooked as ferroelectrics. Future studies may choose to relax this requirement to identify a greater number of promising materials.
To search for compatible nonpolar-polar structure pairs in the Materials Project dataset, we first select compounds possessing nonpolar and polar structures with space groups which are related by a group-subgroup relation. Note that in principle the same compound may display more than one ferroelectric structural transition, and therefore have more than one nonpolar-polar symmetry pair. For each of these pairs, we require that the number of sites in the nonpolar structure is less than or equal to the number of sites in the polar structure. We perform this initial query using pymatgen, spglib, and the Materials Project API37,53–55. We provide the number of nonpolar-polar structures pairs resulting from this query in the top box of Table 1.
At the time of this search, the Materials Project database had approximately 67,000 structures, approximately 15,000 of which are polar. We find approximately 17,000 nonpolar-polar structure pairs related via group-subgroup space group relations. This number is large, in part, because the same polar structure may be paired with multiple possible nonpolar reference structures, and vice versa. This number is also large because the requirement that the polar structure is in a subgroup of the nonpolar space group is a much weaker requirement than the polar structure belongs to an isotropy subgroup of the nonpolar structure–which we check later in the workflow. These roughly 17,000 pairs contain approximately 1,600 of the approximately 10,000 distinct polar compositions in the Materials Project database. The remaining polar compositions in the Materials Project do not have symmetry compatible nonpolar structures within the same composition present in the database. We note that it is possible to propose hypothetical nonpolar reference structures for polar candidates using group theoretic methods or by relaxing the symmetry tolerance between nonpolar-polar distortions7–9,16; this is left for future work.
Naming conventions
We adopt the pymatgen alphabetical_formula method for the Composition class (with spaces and 1 s removed) to output consistent formulas for our candidates. We note that this method orders elements in such a way that does not match conventions in the literature. For example, we use O3 PbTi where the standard in the literature is PbTiO3. Compositions printed by pymatgen also differ from those used in mineralogy, such as for boracite, lawsonite and many other minerals in our dataset. In our datafiles, we also provide formula name output using the pymatgen reduced_formula method for the Composition class, which sorts elements by electronegativity.
Symmetry analysis
The automated nature of our ferroelectric search relies on strict symmetry criteria. As described in the Structure Selection section, we pre-screen our candidate nonpolar-polar structure pairs using the symmetry tools in pymatgen and spglib to ensure that these pairs satisfy preliminary group-subgroup relationships. We then use the Structure Relations symmetry tool provided by the Bilbao Crystallographic Server (BCS)56–58 to impose the symmetry criteria described in the Workflow Overview, namely, to obtain a transformation matrix connecting the lattice parameters and atomic coordinates of the structure pair59,60. The BCS has a freely available web interface for accessing a wide variety of symmetry tools. We create python scripts to automate interaction with and scrape returned data from the BCS to perform our symmetry checks using the python package mechanize61. The Structure Relations tool checks the following:
1.1 The group-subgroup index relations are compatible. The index of a group-subgroup relation indicates the number of ferroelectric domains (distinct polar variants) that arise from the symmetry breaking of the high-symmetry structure.
1.2 There exists a path of maximal subgroups between the high-symmetry structure and low-symmetry structure.
1.3 The Wyckoff position splitting of the high-symmetry structure is compatible with the Wyckoff positions of the low-symmetry structure.
1.4 The lattice of the high-symmetry structure in the low-symmetry setting must be within a defined tolerance of the lattice of the low-symmetry structure (see Symmetry Precision section).
1.5 Each atom in the high-symmetry structure in the low-symmetry setting can be paired to an atom in the low-symmetry structure such that atom pairs are separated by a distance no greater than a given tolerance (see Symmetry Precision section).
Structure Relations takes Crystallographic Information Files (CIFs) of high-symmetry and low-symmetry structures and tolerance threshholds as arguments. We use a lattice tolerance of 3 Å and 10° for lattice parameters and angles, respectively. These tolerances are generous for materials with average sized unit cells (i.e.with lattice parameters less than 20 Å) and permit a wide variety of distortions. For the present work, high-quality candidates are reported for a maximum pairing distance of 1.5 Å. As shown in Table 1, out of the 17,000 structure pairs that we test with Structure Relations, 413 are found to be deformable by symmetry with a maximum distortion less than or equal to 1.5 Å.
Symmetry precision
Symmetry precision is a tolerance factor used to assess whether an atom is equivalent to another after a symmetry operation up to a maximum distance. A symmetry precision between 10−1 and 10−5 Å is typically used. In the Materials Project database, a symmetry tolerance of 10−1 Å is used for the reported space group stored in the database. We use the same tolerance to generate CIFs sent to the BCS Structure Relations.
We evaluated how varying the symmetry tolerance changes the resolved space group for all the structures in the Materials Project. We were able to determine this efficiently by using a binary search on a log10 scale for a maximum and minimum symmetry tolerance of 10−1 Å and 10−5 Å, respectively. Out of the 67,000 structures we checked, 50,000 (75%) structures were resolved into one distinct space group for the entire symmetry precision range. For additional discussion about the sensitivity of symmetry precision on resulting space groups in the search for ferroelectrics, see refs. 16,62.
DFT calculation details
In our workflow, we perform spin-polarized DFT calculations using the Vienna Ab initio Software Package (VASP) version 5.3.563–65. We use the generalized gradient approximation (GGA) functional of Perdew, Burke, and Ernzerhof (PBE)66. Our calculations use PAW pseudopotentials and an energy cutoff of 520 eV for the plane-wave basis67,68; this is 1.3 times the highest cutoff recommended for the pseudopotentials used69. Structures are initialized with ferromagnetic ordering in all cases in this work. Since the default is for parallel alignment of the spins, we expect the workflow to be reliable for nonmagnetic or ferromagnetic materials. Materials with more complicated magnetic ground states, such as antiferromagnets, would require consideration of different antiferromagnetic orderings. Therefore, some common multiferroics possessing antiferromagnetic or near antiferromagnetic ordering may not be identified by this workflow. Extensions to include antiferromagnetic spin arrangements are relegated to future work. These settings correspond to default values used to create the Materials Project database and therefore allow a direct comparison of our results with the Materials Project database.
We use the Berry phase approach from refs. 39,43,44,70,71, as implemented in VASP to calculate the electronic part of the macroscopic spontaneous polarization. We calculate the ionic part of the polarization using the point charge and position for each atom in the unit cell, see the calc_ionic function in pymatgen.analysis.ferroelectricity.polarization for details.
We use the default parameters for VASP inputs as defined in pymatgen (and used by Materials Project) and atomate69,72,73. For details on these parameters, see the documentation for pymatgen.io.vasp.sets.MPStaticSet. We use a Hubbard U correction to correct the DFT-PBE description of d states of select oxides and fluorides following the approach in ref. 74. To see the guidelines for which compounds we apply a U, see refs. 24,69,72,73. We use a reciprocal k-point density of 50 k-points per (1/Å)3 for structural relaxations and 100 k-points per (1/Å)3 for static and polarization calculations. We use total energy convergence criteria of 5 × 10−5 eV per atom for the electronic self-consistent loop and 5 × 10−4 eV/Å per atom for the ionic relaxation loop for structural optimizations. These convergence parameters were tested against higher-accuracy convergence parameters on a set of 182 chemically diverse compounds in ref. 73, yielding total energies within 15 meV/atom and lattice volumes within 7.5% of the higher-accuracy calculations for nearly 96% of the compounds.
We note that while the local density approximation (LDA) is commonly used to describe certain ferroelectric oxides, and therefore to compute their polarizations, use of a generalized gradient approximation (GGA), such as the PBE functional, tends to be standard for wider classes of materials nowadays. PBE is also the default functional used by the Materials Project for structural relaxations and calculating material properties. Thus, we use PBE for this effort. Our results are in line with the typical overestimation of PBE for the lattice parameters, and therefore, we expect a similar overestimation of the polarization. In addition, while DFT-PBE tends to underestimate electronic band gaps, the latter plays a minimal role in the determination of standard ferroelectric materials, and as shown below, will only limit the computation of the spontaneous polarization for a small number of them.
Scientific workflow packages
We construct the scientific workflows to perform the structural relaxations and spin-polarized DFT calculations of energy, band gap, and polarization using the FireWorks and atomate python packages38,75. FireWorks is built for managing computational scientific workflows. atomate is built for constructing workflows for multiple computational material science codes, such as VASP. atomate uses FireWorks classes to develop modules for performing common DFT calculations with VASP, such as structural relaxations and self-consistent calculations of total energy. atomate also provides a framework for building custom modules, which we use to construct our structural interpolations and polarization calculations modules.
DFT workflow
We use the DFT workflow, shown in Fig. 2, to compute the physical properties needed to identify ferroelectric candidates. We perform spin-polarized calculations and for systems with spin-polarized ground states, consider only ferromagnetic ordering. We execute the DFT workflow shown in Fig. 2 for the 413 pairs with continuous nonpolar-polar transformations, with maximum distortions that do not exceed 1.5 Å.
Fig. 2.
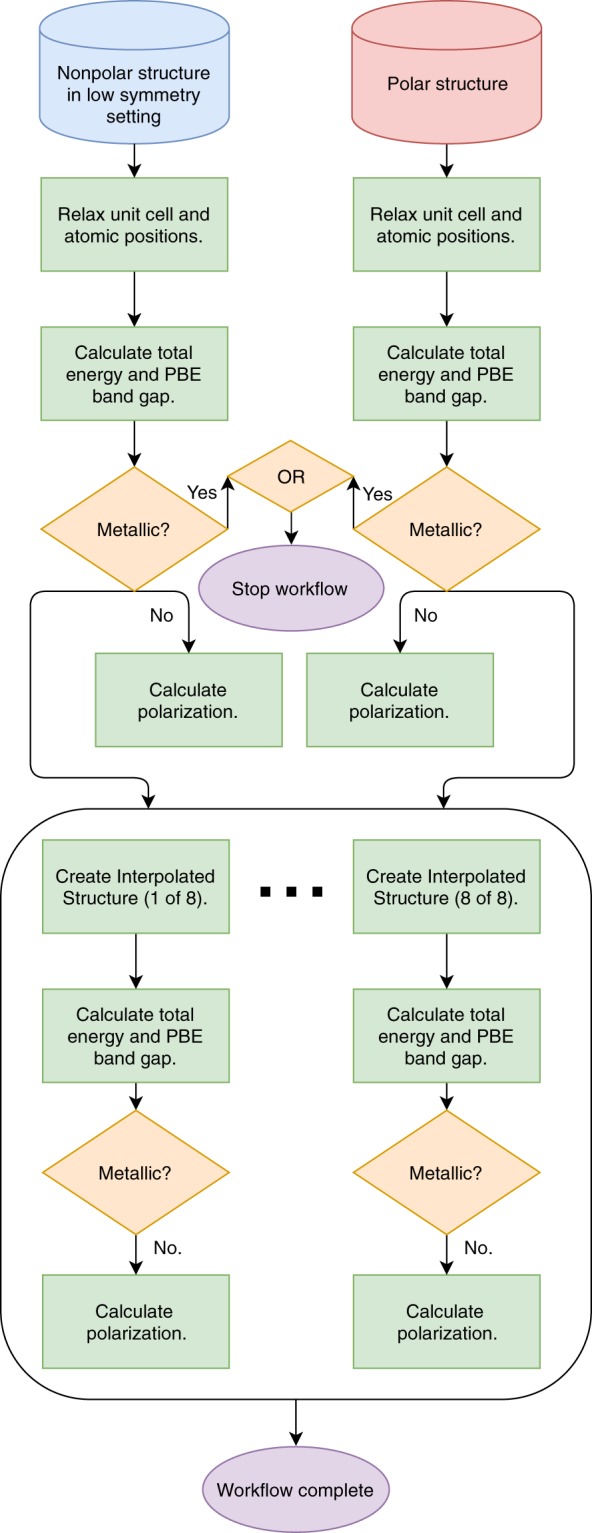
Diagram of DFT workflow written with atomate and Fire Works. Blue and red boxes denote initial nonpolar and polar structures, respectively, green boxes denote DFT calculations, orange rhombuses denote decision steps, and purple ellipses denote exit steps. Black arrows represent passing of data between different software codes. The metallic check for the interpolated structures leads to a similar condition as earlier, where if any of the interpolations are metallic the workflow stops (not illustrated for clarity in figure).
For each structure pair, we begin with the nonpolar structure in the low-symmetry setting (obtained from BCS Structure Relations in the Symmetry Analysis step) and the polar structure. We use the nonpolar structure transformed into the low-symmetry setting so we can perform structure interpolations and polarization calculations across similar lattices. We perform relaxations of the unit cell and atomic positions of both of these structures twice, using a level of convergence similar to what Materials Project uses for its database entries. As mentioned, all calculations are spin-polarized and use PBE, with a Hubbard U correction for systems with non-d0 open-shell cations; our workflow assumes ferromagnetic ordering for all systems. Extensions of our workflows to consider antiferromagnetic and other orderings will be the subject of future work. We then fix the relaxed nonpolar and polar structures, and perform a self-consistent DFT calculation to compute the total energy and band gap. If either the nonpolar structure or polar structure is found to be metallic at the DFT-PBE level in our spin-polarized calculations initialized with ferromagnetic orderings and a standard U–here we define metallic as having a DFT-PBE band gap of less than 10 meV–we stop the workflow for that structure pair.
If the polar and nonpolar structures are both insulating, we compute the polarization along the distortion path. As shown in Table 1, 80 of the 413 structure pairs were computed to have metallic endpoints in our spin-polarized calculations: 30 were found to have a metallic nonpolar structure but insulating polar structure, 2 were found to have a metallic polar structure but insulating nonpolar structure, and 24 were found to have both metallic polar and nonpolar structures. 24 additional structures have at least a metallic nonpolar structure, but these workflows were halted before the polar structures had their band gaps computed.
We compute the DFT total energy, band gap, and polarization of eight evenly-distributed linearly-interpolated structure, or interpolations, of the nonpolar to polar structures. We found eight interpolations to be sufficient for reconstructing a smooth polarization trend for at least 75% of our candidates. Similiar to the previous step where a metallic calculation causes the workflow to stop, metallic interpolations similarly halt the workflow since we would be unable to calculate the polarization of that structure. 59 candidates were found to have metallic interpolations. The DFT workflow is labeled as complete when all polarization calculations along the path have completed. As shown in Table 1, 255 structure pairs successfully completed the workflow, and satisfy our requirements of a ferroelectric phase transition.
Post-processing spontaneous polarization values
As discussed earlier, only polar space groups are compatible with a polarization vector that is not integer or half integer multiples of the polarization quantum46. If a reference nonpolar structure that is continuously deformable into the polar structure can be identified, we can then calculate the polarization of several interpolated structures between the reference nonpolar and the target ferroelectric polar structure. The nonpolar structure is used as a means to calculate the spontaneous polarization; however, we note in general it is not necessary for the nonpolar structure to be experimentally observable for the polar material to be ferroelectric.
We start by calculating the formal polarization of the nonpolar structure, which is either zero or a half quantum of polarization (modulo the quantum of polarization) along the three lattice directions. Then we perform the same calculation for the first interpolated structure along the distortion, and then the next, until we arrive at the final polar structure. For a sufficient number of interpolations between the nonpolar and polar structures, we can trace out smooth, continuous polarization “paths” along the distortion; there will be infinitely many paths due to the periodicity of the polarization lattice. Subtracting the polarization values at the nonpolar and the polar endpoints of the same path or “branch” will give us the spontaneous polarization vector of the polar ferroelectric phase.
We perform the following steps to recover the same branch “proper” polarization, which is independent of choice of branch. The first step, which is crucial, is to readjust the polarization for each structure along the distortion to be in the polar polarization lattice. To do this, we modify the polarization of the intermediate structures by the ratio of the quantum of polarizations of the two lattices (the lattice parameters divided by the volume multiplied by the electron charge), i.e.,
| 2 |
where and are the lattice parameters and volume of the structure along the distortion, and are the lattice parameters and volume of the polar structure, and i is a lattice direction , or . If we do not perform this adjustment, we are calculating what is called the “improper polarization” which will depend on the choice of branch and is therefore unphysical76. See Fig. 3 for an example of the differences between proper and improper polarization for BaTiO3 (here we use conventional notation for the name).
Fig. 3.
Examples of improper (left) and proper (right) polarization curves for BaTiO3 along the direction versus distortion from the nonpolar to polar structure, showing the importance of calculating the proper polarization. Due to the change in lattice parameters and volume across the distortion, the quantum of polarization defined for each structure along the direction is different. Using these different quanta causes the improper spontaneous polarization predicted by different branches to differ, as can be seen in the polarization values given in the right of the image. In contrast for the proper polarization (right), we re-scale the polarization of each intermediate structure to be in the polar structure’s polarization lattice and use the quantum of polarization as defined by the polar structure. This results in predictions that are branch independent, which is what we use to assess candidates. Note that while, in this specific case, the calculated polarization values for all interpolations were on the same branch, this need not generally be the case.
After adjusting our initial polarizations, we then construct a periodic lattice with lengths and angles corresponding to the quantum of polarization along each polar lattice direction; this corresponds to the second term of Eq. (1). For the polarization lattice, the lengths of the lattice vectors are the cell lattice vectors divided by the volume of the unit cell and multiplied by conversion factors for electron charge and length scale.
Our algorithm for adjusting the polarizations to be on the same branch is depicted in Fig. 4. First, we take the nonpolar polarization (adjusted to be in the polar polarization lattice), and choose the “image” (or periodic value) of the polarization value in the nonpolar polarization lattice that is closest to the Cartesian origin (0, 0, 0). The value of the nonpolar polarization along , , and can either be zero or a half-quantum. Then, we find the image of the first interpolation polarization value (again adjusted to be in the polar polarization lattice) that is closest to the Cartesian coordinates of the adjusted nonpolar polarization value. We continue this process until we get to the polarization of the polar structure.
Fig. 4.
A visual demonstration of the same branch polarization algorithm demonstrated in one-dimension (rather than three-dimensions) using BaTiO3. The values for the polarization for each interpolation are those circled in red. In the first panel, we adjust the nonpolar polarization to be on the branch closest to zero. In the second panel, we move the first interpolated polarization to be on the branch closest to the adjusted nonpolar polarization. In the third panel, we adjust the second interpolated polarization to be on the branch closest to the first interpolation polarization. If the algorithm finishes successfully, all the adjusted polarizations will be on the same branch.
This algorithm will find the polarization path with the smallest difference between polarizations of subsequent interpolations. An issue is that this algorithm can incorrectly find the same branch polarization in cases where the change in polarization between interpolations is larger than the quantum of polarization between branches. One example of this type of failure is the polarization resolved for CrO3 with search ID 187, see Fig. 5 (the search ID being a simplified unique identifier, defined for the purposes of our work, for pairs of structures used in our workflow search, see Online-only Table 3). In this example, the algorithm chooses a discontinuous path that has a smaller spontaneous polarization of 78.2 μC/cm2 in red. However, the correct path uses the last three interpolations in the branch shown with a dashed red line and gives a polarization of 122.9 μC/cm2. To correctly reconstruct this polarization with our existing algorithm, more structures would be needed to better interpolate between the nonpolar and polar structures. Alternatively, the curvature of the spline connecting nonpolar and polar structures could be used to identify points on the same branch; we leave this refinement for future work.
Fig. 5.
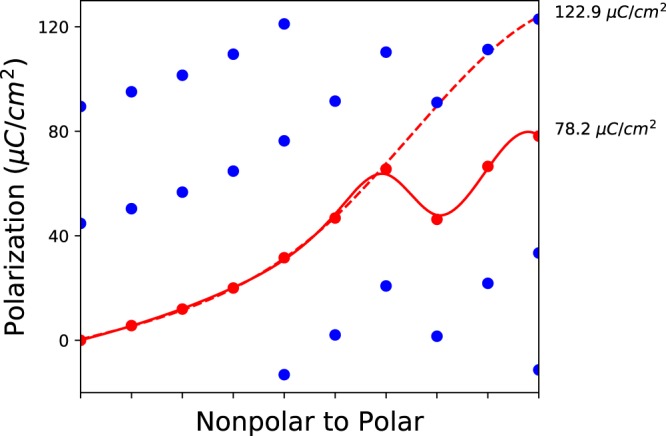
The polarization reconstruction for CrO3 with search ID 187. The polarization along the b lattice parameter is incorrectly reconstructed because the different polarization branches are closer than the change in polarization between structure interpolations.
Online-only Table 3.
Search ID, alphabetical formula, Materials Project ID and Workflow IDs for high quality candidates.
| Search ID | Alphabetical Formula as formatted in Materials Project database | Polar MP ID | Nonpolar MP ID | Workflow ID |
|---|---|---|---|---|
| 1 | Ag10Br3Te4 | mp-568386 | mp-568392 | wfid_1562345081.92745142 |
| 2 | Ag2BiO3 | mp-561113 | mp-558712 | wfid_1562345066.59186560 |
| 3 | Ag2BiO3 | mp-23558 | mp-558712 | wfid_1562345080.63153360 |
| 4 | Ag2O4W | mp-637188 | mp-504466 | wfid_1562345080.72611869 |
| 5 | Ag2S | mp-560025 | mp-556225 | wfid_1562345112.11438196 |
| 6 | Ag2S | mp-560025 | mp-36216 | wfid_1562345112.31901092 |
| 7 | Ag2S | mp-560025 | mp-32791 | wfid_1562345112.28048731 |
| 8 | Ag2S | mp-38511 | mp-32791 | wfid_1562345109.86187522 |
| 9 | Ag2S | mp-32669 | mp-36216 | wfid_1562345080.93250415 |
| 10 | Ag2S | mp-32669 | mp-32791 | wfid_1562345081.72797057 |
| 11 | Ag3IS | mp-675879 | mp-676561 | wfid_1562345089.24703674 |
| 12 | Ag3IS | mp-675879 | mp-558189 | wfid_1562345097.63538177 |
| 13 | Ag3IS | mp-22995 | mp-676561 | wfid_1562345085.94165367 |
| 14 | Ag3IS | mp-22995 | mp-558189 | wfid_1562345089.76230197 |
| 15 | AgAl11O17 | mp-849760 | mp-766293 | wfid_1562345083.68955336 |
| 16 | AgAlO3 | mvc-3476 | mvc-15935 | wfid_1562345112.91840254 |
| 17 | AgC2O2 | mp-600237 | mp-654937 | wfid_1562345064.01802743 |
| 18 | Al2BaO4 | mp-4202 | mp-619456 | wfid_1562345097.07894293 |
| 19 | Al2BaO4 | mp-4202 | mp-3828 | wfid_1562345097.68976538 |
| 20 | Al2CaH4O10Si2 | mp-24603 | mp-733653 | wfid_1562345079.80563577 |
| 21 | Al3F19Pb5 | mp-541732 | mp-557911 | wfid_1562345086.15212454 |
| 22 | Al4La | mp-571423 | mp-21109 | wfid_1562345105.73961799 |
| 23 | AlBiO3 | mp-551918 | mp-23080 | wfid_1562345104.79543572 |
| 24 | AlBiO3 | mvc-3494 | mvc-13972 | wfid_1562345095.70366936 |
| 25 | AlCH2NaO5 | mp-699136 | mp-644506 | wfid_1562345113.04187974 |
| 26 | AlCl4Hg2Sb | mp-570828 | mp-568001 | wfid_1562345074.60128275 |
| 27 | AlCoO3 | mvc-3774 | mvc-13532 | wfid_1562345095.84764302 |
| 28 | AlCrO3 | mvc-3775 | mvc-13996 | wfid_1562345097.53150367 |
| 29 | AlCuO3 | mvc-3501 | mvc-15945 | wfid_1562345104.05261108 |
| 30 | AlF7MgNa2 | mp-19931 | mp-6319 | wfid_1562345084.84452891 |
| 31 | AlH3O3 | mp-625318 | mp-625316 | wfid_1562345113.85119430 |
| 32 | AlH3O3 | mp-626435 | mp-626414 | wfid_1562199295.69225680 |
| 33 | AlH3O3 | mp-626587 | mp-626605 | wfid_1562345066.90756711 |
| 34 | AlMnO3 | mvc-3777 | mvc-15992 | wfid_1562345104.31488404 |
| 35 | AlMo4S8 | mp-554868 | mp-3861 | wfid_1562345097.39878133 |
| 36 | AlMo4S8 | mvc-16083 | mp-3861 | wfid_1562345099.89947666 |
| 37 | AlMoO3 | mvc-3779 | mvc-14006 | wfid_1562345104.48448591 |
| 38 | AlN | mp-661 | mp-13178 | wfid_1562345088.40370432 |
| 39 | AlNiO3 | mvc-3776 | mvc-14043 | wfid_1562345104.16630482 |
| 40 | AlO3Ti | mvc-3466 | mvc-13964 | wfid_1562345113.24875150 |
| 41 | As2NiTm2 | mp-568266 | mp-11581 | wfid_1562345088.19078870 |
| 42 | AsNi | mp-590 | mp-2346 | wfid_1562345096.13686232 |
| 43 | AuCl4K | mp-27181 | mp-568986 | wfid_1562345066.70855532 |
| 44 | AuTe2 | mp-571547 | mp-567525 | wfid_1562345104.42703805 |
| 45 | B13C2Li | mp-638070 | mp-655591 | wfid_1562345084.34740380 |
| 46 | B2K3Nb3O12 | mp-557711 | mp-15248 | wfid_1562345108.76820757 |
| 47 | B2O6Zn3 | mp-559949 | mp-542833 | wfid_1562345069.20163833 |
| 48 | B3CaH5O8 | mp-560899 | mp-705495 | wfid_1562345061.85187620 |
| 49 | B7BrMn3O13 | mp-579836 | mp-567153 | wfid_1562345110.99651178 |
| 50 | B7ClCr3O13 | mp-579770 | mp-566691 | wfid_1562345108.33484522 |
| 51 | B7ClMg3O13 | mp-23087 | mp-23617 | wfid_1562345107.17640773 |
| 52 | B7IMn3O13 | mp-31917 | mp-565322 | wfid_1562345099.25830051 |
| 53 | BC2N | mp-629458 | mp-1008523 | wfid_1562345103.49034383 |
| 54 | BCoLi2O4 | mp-761299 | mp-771049 | wfid_1562345117.22594957 |
| 55 | Ba2Co4Nd2O11 | mp-561781 | mp-24879 | wfid_1562345070.07733415 |
| 56 | Ba2CrO4 | mp-566511 | mp-19703 | wfid_1562345076.48947736 |
| 57 | Ba2F7Y | mp-768350 | mp-777744 | wfid_1562345060.94342955 |
| 58 | Ba3C5Ce2F2O15 | mp-667381 | mp-581090 | wfid_1562199296.78790598 |
| 59 | BaC2CaO6 | mp-644852 | mp-6568 | wfid_1562199296.60378780 |
| 60 | BaCO3 | mp-762225 | mp-34195 | wfid_1562199296.73456920 |
| 61 | BaCl5La | mp-770427 | mp-770125 | wfid_1562345112.71860945 |
| 62 | BaEuFe2O5 | mp-639347 | mp-656144 | wfid_1562345085.29703104 |
| 63 | BaFe2S4 | mp-675078 | mp-27660 | wfid_1562345085.09598476 |
| 64 | BaFe2S4 | mp-675078 | mp-676036 | wfid_1562345085.23366390 |
| 65 | BaMnO3 | mp-19267 | mp-19156 | wfid_1562345090.52467225 |
| 66 | BaNiO3 | mp-19241 | mp-19138 | wfid_1562345089.13746210 |
| 67 | BaO3Ti | mp-995191 | mp-19990 | wfid_1562345103.16533381 |
| 68 | BaO3Ti | mp-5777 | mp-2998 | wfid_1562345097.33024928 |
| 69 | BaO3Ti | mp-12992 | mp-2998 | wfid_1562345085.34572722 |
| 70 | BaO3Ti | mp-5986 | mp-2998 | wfid_1562345085.18772603 |
| 71 | BaO3Ti | mp-5020 | mp-2998 | wfid_1562345096.05165490 |
| 72 | BaO5Ti2 | mp-555966 | mp-3943 | wfid_1562345063.80485743 |
| 73 | BaS3V | mp-3451 | mp-4227 | wfid_1562345096.68042421 |
| 74 | BaSe3V | mp-676597 | mp-27363 | wfid_1562345111.62539924 |
| 75 | BeF4H8N2 | mp-24614 | mp-604245 | wfid_1562345113.37855627 |
| 76 | BeF4H8N2 | mp-24614 | mp-720982 | wfid_1562345114.26291952 |
| 77 | Bi2MoO6 | mp-25708 | mp-567075 | wfid_1562345072.07030301 |
| 78 | Bi2MoO6 | mp-25708 | mp-567326 | wfid_1562345072.66801127 |
| 79 | Bi2Nb2O9Pb | mp-583454 | mp-23101 | wfid_1562345096.76465275 |
| 80 | Bi2O9SrTa2 | mp-23089 | mp-554675 | wfid_1562345092.91429073 |
| 81 | Bi2O9SrTa2 | mp-559951 | mp-554675 | wfid_1562345093.12462394 |
| 82 | Bi4O12Ti3 | mp-723064 | mp-23335 | wfid_1562345067.21007940 |
| 83 | Bi4O12Ti3 | mp-23427 | mp-23335 | wfid_1562345115.68239992 |
| 84 | Bi4O12Ti3 | mp-622198 | mp-23335 | wfid_1562345090.67222161 |
| 85 | BiCl8F4H3K6 | mp-696998 | mp-723540 | wfid_1562345088.64692719 |
| 86 | BiCuO8W2 | mp-565192 | mp-615173 | wfid_1562199296.16002539 |
| 87 | BiCuYb | mp-22953 | mp-22960 | wfid_1562345089.00815378 |
| 88 | BiFeO3 | mp-601706 | mp-561388 | wfid_1562345117.60950601 |
| 89 | BiFeO3 | mp-24942 | mp-561388 | wfid_1562345068.96362730 |
| 90 | BiFeO3 | mp-24932 | mp-561388 | wfid_1562345095.33810901 |
| 91 | BiInO3 | mp-556892 | mp-561102 | wfid_1562345078.25607094 |
| 92 | BiInO3 | mp-556892 | mp-545379 | wfid_1562345104.93967568 |
| 93 | BiO2 | mvc-9645 | mp-32548 | wfid_1562345101.07858072 |
| 94 | BiO3Sc | mp-555313 | mp-555769 | wfid_1562345069.03136189 |
| 95 | BiO3Sc | mp-555313 | mp-550008 | wfid_1562345104.65432837 |
| 96 | BiO3Y | mvc-3479 | mvc-15941 | wfid_1562345100.97005996 |
| 97 | Br3CsGe | mp-642739 | mp-570223 | wfid_1562345114.09410592 |
| 98 | Br3MnRb | mp-568231 | mp-29763 | wfid_1562345090.03425890 |
| 99 | Br3RbV | mp-29314 | mp-570099 | wfid_1562345089.82930048 |
| 100 | Br4K2Zn | mp-23535 | mp-23495 | wfid_1562199296.55106864 |
| 101 | BrH | mp-632229 | mp-634105 | wfid_1562345082.80546132 |
| 102 | BrH | mp-632229 | mp-23903 | wfid_1562345083.08491158 |
| 103 | BrMnSbSe2 | mp-639335 | mp-655834 | wfid_1562345065.32859164 |
| 104 | C2CoLi2O6 | mp-765126 | mp-763828 | wfid_1562345060.79723600 |
| 105 | C2CoLi2O6 | mp-765128 | mp-763828 | wfid_1562345060.64209065 |
| 106 | C2HO2 | mp-675395 | mp-23680 | wfid_1562345111.73469268 |
| 107 | C2HgN2S2 | mp-610992 | mp-655275 | wfid_1562345063.29510504 |
| 108 | C3ClH10NO4 | mp-554570 | mp-560498 | wfid_1562199296.21214937 |
| 109 | C6Cu2H10N4S3 | mp-600236 | mp-555729 | wfid_1562345061.28565377 |
| 110 | CCs4O4 | mp-562815 | mp-605824 | wfid_1562345090.37034900 |
| 111 | CH4N2S | mp-721896 | mp-23930 | wfid_1562345071.44504562 |
| 112 | CHO2Tl | mp-558579 | mp-557687 | wfid_1562345073.70348192 |
| 113 | CK4O4 | mp-551561 | mp-549687 | wfid_1562345114.85602856 |
| 114 | CK4O4 | mp-551561 | mp-549869 | wfid_1562345064.72820430 |
| 115 | CK4O4 | mp-605843 | mp-549869 | wfid_1562345067.39360264 |
| 116 | CK4O4 | mp-545387 | mp-551736 | wfid_1562345092.46694443 |
| 117 | CK4O4 | mp-545630 | mp-551736 | wfid_1562345091.11202201 |
| 118 | CLi4O4 | mp-550320 | mp-551740 | wfid_1562345109.75844212 |
| 119 | CLi4O4 | mp-550320 | mp-551848 | wfid_1562345064.64947472 |
| 120 | CLi4O4 | mp-550498 | mp-551740 | wfid_1562345095.95394592 |
| 121 | CLi4O4 | mp-550593 | mp-546202 | wfid_1562345093.97216898 |
| 122 | CN2Pb | mp-619032 | mp-19727 | wfid_1562345077.98674939 |
| 123 | CNa4O4 | mp-13274 | mp-546551 | wfid_1562345064.95566356 |
| 124 | CNa4O4 | mp-13274 | mp-546707 | wfid_1562345116.92380413 |
| 125 | CNa4O4 | mp-645295 | mp-551886 | wfid_1562345106.21088335 |
| 126 | CNa4O4 | mp-552623 | mp-551886 | wfid_1562345091.53870848 |
| 127 | CNa4O4 | mp-552941 | mp-551886 | wfid_1562345092.72215049 |
| 128 | CO4Rb4 | mp-551176 | mp-550679 | wfid_1562345106.35940545 |
| 129 | CO4Rb4 | mp-551176 | mp-547898 | wfid_1562345115.59588544 |
| 130 | CO4Rb4 | mp-551176 | mp-545760 | wfid_1562345065.02973794 |
| 131 | CO4Rb4 | mp-550314 | mp-546320 | wfid_1562345091.36271002 |
| 132 | CO4Rb4 | mp-551690 | mp-546320 | wfid_1562345111.91150344 |
| 133 | Ca2FeO6W | mvc-12913 | mp-619611 | wfid_1562345117.46280857 |
| 134 | Ca3Mn2O7 | mp-19042 | mp-19610 | wfid_1562345081.50183207 |
| 135 | Ca3Mn2O7 | mvc-11576 | mp-19610 | wfid_1562345099.00022301 |
| 136 | Ca3Mn2O7 | mp-19042 | mp-19124 | wfid_1562345100.32022475 |
| 137 | Ca3Mn2O7 | mvc-11576 | mp-19124 | wfid_1562345098.61366590 |
| 138 | Ca5ClO12P3 | mp-39460 | mp-554236 | wfid_1562345087.78522502 |
| 139 | CaF2 | mp-560030 | mp-554355 | wfid_1562345100.02925969 |
| 140 | CaFe2O4 | mvc-12582 | mvc-8188 | wfid_1562345116.80707800 |
| 141 | CaFe2O4 | mvc-12583 | mvc-8188 | wfid_1562345117.00610059 |
| 142 | CaFeO6W | mvc-10916 | mvc-14934 | wfid_1562345116.27690236 |
| 143 | CaNi2O4 | mvc-12644 | mvc-7742 | wfid_1562345116.53277296 |
| 144 | Cd2ClP3 | mp-29246 | mp-644431 | wfid_1562345068.11764927 |
| 145 | CdCl2 | mp-632403 | mp-695850 | wfid_1562345118.41939438 |
| 146 | CdO3Ti | mp-20940 | mp-14550 | wfid_1562345071.77195440 |
| 147 | CdO3Ti | mp-5052 | mp-14550 | wfid_1562345078.17038961 |
| 148 | CdTe | mp-685146 | mp-1008471 | wfid_1562345102.26130693 |
| 149 | CdTe | mp-685146 | mp-2388 | wfid_1562345082.98370782 |
| 150 | CeCu4Sn | mp-640286 | mp-655580 | wfid_1562345115.39463102 |
| 151 | CeCuSn | mp-22683 | mp-22761 | wfid_1562345088.97236356 |
| 152 | CeKS4Si | mp-22809 | mp-11170 | wfid_1562199297.04974693 |
| 153 | Cl2H8MgO12 | mp-989229 | mp-865188 | wfid_1562345063.58842327 |
| 154 | Cl3CoTl | mp-567430 | mp-569753 | wfid_1562345112.15249459 |
| 155 | Cl3CrCs | mp-610955 | mp-570326 | wfid_1562345089.18755185 |
| 156 | Cl3CrRb | mp-568864 | mp-568887 | wfid_1562345089.52001267 |
| 157 | Cl3CrRb | mp-568864 | mp-30027 | wfid_1562345064.81349297 |
| 158 | Cl3CsPb | mp-675524 | mp-23037 | wfid_1562345092.64050822 |
| 159 | Cl3CuRb | mp-571305 | mp-568857 | wfid_1562345064.33652828 |
| 160 | Cl3CuRb | mp-571305 | mp-569526 | wfid_1562345108.13574082 |
| 161 | Cl4CoRb2 | mp-571242 | mp-23076 | wfid_1562345075.90964892 |
| 162 | Cl4GaHg2Sb | mp-568031 | mp-571190 | wfid_1562345074.87030107 |
| 163 | Cl4K2Zn | mp-653633 | mp-653454 | wfid_1562345109.96773133 |
| 164 | Cl4K2Zn | mp-618177 | mp-653454 | wfid_1562345075.60077746 |
| 165 | Cl4K2Zn | mp-647575 | mp-653454 | wfid_1562345106.46698464 |
| 166 | Cl4Rb2Zn | mp-568350 | mp-608314 | wfid_1562345106.82651466 |
| 167 | Cl4Rb2Zn | mp-616185 | mp-608314 | wfid_1562345076.32521814 |
| 168 | Cl8Na2Ti3 | mp-569978 | mp-29474 | wfid_1562345086.01893685 |
| 169 | ClH | mp-632326 | mp-634101 | wfid_1562345118.36325774 |
| 170 | ClH | mp-632326 | mp-23722 | wfid_1562345083.03981015 |
| 171 | ClH | mp-684609 | mp-634101 | wfid_1562345116.34885480 |
| 172 | ClH3O5 | mp-625175 | mp-625148 | wfid_1562345076.84195890 |
| 173 | ClH4NO4 | mp-698084 | mp-706586 | wfid_1562345077.01048358 |
| 174 | ClIn | mp-571636 | mp-571555 | wfid_1562345080.19562594 |
| 175 | CoLi2O4Si | mp-764958 | mp-764956 | wfid_1562345093.33885886 |
| 176 | CoLiO4P | mp-761753 | mp-18915 | wfid_1562345062.80425054 |
| 177 | CoLiO4P | mp-761753 | mp-761979 | wfid_1562345062.56056403 |
| 178 | CoN | mvc-15478 | mp-1009078 | wfid_1562345115.48425255 |
| 179 | CoO3Y | mvc-3765 | mvc-3570 | wfid_1562345101.77376431 |
| 180 | CoO6Si2 | mvc-12012 | mvc-11366 | wfid_1562345116.15943930 |
| 181 | CoO6Si2 | mvc-15005 | mvc-11366 | wfid_1562345116.64943193 |
| 182 | Cr2S3 | mp-849081 | mp-555569 | wfid_1562345085.83637119 |
| 183 | CrI3Rb | mp-27442 | mp-676553 | wfid_1562345107.98049651 |
| 184 | CrLi3O4 | mp-770632 | mp-777303 | wfid_1562345073.19170804 |
| 185 | CrLiO4P | mp-761391 | mp-25507 | wfid_1562345097.86901705 |
| 186 | CrLiO4P | mp-761399 | mp-761401 | wfid_1562345079.39507654 |
| 187 | CrO3 | mvc-13134 | mp-779986 | wfid_1562345115.52822945 |
| 188 | CrO3 | mp-779941 | mp-779986 | wfid_1562345077.57898854 |
| 189 | CrO3 | mvc-13999 | mvc-11097 | wfid_1562345100.48228079 |
| 190 | CrO3Y | mvc-3768 | mvc-3569 | wfid_1562345101.55871265 |
| 191 | CrO9P3 | mp-566776 | mp-566761 | wfid_1562345068.26681921 |
| 192 | Cs2HgI4 | mp-567594 | mp-28421 | wfid_1562199296.32626762 |
| 193 | Cs2N2Tb6Te7 | mp-646007 | mp-655613 | wfid_1562345117.74137700 |
| 194 | Cs2O3Pb | mp-21521 | mp-21283 | wfid_1562345081.30847872 |
| 195 | CsF3Pb | mp-20282 | mp-5811 | wfid_1562345093.87340147 |
| 196 | CsO4PZn | mp-559752 | mp-18673 | wfid_1562345078.54041242 |
| 197 | Cu2Se | mp-684653 | mp-22297 | wfid_1562345109.82599426 |
| 198 | Cu3Mo2O9 | mp-649957 | mp-639719 | wfid_1562345076.59705060 |
| 199 | Cu4LiO12P3 | mp-761193 | mp-26741 | wfid_1562345069.50145207 |
| 200 | Cu8O | mp-704745 | mp-31217 | wfid_1562345083.27533748 |
| 201 | CuF4Li2 | mp-753171 | mp-753123 | wfid_1562345117.37566277 |
| 202 | CuGeLi2 | mp-676117 | mp-35841 | wfid_1562345108.71707409 |
| 203 | CuGeYb | mp-567768 | mp-5111 | wfid_1562345089.04666899 |
| 204 | CuI | mp-673245 | mp-22895 | wfid_1562199296.66891517 |
| 205 | CuLiO4P | mp-769278 | mp-758750 | wfid_1562345103.23786212 |
| 206 | CuLiO4P | mp-757209 | mp-25449 | wfid_1562345080.06677653 |
| 207 | CuLiO4P | mp-752507 | mp-758750 | wfid_1562345079.49749416 |
| 208 | CuN | mvc-13841 | mp-1008922 | wfid_1562345115.20318466 |
| 209 | CuSbYb | mp-11701 | mp-9439 | wfid_1562345089.09864953 |
| 210 | Er2F7K | mp-27925 | mp-558238 | wfid_1562345077.72055408 |
| 211 | Eu2GeSe4 | mp-629088 | mp-505740 | wfid_1562199296.49909393 |
| 212 | F2HRb | mp-677103 | mp-29764 | wfid_1562345084.74762742 |
| 213 | F2Pb | mp-685150 | mp-315 | wfid_1562345083.62247248 |
| 214 | F3Nd | mp-18511 | mp-18074 | wfid_1562345088.07662185 |
| 215 | F3PbRb | mp-674508 | mp-21043 | wfid_1562345118.45837326 |
| 216 | F4FeLi | mp-777891 | mp-778352 | wfid_1562345073.27618989 |
| 217 | F4FeLi2 | mp-777471 | mp-777588 | wfid_1562345079.15751718 |
| 218 | F4Li2OV | mp-764695 | mp-780857 | wfid_1562345081.19754088 |
| 219 | F4LiV | mp-764895 | mp-766952 | wfid_1562345091.69966218 |
| 220 | F4MgSr | mp-561022 | mp-556290 | wfid_1562345060.28720726 |
| 221 | F5FeK2 | mp-579331 | mp-555882 | wfid_1562345075.11835588 |
| 222 | F5H2Li2OV | mp-868263 | mp-770536 | wfid_1562345112.83065051 |
| 223 | F5V | mp-765140 | mvc-14312 | wfid_1562345115.11396023 |
| 224 | F5V | mp-766786 | mvc-14312 | wfid_1562345115.26181400 |
| 225 | F6LiV | mp-765122 | mp-765966 | wfid_1562345101.99111429 |
| 226 | F7FeNa2Ni | mp-566483 | mp-558817 | wfid_1562345084.18504979 |
| 227 | F7LiMn2 | mp-765204 | mp-763085 | wfid_1562345061.66535445 |
| 228 | FNbO2 | mp-752467 | mp-35171 | wfid_1562345068.05041391 |
| 229 | FTl | mp-558134 | mp-2175 | wfid_1562345083.57628883 |
| 230 | Fe2Li3O12P3 | mp-762728 | mp-853256 | wfid_1562199295.93469828 |
| 231 | Fe2O4Zn | mvc-12661 | mvc-15076 | wfid_1562345116.41517559 |
| 232 | Fe3O4 | mp-612405 | mp-715614 | wfid_1562345066.80008603 |
| 233 | Fe3O4 | mp-715275 | mp-541907 | wfid_1562345071.34228519 |
| 234 | Fe3O4 | mp-715275 | mp-18731 | wfid_1562345071.67063249 |
| 235 | Fe4LiO12P3 | mp-762896 | mp-540020 | wfid_1562345069.75195107 |
| 236 | Fe7S8 | mp-850411 | mp-685128 | wfid_1562345061.12554914 |
| 237 | FeHO2 | mp-625314 | mp-625269 | wfid_1562345062.25044610 |
| 238 | FeHO2 | mp-625314 | mp-605437 | wfid_1562345062.47321464 |
| 239 | FeHO2 | mp-625268 | mp-625233 | wfid_1562345077.64486953 |
| 240 | FeHO2 | mp-625268 | mp-605437 | wfid_1562345078.08008077 |
| 241 | FeHO2 | mp-626102 | mp-743660 | wfid_1562345081.65293768 |
| 242 | FeLi2O4Si | mp-764344 | mp-762566 | wfid_1562345092.81949641 |
| 243 | FeLiO4P | mp-762593 | mp-765913 | wfid_1562345099.64867399 |
| 244 | FeLiO4P | mp-766763 | mp-765913 | wfid_1562345079.60737271 |
| 245 | FeLiO4Si | mp-766664 | mp-762643 | wfid_1562345118.01517942 |
| 246 | FeO2 | mvc-12125 | mp-25519 | wfid_1562345100.60371473 |
| 247 | FeO3Sc | mp-771123 | mp-769970 | wfid_1562345089.93657805 |
| 248 | FeO3Y | mvc-3751 | mvc-3556 | wfid_1562345097.97802299 |
| 249 | GaLuO3 | mp-768505 | mp-755342 | wfid_1562345094.09550293 |
| 250 | GaMo4S8 | mp-559694 | mp-2885 | wfid_1562345089.31591687 |
| 251 | GaMo4Se8 | mp-567394 | mp-5584 | wfid_1562345096.94387271 |
| 252 | GaN5O14 | mp-541950 | mp-557954 | wfid_1562345064.51602404 |
| 253 | GaO3Sc | mp-769079 | mp-754165 | wfid_1562345093.59972440 |
| 254 | Gd3O7Os | mp-567291 | mp-16825 | wfid_1562345112.36603552 |
| 255 | Gd3O7Ru | mp-683963 | mp-17237 | wfid_1562345111.31901335 |
| 256 | H2KO4P | mp-757909 | mp-24262 | wfid_1562345103.54083952 |
| 257 | H2KO4P | mp-23959 | mp-696752 | wfid_1562345096.22998438 |
| 258 | H2Mg | mp-569051 | mp-23711 | wfid_1562345071.87614530 |
| 259 | H2Mg | mp-569051 | mp-1008901 | wfid_1562345095.28203208 |
| 260 | H2MoO4 | mp-625600 | mp-626577 | wfid_1562199295.62978167 |
| 261 | H2MoO4 | mp-626582 | mp-626577 | wfid_1562199296.07296394 |
| 262 | H2MoO4 | mp-626586 | mp-626577 | wfid_1562199295.77439317 |
| 263 | H2NiO2 | mp-626843 | mp-626794 | wfid_1562345090.47289757 |
| 264 | H2O | mp-557082 | mp-558958 | wfid_1562345062.67599870 |
| 265 | H2O | mp-557082 | mp-558226 | wfid_1562345062.31879317 |
| 266 | H2O10U3 | mp-626114 | mp-626104 | wfid_1562199295.82524035 |
| 267 | H2O10U3 | mp-626114 | mp-626062 | wfid_1562199295.87807235 |
| 268 | H2O2Sr | mp-625184 | mp-27425 | wfid_1562345070.54182585 |
| 269 | H2O2Sr | mp-625184 | mp-625191 | wfid_1562345070.86402364 |
| 270 | H2O2Zn | mp-625857 | mp-625830 | wfid_1562345062.14719002 |
| 271 | H2O4PRb | mp-23667 | mp-642831 | wfid_1562345095.48459868 |
| 272 | H2O4S | mp-625475 | mp-690733 | wfid_1562345114.14736365 |
| 273 | H2O4S | mp-625445 | mp-690733 | wfid_1562345068.84228879 |
| 274 | H2O4S | mp-625474 | mp-690733 | wfid_1562345068.50494058 |
| 275 | H2O4Sn3 | mp-625789 | mp-625541 | wfid_1562345091.78627029 |
| 276 | H2O4Te | mp-625526 | mp-625513 | wfid_1562345065.26430213 |
| 277 | H2O4U | mp-626885 | mp-626876 | wfid_1562345081.78625138 |
| 278 | H2O4U | mp-626885 | mp-626864 | wfid_1562345082.84911275 |
| 279 | H3LaO3 | mp-625733 | mp-625394 | wfid_1562345086.50809338 |
| 280 | H3O3Pr | mp-625452 | mp-626361 | wfid_1562345065.11062718 |
| 281 | H3O3Pr | mp-625452 | mp-625447 | wfid_1562345065.17991627 |
| 282 | H3O3Y | mp-625677 | mp-24076 | wfid_1562345086.70080946 |
| 283 | H3O4P | mp-626450 | mp-626464 | wfid_1562345066.41605572 |
| 284 | H3O4P | mp-626450 | mp-626449 | wfid_1562345066.26534577 |
| 285 | H3O4P | mp-626450 | mp-23902 | wfid_1562345065.88747031 |
| 286 | H4O5S | mp-626448 | mp-626109 | wfid_1562345065.45762179 |
| 287 | H4O6Sr | mp-625836 | mp-625812 | wfid_1562345067.79383899 |
| 288 | H4O6Sr | mp-625871 | mp-625821 | wfid_1562345119.03613496 |
| 289 | H5IO6 | mp-625256 | mp-625174 | wfid_1562345066.04864776 |
| 290 | H5IO6 | mp-625256 | mp-27773 | wfid_1562345065.65066324 |
| 291 | H5NO2 | mp-625109 | mp-625108 | wfid_1562345113.93677372 |
| 292 | H8N2O4S | mp-24468 | mp-23876 | wfid_1562345077.14704718 |
| 293 | HInO2 | mp-504535 | mp-632711 | wfid_1562345073.13297542 |
| 294 | HK2NO6S2 | mp-695383 | mp-706912 | wfid_1562345068.66194719 |
| 295 | HNaO | mp-626000 | mp-23940 | wfid_1562199296.04072234 |
| 296 | HNaO | mp-626000 | mp-23891 | wfid_1562345093.29957585 |
| 297 | HNaO | mp-625996 | mp-23891 | wfid_1562345109.01493217 |
| 298 | HO2V | mp-626791 | mp-626787 | wfid_1562345071.60128680 |
| 299 | HO2V | mp-626791 | mp-626796 | wfid_1562345071.21174354 |
| 300 | HORb | mp-626721 | mp-643043 | wfid_1562199296.70345448 |
| 301 | HfO2 | mp-685097 | mp-550893 | wfid_1562345073.07864623 |
| 302 | HfO3Pb | mp-669414 | mp-22734 | wfid_1562345073.51183116 |
| 303 | HfO3Sr | mp-13108 | mp-4551 | wfid_1562345085.42724040 |
| 304 | ILi6PS5 | mp-950995 | mp-985582 | wfid_1562345070.64579894 |
| 305 | ILiO3 | mp-22955 | mp-545343 | wfid_1562345088.90631590 |
| 306 | ILiO3 | mp-613442 | mp-545343 | wfid_1562345088.85588763 |
| 307 | INaO3 | mp-559252 | mp-545825 | wfid_1562345117.14457677 |
| 308 | In3Mg | mp-973320 | mp-973308 | wfid_1562345085.05162970 |
| 309 | K2O4Se | mp-557025 | mp-5226 | wfid_1562345101.21075848 |
| 310 | K2O7Zn6 | mp-559112 | mp-540728 | wfid_1562345085.70573284 |
| 311 | K3S4Sb | mp-9781 | mp-9911 | wfid_1562345091.21940324 |
| 312 | KLaS4Si | mp-861938 | mp-12924 | wfid_1562345060.20349732 |
| 313 | KNbO3 | mp-5246 | mp-935811 | wfid_1562345096.61294252 |
| 314 | KNbO3 | mp-4342 | mp-935811 | wfid_1562345085.39184383 |
| 315 | KNbO3 | mp-7375 | mp-935811 | wfid_1562345096.53537136 |
| 316 | LaN3W | mp-989524 | mp-989455 | wfid_1562345105.24353733 |
| 317 | Li2MnO6Si2 | mp-764791 | mp-767686 | wfid_1562345116.00036545 |
| 318 | Li3Mg | mp-976139 | mp-976254 | wfid_1562345063.43801573 |
| 319 | LiMn4O12P3 | mp-32021 | mp-853253 | wfid_1562345070.20398004 |
| 320 | LiMnO2 | mp-775531 | mp-775236 | wfid_1562345089.69436506 |
| 321 | LiMnO4P | mp-690866 | mp-868359 | wfid_1562345112.01290767 |
| 322 | LiMnO4P | mp-765846 | mp-765871 | wfid_1562345114.75068713 |
| 323 | LiMnO4P | mp-761551 | mp-868359 | wfid_1562345078.67804385 |
| 324 | LiMnO4P | mp-766735 | mp-868359 | wfid_1562345079.01940689 |
| 325 | LiMnO4P | mp-780646 | mp-18997 | wfid_1562345078.43784085 |
| 326 | LiMnO4P | mp-761562 | mp-765871 | wfid_1562345098.18604043 |
| 327 | LiMnO4P | mp-766735 | mp-31939 | wfid_1562345102.64344909 |
| 328 | LiMnO4P | mp-780646 | mp-765871 | wfid_1562345079.70386079 |
| 329 | LiMnO4P | mp-867520 | mp-765871 | wfid_1562345080.29869855 |
| 330 | LiMnO4Si | mp-762828 | mp-780325 | wfid_1562345105.43550629 |
| 331 | LiNbO3 | mp-3731 | mp-552588 | wfid_1562345086.57526556 |
| 332 | LiNi4O12P3 | mp-868339 | mp-868378 | wfid_1562345070.95947283 |
| 333 | LiNiO4P | mp-763217 | mp-25614 | wfid_1562345062.93664125 |
| 334 | LiNiO4P | mp-763217 | mp-762173 | wfid_1562345063.47200918 |
| 335 | LiNiO4P | mp-763217 | mp-761990 | wfid_1562345063.14923175 |
| 336 | LiNiO4P | mp-763061 | mp-32324 | wfid_1562345098.08585876 |
| 337 | LiNiO4P | mp-766636 | mp-761990 | wfid_1562345102.75577260 |
| 338 | LiNiO4P | mp-772673 | mp-761990 | wfid_1562345080.47287897 |
| 339 | LiNiO4P | mp-868169 | mp-32324 | wfid_1562345105.85799320 |
| 340 | LiO12P3W2 | mp-763531 | mp-763372 | wfid_1562345098.77384901 |
| 341 | LiO12P3Zr2 | mp-681439 | mp-541661 | wfid_1562345094.48631430 |
| 342 | LiO4PV | mp-765022 | mp-761338 | wfid_1562345076.06485889 |
| 343 | LiO4PV | mp-765022 | mp-32425 | wfid_1562345102.34349984 |
| 344 | LiO4SiV | mp-767103 | mp-767620 | wfid_1562345079.26097922 |
| 345 | MgN2O6 | mp-776410 | mp-771046 | wfid_1562345119.24225097 |
| 346 | MgO3Si | mp-557803 | mp-5026 | wfid_1562345075.73274781 |
| 347 | MgRb3 | mp-974981 | mp-974940 | wfid_1562345084.61541787 |
| 348 | MnN | mvc-13808 | mp-1009130 | wfid_1562345116.38073018 |
| 349 | MnO3Y | mp-19385 | mp-19227 | wfid_1562345094.72739682 |
| 350 | MnO3Y | mp-19385 | mvc-11553 | wfid_1562345094.87268641 |
| 351 | MnO3Y | mvc-16316 | mvc-11553 | wfid_1562345101.66519989 |
| 352 | MnO3Y | mvc-16316 | mp-19227 | wfid_1562345100.17508190 |
| 353 | MoO3 | mp-715584 | mvc-12752 | wfid_1562345118.94396078 |
| 354 | MoO3 | mvc-13534 | mvc-11096 | wfid_1562345105.14252211 |
| 355 | MoO3Y | mvc-3769 | mvc-3559 | wfid_1562345101.88114837 |
| 356 | N2O6Zn | mp-778973 | mp-772617 | wfid_1562345118.64838432 |
| 357 | N3Na | mp-634410 | mp-570538 | wfid_1562345117.90645376 |
| 358 | N6Pb | mp-620058 | mp-667338 | wfid_1562345078.78578590 |
| 359 | NOs | mp-999317 | mp-1009496 | wfid_1562345106.31147985 |
| 360 | NaNbO3 | mp-4681 | mp-4419 | wfid_1562345096.42937982 |
| 361 | NaNbO3 | mp-558920 | mp-3671 | wfid_1562345071.93467738 |
| 362 | NaNbO3 | mp-558920 | mp-559354 | wfid_1562345072.89491942 |
| 363 | NaO11V6 | mp-567072 | mp-510616 | wfid_1562345107.63740338 |
| 364 | NaO11V6 | mp-25156 | mp-510616 | wfid_1562345088.44942336 |
| 365 | NbO4Sb | mp-3491 | mp-3612 | wfid_1562345074.16515924 |
| 366 | NbO5P | mp-556918 | mp-5803 | wfid_1562345078.33658421 |
| 367 | NiO3Y | mvc-3773 | mvc-14342 | wfid_1562345102.14561677 |
| 368 | O11PbV6 | mp-619128 | mp-25790 | wfid_1562345088.26528020 |
| 369 | O13V7 | mp-715598 | mp-556332 | wfid_1562199296.38256579 |
| 370 | O23Rb6Si10 | mp-27376 | mp-561189 | wfid_1562345094.99343391 |
| 371 | O23Rb6Si10 | mp-555837 | mp-561189 | wfid_1562345094.24965045 |
| 372 | O2Sb | mp-230 | mp-560098 | wfid_1562345073.78468145 |
| 373 | O2Si | mp-555891 | mp-7648 | wfid_1562345105.66292123 |
| 374 | O2Si | mp-555891 | mp-559091 | wfid_1562345063.38077530 |
| 375 | O2Si | mp-972808 | mp-559091 | wfid_1562345063.09303946 |
| 376 | O2Si | mp-553881 | mp-10948 | wfid_1562345104.59178493 |
| 377 | O2Si | mp-553881 | mp-10064 | wfid_1562345067.15640753 |
| 378 | O2Si | mp-557881 | mp-558351 | wfid_1562345067.50179482 |
| 379 | O2Si | mp-555235 | mp-7087 | wfid_1562345099.15877093 |
| 380 | O2Si | mp-554089 | mp-10948 | wfid_1562345074.54062829 |
| 381 | O2Si | mp-554089 | mp-7905 | wfid_1562345080.24041294 |
| 382 | O2Si | mp-554089 | mp-10064 | wfid_1562345080.41388803 |
| 383 | O2Si | mp-16964 | mp-560826 | wfid_1562345082.41349074 |
| 384 | O2Si | mp-556218 | mp-560826 | wfid_1562345083.35483635 |
| 385 | O2Si | mp-557264 | mp-559313 | wfid_1562345083.13307328 |
| 386 | O2Si | mp-554946 | mp-644923 | wfid_1562345086.82500871 |
| 387 | O2V | mp-715553 | mp-714880 | wfid_1562345090.13953873 |
| 388 | O2Zr | mp-556605 | mp-1565 | wfid_1562345072.21799631 |
| 389 | O3PbTi | mp-20459 | mp-19845 | wfid_1562345085.47191419 |
| 390 | O3PbZr | mp-647557 | mp-542903 | wfid_1562345073.88793953 |
| 391 | O3SbY | mvc-3460 | mvc-14740 | wfid_1562345100.87211791 |
| 392 | O3ScY | mp-769007 | mp-768479 | wfid_1562345093.42856192 |
| 393 | O3SnY | mvc-3464 | mvc-13971 | wfid_1562345100.77015926 |
| 394 | O3Te | mvc-14734 | mvc-14413 | wfid_1562345105.02231844 |
| 395 | O3TiY | mvc-3431 | mvc-13995 | wfid_1562345100.06969004 |
| 396 | O3V2 | mp-553955 | mp-715514 | wfid_1562345067.95646032 |
| 397 | O3V2 | mp-553955 | mp-714906 | wfid_1562345118.53916482 |
| 398 | O3VY | mvc-3770 | mvc-13691 | wfid_1562345103.93946099 |
| 399 | O3W | mp-32662 | mp-559175 | wfid_1562345090.19555210 |
| 400 | O3W | mp-32662 | mp-715590 | wfid_1562345090.28098999 |
| 401 | O3W | mp-32662 | mp-32777 | wfid_1562345087.96868747 |
| 402 | O3W | mvc-13988 | mvc-11457 | wfid_1562345101.46683505 |
| 403 | O3WY | mvc-3772 | mvc-15989 | wfid_1562345103.36826836 |
| 404 | O5PTiTl | mp-6706 | mp-559607 | wfid_1562345074.29488196 |
| 405 | O7OsSm3 | mp-555639 | mp-5447 | wfid_1562345109.33811762 |
| 406 | O7RuSm3 | mp-555525 | mp-5779 | wfid_1562345109.06349917 |
| 407 | O7Sr2Ta2 | mp-13664 | mp-12286 | wfid_1562345080.99369532 |
| 408 | O8W3 | mp-715557 | mp-19066 | wfid_1562345114.96113485 |
| 409 | OPb | mp-550714 | mp-20878 | wfid_1562345071.55443872 |
| 410 | PSn | mp-7526 | mp-475 | wfid_1562345111.58481907 |
| 411 | PtU | mp-542817 | mp-569752 | wfid_1562345098.53781532 |
| 412 | Te5U | mp-651772 | mp-28500 | wfid_1562345077.40124852 |
| 413 | U | mp-43 | mp-93 | wfid_1562345085.52036650 |
Graphical interface
To view the DFT ferroelectric candidate data in aggregate, we create an interactive web site for viewing polarization and total energy plots, animations of the distortion, and other data. The interface consists of two main pages: (1) a page containing a sortable table of ferroelectric candidates organized by category (whether the candidate had a value of polarization successfully calculated and if so with what level of confidence) and (2) individual candidate pages that show energy and polarization plots, distortion animations, and other data specific to that candidate. This interface is available at https://blondegeek.github.io/ferroelectric_search_site/.
Data Records
This dataset is available as two JSON files deposited in figshare77 and our GitHub repository (http://github.com/blondegeek/ferroelectric_search_site)78. The JSON files provide details of the symmetry analysis performed for each candidate and data generated by DFT calculations and post-processing from the workflow. Zipped folders of the input and output VASP files for each candidate deposited in figshare77. The title of the zipped folder includes the workflow ID to correlate the VASP files to information in the JSON files provided. We also provide an interface for viewing the dataset at http://blondegeek.github.io/ferroelectric_search_site with the code for the interface located at http://github.com/blondegeek/ferroelectric_search_site.
File format
We contribute the following data:
JSON file with information on workflow status of each calculated candidate and calculation details extracted from VASP inputs and outputs. This includes total energy, band gap, polarization, post-processed information, and validation criteria for candidates with completed calculation. See Tables 2 and 3 for details.
JSON file with information describing all 413 nonpolar-polar structure pairs with group-subgroup relations compatible with a second-order phase transition in the Materials Project determined with BCS Structure Relations and used in this search. See Tables 4 and 5 for details.
Zipped folders with the VASP 5.3.5 INCAR, KPOINTS, OUTCAR, and POSCAR files.
Table 2.
Key, value data type, and value description for workflow_data.json entries.
| Key | Type | Description |
|---|---|---|
| _id | bson.objectid.ObjectId | Automatically created unique identifier. |
| wfid | unicode | The workflow id. |
| cid | unicode | The “connection” or distortion id. The alphanumeric portion of the string after cid_ corresponds to the bson.objectid.ObjectId used in the distortion database. |
| search_id | unicode | Simplified unique identifier for pairs of structures used in the search. |
| workflow_status | unicode | Status of workflow denoted by FireWorks. |
| alphabetical_formula | unicode | Composition with elements sorted alphabetically. |
| pretty_formula | unicode | Composition with elements sorted by electronegativity. |
| polar_id | unicode | Materials Project Id. |
| nonpolar_id | unicode | Materials Project Id. |
| polar_icsd_ids | floats list | ICSD id numbers, if available. |
| nonpolar_icsd_ids | floats list | ICSD id numbers, if available. |
| polar_spacegroup | float | Polar space group, integer between 1 and 230. |
| nonpolar_spacegroup | float | Nonpolar space group, integer between 1 and 230. |
| orig_polar_structure | pymatgen.Structure dict | Polar structure as referenced in distortion JSON file. |
| orig_nonpolar_structure | pymatgen.Structure dict | Nonpolar structure as referenced in distortion JSON file. |
| structures | pymatgen.Structure dicts list | Static calculation structures. Fully complete workflows have 10. |
| relaxation_len | float | Number of relaxation calculations performed. Fully complete workflows have 2. |
| relaxation_task_labels | strs list | The task labels of the relaxation calculations performed. |
| static_len | float | Number of static calculations performed. Fully complete workflows have 10. |
| static_task_labels | strs list | The task labels of the static calculations performed. |
| polarization_len | float | Number of polarization calculations performed. Fully complete workflows have 10. |
| polarization_task_labels | strs list | The task labels of the polarization calculations performed. |
| polarization_change_norm | float | The Cartesian norm of the recovered spontaneous polarization. |
| polarization_change | floats list | The vector along a, b, and c of the recovered spontaneous polarization vector. |
| raw_electron_polarization | floats lists list | Raw electron polarization per structure from VASP along Cartesian directions. |
| raw_ionic_polarization_vasp | floats lists list | Raw ionic polarization per structure from VASP along Cartesian directions. |
| raw_ionic_polarization | floats lists list | Raw ionic polarization per structure from calc_ionic along lattice directions. |
| polarization_quanta | floats lists list | Structure dependent polarization quanta along a, b, and c lattice vectors. |
| same_branch_polarization | floats lists list | Same branch polarization along a, b, and c for each polarization calculation structure. |
| polarization_max_spline_jumps | floats lists list | Max jump between spline and data for polarization along a, b, and c. |
| polarization_smoothness | floats list | Average jump between spline and data for polarization along a, b, and c. |
Table 3.
Key, value data type, and value description for workflow_data.json entries continued.
| Key | Type | Description |
|---|---|---|
| energies | floats list | Energy in eV for each static calculation structure. |
| energies_per_atom | floats list | Energy per atom in eV for each static calculation structure. |
| energies_per_atom_max_spline_jumps | float | Max jump between spline and data for energy per atom. |
| energies_per_atom_smoothness | float | Average jump between spline and data for energy per atom. |
| calculated_max_distance | float | Calculated max distortion distance. Compare to dmax in distortion.json entries. |
| zval_dict | dict | dict with keys of species and values of ZVAL in number of electrons. |
| hubbards | dict | dict with keys of species and values of Hubbard U correction in eV pairs. |
| cbms | floats list | Conduction band minimum per static calculation computed structures. |
| vbms | floats list | Valence band maximum per static calculation computed structures. |
| stresses | floats lists list | Stress tensor per static calculation computed structures. |
| charges | floats dicts lists list | Charges projected onto spd orbitals per atom per static calculation computed structures. |
| magnetization | floats lists list | Magnetization in Bohr magnetons per atom per static calculation computed structures. |
| total_magnetization | floats list | Total magnetization in Bohr magnetons per static calculation computed structures. |
| forces | floats lists list | Cartesian forces per atom per static calculation computed structures. |
| bandgaps | floats list | list of band gaps in eV for static calculation computed structures. |
Table 4.
Key, value data type, and value description for distortion.json entries.
| Key | Type | Description |
|---|---|---|
| _id | bson.objectid.ObjectId | These ids are used to generate cid in workflow_data JSON file. |
| pretty_formula | unicode | Composition with elements sorted by electronegativity. |
| polar_id | unicode | Materials Project Id. |
| nonpolar_id | unicode | Materials Project Id. |
| polar_icsd | float | ICSD id number, if available. |
| nonpolar_icsd | float | ICSD id number, if available. |
| polar_spacegroup | float | Polar space group, integer between 1 and 230. |
| nonpolar_spacegroup | float | Nonpolar space group, integer between 1 and 230. |
| bilbao_polar_spacegroup | float | Polar space group from Bilbao Crystallographic Server, integer between 1 and 230. |
| bilbao_nonpolar_spacegroup | float | Nonpolar space group from Bilbao Crystallographic Server, integer between 1 and 230. |
| distortion | dict | Details pertaining to distortion between nonpolar and polar structure. |
| polar_band_gap | float | Materials Project computed band gap. |
| nonpolar_band_gap | float | Materials Project computed band gap. |
Table 5.
JSON keys, value data type, and value description for distortion dictionary of distortion.json entries.
| Key | Type | Description |
|---|---|---|
| high_symm | dict of pymatgen.Structure | Nonpolar structure in high-symmetry setting. |
| high_low_setting | dict of pymatgen.Structure | Nonpolar structure in low-symmetry setting. |
| low_symm | dict of pymatgen.Structure | Polar structure in low-symmetry setting. |
| high_pre | unicode | Structure information as directly output by Bilbao Crystallographic Server website. |
| high_low_pre | unicode | Structure information as directly output by Bilbao Crystallographic Server website. |
| low_pre | unicode | Structure information as directly output by Bilbao Crystallographic Server website. |
| distortion | list | Table of low-symmetry setting of Wyckoff position, the string “(x, y, z)”, species, distortion in x, y, and z, and the magnitude of distortion. |
| pairings | list | Wyckoff splitting pairing between high symmetry and low symmetry structures. |
| dmax | unicode | Maximum distortion distance between nonpolar and polar structure. |
| s | unicode | Degree of lattice distortion (S) is the spontaneous strain (sum of the squared eigenvalues of the strain tensor divided by 3). |
| dav | unicode | Maximum distortion distance between nonpolar and polar structure. |
| delta | unicode | The measure of compatibility (Δ) (Bergerhoff et al. 1998). |
Reported properties
For each candidate we provide an initial nonpolar-polar pair of structures, including the nonpolar structure in both the nonpolar, high-symmetry setting and polar, low-symmetry setting. We also provide the displacements of each atom and other metrics provided by BCS Structure Relations.
For each successful calculation, we provide the structure used for calculation, the ionic and electronic polarization computed by VASP, the ionic polarization computed via the method of point charges, the total energy and energy per atom of the structure, and other commonly computed quantities such as total magnetization, magnetization per atom, forces, and stresses. We also give details as to which calculations (out of the 22 computed) for a given candidate pair were completed.
For each set of completed calculations we also provide, the recovered spontaneous polarization using the workflow described in the Methods section, as well as spline data characterizing the smoothness of the polarization and energy trends across the nonpolar-polar distortion.
Graphical representation of results
In the top row of Fig. 6, we partition the high-quality candidates found in the Materials Project into known and newly-proposed ferroelectrics and further partition those ferroelectrics into subclasses. In Fig. 6 we see that known and new ferroelectric candidates are well mixed along the metrics of nonpolar-polar structure energy difference, distortion maximum between nonpolar and polar structures, PBE band gap of polar structure, and energy above hull (a measure of the thermodynamic driving force for decomposition79).
Fig. 6.
Validated ferroelectric candidates from our automated search in the Materials Project. Computed spontaneous polarization plotted against nonpolar-polar energy difference, maximum atomic distortion, PBE + U band gap, and energy above hull of the polar structure. All results are generated for spin-polarized DFT-PBE + U calculations. Note, that for spin-polarized systems, we only initialized the calculations with a ferromagnetic ordering. The energy above hull is extracted from the Materials Project. The legend labels different subcategories considered in this work and described in the text.
In the middle row of Fig. 6, the candidates with large polarizations denoted with red triangles belong to the perovskite family. We recover many known perovskite ferroelectrics, such as: LiNbO3, AlBiO3, BiInO3, KNbO3, BaO3Ti, CdO3Ti and O3PbTi. In addition, we recover well-known double perovskite ferroelectrics, such as Bi2Nb2O9Pb and Bi2O9SrTa2. We also recover well-known antiferroelectrics possessing ferroelectric metastable phases, such as NaNbO3, HfO3Pb and O3PbZr. We again note that we do not use conventional notation for these systems but rather use alphabetical order of elements to provide a consistent ordering with our workflow output.
Other classes in the middle row of Fig. 6 are the organic (NH4)2SO4 family in blue and structures already proposed by theory to be ferroelectric in purple. These data show that there are many known and proposed ferroelectrics in the literature with polarizations of 10 μC/cm2 or less.
In the bottom row of Fig. 6, we categorize new ferroelectric candidates into different trending compositions or structure types. There are several candidates containing fluorides, carbon-oxygen compounds, and hydroxyl groups. We highlight these candidates because they are very different in composition from oxide ferroelectrics most common in the literature. We also point out some hypothetical non-magnetic hexagonal manganite-like structures found in the Materials Project database that have polarizations of approximately 10 μC/cm2 and half-quantum nonpolar polarizations.
In Fig. 7, we show trends in the number of pairs with continuous deformation with given nonpolar-polar point group transitions. There are 32 crystallographic point groups; nonpolar and polar point groups are shown in blue and red, respectively. The thickness and color of the line connecting nonpolar and polar point groups indicate the number of structures in the dataset with a continuous deformation between those point groups. We find that point group transitions that correspond to orthorhombic structures such as mmm → mm2, monoclinic structures such as 2/m → 2 or 2/m → m, and hexagonal 6/mmm → 6mm are the most prevalent.
Fig. 7.
Schematic of the number of point group transitions between the 32 crystallographic point groups. The thickness and color of the line connecting nonpolar and polar point groups indicates the number of structures in the dataset with a continuous deformation between those point groups. The legend includes a schematic for nonpolar-polar phase transitions and describes the significance of line weights and colors connecting nonpolar and polar point groups.
In Fig. 8, we show the computed polarization of the ferroelectric candidates plotted with respect to their polar point group, similar to the plot of piezoelectric tensor magnitudes in ref. 4. The majority of candidates have polarization less than 5 μC/cm2, shown on the right. The candidates in point group 4mm with large polarizations are perovskites with a reference structure in point group . The degree of shading of a radial cell is proportional to the number of candidates in that region of the plot. For example, there are many candidates with polar point groups 2 and mm2 that have polarizations within 25 μC/cm2.
Fig. 8.
Diagrams of polarization magnitude vs. point group. The left diagram shows the full range of polarizations from 0 to 140 μC/cm2 and the right diagram zooms in on polarizations in the range 0 to 25 μC/cm2. Point groups are grouped according to symmetry. The darkness of a radial cell is proportional to the number of candidates in that region of the plot.
Technical Validation
Verification of computational methodology
Several checks are needed to ensure our automated calculations have completed satisfactorily and the information automatically extracted from them is reliable. We describe these tests below.
Testing smoothness of energy and polarization trends with distortion
We flag any ferroelectric candidates whose calculations cannot be used to reliably assess the quality of the candidate. For example, if the trend in total energy is not continuous, we cannot be confident that we can extract a meaningful polarization trend. Similarly, if the same branch polarization is not continuous, we cannot be confident that an accurate spontaneous polarization has been determined.
To assess the smoothness of trends in polarization and energy across a distortion, we use UnivariateSplines from scipy.interpolate80. We use cubic splines for fitting polarizations and quartic splines for fitting total energies. We use the default smoothness parameter of 1.0. These splines are generated using the Polarization class in pymatgen.analysis.ferroelectricity.polarization.
We find that 31 out of the 55 materials that do not have smooth interpolations contain atoms with nonzero magnetic moments, mostly containing 3d elements (V, Cr, Mn, Fe, Co, Ni) and one containing the 5d element W. We found 26 materials to have several discontinuities in total energy (even when these calculations resulted in smooth polarizations). These materials were transition metal oxides, fluorides, carbonates, orthosilicates, and phosphates with alkali or alkaline earth metals (Li, Na, and Ba for these specific examples), many being Li-ion battery cathode candidates. The transition metals in these materials (V, Cr, Mn, Fe, Co, Ni) can take multiple oxidation states. Because these discontinuities in energy were coincident with discontinuities in the total magnetization, we believe these jumps were caused by the transition metal species changing oxidation state through the distortion, suggesting the need to asses their ground state magnetic ordering more carefully.
Metallic endpoints and metallic interpolations
Polarization calculations require a nonzero band gap along the distortion path. Therefore, workflows that have either polar or nonpolar structures that are calculated to be metallic are halted. In the workflow_data.json, these workflows are designated by a workflow_status of “DEFUSED”. Of the 413 pairs considered, 80 possess metallic endpoints and therefore interpolations were not performed. Occasionally, interpolated structures between two nonmetallic structure endpoints are metallic and there were 59 that had metallic interpolation structures. If any structure along the path from nonpolar to polar structure is metallic, the quality of automated analysis cannot be guaranteed. We include these candidates in our dataset, but they are noted as having a polarization_len (see Tables 2 and 3) of less than 10 or do not have a polarization_change_norm (in cases where some of the interpolated polarizations are None). If a candidate has a polarization_len equal to 10 and have a polarization_change_norm, all interpolated polarization calculations completed successfully.
We also note that the method used to determine whether a material is insulating differs for pymatgen and VASP. In our workflow, pymatgen determines the band gap by comparing the energies of the band edges. When VASP determines whether to proceed with calculating the polarization, it checks whether the material is insulating by checking the occupations of the band edges. Since the occupations can be sensitive to the choice of smearing and k-grid density, there are instances where using our default settings in the workflow leads to partial occupancies, while the band edge energies suggest the material has a finite gap; therefore VASP will not proceed with calculating the polarization whereas our workflow deems the material to be insulating. This tends to occur for materials containing 3d elements which, as discussed earlier in the context of magnetism, would require more careful calculations to reliably capture their properties, and therefore not necessarily expected to successfully complete the workflow.
Comparison of materials project to relaxed structures
Two structural relaxation calculations are already performed on all structures in the Materials Project. We perform additional relaxations of the unit cell and atomic positions to ensure total energy convergence. We found only less than 5% (10%) of our relaxed structures have lattice parameter differences of more than 3% (1%) from the original Materials Project structures. Because we perform relaxations of nonpolar structures transformed to the low-symmetry polar setting, we compare the relaxed nonpolar structure to the low-symmetry transformed structure output by BCS of the nonpolar structure from Materials Project.
Identifying high-quality candidates
In any high-throughput search, there are calculations that complete without errors and some that require further scrutiny to interpret its results. We deem as high-quality candidates those calculations where the polarization and total energy trends are smooth and continuous; we define this criteria in the following way: the maximum difference between the data and spline fitted to the same branch polarization must be less than 10−1 μC/cm2, and the maximum difference between the data and the spline fitted to the energy trend must be less than 10−2 eV.
As shown in Table 1, out of the 255 candidates, 200 pass through our stringent verification criteria and ensures the polarization and energy trends across the ferroelectric distortion are smooth and continuous. The remaining candidates are still valid candidates; we recommend checking the polarization and energy trends by hand as the algorithms used for analysis may not have reliably recovered the spontaneous polarization in these cases, as in Fig. 5. These high-quality candidates are further described in the section Determining Known and New Ferroelectrics. There are candidates included in this list with polarization values of zero, as computed within the accuracy of our calculations; we include these since they pass the above criteria and could be tuned to host nonzero polarizations such as by chemical substitution. As well, the polarization values may be very small but this is also true of some of the known ferroelectric candidates computed with our workflow, and so for the sake of completeness we also list these candidates. We also call the reader’s attention to the materials with magnetic elements. Since all materials are initialized with ferromagnetic ordering, we do not expect to reliably capture materials with other magnetic orderings (e.g. antiferromagnets); as such, materials with nonzero magnetic moments may not necessarily have been calculated using their true magnetic ground state and those results should be interpreted with caution.
Comparison to DFT calculated polarizations from literature
We verify that our workflow reproduces the first-principles calculated polarizations for a variety of ferroelectrics in the literature. DFT calculated values for the ferroelectric polarization depends heavily on the structures and functional used in the calculation, and for magnetic systems, it will also be sensitive to magnetic ordering. For example, while in our work the endpoint structures are fully relaxed, other works constrain the relaxed polar unit cell to have the same volume as the experimental structure81; these calculated polarizations will be systematically smaller than ours due to PBE optimized structures having larger lattice parameters than experimental values.
We compare to literature where a fully optimized (unit cell, volume, and atomic positions) relaxation procedure is used. For clarity of comparison, we use the chemical formula used by these references rather than the alphabetical_formula that is convention for the rest of this work.
The ferroelectric first-principles literature is largely dominated by studies of perovskites. We compare to calculations for the perovskites BaTiO3, PbTiO3, LiNbO3, BiAlO3, CdTiO3, BiFeO3, and we include in our comparison the double perovskite SrBi2Ta2O9. These comparisons are summarized in Table 6.
Table 6.
Comparison of this work to other first-principles studies of ferroelectrics, primarily perovskites.
| Formula and Space Group | a (Å) | b (Å) | c (Å) | Ps (μC/cm2) | |
|---|---|---|---|---|---|
| BaTiO3 (99) | ref. 87 | 4.005 | — | 4.210 | 43.5 |
| ref. 88 | 4.000 | — | 4.216 | 47.0 | |
| This work (1) | 4.000 | — | 4.224 | 46.7 | |
| This work (2) | 4.001 | — | 4.215 | 45.9 | |
| PbTiO3 (99) | ref. 88 | 3.844 | — | 4.767 | 125.5 |
| This work (3) | 3.871 | — | 4.594 | 116.8 | |
| LiNbO3 (161) | ref. 88 | 5.203 | — | 14.110 | 84.7 |
| This work (4) | 5.216 | — | 14.116 | 84.5 | |
| SrBi2Ta2O9 (36) | ref. 89 | 5.550 | 5.550 | 25.100 | 34.1 |
| This work (5) | 5.602 | 5.614 | 25.520 | 36.9 | |
| CdTiO3 (26) | ref. 90† | 5.250 | 5.387 | 7.570 | 21.0 |
| This work (6) | 5.402 | 5.525 | 7.694 | 37.2 | |
| CdTiO3 (33) | ref. 90† | 5.239 | 5.378 | 7.619 | 29.0 |
| This work (7) | 5.360 | 5.494 | 7.812 | 34.8 | |
| BiAlO3 (161) | ref. 91† | 3.840 (cubic) | — | — | 75.6 |
| This work (8) | 3.844 (cubic) | — | — | 80.3 | |
| KH2PO4 (43) | ref. 88 | 10.800 | 10.710 | 7.110 | 5.5 |
| This work (9) | 10.730 | 10.652 | 7.105 | 5.2 |
For this table, we use the chemical formula conventions used in the works we compare to. We compare to calculations using PBE + U unless otherwise specified. The polar space group is given in parentheses under the chemical formula. The symbol †Indicates the reference being compared to used the Local Density Approximation (LDA) functional in their calculations. LDA polarization values tend to be smaller than polarization values calculated with PBE (which we use in this work) due to smaller predicted lattice parameters by LDA than PBE. The search ids for entries in the table are: (1) 69 (2) 70 (3) 389 (4) 331 (5) 80 (6) 146 (7) 147 (8) 23 (9) 257.
We note again here that because our workflow assumes ferromagnetic ordering, it will fail for many multiferroics since they tend to have other magnetic orderings, such as antiferromagnetic or noncollinear orderings. For example, two important multiferroics are BiFeO3 and YMnO3; the former is only captured to some extent by our workflow and the latter is not reported at all by our database. The standard polar phase of BiFeO3 features G-type antiferromagnetic ordering, and that for YMnO3 features A-type antiferromagnetic ordering. As the present version of our workflow initializes all calculations with ferromagnetic ground states for all magnetic systems, we do not expect to capture most multiferroics using the workflow as implemented for this search with the Materials Project database. Additionally, we note that the standard nonpolar reference structure for BiFeO3 is in space group 167 (Rc); however, the Rc structure of BiFeO3 is not in the Materials Project database. That the R3m and Pmm structures of BiFeO3 calculated in this workflow, with ferromagnetic ordering and the default U value, are found to be insulating is fortuitous and allows it to be reported as a high quality candidate. However, the BiFeO3 experimentally verified ground state structure, 161 (R3c), did not complete our workflow due to metallic interpolations. Conversely, YMnO3 is DEFUSED and does not proceed to the interpolations because its nonpolar structure is found to be metallic in our calculations. Extending the workflows to account for antiferromagnetic and other spin-ordered ground states, as well as to relax the constraint that a nonpolar reference structure exist in the database, will enable casting a wider net for known and new multiferroics, and will be the subject of future work.
Determining known and new ferroelectrics
We distinguish known from new ferroelectrics in our workflow depending on whether or not a material has been reported in the literature as ferroelectric. Thus, we perform a literature review by hand for every considered candidate, and leave automating such literature searches to future work. We find that out of 200 high quality candidates, 74 are known or previously proposed ferroelectrics and 126 are, to our knowledge, new ferroelectric candidates.
In Fig. 6, we plot calculated spontaneous polarization versus nonpolar-polar total energy difference, maximum distortion distance, PBE band gap, and energy difference between the polar structure and convex hull reported in the Materials Project for known, proposed and new ferroelectric candidates. We also provide tables of the known and new candidates grouped by chemical formula and polar space group in Online-only Tables 1 and 2, respectively. Details connecting these candidate to specific workflow calculations are in Online-only Table 3.
Online-only Table 1.
Known and proposed high quality ferroelectric candidates and their space groups, polarizations and band gaps.
| Formula | Polar Space Group | Nonpolar Space Group | Polarization (μ C/cm^2) | Band Gap (eV) | Search ID | Subcategory |
|---|---|---|---|---|---|---|
| Ag3IS | 4 | 155 | 0.7 | 0.3 | 11 | Proposed by theory114 |
| 221 | 0.7 | 0.3 | 12 | |||
| 146 | 155 | 11.7 | 0.5 | 13 | ||
| Al2BaO4 | 173 | 182 | 0.3 | 4.1 | 18 | Proposed by theory115 |
| 173 | 182 | 0.3 | 4.1 | 19 | ||
| Al2CaH4O10Si2 | 33 | 63 | 4.2 | 5.1 | 20 | |
| Al3F19Pb5 | 108 | 140 | 13.9 | 5.2 | 21 | |
| AlBiO3 | 161 | 221 | 80.3 | 3.1 | 23 | Perovskite |
| 185 | 194 | 4.8 | 0.8 | 24 | ||
| AlF7MgNa2 | 46 | 74 | 1.1 | 6.7 | 30 | |
| B2K3Nb3O12 | 26 | 189 | 0.1 | 2.4 | 46 | |
| B3CaH5O8 | 4 | 14 | 0.6 | 5.6 | 48 | |
| B7ClMg3O13 | 29 | 219 | 0.3 | 5.7 | 51 | Boracite |
| BaNiO3 | 186 | 194 | 3.7 | 1.5 | 66 | |
| BaO3Ti | 38 | 221 | 49.9 | 2.4 | 68 | Perovskite |
| 99 | 221 | 46.7 | 1.8 | 69 | ||
| 45.9 | 1.8 | 70 | ||||
| 160 | 221 | 49.9 | 2.5 | 71 | ||
| BaO5Ti2 | 5 | 12 | 15.3 | 2.2 | 72 | |
| BeF4H8N2 | 33 | 62 | 0.6 | 6.6 | 75 | (NH4)2SO4 family |
| 0.6 | 6.6 | 76 | ||||
| Bi2Nb2O9Pb | 36 | 139 | 38.1 | 2.3 | 79 | Perovskite |
| Bi2O9SrTa2 | 36 | 139 | 36.9 | 2.5 | 80 | Perovskite |
| 41 | 139 | 38.3 | 2.3 | 81 | ||
| Bi4O12Ti3 | 7 | 139 | 58.1 | 2.4 | 82 | |
| 41 | 139 | 17 | 2.4 | 83 | ||
| 11.5 | 1.6 | 84 | ||||
| BiCl8F4H3K6 | 186 | 194 | 0.1 | 4.2 | 85 | |
| BiFeO3† | 160 | 221 | 124.5 | 1.8 | 89 | Perovskite |
| BiInO3 | 33 | 62 | 64.7 | 2.8 | 91 | Perovskite |
| 221 | 64.7 | 2.8 | 92 | |||
| BiO3Sc | 9 | 15 | 5.7 | 2.7 | 94 | Hexagonal manganite-like |
| 9 | 221 | 5.7 | 2.7 | 95 | ||
| Br4K2Zn | 4 | 11 | 1.9 | 3.7 | 100 | (NH4)2SO4 family |
| C3ClH10NO4 | 4 | 11 | 0.3 | 5.6 | 108 | Proposed by theory116 |
| CdO3Ti | 26 | 62 | 37.2 | 2.5 | 146 | Perovskite |
| 33 | 62 | 34.8 | 2.4 | 147 | ||
| Cl3CsPb | 38 | 221 | 2.3 | 2.6 | 158 | Perovskite |
| Cl4K2Zn | 33 | 62 | 2.2 | 4.4 | 164 | (NH4)2SO4 family |
| 0.5 | 4.5 | 165 | ||||
| Cl4Rb2Zn | 33 | 62 | 0.5 | 4.5 | 166 | (NH4)2SO4 family |
| 0.3 | 4.4 | 167 | ||||
| ClH | 44 | 139 | 57.4 | 5.2 | 171 | |
| CsF3Pb | 161 | 221 | 0.7 | 3.4 | 195 | Perovskite; Proposed by Theory117 |
| CsO4PZn | 33 | 62 | 1 | 4 | 196 | |
| F4MgSr | 4 | 11 | 10.7 | 6.7 | 220 | Proposed by theory118 |
| H2KO4P | 9 | 14 | 0.5 | 5.2 | 256 | |
| 43 | 122 | 5.2 | 5.4 | 257 | ||
| H2O | 4 | 19 | 13.5 | 5.5 | 264 | |
| 13.5 | 5.5 | 265 | ||||
| H2O4PRb | 43 | 122 | 5.4 | 5.2 | 271 | Hydroxyl |
| H8N2O4S | 33 | 62 | 0 | 5.1 | 292 | (NH4)2SO4 family |
| HfO2 | 29 | 225 | 53.4 | 4.4 | 301 | |
| HfO3Pb | 32 | 55 | 19.8 | 2.8 | 302 | Perovskite |
| HfO3Sr | 99 | 221 | 15.1 | 3.8 | 303 | Perovskite |
| K2O4Se | 33 | 62 | 0.7 | 3.7 | 309 | (NH4)2SO4 family |
| KNbO3 | 38 | 221 | 51.3 | 2.1 | 313 | Perovskite |
| 99 | 221 | 48.7 | 1.6 | 314 | ||
| 160 | 221 | 50.7 | 2.3 | 315 | ||
| LiNbO3 | 161 | 167 | 84.5 | 3.4 | 331 | Perovskite |
| MgO3Si | 33 | 60 | 1.1 | 4.7 | 346 | Perovskite |
| N6Pb | 33 | 62 | 0.4 | 2.3 | 358 | |
| NaNbO3 | 26 | 127 | 53.9 | 2.4 | 360 | Perovskite |
| 29 | 57 | 31.5 | 2.4 | 361 | ||
| 63 | 31.5 | 2.4 | 362 | |||
| NbO4Sb | 33 | 52 | 18.1 | 2.4 | 365 | |
| O2Zr | 29 | 225 | 51.2 | 3.7 | 388 | |
| O3PbTi | 99 | 221 | 116.8 | 2 | 389 | Perovskite |
| O3PbZr | 32 | 55 | 23.5 | 2.8 | 390 | Perovskite |
| O3W | 185 | 191 | 21 | 1.5 | 399 | |
| 21 | 1.5 | 400 | ||||
| 193 | 21 | 1.5 | 401 | |||
| O5PTiTl | 33 | 52 | 22.1 | 2.7 | 404 | |
| O7Sr2Ta2 | 36 | 63 | 3 | 2.9 | 407 | Perovskite |
| 124.5 |
Known candidates are in light gray. All candidates are non-magnetic unless indicated with a † which indicates the candidates are calculated to be ferromagnetic. Only three of all high-quality (know, proposed, and new) candidates contain atoms with nonzero magnetic moments: BiFeO3 (Search ID 89), CrP3O9 (Search ID 191), LiO4PV (Search ID 342). Please see text for discussion of workflow performance on magnetic properties. The search ID being a simplified unique identifier, defined for the purposes of our work, for pairs of structures used in our workflow search. Spaces in table implies the same space group number as the previous row.
Online-only Table 2.
New high quality ferroelectric candidates and their space groups, polarizations and band gaps.
| Formula | Polar Space Group | Nonpolar Space Group | Polarization (μ C/cm^2) | Band Gap (eV) | Search ID | Subcategory |
|---|---|---|---|---|---|---|
| Ag10Br3Te4 | 36 | 63 | 3.9 | 0.9 | 1 | |
| Ag2O4W | 34 | 58 | 1 | 1.8 | 4 | |
| Ag2S | 4 | 11 | 21.1 | 0.4 | 5 | |
| 64 | 17.6 | 0.4 | 7 | |||
| 36 | 63 | 0.4 | 1.4 | 9 | ||
| AgAl11O17 | 40 | 63 | 2.4 | 3.1 | 15 | |
| AgC2O2 | 5 | 15 | 0 | 1 | 17 | |
| AlCH2NaO5 | 46 | 74 | 0.8 | 5 | 25 | |
| AlCl4Hg2Sb | 33 | 60 | 0.5 | 0.9 | 26 | |
| AlH3O3 | 1 | 2 | 0.1 | 5 | 32 | Hydroxyl |
| 7 | 61 | 8.1 | 5 | 33 | ||
| AlN | 186 | 194 | 133 | 4.1 | 38 | |
| AuCl4K | 7 | 14 | 0.3 | 1.4 | 43 | |
| B13C2Li | 44 | 74 | 0.8 | 2.6 | 45 | |
| B2O6Zn3 | 9 | 15 | 0.1 | 2.7 | 47 | |
| Ba2F7Y | 4 | 14 | 0.7 | 6.5 | 57 | |
| BaC2CaO6 | 4 | 11 | 0 | 4.8 | 59 | |
| BaCO3 | 4 | 11 | 1 | 4.5 | 60 | Carbon-oxygen compound |
| BaCl5La | 4 | 62 | 26.1 | 4 | 61 | |
| BiCuO8W2 | 1 | 2 | 0.8 | 1.3 | 86 | |
| BiO3Y | 185 | 194 | 9.7 | 2.1 | 96 | Hexagonal manganite-like |
| Br3CsGe | 8 | 221 | 19.3 | 1.7 | 97 | |
| C2HO2 | 6 | 11 | 3.4 | 2.8 | 106 | Carbon-oxygen compound |
| C2HgN2S2 | 5 | 12 | 0.9 | 2.1 | 107 | |
| C6Cu2H10N4S3 | 4 | 14 | 0 | 2.8 | 109 | |
| CCs4O4 | 146 | 215 | 1.7 | 1.6 | 110 | Carbon-oxygen compound |
| CH4N2S | 26 | 62 | 4.8 | 3.3 | 111 | |
| CHO2Tl | 33 | 52 | 0.8 | 3.5 | 112 | Carbon-oxygen compound |
| CK4O4 | 5 | 121 | 16.7 | 2 | 113 | Carbon-oxygen compound |
| 16.6 | 2 | 114 | ||||
| 8 | 121 | 10.2 | 2.2 | 115 | ||
| 146 | 215 | 2.6 | 2.3 | 116 | ||
| 160 | 215 | 14.6 | 1.9 | 117 | ||
| CLi4O4 | 5 | 121 | 49 | 5 | 118 | Carbon-oxygen compound |
| 49 | 5 | 119 | ||||
| 0.1 | 4.8 | 120 | ||||
| 160 | 215 | 16.6 | 4.2 | 121 | ||
| CN2Pb | 33 | 62 | 10.5 | 1.9 | 122 | |
| CNa4O4 | 5 | 121 | 39.2 | 2.2 | 123 | Carbon-oxygen compound |
| 39.2 | 2.2 | 124 | ||||
| 8 | 215 | 12.6 | 1.7 | 125 | ||
| 146 | 215 | 3.6 | 1.9 | 126 | ||
| 56.2 | 2.2 | 127 | ||||
| CO4Rb4 | 5 | 23 | 14.6 | 1.4 | 128 | Carbon-oxygen compound |
| 121 | 14.6 | 1.4 | 129 | |||
| 14.6 | 1.4 | 130 | ||||
| 146 | 215 | 0.6 | 1.7 | 131 | ||
| 160 | 215 | 42.8 | 0.4 | 132 | ||
| Ca5ClO12P3 | 173 | 176 | 2.1 | 5.4 | 138 | |
| CaF2 | 26 | 123 | 16.5 | 6.3 | 139 | Fluoride |
| Cd2ClP3 | 9 | 15 | 0.8 | 1.3 | 144 | |
| CdCl2 | 5 | 12 | 48.4 | 3.1 | 145 | |
| Cl4GaHg2Sb | 33 | 60 | 0.5 | 0.8 | 162 | |
| ClH3O5 | 33 | 62 | 5.2 | 5.4 | 172 | |
| ClH4NO4 | 33 | 62 | 2.2 | 5.3 | 173 | |
| ClIn | 36 | 63 | 3.8 | 1.4 | 174 | |
| CrO3 | 33 | 62 | 0.4 | 1.6 | 188 | |
| CrO9P3† | 9 | 15 | 0.3 | 3.2 | 191 | |
| Cs2HgI4 | 4 | 11 | 0.3 | 2.1 | 192 | |
| Cs2N2Tb6Te7 | 8 | 12 | 0.2 | 0.8 | 193 | |
| Cs2O3Pb | 36 | 63 | 7.2 | 1.4 | 194 | |
| CuI | 7 | 216 | 0 | 1.2 | 204 | |
| Er2F7K | 33 | 62 | 1.5 | 6.9 | 210 | Fluoride |
| F2HRb | 46 | 140 | 1.6 | 6.7 | 212 | Fluoride |
| F2Pb | 41 | 225 | 5 | 4.4 | 213 | Fluoride |
| F3Nd | 185 | 193 | 17.6 | 7.7 | 214 | Fluoride |
| F3PbRb | 9 | 221 | 4 | 3.8 | 215 | Perovskite |
| F5V | 9 | 15 | 1 | 2.8 | 223 | Fluoride |
| 29.7 | 3.3 | 224 | ||||
| F6LiV | 33 | 225 | 1.3 | 3.2 | 225 | Fluoride |
| FTl | 39 | 225 | 6.4 | 3.1 | 229 | Fluoride |
| GaLuO3 | 185 | 194 | 8 | 2.9 | 249 | Hexagonal manganite-like |
| GaN5O14 | 5 | 82 | 0 | 1.3 | 252 | |
| GaO3Sc | 185 | 194 | 10 | 3.2 | 253 | Hexagonal manganite-like |
| H2Mg | 29 | 60 | 30.9 | 2.4 | 258 | |
| H2MoO4 | 1 | 2 | 0.2 | 3.2 | 260 | |
| 39.2 | 2.5 | 261 | ||||
| 16.3 | 2.1 | 262 | ||||
| H2O10U3 | 1 | 2 | 23 | 1.8 | 266 | |
| 23 | 1.8 | 267 | ||||
| H2O2Sr | 26 | 62 | 1.2 | 4 | 268 | Hydroxyl |
| 1.2 | 4 | 269 | ||||
| H2O4S | 5 | 15 | 20.4 | 6.1 | 272 | Hydroxyl |
| 9 | 15 | 51 | 5.8 | 273 | ||
| H2O4Sn3 | 9 | 114 | 1.6 | 2.5 | 275 | Hydroxyl |
| H2O4U | 36 | 64 | 2.9 | 1.9 | 277 | Hydroxyl |
| 2.9 | 1.9 | 278 | ||||
| H3LaO3 | 173 | 176 | 17.9 | 4 | 279 | Hydroxyl |
| H3O3Pr | 6 | 11 | 0.1 | 3.8 | 280 | Hydroxyl |
| 176 | 0.1 | 3.8 | 281 | |||
| H3O3Y | 173 | 176 | 7.7 | 3.9 | 282 | Hydroxyl |
| H3O4P | 7 | 14 | 4.1 | 5.7 | 283 | |
| 4.1 | 5.7 | 284 | ||||
| H4O5S | 7 | 14 | 1 | 5.7 | 286 | |
| H5IO6 | 7 | 14 | 0.3 | 2.3 | 289 | |
| HInO2 | 31 | 58 | 13.2 | 1.8 | 293 | Hydroxyl |
| HK2NO6S2 | 9 | 15 | 3.2 | 5.3 | 294 | |
| HNaO | 4 | 11 | 10.7 | 3 | 295 | Hydroxyl |
| 63 | 10.7 | 3 | 296 | |||
| HORb | 4 | 11 | 10.5 | 3.4 | 300 | Hydroxyl |
| ILi6PS5 | 9 | 216 | 2.6 | 2.3 | 304 | |
| K2O7Zn6 | 102 | 136 | 2.5 | 0.8 | 310 | |
| K3S4Sb | 36 | 217 | 1 | 2.2 | 311 | |
| KLaS4Si | 4 | 11 | 7.4 | 2.8 | 312 | |
| LiO12P3Zr2 | 5 | 167 | 8 | 4.2 | 341 | |
| LiO4PV† | 33 | 60 | 0.1 | 2.7 | 342 | |
| MgN2O6 | 29 | 205 | 0.7 | 3.5 | 345 | |
| MoO3 | 7 | 62 | 4.7 | 1.9 | 353 | |
| N2O6Zn | 29 | 205 | 1.1 | 3.3 | 356 | |
| N3Na | 5 | 12 | 51.8 | 4.1 | 357 | |
| NbO5P | 33 | 62 | 4 | 2.3 | 366 | |
| O23Rb6Si10 | 38 | 189 | 0.1 | 4.3 | 370 | |
| 0.5 | 4.2 | 371 | ||||
| O2Si | 4 | 20 | 0 | 5.4 | 373 | |
| 182 | 0 | 5.4 | 374 | |||
| 0.4 | 5.6 | 375 | ||||
| 8 | 12 | 0 | 5.5 | 378 | ||
| 9 | 194 | 0.1 | 5.5 | 379 | ||
| 36 | 63 | 0.2 | 5.7 | 383 | ||
| 0 | 5.6 | 384 | ||||
| 64 | 0.2 | 5.4 | 385 | |||
| 44 | 119 | 0 | 5.7 | 386 | ||
| O3SbY | 185 | 194 | 7.5 | 1.5 | 391 | Hexagonal manganite-like |
| O3ScY | 185 | 194 | 6.6 | 3.1 | 392 | Hexagonal manganite-like |
| O3Te | 185 | 194 | 0 | 0.5 | 394 | |
| OPb | 29 | 57 | 54.3 | 2.2 | 409 |
All candidates are non-magnetic unless indicated with a † which indicates the candidates are calculated to be ferromagnetic. Only three of candidates contain atoms with nonzero magnetic moments: BiFeO3 (Search ID 89), CrP3O9 (Search ID 191), LiO4PV (Search ID 342). Please see text for discussion of workflow performance on magnetic properties. The search ID being a simplified unique identifier, defined for the purposes of our work, for pairs of structures used in our workflow search. Spaces in table implies the same space group number as the previous row.
As seen in Fig. 6, known and newly-proposed ferroelectrics display similar dispersion and overlap in the range considered. The middle row of Fig. 6 demonstrates the variety of known ferroelectric candidates that we are able to recover, from perovskites to candidates in the organic (NH4)2 SO4 family to candidates proposed by theory. The bottom row of Fig. 6 shows categories of new ferroelectric candidates we find in the Materials Project, some from previously known ferroelectric classes such as hexagonal manganite-like structures and less-studied categories such as fluorides, carbon-oxygen compounds, and crystals containing hydroxyl groups.
Comparison to hand-curated list of ferroelectrics in the Pauling Files database
The Pauling File is a materials database accessible through SpringerMaterials18. In this database, there are materials tagged as ferroelectric and antiferroelectric. We use these tagged entries to validate whether the workflow is able to successfully identify diverse ferroelectrics by examining which tagged (anti)ferroelectrics complete the workflow. In the Pauling Files, there are 955 distinct compositions tagged as (anti)ferroelectric, 306 of which are pure (not doped) compositions. Out of 306 pure compositions, 95 of those compositions are included in the Materials Project as polar materials. This does not necessarily mean that the Materials Project database contains the same ferroelectric polar structure as referenced in the Pauling Files; rather, it simply means that there exists a polar structure in the Materials Project with the same composition as a tagged ferroelectric or antiferroelectric in the Pauling Files. 57 of these compositions have nonpolar-polar structure pairs in the Materials Project, 40 of which are found to have a continuously distortion by BCS Structure Relations. 32 of the 40 are successfully identified by the workflow as high-quality candidates, meaning the energy and polarization trends are smooth. Out of the 8 candidates that did not successfully make it through the workflow as high quality candidates, 4 of them (CrO3Y, Eu2GeSe4, Cl3CoTl, and MnO3Y) had metallic endpoints, 2 candidates (Cl3CrRb and Br3MnRb) had metallic interpolation structures, and 2 candidates (Cl4CoRb2 and B7ClCr3O13) did not have smooth energy trends due to fluctuating band gaps and magnetic moments in the interpolations. We note that most of these 8 candidates are non-d0 systems, and therefore expected to exhibit magnetic order. This suggests that the primary impact to the robustness of our workflow is the level of DFT used and the magnetic orderings considered; since PBE tends to underestimate band gaps, and since ferromagnetically-ordered systems tend to be overwhelmingly metallic, several of these candidates are experimentally insulating but are metallic in our workflow.
Comparison to experimental measurements in Landolt-Börnstein series
To validate that our workflow calculates polarizations that can be used to guide experimental efforts, we compare to tabulated experimentally measured polarizations of known ferroelectrics in Landolt-Börnstein - Group III Condensed Matter - Ferroelectrics and Related Substances19–23. This series classifies hundreds of ferroelectrics into a 72 class numbering scheme. We note that polarization values for ferroelectrics in the Landolt-Börnstein series volumes 36A, 36B and 36C may be superseded by more recent experimental measurements. Experimentally measured polarizations depend greatly on the quality of the sample and the method used. For many ferroelectrics, polarization measurements made across decades vary greatly depending on these factors. Any comparison between theory must be taken in this context.
Nonetheless, plots of polarizations values calculated by our workflow vs. experimental spontaneous polarizations reported in the Landolt-Börnstein series volumes 36A, 36B and 36C are shown in Fig. 9 and tabulated in Table 7. We only compare search candidates to Landolt-Börnstein entries that match in composition and polar space group. For example, NaNbO3 is LB Number 1A-1 and has a polarization of 12 μC/cm2 for the 161 space group structure. However, all the NaNbO3 found in our search are orthorhombic (space groups 26 and 29), so we do not make the comparison.
Fig. 9.

Log-log plot of experimental vs. calculated polarization for ferroelectric materials in the Landolt-Börnstein series with polarization value larger than 1 μC/cm2. 6 materials with polarization value equal to or smaller than 1 μC/cm2 are not shown in plot but are included in the Table 7. Colored regions show experimental values within ±25%, ±50%, and ±75% of calculated values.
Table 7.
Table of calculated versus experimentally measured polarizations as given in the Landolt-Börnstein - Group III: Condensed Matter - Ferroelectrics and Related Substances19–21.
| Search ID | Formula | Polarization (μC/cm2) | LB number | Exp. | Exp. Ref. |
|---|---|---|---|---|---|
| 51 | B7ClMg3O13 (29) | 0.3 | 18A-1 | 0.08 | 92 |
| 68 | BaO3Ti (38) | 49.9 | 1A-10 | Not available | 93 |
| 69, 70 | BaO3Ti (99) | 46.7, 45.9 | 1A-10 | 26 | 93 |
| 71 | BaO3Ti (160) | 49.9 | 1A-10 | Not available | 93 |
| 79 | Bi2Nb2O9Pb (36) | 38.1 | 9A-10 | Not available | 94 |
| 81 | Bi2O9SrTa2 (41) | 38.3 | 9A-12 | 5.8 | 95 |
| 80 | Bi2O9SrTa2 (36) | 36.9 | 9A-12 | 5.8 | 95 |
| 82 | Bi4O12Ti3 (7) | 58.1 | 9A-15 | 50.2 | 96 |
| 100 | Br4K2Zn (4) | 1.9 | 39A-16 | 3.0 | 97 |
| 111 | CH4N2S (26) | 4.8 | 50A-1 | 3.5 | 98 |
| 146 | CdO3Ti (26) | 37.2 | 1A-9 | Debated | 99 |
| 147 | CdO3Ti (33) | 34.8 | 1A-9 | Debated | 99 |
| 164, 165 | Cl4K2Zn (33) | 2.2, 0.5 | 39A-9 | 0.13 | 100 |
| 166 | Cl4Rb2Zn (33) | 0.5 | 39A-10 | 0.16 | 101 |
| 292 | H8N2O4S (33) | 0.0 | 39A-1 | 0.6 max at −51.5 °C, reversal by 0.05 approaching −260 °C | 102 |
| 302 | HfO3Pb (32) | 19.8 | 1A-16 | Antiferroelectric (62). | 103 |
| 309 | K2O4Se (33) | 0.7 | 39A-2 | 0.15 | 104 |
| 313 | KNbO3 (38) | 51.3 | 1A-2 | Not available | 105 |
| 314 | KNbO3 (99) | 48.7 | 1A-2 | 41.2 | 105 |
| 315 | KNbO3 (160) | 50.7 | 1A-2 | Not available | 105 |
| 331 | LiNbO3 (161) | 84.5 | 2A-1 | 71 | 106,107 |
| 365 | NbO4Sb (33) | 18.1 | 5A-2 | 19.7 | 108 |
| 389 | O3PbTi (99) | 116.8 | 1A-11 | 75 | 109,110 |
| 390 | O3PbZr (32) | 23.5 | 1A-15 | 16 on cooling. Antiferroelectric (55). | 111 |
| 404 | O5PTiTl (33) | 22.1 | 35A-13 | Not available | 112 |
| 407 | O7Sr2Ta2 (36) | 3.0 | 8A-6 | 1.9 | 113 |
“Not available” in the Experimental Reference column (Exp. Ref.) indicates a polarization value was not provided in these references. We make comparisons only between search candidates that have a polar space group compatible with the Landolt-Börnstein reference. The search ID being a simplified unique identifier, defined for the purposes of our work, for pairs of structures used in our workflow search.
For experimental polarizations greater than 10 μC/cm2, the majority of experimental polarizations are between 25% and −50% of those that we calculate, well within an order of magnitude. The exceptions are both polar structures of Bi2O9SrTa2 (space groups 36 and 41), which are calculated to have polarizations much greater than their experimental values. Multiple entries of a given formula indicate multiple calculations for different structure pairs in our dataset for the same compound. Compounds with polarizations of less than or equal to 1 μC/cm2 are not shown on the plot given the log-log scale. For polarizations less than 5 μC/cm2, we see our calculations capture the general trends of the experimental polarizations.
We find that the PBE functional we use for our DFT calculations overestimates polarizations. This is partially due to unit cells relaxed with PBE having larger than experimental volumes and thus larger distortions.
Usage Notes
In this work, we present 413 nonpolar-polar structure pairs in the Materials Project database that are compatible with a second-order phase transition as ferroelectric candidates and perform DFT calculations of total energy, band gap, and polarization for these structures pairs.
This dataset offers the first opportunity to compare a large number of known, previously proposed, and new ferroelectrics side by side with the same methodology. We believe by setting strict criteria for ferroelectricity and casting a wide-net using high-throughput searches, we will find candidates that challenge and advance our understanding of ferroelectric phenomena. As seen in our candidates, there may be ferroelectrics waiting to be discovered that defy our expectations. This dataset will be useful for creating new tools and criteria for analyzing diverse ferroelectrics.
The infrastructure provided by the Bilbao Crystallographic Server, FireWorks, pymatgen, and atomate is crucial to being able to perform these types of searches efficiently. Thus, we also provide our code and data for these searches with the hope they will provide access for others to perform and develop similar searches.
Our code for performing structural interpolations and polarization calculations has been incorporated into the pymatgen and atomate packages. We also provide the code that we use to create the interface that we used to view our candidates in aggregate.
The workflow we have presented can be extended to any crystal structure database, experimental and hypothetical. Several modifications can be made to this workflow to extend the scope of these searches. Notably, extending our workflow to treat different magnetic orderings will enable it to treat multiferroics. Additionally, the same DFT workflow can be used to screen any experimentally measured polar structure - even one without an existing nonpolar reference - by generating nonpolar reference structures with BCS Pseudosymmetry7. Our workflow can also be adapted to perform species substitutions and find symmetry relations between structure types, classes of structures that share space groups, Wyckoff positions, and other lattice similarities.
Acknowledgements
This work supported by the Materials Project funded by the U.S. Department of Energy, Office of Science, Office of Basic Energy Sciences, Materials Sciences and Engineering Division under Contract No. DE-AC02-05-CH11231: Materials Project program KC23MP. This research used resources of the National Energy Research Scientific Computing Center, a DOE Office of Science User Facility supported by the Office of Science of the U.S. Department of Energy under Contract No. DE-AC02-05CH11231. Additional calculations were performed on the High Performance Computing clusters at Lawrence Berkeley Lab. Work at the Molecular Foundry was supported by the Office of Science, Office of Basic Energy Sciences, of the U.S. Department of Energy, and Laboratory Directed Research and Development Program at the Lawrence Berkeley National Laboratory under Contract No. DE-AC02-05CH11231. T.E.S. acknowledges support from the National Science Foundation Graduate Research Fellowship under Grant No. DGE 1106400. S.E.R. acknowledges partial support from FONDECYT Iniciación en Investigación under grant No. 11180590. A.J. was funded by the U.S. Department of Energy, Office of Basic Energy Sciences, Early Career Research Program.
Online-only Tables
Author contributions
All authors contributed to the outline of the workflow. T.E.S. developed the code for the workflow including executing polarization calculations, post-processing calculations to recover the same branch polarization and assess the quality of candidates, and visualizing the results through the graphic web interface. T.E.S. and S.A.M. performed the density functional theory calculations and validated the dataset through comparison to the Pauling Files and Landolt-Börstein series. T.E.S. and S.E.R. performed the literature search to identify known ferroelectrics in the dataset. S.E.R. and A.J. contributed to verification of the workflow. S.E.R., A.J. and J.B.N. were involved in supervising and planning the work. All authors contributed to the writing of the manuscript.
Code availability
VASP version 5.3.5 used to perform DFT calculations is a proprietary code. The Bilbao Crystallographic Server (BCS) is freely available on-line at http://www.cryst.ehu.es. Fireworks, atomate, and pymatgen are python packages accessible on GitHub. Fireworks and atomate are released under a modified Berkeley Software Distribution (BSD) License. pymatgen is released under a Massachusetts Institute of Technology (MIT) License. Both MIT and BSD licenses are open-source and permit both commercial and non-commercial use. Our workflow code is included since atomate version 0.6.7 and our analysis code is available in pymatgen since v2019.2.4. We also use the following python packages in our analysis and Graphical Representation of Results: numpy, scipy, matplotlib, ipython, and jupyter80,82–86. These packages are freely available through the Python Package Index (https://pypi.org/).
Our code for recovering the same branch polarization from polarization calculations has been contributed to pymatgen under the pymatgen.analysis.ferroelectricity module. Our code for the DFT and polarization analysis workflows for performing polarization calculations has been contributed to atomate under the atomate.vasp.workflows.base.ferroelectric module. We also provide code for the interface that we used to view our candidates in aggregate. The web interface for the current work is hosted at http://blondegeek.github.io/ferroelectric_search_site/. The code for the interface can be found at http://github.com/blondegeek/ferroelectric_search_site.
Competing interests
The authors declare no competing interests.
Footnotes
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
References
- 1.Jain, A., Shin, Y. & Persson, K. A. Computational predictions of energy materials using density functional theory. Nature Reviews Materials1, 15004 (2016).
- 2.Yan Q, et al. Solar fuels photoanode materials discovery by integrating high-throughput theory and experiment. Proceedings of the National Academy of Sciences. 2017;114:3040–3043. doi: 10.1073/pnas.1619940114. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Chen R, Po HC, Neaton JB, Vishwanath A. Topological materials discovery using electron filling constraints. Nature Physics. 2017;14:55–61. doi: 10.1038/nphys4277. [DOI] [Google Scholar]
- 4.de Jong M, Chen W, Geerlings H, Asta M, Persson KA. A database to enable discovery and design of piezoelectric materials. Scientific Data. 2015;2:150053. doi: 10.1038/sdata.2015.53. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Abrahams SC. Structurally Based Prediction of Ferroelectricity in Inorganic Materials with Point Group 6mm. Acta Crystallographica Section B. 1988;B44:585–595. doi: 10.1107/S0108768188010110. [DOI] [Google Scholar]
- 6.Abrahams SC. Structurally based predictions of ferroelectricity in seven inorganic materials with space group Pba2 and two experimental confirmations. Acta Crystallographica Section B. 1989;45:228–232. doi: 10.1107/S0108768189001072. [DOI] [Google Scholar]
- 7.Capillas C, et al. A new computer tool at the Bilbao Crystallographic Server to detect and characterize pseudosymmetry. Zeitschrift für Kristallographie. 2011;226:186–196. doi: 10.1524/zkri.2011.1321. [DOI] [Google Scholar]
- 8.Igartua JM, Aroyo MI, Kroumova E, Perez-Mato JM. Search for Pnma materials with high-temperature structural phase transitions. Acta Crystallographica Section B Structural Science. 1999;55:177–185. doi: 10.1107/S0108768198013342. [DOI] [PubMed] [Google Scholar]
- 9.Kroumova E, Aroyo MI, Perez-Mato JM. Prediction of new displacive ferroelectrics through systematic pseudosymmetry search. Results for materials with Pba2 and Pmc21 symmetry. Acta Crystallographica Section B Structural Science. 2002;58:921–933. doi: 10.1107/S0108768102012120. [DOI] [PubMed] [Google Scholar]
- 10.Stokes HT, Sadate C, Hatch DM, Boyer LL, Mehl MJ. Analysis of the ferroelectric phase transition in BaAl2O4 by group theoretical methods and first-principles calculations. Physical Review B. 2002;65:064105. doi: 10.1103/PhysRevB.65.064105. [DOI] [Google Scholar]
- 11.Perez-Mato JM, Withers RL, Larsson AK, Orobengoa D, Liu Y. Distortion modes and related ferroic properties of the stuffed tridymite-type compounds SrAl2O4 and BaAl2O4. Physical Review B - Condensed Matter and Materials Physics. 2009;79:1–12. doi: 10.1103/PhysRevB.79.064111. [DOI] [Google Scholar]
- 12.Smith EH, Benedek NA, Fennie CJ. Interplay of Octahedral Rotations and Lone Pair Ferroelectricity in CsPbF3. Inorganic Chemistry. 2015;54:8536–8543. doi: 10.1021/acs.inorgchem.5b01213. [DOI] [PubMed] [Google Scholar]
- 13.Bennett JW. Discovery and Design of Functional Materials: Integration of Database Searching and First Principles Calculations. Physics Procedia. 2012;34:14–23. doi: 10.1016/j.phpro.2012.05.003. [DOI] [Google Scholar]
- 14.Bennett JW, Garrity KF, Rabe KM, Vanderbilt D. Hexagonal ABC semiconductors as ferroelectrics. Physical Review Letters. 2012;109:167602. doi: 10.1103/PhysRevLett.109.167602. [DOI] [PubMed] [Google Scholar]
- 15.Bennett JW, Rabe KM. Integration of first-principles methods and crystallographic database searches for new ferroelectrics: Strategies and explorations. J. Solid State Chem. 2012;195:21–31. doi: 10.1016/j.jssc.2012.05.013. [DOI] [Google Scholar]
- 16.Garrity KF. High-throughput first-principles search for new ferroelectrics. Phys. Rev. B. 2018;97:024115. doi: 10.1103/PhysRevB.97.024115. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Lines, M. E. & Glass, A. M. Principles and Applications of Ferroelectrics and Related Materials (Oxford University Press, 2001).
- 18.Villars, P. (Chief Editor). PAULING FILE in: Inorganic Solid Phases, SpringerMaterials (online database), Springer, Heidelberg (ed.) (2012).
- 19.Shiozaki, Y., Nakamura, E. & Mitsui, T. (eds.) Landolt-Börnstein - Group III Condensed Matter _Volume 36A1: “Ferroelectrics and Related Substances: Oxides Part 1: Perovskite-type Oxides and LiNbO3Family” (Springer-Verlag, 2001).
- 20.Shiozaki, Y., Nakamura, E. & Mitsui, T. (eds.) Landolt-Börnstein - Group III Condensed Matter _Volume 36A2: “Ferroelectrics and Related Substances: Oxides Part 2: Oxides other than Perovskite-type and LiNbO3Family” (Springer-Verlag, 2002).
- 21.Shiozaki, Y., Nakamura, E. & Mitsui, T. (eds.) Landolt-Börnstein - Group III Condensed Matter _Volume 36B1: “Ferroelectrics and Related Substances: Inorganic Substances other than Oxides Part 1: SbSI family... TAAP” (Springer-Verlag, 2004).
- 22.Shiozaki, Y., Nakamura, E. & Mitsui, T. (eds.) Landolt-Börnstein - Group III Condensed Matter _Volume 36B2: “Ferroelectrics and Related Substances: Inorganic Substances other than Oxides Part 2: (NH4)SO4family... K3BiCl6 _2KCl_KH3F4” (Springer-Verlag, 2006).
- 23.Shiozaki, Y., Nakamura, E. & Mitsui, T. (eds.) Landolt-Börnstein - Group III Condensed Matter _Volume 36C: “Ferroelectrics and Related Substances: Organic crystals, liquid crystals and polymers” (Springer-Verlag, 2006).
- 24.Jain A, et al. The Materials Project: A materials genome approach to accelerating materials innovation. APL Materials. 2013;1:011002. doi: 10.1063/1.4812323. [DOI] [Google Scholar]
- 25.Curtarolo S, et al. AFLOW: An automatic framework for high-throughput materials discovery. Computational Materials Science. 2012;58:218–226. doi: 10.1016/j.commatsci.2012.02.005. [DOI] [Google Scholar]
- 26.Pizzi G, Cepellotti A, Sabatini R, Marzari N, Kozinsky B. AiiDA: automated interactive infrastructure and database for computational science. Computational Materials Science. 2016;111:218–230. doi: 10.1016/j.commatsci.2015.09.013. [DOI] [Google Scholar]
- 27.Bergerhoff, G. & Brown, I. Inorganic crystal structure database (International Union of Crystallography, 1987).
- 28.Hellenbrandt M. The inorganic crystal structure database (ICSD)|present and future. Crystallography Reviews. 2004;10:17–22. doi: 10.1080/08893110410001664882. [DOI] [Google Scholar]
- 29.Saal JE, Kirklin S, Aykol M, Meredig B, Wolverton C. Materials design and discovery with high-throughput density functional theory: The open quantum materials database (OQMD) JOM. 2013;65:1501–1509. doi: 10.1007/s11837-013-0755-4. [DOI] [Google Scholar]
- 30.Kirklin, S. et al. The open quantum materials database (OQMD): assessing the accuracy of DFT formation energies. npj Computational Materials1, 15010 (2015).
- 31.Lines, M. E. & Glass, A. M. chap. Basic Concepts (Oxford University Press, Oxford, 2001).
- 32.Rabe, K. M., Dawber, M., Lichtensteiger, C., Ahn, C. H. & Triscone, J.-M. Modern physics of ferroelectrics: Essential background. In Physics of Ferroelectrics: A Modern Perspective, 1–30 (Springer Berlin Heidelberg, 2007).
- 33.Strukov, B. A. & Levanyuk, A. P. General characteristics of structural phase transitions in crystals. In Ferroelectric Phenomena in Crystals, 1–29 (Springer Berlin Heidelberg, 1998).
- 34.Chandra, P. & Littlewood, P. B. A landau primer for ferroelectrics. In Physics of Ferroelectrics: A Modern Perspective, 69–116 (Springer Berlin Heidelberg, Berlin, Heidelberg, 2007).
- 35.Stokes, H. T. & Hatch, D. M. Isotropy Subgroups of the 230 Crystallographic Space Groups (WORLD SCIENTIFIC, 1989).
- 36.Müller, U. Symmetry relations at phase transitions. In Symmetry Relationships between Crystal Structures, 196–215 (Oxford University Press, 2013).
- 37.Ong SP, et al. Python Materials Genomics (pymatgen): A robust, open-source python library for materials analysis. Computational Materials Science. 2013;68:314–319. doi: 10.1016/j.commatsci.2012.10.028. [DOI] [Google Scholar]
- 38.Mathew K, et al. Atomate: A high-level interface to generate, execute, and analyze computational materials science workows. Computational Materials Science. 2017;139:140–152. doi: 10.1016/j.commatsci.2017.07.030. [DOI] [Google Scholar]
- 39.Resta R. Theory of the electric polarization in crystals. Ferroelectrics. 1992;136:51–55. doi: 10.1080/00150199208016065. [DOI] [Google Scholar]
- 40.Aroyo, M. I. (ed.) International Tables for Crystallography Volume A: Space-group symmetry (International Union of Crystallography, 2016).
- 41.Müller, U. Subgroups and supergroups of point and space groups. In Symmetry Relationships between Crystal Structures, 86–99 (Oxford University Press, 2013).
- 42.King-Smith RD, Vanderbilt D. Theory of polarization of crystalline solids. Phys. Rev. B. 1993;47:1651–1654. doi: 10.1103/PhysRevB.47.1651. [DOI] [PubMed] [Google Scholar]
- 43.Vanderbilt D, King-Smith RD. Electric polarization as a bulk quantity and its relation to surface charge. Physical Review B. 1993;48:4442–4455. doi: 10.1103/PhysRevB.48.4442. [DOI] [PubMed] [Google Scholar]
- 44.Resta R. Macroscopic polarization in crystalline dielectrics: the geometric phase approach. Reviews of Modern Physics. 1994;66:899–915. doi: 10.1103/RevModPhys.66.899. [DOI] [Google Scholar]
- 45.Rabe KM, Waghmare UV. First-principles model hamiltonians for ferroelectric phase transitions. Ferroelectrics. 1992;136:147–156. doi: 10.1080/00150199208016074. [DOI] [Google Scholar]
- 46.Resta, R. & Vanderbilt, D. Theory of polarization: A modern approach. In Physics of Ferroelectrics: A Modern Perspective, 31–68 (Springer Berlin Heidelberg, Berlin, Heidelberg, 2007).
- 47.Spaldin NA. A beginner's guide to the modern theory of polarization. Journal of Solid State Chemistry. 2012;195:2–10. doi: 10.1016/j.jssc.2012.05.010. [DOI] [Google Scholar]
- 48.Rabe, K. M. & Ghosez, P. First-principles studies of ferroelectric oxides. In Topics in Applied Physics, 117–174 (Springer Berlin Heidelberg, 2007).
- 49.Kittel C. Theory of antiferroelectric crystals. Phys. Rev. 1951;82:729–732. doi: 10.1103/PhysRev.82.729. [DOI] [Google Scholar]
- 50.Rabe, K. M. Antiferroelectricity in Oxides: A Reexamination. In Functional Metal Oxides, 221–244 (Wiley-VCH Verlag GmbH & Co. KGaA, 2013).
- 51.Tolédano P, Guennou M. Theory of antiferroelectric phase transitions. Phys. Rev. B. 2016;94:014107. doi: 10.1103/PhysRevB.94.014107. [DOI] [Google Scholar]
- 52.Reyes-Lillo, S. E. & Rabe, K. M. Antiferroelectricity and ferroelectricity in epitaxially strained PbZrO3 from first principles. Physical Review B88, 180102R (2013).
- 53.Toyo, A. spglib, https://atztogo.github.io/spglib/ (2018).
- 54.Togo, A. & Tanaka, I. Spglib: a software library for crystal symmetry search, arxiv:1808.01590 (2018).
- 55.Ong SP, et al. The materials application programming interface (API): A simple, flexible and effcient API for materials data based on REpresentational state transfer (REST) principles. Computational Materials Science. 2015;97:209–215. doi: 10.1016/j.commatsci.2014.10.037. [DOI] [Google Scholar]
- 56.Aroyo, M. I. et al. Crystallography online: Bilbao Crystallographic Server. Bulg. Chem. Commun. 43, 183–197 (2011).
- 57.Aroyo MI, Kirov A, Capillas C, Perez-Mato JM, Wondratschek H. Bilbao crystallographic server. II. representations of crystallographic point groups and space groups. Acta Crystallographica Section A Foundations of Crystallography. 2006;62:115–128. doi: 10.1107/S0108767305040286. [DOI] [PubMed] [Google Scholar]
- 58.Aroyo, M. I. et al. Bilbao Crystallographic Server: I. Databases and crystallographic computing programs. Zeitschrift für Kristallographie - Crystalline Materials221, 15–27 (2006).
- 59.Bilbao Crystallographic Server. Structure relations, http://www.cryst.ehu.es/cryst/rel.html (2019).
- 60.Stokes, H. T., Hatch, D. M. & Campbell, B. J. ISOTROPY Software Suite, iso.byu.edu (2019).
- 61.Aas, G., Lee, J., & Lester, A. Mechanize - stateful programmatic web browsing, version 0.4.4, https://pypi.python.org/pypi/mechanize/ (2019).
- 62.Scott JF. Searching for new ferroelectrics and multiferroics: A users point of view. npj Computational Materials. 2015;1:15006. doi: 10.1038/npjcompumats.2015.6. [DOI] [Google Scholar]
- 63.Kresse G, Furthmüller J. Effciency of ab-initio total energy calculations for metals and semiconductors using a plane-wave basis set. Computational Materials Science. 1996;6:15–50. doi: 10.1016/0927-0256(96)00008-0. [DOI] [Google Scholar]
- 64.Kresse G, Hafner J. Ab initio molecular dynamics for liquid metals. Physical Review B. 1993;47:558–561. doi: 10.1103/PhysRevB.47.558. [DOI] [PubMed] [Google Scholar]
- 65.Kresse, G. & Furthmüller, J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Physical Review B54, 11169 (1996). [DOI] [PubMed]
- 66.Perdew JP, Burke K, Ernzerhof M. Generalized Gradient Approximation Made Simple. Physical review letters. 1996;77:3865–3868. doi: 10.1103/PhysRevLett.77.3865. [DOI] [PubMed] [Google Scholar]
- 67.Blöchl, P. E. Projector augmented-wave method. Physical Review B50, 17953 (1994). [DOI] [PubMed]
- 68.Kresse G, Jourbert D. From ultrasoft pseudopotentials to the projector augmented-wave method. Physical Review B. 1999;59:1758–1775. doi: 10.1103/PhysRevB.59.1758. [DOI] [Google Scholar]
- 69.Materials Project. Materials project calculation guide, https://materialsproject.org/docs/calculations (2019).
- 70.King-Smith RD, Vanderbilt D. Theory of polarization of crystalline solids. Physical Review B. 1993;47:1651–1654. doi: 10.1103/PhysRevB.47.1651. [DOI] [PubMed] [Google Scholar]
- 71.Resta, R. Berry phase in electronic wavefunctions. Troisime Cycle de la Physique en Suisse Romande 899–915 (Anne Academique 1995-1996).
- 72.Jain A, et al. Formation enthalpies by mixing GGA and GGA + U calculations. Physical Review B - Condensed Matter and Materials Physics. 2011;84:1–10. [Google Scholar]
- 73.Jain A, et al. A high-throughput infrastructure for density functional theory calculations. Computational Materials Science. 2011;50:2295–2310. doi: 10.1016/j.commatsci.2011.02.023. [DOI] [Google Scholar]
- 74.Dudarev SL, Savrasov SY, Humphreys CJ, Sutton AP. Electron-energy-loss spectra and the structural stability of nickel oxide: An LSDA+U study. Physical Review B. 1998;57:1505–1509. doi: 10.1103/PhysRevB.57.1505. [DOI] [Google Scholar]
- 75.Jain A, et al. FireWorks: a dynamic workow system designed for high-throughput applications. Concurrency Computation Practice and Experience. 2015;27:5037–5059. doi: 10.1002/cpe.3505. [DOI] [Google Scholar]
- 76.Vanderbilt D. Berry-phase theory of proper piezoelectric response. Journal of Physics and Chemistry of Solids. 2000;61:147–151. doi: 10.1016/S0022-3697(99)00273-5. [DOI] [Google Scholar]
- 77.Smidt TE, Mack SA, Reyes-Lillo SE, Jain A, Neaton JB. 2019. Ferroelectric search distortion and workow data and VASP files. figshare. [DOI]
- 78.Smidt TE, Mack SA, Reyes-Lillo SE, Jain A, Neaton J. 2019. B. blondegeek/ferroelectric search site: Ferroelectric Search Site. Zenodo. [DOI]
- 79.Ong SP, Wang L, Kang B, Ceder G. Li-fe-p-o2 phase diagram from first principles calculations. Chemistry of Materials. 2008;20:1798–1807. doi: 10.1021/cm702327g. [DOI] [Google Scholar]
- 80.Virtanen, P. et al. SciPy 1.0–Fundamental Algorithms for Scientific Computing in Python, https://arxiv.org/abs/1907.10121 (2019). [DOI] [PMC free article] [PubMed]
- 81.Armiento R, Kozinsky B, Fornari M, Ceder G. Screening for high-performance piezoelectrics using high-throughput density functional theory. Phys. Rev. B. 2011;84:014103. doi: 10.1103/PhysRevB.84.014103. [DOI] [Google Scholar]
- 82.Oliphant, T. NumPy: A guide to NumPy. USA: Trelgol Publishing, http://www.numpy.org/ (2006–).
- 83.van der Walt S, Colbert SC, Varoquaux G. The numpy array: A structure for efficient numerical computation. Computing in Science Engineering. 2011;13:22–30. doi: 10.1109/MCSE.2011.37. [DOI] [Google Scholar]
- 84.Hunter JD. Matplotlib: A 2d graphics environment. Computing in Science & Engineering. 2007;9:90–95. doi: 10.1109/MCSE.2007.55. [DOI] [Google Scholar]
- 85.Prez F, Granger BE. IPython: A system for interactive scientific computing. Computing in Science & Engineering. 2007;9:21–29. doi: 10.1109/MCSE.2007.53. [DOI] [Google Scholar]
- 86.Kluyver, T. et al. Jupyter notebooks – a publishing format for reproducible computational workows. In Loizides, F. & Schmidt, B. (eds.) Positioning and Power in Academic Publishing: Players, Agents and Agendas, 87–90 (IOS Press, 2016).
- 87.Wahl R, Vogtenhuber D, Kresse G. SrTiO3 and BaTiO3 revisited using the projector augmented wave method: Performance of hybrid and semilocal functionals. Phys. Rev. B. 2008;78:104116. doi: 10.1103/PhysRevB.78.104116. [DOI] [Google Scholar]
- 88.Zhang Y, Sun J, Perdew JP, Wu X. Comparative first-principles studies of prototypical ferroelectric materials by LDA, GGA, and SCAN meta-GGA. Phys. Rev. B. 2017;96:035143. doi: 10.1103/PhysRevB.96.035143. [DOI] [Google Scholar]
- 89.Yang Q, Cao JX, Ma Y, Zhou YC. First principles study of polarization-strain coupling in SrBi2Ta2O9. AIP Advances. 2013;3:052134. doi: 10.1063/1.4808215. [DOI] [Google Scholar]
- 90.Lebedev AI. Ferroelectric phase transition in orthorhombic CdTiO3: First-principles studies. Physics of the Solid State. 2009;51:802–809. doi: 10.1134/S1063783409040283. [DOI] [Google Scholar]
- 91.Baettig P, Schelle CF, LeSar R, Waghmare UV, Spaldin NA. Theoretical prediction of new high-performance lead-free piezoelectrics. Chemistry of Materials. 2005;17:1376–1380. doi: 10.1021/cm0480418. [DOI] [Google Scholar]
- 92.Adachi, M. et al. Mg3B7O13Cl [F], 18A-1: Datasheet from Landolt-Börnstein - Group III Condensed Matter · Volume 36A2: “Oxides” in SpringerMaterials (2002).
- 93.Adachi, M. et al. BaTiO3 (cubic) [F] Survey, 1A-10: Datasheet from Landolt-Börnstein - Group III Condensed Matter · Volume 36A1: “Oxides” in SpringerMaterials (2001).
- 94.Adachi, M. et al. PbBi2Nb2O9 [(F)], 9A-10: Datasheet from Landolt-Börnstein - Group III Condensed Matter · Volume 36A2: “Oxides” in SpringerMaterials (2002).
- 95.Adachi, M. et al. SrBi2Ta2O9 [F], 9A-12: Datasheet from Landolt-Börnstein - Group III Condensed Matter · Volume 36A2: “Oxides” in SpringerMaterials (2002).
- 96.Adachi, M. et al. Bi4Ti3O12 [F], 9A-15: Datasheet from Landolt-Börnstein - Group III Condensed Matter · Volume 36A2: “Oxides” in SpringerMaterials (2002).
- 97.Deguchi, K., Hasebe, K., Gesi, K. & Asahi, T. 39A-16 K2ZnBr4[F]: Datasheet from Landolt-Börnstein - Group III Condensed Matter · Volume 36B2: “Inorganic Substances other than Oxides” in SpringerMaterials (2005).
- 98.Shiozaki, Y. & Asahi, T. 50A-1: 1-6 SC(NH2)2[F]: Datasheet from Landolt-Börnstein - Group III Condensed Matter · Volume 36C: “Organic crystals, liquid crystals and polymers” in SpringerMaterials (2006).
- 99.Adachi, M. et al. Oxides · CdTiO3, 1A-9: Datasheet from Landolt-Börnstein - Group III Condensed Matter · Volume 36A1: “Oxides” in SpringerMaterials (2001).
- 100.Deguchi, K., Hasebe, K., Gesi, K. & Asahi, T. 39A-9 K2ZnCl4[F]: Datasheet from Landolt-Börnstein - Group III Condensed Matter · Volume 36B2: “Inorganic Substances other than Oxides” in SpringerMaterials (2005).
- 101.Deguchi, K., Hasebe, K., Gesi, K. & Asahi, T. 39A-10 Rb2ZnCl4[F]: Datasheet from Landolt-Börnstein - Group III Condensed Matter · Volume 36B2: “Inorganic Substances other than Oxides” in SpringerMaterials (2005).
- 102.Deguchi, K., Hasebe, K., Gesi, K. & Asahi, T. 39A-1 (NH4)2SO4[F]: Datasheet from Landolt-Börnstein - Group III Condensed Matter · Volume 36B2: “Inorganic Substances other than Oxides” in SpringerMaterials (2005).
- 103.Adachi, M. et al. PbHfO3 [(A)], 1A-16: Datasheet from Landolt-Börnstein - Group III Condensed Matter · Volume 36A1: “Oxides” in SpringerMaterials (2001).
- 104.Deguchi, K., Hasebe, K., Gesi, K. & Asahi, T. 39A-2 K2SeO4[F]: Datasheet from Landolt-Börnstein - Group III Condensed Matter · Volume 36B2: “Inorganic Substances other than Oxides” in SpringerMaterials (2005).
- 105.Adachi, M. et al. Oxides _ KNbO3 [F], 1A-2: Datasheet from Landolt-Börnstein - Group III Condensed Matter · Volume 36A1: “Oxides” in Springer Materials (2001).
- 106.Wemple S, DiDomenico M, Jr., Camlibel I. Relationship between linear and quadratic electro-optic coefficients in linbo3, litao3, and other oxygen-octahedra ferroelectrics based on direct measurement of spontaneous polarization. Applied Physics Letters. 1968;12:209–211. doi: 10.1063/1.1651955. [DOI] [Google Scholar]
- 107.Adachi, M. et al. LiNbO3 [F] Survey, 2A-1: Datasheet from Landolt-Börnstein - Group III Condensed Matter · Volume 36A1: “Oxides” in Springer Materials (2001).
- 108.Adachi, M. et al. SbNbO4 [F, (A)], 5A-2: Datasheet from Landolt-Börnstein - Group III Condensed Matter · Volume 36A2: “Oxides” in Springer Materials (2002).
- 109.Adachi, M. et al. PbTiO3 [F], 1A-11: Datasheet from Landolt-Börnstein - Group III Condensed Matter · Volume 36A1: “Oxides” in Springer Materials (2001).
- 110.Terauchi H, et al. EXAFS Studies on Amorphous PbTiO3. Journal of the Physical Society of Japan. 1981;50:3977–3979. doi: 10.1143/JPSJ.50.3977. [DOI] [Google Scholar]
- 111.Adachi, M. et al. PbZrO3 [A], 1A-15: Datasheet from Landolt-Börnstein - Group III Condensed Matter · Volume 36A1: “Oxides” in Springer Materials (2001).
- 112.Hikita, T. 35A-13 TlTiOPO4[(F)]: Datasheet from Landolt-Börnstein - Group III Condensed Matter · Volume 36B1: “Inorganic Substances other than Oxides. Part 1: SbSI family... TAAP” in SpringerMaterials (2004).
- 113.Adachi, M. et al. Sr2Ta2O7 [F], 8A-6: Datasheet from Landolt-Börnstein - Group III Condensed Matter · Volume 36A2: “Oxides” in SpringerMaterials (2002).
- 114.Abrahams SC. Systematic prediction of new ferroelectrics in space group R3. I. Acta crystallographica. Section B, Structural science. 2006;62(Pt 1):26–41. doi: 10.1107/S0108768105040577. [DOI] [PubMed] [Google Scholar]
- 115.Huang SY, Von Der Mühll R, Ravez J, Hagenmuller P. Structural, ferroelectric and pyroelectric properties of nonstoichiometric ceramics based on BaAl2O4. Journal of Physics and Chemistry of Solids. 1994;55:119–124. doi: 10.1016/0022-3697(94)90192-9. [DOI] [Google Scholar]
- 116.Machida M. Rotational Dynamics of Trimethylammonium Chloride Studied by MD Simulation and NMR. Ferroelectrics. 2006;338:205–209. doi: 10.1080/00150190600740184. [DOI] [Google Scholar]
- 117.Smith EH, Benedek NA, Fennie CJ. Interplay of octahedral rotations and lone pair ferroelectricity in CsPbF3. Inorganic Chemistry. 2015;54:8536–8543. doi: 10.1021/acs.inorgchem.5b01213. [DOI] [PubMed] [Google Scholar]
- 118.Yelisseyev AP, et al. Structures and optical properties of two phases of srmgf4. Phys. Chem. Chem. Phys. 2015;17:500–508. doi: 10.1039/C4CP04689G. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Citations
Data Availability Statement
VASP version 5.3.5 used to perform DFT calculations is a proprietary code. The Bilbao Crystallographic Server (BCS) is freely available on-line at http://www.cryst.ehu.es. Fireworks, atomate, and pymatgen are python packages accessible on GitHub. Fireworks and atomate are released under a modified Berkeley Software Distribution (BSD) License. pymatgen is released under a Massachusetts Institute of Technology (MIT) License. Both MIT and BSD licenses are open-source and permit both commercial and non-commercial use. Our workflow code is included since atomate version 0.6.7 and our analysis code is available in pymatgen since v2019.2.4. We also use the following python packages in our analysis and Graphical Representation of Results: numpy, scipy, matplotlib, ipython, and jupyter80,82–86. These packages are freely available through the Python Package Index (https://pypi.org/).
Our code for recovering the same branch polarization from polarization calculations has been contributed to pymatgen under the pymatgen.analysis.ferroelectricity module. Our code for the DFT and polarization analysis workflows for performing polarization calculations has been contributed to atomate under the atomate.vasp.workflows.base.ferroelectric module. We also provide code for the interface that we used to view our candidates in aggregate. The web interface for the current work is hosted at http://blondegeek.github.io/ferroelectric_search_site/. The code for the interface can be found at http://github.com/blondegeek/ferroelectric_search_site.