Poor estimates of motor variability are associated with longer grooved pegboard times for middle-aged and older adults

Abstract

Goal-directed movements that involve greater motor variability are performed with an increased risk that the intended goal will not be achieved. The ability to estimate motor variability during such actions varies across individuals and influences how people decide to move about their environment. The purpose of our study was to identify the decision-making strategies used by middle-aged and older adults when performing two goal-directed motor tasks and to determine if these strategies were associated with the time to complete the grooved pegboard test. Twenty-one middle-aged (48 ± 6 yr; range 40–59 yr, 15 women) and 20 older adults (73 ± 4 yr; range 65–79 yr, 8 women) performed two targeted tasks, each with two normalized target options. Decision-making characteristics were not associated with time to complete the test of manual dexterity when the analysis included all participants, but slower pegboard times were associated with measures of greater movement variability during the target-directed actions. When the data were clustered on the basis of pegboard time rather than age, relatively longer times for the faster group were associated with greater motor variability during the prescribed tasks, whereas longer times for the slower group were associated with increased risk-seeking behavior (α) and greater variability in the targeted actions.

NEW & NOTEWORTHY This study was the first to examine the association between decision-making choices and an NIH Toolbox test of manual dexterity (grooved pegboard test) performed by middle-aged and older adults. Significant associations were observed between decision-making choices and time to complete the test when the analyses were based on pegboard times rather than chronological age. This result indicates that decision-making choices of middle-aged and older adults, independent of age, were associated with time to complete a test of manual dexterity.

INTRODUCTION

Manual dexterity is such an essential attribute that it is included in the NIH Toolbox as a biomarker of neurological health and function across the life span. It is quantified as the time to complete a pegboard test (Reuben et al. 2013; Wang et al. 2011). Cross-sectional studies indicate that pegboard times increase progressively across the adult life span, but the underlying adaptations are unknown. The functional significance of the pegboard test is underscored by its capacity to predict motor performance of healthy adults 20–88 yr old (Bowden and McNulty, 2013), activities of daily living in adults >65 yr old (Seidel et al. 2009), and the level of dependency among adults >63 yr old (Williams et al. 1982).

One of the adaptations that may underlie the longer pegboard times of older adults is the increase in movement variability (Stergiou et al. 2006; Stergiou and Decker 2011) that accompanies advancing age (Christou et al. 2007; Poston et al. 2008a, 2008b). The pegboard test involves two targeted actions, picking up a peg and inserting it into a hole, that are likely more variable in older adults. Based on the speed-accuracy trade-off, one strategy that can be used to reduce the variability is to move more slowly, which would prolong pegboard time. The decision to move slowly or quickly depends on the risk characteristics of the individual. Given that risk can be defined as the variance in the outcome of a prescribed action (O’Brien and Ahmed 2016), goal-directed tasks that involve greater variance in endpoint location are riskier because there is a greater chance that the intended goal will not be achieved. The ability to estimate motor variability when performing goal-directed actions varies across individuals (Wu et al. 2009, 2011), and consistency of decision making appears to decline with age (Tymula et al. 2013). As a result of the greater motor variance exhibited by older adults (Christou et al. 2007; Galganski et al. 1993; Poston et al. 2008a, 2008b), they inherently move about their environment with greater risk of not achieving intended goals during targeted actions. This greater motor risk may decrease the attraction to the reward of successfully completing a riskier goal-directed movement (Chen et al. 2018; Valsecchi et al. 2018) and influence how older adults decide to move about their environment.

Decision-making strategies can be quantified with probability-based lotteries. By providing variable monetary outcomes paired with the probability that the provided outcome will occur, it is possible to assess how individuals make decisions based on economic risk. This economic framework can be expanded to understand how perceptions of risk influence motor decisions (Trommershäuser et al. 2008). For example, O’Brien and Ahmed (2013) used this framework to demonstrate that young adults exhibited risk-seeking behavior in both arm-reaching and whole body lean tasks to prescribed targets, but the degree to which participants were risk seeking differed between tasks; the young adults were more risk seeking during the whole body lean task. The interpretation was that greater risk sensitivity when performing goal-directed actions may be related to a skewed sense of motor variance, or distorted probability weighting (O’Brien and Ahmed 2013). If older adults exhibit a less accurate sense of motor variance than young adults, as they do in explicit economic probabilities (Tymula et al. 2013), there may be negative consequences for the strategies they use during targeted activities of daily living.

The aim of the study was to identify the decision-making strategies used by middle-aged and older adults when performing two goal-directed motor tasks and to determine if these strategies were associated with the time to complete the grooved pegboard test. We compared the risk-behavior characteristics of middle-aged and older adults in two tasks: a seated wrist-extension task and a standing whole body lean task. Manual dexterity was quantified as the time taken to complete the grooved pegboard test (Wang et al. 2011). The hypothesis was that the decision-making choices of older adults would be more risk averse than those of middle-aged adults when performing the goal-directed actions, which would be associated with longer times to complete the pegboard test. We expected to find that the relative risk-averse actions of older adults during these tasks, compared with the more risk-seeking actions of middle-aged adults, would be associated with more variable neuromuscular properties, motor variability, and longer pegboard times. Because differences in motor variance during target-matching tasks are attributable to changes in the cumulative activity of the involved motor units (Barry et al. 2007; Negro et al. 2009; Thompson et al. 2018), older adults were also expected to be more variable in the coefficient of variation for force during wrist extension, mediolateral variability about the target, and maximal endpoint distance.

METHODS

Twenty-one middle-aged (48 ± 6 yr; range 40–59 yr, 15 women) and 20 older adults (73 ± 4 yr; range 65–79 yr, 8 women) met the inclusion criteria and provided written informed consent before participating in the study. All participants were right handed (97.3 ± 6.5; range: 75–100) as determined with the Edinburgh Handedness Inventory Short Form (Veale 2014), were free from neurological disease, had no reported orthopedic problems that could influence upper- or lower-limb function, did not experience regular episodes of dizziness or fainting, and were not taking any medications known to influence neuromuscular or cognitive function. The Institutional Review Board at the University of Colorado Boulder approved the protocol (Protocol no. 17-0319).

Experimental Protocol

Participants completed either one or two experimental sessions that lasted ~2.5 h in total. Functional capabilities were assessed using the Lafayette grooved pegboard test of manual dexterity (Wang et al. 2011), muscle strength during maximal isometric contractions (Reuben et al. 2013), and the Mini Mental State Exam to quantify cognitive function (Molloy et al. 1991). Force variability and endpoint distributions (Almuklass et al. 2016; Christou et al. 2007; Marmon et al. 2011; Poston et al. 2008b, 2008a) were calculated for the two goal-directed tasks to assess decision-making strategies (O’Brien and Ahmed 2013, 2015, 2016). The primary outcome was time to complete the grooved pegboard test with secondary outcomes used to identify variables associated with the time it took middle-aged and older adults to complete the pegboard test.

Functional Assessment

The Lafayette 25-hole grooved pegboard test requires participants to place keyhole-shaped pegs into 25 holes on a board as quickly as possible. The holes are arranged in a 5-by-5 grid, with varying keyhole orientation across the board. Participants insert pegs into the board one at a time, completing the rows from left to right, top to bottom. Participants practiced the task by completing the top row before performing the entire test. Normative data for the time to complete the grooved pegboard test (mean ± SD) are 57 ± 8 s for middle-aged adults (31–45 yr), 69 ± 18 s for older adults (66–75 yr), and 87 ± 16 s for oldest adults (76–85 yr) (Wang et al. 2011).

Maximal handgrip strength was measured with a hand dynamometer (Baseline hydraulic hand dynamometer; Baseline Evaluation Instruments, Irving, TX) (Reuben et al. 2013). Three maximal voluntary contractions (MVC) were performed with the right hand while holding the handgrip device. Subjects were instructed to increase force gradually to reach a maximal value in 3 s and sustain that force for ~2 s. Strong verbal encouragement was provided during each MVC trial with at least 90 s of rest between trials. The maximal value recorded for the right hand was used as MVC force.

Cognitive function was assessed with the Standardized Mini-Mental State Examination (SMMSE) (Molloy et al. 1991). The assessment comprises a 30-point questionnaire that examines cognitive abilities, which include repeating named prompts, attention, recall, language, ability to follow simple commands, and object orientation. A score of ≥25 indicates the absence of cognitive impairment (Folstein et al. 1975).

Force Variability

Maximal wrist extension force.

The maximal force exerted by the wrist extensors was measured with a six-axis transducer (0.011 V/N in the vertical direction, 0.15 V/N·m about the wrist pronation/supination axis; model UFS-45A100-U760, JR3, Woodland, CA). The signals were sampled at 200 Hz and stored on a computer for offline analysis. Participants were instructed to increase force gradually from rest to maximum in 3 s and then hold that maximal force for ~2 s. At least three MVCs were performed, with the maximal value recorded as the peak force taken from one of two trials within 5% of each other. When the difference in peak force between the three MVCs was not 5% or less, subsequent MVC trials were performed until peak force from two trials fell within the criterion, with no more than five MVC trials performed by each participant. At least 90 s of rest were provided between each MVC trial.

Force steadiness.

The coefficient of variation for force (force steadiness) was measured as participants performed submaximal isometric contractions with the wrist extensors of the right arm (Almuklass et al. 2017; Hamilton et al. 2017). Participants were instructed to place their third digit under the center of a rigid restraint to ensure that the hand was centered for all wrist extension tasks (Fig. 1A). Two 30-s contractions were sustained at a target force of 10% MVC with 45 s of rest provided between trials.

Fig. 1.

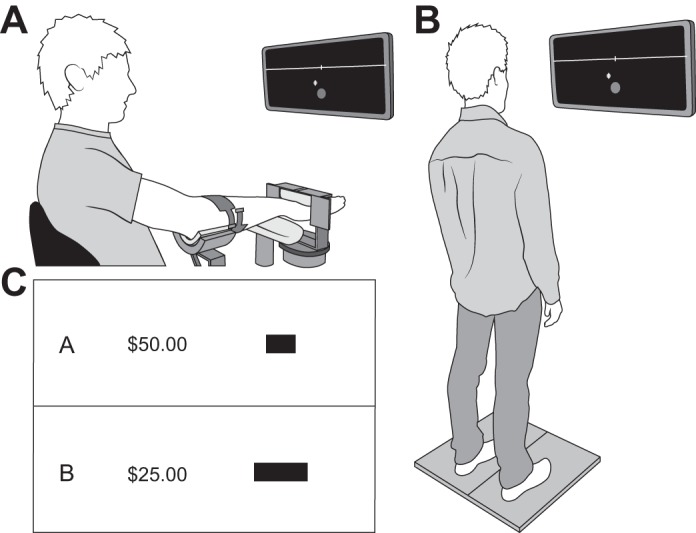
Experimental setup for wrist-extension (A) and whole body lean (B) tasks. Each task involved out-and-back displacements of the cursor to a target. Target options were constructed using a 4 × 4 outcome-probability matrix, where each block presented a monetary reward and target size (C; in black).

Visual feedback was displayed on a computer screen ~1 m in front of the participant. A circular yellow cursor (5-mm diameter) moved across the screen at 0.79 cm/s from left to right, and performing an isometric contraction with the wrist extensors by pushing upward with the back of the hand against the rigid restraint moved the cursor vertically. The target force was located 2 cm above baseline (visual angle 1.15°) and was indicated with a 2-mm thick white line. Participants were instructed to maintain a steady contraction once the target was reached. Force steadiness was quantified as the coefficient of variation for force (SD/mean × 100; Galganski et al. 1993) during the steadiest 10 s of each force-matching trial.

Muscle activity.

Activation of the right forearm muscles was measured during the force-steadiness trials. A high-density surface electromyography (EMG) system (Sessantaquattro; OT Bioelettronica, Torino, Italy) was used to measure the absolute EMG amplitude of the wrist extensors and wrist flexors with one grid of electrodes (4 × 8 detection points; 10-mm interelectrode distance) centered over the belly of each muscle group (Fig. 1A). Each muscle group was identified through palpation and a series of prescribed wrist extension and flexion tasks with the location of the ulna used to orient the placement of the electrodes over each muscle group. The electrodes provided 32 monopolar surface EMG signals for each muscle group with a remote reference placed over the olecranon process. The monopolar EMG signals were amplified, bandpass filtered (3-dB bandwidth, 100–500 Hz), sampled at 2,000 Hz, and stored on a computer for offline analysis.

Before the electrodes were attached, the skin was shaved and carefully prepared with an abrasive gel and rubbing alcohol. The electrode grid was affixed to the skin with double-adhesive foam with small cavities over the electrode locations. Conductive paste was placed in the cavities of the foam to minimize impedance of the electrode–skin interface.

The EMG signals were visually inspected for erroneous waveforms, and contaminated channels were removed from the recordings obtained with both electrodes and all trials to maintain a consistent number of recording channels for each participant. The root mean square amplitude of each monopolar channel was then summed for the respective electrode grid to provide a measurement of absolute EMG amplitude (in mV) for the wrist extensors and wrist flexors. A coactivation index [wrist extensors/(wrist extensors + wrist flexors) × 100] was calculated to assess the change in the relative muscle activity of the two muscle groups (Falconer and Winter 1985).

Performance variability.

Variance in performance was quantified in two goal-directed tasks: wrist extension and whole body lean (Fig. 1, A and B). In the wrist-extension task, the vertical displacement of the cursor was controlled by wrist-extension force and the mediolateral displacement was controlled by the rotational moment about the longitudinal axis of the forearm. Supination of the hand-forearm moved the cursor to the right, and pronation moved the cursor to the left. The task was to move the cursor quickly upward by 6 cm to a target (10% MVC force) shown on the screen.

In the whole body lean task, participants stood on a platform with two force plates (dual-top AccuSway; AMTI, Watertown, MA) that measured three-dimensional forces (Fx, Fy, Fz) and moments of force (Mx, My, Mz) about the center of each plate at 200 Hz. The center of pressure (CoP) for each plate was calculated relative to the center of the dual-top force platform, [Cx Cy], as [CoPx CoPy] = [Cx Cy] + [Mx My]/Fz, where x refers to the mediolateral direction and y denotes the anteroposterior direction. The combined CoP was calculated as the weighted average of each plate (Winter et al. 1996) to provide one measurement for visual feedback. The 6-cm distance to the target was scaled to 50% of maximal anterior CoP distance for the whole body lean.

The initial location of the cursor, which was a yellow circle (1-cm diameter) with a red vertical line to mark its center, was a green circle (3-cm diameter). The target was a white horizontal line that spanned the entire width of the screen with a white vertical line to indicate its center. Participants were instructed to make a quick out-and-back movement from the initial location to the target, trying to move in a straight line to pass the center of the cursor through the center of the target. To limit visually based corrective actions, the cursor was obscured after it remained in the initial location for 500 ms until the target line was crossed.

The horizontal position of the cursor and the speed of the movement to the target were shown on the monitor briefly after each trial. Participants were instructed to reach the target within 1,000 ms for the whole body lean task and within 800 ms for the wrist-extension task. The target line flashed green when the movement was performed within the desired time, yellow when it was within 100 ms after the desired time, and gray when the movement was too slow. Participants were instructed to adjust their performance on the basis of this feedback.

Task order was randomized, but all wrist-extension tasks (i.e., maximal strength, force steadiness, and movement variability) were performed together to limit variability in the measurement setup. Two blocks of 50 practice trials (100 total) were performed for each goal-directed action during which performance was not quantified and participants were able to gain familiarity with the tasks. These 100 trials were sufficient for all participants to learn how to perform the wrist-extension and whole body lean tasks at the desired speed. Participants then completed an additional 100 trials (2 blocks of 50 trials) of each action to quantify timing and movement variance and to help them prepare for the subsequent decision-making portion of the protocol.

The trial-to-trial variability and timing were quantified for each goal-directed action (mean, SD, and the coefficient of variation) at both the target line and at maximal vertical distance, or endpoint (Fig. 2). The target-line measurements included the time to reach the line and mediolateral variability about the center of the target line. At the maximal distance of the cursor, the measurements included time to reach the endpoint, absolute vertical distance of the cursor, and the mediolateral distance from the centerline. All distance variance measures were quantified as the mean, SD, and coefficient of variation for the distance.

Fig. 2.

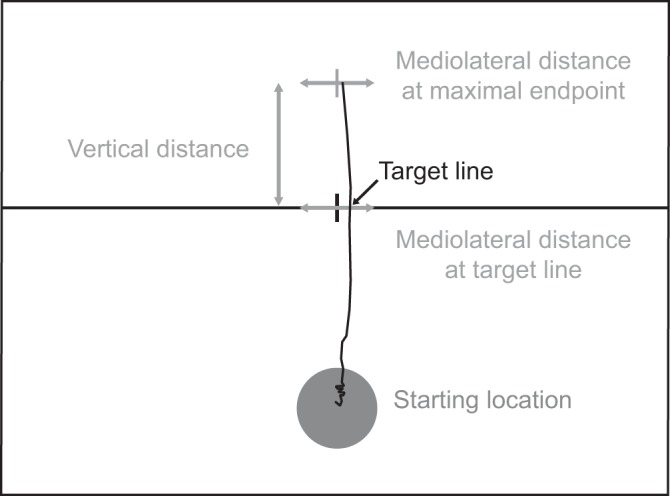
Representative force trajectory showing performance variability measurements. Participants received feedback regarding their mediolateral variability at the target line after completing each trial but did not receive feedback about the path or maximal vertical distance.

Decision Making

Choice trials.

Participants were then asked to choose between pairs of target options (A and B), each of which had a different monetary reward and target size (Fig. 1C). Construction of target sizes was based on the design of Wu et al. (2009) as implemented by O’Brien and Ahmed (2015). Each pair of targets comprised a “safe” and a “risky” option to denote the variance of each choice.

$$Var[option]=p{\text{\$}}^2(1-p)$$

where p represents the probability of winning the reward (target size) and $ represents the numerical value of the monetary reward. The option with the higher variance was considered to be a riskier choice for the goal-directed action. For example, if option A involved a probability of winning that was 0.35 (target width = 0.24 cm) and a reward of $6.72 (Var[A] = 10.27), and option B involved a probability of winning that was 0.80 (target width = 0.67 cm) and a reward of $3.00 (Var[B] = 1.44), then option A would be considered the riskier choice because of the relatively higher variance.

Target size was normalized across individuals by adjusting target width to represent the probability that the participant would reach the target based on the standard deviation of the mediolateral cursor position at the target line (O’Brien and Ahmed 2015; Wu et al. 2011; Fig. 1C). Seven possible monetary outcomes ranging from $2.40 to $48, and seven probabilities ranging from 0.05 to 0.95, were implemented to create the target options.

Participants performed 72 target-choice trials for each motor task (wrist extension and whole body lean) after completing the 100 endpoint trials for the task. Within each trial, the target options and monetary values were shown for 4 s before the target options disappeared, and subjects were given 2 s to select a preferred target with a handheld clicker. When a participant failed to select an option, the screen advanced with no selection recorded and that trial was not included in the analysis.

To assess participants’ understanding of their ability to reach the target, all 72 options for target A were presented again, and participants were asked to state the probability that they could achieve the target. Average error (verbal response − actual probability) was calculated to indicate whether participants consistently over- or underestimated their performance, whereas root mean square error (RMSE) was used to provide a nondirectional measure of accuracy. The responses for each participant were characterized as the slope across the entire range of presented probabilities. It was calculated as the linear relation (β coefficient) between the actual probabilities and the verbal responses across the entire range of target widths (probabilities).

Assessment of risk sensitivity.

Maximum-likelihood estimation was used to determine subject-specific distortions in utility and probability (Tversky and Kahneman 1992) for each task (O’Brien and Ahmed 2015). Cumulative prospect theory was used to model the subjective value function of monetary rewards v(O) and probability weighting w(P) for the target-option tasks as

$$v(O)=O^{\alpha },O\ge 0$$

$$w(P)=\exp \left\{-{\left[-\ln (P)\right]}^{\gamma }\right\},0<P<1$$

where parameters for utility and probability weightings are α and γ, respectively. Distortions in utility and probability (α, γ ≠ 1) characterize risk behavior, with α < 1 indicating risk aversion and γ < 1 indicating an overweighting of small probabilities. Conversely, α > 1 indicates risk-seeking behavior and γ > 1 indicates an underweighting of small probabilities, which means that participants who overvalue greater rewards and underestimate their goal-directed variability would likely choose riskier strategies. Additionally, randomness in a subject’s choices was quantified with the stochasticity parameter k, where k = 0 characterizes random choice.

Risk behavior was also quantified as the frequency of risky choices in each task. This value was expressed as the proportion of times the option with the greater variance was selected relative to the total number of trials. This parameter provides a global view of individual risk behavior, which can be compared across tasks and between participants (O’Brien and Ahmed 2015).

Statistics

Normality of data was assessed using the Shapiro-Wilkes test and verified visually with box plots and quantile-quantile plots (theoretical vs. sample quantiles). Age-group comparisons of functional performance were performed initially with a parametric t-test, fit with a linear model to identify a difference statistic, and verified with a linear model treating age (yr) as continuous. Decision-making characteristics were expressed as the median and 95% confidence interval of the median.

All repeated measures were examined using linear mixed-effects models controlling for random effects (subject) and the interactions between fixed effects. Differences in endpoint performance, utility, weighted probability, and frequency of risky choices were calculated using an age group-by-task (wrist extension vs. whole body lean) comparison. Analysis of wrist-extension force steadiness and EMG characteristics was performed using an age group-by-time (before vs. after endpoint practice) comparison. To assess the appropriate use of a linear model, the residuals for each model were plotted and inspected visually. When plotted residuals were visually identified to be nonuniform, as in the case with decision-making characteristics, a bootstrapping procedure was used to construct an empirical distribution of the difference between the median parameters (5,000 iterations), thereby making no assumptions about the distribution of these parameters.

To identify the association between decision-making characteristics and participant understanding of the ability to reach the target, Pearson correlation coefficients between measures were calculated. To verify significant associations and limit the influence of potential outliers, Pearson correlation and linear regression coefficients were bootstrapped by case resampling across 10,000 iterations to provide the bias-corrected and accelerated (BCa) 95% confidence interval.

A multiple regression analysis was used to identify the variables that could explain the variance in the time to complete the grooved pegboard test. Pearson correlation coefficients were calculated for all potential explanatory variables and verified with a bootstrapping procedure to provide the BCa 95% confidence interval. Variables with a significant Pearson correlation and a BCa 95% confidence interval that did not include zero were incorporated in the multiple regression analysis. The potential explanatory variables included functional measures (cognitive function, grip strength, and wrist extensor MVC force), movement variance and timing for each task (mean, SD, and coefficient of variation) at the target line and at maximal vertical distance (Fig. 2), decision-making characteristics (α, γ, and frequency of risky choices), and verbal response characteristics (average error of verbal response, RMSE of verbal response, and slope of the verbal response). Significantly associated variables were entered into a backward, stepwise regression analysis to identify significant explanatory variables for all participants (age collapsed), each age group (middle-aged and older adults), and two performance-based groups (slower and faster pegboard times). The number of explanatory variables was limited to one for approximately every 10 participants included in the sample. Multicollinearity of the explanatory variables was assessed with the variance inflation factor (VIF).

The selection of two performance-based groups was determined by the visually identified bimodal distribution of time to complete the grooved pegboard test and verified using the average silhouette approach. Participants were assigned to their respective group using K-means clustering with the maximum number of iterations set to 10. To verify the appropriate group assignment, the K-medoids method was used to select grooved pegboard times that corresponded to the most centrally located points (root sum of squares of differences) within the cluster, which are less influenced by potential outliers. An α level of P < 0.05 was used to identify significant differences, and all statistical analyses were performed using R (version 3.3.1).

RESULTS

The primary outcome variable was the time it took middle-aged and older adults to complete the grooved pegboard test. Secondary outcomes derived from measurements of motor function, performance variability, and decision-making strategies were used as inputs to regression analyses to explain the variance in pegboard times.

Functional Assessment

Time to complete the grooved pegboard test (Table 1) was 24.1% longer for older adults than middle-aged adults (P = 2.71e⁻⁶). On average, every year of increase in age was accompanied by a 0.66-s increase in time to complete the grooved pegboard test ([95% confidence interval], P value; [0.42, 0.89], P = 1.29e⁻⁶). In contrast, there were no differences in muscle strength between the two groups, with older adults having similar grip strength (7.3% difference, P = 0.41) and wrist-extension strength (6.8% difference, P = 0.49) relative to middle-aged adults (Table 1). Similarly, there were no group differences in cognitive function (0.4% difference, P = 0.59). However, middle-aged adults were able to lean slightly farther in the anterior direction (8.6% difference in CoP distance, P = 0.017) than the older adults; every year of increase in age was associated with a 0.033-cm decrease in maximal anterior lean ([0.009, 0.059], P = 0.0098). These results illustrate that only two of the five functional measures differed between the two age groups.

Table 1.

Participant characteristics

	Middle-Aged	Older	Difference	P Value
Age, yr	48 ± 6	73 ± 4	25 ± 2	2.20e−16
	[45, 51]	[71, 75]	[21, 28]
Pegboard time, s	53.1 ± 8.8	70 ± 11	17 ± 3	2.71e−6
	[49.1, 57.1]	[65, 76]	[11, 24]
Grip strength, kg	41 ± 11	38 ± 10	2.8 ± 3.4	0.4122
	[36, 46]	[33, 43]	[−9.53, 3.99]
Cognitive function, au	29.71 ± 0.56	29.60 ± 0.75	0.11 ± 0.21	0.5867
	[29.46, 29.97]	[29.25, 29.95]	[−0.54, 0.31]
Wrist extension strength, N	103 ± 38	96 ± 28	7.2 ± 10.5	0.4927
	[86, 120]	[82, 109]	[−28, 14]
CoP distance, cm	9.52 ± 0.97	8.7 ± 1.2	0.85 ± 0.34	0.0168
	[9.08, 9.96]	[8.1, 9.2]	[0.2, 1.5]

Values are means ± SD [95% confidence interval] for middle-aged and older adults. Difference values are means ± SE [95% confidence interval]. Center of pressure (CoP) distance represents the maximal anterior distance (cm) during maximal whole body lean.

Force Variability

Force steadiness.

Linear mixed-effects analysis indicated that there was no initial difference in force steadiness (coefficient of variation) for wrist-extension between middle-aged and older adults (β coefficient [95% confidence interval], P value; 0.25% [−0.06, 0.56] greater for older adults, P = 0.108; Table 2). Similarly, the absence of a difference in force steadiness was still present after practice of the movement variability task (0.04% [−0.25, 0.17] decrease after vs. before, P = 0.692; Table 2) with no significant group-by-time interaction (i.e., before vs. after endpoint practice) (0.04% [−0.26, 0.35], P = 0.779).

Table 2.

Force steadiness and EMG amplitude during steady contractions with wrist extensors at 10% MVC force performed before and after practicing the wrist-extension task

	Middle-Aged Adults		Older Adults
	Before	After	Before	After
CV for force, %	1.47 ± 0.69	1.38 ± 0.74	1.53 ± 0.45	1.64 ± 0.63
	[1.15, 1.78]	[1.04, 1.71]	[1.32, 1.74]	[1.34, 1.95]
Wrist extensors, mV	2.48 ± 0.83	2.76 ± 0.92*	2.81 ± 0.95	2.98 ± 0.97*
	[2.09, 2.86]	[2.33, 3.19]	[2.37, 3.26]	[2.50, 3.46]
Wrist flexors, mV	1.55 ± 0.63	1.56 ± 0.69	1.77 ± 0.74	1.66 ± 0.59
	[1.25, 1.84]	[1.26, 1.85]	[1.43, 2.12]	[1.38, 1.97]
Coactivation index, %	62.2 ± 4.1	64.4 ± 4.1*	62.1 ± 4.7	64.2 ± 5.1*
	[60.3, 64.1]	[62.5, 66.3]	[59.9, 64.3]	[61.7, 66.8]

Values are means ± SD [95% confidence interval]. Electromyography (EMG) amplitude (mV) was calculated as the sum of the monopolar recordings with the high-density electrodes. CV, coefficient of variation; MVC, maximum voluntary contraction.

^*P ≤ 0.0206 relative to before.

EMG activity.

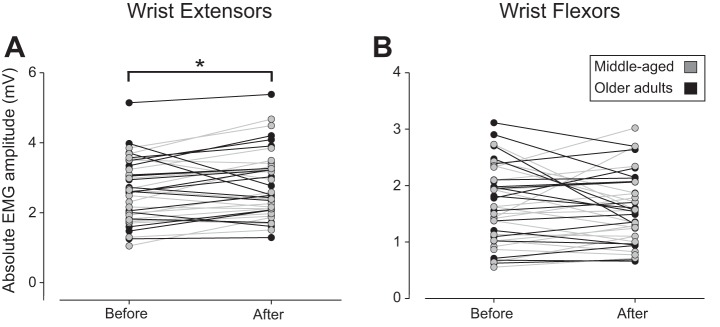
Absolute EMG amplitude of the wrist extensor muscles during the steady contractions increased by 0.18 mV ([0.03, 33], P = 0.0206; Fig. 3A) after participants practiced the movement-variability task with no difference between age groups (0.29 mV [−0.28, 0.86], P = 0.3019) and no significant group-by-time interaction (−0.12 mV [−0.34, 0.10], P = 0.2739; Table 2). Flexor EMG amplitude remained similar across time (−0.03 mV [−0.17, 0.11], P = 0.655; Fig. 3B) for both age groups (0.13 mV [−0.27, 0.52] middle-aged vs. older, P = 0.518) with no significant group-by-time interaction (−0.07 mV [−0.26, 0.13], P = 0.489).

Fig. 3.

Absolute electromyography (EMG) amplitude during the steadiness task (10% maximal voluntary contraction force) with the wrist extensors before and after participants practiced the movement-variability task with the wrist extensors. EMG amplitude (mV) was calculated as the sum of the monopolar recordings with the high-density electrodes for the wrist extensors (A) and wrist flexors (B). *P = 0.0206 for after relative to before task. Gray symbols indicate middle-aged adults; black symbols indicate older adults.

Because of the increase in wrist-extensor EMG amplitude and no change in flexor EMG amplitude, the coactivation index increased 1.89% ([0.93, 2.84]; P = 9.33e⁻⁵) from before to after practice. However, there was no statistical difference between age groups (difference = 0.81% [−1.87, 3.50]; P = 0.544) or group-by-time interaction (−0.53% [−1.88, 0.83]; P = 0.444) for the coactivation index. These findings indicate that the absolute EMG amplitude for the middle-aged and older adults was relatively similar before and after they practiced the movement-variability task, including the increase in wrist-extensor amplitude after the practice trials.

Performance Variability

Target line.

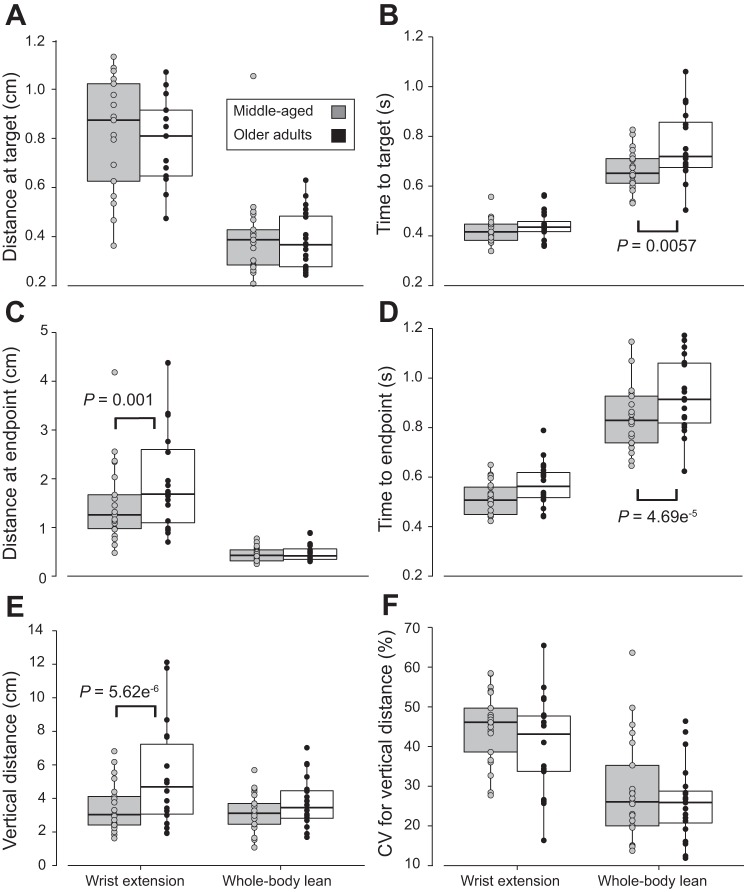
There was no age-group effect on the mediolateral location at which the cursor passed through the target line during either task (Fig. 4A). On average, middle-aged adults passed through the target line 1.01 cm lateral to the center during the wrist-extension task, whereas older adults passed through it 1.07 cm lateral to the center (difference = 0.055 cm [−0.103, 0.213], P = 0.4855). Similarly, middle-aged adults passed through the target line 0.40 cm lateral to the center during the whole body lean task, whereas older adults passed through it 0.38 cm lateral to the center (difference = −0.017 cm [−0.174, 0141], P = 0.8311).

Fig. 4.

Box plots showing distance and time measures for the movement-variability tasks of the middle-aged and older adults. A: mediolateral distance (cm) at the target. B: time (s) to reach the target. C: mediolateral distance (cm) at the endpoint. D: time (s) to reach the endpoint. E: maximal vertical distance at the endpoint (cm). F: coefficient of variation (CV) for maximal vertical distance (%). Horizontal lines of the box plot represent quartiles (25th, 50th, and 75th percentiles) of the distribution. Gray circles indicate middle-aged adults; black circles indicate older adults.

Similar to mediolateral location at the target line, no age-specific difference in time to pass through the target was identified during wrist extension with middle-aged adults passing through the target line in 0.42 s and older adults passing through it in 0.44 s (Fig. 4B; difference = 0.020 s [−0.023, 0.063], P = 0.349). In contrast, the average time to pass through the target line during the whole body lean task was significantly longer for older adults (0.76 s) than middle-aged adults (0.66 s) (difference = 0.10 s [0.06, 0.14], P = 0.0057).

Endpoint location.

Older adults exhibited greater average lateral distance (1.96 cm) from the centerline than middle-aged adults (1.49 cm) at wrist-extension endpoint (difference = 0.51 cm [0.20, 0.82], P = 0.00104; Fig. 4C), whereas the average lateral distance at the endpoint during whole body lean was similar between age groups (middle-aged = 0.45 cm; older adults = 0.48 cm; difference = 0.032 cm [−0.279, 0.342], P = 0.837). Time to reach the endpoint was not statistically different between age groups during wrist extension (middle-aged = 0.51 s; older adults = 0.56 s; difference = 0.058 s [−0.009, 0.124], P = 0.081), but middle-aged adults (0.84 s) were faster than older adults (1.02 s) during whole body lean (difference = 0.13 s ([0.07, 0.20], P = 4.69e⁻⁵; Fig. 4D). Interestingly, older adults reached a maximal vertical distance (6.88 cm) almost twice that of the middle-aged adults (3.48 cm) during wrist extension (difference = 3.40 cm [1.89, 4.90], P = 5.62e⁻⁶; Fig. 4E), whereas there was no significant difference in maximal vertical distance between the middle-aged (3.17 cm) and older adults (3.72 cm) during whole body lean (difference = 0.54 cm [−0.96, 2.04], P = 0.468). In contrast, the coefficient of variation for maximal vertical distance was similar between middle-aged (45%) and older adults (40%) for both wrist extension (difference = 4.4% [−1.3; 11.0]; P = 0.19) and whole body lean (middle-aged = 29%; older adults = 26%; difference = 2.9% [−4.4, 10.1,]; P = 0.428; Fig. 4F).

Decision Making

Measures of risk sensitivity.

Linear mixed-effects analysis indicated that there was no significant difference in utility (α) levels between age groups (−0.14 [−1.33, 1.05], P = 0.8185) or task (−0.19 [−1.20, 0.83], P = 0.7119) and no significant group-by-task interaction (0.54 [−0.92, 1.99], P = 0.4598; Table 3). Similarly, weighted probability (γ) values did not differ between age groups (0.34 [−2.16, 2.84], P = 0.789) or tasks (−0.11 [−2.58, 2.35], P = 0.928), and there was no significant group-by-task interaction (1.43 [-2.11, 4.97], P = 0.418). As with the other decision-making characteristics, the frequency of risky choices did not differ between age groups (0.087 [−0.1080, 0.1255], P = 0.882) or tasks (−0.01 9 [−0.089, 0.051], P = 0.582), and there was no interaction between age group and task (0.046 [−0.054, 0.146], P = 0.354).

Table 3.

Median parameter fits for measures derived from cumulative prospect theory

	Utility (α)	Weighted Probability (γ)	Stochasticity (k)
Middle-aged adults
Wrist extension	0.47	1.6	2.9
	[0.26, 0.99]	[1.0, 1.9]	[1.5, 16.4]
Whole body lean	0.51	1.3	4.7
	[0.19, 1.04]	[1.0, 1.8]	[2.3, 9.8]
Older adults
Wrist extension	0.5	1.4	3.8
	[0.23, 0.93]	[0.5, 2.3]	[2.5, 12.7]
Whole body lean	0.56	1.1	4.8
	[0.28, 1.03]	[0.63, 1.9]	[2.8, 10.8]

Values are medians [95% confidence interval of median]. α > 1 indicates risk-seeking behavior, γ > 1 denotes an underweighting of small probabilities, and k = 0 characterizes random choice. There were no significant differences between age groups and tasks.

To validate these comparisons, bootstrapping of the difference between the median parameters (5,000 iterations) verified the results of the linear mixed-effects analysis for α, γ, and frequency of risky choices. Furthermore, linear regression analysis (treating age as a continuous variable) yielded no effect of age on α (whole body lean = −0.004 [−0.049, 0.041], P = 0.86; wrist extension = 0.017 [−0.032, 0.065], P = 0.49), γ (whole body lean = 0.008 [−0.059, 0.075], P = 0.81; wrist extension = 0.045 [−0.077, 0.128], P = 0.46), or frequency of risky choices (whole body lean = 0.001 [−0.003, 0.006], P = 0.59; wrist extension = 0.003 [−0.002, 0.007], P = 0.24).

Because of the variable distributions of the residuals for the stochasticity parameter (k) (Table 3), only the bootstrapping procedure was used to examine age-group and task-specific differences in choice randomness. Stochasticity of choice (k) did not differ between wrist extension and whole body lean for middle-aged (median difference = 0.0009 [−0.91, 36.48], P = 0.4224) or older adults (median difference = 0.48 [−3.98, 7.79], P = 0.7526). Similarly, no differences were found between middle-aged and older adults in stochasticity parameter (k) for either wrist extension (median difference = 0.051 [−15.02, 1.32], P = 0.5754) or whole body lean (median difference = 0.0078 [−5.84, 3.66], P = 0.921).

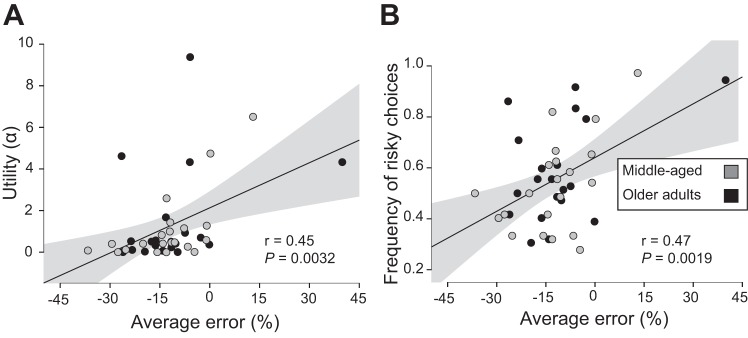
Despite the lack of differences in risk-sensitivity characteristics between age groups and the two goal-directed tasks, participants’ understanding of the variability in their performance was significantly related to risk profile when the two age groups were combined (Figs. 5 and 6). Average error of the perceived probability to pass through the displayed target indicated that participants tended to underestimate their ability to pass through a given target width (wrist extension: −12 ± 13% [−16, −8]; whole body lean: −14 ± 22% [−20, −7]). Each unit increase in average error was associated with a 0.072 [0.027, 0.142] unit increase in wrist-extension α (Pearson’s r = 0.45 [0.08, 0.70], P = 0.0032; Fig. 5A), a 0.007 [0.0014, 0.0112] unit increase in the frequency of risky choice during wrist extension (Pearson’s r = 0.47 [0.09, 0.70], P = 0.0019; Fig. 5B), a 0.035 unit increase in whole body lean α (Pearson’s r = 0.40, P = 0.0089; Fig. 6A), and a 0.0046 [0.0003, 0.0068] unit increase in the frequency of risky choice during whole body lean (Pearson’s r = 0.53 [0.10, 0.76], P = 0.00042; Fig. 6B).

Fig. 5.

Pearson’s r between measures derived from cumulative prospect theory and measures of performance variability for the wrist-extension task. Utility (α) denotes risk sensitivity with α < 1 showing risk-averse behavior and α > 1 showing risk-seeking behavior. Frequency of risky choices was quantified as the ratio of number of times the riskier option was chosen. The average error between the verbal response and actual probability (average difference) provides a directional assessment of underestimating (negative) or overestimating (positive) motor variability. A: average error of the perceived probability and utility (α). B: average error of the perceived probability and the frequency of risky choices. Gray circles indicate middle-aged adults; black circles indicate older adults. Shaded area about the regression line denotes the SE of the regression.

Fig. 6.

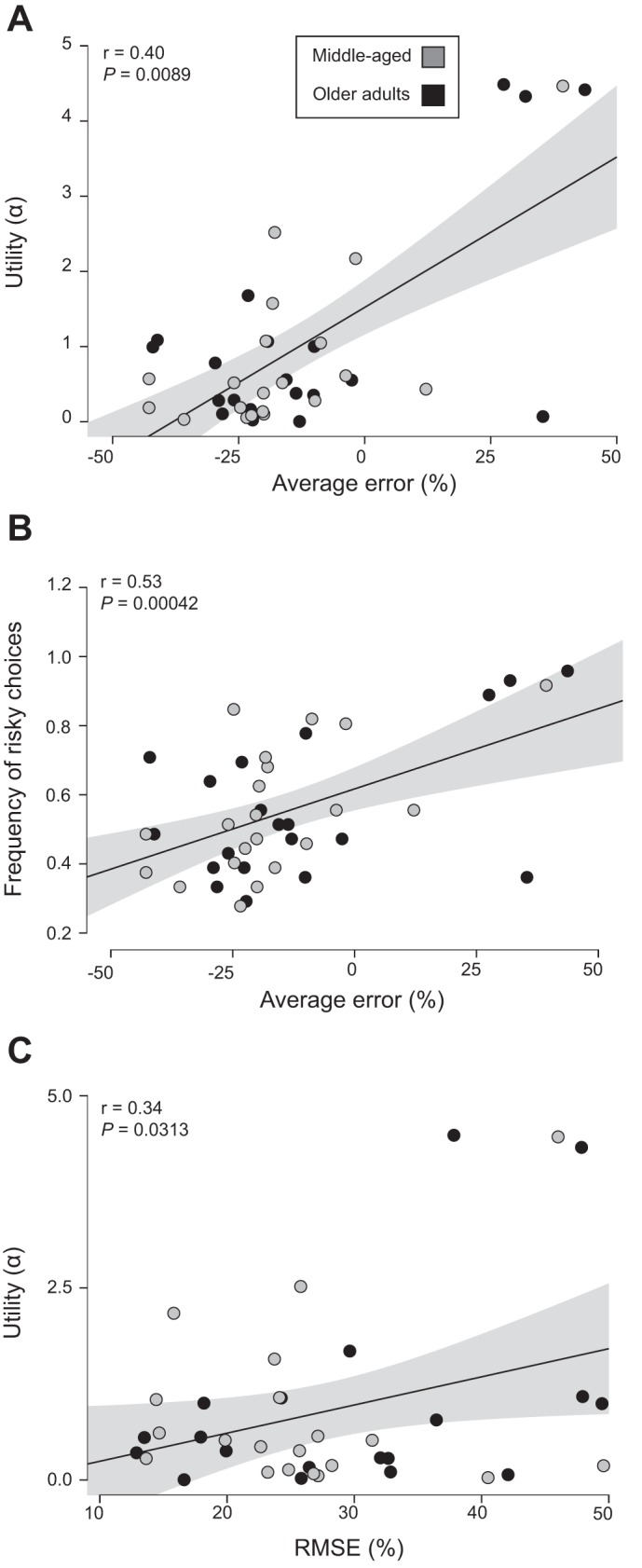
Pearson’s r between measures derived from cumulative prospect theory and measures of performance variability for whole body lean. Utility (α) denotes risk sensitivity with α < 1 showing risk-averse behavior and α > 1 showing risk-seeking behavior. Frequency of risky choices was quantified as the ratio of number of times the riskier option was chosen. The average error between the verbal response and actual probability (average difference) provides a directional assessment of underestimating (negative) or overestimating (positive) motor variability. Root mean square error (RMSE) of the difference between the verbal response and actual probability provided a nondirectional measure of accuracy of motor variability. A: average error of the perceived probability and utility (α). B: average error of the perceived probability and the frequency of risky choices. C: RMSE of perceived motor variability and utility (α). Gray circles indicate middle-aged adults; black circles indicate older adults. Shaded area about the regression line denotes the SE of the regression.

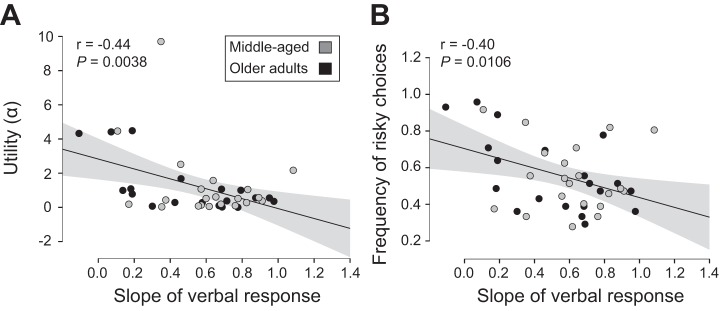
Similar to average error, the RMSE of the difference between the verbal response (perceived probability of passing through a target) and actual probability was significantly associated with risk profile; each unit increase in RMSE was associated with a 0.057 [0.012, 0.107] unit increase in whole body lean α (Pearson’s r = 0.34 [0.08, 0.60], P = 0.0313; Fig. 6C). Also, the slope of the participant verbal response across the probability range was negatively associated with risk profile; every unit increase in the slope of the verbal response was associated with a 2.90 [0.94, 4.93] unit decrease in whole body lean α (Pearson’s r = −0.44 [−0.68, −0.14], P = 0.0038; Fig. 7A) and a 0.267 [−0.003, 0.478] unit decrease in the frequency of risky choice for the whole body lean (Pearson’s r = −0.395 [−0.671, −0.002], P = 0.0106; Fig. 7B). These results indicated that those who had a better understanding of their motor variance exhibited less risk-seeking behavior. Similar age-specific associations between decision-making characteristics and risk profile were observed for each age group (data not shown).

Fig. 7.

Pearson’s r between the slope of the verbal response and measures of performance variability for whole body lean. Utility (α) denotes risk sensitivity with α < 1 showing risk-averse behavior and α > 1 showing risk-seeking behavior. Frequency of risky choices was quantified as the ratio of number of times the riskier option was chosen. Slope of the verbal response represents the linear relation between participant estimates of ability to pass through the target throughout the range of presented target widths. A: slope of the perceived probability and utility (α). B: slope of the perceived probability and the frequency of risky choices. Shaded area about the regression line denotes the SE of the regression.

Predictive Pegboard Models

Combined model.

The analysis to explain the variance in pegboard times for all participants (middle-aged + older adults) converged on a model with two variables: 1) age (β coefficient = 0.62 [0.38, 0.87], VIF = 1.0388; partial r = 0.66) and 2) coactivation index during the steadiness task with the wrist extensors (β coefficient = 0.68 [0.03, 1.32], VIF = 1.0388; partial r = 0.34). This model indicated that longer times to complete the grooved pegboard test were positively associated with advancing age and a greater relative amount of wrist-extensor EMG activity during the force-steadiness task. This model explained 51% of the variance in time to complete the grooved pegboard test (P = 3.615e⁻⁶). The secondary variables included in the stepwise-regression approach were age (β coefficient = 0.65 [0.43, 0.86]; Pearson’s r = 0.68 [0.43, 0.79], P = 1.29e⁻⁶) and the variables listed in Table 4.

Table 4.

Correlations between pegboard times and performance outcomes for both age groups combined

	Pearson’s r	β Coefficient	P Value
Wrist extension
Average time to endpoint, s	0.34	55.7	0.0289
	[0.03, 0.59]	[6.4, 95.3]
SD of vertical distance, cm	0.38	4.91	0.0136
	[0.01, 0.67]	[−0.27, 8.16]
Average of vertical distance,  cm	0.45	1.33	0.0034
	[0.07, 0.71]	[0.09, 1.87]
SD of mediolateral distance  at endpoint, cm	0.48	6.67	0.0014
	[0.19, 0.72]	[2.49, 8.73]
Average mediolateral  distance endpoint, cm	0.46	5.96	0.0028
	[0.13, 0.70]	[1.48, 8.58]
Whole body lean
Maximal anterior lean, cm	−0.41	−4.67	0.0080
	[−0.63, −0.12]	[−7.13, −1.45]
Coactivation index, %	0.34	1	0.0200
	[0.002, 0.63]	[0.03, 1.80]
RMSE	0.38	0.4	0.0329
	[0.03, 0.58]	[0.05, 0.72]
Average time to target line, s	0.44	47	0.0039
	[0.20, 0.67]	[17.1, 79.5]
Average time to endpoint, s	0.33	26.1	0.0215
	[0.09, 0.61]	[5.2, 52.0]

Values are coefficients [bias-corrected and accelerated 95% confidence interval]. SD, standard deviation; RMSE, root mean square error.

Middle-aged adults.

The analysis for explaining the variance in pegboard times of middle-aged adults converged on a model (R² = 0.50, P = 0.002039) with two variables: 1) coefficient of variation for the maximal vertical distance during whole body lean (β coefficient = 0.18 [−0.08, 0.56], VIF = 1.2875; partial r = 0.32) and 2) average mediolateral error at the center of the target line during wrist extension (β coefficient = −5.82 [−10.17, −1.48], VIF = 1.2875; partial r = −0.55). To account for two potential outliers identified by visual inspection of the plotted residuals, regression coefficients were bootstrapped by case resampling across 10,000 iterations and yielded 1) coefficient of variation for the maximal vertical distance during whole body lean (β coefficient = 0.18 [−0.11, 0.56], boot bias = −0.0063) and 2) average mediolateral error at the center of the target line during wrist extension (β coefficient = −5.54 [−11.16, 1.09], boot bias = 0.9372). However, average mediolateral error at the center of the target line during wrist extension by itself explained 44% of the variance in time to complete the grooved pegboard test. Therefore, increased variability of a kinematic measure during a whole body, target-matching task and wrist extensor variability were associated with longer pegboard times. The secondary variables included in the middle-aged stepwise analysis are listed in Table 5.

Table 5.

Correlations between pegboard times and outcome variables for the two age groups

	Pearson’s r	β Coefficient	P Value
Middle-aged adults
Wrist extension
Average mediolateral error  at target line, cm	−0.66	−7.23	0.0011
	[−0.94, −0.01]	[−10.03, −0.13]
CV for mediolateral variance  at target line, %	−0.59	−0.37	0.0048
	[−0.89, −0.10]	[−0.66, −0.4]
Whole body lean
Average vertical distance,  cm	−0.47	−3.67	0.0296
	[−0.76, −0.09]	[−8.99, −0.82]
CV for vertical  distance, %	0.53	0.35	0.0144
	[0.09, 0.76]	[0.14, 0.89]
Average time to target  line, s	0.51	55.46	0.0193
	[0.08, 0.82]	[7.5, 124.9]
Older adults
Wrist extension
Average mediolateral error  at target line, cm	0.6	7.85	0.0056
	[0.18, 0.82]	[4.40, 11.16]

Values are coefficients [bias-corrected and accelerated 95% confidence interval]. CV, coefficient of variation.

Older adults.

The analysis for explaining the variance in pegboard times of older adults converged on a model with one variable: average mediolateral error at the center of the target line during wrist extension (β coefficient = 7.85 [2.60, 13.10], P = 0.00564; Pearson’s r = 0.60). This result showed that a relative mediolateral error to the right of the target line during wrist extension was associated with longer pegboard times, which explained 35% of the variance in the pegboard times of the older adults (Table 5).

K-means cluster analysis.

To identify explanatory variables independent of age category, a K-means cluster analysis separated participants into a slower group (pegboard time = 76.6 ± 7.4 s, n = 15) and a faster group (pegboard time = 52.9 ± 5.5 s, n = 26; difference = 23.8 s [20.9, 26.6], P = 2.2e⁻¹⁶). Despite the slower group (70 ± 8 yr) being, on average, 15 yr older (P = 3.92e⁻⁵; Table 6) than the faster group (55 ± 13 yr), the range of ages encompassed by both groups was similar (slower group = 51–79 yr; faster group = 40–78 yr; Fig. 8). Similar to age-group comparisons, no difference was found between the slower group (1.47% ± 0.44 [1.23, 1.72]) and the faster group (1.33% ± 0.49 [1.13, 1.53]) for the average coefficient of variation for force during wrist extension (difference = 0.14% [−0.17, 0.45]; P = 0.3703). The only other significantly different functional measure between the groups was maximal forward lean (Table 6), with the faster group (9.56 ± 1.02 cm) leaning 11% farther than the slower group (8.50 ± 1.13 cm; P = 0.0081). This result shows that only two of the five functional measures differed between groups when category was determined by grooved pegboard time.

Table 6.

Characteristics of the two groups identified by K-means cluster analysis

	Slower	Faster	Difference	P Value
Age, yr	70 ± 8	55 ± 13	15 ± 4	3.92e−5
	[65, 74]	[49, 60]	[9,22]
Pegboard time, s	77 ± 7	53 ± 5	24 ± 2	1.87e−10
	[72, 81]	[51, 55]	[19, 28]
Grip strength, kg	40 ± 12	39 ± 10	1.55 ± 3.50	0.6778
	[34, 47]	[35, 43]	[-6.06, 9.16]
Cognitive function, au	29.60 ± 0.83	29.69 ± 0.55	0.09 ± 0.21	0.7306
	[29.14, 30.06]	[29.47, 29.91]	[−0.59, 0.41]
Wrist extension strength, N	98 ± 26	101 ± 37	3 ± 11	0.7617
	[83, 112]	[86, 116]	[−23, 17]
CoP distance, cm	8.50 ± 1.13	9.46 ± 1.02	0.96 ± 0.34	0.0081
	[7.87, 9.13]	[9.05, 9.87]	[0.23, 1.69]

Values are means ± SD [95% confidence interval] for the slower and faster group values. Difference values are means ± SE [95% confidence interval]. Center of pressure (CoP) distance represents the maximal anterior distance (cm) during maximal whole body lean.

Fig. 8.

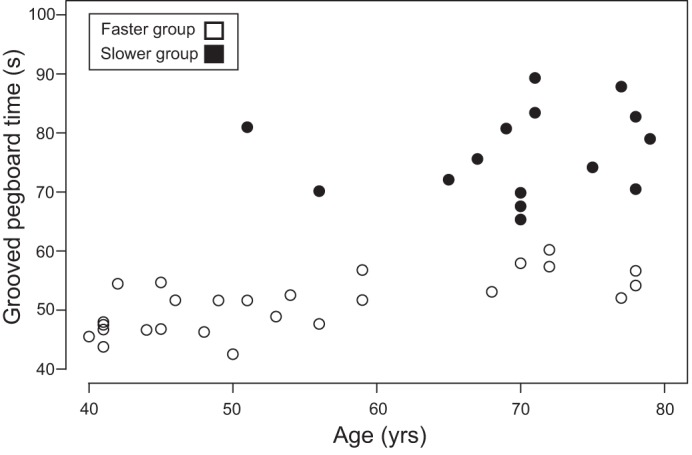
K-means clustered pegboard times (s) for the slower group and faster group plotted by age (yr). Closed circles indicate the slower group; open circles indicate the faster group.

Linear mixed-effects analysis indicated that there was no significant difference in utility (α) values between clusters (0.03 [−1.18, 1.25], P = 0.9600) and task (0.82 [−0.35, 2.00], P = 0.1606), and there was no significant cluster-by-task interaction (−1.17 [−2.65, 0.30], P = 0.1091; Table 7). Similarly, weighted probability (γ) values did not differ between clusters (−0.89 [−3.46, 1.68], P = 0.493) or tasks (1.62 [−1.28, 4.51], P = 0.2682), and there was no significant cluster-by-task interaction (−1.62 [−5.26, 2.01], P = 0.376). Resampling of the median difference between clusters (5,000 iterations) verified the results of the linear mixed-effects analysis for α and γ, and identified no difference in stochasticity of choice (k) between wrist extension and whole body lean for the slower group (median difference = 0.0009 [−0.91, 36.48], P = 0.4224) or faster group (median difference = 0.48 [−3.98, 7.79], P = 0.7526). Furthermore, no differences were found between the slower group and faster group in stochasticity parameter (k) for either wrist extension (median difference = 0.051 [−15.02, 1.32], P = 0.5754) or whole body lean (median difference = 0.0078 [−5.84, 3.66], P = 0.921).

Table 7.

Cumulative prospect theory parameter fits for the two groups identified by K-means cluster analysis

	Utility (α)	Weighted Probability (γ)	Stochasticity (k)
Slower
Wrist extension	0.7	1.8	2.9
	[0.11, 2.59]	[0.02, 2.4]	[0.4, 9.6]
Whole body lean	0.56	1.1	3.6
	[0.28, 1.07]	[0.4, 1.9]	[1.9, 6.4]
Faster
Wrist extension	0.41	1.5	3.9
	[0.23, 0.56]	[1.0, 1.9]	[2.1, 15.8]
Whole body lean	0.48	1.3	5.2
	[0.16, 0.78]	[0.8, 1.8]	[2.3, 12.6]

Values are medians [95% confidence interval of median]. α > 1 indicates risk-seeking behavior, γ > 1 denotes an underweighting of small probabilities, and k = 0 characterizes random choice. There were no significant differences between age groups and tasks.

In contrast to the results from the age-group comparisons, the frequency of risky choices did not differ between clusters (−0.03 [−0.1080, 0.1255], P = 0.5723) or tasks (0.07 [−0.089, 0.051], P = 0.075), but a significant cluster-by-task interaction was identified (−0.11 [−0.21, −0.006], P = 0.0333). Resampling of the mean difference between clusters (5,000 iterations) identified a significant difference between the slower group and faster group in frequency of risky choice for the wrist-extension task (mean difference = 0.14 [0.02, 0.26], P = 0.0212). This result indicated that the slower group (0.65 ± 0.20 [0.53, 0.76]) more frequently chose the riskier option than the faster group (0.51 ± 0.17 [0.44, 0.57]) during wrist extension. However, no difference was found between the slower group and faster group in frequency of risky choice for whole body lean (mean difference = 0.001 [−0.064, 0.190], P = 0.6226) or between wrist extension and whole body lean for the slower group (mean difference = 0.002 [−0.28, 0.0018], P = 0.3424) or faster group (mean difference = 0.001 [−0.029, 0.175], P = 0.4892).

The regression analysis for the slower group identified a model (R² = 0.44, P = 0.02969) with two explanatory variables: 1) whole body lean α (β coefficient = 2.29 [−0.24, 4.83], VIF = 1.09; partial r = 0.49) and 2) standard deviation of the mediolateral distance from the centerline at the endpoint of the wrist-extension task (β coefficient = 3.26 [−0.90, 7.42], VIF = 1.09; partial r = 44). This model showed a relative increase in risk-seeking behavior, and increased motor variability during one of the goal-directed tasks was associated with slower pegboard times. The secondary variables included in the stepwise model are listed in Table 8.

Table 8.

Correlations between pegboard times and outcome variances for the two groups identified by K-means cluster analysis

	Pearson’s r	β Coefficient	P Value
Slower group
Wrist extension
SD of mediolateral distance  at endpoint, cm	0.51	4.36	0.0496
	[0.04, 0.86]	[0.33, 6.58]
Average mediolateral distance  at endpoint, cm	0.53	2.95	0.0430
	[0.10, 0.86]	[0.93, 4.69]
Whole body lean
Utility (α)	0.56	2.88	0.0317
	[0.02, 0.87]	[0.38, 4.47]
Faster group
Wrist extension
CV for wrist extension force	0.45	3.21	0.0219
	[0.06, 0.69]	[0.82, 5.01]
Whole body lean
CV for vertical distance, %	0.41	0.18	0.0350
	[0.05, 0.67]	[0.02, 0.33]
SD of time to target line, s	0.47	37.021	0.0154
	[0.1, 0.70]	[8.28, 62.15]

Values are coefficients [bias-corrected and accelerated 95% confidence interval]. SD, standard deviation; CV, coefficient of variation.

Regression analysis for the faster group identified a model (R² = 0.59, P = 3.691e⁻⁵) with two variables: 1) age (yr) (β coefficient = 0.27 [0.16, 0.39], VIF = 1.0125; partial r = 0.71) and 2) coefficient of variation for maximal vertical distance during whole body lean (β coefficient = 0.15 [0.03, 0.27], VIF = 1.0125; partial r = 0.47). Alternatively, regression analysis that did not include age identified a model (R² = 0.32, P = 0.0127) with two variables: 1) coefficient of variation for force during wrist extension (β coefficient = 2.76 [0.16, 5.36], VIF = 1.05; partial r = 0.42) and 2) coefficient of variation for maximal vertical distance during whole body lean (β coefficient = 0.15 [−0.007, 0.302], VIF = 1.05; partial r = 0.38). The models indicated that advancing age and increased motor variability during target-directed actions were associated with longer pegboard times. Secondary variables included in the stepwise regression analysis included age (β coefficient = 0.29 [0.17, 0.40]; Pearson’s r = 0.69 [0.41, 0.83]; P = 0.0001054) and the variables listed in Table 8.

DISCUSSION

The goal of our study was to identify the decision-making strategies used by middle-aged and older-adults when performing two goal-directed motor tasks and to determine if these strategies were associated with the time to complete the grooved pegboard test. Decision-making strategy was assessed by measuring movement variability during targeted whole body lean and wrist-extension actions, and then quantifying perceived motor variability in these tasks and risk sensitivity through monetary choices tied to performance. The main finding of the study was that the pegboard times of each age group were not related to decision-making characteristics, but were associated with measures of performance variability during goal-directed wrist-extension and whole body lean tasks, with greater variability predicting slower pegboard times. When the data were clustered on the basis of pegboard time rather than age, however, one of the explanatory variables for the slower group was a measure of risk sensitivity with a relative increase in risk-seeking behavior (α) being associated with a longer time to complete the pegboard test. This result underscores the need for studies on sensorimotor function in middle-aged and older adults to categorize participants on the basis of a performance metric rather than chronological age.

Decision-Making Characteristics

Previous research has used cumulative prospect theory to characterize the risk-behavior profiles of individuals with weightings of reward and probability. O’Brien and Ahmed (2013) found that healthy young adults exhibit risk-seeking behavior in whole body lean and arm-reaching tasks to the edge of a virtual cliff. Participants overvalued the rewards (α > 1) and underweighted probability (γ >1), moving closer to the edge of the virtual cliff than predicted with subject-specific risk-neutral models of movement planning (O’Brien and Ahmed 2013). When young adults performed similar targeted leaning and reaching tasks on a platform that was raised 0.8 m, however, their behavior became more risk averse (O’Brien and Ahmed 2015). The reward achieved by successfully completing a desired goal-directed action, therefore, was valued less when the action became riskier due to the increased postural threat.

Contrary to our hypothesis, risk profile did not differ between middle-aged and older adults (Table 3). However, our results on median utility (α) values were comparable to those reported for young adults when the tasks were performed on a raised platform (arm reaching high = 0.53 [0.29, 0.87]; whole body lean high = 0.49 [0.36, 0.92]; O’Brien and Ahmed 2015). This similarity suggests that valuation of movement reward by middle-aged and older adults was skewed by an internal assessment of movement risk, or trial-to-trial variability (Stergiou et al. 2006; Stergiou and Decker 2011), when they performed goal-directed actions. Consistent with this interpretation, O’Brien and Ahmed (2013) suggested that variability in risk behavior could result from an inappropriate estimate of movement variability about a prescribed endpoint. Specifically, when participants perceive their movement variability to be less than the actual variability, they would be more willing to choose riskier movements. Conversely, when participants perceive movement variability about a prescribed endpoint to be greater than its actual value, they would assign a lower probability to reaching a given target (O’Brien and Ahmed 2013, 2016). This interpretation is consistent with our findings of a positive correlation between the perceived ability to reach a target and risk-seeking behavior (Fig. 5 and 6). Consequently, middle-aged and older adults who overestimated their ability to reach a target were more likely to choose riskier movement options, and conversely for those who underestimated their ability.

To further support this finding, we measured subject-specific characteristics as the slope of each participant’s verbal response across a range of target widths (probabilities). A slope of less than 1 indicated a verbal response with a progressively lower value below the larger targets (higher probabilities), a slope of exactly 1 represented a proportional value of the target width presented across the entire range, and a slope of greater than 1 denoted a progressively greater value for the larger target widths. The negative association between slope of the verbal response and risk profile (Pearson’s r = −0.44, P = 0.0038) indicated that those who had a better understanding of their motor variability exhibited less risk-seeking behavior and a lower frequency of risky choices (Pearson’s r = −0.40, P = 0.0106). Taken together, these findings indicate that middle-aged and older adults (independent of age) who had a better understanding of their motor variability during goal-directed actions, particularly across the entire range of target widths, exhibited a more rational movement strategy. Understanding changes in motor variability, therefore, seems to be as important as knowing changes in movement capabilities.

Predictive Pegboard Models

The statistical model for all participants explained 51% of the variance in pegboard time. The explanatory variables were age (partial r = 0.66) and the EMG coactivation index during the steady wrist-extension task (partial r = 0.34). Advancing age is commonly associated with declines in manual dexterity (Reuben et al. 2013; Wang et al. 2011, 2015), and adjustments in muscle activation (Christou et al. 2007; Kornatz et al. 2005; Laidlaw et al. 1999, 2000) likely contribute to decreases in manual dexterity, although age was the more dominant variable in our cohort.

A cross-sectional study of young, middle-aged, and older adults (n = 25 in each group) found two variables (force steadiness for index finger abduction and grip strength) explained a significant amount of the variance (R² = 0.36) in the time to complete the grooved pegboard test (Marmon et al. 2011). When these data were examined for each age group, however, a statistically significant regression model (R² = 0.59) was only identified for older adults (75 ± 6 yr, n = 25); the three predictor variables were age, force steadiness for index finger abduction, and pinch-grip strength.

Our subsequent studies have developed models for each age group separately to increase the explanatory power when predicting time to complete the grooved pegboard (Almuklass et al. 2017; Feeney et al. 2018; Hamilton et al. 2017). For example, Hamilton et al. (2017) used a data-reduction approach to identify latent variables underlying the variance in pegboard times for middle-aged and older adults. This approach yielded six latent variables for middle-aged adults (51.3 ± 6.8 yr) with the first three latent variables describing 72.4% of the covariance. The latent variables included measures of force steadiness (coefficient of variation) for index finger abduction at 5% and 10% MVC force. The analysis for older adults (73.8 ± 6.9 yr) yielded three latent variables that described 100% of the covariance and included measures of age and working memory.

A significant feature of the two studies on older adults (65–89 yr) was the emergence of age as an explanatory variable (Hamilton et al. 2017; Marmon et al. 2011), which underscores a limitation of using chronological age as a factor to distinguish groups. In our current study, for example, 35% of the variance in the time for older adults to complete the grooved pegboard was associated with the amount of supination of the forearm as the hand crossed the target line, which provides limited insight on the underlying physiology. As an alternative approach, we stratified performance on the basis of pegboard time rather than age. The approach was based on the rationale that the distribution of pegboard times becomes more variable with advancing age (Wang et al. 2011, 2015) and outcomes depend on the physiological characteristics of the individuals included in the sample. This performance-based approach used K-means clustering to identify two groups independent of age: one group of individuals whose pegboard times were faster than another group of participants.

The statistical model for the slower group explained 44% of the variance in pegboard times with two variables: whole body lean utility (α) and standard deviation of the mediolateral distance at the endpoint of the wrist-extension task. The first explanatory variable indicates that each unit increase in the value for the whole body lean utility was associated with a 2.29-s increase in pegboard time (partial r = 0.49). Thus participants who were relatively more risk seeking when performing the whole body lean task to the prescribed target took longer to complete the pegboard test. This result ran counter to our hypothesis that risk aversion would be associated with longer pegboard times. Perhaps the relatively more risk-seeking individuals underestimated their movement variability during goal-directed actions and took longer to select and insert each peg into its hole during the pegboard test (Almuklass et al. 2018b). Consistent with this interpretation, we observed a 0.14 proportional increase in the frequency of risky choices for the slower group during the wrist-extension task; the slower group (0.65 ± 0.20 [0.53, 0.76]) more frequently chose the riskier option than the faster group (0.51 ± 0.17 [0.44, 0.57]). The other explanatory variable for the slower group was a measure of movement variability during targeted actions. Each unit increase in the standard deviation of the mediolateral distance from the centerline at the endpoint during the wrist-extension task was associated with a 3.26-s increase in pegboard time (partial r = 0.44).

The statistical model for the faster group explained 59% of the variance in pegboard times with two variables: age and the coefficient of variation for endpoint vertical distance during the whole body lean task. Similar to the findings reported by Marmon et al. (2011), each year increase with advancing age was associated with a 0.27-s increase in time to complete the grooved pegboard test (partial r = 0.71). The second explanatory variable for the faster group indicated that each unit increase in the coefficient of variation for maximal distance during whole body lean was associated with a 0.15-s increase in pegboard time (partial r = 0.47). It is somewhat surprising that a specific measure of movement variability involving a goal-directed whole body task was significantly associated with pegboard times rather than an action involving the upper limbs. However, the finding is consistent with the interpretation that tests of manual dexterity provide global measures of physical function (Almuklass et al. 2018a).

The statistical model that excluded age for the faster group explained 32% of the variance in grooved pegboard times with two variables: force steadiness (coefficient of variation for force) during wrist extension and the coefficient of variation for endpoint vertical distance during the whole body lean task. The first explanatory variable indicates that each unit increase in the coefficient of variation for force during the wrist-extension task was associated with a 2.76-s increase in pegboard time (partial r = 0.42). The emergence of force steadiness as an explanatory variable for differences in pegboard times is consistent with previous reports (Almuklass et al. 2016; Hamilton et al. 2017; Marmon et al. 2011). This result indicates that those participants with worse force steadiness, and hence greater variability in the common modulation of motor unit discharge rates during a force-matching task (Farina and Negro 2015; Feeney et al. 2017; Negro et al. 2009; Thompson et al. 2018), had longer pegboard times. Similar to the model for the faster group that included age, a 1-unit increase in coefficient of variation for maximal distance during whole body lean was associated with a 0.15-s increase in pegboard time (partial r = 0.38).

One consistent result in our statistical models was that greater motor variability during target-directed tasks was associated with longer pegboard times. Previous research strongly supports this observation (Almuklass et al. 2016; Hamilton et al. 2017; Marmon et al. 2011) and highlights the importance of reducing motor variability to improve functional performance. However, counter to our hypothesis that the coefficient of variation during the steady wrist-extension task would be greater for older adults compared with middle-aged adults, the values did not differ between middle-aged and older adults (Table 2). In contrast, other studies have shown that older adults consistently have a greater coefficient of variation for force during wrist-extension tasks (Feeney et al. 2018; Hamilton et al. 2017). Furthermore, the pegboard performance of the middle-aged adults (53.1 ± 8.8 s) and older adults (70 ± 11 s) was remarkably faster than those reported previously: 60.0 ± 8.5 and 80.8 ± 18.1 s for middle-aged and older adults, respectively (Hamilton et al. 2017), and 65.7 ± 8.6 and 88.9 ± 15.7 s, respectively (Marmon et al. 2011). This difference in pegboard times may be due to some potential volunteers not being willing to perform the whole body lean task while standing on a platform, possibly resulting in a self-selected group of higher functioning older adults.

One of the limitations of our study, therefore, is that the results may not generalize to all healthy older adults, because our participant group was more homogenous than previous cohorts. Also, the amount of variance in the time to complete the grooved pegboard test explained by the regression models was rather limited. In a study measuring manual dexterity performance in 30 young men and women (24.2 ± 4.0 yr; 15 women), 70% of the variance in time to complete the grooved pegboard test was explained by time to match a rapid 10% MVC pinch target during wrist extension and the coefficient of variation for force during 10% MVC wrist extension (Almuklass et al. 2016). Similarly, the results of Marmon et al. (2011) revealed that 59% of the variance in time it took 25 older adults (74.5 ± 6.3 yr) to complete the grooved pegboard test was explained by age, force steadiness (coefficient of variation) for index finger abduction, and pinch grip strength. Additionally, time to complete the grooved pegboard test for 25 middle-aged adults (51.3 ± 6.8 yr; 14 women) was associated with force steadiness of index finger abduction during wrist extension at 5% and 10% MVC forces and 5% MVC force steadiness during index finger abduction only (Hamilton et al. 2017). All three of these studies included at least one measure of index finger abduction in relation to time to complete the grooved pegboard test. Unfortunately, we did not include any measure of index finger abduction in our study, which likely limited the amount of variance explained by the emergent regression models.

Conclusions

Decision-making characteristics were not associated with time to complete the test of manual dexterity when the analysis included both the middle-aged and older participants. However, when groups were stratified on the basis of pegboard time, the utility (α) function during whole body lean to a prescribed target, along with the standard deviation of mediolateral variability at maximal endpoint during wrist extension, was found to explain 44% of the variance in time to complete the grooved pegboard test for slower performers. Similarly, the pegboard times for the faster cohort were explained by the coefficient of variation for force during wrist extension and variability (coefficient of variation) in maximal vertical distance during whole body lean. Overall, greater motor variability during goal-directed actions, and thus greater motor risk, was associated with longer pegboard times. The results showed that, independent of age, middle-aged and older adults who underestimated their movement variability during targeted actions chose riskier movement strategies that were associated with longer grooved pegboard times. A key finding of our study is that future work on the sensorimotor capabilities of middle-aged and older adults should not rely exclusively on the categorization of participants by chronological age.

DISCLOSURES

No conflicts of interest, financial or otherwise, are declared by the authors.

AUTHOR CONTRIBUTIONS

L.D.H., A.A.A., and R.M.E. conceived and designed research; L.D.H., M.R.M., and L.P. performed experiments; L.D.H. and L.P. analyzed data; L.D.H. interpreted results of experiments; L.D.H. and M.R.M. prepared figures; L.D.H. and R.M.E. drafted manuscript; L.D.H., M.R.M., L.P., A.A.A., and R.M.E. edited and revised manuscript; L.D.H., M.R.M., L.P., A.A.A., and R.M.E. approved final version of manuscript.