Abstract
Protective arm reactions were evoked in 14 younger adults to determine the effect of fall height on protective arm reaction biomechanics. Participants were supported in a forward-leaning position on top of an inverted pendulum that isolated arm reaction by preventing any fall arresting contribution that may come from the ankle, knees, or hip. At an unpredictable time, the pendulum was released requiring participants to rapidly oriented their arms to protect the head and body. Vertical ground reaction force (vGRF), arm kinematics, and electromyographic (EMG) measures of the biceps and triceps were compared at four initial lean angles. The time following perturbation onset and prior to impact consisted of two phases: rapid extension of the elbows and co-activation of the biceps and triceps in preparation for impact. The rapid orientation phase was modulated with fall height while the co-activation of the biceps and triceps in preparation for landing was minimally affected. Larger lean angles resulted in increased vGRF, increased elbow extension at impact, decreased elbow angular extension velocity at impact, and increased neck velocity at impact while hand velocity at impact was not significantly affected. The neuromuscular control strategy appears to optimize elbow extension angle/angular velocity prior to co-activation of the biceps and triceps that occurs about 100 ms prior to impact. Future work should investigate how the neuromuscular control strategy handles delayed deployment of protective arm reactions.
Keywords: Upper extremity, falls, injury
1. Introduction
Hip fractures represent a significant societal burden. The number of hip fractures (Brauer et al., 2009), the high mortality (see Schnell et al., 2010 for a summary), the health and care costs (Williamson et al., 2017), and the loss of independence (Osnes et al., 2004) represent a major public health concern. More than 97% of hip fractures result from a fall (Grisso et al., 1991; Palvanen et al., 2000) although most falls do not result in serious injury such as fracture (DeGoede et al., 2003; Kannus et al., 2005). Load sharing between the hands and hip/body has been identified as an important mechanism to reduce an individuals’ risk for fall injury (Feldman and Robinovitch, 2007; Hsiao and Robinovitch, 1998). It has been proposed that there are characteristic protective responses, such as arm rescue reactions, that normally allow for a safe landing during a fall, and that these responses become less effective with aging (Cummings and Nevitt, 1989; Lattimer et al., 2018; Lee and Ashton-Miller, 2015, 2011; Lo et al., 2003; Sran et al., 2010). However, landing on the hands and wrist during protective arm movements is not without risk as wrist fractures are also a prevalent health problem (Donaldson et al., 1990; MacIntyre and Dewan, 2016). Therefore, it is important to identify underlying factors that lead to successful protective responses that allow for a safe landing during a fall.
The amount of time required to effectively orient the hands and arms in a protective manner while falling is affected by several factors: the speed, height, and direction of the fall, etc. There is an estimated 715 to 1200 ms between loss of balance and unintentional ground impact (Choi et al., 2015; Hsiao and Robinovitch, 1998). The time required for a protective arm reaction may be affected by muscle co-activation that occurs in preparation for landing. Studies of drop landings (Greenwood and Hopkins, 1976; Santello and McDonagh, 1998), volitional falls (Dietz and Noth, 1978), and unexpected falls (Burkhart and Andrews, 2013; Lattimer et al., 2016) have demonstrated a characteristic burst of electromyographic (EMG) activity of the relevant musculature about 100 ms prior to impact. The burst of EMG activity of the landing musculature preceding impact has been proposed to be required to achieve muscular control in landing (Melvill Jones and Watt, 1971). Additionally, it is not clear how or if muscle activity is modulated to fall height/velocity, or in other words it is not clear how pre-impact EMG activity is modified in time or magnitude with fall height/velocity.
Previous investigations of protective arm reactions, pre-positioned the hands and arms in an orientation that was either prepared to accept weight prior to falling (Burkhart and Andrews, 2013; Chiu and Robinovitch, 1998; Chou et al., 2001; Dietz et al., 1981; Johnston et al., 2019; Lattimer et al., 2018, 2016; Lo et al., 2003; Sran et al., 2010), and/or the reaction was instructed to be volitional rather than occurring spontaneously (Dietz et al., 1981; Dietz and Noth, 1978). There have been a few studies of rapid orientation of the hands and arms in forward falls, however the landing position did not require body weight to be fully supported (DeGoede et al., 2001; Kim and Ashton-Miller, 2003; Robinovitch et al., 2005). Other studies involving rapid hand/arm orientation did not investigate multiple fall heights (Tan et al., 2006; Troy and Grabiner, 2007). Another limitaion of these previous studies is that fall arresting contributions of the ankle, knee, and/or hip were not controlled. Following rapid orientation of the hands and arms, elbow angle, vertical hand velocity, vertical neck velocity, elbow angular acceleration, and muscle activity affect the maximum vertical ground reaction force (vGRF) and the ability to avoid unintentional ground impact as a result of elbow flexion buckling (Chou et al., 2001; DeGoede and Ashton-Miller, 2003; Dietz et al., 1981; Lattimer et al., 2018; Lee and Ashton-Miller, 2011). The effectiveness of such reactions would no doubt be affected by the fall height/velocity.
The aim of this study was to characterize the neuromechanical/neuromuscular control of protective arm reaction strategies as a function of fall height/velocity following an externally applied postural perturbation. The hypothesis is that protective arm reaction strategies are modulated according to fall height. Specifically, decreased fall height will result in decreased elbow extension angle at impact (more flexed), increased hand velocity at impact, and increased elbow extension angular velocity at impact. A secondary aim was to determine if pre-impact activation amplitude and timing of landing muscle activity is affected by fall height.
2. Methods
2.1. Participants
Fourteen younger adults (5 males/9 females; mean age: 25.1±3.5 years; mean height: 173.9±10.0 cm; mean body mass: 78.9±4.6 kg) participated in this study. Exclusion criteria were: injury or surgery within the past 6 months; abnormal gait, kinematics, and/or physical disability; medical condition that precludes participation in regular exercise; significant cognitive disability; history of neurological or sensory disorders; dizziness or unsteadiness; use of medication that affects strength, balance, and/or motor function; and grip weakness. Participants all reported right hand dominance. All participants provided written informed consent prior to participation. The study was approved by the Institutional Review Board at the University of Maryland School of Medicine.
2.2. Protocol
Participants were strapped to a custom-built inverted pendulum system (Fig. 1). Participants “laid” on top of the pendulum with their feet in plantar flexion to minimize contribution of the ankle flexors. An adjustable surface was positioned so that participants’ toes just contacted the ground. The starting hand position was chosen to avoid muscle activation prior to perturbation onset and require rapid hand and arm movement to prepare for absorbing impact energy and protecting the head/torso from impact. Holding the arms parallel to the body or ‘hanging’ the arms straight down were considered but rejected for it would have required muscle activation to hold the arm in place and require minimal rapid orientation following perturbation onset respectively. Participants placed their hands on top of the pendulum with their arms relaxed as shown in Fig. 1. The acromion was approximately 12 inches above the top of the pendulum. Participants were instructed to look at the landing surface. The pendulum was held in an upright position with an electromagnet (MagneTool Inc., Troy, MI). At an unpredictable time after the start of each trial (2.7 ±0.6 s, range: 1.3-4.4 s), the pendulum was released causing the pendulum and participant to fall under the acceleration due to gravity. Participants were instructed to “land on their hands as softly as possible.” Upon landing each acromion was centered, horizontally, over an AMTI force platform (AMTI, Watertown, MA). The force platforms and landing surface were covered with custom 12-inch-thick gymnastics crash pads (Carolina Gym Supply, Hillsborough, NC).
Figure 1:

Participants began each trial leaning against an inverted pendulum system (A). A strap wrapped around the participant’s midsection secured them to the inverted pendulum. At an unpredictable time, the pendulum was released, causing the pendulum and the participant to fall under the acceleration due to gravity (B). The landing area was covered with 12-inch-thick gymnastic crash pads. Following release, each of the participants hands landed on different gymnastics mat with a force platform under each gym mat. The shaft that the pendulum pivots about has a sprocket on the opposite side of the safety barrier (C). A chain and cable system connected the sprocket to an electromagnet which held the pendulum at a specific angle. Two angle-irons were bolted together to control the distance between an anchor point and the electromagnet. At about 5 degrees above horizontal, the pendulum first impacts the gymnastics mat closest to the pivot point. If the pendulum reaches the horizontal (0 degrees), a pair of dampers (600 in-lbs. energy capacity) assisted the participant in absorbing impact energy. A mechanical stop (not shown) stopped the pendulum from falling further than 5 degrees below the horizontal.
2.3. Apparatus
Participants were released twice from each of four lean angles following a practice trial. The practice trials had the same initial lean angle as the first two test trials. The order of initial lean angles was randomly selected for each participant. Initial lean angles between 26 and 52 degrees (Low: 26±2, Medium: 39±2, Medium-Hight: 46±2, and High: 52±2 degrees) were selected to yield drop durations between 350 and 600 ms (368±29, 459±34, 521±28, and 575±45 ms). Drop duration was defined as the time from perturbation onset until the right force platform recorded more than 10 Newtons (N). Perturbation onset was defined at the time that the angular acceleration of the pendulum exceeded 10 degrees/s2. Lean angles were selected through pilot testing to give a range of drop durations slightly shorter than reported perturbation-evoked reach-to-grasp and protective arm reactions, between 400 and 700 ms (Gage et al., 2007; Hsiao and Robinovitch, 1998; Robinovitch et al., 2005).
The vertical vGRF under the hands after impact was measured with a pair of force platforms located beneath gymnastics mats and reported as percent body weight (%BW). Participants were outfitted with retroreflective markers bilaterally on the acromion, lateral and medial elbow, and ulnar and radial wrist. Additional markers were placed on the inverted pendulum to measure the angle relative to the horizontal. EMG data (Noraxon Wireless Telemyo DTS System, Scottsdale, AZ) was collected bilaterally from the biceps brachii and triceps brachii. Electrode placement followed guidelines given by the surface electromyography for the non-invasive assessment of muscles project (www.seniam.org).
2.4. Signal Processing
Force platform data were sampled at 600 Hz. Motion capture data (Vicon, Oxford, UK) were sampled at 120 Hz. Kinetic and kinematic data were low-pass filtered using a dual-pass second-order Butterworth filter with a cut-off frequency of 30 Hz and 10 Hz respectively. Power analysis revealed that 99% of the signal power was below 30 Hz and 10 Hz for all kinetic and kinematic variables respectively. EMG data were collected at 1500 Hz, band-pass filtered with a dual-pass second-order Butterworth filter with a cut-off frequency of 16 Hz and 500 Hz. EMG data was full-wave rectified and low-pass filtered with a dual-pass second-order Butterworth filter with a cut-off of 50 Hz yielding a linear envelope. EMG onset latency (described below) was calculated using a linear envelope of the EMG data. The remaining EMG based quantities were normalized and processed further (described below). All EMG analysis was performed with custom software written in Matlab (MathWorks, Natick, MA). Force platform, motion capture, and EMG signals were collected simultaneously in Vicon Nexus.
2.5. Dependent Variables
Movement time, maximum vGRF, elbow angle at impact, elbow angular velocity at impact, vertical hand velocity at impact, and vertical neck velocity at impact were included as dependent variables. Initial EMG onset latency, pre-impact EMG time, mean biceps and triceps EMG amplitude 50 ms prior to impact and mean co-activation index 50 ms prior to impact were also included (see Table 1).
Table 1:
Description of dependent variables.
| Dependent Variables | Units | Description |
|---|---|---|
| Movement time | ms | The time between the onset of the first burst of EMG activity of the biceps or triceps (described below) and hand contact* |
| Maximum vertical ground reaction force | Percent body weight | Maximum vertical ground reaction force following hand contact |
| Elbow angle at impact | Degrees | Angle between the vectors connecting the midpoint of the ulnar and radial wrist and the midpoint of the lateral and medial elbow and the midpoint of the elbow and the acromion with 180 degrees representing full extension |
| Elbow angular velocity at impact | Degrees/s | Elbow angle was numerically differentiated to determine the elbow angular velocity at impact with positive values for extension and negative values for flexion |
| Vertical hand velocity at impact | m/s | The position of the midpoint of the ulnar and radial wrist markers were integrated to determine hand velocity at impact |
| Vertical neck velocity at impact | m/s | The position of the midpoint of the right and left acromion was numerically differentiated to determine the vertical neck velocity at impact (vertical neck position represents the position of the torso at shoulder height or the base of the neck) |
| Initial EMG onset | ms | The point in time when the linear envelope of the EMG exceeded 3 standard deviations of the average baseline signal measured 100 ms prior to perturbation onset for more than 30 ms following perturbation onset |
| EMG onset latency | ms | The period of time between perturbation onset and initial EMG onset |
| Pre-impact onset | ms | Pre-impact EMG onset is the largest change in the rate of growth of the rectified, integrated, and normalized EMG signal prior to ground contact (Santello et al., 2001; Santello and McDonagh, 1998) |
| Pre-impact time | ms | Period of time between the burst of EMG activity and hand contact |
| Mean amplitude of EMG activity 50 ms prior to impact | Percent | Average EMG amplitude 50 ms prior to contact |
| Mean co-activation index 50 ms prior to impact | Percent | Calculated following the method of Winter (1990) and averaged over 50 ms prior to impact. Calculated for the biceps with respect to the triceps. |
Hand contact was defined as the time when the vertical ground reaction force exceeded 10 Newtons.
Muscular activity of the biceps and triceps could be characterized as having two distinct phasic burst patterns separated by a period of relative quiescence or lower level tonic EMG activity: immediately following perturbation onset (initial EMG onset) and immediately preceding hand contact (pre-impact EMG onset). The EMG signal used in the calculation of pre-impact onset was normalized to the value at impact for each trial (see Fig. 2 for more details). Most trials (>75%) exhibited pre-impact EMG times greater than 50 ms.
Figure 2:

Data from a single trial at the M-angle with a drop duration of 455 ms from perturbation onset until hand contact. The angle of the inverted pendulum is shown in A, the ground reaction force is shown in B, the elbow angle (180 degrees is full extension) is shown in C, and the normalized EMG amplitude of the biceps and triceps is shown in D. Perturbation onset, initial EMG onset, and pre-impact EMG onset of the triceps and biceps are shown with vertical lines. EMG onset latency is defined as the time between the first burst of EMG and perturbation onset. Pre-impact time is defined as the time between the pre-impact EMG onset and hand contact. Pre-impact EMG onset is the largest change in the rate of growth of the rectified, integrated, and normalized EMG signal prior to ground contact (Santello et al., 2001; Santello and McDonagh, 1998). The algorithm was accurate in almost 90% of trials. The pre-impact EMG onset was manually adjusted in about 11% of trials (12, 4, 12, and 6 out of 112 trials for the right biceps, left biceps, right triceps, and left triceps respectively). In some trials two bursts of muscular activity preceded the pre-impact onset. The algorithm automatically picked the burst immediately following the initial EMG onset in these trials and was manually changed to the burst occurring closer (in time) to impact.
The EMG signals used in the calculation of the mean EMG amplitude prior to impact and average co-activation index prior to impact were normalized to the peak signal recorded during all trials for each participant for the respective muscle. Normalizing EMG signal to a functional task generally results in less inter-participant variability compared to a maximum voluntary activation (Burden, 2010; Rand and Ohtsuki, 2000; Suydam et al., 2017).
2.6. Statistical analyses
Linear regression analysis was used to determine the variance in drop duration accounted for by lean angle. One-way repeated measures ANOVA (RmANOVA) was used to determine whether initial lean angle (low (L), medium (M), medium-high (MH), or high(H)) significantly affected the dependent variables. Greenhouse-Geisser correction was used when Mauchly’s sphericity was significant (p<0.05). Analysis focused on the right upper extremity because all participants reported right arm dominance. When statistically significant effects (p<0.05) were found, post-hoc comparisons using Bonferroni’s correction were used to evaluate pairwise differences. Statistical analysis was performed using SPSS 22 (IBM Corp, Armonk, NY).
3. Results
Representative table angle (Fig. 3A), vGRF (Fig. 3B), elbow angle (Fig. 3C), and EMG activity of the biceps and triceps (Fig. 3D) from a single trial is shown in Fig. 2. None of the participants hit the mechanical stop (5 degrees below horizontal). Seventy nine percent (88/112) of trials resulted in the pendulum hitting the damping mechanism. The average minimum angle reached by the pendulum was −0.5±0.8 degrees. The pendulum generally hit the gym mats prior to the hand (81/112). On average the hand contacted the gym mat 16±39 ms after the pendulum hit the mat. Increasing lean angle resulted in an increase in drop duration. The lean angle accounted for 84% of the variance of the drop duration (Fig. 4A). Lean angle had a significant effect on the drop duration (p<0.001). Post-hoc analysis showed significant differences in drop duration for all pairwise comparisons of lean angle (Fig. 4B).
Figure 3:

Representative plot demonstrating the method for calculating the pre-impact EMG onset following Santello and McDonagh (1998). The data is from the same trial as shown in Figure 2. The full-wave rectified EMG signal for the right biceps is shown in A. The signal is then integrated between initial EMG onset and hand contact (B). The integrated EMG signal (IEMG) is normalized to the value at hand contact. The integrated signal is plotted against a reference line with slope equal to 1/Δt. The time between initial EMG onset latency and hand contact is defined as Δt. The reference line represents what the IEMG signal would look like if there were a constant level of EMG amplitude. The pre-impact EMG onset was defined at the point in time when the distance between the normalized IEMG and the reference line was the greatest (D). This represents the point in time when the IEMG starts to increase continuously, i.e. continuous build-up of muscle activity.
Figure 4:
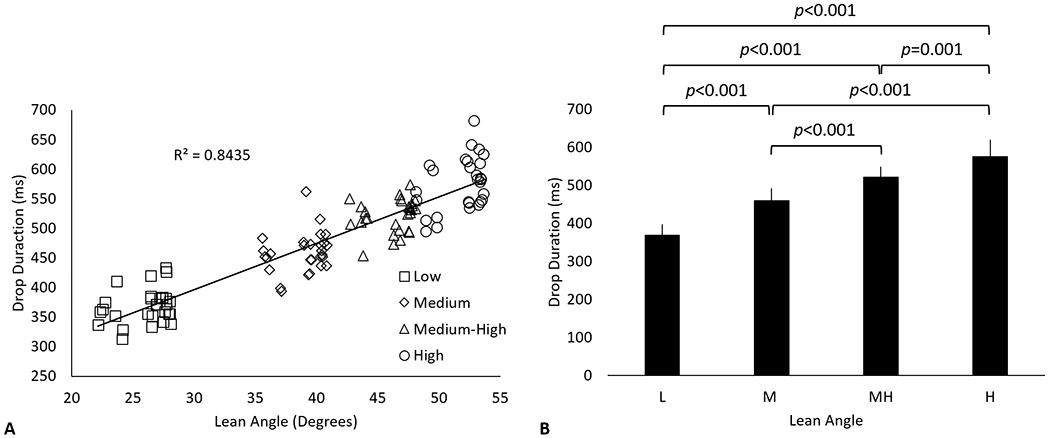
The relationship between lean angle and drop duration is shown in A. The mean and standard deviation of drop duration associated with low (L), medium (M), medium-high (MH), and high (H) lean angles are shown in B. Drop duration was defined as the time between perturbation onset and impact with the ground (>10N load on the right hand).
The maximum vGRF amplitude increased with increasing lean angle (p<0.001, Fig. 5A). The vGRF was 54.6±11.3 %BW, 62.6±12.6, 69.0±12.7, and 71.9±14.7 %BW for the low, medium, medium-high, and high lean angles respectively. Movement time increased with increasing lean angle (p<0.001, Fig. 5B).
Figure 5:
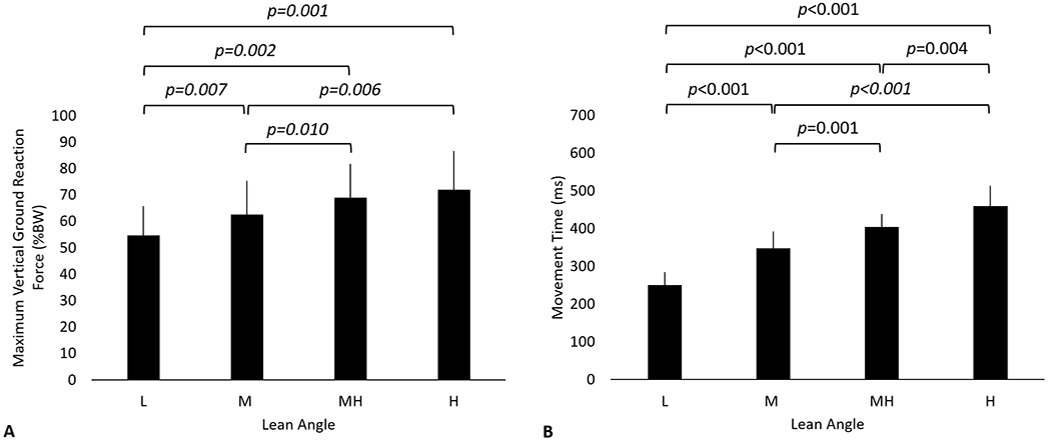
Mean and standard deviation of the vertical ground reaction force (A) and movement time (B) as a function of initial lean angle. The movement time was defined as the time between EMG onset latency (initial EMG onset of the biceps or triceps) and impact (>10 N) with the ground.
Vertical neck velocity at impact increased (L-angle: 2.4±0.3; M-angle: 2.9±0.3; MH-angle: 3.1±0.2; H-angle: 3.2±0.2 m/s) with increasing lean angle (p<0.001, Fig. 6A). Vertical hand velocity at impact, however, was not significantly affected by lean angle (p=0.113, Fig. 6B). Participants exhibited increasing elbow extension at impact (L-angle: 100±17; M-angle: 121±15; MH-angle: 127±14; H-angle: 131±12 degrees) with increasing fall angle (p<0.001, Fig. 6C). Elbow angular velocity at impact (p=0.015, Fig. 6D) decreased with increasing fall angle (elbow angular velocity is position for extension); however, the differences were not statistically significant in post-hoc tests.
Figure 6:

Vertical neck velocity at impact (A), vertical hand velocity at impact (B), elbow angle at impact (C), and elbow angular velocity at impact (D). Elbow angle was defined with 180 degrees as full extension. Positive values of angular velocity are extension.
Initial lean angle did not significantly affect the initial EMG onset latency for the biceps (p=0.30, Fig. 7A) or the triceps was (p=0.75, Fig. 7B). The initial EMG onset latency of the biceps and triceps were 120±18 ms and 126±17 ms respectively. The biceps (Fig. 7C) and triceps (Fig. 7D) pre-impact were significantly affected by lean angle (p <0.001). The pre-impact time of the biceps (L-angle: 36±34 ms; M-angle: 84±47 ms; MH-angle: 89±38 ms; H-angle: 91±53 ms) and triceps (L-angle: 72±45 ms; M-angle: 79±45 ms; MH-angle: 110±40 ms; H-angle: 121±40 ms) occurred between 80 and 120 ms with the exception of the biceps at the L-angle and the triceps at the L- and M-angle, which occurred later (i.e. shorter pre-impact time).
Figure 7:

Mean and standard deviation of biceps (A) and triceps (B) initial EMG onset latency, and pre-impact time for the biceps (C) and triceps (D). Initial EMG onset latency is relative to perturbation onset while pre-impact time is relative to impact.
The co-activation index was not significantly affected by lean angle (p=0.091, Fig. 8A). The mean biceps EMG amplitude 50 ms prior to impact increased with increasing lean angle (p=0.029, Fig. 8B). The mean biceps EMG amplitude 50 ms prior to impact was significantly larger in the H-angle (21±15%), MH-angle (21±13%), and M-angle (23±15%) compared to the L-angle (14±11 %). The mean triceps EMG amplitude 50 ms prior to impact was not significantly affected by lean angle (p=0.97, Fig. 8B).
Figure 8:

The co-activation index (A) and mean EMG activity of the biceps and triceps (B) are the average value taken for 80 ms prior to impact. The mean EMG amplitude is normalized to the maximum EMG signal recorded in all of the trials for each participant and respective muscle.
4. Discussion
The aim of this study was to investigate the effect of fall height, or initial lean angle, on protective arm reaction biomechanics. Falls from increased height resulted in increased elbow extension at impact, decreased elbow extension angular velocity at impact, and increased pre-impact time. The results support the hypothesis that protective arm reaction strategies are modulated to initial lean angle or fall height. The findings also confirm that protective arm reactions consist of two phases: rapid orientation followed by co-activation of the biceps and triceps in preparation for landing.
Factors affecting the magnitude of the impact force and the ability to avoid head/torso impact as a result of elbow buckling were affected by initial lean angle. However, it is not clear if these factors were affected detrimentally or were an attempt to optimize the performance based on initial lean angle and expected vGRF at impact. Elbow extension angular velocity at impact decreased with increasing initial lean angle. The elbow extension velocity at impact reported here is consistent with previous reports (Kim and Ashton-Miller, 2003; Lo et al., 2003). Elbow angular velocity has been shown to affect initial GRF (Chou et al., 2001) and suggested to affect the ability to avoid elbow flexion buckling (Lattimer et al., 2018) with increased elbow extension angular velocity having a negative effect.
The present study and others have identified co-activation of the triceps and biceps prior to impact (Burkhart and Andrews, 2013; Lattimer et al., 2018). Following impact, the triceps are activated eccentrically to control descent and the biceps should be relatively inactive (Lattimer et al., 2017). Activation/co-activation level affects stiffness and damping of the elbow joint and potential for musculoskeletal injury (Butler et al., 2003; Lee and Ashton-Miller, 2015, 2011) and plays a role in avoiding elbow buckling by establishing the level of fall energy that can be absorbed (DeGoede et al., 2003). In the present study, activation of the biceps prior to impact may be at least partially explained as an effort to reduce elbow extension angular velocity at impact. Avoiding elbow buckling during the post-impact phase is also a function of elbow extension angle at impact and elbow torque (DeGoede and Ashton-Miller, 2003). Elbow extension at impact decreased with decreased initial lean angle, which is consistent with previous findings (Kim and Ashton-Miller, 2003). Individuals with weaker elbow extensor muscle strength require greater elbow extension at impact to avoid elbow buckling (DeGoede et al., 2003). Given the same level of strength, less elbow extension would be required to avoid elbow buckling at decreasing fall heights. Some support for this argument may be provided by the fact that post-hoc analysis of the minimum elbow angle after impact (68±16 degrees) was not significantly affected by initial lean angle (p=0.415). This may provide some explanation for the minimal increase in co-activation and pre-impact times.
In previous studies, rapid orientation of the hands and arms was not required (Burkhart and Andrews, 2013; Chiu and Robinovitch, 1998; DeGoede and Ashton-Miller, 2002; Lattimer et al., 2018; Lo et al., 2003; Sran et al., 2010), or the impact energy of the body was not entirely absorbed through the hands and arms (DeGoede et al., 2001; Kim and Ashton-Miller, 2003; Robinovitch et al., 2005). Protective arm reaction performances reported by these studies may be optimistic because a rapid orientation and preparation for landing phase were not both included. About 530 ms (between the go cue and impact) is required to reach an elbow extension angle of 135 degrees at impact when body weight support is not required (Robinovitch et al., 2005). Alternatively, only 127 degrees of elbow angle at impact was achieved when 520 ms was available (at the MH-angle). In a study that required partial weight bearing, 126 degrees of elbow extension at impact was reached in 545 ms (Kim and Ashton-Miller, 2003). Decreased elbow extension angle at impact in studies involving weight bearing is likely the result of increased stiffness at the elbow joint brought on by co-activation in preparation for landing which has been shown to affect rotational stiffness (Lee and Ashton-Miller, 2015, 2011).
There were two distinct phasic bursts of EMG activity following perturbation onset, similar to studies of unpredictable drop landings where phasic bursts of EMG activity were reported in the legs (Greenwood and Hopkins, 1976; Melvill Jones and Watt, 1971; Sanders et al., 2015). The initial rapid burst of EMG activity has been proposed to contain a generalized startle response (Carlsen et al., 2007; Greenwood and Hopkins, 1976; Melvill Jones and Watt, 1971; Sanders et al., 2015), mediated mainly by the reticulospinal system that contributes little to the neuromechanical control of landing (Greenwood and Hopkins, 1976; Sanders et al., 2015; Yeomans et al., 2002). In falls lasting longer than 200 ms, a second burst of neuromuscular activity of the landing musculature, likely involving voluntary corticospinal control, was evident and scaled in time to the instant of landing to provide neuromechanical control at ground impact (Greenwood and Hopkins, 1976). Although there have been a few studies of protective arm reactions that reported muscular activity between unexpected release and impact, onset timing and/or number of bursts of muscular activity was not reported (Burkhart and Andrews, 2013; DeGoede and Ashton-Miller, 2002; Lattimer et al., 2018). Additionally, the fall times were relatively short in those studies. For example, one study (Lattimer et al., 2016) reported an average of 257 ms, and another (Burkhart and Andrews, 2013) did not report a pre-impact time but with the hands held 1 cm above the landing surface, pre-impact times could have been as short as 140 ms assuming gravitational acceleration. During drop landings, the presence of a startle reaction was shown to increase muscle co-activation and increased vGRF at impact (Sanders et al., 2019). Future studies should investigate whether the early startle-like arm reactions interfere with the functional performance of landing in the same way as drop landings.
In the present study, participants knew a protective arm reaction was required. Pre-selecting a reaction strategy may result in a more rapid response (Rogers et al., 2003; Weaver and Tokuno, 2013) than when required to rapidly choose between attempting to recover balance through a reach-to-grasp reaction, counterbalancing, or protecting the body on landing. This may require a sequence of responses if attempts to recover balance through an initial balance recovery strategy fail. The possibility of a sequence of arm reactions (attempting to recover balance prior to deploying a protective reaction) is consistent with the fact that there is often more time than necessary to deploy a protective arm reaction. Arm reactions and movement times observed in the present study, were shorter than the average time between fall initiation and hand contact and/or hip contact (about 680-1300 ms) reported in previous studies (Choi et al., 2015; Hsiao and Robinovitch, 1998). This suggests that there may be sufficient time to initially attempt to recover balance and then deploy a protective reaction if balance recovery fails. Additional information is needed about individuals’ ability to precisely time deployment of protective strategies and/or the response characteristics during more complex and demanding situations. For example, pre-planning (Weaver and Tokuno, 2013), cognitive load (Brauer et al., 2001), or attention shifting (Maki et al., 2001; Westlake et al., 2016) have been shown to affect reactive performance.
In summary, this is possibly the first work that involved a perturbation-evoked rapid orientation of the hands and arms at multiple fall heights where the landing musculature had to accept the weight of the body. Additionally, potential fall arresting contributions of the ankle, knee, and/or hip were removed, isolating the arm reactions. The findings demonstrate that a protective arm reaction strategy is modulated according to fall height. Deceased fall heights, or initial lean angles, resulted in reduced elbow extension and increased elbow angular velocity at impact - factors that have been reported to negatively influence impact load and an individual’s ability to prevent head/torso/hip impact due to elbow buckling. However, the present study cannot disentangle whether these modulations represent diminished performance or an attempt to optimize the landing configuration given the fall height. Future work should investigate the effects of delaying the response following perturbation onset on functional performance. Additional insights about the neuromuscular control strategies associated with protective arm reactions indicated that a phasic preparatory burst of muscle activation of the triceps and biceps appears somewhat time-dependent and scaled in magnitude with the instant of ground impact. In addition to providing new information about the neuromechanical control of the pre-impact phase of protective arm reactions when a fall is unavoidable, the data can serve as a normative baseline for understanding the impairments in protective arm reactions due to aging and clinical conditions that contribute to injuries due to falls.
Acknowledgements:
JB was supported by the University of Maryland Advanced Neuromotor Rehabilitation Research Training (UMANRRT) Program (NIDRR 90AR50280, NIDILRR 90AR5004 formerly H133P100014). This project was supported by the University of Maryland Claude D Pepper-OAIC NIH/NIA grant P30AG028747.
Footnotes
Conflict of interest: The authors have no conflicts of interest in relation to the work reported here.
References
- Brauer CA, Coca-Perraillon M, Cutler DM, Rosen AB, 2009. Incidence and mortality of hip fractures in the United States. JAMA - J. Am. Med. Assoc 302, 1573–1579. 10.1001/jama.2009.1462 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brauer SG, Woollacott M, Shumway-cook A, 2001. The Interacting Effects of Cognitive Demand and Recovery of Postural Stability in Balance-Impaired Elderly Persons 56, 489–496. [DOI] [PubMed] [Google Scholar]
- Burden A, 2010. How should we normalize electromyograms obtained from healthy participants ? What we have learned from over 25 years of research. J. Electromyogr. Kinesiol 20, 1023–1035. 10.1016/j.jelekin.2010.07.004 [DOI] [PubMed] [Google Scholar]
- Burkhart TA, Andrews DM, 2013. Kinematics, kinetics and muscle activation patterns of the upper extremity during simulated forward falls. J. Electromyogr. Kinesiol 23, 688–695. 10.1016/j.jelekin.2013.01.015 [DOI] [PubMed] [Google Scholar]
- Butler RJ, Crowell HP, Davis IMC, 2003. Lower extremity stiffness: Implications for performance and injury. Clin. Biomech 18, 511–517. 10.1016/S0268-0033(03)00071-8 [DOI] [PubMed] [Google Scholar]
- Carlsen AN, Dakin CJ, Chua R, Franks IM, 2007. Startle produces early response latencies that are distinct from stimulus intensity e V ects. Exp. Brain Res 176, 199–205. 10.1007/s00221-006-0610-8 [DOI] [PubMed] [Google Scholar]
- Chiu J, Robinovitch SN, 1998. Prediction of upper extremity impact forces during falls on the outstretched hand. J. Biomech 31, 1169–1176. 10.1016/S0021-9290(98)00137-7 [DOI] [PubMed] [Google Scholar]
- Choi WJ, Wakeling JM, Robinovitch SN, 2015. Kinematic analysis of video-captured falls experienced by older adults in long-term care. J. Biomech 48, 911–920. 10.1016/j.jbiomech.2015.02.025 [DOI] [PubMed] [Google Scholar]
- Chou PH, Chou YL, Lin CJ, Su FC, Lou SZ, Lin CF, Huang GF, 2001. Effect of elbow flexion on upper extremity impact forces during a fall. Clin. Biomech 16, 888–894. 10.1016/S0268-0033(01)00086-9 [DOI] [PubMed] [Google Scholar]
- Cummings SR, Nevitt MC, 1989. A HYPOTHESIS: The Causes of Hip Fractures. J. Gerontol. Med. Sci 44, M107–M111. [DOI] [PubMed] [Google Scholar]
- DeGoede KM, Ashton-Miller JA, 2003. Biomechanical simulations of forward fall arrests: Effects of upper extremity arrest strategy, gender and aging-related declines in muscle strength. J. Biomech 36, 413–420. 10.1016/S0021-9290(02)00396-2 [DOI] [PubMed] [Google Scholar]
- DeGoede KM, Ashton-Miller JA, 2002. Fall arrest strategy affects peak hand impact force in a forward fall. J. Biomech 35, 843–848. 10.1016/S0021-9290(02)00011-8 [DOI] [PubMed] [Google Scholar]
- DeGoede KM, Ashton-Miller JA, Liao JM, Alexander NB, 2001. How quickly can healthy adults move their hands to intercept an approaching object? Age and gender effects. Journals Gerontol. - Ser. A Biol. Sci. Med. Sci 56, 584–588. 10.1093/gerona/56.9.M584 [DOI] [PubMed] [Google Scholar]
- DeGoede KM, Ashton-Miller JA, Schultz AB, 2003. Fall-related upper body injuries in the older adult: A review of the biomechanical issues. J. Biomech 36, 1043–1053. 10.1016/S0021-9290(03)00034-4 [DOI] [PubMed] [Google Scholar]
- Dietz V, Noth J, 1978. Pre-innervation and stretch responses of triceps bracchii in man falling with and without visual control. Brain Res. 142, 576–579. 10.1016/0006-8993(78)90921-6 [DOI] [PubMed] [Google Scholar]
- Dietz V, Noth J, Schmidtbleicher D, 1981. Interaction between pre-activity and stretch reflex in human triceps brachii during landing from forward falls. J. Physiol 311, 113–125. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Donaldson LJ, Cook A, Thomson RG, 1990. Incidence of fractures in a geographically defined population. J. Epidemiol. Community Health 44, 241–245. 10.1136/jech.44.3.241 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Feldman F, Robinovitch SN, 2007. Reducing hip fracture risk during sideways falls: Evidence in young adults of the protective effects of impact to the hands and stepping. J. Biomech 40, 2612–2618. 10.1016/j.jbiomech.2007.01.019 [DOI] [PubMed] [Google Scholar]
- Gage WH, Zabjek KF, Hill SW, McIlroy WE, 2007. Parallels in control of voluntary and perturbation-evoked reach-to-grasp movements: EMG and kinematics. Exp. Brain Res 181, 627–637. 10.1007/s00221-007-0959-3 [DOI] [PubMed] [Google Scholar]
- Greenwood BYR, Hopkins A, 1976. Muscle responses during sudden falls in man. J. Physiol 254, 507–518. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Grisso JA, Kelsey JL, Strom BL, Chiu GY, Maislin G, OO’Brien LA, Hoffman S, Kaplan F, Group NHFS, 1991. Risk factors for falls as a cause of hip fracture in women. N. Engl. J. Med 324, 954–960. 10.1056/NEJM199104043241404 [DOI] [PubMed] [Google Scholar]
- Hsiao ET, Robinovitch SN, 1998. Common protective movements govern unexpected falls from standing height. J. Biomech 31, 1–9. 10.1016/S0021-9290(97)00114-0 [DOI] [PubMed] [Google Scholar]
- Johnston JD, Kawalilak CE, Lanovaz JL, Kontulainen SA, 2019. A single-spring model predicts the majority of variance in impact force during a fall onto the outstretched hand. J. Biomech 90, 149–152. 10.1016/j.jbiomech.2019.04.042 [DOI] [PubMed] [Google Scholar]
- Kannus P, Sievänen H, Palvanen M, Järvinen T, Parkkari J, 2005. Prevention of falls and consequent injuries in elderly people. Lancet 366, 1885–1893. 10.1016/S0140-6736(05)67604-0 [DOI] [PubMed] [Google Scholar]
- Kim KJ, Ashton-Miller JA, 2003. Biomechanics of fall arrest using the upper extremity: Age differences. Clin. Biomech 18, 311–318. 10.1016/S0268-0033(03)00005-6 [DOI] [PubMed] [Google Scholar]
- Lattimer LJ, Lanovaz JL, Farthing JP, Madill S, Kim S, Arnold C, 2016. Upper limb and trunk muscle activation during an unexpected descent on the outstretched hands in young and older women. J. Electromyogr. Kinesiol 30, 231–237. 10.1016/j.jelekin.2016.08.001 [DOI] [PubMed] [Google Scholar]
- Lattimer LJ, Lanovaz JL, Farthing JP, Madill S, Kim S, Robinovitch S, Arnold C, 2017. Female Age-Related Differences in Biomechanics and Muscle Activity During Descents on the Outstretched Arms. J. Aging Phys. Act 25, 474–481. [DOI] [PubMed] [Google Scholar]
- Lattimer LJ, Lanovaz JL, Farthing JP, Madill S, Kim SY, Robinovitch S, Arnold CM, 2018. Biomechanical and physiological age differences in a simulated forward fall on outstretched hands in women. Clin. Biomech 52, 102–108. 10.1016/j.clinbiomech.2018.01.018 [DOI] [PubMed] [Google Scholar]
- Lee Y, Ashton-Miller JA, 2015. Effects of Age, Gender and Level of Co-contraction on Elbow and Shoulder Rotational Stiffness and Damping in the Impulsively End-Loaded Upper Extremity. Ann. Biomed. Eng 43, 1112–1122. 10.1007/s10439-014-1185-3 [DOI] [PubMed] [Google Scholar]
- Lee Y, Ashton-Miller JA, 2011. The effects of gender, level of co-contraction, and initial angle on elbow extensor muscle stiffness and damping under a step increase in elbow flexion moment. Ann. Biomed. Eng 39, 2542–2549. 10.1007/s10439-011-0308-3 [DOI] [PubMed] [Google Scholar]
- Lo J, McCabe GN, DeGoede KM, Okuizumi H, Ashton-Miller JA, 2003. On reducing hand impact force in forward falls: Results of a brief intervention in young males. Clin. Biomech 18, 730–736. 10.1016/S0268-0033(03)00124-4 [DOI] [PubMed] [Google Scholar]
- MacIntyre NJ, Dewan N, 2016. Epidemiology of distal radius fractures and factors predicting risk and prognosis. J. Hand Ther 29, 136–145. 10.1016/j.jht.2016.03.003 [DOI] [PubMed] [Google Scholar]
- Maki BE, Zecevic CAA, Bateni H, Kirshenbaum N, Mcilroy WE, 2001. Cognitive demands of executing postural reactions : does aging impede attention switching ? 12, 3583–3587. [DOI] [PubMed] [Google Scholar]
- Melvill Jones G, Watt DGD, 1971. Muscular control of landing from unexpected falls in man. J. Physiol 219, 729–737. 10.1113/jphysiol.1971.sp009685 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Osnes EK, Lofthus CM, Meyer HE, Falch JA, Nordsletten L, Cappelen I, Kristiansen IS, 2004. Consequences of hip fracture on activities of daily life and residential needs. Osteoporos. Int 15, 567–574. 10.1007/s00198-003-1583-0 [DOI] [PubMed] [Google Scholar]
- Palvanen M, Kannus P, Parkkari J, Pitkäjärvi T, Pasanen M, Vuori I, Järvinen M, 2000. The Injury Mechanisms of Osteoporotic Upper Extremity Fractures Among Older Adults: A Controlled Study of 287 Consecutive Patients and Their 108 Controls. Osteoporos. Int 11, 822–831. [DOI] [PubMed] [Google Scholar]
- Rand MK, Ohtsuki T, 2000. EMG analysis of lower limb muscles in humans during quick change in running directions. Gait Posture 12, 169–183. [DOI] [PubMed] [Google Scholar]
- Robinovitch SN, Normandin SC, Stotz P, Maurer JD, 2005. Time requirement for young and elderly women to move into a position for breaking a fall with outstretched hands. Journals Gerontol. - Ser. A Biol. Sci. Med. Sci 60, 1553–1557. 10.1093/gerona/60.12.1553 [DOI] [PubMed] [Google Scholar]
- Rogers MW, Hedman LD, Johnson ME, Martinez KM, 2003. Triggering of protective stepping for the control of human balance : age and contextual dependence. Cogn. Brain Res 16, 192–198. 10.1016/S0926-6410(02)00273-2 [DOI] [PubMed] [Google Scholar]
- Sanders O, Hsiao H, Savin DN, Creath RA, Rogers MW, 2019. Aging effects of motor prediction on protective balance and startle responses to sudden drop perturbations 91, 23–31. 10.1016/j.jbiomech.2019.05.005 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sanders OP, Savin DN, Creath RA, Rogers MW, 2015. Protective balance and startle responses to sudden freefall in standing humans. Neurosci. Lett 586, 8–12. 10.1016/j.neulet.2014.11.034 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Santello M, McDonagh MJN, 1998. The control of timing and amplitude of EMG activity in landing movements in humans. Exp. Physiol 83, 857–874. [DOI] [PubMed] [Google Scholar]
- Santello M, McDonagh MJN, Challis JH, 2001. Visual and non-visual control of landing movements in humans. J. Physiol 537, 313–327. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schnell S, Friedman SM, Mendelson DA, Bingham KW, Kates SL, 2010. The 1-year mortality of patients treated in a hip fracture program for elders. Geriatr. Orthop. Surg. Rehabil 1, 6–14. 10.1177/2151458510378105 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sran MM, Stotz PJ, Normandin SC, Robinovitch SN, 2010. Age differences in energy absorption in the upper extremity during a descent movement: Implications for arresting a fall. Journals Gerontol. - Ser. A Biol. Sci. Med. Sci. 65 A, 312–317. 10.1093/gerona/glp153 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Suydam SM, Manal K, Buchanan TS, 2017. The Advantages of Normalizing Electromyography to Ballistic Rather than Isometric or Isokinetic Tasks. J. Appl. Biomech 33, 189–196. [DOI] [PubMed] [Google Scholar]
- Tan J, Eng JJ, Robinovitch SN, Warnick B, 2006. Wrist impact velocities are smaller in forward falls than backward falls from standing. J. Biomech 39, 1804–1811. 10.1016/j.jbiomech.2005.05.016 [DOI] [PubMed] [Google Scholar]
- Troy KL, Grabiner MD, 2007. Asymmetrical ground impact of the hands after a trip-induced fall : Experimental kinematics and kinetics 22, 1088–1095. 10.1016/j.clinbiomech.2007.07.014 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Weaver TB, Tokuno CD, 2013. The influence of handrail predictability on compensatory arm reactions in response to a loss of balance. Gait Posture 38, 293–298. 10.1016/j.gaitpost.2012.12.003 [DOI] [PubMed] [Google Scholar]
- Westlake KP, Johnson BP, Creath RA, Neff RM, Rogers MW, 2016. HHS Public Access. Gait Posture 45, 51–55. 10.1016/j.gaitpost.2016.01.007.Influence [DOI] [PMC free article] [PubMed] [Google Scholar]
- Williamson S, Landeiro F, McConnell T, Fulford-Smith L, Javaid MK, Judge A, Leal J, 2017. Costs of fragility hip fractures globally: a systematic review and meta-regression analysis. Osteoporos. Int 28, 2791–2800. 10.1007/s00198-017-4153-6 [DOI] [PubMed] [Google Scholar]
- Winter DA, 1990. Biomechanics and Motor Control of Human Movement, Second Edi. ed. John Wiley & Sons, Inc., New York. [Google Scholar]
- Yeomans JS, Li L, Scott BW, Frankland PW, 2002. Tactile, acoustic and vestibular systems sum to elicit the startle reflex. Neurosci. Biobehav. Rev 26, 1–11. [DOI] [PubMed] [Google Scholar]


