Cortical contraction drives the 3D patterning of epithelial cell surfaces

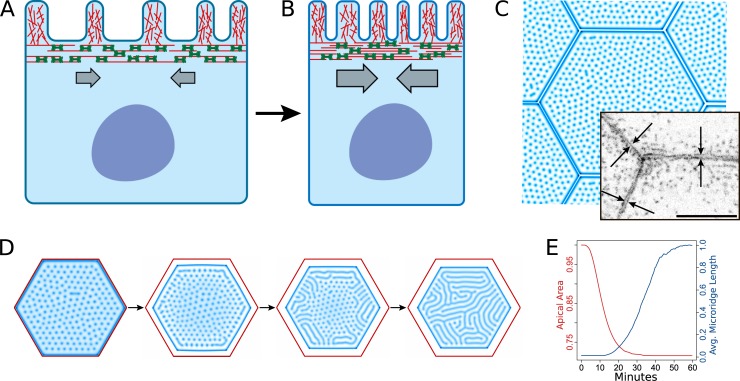
Microridges, elongated 3D protrusions arranged in maze-like patterns on zebrafish skin cells, form by the accretion of simple precursor projections. Modeling and in vivo experiments showed that cortical contractions promote the coalescence of precursors into microridges by reducing surface tension.

Abstract

Cellular protrusions create complex cell surface topographies, but biomechanical mechanisms regulating their formation and arrangement are largely unknown. To study how protrusions form, we focused on the morphogenesis of microridges, elongated actin-based structures that are arranged in maze-like patterns on the apical surfaces of zebrafish skin cells. Microridges form by accreting simple finger-like precursors. Live imaging demonstrated that microridge morphogenesis is linked to apical constriction. A nonmuscle myosin II (NMII) reporter revealed pulsatile contractions of the actomyosin cortex, and inhibiting NMII blocked apical constriction and microridge formation. A biomechanical model suggested that contraction reduces surface tension to permit the fusion of precursors into microridges. Indeed, reducing surface tension with hyperosmolar media promoted microridge formation. In anisotropically stretched cells, microridges formed by precursor fusion along the stretch axis, which computational modeling explained as a consequence of stretch-induced cortical flow. Collectively, our results demonstrate how contraction within the 2D plane of the cortex can pattern 3D cell surfaces.

Introduction

Animal cells generate a broad repertoire of dynamic structures based on the highly versatile and plastic actin cytoskeleton (Pollard and Cooper, 2009; Blanchoin et al., 2014). Actin generates both the protrusive forces that shape the membrane and, in conjunction with myosin, contractile forces that can alter cell geometry. Rapid restructuring of the actin cytoskeleton is controlled by a core of conserved actin regulatory proteins, including nucleators, elongators, bundlers, depolymerizers, and myosin motors (Pollard, 2016). Despite their universality, the divergent patterns of self-organization between these regulators generate a remarkable diversity of actin-based structures, including filopodia, lamellipodia, microvilli, dorsal ruffles, and podosomes (Blanchoin et al., 2014; Buccione et al., 2004). While actin regulatory proteins have been extensively studied, neither molecular mechanisms nor biophysical principles that generate and switch between specific actin structures are well understood. The coexistence and competition of distinct actin-based structures within the same cell makes these problems even more complex (Rotty and Bear, 2014; Lomakin et al., 2015).

Microridges are membrane protrusions extended in one spatial dimension and arranged in remarkable fingerprint-like patterns on the apical surface of mucosal epithelial cells (Fig. 1 A; Straus, 1963; Olson and Fromm, 1973). Microridges are found in a wide array of species on a variety of tissues, including the cornea, oral mucosa, and esophagus (Depasquale, 2018), and are thought to aid in mucus retention (Sperry and Wassersug, 1976; Pinto et al., 2019). Microridges are filled with actin filaments and associate with several actin-binding proteins (Depasquale, 2018; Pinto et al., 2019). Interestingly, microridges do not emerge as fully spatially extended structures like dorsal ruffles. Instead, they assemble from short vertically projecting precursors (Raman et al., 2016; Lam et al., 2015; Uehara et al., 1988; Gorelik et al., 2003). Ultrastructural analyses have demonstrated that actin filaments in microridges have mostly branched actin networks (Bereiter-Hahn et al., 1979; Pinto et al., 2019), and, therefore, it is unclear if microridge precursors are more similar in their actin organization to podosomes or microvilli, to which they had been frequently compared. To emphasize this distinction, we have dubbed these precursors actin “pegs.” Inhibiting Arp2/3 prevents aggregation of actin pegs into microridges, suggesting that branched actin networks are also required for microridge assembly (Lam et al., 2015; Pinto et al., 2019). Factors regulating nonmuscle myosin II (NMII) activity have been found to promote microridge elongation (Raman et al., 2016), but reports differ about whether NMII plays a direct role in microridge morphogenesis (Lam et al., 2015).

Figure 1.

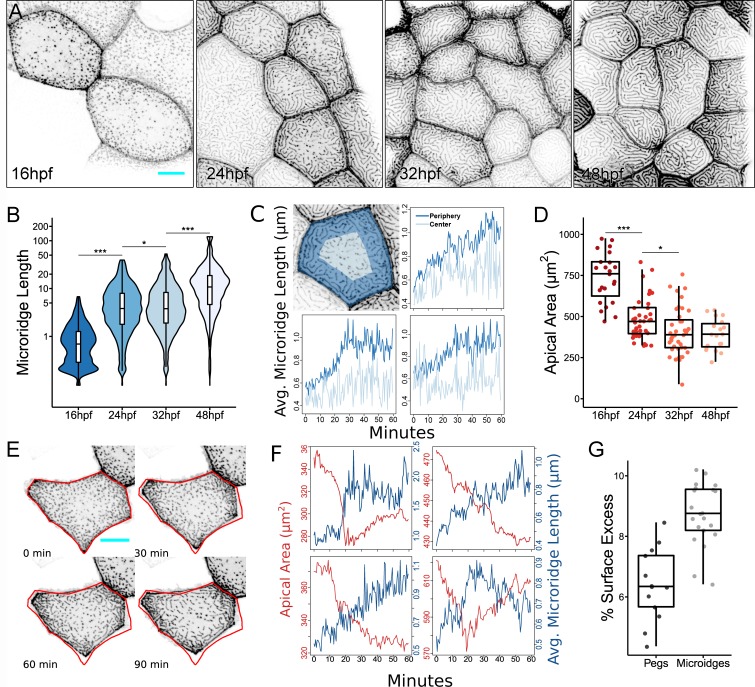
Microridge length changes in tandem with apical cell area. (A) Representative projections of Lifeact-GFP in periderm cells on zebrafish larvae at the indicated stages of zebrafish development. (B) Box and violin plot of microridge length at the indicated stages of zebrafish development. Data displayed are a weighted distribution of microridge length, in which frequency is proportional to microridge length, approximating occupied area. For a nonweighted presentation of the same data, see Fig. S1 K. *, P < 0.05; ***, P < 0.001; Kruskal–Wallis test followed by Dunn’s test (n = 15,582 structures in 23 cells from 10 fish at 16 hpf; n = 5,096 structures in 40 cells from nine fish at 24 hpf; n = 4,572 structures in 40 cells from nine fish at 32 hpf; n = 1,309 structures in 19 cells from six fish at 48 hpf). (C) Top left: Representation of cell “periphery” (dark blue) and “center” (light blue) zones, representing 75% and 25% of apical cell area, respectively. Other panels: Line graphs comparing the average microridge length in the cell periphery versus the cell center over time. (D) Dot and box plot of periderm cell apical area at the indicated stages of zebrafish development. *, P < 0.05; ***, P < 0.001; Kruskal–Wallis test followed by Dunn’s test (n = 23 cells from 10 fish at 16 hpf; n = 40 cells from nine fish at 24 hpf; n = 40 cells from nine fish at 32 hpf; n = 19 cells from six fish at 48 hpf). (E) Sequential projections from a time-lapse video of Lifeact-GFP in a single periderm cell during apical constriction. Red outline shows position of cell border at 0 min. (F) Line plots of apical area and average microridge length in single periderm cells over time. Top right panel corresponds to cell shown in E. (G) Dot and box plot of surface excess (relative difference between total surface area and projected surface area as seen in microscope) in regions of the apical cell membrane composed of only microridges or only pegs (n = 13 regions with pegs, n = 21 regions with microridges). Further details of this analysis are provided in Materials and methods. Scale bars, 10 µm (A and E). Avg., average. For box plots, middle box line is the median, and lower and upper ends of boxes are 25th and 75th percentiles, respectively.

Although microridges are less studied than other actin-based structures, they offer an excellent opportunity to probe systemic properties of cytoskeletal regulation. Microridge patterns possess several characteristic parameters, including their spatial orientation, length distribution, and periodicity, which can be readily quantified from live-cell images. These parameters reflect biochemical and biomechanical processes that regulate the morphogenesis of actin structures and are sensitive to experimental intervention. Multiple genetic and pharmacological perturbations can thus be applied to dissect principles of patterning and test theoretical hypotheses.

By imaging microridge development on the skin of larval zebrafish, we found that cortical contraction couples apical constriction to microridge morphogenesis. In vivo experiments and modeling suggest that contraction of the apical actomyosin cortex relieves surface tension to facilitate the coalescence of pegs to form, elongate, and orient microridges. Thus, cortical contraction not only determines the size and shape of the apical surface but also concomitantly sculpts its 3D surface.

Results

The apical surfaces of periderm cells shrink as microridges form

We first asked if we could identify overarching organizational principles in the emergence of microridges from pegs. To characterize the process of microridge development in live animals, we imaged transgenic zebrafish expressing the F-actin reporter Lifeact-GFP specifically in periderm cells during development (Rasmussen et al., 2015; Helker et al., 2013). We developed an automated image analysis protocol to segment microridges from these images and quantify microridge length in an unbiased manner (Fig. S1). As previously reported (Lam et al., 2015; Raman et al., 2016; Pinto et al., 2019), early in development (16 h post-fertilization [hpf]), periderm cells projected actin pegs that superficially resemble short microvilli (Fig. 1, A and B). By 24 hpf, elongated microridges appeared near cell borders, whereas pegs still populated the center of the apical cell surface (Fig. 1, A and B). By 32 hpf, microridges filled the apical surface and continued to elongate through at least 48 hpf (Fig. 1, A and B). This temporal progression of microridge growth was apparent from plotting the distribution of the pooled population of protrusions (Fig. 1 B and Fig. S2 A), or from measuring the average protrusion length per cell (Fig. S2 B). To determine how cells transitioned from pegs to microridges, we imaged microridge growth in live animals at 15–30-s intervals. These videos revealed that pegs were dynamic and coalesced to both form and elongate microridges (Fig. S3 and Video 1). Time-lapse imaging also demonstrated that microridges form in a centripetal manner: assembly of microridges from pegs started in the cell periphery and progressed toward the cell center (Fig. 1 C and Video 1). These observations confirmed previous studies suggesting that actin pegs are precursors to microridges that coalesce to form and elongate microridges (Lam et al., 2015; Pinto et al., 2019).

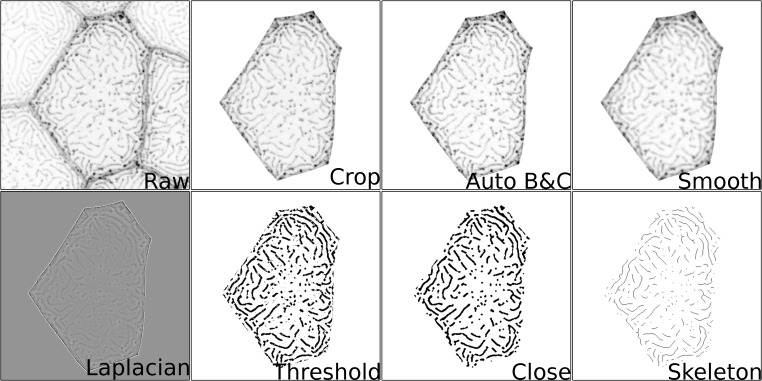
Figure S1.

Image analysis method for microridge detection. Stepwise illustration of image analysis pipeline, as described in Materials and methods.

Figure S2.

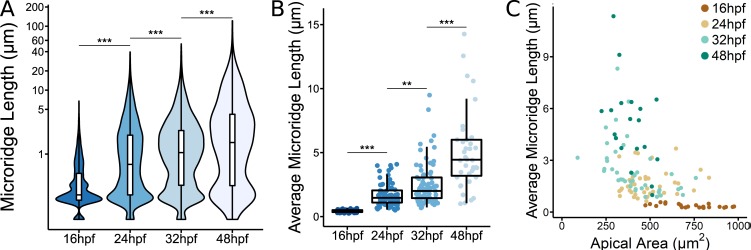
Additional analyses of microridge development. (A) Box and violin plot of microridge length in periderm cells at the indicated stages of zebrafish development. For a weighted presentation of this data, see Fig. 1 B. ***, P < 0.001; Kruskal–Wallis test followed by Dunn’s test (n = 15,582 structures in 23 cells from 10 fish at 16 hpf; n = 5,096 structures in 40 cells from nine fish at 24 hpf; n = 4,572 structures in 40 cells from nine fish at 32 hpf; n = 1,309 structures in 19 cells from six fish at 48 hpf). (B) Dot and box plot of average microridge length per periderm cell at the indicated stages of zebrafish development. **, P < 0.01; ***, P < 0.001; Kruskal–Wallis test followed by Dunn’s test (n = 15,582 structures in 23 cells from 10 fish at 16 hpf; n = 5,096 structures in 40 cells from nine fish at 24 hpf; n = 4,572 structures in 40 cells from nine fish at 32 hpf; n = 1,309 structures in 19 cells from six fish at 48 hpf). (C) Scatter plot of average microridge length per cell versus apical cell area at the indicated stages of zebrafish development (n = 15,582 structures in 23 cells from 10 fish at 16 hpf; n = 5,096 structures in 40 cells from nine fish at 24 hpf; n = 4,572 structures in 40 cells from nine fish at 32 hpf; n = 1,309 structures in 19 cells from six fish at 48 hpf). For box plots, middle box line is the median, and lower and upper ends of boxes are 25th and 75th percentiles, respectively.

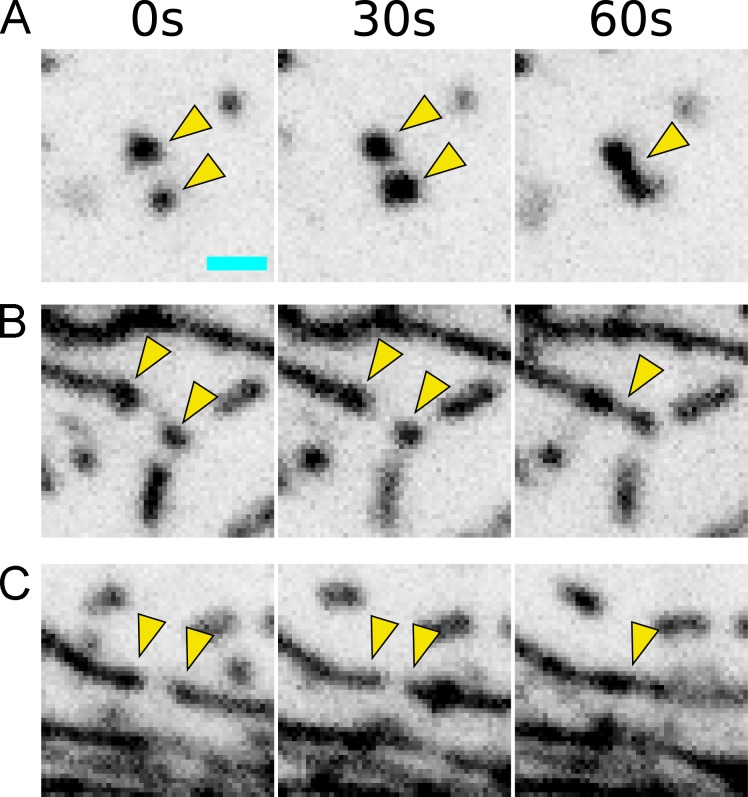
Figure S3.

Three modes of microridge formation and growth. (A-C) Time-lapse sequences show examples of two pegs coalescing to form an incipient microridge (A), the addition of a peg to the end of a preexisting microridge (B), and the joining of two preexisting microridges (C). Scale bar, 1 µm (A).

Video 1.

Live imaging of Lifeact-GFP in periderm cells during microridge development, beginning at 18 hpf. All images are maximum intensity projections; time stamp represents hours:minutes:seconds. Frame rate is 25 frames/s.

https://movie.rupress.org/media/by_doi/10.1083/JCB_201904144.v1/source

We next considered if microridge morphogenesis is associated with other changes in the morphology or biomechanical properties of the developing epithelium. Indeed, we noticed that during the period of transition from pegs to microridges (~16–32 hpf), the apical area of periderm cells decreased (44.7% on average), but stabilized between 32 hpf and 48 hpf (Fig. 1 D). Moreover, average microridge length in individual cells inversely correlated with apical cell area: smaller cells had, on average, longer microridges (Fig. S2 C), suggesting that apical area may influence microridge length. To determine whether cell areas shrank predominantly by apical constriction or cell division, we imaged actin dynamics at 30-s intervals during an early stage of microridge elongation (18–19 hpf). These videos demonstrated that cells underwent intermittent bouts of apical constriction and relaxation, but predominantly constricted, similar to the ratchet-like process that has been described in other instances of apical constriction (Martin et al., 2009; Solon et al., 2009; Blanchard et al., 2010). Microridge length closely tracked changes in apical cell area: microridges elongated, likely by peg accretion, as apical areas shrank, and microridges shortened as apical areas increased (Fig. 1, E and F). We conclude that pegs and microridges are in a dynamic equilibrium and that apical constriction promotes microridge formation.

A model for microridge formation reproduces experimental observations

Apical constriction significantly reduces the 2D-projected apical area of epithelial cells, as illustrated by our live-cell imaging (Fig. 1, E and F). However, it was not clear how actin pegs and microridges, which determine the 3D topography of the membrane, affect the total surface area of the apical membrane. We therefore asked whether cells with pegs or cells with microridges have a larger 3D apical surface when their projected apical areas are identical. To answer this question, we assumed that actin pegs and microridges are of equal and uniform height and computationally evaluated the total 3D surface of apical regions with only microridges or only pegs. Surprisingly, after normalization by the 2D-projected area of the regions, we found that microridges induce larger membrane surfaces (Fig. 1 G). Therefore, while apical constriction reduces the apical membrane surface, the associated transition from pegs to microridges increases it.

To gain quantitative insight into these observations, we developed a simple biophysical model of the cellular apical domain. We hypothesized that apical morphogenesis is generated by the dynamics of three closely interacting subsystems with distinct biomechanical properties: the membrane itself, the immediately underlying branched actin structure that fills pegs and microridges, and the deeper actomyosin cortex (Fig. 2 A). Actin filaments within the branched structure are largely disordered but project into the neighboring membrane (Uehara et al., 1991; Pinto et al., 2019), similar to the actin structures that power lamellipodia protrusion. We thus assumed that their polymerization stretches the membrane and expands the membrane surface. Conversely, filaments in the deeper actomyosin cortex are largely aligned parallel to the basal surface of cells (Pinto et al., 2019). Contraction of the cortex drives apical constriction (Martin and Goldstein, 2014) and reduces surface tension (Fig. 2 B). Excess membrane is presumably removed by endocytosis (Sonal et al., 2014). We thus propose that the two actin subsystems have opposing effects on membrane area and tension; branched actin and the contractile actomyosin cortex increase and decrease surface tension, respectively. Pattern formation in our model is driven by the autocatalytic branched polymerization of actin at the membrane–cytoskeleton interface. To ensure formation of both pegs and microridges, we resorted to a prototypical activator-inhibitor model described by Gierer and Meinhardt (1972), in which the role of the inhibitor is played by the height, h, of the actin structure. This heuristic assumption mimics the opposition that surface tension produces to actin polymerization (Gov, 2006; Gov and Gopinathan, 2006; Atilgan et al., 2006; Mogilner and Rubinstein, 2005). Conversely, surface tension is relaxed by myosin motor-driven contraction of the actomyosin cortex, whose dynamics are described by the well-established active gel model (Prost et al., 2015). A detailed description of the model equations and parameters is provided in Materials and methods.

Figure 2.

In silico simulation of apical constriction mimics microridge development in vivo. (A) Diagram of a periderm cell in homeostatic conditions with actin-filled microridges projecting from the apical surface. The underlying apical cortex is rich in actin (red filaments) and NMII (green bipolar mini-filaments) and attached to the cell membrane. (B) Diagram of a periderm cell undergoing apical constriction. NMII contraction in the apical cortex relieves tension in the attached cell membrane, allowing actin to protrude. (C) Cells from in silico simulations developed a long microridge at the cell border before microridge formation elsewhere on the apical membrane. Arrows in the inset image point to a similar structure in periderm cells expressing Lifeact-GFP before microridge development. (D) In silico simulation of apical constriction in our biomechanical model recapitulates the centripetal progression of microridge development observed in vivo. (E) Average change in apical area and average microridge length in 20 simulations. Scale bar, 10 µm (C).

In our model, spatially uniform isotropic contraction of the apical actomyosin cortex produced a transition from pegs to microridges, which occurred uniformly on the apical surface (Video 2, right). We noticed that even with parameters corresponding to the initially relaxed cortex, when the interior of the apical domain is populated only by pegs, a single closed microridge had formed immediately proximal to the cell boundary (Fig. 2 C). Interestingly, such microridges, positioned next to the tight junctions between cells, have been routinely observed in experiments by us and others (Depasquale, 2018). Remarkably, as in the model, they typically form before the formation of microridges in the interior of the apical domain. In live-cell images, they emerged first as discontinuous paired structures positioned on each side of, and strictly parallel to, the tight junctions (Fig. 2 C, inset). As microridges developed within the apical interior, these junction-associated structures matured into proper microridges and continuously surrounded the entire apical domains of cells (Fig. 1 A). In the model, formation of this outer microridge is determined by the boundary condition that fixes vertical membrane deflection on the boundary to h = 0. Thus, our model predicts that formation of these circumferential microridges is determined by the singularity in the surface tension imposed by unyielding tight junctions.

Video 2.

Simulation of microridge formation. In silico simulation of apical constriction in our biomechanical model recapitulates the centripetal progression of microridge development observed in vivo (left panel). As the cell constricts its surface, surface tension is relieved in a centripetally moving wave, promoting peg coalescence in a similar pattern. For comparison, right panel shows constriction in response to the spatially homogeneous increase in active stress. Frame rate is 14 frames/s.

https://movie.rupress.org/media/by_doi/10.1083/JCB_201904144.v2/source

Model simulations showed that uniform contraction of the apical actomyosin cortex cannot explain centripetal emergence of microridges from the cell boundaries. We thus surmised that the apical actomyosin cortex could also undergo a process of maturation. Possibly, its contractility increases first at the tight junctions, where Rho GTPase activity that drives actin polymerization and myosin contraction is typically enriched (Zihni and Terry, 2015; Ratheesh et al., 2012), and then progresses inwards. Simulations of the model augmented with this additional hypothesis reproduced the experimental observations. Starting at the cell boundary, pegs coalesced into microridges, which eventually filled the entire apical domain (Fig. 2, D and E; and Video 2, left).

NMII is required for apical constriction and microridge formation

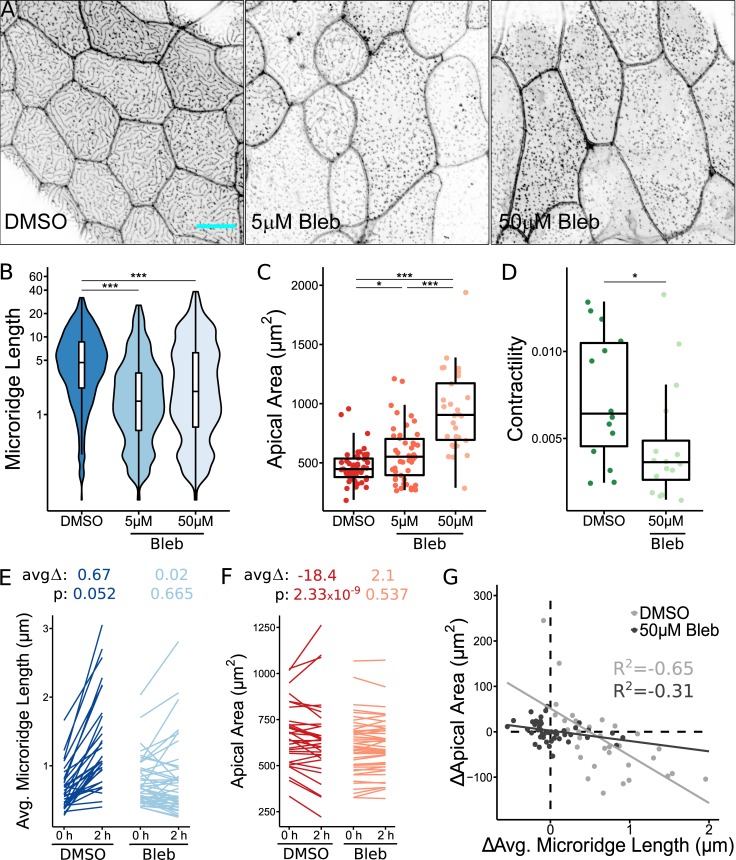
A previous study suggested that NMII is involved in lengthening microridges (Raman et al., 2016), but did not determine how it contributes to microridge formation, nor whether it is linked to apical constriction. We therefore sought direct evidence that NMII produces apical constriction and induces microridge morphogenesis from actin pegs. We first inhibited NMII contractility by treating zebrafish larvae with the specific small molecule inhibitor blebbistatin (Straight et al., 2003) for 24 h spanning the period of microridge development (16–40 hpf). Blebbistatin reduced apical constriction in a concentration-dependent manner and inhibited the coalescence of pegs into microridges (Fig. 3, A–C). Since extended exposures to blebbistatin could affect microridges in a variety of direct or indirect ways, we examined the effects of shorter treatments; periderm cells expressing the actin reporter were imaged before and after 2 h of blebbistatin exposure. During this short period of exposure, blebbistatin inhibited microridge elongation and reduced apical constriction, compared with controls (Fig. 3, E and F). In control cells, microridge length and apical cell area were inversely correlated (R² = –0.65), but this relationship was diminished by treatment with blebbistatin (R² = –0.31; Fig. 3 G).

Figure 3.

NMII contraction is required for apical constriction and microridge development. (A) Representative projections of Lifeact-GFP in periderm cells on 40 hpf zebrafish larvae after 24-h treatment with either 1% DMSO or indicated concentration of blebbistatin (Bleb). (B) Box and violin plot of microridge length in 40 hpf zebrafish embryos after 24-h treatment with either 1% DMSO or indicated concentration of blebbistatin. Data are presented as a weighted distribution of microridge length, in which frequency is proportional to length, approximating occupied area. ***, P < 0.001; Kruskal–Wallis test followed by Dunn’s test (n = 6,772 structures in 53 cells from 10 fish for 1% DMSO, n = 9,587 structures in 46 cells from 11 fish for 5 µM blebbistatin; n = 8,623 structures in 29 cells from 13 fish for 50 µM blebbistatin). (C) Dot and box plot of periderm cell apical area in 40 hpf zebrafish embryos after 24-h treatment with either 1% DMSO or indicated concentration of blebbistatin. *, P < 0.05; ***, P < 0.001; Kruskal–Wallis test followed by Dunn’s test (n = 53 cells from 10 fish for 1% DMSO, n = 46 cells from 11 fish for 5 µM blebbistatin, n = 29 cells from 13 fish for 50 µM blebbistatin). (D) Dot and box plot of frame average NMII reporter contraction area summed over a 10-min period (30-s intervals), after 1-h treatment with either 1% DMSO or 50 µM blebbistatin. *, P < 0.05; Wilcoxon rank-sum test (n = 10,416 contractions in 29 cells from 18 fish for 1% DMSO, n = 2,259 contractions in 16 cells from nine fish for 50 µM blebbistatin). (E) Line plots of average microridge length in individual periderm cells before (18 hpf) and after (20 hpf) 2-h treatment with either 1% DMSO or 50 µM blebbistatin. Above, average change in average microridge length and P values (Wilcoxon signed-rank test; n = 17,039 structures in 64 cells from 10 fish for 1% DMSO, n = 20,873 structures in 92 cells from 11 fish for 50 µM blebbistatin). (F) Line plots of periderm cell apical area in individual cells before (18 hpf) and after (20 hpf) 2-h treatment with either 1% DMSO or 50 µM blebbistatin. Above, average change in periderm cell apical area and P values (Wilcoxon signed-rank test; n = 64 cells from 10 fish for 1% DMSO, n = 92 cells from 11 fish for 50 µM blebbistatin). (G) Scatter plot of change in average microridge length versus change in periderm cell apical area after 2-h treatment with 1% DMSO or 50 µM blebbistatin. R² determined using Pearson’s correlation coefficient (n = 17,039 structures in 64 cells from 10 fish for 1% DMSO, n = 20,873 structures in 92 cells from 11 fish for 50 µM blebbistatin). Scale bar, 10 µm (A). For box plots, middle box line is the median, and lower and upper ends of boxes are 25th and 75th percentiles, respectively.

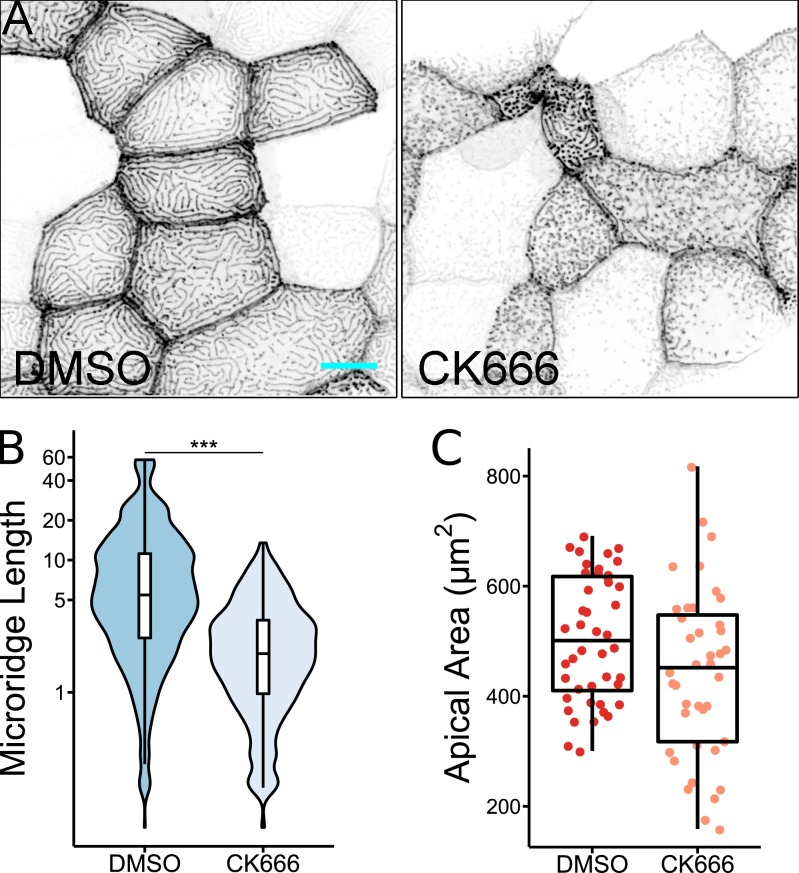
The branched actin nucleator Arp2/3 is required for microridge formation and maintenance (Lam et al., 2015). As expected, an inhibitor of Arp2/3, CK666 (Nolen et al., 2009), prevented coalescence of actin pegs into microridges (Fig. S4, A and B), but did not prevent pegs from forming or reduce their dynamics (not shown). Interestingly, however, CK666 failed to reduce apical constriction and, in fact, appeared to promote it (Fig. S4 C). This observation is consistent with our hypothesis that polymerization of the branched actin subsystem, for which Arp2/3 is required, induces membrane surface expansion and thus opposes apical constriction, which is driven by the underlying actomyosin layer.

Figure S4.

Arp2/3 activity is required for microridge development, but not apical constriction. (A) Representative projections of Lifeact-GFP in periderm cells on 24 hpf zebrafish larvae after 8-h treatment with either 1% DMSO or 100 µM CK666. (B) Box and violin plot of microridge length in 24 hpf zebrafish larvae after 8-h treatment with either 1% DMSO or 100 µM CK666. Data displayed are a weighted distribution of microridge length where frequency is proportional to microridge length, approximating occupied area. ***, P < 0.001; Wilcoxon rank-sum test (n = 5,283 structures in 44 cells from 11 fish for 1% DMSO, n = 6,130 structures in 40 cells from 12 fish for 100 µM CK666). (C) Dot and box plot of periderm cell apical area in 24 hpf zebrafish embryos after 8-h treatment with either 1% DMSO or 100 µM CK666. P = 0.052; Wilcoxon rank-sum test (n = 44 cells from 11 fish for 1% DMSO, n = 40 cells from 12 fish for 100 µM CK666). Scale bar, 10 µm (A). For box plots, middle box line is the median, and lower and upper ends of boxes are 25th and 75th percentiles, respectively.

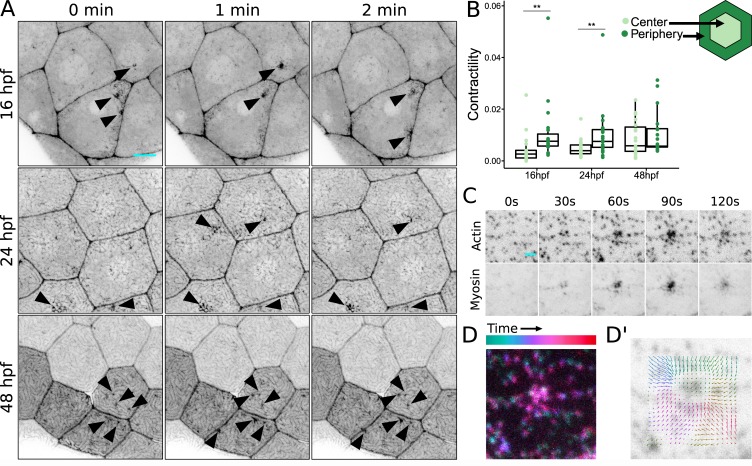
To directly visualize the localization and activity of NMII in periderm cells during apical constriction and microridge development, we created a transgenic zebrafish line that expresses an NMII reporter (Maître et al., 2012) specifically in periderm cells. As expected, this reporter localized to cell–cell junctions and appeared to be distributed across the apical cortex. Time-lapse imaging revealed transient local flashes of reporter fluorescence at the apical surface, which we interpreted as contractile pulses that concentrated NMII at their foci (Fig. 4 A and Video 3). Indeed, 1 h of exposure to blebbistatin was sufficient to significantly decrease these pulses (Fig. 3 D), confirming that they reflect contractile activity of NMII. These apical NMII pulses temporally and spatially resembled pulsatile contractions that drive apical constriction in other systems (Fernández et al., 2007; Solon et al., 2009; Blanchard et al., 2010; David et al., 2010). Contractile events concentrated toward the periphery of zebrafish periderm cells early in microridge development (16 hpf), progressed toward the center as development proceeded (24 hpf), and equalized across the apical surface after microridge formation (48 hpf; Fig. 4 B), supporting our hypothesis that apical constriction initiates at, and centripetally propagates from, junctions. This outside-in progression of cortical activity mirrors the spatial progression of microridge formation (Fig. 1 C). Time-lapse imaging of periderm cells expressing both actin and NMII reporters demonstrated that contraction events pulled nearby actin pegs toward myosin foci (Fig. 4, C and D; and Video 3).

Figure 4.

Apical NMII contractions pinch the cell membrane. (A) Sequential projections from time-lapse videos of Myl12.1-EGFP in periderm cells at indicated stages of zebrafish development. Arrowheads: dynamic concentrations of NMII reporter fluorescence at the apical membrane. (B) Dot and box plot of frame average NMII reporter contraction area summed over a 10-min period (30-s intervals) at specified time points during zebrafish development. Contractions were categorized based on whether the majority of contraction area was within the inner 25% of the cell surface (Center) or in the remaining outer 75% (Periphery). **, P < 0.01; Wilcoxon signed-rank test (n = 11,794 contractions in 19 cells from 13 fish at 16 hpf; n = 18,776 contractions in 25 cells from 13 fish at 24 hpf; n = 6,303 contractions in 19 cells from seven fish at 48 hpf). (C) Sequential projections from a time-lapse video of Lifeact-Ruby and Myl12.1-EGFP during an apical NMII pulse in a 16 hpf periderm cell. (D and D’) Superimposition of sequential frames from a time-lapse video (D) and particle image velocimetry (D’) show the centripetal trajectory of actin structures toward the focus of contraction. Scale bars, 10 µm (A) and 2 µm (C). For box plots, middle box line is the median, and lower and upper ends of boxes are 25th and 75th percentiles, respectively.

Video 3.

NMII (Myl12.1-EGFP) contractions in the apical cortex pull on actin microridges (Lifeact-Ruby) of periderm cells at various stages in microridge development, indicated by title cards. All images are maximum intensity projections; time stamp represents minutes:seconds. Frame rate is 5 frames/s.

https://movie.rupress.org/media/by_doi/10.1083/JCB_201904144.v3/source

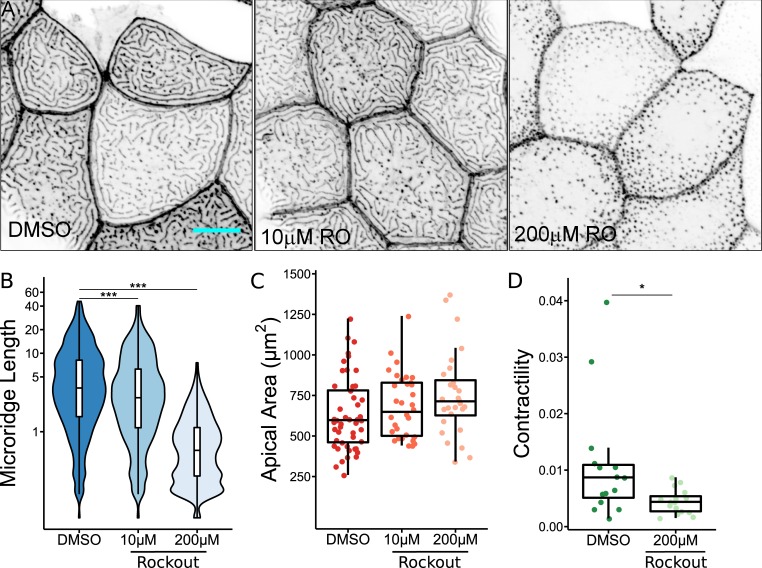
Contractile activity of NMII is activated via phosphorylation of the myosin regulatory light chain by multiple kinases, such as Rho GTPase effector kinase (ROCK) and myosin light chain kinase (MLCK; Matsumura, 2005). To determine if these kinases regulate microridge morphogenesis, we inhibited ROCK or MLCK with the small molecule inhibitors Rockout or ML-7, respectively, between 16 and 24 hpf. While ML-7 had no effect on microridge formation (data not shown), Rockout significantly decreased microridge length and increased apical cell area in a concentration-dependent manner (Fig. 5, A–C). Additionally, 1 h of Rockout treatment significantly reduced NMII pulses (Fig. 5 D). Rockout did not dramatically affect peg dynamics, indicating that contraction specifically regulates peg coalescence, not peg formation (data not shown). This result indirectly supports the hypothesis that contraction of the actomyosin cortex is driven by activity of RhoA via its effector ROCK. We conclude that, regardless of its upstream regulation, NMII-driven contraction of the apical actomyosin cortex is required for both apical constriction and formation of microridges from actin peg precursors.

Figure 5.

ROCK activity is required for microridge development. (A) Representative projections of Lifeact-GFP in periderm cells on 24 hpf zebrafish larvae after 8-h treatment with either 0.2% DMSO or indicated concentration of Rockout (RO). (B) Box and violin plot of microridge length in 24 hpf zebrafish embryos after 8-h treatment with either 0.2% DMSO or indicated concentration of Rockout. Data displayed are a weighted distribution of microridge length, where frequency is proportional to microridge length, approximating occupied area. ***, P < 0.001; Kruskal–Wallis test followed by Dunn’s test (n = 10,385 structures in 49 cells from 15 fish for 0.2% DMSO, n = 8,353 structures in 34 cells from 11 fish for 10 µM Rockout, n = 7,501 structures in 28 cells from 10 fish for 200 µM Rockout). (C) Dot and box plot of periderm cell apical area in 24 hpf zebrafish embryos after 8-h treatment with either 0.2% DMSO or indicated concentration of Rockout. P = 0.063; Kruskal–Wallis test (n = 49 cells from 15 fish for 0.2% DMSO, n = 34 cells from 11 fish for 10 µM Rockout, n = 28 cells from 10 fish for 200 µM Rockout). (D) Dot and box plot of frame average NMII reporter contraction area summed over a 10-min period (30-s intervals), after 1-h treatment with either 0.2% DMSO or 200 µM Rockout. *, P < 0.05; Wilcoxon rank-sum test (n = 9,048 contractions in 15 cells from 10 fish for 0.2% DMSO, n = 3,495 contractions in 16 cells from 10 fish for 200 µM Rockout). Scale bar, 10 µm (A). For box plots, middle box line is the median; lower and upper ends of boxes are 25th and 75th percentiles, respectively.

Surface tension directly controls microridge formation

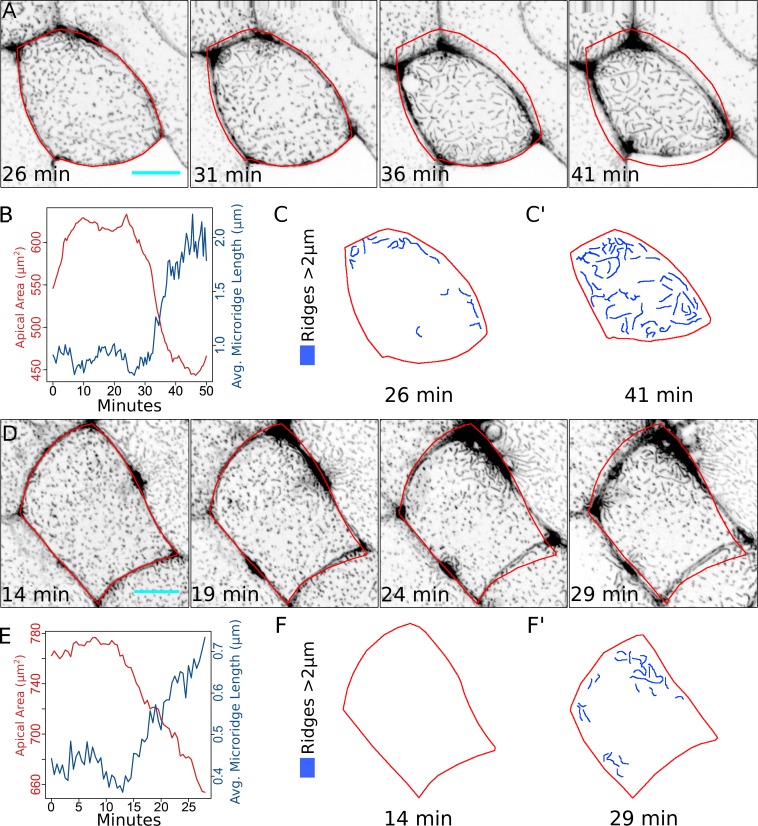
Although the activity of NMII and its activation by ROCK are required for apical constriction and microridge formation, it is possible that myosin affects microridge formation by a means not related to its biomechanical function—for example, by serving as a scaffold for signaling complexes. We therefore sought to directly test whether surface tension or an unrelated function of NMII controls microridge formation. To alter surface tension, we exposed zebrafish embryos to hyperosmolar media during early stages of microridge development. Placing animals in a hyperosmolar environment should draw water from periderm cells, causing them to “deflate,” thus reducing surface tension independent of myosin contraction. Indeed, exposing zebrafish embryos to either high-salt media or glycerol-supplemented media at a stage when cells are dominated by actin pegs, but before significant microridge formation typically occurs (16 hpf), caused cells to shrink rapidly (Fig. 6). Time-lapse imaging demonstrated that as cells shrank, actin pegs rapidly coalesced into microridges (Fig. 6 and Video 4). Thus, reducing surface tension is sufficient to promote microridge formation, in agreement with our in silico model.

Figure 6.

Membrane surface energy regulates microridge formation. (A) Sequential projections from a time-lapse video of Lifeact-GFP in periderm cells after exposure to water with 500× Instant Ocean salt. Red outline shows position of cell border at 26 min. (B) Line plot of apical area and average microridge length in the periderm cell shown in A after exposure to water with 500× Instant Ocean salt. (C and C’) Diagram of cell in A at the indicated time points with microridges longer than 2 µm traced in blue. (D) Sequential projections from a time-lapse video of Lifeact-GFP in periderm cells after exposure to 12.5% glycerol. Red outline shows position of cell border at 14 min. (E) Line plot of apical area and average microridge length in the cell shown in D after exposure to 12.5% glycerol. (F and F’) Diagram of cell in E at the indicated time points with microridges longer than 2 µm traced in blue. Scale bars, 10 µm (A and D).

Video 4.

Live imaging of Lifeact-GFP in 16 hpf periderm cells, beginning 3 min after exposure to high-salt media. All images are maximum intensity projections; time stamp represents minutes:seconds. Frame rate is 10 frames/s.

https://movie.rupress.org/media/by_doi/10.1083/JCB_201904144.v4/source

Anisotropy of microridge formation indicates that peg coalescence is an active process

To further our understanding of microridge formation, we sought to direct this process in a well-controlled experimental setup. To achieve this goal, we leveraged the natural wound-healing behavior of epithelial sheets. In response to ablation of individual cells, neighboring cells generate a powerful biomechanical response to rapidly constrict the wound (Lam et al., 2015; Rosenblatt et al., 2001). If two cells are ablated simultaneously, intervening cells will sometimes undergo near-perfect uniaxial stretching along the axis connecting the two wounds (Fig. 7, A–C). For these experiments, we chose to ablate periderm cells at an early developmental stage with few microridges (16 hpf), using a laser on a two-photon microscope (Video 5). Cells were selected for analysis if they exhibited robust uniaxial stretch. These analyses showed that stretch was accompanied by a small reduction of the apical surface, on average 10% of the projected area (Fig. 7 E). Remarkably, as they stretched, all cells formed new microridges, which were predominantly aligned along the stretch axis (Fig. 7, B–D and F; and Video 5). The highest anisotropy of microridge orientation was coincident with the maximal distortion of stretched cells (~10 min after ablation). This alignment slightly decreased as the epithelium relaxed into a new steady-state configuration.

Figure 7.

Cell stretching promotes formation of microridges along the elongation axis. (A) Projection of Lifeact-GFP in periderm cells on a 16 hpf zebrafish embryo before laser cell ablation. Eye: observed cell. Target: cell to be ablated. (B) Still images from a time-lapse sequence of the cell in A elongating over 10 min. (C and C′) Outline of the elongating cell in B, shown at the initial time-point (C), and 10 min after ablation (C’). Microridges longer than 2 µm are highlighted in blue. (D) Averaged histogram of directions of peg coalescence events (normalized to maximal bin, direction of elongation at 0°). (E) Projected area for five cells used in this analysis. Areas were normalized to the initial value. (F) Elongation factor (ratio of longest axis to shortest axis for the transformation of the cell) for five analyzed cells. Scale bars, 10 µm (A and B).

Video 5.

Live imaging of Lifeact-GFP in 16 hpf periderm cells, beginning immediately after ablation of periderm cells on opposite sides of the central cell. All images are maximum intensity projections; time stamp represents minutes:seconds. Frame rate is 10 frames/s.

https://movie.rupress.org/media/by_doi/10.1083/JCB_201904144.v5/source

Cell stretch produced by neighbor ablation temporarily induces flow of the viscoelastic actomyosin cortex, which is transmitted to the plasma membrane and the underlying branched F-actin cortex via multiple protein–protein links. The observed orientation of microridges along the stretch axis could be potentially explained by two distinct sources, both induced by flow. First, the torque generated by the actomyosin flow could reorient preexisting microridges along the direction of stretch. However, quantification (Fig. 7, C and C′) showed that, before cell stretch, microridges were essentially nonexistent and largely formed during the stretch itself. Thus, reorientation of preexisting microridges contributes little, if at all, to the aligned microridges seen in the experiment. Alternatively, microridges could form in an oriented manner if the fusion of pegs occurred preferentially along the direction of stretch. To test this second hypothesis, we quantified the angle at which actin peg fusion occurred after laser ablation. This analysis demonstrated that, in all analyzed cells, peg fusion was strongly anisotropic, on average three times more frequent along the stretch axis than perpendicular to it (Fig. 7 D), confirming that microridges indeed form in an oriented manner.

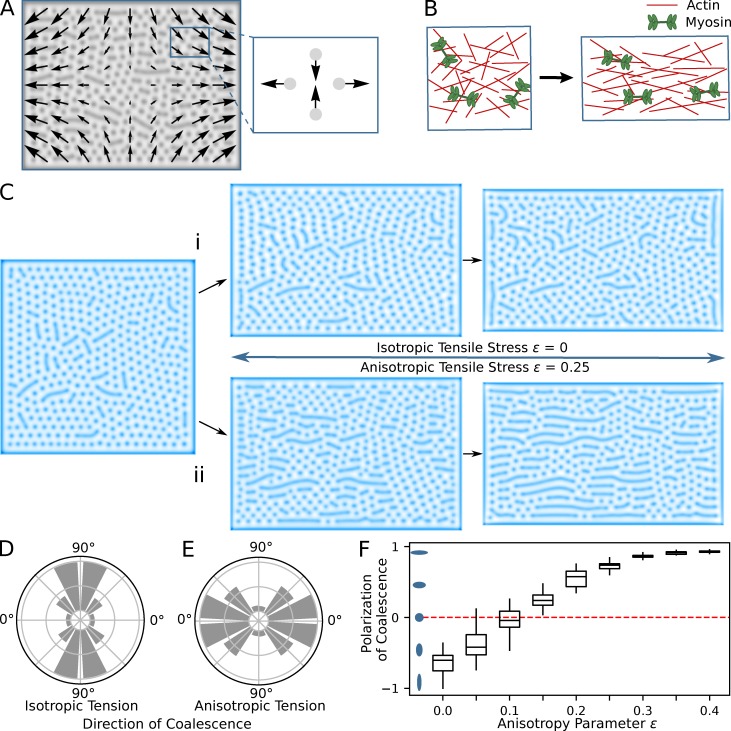
The observation that pegs fuse along the stretch axis is surprising, as actin pegs sandwiched between the membrane and the actomyosin cortex are transported by the cortical flow and thus would be expected to collide preferentially along the direction orthogonal to the stretch axis (Fig. 8 A). Theory predicts that peg fusion is energetically preferable (Gov, 2006; Derényi et al., 2002), as it reduces membrane-bending energy. Hydrodynamic flow-induced collision of pegs should reduce the potential barrier to fusion, and therefore promote peg fusion perpendicular to the direction of stretch. Indeed, in agreement with this theoretical argument, and contrary to experimental results, simulations of our model that emulated cell stretch produced preferential fusion of pegs perpendicular, rather than parallel, to the stretch axis (Fig. 8, C and D). This discrepancy suggested that our model failed to capture the full complexity of cortical biomechanics. Hydrodynamic flow could potentially order initially isotropic actin filaments along the stretch axis and thus induce orientation of force-generating NMII filaments (Fig. 8 B). Counterintuitively, this passive reorientation would increase the active stress generated by the actomyosin gel in the direction of stretch and reduce it in the opposite direction. Introduction of this hypothesis into our model produced simulation results in full agreement with the experiment (Fig. 8, C, E, and F; and Video 6). Furthermore, the model revealed the existence of a minimal value of the flow-induced actomyosin anisotropy, below which peg fusion still occurs predominantly perpendicular to the stretch axis (Fig. 8 F). Since our analysis of experimental data identified a significant (3:1) preference for pegs to fuse along the stretch axis, we conclude that stretch-induced cortical flow must induce substantial orientation of F-actin fibers and NMII motors.

Figure 8.

Flow-induced actomyosin anisotropy directs peg fusion along the cell stretch axis. (A) Approximated cortex flow during uniaxial stretch. Flow can be locally represented as elongation along one axis and compression along an orthogonal axis. (B) Scheme of rapid stretch that leads to partial alignment of actin and myosin filaments. (C) Modeling of cell stretching with isotropic (i) and anisotropic (ii) tensile stress. (D and E) Corresponding histograms of distributions of structure fusions (averaged over 100 simulations with different initial conditions). If tension does not depend on the anisotropic flow, the fusions occur mostly in the direction perpendicular to the elongation (D). In the case of anisotropic tensile stress, the fusions occur in the direction of elongation (E). (F) Polarization of coalescence histogram for different values of the anisotropy parameter. Polarization value −1 corresponds to coalescence in the perpendicular direction and value 1 corresponds to coalescence in the direction parallel to elongation. For box plots, middle box line is the median, and lower and upper ends of boxes are 25th and 75th percentiles, respectively.

Video 6.

In silico simulation of uniaxial elongation of a model rectangular cell. Left panel shows pattern formation in the absence of sensitivity to anisotropic flow $\left(\epsilon =0\right)$. Right panel shows pattern formation with surface tension depending on underlying anisotropic actomyosin flow. Frame rate is 14 frames/s.

https://movie.rupress.org/media/by_doi/10.1083/JCB_201904144.v6/source

Discussion

NMII-based contraction is well known to alter cell surfaces in two dimensions: for example, polarized contractions at junctions regulate polarized cell rearrangements (Bertet et al., 2004; Blankenship et al., 2006), and cortical contraction shrinks surfaces during apical constriction (Martin and Goldstein, 2014). Here, we demonstrate that contraction in zebrafish periderm cells not only changes 2D cell surface geometry but also simultaneously sculpts the 3D topography of cells: NMII-based cortical contractions couple apical constriction to the patterning of microridges, which protrude from the apical surface of zebrafish periderm cells, orthogonal to the cortex. Computational modeling and in vivo experiments together support a model in which cortical contractions lower surface tension to permit the coalescence of actin pegs into microridges, and cortical flow influences the organization of contractile machinery, which determines microridge orientation.

Microridges form by the accretion of precursor structures (pegs), a feature that distinguishes them from better-studied protrusions, such as lamellipodia and dorsal ruffles, which emerge and expand as a single unit. Inhibiting Arp2/3, NMII, or ROCK prevented peg coalescence into microridges, but did not appear to affect the pegs themselves. Thus, peg formation and peg coalescence are two separate morphogenetic steps under distinct biomechanical and biochemical regulation. Understanding peg formation, actin dynamics in pegs, and the regulation of peg density will be critical to fully understanding microridge morphogenesis. For example, aggregation of similar peg-like precursors to form ridge-like structures in cultured kidney cells is influenced by actin dynamics (Gorelik et al., 2003). A critical local peg density may be required for microridge formation, but our observations suggest that it is not sufficient, since peg density remains relatively constant in the peripheral domain of cells for several hours before microridge formation begins (data not shown). Upon integrating into microridges, pegs may, at least in part, retain their integrity as substructures, as we and others (Depasquale, 2018) have noted intensely labeled F-actin puncta within microridges. In fact, one ultrastructural study reported that periodic actin bundles could be discerned within microridges by electron microscopy (Bereiter-Hahn et al., 1979), though a more recent study using high-resolution techniques did not identify these substructures (Pinto et al., 2019). Whether pegs contain bundled parallel actin filaments, like microvilli, or only branched filaments, like podosomes, is thus unclear. Identifying the bundling proteins, nucleators, and motors that localize to pegs may resolve whether they resemble microvilli or podosomes, or are unique structures with a distinct actin organization and protein composition.

The cortical contractions we observed in periderm cells resemble contractions driving well-characterized behaviors in other, better studied systems, like Caenorhabditis elegans and Drosophila melanogaster gastrulation (Roh-Johnson et al., 2012; Martin et al., 2009). In those other systems, contraction is driven by Rho family GTPase signaling networks (Mason et al., 2013; Munjal et al., 2015; Marston et al., 2016). It is thus likely that contraction of zebrafish periderm cells during microridge formation also depends on Rho family GTPases. Indeed, we found that the RhoA effector ROCK is required for apical contraction and microridge development in periderm cells, and previous work showed that RhoA inhibition can alter microridge patterning (Lam et al., 2015). Our observation that contractions initially predominate near cell borders may result from the association of RhoA regulators with cell–cell junctions (Ratheesh et al., 2012; Zihni and Terry, 2015), and could contribute to the centripetal progression of microridge formation. Defining the contribution of cell–cell junctions and Rho signaling networks could help explain how cortical contractions are tuned to create biomechanical conditions conducive to apical constriction and microridge morphogenesis.

Our theoretical model predicted that reducing surface tension is sufficient to promote peg coalescence into microridges. This prediction was supported by experiments showing that microridges rapidly formed as cells shrank in hyperosmolar media. Conversely, cell swelling would be predicted to prevent microridge formation or cause microridge disassembly. Unfortunately, fish larvae and periderm cells appeared to be unaffected by treatment with hypo-osmolar media (not shown), potentially due to homeostatic regulatory mechanisms. Nonetheless, a previous study showed that in zebrafish with myosin Vb mutations, cells swell due to defects in vesicular trafficking and lose microridges (Sonal et al., 2014), consistent with the idea that increasing surface tension opposes microridge formation.

Contractile patterns are shaped by the flow of contractile machinery and NMII regulators within the plane of the cortex (Munjal et al., 2015; Rauzi et al., 2010; Bray and White, 1988). Our experiments and biomechanical modeling demonstrated that when cortical flow is anisotropically oriented by cell stretching, pegs coalesce into microridges in an oriented manner, aligning nascent microridges along the stretch axis. This phenomenon could explain microridge orientation during naturally anisotropic cell behaviors, like cytokinesis. Just before cytokinesis, cells expand and microridges dissolve back into pegs; during cytokinesis, cells contract dramatically and microridges rapidly reform (Lam et al., 2015). These new microridges are initially oriented predominantly perpendicular to the cytokinetic furrow, consistent with the observation that, during cytokinesis, ingression drives polarized cortical flow toward the furrow (Khaliullin et al., 2018; Cao and Wang, 1990; DeBiasio et al., 1996).

Microridges (and closely related structures called microplicae) are found on a variety of mucosal tissues in many vertebrate animals, suggesting that they play a common role in mucus retention (Depasquale, 2018). Nonetheless, their morphologies vary significantly in length, spacing, and branching, perhaps reflecting optimized morphologies for their function in different tissue contexts. Intriguingly, microridge morphology even varies in different parts of the zebrafish skin that are likely under distinct mechanical strains; for example, microridges are shorter and more branched in cells covering pectoral fins, and are reduced in periderm cells that stretch over bulges in the skin, such as those created by neuromast mechanosensory organs (data not shown). This variation in microridge patterns provides an opportunity to further explore how actin regulators, contraction, and membrane biomechanics contribute to sculpting complex 3D membrane topographies.

Materials and methods

Zebrafish

Zebrafish (Danio rerio) were raised at 28.5°C on a 14-h/10-h light/dark cycle. Embryos were raised at 28.5°C in embryo water composed of 0.3 g/liter Instant Ocean salt (Spectrum Brands, Inc.) and 0.1% methylene blue. Previously characterized zebrafish lines in this paper include AB wild-type fish (ZFIN: ZDB-GENO-960809-7), Tg(krt5:Gal4) (Rasmussen et al., 2015), and Tg(UAS:Lifeact-GFP) (Helker et al., 2013). Transgenic zebrafish lines Tg(krt5:Lifeact-GFP), Tg(krt5:Lifeact-Ruby), and Tg(krt5:Myl12.1-EGFP) were created for this publication. All experimental procedures were approved by the Chancellor’s Animal Research Care Committee at the University of California, Los Angeles.

Plasmids and transgenes

Plasmids were constructed using the Gateway-based Tol2kit (Kwan et al., 2007). The following plasmids have been described previously: p5E-krt5 (Rasmussen et al., 2015), pME-myl12.1 (Maître et al., 2012), p3E-polyA, p3E-EGFPpA, and pDestTol2pA2 (Kwan et al., 2007).

To construct pME-lifeact-GFP, the following primers were used: 5′-GGG​GAC​AAG​TTT​GTA​CAA​AAA​AGC​AGG​CTT​AAT​GGG​TGT​CGC​AGA​TTT​G-3′ and 5′-GGG​GAC​CAC​TTT​GTA​CAA​GAA​AGC​TGG​GTA​TTA​CTT​GTA​CAG​CTC​GTC-3′; actb1:lifeact-GFP (Behrndt et al., 2012).

To construct pME-lifeact-Ruby, the following primers were used: 5′-GGG​GAC​AAG​TTT​GTA​CAA​AAA​AGC​AGG​CTT​AAT​GGG​TGT​CGC​AGA​TTT​G-3′ and 5′-GGG​GAC​CAC​TTT​GTA​CAA​GAA​AGC​TGG​GTA​TTA​AGC​GCC​TGT​GCT​ATG-3′; actb1:lifeact-RFP (Behrndt et al., 2012).

krt5:lifeact-GFP, krt5:lifeact-Ruby, and krt5:myl12.1-EGFP plasmids were created by combining the appropriate Gateway entry vectors with the pDestTol2pA2 destination vector in an LR reaction. To generate zebrafish lines with each of these transgenes, wild-type zebrafish embryos were injected at the one-cell stage with the appropriate plasmid (50 pg/embryo) and Tol2 mRNA (50 pg/embryo).

Live imaging of zebrafish embryos

Live zebrafish embryos were anesthetized with 0.2 mg/ml MS-222 (Western Chemical) in system water before mounting. Embryos were embedded in 1.2% agarose on a coverslip and sealed within a microscope chamber, as previously described (O’Brien et al., 2009). Chambers were filled with 0.2 mg/ml MS-222 solution and sealed with vacuum grease. Images taken up to 32 hpf show the top of the head, and images taken after 32 hpf show the side of the trunk, avoiding the yolk extension.

Hyperosmolar media treatment

After mounting zebrafish embryos on coverslips in 1.2% agarose, slide chambers were filled with solutions of either 0.15 g/ml Instant Ocean salt mix in deionized water, or 12.5% glycerol in Ringer’s solution, with 0.2 mg/ml MS-222. Time-lapse imaging was started immediately after filling the slide chamber with hyperosmolar media.

Drug treatments

All drugs were dissolved in DMSO. Treatment solutions were created by adding the appropriate volume of blebbistatin (Cayman Chemical), Rockout (Santa Cruz Biotechnology), ML-7 (Tocris Bioscience), or an equivalent volume of DMSO (≤1%) to Ringer’s solution with 0.2 mg/ml MS-222. Zebrafish larvae were immersed in treatment solutions for the specified periods of time, then mounted in agarose and imaged while bathed in the same solution. For treatment periods longer than 2 h, larvae were initially exposed to treatment solutions prepared without MS-222, then transferred to a treatment solution containing MS-222 at least 30 min before mounting and imaging.

Microscopy

Live fluorescent images and videos of microridge development, drug experiments, and hyperosmolar media experiments were performed on a Zeiss LSM510 or LSM800 confocal microscope. Images were acquired with Zeiss Zen software using an EC Plan-Neofluar 40×/1.30 oil DIC M27 objective with 2–3× digital zoom. During imaging, zebrafish slide chambers were mounted on a heated stage set to 28°C. The x-y position and z-stack were occasionally adjusted during time-lapse imaging to keep the cells of interest in the frame.

To ablate cells, we adapted a previously described method (O’Brien et al., 2009). Videos of cell stretching by periderm cell ablation were acquired using Zeiss Zen Software on a Zeiss LSM 880 microscope equipped with an EC Plan-Neofluar 40×/1.30 oil DIC M27 objective and a Coherent Chameleon Ultra II two-photon laser set to 813 nm. A 488-nm laser was used to find and focus on the cell surface at 250× digital zoom, and the cell was then exposed to two-photon laser illumination for 3–4 s at 5–6% laser power using “live” scanning.

Image analysis and statistics

Statistical analyses and data presentation were conducted in RStudio (RStudio, Inc.). All distributions were statistically tested for normality using the Shapiro–Wilks test for normality, and visually tested for normality using Q-Q plots. All statistical comparisons contained one or more nonnormal distributions, so nonparametric tests were chosen to analyze all data. P values generated by Dunn’s tests were adjusted using the Benjamini–Hochberg method.

Image analysis was performed with Fiji (Schindelin et al., 2012). For display purposes, confocal z-stack images were projected (maximum intensity projection) and brightness and contrast were enhanced.

To analyze microridge length and other cell parameters, we developed an ImageJ script to automatically process cells in each image (Fig. S1). Cell outlines were traced by hand with the polygon selection tool to measure apical cell area. Brightness and contrast were automatically enhanced, and the area around the cell was cleared. Images were then blurred using the Smoothen function three times and passed through a Laplacian morphological filter from the MorphoLibJ plugin (Legland et al., 2016), using the square element and a radius of 1. Filtered images were automatically thresholded using the Triangle method and skeletonized. The Analyze Skeleton (2D/3D) feature was then used to measure microridge length.

To calculate surface excess for pegs and microridges (Fig. 1 G), we cropped 10 × 10–µm samples showing regions occupied by pegs or microridges in several cell images and estimated the surface area of those samples with the following algorithm. We assumed that the height of the surface is proportional to the signal, and that both pegs and microridges have the same maximal height of $h=400$ nm. We normalized the samples so that the 10th percentile became 0 and the 90th percentile became 1 and then used the formula

$$A_{surf}=\int \int \sqrt{1+h^2{\left(\nabla I\right)}^2}dA=\sum s^2\sqrt{1+{\left(h/s\right)}^2\left(I_x^2+I_y^2\right)},$$

where $\nabla I$ is the gradient of the image, $I_x$ and $I_y$ are normalized Sobel filters along x and y directions, $s$ is the absolute pixel size, and summation is taken over all pixels of the image. Surface excess of each sample was calculated as $ϵ=A_{surf}/A_{proj}-1,$ where $A_{proj}$ is the area of the projected surface (width × length of the image).

To quantify NMII contraction, time-lapse z-stack images were projected and smoothened. Cell outlines were traced by hand and cells were cropped from each time-lapse frame. Brightness and contrast of each time-lapse frame were automatically adjusted, and then images were automatically thresholded using the Triangle method. Thresholded pulses were measured using the ImageJ Analyze Particles function, excluding particles with <4 pixels.

To construct the optic flow diagram (Fig. 4 D′), we used the FlowJ plugin in Fiji (Lucas and Kanade algorithm).

To study the angular distribution of surface structure coalescence (Fig. 7 D), we analyzed videos from ablation experiments. We isolated distinct peg coalescence events and determined their direction (the line connecting pegs on a frame just before fusion).

To calculate the direction and amount of elongation (Fig. 7 F), we calculated the moment matrices M of cell shapes approximated with polygons (shifted to the polygons’ centroids). We then calculated nonrotational affine transformations that better transform the moment matrix at frame n to the moment matrix at frame n + 1. The median direction of these transformations was defined as the direction of elongation. A ratio of the axes was defined as the elongation factor.

To calculate angular histograms for peg coalescence in the model (Fig. 8, D and E), we created an automated version of the algorithm, which was used in the preparation of Fig. 7 D. This algorithm was applied to multiple (n = 100) simulations with random initial conditions and the results were plotted in the averaged histograms in Fig. 8, D and E.

To study how the angular distribution of peg coalescence in the model changes with the anisotropy parameter ϵ (Fig. 8 F), we decreased the number of bins in the previous analysis to two. All peg coalescence events with angles from –45° to 45° were considered to be parallel to the axis of stretch, whereas those with angles from 45° to 135° were considered perpendicular to it. We then calculated the polarization parameter

$$p=\frac{n_{\left|\right|}-n\perp }{n_{\left|\right|}+n\perp },$$

using the number of coalescence events in both bins. As defined, the value p = −1 corresponds to all pegs merging perpendicular to the stretch axis, whereas p = 1 corresponds to all coalescence events parallel to it.

Modeling

We built a model as a system of partial differential equations and solved it with a finite element method. Calculations were performed with COMSOL Multiphysics (COMSOL, Inc.); postprocessing was done with custom Python code.

A two-layer model

We subdivided the apical surface of the cell into two interacting subsystems. The first layer represents a composite of the lipid membrane and the branched actin cytoskeleton, which fills pegs and microridges. The second layer represents the actomyosin cortex. The vertical component of interaction between the two layers results from the actin polymerization force of the top layer and is opposed by the oppositely directed force of the bottom layer (Gov, 2006). For simplicity, we assumed that the interface between the two layers is flat and neglected its deformation, following an estimate based on the characteristic values of cortical tension (Balaban et al., 2001; Bischofs et al., 2009; Fischer-Friedrich et al., 2014) and the protrusive force of polymerizing actin (Lan and Papoian, 2008; Mogilner and Oster, 2003). This assumption is also consistent with the published ultrastructural analyses of the cytoskeleton in fish epidermal cells (Bereiter-Hahn et al., 1979; Pinto et al., 2019; Uehara et al., 1991).

The two layers are mechanically coupled. Due to the presence of extensive cytoskeletal linkers connecting actomyosin to the transmembrane proteins embedded in the lipid bilayer, we introduced a no-slip boundary condition. Thus, the two layers are coupled by the common strain field. This coupling has two important consequences. First, velocity fields in the actomyosin layer induced by the forces directly translate onto the top layer. Second, these velocity fields produce advection of the patterned structures positioned there, such as pegs or microridges.

The cortex layer

To describe the actomyosin layer, we used the active gel approach (Marchetti et al., 2013; Prost et al., 2015). Since we are interested in the behavior on a very long timescale (minutes and hours), we neglected inertia and shear elasticity and reduced the mechanics of the layer to a 2D compressible isotropic fluid with high viscosity and active stress. Following the active gel model (Prost et al., 2015), we formulated a standard force balance equation:

$$\frac{\partial }{\partial x_{\beta }}\left({\sigma }_{\alpha \beta }^a+{\sigma }_{\alpha \beta }^h+\Pi {\delta }_{\alpha \beta }\right)=0.$$

In the force balance equation, the indices α, β, and γ belonging to {1,2} refer to the spatial coordinates x,y (x₁,x₂) in the plane of the layer, ${\sigma }_{\alpha \beta }^a$ is the active stress, ${\sigma }_{\alpha \beta }^h$ is the hydrodynamic (viscous) stress, and, finally, $\Pi$ is the pressure. In all formulae, repeating indices imply the Einstein summation convention, and ${\delta }_{\alpha \beta }$ is the Kronecker delta. Hydrodynamic stress for a 2D fluid was defined as

$${\sigma }_{\alpha \beta }^h={\mu }_1{U}_{\gamma \gamma }\frac{{\delta }_{\alpha \beta }}{2}+{\mu }_2\left(U_{\alpha \beta }-U_{\gamma \gamma }\frac{{\delta }_{\alpha \beta }}{2}\right),$$

where $U_{\alpha \beta }=\partial u_{\alpha }/\partial x_{\beta }+\partial u_{\beta }/\partial x_{\alpha }$ is a symmetric strain rate tensor, u_α is the velocity of the layer, and μ₁ and μ₂ are the bulk and shear viscosities.

Although in vivo the actomyosin cortex is constantly assembled and disassembled (Clark et al., 2013), for the sake of simplicity, we assumed in our model that the total mass of actomyosin is constant. In line with this assumption, we adopted a logarithmic continuation of Hooke’s law as the constitutive relation describing the mechanical properties of actomyosin: $\Pi ={\Pi }_{0}log\rho .$

Here we defined the dimensionless density $\rho =V_0/V_1$, where $V_0$ and $V_1$ are infinitesimal volumes within the layer before and after deformation, and ${\Pi }_0$ is the effective stiffness of actomyosin. As defined, $\rho$ follows the conservation law:

$$\frac{\partial \rho }{\partial t}+\frac{\partial \left(\rho u_{\alpha }\right)}{\partial x_{\alpha }}=0.$$

The top composite layer

We described the state of the top composite layer with a heuristic activator-inhibitor model of the Gierer–Meinhardt type (Gierer and Meinhardt, 1972), consisting of two spatially distributed variables: the autocatalytic activator of actin polymerization, $c\left(x,y\right),$ and the height of the membrane, $h\left(x,y\right)$, measured relative to an initial plane. The latter variable plays the role of the inhibitor and is presented in the Monge parametrization that is commonly used to describe membrane geometry under the assumption $\left|\nabla h\right|\ll 1$ (Kabaso et al., 2011; Gov, 2006).

The dynamics of the activator $c$ was represented by the following equation that directly follows the Gierer-Meinhardt form:

$$\underset{\begin{array}{l}\mathrm{material}\\ \mathrm{derivative}\end{array}}{\underbrace{\frac{\partial c}{\partial t}+\frac{\partial \left(c{u}_{\alpha }\right)}{\partial x_{\alpha }}}}=\underset{\mathrm{Diffusion}}{\underbrace{D_c{\nabla }^{2}c}}+\underset{\mathrm{production}}{\underbrace{k_{on}}}\underset{\mathrm{degradation}}{\underbrace{-k_{off}c}}+\underset{\begin{array}{l}\mathrm{height}‐\mathrm{inhibited}\\ \mathrm{activation}\end{array}}{\underbrace{k_{h}H\left(c\right)K\left(h\right)}}.$$

Parameters $D_c,$ $k_{on},$ $k_{off},$ $k_h,$ $c_0,$ and $h_0$ are constants whose values are given in Table S1. The last term corresponds to the process of positive feedback with a rate that saturates as the concentration $c$ increases and diminishes when $h$ increases:

$$H\left(c\right)=\frac{{\left(c/c_0\right)}^2}{1+{\left(c/c_0\right)}^{2 }};$$

$$K\left(h\right)=\frac{1}{1+h/h_0}.$$

Following Gierer and Meinhardt (1972), we chose the second power in the Hill-like term $H\left(c\right)$ as the smallest integer power, allowing the system to be unstable and form spatial patterns.

We described mechanical properties of the layer with the Helfrich Hamiltonian (Helfrich, 1973):

$$E=\int \left\{\Omega h^2+S{\left[\nabla h\right]}^2\right\}dxdy,$$

where $S$ is the effective layer tension coefficient. We added a spring-like “cytoskeletal confinement” term $\Omega h^2$ to prevent unlimited spatially homogeneous autocatalytic actin polymerization (Gov et al., 2003; Ben Isaac et al., 2013; Daniels et al., 2006; Gov, 2006), and neglected the curvature-dependent energy terms. Minimizing energy $E,$ we obtained

$$\underset{\begin{array}{c}\mathrm{material}\\ \mathrm{derivative}\end{array}}{\underbrace{\frac{\partial h}{\partial t}+u_{\alpha }\frac{\partial h}{\partial x_{\alpha }}}}=\underset{\begin{array}{c}\mathrm{actin}\\ \mathrm{polymerization}\end{array}}{\underbrace{\frac{F_c}{\gamma }\left(c^2-c_1^2\right)}}+\frac{1}{\gamma }\left(-\frac{\delta E}{\delta h}\right).$$

The actin polymerization force is postulated to depend quadratically on the concentration of activator $c$ with the preferred concentration $c_1$ and $\gamma$ is the local Oseen parameter. The functional derivative has the form

$$\frac{\delta E}{\delta h}=\underset{\begin{array}{c}\mathrm{restoring}\\ \mathrm{force}\end{array}}{\underbrace{\Omega h}}-S\underset{\begin{array}{c}\mathrm{membrane}\\ \mathrm{tension}\end{array}}{\underbrace{\frac{{\partial }^{2}h}{\partial x_{\alpha }\partial x_{\alpha }}}}.$$

In the force equilibrium, the actin polymerization force is balanced by the restoring force and surface tension.

We posited that tension of the top composite layer depends on its bulk strain

$$S\left(\frac{V_1-V_0}{V_0}\right),$$

where $V_0$ and $V_1$ are the infinitesimal volumes before and after deformation. This constitutive relation can be written as $S\left({\rho }^t\right)$, where ${\rho }^t$ is the nondimensional density of the top layer defined as ${\rho }^t=V_0/V_1.$ Thus, introduced nondimensional ${\rho }^t$ is a variable representing the bulk strain and does not describe molecules, such as myosin. Following from the earlier introduced tight mechanical coupling between the layers by strain, we conclude that ${\rho }^t=\rho .$ In other words, when the actomyosin layer contracts, the produced negative strain reduces the tension of the top layer. Making the simplest possible assumption about the response of this composite layer to strain, we adopted a linear relation in the form

$$S=S_0-S_1\left(\rho -1\right).$$

Apical constriction

To model pattern formation during apical surface constriction, we applied time- and space-dependent active stress to a hexagonal cell with the side length $L$. We generated the initial pattern by simulating the equations for the lipid membrane layer with a zero-velocity field and zero pressure in the cortex layer.

We first used a spatially uniform active stress function,

$${\sigma }_{\alpha \beta }^a\left(t,x,y\right)={\delta }_{\alpha \beta }{\sigma }_0^{a}g\left(t\right),$$

where ${\sigma }_0^a$ is the magnitude of active stress, and g(t) is a function representing temporal evolution,

$$g\left(t\right)=\frac{1-exp\left(-t/t_{AS}\right)}{1-exp\left(-t_1/t_{AS}\right)},$$

where $t_{AS}$ is a parameter given in Table S1 and $t_1$ is the total simulation time. To model the hypothesis that apical constriction initiates at the cell periphery, we introduced a radially symmetric wave-like active stress function in the form

$${\sigma }_{\alpha \beta }^a\left(t,x,y\right)={\delta }_{\alpha \beta }{\sigma }_0^{a}step\left\{\frac{\sqrt{x^2+y^2}-L/2}{l_1} + \frac{L}{v_1{t}_1}\left[g\left(t\right)-\frac{1}{2}\right]\right\},$$

where ${\sigma }_0^a$ is the magnitude of active stress, $l_1$ is the transition half-length, $v_1$ is a typical wave propagation speed, and $step\left(z\right)$ is a continuous step function,

$$step\left(z\right)=\left(\frac{3}{16}{z}^5-\frac{5}{8}{z}^3+\frac{15}{16}z+\frac{1}{2}\right)\theta \left(1-z^2\right)+\theta \left(z-1\right),$$

where $\theta \left(z\right)$ is the Heaviside step function.

Anisotropic elongation

We speculate that during rapid uniaxial stretch of the cell, actomyosin filaments reorient in the direction of elongation (Fig. 8 B) and thus introduce tensile anisotropy that propagates to the top layer. The surface tension term becomes

$$f^{aniso}=S\frac{\partial }{\partial x_{\alpha }}\left(A_{\alpha \beta }\frac{\partial h}{\partial x_{\beta }}\right),$$

where $A_{\alpha \beta }$ represents tensile anisotropic tensor, which we chose as

$$A_{\alpha \beta }={\delta }_{\alpha \beta }-\epsilon \left\{1-exp\left[-\frac{\widehat{U}}{{\widehat{U}}_0}\right]\right\}\frac{U_{\alpha \beta }^{*}}{{\widehat{U}}_0}.$$

Here, $U_{\alpha \beta }^{*}=U_{\alpha \beta }-\frac{{\delta }_{\alpha \beta }}{2}{U}_{\gamma \gamma }$ is the traceless component of the strain rate $U_{\alpha \beta },$ $\widehat{U}=\sqrt{\frac{1}{2}{U}_{\alpha \beta }{U}_{\alpha \beta }}$ is the positive eigenvalue of traceless matrix $U_{\alpha \beta },$ $\epsilon$ is the maximal relative increment, and ${\widehat{U}}_0$ is a typical strain-rate stress at which actomyosin filaments become partially ordered and surface tension becomes sensitive to anisotropic flow. The idea behind this dependency is as follows: without shear flow $\left({\widehat{U}}_0=0\right),$ the tension tensor is isotropic. With very large shear flow $\left({\widehat{U}}_0\to \infty \right),$ tension in the direction of elongation becomes smaller by factor $1-\epsilon$ and tension in the orthogonal direction becomes greater by factor $1+\epsilon .$ The transition occurs at a typical strain rate of ${\widehat{U}}_0.$

To simulate the elongation itself, we used a time-dependent affine transformation applied to the square border of the cell to simulate the experimental data (Fig. 7, E and F). The duration of simulation was $t_2=15$ min. We varied parameter $\epsilon$ from 0 (isotropic case; Video 6, left panel) to 0.4. An anisotropic case with $\epsilon =0.25$ is shown in Video 6 on the right.

Online supplemental material

Fig. S1 shows the automatic image processing pipeline used to measure microridge length. Fig. S2 shows additional quantification methods and demonstrates that microridges lengthen as apical surfaces constrict during development. Fig. S3 shows time-lapse sequences illustrating three mechanisms of microridge growth. Fig. S4 illustrates the consequences of Arp2/3 inhibition on microridge length and apical constriction. Video 1 shows live imaging of microridge morphogenesis during development, demonstrating that microridges form from the accretion of pegs. Video 2 shows simulations of a biomechanical model, demonstrating that reduction of surface tension can promote centripetal microridge development. Video 3 shows live imaging of an NMII reporter at three different developmental stages, revealing pulsatile apical contractions that pinch the membrane. Video 4 shows an in vivo live-imaging experiment, demonstrating that reducing surface tension with hyperosmolar media promotes microridge development. Video 5 shows a time-lapse sequence of a cell stretching after ablating neighboring cells. Video 6 shows simulations of a computational model demonstrating the effect of anisotropic cortical flow on the orientation of microridges during cell stretching. Table S1 summarizes the parameters of the computational model.

Supplementary Material

Table S1

summarizes the parameters of the computational model.