Robust Rate-Place Coding of Resolved Components in Harmonic and Inharmonic Complex Tones in Auditory Midbrain

Harmonic complex tones (HCTs) commonly occurring in speech and music evoke a strong pitch at their fundamental frequency (F0), especially when they contain harmonics individually resolved by the cochlea. When all frequency components of an HCT are shifted by the same amount, the pitch of the resulting inharmonic tone (IHCT) can also shift, although the envelope repetition rate is unchanged.

Abstract

Harmonic complex tones (HCTs) commonly occurring in speech and music evoke a strong pitch at their fundamental frequency (F0), especially when they contain harmonics individually resolved by the cochlea. When all frequency components of an HCT are shifted by the same amount, the pitch of the resulting inharmonic tone (IHCT) can also shift, although the envelope repetition rate is unchanged. A rate-place code, whereby resolved harmonics are represented by local maxima in firing rates along the tonotopic axis, has been characterized in the auditory nerve and primary auditory cortex, but little is known about intermediate processing stages. We recorded single-neuron responses to HCT and IHCT with varying F0 and sound level in the inferior colliculus (IC) of unanesthetized rabbits of both sexes. Many neurons showed peaks in firing rate when a low-numbered harmonic aligned with the neuron's characteristic frequency, demonstrating “rate-place” coding. The IC rate-place code was most prevalent for F0 > 800 Hz, was only moderately dependent on sound level over a 40 dB range, and was not sensitive to stimulus harmonicity. A spectral receptive-field model incorporating broadband inhibition better predicted the neural responses than a purely excitatory model, suggesting an enhancement of the rate-place representation by inhibition. Some IC neurons showed facilitation in response to HCT relative to pure tones, similar to cortical “harmonic template neurons” (Feng and Wang, 2017), but to a lesser degree. Our findings shed light on the transformation of rate-place coding of resolved harmonics along the auditory pathway.

SIGNIFICANCE STATEMENT Harmonic complex tones are ubiquitous in speech and music and produce strong pitch percepts when they contain frequency components that are individually resolved by the cochlea. Here, we characterize a “rate-place” code for resolved harmonics in the auditory midbrain that is more robust across sound levels than the peripheral rate-place code and insensitive to the harmonic relationships among frequency components. We use a computational model to show that inhibition may play an important role in shaping the rate-place code. Our study fills a major gap in understanding the transformations in neural representations of resolved harmonics along the auditory pathway.

Introduction

The spectral pattern of an acoustic stimulus plays important roles in the perception of the pitch and timbre of voice and musical instruments, and the vertical angle of sound sources (Town and Bizley, 2013; Middlebrooks, 2015; Oxenham, 2018). A general principle for the neural representation of spectral patterns is rate-place coding (Sachs, 1984), which is created in the cochlea via a mechanical frequency analysis and conveyed along the ascending auditory pathway via tonotopic mappings. The effectiveness of rate-place coding is limited by both the frequency resolution of the cochlea and the “dynamic range problem,” the observation that the firing rates (FRs) of a majority of auditory-nerve fibers saturate at moderate sound levels, so that they can no longer encode spectral features at higher sound levels (Sachs and Young, 1979).

Accounting for the pitch of harmonic complex tones (HCTs), in which all frequency components are integer multiples of a common fundamental frequency (F0), is especially challenging for rate-place codes because it requires that individual frequency components be represented rather than just the broader spectral envelope. HCTs are common in speech, music, and animal vocalizations (Bregman, 1994; Plack and Oxenham, 2005b), and their pitch plays an important role in the perceptual organization of sound (Oxenham, 2018). The spectral pattern of HCTs containing low-numbered, resolved harmonics provides the most salient cue for pitch (Plack and Oxenham, 2005a). HCTs containing only high-numbered, unresolved harmonics evoke a weaker pitch derived from neural phase locking to the stimulus envelope (Houtsma and Smurzynski, 1990; Shackleton and Carlyon, 1994; Bernstein and Oxenham, 2003). When all harmonics of an HCT with resolved components are shifted in frequency by the same amount, the pitch of the resulting inharmonic complex tone (IHCT) shifts in rough proportion to the frequency shift, even though the envelope repetition rate (ERR) is unchanged (De Boer, 1956; Schouten et al., 1962; Patterson and Wightman, 1976). Although resolved harmonics produce the most salient pitch percepts, the neural mechanisms for extracting pitch from resolved harmonics are poorly understood.

Rate-place coding of resolved harmonics in HCTs has been described in the auditory nerve (AN) fibers of anesthetized cats (Cedolin and Delgutte, 2005, 2010; Larsen et al., 2008), as well as single units and multiunits in the primary auditory cortex (A1) of awake macaques (Schwarz and Tomlinson, 1990; Fishman et al., 2013). While pitch perception is invariant over a wide range of sound levels, the AN rate-place code degrades within 20–30 dB above threshold due to saturation of most AN fibers (Cedolin and Delgutte, 2010), although the cortical code appears more robust (Schwarz and Tomlinson, 1990; Fishman et al., 2013). How and where along the ascending pathway level tolerance emerges are unknown. The pitch of harmonic and inharmonic tones may be extracted from neural representations of resolved harmonics using harmonic templates (Goldstein, 1973; Wightman, 1973; Terhardt, 1974; Cohen et al., 1995; Shamma and Klein, 2000). However, the only physiological evidence for harmonic templates is a report of “harmonic template neurons” (HTNs) in A1 of marmoset monkeys (Feng and Wang, 2017). These neurons show FR facilitation at a particular F0 of HCT compared with a pure tone at characteristic frequency (CF), and are sensitive to stimulus harmonicity.

The inferior colliculus (IC) is a logical site to investigate how rate-place coding transforms along the auditory pathway, and possibly shed light on the emergence of harmonic templates. Its tonotopically organized central nucleus receives convergent excitatory and inhibitory inputs from most brainstem auditory nuclei (Adams, 1979; Malmierca et al., 2005), as well as inputs from within IC (Saldaña and Merchán, 1992). A handful of IC studies that used HCT stimuli containing many harmonics (Sinex et al., 2002; Sinex and Li, 2007; Shackleton et al., 2009; Schnupp et al., 2015; Peng et al., 2018) focused on the coding of stimuli with low F0s, mostly within the range of human voice, which are not likely to be resolved in small laboratory animals (Sumner et al., 2018).

Here, we characterize rate-place coding of resolved harmonics in the IC of unanesthetized rabbits by measuring single-unit responses to HCT and IHCT with varying F0 and sound level. Spectral receptive field models were fit to neural responses to evaluate the role of inhibition in shaping the IC rate-place code. We also compared responses to HCT and pure tone stimuli to assess whether IC neurons exhibit properties of cortical HTNs (Feng and Wang, 2017). We find that IC neurons can represent resolved harmonics over a wide range of F0 via a rate-place code that is robust across sound levels but not sensitive to harmonicity.

Materials and Methods

Four female and one male adult Dutch-belted rabbits were used for the experiments. All animal procedures were approved by the Animal Care Committee of Massachusetts Eye & Ear. Surgical and electrophysiological procedures to record from the IC of unanesthetized rabbits are the same as in a companion study (Su and Delgutte, 2019). Here we mainly focus on describing the acoustic stimuli and data analyses that are specific to this paper.

Surgical preparation.

Each rabbit underwent two aseptic surgeries before the first electrophysiological recording session: implantation of a cylinder and head bar to hold the animal during recording sessions, and a small craniotomy (2–3 mm diameter) to allow access to the IC. In both surgeries, anesthesia was induced with xylazine (6 mg/kg) and ketamine (35–44 mg/kg), and maintained by either injection of one-third initial dose of xylazine/ketamine mix or facemask delivery of isoflurane gas mixed with oxygen (0.8 L/min, isoflurane concentration gradually increased to 2.5%). In the 8–10 d between the two surgeries, the rabbit was trained to sit still in the experimental apparatus with head attached. Single-unit recording sessions began 3 d after the craniotomy and lasted for 6–18 months. Occasionally over the period of recording sessions, the craniotomy was enlarged or moved to the contralateral side using the same procedure.

Single-unit recording.

Each recording session lasted 1.5–2.5 h, during which the rabbit was strapped in a spandex sleeve with its head fixed via the brass bar in a double-walled, electrically shielded and soundproof chamber. At the beginning of each session, the acoustic assembly was calibrated using broadband chirp stimuli, and an inverse digital filter was created for the assembly frequency response over 0.05–18 kHz. The animal was monitored via a closed-circuit video throughout the session, and the recording session was terminated if the animal showed signs of distress or moved excessively.

The majority of single-neuron recordings were made with polyimide-insulated platinum-iridium linear microelectrode arrays (MicroProbes) with 4–6 contacts spaced 150 μm apart. Some early recordings were made using epoxy-insulated tungsten electrodes (A-M Systems). The IC was identified by audio-visual cues of entrainment to a search stimulus consisting of 200 ms broadband noise bursts presented diotically at 60 dB SPL. The recorded signals were first amplified and bandpass filtered (300–5000 Hz), then sampled at 100 kHz (National Instruments, PXI-6123). Spike times were identified by crossing of a manually set voltage threshold and recorded for later analysis. Isolation of a single unit was determined based on the stable shape and amplitude of the spike waveform and absence of interspike intervals <1 ms.

Stimuli.

Acoustic stimuli were first created in MATLAB (The MathWorks) and passed through the digital filter created from the acoustic calibration to equalize the frequency response of the acoustic assembly. The filtered signals were then converted to analog signals (24 bits, 100 kHz) and delivered to the animal ear by a pair of speakers via plastic tubes fitted through the ear inserts fitted to the ear canals of each animal. Once a neuron was isolated, we characterized its frequency tuning with pure tones and then measured responses to complex tones. The measurement of frequency tuning was the same as in Su and Delgutte (2019).

Pure-tone frequency tuning.

In half of the neurons, we measured the frequency response area (FRA) to characterize pure-tone tuning. Tone bursts (100 ms on, 100 ms off) varying in frequency from 0.2 to 18 kHz (0.25 octave step or finer) and in level from 5 to 70 dB SPL were presented in random order, and each was repeated 3 times. The evoked FR was measured for each tone and plotted as a heat map on the log frequency versus intensity plane. The heat map was then interpolated 10×. Contours on the interpolated map were identified using the MATLAB image processing toolbox. The CF was defined as the frequency corresponding to the lowest sound level on the longest contour (for examples, see Fig. 4).

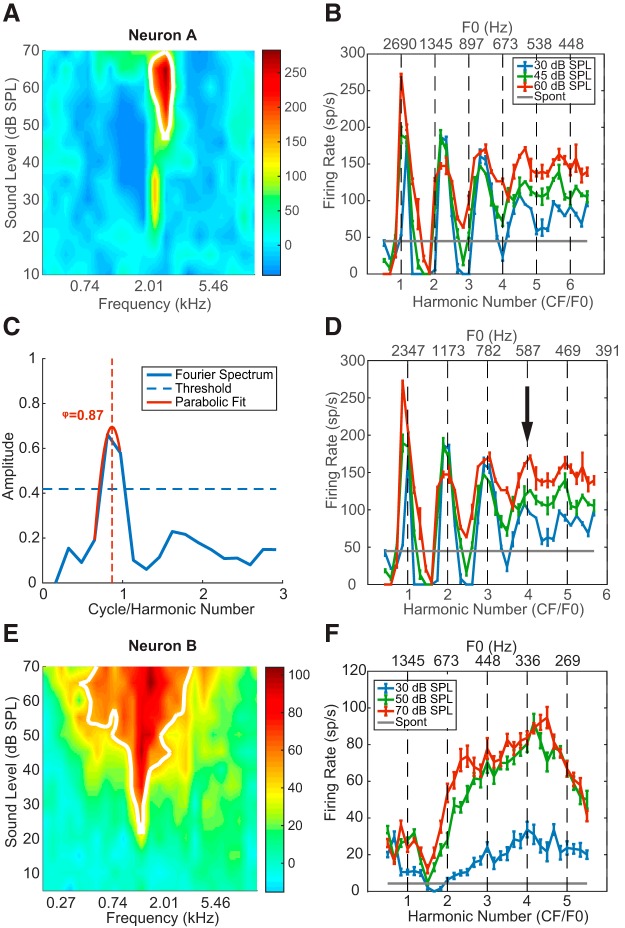
Figure 4.

Example neural responses to HCTs. A, Pure-tone FRA of Neuron A. Colors represent the neuron's FR minus the SR. B, Rate-place profile of Neuron A before the CF adjustment (see Materials and Methods). Error bars indicate ± 1 standard error throughout this report unless specified otherwise. C, Fourier transform of the rate-place profile at 30 dB SPL in B. Horizontal dashed line indicates the 95th percentile of the permutation test. Vertical dashed line indicates the location of the “true” spectrum peak (i.e., the adjustment factor φ) inferred from the parabolic fit (red solid line). D, Rate-place profiles of Neuron A after adjustment. Arrow indicates the neuron's lowest resolved F0. E, Pure-tone FRA of Neuron B, CF = 1.35 kHz. F, Rate-place profile of Neuron B.

Before the FRA measurement was implemented, pure-tone frequency tuning was characterized with either an automatic threshold tracking algorithm (Kiang and Moxon, 1974) or, when the tracking procedure failed to converge, an iso-level method in which tone bursts varying in frequency from 0.5 to 18 kHz (0.1 octave steps) were presented at ∼10 dB above the threshold to broadband noise. Details of these two methods for characterizing frequency tuning were described by Su and Delgutte (2019).

Most pure tone responses were measured for monaural stimulation of the contralateral ear. In rare cases, when a neuron responded more strongly to ipsilateral sounds, frequency tuning was characterized for monaural stimulation of the ipsilateral ear. For brevity, we will refer to both the CFs measured from the FRA or the tracking method and the best frequency (BF) measured by the iso-level method as “CF” in this report.

HCTs.

Rate-place coding of resolved harmonics by single neurons was tested using an HCT paradigm adapted from previous studies in the AN (Cedolin and Delgutte, 2005; Larsen et al., 2008) and auditory cortex (Fishman et al., 2013). This paradigm was designed to optimize the chance of observing responses to resolved harmonics by selecting the range of F0s based on each neuron's CF. Each HCT consisted of equal-amplitude harmonics in cosine phase, ranging from the fundamental (F0) to the lowest of either the 12th harmonic or 18 kHz, where the frequency response of our acoustic system showed a sharp drop-off. The power spectrum and temporal waveform of a harmonic complex with F0 equal to 500 Hz are shown in Figure 1 (second row, orange).

Figure 1.

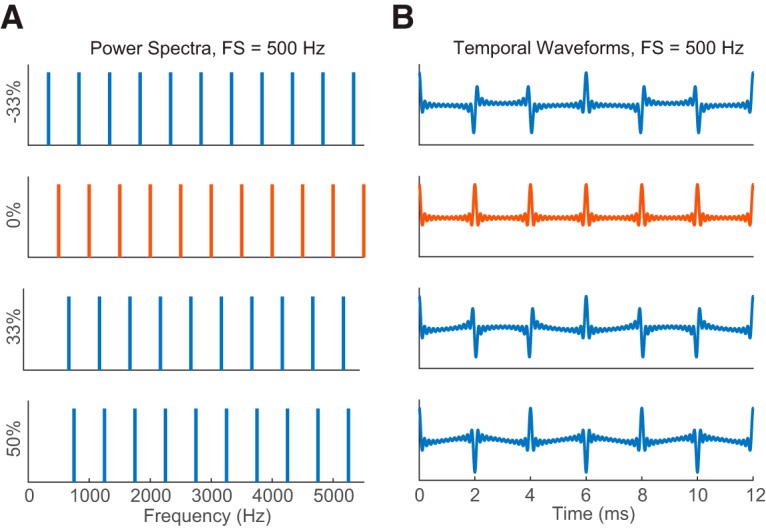
HCTs and IHCTs. A, Power spectra of HCT (0% shift, orange) and IHCTs (non-zero shift, blue) with the same FS = 500 Hz. Y labels indicate amounts of frequency shift from the HCT as percentages of FS. For the harmonic tone, FS is equivalent to F0. B, Temporal waveforms of the corresponding complex tones in A.

For each neuron, the F0 of HCTs was varied so that the “neural harmonic number,” NH = CF/F0, varied from 0.5 to 5.5 or higher in linear steps of 1/6. When NH is a small integer (Fig. 2A), the NH^th component of the complex tone coincides with the neuron's CF; therefore, the stimulus should evoke a high FR if this harmonic is resolved. When NH is an integer + 1/2 (Fig. 2C), the neuron's CF falls halfway between two harmonics, so that a low FR is expected if the harmonics are resolved. As NH increases (Fig. 2D), F0 decreases as does the spacing between adjacent harmonics (i.e., F0). When F0 becomes smaller than the bandwidth of the neuron's FRA, the FR should no longer depend on F0. In this way, HCTs with low-number harmonics (large F0) are expected to be resolved by the neuron, whereas HCTs with high-number harmonic (small F0) should be unresolved.

Figure 2.

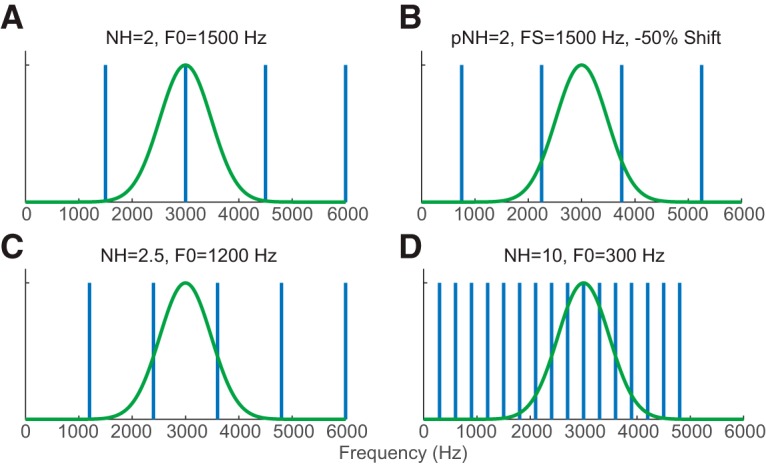
Schematics for testing rate-place coding in a hypothetical neuron with CF = 3000 Hz (green curves). Vertical bars represent power spectra of the corresponding complex tone. A, NH = 2 (F0 = 1500 Hz), the second harmonic of the corresponding HCT coincides with the neuron's CF. B, For an IHCT with the same FS as in A but −50% shift (750 Hz to lower frequency), the neuron's CF is between two adjacent components. C, NH = 2.5 (F0 = 1200 Hz), CF between two adjacent harmonics. D, NH = 10 (F0 = 300 Hz), the neuron's auditory filter encompasses many harmonics.

HCTs with each F0 were presented at three different sound levels: low (≤30 dB SPL/harmonic), medium (31–55 dB SPL/harmonic), and high (55–70 dB SPL/harmonic). Sound level was specified for each harmonic rather than overall RMS amplitude so that the amplitude of individual harmonics would stay the same when F0 is varied. When the stimulus contains 12 harmonics, the overall SPL is ∼11 dB higher than the level per harmonic. The three sound levels used in each neuron were originally chosen in 15 dB increments, but this was later increased to 20 dB increments to test a wider range. In each measurement, HCTs with different F0s and sound levels were randomly interleaved for 10 total repetitions. Each complex tone was presented diotically for 200 ms with a 10 ms raised-cosine ramp at onset and offset, and followed by a 300 ms silent (off) period.

For a subset of neurons, HCT stimuli were interleaved with pure tones at frequencies such that the ratio CF/F ranged from 0.5 to 1.5 in steps of 1/6, with the same duration (200 ms), interstimulus interval (300 ms), and per-component sound levels as the HCTs.

IHCTs.

In a subset of neurons, we measured responses to IHCTs that were generated by shifting all frequency components in an HCT by a fixed proportion of its F0. For an inharmonic tone, the frequency spacing (FS) between adjacent components is always equal to the F0 of the original HCT, and the temporal ERR is 1/FS (Fig. 1). For the majority of neurons, inharmonic tones were generated with shifts of ±1/3, ±1/6, 0 (harmonic), and 1/2 of the original F0. In a few early measurements, frequency shifts of 0, ±1/10, ±1/4, and 1/2 were used.

A pseudo-harmonic number (pNH) was defined for each IHCT as pNH = CF/FS. For each neuron and each value of frequency shift, pNH was varied over the same range (0.5–6.5) as the NH of harmonic tones. Because of the frequency shift, an IHCT with integer pNH no longer has a component at the neuron's CF (Fig. 2B). Instead, for the N^th component of an IHCT with shift s to align with the neuron's CF, the tone should satisfy the following:

Therefore, if a neuron's response is dependent on the presence of resolved components near the CF regardless of harmonicity, it would show peaks in FR when pNH = N (a small integer) + s (percent shift relative to FS).

Due to the large number of stimulus conditions tested (36 FS values × 6 frequency shifts), IHCTs were only presented at 30 dB SPL per component.

Data analysis.

For all HCT and IHCT paradigms, we computed the average FR over the stimulus duration as a function of (pseudo) harmonic number. The response in the first 10 ms was excluded to eliminate the onset response. The neuron's background FR was calculated as the average FR during the last 200 ms of the 300 ms interstimulus interval averaged across all the complex tone stimuli. Assuming that there exists a population of IC neurons having the same response properties as the recorded neuron, except for their position along the tonotopic axis (mapped to CF), a plot of FR against neural harmonic number (or F0) should resemble the response of the hypothetical neural population to an HCT with a specific F0 as a function of CF (LePrell et al., 1996; Larsen et al., 2008). Therefore, we refer to the patterns of FR against neural harmonic number as “rate-place profiles.” This terminology is consistent with previous studies of the AN and cortex (LePrell et al., 1996; Cedolin and Delgutte, 2005; Fishman et al., 2013).

Fourier-based analysis of rate-place profiles.

The rate-place profile of a neuron demonstrating rate-place coding should have peaks at small integer harmonic numbers and troughs in between small integers, producing a periodic pattern with a periodicity of 1 (in units of harmonic number NH). Following Fishman et al. (2013), we harnessed this periodicity by using a Fourier-based analysis to characterize rate-place coding in our neurons.

The discrete Fourier transform (DFT) of the rate-place profile was first computed and normalized by half the average FR across the entire profile so that the DFT amplitude fell in the range [0, 2]. The component at 0 frequency was then set to 0 to simplify the following analysis. The “harmonic modulation depth” was defined as the amplitude of the Fourier component at 1 cycle/harmonic number. A fully modulated sinusoidal profile with a periodicity of 1 cycle/NH would have a harmonic modulation depth of 1, whereas a profile consisting of impulses at integer values of NH would have a depth of 2. The statistical significance of the harmonic modulation depth was determined by a permutation test (10,000 permutations), where data points on the rate-place profile were randomly shuffled across NH and the harmonic modulation depth was computed for each permutation. The neuron was identified as showing rate-place coding if the original modulation depth exceeded the 95th percentile of the permutation values.

CF adjustment.

We observed that the periodicity of rate-place profiles was sometimes not exactly at, but still close to, 1 cycle/NH. This was possibly due to inaccuracy in CF measurement or to differences in frequency selectivity between pure tones and HCTs as a result of nonlinear processing. Such deviations from the expected periodicity could accumulate and have a pronounced effect on rate profiles at large harmonic numbers. We adapted a method from Fishman et al. (2013) to adjust for these deviations and obtain a revised estimate of CF that better describes frequency selectivity for HCT. Specifically, we estimated the location of the maximum of the Fourier spectrum by fitting a parabola to the Fourier spectrum at the peak location and the two neighboring points, and then computing the location of the peak, φ, of the fitted parabola. This procedure was done for each of the three sound levels separately, and the final φ value was set based on the level that had the most significant harmonic modulation depth (the lowest p value in the permutation test). The adjusted CF was defined as CF_adjusted = φ × CF_measured because the adjustment is equivalent to scaling the DFT axis by a factor of φ so that the parabola peak occurs exactly at 1 cycle/NH. All NH values corresponding to the tested F0s were adjusted as well using the formula NH_adjusted = CF_adjusted/F0 = φ × NH_nominal. The harmonic modulation depth was also redefined as the amplitude of the scaled Fourier spectrum at 1 cycle/NH_adjusted.

Identification of resolved harmonics.

Peaks in the rate-place profile corresponding to resolved harmonics were identified by applying the Fourier analysis recursively. When a significant spectral peak at 1 cycle/NH was identified in the Fourier spectrum of the rate-place profile, data points for the first peak (NH from 0.5 to 1.5) were removed from the profile. The same procedure was then applied to the remainder of the rate-place profile and repeated until the harmonic modulation depth became insignificant. For a profile with N peaks identified by this procedure, the total number of resolved harmonics is N + 1 because a profile must have at least 2 peaks to show periodicity. Thus, a neuron that resolves the fundamental but not the second harmonic is not considered to exhibit rate-place coding based on our conservative criterion.

Quantification of neural coding strength.

To characterize neural sensitivity to F0 independently of whether the rate-place profile showed resolved harmonics or not, we computed the signal-to-total variance ratio (STVR) (Hancock et al., 2010, 2012). STVR is an ANOVA-based metric derived from the spike counts on each stimulus trial that represents the ratio of the variance in FRs attributable to their dependence on F0 to the total variance, including variability across multiple presentations of the same stimulus. STVR = 1 implies perfectly reliable sensitivity to F0; that is, all the response variability can be attributed to the change in F0, and 0 implies no sensitivity (flat rate profile).

Spectral receptive fields models.

For neurons demonstrating resolved harmonics in HCT responses, we used linear spectral receptive field models to predict the rate-pace profile from the stimulus spectra at each F0 (Fig. 3). Two spectral receptive field models were tested. A simple Gaussian function as follows:

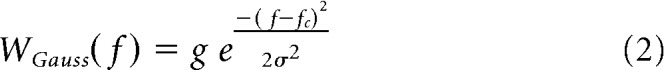A Difference of Gaussians (DoG) function to simulate the interaction of excitation and inhibition follows:

In both functions, the amplitude g has a unit of neural FRs in spikes/s. The center frequency f_c is expected to correspond to the neuron's CF, and the SD σ specifies bandwidth for the corresponding Gaussian filter. For both models, the FR r is computed from the stimulus spectrum S(f) by the following equation:

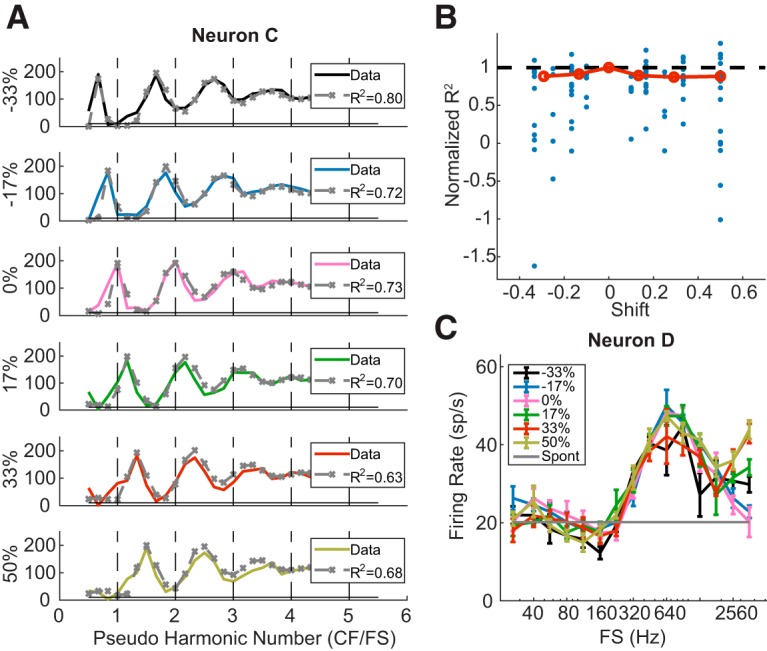
where f_k indicates the frequency components of the stimulus and r₀ is the spontaneous FR. Parameters of the two models were fitted separately by minimizing the city-block distance (sum of absolute distances across F0s) between the model prediction and the neuron's rate profile using the MATLAB function fmincon. The fitted rate profiles were half-wave rectified (i.e., any negative predicted FRs were set to 0 in the model output). Goodness of fit of each model was assessed using adjusted R² to take into account the different number of parameters in the two models (Theil, 1961) as follows:

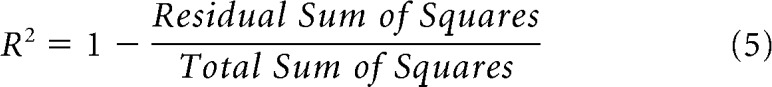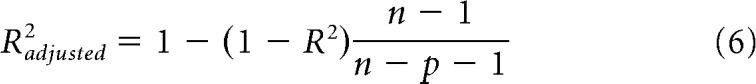Where n is the number of data points and p is the number of model parameters. We also compared the goodness of fit of the two models using single-sided F tests, for which the null hypothesis was that the two models fit equally well, and the alternative hypothesis that the DoG fit better than the Gaussian model.

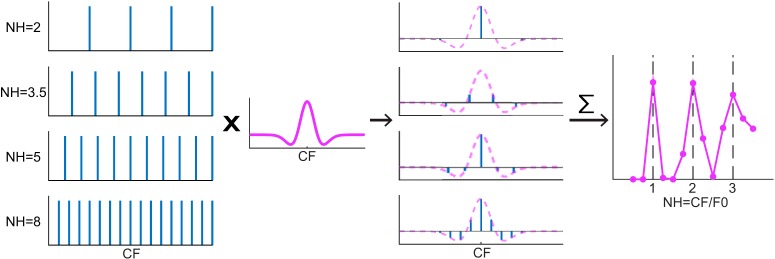
Figure 3.

DoG spectral weighting model diagram. Column 1: Power spectra of HCTs at different NHs. Column 2: A DoG weighting functions centered at the neuron's CF. Column 3: Weighted power spectra by multiplying the HCT spectra with the weighting function (purple dashed lines). Horizontal lines in each panel indicate 0 amplitude. Column 4: Modeled rate-place profile of the neuron. Each point is obtained by summing the weighted power spectrum in Column 3 of an HCT at the corresponding F0, or equivalently, the convolution of the power spectrum and the weighting function at 0 shift.

The Gaussian function has a purely excitatory (g > 0) or inhibitory (g < 0) band centered at f_c, whereas the DoG has a more complicated morphology depending on the interaction between the excitatory and the inhibitory components. For most neurons, the inhibitory component of the best-fitting DoG model had a smaller amplitude and wider bandwidth than the excitatory component (g_i < g_e, σ_i > σ_e), resulting in a narrower excitatory center band flanked by two symmetrical inhibitory sidebands as illustrated in Figure 3. In cases when σ_i < σ_e, the receptive field has a broad excitatory band with a notch in its center.

Experimental design and statistical analysis.

Each neuron's responses to different stimulus conditions (F0s, sound levels, or frequency shifts of IHCTs) were obtained using randomly interleaved presentations to minimize the effect of possible fluctuations in overall neural responsiveness. Whenever possible, we used nonparametric statistical tests to compare neural response metrics (e.g., the STVR) between stimulus conditions across the neuronal population. When comparing two conditions, we used the Wilcoxon signed rank test (for paired data) or rank-sum test (for independent variables), and the Kolmogorov–Smirnov test for comparing the distributions. For three or more conditions, we used the Friedman test (Friedman, 1937) to compare across all conditions, and obtained pairwise comparison by applying multiple comparison (with Bonferroni correction) to the Friedman test statistics. We used the χ² test for comparing distributions of discrete data such as the number of resolved harmonics among different sound levels. Significance of the correlation between two quantities was determined by the Kendall tau test (Kendall, 1948). Goodness of fit of two spectral receptive field models were quantified as adjusted R² values and compared using the F test for each neuron. For all tests, p < 0.05 was considered as statistically significant. All statistical tests were performed using the MATLAB statistics toolbox.

Results

We recorded responses to HCT stimuli from 252 IC neurons in 5 unanesthetized rabbits; 194 of these neurons had an identifiable CF so that the stimulus F0s could be set based on the desired range of neural harmonic numbers (0.5–5.5 or higher) to test for rate-place coding of resolved harmonics. Responses of these 194 neurons to HCTs were studied as a function of F0 and sound level. The remaining 58 neurons that did not have a clearly identifiable CF were used to study responses to HCTs with unresolved harmonics as reported in a companion paper (Su and Delgutte, 2019). These 58 neurons are not included in the present dataset. Among the 194 neurons included in the present dataset, 25 were also tested with IHCTs and 37 were tested with pure tones interleaved with HCTs to determine whether they behave like cortical HTNs (Feng and Wang, 2017). Pure-tone CFs of the neurons ranged from 0.4 to 24.3 kHz, with a median of 4.6 kHz.

Rate-place coding of resolved harmonics in HCT

Figure 4 shows the pure-tone FRAs and HCT rate-place profiles of two IC neurons. Neuron A (Fig. 4A–D) had a sharply tuned, nearly “I”-shaped FRA with two excitatory zones. The contour-based algorithm (see Materials and Methods) identified 2.69 kHz (the tip of the high-threshold zone) as the CF (Fig. 4A), and this value was used to set the range of F0s of the HCT stimuli from 414 Hz (NH = 6.5) to 5380 Hz (NH = 0.5). The rate-place profiles (Fig. 4B) showed peaks near the first four integer harmonic numbers at all three stimulus levels tested but were “stretched” so that the interpeak intervals were slightly >1 NH. Figure 4C shows the Fourier transform of the neuron's rate-place profile at 30 dB SPL. The peak amplitude (i.e., the harmonic modulation depth) was 0.66, which exceeded the 95% percentile of the permutation test (horizontal dashed line). Using parabolic interpolation, the peak in the spectrum was identified at φ = 0.87 cycle/NH (vertical dashed line) rather than the predicted 1 cycle/NH. Therefore, the CF was adjusted to 0.87 × 2.69 = 2.34 kHz. The adjusted CF corresponds to the tip of the low-threshold zone of the FRA, which was not identified as the CF by the automatic algorithm because its contour had a shorter length than the high-threshold zone (Fig. 4A, white line). After CF adjustment, peaks in the rate profiles were aligned at integer NHs (Fig. 4D). For neurons showing peaks in FR at resolved harmonics in their rate profile, like Neuron A, we define the “lowest resolved F0” as the F0 corresponding to the largest integer NH that yielded a significant peak the rate profile according to the DFT-based algorithm (see Materials and Methods). The lowest resolved F0 for Neuron A was 587 Hz (fourth harmonic, Fig. 4D, arrow) for all three sound levels.

Although Neuron B had a “V”-shaped pure-tone FRA with a clear CF at 1.35 kHz (Fig. 4E), unlike Neuron A, its rate profile failed to show peaks in FR near integer harmonic numbers (Fig. 4F), and the peak in the spectrum of the rate profile lay below the 95th percentile of the shuffled values (data not shown). Such “non-place coding” neurons were a majority in our sample. In total, 80 of 194 neurons (41%) demonstrated rate-place coding of resolved harmonics, whereas the remaining 59% showed no evidence of rate-place coding. Our experimental design only measured responses to HCTs in neurons with a clearly identifiable CF in response to pure tones. Because neural processing is nonlinear, it is theoretically possible that a neuron without a pure-tone CF would still show harmonically related peaks in FR in response to HCTs. Nevertheless, it seems likely that the proportion of rate-place coding neurons was overestimated overall because we only tested neurons with an identifiable pure-tone CF.

Rate-place coding of resolved harmonics was observed in IC neurons across a wide range of CFs. Figure 5A shows the distribution of adjusted CF for place coding (dark green) and original CF for non-place coding (light green) neurons. The distributions for both groups extended from a few hundred Hz to >10 kHz, with more neurons at higher CFs. However, the median CF was significantly higher for place coding neurons (6998 Hz) than for noncoding neurons (3707 Hz) (p = 7.25 × 10⁻⁵, Wilcoxon rank-sum test).

Figure 5.

Frequency distribution of IC rate-place code. A, Distribution of CF for rate-place coding neurons (dark green, bottom) and non–rate-place coding neurons (light green, top). B, Distribution of STVR for coding (dark green) and noncoding (light green) neurons. Neurons tested with less than five total stimulus repetitions were excluded. C, Relationship between the lowest resolved F0 and CF of individual rate-place coding neurons (N = 80). Dashed lines indicate NH = 2, 4, 6, 8, 10. D, Percentage of neurons that were able to resolve F0 in different frequency bands.

We used an ANOVA-based metric, the STVR (see Materials and Methods), to quantify the strength of F0 coding in both groups of neurons independently of the shape of their rate-place profiles. The distribution of F0 STVRs (Fig. 5B) was skewed toward higher values (close to 1) in place coding neurons but was relatively uniform for noncoding neurons, and the median STVR was higher for place coding neurons than for noncoding neurons (0.80 vs 0.58, p < 10⁻⁹, single-sided Wilcoxon rank sum test test). A higher STVR implies that a greater amount of the variance in FRs can be explained by the variation in F0 as opposed to intrinsic variability in neural firing. The greater ability of place coding neurons to reliably encode F0 justifies our focus on this group of neurons in the remainder of this paper.

For each place coding neuron, the lowest resolved F0 over all three sound levels (e.g., 587 Hz for Neuron A) is plotted as a function of adjusted CF in Figure 5C. Neurons with CF < 1000 Hz were only able to resolve the first two harmonics, and the lowest resolved F0 found among all neurons was 300 Hz, corresponding to the second harmonic of a neuron with CF = 600 Hz. Neurons with higher CFs were able to resolve more harmonics (typically 3–5, but up to 11 in 1 case), but the lowest resolved F0 remained >400 Hz. To estimate the availability of the rate-place code as a function of F0, we computed the proportion of neurons that were able to resolve an F0 within a half-octave frequency band relative to the total number of neurons tested with HCTs in that band (including non-place coding neurons). As shown in Figure 5D, the proportion monotonically increases with F0 and reaches a plateau of ∼40% for F0 of ≥3200 Hz. Thus, rate-place coding is more effective at high F0s compared with low F0s, consistent with the improvement in cochlear frequency selectivity (Q10) with increasing CF (Borg et al., 1988).

Moderate dependence of IC rate-place coding on sound level

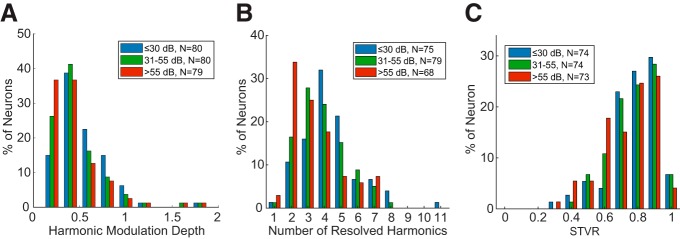
For human listeners, pitch perception of HCTs is robust across a wide range of sound levels (Zheng and Brette, 2017). In contrast, rate-place coding in the AN degrades at levels 20–30 dB above threshold due to spike rate saturation (Cedolin and Delgutte, 2010). However, many of our IC neurons demonstrated strong rate-place coding at high sound levels (>55 dB and up to 70 dB SPL per harmonic) that was similar to their response at lower sound levels in terms of harmonic resolvability. To characterize the dependence of IC rate-place coding on sound level, we used four different measures. First, we compared the “harmonic modulation depth” of the spectrum of the rate-place profile at low (≤30 dB per harmonic), medium (31–55 dB), and high (>55 dB) SPLs in neurons showing rate-place coding for at least one sound level (Fig. 6A). In general, the harmonic modulation depth tended to decrease slightly with increasing sound level, with medians of 0.45, 0.41, and 0.35 for low, medium, and high SPL, respectively (compare with 0.66 for Neuron A in Fig. 4 at the low level). Differences in median harmonic modulation depths were significant across all three sound levels (p = 3.5 × 10⁻⁶, Friedman test, N = 79), and also between low versus medium (p = 0.026, multiple comparison on the Friedman test statistic with Bonferroni correction) and low versus high (p = 1.6 × 10⁻⁶) sound levels. The difference between medium and high sound levels was close to significance (p = 0.051).

Figure 6.

Level dependence of IC rate-place code. A, Distribution of harmonic modulation depth for all neurons demonstrating rate-place coding in at least one sound level. B, Distribution of total number of resolved harmonics at three sound levels. Only neurons showing resolved harmonics at the corresponding sound level are included. C, Distributions of STVR at three sound levels in place coding neurons.

Figure 6B shows the distributions of the number of resolved harmonics in the three sound level ranges for rate-place coding neurons. The distributions spanned a similar range for all three sound levels, but their centroids shifted slightly toward lower numbers as sound level increased, indicating a reduction in the effective frequency range of rate-place coding at higher sound levels. The difference among the three distributions was statistically significant (p = 0.037, χ² test). (The numbers of neurons contributing to the histogram were smaller than the total number of rate-place coding neurons because some neurons only showed rate-place coding at one or two of the sound levels.)

Figure 6C compares the distribution of F0 STVR among place coding neurons across sound levels. Median STVR values were 0.80, 0.81, and 0.77 for low, medium, and high SPL, respectively. Differences in median STVRs were significant across all three sound levels (p = 8.9 × 10⁻⁴, Friedman test, N = 73), but pairwise comparison revealed only a significant difference between low and high sound levels (p = 0.41 for low vs mid, p = 0.076 for mid vs high, and p = 5.9 × 10⁻⁴ for low vs high; multiple comparison on the Friedman test statistics with Bonferroni correction).

Finally, we tested how the adjusted CF (or, equivalently, the CF adjustment factor φ) depends on sound. The median φ values were 0.997, 1.010, and 0.971 for low, medium, and high levels, respectively. Using signed rank tests, paired comparisons of medians were statistically significant for low versus high levels (p = 0.0012, single-sided) and mid versus high (p = 7.8 × 10⁻⁵, single-sided), but not for low versus mid levels (p = 0.20, two-sided). The small decrease in φ at the higher level indicates a decrease in CF, consistent with the peak shift of basilar membrane vibration (Russell and Nilsen, 1997) and auditory nerve fiber tuning (Carney and Yin, 1988) at high stimulus intensities. These level-dependent CF shifts may lead to degradation in rate-place coding of resolved harmonics, although a more sophisticated rate-place code in which frequency and level are jointly estimated should be able to handle these small shifts.

Overall, the strength and effective frequency range of rate-place coding showed a moderate degradation as sound level increased. Although the performance of human listeners in F0 discrimination for HCTs with resolved harmonics degrades somewhat with increasing stimulus level (Bernstein and Oxenham, 2006), the degradation does not occur until fairly high levels (>70 dB SPL). It is unclear to what degree such degradation in behavioral performance can be accounted for by the dependence of the IC rate-place code on sound level.

Spectral receptive field model suggests a role for inhibition in rate-place coding

In many rate-place coding neurons, for example, Neuron A (Fig. 4B), the trough FRs between peaks associated with resolved harmonics were below the neuron's spontaneous FR, and sometimes even reached 0, suggesting inhibition or suppression at these F0s. Such response patterns contrast with the rate-place profiles from the AN of anesthetized cats (Cedolin and Delgutte, 2005), where the trough FRs were always above spontaneous rates (SRs). To explore possible mechanisms of the suppressed IC response, we fitted two spectral receptive field models to the rate-place profiles of neurons demonstrating rate-place coding: a Gaussian function with a single excitatory band and a DoG function with both excitatory and inhibitory bands centered at the same frequency. When the inhibition is broader than the excitation in the DoG model, the net receptive field has a center excitatory band flanked by two inhibitory sidebands (see Materials and Methods). For both models, the parameters (center frequency, bandwidths, and, for the DoG, relative amplitude of excitatory and inhibitory components) were fitted to minimize the distance between predicted and measured rate profiles.

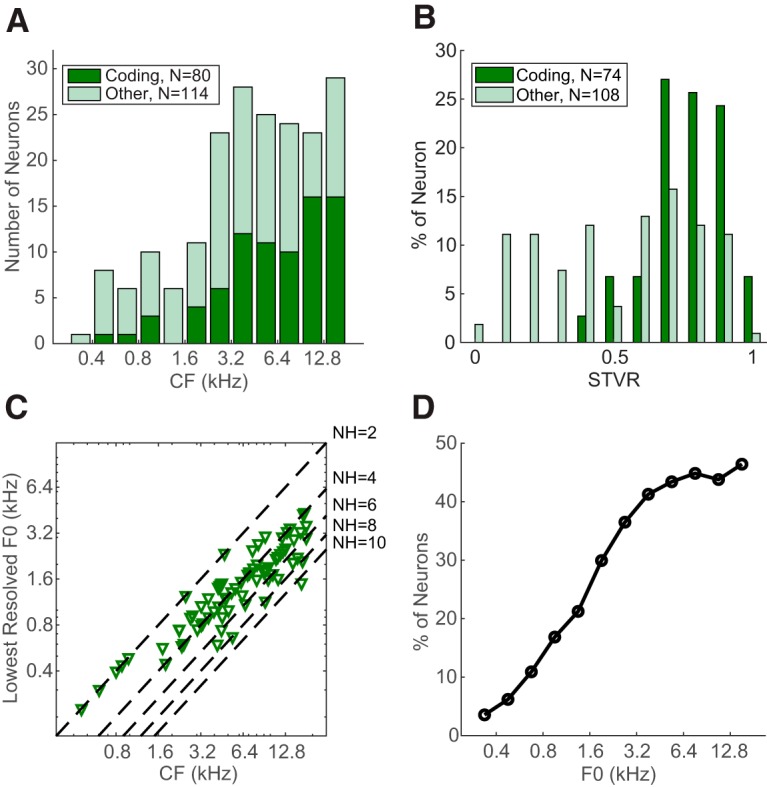
Figure 7A shows the Gaussian and DoG fits to the rate-place profile of Neuron A at 30 dB. Both models produced a rate-place profile with multiple peaks at low integer harmonic numbers. However, the DoG model was better at capturing the peak amplitudes: high rates for the first three peaks followed by a much lower rate for the fourth peak, and an almost indistinguishable fifth peak. In contrast, the Gaussian model produced similar peak FRs for NH from 1 to 5, thereby underestimating the amplitudes of first three peaks and overestimating the height of the fifth peak compared with the neural data. The best-fitting DoG and Gaussian models are shown in Figure 7B along with key model parameters. For both models, the best-fitting center frequencies were close to the adjusted CF obtained by the Fourier method. The finding that the DoG model fits better than the Gaussian model in this neuron suggests a role for inhibition in shaping the rate-place profile. Inhibition is also apparent in the neuron's FRA (Fig. 4A), where the FR fell below SR in frequency bands (dark blue) on either side of both center excitatory zones.

Figure 7.

Receptive field model for HCT responses. A, Neural (blue with error bar) and fitted (purple represents DoG model; green represents Gaussian model) rate-place profiles of Neuron A at 30 dB SPL. The 10 dB bandwidth was calculated from FRA at 30 dB SPL. B, Morphology and key parameters of the optimal DoG (purple) and Gaussian (green) weighting functions. C, Comparison of R² values using the DoG model (y axis) versus the Gaussian model (x axis) for individual neurons (N = 80). D, F test statistics to compare the goodness of fit from the two models. Dashed line indicates p = 0.05, the criterion for statistical significance. E, CF (orange circle), excitatory bandwidth (purple dots), and inhibitory bandwidth (blue “x”) of the optimized DoG model as a function of measured CF in individual neurons. Purple dashed curve indicates exponential fit of the σ_e versus CF relationship. F, The 10 dB bandwidth estimated from Borg et al. (1988). AN data (gray shaded area, 95% boundary of original data points), FRA of IC neurons showing rate-place coding (N = 53, blue triangle), DoG fitting of IC neurons with rate-place coding (N = 68, purple circle), and human periphery (short red curve) as functions of CF. Black dashed line at the middle of the shaded area indicates a custom fitting of Borg et al. (1988) data.

In Figure 7C, the goodness of fit for the two models is compared in each neuron using the adjusted R² metric. Most neurons (62 of 80) showed a higher R² for the DoG model than for the Gaussian model. For 70% of neurons (56 of 80), the DoG fit yielded R² > 0.5. Further examination of neurons with R² < 0.5 in DoG fits reveals that the rate-place profiles of these neurons were either irregular (e.g., containing minor peaks between integer harmonic numbers) or showed a dramatic difference in the peak FRs at different harmonic numbers (e.g., very high peak FRs at NH = 1 and 2, but much lower rates at NH = 3, 4, …). The mechanism yielding such rate-place profiles is not clear.

To further verify the benefit of adding inhibition to the model, we ran an F test in each neuron to compare the goodness of fit for the two models. As shown in Figure 7D, the F test p value was <0.05 for the majority of neurons (N = 62), indicating that the DoG model fit the rate profiles significantly better than the Gaussian model. Equally good fits from the two models were only observed in neurons with CF >1500 Hz, but this may be just due to the smaller number of low-CF neurons in our sample.

The center frequency (f_c), excitatory bandwidth (σ_e), and inhibitory bandwidth (σ_i) of the best-fitting DoG model are shown for each neuron as functions of adjusted CF in Figure 7E. The f_c values were all distributed along the identity line (black dashed), as expected. The dependence of the excitatory bandwidth of the DoG filter on CF (both in Hz) could be approximated by an exponential function shown as the purple dashed curve. In contrast, the inhibitory bandwidths showed a great deal of scatter so that a clear CF dependence could not be identified.

In effect, the inhibition in the DoG model sharpens the central excitatory band. Figure 7F shows the relationship between CF and 10 dB bandwidth of IC neurons calculated from the central excitatory band of the DoG model (N = 68, fits with negative R² or bandwidth >8000 Hz excluded). The bandwidths showed an increasing trend with increasing CF, but the data points were very scattered. A similar trend can be discerned for 10 dB bandwidths calculated from the pure-tone FRA at the same sound level as the HCTs (blue triangles, N = 53, only place coding neurons included). There was no significant difference between the two measures of bandwidths from the same neuron across the population (p = 0.49, two-sided Wilcoxon signed-rank test).

To compare the IC bandwidths with those in the AN, we fit a sigmoidal function to the Q₁₀-CF relationship measured in rabbit AN by Borg et al. (1988), and calculated the 10 dB bandwidths from the fitted curve (black dashed line). The gray shaded area encompasses 95% of the data points for rabbit AN 10 dB bandwidths. A majority of both FRA and DoG 10 dB bandwidths for IC neurons lay below the lower bound of AN bandwidths. Both IC bandwidths were significantly smaller than the AN bandwidths (p < 10⁻⁶ for DoG, p < 10⁻⁴ for FRA, single-sided Wilcoxon signed-rank tests), suggesting a sharpening of frequency tuning in the auditory midbrain, at least for place coding neurons.

IC neural responses to inharmonic tones

When all harmonics of an HCT containing resolved harmonics are shifted in frequency by the same amount, the perceived pitch of the resulting IHCT shifts in the same direction as the frequency shift (Schouten et al., 1962), although the temporal ERR is unchanged (Fig. 1). To shed light on mechanisms of pitch shift perception and to test whether IC neurons are sensitive to the harmonicity of complex tones, we measured the responses to harmonic and inharmonic tones in 25 neurons.

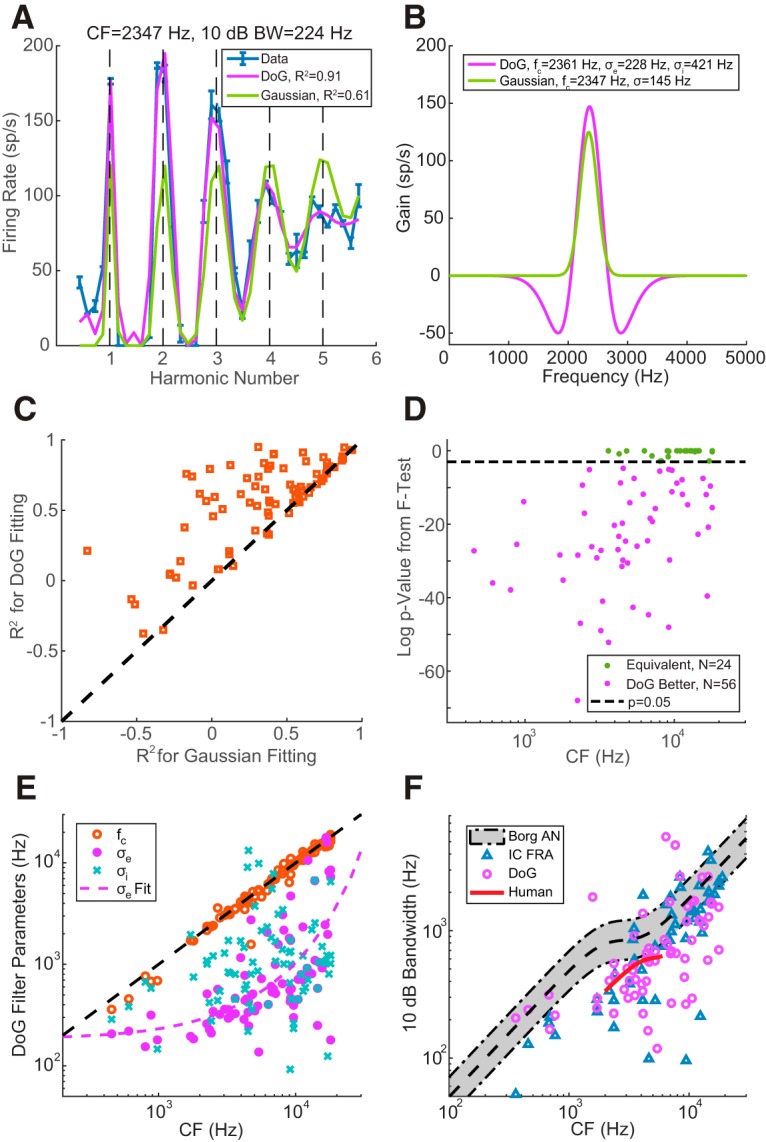
Figure 8A (solid lines) shows the FR of Neuron C (CF = 3.2 kHz) in response to complex tones with and without frequency shifts plotted against pNH = CF/FS (where FS is the frequency separation between adjacent frequency components, equals to F0 in the harmonic case). In the 0% shift (harmonic) condition, the neuron showed distinct peaks at NH = 1, 2, 3. With inharmonic tones, the neuron's profiles were similar to those in the harmonic condition with respect to numbers of peaks and peak FRs, but were shifted in the same direction as the frequency components. Peaks in the inharmonic profile approximately occurred when pNH = integer + shift, consistent with the prediction that FR is maximum when a component of the shifted tone aligns with the CF (see Materials and Methods).

Figure 8.

Neural and model responses to IHCTs. A, Rate-place profiles of Neuron C in response to harmonic and inharmonic tones at 30 dB per component (solid lines). A DoG model was fit to the response to 0% shift and then used to predict responses to non-0 shifts (gray dashed lines with “x”). B, Normalized R² values of DoG fitting to rate-place profiles at different proportions of frequency shift in individual neurons (blue dots) and their medians (red circles). C, Rate-FS profile of Neuron D at different amounts of frequency shift.

To further verify that the neuron's responses to the frequency-shifted tones were not dependent on harmonicity, we first fit a DoG model to the rate-place profile for 0% shift, and then used the same model parameters to predict the rate profiles in response to inharmonic tones (Fig. 8A, dashed lines) using the shifted power spectra as inputs to the model. The DoG model predictions were very close to the neuron's FRs in all conditions. Adjusted R² values indicated similar goodness of fit for the different amounts of shift. Among the 25 neurons tested with inharmonic tones, five either had negative R² values in the 0% shift condition or showed weak rate-place coding. For the remaining 20 neurons, we computed the normalized R² as a function of frequency shift (Fig. 8B), where the R² values at non-0 shifts were normalized by the value at 0% shift in the same neuron. Although the median normalized R² slightly decreased with increasing absolute shift, the trend was not statistically significant (Kendall's tau = 0.157, p = 0.8304).

It is worth noting that because the shifts in rate-place profiles are dependent on a neuron's ability to resolve frequency components, not all neurons showed an effect of frequency shift. For example, Neuron D (CF = 9.05 kHz) in Figure 8C did not show peaks in FR for resolved harmonics for either harmonic or inharmonic tones. Its rate profiles for inharmonic tones were almost identical to the profile in the harmonic case, with a broad peak at 640 Hz that was not a subharmonic of the CF. By manipulating the phase relationships among the harmonics to dissociate F0 from ERR in the stimulus waveform (Su and Delgutte, 2019), we ascertained that this neuron was sensitive to ERR rather than F0 per se (data not shown). Such envelope sensitivity is consistent with the lack of an effect of frequency shift on rate profiles because the ERR equals 1/Fs regardless of the amount of shift (Fig. 1B).

Are there “HTNs” in IC?

Feng and Wang (2017) have identified a class of “HTNs” in the auditory cortex of awake marmoset monkeys that were defined by two properties: (1) facilitation: the FR in response to an HCT at the “best F0” (BF0, which evokes the maximum FR to HCTs) was at least 100% higher than the rate for a pure tone at the BF; and (2) shift periodicity: in response to inharmonic tones created by shifting all the frequency components of an HCT by the same amount, the FR showed a quasi-periodic pattern as a function of the amount of shift, with maxima at integer multiples of BF0. The above results with inharmonic tones show that the shift-periodicity property holds for rate-place coding IC neurons. Therefore, we focused on testing the facilitation property of HTN by comparing the FRs produced by pure tones and HCT as a function of frequency. Although Feng and Wang (2017) tested only one stimulus level, we analyzed responses at three sound levels to assess whether the facilitation property is dependent on intensity.

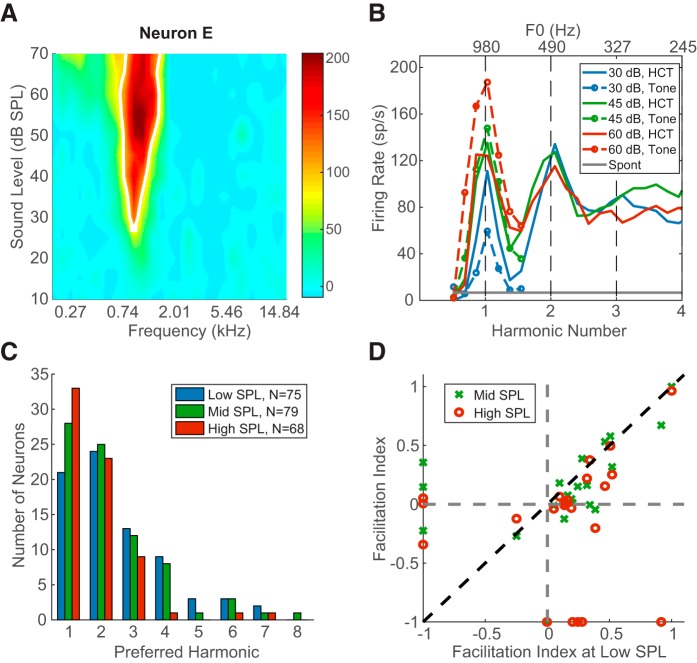
To test the facilitation property of HTN, we measured responses to both pure tones near the CF and HCT stimuli at the same stimulus level per component for 37 neurons, 22 of which showed rate-place coding of resolved harmonics. The pure-tone FRA and rate profiles for pure and complex tones of Neuron E are shown in Figure 9A and Figure 9B, respectively. This low-CF neuron (980 Hz) could resolve the first two harmonics at all three stimulus levels. The best F0 producing the highest FR for HCT was equal to the CF at 45 and 60 dB SPL/component but to CF/2 at 30 dB SPL/component, indicating that the neuron was more responsive to the second harmonic than the fundamental at this SPL. Such preference for a particular harmonic other than the fundamental was common in our neuronal sample. Figure 9C shows the distribution of preferred harmonics for all neurons demonstrating rate-place coding (N = 80). For all three sound levels, more than one-fourth of the neurons preferred the second harmonic over the first, and some responded strongest to even higher harmonics up to the eighth. The preferred harmonic shifted slightly toward lower values as sound level increased, but the trend was not statistically significant (χ² test, p = 0.28). The distribution of preferred harmonics for rate-place coding IC neurons qualitatively resembles the distribution for cortical HTNs (Feng and Wang, 2017, their Fig. 4A), but the mode of the distribution is at the second harmonic for cortical neurons as opposed to the fundamental for IC neurons.

Figure 9.

Evidence of harmonic templates in IC. A, Pure-tone FRA of Neuron E. B, Rate profile of Neuron E in response to pure tone and HCT at different sound levels. The original measurement used HCT with harmonic number up to 6.5, and is truncated here to show detail. C, Distribution of preferred harmonic across all neurons demonstrating rate-place coding (N = 80). D, Facilitation indices of neurons measured with interleaved pure tone and HCT, and showing rate-place coding (N = 22).

Feng and Wang (2017) defined a “facilitation index” (FI) to quantify the enhancement of FR for HCTs relative to pure tones: FI = (FR_BF0 − FR_BF)/(FR_BF0 + FR_BF). FI > 0 indicates that a neuron's FR is facilitated for an HCT at BF0 compared with a pure tone at CF, whereas FI < 0 indicates suppression for HCT. The neuron of Figure 9B shows modest facilitation at 30 dB SPL (FI = 0.3), but not at 45 and 60 dB, where the response to HCTs is actually slightly suppressed relative to the CF tone response. This occurred because the FR increased with stimulus level for the pure tone at CF but stayed nearly constant across levels for the HCT at BF0. Figure 9D shows a scatter plot of FI at a mid and high levels against FI at the low level for the 22 rate-place coding IC neurons tested with both pure tone and HCT stimuli. Some neurons did not demonstrate rate-place coding at all three sound levels, and therefore did not have a best F0 at some sound levels. Such neurons are plotted along either the x axis (neurons with a best F0 at the low SPL but not at mid or high SPLs) or the y axis (neurons with a best F0 at mid or high SPL but not at the low SPL). Among the 22 neurons, 17 showed facilitation at the lowest sound level, but only 5 showed suppression. The number of facilitated neurons decreased to 15 at the medium sound level and 11 at the highest sound level. For a given neuron, FI was usually maximum at the low SPL, as data for most neurons lay under the identity line in Figure 9D. While facilitation was observed in many neurons, only 9 neurons reached the FI > 0.33 criterion of Feng and Wang (2017) for HTN, which means the FR for an HCT at BF0 was at least 100% higher than the rate for a pure tone at CF. For the few neurons with FI < 0, the FI values were fairly close to 0, meaning the amount of suppression for HCTs was very modest. The dependence of suppression on sound level cannot be reliably assessed due to the small sample size.

Overall, facilitation of HCT responses relative to pure-tone responses in IC neurons was not as strong as for cortical HTNs, and its prevalence was dependent on stimulus intensity. However, because we only tested IC neurons that had an identifiable pure-tone CF, while some HTNs in the marmoset cortex did not respond to pure tones, we may have missed possible HTN-like neurons that responded poorly to pure tones.

Discussion

Using single-neuron recordings from the IC of unanesthetized rabbits in response to harmonic and inharmonic complex tones, we characterized rate-place coding of the spectral pattern of resolved frequency components, which was observed mainly for F0 > 800 Hz. Many IC neurons could resolve the first 3–5 harmonics, and this rate-place code was moderately dependent on sound level and not sensitive to harmonicity. Using spectral receptive field models, we found indirect evidence that inhibition may enhance the IC rate-place code. Some IC neurons had some properties of cortical HTNs in that they demonstrated modest facilitation to HCTs compared with pure tones at CF or responded most strongly to higher harmonics rather than to the fundamental. These results suggest relationships between the neural coding and the perception of pitch.

Rate-place coding along the auditory pathway

Rate-place coding of resolved harmonics in HCTs has been described in AN fibers (Cedolin and Delgutte, 2005, 2010) in anesthetized cats and single units and multiunits in A1 of awake macaques (Schwarz and Tomlinson, 1990; Fishman et al., 2013). In the cat AN, rate-place coding of resolved harmonics is observed in neurons with CFs >400 Hz, and can encode F0s >400–500 Hz (Cedolin and Delgutte, 2005). However, the AN rate-place code degrades rapidly with increasing sound level (Cedolin and Delgutte, 2010). Although IC rate-place coding appears to be more robust across sound levels than its AN counterpart, a quantitative comparison with the data of Cedolin and Delgutte (2005, 2010) cannot be made due to differences in both stimuli (different NH ranges) and preparation (unanesthetized rabbit vs anesthetized cat).

In both cortical studies (Schwarz and Tomlinson, 1990; Fishman et al., 2013), rate-place coding was also more prevalent in neurons with higher CFs (>300–400 Hz), and was only effective for F0s ∼>80 Hz. Schwarz and Tomlinson (1990) observed peaks in FRs at resolved harmonics over a 40 dB range of SPLs, and Fishman et al. (2013) stated that the rate-place code was prominent at 60 dB SPL per harmonic. Thus, the cortical representation is more robust to variations in sound level than the peripheral code.

In the current study, 41% of IC neurons demonstrated rate-place coding of resolved harmonics. The CFs of these neurons were all >600 Hz, and the lowest resolved F0 was ∼300 Hz. Compared with the single-unit results from cat AN (Cedolin and Delgutte, 2005) and macaque A1 (Schwarz and Tomlinson, 1990), the CF ranges of these neurons are comparable at different stages, but the prevalence of rate-place coding neurons shows a decreasing trend along the ascending auditory pathway, likely because different types of neurons at higher processing stages specialize in encoding diverse stimulus properties (Chechik et al., 2006). In addition, IC rate-place coding was observed up to 70 dB SPL per harmonic and was only moderately dependent on stimulus level. This evidence suggests a key role for the IC in transforming the rate-place code between the periphery and the auditory cortex. However, comparisons are made difficult by differences in methodology and also known differences between cats, rabbits, and macaques with respect to cochlear frequency selectivity (Liberman, 1978; Borg et al., 1988; Joris et al., 2011).

Role of inhibition in IC

Our experimental and modeling results suggest that inhibition may play a role in shaping rate-place coding in IC neurons. Specifically, we found that the 10 dB bandwidths of rate-place coding IC neurons were narrower than those of AN fibers (Fig. 7F). A sharpening of frequency tuning relative to the AN has been observed for some classes of IC neurons with pure-tone stimulation (Ramachandran et al., 1999; Palmer et al., 2013). A recent study in mice also suggested a role of inhibition in shaping the pure-tone frequency selectivity of IC neurons (Lee et al., 2019). Our observations are also consistent with studies showing a central excitatory area flanked by inhibitory bands in spectral or spectro-temporal receptive fields of IC neurons measured with broadband stimuli (Qiu et al., 2003; Lesica and Grothe, 2008; Yu and Young, 2013). However, using binaural broadband noise stimuli, McLaughlin et al. (2007) found no difference between AN and IC bandwidths in low-CF neurons sensitive to interaural time differences.

Another possible role for inhibition is to make the neural response invariant to stimulus intensity, which is highly relevant for pitch and timbre perception. Lesica and Grothe (2008) found that the STRF of IC neurons often displayed more inhibitory regions at high SPLs compared with low SPLs. They suggested that the increase in inhibition at high levels can be attributed to the activation of high-threshold inhibitory inputs, which is in turn supported by intracellular studies that showed higher response thresholds for inhibitory compared with excitatory inputs (Covey et al., 1996; Xie et al., 2007). Thus, our finding that IC rate-place coding is fairly robust against sound level, together with previous studies showing level-invariant tuning in the primary auditory cortex (Sutter, 2000; Sadagopan and Wang, 2008), suggests that the neural representation of auditory stimuli may progressively become invariant to intensity by accumulating intensity-dependent inhibition along the ascending pathway.

However, inhibition in IC can only enhance rate-place cues at high sound levels if such cues are not completely absent in the periphery. While AN fibers with high SRs saturate at moderate sound levels (Sachs and Young, 1979), the smaller populations of low- and medium-SR fibers contain rate-place cues to the spectrum of broadband stimuli, such as vowels up to 80 dB SPL and above (Rice et al., 1995; LePrell et al., 1996), and even high-SR fibers preserve significant rate-place information at high levels when studied with appropriate methods (Young and Calhoun, 2005). Moreover, rate-place coding of complex sounds exhibits a wider dynamic range in certain cell types of the ventral cochlear nucleus relative to the AN (Blackburn and Sachs, 1990; May et al., 1998), suggesting an enhancement of rate-place cues via the pattern of convergence from AN fibers onto ventral cochlear nucleus cells (Lai et al., 1994). In this view, the role of IC may be to further enhance the spectral contrast for resolved harmonics at high sound levels.

An alternative possibility is that rate-place information in the IC is derived from temporal cues in the periphery, since peripheral temporal cues to both pitch and vowel formants are robust at high sound levels (Young and Sachs, 1979; Cariani and Delgutte, 1996). Several models have been proposed for converting temporal cues to pitch into rate-place cues (Loeb et al., 1983; Srulovicz and Goldstein, 1983; Shamma and Klein, 2000; Cedolin and Delgutte, 2010; Shamma and Dutta, 2019), although direct evidence that such schemes are actually implemented in the auditory brainstem remains elusive. However, it is unlikely that the IC rate-place code is entirely derived from AN temporal cues because a majority of our rate-place coding neurons had CFs >3–5 kHz, the upper frequency limit of phase locking to the temporal fine structure in the AN (Johnson, 1980; Palmer and Russell, 1986).

No compelling evidence for harmonic templates in IC

It has long been known that models of pitch processing incorporating harmonic templates can account for a wide variety of pitch phenomena for stimuli with resolved harmonics, including the pitch shift of IHCTs (Goldstein, 1973; Wightman, 1973; Terhardt, 1974; Gerson and Goldstein, 1978; Cohen et al., 1995). Shamma and Klein (2000) proposed a biologically plausible model for the emergence of harmonic templates based on across-frequency coincidence detection. Because the operation of coincidence detectors requires precise phase locking, the harmonic templates in this model must emerge early on in the auditory pathway, and not beyond the IC (Shamma and Dutta, 2019) where phase locking degrades sharply (Joris et al., 2004). So far, neurons with properties of harmonic templates have only been reported in marmoset auditory cortex (Feng and Wang, 2017).

We explored whether IC neurons might exhibit some of the response properties of cortical HTNs. Specifically, we tested whether rate-place coding IC neurons meet the facilitation property of HTNs according to Feng and Wang (2017). A majority of IC neurons showed facilitation in response to HCTs compared with pure tones, but to a lesser degree than cortical HTNs because: (1) only a few neurons showed >100% facilitation and (2) fewer IC neurons responded maximally to high harmonics compared with cortical HTNs. Both of these properties were dependent on sound level.

The other defining property of cortical HTNs according to Feng and Wang (2017), periodicity in response to frequency shifted inharmonic tones, did hold for IC rate-place coding neurons (Fig. 8), but this property was a direct consequence of peripheral frequency selectivity rather than to central processing specific to harmonic stimuli, suggesting that the shift-periodicity property of cortical HTN is not sufficiently selective. Sensitivity to spectral jitter in the harmonics, which provided some of the strongest evidence for harmonic templates in the Feng and Wang (2017) study, may provide a better defining criterion for HTNs.

Overall, we did not find compelling evidence for harmonic templates in the IC, even though rate-place coding IC neurons could exhibit some of the properties of cortical HTNs as defined by Feng and Wang (2017). We suggest that the criteria of Feng and Wang (2017) for defining HTNs need to be revised to exclude properties that can be explained by peripheral frequency selectivity. More generally, additional evidence for harmonic templates in the auditory system is needed.

Implications for pitch perception

The lowest F0 for which we observed rate-place coding of resolved harmonics in rabbit IC (∼300 Hz) lies at the upper range of adult human voice (∼80–320 Hz) (Matteson et al., 2013), and the most effective F0 range for IC rate-place coding (>3000 Hz; Fig. 5D) lies mostly above the upper limit of musical pitch ∼5 kHz (Semal and Demany, 1990; Plack and Oxenham, 2005a). Such differences can be partly attributed to broader cochlear tuning in rabbit, as shown in Figure 7F by the comparison of 10 dB bandwidths of rabbit auditory nerve fibers (Borg et al., 1988) with estimates of human AN bandwidths from compound action potentials (Verschooten et al., 2018). Extrapolating the trends in human AN bandwidths to lower CFs, the bandwidths of neurons with CFs in the first formant region (200–800 Hz) should be narrow enough to resolve harmonics of F0s in the range of male voices, and this would a fortiori be true for human IC neurons if the sharpening observed in the rabbit IC also occurs in humans. The few available studies on rabbit phonation suggest F0s in the range of 500–1200 Hz (Swanson et al., 2010; Mills et al., 2017; Döllinger et al., 2018), which is at the low end of the effective range for rate-place coding by IC neurons. Although behavioral studies have concluded that small mammals use primarily temporal envelope cues to discriminate the F0 of HCTs (Shofner and Chaney, 2013; Sumner et al., 2018; Walker et al., 2019), our own study suggests that rabbits can also do so based on resolved harmonics for F0s in the range of their vocalizations (Delgutte et al., 2018).

Human psychophysical experiments using HCTs with identical power spectra but different temporal ERRs (Krumbholz et al., 2000; Pressnitzer et al., 2001) showed that, at very low frequencies (<50 Hz), the pitch of HCTs is dependent on ERR rather than F0. Therefore, the lower limit of pitch perception is likely not conveyed by resolved spectral components, but by temporal phase locking to the ERR. In a companion paper (Su and Delgutte, 2019), we showed that a temporal code for ERR was available in the IC up to 900 Hz, and bandpass rate tuning to ERR was observed between 56 and 1600 Hz. Therefore, the three neural codes available in IC are effective in complementary frequency ranges and, together, cover the entire behaviorally relevant range of F0.

Our findings on IC rate-place coding shed light on the transformation of neural representations of resolved harmonics along the auditory neuraxis, and suggest how a higher processing center could extract pitch from resolved frequency components. An important goal for future studies will be to determine whether the level robustness of the IC rate-place code emerges through enhancement of rate cues already present in the periphery or transformations from a temporal code to a rate code.