Validation of in-house knowledge-based planning model for advance-stage lung cancer patients treated using VMAT radiotherapy

Abstract

Objectives:

Radiotherapy plan quality may vary considerably depending on planner’s experience and time constraints. The variability in treatment plans can be assessed by calculating the difference between achieved and the optimal dose distribution. The achieved treatment plans may still be suboptimal if there is further scope to reduce organs-at-risk doses without compromising target coverage and deliverability. This study aims to develop a knowledge-based planning (KBP) model to reduce variability of volumetric modulated arc therapy (VMAT) lung plans by predicting minimum achievable lung volume-dose metrics.

Methods:

Dosimetric and geometric data collected from 40 retrospective plans were used to develop KBP models aiming to predict the minimum achievable lung dose metrics via calculating the ratio of the residual lung volume to the total lung volume. Model accuracy was verified by replanning 40 plans. Plan complexity metrics were calculated using locally developed script and their effect on treatment delivery was assessed via measurement.

Results:

The use of KBP resulted in significant reduction in plan variability in all three studied dosimetric parameters V5, V20 and mean lung dose by 4.9% (p = 0.007, 10.8 to 5.9%), 1.3% (p = 0.038, 4.0 to 2.7%) and 0.9 Gy (p = 0.012, 2.5 to 1.6Gy), respectively. It also increased lung sparing without compromising the overall plan quality. The accuracy of the model was proven as clinically acceptable. Plan complexity increased compared to original plans; however, the implication on delivery errors was clinically insignificant as demonstrated by plan verification measurements.

Conclusion:

Our in-house model for VMAT lung plans led to a significant reduction in plan variability with concurrent decrease in lung dose. Our study also demonstrated that treatment delivery verifications are important prior to clinical implementation of KBP models.

Advances in knowledge:

In-house KBP models can predict minimum achievable lung dose-volume constraints for advance-stage lung cancer patients treated with VMAT. The study demonstrates that plan complexity could increase and should be assessed prior to clinical implementation.

Introduction

Technological advancements in radiotherapy planning and delivery techniques, such as volumetric modulated arc therapy (VMAT), have allowed reduction of dose to critical structures while maintaining target coverage.^1–3 Nevertheless, achieving the lowest possible organ-at-risk (OAR) doses for a given patient geometry remains challenging as there are large population variations in OAR and target structure geometries.^4,5 Several studies reported large heterogeneity in treatment plans produced by planners with different experience levels.^4–7 A treatment plan meeting OAR constraints and with adequate target coverage may still be considered suboptimal if OAR doses are possible to be further reduced without compromising target coverage.

To reduce variability between planners, different knowledge-based planning (KBP) methods have been implemented. KBP utilises prior patients’ geometries, plans and resultant dosimetric coverage to estimate lowest achievable OAR doses for prospective patients prior to treatment plan optimisation.⁸ KBP offers several benefits including improvements in treatment plan quality, reduction of interobserver variability and improvement of treatment planning efficiency.^9–11 In addition to OAR dose prediction, KBP methods have also been used successfully to determine optimal gantry angle for Intensity Modulated Radiation Therapy (IMRT) patients.^12,13

A number of different metrics have been explored for predicting OAR doses prior to treatment plan optimisation. The most commonly used metric is an overlap volume histogram (OVH); this is used to characterise the 3D spatial relationship between an OAR and a target.^14–16 Other metrics can include overlap of OAR volume with target structure(s),¹⁷ OAR volume within and outside a target structure¹⁸ and similarity coefficient between retrospective and prospective patents’ geometry.¹⁹

KBP methods have been largely used for prostate and head and neck planning;^8,20–22 however, only a limited number of studies have reported on its benefit for lung cancer patients.^8,23 A study performed by Fogliata et al utilised commercial software (Varian’s RapidPlan^TM) for VMAT lung planning and reported that the RapidPlan^TM KBP model facilitated achieving the desired clinical constraints in 4% more patients.⁸ Cui et al produced an in-house model for predicting lung doses using a line of best fit to the data for patients treated with IMRT fields.²³ In this study, 15 ring structures from the planning target volume (PTV) were produced and the overlap of lungs with each of the rings was used to determine V₁₀ (i.e., volume receiving 10 Gy), V₂₀ and V₃₀. Furthermore, Zawadzka et al developed an in-house model to predict minimum achievable mean lung dose (MLD) for a given geometry.²⁴ They predicted MLD using the dose calculated from 36 equidistance fields.

At the time of writing, none of the studies in the literature include predictions of minimum achievable V₅ (percentage of lungs receiving a dose of 5 Gy) and minimum achievable V₂₀ for lung cancer patients treated with VMAT. V₅ is a valuable metric as it has been widely reported as a predictor of radiation pneumonitis for advanced-stage lung cancer patients (not limited to only mesothelioma patients).^25–28 V₅ constraints are routinely used at our institution for all advanced-stage lung cancer patients; therefore, a KBP modelling study involving this metric has been of particular interest to our department and is expected to add a missing piece to the literature.

The aim of this study was to develop in-house KBP models to predict minimum lung-dose constraints for V₅, V₂₀ and MLD for a given patient geometry. Combinations of volumes and dose-volume histogram were used to build the models. Of note is the fact that treatment plans optimised using the lower bound model to achieve lowest OAR doses could produce highly modulated plans, thereby increasing uncertainties in treatment delivery as compared to the plan optimised without the model. Furthermore, any error in treatment plan delivery could significantly alter delivered dose distributions especially within high dose gradient regions. Therefore, an important objective of our study is to verify the treatment delivery accuracy of plans produced using KBP models and compare it with the respective delivery accuracy of plans optimised without the model so that an optimal trade-off between lower OAR dose and plan delivery can be established. In the present study, the produced treatment plans were verified using treatment planning and measurements on the TrueBeam^TM (V2.5 Varian Medical Systems, Palo Alto, CA) linear accelerator which is a novel approach not yet reported in the KBP field.

Methods

Data collection

The clinical patients were planned with RapidArc^®/VMAT within the Eclipse^TM treatment planning system (Version 13.7, Varian Medical Systems, Palo Alto, CA) with 6 MV beams. Two partial arcs (0^o to 181^o for right-sided tumours and 0^o to 179^o for left-sided tumours) were used avoiding direct entry through the contralateral lung to minimise the dose received by it. Plan dose was calculated using the Acuros^® algorithm (dose to water) with a uniform dose grid of 0.25 cm. The prescribed dose for patients included in the study was 55 Gy in 20 fractions. Treatment plans were optimised to meet the planning goals as described in Table 1. The normal tissue objective (NTO) function was used to limit dose to healthy structures with the same priority as the PTV. The NTO is a function in the Eclipse planning system which reduces dose to healthy tissue as a function of distance from the PTV’s outer boarder.²⁹ Automatic NTO settings were used (i.e., distance from target boarder 1.0 cm, start dose 105%, end dose 60% and fall-off 0.05) with priority set to 300 manually.

Table 1.

Treatment planning objective used for planning NSCLC patients at our clinic

Volume	Parameters	Clinical constraints
Spinal Cord Planning Organ at Risk Volume	D0.01cc	<45 Gy
Planning target volume (PTV)	V95	≥99 %
	V107	<1.8 cc
Lungs-gross tumour volume (GTV)	V5Gy	<60 %
	V20Gy	<35 %
Heart	V30Gy	<45 %
	Mean Dose	<26 Gy

A total of 40 pre-existing treatment plan data sets from our database were used to build the models in this study; all were calculated with Acuros algorithm within the same version of Eclipse planning system. Volumes (in cubic centimetre (cc)) for numerous of structures including gross tumour volume (GTV), PTV, lungs (lungs minus GTV), PTV outside lungs, overlap of lungs with PTV, lungs volume cropped back from the PTV by 1 to 5 cm (with 1 cm increment) and field size were collected. Then, dosimetric parameters such as percentage of lungs volume receiving 5 Gy (V₅), V₂₀ and MLD were collected from the Eclipse treatment planning system for the above.

Development of KBP model

To determine suitable volumes (including ratio of different volumes (e.g., Lungs/PTV)) for our KBP model, correlation coefficients (R²) of all collected volumes with the dosimetric data (i.e., V₅, V₂₀ and MLD) were determined. The commonly used parameters (e.g., OVH) and number of volumes (e.g., lungs, PTV, lungs within PTV etc) showed very poor positive correlation. Finally, the residual lung volume (Lung_Residual) was calculated.

$${\displaystyle Lun{g}_{Residual}-\left(\frac{V2-V1}{V2}\right)}$$ (1)

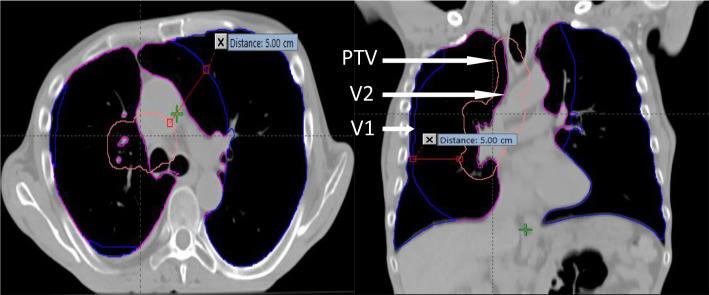
V₂ is total lung volume excluding GTV and V₁ is the total lung cropped back from PTV by 5 cm (V₁: Lungs5cmCrop – volume was produced by cropping total lung (total lung = lungs GTV) volume extending inside PTV with an additional margin of 5.0 cm using the crop function within the planning system) demonstrated in Figure 1. Furthermore, in this study, a lower bound model was developed to predict lowest achievable volume-dose (Predict_volume-dose) for a given geometry (i.e., Lung_Residual).

Figure 1.

Displaying the total lung volume excluding GTV (volume V2) in magenta and the volume V1 (i.e. the lung volume crop back from PTV (pink) by 5cm (blue).

$${\displaystyle Predic{t}_{Volume-Dose}=m\times Lun{g}_{Residual}+c}$$ (2)

The prediction model was developed based on prescription of 55 Gy in 20 fractions (typically used in our clinic). However, to use the model for different prescriptions (i.e., 66 Gy in 33 fractions and 60 Gy in 30 fractions), it was normalised using factor ∆ (see equation 3 and 4) to predict minimum achievable doses. Note: the 55 Gy model data was used in the normalised model.

$${\displaystyle \mathrm{\Delta }=\left(\frac{PrescriptionDose\left(Gy\right)}{55Gy}\right)}$$ (3)

$${\displaystyle Predic{t}_{Volume-Dose}=\left(m\times Lun{g}_{Residual}+c\right)\times \mathrm{\Delta }}$$ (4)

Verification of model using treatment planning

A total of 40 previously treated patients (not included in the training data) were replanned using the values predicted by the models. For replanning, optimisation objectives for V₅, V₂₀ and MLD were set to achieve the model predicted values, whereas all other objectives were kept the same as the original plans. Difference in dosimetric parameters between predicted and replanned, predicted and original, replanned and original plan were compared.

In addition, the prediction accuracy of the normalised model (see equation 4) was assessed by reoptimising 10 plans from the test data set (originally prescribed 55 Gy in 20 fractions but for the validation of model prescription doses were changed within the planning system). The difference between predicted and achieved doses were calculated for both 60 Gy and 66 Gy prescriptions.

Verification of model using treatment delivery

All VMAT plans are routinely verified with portal dosimetry measurements on a linear accelerator prior to delivering it to patients. All the plans optimised using the KBP model were verified by measuring the fluence on the electronic portal imaging device (EPID) panel, without the presence of a patient, and comparing it with the planned fluence in the portal dosimetry image prediction software within the Eclipse planning system. Gamma analysis (criteria 3%/2mm ≥ 98% (optimal tolerances set locally) or ≥95% (mandatory tolerance) results were collected and compared with the original plan results to assess the effect of KBP on plan delivery. For analysis, lower dose cut-off threshold was set to 20 %, the measured and predicted images were auto-aligned and improved γ evaluation was used.

Plan complexity measurements

Treatment plan complexity is dependent on the total number of μ and level of modulation within a plan. Simpler treatment plans (i.e., lower μ, less modulated with larger leaf pair opening) are preferable as these are relatively less dependent on MLC motion/position accuracy during delivery.²⁹ Highly complex plans generally have higher number of μ, which increase treatment delivery time, increase dose to the patient—due to MLC transmission—and are more susceptible to interplay effects. A number of treatment plan complexity metrics were calculated both for the original plans as well as the plans produced using the KBP model. The treatment plan complexity parameters, including μ/Gy, μ/Degree, islands below 1cc (i.e., small islands), small aperture score (SAS: calculated as the ratio of open leaf pairs where the aperture was less than a defined criterion (2 mm, 5 mm, 10 mm and 20 mm in our study) to all open leaf pairs (see equation 5)³⁰ were calculated using a locally developed script. The effect of KBP on plan complexity was assessed.

$${\displaystyle SAS\left(x\right)beam=\sum _{i=1}^1\frac{N\left(x>a>0\right)i}{N\left(a>0\right)i}\times \frac{MUi}{MUbeam}}$$ (5)

where x is the aperture criteria, i is the number of segments in the beam, N is the number of leaf pairs not positioned under the jaw, and a is the aperture distance between opposing leaves.³⁰

Statistical analysis

To determine the optimal volumes for predicting dose metrics, Pearson correlation coefficient values were calculated. All other comparisons were tested for significance using the Student’s paired t-test. p-values < 0.05 were considered as suggesting statistically significant differences. Normality of data was tested with Kurtosis analysis.³¹

Results

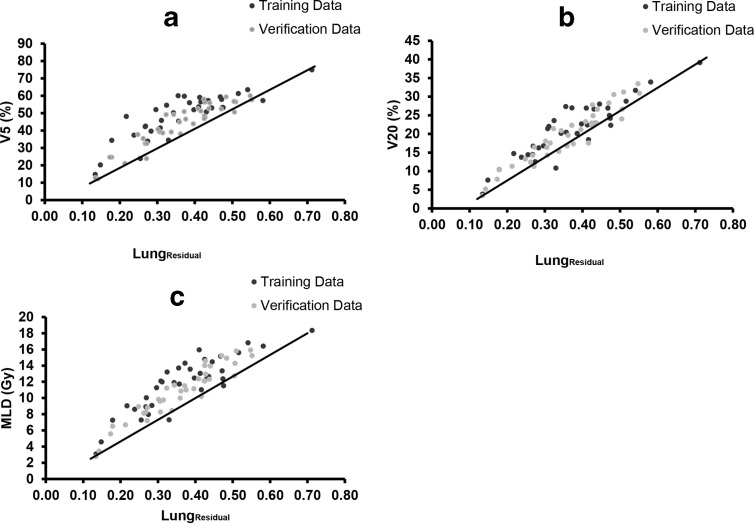
The clinical KBP models were developed to determine the minimum achievable dose metrics using the Lung_Residual volume (Figure 2). A significant reduction in variability in treatment plans among different planners was observed following the implementation of the model (Table 2 and Figure 3).

Figure 2.

The plots showing training and verification data and the linear line showing the lower bound model for V5 (a), V20 (b), and MLD (c)

Table 2.

Mean and standard deviation of the differences between achieved and predicted dose-volume parameters for lung before and after implementation of model. The minimum achievable values for each dose-volume parameter were predicted prior to plan optimisation using Eclipse Scripting Application Plugg-In (ESAPI)

Dose-volume parameter	Before model		After model		p value
	Mean	SD	Mean	SD
V5	10.8 %	7.1 %	5.9 %	4.6 %	0.007
V20	4.0 %	3.1 %	2.7 %	2.1 %	0.038
Mean lung dose (MLD)	2.5 Gy	1.6 Gy	1.6 Gy	1.0 Gy	0.012

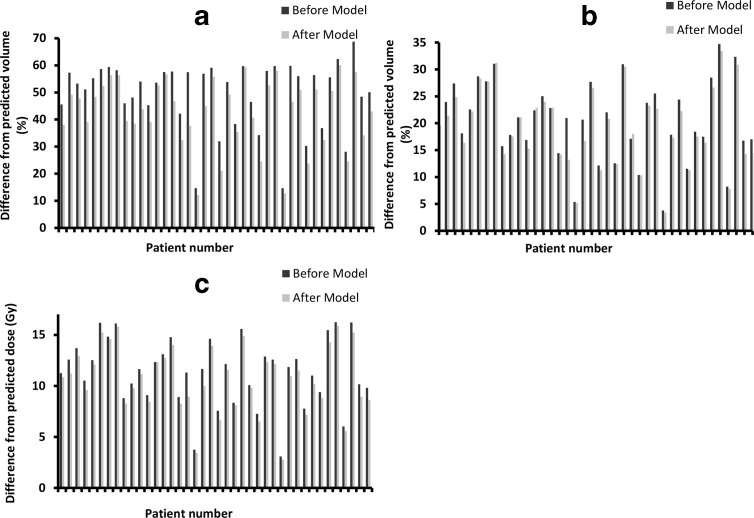
Figure 3.

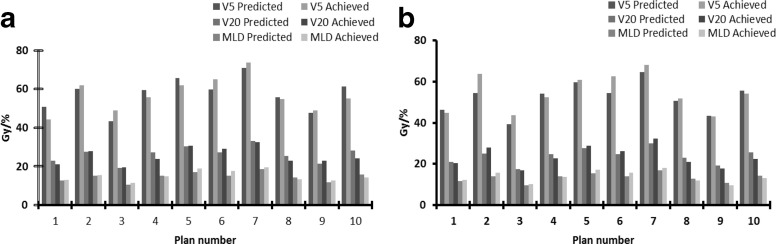
Plots A, B and C showing reduction plan variability in plans produced after the models compared for V5, V20 and MLD respectively. The original plans were planned without model predicted values whereas, achieved values were obtained by re-optimizing plans with the model predicted values. Three separate models were produced for each dose-volume parameter shown in Figure 2, using residual lung volume. The minimum achievable dose-volume parameters were predicted prior to the plan optimisation and the predicted values for each parameter were entered in optimiser.

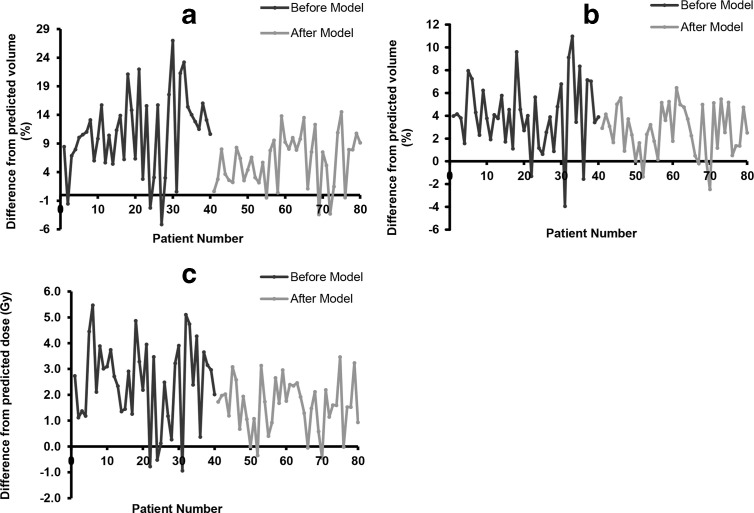
Furthermore, the plans optimised using the model showed significant reduction in dose-volume in all three, V₅, V₂₀ and MLD, dosimetric parameters. The mean difference between predicted and achieved values was reduced from 10.8 to 5.9%, 4.0 to 2.7% and 2.5 to 1.6Gy for V₅, V₂₀ and MLD, respectively, with the model (Figure 3). In Figure 3, it can be observed that negative differences indicate that the model predicted values were higher than the achieved values and positive differences indicate model predicted values were lower.

Furthermore, treatment plans produced using the model-predicted values resulted in concurrent reduction in all three dosimetric parameters compared to the original plans (Figure 4). The average reduction observed in V₅, V₂₀ and MLD was 6.6% (range: 0.4–19.78%), 1.1% (range: −0.93–7.77%) and 0.7 Gy (range: 0.03 – 2.38Gy), respectively. The reduction in lung doses was achieved without compromising the overall plan quality. All test plans were evaluated by a clinician and were deemed acceptable for clinical delivery.

Figure 4.

Showing difference in dose-volume parameters before and after the model. Concurrent reduction was seen in all the dosimetric parameters studied V5 (a), V20 (b) and MLD (c) after the model. The achievable dosimetric parameters were determined using the models prior to optimisation and the predicted values were entered in the optimiser.

In addition, the model developed for the prescription used in our clinic (55 Gy in 20 fractions) was normalised for use with different prescriptions. The normalised model (equation 3) was validated for two additional prescriptions (66 Gy in 33 fractions and 60 Gy in 30 fractions) by replanning 10 patients. The indicated accuracies of the models were clinically acceptable; mean difference between predicted and achieved doses at V₅ was 0.5 and 2.3% for 66 Gy and 60 Gy prescriptions, respectively, and for V₂₀ and MLD, it was 2.1% and 1.2 Gy for both prescriptions, respectively (Figure 5).

Figure 5.

Showing difference in dose-volume parameters before and after the model for 66Gy in 33 fractions (a) and 60Gy in 30 fractions (b) prescriptions. The normalised model was verified using ten plans, minimum achievable doses were predicted using the normalised model and these valued were used during plan optimisation.

It was noted in the KBP model-based plans that the total number of μ increased significantly in majority of plans compared to the original clinical plans (mean increase = 46.21 MU (range: −48MU – 186MU), p = 0.011). Therefore, a number of treatment plan complexity metrics were calculated using a locally developed script for both the original and re-optimised plans. The results are shown in Table 3.

Table 3.

Comparison of treatment plan complexity measurements for the original and replanned plans. Mean, standard deviation and p values for different parameters

Parameters	Original Plan	SD	Replanned Plan	SD	p value
μ/Gy	236.6	29.0	253.4	29.4	0.0002
μ/Degree	1.8	0.2	2.0	0.2	0.0001
Fraction of islands < 1cc	0.5	0.2	0.6	0.1	0.0002
Islands/control point SAS2 SAS5 SAS10 SAS20	3.9 0.2 0.2 0.3 0.4	2.1 0.1 0.1 0.1 0.1	4.9 0.2 0.3 0.3 0.5	2.3 0.1 0.1 0.1 0.1	0.0001 0.0003 0.0002 0.0002 0.0002

The results show that all studied complexity metrics increased significantly in the replans optimised using KBP models, when compared to the original plan (Table 3). This indicates that KBP plans were relatively highly modulated compared to the original plans.

Treatment verification measurements performed on linear accelerators showed that both original and KBP plans delivered as planned. Differences in treatment verification measurements for all parameters were within the optimal tolerance limits set locally (≥98% pixels passing with γ criteria of 3%/2 mm) except two arcs from the KBP plans showed slightly higher differences with γ pass rates at 96.9 and 97.2%. However, these were within the mandatory tolerance limit of ≥95%; therefore, these plans were deemed as clinically acceptable for treatment delivery.

Discussion

The aim of treatment planning is to achieve optimal target coverage while reducing OAR doses as low as reasonably achievable without compromising target coverage.³² However, in routine clinical practice, due to treatment planners’ experience and clinical workload, this is not always achieved for all patients.^4–7 Furthermore, not all plans meeting target coverage and OAR constraints are optimal if there are opportunities to minimise OAR doses further without compromising target coverage. This balance may be difficult to be achieved efficiently in the absence of KBP methods, especially for relatively inexperienced treatment planners.

Building KBP models for lung cancer patients could be more complex compared with some other sites (e.g., prostate) as there are large variations in the location, shape, size and orientation of lung tumour with respect to OAR volumes. Several combinations of volumetric parameters (e.g., PTV and OAR volumes, overlap volumes and field size) and their correlation with studied lung dose-volume parameters were evaluated. However, the lung_Residual volume calculated using total lung volume and the lungs crop back from PTV by 5.0 cm (equation 1) showed highest correlation with all the studied lung dose-volume parameters.

Only two studies have reported on the use of in-house KBP modelling for optimising lung plans.^23,24 However, as none of these models predicts minimum dose to V₅ and V₂₀ of lungs, we felt it was important to develop local models that predict the minimum achievable dose to these percentages of lung volumes for a given patients’ geometry. Furthermore, none of the studies in the literature has investigated the effect of KBP models on the complexity of plans and hence on the delivery of these plans. In this study, accuracy of the models was verified using a planning study while the effect of KBP models on plan complexity and delivery was assessed by calculating complexity metrics and performing measurements on a linear accelerator.

Our models were built to predict minimum doses to three lung dose parameters for lung patients treated with VMAT. This study demonstrated that minimum lung dose-volume prediction models can be developed and used in the routine clinical setting. Relatively simple and cost-effective models reduced variability/heterogeneity in treatment plans significantly compared to the original clinical plans, which was the primary aim of this study. Predicting dose-volume parameters prior to optimising a plan could reduce number of optimisations/iterations required to achieve the optimal plan and reduce the overall planning time.

Additionally, the treatment planning study performed showed that the use of a KBP model led to a larger reduction in V₅ as compared to V₂₀ and MLD (Figure 4). The moderate reduction observed for the V₂₀ (1.4%) and MLD (0.7 Gy) may be attributed to the use of the NTO function in the original and re-optimised plans with same priority as PTV. Results from number of commercial auto-planning software showed similar results as our in-house developed model.^33–35 One of the auto-planning studies reported statistically insignificant increased V₅ whereas our study showed consistent and significant reduction in this dosimetric parameter.³⁴ The normalised model shows that the model could be used for different prescription.

In addition, we also assessed the accuracy of the model for oesophagus cancers (commonly treated with 45 Gy and 50 Gy in 25 fractions), treated with full-arc geometry but the prediction accuracy of V₅ was not clinically acceptable. However, prediction accuracy of V₂₀ and MLD was clinically acceptable but the difference seen between predicted and achieved dose were higher compared to the lung plan. Mean difference between predicted and achieved values for 50 Gy and 45 Gy prescriptions were V₅ = 29.7 and 30.8%, V₂₀ = 1.8% and 3.4% and MLD = 2.3 Gy and 2.1 Gy respectively. This could be due to the difference in the beam geometry.

Furthermore, it was noted that the largest reduction in all three dosimetric parameters investigated was achieved with the use of KBP models in the subset of plans produced by relatively less-experienced planners, compared to experienced planners (see patient numbers 2, 4, 17, 19, 30 and 39 in Figure 4), due to not driving optimiser harder. However, almost all the original clinical plans considered met planning goals given in Table 1 and therefore acceptable, some were not classed as “optimal” as lung dosimetric parameters could be reduced further to some extent without compromising target coverage. Some of these plans were produced by experienced staff indicates the potential benefits of KBP for all planners. In addition, a relatively smaller reduction in the studied parameters was noted in plans where lung constraints were either exceeding or were very close to the tolerance levels in the original plans as compared with the plans where lung constraints were well within tolerance—potentially due to the fact that the original plans were increasingly optimised to bring doses within tolerance. These results indicate the importance and efficiency of KBP modelling for this type of patients in reducing OAR dose variability in treatment plans produced by planners of variable experience.

Webb et al and Abdellatif et al reported that plan complexity increases with increasing number of small segments, μ/cGy and number of µs per control point.^36,37 An increase in the total number of µs seen in the KBP optimised plans warranted further investigation: Treatment plan complexity metrics were calculated and delivery verification measurements were performed on a linear accelerator. Plan complexity metrics indicated a significant increase in smaller islands (i.e., smaller than 1cc), number of µs per control point and small aperture segments in the KBP plans. These plans were optimised to achieve minimum achievable doses, rather than generic OAR tolerances; therefore, an increase in plan complexity was expected. A study by Crowe et al reported that SAS could be used as an indicator of level of plan modulation; they showed positive correlation between quality assurance (QA) results and SAS was set at 0.5 cm.³⁰ In this study, SAS at 0.2 cm, 0.5 cm, 1.0 cm and 2.0 cm increased for all studied plans indicating increase in modulation in these plans.

Although the plan complexity parameters for KBP model-based plans were relatively higher than the ones of clinical plans, their impact on the measured fluence was relatively minimal for the majority of the test plans. Similar results are reported in the literature.^38,39 The measurements showed overall good agreement with the planned fluence except for two arcs where differences exceeded the locally determined optimal γ tolerance limits. These measurements showed that KBP may increase modulation and hence affect delivery therefore the model must be verified using treatment delivery measurements prior to implementing it clinically. Furthermore, in this study, delivery measurements were performed using EPID panel (without patient or moving phantom) that do not fully verify the impact of an increase in modulation on the robustness of plan. Further investigation, using a moving phantom, is needed to quantify the effect of high modulation of the delivery especially for treatment of thoracic tumours.

Finally, the model was implemented clinically in our clinic using the Eclipse scripting tool (ESAPI: Eclipse Scripting Application Plugg-In). Planners produce the structure (Lungs5cmCrop = crop total lung volume extending inside PTV with an additional margin of 5.0 cm) using the crop function and then run the script within the Eclipse planning system prior to proceeding with plan optimisation. The script displays the minimum achievable dosimetric metrics based on the residual lung volume for the selected patient. The predicted values are then manually entered in the optimiser (priorities are set within the clinical protocol template) during the optimisation of the plan.

Conclusion

This study showed that a relatively simple KBP model can significantly reduce variability in lung planning between planners. The clinical implementation of these models demonstrated increase in lung sparing. It is, however, important to assess plan deliverability prior to clinical implementation of such models to ensure that the potential increase in plan complexity will not affect the dosimetrical accuracy required.