A global model of island species–area relationships

Significance

The island species–area relationship (ISAR) is a fundamental diversity pattern, best described by the power model. Biogeographic theory assumes predictable variation in power model parameters in relation principally to system isolation, but these assumptions are only weakly supported by previous work, which has been limited in considering the two parameters separately and oversimplistically. By developing and testing a hierarchical (structural equation) model of factors influencing ISAR form, we show that island species diversity patterns are shaped by intra-archipelago processes more strongly than by isolation from mainland source pools. These findings point to a need to quantify the role of differing scales of isolation in influencing propagule exchange among insular systems to develop improved predictive diversity models.

Abstract

The increase in species richness with island area (ISAR) is a well-established global pattern, commonly described by the power model, the parameters of which are hypothesized to vary with system isolation and to be indicative of ecological process regimes. We tested a structural equation model of ISAR parameter variation as a function of taxon, isolation, and archipelago configuration, using a globally distributed dataset of 151 ISARs encompassing a range of taxa and archipelago types. The resulting models revealed a negative relationship between ISAR intercept and slope as a function of archipelago species richness, in turn shaped by taxon differences and by the amount and disposition of archipelago area. These results suggest that local-scale (intra-archipelago) processes have a substantial role in determining ISAR form, obscuring the diversity patterns predicted by island theory as a function of archipelago isolation. These findings have implications for the use and interpretation of ISARs as a tool within biogeography, ecology, and conservation.

The island species–area relationship (ISAR) is a fundamental macroecological pattern, the study of which has been closely connected with the investigation of processes responsible for the generation, maintenance, and loss of biological diversity (1–5). The ISAR is commonly described by the power model, which in its logarithmic form is given by logS = logC + zlogA (where S = island species richness, A = island area, and z and logC are fitted parameters representing the slope and intercept of the model, respectively). Meta-analyses of 612 island datasets have shown the power model to provide (i) significant fits in 75% of cases and (ii) the best general model from 20 SAR models tested (6, 7). Island biogeographical theory posits that logC and z should increase, respectively, as a function of the biotic richness of the source pool region and the isolation of the archipelagos, the latter reflecting increased importance of the evolutionary process with distance from the mainland (1, 2, 7, 8). These trends are evident in the aforementioned meta-analyses and the wider literature, but only weakly so, reflecting the many confounding factors involved and undermining confidence in the biological interpretation of logC and z. Intriguingly, while both parameters are necessary to specify any given ISAR, variation in each has traditionally been examined separately (1, 6–11). We therefore set out to explore whether departure from expected patterns of variation in z might in part be coupled to variation in logC.

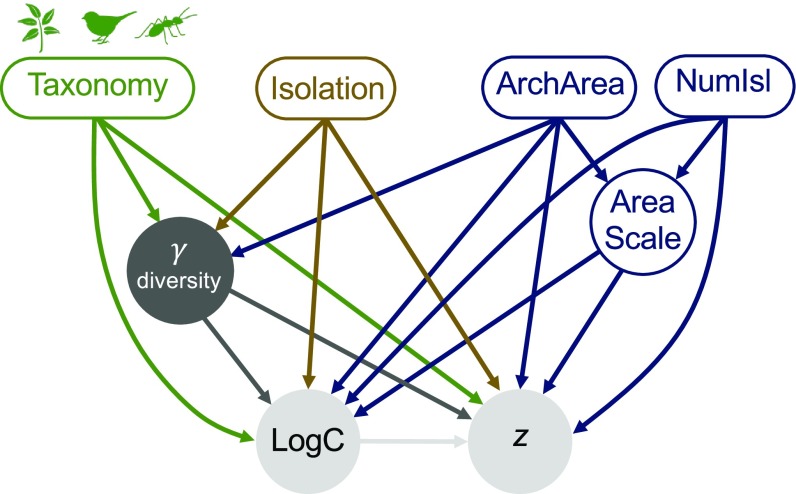
Through exploratory analyses of our database of significant power-model ISARs (Materials and Methods), we observed that despite logC and z values being statistically unrelated in bivariate correlation (below), negative covariation between them appeared to emerge with increasing archipelago species richness (herein Gamma). This led us, in turn, to question how the characteristics of each archipelago may modify the ISAR variation otherwise predicted to occur as a function of increasing isolation from mainland sources (above, and see refs. 1, 12, and 13). Drawing on previous work, we selected a set of key archipelagic properties shown or hypothesized to influence ISAR form and developed a statement of plausible hierarchical causal influences (e.g., archipelago area and isolation may both influence Gamma but not vice versa), constituting a general hypothesis of ISAR parameter variation (Fig.1 and SI Appendix, Materials and Methods). The model encapsulates classic hypothesized roles for differences between major taxa, geographical isolation, and archipelago configuration (Fig. 1) (1, 11, 12).

Fig. 1.

Model structure. A priori pathways were hypothesized between exogenous variables (rectangles) and endogenous variables (circles) based on arguments from the literature (see text). Three categories of taxa (green) were considered: Plants (i.e., vascular plants), Vertebrates (e.g., birds, mammals), and Invertebrates (e.g., land snails, beetles). Archipelago configuration (blue) was represented by NumIsl = Number of islands, AreaScale = ratio between the largest and the smallest islands within each archipelago, and ArchArea = total land area of the archipelago. Isolation (brown) = archipelago distance from the mainland. Diversity properties (gray) are represented by Gamma diversity = total species richness of an archipelago, and by logC, and z (i.e., the parameters of the ISAR of each archipelago). Archipelago identity (not shown) is included as a random factor because some archipelagos are represented by separate datasets for different taxa. For the full set of variables initially considered and their pairwise correlations, see SI Appendix, Table S1.

We then applied piecewise structural equation modeling [SEM (14)], using backward stepwise selection and AIC_c, to a database of ISARs (n = 151) to test our general model (Materials and Methods). The parent–child relationships (paths) of variables in the full model were specified but not the path sign. Within the SEM, AreaScale (the ratio between the area of the largest and the smallest island within each archipelago), Gamma, logC, and z are all classed as endogenous variables (those influenced by one or more other variables), while the remaining variables are exogenous (Fig. 1). The model structure ultimately focuses attention on how richness scales with area and thus on z, which, together with variation in logC, is crucial to biological interpretations and applications of ISARs in, for example, island biogeography and conservation science (3–5, 15–17). Also of interest is the extent to which archipelagos of differing long-term geoenvironmental dynamics (e.g., hotspot oceanic vs. land bridge) generate different ISAR forms (6–8, 13, 16, 18–20). Accordingly, we also report analyses for our two largest subsets, oceanic (n = 39) and continental (n = 64) archipelagos.

Results

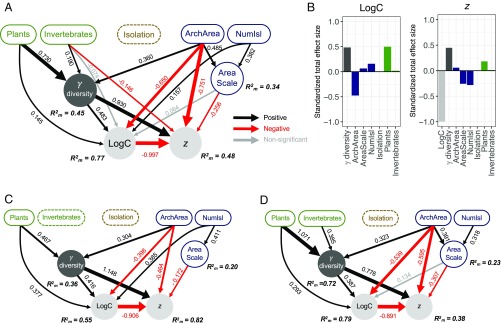
Our full dataset (hereafter “all-ISARs”) encompasses globally representative variation in: Gamma diversity from 5 to 3,394 species; total archipelago area (ArchArea) from <1 km² to 1,594,760 km²; system type from islands within lakes to continental and oceanic archipelagos; and number of islands (NumIsl) from 6 to 86 (Dataset S1). The best all-ISARs model was identified using a backward stepwise procedure and AIC_c (Fig. 2 and SI Appendix, Table S2), and it shows that Gamma increases from Vertebrates to Invertebrates to Plants (the largest effect), which reflects trophic and general ecological differences (compare with ref. 21) and that our plant data are in each case for all higher plants, while the animal datasets are for limited subtaxa (e.g., spiders, snails, birds, lizards). Gamma is also, predictably (19), a positive function of ArchArea (Fig. 2A). AreaScale increases with NumIsl and with ArchArea. The model has high explanatory power for both logC and z (Fig. 2A). The marginal R²_m values (fixed factors only) for z, logC, and Gamma (respectively 0.48, 0.77, and 0.45) were almost identical to the conditional R²_c values (all factors, including the random effect, respectively 0.48, 0.8, and 0.53), indicating that the random factor “Archipelago identity” accounted for very little additional variance in the analysis except for AreaScale, for which “Archipelago identity” captured a substantial amount of variance (R²_m = 0.34, R²_c = 0.81). At the core of the path diagram, there is a strong negative relationship between logC and z, driven by increasing values of Gamma (Figs. 2A and 3A). In declining order of the size of the model coefficients (i.e., direct effects of predictors), logC values decrease in response to ArchArea and increase in response to Gamma and NumIsl, with a further taxon effect of Plants (Fig. 2A and SI Appendix, Table S3). There is also a small positive net effect of Invertebrates on logC through Gamma (SI Appendix, Table S4). ISAR slope (z) values decrease in response to logC, ArchArea, AreaScale, and Invertebrates, and increase in response to Gamma (Fig. 2 and SI Appendix, Table S3). There is also a negative, indirect effect of NumIsl and a positive indirect effect of Plants on z (SI Appendix, Table S4).

Fig. 2.

Best-path models for all-ISARs (n = 151) (A and B), oceanic-ISARs (n = 39) (C), and continental-ISARs (n = 64) (D). Best path models were obtained using a backward stepwise selection procedure and AIC_c. Pathways show how Taxon (with vertebrates the base level), isolation, archipelago configuration (ArchArea, NumIsl, and AreaScale), and Gamma influence logC and, together, z (SI Appendix, Table S2). Piecewise structural equation models were fitted using linear mixed models with Archipelago identified as a random effect. These models were supported by the data (all-ISARs: Fisher’s C = 16.02, df = 12, P = 0.190; oceanic-ISARs: respectively 14.36, 14, 0.423; continental-ISARs: respectively 16.06, 18, 0.588). Arrow widths are proportional to standardized path coefficients (values are also given), and marginal R²_m values (fixed effect) are given for each endogenous variable. (B) Standardized total effect size of logC and of z, calculated by summing the direct and indirect effects derived from the best all-ISARs path model (Materials and Methods and SI Appendix, Tables S3 and S4).

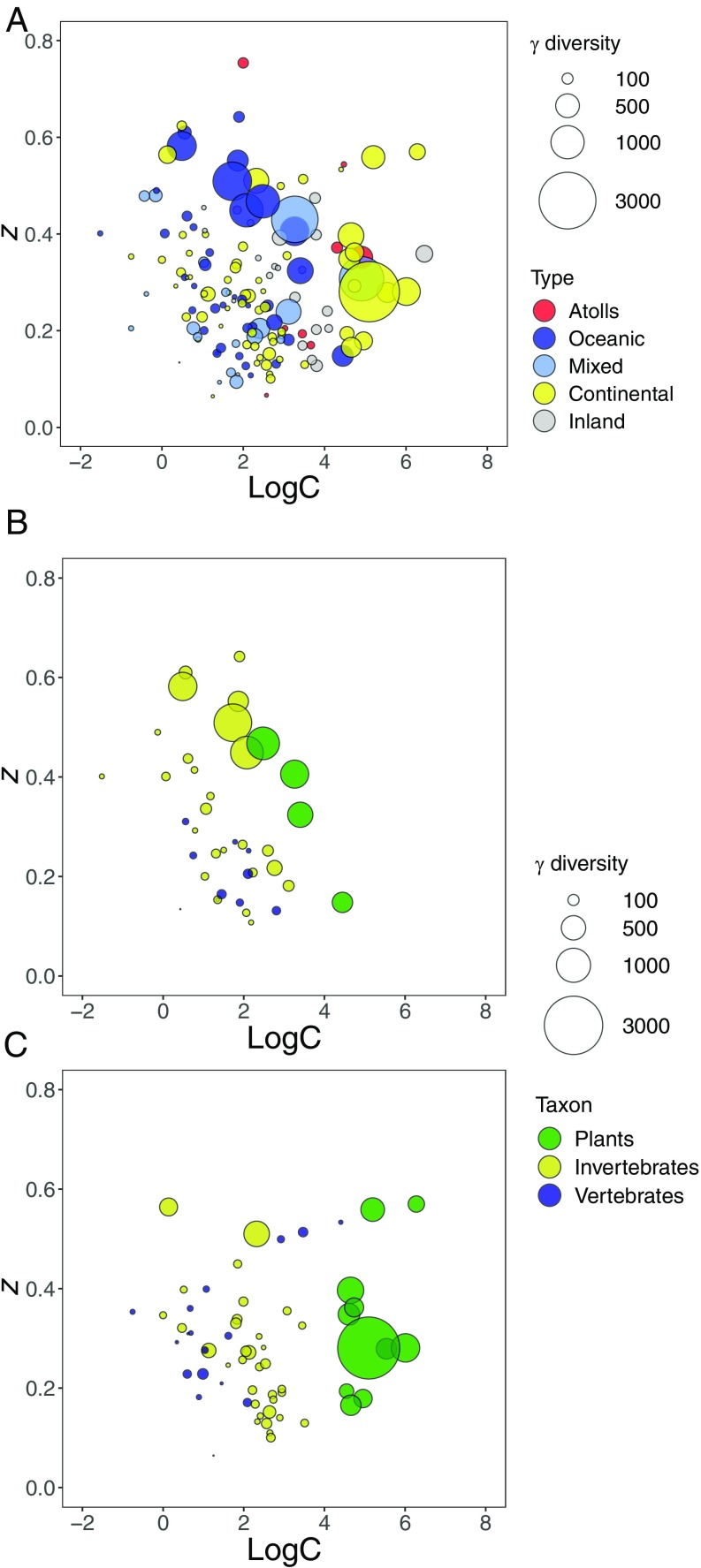
Fig. 3.

Archipelago richness (Gamma) in relation to the parameters of each ISAR. The five archipelago types are distinguished for the all-ISARs dataset (n = 151) (A); vascular plants, vertebrates, and invertebrates (note that animal datasets are for subsets such as birds or spiders) for the oceanic-ISARs dataset (n = 39) (B) and continental-ISARs dataset (n = 64) (C) (Dataset S1).

Simplifying the contributions of each variable to the variation in ISAR parameters for the all-ISARs dataset (Fig. 2B): (i) for logC, it is apparent that taxon, archipelago configuration, and Gamma are each important, with plants and increasing Gamma driving higher values and archipelago configuration having more complex effects; (ii) for z, the interplay between logC and Gamma is of central importance, as are the effects of archipelago configuration, while there are relatively limited net effects deriving from taxon differences. Effects of archipelago configuration on z are also complex, involving a combination of direct and indirect effects, such that there is, for instance, a negligible net (positive) role for ArchArea on z (standardized path coefficient = 0.058) despite its large contribution to the overall model structure and its direct (negative) linkage to z (SI Appendix, Tables S3 and S4). It is also notable that (i) based on standard bivariate Pearson’s correlation coefficients, there is no relationship between logC and z (r = −0.07; P = 0.42) (SI Appendix, Table S2) and it is only through analysis of the interactions with Gamma within the SEM that the relationship emerges; and (ii) the theoretical expectation of steeper slopes and lower intercepts with increased system isolation is not supported.

Theoretically, we may expect differences in ISAR parameters to arise between different types of archipelagos (e.g., oceanic volcanic, atolls, continental, mixed groups, inland) that have distinct and contrasting geodynamics. Visual scrutiny of the Gamma, logC, and z interrelationship appears to support this proposition (Fig. 3A). However, reanalysis of the two best represented subsets, oceanic and continental archipelagos, generated remarkably similar overall model structures (Fig. 2 and SI Appendix, Fig. S1A). We found that the oceanic-ISARs model (Fig. 2C) has a much higher explanatory power for z (R²_m = 0.82), explains slightly less variation in logC (R² = 0.55), and differs in paths in just two respects from the all-ISARs model (Fig. 2 A and C and SI Appendix, Tables S2–S4). First, the taxon signal is reduced to a plant-vs.-animal effect (links from Invertebrates to Gamma and z being absent), perhaps simply reflecting the smaller number of datasets by which to demonstrate clear differences (Fig. 3B). Second, the link from ArchArea to AreaScale disappears. The model for continental ISARs is comparable in power for logC (R²_m = 0.79) and poorer for z (R²_m = 0.38) than the all-ISARs analysis. These differences are evident also in the Gamma, logC, and z interrelationships shown in Fig. 3, wherein the relationship is not so evident for continental ISARs, especially for the plant datasets, most of which are from land-bridge archipelagos ranging from the Mediterranean to the Baltic and Canada (Dataset S1). Nonetheless, the respective importance of Gamma and archipelago configuration effects is little changed while the influence of taxon differences on logC and z are more pronounced than for the (smaller) oceanic-ISARs subset (Fig. 2B and SI Appendix, Fig. S1B and Tables S2–S4).

Further sensitivity tests were run to evaluate the predictive power of the best path models for all three datasets, using a repeated k-fold cross-validation approach. Outputs produced an average Pearson’s correlation between the observed and the predicted endogenous variable values >0.5 for the four endogenous variables with the exception of AreaScale (SI Appendix, Table S5). Finally, we also tested for interactions between Taxon and the three other main endogenous variables (SI Appendix, Materials and Methods), which once again showed the model structure to be stable (SI Appendix, Figs. S2 and S3 and Table S6, and compare with Fig. 2). These findings support the generality of our best path models and indicate that the biological relationships described have predictive power; that is, they may extend to other archipelagos and island systems.

In summary, the SEMs reveal that, for a diverse range of taxa from archipelagos ranging from inland lakes to remote atolls: (i) increases in Gamma are found for larger archipelagos and taxa that are known to have higher densities at the community level (e.g., plants versus vertebrate groups such as reptiles), (ii) increases in Gamma drive a trade-off between logC and z values, (iii) the values of which are further modified by archipelago configuration (the distribution of archipelago area across variable numbers of islands); and (iv) the role of system isolation in relation to Gamma and ISAR parameters anticipated in classic island theory (1) is not evident regardless of the dataset analyzed (Fig. 2 and SI Appendix, Tables S1–S5).

Discussion

Notwithstanding recent advances, we lack a general consensus as to how individual factors and mechanisms contribute to ISAR form across different taxa, environmental conditions, and spatial and temporal scales (7–11, 16, 17, 21–24). Such an understanding is essential if the ISAR is to be used effectively as a predictive tool in applied biodiversity science (3–5, 15). Previous work has, however, established a number of broad generalizations. First, species richness variation across islands and archipelagos is primarily a function of area, which not only provides more space for individual plant and animal populations but also is frequently indicative of available resources, energy supply, elevational range, or habitat diversity (11, 22, 23). The inclusion of, for example, climate, habitat, environmental change, and island age data can often also raise the explanatory power of diversity models (19, 22–24). Second, while logC tends to decrease and z to increase with geographical isolation, consistent with reduced immigration rates and consequent increases of in situ speciation (1, 6, 8), the ISAR parameter space occupied by distant, nearshore, inland, and even habitat islands shows a great deal of overlap (6, 7, 11)—the prompt for the present work. Third, alongside differences in ISAR parameters with isolation and between taxa, previous work has shown scale effects on the ISAR slope (z) linked to range in island area (6, 7, 10, 25). Fourth, considering whole archipelagos as islands, it has been shown elsewhere that strong archipelago species–area relationships (ASARs) can be obtained when fitting power models to a set of 14 oceanic archipelagos (18), and that steeper slopes are found when restricting those analyses to archipelago-endemic species, reflecting enhanced diversification effects among larger (isolated) archipelagos.

In the present analyses, we drew on these prior observations in developing a general hierarchical model of factors that may explain departure from the variation in ISAR form predicted by theories of island biogeography that are framed in relation to the notion of single, dominant source pools. These classic island theories predict increased slope (z) with increasing isolation as rates of immigration and accompanying gene flow (rescue effects) are reduced and in-situ anagenesis and cladogenesis lead to high incidence of local endemics. Similarly, within conservation science, habitat loss and increased isolation of habitat remnants are hypothesized to cause adjustment (“relaxation”) of ISAR form, generating time-lagged extinctions (2–4).

Here we have shown that (i) archipelago area provides first-order control over archipelago diversity (Gamma), (ii) the distribution of that diversity within archipelagos responds to the internal configuration of the archipelago such that (iii) regionally structured variation in ISAR parameters (decreasing logC, increasing z with isolation) is modulated by local properties of archipelagos (compare with refs. 1,10, 12, and 13). Thus, whereas ISAR slope (z) may indeed be responding to a changing balance in the role of ecological vs. evolutionary processes (2, 8, 20), these effects are only evident in the all-ISARs model via variations in archipelago richness and configuration, and neither the expected negative relationship between system isolation and Gamma nor the importance of system isolation for ISAR parameters is evident for our full all-ISARs dataset or for either the continental or the oceanic subsets (Fig. 1 and SI Appendix, Tables S1–S4).

It is remarkable how much of the global variation in ISAR parameters can be captured by models including taxon effects, Gamma, archipelago area, and two simple metrics of how that area is subdivided, without the need to consider other archipelagic features that are known to have explanatory power for island diversity patterns—for example, elevational range, island age, climate, or energy flow (20–24, 26). Further work could usefully explore how incorporation of such variables might improve model fits, although the development of more complex models is analytically challenging with the available data if overfitting is to be avoided.

While previous work has shown that switching attention from generalist to specialist species groups and from wide-ranging natives to restricted endemics is accompanied by increasing ISAR slope (8, 27), as predicted with a shift from “ecological” toward “evolutionary” process regimes with geographical isolation, the expected combination of increasing slope and decreasing intercepts with distance from mainland sources (1, 2) fails to feature in our path models (Fig. 1), as combinations of taxon and archipelagic features drive local adjustment of ISAR fits.

We interpret these findings as supporting the importance of archipelago configuration (area distribution, number and spacing of islands), in turn influencing intra-archipelago dynamics, such as metapopulation-like “rescue effects” between islands (12, 28), for adjustment of ISAR form. Interestingly, when considering solely volcanic oceanic islands, typically systems of high local endemism (13, 20), as Gamma increases, an increasingly constrained range of logC vs. z combinations is apparent—a pattern which does not appear to have previously been documented empirically. The trade-off in ISAR slope and intercept as a function of archipelago richness (Figs. 2 and 3) is consistent with the importance of dynamic processes of propagule exchange, population extinction, and in situ diversification within archipelagos (1, 2, 20, 26), but demonstrates that these processes need not result in a single or narrow band of canonical slope values determined primarily by distance from major source pools. Future ISAR studies should (i) consider logC and z values in tandem and approach system description in ways that better capture scale dependency in ISAR form and (ii) extend the approach developed herein to other forms of insular system (e.g., forest fragments, sky islands). Finally, to test these ideas and to improve understanding of the biological mechanisms at play, further work is needed to determine how the configuration of the constituent islands within archipelagos and the multiple scales of geographical isolation involved (within archipelagos, between archipelagos, and with mainland areas; refs. 12, 13, and 26) influence propagule exchange.

Materials and Methods

Data Compilation and ISAR Models.

The datasets were sourced from the literature according to protocols detailed elsewhere (6, 7). In brief, we used two main abstracting/indexing systems (ISI Web of Science and Scopus) with a wide range of search strings. More than 800 journal papers, books, doctoral theses, online databases, reports, and unpublished resources were screened. For present purposes, all datasets were checked (as explained more fully in SI Appendix, Materials and Methods) to ensure that each dataset retained for analysis provided (i) a significant power model; (ii) a unique taxon/archipelago combination; and (iii) a system of real islands (land surrounded by water). Each of the resulting datasets represented, for that archipelago, a well-sampled taxonomic group (e.g., higher plants, birds, mammals, land snails, Homoptera: Cicadoidea), which we coded for analysis as belonging to plants, invertebrates, or vertebrates.

Where possible, we extracted the binary presence-absence matrix and used this to calculate archipelago species richness ourselves. However, certain studies did not provide the presence-absence matrix but instead simply reported the number of species on each island and separately for the archipelago (Gamma). All island area values were converted to square kilometers before analysis to ensure comparability of logC values. We fitted the power (log-log) ISAR model using linear regression in R (29), extracting the slope (z) and intercept (logC) values. The power model was chosen because it has been shown to be the best-performing general model, significantly fitting and thus adequately describing high proportions of ISAR datasets (6, 7), and because the parameters permit comparison between studies and are used in further biogeographical analyses (e.g., refs. 4, 5, and 15). Natural logarithms were used. Following ref. 6, for datasets that contained islands with zero species we added 1 to all island richness values before analysis. In total, we retrieved 151 datasets (= all-ISARs) meeting the above criteria from 113 separate sources (Dataset S1).

Other variables of interest were extracted from the source papers. These included the taxon sampled (Taxon, classified as vertebrates, invertebrates, or plants), archipelago richness (Gamma), number of islands (NumIsl), total area of the archipelago (ArchArea) in square kilometers, areas of the smallest (MinArea) and largest islands (MaxArea) in the archipelago, and ratio of the largest island area to the smallest island area (AreaScale). We also measured the geographical isolation of the archipelago (Isolation) in meters. Measuring archipelagic isolation is not straightforward (26), but for these purposes and given the wide variety of island types/locations, we used the minimum distance of each archipelago to the closest mainland (or lake edge for islands within lakes), where mainlands were taken to include the world’s continents plus Madagascar (the world’s largest continental fragment island at 587,040 km²) and the largest (>130,000 km²) of the world’s land-bridge islands that were relevant to our study systems (New Guinea, Java, Sumatra, Borneo, Great Britain). This provided an objective, conventional metric, although we recognize that, for some archipelagos, it might not be the best possible indicator of their isolation from their key source pools (26). The type of archipelago was classified using information in the source papers and the wider literature (e.g., ref. 30) as inland water body (i.e., islands within lakes), continental (land-bridge and other continental-shelf islands), oceanic (islands of volcanic origin over an oceanic plate and with no history of connection to continental land masses), atolls, or mixed (a mix of oceanic and other island types found within oceans) (SI Appendix, Materials and Methods).

Analytical Strategy.

Structural equation models (SEMs) are well suited for evaluating multivariate hypotheses because the direct and indirect effects of predictor variables can be tested simultaneously (31) and, if the SEM is set up correctly, it allows the user to infer causality from observational data (32). Whereas in multiple linear regressions, the test is for whether a response variable is a linear function of a set of predictor variables, in SEMs we are testing whether the endogenous variables are caused by a set of other variables (which can be a mix of endogenous and exogenous variables) (32).

The first stage of a SEM is to develop a theoretical causal model that outlines the specific hypothesized causal structure between variables. Our model is illustrated in Fig. 1 and described fully in SI Appendix, Materials and Methods. Based on the previous demonstration of power archipelago species–area relationships (ASARs; ref. 19), Gamma was hypothesized to be primarily a function of Taxon and ArchArea, both of which were included as exogenous variables. Gamma was also hypothesized to be a function of geographical isolation (e.g., refs. 1, 12, and 13). NumIsl was included as an exogenous variable as it captured additional information concerning the subdivision of total archipelago area. AreaScale was hypothesized to be a function of both ArchArea and NumIsl and was included as an endogenous variable in the model (Fig. 1). Gamma was also included as an endogenous variable, and both Gamma and AreaScale were hypothesized to potentially explain variation in logC and z (10, 25). Based on previous work and theoretical considerations (e.g., refs. 1, 2, and 6–9), we also permitted paths between the exogenous variables ArchArea, NumIsl, Taxon, and Isolation, and between z and logC.

Whereas initial analysis demonstrated no significant bivariate correlation between logC and z (SI Appendix, Table S1), we hypothesized a trade-off between the two ISAR parameters, conditioned by the foregoing causal network (see e.g., ref. 10). The rationale for a link from logC to z rather than vice versa is based on the notion that, given the same biological process regime, z values should be equivalent while logC may vary in relation to the biotic richness of the available species pool, reflected at the archipelago level by Taxon and Gamma. We tested whether this rationale could be supported analytically using the method of Vinod Causality (33; SI Appendix, Materials and Methods). The model posits that, taking account of variation between taxa and in the location of archipelagos, increases in Gamma reflecting larger archipelagos and richer species pools may drive a trade-off between logC and z values, further modified by the distribution of total archipelago area across variable numbers of islands (cf. 10, 12, 13, 25, and 26).

The processes driving community assembly differ in balance between island types. In particular, the process regime of volcanic oceanic islands is distinct from that of other categories of island, as diversity patterns are strongly shaped by the geological dynamics of the archipelagos and by the opportunities for diversification presented by their permanent and significant isolation from mainland species pools (e.g., 19, 20, 30, 34, and 35). To assess the generality of our model for specific archipelago types, we reran our analyses using the subset of oceanic-ISARs datasets (n = 39) and also the subset of continental-ISARs datasets (n = 64), a high proportion of which comprise land-bridge islands (likely connected to larger landmasses during Pleistocene sea-level minima), since these represent the two largest groups of ISARs in our dataset. The remaining subsets of island types contained too few datasets for analysis.

Model Fitting and Validation.

The SEMs were fitted using piecewise structural equation modeling [piecewise SEM (14)]. This SEM method enables the overall fit of a multifaceted hierarchical network to be tested, including the estimation of indirect effects, while allowing for the consideration of random effects (36). We assessed overall model fit using direct separation tests (d‐sep) based on Fisher’s C statistic, with the model being accepted where the associated P > 0.05 (36). We first assessed the fit of our hypothetical causal model before simplifying the model using a backward stepwise selection procedure (37–39). At each step of the backward procedure, the nonsignificant path with the highest P value was dropped from the model and the fit of the resultant reduced model was evaluated using Fisher’s C statistic (a model was accepted if Fisher’s C was nonsignificant; i.e., P > 0.05). The AIC_c value of the resultant reduced model was also stored. This backward process carried on until there were no nonsignificant paths remaining in the model. Finally, the best model was chosen by selecting the model, across all accepted models (i.e., the full model and any of the reduced models with a nonsignificant Fisher’s C statistic), with the lowest AIC_c value (38, 39).

As different archipelagos feature contrasting environmental and biological dynamics (6–8, 11, 13, 20), likely contributing both noise and signal, archipelago identity (i.e., the archipelago name; Dataset S1) was accounted for in the analysis as a random effect within linear mixed models (LMMs) fitted using restricted maximum likelihood (14).

For all endogenous variables (z, logC, Gamma, and AreaScale), both the conditional R²_c (all factors, including the random effect) and marginal R²_m (fixed factors only) were computed following ref. 40. In all best models, the effect of each predictor on the endogenous variables was evaluated through their standardized path coefficients. An overview of the backward procedure for all datasets and the two subsets (oceanic and continental) is provided in SI Appendix, Table S2. Our hypothesized causal models (the full model including all hypothesized paths), as well as our best models, all had satisfactory fits (SI Appendix, Table S2).

The direct and indirect effects of the predictors on z and logC were calculated using the standardized path coefficients (41). For a given predictor A, the strength of its indirect effect on C through B is obtained by multiplying the direct standardized path coefficients of A on B and B on C. The total effect of A on C is then calculated by summing the standardized path coefficient of its direct effect and the sum of its indirect effects (Fig. 2 B and D and SI Appendix, Tables S3 and S4).

Finally, we evaluated the predictive power of the best path models using a repeated k-fold cross-validation approach; this procedure was undertaken separately for the all-ISARs and the two island type subsets (SI Appendix, Materials and Methods). As a further test of the sensitivity of our modeling approach, we also explored an alternative model with several potential interactions involving the variable Taxon as the moderator (SI Appendix, Materials and Methods). All of the analyses were undertaken in R (29). Piecewise SEM models were fitted using the piecewiseSEM package (14). The LMM models were implemented with the nlme R package (42).