Original Article: A Tool for Empirical Equipoise Assessment in Multi-group Comparative Effectiveness Research

Abstract

PURPOSE:

In observational research, equipoise concerns whether groups being compared are similar enough for valid inference. Empirical equipoise was previously proposed as a tool to assess patient similarity based on propensity scores (PS). We extended this work for multi-group observational studies.

METHODS:

We modified the tool to allow for multinomial exposures such that the proposed definition reduces to the original when there are only two groups. We illustrated how the tool can be used as a method to assess study design within three-group clinical examples. We then conducted three-group simulations to assess how the tool performed in a setting with residual confounding after PS weighting.

RESULTS:

In a clinical example based on rheumatoid arthritis, 44.5% of the sample fell within the region of empirical equipoise when considering first-line biologics, whereas 57.7% did so for second-line biologics, consistent with the expectation that a second-line design results in better equipoise. In a simulation where the unmeasured confounder had the same magnitude of association with the treatment as the measured confounders and a 25% greater association with the outcome, the tool crossed the proposed threshold for empirical equipoise at a residual confounding of 20% on the ratio scale. When the unmeasured variable had a twice larger association with treatment, the tool became less sensitive and crossed the threshold at a residual confounding of 30%.

CONCLUSION:

Our proposed tool may be useful in guiding cohort identification in multi-group observational studies, particularly with similar effects of unmeasured and measured covariates on treatment and outcome.

INTRODUCTION

Pharmacoepidemiologists are often concerned with whether the exposure groups in an observational study are similar enough for unbiased causal inference. Lack of similarity can imply dangers of positivity violation¹ and residual confounding from imperfectly measured and unmeasured variables. Statistical analyses alone cannot fully address these issues and design stage efforts², such as the active comparator design^3,4, are necessary. However, no well-accepted measure exists for deciding whether groups are similar enough, particularly in comparisons among three or more treatments.

Walker et al. introduced the concept of empirical equipoise⁵ in the setting of two-group comparative effectiveness research (CER). Empirical equipoise is a manifestation of underlying clinical equipoise⁶: a state of collective uncertainty among medical providers regarding the best treatment option for a specific patient population. In this circumstance, prescriber opinions, rather than patient characteristics, largely determine treatment choices⁵. A treatment assignment mechanism that is mostly independent of patient characteristics results in treatment groups that are similar and overlapping in covariates.

Since clinical equipoise pertains to prescriber opinions, it is not directly measurable in typical CER datasets such as administrative claims. Empirical equipoise is a measure of similarity of the distributions of potential confounders available in CER datasets and can be useful as a study design assessment tool⁷. To our knowledge, no such tool exists for studies with three or more groups even though multi-group CER is increasingly relevant due to the development of many treatment options for rheumatoid arthritis (RA)⁸, diabetes mellitus⁹, and atrial fibrillation¹⁰ to name a few. In this paper, we provide a detailed explanation of Walker et al.’s empirical equipoise tool, propose an extension to the multi-group CER setting, illustrate its face validity in empirical data, and examine its performance in simulations.

METHODS

Empirical equipoise assessment tool

Consider a two-group CER study. Let A_i be an indicator of the binary treatment for the i-th study participant, X_i a vector of potential confounders, and consider the following logistic model for the propensity score (PS), denoted e_i:

$$\text{log}\left(\frac{e_i}{1-e_i}\right)=\text{logit}\left(E[A_i|X_i]\right)={\alpha }_0+X_i^T{\alpha }_X$$

Walker et al. proposed a prevalence-adjusted version of PS, the preference score, denoted π_i defined by:

$$\text{log}\left(\frac{{\pi }_i}{1-{\pi }_i}\right)=\text{log}\left(\frac{e_i}{1-e_i}\right)-\text{log}\left(\frac{p}{1-p}\right)$$

where p is the marginal prevalence of treatment. The second term has the same form as the intercept adjustment for risk prediction from case-control data.^11–13 Given this, the model for the preference score can re-written as:

$$\text{log}\left(\frac{{\pi }_i}{1-{\pi }_i}\right)=\left[{\alpha }_0-\text{log}\left(\frac{p}{1-p}\right)\right]+X_i^T{\alpha }_X$$

Thus, the preference score considers treatment assignment in a hypothetical population with a treatment prevalence of 50% but for which the covariate effect on assignment remains the same as in the study population (eAppendix 1.2). If the covariates have no effect on the treatment assignment (i.e., α_X = 0), the right-hand side reduces to zero, giving a preference score of 0.5 for every individual⁵. Solving the defining equation for the preference score gives:

$${\pi }_i= \frac{\frac{e_i}{p}}{\frac{1-e_i}{1-p}+\frac{e_i}{p}}$$

for which the numerator can be considered as an inverse prevalence scaled PS and the denominator can be seen as a normalizer to constrain π_i within [0,1]. This transformation eliminates the influence of the treatment prevalence. For example, if the treatment is rare (small p), e_i is generally small whereas π_i is not because of the e_i/p operation (small value/small value).

Walker and colleagues proposed an assessment tool based on the proportion of each exposure group that falls within the central region of the preference score distribution [0.3, 0.7] (i.e., 0.5 ± 0.2). Specifically, they proposed that having 50% or more of the subjects in this region indicates that the two drugs are in empirical equipoise.⁵ That is, the measured prognostic factors do not distinguish the users of one drug from the other, suggesting less danger of confounding by indication.

Extension to the multi-group setting

Here we propose an extension of the tool to settings where interest lies in comparing more than two treatments. Specifically, suppose there are J + 1 treatment groups so that A_i is a categorical variable taking on a value in {0, 1, …, J}. The generalized PS¹⁴ is defined as e_ji = P[A_i = j | X_i] for j ∈{0, 1, …, J} where ∑_j e_ji = 1 for all i. One option for modeling the generalized PS is to adopt a baseline-category logit PS model¹⁵, defined by the following J linear predictors:

$$\text{log}\left(\frac{e_{ji}}{e_{0i}}\right)=\text{log}\left(\frac{P[A_i=j|X_i]}{P[A_i=0|X_i]}\right)={\alpha }_{0j}+X_i^T{\alpha }_{Xj}\text{for} j\in \left\{1,\dots ,J\right\}$$

Let p_j (j = 0, …, J) describe the marginal prevalence of j-th treatment (∑_j p_j = 1) and π_ji denote the multinomial preference score defined for the treatment group j for the i-th subject. We propose the generalized preference score, defined by the following J equations:

$$\text{log}\left(\frac{{\pi }_{ji}}{{\pi }_{0i}}\right)=\text{log}\left(\frac{e_{ji}}{e_{0i}}\right)-\text{log}\left(\frac{p_j}{p_0}\right) \text{for} j\in \left\{1,\dots ,J\right\}$$

Solving these equations for π_ji using a constraint ∑_jπ_ji = 1 (eAppendix 2.1) gives:

$${\pi }_{ji}= \frac{\frac{e_{ji}}{p_j}}{{\sum }_{k=0}^J\frac{e_{ki}}{p_k}}\text{for}j\in \left\{0,1,\dots ,J\right\}$$

which can be interpreted as the generalized PS scaled by the corresponding group’s marginal prevalence.

In extending the definition of the region of empirical equipoise, the threshold value needs to account for the number of groups. Thus, we propose the generalized threshold as:

$${\pi }_{ji}\ge \left(\frac{3}{5}\right)\left(\frac{1}{J+1}\right) \text{for}\text{all}j\in \left\{0,1,\dots ,J\right\}$$

The threshold is 0.3 in the two-group setting and becomes more lenient with the number of groups, for example, 0.2 in the three-group setting. This is necessary because once there are four groups, no individual can have π_ji ≥ 0.3 for all four treatments (eAppendix 2.2). We note that an appealing feature of the proposed region is that it reduces to [0.3, 0.7] in the two-group case (eAppendix 2.3).

Data examples in the three-group setting

We use two observational datasets to demonstrate the face validity of the tool. We used ternary plots (eAppendix 3.1).¹⁶ The Partners Healthcare Institutional Review Board approved these analyses.

Non-steroidal anti-inflammatory drugs example

This example was an observational study of non-steroidal anti-inflammatory drugs (NSAIDs) taken from an original study of cardiovascular and gastrointestinal safety of analgesics among Medicare beneficiaries with osteoarthritis or rheumatoid arthritis (eAppendix 3.2).¹⁷ The dataset included 23,532 naproxen, 21,880 ibuprofen, and 5,261 diclofenac users. As they belong to the same pharmacological class, we expected clinical equipoise. In Figure 1 (left panel), closeness to each corner indicates a high propensity for the corresponding group. The prevalence imbalance drove the center of the distribution away from the smallest diclofenac corner (right lower). Preference scores (Figure 1, right panel) re-centered the distribution. Of the entire cohort, 86.6 percent fell within the proposed region of empirical equipoise, suggesting feasibility of the three-way comparison. The individual covariates mostly gave absolute standardized mean distance (SMD) less than 0.1 (eFigure 1).^18,19 Table 1 shows the myocardial infarction outcome analyses. The generalized PS approach, which we advocate in this paper, resulted in transitive results, whereas the pairwise PS approach, which is more commonly done, resulted in non-transitive results.

Figure 1.

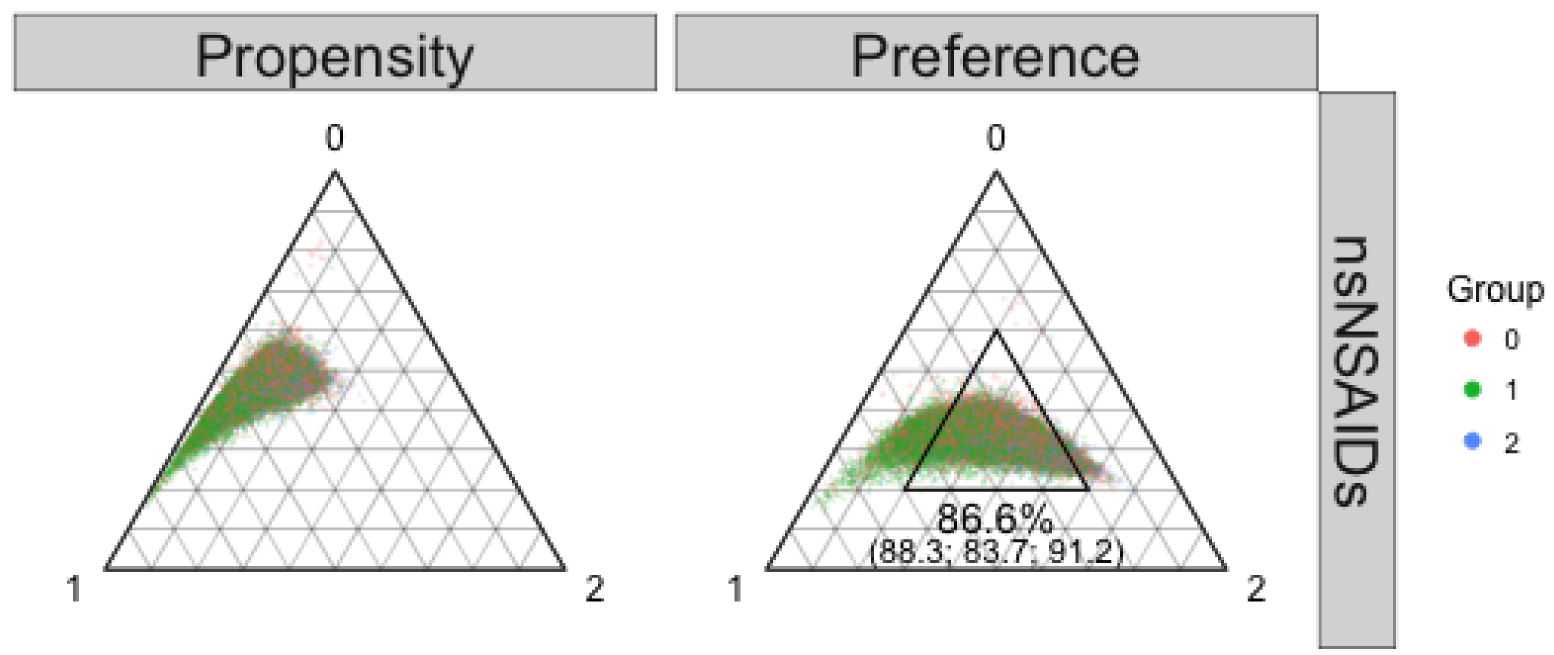
Propensity score (left) and preference score (right) distributions in the naproxen (0 red; n = 23,532), ibuprofen (green 1; n = 21,880), and diclofenac (2 blue; n = 5,261) example.

The inner triangular area in the right panel indicates the region of empirical equipoise proposed in the text. Overall 86.6% of the cohort fell into this region (88.3% of naproxen users, 83.7% of ibuprofen users, and 91.2% of diclofenac users).

Abbreviations: nsNSAIDs: non-selective non-steroidal anti-inflammatory drugs.

Table 1.

Hazard ratios and 95% confidence intervals for myocardial infarctions for the non-steroidal anti-inflammatory drugs example.

PS	Adjustment	Diclofenac vs Naproxen	Ibuprofen vs Naproxen	Diclofenac vs Ibuprofen†	Expected for third contrast‡
-	Unadjusted	0.899 [0.635, 1.274]	1.022 [0.833, 1.253]	0.880 [0.620, 1.248]	0.880
Multi	IPTW	0.901 [0.626, 1.295]	0.940 [0.765, 1.155]	0.958 [0.665, 1.380]	0.958
Multi	MW	0.886 [0.623, 1.260]	0.877 [0.700, 1.099]	1.010 [0.705, 1.447]	1.010
Multi	OW	0.904 [0.636, 1.286]	0.899 [0.724, 1.115]	1.006 [0.704, 1.439]	1.006
Pair	IPTW	0.906 [0.634, 1.294]	0.947 [0.771, 1.164]	0.943 [0.652, 1.363]	0.957
Pair	MW	0.883 [0.621, 1.256]	0.944 [0.767, 1.160]	1.010 [0.705, 1.446]	0.936§
Pair	OW	0.894 [0.629, 1.271]	0.946 [0.770, 1.163]	1.006 [0.704, 1.438]	0.945§

Abbreviations: PS: propensity score; Multi: multinomial generalized propensity score; IPTW: inverse probability of treatment weights; MW: matching weights; OW: overlap weights; Pair: pairwise propensity score.

^†Direct comparison results for diclofenac vs ibuprofen.

^‡Indirect comparison results for diclofenac vs ibuprofen based on the first two contrast. That is, (hazard ratio for diclofenac vs naproxen) / (hazard ratio for ibuprofen vs naproxen).

^§Non-transitive results for the third contrast. The direct comparison estimates and the indirect comparison estimates are on the opposite side of 1.0 although the difference is small.

Biological disease-modifying anti-rheumatic drugs example

This example was an observational dataset of new users of biological disease-modifying anti-rheumatic drugs (bDMARDs) taken from original studies of cardiovascular safety among rheumatoid arthritis patients (eAppendix 3.3)^20,21. We constructed a first-line bDMARDs cohort and a second-line (switch) bDMARDs cohort after prior use of one of the five tumor necrosis factor inhibitors (TNFi). The most up-to-date recommendations list all bDMARDs as equally indicated,^8,22 however, abatacept and tocilizumab were more typically employed after TNFi failure. Thus, we reasoned that first-line abatacept and tocilizumab users would be somewhat atypical patients.²³ Thus, we expected better equipoise in the second-line design (eAppendix 3.3). We used this example to assess if the tool correctly identified the second-line design as superior. In the first-line cohort, there were 2,260 abatacept, 645 tocilizumab, and 27,939 TNFi users. The second-line cohort had 475 abatacept, 187 tocilizumab, and 1,277 second TNFi users (switch within TNFi). Only 44.5% of the first-line cohort fell in the proposed region of empirical equipoise (Figure 2, right upper panel), indicating a need to revise eligibility, for example, regarding comorbidities and prior drug use. Using the second-line design (Figure 2, right lower panel) resulted in improvement with a higher proportion of the cohort (57.7%) falling in the proposed region of empirical equipoise although the second-line design did modify the clinical question. Absolute SMDs generally decreased, particularly for relevant risk factors such as oral glucocorticoids (eFigure 2). We could not pursue outcome analyses due to insufficient numbers of cardiovascular outcome events.

Figure 2.

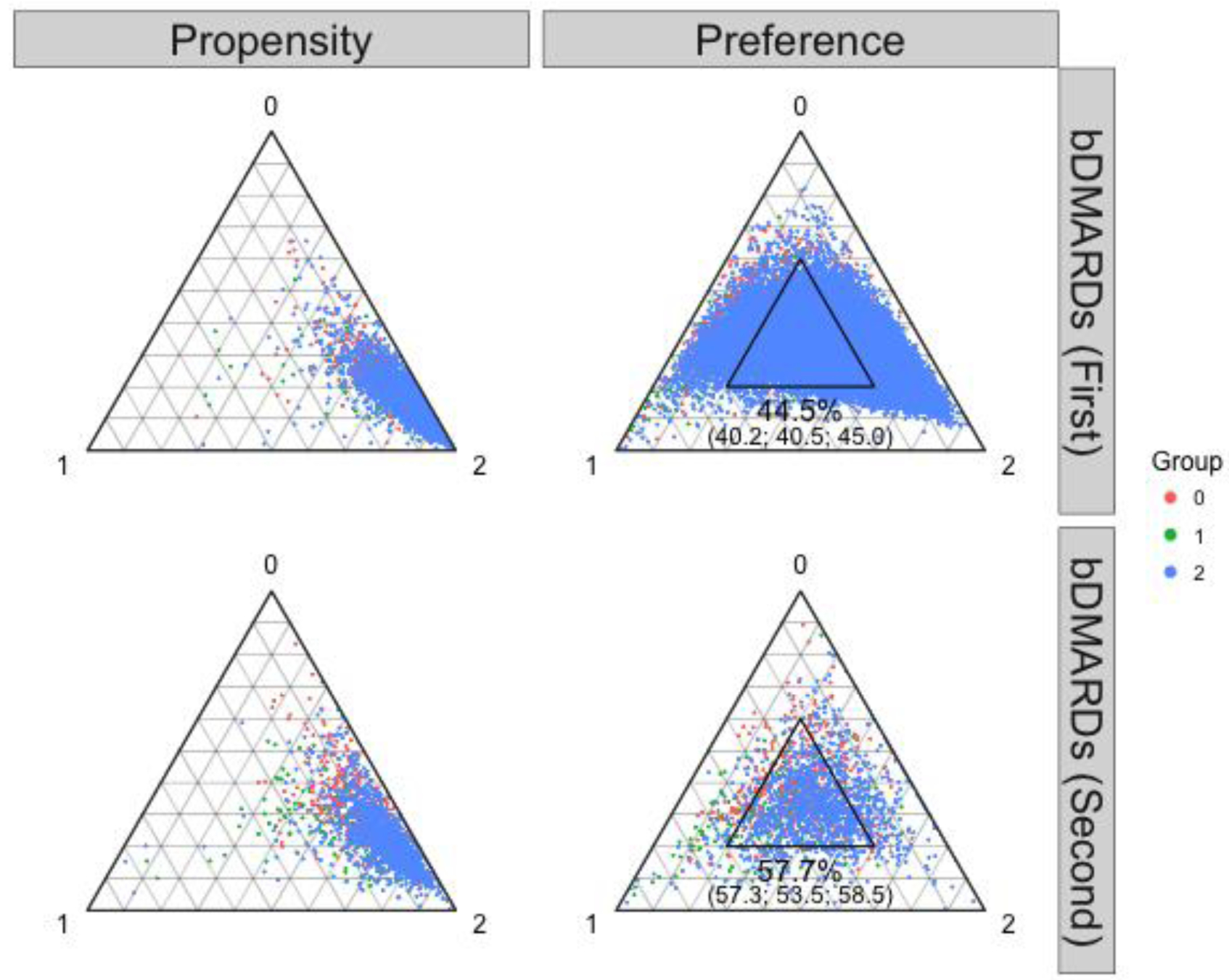
Propensity score (left) and preference score (right) distributions in the abatacept (0 red), tocilizumab (1 green), and TNFi (2 blue) examples.

The inner triangular area in the right panel indicates the region of empirical equipoise proposed in the text. Among the first-line bDMARD users, 44.5% of the cohort fell into this region (40.2% of abatacept users, 40.5% of tocilizumab users, and 45.0% of TNFi users). Among the second-line bDMARD users, 57.7% of the cohort fell into this region (57.3% of abatacept users, 53.5% of tocilizumab users, and 58.5% of TNFi users).

Abbreviations: TNFi (tumor necrosis factor inhibitor); bDMARD: biological disease-modifying antirheumatic drug.

Simulation setup

We conducted a simulation study to examine the settings under which the proposed tool reflected the risk of residual confounding (R code at [to be posted at the time of publication]).

Data generating mechanism.

Details regarding the data generating models are provided in the eAppendix 4.1. Briefly, we generated covariates X₁ through X₇ of various types and used them to assign treatment A_i via a three-group multinomial logistic regression model. The coefficient for X₇ took on values zero, half, same, or twice as large as the coefficients for X₁- X₆. The coefficients were then simultaneously increased (less equipoise) or decreased (more equipoise). The outcome Y_i was generated as a count outcome using a log-linear model. The rate ratio (RR) for X₇ was 1.2 (same as other covariates), 1.5, or 2.0. We handled X₇ as an unmeasured continuous variable in the subsequent analysis.

Methods to be evaluated.

The region of empirical equipoise was defined at the threshold of 0.2 as stated above. We examined two assessment rules of three-group empirical equipoise: (1) whether the proportion of those who were in the region of empirical equipoise in the entire sample was greater than 50% (overall proportion); (2) whether the minimum of three group-specific proportions was greater than 50% (group-specific proportion).

Estimands of interest.

The estimands were the RRs for groups 1 vs. 0, groups 2 vs. 0, and groups 2 vs. 1. We conducted unadjusted analysis as well as three PS-weighted analyses with inverse probability of treatment weights (IPTW)²⁴, matching weights (MW)^25,26, and overlap weights (OW)^27–29. See eAppendix 4.2 for weight definitions.

Performance measures.

We examined the relationship between the residual confounding after PS weighting and the proportions in the region of empirical equipoise. The desired result was a decreasing trend in the proportions in the region with increasing residual confounding.

RESULTS

Figures 3 and eAppendix 5.1 summarize the results from scenarios with no correlation among covariates (ρ = 0) and approximately equal group sizes (33:33:33). The columns of panels correspond to PS weighting methods. The rows of panels correspond to the RR for the unmeasured X₇. Focusing on the panel in the MW column and RR 1.5 row (third column, second row) in Figure 3, the X-axis represents the multiplicative bias in RR estimates, whereas the Y-axis represents the average proportion of the simulated cohorts within the region of empirical equipoise (overall proportion).

Figure 3.

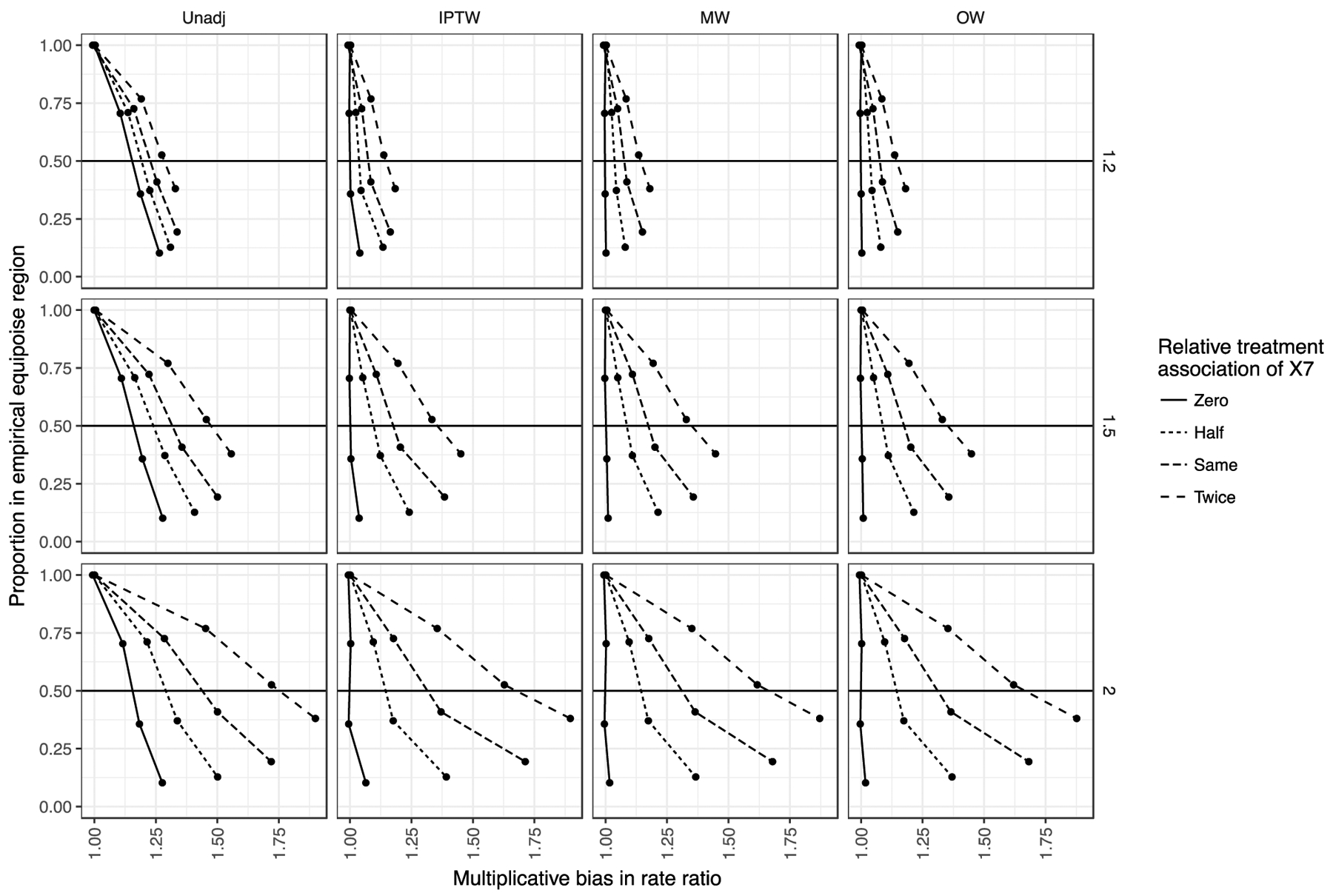
Simulation results from scenarios with equal group sizes (1 vs 0 contrast).

The columns of panels denote different confounding adjustment methods. The rows of panels denote different levels of associations between X₇ (unmeasured covariate) and outcome. A rate ratio of 1.2 was the same strength of association as the measured covariates, whereas only X₇ had a stronger outcome association at a rate ratio of 1.5 and 2.0. In each panel, the X-axis represents the multiplicative bias in RR estimates, whereas the Y-axis represents the average proportion of the simulated cohorts within the region of empirical equipoise (overall proportion). The line types denote different levels of associations between X₇ and treatment relative to the associations between measured variables and treatment.

Abbreviations: Unadj.: unadjusted; IPTW: inverse probability of treatment weights; MW: matching weights; OW: overlap weights.

The relationship between the residual confounding after PS weighting and the overall proportion varied with the relative strength of association of X₇ with the treatment (denoted by line types). Given an unmeasured confounder with a similar association with treatment (Same line type), having an overall proportion of 50% in the region of empirical equipoise (crossing of the horizontal 50% line) corresponded to residual confounding of roughly 1.2 (20% upward bias in RR estimates). This indicates in a setting where the unmeasured factor’s treatment association is similar to those of measured factors and the outcome association is only modestly stronger (+25%), the empirical equipoise tool would give an alert (overall proportion would drop below 50%) once the residual confounding is greater than 20%. A proportion above 50% means less bias.

Still focusing on the same panel in Figure 3, the level of residual confounding at which the empirical equipoise tool gave an alert depended on the associations of X₇ with the treatment and outcome. On the other hand, the type of PS weights (IPTW, MW, and OW) made little difference. When the relative treatment association of X₇ was decreased to the lower extreme end (no unmeasured confounding; solid line), the tool became overly sensitive. That is, the 50% threshold was crossed without a corresponding increase in residual confounding. On the other hand, as we increased the association of the unmeasured variable X₇ and the treatment to twice as large as the measured ones, the slopes became shallower. This means the tool became less sensitive to residual confounding, only crossing the 50% overall proportion threshold at a residual confounding level of about 1.37. That is, the unmeasured variable increasingly had a stronger effect on treatment not represented by the association between measured variables and treatment.

We also varied the level of unmeasured confounding by changing the RR between the unmeasured variable X₇ and the outcome (rows of panels; RR 1.2, 1.5, and 2.0). For example, decreasing the unmeasured variable-outcome association to the same level as the other variables (third column, top row in Figure 3) resulted in the tool giving an alert at a residual confounding of roughly 1.1 (more sensitive) when X₇ had the same treatment association. When increasing the RR between the unmeasured variable X₇ and the outcome to 2.0 (67% increase over measured variables), the tool gave an alert at a residual confounding of around 1.3 (less sensitive). When both associations were strong for the unmeasured variable X₇, the 50% overall proportion threshold was crossed at a residual confounding of around 1.6. This means having barely 50% of the cohort in this region does not assure a small level of unmeasured confounding in this setting.

DISCUSSION

We extended Walker et al.’s tool⁵ for assessing simultaneous empirical equipoise among multiple treatment groups in CER. We demonstrated its face validity in empirical data and examined its performance in simulations with three groups. Our simulations showed that having at least 50% of the overall cohort in the region of empirical equipoise can give a reasonable assurance of relatively small magnitude of residual bias. However, in settings with a strong unmeasured variable (outcome association RR of 2.0) and a strong influence of the unmeasured variable on treatment choice (twice more on the logit scale), a relatively large residual bias went undetected by the 50% threshold. As a result, the tool was most useful when we could assume the unmeasured confounder had covariate-treatment associations similar in magnitude to the measured confounders.

There are several ways this empirical equipoise assessment tool could be useful in the implementation of multi-group CER. First, when several datasets are available for a specific multi-group CER question, the tool could indicate which dataset may suffer less from residual confounding as well as positivity issue. Second, when dealing with one dataset, the tool may help in choosing eligibility criteria although sample size issues may need to be taken into consideration. Thirdly, another potential change in the study design is to refrain from conducting all comparison if the groups do not achieve reasonable simultaneous empirical equipoise (e.g., if key covariates are highly imbalanced in one group but not in the others). In this case, dropping one or more groups from the comparison may identify a subset of groups in better equipoise.

Our tool is designed to assess feasibility⁷ of simultaneous multi-group comparison in a single outcome analysis dataset, which attempts to emulate³⁰ one multi-arm RCT. However, when there are three or more groups, pairwise PS-matched or PS-weighted cohort construction is common. A drawback of the pairwise approach is that it produces multiple outcome analysis datasets, one for each pairwise comparison, attempting to emulate separate pairwise RCTs. The pairwise approach can suffer from non-transitivity.³¹ This loosely used term can be understood by considering actual RCTs. Network meta-analysis (NMA)^32,33 is another CER approach given multiple treatments of interest, which combines information from several, typically pairwise, RCTs to form indirect comparisons of drugs that have not been compared in head-to-head RCTs. When such a pairwise RCT does exist (direct comparison), non-transitivity can manifest.³³ Assume drugs A, B, and C and respective pairwise RCTs, we can derive indirect comparison of A-B based on RCT A-C and RCT B-C (for example, A>B), which may qualitatively contradict direct comparison in RCT A-B (for example, A<B). Even though each pairwise RCT should have near-perfect covariate balance, differential distributions of treatment effect modifiers across pairwise RCT (different target populations) can cause non-transitivity.³⁴ The fundamental issue is the lack of an A-B-C multi-group trial in a single target population, which necessitated NMA. The generalized PS approach attempts to emulate this type of trial. In our NSAIDs example (Table 1 last row), we had a pairwise hazard ratio (HR) of 0.894 for the diclofenac-naproxen comparison, 0.946 for the ibuprofen-naproxen comparison. The indirect comparison for the third contrast (diclofenac-ibuprofen) is 0.894 / 0.946 = 0.945, a protective HR estimate. However, the direct pairwise analysis gave an HR of 1.006, a result on the opposite side of 1.0 (more formally the margin of error needs consideration³⁵). Simultaneous empirical equipoise assessment followed by construction of a single PS weighted cohort avoided this issue as seen in Table 1.

There are differences between the context in which Walker et al. developed the original empirical equipoise tool⁵ and the context for our proposed tool. We considered the drugs of interest that we want to compare in the proposed multi-group CER as given. Walker et al. proposed the tool as a prioritization tool given a source dataset that contains information on the use of many drugs. They developed their tool to assess the empirical equipoise of all possible pairwise contrasts of groups for prioritization. On the other hand, we framed our problem in a setting where we already had several drugs of interest a priori, with several alternative data sources or alternative designs to choose from.

One further point to consider in implementation is what variables we should include in the PS model for preference score construction. The tool’s usefulness rests on the assumption that the presence of strong measured clinical determinants of treatments (e.g., past medications) can inform the presence of strong unmeasured clinical determinants of treatments (e.g., physical frailty). If prescribers are sensitive to measured clinical factors in treatment choice, it is not unreasonable to assume they are also sensitive to an important unmeasured clinical factor. On the other hand, we can reason that how prescribers are influenced by administrative factors (e.g., formulary restrictions) is less representable of how they take into account clinical factors in choosing treatment. As a result, it is more prudent to include clinical factors into the PS model and to exclude purely administrative factors.

In conclusion, to examine the roles that equipoise assessment may play in the setting of multi-group CER, we extended Walker et al.’s empirical equipoise tool. Our tool gave reasonable guidance for unmeasured confounding when the associations of the unmeasured variables to the treatment and outcome were similar to associations of measured covariates. With this assumption, when the proportion in the region of empirical equipoise is very high, for example, > 75%, we can reasonably assume that the level of residual confounding is small. A lower value, particularly < 50%, should prompt reconsideration of the study design or data source.

KEY POINTS:

• We extended Walker et al.’s empirical equipoise tool (Comp Eff Res 2013;3:11) into the general multi-group settings.

• We verified a known improvement in the study design with three groups resulted in a corresponding improvement in multi-group empirical equipoise.

• Three-group simulations indicated that the tool was useful in signaling potential for residual confounding when the unmeasured variable had coefficients similar to measured variables.

• In practice, a high (e.g., > 75%) proportion of the multi-group cohort in the region of empirical equipoise likely indicates less risk of residual confounding in simultaneous comparison.

• A lower proportion, particularly < 50%, should prompt a reassessment and revision of the multi-group study design, including eligibility criteria, data source, and whether to drop one or more groups.