A Guide to Representational Similarity Analysis for Social Neuroscience

Abstract

Representational similarity analysis (RSA) is a computational technique that uses pairwise comparisons of stimuli to reveal their representation in higher-order space. In the context of neuroimaging, mass-univariate analyses and other multivariate analyses can provide information on what and where information is represented but have limitations in their ability to address how information is represented. Social neuroscience is a field that can particularly benefit from incorporating RSA techniques to explore hypotheses regarding the representation of multidimensional data, how representations can predict behavior, how representations differ between groups and how multimodal data can be compared to inform theories. The goal of this paper is to provide a practical as well as theoretical guide to implementing RSA in social neuroscience studies.

Introduction

Neuroimaging has allowed social neuroscientists unprecedented access to the neurobiological basis of social behavior. For many years, the neuroimaging literature in social neuroscience was dominated by studies using mass-univariate statistical techniques. After some time, this was partially supplanted by multivariate techniques, one of which is the focus of this paper: representational similarity analysis (RSA). Although RSA is over a decade old, its adoption in social neuroscience has been limited. The goal of this paper is to provide an easy guide to RSA with an emphasis on how it can be used in social neuroscience to test hypotheses and inform theory.

It is already known that mass-univariate neuroimaging techniques are limited in their ability to analyze multidimensional information. Mass-univariate methods in functional magnetic resonance imaging (fMRI) are typically used to compare the neural activation of one group of stimuli to the neural activation of another group of stimuli, by creating a contrast that averages the response of stimuli within a group. For example, if one wants to study the neural representation of social status, the mass-univariate contrast will show us regions of the brain that respond more strongly to high social status by subtracting the neural activation for low status faces from the activation for high status faces (Chiao et al., 2009). However, this only tells us a little bit about the neural processing of social status, as relying on an overall response magnitude across voxels in a region provides limited information. A brain region may have a minimal overall, but consistent, response to low status faces, that is overshadowed by a much larger overall response to high status faces (Haxby, 2012). We are unable to determine, for instance, if brain regions that respond more strongly for one category might also have some sensitivity to information from another category (Haxby, 2012). We also do not know if regions represent information about both categories, but in different ways, that the task did not account for (e.g. attention, motivation). In addition, some functionally heterogeneous areas can be commonly activated by multiple tasks and we cannot determine whether the activated brain region is specialized for information integration (e.g. for instance, the anterior temporal lobe [ATL] appears to integrate social, semantic and emotional processing; Olson et al., 2007), whether it represents the same information but along different dimensional spaces (e.g. self-relatedness and positivity are co-represented in medial prefrontal cortex [MPFC]; Chavez et al., 2017) or perhaps there is just a lack of spatial resolution to disentangle specialized sub-neural clusters (e.g. social and physical pain are represented next to each other but separately in anterior cingulate cortex [ACC]; Woo et al., 2014). Lastly, when multiple neural regions respond to the same category, we cannot differentiate the functional specificity of these regions. With univariate approaches, there is no information about what is specifically represented in the activated regions or how information is architecturally represented, and this is partially due to the loss of information caused by signal averaging across many voxels (Norman et al., 2006).

To address some of these limitations, multivariate analyses have been introduced (Haxby et al., 2001; Lewis-Peacock and Norman, 2014). Multivariate pattern analysis (MVPA) focuses on whether information relating to specific stimuli is encoded in patterns of activity across multiple voxels. It does not average signals but rather jointly analyzes multi-voxel data to predict or characterize states of the brain (Haxby et al., 2001; Lewis-Peacock and Norman, 2014). In a typical implementation of MVPA classification, a linear or non-linear classifier is trained to distinguish stimuli for different categories within a subset of the data. The trained model is then tested by using it to predict the categories of the remaining (independent) data. If a stimulus can be predicted, or decoded, solely from the pattern of fMRI activity, there must be some information about that stimulus represented in the brain region where the pattern was identified (Chadwick et al., 2012). Accordingly, MVPA goes beyond the simple task/state level of inference that mass-univariate analysis usually draws about a brain region (e.g. ATL plays some role in identifying people as compared to objects) while also boosting the sensitivity to reveal a region’s representational content (e.g. the ATL represents individual person identity; Wang et al., 2017).

Although MVPA classification is a powerful decoding tool that allows us to infer whether category-level representation occurs in a region, it is relatively agnostic about what the specific information is and in what format that information is organized. There are many aspects of the stimuli or the behaviors (e.g. attentional differences or low-level visual feature differences) that can cause a brain region to successfully classify different categories, and MVPA classification has limited power for disentangling these differences. A confusion matrix analysis can be generated to determine if a classifier for a brain region responds similarly to different categories, leading to an indirect measure of the geometry of the representation of the categories (Liang et al., 2013). However, this approach is still limited by the constraints of classification, in that it requires many repetitions of trials to train the classifier. In addition, statistical inference on MVPA classification is prone to false positives when the number of categories is high but the sample size is low (Combrisson and Jerbi, 2015; Jamalabadi et al., 2016). Moreover, neural representations of the social world often entail a continuous dimension of information (e.g. mental states or subjective feeling; Nummenmaa et al., 2018; Tamir et al., 2016) and a large number of features, such as body parts (Bracci et al., 2015), stereotype knowledge (Stolier and Freeman, 2016) or action perception (Urgen et al., 2019; Wurm et al., 2017). MVPA classification can examine these characteristics in a coarse and complicated way (e.g. via confusion matrix analysis), but stimuli must be categorized in an unnatural way and the individual differences between every stimulus are typically lost. This loss of within-category features limits the number of features or conditions that can be representationally explored, to only the between-category features. Regression-based MVPA decoding analyses alleviate some of these issues, such as being able to explore the dimensional representation of information. However, these techniques still require a large number of trials and these techniques are not sensitive to the representation of information along a multi-dimensional space. Thus, the family of MVPA decoding analyses, including classification and regression, lacks the ability to explore the entire representational space between stimuli (Diedrichsen and Kriegeskorte, 2017).

Another type of multivariate method—RSA—lends itself to looking at higher-order representational space as well as testing different computational models of cognition (Haxby et al., 2014; Kriegeskorte et al., 2008a). In RSA, the multivoxel pattern responses of stimuli, derived from the same method as classification-based MVPA, are compared to each other, providing a direct higher-order representation of the stimuli. In our example, RSA can be used to compare status representations across multiple dimensions (e.g. economic status vs career status vs reputational status vs body-gesture status vs face-based status; Koski et al., 2017). From this perspective, mass-univariate analyses provide the first step to understanding the underlying architecture involved in cognitive processes by showing which areas ramp up in activity, while MVPA decoding can provide more detail about which areas contribute to a process and some information on how areas can distinguish information. RSA goes further than both by providing information about how regions of the brain represent information, by directly comparing individual responses to get a complete picture of the structure of representation of information across some higher-order dimension space, hereby referred to as the geometric representation of information. Different from MVPA confusion matrix analysis, RSA uses distance measures instead of a classifier to characterize the representational space in brain regions and has the potential benefit of revealing the representation of individual stimuli and not just categories of stimuli. With this full representation via RSA, all features of stimuli can be characterized, whereas MVPA decoding only reveals a subset of features (Diedrichsen and Kriegeskorte, 2017). Ultimately, the comparison between MVPA decoding and RSA traces to the discussion benefits and limitations of decoding vs encoding models (Kriegeskorte and Douglas, 2019). A comparison between mass-univariate analyses, MVPA decoding analyses and RSA can be found in Table 1.

Table 1. Comparison between different fMRI analytic approaches.

	Mass-Univariate	MVPA Decoding	RSA
Granularity of representational inference	Task/state level of information	Category and item level of information	Item level of information
Handling multivoxel data	Averaged across voxels	Jointly analyze across voxels	No requirement
Inferred format of representation	Discrete categories	Classification for discrete categories, regression for continuous dimensions	Discrete categories and continuous dimensions
Implementation	Contrast subtraction	Train-test learning phase	Representational dissimilarity matrix
Algorithm	Linear	Both linear and non-linear classifier	Mostly linear
Data modelling in GLM	Single-category modelling and aggregated across runs	Single-category modelling and then cross-validate across runs	Single-trial modelling, within- or between-runs
Optimal study design	Factorial design	Only few numbers of stimulus categories (<5), each with many repetitions for train-test learning	No limits on number of categories, stimuli with many features
Testing computational models	Easy (but univariate encoding models have to fit a model first using separate data)	Difficult (due to its decoding nature)	Easy (due to its encoding nature)
Linking multimodal data	Difficult	Difficult	Easy

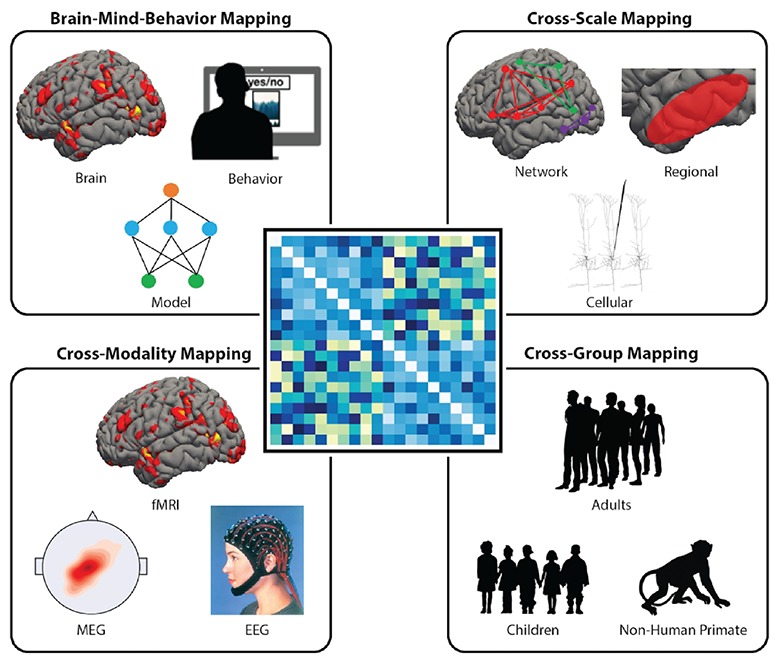
A unique feature of RSA is its ability to compare data from different sources (see Figure 1). For instance, RSA can be used to compare data from behavioral measures related to social scenes (e.g. ratings, reaction times, error rates or latent semantic analysis indices) and data from neural activations in response to the same stimuli. Indeed, this comparison can even be done for data from different spatial scales (e.g. single-neuronal recording vs regional activation) and data from different species (monkey vs human) (Kriegeskorte et al., 2008b). When linked to computational models, RSA can study not only the fine-grained representations of social information but also explore the dynamic neural computations that undergird social processing (e.g. bottom-up vs top-down processes; Brooks and Freeman, 2018). RSA is best applied to stimuli or states that can be systematically ‘dimensionalized’. In vision research, stimulus dimensions such as hue, luminance and line orientation can be parametrically manipulated and the representational sensitivity of visual cortex measured. In social neuroscience, many stimuli can also be dimensionalized, for instance faces can vary on several dimensions (e.g. attractiveness, age, gender and trustworthiness; Dobs et al., 2019; Freeman et al., 2018; Stolier and Freeman, 2016; Stolier et al., 2018b), actions can vary on kinematics, effectors, transitivity and intentions (Urgen et al., 2019; Wurm et al., 2017), social concepts can vary on affective and psycholinguistic dimensions (Thornton and Tamir, 2017) and friendships can vary in their social distance and network topology (Parkinson et al., 2014; Parkinson et al., 2017). With this new tool, researchers can even investigate complex representations such as morality (Pegado et al., 2018a; Pegado et al., 2018b; van Baar et al., 2019; Volz et al., 2017; Wasserman et al., 2017) and the development of object concepts (Long et al., 2018).

Figure 1. RSA combines data from different sources by using a common representational space. RSA is unique in its ability to incorporate data from a variety of sources. By using a common stimulus set, RDMs can be created from different sources, such as brain data, cognitive models and behavioral data, to analyze the common representational mapping. Other examples of social neuroscience uses for RSA include combining fMRI, MEG and EEG data to do cross-modality mapping, network, regional and cellular data to explore cross-scale mapping and data from different populations or species to explore cross-individual and species mapping of representations.

Nuts and bolts: how to do RSA

RSA allows us to explore the underlying representational content of brain regions by comparing the neural response pattern (with an emphasis on ‘pattern’) across different stimuli. The basis of RSA is the representational dissimilarity matrices (RDMs), which can be created from any type of data one might have: neuroimaging data, behavioral data or even computational data. This is an important benefit for analytic flexibility, and RSA should not be considered an exclusive fMRI technique. There are already multiple RSA studies in social neuroscience that do not use fMRI data at all (see Brooks and Freeman, 2018; Costa et al., 2014; Dobs et al., 2019; Stolier et al., 2018b; Thornton and Tamir, 2017). Once RDMs are compared across different sources, RSA has the greatest power to link representational information between brain data, behavioral data and computational data (see Figure 1). The analytic pipeline for RSA is actually quite simple, as outlined in the following paragraphs.

Step 1. Optimize your study design

RSA can be easily implemented in both block and event-related fMRI tasks (Mur et al., 2009). However, special attention needs to be given to the spacing of individual trials because the unit of measure for each type of RDM is an individual stimulus. This makes RSA unique among neuroimaging methods because typically in neuroimaging, we group the signals from similar stimuli to create a contrast.

In fMRI, trials that are closer together will have more correlated signal because of the lag of the hemodynamic response. To fully capitalize benefits of RSA and effectively compare individual trials, it has been suggested that within-run trials should be randomized between all subjects or if randomization is not possible, only between-run trials should be compared (Mumford et al., 2014). Since we are modeling each trial in isolation, we have to space trials further apart (a jittered design will not help) and include more trials per run to increase power (Dimsdale-Zucker and Ranganath, 2019).

Typically, RSA does not require as many trial repetitions as MVPA decoding, because RSA does not require machine learning algorithms. In other words, you don’t need to do training then testing. It is important to note that all possible stimuli within a domain of interest should be included so that the representational space is completely explored. For example, neuroimaging research on semantic memory research has traditionally omitted social and abstract words from the stimuli corpus, which leads to findings that fail to include the entire representational space, and also fails to reveal the roles of social brain regions in semantic representation and processing (Leshinskaya et al., 2017; Olson et al., 2007; Troche et al., 2014). Other suggestions for optimizing RSA experimental design (e.g. preprocessing, noise reduction, unequal trial numbers between conditions) can be found in detail elsewhere (Dimsdale-Zucker and Ranganath, 2019).

Step 2. Construct RDMs

To construct an RDM, all stimuli are compared to each other, resulting in a matrix that is symmetrical along its diagonal. Stimuli can be compared by calculating the similarity or dissimilarity between stimuli (Kriegeskorte et al., 2008a). Using a measure of similarity (e.g. Pearson’s r) vs a measure of dissimilarity (1—Pearson’s r) when constructing RDMs does not have a statistical impact on results, but a dissimilarity measure seems to be favorable because it is commonly used in other techniques (e.g. multidimensional scaling, latent semantic analysis) and has advantages for conceptually understanding the results. Dissimilarity is accompanied by an intuitive organization of stimuli in space where more dissimilar stimuli are further apart and thus can be mapped out in a network-style visualization (Haxby et al., 2014; Kriegeskorte et al., 2008a).

It is also important to consider which similarity/dissimilarity measure should be used for your type of data. For fMRI data, it is common to use a similarity measure, such as Pearson or Spearman correlation, to compare the neural response to two stimuli classes since these metrics are magnitude-insensitive (e.g. the magnitude of BOLD signals varies across brain regions). For behavioral data where measures are not directly compared, such as when all stimuli are rated on a scale, a dissimilarity measure, such as Euclidean distance, might be more suitable. The reliability of Pearson correlations and Euclidean and Mahalanobis distance metrics have been compared and found to be not only reliable among each other but also more reliable than MVPA classification (Walther et al., 2016). When choosing a similarity/dissimilarity measure, it is important to choose a measure that is specifically appropriate to the original data. For example, it has been recommended that Euclidean distance would ‘not’ be appropriate for finding the dissimilarity of data that is binary. Manhattan distance should be used instead (Nguyen and Holmes, 2019). Regardless of which similarity/dissimilarity measure is used, all RDMs are recommended to be cross-validated as noise in the dataset can make stimuli more dissimilar than they are in reality (Walther et al., 2016).

For neural RDMs, the response pattern from a single region of interest (ROI) is used as the response to correlate between stimuli. In fMRI, this would be the multi-voxel activation pattern that is also used in MVPA decoding. The response pattern from one stimulus is correlated to another, resulting in an r-value. Dissimilarity between stimuli is calculated as r subtracted from 1 (Figure 2A). For example, the dissimilarity between a stimulus and itself would be 0, as the correlation between the two stimuli would be 1. To make this concrete, the dissimilarity between two social stimuli should be lower than the dissimilarity between a social and non-social stimulus, in a brain region that makes this distinction. A matrix is then created where each row depicts a vector of the neural response comparisons of one stimulus to all stimuli, including itself. The matrix is an RDM representing the dissimilarity between all stimulus neural responses. To increase power, trials are often repeated and averaged together. Trials can also be grouped together based on categories of interest, similar to designs used for mass-univariate analyses or MVPA classification; however, this is not necessary. RSA has an advantage over other techniques in that it allows for stimuli to remain ungrouped so that the underlying representational geometry of the stimuli can be explicitly explored (e.g. mental states; Tamir et al., 2016). These steps to create a neural RDM can be repeated for all subjects, and the subject-level RDMs can be averaged together to create a group-level RDM. Alternatively, RDMs can be compared on an individual subject level; for example, a subject’s neural RDM to their behavioral RDM of their ratings from a task.

Figure 2. Construction of RDMs. (A) An RDM is constructed from neural data by extracting the multi-voxel pattern response from a ROI, from a single participant, for each individual stimulus. The dissimilarity, or 1 minus the correlation coefficient, is found between all possible stimuli comparison pairs, to create a dissimilarity matrix. (B) An RDM is constructed from behavioral data by collecting the response from a participant for each individual stimulus. The dissimilarity between all individual stimuli pairs is found using a distance measure calculation, such as the Euclidean distance. (C) A conceptual model RDM is constructed by pinpointing a feature of interest from the stimulus set. The dissimilarity matrix represents which stimuli share the common feature and which do not. (D) In the final step of the analysis, the bRDM and two mRDMs are compared to the nRDM. A noise ceiling (the gray horizontal bar) is calculated to see how well a perfect model would perform. Significance tests show that the bRDM and the mRDM1 are significantly similar to the nRDM. A pairwise comparison shows that the bRDM performs significantly better than the mRDM1 and mRDM2, in terms of relating to the nRDM.

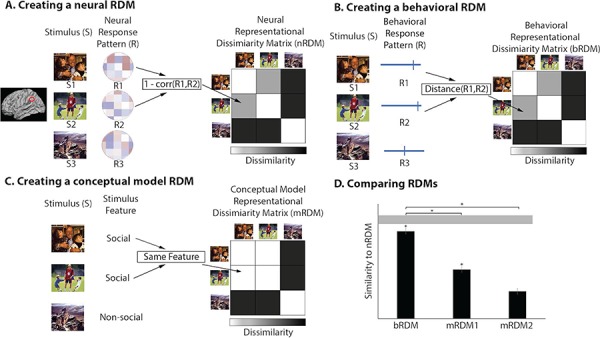
For behavioral RDMs, the ratings or measures between pairs of stimuli are compared to create an RDM. Comparisons between two different behavioral ratings in a task, for instance, valence or arousal, can be calculated using measures of distance, such as Euclidean distance (Freeman et al., 2018; Kragel and LaBar, 2016). The RDM is created in the same manner as a neural DMN, resulting in a matrix that is also symmetrical about its diagonal and has the same number of rows and columns, as the same stimuli must be used in both tasks (Figure 2B).

Model RDMs can be used in a few ways depending on the researcher’s needs. There are two styles of models. One type, called a ‘conceptual model’, can be used by creating a matrix based on a presumed relationship between the stimuli (Kriegeskorte et al., 2008a). A conceptual model RDM highlights the difference between stimuli along a feature of interest. The dimensions and stimulus order of a conceptual model RDM matches the other RDMs that will be compared with the model. In an example where there are two categories of interest, the values of the conceptual model RDM will be ‘0’ for stimuli that are of the same category or share a similar feature of interest, for instance animate objects, and ‘1’ for stimuli that are not of the same category or do not share a similar feature of interest, for instance, animate objects and inanimate objects (Figure 2C). This is similar to creating a contrast in a mass-univariate analysis; however, the difference is that in RSA betas from individual stimuli are first compared to each other, rather than grouped and averaged together. Conceptual RDMs can also be created to account for multiple categories or features, based on some hypothesized relationship between stimuli, such as faces, non-face animate objects and inanimate objects. In this example, faces and non-face animate objects will be ‘1’, as they differ on only one category (face vs non-face), and faces and inanimate objects will be ‘2’, as they differ on two categories (face vs non-face and animate vs inanimate). The second type of model is called a ‘computational model’ where values of an RDM are outputs of some function or algorithm. For example, a computational model that mimics the processing of V1 in humans can be fed images and a computational RDM can be produced (Nili et al., 2014). This has been done for different types of stimuli including luminance patterns of images (Cichy et al., 2016; Kriegeskorte et al., 2008), semantic features of words (Carota et al., 2017; Chen et al., 2016) and motion trajectory patterns of action videos (Urgen et al., 2019).

Step 3. Compare the RDMs

A single RDM can be used to complete an analysis, but the greatest advantage of RSA is the ability to compare RDMs, hence the word ‘similarity’ in RSA. RDMs can be compared in a variety of iterations depending on the researcher’s questions and hypotheses. In a simple example, a neural RDM and conceptual model RDM (e.g. social vs non-social) can be correlated to see how well social information is represented in the neural RDM (Figure 2D).

Multiple ROIs can be compared to see which region better represents a category. For example, an RDM constructed from the BOLD response in inferior temporal cortex would better represent animate as compared to inanimate objects than a neural RDM from early visual cortex as the model RDM for animacy is more similar to the neural RDM in inferior temporal cortex than in early visual cortex (Kriegeskorte et al., 2008). Comparing RDMs among multiple ROIs can also reveal the relationships between their representations (‘representational connectivity’). In analogy to functional connectivity analyses, this representational connectivity analysis (when combined with a searchlight approach) can powerfully inform us which regions are representationally connected to a given region(Kriegeskorte et al., 2008a). Just as in RDM construction, instead of using similarity, a second-order dissimilarity can be used to compare RDMs (Kriegeskorte et al., 2008a).

RDMs can be quantitatively compared with different metrics, though it has been recommended that rank-correlation distance (e.g. Spearman correlation, Kendall’s Tau) should be used since the noise within each RDM differs based on what the RDM was created from [e.g. fMRI data, MEG (magnetoencephalography) data, behavioral measures], therefore avoiding an assumption of a linear match between the RDMs (Kriegeskorte et al., 2008a). Similarly, when comparing the performance of multiple model RDMs (e.g. which is more closely related to the measured neural RDMs), non-parametric signed-rank test should be used (rather than the paired Student’s t-test) (Nili et al., 2014). Using these non-parametric rank-based tests also has the advantage of being robust against outliers. In order to reduce the likelihood of false-positive correlations, it is important that the diagonal and off-diagonal triangle of RDMs be excluded when comparing RDMs, thereby only leaving the lower or upper triangle of RDMs (Ritchie et al., 2017).

There are two general steps that should be taken to determine if RDMs are statistically similar. First, a noise ceiling should be calculated to determine the maximum possible similarity between an RDM of interest and the theoretical ‘true’ model RDM, given the level of noise in the data (for how to compute the noise ceiling, please read Nili et al., 2014). Second, a significance test should be done. A popular option is to use a permutation test, where the labels of the original data are shuffled, and an RDM is calculated on the permuted labels. The resulting permuted RDM is correlated to a second unpermuted RDM, repeatedly, in order to find the null distribution under the assumption that the RDMs are different (Dimsdale-Zucker and Ranganath, 2019; Kriegeskorte et al., 2008a; Nili et al., 2014; Walther et al., 2016). When RDMs are significantly correlated, researchers can articulate clearer conclusions by stating that the representation of stimuli is more similar in two brain regions, whose RDMs are significantly correlated, than in a third brain region, whose RDM is not significantly correlated with the others.

A common technique for exploratory brute-force search of neural representations is whole-brain searchlight RSA. The premise of this technique is similar to MVPA decoding searchlight in which a spherical ROI is made around each voxel in the brain for the analysis (Kriegeskorte et al., 2006). A neural RDM is created for each spherical ROI, and this is compared to other RDMs of interest (e.g. behavioral or model RDMs). Maps can be created to show which voxels across the whole brain are significantly related to the comparison RDMs (Tamir et al., 2016). When using a searchlight, testing for significance is done in the same manner as traditional fMRI methods, such as by using an FDR/FWE correction, Monte Carlo simulation or permutation test (Carlin et al., 2011).

Social neuroscience problems for which RSA is useful

RSA can be used to investigate social categories and dimensions

RSA has been used to test hypotheses about the neural representation of social categories and dimensions (Chavez and Heatherton, 2014; Freeman et al., 2018; Pegado et al., 2018; Vida et al., 2017; Wasserman et al., 2017). In most of these studies, the stimuli that are compared can be dimensionalized along some predefined metric. For instance, Parkinson et al. (2014) used RSA to ask whether social distance (how psychologically close you are to various friends and acquaintances), physical distance (the proximity between two objects in space and temporal distance (how far apart two events are in time) are represented in a single domain-general region. A key feature of the experimental design is that psychological closeness can be measured parametrically in terms of distance, just like real physical distance. The findings showed that the right inferior parietal lobule was significantly related to social, physical and temporal distance, suggesting that some high level social processes co-opted neural processes that evolved to process basic sensory information about spatial–temporal distance (Parkinson et al., 2014).

RSA has also been used to reveal how the brain represents the richness and complexity of social knowledge such as the self (Chavez et al., 2017; Feng et al., 2018; Wagner et al., 2018) and others’ mental states (Tamir et al., 2016; Thornton et al., 2019a; Thornton et al., 2019b). For instance, Tamir and colleagues asked subjects to rate mental state terms (e.g. awe, worry, curiosity, rage) on a variety of attributes such as warmth, competence, agency, experience and arousal. Their behavioral results showed that individual mental states can be represented by four unique dimensions (i.e. rationality, social impact, human mind and valence). They then created a behavioral RDM for each dimension based on the pairwise similarity of each mental state projecting on that dimension. Later, they asked subjects to think about each mental state term in the scanner and derived a neural RDM for each region of the brain based on the pairwise similarity of local neural activation patterns associated with each mental state. By linking behavioral and neural RDMs using searchlight RSA, they localized the neural correlates of three dimensions (rationality, social impact and valence) in the MPFC, precuneus, TPJ (temporoparietal junction) and ATL (Tamir et al., 2016). This study demonstrates that RSA is a very powerful analytic technique to reveal how the brain organizes a complex and multidimensional system like social knowledge.

RSA can be used to investigate emotions and valence

RSA has also been used in affective neuroscience to better understand the neural representation of emotions and valence (Chikazoe et al., 2014; Costa et al., 2014; Nummenmaa et al., 2012). RDMs from different ROIs can be compared to see how different brain regions represent distinct stimulus features such as the emotional valence of images. Chikazoe et al. (2014) found that when mean activations were used to measure representations in the orbitofrontal cortex, specificity of valence was not found as the similarity of between-valence stimuli (positive vs negative stimuli) was similar to within-valence stimuli (positive vs positive and negative vs negative). However, when the pattern of activation across the orbitofrontal cortex was used, valence could be seen to be represented in a dimensional manner where within-valence stimuli had greater similarity than between-valence stimuli. This was interesting because prior meta-analyses of data from mass-univariate fMRI studies showed that neural activations for positive and negative valenced items tended to overlap (Lindquist et al., 2012). Chikazoe and colleagues showed that although mass-univariate analyses can reveal that a region is activated for stimuli of two opposing sides of a dimension, RSA can reveal how information of that dimension is represented (Chikazoe et al., 2014).

RSA can be used to compare models with neural representations

A unique feature of RSA is its ability to compare neural representations with psychological or computational models. In a recent study, representations of observed socio-affective touch experiences, such as hugging and holding hands, were compared to representations of non-socio-affective touch experiences, such as holding objects (Lee Masson et al., 2018). The mass-univariate analysis from this study showed that the social vs non-social touch contrast implicated social brain network regions such as the TPJ and superior and middle temporal gyrus. A multiple regression analysis was used to show that a social vs non-social conceptual RDM could be related to neural RDMs from different ROIs representing various networks and not just the social brain network. The analysis revealed that social information from touch experiences can be represented across a variety of regions belonging to somatosensory, pain, theory of mind and visual networks. Affective information from touch experiences, on the other hand, was selectively represented in regions belonging to somatosensory and theory of mind regions.

RSA can be used to compare data from different age groups, diagnostic groups or even species

The neural representation of a category, dimension or task can be easily compared using RSA between different individuals (Guntupalli et al., 2016; Nguyen et al., 2019; van Baar et al., 2019) and groups (Golarai et al., 2017; Lee et al., 2017). For instance, one could ask: do children and adults have similar or different neural representations for different visual categories? And in fact, using RSA, it has been shown that category representations of faces, scenes and objects in the ventral temporal cortex does not differ between children, ages 7 to 11, and adults (Golarai et al., 2017). In another study with a slightly younger age group of five to seven-year olds, a univariate analysis showed that category-selectivity was not present in regions that typically encode faces, bodies and places. However, RSA was able to show that response patterns were still similar to adults who did have category selectivity in those same regions, suggesting that very young children have distributed response patterns that serve as a foundation for category-selective regions (Cohen et al., 2019). Another study asked whether a mother’s empathy for her child is equivalent to the child’s empathy for their mother. This question was based on the premise that empathy, to some degree, blurs the line between self and other, thus if one group has higher empathy for the other group, there should be greater representational similarity. Using RSA, the results showed that mothers had more similar neural representations for harm to self and harm to family members than did their adolescent children (Lee et al., 2017). When comparing common representational space across individuals, RSA can even be employed for functional parcellation of the cortex (Guntupalli et al., 2016).

Not only can different groups of human participants be compared using RSA but also different species of animals as well. In an early RSA study, researchers asked if object and face representations in the inferior temporal lobe are similar in macaques and humans (Kriegeskorte et al., 2008). Humans and macaques were shown the same images of natural and artificial objects, animate non-human faces and body parts and human faces and body parts while either undergoing an fMRI scan or while having the electrical activity of neurons recorded. The dissimilarity between the neural response to visual stimuli in human inferior temporal cortex was compared to the dissimilarity of the neural response to visual stimuli in macaque inferior temporal cortex. The results showed that both species represent objects and faces in a highly similar way in inferior temporal cortex. This example shows how RSA can create a bridge to directly compare non-human primate research to human research, even when the data that are being compared are from distinct methodologies.

RSA can be used to compare data from different techniques

As hinted at in the last section, RSA enables us to compare neural data from different modalities. Kriegeskorte and colleagues (2008) not only compared different species, but they also compared fMRI and extracellular recording data (Kriegeskorte et al., 2008). In short, any modality (with different spatial and temporal scales) can be used in combination together as input in RSA, as long as the same tasks are used across studies. It can provide a bridge between data gathered using different modalities in social neuroscience (e.g. eye-tracking, electromyography and electrocorticography). For instance, the sluggish temporal resolution of the BOLD response can be partly overcome by using RSA to complement fMRI with data from techniques with excellent temporal resolution such as MEG (Cichy et al., 2017) or EEG (electroencephalography) (Salmela et al., 2018). RSA has also been used to compare data from MEG to EEG (Cichy and Pantazis, 2017). RSA can even be combined with diffusion imaging to reveal the neural representation in white matter (Fang et al., 2018). As data accumulate in social neuroscience, comparisons across techniques will allow us to gain convergent and complimentary viewpoints.

RSA can be used to make predictions about future behavior

Since RSA can reveal how information is represented in the brain, an interesting extrapolation is to use the current state of an individual’s neural representations to predict the same individual’s future behavior. This is particularly useful for persuasion neuroscience where the aim is to investigate how messages are firstly encoded in the brain and then influence people’s mind and subsequent behavior. In one such experiment, study participants who were smokers were recruited and they were shown images that contained social or health themes related to quitting smoking. Conceptual model RDMs were created for health information, social information and valence of message content. These model RDMs were correlated with neural RDMs to see how well an ROI represented a given type of information. The correlations from the neural RDM and each of the model RDMs were inputted into a regression analysis to predict change in frequency of smoking. It was found that the more health information was represented in the MPFC, the more likely participants were to reduce smoking (as indexed by self-report, ~38 days later) (Pegors et al., 2017). Future extensions of this work could look to see if neural data predict behavior at longer time frames, which is more relevant for public health, and also use direct measures of smoking cessation to improve model prediction.

RSA has also been used to predict physiological indices of fear. Visser et al. (2013) presented participants with visual stimuli, such as a face or a house, and some of these were paired with shocks. The similarity between neural responses for different category stimuli, which were both presented with an electric shock (and therefore had a shared feature of fear), predicted pupil dilation similarity in a separate test given weeks after the initial learning experiment (Visser et al., 2013). Note that the average activation to the stimuli was not able to predict pupil dilation, but RSA could—further highlighting RSA’s greater sensitivity over mass-univariate analyses.

RSA limitations

Although the focus of this paper has been on highlighting the advantages of RSA over other methods, RSA still shares some limitations of more commonly used techniques. One limitation of RSA is that it is still susceptible to pitfalls of any correlation-based methods. RSA attempts to understand how information is represented in a brain region by correlating RDMs, which are themselves made of correlations. Although neural RDMs may be correlated with model RDMs of a specific attribute (i.e. high-status vs low-status), the correlations will not explain all of the shared variances between stimuli. One solution to this may be to direct attention during a task to specific attributes that can tell the researcher how information is represented (Nastase et al., 2017; Popov et al., 2018). Another solution would be to use other non-correlation-based representational analyses (e.g. encoding analysis, pattern component analysis, multivariate pattern dependence, repetition suppression) to validate RSA results in the same study (Anzellotti and Coutanche, 2018; Diedrichsen and Kriegeskorte, 2017; Hatfield et al., 2016; Wagner et al., 2018).

A second limitation is that RSA can be heavily influenced by outliers, in much the same way that all correlation-based analyses are. As mentioned previously, a rank-based correlation can be used to curb the influence of outliers when correlating RDMs, and large sample size (n > 12) and rich stimuli for each condition (>20) are needed for population inference and stimulus-label randomization test (Nili et al., 2014).

General discussion

RSA can uniquely address questions about the neural representation of information from features of stimuli. Because RSA directly captures the differences between individual stimuli, it has an advantage over mass-univariate methods and MVPA decoding in analyzing the multidimensional features of stimuli. This is in addition to its greater sensitivity by accounting for the multivariate nature of data, rather than an aggregate response that is used in mass-univariate methods. Although some earlier univariate techniques can also be used to study the representation of stimulus features, such as repetition suppression (Grill-Spector et al., 2006), these techniques still suffer from limitations that multivariate techniques do not have.

In addition, although traditional univariate encoding models provide an alternative to RSA for testing computational models of brain information processing (Kay et al., 2008), it first needs a separate dataset and stimuli for model fitting. In contrast, RSA offers an easy and simple way of comparing models, naturally handles noise correlations between voxels and reduces the need for a training dataset (Nili et al., 2014). When RSA incorporates other encoding models (e.g. multiple regression RSA), it can provide a flexible and powerful quantitative means to characterize dynamic, rather than fixed representational spaces, shaped by bottom-up and top-down factors, thus promising better predictions of social cognition and behavior (Stolier et al., 2018a).

Future implementations of RSA can be used to explore differences in representation in clinical populations. Alterations in the representation of a particular type of information can be explored in clinical populations that have a clear deficit in representations, such as semantic memory deficits in semantic variant primary progressive aphasia or social knowledge in autism spectrum disorders. A novel use of RSA seeks to understand individual differences between subjects by having subjects as features of RDMs and using inter-subject correlations to see how subjects respond differently to naturalistic stimuli (Finn et al., 2018).

In sum, RSA is an important and promising computational technique for understanding how our brain represents the social world. RSA is easy to use and can fully integrate the entire repertoire of techniques used in social neuroscience including single-unit recordings, fMRI, EEG, physiological recordings and behavioral reactions (Figure 1). Several toolboxes exist that allow researchers to handily use RSA, such as the RSA toolbox (Nili et al., 2014), CosMoMVPA (Oosterhof et al., 2016), The Decoding Toolbox (Hebart et al., 2015) and PyMVPA (Hanke et al., 2009). Compared to MVPA decoding, the learning curve for RSA is far lower as users do not need to understand various machine learning algorithms that if implemented poorly can provide ambiguous or even misleading results.

We hope that this introduction to RSA allows researchers to see that the technique is easy to understand and implement, thus paving the way for future research using this technique.

Funding

This work was supported by a National Institute of Health grant to I. Olson [RO1 MH091113].