Investigating Conformational Dynamics of Lewis Y Oligosaccharides and Elucidating Blood Group Dependency of Cholera Using Molecular Dynamics

Abstract

Cholera is caused by Vibrio cholerae and is an example of a blood-group-dependent disease. Recent studies suggest that the receptor-binding B subunit of the cholera toxin (CT) binds histo–blood group antigens at a secondary binding site. Herein, we studied the conformational dynamics of Lewis Y (Le^Y) oligosaccharides, H-tetrasaccharides and A-pentasaccharides, in aqueous solution by conducting accelerated molecular dynamics (aMD) simulations. The flexible nature of both oligosaccharides was displayed in aMD simulations. Furthermore, aMD simulations revealed that for both oligosaccharides in the free form, ⁴C₁ and ¹C₄ puckers were sampled for all but GalNAc monosaccharides, while either the ⁴C₁ (GlcNAc, Gal, GalNAc) or ¹C₄ (Fuc2, Fuc3) pucker was sampled in the CT-bound forms. In aMD, the complete transition from the ⁴C₁ to ¹C₄ pucker was sampled for GlcNAc and Gal in both oligosaccharides. Further, we have observed a transition from the open to closed conformer in the case of A-pentasaccharide, while H-tetrasaccharide remains in the open conformation throughout the simulation. Both oligosaccharides adopted an open conformation in the CT binding site. Moreover, we have investigated the molecular basis of recognition of Le^Y oligosaccharides by the B subunit of the cholera toxin of classical and El Tor biotypes using the molecular mechanics generalized Born surface area (MM/GBSA) scheme. The O blood group determinant, H-tetrasaccharide, exhibits a stronger affinity to both biotypes compared to the A blood group determinant, A-pentasaccharide, which agrees with the experimental data. The difference in binding free energy between O and A blood group determinants mainly arises due to the increased entropic cost and desolvation energy in the case of A-pentasaccharide compared to that of H-tetrasaccharide. Our study also reveals that the terminal Fuc3 contributes most to the binding free energy compared to other carbohydrate residues as it forms multiple hydrogen bonds with CT. Overall, our study might help in designing glycomimetic drugs targeting the cholera toxin.

Introduction

There is a strict variation in the blood group type and frequencies among the human population throughout the world, which is a result of the genetic pressure giving protection from different infectious diseases.¹ Among all of these blood-group-dependent diseases, cholera is one of the deadliest and epidemic diseases in human history and most prevalent in the African subcontinent. More than 1.2 million cases were reported in 2017 all over the world, with a fatality rate of 0.5. Cholera is caused by the pathogen Vibrio cholerae.(2) The relationship between blood groups and cholera was first shown by Barua and Paguio.³ People with the O blood group tend to acquire a higher risk in the development of severe cholera symptoms.⁴⁻⁷ Further, evolutionary history also suggests an association between the blood group O and cholera. The Ganges delta is a region where cholera is prevalent from ancient times. As a result of the genetic pressure, the O blood group is decidedly less prominent in the Ganges delta region.⁸ All of these studies indicate an active role of the blood groups, especially the O blood group, in the infection and development of cholera. Despite several experimental analyses, a detailed understanding of the molecular mechanism underlying this cause is still missing, and this needs to be addressed.⁹

Throughout the world, cholera infection can be divided into two serogroups, O1 and O139. Further, O1 can be classified into classical and El Tor biotypes.^10,11 Both biotypes produce cholera toxins (cCT and ET CT) differing in two residues of the B subunit, H18Y and T47I (classical and El Tor). The interaction of the blood group with El Tor was observed to be stronger compared to that with the classical strain.¹²

Blood group antigens (BGAs) are cell surface carbohydrates that are conjugated with glycolipids (e.g., GM1) or membrane glycoproteins expressed mainly in red blood cells and epithelial cells. The Lewis blood group antigens are mostly fucosylated glycans and possess a typical basic structure composed of galactose (Gal), N-acetylglucosamine (GlcNAc), and fucose (Fuc) residues.¹³ There are four Lewis antigens, namely, Lewis A (Le^A), Lewis B (Le^B), Lewis X (Le^X), and Lewis Y (Le^Y). Further, Le^A or Le^X can often be found sialylated to yield sialyl Lewis A (sLe^A) or sialyl Lewis X (sLe^X), respectively. For Le^X, the sequence of the core trisaccharide is found to be Galβ(1–4)(Fucα(1–3))GlcNAcβ.¹⁴ Le^Y is obtained when a second Fucα(1–2) is attached to the terminal Gal residue of Le^X. All of these determinants are characteristics of blood group O. An enzymatic addition of N-acetylgalactosamine (GalNAc) or galactose (Gal) yields A or B blood group, respectively. In this study, we consider only Le^Y oligosaccharides, as shown in Figure 1B. Recently, Heggelund et al.¹⁵ reported the crystal structure of cCT and ET CT with Le^Y blood group determinants, H-tetra and A-penta BGAs, which opens the possibility of systematic dynamical studies of interactions between blood groups and cholera toxins. Moreover, it was shown that H-tetrasaccharide binds to CT with a much higher affinity in comparison to A-pentasaccharide.

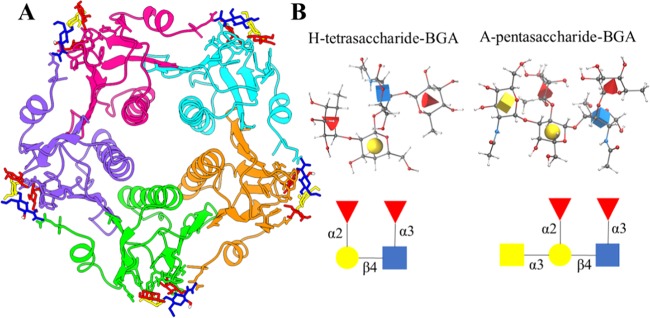
Figure 1.

(A) Crystal structure of the pentameric cholera toxin B subunit in complex with glycans. Each protein chain is shown in a different color, and the glycan is represented in the ball-and-stick model. (B) Structure and nomenclature of Lewis Y (Le^Y) blood group determinants: H-tetrasaccharide and A-pentasaccharide BGAs. The structure and nomenclature of Le^Y blood group determinants are displayed in three-dimensional (3D) symbol nomenclature for glycans (SNFG) icon mode. In this representation, N-acetylglucosamine is shown as a blue cube, l-fucose is shown as a red cone, d-galactose is shown as a yellow sphere, and N-acetylgalactosamine is shown as a yellow cube. All images were generated using Visual Molecular Dynamics (VMD) with the help of the 3D-SNFG plugin available at www.glycam.org/3d-snfg. A detailed atomic structure is also shown in the ball-and-stick model, where the standard color scheme is used to depict different types of atoms.

The interaction between carbohydrates and the cholera toxin is highly specific and depends on the conformational variation. The cholera toxin binds to not only GM1 but also various analogues of GM1.¹⁶ A previous study on the interaction of the cholera toxin with several monosialogangliosides describes the possible binding modes of carbohydrates to the toxin and elucidates the role of water-mediated hydrogen bonds that stabilize the interaction.¹⁷ Several studies involving different analogues of sialic acid against the cholera toxin showed that it is successfully recognized and interacts with the analogues.^18,19 Cervin et al. show that CT can induce toxicity in the absence of GM1 and support a role for host glycoproteins in CT intoxication. It is worth noting here that these glycoprotein receptors are fucosylated since human intestinal epithelial cells are heavily fucosylated.²⁰ Fazil and co-workers have shown by utilizing molecular dynamics simulations that the binding efficiency of the carbohydrate units of GM1 receptors varies against different genotypes of CT.²¹

In this study, we focus on investigating the conformational dynamics of Lewis Y oligosaccharides (i.e., H-tetra and A-pentasaccharides) and elucidating the biophysical basis of their recognition by the cholera toxin of two biotypes. Previously, various computational methods have been employed to study the conformational dynamics of glycans.²²⁻²⁹ In general, Lewis sugars behave as a rigid structure in solution stabilized by the stacking interaction between fucose and galactose rings.³⁰ In this study, we have utilized the accelerated molecular dynamics (aMD)³¹ technique for investigating the conformational dynamics of free Le^Y oligosaccharides. We compare the conformational preferences in solution and bound to CT by constructing the underlying free energy surfaces corresponding to the glycosidic linkages. It is worth noting here that the conformational dynamics of H-tetra and A-pentasaccharides have not been studied previously. Finally, we calculate the binding free energy of each glycan complexed with both biotypes of CT by employing the popular MM-GBSA³² scheme, which is an average estimation of molecular mechanics and solvation free energy. Since the binding event occurs in aqueous solution,³³ MD simulations were conducted in an explicit water environment.

Results and Discussion

Structural Stability and Flexibility of the Complexes

First, we have computed the root-mean-squared deviations (RMSDs) of backbone atoms compared to the initial structure for all four protein–glycan systems, and the time evolution of RMSD is shown in Figure 2A. In the case of all four complexes, the RMSD values quickly reach the plateau and remain stable throughout simulations, suggesting the convergence of simulations. The average RMSD is estimated to be 1.2 Å for the classical strain bound to H-tetra and A-pentasaccharides. Similarly, average RMSDs of 1.3 and 1.4 Å are obtained when the El Tor (ET) strain is complexed with the H-tetra and A-pentasaccharides, respectively. The main reason for the structural stability of the pentameric cholera toxin could be a conserved intermonomer hydrogen bond.

Figure 2.

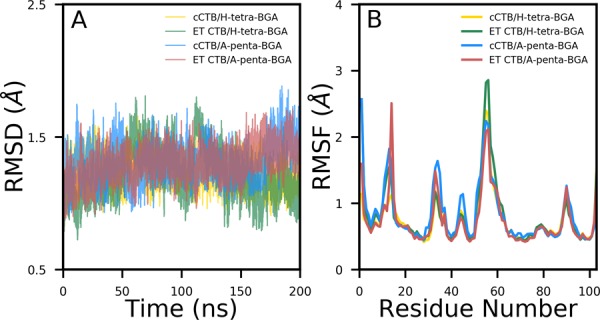
(A) Time evolution of the root-mean-square deviations (RMSDs) of backbone atoms with respect to the initial structure and (B) root-mean-square fluctuations (RMSFs) of C_α atoms for all four complexes.

Next, we investigated the flexibility of each residue by computing root-mean-squared fluctuations (RMSFs) of C_α atoms, which are shown in Figure 2B. A similar variation is observed for all four protein–glycan complexes. Further, it is revealed in Figure 2B that the region between residues 51 and 58 is the most flexible region. Another highly flexible region is located between residues 8 and 12. Both the areas correspond to a dynamic loop and are solvent-exposed.

Conformational Dynamics of Glycans Bound to CT

To investigate the conformational features of glycans, we have calculated the RMSD of each glycan bound to each monomer of the pentameric cholera toxin of both biotypes, which is shown in the Supporting Information (see Figures S1–S4). For both biotypes, the RMSD of each of the five H-tetrasaccharides is very stable (see Figures S1 and S2). In contrast, the RMSD of A-pentasaccharide is found to be varying and fluctuating (see Figures S3 and S4), suggesting a more flexible nature of A-pentasaccharide compared to that of H-tetrasaccharide in the binding site. Such a flexible nature was observed for the Le^X trisaccharide bound to RSL.²⁸ In the case of H-tetrasaccharide, an average RMSD of ∼0.9 Å is obtained when it is bound to either cCTB or ET CTB (see Table 1). On the other hand, average RMSDs of 1.3 and 1.6 Å are obtained for A-pentasaccharide bound to cCTB and ET CTB, respectively (see Table 1). Furthermore, it is evident from Figures S3 and S4 that the flexibility of A-pentasaccharide is biotype-specific as it is found to be more flexible when it is bound to ET CTB than to cCTB. An addition of GalNAc monosaccharide to A-pentasaccharide causes a higher degree of flexibility compared to that for H-tetrasaccharide.

Table 1. Average RMSDs Obtained from Simulations of Free Glycans as Well as Complex Simulations^a.

		complex				free
		cCT/H-tetra	ET CT/H-tetra	cCT/A-penta	ET CTB/A-penta	H-tetra	A-penta
						aMD	aMD
chain	A	0.9 (0.2)	1.2 (0.2)	1.1 (0.2)	1.7 (0.3)	3.3 (0.7)	3.9 (0.7)
	B	0.9 (0.2)	1.0 (0.2)	1.5 (0.5)	1.7 (0.4)
	C	0.9 (0.2)	0.6 (0.1)	1.5 (0.5)	1.8 (0.5)
	D	0.9 (0.2)	0.6 (0.2)	1.1 (0.2)	1.3 (0.5)
	E	0.8 (0.2)	0.8 (0.2)	1.2 (0.2)	1.5 (0.3)
global		0.9 (0.2)	0.9 (0.2)	1.3 (0.4)	1.6 (0.4)

^aAll values are in Å. Standard deviations are provided in parentheses.

Further, we analyzed the flexibility of the glycosidic linkages for both glycans bound to both biotypes by constructing two-dimensional (2D) free energy surfaces of φ/ψ glycosidic torsions (see Figures S5–S6, Supporting Information). Three glycosidic linkages of H-tetra are Galβ(1–4)GlcNAc, Fucα(1–2)Gal, and Fucα(1–3)GlcNAc, while four glycosidic linkages of A-penta are Galβ(1–4)GlcNAc, Fucα(1–2)Gal, Fucα(1–3)GlcNAc, and GalNAc(1–3)Gal. For constructing the φ/ψ map, we generated a 1 μs trajectory by extracting the trajectory of each BGA at the five binding sites and combining such five trajectories (5 × 200 ns). For both glycans bound to both biotypes, the free energy surfaces are similar, and we obtained a narrow and single free energy minimum for all of the glycosidic linkages. In the case of H-tetra, the principal minima corresponding to Galβ(1–4)GlcNAc, Fucα(1–2)Gal, and Fucα(1–3)GlcNAc linkages almost coincide with the corresponding linkages of A-penta. However, the φ/ψ distribution of the Fucα(1–2)Gal linkage shows a slightly broader free energy minimum in H-tetra compared to that in A-pentasaccharide. Moreover, the free energy surface of the GalNAcα(1–3)Gal linkage in A-pentasaccharide is also found to be a little broad. This observation suggests that the movements of the glycans get restricted while they are bound to CT.

Conformational Dynamics of Free Oligosaccharides in Aqueous Solution

The flexible nature of the glycan is revealed in 1 μs long aMD simulations. The time evolutions of RMSD of nonhydrogen atoms for both BGAs are displayed in Figure S7A,B. The average RMSD for both BGAs obtained from the aMD simulation is reported in Table 1. It can be noted from Table 1 that the average RMSD value of the free oligosaccharide is much higher compared to that of the oligosaccharide at the binding sites and is estimated as 3.3 and 3.9 Å for H-tetra and A-penta BGA, respectively (see Table 1). We have also calculated and plotted the probability distribution of RMSD for both glycans in Figure S7C,D. It displays a single peak at ∼3.3 Å for H-tetra BGA, while three peaks at 3.3, 3.7, and 4.7 Å are obtained for A-penta BGA. Furthermore, the conformational dynamics of both BGAs are illustrated by the free energy landscape (FEL) of RMSD and the radius of gyration (R_g) and are shown in Figure S8A,B. It is evident from Figure S8 that in H-tetra BGA, a single broad conformational space is explored with a global free energy minimum at RMSD/R_g ∼3.3/∼4.6 Å, while the FEL of A-penta BGA is characterized by three dispersed basins (RMSD/R_g: ∼3.3/∼5.3, ∼3.7/∼5.2, ∼4.7/∼4.9 Å). The global free energy minimum in A-penta BGA is located at ∼4.7, ∼4.9 Å. In contrast, in the case of bound H-tetra BGA, the free energy minimum is located at ∼0.8, ∼5.1 Å, as shown in Figure S9. On the other hand, in the case of A-penta BGA, the global free energy minimum is located at ∼1.0, ∼5.2 and ∼1.8, ∼5.1 Å for cCTB and ET CTB, respectively. Overall, this suggests that the conformational ensemble of A-penta BGA in solution is more diverse compared to that of H-tetra.

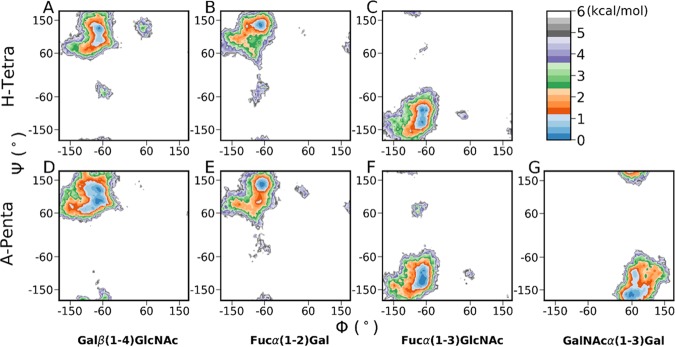
Next, we constructed the free energy surfaces of the glycosidic linkages for both H-tetra and A-penta BGAs, which are shown in Figure 3. Overall, Figure 3 indicates a broad sampling around the principal minimum for all of the glycosidic linkages. On comparing Figure 3 with Figure S5 (Supporting Information), we find out that the locations of principal minima for all glycosidic linkages are almost similar in the free and CT-bound states. However, the regions of minima of both glycans are much broader in solution compared to those in the CT-bound form. It is worth noting here that in the case of A-pentasaccharide, the core linkage [Galβ(1–4)GlcNAc] displayed two distinct minima closely connected by a very shallow free energy barrier (Figure 3D), while a single minimum was obtained for H-tetrasaccharide (Figure 3A).

Figure 3.

Free energy surfaces (kcal/mol) of the φ/ψ glycosidic angles of (A–C) H-tetra and (D–G) A-penta BGAs obtained from accelerated MD simulations. Top panel (H-tetra): (A) Galβ(1–4)GlcNAc, (B) Fucα(1–2)Gal, and (C) Fucα(1–3)GlcNAc. Bottom panel (A-penta): (D) Galβ(1–4)GlcNAc, (E) Fucα(1–2)Gal, (F) Fucα(1–3)GlcNAc, and (G) GalNAcα(1–3)Gal.

Investigating Closed and Open Conformations of Free A-Penta BGA in Solution

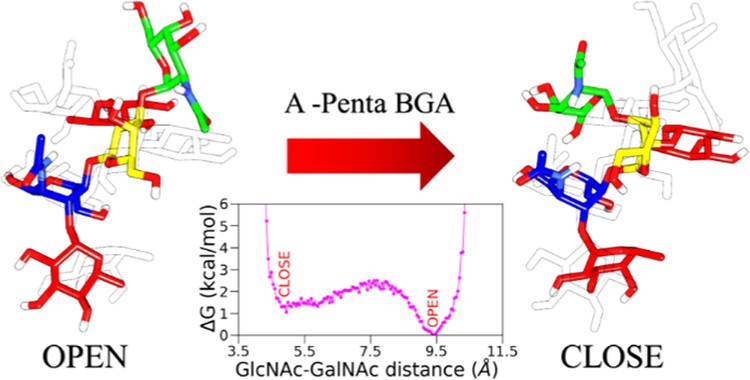
To further characterize the structural features, the distances between GlcNAc-GalNAc (R₁) and GalNAc-Fuc3 (R₂) for each CTB-bound A-penta BGA are calculated from the PDB (Protein Data Bank) structure for both biotypes and are listed in Table S1 (Supporting Information). It can be seen in Table S1 that R₁ varies between 8.9 and 9.4 Å while R₂ varies between 9.2 and 9.6 Å for both biotypes. This suggests that A-penta adopts an extended conformation in the binding site. To explore conformational preferences of unbound A-penta in aqueous solution, we constructed a two-dimensional potential of mean force (2D PMF) from the aMD simulation with R₁ and R₂ as reaction coordinates (see Figure 4). It is characterized by two distinct free energy wells separated by a relatively high free energy barrier. R₁ varies between 5 and 9 Å, suggesting that both open and closed conformations are explored by free A-penta in solution, which is in contrast to what has been observed in the CTB-bound X-ray structure. Further, Figure 4 suggests that the open conformation, characterized by R₁/R₂: ∼9.4/11.1 Å, is more probable compared to the closed structure (R₁/R₂: ∼5.3/9.3 Å). The three-dimensional structures of both conformations are also shown in Figure 4. The closed structure is characterized by a hydrogen bond between O5@GlcNAc and O6@GalNAc, which is absent in the open structure. The extended or open conformation is linear, and all of the terminal fucose residues are also perpendicular to the main branch. These two different forms of A-penta oligosaccharide can bind to different targets, as is the case with Lewis X.^34,35 The same 2D PMF was generated for A-penta BGA from the complex simulations and is shown in Figure S10 (Supporting Information). Here, for both biotypes, only the open conformation, characterized by R₁/R₂: ∼10/9 Å, is explored. Overall, our simulations suggest that A-penta can adopt both open and closed conformations in solution, while only the open conformation is preferred when it is bound to pentameric CTB.

Figure 4.

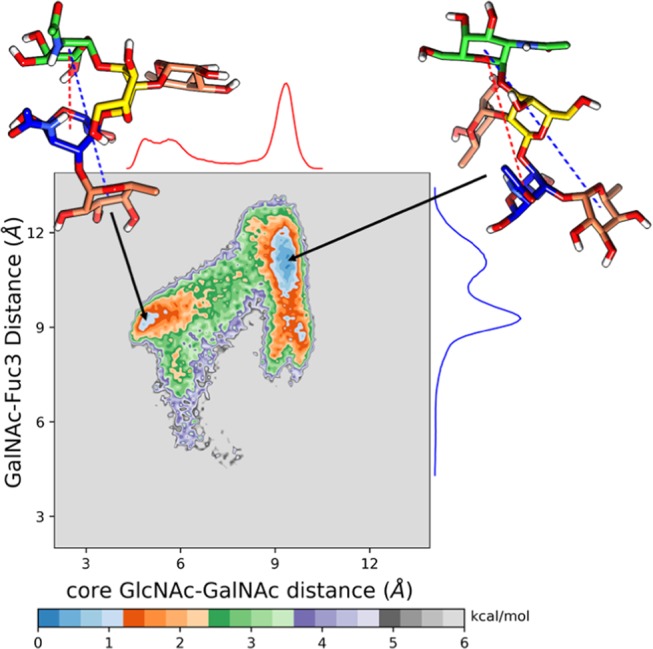
Two-dimensional potential of mean force for A-penta BGA in solution obtained from the aMD simulations. The distances between GlcNAc and GalNac and GalNac and terminal fucose residue (Fuc3) were considered as reaction coordinates.

Puckering Conformations of the Pyranose Ring

Next, we characterized the shape variation of the individual sugar ring pucker for both oligosaccharides in solution and compared it with the protein-bound state. The IUPAC convention was used to calculate the canonical puckering conformations, and the Mercator representations of the Cremer–Pople sphere³⁶ depicting pyranose shapes for aMD simulations of both BGAs in solution are shown in Figure 5. Both chair conformations (⁴C₁ and ¹C₄) were sampled for all (GlcNAc, Gal, Fuc2, and Fuc3) but GalNAc monosaccharides, as is evident from Figure 5. On the other hand, either the ⁴C₁ (GlcNAc, Gal, GalNAc) or ¹C₄ (Fuc2, Fuc3) pucker conformation was sampled in all monosaccharides for both BGAs bound to CT (Figure S11, Supporting Information).

Figure 5.

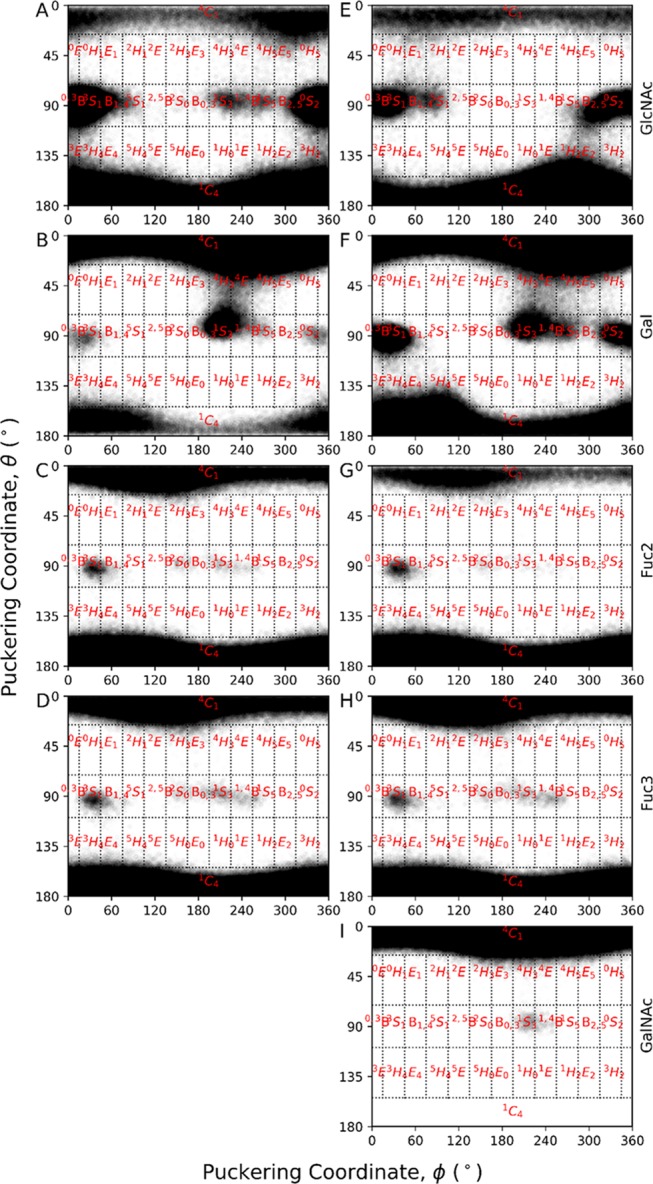
Mercator representation of the Cremer–Pople Sphere for all of the monosaccharides in solution derived from the accelerated MD simulations. Left-hand images (A)–(D) correspond to the GlcNAc, Gal, Fuc2, and Fuc3, respectively, from H-tetra BGA, whereas right-hand images (E)–(I) correspond to GlcNAc, Gal, Fuc2, Fuc3, and GalNAc, respectively, from A-penta BGA.

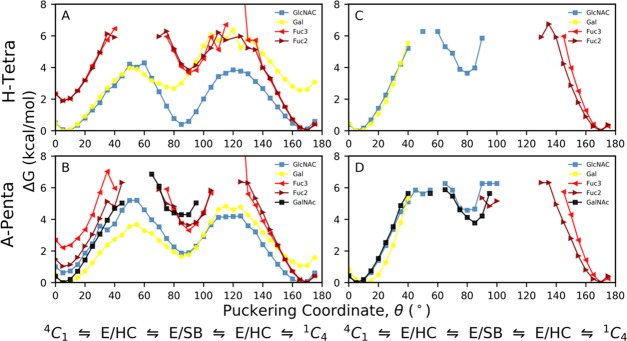
Next, we computed the one-dimensional (1D) puckering free energy profiles for all monosaccharides in both BGAs, which are shown in Figure 6. It is observed from Figure 6A,B that only for GlcNAc and Gal monosaccharides in both H-tetra and A-penta BGAs, the complete ⁴C₁ to ¹C₄ pucker transition was sampled in solution. A similar trend was obtained by Alibay and co-workers for the Lewis X trisaccharide.¹⁴Figure 6C,D further reveals that for both BGAs bound to CTB, only the ⁴C₁ pucker was sampled for GlcNAc, GalNAc, and Gal monosaccharides, while the ¹C₄ pucker conformation was populated for both fucoses (Fuc2, Fuc3). On computing the puckering angle ⊖ as a function of simulation time from aMD simulations of free BGAs in solution, we noted that for GlcNAc in both BGAs, the ¹C₄ pucker was sampled more frequently than ⁴C₁ with significant time in ^0,3B, ³S₁, and ⁰S₂ (Figure S12, Supporting Information). Further, Figure 6A,B suggests that the boat/skewed-boat conformations in GlcNAc are energetically more favorable by ∼1.5 kcal/mol for H-tetra than for A-penta. In contrast, for Gal in H-tetra BGA, the ⁴C₁ pucker was more populated compared to ¹C_4, while both pucker conformations (⁴C₁,¹C₄) were almost equally sampled in A-penta BGA (Figure S12, Supporting Information). This is because the ⁴C₁ pucker in Gal is energetically more favorable by ∼2 kcal/mol compared to the ¹C₄ shape in H-tetra BGA (see Figure 6A,B). Furthermore, in the case of Gal, ^0,3B, ¹S₃, ^1,4B, and ⁰S₂ puckers were also sampled more significantly in A-penta BGA than in H-tetra BGA, as these conformations have lower free energies in A-penta than in H-tetra BGA (see Figure 6A,B). Although both the chair conformations (⁴C₁, ¹C₄) were sampled for Fuc2 and Fuc3 monosaccharides in solution with a short time in the ³S₁ shape, the ¹C₄ pucker conformation was found to be energetically more favorable than ⁴C₁ for both fucose monosaccharides, as is evident from Figure 6A,B. In the case of GalNAc, mostly, the ⁴C₁ pucker conformation was sampled with the only optimization passage to the ¹S₃ and ^1,4B puckers when A-penta BGA is either in solution or at the binding sites (Figure 6B,D). Finally, Figure 6C,D displays that the boat/skewed-boat puckers are free energetically unfavorable for Gal, Fuc2, and Fuc3 monosaccharides when BGAs are bound to CTB.

Figure 6.

Cremer–Pople 1D ⊖ puckering profiles of H-tetra and B-penta BGAs (A, B) in solution and (C, D) in complex states. (A) and (B) were generated from aMD simulations, while (C) and (D) were obtained from cMD simulations of the complex structures.

Recognition of H-Tetra and A-Penta by the Cholera Toxin

Binding Energetics

To elucidate the mechanism of recognition of H-tetra and A-penta BGAs by the cholera toxin, we have calculated the total binding free energy and decomposed the same into various components including electrostatics, van der Waals, polar and nonpolar solvation free energies, and entropy (see Table 2). The total binding free energy and its different components for all four complexes are listed in Table 2. Overall, it is evident from Table 2 that the complex formation is mainly favored by the intermolecular electrostatic (ΔG_elec) and van der Waals (ΔG_vdW) interactions. The nonpolar component of the solvation free energy also favors the complexation. On the contrary, polar solvation free energy (ΔG_polar) and configurational entropy (−TΔS) oppose the binding of BGAs to CT.

Table 2. Binding Free Energies of All Four Complexes along with the Different Energy Components from the MM/GBSA Scheme^a.

energy term	cCT/H-tetra	ET CT/H-tetra	cCT/A-penta	ET CT/A-penta
ΔGvdW	–35.4 (0.1)	–32.9 (0.1)	–42.8 (0.1)	–40.24 (0.1)
ΔGelec	–41.1 (0.1)	–39.1 (0.1)	–47.6 (0.1)	–45.6 (0.1)
ΔGpolar	52.8 (0.1)	48.2 (0.1)	62.1 (0.1)	58.4 (0.1)
ΔGnonpolar	–4.4 (0.0)	–4.2 (0.0)	–5.5 (0.01)	–5.1 (0.0)
–TΔS	23.3 (1.6)	25.3 (1.7)	31.2 (2.1)	29.9 (1.8)
ΔGbind	–4.8 (1.6)	–2.7 (1.7)	–2.6 (2.1)	–2.8 (1.8)
ΔGexp	–4.1	–3.9	–3.7	–2.1

^aAll values are given in kcal/mol.

As shown in Table 2, the calculated binding free energies (ΔG_bind) are −4.8, −2.7, −2.6, and −2.8 kcal/mol for cCTB/H-tetra, ET/H-tetra, cCTB/A-penta, and cCTB/A-penta, respectively. This suggests that H-tetra (i.e., the O blood group determinant) binds more strongly to both classical and El Tor (ET) biotypes compared to A-penta (the A blood group determinant). This observation is in agreement with the experimental study.¹⁵ It should be noted that ΔG_elec varies between −39.1 and −47.6 kcal/mol, while ΔG_vdW varies between −32.9 and −42.8 kcal/mol for all four complexes. This means that ΔG_elec contributes more favorably to the complexation compared to ΔG_vdW. This is in contrast to what has been observed for HIV-1 protease-inhibitor³⁷⁻⁴⁰ or with-no-lysine kinase-inhibitor complexes.^41,42 It is also worth mentioning here that for both oligosaccharides, ΔG_elec and ΔG_vdW are more favorable for the classical strain than for El Tor.

In the case of cCTB/A-penta, both ΔG_elec (−47.6 kcal/mol) and ΔG_vdW (−42.8 kcal/mol) are more favorable for the binding compared to the binding of H-tetra to cCTB (ΔG_elec = −41.1 kcal/mol, ΔG_vdW = −35.4 kcal/mol). However, in the case of cCTB/A-penta, both ΔG_polar (62.1 kcal/mol) and −TΔS (31.2 kcal/mol) oppose more to the binding compared to cCTB/H-tetra (ΔG_polar = 52.8 kcal/mol, −TΔS = 23.3 kcal/mol). Overall, A-penta binds less strongly to cCTB compared to H-tetra due to the increased polar solvation free energy and configurational entropy. However, in the case of the El Tor strain, a similar binding free energy (ΔG_bind = ∼−2.7 kcal/mol) is obtained for both H-tetra and A-penta.

Quantification of per-Residue Contributions to ΔG_bind

To provide further insights into the mechanism of recognition of BGAs by CT, we calculated the contribution of each monosaccharide to ΔG_bind for all four complexes, which is listed in Table 3. For all four complexes, Fuc3 and GlcNAc contribute more favorably to the binding compared to other monosaccharides, as is evident from Figure 7. The contribution from GlcNAc ranges between −3.1 and −3.9 kcal/mol, while Fuc3 contributes between −8.6 and −8.9 kcal/mol toward the total binding free energy for all cases (see Table 2). The contribution from Fuc3 in H-tetra BGA accounts for ∼70% of the total binding energy for both strains, while it reduces to ∼55% in the case of A-penta complexed with either strain (see Figure 7). Further, Figure 7 reveals that GlcNAc is the next important monosaccharide for the binding for all four complexes, accounting for ∼25% of the binding energy. Interestingly, only in the case of A-penta BGA bound to the El Tor strain, the contribution of Gal (−2.6 kcal/mol) to ΔG_bind is significant compared to the other three cases (Figure 8). Gal in A-penta BGA contributes approximately 4 times more favorably to the binding with ET compared to the classical strain because of the ∼3-fold increase in favorable interatomic electrostatic interactions (T_ele = −5.5 kcal/mol) relative to classical (T_ele = −1.9 kcal/mol). A careful inspection of Table 3 reveals that the electrostatic (T_ele) contribution from GlcNAc and Fuc3 to the binding is more favorable compared to van der Waals (T_vdW) interactions and varies between −6.6 and −12.9 kcal/mol for all complexes. However, it gets nearly canceled due to unfavorable polar desolvation free energy (T_GB). Therefore, the key contributor to the binding from these two monosaccharides is T_vdW, which varies between −3.4 and −7.6 kcal/mol.

Table 3. Decomposition of ΔG on a per-Monosaccharide Basis for All Four Complexes^a.

monosaccharide	TvdW	Tele	TGB	Tnp	TTOT
cCTB/H-Tetra BGA
reducing end OH	–0.2	–0.3	0.5	0.0	–0.1
GlcNAc	–4.3	–8.0	9.2	–0.6	–3.8
Gal	–2.3	–0.1	3.4	–0.3	0.7
Fuc3	–7.6	–12.3	12.5	–1.2	–8.7
Fuc2	–3.1	0.2	2.9	–0.6	–0.6
El Tor/H-Tetra BGA
reducing end OH	–0.3	0.1	0.2	–0.1	–0.1
GlcNAc	–3.4	–6.9	7.7	–0.5	–3.1
Gal	–2.0	–1.7	3.9	–0.2	0.0
Fuc3	–7.3	–12.0	11.6	–1.2	–8.9
Fuc2	–3.5	1.0	2.8	–0.7	–0.4
cCTB/A-Penta BGA
reducing end OH	–0.3	–1.6	2.2	–0.2	0.1
GlcNAc	–4.1	–6.6	7.2	–0.5	–3.9
Gal	–2.1	–1.9	3.5	–0.1	–0.6
GalNAc	–4.9	–1.5	5.2	–0.9	–2.1
Fuc3	–7.6	–12.9	13.0	–1.2	–8.6
Fuc2	–2.4	0.7	1.8	–0.5	–0.4
El Tor/A-Penta BGA
reducing end OH	–0.6	–1.3	1.9	–0.2	–0.3
GlcNAc	–3.4	–6.6	7.2	–0.4	–3.1
Gal	–1.8	–5.5	4.8	–0.1	–2.6
GalNAc	–3.9	–0.3	4.7	–0.8	–0.2
Fuc3	–7.3	–11.2	10.8	–1.2	–8.8
Fuc2	–3.2	2.0	1.4	–0.6	–0.4

^aEnergies are shown as contributions from the van der Waals (vdW), electrostatic (ele), polar (GB), and nonpolar solvation energy (np) of the side chain (S), backbone (B), and their sum (TOT) for CT-BGA complexes. All values are given in kcal/mol.

Figure 7.

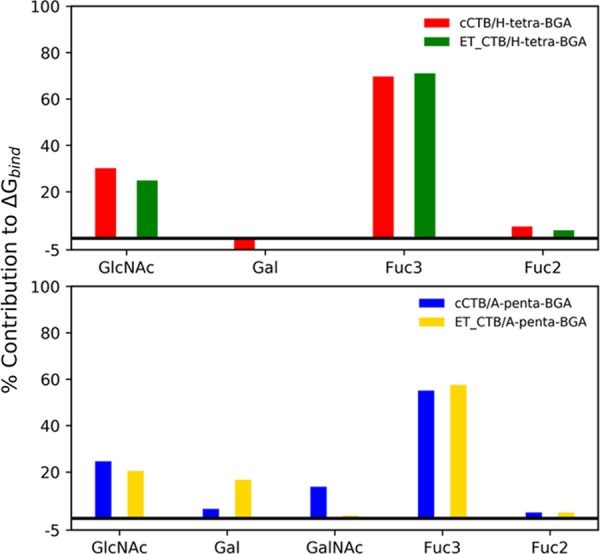
Percentage contribution by each monosaccharide in the total ΔG made by each BGA.

Figure 8.

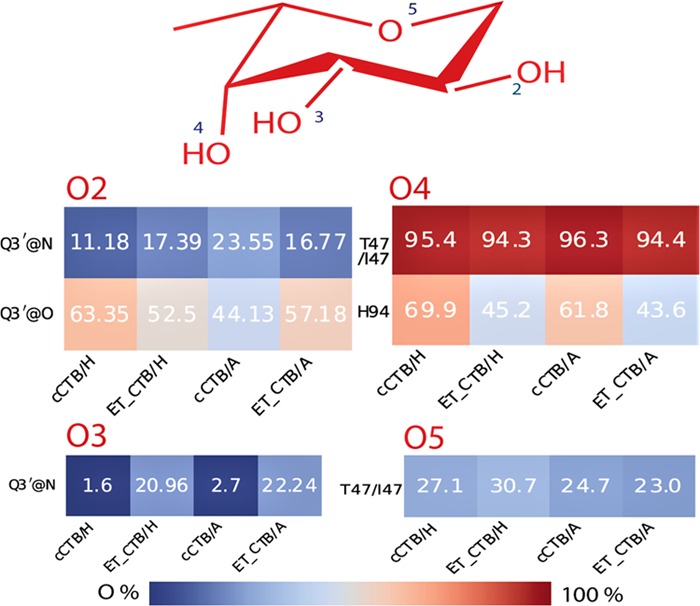
Hydrogen-bond profile of Fuc3.

Next, we calculated the contribution of each amino acid to the binding (Table 4) and plotted the CT/BGA interaction energy spectra (Figure S13, Supporting Information). A similar spectrum is obtained for all four cases. We note that H18/Y18, A46 T47/I47, P93, H94, and Q3′ are important residues for the binding of BGA and contributed to the binding by ≥−1.5 kcal/mol (Table 4). In the case of the classical biotype, T47 contributed by ∼−3.1 kcal/mol, while the corresponding residue (I47) in El Tor contributed by ∼−4.0 kcal/mol. In T47 (i.e., classical), the backbone (T_B) contributed more favorably to the binding than the side chain (T_S), while T_S is more favorable than T_B in I47 (El Tor). Table 4 further reveals that in cases of A46, H94, and Q3′, T_S is more favorable than T_B for all four complexes. In contrast, T_B is more favorable than T_S in P93 for all complexes. Here, it is worth mentioning that T_vdW (−1.9 to −3.9 kcal/mol) is more favorable compared to T_ele (−0.2 to −3.5 kcal/mol) for both A46 and H94 and T_ele is overcompensated by T_GB.

Table 4. Decomposition of ΔG on a per-Residue Basis for All Four Complexes^a,b.

residue	TvdW	Tele	TGB	Tnp	TS	TB	TTOT
cCTB/H-Tetra BGA
T47	–2.1	–3.4	2.5	–0.2	–0.5	–2.6	–3.1
H94	–2.5	–1.5	1.5	–0.3	–1.6	–1.2	–2.8
Q3′	–0.8	–5.5	4.5	–0.3	–2.3	0.1	–2.2
P93	–1.3	–1.5	0.7	–0.1	–0.7	–1.4	–2.1
A46	–2.1	–0.9	1.1	–0.2	–1.2	–0.9	–2.1
G45	–1.4	–2.5	2.3	–0.3	–0.4	–1.5	–1.9
El Tor/H-Tetra BGA
I47	–2.2	–3.7	2.2	–0.3	–1.9	–2.1	–4.0
H94	–2.9	–2.6	3.1	–0.4	–2.0	–0.8	–2.8
A46	–2.1	–0.5	0.7	–0.2	–1.3	–0.8	–2.1
Q3′	–0.4	–4.8	3.4	–0.2	–2.1	0.1	–2.0
P93	–1.0	–1.4	0.6	0.0	–0.6	–1.2	–1.8
cCTB/A-Penta BGA
H94	–3.2	–2.6	2.8	–0.5	–2.3	–1.1	–3.4
T47	–1.8	–3.7	2.5	–0.2	–0.6	–2.6	–3.2
Q3′	–0.8	–5.3	4.1	–0.3	–2.4	0.1	–2.3
G45	–1.5	–2.3	1.8	–0.2	–0.4	–1.8	–2.2
P93	–1.3	–1.3	0.7	0.0	–0.7	–1.3	–2.0
H18	–2.6	–2.5	3.5	–0.4	–1.9	–0.1	–2.0
A46	–1.9	–0.4	0.8	–0.2	–1.0	–0.7	–1.7
F48	–1.4	–0.7	0.7	–0.1	–1.1	–0.4	–1.5
El Tor/A-Penta BGA
I47	–2.1	–3.8	2.2	–0.3	–1.9	–2.1	–4.0
H94	–3.9	–3.5	4.4	–0.5	–2.7	–0.8	–3.5
Q3′	–0.4	–4.7	3.3	–0.2	–2.1	0.1	–2.0
A46	–2.2	–0.2	0.7	–0.2	–1.3	–0.5	–1.8
P93	–1.0	–1.2	0.6	0.0	–0.5	–1.2	–1.7

^aOnly residues with |T_TOT| ≥ 1.5 kcal/mol are listed.

^bEnergies are shown as contributions from the van der Waals (vdW), electrostatic (ele), polar (GB), and nonpolar solvation energy (np) of the side chain (S), backbone (B), and their sum (TOT) for CT-BGA complexes. All values are given in kcal/mol.

Subsequently, we performed the hydrogen-bond (h-bond) analysis for all four complexes to complement the above results, and the critical h-bonds between BGA and CT with their occupancies are shown in Table S2 (Supporting Information). It is observed from Table S2 that H94, T47/I47, Q3′, and G45 form h-bonds with BGAs for all cases during MD simulations, explaining high intermolecular electrostatic contributions to the binding from these residues (Figure S14, Supporting Information). Further, we observe that mainly Fuc3 and GlcNAc monosaccharides participated in forming h-bonds with CT.

In Figure 8, we have shown h-bonds between Fuc3 and CT. The h-bond between T47/I47@O and Fuc3@O4 remains nearly conserved (∼95%) during the simulation for all four complexes (Figure 8). Furthermore, an h-bond with an occupancy of ∼23–30% was formed between Fuc3@O5 and T47/I47@N-H. Since h-bonds were formed with the backbone atoms, T_B was found to be more favorable in T47/I47 than T_S. The glutamine residue from the neighboring monomer (i.e., Q3′) was also found to be interacting with Fuc3 by forming h-bonds with O2 and O3 atoms of the fucose ring. We complemented the above result by calculating the pairwise correlation function or the radial distribution function, g(r), of the water molecules with respect to the oxygen atoms of individual monosaccharide in the free (Figure S15A,B) and protein-bound (Figure S15C,D) states. In the case of free glycans, the intensity of the peak corresponding to Fuc2 and Fuc3 is found to be much higher compared to that of other monosaccharides (see Figure S15A,B). However, in the protein-bound form, the intensity of the peak of Fuc3 in both BGAs is greatly diminished (Figure S15C,D), while it remains unchanged for Fuc2. This is because Fuc3 was found to be involved in forming multiple h-bonds with the cholera toxin (Figure 8). Finally, for the whole glycan, the distribution of g(r) is the same, irrespective of whether the glycan is in the protein-bound or free states.

Overall, Fuc3 is found to be critical in recognizing the cholera toxin by BGA as the maximum number of h-bonds is formed by Fuc3 with CT (Figure 8). This is in agreement with a previous experimental study, elucidating the role of fucosylated molecules in interaction with CT.⁴³

Conclusions

First, in this study, we have elucidated the conformational dynamics of the Lewis Y blood group antigens, H-tetra, and A-penta oligosaccharides, in aqueous solution using 1 μs long accelerated molecular dynamics (aMD) simulations. We have also investigated the conformational preferences of BGAs bound to CT using cMD. Both oligosaccharides in aqueous solution were found to be flexible. A similar result was obtained for the core Le^X trisaccharide [Galβ(1–4)(Fucα(1–3))GlcNAcβ] in solution.^14,28 The aMD simulations suggest that the conformational ensemble of A-penta BGA is more diverse compared to that of H-tetra BGA. Three different conformers with varying populations were sampled for A-pentasaccharides, while a single conformer was populated in the case of H-tetrasaccharide. Moreover, the free energy surfaces of glycosidic linkages for both BGAs obtained from aMD simulations were found to be broader compared to those of the protein-bound form.

Interestingly, only aMD simulations revealed that A-pentasaccharide could adopt both open and closed forms in solution (Figure 5), while it takes an open conformation in the binding site. In contrast, H-tetrasaccharide remained in an open conformation in solution or bound form. Furthermore, aMD simulations revealed that for both oligosaccharides in the unbound state, ⁴C₁ and ¹C₄ puckers were sampled for all (GlcNAc, Gal, Fuc2, and Fuc3) but GalNAc monosaccharides, while either the ⁴C₁ (GlcNAc, Gal, GalNAc) or ¹C₄ (Fuc2, Fuc3) pucker conformation was sampled in cMD simulations of protein–glycan complexes. In the time scale of our cMD simulation, the other puckering states were not sampled due to the high energy barrier caused by the cyclization of the sugar ring.⁴⁴ The 1D free energy profile of the puckering angle (⊖) shows that only for the GlcNAc and Gal rings in H-tetra and A-pentasaccharides, the aMD simulations sampled the complete ⁴C₁ to ¹C₄ pucker transition. In the case of Le^X trisaccharide, the complete transition was observed only for GlcNAc, while only the ⁴C₁ pucker was sampled for the Gal ring.¹⁴

Second, we have studied the mechanism of binding of H-tetra and A-penta BGAs with the cholera toxin using the MM/GBSA scheme. A relatively stronger binding affinity was obtained for the O blood group determinant, H-tetrasaccharide, complexed with both biotypes compared to the A blood group determinant, A-pentasaccharide. This agrees with the experimental data. In the case of the CT/H-tetrasaccharide complex, both polar solvation free energy and configurational entropy were less disfavored compared to those in CT/A-pentasaccharide, resulting in higher binding free energy. Per residue decomposition of the total binding free energy shows that the terminal Fuc3 monosaccharide contributes most to the binding free energy compared to other carbohydrate residues, and it forms multiple h-bonds with CT. Overall, our study provides a detailed overview of the conformational preferences of Le^Y BGAs in solution and the protein-bound form and molecular basis of recognition of BGAs by the cholera toxin, which may further help in designing a more potent and reliable cholera toxin inhibitor as well as a vaccine to fight this century-old deadly disease.

Materials and Methods

MD Simulations of CT-BGA Complexes

We have simulated the pentameric CT-BGA complexes in aqueous solution using conventional molecular dynamics (cMD) simulations at 300 K. Initial coordinates of the four complexes were obtained from the Protein Data Bank (PDB IDs: 5ELB and 5ELC for H-tetra BGA with cCT and ET CT, respectively, and 5ELD and 5ELE for A-penta BGA with cCT and ET CT, respectively).¹⁵ The missing part of the crystal structure was built using the University of California, San Francisco, Chimera software.⁴⁵ In cases where the glycan was missing in the binding site of a monomer, we placed it by geometrically translating the glycan from the neighboring monomer. For all complexes, the AMBER ff14SB force field⁴⁶ was used for modeling the protein, and glycam06j-1⁴⁷ was employed for describing the glycan. All of the systems were solvated using TIP3P⁴⁸ water molecules in a truncated octahedral box, having a 10 Å distance between the solute and the wall of the box. An appropriate number of sodium ions were added to neutralize the system. Bonds involving hydrogen atoms were constrained using the SHAKE algorithm,⁴⁹ and the long-range electrostatic interactions were estimated using the particle-mesh Ewald (PME)⁵⁰ method. The nonbonded cutoff was set to 10 Å, and the temperature was kept fixed at 300 K using the Langevin thermostat⁵¹ with a collision frequency of 2 ps^–1. The energy minimization of the system was carried out in two stages: (i) 500 steps of steepest descent followed by another 500 steps of conjugate gradient with a harmonic restraint of 2 kcal/(mol Ų) applied on the solute and (ii) without any restraint on the solute using the steepest descent followed by conjugate gradient schemes. After the minimization, the systems were heated stepwise from 0 to 300 K with a restraint force of 2 kcal/(mol Ų) acting on the solute. A 50 ps simulation with the restraint of 2 kcal/(mol Ų) on the solute was carried out at a pressure of 1 atm to equilibrate the density. After that, we conducted 1 ns simulation under the NPT ensemble without any restraint on the solute. Finally, the production simulations were carried for 200 ns in the NPT ensemble with a time step of 2 fs using the pmemd.cuda module of AMBER 16.⁵²⁻⁵⁴ We recorded coordinates every 10 ps, resulting in 20 000 configurations.

aMD Simulations of Free Glycans

For better sampling, we also simulated BGAs in aqueous solution using the accelerated molecular dynamics (aMD) technique. We equilibrated the solute for 10 ns before applying the aMD boost to get the average potential energy and dihedral energy. After that, we used a dual boost potential using the following boost parameters. For H-tetrasaccharide, dihedral energies E_dih = 24.22 kcal/mol, α_dih = 3.5 kcal/mol; total potential energy E_tot = −13 222.0 kcal/mol; and α_tot = 807.1 kcal/mol were used. Similarly, in the case of A-pentasaccharide, dihedral energies E_dih = 16.6 kcal/mol, α_dih = 4.2 kcal/mol; total potential energy E_tot = −17 222.6 kcal/mol; and α_tot = 1047.0 kcal/mol were employed. Finally, aMD simulations were carried out for 1 μs under the NPT ensemble and the coordinates were stored every 10 ps.

Analysis

All of the trajectories obtained from the unbiased and biased simulations were analyzed using the Cpptraj⁵⁵ module of AMBER 16. Glycosidic torsion angles were defined as φ = O₅–C₁–O–C_n, ψ = C₁–O–C_n–C_(n–1) for α/β(1 – n) linkages. The relative free energy surfaces corresponding to the glycosidic angles were computed using the expression ΔG_x = −k_BT ln(ρ_x), where k_B is the Boltzmann constant, T is the temperature, and ρ_x is the probability density of the geometric coordinate x. As the value of this logarithm function is negative or zero, the final free energy value remains zero or positive. The state having the highest probability will always be 1; therefore, the minimum always stays at zero. For estimating the puckering conformation of the pyranose rings, we have adopted the generalized pseudorotation coordinates coined by Cremer and Pople.³⁶ Further, we followed the IUPAC convention to show different puckerings, which lead to the partition of ⊖ and φ plane in 38 regions. The one-dimensional free energy surface was also generated using the already stated Boltzmann formula, taking ⊖ from the puckering parameter as a reaction coordinate. For aMD simulations, we have employed the Pyreweighting scripts developed by the McCammon group⁵⁶ for constructing the potential of mean force (PMF) surface from the biased potential. This script uses the 10th-order Maclaurin series expansion to reweigh the total boost energy from each frame.

For estimating the binding free energy of CT-BGA complexes, the popular molecular mechanics generalized Born surface area (MM/GBSA)³² scheme was used. For protein–glycan systems, it has been shown in previous studies^57,58 that MM/GBSA outperforms the computationally expensive MM/PBSA.⁵⁹⁻⁶¹ The MM/GBSA scheme has been discussed elsewhere.^{37−39,41,62,63} We have used the option (igb = 2)⁶⁴ within the MM-GBSA framework for all cases. We extracted the trajectory of a dimer pair with one oligosaccharide from the pentameric complex trajectory for estimating the binding free energy. Two adjacent monomers were considered because the ligand was found to form a stable hydrogen bond with the glutamine residue of the neighboring monomer (Q3′). We have considered 8000 frames for computing the binding free energy. The normal mode analysis (NMA) method was employed for calculating the configurational entropy, and 50 frames were used for the calculation.

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acsomega.9b03398.

• Hydrogen-bond occupancy, 2D free energy landscapes, ligand RMSD, time evolution of puckering conformation, Mercator representations of puckering conformations, puckering free energy profiles, per-residue decomposition of free energy, and pairwise correlation function (PDF)

The authors declare no competing financial interest.