Using the density of Kuiper Belt Objects to constrain their composition and formation history

Abstract

Telescopic observations of Kuiper Belt objects have enabled bulk density determinations for 17 objects. These densities vary systematically with size, perhaps suggesting systematic variations in bulk composition. We find this trend can be explained instead by variations in porosity arising from the higher pressures and warmer temperatures in larger objects. We are able to match the density of 14 of 17 KBOs within their 2σ errors with a constant rock mass fraction of 70%, suggesting a compositionally homogeneous, rock-rich reservoir. Because early ²⁶Al would have removed too much porosity in small (~100 km) KBOs we find the minimum formation time to be 4 Myr after solar system formation. This suggests that coagulation, and not gravitational collapse, was the dominant mechanism for KBO formation. We also use this model to make predictions for the density of Makemake, 2007 OR₁₀, and MU₆₉

1. Introduction

As of this writing there are 17 Kuiper Belt systems in which the orbit of the secondary has been determined well enough to meaningfully estimate the system mass (Table A.2). In these cases, with the addition of radii measurements from either occultation or direct imaging, the primary’s density can be determined. In small KBOs the uncertainty in radius can be large, leading to a large uncertainty in density. Despite this there is a clear systematic trend of larger objects also having a higher density (Brown, 2012).

There are at least three mechanisms that could generate the oberved KBO density distribution. The first is that large KBOs could contain higher density ice phases. However, the low internal pressures in even the largest KBOs (Grundy et al., 2007; Brown, 2012), along with an absence of any evidence for such high-pressure phases in Pluto (McKinnon et al., 2017), rules out this possibility. The second is there could be a compositional difference between small and large KBOs. This would require smaller KBOs to be significantly more ice rich than their larger counterparts (Brown, 2012). The most commonly discussed mechanism to generate such a difference is large disruptive impacts. Modeling has been done to estimate the effect impacts could have on the bulk density of particular systems (Leinhardt et al., 2010; Canup, 2011; Barr and Schwamb, 2016) but not on the overall density distribution. Estimates using existing scaling laws suggest that impacts are an implausible explanation due to the large fraction of material that would need to be removed from the system (Brown, 2012). A compositional gradient could also arise if larger bodies could lose volatiles preferentially due to accretional heating (McKinnon and Mueller, 1988; Bierson et al., 2018) but we show below that this mechanism is not plausible (see Appendix C). The third possibility is that small KBOs contain substantial porosity (Brown, 2012) not present in larger bodies, and is the focus of this work.

Experimental work has shown a series of processes that remove macro-porosity in different temperature-pressure regimes. Below 1 MPa significant macro porosity can be maintained in cold water ice (Durham et al., 2005; Yasui and Arakawa, 2009). Between 1 and 10’s of MPa brittle failure begins to cause the porosity to fall rapidly. In this regime pore closure is independent of temperature. The degree of pore closure due to brittle failure is dependent on the rock mass fraction. At pressures greater than 10’s of MPa ductile deformation dominates. In this high pressure regime compaction depends on both temperature and rock mass fraction. Durham et al. (2005) found that pure water ice at temperatures of 77 K could support porosity of 10%–20% beyond 100 MPa. In contrast Yasui and Arakawa (2009) found pure water ice samples at 260 K would contain only ~1% porosity at 30 MPa.

In this work we test if porosity is able to explain the observed density distribution of KBOs. This is done with a model of KBO thermal evolution coupled with the porosity evolution. We examine the sensitivity of these results to the KBO rock mass fraction and formation time. We find that the observed density distribution can be well fit with a nearly uniform rock mass fraction. We also find that small KBOs ( ~ 100 km) must have formed after the decay of ²⁶Al to maintain their high porosity. We discuss the implications of these results for KBO formation.

2. Model

We use a 1D model to probe the effect of the two different pore-closure processes on the bulk density. All model runs begin with an undifferentiated KBO that has an initial bulk porosity ϕ₀ and rock mass fraction f_m = M_s/(M_s+ M_i). Here M_s is the mass of the silicates and M_i is the mass of the ice. For each model run the effect of brittle failure is calculated followed by the thermal-ductile pore closure modeling.

Brittle failure is assumed to take place on geologically rapid timescales and is modeled following the empirical results of Yasui and Arakawa (2009). This is done by iteratively calculating the internal pressure and updating the ice and silicate porosity via

$${\varphi }_i\left(P\right)=\max \left({\varphi }_0\exp \right(b_{1}P),{\varphi }_c)$$ (1)

$${\varphi }_s\left(P\right)=\min ({\varphi }_0{P}^{b_2},{\varphi }_0)$$ (2)

where P is the local lithostatic pressure in MPa. The value ϕ_c is the assumed porosity that can be supported by matrix in cold conditions (Durham et al., 2005). Values for the empirical constants used are given in Table 1. These components are then mixed by their volume fractions to get the bulk porosity of each layer. Recalculation of the pressure profile and updating of the porosity profile is iterated until the porosity profile converges. This sets the initial porosity profile for the thermal modeling.

Table 1:

Parameters used. Values for b₁, b₂ based on Yasui and Arakawa (2009). ϕ_c value based on Durham et al. (2005). Other parameter values are from Bierson et al. (2018).

	Symbol	Nominal Value	Units
Ice Reference Viscosity	η0	1014	Pa s
Viscosity Reference Temperature	T0	270	K
Activation Energy	Q	60	kJ/mol
Ice Thermal Conductivity	kice	0.4685 + 488.12/T	W/(m K)
Silicate Thermal Conductivity	ks	3.0	W/(m K)
Surface Temperature	Ts	40.0	K
Initial Temperature	T0	100.0	K
Specific Heat	Cp	1000	J/(kg K)
Ice Density	ρice	920	kg/m3
Silicate Density	ρs	3500	kg/m3
Initial Porosity	ϕ0	0.60
Strength supported porosity	ϕc	0.20
Empirical compaction parameter (ice)	b1	−0.1	MPa−1
Empirical compaction parameter (silicate)	b2	−0.11

Modeling the subsequent evolution of the porous structure of KBOs is handled by the thermal evolution model of Bierson et al. (2018). The numerical methods used are presented in Appendix B. This model assumes that porosity is primordial and removed over time. The final porosity structure is then dependent on the thermal history. Following Besserer et al. (2013) we model the change in porosity as a function of pressure (P) and viscosity (η) via

$$\frac{d\varphi }{dt}=\varphi \frac{P}{\eta \left(T\right)}.$$ (3)

Here the ice viscosity is taken to be Newtonian and is assumed to vary as

$$\eta \left(T\right)={\eta }_0\exp \left(\frac{Q}{R_{g}T}-\frac{Q}{R_g{T}_0}\right)$$ (4)

where Q is the activation energy, R_g is the gas constant and η₀ is the reference viscosity at T₀ (Table 1). It was shown by Besserer et al. (2013) that equation (3) provides a reasonable approximation to more complicated pore-closure models (Eluszkiewicz, 1990; Leliwa-Kopystyński and Kossacki, 2000).

This model was updated from Bierson et al. (2018) to include short-lived radioisotopes. The method by which porosity affects thermal conductivity has also been updated. The effect of porosity on thermal conductivity is one of the largest uncertainties in modeling high porosity objects. The true conductivity of a porous mixture depends on the geometry of the matrix (how interconnected the pores are) and the effective thermal conductivity of the pore space itself. While there are no direct constraints on the thermal conductivity of KBOs, there exists a wealth of theoretical work to bound the value. A detailed review of different physical models is given in Carson et al. (2005).

In this work the thermal conductivity is computed for each timestep as follows. We begin by assuming the rock-ice matrix itself is well mixed. As such we use the parallel model to combine an assumed constant silicate conductivity and temperature dependent ice conductivity (see values in Table 1).

$$k_0(f_{rock},T)=k_s\left(f_m\frac{{\rho }_s}{\rho }\right)+k_{ice}\left(1-f_m\frac{{\rho }_s}{\rho }\right)$$ (5)

We then assume heat transfer through the porosity itself is highly inefficient and apply the parallel model via

$$k\left(\varphi \right)=k_0(f_{rock},T)(1-\varphi )$$ (6)

The parallel model is the upper bound for the thermal conductivity in a solid medium. Any lower values chosen for the thermal conductivity would lead to higher densities (more porosity removed) for smaller objects. Radiation may slightly enhance the heat transfer in a porous material. Shoshany et al. (2002) calculated the effective thermal conductivity including radiation and the parallel model is in the middle of the range of values they predict. Changing our thermal conductivity model to the maximum conductivity model of Shoshany et al. (2002) results in at most an 8% decrease in predicted density at intermediate ( 400 km) radii, and less at larger or smaller radii. Neglecting the effect of porosity on thermal conductivity entirely results in at most a 10% change in the final density. This change is too small to alter any of our conclusions.

2.1. Parameters and sensitivity

Table 1 gives the nominal values for all the parameters used in this modeling. These values are generally taken from Bierson et al. (2018). The new parameters are those for the brittle failure modeling taken from Durham et al. (2005) and Yasui and Arakawa (2009). The other important controlling parameter is the initial porosity. Here a nominal value of 60% is used as this gives an object with f_m = 70% a density of ~750 kg/m³. This high porosity is consistent with measurements made for asteroids, which Baer et al. (2011) find exhibit a range of porosity from 10%–70% for radii up to ~150 km. While porosity is difficult to infer for comets as we do not know the grain density, the bulk density of comets like 67P/Churyumov-Gerasimenko (532 ± 7 kg m³, Jorda et al. (2016)) imply a porosity of > 40%.

Our model has very little sensitivity to most of the parameters in Table 1. A factor of two change in C_p leads to a 4% change in the bulk density (~50 kg m³). Changing η₀ to 10¹⁷ Pa s also changes the final density by up to 4%. Changing the initial porosity changes the density of small KBOs (as expected) but does not notably change the radius at which density begins to increase. While each of these parameters may change the rate of change or the timing of when porosity closes, the final bulk density is a robust outcome of our model runs.

2.2. Processes not modeled

The modeling in this work does not include melt production, differentiation, convection, impacts, and tidal heating. Here we discuss each of these process in turn and their potential impact on our results. Melting to form a subsurface ocean will increase the bulk density while the ocean is present, but the effect is small and will disappear once the ocean freezes (McKinnon et al., 2017; Bierson et al., 2018). Differentiation redistributes the mass within the body; however, because no mass is lost the bulk density is unchanged. As differentiation occurs a small amount of extra gravitational energy will be released which is not included here (Desch et al., 2009; Malamud and Prialnik, 2015). The redistribution of ice and silicates will also change the magnitude of compression but given the low internal pressures of KBOs we expect this to have only a minor effect (Bierson et al., 2018). Since differentiation redistributes the heat source (silicates) towards the center of the body, higher internal temperatures will result, making our porosity estimates conservatively high. Convection will remove heat more rapidly than in our conductive models, but if ice is warm enough to convect, all porosity will already have been removed.

In a high porosity surface, impacts will also reduce the bulk porosity. This effect is limited to the upper tens of kilometers (Milbury et al., 2015), small compared to the size of objects considered here. It is possible that during the formation of larger KBOs, impacts may have removed porosity in a significant fraction of the outer ice shell. Large disruptive impacts into differentiated KBOs could change f_m and are further discussed in section 3.

All the KBOs discussed here are either in binary systems or experienced capture (Goldreich et al., 1989; Agnor and Hamilton, 2006). Because of this tidal heating may have been an extra energy source. The amount of energy and its importance to the overall thermal evolution is dependent on the initial orbital configuration and internal structure of the KBOs (Saxena et al., 2018).

The important point for this work is that all these processes have the same net effect of removing more porosity than predicted by our model. Similarly, we assume an upper limit for the thermal conductivity at a given porosity. A lower thermal conductivity would allow more heat to build up in the interior, removing additional porosity. As a result our model runs represent a lower bound on the bulk density (the most porosity that can be retained).

In this work we also assume that the ‘ice’ component is dominated in composition by H₂O. Depending on their formation conditions, some KBOs may have incorporated ices during formation such as N₂, NH₃, CO, CO₂, and CH₄. Most of these ices have densities close to that of water ice (950, 850, 1000, 1000–1600, 500 kg/m³ respectively) and so cannot have a significant effect on the bulk density at reasonable concentrations (Satorre et al., 2008, 2013; Umurhan et al., 2017). For example, to change the bulk density by ~300 kg/m³ through the addition methane (the ice with the lowest density) would require adding ~8% of the total body mass. There is also no clear reason these compositional differences would depend on size, the main focus of this work.

3. Results

A comparison of our model results with the observed KBO values are shown in Figure 1a. Our model predicts that the transition from small porous objects to dense KBOs occurs quickly between a radius of 200km-500km. This transition radius is set by the balance between heat production (which depends on f_m and radioactive half-life) and conductive heat loss (which depends on the body size). An analogous argument has been made for understanding the minimum size of differentiation in asteroids (Grimm and McSween Jr, 1993).

Figure 1:

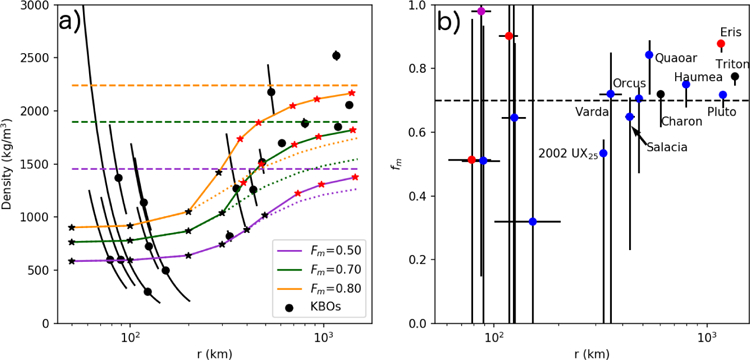
a) Density of observed KBOs with 1σ errors in black. Error bars only account for uncertainty in radius. See Table A.2 for citations. Each color refers to a fixed rock mass fraction indicated in the legend. Flat dashed lines show the density of a non-porous object. Dotted line shows the expected density only accounting for brittle failure. Solid lines show model results that include the effects of thermally controlled viscous relaxation. Individual model runs are show with stars. Red stars indicate models where internal temperatures met or exceeded 250 K at some point. All thermal models were started at 10 Myr to avoid the effects of ²⁶Al decay (See Figure 2). b) Estimated rock mass fraction of each KBO by interpolating model runs. Horizontal line is f_m = 0.7. Colors indicate object class where blue are classical and resonant KBOs, red is scattered disk object, magenta is centaur, and black are satellites. The upper f_m limit is the interpolated model value using the 1σ density upper bound. The lower f_m limit is the f_m calculated assuming no porosity and the 1σ density lower bound.

Around this transition diameter internal temperatures begin to reach or exceed the melting point of water (red stars). For the reasons presented in Section 2.2 these points are more likely to underestimate the bulk density. The maximum bulk density for a given f_m (neglecting compression) is shown by the dashed lines. This is the density an object of a given f_m would have with no porosity. We estimate the f_m for each KBO in Figure 1b with error bars that include the observational uncertainty and in addition treat our model and zero porosity values as limiting cases (see Figure caption for details). This is a conservative estimate that likely overestimates our error particularly for small KBOS and on the lower limits.

For a rock mass fraction of 70% our model matches the density observations for ten of seventeen KBOs within 1σ and fourteen of seventeen within 2σ (Figure 1b). The three objects not well fit by this model are Triton, Eris, and 2002 UX₂₅. Eris and Triton both require f_m > 70%. Triton’s high rock fraction might be a consequence of the extreme heating it experienced during capture (Goldreich et al., 1989). There is also a hint that scattered disk objects may have a higher f_m compared with classical KBOs. This could be due to more energetic collisions caused by their more dynamically excited orbits; such collisions will have preferentially removed the ice-rich mantles of differentiated objects, potentially explaining the higher rock fraction of Eris (Lissauer and Stewart, 1993; Barr and Schwamb, 2016). 2002 UX₂₅ is below our expected density. We are not aware of any processes that might significantly lower the bulk density without lowering f_m. Our model predicts that f_m~50% for 2002 UX₂₅. It is worth noting that at present no light curve or occultation measurements have been used to constrain the shape of 2002 UX₂₅. If it is significantly non-spherical in shape this could lead to an overestimation of its volume, and thereby an underestimation of the density. Whatever the case, this object remains enigmatic but is also only a single data point.

We can also place a constraint on the formation time of KBOs as follows. The earlier in solar system history KBOs form the more short lived radiogenic isotopes will be incorporated. It is these isotopes that are responsible for differentiation of small asteroids (Grimm and McSween Jr, 1993); in the case of KBOs, if these objects form too early, sufficient ²⁶Al will be present that all porosity is removed. We assume chondritic abundances of ²⁶Al, ⁶⁰Fe, ⁵³Mn in the silicate component of modeled KBOs (Table A.3). Figure 2 shows the final density of modeled KBOs as a function of their formation time. If a small KBO with f_m = 0.7 forms before 5 Myr after CAI the internal porosity will be removed by the heat from the decay of short lived isotopes (primarily ²⁶Al). At f_m = 0.5 this limit is pushed to 4 Myr after CAI. As previously noted other feedbacks would further remove porosity once the object starts to warm. Based on these results we conclude that 4 Myr is a lower bound on the KBO formation time. This is consistent with the modeling of Merk and Prialnik (2006) who found that objects larger than a few kilometers radius reach internal temperatures sufficient for liquid water if formed with ²⁶Al still live. A similar argument has been made in favor of a low ²⁶Al in the small Saturnian satellites(Leliwa-Kopystyński and Kossacki, 2000). This is also consistent with McKinnon et al. (2017) who argue that Pluto couldn’t be fully differentiated before the Charon-forming impact, and therefore that Pluto did not form while ²⁶Al was live.

Figure 2:

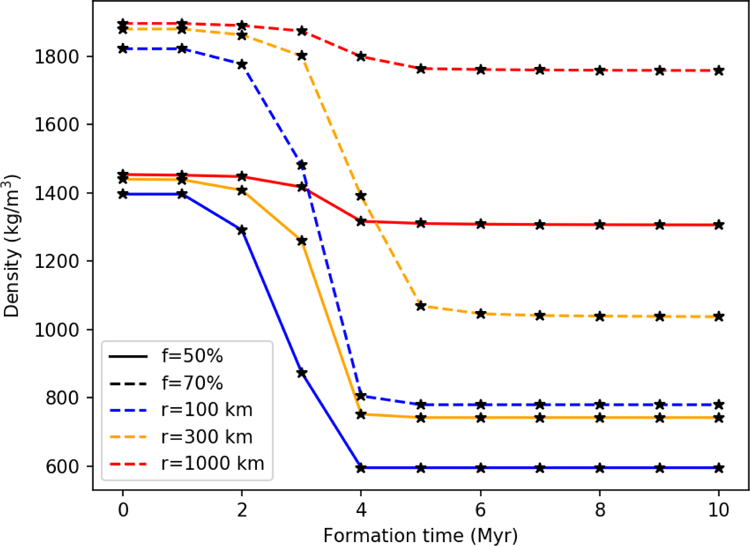
Modeled final density of three KBOs of different sizes formed a different times after CAI. Models are shown with f_m=0.70 or 0.50 and with an initial temperature of 40 K. If any small (~100 km-scale) KBOs formed earlier than 4 Myr after CAI the heat from short lived radioisotopes would remove a significant fraction of their internal porosity.

An analogous argument can be made that small, low density KBOs cannot have experienced large amounts of tidal heating. As more precise estimates of the orbits and individual masses of KBO binary systems become available this should allow constraints to be placed on the tidal parameters such as k₂/Q (Saxena et al., 2018).

4. Dicussion

The results above show that small KBOs cannot have formed prior to 4 Ma, as otherwise they would have experienced too much porosity reduction. Placing this timing constraint on the formation of KBOs allows us to test the formation models that have been proposed. There are currently two main models for KBO formation. The coagulation model proposes that KBOs formed from kilometersized precursors that interacted dynamically to form larger bodies (Kenyon, 2002; Kenyon et al., 2008; Schlichting and Sari, 2011). Because of the long orbital periods this process takes tens of millions of years to form the large KBOs. Alternatively the Nesvorný et al. (2010) model proposes that decimeter sized ‘pebbles’ could be aggregated by the streaming instability to undergo gravitational collapse. This gravitational collapse model naturally forms binary systems which are common in the Kuiper belt and dynamical evidence suggests may have been more common early in the solar system (Petit and Mousis, 2004; Fraser et al., 2017). KBO binaries could form through gravitational interactions (Goldreich et al., 2002) although it remains open if this mechanism is efficient enough to form the inferred number of binary systems.

Because the Nesvorný et al. (2010) model invokes the streaming instability, it requires the presence of a gas disk. Astronomical observations of disks around young systems suggest disk lifetimes of three to ten million years (Haisch et al., 2001; Williams and Cieza, 2011). Constraints from the inner solar system suggest that the gas was present until 4 – 5 Myr after solar system formation (Johnson et al., 2016; Wang et al., 2017; Kruijer et al., 2017). Our results constrain KBO formation to be after 4 – 5 Myr, around the same time the gas disk is dispersing in the inner solar system.

One interpretation of this result could be that the gas disk must have persisted longer in the outer solar system. How plausible this is depends on what mechanism(s) are responsible for removing the gas disk in the outer solar system (Matsuyama et al., 2003). This explanation would also require that KBO formation only occur after 4 Myr; if collapse were operating before 4–5 Myr, small dense KBOs should have formed, but are not observed. The alternative interpretation is that our constraint favors KBO formation via the coagulation model. In this case there is no need for special timing because the ~100 km KBOs naturally form long after the shortlived isotopes are extinct.

This work also has implications for the dynamical environment of the Kuiper Belt. The near constant f_m is in stark contrast with the inner solar system where core mass fractions vary from 2% (the Moon, Weber et al. 2011) to 70% (Mercury, Rivoldini et al. 2009). This suggests that there was much less erosion of material by impacts relative to the inner solar system. This may be due to the fact that giant impacts between KBOs, such as the one that may have formed the Pluto-Charon system, do not necessarily lead to large changes in the bulk composition (Canup, 2011). A relative absence of giant impacts is also consistent with the preponderance of binary systems being formed by long-range dynamical interactions (Goldreich et al., 2002).

Our results suggest that KBOs form a homogenous population, in terms of their bulk composition. While variations in surface color certainly exist, and appear to be related to dynamical characteristics (Brown, 2012; Dalle Ore et al., 2013; Tegler et al., 2016), we see little evidence of systematic variations in bulk composition, except for a hint that scattered disk objects are more rock-rich (Fig 1b).

Going forward we expect future observations to be able to test the model presented here. Moons have recently been discovered for Makemake (Parker et al., 2016) and 2007 OR₁₀ (Kiss et al., 2017) making density measurements likely in the near future. Our results that both of these objects should have bulk densities similar to, or slightly less than, that of Pluto (≈1800 kg m⁻³). In contrast, if a mass measurement is possible during the New Horizons flyby of 2014 MU₆₉ (r∼ 30 km) we expect it to have a low density of ∼ 750 kg/m³.

5. Conclusion

We find the density distribution of KBOs is best explained not by variations in composition, but in bulk porosity. KBOs transition from highly porous to having only a surface porous layer when the internal heat production by radioactive decay outpaces the rate of energy transport by thermal conduction. Because the large amount of energy in ²⁶Al would have melted even small KBOs (r ~ 100 km) we conclude they must have formed ~5 Myr after CAI. As observations of KBO density are refined and more acquired more narrow constraints will be placed on the range of compositions within the Kuiper Belt.

Appendix A. Observations and parameters

Table A.2:

Density values used.

Name			Density (kg/m3)	Diameter (km)	Source
Typhon	42355	2002 CR46	600	157 ± 34	Stansberry et al. (2012)
Ceto	65489	2003 FX128	1370	174 ± 17	Grundy et al. (2007)
Teharonhiawako	88611	2001 QT297	600	${178}_{-36}^{+33}$	Vilenius, E. et al. (2014)
		2001 QC298	1140	${235}_{-23}^{+21}$	Vilenius, E. et al. (2014)
Altjira	148780	2001 UQ18	300	${123}_{-69}^{+19}$	Vilenius, E. et al. (2014)
Sila	79360	1997 CS29	730	${249}_{-31}^{+30}$	Vilenius, E. et al. (2014)
Lempo	47171	1999 TC36	500	304 ± 101	Stansberry et al. (2006)
	55637	2002 UX25	820	652 ± 12	Brown (2013)
Varda	174567	2003 MW12	1270	${705}_{-75}^{+81}$	Vilenius, E. et al. (2014)
Salacia	120347	2004 SB60	1260	866 ± 37	Brown and Butler (2017)
Orcus	90482	2004 DW	1520	958 ± 23	Fornasier, S. et al. (2013)
Quaoar	50000	2002 LM60	2180	1070 ± 38	Vilenius, E. et al. (2014)
Charon			1700	1212 ± 2	Nimmo et al. (2016)
Haumea	136108	2003 EL61	1885	1595 ± 11	Ortiz et al. (2017)
Eris	136199	2003 UB313	2520	2326 ± 12	Brown et al. (2011)
Pluto	134340		1850	2376 ± 3	Nimmo et al. (2016)
Triton			2060	2706 ± 1.8	Thomas (2000)

Table A.3:

Radioactive isotope values used. Long lived isotope values from Robuchon and Nimmo (2011). Short lived isotope values from Castillo-Rogez et al. (2007) and Castillo-Rogez et al. (2009). Concentration is the abundance of that element relative within the silicate. For ⁶⁰Fe we use the value from Tang and Dauphas (2012).

Isotope	Concentration (ppb)	Specific heat production (W/kg)	Half-life (yrs)
235U	5.4	568.7 × 10−6	7.04 × 108
238U	19.9	94.65 × 10−6	4.47 × 109
40K	737.9	29.17 × 10−6	1.28 × 109
232Th	38.7	26.38 × 10−6	1.4 × 1010
26Al	600	0.355	7.16 × 105
60Fe	100	7.0 × 10−2	1.5 × 106
53 Mn	25.7	2.7 × 10−2	3.7 × 106

Appendix B. Thermal model details

This section details the methods used in our numerical model. Everything in this section is consistent with the description in Bierson et al. (2018). For differences between this model and Bierson et al. (2018) see Section 2.

To account for the radial variation in conductivity (k), layer thickness (∆z), and density (ρ) of each grid point (subscript i), we use the heat conduction equation from (Kieffer, 2013) modified to spherical geometry. The following equation is derived in Bierson et al. (2018).

$$\mathrm{\Delta }{T}_i=\frac{-2\mathrm{\Delta }t}{{\rho }_{i}C{p}_i\mathrm{\Delta }{z}_i{r}_i^2}\left[r_{i+1/2}^2\frac{T_{i+1}-T_i}{\frac{\mathrm{\Delta }{z}_{i+1}}{k_{i+1}}+\frac{\mathrm{\Delta }{z}_i}{k_i}}-r_{i-1/2}^2\frac{T_i-T_{i-1}}{\frac{\mathrm{\Delta }{z}_{i-1}}{k_{i-1}}+\frac{\mathrm{\Delta }{z}_i}{k_i}}\right].$$ (B.1)

Here ∆t is the model timestep and r_i is the radial location of the cell i.

As pore space closes the local density and therefore the layer thickness will change. To calculate the change in layer thickness it is convenient to define a quantity, Ψ, that is the ratio of the initial and final layer density

$$\mathrm{\Psi }=\frac{{\rho }_0}{{\rho }_f}.$$ (B.2)

As derived in Bierson et al. (2018), Ψ is related to the change in the radial position of the top of the layer (∆R) in terms of the initial layer thickness (∆z₀) and the original location of the layer top (R_t,0) assuming a fixed bottom boundary.

$$\mathrm{\Delta }{R}_t=\left\{{\left[{\left(1-\frac{\mathrm{\Delta }{z}_0}{R_{t,0}}\right)}^3(1-\mathrm{\Psi })+\mathrm{\Psi }\right]}^{1/3}-1\right\}{R}_{t,0}$$ (B.3)

After a layer expands or contracts the radial position of all the layers above needs to be adjusted accordingly. The spherical geometry causes the change in the radial position of the layer bottom (∆a) to be different from the change of the radial position of the layer top (∆b). For the layer immediately above the layer that has changed density, ∆R = ∆a. With this constraint, and conservation of volume, we can calculate the change in layer thickness (∆(∆z)) for each layer above the layer that changed density.

$$\mathrm{\Delta }b=\left\{{\left[\left(1+\frac{\mathrm{\Delta }a-\mathrm{\Delta }{z}_0}{R_{t,0}}\right)-{\left(1-\frac{\mathrm{\Delta }z}{R_{t,0}}\right)}^3\right]}^{1/3}-1\right\}{R}_{t,0}$$ (B.4)

$$\mathrm{\Delta }\left(\mathrm{\Delta }z\right)=\mathrm{\Delta }b-\mathrm{\Delta }a$$ (B.5)

Because the radial position of each layer, R, is assumed to be at the layer center (not the center of mass), the change in the layer center is given as

$$\mathrm{\Delta }R=\frac{\mathrm{\Delta }a+\mathrm{\Delta }b}{2}$$ (B.6)

The model ∆t is recalculated at the start of each timestep using the Courant criterion as

$$\mathrm{\Delta }t=0.3\min \left(\mathrm{\Delta }{z}_i^2{\rho }_{i}C{p}_i/k_i\right).$$ (B.7)

Appendix C. Mass loss during formation

In Bierson et al. (2018) it was suggested that the gravitational potential energy of a forming KBOs could cause a density gradient with size. The idea is that if accretion is sufficiently rapid, the surface temperatures could exceed the melting point of water ice. At this point a temporary atmosphere would form in vapor pressure equilibrium with the liquid surface. Given the low gravity of KBOs this atmosphere would be rapidly lost via hydrodynamic escape. The very fast accretion times of the gravitational collapse model (~100 yrs) made this plausible (Nesvorný et al., 2010). Because the gravitational potential energy scales roughly as r⁵ we suggested that much more water could be driven off larger KBOs, leading to their higher density. In this appendix we construct a model for this process and find it cannot significantly affect the bulk density of KBOs.

Following the work of Kuramoto and Matsui (1994), we can write the energy balance of a forming KBO following

$$\begin{gathered} \underset{\begin{array}{l}\text{Gravitational}\hspace{0.17em}\text{potential}\\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\text{energy}\end{array}}{\underbrace{\frac{GM\dot{M}}{r}}}=\underset{\text{Blackbody}\hspace{0.17em}\text{radiation}}{\underbrace{4\pi r^2\sigma T^4}}+\underset{\begin{array}{l}\text{Warming}\hspace{0.17em}\text{incomming}\\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\text{material}\end{array}}{\underbrace{C_p\dot{M}(T-T_0)}} \\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}+\underset{\text{Warming}\hspace{0.17em}\hspace{0.17em}\text{surface}\hspace{0.17em}\hspace{0.17em}\text{layer}}{\underbrace{C_{p}fM\dot{T}}}+\underset{\text{Mass}\hspace{0.17em}\hspace{0.17em}\text{loss}}{\underbrace{\mathrm{\Phi }\left(T\right)\left(L_v+\frac{GM}{R}\right)}} \end{gathered}$$ (C.1)

Here dots indicate time derivative, M is the object mass, r is the radius, σ is the Stefan-Boltzmann constant, T is the surface temperature, C_p is the specific heat at constant pressure, T₀ is the temperature of objects before accretion, f is the fraction of the body mass in equilibrium with the surface temperature, L_υ is latent heat of vaporization, and Φ(T) is the hydrodynamic escape rate (kg/s) assuming an isothermal atmosphere (Catling and Kasting, 2017). This formulation assumes internal thermal diffusion is not important on the timescale of formation. It also ignores the energy input from solar radiation which would effectively set a lower limit on the temperature. We solve Equation C.1 by assuming a function for $\dot{M}$. We found through sensitivity testing that the resulting temperature distribution is very insensitive to the chosen form of $\dot{M}$. For the results presented here we use the following equation from (Kuramoto and Matsui, 1994).

$$\dot{M}=7.15{\left(\frac{M}{M_f}\right)}^{2/3}\frac{M_f-M}{\tau }$$ (C.2)

Here M_f is the final satellite mass and τ is the accretion time.

The results of this modeling are shown in Figure C.3. In agreement with Kuramoto and Matsui (1994) we find that the most loss occurs around a formation timescale of ~10⁴ years. This is because this timescale balances the requirement that the energy delivery rate be high enough while providing a relatively long period over which escape can occur. We find however that very little mass is lost as most of the energy goes into warming the material from the cold background temperature (40 K). Lowering the initial density further to try and match the observed density of small KBOs would further reduce the energy budget and allow for even less mass loss than is shown here. From this we conclude that this process of accretional heating followed by hydrodynamic escape could not have significantly contributed to the density contrast observed in KBOs.

Figure C.3:

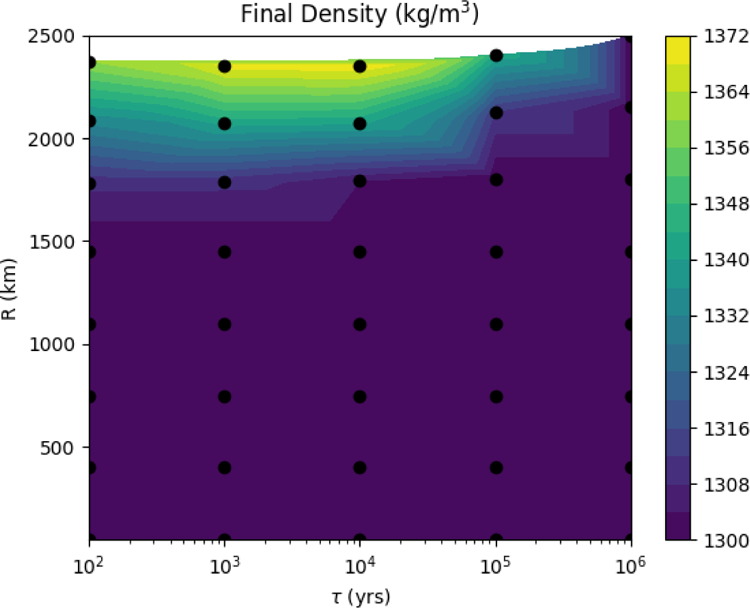
Final density obtained after integrating Equation C.1. Black dots are individual model runs. The initial material density used is 1300 kg/m³ and the background temperature is 40K. Even in ideal conditions (large objects forming in ~10⁴ yrs) very small changes in the final bulk density are found.