Abstract
PURPOSE:
To investigate the accuracy of Zernike and Fourier reconstruction algorithms in describing simulated wavefront data from corneal topography of normal and abnormal eyes.
METHODS:
Corneal topography (Orbscan IIz) was collected on 87 normal, 27 keratoconus, 9 penetrating keratoplasty (PKP), and 20 postoperative LASIK symptomatic eyes over a 6-mm pupil. Raw data from slit images were converted into elevation maps, which were then resampled at resolutions of 100, 300, and 500 μm. Differences in elevation between adjacent pixels were used to generate simulated wavefront slope data. Both conventional Zernike and iterative Fourier algorithms were used to reconstruct the elevation map from the same slope information. The difference between the reconstructed and original maps was used to evaluate reconstruction performance, quantified by the residual root-meansquare (RMS) error.
RESULTS:
When using the Zernike-based method, residual RMS error decreased substantially as the number of modes used in the reconstruction increased up to approximately the 10th order. Both Zernike and Fourier algorithms performed best when reconstructing simulated wavefronts from normal eyes and worst with PKP eyes. Using a large number of Zernike modes to reconstruct simulated wavefronts of low spatial resolution lead to inaccurate reconstructions. The Fourier method had better reconstruction reliability in the center of the pupil than peripherally. Only 2nd through 5th order Zernike modes were required to produce less residual RMS error than the Fourier method.
CONCLUSIONS:
For all conditions tested, the Zernike method outperformed the Fourier method when representing simulated wavefront data from topography maps. Even 2nd through 5th order Zernike polynomials were enough to outperform the Fourier method in all populations. Up to 9th order Zernike modes may be required to accurately describe the simulated wavefronts in some abnormal eyes.
For nearly 30 years, the eye’s wavefront aberration has been objectively measured using a number of different aberrometry techniques.1–4 To facilitate application of the technology clinically, it has become necessary to express the eye’s aberration mathematically. The Zernike polynomials, an orthogonal base function used to describe optical systems with circular pupils, have thus far fulfilled this need.5 In 2001, Porter et al6 showed through a principal components analysis that the Zernike polynomials efficiently described the eye’s wavefront aberration. Although they demonstrated that the Zernike fitting method was not perfect and that it resulted in residual root-mean-square (RMS) error, the amount of error was undefined and uncorrelated to the number of modes used.
Despite previous acceptance of the Zernike polynomials, there has been recent scrutiny concerning the accuracy with which they can represent the total ocular wave aberration, especially in abnormal eyes such as those having keratoconus, penetrating keratoplasty, or severe trauma.7–10 In 2003, Smolek and Klyce9 showed that the corneal fit error of the Zernike polynomials strongly correlated with visual acuity. They concluded from this that the polynomials did not fully characterize the surface features that affect vision. They also observed an unpredictable increase in wavefront error when using a larger expansion series (10th order) to represent the corneal aberration. In 2004, Klyce et al10 reiterated their concern with respect to using Zernike polynomials in surgical or pathological eyes. They found that using Zernike polynomials in normal eyes was acceptable, but that large amounts of higher order aberration present in pathologic eyes cause significant fit error and an underestimation of the total higher order corneal aberration present.10
Other methods including zonal reconstruction using bi-cubic splines and use of a Fourier series have been suggested as alternatives for representation of the wave aberration in eyes.11,12 Of these, the Fourier series has become of particular interest recently. Similar to the Zernike polynomials, the Fourier series is an infinite expansion that can be used to represent any complex shape (including a wave aberration) by breaking it into its frequency components. Previous studies by Smolek and Klyce that used a Fourier-based algorithm worked by directly fitting the surface of the cornea.9 However, most commercially available ophthalmic wavefront sensors use a different method, namely wavefront slope fitting. Therefore, their results may not be directly applicable to most scientific and clinical studies involving wavefront sensors.
More recently, Dai13 published the first study comparing Fourier and Zernike reconstruction algorithms using the wavefront slope fitting method. He concluded that the Fourier algorithm outperformed the Zernike algorithm on highly aberrated wavefront shapes, but the study made several assumptions that may compromise objectivity and clinical applicability. For example, his choice of randomly regenerated Zernike coefficients up to the 15th order as a gold standard makes it difficult to correlate performance of these algorithms to wavefront shapes similar to those found in normal and abnormal eyes. Perhaps more importantly, Dai started with a 10-mm pupil but based reconstruction performance on only the central 6 mm. Because it is impractical to measure wavefront slope over a 10-mm pupil clinically, true reconstruction performance should be based on a smaller reference pupil size. These shortcomings are outlined in greater detail in the discussion.
The purpose of this study was to investigate the relative accuracy with which the Zernike polynomials and Fourier series can represent the corneal surface aberration in both normal and abnormal eyes.
MATERIALS AND METHODS
Zernike and Fourier Reconstructions
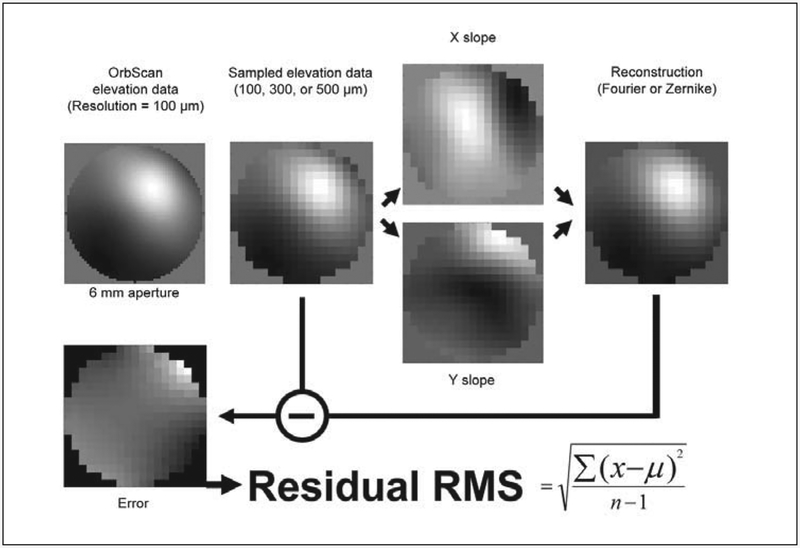
Because no gold standard exists to represent the total ocular aberration perfectly, corneal topography data were used as a reference. Using an Orbscan IIz (Bausch & Lomb, Rochester, NY) videokeratographer, corneal topography maps were acquired on 87 normal, 27 keratoconic, 9 penetrating keratoplasty, and 20 postoperative LASIK symptomatic eyes. Careful attention was given to ensuring that no data points were missing within a 6.0-mm pupil before proceeding. Sampling resolution of the topography measurements was 100 μm. For each measurement, raw data from the slit images were converted to an elevation matrix by subtracting each data point from a best fit sphere as calculated by the manufacturer’s software. All further processing was based on the difference from sphere elevation matrix. Data points outside a 6.0-mm pupil were forced to zero. The processing method is illustrated in Figure 1. For each map, the elevation matrix was first resampled at 100-, 300-, and 500-μm resolutions by averaging the elevation across adjacent pixels. This was done to simulate the sampling that would typically be observed from Shack-Hartmann wavefront sensors with comparable lenslet spacings. Two matrices of x- and y-slopes were generated from the elevation matrix by using MATLAB’s (The MathWorks Inc, Natick, Mass) “gradient” function, which calculates slope based on the first order central difference. The wavefront slopes were computed from the elevation matrix for each lenslet size before applying the two reconstruction methods. Therefore, both algorithms used the exact same wavefront slope data as a starting point.
Figure 1.
Method for reconstruction of elevation data. First the original corneal topography elevation map was resampled at 100, 300, and 500 μm. For each of the three sampled elevation maps, the x- and y-slopes were calculated across the entire pupil by comparing differences in elevation between adjacent pixels. Zernike and Fourier reconstruction algorithms were applied to reconstruct the original, sampled wavefront from wavefront slope data. Subtraction of the reconstructed map from the originally sampled one resulted in an objective measure of reconstruction accuracy, expressed as residual root-mean-square (RMS). In this equation, x is defined as the elevation of a single data point within the given pupil, μ is the ideal elevation of a single data point (zero), and n is the number of sampling points.
A conventional Zernike reconstruction algorithm that works from wavefront slopes3 was applied to each pair of x- and y-slope matrices to produce a reconstructed map with the same resolution as the originally sampled elevation map. This was first done using only 1 Zernike mode, then 2, 3, etc. In each successive reconstruction, one additional Zernike mode was used until 130 Zernike modes (15th order) were used to reconstruct the wavefront. Each new wavefront map generated was directly compared to the originally sampled wavefront and the residual root-mean-square (RMS) error between the original and reconstructed map was recorded. When the 300- and 500-μm resolution reconstructed wavefront maps were generated, the RMS error calculation was based on the number of data points in those maps, and not on the number present in the original wavefront map. Ultimately, for each eye the Zernike analysis resulted in three plots (one at each simulated lenslet spacing—100, 300, and 500 μm) of RMS difference between original and reconstructed wavefronts versus the number of Zernike modes used. The residual RMS error as a function of the number of Zernike modes used was averaged across each population.
An iterative Fourier algorithm that works from wavefront slope data12 was also used to reconstruct each sampled elevation map from the exact same pair of x- and y-slope matrices used for the Zernike reconstruction. First, a discrete Fourier transform was taken over a 6-mm pupil containing the x- and y-slope data so that they were expressed as functions of u and v, respectively. The variables u and v are defined as the horizontal and vertical frequency components of the spatially defined arrays. The Fourier transform of the x-slope was multiplied by u and that of the y-slope by v. After adding the results, the inverse Fourier transform was computed to produce a wavefront estimate. For simplicity, this process was iterated six times for each eye to ensure convergence and minimize error (a separate test showed that more iterations did not significantly decrease error any further). Because no modes are present in the Fourier algorithm, only one reconstruction per patient was required. Each reconstructed elevation map consisted of the same number of sampling points as the original sampled elevation map, which may also be thought of as the number of lenslets within a given pupil diameter. The reconstructed elevation map was subtracted from the originally sampled elevation map and the residual RMS error was measured.
Validation of Fourier Reconstruction Algorithm
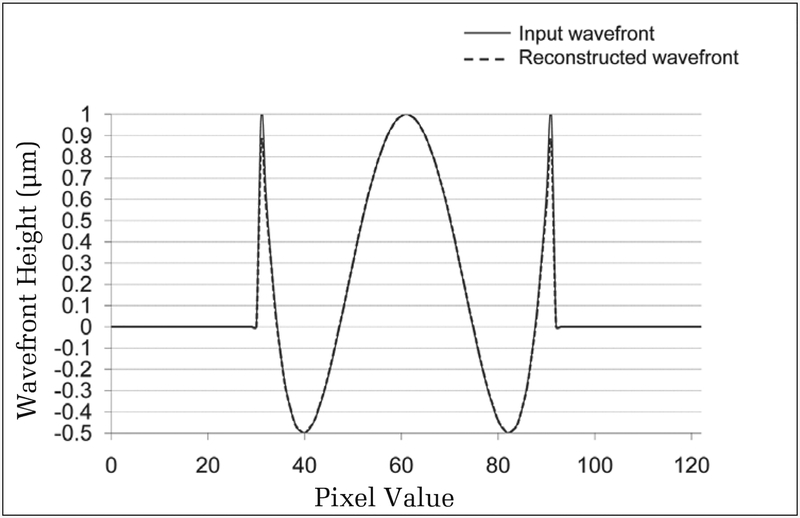
In 1991, Roddier and Roddier12 published a method of reconstructing wavefronts based on iterative Fourier transforms (discussed further below). Data from their work was used to validate our own implementation. In their paper, primary spherical aberration was used as the input function. The same exact test was used in our study, and the results are shown in Figure 2. Although the input function and the reconstructed waveform differed slightly peripherally (discussed later), our algorithm appeared to perform as well or better than the original Roddier simulation from 1991.
Figure 2.
Validation of the Fourier reconstruction algorithm. The input function was primary spherical aberration, represented by a solid line. The reconstructed waveform is represented by a dashed line. Original and reconstructed waveforms differ slightly peripherally, however, results actually outperform the original algorithm presented by Roddier in 1991.12
Condition Number Calculation
As described elsewhere,3,14 calculation of the Zernike coefficients from wavefront aberrometer data requires solving the following equation:
| (1) |
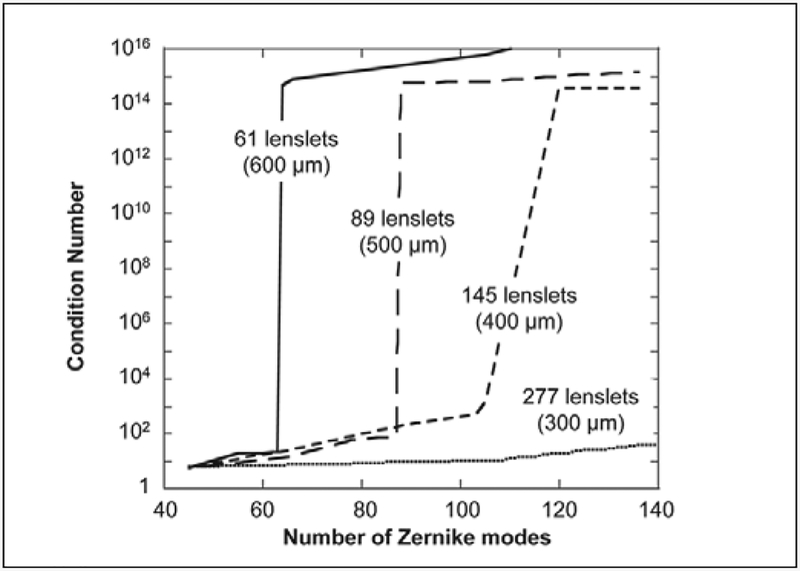
where c is the vector of Zernike coefficients to be calculated, D is a rectangular matrix consisting of 1st derivatives of each Zernike polynomial with respect to x and y at each lenslet position, and s is the vector of spot displacements (x- and y-slopes) measured with the wavefront sensor. Because D is a rectangular matrix, its inverse cannot be calculated directly. To solve Eq.(1), a method called singular value decomposition (SVD)15 can be used. Inaccuracies in calculating the SVD result in error calculating the Zernike coefficients, which in turn leads to wavefront reconstruction error. The condition number can be used to quantify the reliability of this calculation. The condition number is the ratio of the absolute values of the largest to smallest singular values. Condition numbers near 1 indicate a well-conditioned matrix. As the condition number increases, the SVD calculation becomes less reliable and more sensitive to a small error in the measured wavefront slopes, which in turn causes an increase in reconstruction error.
Given a fixed number of sampling points, the condition number will increase with the increasing number of Zernike polynomials chosen to represent the wavefront. It is important to note that this relationship is not linear and will not be identical for every patient because error in reconstructed wavefronts depends on the individual’s amount of aberration. In other words, no constant relationship exists between the absolute value of the condition number and reconstruction accuracy.
To evaluate the SVD calculation, four conditions were tested: 277, 145, 89, and 61 sampling points, which corresponded to sampling resolutions of 300, 400, 500, and 600 μm over a 6.0-mm pupil, respectively. For each fixed number of sampling points, the condition number of the matrix was calculated using varying numbers of Zernike modes (from 45 to 140). A plot was constructed to illustrate the relationship between condition number and number of Zernike modes used (Fig 3).
Figure 3.
Condition number versus number of Zernike modes used in reconstruction. The condition number is a mathematical quantification of the accuracy of matrix conversion; accurate matrix conversion, in turn, leads to reliable reconstruction with the Zernike polynomials. If the number of Zernike modes used during reconstruction is too many relative to the number of sampling points (lenslets), the condition number will be exponentially large, and reconstruction accuracy will be poor.
RESULTS
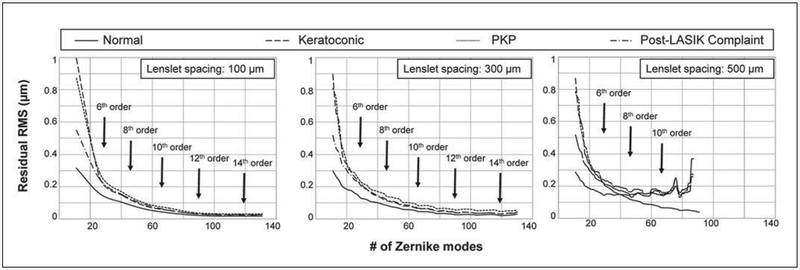
The results from studying reliability of the Zernike reconstruction algorithm are displayed in Figure 4. For all four of the populations studied, the residual RMS error in reconstruction decreased logarithmically as the number of Zernike modes used in the reconstruction increased. This was especially true when the wavefront was sampled at resolutions of 100 and 300 μm. The Zernike reconstruction algorithm was more efficient (obtained good representation with fewer modes) in its ability to reconstruct wavefronts from normal eyes than abnormal eyes. For both 100- and 300-μm resolution wavefront maps, the Zernike method was most efficient in reconstructing eyes from the normal population and least accurate with regards to PKP eyes. For wavefront reconstructions at a resolution of 500 μm, the trend was less consistent. Although the reconstruction error decreased initially with increasing Zernike modes, the trend destabilized and eventually began to increase as the number of Zernike modes used for the reconstruction became greater than 70 modes. Interestingly, the only population that did not destabilize at this resolution of 500 μm was the symptomatic postoperative LASIK group.
Figure 4.
Residual root-mean-square (RMS) reconstruction error as a function of number of Zernike modes used (100-, 300-, and 500-μm cases). For both 100- and 300-μm lenslet spacings, reconstruction accuracy increased and residual RMS error decreased logarithmically as more Zernike modes were used (up to 130). The Zernike reconstruction algorithm consistently performed best on normal eyes and worst on penetrating keratoplasty (PKP) eyes. When a resolution of 500 μm was used, residual RMS error initially decreased logarithmically as the number of modes used in the reconstruction increased; however, when a large number of modes were used, residual RMS error actually began to increase for three of the four populations (not for the postoperative LASIK complaint). The result emphasizes that trying to use too many Zernike modes when sampling resolution is relatively low leads to greater reconstruction error.
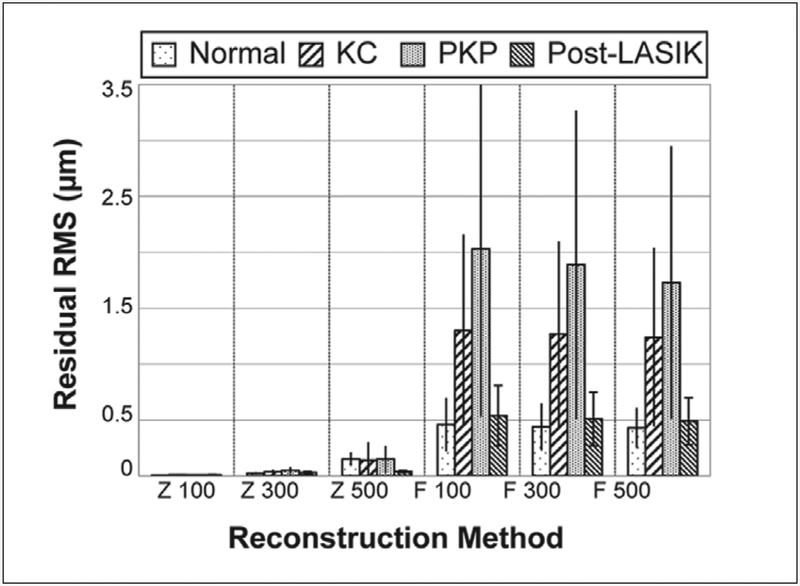
Resolution used with the Fourier method was not manipulated and was directly determined by the sampling resolution. The sampling resolutions used with the Fourier method may be thought of as three different lenslet sizes (100, 300, and 500 μm). Results from studying reliability of the Fourier reconstruction algorithm are shown in Figure 5. The residual RMS error from the Fourier reconstruction is compared to the error resulting from the Zernike method when it was performing at its best (ie, the lowest stable residual RMS error for each population and resolution was chosen to represent the performance of the Zernike algorithm at each of the tested conditions). For the Zernike method, the residual RMS reconstruction error decreased as the sampling resolution of the original elevation map increased. This trend was statistically significant for the normal population (P<.01), but not for any of the others. For the Fourier method, as the sampling resolution became less fine, reconstruction error actually decreased; however, the observation was not statistically significant. Both methods were best at representing wavefronts from the normal population whereas abnormal eyes had significantly larger errors. Regardless of the resolution used or population measured, the Zernike reconstruction algorithm appeared to outperform the Fourier method (P<.01). In fact, only up to the 5th order Zernike modes (20 terms excluding piston) were required to outperform the Fourier method at every condition tested; more Zernike modes resulted in even greater accuracy.
Figure 5.
Zernike versus Fourier comparison of reconstruction performance. As the number of sampling points decreased, the Zernike reconstruction algorithm performed more poorly; however, the Fourier method actually improved slightly in accuracy as the number of sampling points decreased. When performing optimally, the Zernike reconstruction algorithm appeared to outperform the iterative Fourier method for all populations and conditions tested. KC = keratoconic, PKP = penetrating keratoplasty
DISCUSSION
In this study, we used simulated wavefront slope data to reconstruct corneal shapes using both Zernike and iterative Fourier algorithms. The algorithms were compared by determining what conditions minimized residual RMS error between original and reconstructed elevation data. The simulation was done on both normal and abnormal eyes, as speculation has suggested that each algorithm might be best suited for a respective population. Our findings suggested that when both the Fourier and Zernike algorithms are performing optimally under the conditions tested, the Zernike reconstruction algorithm always outperforms Fourier, irrespective of the normal and abnormal aberrations present.
Many commercial wavefront sensors for the eye, such as the Shack-Hartmann, spatially resolved refractometer, and laser ray tracing techniques, are based on measurement of wavefront slopes. The true wavefront is always sampled by a lenslet array, an aperture, or a laser beam that generates a laser beacon on the retina when using these techniques. One limitation is that wavefront structures with higher spatial frequency components than the sampling frequency are not available for wavefront reconstruction. These high spatial frequency components cannot be restored by wavefront reconstruction, regardless of the algorithm used (Zernike or Fourier). Therefore, determining lenslet parameters such as size and focal length are important determinants of reconstruction accuracy and must be chosen before making a decision regarding the type of reconstruction algorithm to use.16
In 2003, Smolek and Klyce9 also evaluated the performance of Zernike polynomials when reconstructing wavefront maps. Their study and ours are similar in that both used corneal topography maps to represent wavefront aberration of normal and abnormal eyes. However, the studies from Smolek and Klyce used a surface-based reconstruction algorithm that fitted the original elevation map directly with the Zernike polynomials. In contrast, the study presented here decomposed the original elevation matrix into two matrices of x- and y-slopes first, then proceeded to reconstruct a wavefront map from these two matrices. We chose this method because it is most similar to how ophthalmic wavefront sensors calculate the wavefront error when measuring an eye’s aberration. The original surface of the wavefront error is never truly known, and so a wavefront aberrometer is forced to reconstruct the surface from an array of x- and y-slopes as measured by a lenslet array.
Despite the difference in methods above, Smolek and Klyce9 drew similar conclusions to those presented here. They showed that using 10th order Zernike modes to reconstruct corneal topography maps led to decreased “elevation fit error” when compared to using only 4th order terms. This means that the 4th order Zernike reconstruction must have left some amount of higher order aberration unaccounted for; when up to 10th order terms were included, the true (albeit increased) wavefront error became apparent and the residual error left between the reconstructed and original maps decreased. This finding is consistent with results from our study, which showed that residual RMS error decreased as the number of Zernike modes used in the reconstruction increased (see Fig 4).
In 2004, Klyce et al10 evaluated the ability of both Fourier- and Zernike-based algorithms to represent a point spread function (PSF) derived from corneal topography data. Once again, their methodology differed from ours in that their comparison was based on surface fitting of the cornea, while ours was based on wavefront slope. The main conclusion from this comparison was that even 30th order Zernike modes were not enough to produce a PSF identical to that derived from the Fourier method. It is important to recognize that the raw data from which the Fourier-based PSF was derived had over 51,000 data points. When the PSF was generated directly via a Fourier transform, the transform used all of the data points. However, the PSF generated from the Zernike polynomials (up to 30th order) was constructed from only 496 terms. If the number of Zernike modes used had been significantly more than the 30th order, the PSF might have more closely represented that produced using the Fourier algorithm. Using so many Zernike polynomials also would have been prohibitively time consuming, as they pointed out. However, most of the time required for wavefront fit is used to compute the SVD of the matrix including Zernike polynomials described earlier. This can be pre-computed once for a certain pupil size, which obviates the time constraint noted with the Zernike method.
Another important shortcoming in the 2004 study by Klyce et al10 is that noise inherently present in corneal topography data may have been fit in the reconstruction. Any measured wavefront map, whether it includes total ocular aberration or only corneal surface data, has inherent noise with a wide range of spatial frequencies caused by factors such as tear film uniformity, eye movement, alignment, etc. As the goal of reconstruction is to extract the underlying wavefront shape from the overlying noise, the effects of the noise need to be removed properly before fitting the measured topography. Using lower spatial frequency Zernike modes and Fourier series permits extraction of the true wavefront aberration and avoids fitting high frequency random measurement noise.
Dai’s 2006 study directly comparing Zernike and Fourier algorithms is unique in that it is the first to use wavefront slope fitting—the same method used by most commercially available wavefront sensors.13 Despite using the same exact method in the study presented here, our conclusions are opposite those proposed by Dai. There are several reasons for this discrepancy. First, Dai used randomly generated wavefront aberration maps to test reconstruction performance, whereas real corneal topography maps acquired from normal and abnormal eyes were used in our study. The difference in choice of a gold standard may affect the result significantly. Corneal aberrations calculated from corneal topography data resemble total ocular aberration, especially in the keratoconic and PKP populations. For this reason, we believe using corneal topography maps more accurately represents the aberration patterns found clinically. The wavefront aberration maps in Dai’s study were also generated using up to 15th order Zernike polynomials, but when reconstruction performance was tested, only up to 10th order Zernike polynomials were included in the analysis. The results could be significantly different if polynomials up to the 15th order were used.
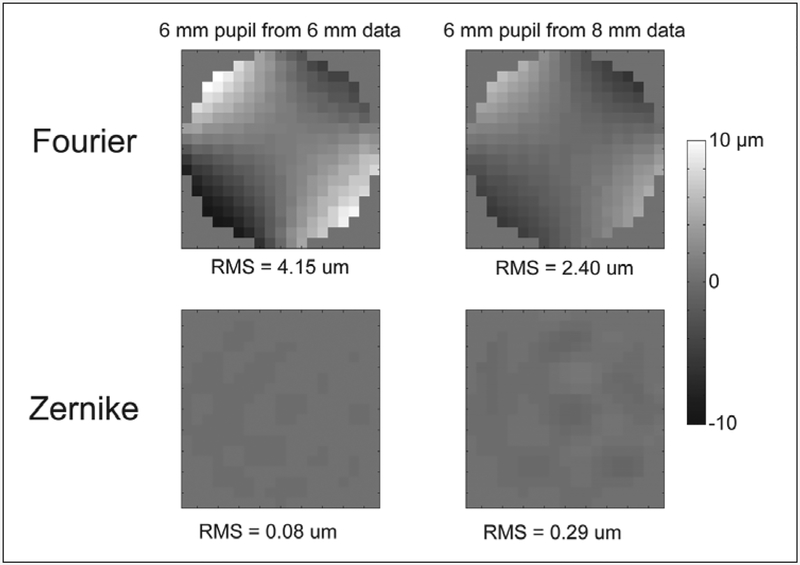
Perhaps most importantly, Dai’s wavefront aberration maps were generated over a 10-mm pupil, but reconstruction performance was only based on each algorithm’s respective ability to represent the central 6 mm. It is impractical to measure wavefront slope over a 10-mm pupil clinically, therefore true reconstruction performance should be based on a smaller reference pupil size. The effects of peripheral reconstruction error in the Fourier algorithm can be understood better by studying Figure 6. In this example, a typical keratoconic corneal topography map over which 8-mm data were available was used. First, reconstruction performance was assessed exactly as described previously for the study, meaning that the raw topography data for only the central 6 mm were used to reconstruct the wavefront for the 6-mm cornea and reconstruction error was evaluated for the 6-mm pupil. Afterwards, reconstruction performance was evaluated as described by Dai—the same raw data were used, but instead the 8-mm cornea was used to reconstruct the wavefront for the 8-mm cornea. After reconstruction, reconstruction error was only based on the central 6 mm.
Figure 6.
Effect of original pupil size on reconstruction accuracy. The Fourier algorithm performs poorly when used to reconstruct the wavefront over the entire original pupil size. Therefore, reconstruction over a pupil that is larger than the actual area of interest is required to reduce reconstruction error. The Zernike algorithm performs best when reconstruction is based on the entire original pupil size.
For the Fourier algorithm, reconstruction performance was poor when wavefront reconstruction for the 6-mm cornea was done from the 6-mm topography data; however, reconstruction error for the same 6-mm cornea was reduced by approximately 73% when the reconstruction was performed from the 8-mm corneal topography data. This indicates that larger topography data are required to reduce edge effect of the Fourier algorithm. In the case of the Zernike algorithm, reconstruction performance for the 6-mm cornea actually worsened by more than a factor of three when it was based on the 8-mm topography data. This may be because the algorithm was used to best fit the entire 8-mm pupil (not just the central 6 mm), which required that it sacrifice some performance centrally to better fit large aberrations peripherally.
Two parameters that may be especially helpful to clinicians are the number of Zernike modes needed to accurately represent the wavefront and the number of terms needed to optimally represent the wavefront. For the sake of discussion, we have defined accurate representation of the wavefront as the number of Zernike modes needed to achieve a residual RMS error less than 1/10 of a diopter, or approximately 0.13 μm for a 6-mm pupil. Optimal wavefront reconstruction was defined as the number of Zernike modes needed to produce the lowest RMS error possible. The Table displays the number of Zernike modes needed for accurate and optimal representation for each of the four populations tested when the sampling resolution is 300 μm.
TABLE.
Number of Zernike Modes Needed for Reconstruction
| Population | Accurate (Zernike Order) | Optimal (Zernike Order) |
|---|---|---|
| Normal | 29 (~6th) | 92 (~12th) |
| Keratoconus | 44 (~8th) | 92 (~12th) |
| PKP | 52 (~9th) | 104 (~13th) |
| Postoperative LASIK complaint | 44 (~8th) | 120 (14th) |
PKP = penetrating keratoplasty
Disadvantages of Zernike and Fourier Reconstruction Methods
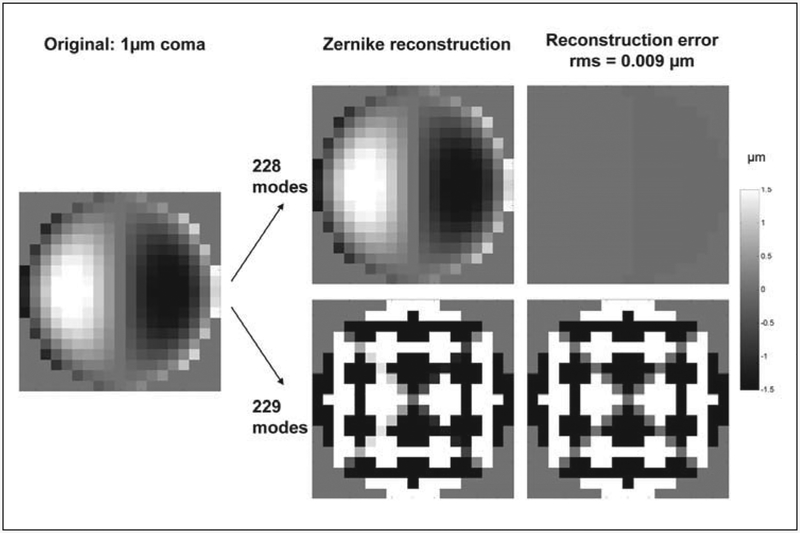
Each method of reconstructing the corneal shapes had its respective disadvantages. These are best illustrated in Figure 7. In this figure, the Zernike reconstruction algorithm was used to reconstruct a map consisting of exactly 1 μm of horizontal coma. The resolution of the original image was 300 μm and the algorithm was run once using 228 Zernike modes, corresponding to approximately 20th order, and a second time using 229 Zernike modes. The reconstructed map and residual RMS (original – reconstructed) are shown. When 228 modes were used, the reconstructed map closely resembled the original one and residual error was negligibly small. When 229 modes were used, the reconstructed map was grossly miscalculated, and the residual RMS error was ten orders of magnitude higher than that of the 228 mode case. The example demonstrates that good reconstruction can be obtained as long as the number of modes used is carefully chosen. Attempting to use too many Zernike modes when resolution is limited by a large lenslet spacing will cause large errors in reconstruction and inaccurate results.
Figure 7.
Disadvantages of Zernike reconstruction method. Resolution of the original image is 300 μm. When 228 Zernike modes are used to reconstruct the wavefront, good reconstruction is achieved. However, when 229 modes are used, reconstruction performance is extremely poor, and residual error is exponentially larger. Resolution of the original wavefront directly determines the number of modes that can be used to accurately reconstruct it. Careful selection of the number of modes used will ensure good reconstruction performance.
The errors in reconstruction described above can be explained mathematically by the condition number (described above), which varies as a function of the number of modes used. Figure 3 illustrates that the condition number increased slowly when the number of lenslets was substantially larger than the number of Zernike coefficients being calculated in the reconstruction. Because the matrix including the 1st derivatives of each Zernike polynomial with respect to x and y was well-conditioned under these conditions, the Zernike coefficients (and thus reconstruction accuracy) were reliable. However, when the number of lenslets was approximately the same or smaller than the number of Zernike coefficients calculated, the condition number dramatically increased. In this situation, the matrix was ill-conditioned. This resulted in unreliable Zernike coefficients and large reconstruction error.
Roddier and Roddier12 presented the iterative Fourier algorithm in 1991. They reconstructed a two-dimensional representation of spherical aberration using the algorithm and revealed one disadvantage of Fourier-based reconstruction. Although the Fourier method has good reconstruction centrally, most of the residual RMS error comes from poor reconstruction ability along the periphery. Their findings are consistent with our own, shown previously in Figure 6. Namely, when the sizes of the reference pupil and the reconstructed wavefront map are equal, larger peripheral error results. Again, this may be due to the sharp delineation between the border of the pupil and the points outside that pupil. One way of reducing this error would be to acquire data over a larger diameter than the area of interest.
Despite the finding that the Zernike algorithm is superior to Fourier when reconstructing wavefront aberrations from slope data, the Fourier method has some advantages. For instance, when the pupil is not circular, the Zernike polynomials cannot be used because they are defined about a circular aperture. Second, the Fourier method may be better at representing extremely high frequency wavefront slopes, such as those caused by tear film or corneal scar.17 It is also well-established that Fourier-based algorithms are faster to implement computationally,10 though this fact becomes less relevant as the speed of computers increases.
Conclusions
The Zernike reconstruction algorithm can outperform the iterative Fourier method when representing shapes that are similar to those obtained from wavefront aberrometers. This is true in both normal and abnormal eyes. For the sampling resolutions (100, 300, and 500 μm) and pupil size (6-mm diameter) tested here, the best reconstruction occurs when the number of Zernike modes used is roughly one half the total number of sampling points (lenslets) in the pupil image. For example, approximately 184 lenslets are required to achieve optimal wavefront reconstruction for normal eyes. It should be noted that obtaining higher resolution data (ie, by using aberrometers with small lenslet spacings) reduces residual reconstruction error, but sacrifices the dynamic range of the wavefront sensor.
Acknowledgments
This research was funded by grants from the NIH (R01-EY014999) and Research to Prevent Blindness Inc, New York, NY.
Footnotes
The authors have no proprietary interest in the materials presented herein.
REFERENCES
- 1.Smirnov MS. Measurement of the wave aberration of the human eye [Russian]. Biofizika. 1961;6:687–703. [PubMed] [Google Scholar]
- 2.Walsh G, Charman WN, Howland HC. Objective technique for the determination of monochromatic aberrations of the human eye. J Opt Soc Am A. 1984;1:987–992. [DOI] [PubMed] [Google Scholar]
- 3.Liang J, Grimm B, Goelz S, Bille J. Objective measurement of the wave aberrations of the human eye with the use of a Hart-mann-Shack wavefront sensor. J Opt Soc Am A. 1994;11:1949–1957. [DOI] [PubMed] [Google Scholar]
- 4.Mrochen M, Kaemmerer M, Mierdel P, Krinke HE, Seiler T. Principles of Tscherning aberrometry. J Refract Surg. 2000;16: S570–S571. [DOI] [PubMed] [Google Scholar]
- 5.Born M, Wolf E. Principles of Optics. Oxford, United Kingdom: Pergamon Press; 1975. [Google Scholar]
- 6.Porter J, Guirao A, Cox IG, Williams DR. Monochromatic aberrations of the human eye in a large population. J Opt Soc Am A. 2001;18:1793–1803. [DOI] [PubMed] [Google Scholar]
- 7.Carvalho LA. Accuracy of Zernike polynomials in characterizing optical aberrations and the corneal surface of the eye. Invest Ophthalmol Vis Sci. 2005;46:1915–1926. [DOI] [PubMed] [Google Scholar]
- 8.Iskander DR, Morelande MR, Collins MJ, Buehren T. A refined bootstrap method for estimating the Zernike polynomial model order for corneal surfaces. IEEE Trans Biomed Eng. 2004;51:2203–2206. [DOI] [PubMed] [Google Scholar]
- 9.Smolek MK, Klyce SD. Zernike polynomial fitting fails to represent all visually significant corneal aberrations. Invest Ophthalmol Vis Sci. 2003;44:4676–4681. [DOI] [PubMed] [Google Scholar]
- 10.Klyce SD, Karon MD, Smolek MK. Advantages and disadvantages of the Zernike expansion for representing wave aberration of the normal and aberrated eye. J Refract Surg. 2004;20:S537–S541. [DOI] [PubMed] [Google Scholar]
- 11.Southwell WH. Wave-front estimation from wave-front slope measurements. J Opt Soc Am. 1980;70:998–1009. [Google Scholar]
- 12.Roddier F, Roddier C. Wavefront reconstruction using iterative Fourier transforms. Appl Opt. 1991;30:1325–1327. [DOI] [PubMed] [Google Scholar]
- 13.Dai GM. Comparison of wavefront reconstructions with Zernike polynomials and Fourier transforms. J Refract Surg. 2006;22:943–948. [DOI] [PubMed] [Google Scholar]
- 14.Thibos LN, Applegate RA, Schwiegerling JT, Webb R; VSIA Standards Taskforce Members. Standards for reporting the optical aberrations of eyes. J Refract Surg. 2002;18:S652–S660. [DOI] [PubMed] [Google Scholar]
- 15.Press WH, Vetterling WT, Teukolsky SA, Flannery BP. Numerical Recipes in C: The Art of Scientific Computing. 2nd ed New York, NY: Press Syndicate of the University of Cambridge; 1992. [Google Scholar]
- 16.Yoon GY, Pantanelli SM, MacRae SM. Optimizing the Shack-Hartmann wavefront sensor In: Krueger R, Applegate RA, MacRae SM, eds. Wavefront Customized Visual Correction: The Quest for Supervision II. Thorofare, NJ: SLACK Incorporated; 2004:131–136. [Google Scholar]
- 17.Li KY, Yoon G. Changes in aberrations and retinal image quality due to tear film dynamics. Optics Express. 2006;14:12552–12559. [DOI] [PubMed] [Google Scholar]