Mutation effect estimation on protein–protein interactions using deep contextualized representation learning

Abstract

The functional impact of protein mutations is reflected on the alteration of conformation and thermodynamics of protein–protein interactions (PPIs). Quantifying the changes of two interacting proteins upon mutations is commonly carried out by computational approaches. Hence, extensive research efforts have been put to the extraction of energetic or structural features on proteins, followed by statistical learning methods to estimate the effects of mutations on PPI properties. Nonetheless, such features require extensive human labors and expert knowledge to obtain, and have limited abilities to reflect point mutations. We present an end-to-end deep learning framework, MuPIPR (Mutation Effects in Protein–protein Interaction PRediction Using Contextualized Representations), to estimate the effects of mutations on PPIs. MuPIPR incorporates a contextualized representation mechanism of amino acids to propagate the effects of a point mutation to surrounding amino acid representations, therefore amplifying the subtle change in a long protein sequence. On top of that, MuPIPR leverages a Siamese residual recurrent convolutional neural encoder to encode a wild-type protein pair and its mutation pair. Multi-layer perceptron regressors are applied to the protein pair representations to predict the quantifiable changes of PPI properties upon mutations. Experimental evaluations show that, with only sequence information, MuPIPR outperforms various state-of-the-art systems on estimating the changes of binding affinity for SKEMPI v1, and offers comparable performance on SKEMPI v2. Meanwhile, MuPIPR also demonstrates state-of-the-art performance on estimating the changes of buried surface areas. The software implementation is available at https://github.com/guangyu-zhou/MuPIPR.

INTRODUCTION

Protein–protein interactions (PPIs) govern a wide range of biological mechanisms ranging from metabolic and signaling pathways, cellular processes, and immune system (1,2). Mutations in proteins can affect protein folding and stability (3–5); consequently, these mutations alter the kinetic and thermodynamics of PPIs (6,7). Such mutations can either be selectively advantageous to the organism through evolution (8), or be deleterious and causing a disease phenotype (9). Understanding the effects of these mutations, specifically the conformation and thermodynamic changes of the interacting proteins, is vital to various biomedical applications, including disease-associated mutation analyses (10), drug design (11) and therapeutic intervention (12).

The quantitative measures of different aspects of PPIs are often determined experimentally through biophysical techniques, including but not limited to, isothermal titration calorimetry for measuring the binding affinity (13), and BN-PAGE for the stability of the protein complex (14). However, these in vivo or in vitro techniques are laborious and expensive due to the need of purifying each protein. In addition, estimating the mutation effects requires the physical presence of both wild-type and mutated proteins, while the interaction involving a mutated protein is not always available.

To enable large scale studies of the mutation effects of PPIs, significant efforts have been made to computationally estimating the changes of PPIs properties upon mutations. One of these estimates, the change of binding affinity (ΔΔG), has been widely investigated. The binding affinity (ΔG) measures the strength of the interaction between two single biomolecules, and is reported by the equilibrium dissociation constant. Here, the basis of a biomolecule can be a protein or a sub-unit of a protein. Earlier methods estimating the ΔΔG derive empirical linear functions based on physical energies (15) or known protein structures (16,17). Instead of training parameters on existing data, these methods require a set of pre-determined coefficients for the linear models. Hence, they suffer from poor generalizability and lead to low accuracy. With the increasing availability of large mutation databases, statistical learning algorithms have been proposed to capture the relations between a variety of energetic or structural features and the binding affinity of two biomolecules (8,18–20). Nevertheless, features used in these methods are hand-crafted, requiring extensive human labors and expert knowledge.

Recently, deep learning methods show the potential of automatically extracting comprehensive features from protein sequences, and gain unprecedented success in PPI tasks. Corresponding methods, including DNN-PPI (21), DPPI (22) and PIPR (23) employ various neural sequence pair models to predict PPI information based on protein sequences. In the application of predicting the structural properties of a protein complex, NetSurfp-2.0 (24) employs a neural sequence model to predict the solvent accessible surface area (ASA) of a protein. A more pronounced feature to describe the PPI property is the buried surface area (BSA), which measures the size of the interface in a protein-protein complex. Estimating the change of BSA upon mutation provides insight to the potential deleterious mutations buried inside an interacting protein pair, which is crucial for understanding diseases (25). However, none of the existing methods can directly estimate the BSA score, or the change in BSA upon mutation. BSA is often computed from the ASA scores of individual proteins and the protein complex (19).

To capture the features of the raw protein sequence from scratch, neural sequence models require a mechanism to characterize and represent the amino acids in a protein sequence. Such mechanisms deploy fixed representations, e.g. one-hot vectors (21), physicochemical property-aware encoding (23) or static amino acid embeddings (23). However, these representations face several crucial problems for PPI property predictions upon mutations. First, these representation mechanisms fall short of reflecting mutations, inasmuch as point mutations will only lead to subtle differences in the corresponding amino acid representations of a long protein sequence. Second, as these mechanisms independently characterize each amino acid, they do not consider the contextual information of surrounding amino acids and do not highlight those that are critical to PPIs. Moreover, the aforementioned methods fail to deploy a learning architecture dedicated to modeling the change between a wide-type protein pair and its mutant counterparts.

In this paper, we introduce a comprehensive learning framework, MuPIPR (Mutation Effects in Protein–protein Interaction PRediction Using Contextualized Representations), to estimate the changes of quantifiable PPI properties upon amino acid mutations. MuPIPR incorporates a contextualized representation learning mechanism of amino acids, which seeks to sensitively capture mutations. In particular, MuPIPR pre-trains a multi-layer bidirectional long short-term memory (LSTM) (26) language model on a collection of protein sequences, and alters the representation of each amino acid based on the surrounding context captured by the language model. The benefits of this representation learning mechanism are two-fold: (i) it automatically extracts more refined amino-acid-level features that are differentiated between different contexts of the proteins; (ii) it propagates the mutation effects to the representations of surrounding amino acids, therefore amplifying the subtle signal of each mutation in a long protein sequence. On top of the contextualized animo acid representations, a deep neural learning architecture is carefully designed to subsequently estimate the quantifiable PPI property changes between a wild-type pair and a mutant pair of proteins. The architecture features an end-to-end learning of two stages: (i) a 4-fold Siamese residual recurrent convolutional neural network (RCNN) encoder characterizes the two protein pairs based on their contextualized amino acid representations, which seeks to seize the differences of their latent features; (ii) a main multi-layer perceptron (MLP) regressor is stacked to the encoder to estimate the property change between the two protein pairs, with two auxiliary regressors to enhance the estimation by jointly estimating the individual PPI properties of each protein pair. In practice, MuPIPR demonstrates the benefits of alleviating the need of hand-crafted features, and generalizes well to tasks of estimating the changes of different PPI properties upon mutations. The evaluation on the protein binding affinity change estimation task and protein buried surface area change estimation task on three benchmark datasets shows that MuPIPR significantly outperforms state-of-the-art methods on both tasks. Detailed ablation study on MuPIPR also provides insightful understanding of the effectiveness of each model component.

MATERIALS AND METHODS

In this section, we present the detailed design of the proposed framework MuPIPR to address two regression tasks in PPI. Figure 1 illustrates the architecture of MuPIPR with three components: (i) a contextualized amino acid representation mechanism, (ii) a protein sequence level Siamese encoder by leveraging the RCNN, (iii) multiple-layer perceptron regressors for estimating quantifiable property changes in PPIs upon mutations.

Figure 1.

Architecture of MuPIPR.

Preliminary

We represent a protein as a sequence of amino acid residues S = (r₁, r₂, ⋅⋅⋅, r_N), where each r_i is an amino acid residue. Let I = {(p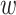, p_m)} be a set of doublets, where each doublet contains a wild-type protein pair and its corresponding mutant protein pair 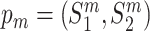. The mutant pair contains at least one mutant of the proteins from the wild-type pair, such that 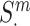could be the mutant form of the . Our goal is to estimate the change of quantifiable PPI properties between a wild-type pair and its mutant pair. Such changes can be that of binding affinity, buried surface area or other quantifiable properties.

Protein sequence encoding with contextualized representations

Primary sequence is the fundamental information to describe a protein. Apprehending the sequence information serves as the basis of estimating the effects caused by protein mutations. To better characterize the sequence information and the mutation, MuPIPR adopts two levels of encoding processes respectively on individual amino acids and on the sequence.

Contextualized amino acid embedding

Given an amino acid in a protein sequence, we seek to generate an adaptive representation according to its surrounding amino acids (referred as the context). The contextualized amino acid embedding produces a sequence of vector representations for the amino acid residues, 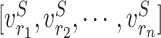, where each vector is the representation of residue r_i that is specific to the context of protein S. The detailed framework of training the contextualized amino acid embedding (E_co) is shown in Figure 2A.

Figure 2.

The detailed framework of the two encoders.

Compared to the static representations of the amino acid such as the one-hot encoding and co-occurrence based embeddings (23), the contextualized embedding seeks to incorporate the information of neighboring amino acids. Inspired by the recent success of ELMo (27) for word representations under different linguistic contexts, we obtain the contextualized representations of amino acids by leveraging a pre-trained bidirectional language model (BiLM). The BiLM is crucial to capturing the context information of a given amino acid in a sequence.

The forward language model computes the sequence probability of residue r_i given the context (r₁, r₂, ..., r_{i − 1}):

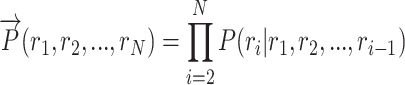(1)

The backward language model computes the sequence probability in the reverse order. Given the later context, (r_{i + 1}, r_{i + 2}..., r_N), it predicts the previous residue as:

(2)

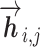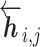The language model of each direction is implemented with M stacked layers of LSTM models (26). The LSTM layers of both directions output intermediate embedding vectors (i.e. hidden state vectors) or based on the context for the forward and backward language models respectively, where j = 1, ...M. These intermediate embedding vectors from different layers represent different levels of contextual information. The vectors from higher-level layers capture the information of more long-term contexts, while lower-level vectors extract more fine-grained information of the neighboring amino acids. Specially, the output of the LSTM’s top laye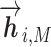r, or 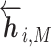, is passed through a Softmax layer to predict the next or previous residue r_{i + 1} or r_{i − 1}.

By combining the above two language models, the objective of the BiLM is defined as follows:

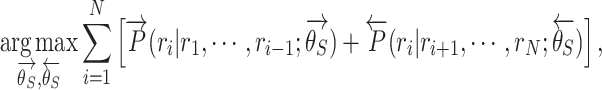(3)

where and are the learnable parameters of either direction of LSTM.

We pre-train our BiLM on a selected set of raw protein sequences from the STRING protein database (28), which is described in detail in the ‘Datasets’ section. Then the pre-trained BiLM can be applied on each protein sequence of up to N amino acid residues. For each amino acid r_i, the M-layer BiLM computes a total of 2M + 1 embeddings, denoted as 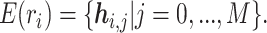Here, 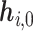is a trainable single-layer affine projection (29) on one-hot vectors of amino acids and 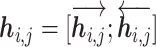are the intermediate results for each layer of the BiLM. Different layers of the stacked BiLM capture different widths of the neighboring contexts of the amino acid in the sequence. Therefore, for each amino acid, we aggregate the representations of different BiLM layers to obtain its contextualized representation: 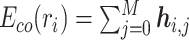. Then the encoding for S = (r₁, r₂, ..., r_N) is produced as a sequence of contextualized amino acid embedding vectors: E_co(S) = [E_co(r₁), E_co(r₂), ⋅⋅⋅, E_co(r_N)].

Protein sequence encoding

Upon obtaining the embeddings of amino acids for the protein sequence, we employ a deep 4-fold Siamese architecture of neural network to capture latent semantic features of the protein sequence doublets. Following PIPR (23), we choose to build a sequence level encoder based on the RCNN, due to its benefits with sequential and multi-granular feature aggregation for the protein sequence. MuPIPR can be easily adapted to use other sequence encoding techniques such as convolutional neural network (CNN) (21,22) or self-attentive encoders (30,31).

As depicted in Figure 2B, the residual RCNN sequence encoding process E_RCNN starts with an iterative process of the residual RCNN unit, consisting of two modules: a convolution module and a recurrent module. The convolution module serves as the initial encoder to extract local features from the input, followed by a recurrent module. Then the output of the recurrent module is used as the input of the next convolution module. This iterative process helps to generate and aggregate features while maintaining the contextualized features across different layers.

The convolution module contains a convolution layer with pooling. Let X be the input sequence of vectors. The convolution layer (Conv) applies a weight-sharing kernel of size k to generate a latent vector 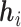from each k-gram X_{i: i + k} of X. By sliding through the whole sequence, the convolution layer produces a sequence of the latent vectors: . Then the p-max-pooling applies on every p-strides of the sequence (i.e. non-overlapping subsequences of length p). We use the max-pooling mechanism to preserve the most significant features within each stride. The output of this module is summarized as below:

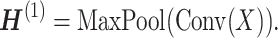(4)

The recurrent module consists of the bidirectional gated recurrent units (BiGRU). Note that the gated recurrent units (GRU) is an alternative to LSTM without extra parameters on memory gates. Typically GRU performs better than LSTM on small data (32). Consider that there are much fewer data for protein pairs with mutations than the raw sequence data for pre-training the BiLM, we use GRU instead of LSTM in this module. We also add the residual mechanism, which is designed to improve the learning of non-linear neural layers (33). Given an input vector , the recurrent module with residual is defined as: 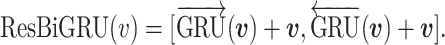A residual RCNN unit stacks two modules:

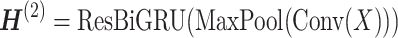(5)

After a chain of residual RCNN units, the output of the last iteration is passed through a final convolution layer with global average pooling (34). This produces the final sequence embedding:

(6)

Design and learning objective of MuPIPR

Learning architecture

In order to estimate the changes of PPI properties upon mutations, our model needs to handle the inputs of four sequences of a doublet (p, p_m) at a time, i.e two from a wild-type pair p and the other two from a mutant pair p. Therefore, we deploy a 4-fold Siamese architecture to capture the mutual interaction between p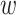 and p_m.

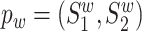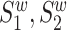Given two protein pairs and , where and 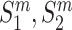are the wild-type proteins and their mutant respectively, the pre-trained contextualized model is applied to obtain the amino acid level representations for each sequence: 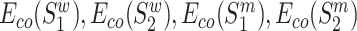. The amino acid embeddings of these four sequences are then served as inputs to one RCNN encoder, which yields , , , 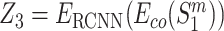and 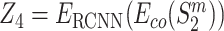. The encodings of two proteins in each pair are then combined by the concatenation of their element-wise product (⊙) and their absolute element-wise differences: Z 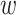= [Z₁⊙Z₂; |Z₁ − Z₂|], and Z_m = [Z₃⊙Z₄; |Z₃ − Z₄|], where Z and Z_m refer to the final encoding of the wild-type pair and the mutant pair, respectively. Intuitively, we use the integration technique defined for Z and Z_m to apprehend the mutual influence of a pair of protein sequences, as this is a widely used technique for symmetric pairwise comparison in neural sequence pair modeling. Afterward, Z_c is obtained by the ordered concatenation of Z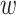 and Z_m, i.e., Z_c = [Z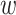; Z_m], as we specify the second pair to be the mutant one.

Primary learning objective

The property change upon mutation is estimated with an MLP-based regressor. Particularly, an MLP with leaky ReLU (35) is stacked on Z_c, and outputs a scalar to estimate the PPI property change. The main learning objective is to minimize the following mean squared loss:

(7)

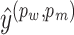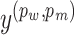where I is the set of doublets; and are the predicted and the true scores changes, respectively. Both scores are normalized to [0,1] by using the min–max scaling during the optimization process.

Joint learning with auxiliary regressors

It has been observed in many prior works that jointly learning of multiple correlated tasks can help improve the performance of each task (36,37). In addition to predicting the property changes in PPI by the main MLP regressor, MuPIPR is able to predict the original measure of the properties for the wild-type pair and the mutant pair. This is achieved by using two auxiliary regressors, which is jointly learned to enhance the estimation of the changes. 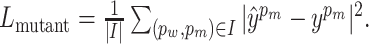Similar to L_change, we use the mean squared loss for both the wild-type pair and the mutant pair: , and Then, the learning objective is to minimize the joint loss L_joint = L_change + L_wild + L_mutant.

Implementation details

The BiLM for contextualized amino acid embeddings is implemented as two stacked layers of bidirectional LSTMs, for which the hidden dimension is set to 32. The protein sequence encoder E_RCNN consists of 3 RCNN units. The kernel size k of the convolution layer is set to 3 and 3-max-pooling is adopted. The hidden state of the convolution size is set to be 50, and the residual RCNN output size is set to be 100. We also zero-pad short sequences to the longest sequence length in the dataset, as a widely adopted technique in bioinformatics (38–40) for efficient training. Both the main MLP and the auxiliary MLP have 1 hidden layer with 100 neurons.

We use batched training based on the AMSGrad optimizer (41) to optimize the parameters, for which we fix the batch size as 32, the learning rate α as 0.005, the linear and quadratic exponential decay rates as 0.9 and 0.999, respectively. We also implement 5 simplified variants of MuPIPR. Specifically, MuPIPR-noAux removes the two auxiliary MLP regressors in the estimation stage. MuPIPR-static uses the same four-sequence residual RCNN encoders, but replaces the contextualized amino acid representations with the static amino acid embeddings as used in PIPR (23). MuPIPR-static-noAux removes the two auxiliary MLP regressors and uses the static embeddings simultaneously. MuPIPR-CNN substitutes the residual RCNN encoder with convolution layers by removing the residual BiGRUs. At last, MuPIPR-CNN-noAux further removes the auxiliary regressors. All model variants are trained until converge for each fold of the cross-validation.

Datasets

We obtain data from three resources for different purposes. Data from the SKEMPI (Structural database of Kinetics and Energetics of Mutant Protein Interactions) database (42) are used to conduct the task of binding affinity change estimation. The dataset for the task of BSA change estimation is constructed from the PDB (protein data bank) (43). To pre-train the contextualized representations of amino acids, we collect protein sequences from the STRING database (28). Details of these datasets are described below. The processed data are available at our GitHub repository.

SKEMPI datasets

Two datasets generated from the SKEMPI database are used for the binding affinity task. The first one is a benchmark dataset extracted by Xiong et al. (20). We denote it as SKP1400m. This dataset contains the changes of binding affinity between wild-type and mutated protein complexes that are experimentally measured. These mutations include single and multiple amino acid substitutions on the protein sequences. For duplicated entries of two protein pairs with the same mutations, we take the average ΔΔG of those reported in SKEMPI.

As a result, this dataset contains 1400 doublets for 113 proteins, among which, 1129 doublets contain single-point mutations, 195 contain double-points mutations and 76 contain three or more mutations. The second dataset is provided by Geng et al. (19), which considers only single-point mutation of dimeric proteins. It contains 1102 doublets for 57 proteins. We denote this dataset as SKP1102s. Of these 1102 doublets, the majority (759 doublets) are new entries that are not found in SKP1400m.

PDB dataset

We use this dataset for the task of estimating BSA changes. To construct the wild-type pairs and their mutant pairs, we extract protein sequences from PDB and keep those with only two chains. Sequences with <20 amino acids are removed. Here a wild-type pair or a mutant pair refers to the two chains of a protein. We concatenate such two chains of a protein for pairwise sequence comparisons and retain those with one amino acid substitution. Note that given each doublet of protein complexes, we always regard the complex with a smaller PDB ID in the lexicographical order as the wild-type and the other as the mutant one. This process produces 2948 doublets. To compute the true value of BSA, we first run DSSP (44) to obtain the ASA of the proteins based on the 3D structures provided by PDB. The standard estimation of BSA is calculated by taking the difference between the sum of ASA for the individual chains in a protein complex and the ASA of the protein complex (19).

Contextualized amino acid training corpus

We obtain the corpus to pre-train the contextualized amino acid encoder from the STRING database. A total of 66 235 protein sequences of four species from the STRING database are extracted, i.e. Homo sapiens, Bos taurus, Mus musculus and Escherichia coli. These are the four most frequent species in the SKP1400m dataset.

RESULTS

To demonstrate the effectiveness of MuPIPR, we conduct comprehensive experiments on two tasks. These two tasks estimate the mutation effects on different aspects of the alteration of the PPI properties: the change of binding affinity (ΔΔG) and the change of buried surface area (ΔBSA).

Task 1: binding affinity change estimation

Binding affinity change estimation is a widely attempted task in previous works (8,15,17,18,20,45). Given a wild-type protein pair and its mutant pair, the goal is to estimate the difference of their binding affinities (ΔΔG).

Evaluation protocol

Following the convention (8,18), the performance of binding affinity change estimation is evaluated based on the Pearson’s correlation coefficient (Corr) and the root mean square error (RMSE), which are two widely used metrics for regression tasks. To be consistent with the baseline experiments, we carry out a 5-fold cross-validation on SKP1400m and a 10-fold cross-validation on SKP1102s. Note that the configurations of MuPIPR is described in Implementation details of the ‘Materials and Methods’ section, and the study of different hyperparameter values is presented in Hyperparameter study of this section.

Baseline methods

We compare MuPIPR with two groups of baselines for this task: (i) BeAtMusic (17), Dcomplex (16) and FoldX (15) are empirical linear methods; (ii) mCSM (8), BindProfX (20) and Mutabind (18) are statistical learning methods leveraging structural and/or energy features. Note that we cannot run iSEE (19) on SKP1400m, since the service of generating features used in iSEE is not provided. Hence, the comparison of iSEE is only conducted on the SKP1102s dataset used by Geng et al. (19).

Experimental results

The results are reported in Table 1. For ΔΔG estimation on single-point mutation, empirical linear methods perform the worst. This shows that the pre-determined coefficients cannot be generalized well to reflect the mutation effects. On the contrary, statistical learning methods generally perform better. The best-performing baseline on SKP1400m is Mutabind, which trains a Random Forest regressor based on a variety of energetic, structural and conservation features. MuPIPR outperforms Mutabind by 0.038 in Corr and 0.376 kcal/mol in RMSE. As for the comparison with iSEE, we achieve Corr of 0.858 and RMSE of 1.236 kcal/mol on SKP1102s, outperforming iSEE which achieves a Corr of 0.80 and an RMSE of 1.41 kcal/mol. This is attributed to the fact that MuPIPR is able to discover important features reflecting the mutation effects. The average evaluation time of MuPIPR for each mutant is around 0.03 seconds on one NVIDIA Tesla V100-SXM2-16GB GPU.

Table 1.

Corr and RMSE (kcal/mol) of ΔΔG estimation by different methods using the SKP1400m dataset

N mut	All		1		2		≥3
Methods	Corr	RMSE	Corr	RMSE	Corr	RMSE	Corr	RMSE
BeAtMusic	NA	NA	0.272	2.389	NA	NA	NA	NA
mCSM	NA	NA	0.579	2.019	NA	NA	NA	NA
Mutabind	NA	NA	0.816	1.675	NA	NA	NA	NA
Dcomplex	0.183	3.068	0.056	2.684	−0.057	4.435	0.015	3.999
FoldX	0.480	2.629	0.470	2.265	0.289	3.487	0.095	4.471
BindProfX	0.690	1.914	0.663	1.854	0.584	2.558	0.840	2.304
MuPIPR	0.883	1.324	0.854	1.299	0.899	1.462	0.898	1.303

For cases with multiple mutations, explicit feature-based learning methods often fall short of modeling more than one mutation. Therefore, we evaluate the capabilities of MuPIPR in capturing the effects of different numbers of mutations (N_mut) in Table 1, and compare with baselines that support multiple mutations. Dcomplex is the only empirical linear method that can model multiple mutations; however, it performs poorly in all cases. The estimations under multi-mutation cases are further impaired compared to single-point mutations. The statistical learning baseline that supports estimation upon multi-point mutations, i.e. BindProfX, shows better generalizability and offers better performance. MuPIPR significantly outperforms BindProfX in all cases with different number of mutations. In particular, MuPIPR offers a drastic improvement of 0.280 in Corr on two-mutation cases, and that of 0.058 on cases with more than two mutations. Hence, MuPIPR can precisely capture the effects of multi-point mutations, where other systems typically fall short.

To further demonstrate the contributions of each component of MuPIPR, we conduct an ablation study with simplified variants as shown in Table 2. Specifically, MuPIPR-static replaces the contextualized embedding with static amino acid embeddings; MuPIPR-CNN substitutes the residual RCNN encoder by removing the residual BiGRUs and uses convolution layers only; noAux remarks for removing the two auxiliary MLP regressors from the model. By adopting contextualized amino acid representations, MuPIPR and MuPIPR-CNN perform better than MuPIPR-static in both Corr and RMSE. This is due to the fact that contextualized representation mechanism can extract more-refined amino-acid-level features to distinguish among different contexts of the proteins. By propagating the mutation effects to surrounding amino acid representations, the subtle changes in the protein sequence can be competently captured. The complete version of MuPIPR outperforms MuPIPR-CNN with the improvement of 0.027 in Corr and 0.12 kcal/mol in RMSE. This shows that residual RCNN is superior in leveraging sequential and local significant features that are important to predict PPI properties.

Table 2.

Corr and RMSE (kcal/mol) of ΔΔG estimation by different variants of MuPIPR using the SKP1400m dataset

N mut	All		1		2		≥3
MuPIPR variants	Corr	RMSE	Corr	RMSE	Corr	RMSE	Corr	RMSE
MuPIPR-static-noAux	0.773	1.832	0.741	1.783	0.794	2.032	0.744	2.001
MuPIPR-static	0.795	1.721	0.754	1.684	0.821	1.946	0.858	1.654
MuPIPR-CNN-noAux	0.819	1.596	0.779	1.559	0.829	1.728	0.797	1.773
MuPIPR-CNN	0.856	1.449	0.822	1.410	0.869	1.663	0.867	1.435
MuPIPR-noAux	0.853	1.462	0.829	1.406	0.848	1.751	0.860	1.473
MuPIPR	0.883	1.324	0.854	1.299	0.899	1.462	0.898	1.303

To verify the effectiveness of adopting auxiliary regressors, we train the noAux variants to learn ΔΔG without the original binding affinities, ΔG_w for wild-type and ΔG_m for mutant. Table 2 demonstrates that the variants with auxiliary regressors (MuPIPR-static, MuPIPR-CNN and MuPIPR) consistently outperform their counterparts (MuPIPR-static-noAux, MuPIPR-CNN-noAux and MuPIPR-noAux) by 0.022, 0.037 and 0.030 in Corr, respectively. The auxiliary MLP regressors jointly learn the original scores, which can effectively guide the learning of ΔΔG and hence improve the performance. We further evaluate the performance of the auxiliary MLP regressors in estimating the original binding affinities. Table 5 shows that while all variants perform comparably well on estimating the ΔG, MuPIPR-CNN and MuPIPR ameliorate the estimation of ΔG_m through contextualized amino acid representations.

Table 5.

Corr and RMSE (kcal/mol) of binding affinity estimation by different variants of MuPIPR using the SKP1400m dataset

	ΔG		ΔGm
Methods	Corr	RMSE	Corr	RMSE
MuPIPR-static	0.978	0.722	0.860	1.775
MuPIPR-CNN	0.964	0.872	0.901	1.520
MuPIPR	0.966	0.872	0.903	1.483

To remove the bias of training and testing of our model on proteins with high sequence similarity, we evaluate the performance of MuPIPR by removing homologous proteins at different sequence similarity thresholds. Specifically, we use CD-HIT (46,47) to cluster the wild-type protein sequences from SKP1102s with 75 and 45% as thresholds. For each cluster, we select one protein as the representative and remove the entries of other proteins. Accordingly, we retain 652 and 637 protein pairs at the thresholds of 75 and 45%, respectively. After conducting 10-fold cross-validation, MuPIPR achieves a Corr of 0.794 and an RMSE of 1.340 kcal/mol on the subset with less than 75% sequence identity. On the subset with <45% sequence identity, it achieves a Corr of 0.758 and an RMSE of 1.434 kcal/mol. By removing the homologous proteins in the data, MuPIPR still performs reasonably well based on the evaluation metrics. This demonstrates MuPIPR is robust in identifying the important physicochemical changes regarding the changes of binding affinity.

Blind test evaluations

To show the generalizability of MuPIPR, we evaluate the performance of different methods on two external validation sets. The first blind test is provided by Benedix et al. (48), which contains the mutations on chain B of the interleukin-4 receptor (PDB ID: 1IAR). We denote this set as the NM test set. The second blind test contains the mutations of the MDM2-p53 complex (PDB ID: 1YCR) provided by Geng et al. (19). These mutations have been shown important in cancer development (49).

We follow the same experimental settings as Geng et al. (19) and apply the same data filtering criteria for the test sets. In addition, we use BLASTp (50) to verify that these test sets are unknown to the training phase. We search all the sequences from the test sets against all the wild-type sequences from SKP1102s and find that the best E-values are 0.35, 2.1 and 0.15 for the interleukin-4 receptor, MDM2 and p53, respectively. The BLASTp results indicate that the sequences of these test sets are significantly different from those in the training data.

We compare MuPIPR with four baselines including mCSM, BeAtMuSic, FoldX and iSEE. The results reported in Table 3 show that MuPIPR outperforms other methods on NM by achieving a 0.74 in Corr and a 1.13 kcal/mol in RMSE. While all baseline methods fall short of predicting ΔΔG on MDM2-p53, MuPIPR drastically outperforms others on MDM2-p53 with a significantly higher Corr of 0.43 and a lower RMSE of 0.70 kcal/mol. The comparative results of MuPIPR on the NM and MDM2-p53 sets demonstrate that MuPIPR can generalize better than other methods to mutations on protein complexes that share low sequence similarity with the training set.

Table 3.

Corr and RMSE (kcal/mol) of ΔΔG estimation on the external validation sets NM and MDM2-p53

Blind test set	NM		MDM2-p53
Methods	Corr	RMSE	Corr	RMSE
mCSM	0.154	1.828	0.225	0.826
BeAtMuSic	0.242	1.703	−0.226	0.913
FoldX	0.720	1.147	−0.140	0.903
iSEE	0.731	1.367	0.238	0.805
MuPIPR	0.742	1.134	0.434	0.697

Analysis on SKEMPI v2

SKEMPI v2 is a recently released dataset (51). It features a more diverse set of proteins that are not seen in SKEMPI v1. We use the same subset as described in Geng et al. (19) to evaluate MuPIPR, FoldX, mCSM and iSEE. The subset (SKPv2-487) contains 487 mutations in 56 protein complexes. MuPIPR is trained on SKEMPI v1 (SKP1102s). Notably, none of the predictors perform well as shown in Table 4. FoldX performs the best in Corr (0.34) but the worst in RMSE (1.53 kcal/mol). mCSM, iSEE and MuPIPR all achieve a Corr of 0.25. Among them, iSEE presents a slightly better RMSE of 1.32 kcal/mol.

Table 4.

Corr and RMSE (kcal/mol) of binding affinity estimation by different methods on the SKPv2-487 dataset

Methods	Corr	RMSE
mCSM	0.25	1.35
iSEE	0.25	1.32
FoldX	0.34	1.53
MuPIPR	0.25	1.36

Using the SKEMPI v1 as the learning resource to predict new proteins in SKEMPI v2 is very challenging. MuPIPR extracts the protein features from scratch on raw sequences, which inevitably fall short for cases where test data have distinct distributions on the sequence level. Therefore, MuPIPR is mostly suitable for estimating the mutation effects when there is adequate sequence relatedness. To support our assumption, we examine the relationship between RMSE and sequence similarity. Specifically, we run BLASTp for all wild-type sequences in SKPv2-487 (test set) against the SKP1102s dataset (training set) and record the smallest E-value for each test sequence from the BLASTp results. Then, We divide the protein pairs in the test set into four groups based on their E-values and report the RMSE of all methods as shown in Figure 3. The smaller E-value reflects a higher sequence similarity between the test and training. It is a clear trend that with the increasing of the E-value, the prediction performance drops more significantly. This demonstrates the importance of adequate sequence relatedness between the training and test set, and shows an intrinsic limitation of MuPIPR. Yet, we note that MuPIPR still offers a close performance to the other methods that employ experimental features.

Figure 3.

The performance of different predictors on SKEMPI v2 based upon different thresholds of sequence similarity (by the log E-value) when compared with the SKEMPI v1 training set. The number of samples in the four bins are 128, 78, 104 and 177, respectively.

Analysis of mutation types

Consider that different types of point mutations can occur to a protein sequence and yield different impacts on the protein complex, we provide an analysis to demonstrate how MuPIPR captures the mutation effect for specific types of mutations. In particular, we consider the most common point mutation where one amino acid is mutated to alanine. For simplicity, we regard such a mutation as an ‘ALA’ mutation, and others as a ‘NonALA’ mutation. In Figure 4, we use the scatter plot to show the correlations between predicted and experimental ΔΔG values for these two groups in SKP1102s, in which 335 out of 1102 samples are ALA mutations and 767 are NonALA mutations. MuPIPR achieves a Corr of 0.61 and an RMSE of 1.17 kcal/mol for the ALA mutations, and a Corr of 0.89 and an RMSE of 1.24 kcal/mol for the NonALA mutations. We compare our findings to the results reported by iSEE (19). iSEE attains lower Corrs (0.50 for ALA and 0.84 for NonALA) and higher RMSEs (1.21 kcal/mol for ALA and 1.48 kcal/mol for NonALA) than MuPIPR. Thus, MuPIPR is more effective in capturing the effects of alanine mutations.

Figure 4.

Correlations between predicted and experimental ΔΔG values for different types of mutated amino acids (i.e. ‘ALA’ and ‘NonALA’) in the SKP1102s dataset.

We further investigate the ability of MuPIPR on predicting the mutation effects of all 20 amino acids. Figure 5 summarizes the distribution of prediction errors for different amino acids. These amino acids are regarded as the outcomes of the mutation. The prediction error is calculated as the difference between experimental and predicted ΔΔG values. The boxplots show that MuPIPR consistently maintains high-quality predictions with all mutation types.

Figure 5.

Boxplots of prediction errors for different mutant types from the SKP1400m dataset.

Overall, MuPIPR performs consistently well on different mutation types, demonstrating that the predictions from MuPIPR are not biased toward any specific amino acid.

Task 2: Buried surface area change estimation

The second task estimates the change of buried surface area (ΔBSA) of two chains of a protein complex upon mutations.

Evaluation protocol

Similar to the first task, the performance of BSA change estimation is evaluated with Corr and RMSE. We also carry out a 5-fold cross-validation on the PDB dataset.

Baseline method

>To the best of our knowledge, the state-of-the-art methods only focus on estimating the solvent accessible surface area (ASA), instead of BSA and ΔBSA. Among these methods, we choose the best performing one, NetSurfP-2.0 (24), as our baseline. NetSurfP-2.0 is a deep learning model, which learns an architecture composed of convolutional and LSTM networks using sequence information. It estimates the ASA at the residue level for each protein sequence. The ASA of a chain of protein is then calculated by summing up the ASA of all residues in the sequence. The BSA and its change are then calculated based on the predicted ASA. In addition, we take three variants of MuPIPR into comparison, including MuPIPR-static, MuPIPR-noAux and MuPIPR-CNN as described in Task 1.

Experimental results

MuPIPR provides a direct estimation of ΔBSA, BSA for wild-type and BSA_m for mutant, without pre-estimating the ASA. Table 6 shows the estimations on the PDB dataset. All the MuPIPR variants drastically outperform NetSurfP-2.0 on both BSA and ΔBSA. The worst-performing variant MuPIPR-static, has already outperformed NetSurfP-2.0 with more than 1.4-fold of Corr on both BSA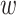 and BSA_m, As for ΔBSA estimation, MuPIPR-static almost doubles (1.9-fold) the Corr reported by NetSurfP-2.0. Similar to what we have observed in Task 1, incorporating both contextualized amino acid representations and auxiliary regressors leads to the best performance. MuPIPR offers a fold change of 2.1 in Corr over the results of NetSurfP-2.0. This once again indicates the importance of contextualized representations in highlighting the mutations in sequences, and the benefits of jointly capturing the original BSA. The average evaluation time of MuPIPR on ΔBSA estimations for each mutant is similar as the ΔΔG task, which is around 0.03 s on one GPU.

Table 6.

Corr and RMSE (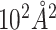) of BSA and ΔBSA estimation by different methods using the PDB dataset

	BSA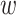		BSAm		ΔBSA
Method	Corr	RMSE	Corr	RMSE	Corr	RMSE
NetSurfP-2.0	0.670	25.994	0.685	22.731	0.329	3.405
MuPIPR-static	0.978	4.833	0.980	4.681	0.624	2.031
MuPIPR-noAux	NA	NA	NA	NA	0.667	2.021
MuPIPR-CNN	0.985	4.079	0.987	3.794	0.673	1.913
MuPIPR	0.986	3.844	0.988	3.616	0.695	1.859

Case studies of contextualized amino acid embeddings

We further demonstrate the effectiveness of contextualized representations in capturing the effect of mutations on both tasks using specific examples.

Table 7 depicts three different cases of mutations on the barnase-barstar complex (1B3S): (i) The mutation at position 25 of Chain D (Phe to Tyr) leads to a small change of binding affinity; (ii) The mutation at position 102 of Chain A (Ala to His) causes a substantial change; (iii) Combining the mutations of these two brings a significant change in the binding affinity of this complex. For each case, we also investigate the L₂ differences of sequence pair encodings between the wild-type pair and the mutant pair. The corresponding L₂ differences under static and contextualized amino acid representations are denoted by D_static and 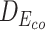, respectively. D_static is consistently small, which indicates the subtle changes to sequences are inadequately captured. As a result, its ΔΔG is more erroneously estimated. On the other hand, the ΔΔG for 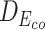is estimated more accurately. This shows the contextualized representations amplify the mutation effects, as reflected by 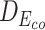. These observations show that the contextualized amino acid embeddings better benefit the downstream sequence encoder to capture the subtle changes of a sequence, such as point mutations, and lead to a more accurate estimation of binding affinity changes.

Table 7.

Case study of the effects of contextual amino acid embeddings on two chains of a protein complex, 1B3S_A for barnase and 1B3S_D for barstar

	L 2 distances		Ground truth	ΔΔG Predictions
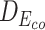
Mutation(s)	D static		ΔΔG	MuPIPR-static	MuPIPR
D_F30Y	−0.0027	−0.0073	0.596	−5.534	0.185
A_A102H	0.0021	−0.0518	−5.682	−5.032	−6.141
A_A102H, D_F30Y	−0.0006	−0.0591	−9.549	−2.082	−8.868

For the change of BSA estimation, Figure 7 depicts the 3D structures of two chains of the Human Insulin complex. Phe at position 25 of Chain B is mutated to His, causing a significant conformational alteration of the complex. The BSA therefore changes from −1401 to −1055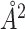. The true ΔBSA here (−346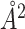) is more precisely estimated by MuPIPR with an absolute error of 1.61 than MuPIPR-static with an absolute error of 126.95. The static amino acid embeddings again fall short of capturing the changes upon mutation and lead to a notably less accurate estimation.

Figure 7.

Mutation effects on structures and BSA. The structures of Chain A and Chain B of the Human Insulin protein complex are depicted respectively on the left and right of the complex. The mutation is highlighted on Chain B. The wild-type (2HIU) and mutant (2M2P) complexes are retrieved from PDB.

In addition, we provide a comprehensive analysis of all the samples in the PDB dataset to further demonstrate the merits of using the contextualized amino acid embeddings over the static embeddings. Based on the predictions, we calculate the absolute errors for both model variants and use a scatter plot to compare this metric in Figure 6. The absolute error is calculated as the absolute difference between experimental and predicted ΔΔBSA values. As we can see, there are many more points (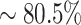) below the diagonal line than above (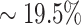), which indicate that most cases predicted by the complete version of MuPIPR have smaller errors than those predicted by MuPIPR-static. The errors of the complete version of MuPIPR are also statistically significantly smaller than the errors of MuPIPR-static by the one-tailed paired Student’s t-test (t-statistic of −5.58 and P-value < 0.001). This improvement in performance is due to the contribution of the contextualized amino acid embeddings, which help the downstream sequence encoder to capture the subtle changes of a sequence, therefore leading to a more accurate estimation of BSA changes.

Figure 6.

Scatter plot to compare the absolute errors by the complete version of MuPIPR and MuPIPR-static variant. The majority of points () are below the diagonal line, showing the predictions by the complete model to be generally more accurate.

Hyperparameter study

We conduct the study on the configuration of critical factors that affects the performance of the amino acid contextualized embeddings: (i) the dimensionality of hidden states for E_co; (ii) the number of LSTM layers used in E_co; (iii) the dimensionality of hidden states for the residual RCNN; (iv) the number of residual RCNN units. Figure 8 shows the performances of different settings for these four hyperparameters based on the change of binding affinity estimation task using the SKP1400m dataset.

Figure 8.

Performance evaluation on using different hyperparameters on the SKP1400m dataset for ΔΔG estimation. The Pearson’s correlation coefficient (Corr) and the root mean square error (RMSE) are reported in blue squares (left) and red triangles (right), respectively.

The dimensions of hidden states for E_co are chosen from {2, 4, 8, 16, 32, 64}. As illustrated in Figure 8A, the performance of MuPIPR gets better as we increase the dimensionality of the hidden states until it reaches 32 and then the performance slightly drops with dimension of 64. The number of LSTM layers in E_co is another factor. Different layers of the stacked LSTM captures different widths of the neighbouring contexts of the amino acid on the sequence and we examine the cases with one to four layers. Figure 8B shows that two layers is the optimum.

Apart from the parameters of E_co, we also exam the hidden states and the number of residual RCNN units for E_RCNN. As shown in Figure 8C, the model offers the best performance when the hidden states of residual RCNN is 100. As for the residual RCNN unit, it contributes to the different levels of granularity in feature aggregation where more units correspond to more aggregation. Figure 8D demonstrates that the performances increase with more residual RCNN units. However, the improvement from three to five units is marginal because too many residual RCNN units can lead to over-compressing the features. Our framework is robust to this setting as long as there are more than three residual RCNN units.

CONCLUSION

In this paper, we introduce a novel and comprehensive learning framework to estimate mutation effects on protein-protein interactions. Our proposed framework, MuPIPR, incorporates a contextualized representation mechanism of amino acids, which automatically extracts amino-acid-level features that are differentiated among different contexts of the proteins. Therefore this mechanism propagates the mutation effects to surrounding amino acid representations. By incorporating the contextualized representation mechanism to a carefully designed 4-fold Siamese deep learning architecture, MuPIPR effectively captures the PPI property changes between a wild-type pair and a mutant pair of proteins. Moreover, auxiliary regressors are provided to further improve estimation whenever original measures of the PPI property are available. Extensive experiments conducted on two different tasks demonstrate the promising performance of MuPIPR. As a future direction, we plan to explore more tasks of PPI property changes upon mutations. To further improve the performance, we seek to incorporate multi-task learning (36) to augment the learning of tasks that complement each other.

FUNDING

National Institutes of Health [U01HG008488, R01GM115833, U54GM114833, in part]; National Science Foundation [IIS-1313606, DBI-1565137, DGE-1829071].

Conflict of interest statement. None declared.