Abstract
Background
Clinical prediction tasks such as patient mortality, length of hospital stay, and disease diagnosis are highly important in critical care research. The existing studies for clinical prediction mainly used simple summary statistics to summarize information from physiological time series. However, this lack of statistics leads to a lack of information. In addition, using only maximum and minimum statistics to indicate patient features fails to provide an adequate explanation. Few studies have evaluated which summary statistics best represent physiological time series.
Methods
In this paper, we summarize 14 statistics describing the characteristics of physiological time series, including the central tendency, dispersion tendency, and distribution shape. Then, we evaluate the use of summary statistics of physiological time series as features for three clinical prediction tasks. To find the combinations of statistics that yield the best performances under different tasks, we use a cross-validation-based genetic algorithm to approximate the optimal statistical combination.
Results
By experiments using the EHRs of 6,927 patients, we obtained prediction results based on both single statistics and commonly used combinations of statistics under three clinical prediction tasks. Based on the results of an embedded cross-validation genetic algorithm, we obtained 25 optimal sets of statistical combinations and then tested their prediction results. By comparing the performances of prediction with single statistics and commonly used combinations of statistics with quantitative analyses of the optimal statistical combinations, we found that some statistics play central roles in patient representation and different prediction tasks have certain commonalities.
Conclusion
Through an in-depth analysis of the results, we found many practical reference points that can provide guidance for subsequent related research. Statistics that indicate dispersion tendency, such as min, max, and range, are more suitable for length of stay prediction tasks, and they also provide information for short-term mortality prediction. Mean and quantiles that reflect the central tendency of physiological time series are more suitable for mortality and disease prediction. Skewness and kurtosis perform poorly when used separately for prediction but can be used as supplementary statistics to improve the overall prediction effect.
Keywords: Patient representation, Clinical prediction tasks, Genetic algorithm, Summary statistics
Background
Clinical prediction tasks such as patient mortality and disease prediction are highly important for early disease prevention and timely intervention [1, 2]. Patient mortality prediction in intensive care units (ICUs) is a key application for large-scale health data and plays an important role in selecting interventions, planning care, and allocating resources. Accurate assessment of mortality risk and early identification of high-risk populations with poor prognoses followed by timely intervention are key in improving patient outcomes. A preliminary disease diagnosis assists doctors in making decisions. With the goal of accurately predicting clinical outcomes, studies have proposed methods that include scoring systems and machine learning models [3, 4]. The scoring systems for mortality prediction in widely clinical use include the Sepsis-related Organ Failure Assessment (SOFA) [3], the New Simplified Acute Physiology Score (SAPSII) [5], and the Multiple Organ Dysfunction Syndrome (MODS) [6]. However, most scoring systems based on simple logistic regression for patient mortality prediction have limited prediction performance. With the development of machine learning and deep learning models, studies have applied trained models to clinical prediction tasks and achieve better performance compared to earlier approaches [4, 7].
Feature extraction and patient representation are the underlying premise for constructing prediction models; consequently, these factors are important and affect the prediction performance. An increasing number of monitoring devices and laboratory tests in modern ICUs collect multivariate time series data of varying lengths from patients. Variable-length multivariate time series means that more than one physical measurement will be collected from a patient after admission to the ICU and that the sampling frequency of each predictor differs within a given time window. Overall, patient data consisting of physiological measurements have typical characteristics, such as high resolution, varying lengths, noisy values, and system bias, making the extraction of the temporal features of time series challenging. Most of the existing models select specific summary values for each predictor over a given time period and concatenate them to form patient vectors. Statistics are a form of summary values, and studies have shown that summary statistics can reflect the characteristics of time series. Moreover, they have advantages such as simple extraction, high robustness and strong representativeness [8–10]. The features of time series can be divided into three aspects: central tendency, dispersion tendency and distribution shape. The distribution and trends of time series can be reflected by combining multiple summary statistics, thus approximating the original data distribution and reducing the impact of noise on the prediction results.
Existing studies based on machine learning models have mainly used simple summary statistics to summarize time series information, such as maximum and minimum observations, as of physiological time series features. However, this lack of more comprehensive summary statistics leads to a lack of information in physiological time series. In addition, using only the maximum and minimum statistics to indicate patient features fails to provide adequate explanations. Despite the likelihood that more comprehensive features would have clinical implications, few existing studies have experimentally evaluated which summary statistics can best represent physiological time series. In this paper, we report an exhaustive set of results based on different combinations of summary statistics used as features of physiological time series for three clinical prediction tasks. The contributions of this study are twofold: on the one hand, we summarize and use 14 statistics as options for physiological time series representation compared with previous studies that used only a few statistics. On the other hand, we experimentally evaluate the performance of different summary statistics as features of physiological time series for different prediction tasks and obtain many conclusions that have practical implications and can provide guidance for subsequent related research.
The remainder of this paper is arranged as follows. First, we outline the related works. Second, we describe our method and its details and then present the experiments and results. Next, we discuss the results of the previous section. Finally, conclusions and future prospects are provided in the last section.
Related works
Methods for representing physiological time series
The most common method for representing physiological time series is to summarize the changing features of data contained in predictors using summary features and concatenate them as representative of a patient. Such statistics are simple and easy to calculate and have wide applications. Some studies also adopt the first measurement of predictors as the characteristic value of time series. The statistics used in some of the existing studies are listed in Table 1. From Table 1; these include maximum, minimum and mean values, which are widely used. One reason for their wide use is that these statistics are easy to acquire. Another is that experts tend to believe that the maximum and minimum observations reflect the normality or abnormality of the patient index, while the mean value reflects the average fluctuation range of the index over a period of time. A few studies have attempted to characterize time series features using statistics such as standard deviation, median and skewness.
Table 1.
Statistics used in existing research works
| No. | Research works | Min | Max | Mean | First | Others |
|---|---|---|---|---|---|---|
| 1 | Pollack M M, Patel K M, et al. (1996) [11] | ✓ | ✓ | |||
| 2 | Ribas V J, Lpez, et al. (2011) [12] | ✓ | ||||
| 3 | Fialho A S, Cismondi F, et al. (2012) [13] | ✓ | ||||
| 4 | Bosnjak A, Montilla G (2012) [14] | ✓ | ✓ | ✓ | std | |
| 5 | Wiens J, Horvitz E, et al. (2012) [15] | ✓ | ✓ | ✓ | std | |
| 6 | Eren Gultepe, Jeffrey P Green, et al. (2013) [16] | ✓ | std, CV, median, IQR | |||
| 7 | Pirracchio R, Petersen M L, et al. (2015) [17] | ✓ | ✓ | |||
| 8 | Lee J, Maslove D M, et al. (2015) [18] | ✓ | ✓ | |||
| 9 | NM Arzeno, KA Lawson, et al. (2015) [19] | ✓ | ✓ | |||
| 10 | Lipton Z C, Kale D C, et al. (2015) [20] | ✓ | ||||
| 11 | Lee J, Dubin J A, et al.(2016) [21] | ✓ | ||||
| 12 | Awad A, Baderelden M, et al. (2017) [22] | ✓ | ✓ | |||
| 13 | Morid M A, Sheng O R L, et al.(2017) [23] | ✓ | ✓ | ✓ | ✓ | median |
| 14 | Harutyunyan H, Khachatrian H, et al. (2017) [9] | ✓ | ✓ | ✓ | ✓ | std, skew |
| 15 | Sherman E, Gurm H, et al. (2017) [24] | ✓ | ✓ | ✓ | ||
| 16 | Purushotham S, Meng C, et al. (2018) [10] | ✓ | ✓ | ✓ | ||
| 17 | Mayhew M B, Petersen B K, et al. (2018) [25] | ✓ | ✓ | ✓ | std |
In addition to the above studies, many studies have attempted to fully understand the temporal trends hidden in multivariate time series data. Hug et al. considered a comprehensive set of physiologic measurements and manually defined a set of trend patterns [26]. McMillan et al. used temporal pattern mining to discover time series feature patterns [27]. Cohen et al. identified clinically relevant patient physiological states from physiologic measurements based on hierarchical clustering [28]. Yuan et al. applied nonnegative matrix factorization to group trends in a way that approximates patient pathophysiologic states [29]. Compared with these methods, patient representation based on summary statistics is a simple concept that is easy to calculate and can improve the interpretability of the results. However, the above studies based on summary statistics do not provide a clear reason why only these statistics were selected. It can be surmised that these choice were subjective and lack theoretical and experimental support. In addition, relevant research to determine which summary statistics can achieve the best performances for physiological time series is lacking. Therefore, the goals of this paper are to discover statistics that yield important summary performances and thus provide support for these studies and to improve model prediction performance based on representations of these summary statistics.
Feature selection methods
Datasets containing massive amounts of features can reduce classification accuracy, raise the computational cost and increase the risk of overfitting [30, 31]. Varying length multivariate time series can be characterized by multiple summary statistics; however, some statistics may contain useless or redundant information, and some features may be coupled. If representative features are not selected, algorithm resources will be consumed, but accurate classification results will not be obtained. Thus, it is beneficial to use feature selection mechanisms not only to identify the most representative features but also to reduce the number of features. To select a suitable combination of important summary statistics, feature selection is critical [32]. Previous works used three feature selection categories: filter methods, wrapper methods and embedded methods. Genetic algorithms are classically used for feature selection and have wide applicability because they can overcome the shortcomings of exhaustive methods that have high time complexity. Additionally, the genetic algorithm is a feature selection method of combinatorial optimization that can fully consider the relationships between features and find the most suitable feature combinations. Many previous works have selected features based on genetic algorithms and achieved satisfactory results. Leardi R et al. first proposed that the genetic algorithm can be a valuable tool for solving feature selection problems [33]. Mahdi Mohammadi et al. used a genetic algorithm to identify the most significant features of EEG signals and find their diagnostic value for depression [34]. Dino et al. combined a genetic algorithm with gene expression data to classify gene expression data in two steps [35]. Lei et al. proposed a new electrocardiograph pattern recognition method by combining a genetic algorithm with a support vector machine [36].
Method
Clinical prediction tasks include mortality, length of hospital stay, and disease prediction. The distribution characteristics of physiological time series are the manifestations of physiological states, including dispersion tendency, central tendency, and distribution shape, and these correspond to multiple statistics. By comparing the effects of different statistical combinations on different prediction tasks, the commonalities and differences of the optimal statistical combinations can be found, which can guide subsequent prediction tasks. The premise for finding the best combination of statistics is global search; however, global search is laborious and difficult in practice. This paper considers a feature selection method based on combinatorial optimization, that is, using the genetic algorithm to find the best combinations of statistics.
Identification of the distribution features of physiological time series
To characterize the time series distribution features of different predictors, it is critical to explore many different aspects of the data distribution. Based on statistical theory and existing research, this paper approximates the original data distribution by analysing the central tendency, the dispersion tendency and the distribution shape of each predictor. The central tendency reflects the representative value of the general level of the data or the central value, including statistics such as the mean, median, mode and quantile. The dispersion tendency of the distribution reflects trends describing how far the data are from the central value, including statistics such as maximum, minimum, standard deviation, coefficient of variation, range and interquartile range. The shape of the distribution reflects whether the distribution is symmetrical, the degree of skewness and the flatness of the distribution, including statistics such as skewness and kurtosis.
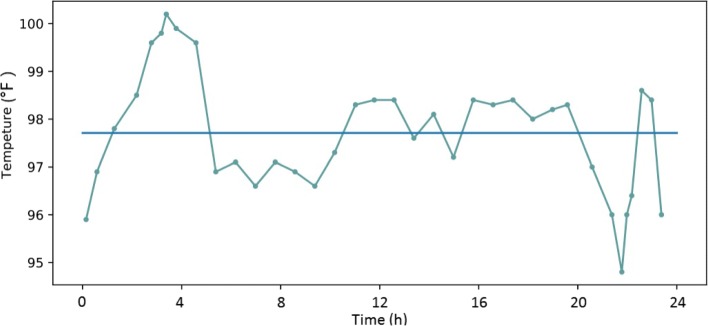
Figure 1 shows the temperature fluctuation of a patient within 24 hours of admission to the ICU. The minimum and maximum values reflect the range of temperature change of the patients and can reflect the trend of the data from the centre value. The mean value reflects the average temperature of the patients over 24 hours and can reflect the degree to which the data distribution aggregates to its centre value. Furthermore, the mode reflects the temperature value that appears most frequently within the 24 hours. The median reflects the average value, and the quantile reflects values in a specific position. The range and interquartile range reflect the degree of difference among the whole data distribution. The variance and standard deviation reflect the dispersion degree of the temperature distribution and the stability of the temperature data: a larger variance indicates that the patient’s temperature fluctuates widely, which may indicate that the disease is more severe. The coefficient of variation also reflects the degree of discreteness of the data. However, the central tendency and the dispersion tendency of the temperature distribution cannot reflect the order of temperature measurements; therefore, the shape of the distribution should be considered. The shape of the distribution can reflect the evolution of the disease. Skewness can reflect the symmetry of the data distribution. Generally, the symmetry of the data distribution can be understood as the stability of the temperature change. Both left and right skewness can reflect changes in temperature. Kurtosis reflects sharpness of the peak and the peak degree of the data distribution and reveals the fluctuation trend and the patients’ physiologic state.
Fig. 1.
Temperature fluctuation of a patient within 24 hours of admission to the ICU. The straight line represents the mean temperature within 24 hours
The summary statistics used in this study included the 13 statistics mentioned above, namely, minimum (min), maximum (min), mean, standard variation (std), median, lower quartile (Q1), upper quartile (Q3), mode, range, interquartile range (IQR), coefficient of variation (CV), skewness (skew) and kurtosis (kurt). Based on previous works, the first measurement (first) is also added.
Selection of best statistical combination based on the genetic algorithm
To explore the impact of different combinations of statistics on prediction performance and find the optimal combination, we formalize the problem. Let V={V1,V2,⋯,VP} represent a collection of P multivariate time series. Series Vi consists of a multidimensional time series of m variables, and the time series of each variable j has nj observations. For a variable-length time series, nj may differ for each variable j. Vi can be written as follows:
| 1 |
The j-th component of the i-th time series, that is, , is a univariate time series. For every univariate time series Vij, the different variables have different dimensions (observations), but every time series can be represented and transformed into L summary statistics extracted from the time series. In this paper, according to the 14 statistics mentioned, we set L=14.
Multiple clinical predictors with different sampling frequencies from multiple patients are collected in the ICU. Thus, V is a set of time series of varying length multivariate time series. Specifically, in Formula (1), P represents the number of patients, m corresponds to predictor dimensions such as heart rate, blood pressure, temperature and other vital signs and laboratory predictors and t is the time measurement point, and the length of t differs for different predictor sampling frequencies. Thus, Vijt denotes the t-th measurements of the j-th predictor in the i-th patient. Because of the different sampling frequencies of different predictors in different patients, the total lengths of the vectors obtained by concatenating them differ. We can summarize the measurements of different variables by statistics of fixed numbers and concatenate them to obtain vectors of the same length for patients. The time series of patient i after extracting the time series features using the L summary statistics can be expressed as follows:
| 2 |
Note that different statistics have specific statistical meanings. Some problems, such as information overlap, may exist among the statistics. Not all the statistics may perform well for prediction; thus, using all the statistics directly to represent a patient will increase the modelling complexity and can lead to overfitting. Let binary variable xk denote whether statistic k is selected in the best combination, that is,
| 3 |
Then, the selection vector X of the best combination of statistics can be expressed as
| 4 |
and thus, the representation of patient i after statistical selection can finally be expressed as
| 5 |
To select the combination of statistics that best reflects the physiological time series, we regard the selection vector X as an unknown parameter and construct an objective function to solve the optimization problem. The optimal objective function can be written as follows:
| 6 |
where E is an evaluation function used to measure the prediction performance; in this study, the area under the receiver operating characteristic curve (AUROC) is chosen in this paper. Here, yi is the true label of the patient in different prediction tasks, and f is the prediction model, which is the random forest algorithm in this study. Because the objective function in Formula (6) cannot be written using explicit expression levels, the simplest and most direct way to find the optimal solution of X is to adopt a global search strategy, that is, to find the prediction effect of all statistical combinations and then select the optimal combination. However, the time complexity of this method is O(2n−1), which has practical limitations. The purpose of this paper is to evaluate which statistical combination is most effective for time series representation, and the final result of feature selection is a combination of statistics (such as [minimum, maximum and mean]). The optimal combination can be achieved by chromosome coding in a genetic algorithm. The genetic algorithm is a combinatorial optimization algorithm that approximates a global search; it can fully consider the relationships between features and find the most suitable feature combination.
The parameter settings in the genetic algorithm are as follows. (1) Coding and decoding: Because the selection vector of summary statistics is a binary variable, we use binary coding, and no decoding process is needed. (2) Population: We select the size of the population as 20, and the initial population is generated randomly. (3) Fitness function: In this paper, we select the AUROC as the fitness function to select the feature subset with a better classification effect. The fitness function corresponds to E in Formula (6). (4) Genetic operators: We use the roulette wheel selection scheme as the selection strategy, single point crossover with a probability of 0.6 as the cross strategy and uniform mutation with a probability of 0.1 as the mutation strategy. (5) Termination condition: To determine the convergence of the algorithm adaptively during the iteration process, the termination condition for the genetic algorithm used in this paper combines the maximum genetic algebra with the stationary fitness value. When the continuous fluctuation range of the fitness value is less than the specified threshold or the genetic algebra is larger than the specified algebra, the solution of the algorithm is complete.
To avoid optimistically biased performance estimates from conducting feature selection on the full dataset, we refer to previous work by Ozcift and Gulten, who embedded a genetic algorithm for feature selection into Bayesian network classifier training using a nested cross-validation approach [37]. The general flow of feature selection with the genetic algorithm is given in Table 2. The feature selection based on the genetic algorithm is embedded in a 5-fold cross-validation. For each fold of test data, a set of summary statistics will be obtained by the genetic algorithm; thus, five groups of summary statistics will be obtained under 5-fold cross-validation. Then, based on the summary statistics of each group, the random forest model is used for prediction, and the mean and standard error of the metrics index is taken as the experimental result.
Table 2.
The general flow of feature selection by the genetic algorithm
| Divide data into k=5 folds |
| for k=1 to 5 |
| Assign |
| A = test data (1 fold reserved for random forest) |
| B = train data (3 folds train for random forest) |
| C = validation data (1 fold validation for random forest) |
| Repeat for train and validation data |
| step 1: Encode features as binary chromosomes |
| step 2: Generate a population of 20 chromosomes randomly |
| step 3: Evaluate AUROC of random forest algorithm for step 2 |
| step 4: Determine if termination conditions are met |
| if yes: |
| Terminate |
| else: |
| step 5.1: Apply Single point crossover with probability |
| of 0.6 |
| step 5.2: Apply uniform mutation with probability of 0.1 |
| step 5.3: Calculate AUROC of new chromosomes by |
| random forest and compare it with step 3 |
| step 5.4: Select best chromosomes with highest fitness |
| step 5.5: Replace chromosomes with lowest fitness, |
| back to step 4 |
| Train random forest with data (B+C) based on statistics obtained by |
| the genetic algorithm |
| Test random forest with data (A) |
| Calculate AUROC for fold k |
| End for |
| Calculate average AUROC for 5 folds |
Experiments and results
We explored the performances of different statistical combinations for different clinical prediction tasks, including patient mortality, length of hospital stay and disease prediction, and obtained the optimal statistical combination based on a genetic algorithm. Then, we analysed the results to find the commonalities and differences of the optimal combinations under different tasks.
Dataset and preprocessing
We used the MIMIC-III dataset collected from a variety of ICUs between 2001 and 2012 [38]. MIMIC-III is a large, freely available critical care database developed by the Laboratory for Computational Physiology of Massachusetts Institute of Technology (MIT). The database integrates deidentified, comprehensive, health-related data of 58,976 admissions admitted to the ICU of the Beth Israel Deaconess Medical Center (BIDMC) in Boston, Massachusetts.
To reflect the universality of the results, we did not target patients with a certain disease, but accepted all patients. After removing duplicates, we obtained a total of 42,145 admission records; patients less than 15 years of age were excluded. To prevent possible information leakage and to ensure similar experimental settings compared with related works, we used only the first ICU admission for each patient [39]. In the MIMIC-III database, bedside monitoring data, laboratory test data, input events and output events all consist of time series with time tags. The data for the predictors selected in this paper came from three tables: chartevents, labevents and outputevents. Following the related research, we chose the predictors used in SAPS II, as shown in Table 3 [10, 17, 21]. For each predictor, we used raw data instead of calculated data. For example, we treated GCSVerbal, GCSMotor, and GCSEyes from the Glasgow Coma Scale (GCS) score as separate features. All the extracted predictors shown in the table came from the first 24 hours after the patient was admitted to the ICU.
Table 3.
Predictors used in the experiments
| Feature | Item ID | Item Name | Table |
|---|---|---|---|
| Glasgow Coma Scale | 184 | GCSEyes | chartevents |
| 220739 | Eye Opening | chartevents | |
| 454 | GCSMotor | chartevents | |
| 223901 | Motor Response | chartevents | |
| 723 | GCSVerbal | chartevents | |
| 223900 | Verbal Response | chartevents | |
| White Blood Cells Count | 51301 | White Blood Cells | labevents |
| 51300 | WBC Count | labevents | |
| Potassium Level | 50971 | Potassium | labevents |
| 50822 | Potassium, whole Blood | labevents | |
| Po2 | 50821 | pO2 | labevents |
| Serum Bicarbonate Level | 50882 | Bicarbonate | labevents |
| Sodium Level | 50983 | Sodium | labevents |
| Urea Nitrogen (Bun) | 51006 | Urea Nitrogen | labevents |
| Bilirubin, Total | 50885 | Bilirubin, Total | labevents |
| Temperature | 678 | Temperature_F | chartevents |
| 223761 | Temperature_Fahrenheit | chartevents | |
| 676 | Temperature_C | chartevents | |
| 223762 | Temperature_Celsius | chartevents | |
| Urine Output | 40055 | Urine Out Foley | outputevents |
| FiO2 | 223835 | Inspired O2 Fraction | chartevents |
| 190 | FiO2 Set | chartevents | |
| Heart Rate(HR) | 211 | Heart Rate | chartevents |
| 220045 | Heart Rate | chartevents | |
| Systolic Blood Pressure(SBP) | 220179 | Noninvasive Systolic Blood Pressure | chartevents |
| 455 | NBP[Systolic] | chartevents | |
| Age | - | - | patients |
| Admission_Type | - | - | admissions |
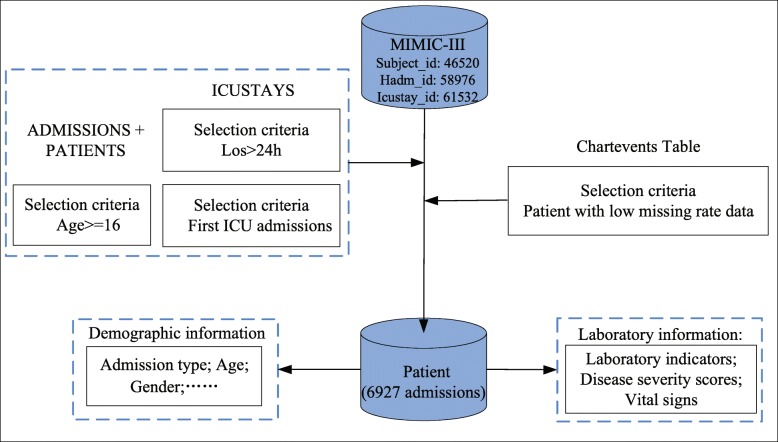
Data preprocessing mainly included processing missing values, noisy values and duplicate values. The missing value processing process was divided into three aspects: patients, predictors and statistics. We eliminated patients missing more than 30% of their data and predictors missing more than 40%. Because the sampling frequency of each predictor is different and the calculation of statistics such as std, kurt and skew have requirements for sampling frequency, some indicators with very low sampling frequency led to the inability to calculate those statistics. We eliminated the statistics in which the missing data rate was greater than 20% under these indicators. Then, we used mean interpolation to interpolate the remaining missing values. Abnormal values were processed for each predictor. The outliers were found and dealt with by the box-plot combined with the clinical normal range of the different predictors. For example, to protect information about surviving patients older than 90 years old, the age of these patients is recorded as 300 years old. Here, we replaced it with the median value. In addition, duplicate records were deleted, and inconsistent units were converted. For the interval value, we chose the median value to represent the predictor value of the time point. Ultimately, 6,927 admission records remained after preprocessing. Figure 2 shows the patient cohort selection inclusion criteria and the data extraction process, and Table 4 shows the baseline characteristics and outcome measure of our dataset. The median age of the adult patients was 65 years, and 58.8% of patients were male. In-hospital mortality was approximately 19.5%, and the median length of stay in the ICU was 4.7 days. We did not process non-time series predictors such as age and sex. For the time series predictors, we calculated 14 statistics, including min, max, mean, std, median, Q1, Q3, mode, range, IQR, CV, skew, kurt and the first measurement of each predictor from the first 24 hours after admission to the ICU.
Fig. 2.
Patient cohort selection inclusion criteria and data extraction process. Adult patients at their first hospital admission with a low missing data rate were selected as the patient cohort, and then, the clinical data of these patients, such as cohort demography, vital signs, and laboratory examinations, were extracted
Table 4.
Baseline characteristic and mortality outcome measures. Categorical variables are presented as counts (%), and continuous variables are presented as medians [inter-quartile range Q1-Q3]
| Overall | Died in the hospital | Survived in the hospital | |
|---|---|---|---|
| General | |||
| Admissions | 6927 | 1350 | 5577 |
| Age | 65.0 [53.0,77.0] | 71.0 [58.0,81.0] | 64.0 [52.0,75.0] |
| Gender (Female) | 2853 (41.2%) | 602 (44.6%) | 2251 (40.4%) |
| First SOFA | 6.0 [4.0,8.0] | 8.0 [5.0,11.0] | 5.0 [4.0,8.0] |
| First SAPS | 21.0 [18.0,25.0] | 24.0 [21.0,28.0] | 21.0 [18.0,24.0] |
| First SAPS II | 41.0 [32.0,52.0] | 53.0 [44.0,64.0] | 39.0 [31.0,49.0] |
| Origin | |||
| Elective | 1269 (18.3%) | 64 (4.7%) | 1205 (21.6%) |
| Emergency | 5463 (78.9%) | 1237 (91.6%) | 4226 (75.8%) |
| Urgent | 195 (2.8%) | 49 (3.6%) | 146 (2.6%) |
| Site | |||
| MICU | 1974 (28.5%) | 600 (44.4%) | 1374 (24.6%) |
| SICU | 1359 (19.6%) | 266 (19.7%) | 1093 (19.6%) |
| CCU | 660 (9.5%) | 163 (12.1%) | 497 (8.9%) |
| CSRU | 1599 (23.1%) | 98 (7.3%) | 1501 (26.9%) |
| TSICU | 1335 (19.3%) | 223 (16.5%) | 1112 (19.9%) |
| Lab Results | |||
| HR (BPM) | 88.0 [76.0,102.0] | 92.0 [78.0,109.0] | 87.0 [76.0,100.0] |
| NBP (MMHG) | 113.0 [100.0,130.0] | 109.0 [95.0,127.0] | 114.0 [101.0,129.0] |
| RR (CPM) | 20.56 [17.71-23.88] | 20.78 [17.90-24.19] | 20.31 [17.57-23.53] |
| NA (MMOL/L) | 139.0 [137.0,142.0] | 140.0 [136.0,143.0] | 139.0 [137.0,142.0] |
| K (MMOL/L) | 4.1 [3.8,4.6] | 4.2 [3.7,4.7] | 4.1 [3.8,4.6] |
| HCO3 (MMOL/L) | 23.0 [19.0,25.0] | 21.0 [17.0,24.0] | 23.0 [20.0,26.0] |
| WBC (103/MM3) | 11.7 [8.2,16.1] | 12.3 [7.5,17.8] | 11.7 [8.4,15.8] |
| P/F Ratio | 235.13 [227.10-235.13] | 235.13 [207.50-235.23] | 235.13 [235.13-235.13] |
| Ht (%) | 28.40 [25.00-32.30] | 27.90 [24.40-31.70] | 29.10 [25.80-32.70] |
| Urea (mmol/l) | 77.79 [46.35-120.52] | 70.27 [34.77-94.43] | 104.25 [60.69-140.53] |
| Bilirubin (mg/dl) | 1.00 [0.50-2.36] | 1.25 [0.50-2.88] | 0.88 [0.45-1.66] |
| Outcomes | |||
| ICU LOS (days) | 4.7 [2.4,10.5] | 5.7 [2.7,11.7] | 4.5 [2.3,10.2] |
| ICU Death (%) | 1129 (16.3%) | 1129 (83.6%) | - |
| Hospital Death (%) | 1350 (19.5%) | 1350 (100%) | - |
Clinical prediction tasks
The clinical prediction tasks selected in the experiment included patient mortality, length of hospital stay, and disease prediction. Mortality prediction is a primary patient outcome, including short-term, in-hospital and long-term mortality. In the experiment, whether the patient died within 72 hours after entering the ICU was selected as the short-term mortality label, and the 30-day and 1-year mortality rates were used as the long-term mortality label. The length of the hospital stay of an admission can be defined as the time interval between admission and discharge; we calculated the length of hospital stay for each admission in hours. When a patient is discharged, there will be multiple diagnosis, which are represented by the ICD(international statistical classification of disease)-9 diagnosis codes. We followed [10] and divided all the ICD-9 codes into 20 diagnostic groups; each diagnostic group had similar diseases (e.g. respiratory system diagnosis). Thus, the task of disease prediction is transformed into the task of predicting the ICD-9 code groups.
Experimental design
For the three prediction outcomes, we approximated a global search to obtain the best combination of statistics using a genetic algorithm. To improve the generalizability of the statistical combinations obtained by the genetic algorithm, we embedded the genetic algorithm in a cross-validation procedure, as shown in Table 2. For each data fold, we obtain a set of optimal statistical combinations (i.e., fivefold cross-validation yields 5 sets of statistical combinations). To reduce the effect of randomly partitioning the data during cross-validation, we repeated the entire process five times, selecting different random seeds for dividing the data each time. For the 25 sets of statistical combinations obtained under each prediction task, on the one hand, we compared their prediction performance with the combination of statistic commonly used in previous studies, and on the other hand, we conducted an in-depth analysis of these combinations. Then, we constructed two indexes to quantify the importance of different statistics used for prediction (see the Discussion section). The most important statistics were found by comparing the commonalities and differences of the optimal combination of statistics under different prediction tasks. As performance measures, we choose the AUROC and the area under the precision-recall curve (AUPRC) for the classification tasks and Mean Squared Error (MSE) for the regression tasks. AUROC and AUPRC evaluate the discrimination ability of the model, namely, the ability to assign higher severity scores to patients who died in the hospital compared with those who did not. The higher the AUROC and the AUPRC are, the better the model is. We calculated the mean and standard error of AUROC, AUPRC and MSE scores based on cross-validation as the final result.
All the experiments in this paper were programmed in the Python language, using Spyder 3.6 on a PC equipped with an Intel (R) Core (TM) i7-6700 CPU @ 3.40 GHz processor. The iterations of the genetic algorithm were terminated when the fluctuation in the fitness value became less than δ=10−3 for 50 consecutive iterations or when the total number of iterations exceeded 200. The crossover probability was set to 0.6, the mutation probability of the genetic algorithm was set to 0.1, and the size of the population was set to 20.
Results
We report the results under different prediction tasks separately. For each prediction task, we list the prediction results based on a single statistic, commonly used combinations of statistics, and the optimal combinations of statistics obtained by the genetic algorithm.
Results of mortality prediction
Patient mortality prediction tasks are divided into short-term, in-hospital, and long-term mortality prediction by survival time. In the experiment, the mortality of patients at 72 hours, in-hospital, 30 days and 1 year were predicted based solely on patients data collected within 24 hours after they entered the ICU. A single statistic can directly reflect the prediction effect. Table 5 shows the AUROC and AUPRC of the 14 selected statistics applied separately for the four mortality prediction tasks. When using a single statistic for mortality prediction, mean, median and Q3 achieved the best results under different prediction tasks. In other words, the statistic that reflects the concentrated trend of the physiological time series achieved the best and near-best prediction results on the mortality prediction task whether in the short or long term prediction. In addition, for short-term mortality prediction, the effect of the max statistic is also significantly greater, which is a statistic that reflects dispersion trends. It is not difficult to understand that if the short-term mortality is predicted using the data of patients 24 hours after entering the ICU, the values that will be significantly related to the predictive label are the degrees of fluctuation of the patient predictors. If the predictors are relatively stable, patient state can also be considered relatively stable. In contrast, large fluctuations are considered to indicate an unstable patient condition; such patients have a higher mortality rate. For the long-term prediction, the average levels of the predictors at a certain stage are closely related to the prediction results over extended periods. If the predictor remain at a consistently abnormal level, the mortality rate is higher over longer time spans.
Table 5.
Performance of mortality prediction by a single statistic
| Statistic | AUROC | AUPRC | AUROC | AUPRC |
|---|---|---|---|---|
| 72-hour | in-hospital | |||
| min | 0.8113 ±0.0023 | 0.1974 ±0.0040 | 0.7869 ±0.0028 | 0.4627 ±0.0073 |
| max | 0.8310 ±0.0034 | 0.2178 ±0.0081 | 0.8101 ±0.0013 | 0.4826 ±0.0035 |
| range | 0.7789 ±0.0077 | 0.1782 ±0.0065 | 0.7622 ±0.0014 | 0.4188 ±0.0048 |
| mean | 0.8517 ±0.0033 | 0.2282 ±0.0071 | 0.8248 ±0.0016 | 0.5128 ±0.0050 |
| std | 0.7671 ±0.0017 | 0.1625 ±0.0026 | 0.7585 ±0.0014 | 0.4096 ±0.0072 |
| CV | 0.7739 ±0.0033 | 0.1495 ±0.0054 | 0.7545 ±0.0015 | 0.4046 ±0.0037 |
| median | 0.8498 ±0.0048 | 0.2191 ±0.0061 | 0.8234 ±0.0017 | 0.5091 ±0.0041 |
| Q1 | 0.8330 ±0.0034 | 0.2042 ±0.0044 | 0.8085 ±0.0013 | 0.4918 ±0.0027 |
| Q3 | 0.8467 ±0.0010 | 0.2224 ±0.0089 | 0.8233 ±0.0020 | 0.5094 ±0.0036 |
| IQR | 0.7463 ±0.0064 | 0.1287 ±0.0043 | 0.7447 ±0.0021 | 0.3854 ±0.0031 |
| mode | 0.8395 ±0.0014 | 0.1995 ±0.0023 | 0.4804 ±0.0059 | |
| skew | 0.6886 ±0.0039 | 0.0890 ±0.0018 | 0.7074 ±0.0008 | 0.3418 ±0.0027 |
| kurt | 0.6492 ±0.0118 | 0.0840 ±0.0042 | 0.6908 ±0.0018 | 0.3301 ±0.0025 |
| first | 0.7206 ±0.0054 | 0.1115 ±0.0025 | 0.7366 ±0.0017 | 0.3665 ±0.0014 |
| 30-day | 1-year | |||
| min | 0.7508 ±0.0015 | 0.5126 ±0.0043 | 0.7674 ±0.0009 | 0.7203 ±0.0026 |
| max | 0.7671 ±0.0028 | 0.5237 ±0.0063 | 0.7790 ±0.0021 | 0.7289 ±0.0033 |
| range | 0.7590 ±0.0018 | 0.5211 ±0.0059 | 0.7597 ±0.0013 | 0.7070 ±0.0028 |
| mean | 0.7716 ±0.0033 | 0.5314 ±0.0049 | 0.7838 ±0.0017 | 0.7324 ±0.0034 |
| std | 0.7609 ±0.0027 | 0.5239 ±0.0053 | 0.7608 ±0.0033 | 0.7087 ±0.0049 |
| CV | 0.7482 ±0.0025 | 0.5188 ±0.0033 | 0.7526 ±0.0011 | 0.6991 ±0.0022 |
| median | 0.7675 ±0.0022 | 0.5319 ±0.0042 | 0.7789 ±0.0021 | 0.7279 ±0.0039 |
| Q1 | 0.7632 ±0.0027 | 0.5274 ±0.0047 | 0.7739 ±0.0017 | 0.7247 ±0.0023 |
| Q3 | 0.7757 ±0.0025 | 0.5368 ±0.0032 | 0.7808 ±0.0020 | 0.7310 ±0.0034 |
| IQR | 0.7533 ±0.0037 | 0.5212 ±0.0024 | 0.7505 ±0.0016 | 0.6956 ±0.0016 |
| mode | 0.7611 ±0.0022 | 0.5280 ±0.0066 | 0.7700 ±0.0022 | 0.7205 ±0.0023 |
| skew | 0.7304 ±0.0020 | 0.5020 ±0.0033 | 0.7233 ±0.0023 | 0.6728 ±0.0054 |
| kurt | 0.7210 ±0.0025 | 0.5017 ±0.0065 | 0.7196 ±0.0015 | 0.6781 ±0.0024 |
| first | 0.7597 ±0.0036 | 0.5281 ±0.0069 | 0.7561 ±0.0018 | 0.7031 ±0.0028 |
Table 6 provides the results of mortality prediction by the commonly used combinations of statistics including [mean], [first], [min, max], [min, max, min] and [min, max, mean, std]. Using a single statistic to represent physiological time series obviously leads to information loss and affects the prediction effect. Although the mean performs best as a single statistic, its prediction effect is worse than the prediction effect from combining multiple statistics. The first measurement, which has been used in previous studies, performed the worst; therefore, if only one statistic is used, the first value should not be applied, revealing irrationality in some previous studies. For the different prediction tasks (short-term, in-hospital and long-term mortality), [min, max], [min, max, mean], and [min, max, mean, std] top the list. [min, max, mean] performs best for 72-hour short-term mortality and in-hospital mortality prediction, which shows that the combination of dispersion and central tendency is better. It is further demonstrated that for short-term prediction, statistics that reflect the dispersion tendency have a better representation effect and can reveal fluctuations in the patient’s physiological state. For longer-term mortality prediction tasks (such as 30-day and 1-year), the addition of the std statistic enriches the physiological time series fluctuation information. Even knowing the min, max and mean value of the physiological time series, it is difficult for these statistics to reflect violent fluctuations in the patient’s physiological state. Long-term prediction causes a reduction in the time dependence of the prediction; thus, more information needs to be added to achieve good results.
Table 6.
Performance of mortality prediction by commonly used combinations of statistics
| Statistic | AUROC | AUPRC | AUROC | AUPRC |
|---|---|---|---|---|
| 72-hour | in-hospital | |||
| mean | 0.8517 ±0.0033 | 0.2282 ±0.0071 | 0.8248 ±0.0016 | 0.5128 ±0.0050 |
| first | 0.7206 ±0.0054 | 0.1115 ±0.0025 | 0.7366 ±0.0017 | 0.3665 ±0.0014 |
| min, max | 0.8590 ±0.0042 | 0.2558 ±0.0080 | 0.8308 ±0.0021 | 0.5289 ±0.0042 |
| min, max, mean | 0.8607 ±0.0021 | 0.2494 ±0.0031 | 0.8310 ±0.0012 | 0.5297 ±0.0030 |
| min, max, mean, std | 0.8589 ±0.0022 | 0.2498 ±0.0058 | 0.8282 ±0.0005 | 0.5262 ±0.0020 |
| 30-day | 1-year | |||
| mean | 0.7716 ±0.0033 | 0.5314 ±0.0049 | 0.7838 ±0.0017 | 0.7324 ±0.0034 |
| first | 0.7597 ±0.0036 | 0.5281 ±0.0069 | 0.7561 ±0.0018 | 0.7031 ±0.0028 |
| min, max | 0.7760 ±0.0021 | 0.5351 ±0.0031 | 0.7844 ±0.0011 | 0.7298 ±0.0020 |
| min, max, mean | 0.7734 ±0.0017 | 0.5353 ±0.0041 | 0.7840 ±0.0022 | 0.7330 ±0.0049 |
| min, max, mean, std | 0.7770 ±0.0016 | 0.5430 ±0.0058 | 0.7872 ±0.0020 | 0.7391 ±0.0030 |
Tables 7, 8, 9, 10 presents the optimal ten combinations of statistics obtained by the genetic algorithm and their performances for short-term, in-hospital and longterm mortality prediction. As shown, the prediction effect of the optimal combination of statistics obtained by the genetic algorithm is rarely weaker than the prediction effect of the commonly used combinations of statistics. As the prediction interval is extended, the prediction performance decreases, which indicates that predicting long-term mortality based only on data collected within 24 hours after patient entering the ICU not ideal. For short-term mortality prediction tasks, Q1 and Q3 appear more frequently. And the statistics that show dispersion tendency also appear frequently, such as min, max and so on. Skew and kurt, two statistics that describe the shape of the time series distribution and are often ignored, appear quite frequently and reflect the role of these two statistics in supplementing the other available information. Under longer-term mortality prediction tasks, mean, Q1 and Q3, which are concentrated statistics, also achieve better results. Combining statistics such as min, max, and mean can better characterize the distribution of physiological time series. In addition, the commonly used combinations of statistics such as [min, max] and [min, max, mean, std] also achieve good prediction results on both in-hospital and long-term mortality prediction tasks. In other words, this paper used experiments to demonstrate why the existing studies chose these particular statistical combinations to represent physiological time series.
Table 7.
The optimal ten combinations of statistics obtained by the genetic algorithm and their prediction performance for 72-hour mortality prediction
| Combination | AUROC | AUPRC |
|---|---|---|
| min, max, mean, median, Q1, IQR, kurt | 0.8627 ±0.0023 | 0.2493 ±0.0114 |
| min, max, CV, Q1, Q3, IQR, kurt | 0.8620 ±0.0027 | 0.2398 ±0.0028 |
| min, max, range, mean, Q1, Q3, IQR, skew | 0.8609 ±0.0041 | 0.2427 ±0.0072 |
| min, max, mean, std, Q3 | 0.8609 ±0.0022 | 0.2471 ±0.0031 |
| min, std, median, Q1, Q3, skew | 0.8607 ±0.0041 | 0.2444 ±0.0074 |
| min, max, mean | 0.8607 ±0.0021 | 0.2494 ±0.0031 |
| max, mean, Q1, Q3, IQR, kurt | 0.8606 ±0.0056 | 0.2455 ±0.0102 |
| min, mean, std, median, Q1, Q3 | 0.8605 ±0.0025 | 0.2485 ±0.0060 |
| min, max, range, mean, CV, Q1, Q3, kurt | 0.8604 ±0.0023 | 0.2454 ±0.0050 |
| min, max, mean, CV, median, Q1, Q3, IQR, kurt | 0.8603 ±0.0033 | 0.2433 ±0.0102 |
Table 8.
The optimal ten combinations of statistics obtained by the genetic algorithm and their prediction performances for in-hospital mortality prediction
| Combination | AUROC | AUPRC |
|---|---|---|
| min, max, range, median | 0.8316 ±0.0015 | 0.5308 ±0.0042 |
| min, max, mean | 0.8310 ±0.0012 | 0.5297 ±0.0030 |
| min, max | 0.8308 ±0.0021 | 0.5289 ±0.0042 |
| min, max, CV, Q1, Q3, kurt, first | 0.8285 ±0.0012 | 0.5268 ±0.0046 |
| max, range, Q1, IQR, mean | 0.8280 ±0.0012 | 0.5236 ±0.0027 |
| range, mean, std, median, Q1, Q3 | 0.8267 ±0.0008 | 0.5225 ±0.0025 |
| min, std, Q1, Q3, skew, first | 0.8261 ±0.0014 | 0.5234 ±0.0025 |
| range, mean, std, median, Q1, Q3 | 0.8257 ±0.0014 | 0.5216 ±0.0034 |
| min, mean, std, IQR, Q1, kurt | 0.8254 ±0.0014 | 0.5198 ±0.0041 |
| min, range, std, median, Q3, skew, first | 0.8253 ±0.0017 | 0.5225 ±0.0034 |
Table 9.
The optimal ten combinations of statistics obtained by the genetic algorithm and their prediction performances for 30-day mortality prediction
| Combination | AUROC | AUPRC |
|---|---|---|
| min, max, mean, CV, skew, first | 0.7780 ±0.0028 | 0.5351 ±0.0061 |
| min, max, mean, std | 0.7770 ±0.0016 | 0.5430 ±0.0058 |
| mean, std, CV, Q1, min, skew | 0.7749 ±0.0027 | 0.5338 ±0.0058 |
| min, max, std, CV, Q1, Q3, kurt | 0.7746 ±0.0015 | 0.5311 ±0.0061 |
| min, range, std, Q1, Q3, skew, kurt, first | 0.7742 ±0.0015 | 0.5368 ±0.0027 |
| min, range, Q3, skew | 0.7741 ±0.0020 | 0.5348 ±0.0048 |
| max, IQR, kurt | 0.7740 ±0.0011 | 0.5332 ±0.0049 |
| min, range, mean, Q3, IQR | 0.7735 ±0.0015 | 0.5334 ±0.0045 |
| min, max, CV, skew, first | 0.7732 ±0.0040 | 0.5296 ±0.0083 |
| min, max, Q1, Q3, skew | 0.7731 ±0.0015 | 0.5328 ±0.0036 |
Table 10.
The optimal ten combinations of statistics obtained by the genetic algorithm and their prediction performance for 1-year mortality prediction
| Combination | AUROC | AUPRC |
|---|---|---|
| max, mean, std, Q1, kurt | 0.7876 ±0.0014 | 0.7408 ±0.0026 |
| min, max, mean, std | 0.7872 ±0.0020 | 0.7391 ±0.0030 |
| range, mean, std, mode | 0.7852 ±0.0020 | 0.7290 ±0.0021 |
| std, CV, Q1, Q3, skew, kurt | 0.7846 ±0.0031 | 0.7299 ±0.0047 |
| min, max, range, Q1, skew, kurt | 0.7846 ±0.0024 | 0.7347 ±0.0024 |
| range, CV, Q1, Q3, mode, skew, kurt | 0.7834 ±0.0012 | 0.7293 ±0.0031 |
| mean, std, Q1, Q3, skew, first | 0.7831 ±0.0010 | 0.7276 ±0.0013 |
| range, median, Q3, mode, first | 0.7823 ±0.0015 | 0.7263 ±0.0023 |
| range, mean, CV, Q3, skew | 0.7821 ±0.0012 | 0.7275 ±0.0019 |
| max, range, mean, std, CV, median | 0.7819 ±0.0013 | 0.7258 ±0.0016 |
Results of length of hospital stay
Table 11 shows the performance of a single statistic for length of hospital stay prediction. A certain level of correlation exists between the length of hospital stay and mortality prediction. Generally, patients with higher mortality have more severe symptoms; consequently, their hospital stays are relatively long. Consistent with mortality prediction, range works best when based on a single statistic. At the same time, std, CV, and IQR, which reflect the dispersion tendency, have better effects. In addition to indicating the dispersion tendency, the better performing statistics also constitute crossover features, just as range=max−min. Therefore, the importance of cross features is self-evident.
Table 11.
Performances of single statistics for predicting length of hospital stay
| Statistic | MSE |
|---|---|
| min | 59562.72 ±309.59 |
| max | 54602.26 ±296.81 |
| range | 47071.82 ±273.31 |
| mean | 58583.26 ±395.47 |
| std | 48985.76 ±321.89 |
| CV | 50047.97 ±336.91 |
| median | 59286.18 ±397.62 |
| Q1 | 59449.26 ±330.22 |
| Q3 | 58534.13 ±363.85 |
| IQR | 51209.18 ±269.86 |
| mode | 60160.49 ±351.09 |
| skew | 58055.02 ±333.20 |
| kurt | 57259.82 ±178.34 |
| first | 61832.78 ±246.62 |
Table 12 shows the performances of commonly used combinations of statistics for predicting length of hospital stay. [min, max, mean, std] corresponds to the smallest MSE and the best prediction performance. Table 13 shows the optimal ten combinations of statistics obtained by the genetic algorithm and their prediction performances for length of hospital stay prediction. The effect of the combinations of statistics obtained by the genetic algorithm is superior to the effect of the common combinations of statistics. Range appears in each group, illustrating the validity of this statistic for predicting the length of hospital stay of patients. A larger range indicates an unstable condition, and patients with unstable conditions will naturally be hospitalized longer. In contrast, statistics such as the mean, which reflects the central tendency, appear less frequently. When predicting the length of hospital stay, the stability of the patient’s condition is the most important factor; thus, statistics that indicate the dispersion tendencies of time series function better.
Table 12.
Performances of commonly used combinations of statistics for predicting length of hospital stay
| Combination | MSE |
|---|---|
| mean | 58583.26 ±395.47 |
| first | 61832.78 ±246.62 |
| min, max | 48969.03 ±508.88 |
| min, max, mean | 49890.57 ±383.63 |
| min, max, mean, std | 46459.67 ±181.91 |
Table 13.
The optimal ten combinations of statistics obtained by the genetic algorithm and their prediction performances for predicting length of hospital stay
| Combination | MSE |
|---|---|
| min, max, range, std, CV, Q1, Q3, kurt, first | 43827.77 ±227.26 |
| min, max, range, CV, median, skew, kurt | 43854.10 ±405.73 |
| min, max, range, CV, median, Q3, skew | 43854.53 ±297.85 |
| max, range, mean, std, kurt | 43868.48 ±314.05 |
| range, CV, Q3, kurt, first | 43879.73 ±302.22 |
| min, range, CV, Q3, IQR, skew, kurt, first | 43985.47 ±313.01 |
| min, range, CV, Q3, skew, kurt, first | 44200.31 ±188.89 |
| min, range, CV, IQR, skew, first | 44308.55 ±276.67 |
| max, range, mean, std, Q1, IQR, skew, kurt, first | 44318.11 ±323.34 |
| min, max, range, mean, std, median, Q1, Q3, IQR, skew | 44334.44 ±301.66 |
Results of disease prediction
We treat disease prediction as a multilabel classification task and calculate the AUROC and AUPRC. Table 14 shows the performances of single statistics for disease prediction. On this task, a comparison of the results shows that the mean, median, Q1, Q3 and other statistics that reflect centralized trends have the best effect. In contrast, the effects of statistics that reflect the dispersion tendency are not very good. The performances of skew and kurt, which reflect the shape of the time series distribution, are the worst. This result shows that if only one statistic is used for patient disease prediction, the shape of the distribution is unimportant; the level of the value is more important.
Table 14.
Performances of single statistics for disease prediction
| statistic | AUROC | AUPRC |
|---|---|---|
| min | 0.6460 ±0.0097 | 0.4416 ±0.0131 |
| max | 0.6494 ±0.0108 | 0.4431 ±0.0086 |
| range | 0.6371 ±0.0097 | 0.4208 ±0.0134 |
| mean | 0.6602 ±0.0080 | 0.4470 ±0.0124 |
| std | 0.6271 ±0.0162 | 0.4230 ±0.0153 |
| CV | 0.6173 ±0.0127 | 0.4094 ±0.0152 |
| median | 0.6506 ±0.0073 | 0.4454 ±0.0110 |
| Q1 | 0.6503 ±0.0124 | 0.4396 ±0.0121 |
| Q3 | 0.6561 ±0.0070 | 0.4457 ±0.0070 |
| IQR | 0.6174 ±0.0142 | 0.4211 ±0.0106 |
| mode | 0.6369 ±0.0128 | 0.4364 ±0.0138 |
| skew | 0.5893 ±0.0159 | 0.3945 ±0.0110 |
| kurt | 0.5915 ±0.0082 | 0.3923 ±0.0111 |
| first | 0.6486 ±0.0158 | 0.4393 ±0.0082 |
The corresponding prediction performances of combinations of multiple statistics are shown in Table 15. Among the five commonly used combinations, it is surprising that the single mean statistic works best—even better than combinations of multiple statistics. From the optimal ten combinations obtained by the genetic algorithm shown in Table 16, we can see that the mean statistic appears in almost all the combinations, indicating its core role in disease prediction. Furthermore, min, max, and range are evenly distributed among the multiple combinations. We speculate that these metrics provide good auxiliary data for disease prediction; however, using these statistics alone does not result in good prediction.
Table 15.
Performances of commonly used combinations of statistics for disease prediction
| Combination | AUROC | AUPRC |
|---|---|---|
| mean | 0.6602 ±0.0080 | 0.4470 ±0.0124 |
| first | 0.6486 ±0.0158 | 0.4393 ±0.0082 |
| min, max | 0.6558 ±0.0179 | 0.4488 ±0.0079 |
| min, max, mean | 0.6477 ±0.0126 | 0.4462 ±0.0169 |
| min, max, mean, std | 0.6578 ±0.0169 | 0.4483 ±0.0096 |
Table 16.
The optimal ten combinations of statistics obtained by the genetic algorithm and their prediction performances for disease prediction
| Combination | AUROC | AUPRC |
|---|---|---|
| max, mean, Q3, IQR, first | 0.6610 ±0.0088 | 0.4455 ±0.0127 |
| max, mean, std, Q1, IQR, mode, first | 0.6585 ±0.0119 | 0.4483 ±0.0104 |
| min, range, std, median, Q3, mode, skew, first | 0.6581 ±0.0132 | 0.4462 ±0.0123 |
| range, mean, std, mode | 0.6569 ±0.0096 | 0.4450 ±0.0131 |
| max, std, CV, Q3, IQR, kurt, first | 0.6568 ±0.0100 | 0.4430 ±0.0106 |
| max, range, mean, std, CV, median | 0.6565 ±0.0115 | 0.4442 ±0.0080 |
| range, mean, std, CV, Q1, IQR, skew, first | 0.6563 ±0.0068 | 0.4435 ±0.0100 |
| min, max, mean, std, CV, Q1, IQR, kurt | 0.6553 ±0.0141 | 0.4429 ±0.0105 |
| range, mean, std, median, Q1, Q3 | 0.6546 ±0.0116 | 0.4556 ±0.0113 |
| min, mean, std, median, mode | 0.6540 ±0.0137 | 0.4546 ±0.0106 |
In summary, through the analysis of the prediction performances of different prediction tasks based on single statistics, commonly used combinations of statistics, and approximately optimal combinations of statistics obtained by the genetic algorithm, we discovered many interesting and clinically significant phenomena. We have indirectly demonstrated the rationality of using various combinations of statistics that were applied in previous research. Additionally, we found the statistics that are extremely important in clinical prediction tasks, which can provide guidance for future research.
Discussion
In the experiments, we used a genetic algorithm to obtain combinations with approximately optimal prediction results for different prediction tasks. Taking 72-hour mortality prediction as an example, the 5-fold cross-validation genetic algorithm was repeated 5 times to obtain 25 groups of combinations. Each group corresponds to multiple statistics, and the prediction performance varies among the different combinations. Which statistics appear most frequently and which statistics will achieve better prediction results are meaningful research questions. In the previous chapter, we performed a rough analysis. In this chapter, we quantitatively analyse the frequency of each statistic in the optimal combinations and the mean values of indexes under different tasks. Since we chose random forest as the classifier in the experiments, it is necessary to verify the performances of other classifiers based on the obtained statistics. So we also discuss this issue.
Tables 17, 18, and 19 show the results of each statistic regarding patient mortality, length of hospital stay and disease prediction, respectively. Frequency represents the number of occurrences of a statistic in the 25 combinations, and Mean_AUROC and Mean_AUPRC represent the average AUROC and AUPRC for all the combinations in which the statistic appears.
Table 17.
Quantitative analysis results of each statistic for mortality prediction
| Statistic | Frequency | Mean_AUROC | Mean_AUPRC | Frequency | Mean_AUROC | Mean_AUPRC |
|---|---|---|---|---|---|---|
| 72-hour | In-hosp | |||||
| min | 22 | 0.8598 | 0.2447 | 14 | 0.8262 | 0.5221 |
| max | 22 | 0.8597 | 0.2446 | 12 | 0.8264 | 0.5222 |
| range | 7 | 0.8592 | 0.2429 | 8 | 0.8258 | 0.5215 |
| mean | 17 | 0.8598 | 0.2453 | 12 | 0.8253 | 0.5197 |
| std | 10 | 0.8594 | 0.2459 | 14 | 0.8245 | 0.5195 |
| CV | 9 | 0.8596 | 0.2433 | 8 | 0.8242 | 0.5187 |
| median | 5 | 0.8605 | 0.2461 | 13 | 0.8249 | 0.5205 |
| Q1 | 20 | 0.8599 | 0.2440 | 11 | 0.8255 | 0.5208 |
| Q3 | 20 | 0.8597 | 0.2438 | 13 | 0.8249 | 0.5201 |
| IQR | 12 | 0.8599 | 0.2443 | 9 | 0.8245 | 0.5191 |
| mode | 3 | 0.8592 | 0.2463 | 7 | 0.8235 | 0.5179 |
| skew | 5 | 0.8596 | 0.2429 | 13 | 0.8241 | 0.5192 |
| kurt | 14 | 0.8598 | 0.2443 | 12 | 0.8244 | 0.5180 |
| first | 3 | 0.8584 | 0.2429 | 11 | 0.8248 | 0.5192 |
| 30-day | 1-year | |||||
| min | 17 | 0.7726 | 0.5323 | 5 | 0.7830 | 0.7311 |
| max | 14 | 0.7721 | 0.5305 | 13 | 0.7819 | 0.7280 |
| range | 12 | 0.7710 | 0.5306 | 12 | 0.7817 | 0.7269 |
| mean | 14 | 0.7718 | 0.5312 | 16 | 0.7819 | 0.7274 |
| std | 12 | 0.7722 | 0.5314 | 17 | 0.7820 | 0.7272 |
| CV | 12 | 0.7719 | 0.5305 | 12 | 0.7813 | 0.7258 |
| median | 10 | 0.7704 | 0.5289 | 7 | 0.7810 | 0.7259 |
| Q1 | 14 | 0.7712 | 0.5302 | 15 | 0.7819 | 0.7275 |
| Q3 | 12 | 0.7715 | 0.5305 | 10 | 0.7816 | 0.7262 |
| IQR | 11 | 0.7708 | 0.5298 | 8 | 0.7802 | 0.7242 |
| mode | 12 | 0.7699 | 0.5285 | 10 | 0.7814 | 0.7262 |
| skew | 17 | 0.7717 | 0.5308 | 13 | 0.7815 | 0.7264 |
| kurt | 10 | 0.7718 | 0.5301 | 9 | 0.7827 | 0.7291 |
| first | 9 | 0.7718 | 0.5309 | 10 | 0.7809 | 0.7253 |
Table 18.
Quantitative analysis results of each statistic for predicting length of hospital stay
| Statistic | Frequency | Mean_MSE |
|---|---|---|
| min | 15 | 44758.80 |
| max | 14 | 44706.94 |
| range | 18 | 44440.71 |
| mean | 12 | 44979.37 |
| std | 11 | 44800.35 |
| CV | 14 | 44770.15 |
| median | 10 | 44894.44 |
| Q1 | 11 | 45090.02 |
| Q3 | 15 | 44772.27 |
| IQR | 11 | 44770.07 |
| mode | 7 | 45325.18 |
| skew | 16 | 44670.12 |
| kurt | 14 | 44678.53 |
| first | 13 | 44771.67 |
Table 19.
Quantitative analysis results of each statistic for disease prediction
| Statistic | Frequency | Mean_AUROC | Mean_AUPRC |
|---|---|---|---|
| min | 6 | 0.6541 | 0.4447 |
| max | 14 | 0.6544 | 0.4443 |
| range | 13 | 0.6542 | 0.4464 |
| mean | 13 | 0.6550 | 0.4464 |
| std | 16 | 0.6547 | 0.4454 |
| CV | 9 | 0.6541 | 0.4434 |
| median | 11 | 0.6538 | 0.4476 |
| Q1 | 13 | 0.6539 | 0.4459 |
| Q3 | 11 | 0.6543 | 0.4467 |
| IQR | 10 | 0.6550 | 0.4436 |
| mode | 9 | 0.6539 | 0.4450 |
| skew | 8 | 0.6534 | 0.4435 |
| kurt | 8 | 0.6532 | 0.4441 |
| first | 11 | 0.6541 | 0.4451 |
In the mortality prediction task, the statistics with the highest frequency for 72-hour short-term mortality prediction are min, max, Q1 and Q3. The mean_AUROC and mean_AUPRC values corresponding to median and Q1 are high, while first are low. Statistics that embody the dispersion tendency, such as min and max, play a central role in short-term mortality prediction, while statistics such as first are more irrelevant to patients’ physiological status information. For the in-hospital mortality prediction task, min and std occurred most frequently, and min and max achieved the highest Mean_AUROC and Mean_AUPRC, respectively. For the long-term mortality prediction task, min, std, and kurt performed best. Kurtosis and skew measures have rarely been used in previous studies to measure the shapes of physiological time series distributions. However, the experiments in this paper show that these two statistics provide supplementary information and should not be discarded. Apart from this lack, we can clearly see that the statistics widely used in previous studies have indeed played a better role in predicting mortality. When predicting the length of hospital stay, range appears most often, and its effect is the best. In the disease prediction task, the most frequent occurrence is std, but the measures that perform the best are statistics that reflect the central tendency.
To verify whether the combinations of statistics obtained in this paper can also obtain good prediction results using other classifiers, we select logistic regression, SVM and decision tree. We compare the prediction performance of the optimal combination of statistics and the commonly used combinations of statistics under different prediction tasks by multiple classifiers. Tables 20, 21, 22 and 23 show the results of the 72-hour, in-hospital, 30-day, and 1-year mortality prediction, respectively. Tables 24 and 25 show the results of the length of hospital stay and the disease group prediction.
Table 20.
Performance of 72-hour mortality prediction by multiple classifiers
| Combination | AUROC | AUPRC | AUROC | AUPRC |
|---|---|---|---|---|
| Logistic regression | Random forest | |||
| mean | 0.8356 ±0.0014 | 0.2277 ±0.0037 | 0.8517 ±0.0033 | 0.2282 ±0.0071 |
| first | 0.7147 ±0.0030 | 0.1440 ±0.0031 | 0.7206 ±0.0054 | 0.1115 ±0.0025 |
| min, max | 0.8374 ±0.0019 | 0.2395 ±0.0031 | 0.8590 ±0.0042 | 0.2558 ±0.0080 |
| min, max, mean | 0.8475 ±0.0023 | 0.2469 ±0.0044 | 0.8607 ±0.0021 | 0.2494 ±0.0031 |
| min, max, mean, std | 0.8484 ±0.0022 | 0.2506 ±0.0065 | 0.8589 ±0.0022 | 0.2498 ±0.0058 |
| min, max, mean, median, Q1, IQR, kurt | 0.8426 ±0.0029 | 0.2377 ±0.0039 | 0.8627 ±0.0023 | 0.2493 ±0.0114 |
| SVM | Decision tree | |||
| mean | 0.8307 ±0.0031 | 0.2191 ±0.0080 | 0.6050 ±0.0164 | 0.0778 ±0.0066 |
| first | 0.6950 ±0.0082 | 0.1147 ±0.0074 | 0.5356 ±0.0163 | 0.0572 ±0.0050 |
| min, max | 0.8345 ±0.0031 | 0.2163 ±0.0041 | 0.5972 ±0.0112 | 0.0795 ±0.0052 |
| min, max, mean | 0.8372 ±0.0042 | 0.2158 ±0.0035 | 0.6040 ±0.0165 | 0.0835 ±0.0082 |
| min, max, mean, std | 0.8331 ±0.0043 | 0.2196 ±0.0088 | 0.5895 ±0.0118 | 0.0752 ±0.0054 |
| min, max, mean, median, Q1, IQR, kurt | 0.8377 ±0.0023 | 0.2275 ±0.0058 | 0.5952 ±0.0121 | 0.0777 ±0.0058 |
Table 21.
Performance of in-hospital mortality prediction by multiple classifiers
| Combination | AUROC | AUPRC | AUROC | AUPRC |
|---|---|---|---|---|
| Logistic regression | Random forest | |||
| mean | 0.8122 ±0.0040 | 0.5147 ±0.0021 | 0.8248 ±0.0016 | 0.5128 ±0.0050 |
| first | 0.7354 ±0.0033 | 0.4019 ±0.0022 | 0.7366 ±0.0017 | 0.3665 ±0.0014 |
| min, max | 0.8277 ±0.0041 | 0.5328 ±0.0020 | 0.8308 ±0.0021 | 0.5289 ±0.0042 |
| min, max, mean | 0.8301 ±0.0034 | 0.5365 ±0.0016 | 0.8310 ±0.0012 | 0.5297 ±0.0030 |
| min, max, mean, std | 0.8315 ±0.0018 | 0.5416 ±0.0010 | 0.8282 ±0.0005 | 0.5262 ±0.0020 |
| min, max, range, median | 0.8330 ±0.0022 | 0.5429 ±0.0013 | 0.8316 ±0.0015 | 0.5308 ±0.0042 |
| SVM | Decision tree | |||
| mean | 0.7997 ±0.0018 | 0.5121 ±0.0037 | 0.6163 ±0.0014 | 0.2652 ±0.0012 |
| first | 0.7190 ±0.0029 | 0.3779 ±0.0023 | 0.5797 ±0.0039 | 0.2359 ±0.0031 |
| min, max | 0.8056 ±0.0026 | 0.5237 ±0.0018 | 0.6243 ±0.0039 | 0.2724 ±0.0024 |
| min, max, mean | 0.8124 ±0.0026 | 0.5377 ±0.0026 | 0.6256 ±0.0015 | 0.2739 ±0.0024 |
| min, max, mean, std | 0.8165 ±0.0019 | 0.5424 ±0.0017 | 0.6241 ±0.0041 | 0.2719 ±0.0027 |
| min, max, range, median | 0.8186 ±0.0026 | 0.5446 ±0.0015 | 0.6337 ±0.0030 | 0.2800 ±0.0024 |
Table 22.
Performance of 30-day mortality prediction by multiple classifiers
| Combination | AUROC | AUPRC | AUROC | AUPRC |
|---|---|---|---|---|
| Logistic regression | Random forest | |||
| mean | 0.7257 ±0.0024 | 0.5118 ±0.0005 | 0.7716 ±0.0033 | 0.5314 ±0.0049 |
| first | 0.7321 ±0.0029 | 0.5139 ±0.0027 | 0.7597 ±0.0036 | 0.5281 ±0.0069 |
| min, max | 0.7376 ±0.0022 | 0.5140 ±0.0018 | 0.7760 ±0.0021 | 0.5351 ±0.0031 |
| min, max, mean | 0.7380 ±0.0035 | 0.5148 ±0.0038 | 0.7734 ±0.0017 | 0.5353 ±0.0041 |
| min, max, mean, std | 0.7404 ±0.0017 | 0.5184 ±0.0034 | 0.7770 ±0.0016 | 0.5430 ±0.0058 |
| min, max, mean, CV, skew, first | 0.7403 ±0.0041 | 0.5178 ±0.0045 | 0.7780 ±0.0028 | 0.5351 ±0.0061 |
| SVM | Decision tree | |||
| mean | 0.7322 ±0.0015 | 0.5162 ±0.0013 | 0.5778 ±0.0029 | 0.3550 ±0.0010 |
| first | 0.7164 ±0.0012 | 0.5055 ±0.0046 | 0.5102 ±0.0035 | 0.3069 ±0.0018 |
| min, max | 0.7282 ±0.0011 | 0.5034 ±0.0041 | 0.5566 ±0.0010 | 0.3444 ±0.0048 |
| min, max, mean | 0.7395 ±0.0033 | 0.5121 ±0.0046 | 0.5756 ±0.0034 | 0.3536 ±0.0012 |
| min, max, mean, std | 0.7218 ±0.0024 | 0.5039 ±0.0013 | 0.5867 ±0.0003 | 0.3619 ±0.0005 |
| min, max, mean, CV, skew, first | 0.7454 ±0.0015 | 0.5271 ±0.0035 | 0.5831 ±0.0026 | 0.3592 ±0.0024 |
Table 23.
Performance of 1-year mortality prediction by multiple classifiers
| Combination | AUROC | AUPRC | AUROC | AUPRC |
|---|---|---|---|---|
| Logistic regression | Random forest | |||
| mean | 0.7704 ±0.0025 | 0.7398 ±0.0030 | 0.7838 ±0.0017 | 0.7324 ±0.0034 |
| first | 0.7505 ±0.0043 | 0.7171 ±0.0024 | 0.7561 ±0.0018 | 0.7031 ±0.0028 |
| min, max | 0.7759 ±0.0036 | 0.7404 ±0.0046 | 0.7844 ±0.0011 | 0.7298 ±0.0020 |
| min, max, mean | 0.7776 ±0.0033 | 0.7413 ±0.0015 | 0.7840 ±0.0022 | 0.7330 ±0.0049 |
| min, max, mean, std | 0.7899 ±0.0024 | 0.7534 ±0.0040 | 0.7872 ±0.0020 | 0.7391 ±0.0030 |
| max, mean, std, Q1, kurt | 0.7998 ±0.0007 | 0.7642 ±0.0028 | 0.7876 ±0.0014 | 0.7408 ±0.0026 |
| SVM | Decision tree | |||
| mean | 0.7996 ±0.0015 | 0.7634 ±0.0018 | 0.6367 ±0.0019 | 0.5653 ±0.0037 |
| first | 0.7694 ±0.0024 | 0.7343 ±0.0026 | 0.6218 ±0.0006 | 0.5495 ±0.0024 |
| min, max | 0.7923 ±0.0024 | 0.7552 ±0.0024 | 0.6368 ±0.0026 | 0.5654 ±0.0013 |
| min, max, mean | 0.7959 ±0.0023 | 0.7607 ±0.0021 | 0.6375 ±0.0030 | 0.5658 ±0.0014 |
| min, max, mean, std | 0.7978 ±0.0019 | 0.7619 ±0.0017 | 0.6409 ±0.0028 | 0.5689 ±0.0023 |
| max, mean, std, Q1, kurt | 0.8090 ±0.0013 | 0.7734 ±0.0007 | 0.6370 ±0.0018 | 0.5654 ±0.0028 |
Table 24.
Performance of length of hospital stay prediction by multiple classifiers
| Combination | Logistic regression | Random forest |
|---|---|---|
| mean | 87295.21 ±136.38 | 58583.26 ±395.47 |
| first | 85075.99 ±141.76 | 61832.78 ±246.62 |
| min, max | 83285.19 ±248.05 | 48969.03 ±508.88 |
| min, max, mean | 81878.83 ±348.28 | 49890.57 ±383.63 |
| min, max, mean, std | 80245.68 ±234.80 | 46459.67 ±181.91 |
| min, max, range, std, CV, Q1, Q3, kurt, first | 75391.36 ±642.39 | 43827.77 ±227.26 |
Table 25.
Performance of disease prediction by multiple classifiers
| Combination | AUROC | AUPRC | AUROC | AUPRC |
|---|---|---|---|---|
| Logistic regression | Random forest | |||
| mean | 0.6537 ±0.0073 | 0.5251 ±0.0053 | 0.6602 ±0.0080 | 0.4470 ±0.0124 |
| first | 0.6229 ±0.0055 | 0.4932 ±0.0069 | 0.6486 ±0.0158 | 0.4393 ±0.0082 |
| min, max | 0.6395 ±0.0054 | 0.5053 ±0.0055 | 0.6558 ±0.0179 | 0.4488 ±0.0079 |
| min, max, mean | 0.6509 ±0.0123 | 0.5203 ±0.0115 | 0.6477 ±0.0126 | 0.4462 ±0.0169 |
| min, max, mean, std | 0.6483 ±0.0084 | 0.5153 ±0.0077 | 0.6578 ±0.0169 | 0.4483 ±0.0096 |
| max, mean, Q3, IQR, first | 0.6521 ±0.0081 | 0.5262 ±0.0077 | 0.6610 ±0.0088 | 0.4455 ±0.0127 |
| SVM | Decision tree | |||
| mean | 0.6407 ±0.0109 | 0.4399 ±0.0120 | 0.5267 ±0.0032 | 0.3329 ±0.0030 |
| first | 0.6370 ±0.0083 | 0.4281 ±0.0087 | 0.5203 ±0.0079 | 0.3291 ±0.0053 |
| min, max | 0.6399 ±0.0067 | 0.4293 ±0.0069 | 0.4983 ±0.0109 | 0.3020 ±0.0021 |
| min, max, mean | 0.6407 ±0.0109 | 0.4407 ±0.0099 | 0.5196 ±0.0110 | 0.3203 ±0.0063 |
| min, max, mean, std | 0.6437 ±0.0054 | 0.4426 ±0.0064 | 0.5234 ±0.0070 | 0.3281 ±0.0083 |
| max, mean, Q3, IQR, first | 0.6401 ±0.0115 | 0.4374 ±0.0073 | 0.5201 ±0.0119 | 0.3266 ±0.0086 |
In the task of mortality prediction, regardless of short-term, in-hospital or long-term prediction, from a horizontal perspective, the decision tree has a poor prediction effect. The performance of SVM is similar to random forest, but the time complexity is high. Logistic regression is usually able to achieve higher AUPRC. The time complexity of the random forest is low, and it can obtain the best prediction effect in most cases compared to other classifiers. This is why we choose the random forest as the classifier at the stage of calculating the fitness value by the genetic algorithm. Vertically, patient representation based on the best combination of statistics has achieved the best prediction results in most cases compared to the commonly used combinations of statistics. A single statistic such as mean and first is less effective than the combination of multiple statistics. In the cases where the optimal combination of statistics does not achieve the optimal effect, the combination of [min, max, mean, std] has achieved the optimal effect many times. On the one hand, it shows that the statistical combinations obtained by random forest and the analysis of effective statistics are also applicable to other classifiers. On the other hand, it also reflects the scientific nature of the commonly used combinations of statistics such as [min, max, mean, std].
In the length of stay prediction task, the MSE of random forest is much smaller than the MSE of logistic regression. The MSE corresponding to the optimal combination is smaller than the commonly used combination, and much smaller than the MSE corresponding to a single statistic. In the disease prediction task, the optimal combination of statistics only performs best when the random forest is used as a classifier. When logistic regression and decision tree are used as classifiers, the performance based on a single statistic ’mean’ is the best. Although the optimal combination of statistics do not achieve the best prediction effect, in the results of random forest, we can also find that the effect of mean and optimal combination of statistics is not much different. It is also consistent with the conclusion that the statistic ’mean’ plays an important role in disease prediction. In general, the effective statistical combinations based on random forest in this paper can also achieve better prediction results when selecting other classifiers. It shows that the discussion of effective statistics under different prediction tasks in this paper has a strong generalization ability.
Conclusion
In this paper, we summarized 14 statistics that describe the characteristics of physiological time series, of which three involve aspects of the central tendency, dispersion tendency, and distribution shape. Then, we evaluated the performances of these summary statistics of physiological time series as features for clinical prediction tasks, including patient mortality, length of hospital stay and disease prediction. We performed experiment on patient representations based on both single statistics and commonly used combinations of statistics. To find the combinations of statistics with the best prediction performances under different tasks (limited by the high time complexity of global search), we used a cross-validation-integrated with a genetic algorithm to obtain the combinations of statistics with approximately optimal performances. A quantitative analysis was performed on each statistic in the optimal combinations. Through in-depth analysis of the experimental results, we have reached the following conclusions: (1) As the prediction time becomes longer, the prediction performance becomes increasingly worse. Using data acquired only within 24 hours after the patient entered the ICU was insufficient to make reasonable long-term mortality prediction. (2) Statistics that reflect centralized trends, such as mean and median, play an important role in almost all mortality prediction tasks. (3) For short-term mortality prediction, statistics that show dispersion tendency are also representative, such as min, and max. Cross-features such as range may contain more information. (4) For the length of hospital stay prediction task, the statistics that reflect the dispersion tendency perform better. The length of hospital stay is closely related to the stability of the patient’s physiological state: unstable patients have a higher probability of staying longer. (5) For the disease prediction task, statistics that reflect the centralized trend, such as the mean, make larger contributions to the prediction result.
The mean represents the average level of different predictors is sig- nificantly correlated with judgements concerning whether the patient’s condition is due to a specific disease. (6) Commonly used combinations of statistics such as [min, max, mean] and [min, max, mean, std] achieve good prediction results in most cases; thus, these experiments help to verify the rationality of previous research. (7) Skew and kurt, which reflect the shape of a distribution, perform poorly when used individually as features for prediction, but they appear frequently in the optimal combinations, indicating that they can play a role as supplemental information.
Although we evaluated the effect of statistics of physiological time series under different prediction tasks, some limitations still exist. This paper considers the central tendency, dispersion tendency and distribution shape when choosing statistical features but does not fully consider latent characteristics, such as periodicity. Moreover, due to limitations in the sampling frequencies of some of the clinical predictors, the analysis of kurt and skew, which describe shape of a distribution, was insufficient. Furthermore, these experiments were applied only to patient mortality, length of hospital stay and disease prediction. Research on other clinical tasks still needs to be performed. In future work, we plan to correct the deficiencies of this study and design a more suitable patient representation method and model to improve the results of clinical task prediction.
Acknowledgements
The authors thank the National Natural Science Foundation of China, the Science and Technology Program of Jieyang and the Scientific and Technological Innovation Foundation of Dalian for funding our research and the MIT Laboratory for Computational Physiology and collaborating research groups for providing the freely available database (MIMIC-III).
Abbreviations
- APACHE
Acute physiology and chronic health evaluation
- AUPRC
Area under the precision-recall curve
- AUROC
Area under the receiver operating characteristic curve
- Bun
Urea nitrogen
- CV
Coefficient of variation
- EHR
Electronic health record
- GCS
Glasgow coma scale
- HR
Heart rate
- ICD
International statistical classification of disease
- ICU
Intensive care unit
- IQR
Interquartile range
- kurt
kurtosis
- max
Maximum
- MIMIC
Medical information mart for intensive care
- min
Minimum
- MODS
Multiple organ dysfunction syndrome
- SAPSII
New simplified acute physiology score
- SBP
Systolic blood pressure
- Q1
Lower quartile
- Q3
Upper quartile
- skew
Skewness
- SOFA
Sepsis-related organ failure assessment
- SOI
Severity of illness
- std
Standard variation
Authors’ contributions
CG conceived and designed the study. ML and JC performed the data collection, processing, and experiments. ML wrote the first full draft. ML and JC added further improvements to the paper. CG and JC reviewed and edited the manuscript. All the authors read and approved the final manuscript.
Funding
This research is supported in part by the National Natural Science Foundation of China (No. 71771034, 71421001), which provides financial support in the design of study and analysis of data, the Science and Technology Program of Jieyang (No. 2017xm041) and the Scientific and Technological Innovation Foundation of Dalian (No. 2018J11CY009), which provide financial support in analysis and interpretation of data and writing the manuscript.
Availability of data and materials
The data (MIMIC-III Dataset) used in our experiment can be obtained from https://mimic.physionet.org/. Researchers seeking to use the database must formally request access following the steps listed on that website.
Ethics approval and consent to participate
Not applicable.
Consent for publication
Not applicable.
Competing interests
The authors declare that they have no competing interests.
Footnotes
Publisher’s Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
References
- 1.Zimmerman LP, Reyfman PA, Smith AD, Zeng Z, Kho A, Sanchez-Pinto LN, Luo Y. Early prediction of acute kidney injury following icu admission using a multivariate panel of physiological measurements. BMC Med Inf Decis Making. 2019;19(1):16. doi: 10.1186/s12911-019-0733-z. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Kramer AA, Zimmerman JE. A predictive model for the early identification of patients at risk for a prolonged intensive care unit length of stay. BMC Med Inf Decis Making. 2010;10(1):27. doi: 10.1186/1472-6947-10-27. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Vincent J-L, Moreno R, Takala J, Willatts S, De Mendonça A, Bruining H, Reinhart C, Suter P, Thijs L. The SOFA (Sepsis-related Organ Failure Assessment) score to describe organ dysfunction/failure. Intensive Care Med. 1996;22:707–10. doi: 10.1007/BF01709751. [DOI] [PubMed] [Google Scholar]
- 4.Verplancke T, Looy SV, Benoit D, Vansteelandt S, Depuydt P, Turck FD, Decruyenaere J. Support vector machine versus logistic regression modeling for prediction of hospital mortality in critically ill patients with haematological malignancies. BMC Med Inf Decis Making. 2008;8(1):56. doi: 10.1186/1472-6947-8-56. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Le Gall J-R, Lemeshow S, Saulnier F. A new simplified acute physiology score (SAPS II) based on a european/north american multicenter study. JAMA. 1993;270(24):2957–63. doi: 10.1001/jama.1993.03510240069035. [DOI] [PubMed] [Google Scholar]
- 6.Baue AE, Durham R, Faist E. Systemic inflammatory response syndrome (SIRS), multiple organ dysfunction syndrome (MODS), multiple organ failure (MOF): are we winning the battle. Shock. 1998;10(2):79–89. doi: 10.1097/00024382-199808000-00001. [DOI] [PubMed] [Google Scholar]
- 7.Sakr S, Elshawi R, Ahmed AM, Qureshi WT, Brawner CA, Keteyian SJ, Blaha MJ, Al-Mallah MH. Comparison of machine learning techniques to predict all-cause mortality using fitness data: the henry ford exercise testing (fit) project. BMC Med Inf Decis Making. 2017;17(1):174. doi: 10.1186/s12911-017-0566-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Chandrakala S, Sekhar CC. International Conference on Pattern Recognition and Machine Intelligence. Berlin: Springer; 2009. Classification of multi-variate varying length time series using descriptive statistical features. [Google Scholar]
- 9.Harutyunyan H, Khachatrian H, Kale DC, Galstyan A. Multitask learning and benchmarking with clinical time series data. 2017. arXiv preprint arXiv:1703.07771. https://arxiv.org/abs/1703.07771. [DOI] [PMC free article] [PubMed]
- 10.Purushotham S, Meng C, Che Z, Liu Y. Benchmarking deep learning models on large healthcare datasets. J Biomed Inf. 2018;83:112–34. doi: 10.1016/j.jbi.2018.04.007. [DOI] [PubMed] [Google Scholar]
- 11.Pollack MM, Patel KM, Ruttimann UE. PRISM III: an updated pediatric risk of mortality score. Crit Care Med. 1996;24(5):743–52. doi: 10.1097/00003246-199605000-00004. [DOI] [PubMed] [Google Scholar]
- 12.Ribas VJ, López JC, Ruiz-Sanmartín A, Ruiz-Rodríguez JC, Rello J, Wojdel A, Vellido A. Engineering in Medicine and Biology Society, EMBC, 2011 Annual International Conference of the IEEE. Piscataway: IEEE; 2011. Severe sepsis mortality prediction with relevance vector machines. [DOI] [PubMed] [Google Scholar]
- 13.Fialho AS, Cismondi F, Vieira SM, Reti SR, Sousa JM, Finkelstein SN. Data mining using clinical physiology at discharge to predict ICU readmissions. Expert Syst Appl. 2012;39(18):13158–65. doi: 10.1016/j.eswa.2012.05.086. [DOI] [Google Scholar]
- 14.Bosnjak A, Montilla G. Predicting mortality of ICU patients using statistics of physiological variables and support vector machines. Comput Cardiol. 2012;39:481–4. [Google Scholar]
- 15.Wiens J, Horvitz E, Guttag JV. Advances in Neural Information Processing Systems. Cambridge: MIT; 2012. Patient risk stratification for hospital-associated c. diff as a time-series classification task. [Google Scholar]
- 16.Gultepe E, Green JP, Nguyen H, Adams J, Albertson T, Tagkopoulos I. From vital signs to clinical outcomes for patients with sepsis: a machine learning basis for a clinical decision support system. JAMA. 2013;21:315–25. doi: 10.1136/amiajnl-2013-001815. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Pirracchio R, Petersen ML, Carone M, Rigon MR, Chevret S, van der Laan MJ. Mortality prediction in intensive care units with the Super ICU Learner Algorithm (SICULA): a population-based study. Lancet Respir Med. 2015;3(1):42–52. doi: 10.1016/S2213-2600(14)70239-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Lee J, Maslove DM, Dubin JA. Personalized mortality prediction driven by electronic medical data and a patient similarity metric. PloS ONE. 2015;10(5):0127428. doi: 10.1371/journal.pone.0127428. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Arzeno NM, Lawson KA, Duzinski SV, Vikalo H. Designing optimal mortality risk prediction scores that preserve clinical knowledge. J Biomed Inf. 2015;56:145–56. doi: 10.1016/j.jbi.2015.05.021. [DOI] [PubMed] [Google Scholar]
- 20.Lipton ZC, Kale DC, Elkan C, Wetzel R. Learning to diagnose with LSTM recurrent neural networks. 2015. arXiv preprint arXiv:1511.03677. https://arxiv.org/abs/1511.03677.
- 21.Lee J, Dubin JA, Maslove DM. Secondary Analysis of Electronic Health Records. Cambridge: Springer; 2016. Mortality prediction in the ICU. [PubMed] [Google Scholar]
- 22.Awad A, Bader-El-Den M, McNicholas J, Briggs J. Early hospital mortality prediction of intensive care unit patients using an ensemble learning approach. Int J Med Inform. 2017;108:185–95. doi: 10.1016/j.ijmedinf.2017.10.002. [DOI] [PubMed] [Google Scholar]
- 23.Morid MA, Sheng ORL, Abdelrahman S. PPMF: A Patient-based Predictive Modeling Framework for Early ICU Mortality Prediction. 2017. arXiv preprint arXiv:1704.07499. Available from https://arxiv.org/abs/1704.07499.
- 24.Sherman E, Gurm H, Balis U, Owens S, Wiens J. AMIA Annual Symposium Proceedings, vol 2017. Bethesda: American Medical Informatics Association; 2017. Leveraging clinical time-series data for prediction: a cautionary tale. [PMC free article] [PubMed] [Google Scholar]
- 25.Mayhew MB, Petersen BK, Sales AP, Greene JD, Liu VX, Wasson TS. Flexible, cluster-based analysis of the electronic medical record of sepsis with composite mixture models. J Biomed Inf. 2018;78:33–42. doi: 10.1016/j.jbi.2017.11.015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Hug CW, Szolovits P. AMIA Annual Symposium Proceedings, vol 2009. Bethesda: American Medical Informatics Association; 2009. ICU acuity: real-time models versus daily models. [PMC free article] [PubMed] [Google Scholar]
- 27.McMillan S, Chia C-C, Van Esbroeck A, Rubinfeld I, Syed Z. Computing in Cardiology (CinC) Piscataway: IEEE; 2012. ICU mortality prediction using time series motifs. [Google Scholar]
- 28.Cohen MJ, Grossman AD, Morabito D, Knudson MM, Butte AJ, Manley GT. Identification of complex metabolic states in critically injured patients using bioinformatic cluster analysis. Crit Care. 2010;14(1):10. doi: 10.1186/cc8864. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Luo Y, Xin Y, Joshi R, Celi LA, Szolovits P. AAAI. Menlo Park: AAAI; 2016. Predicting ICU mortality risk by grouping temporal trends from a multivariate panel of physiologic measurements. [Google Scholar]
- 30.Demel MA, Janecek AG, Thai K-M, Ecker GF, Gansterer WN. Predictive qsar models for polyspecific drug targets: The importance of feature selection. Curr Comput Aided Drug Des. 2008;4(2):91–110. doi: 10.2174/157340908784533256. [DOI] [Google Scholar]
- 31.Abdi MJ, Giveki D. Automatic detection of erythemato-squamous diseases using PSO–SVM based on association rules. Eng Appl Artif Intell. 2013;26(1):603–8. doi: 10.1016/j.engappai.2012.01.017. [DOI] [Google Scholar]
- 32.Wei W, Guo C. A text semantic topic discovery method based on the conditional co-occurrence degree. Neurocomputing. 2019;368:11–24. doi: 10.1016/j.neucom.2019.08.047. [DOI] [Google Scholar]
- 33.Leardi R, Boggia R, Terrile M. Genetic algorithms as a strategy for feature selection. J Chemom. 1992;6(5):267–81. doi: 10.1002/cem.1180060506. [DOI] [Google Scholar]
- 34.Mohammadi M, Alazab F, Raahemi B, Richards G, Jaworska N, Smith D, Salle SDL, Blier P, Knott V. Data mining eeg signals in depression for their diagnostic value. BMC Med Inf Dec Making. 2015;15(1):108. doi: 10.1186/s12911-015-0227-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Kečo D, Subasi A, Kevric J. Cloud computing-based parallel genetic algorithm for gene selection in cancer classification. Neural Comput Applic. 2018;30(5):1601–10. doi: 10.1007/s00521-016-2780-z. [DOI] [Google Scholar]
- 36.Lu L, Yan J, de Silva CW. Feature selection for ECG signal processing using improved genetic algorithm and empirical mode decomposition. Measurement. 2016;94:372–81. doi: 10.1016/j.measurement.2016.07.043. [DOI] [Google Scholar]
- 37.Özçift A, Gülten A. Genetic algorithm wrapped bayesian network feature selection applied to differential diagnosis of erythemato-squamous diseases. Digit Signal Process. 2013;23(1):230–7. doi: 10.1016/j.dsp.2012.07.008. [DOI] [Google Scholar]
- 38.Johnson AE, Pollard TJ, Shen L, Li-wei HL, Feng M, Ghassemi M, Moody B, Szolovits P, Celi LA, Mark RG. MIMIC-III, a freely accessible critical care database. Sci Data. 2016;3:160035. doi: 10.1038/sdata.2016.35. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Johnson AE, Pollard TJ, Mark RG. Reproducibility in critical care: a mortality prediction case study. In: Proceedings of the 2nd Machine Learning for Healthcare Conference. Boston: 2017. p. 361–76. http://proceedings.mlr.press/v68/johnson17a.html.
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
The data (MIMIC-III Dataset) used in our experiment can be obtained from https://mimic.physionet.org/. Researchers seeking to use the database must formally request access following the steps listed on that website.