Cooperative dynamics of proteins unraveled by network models

Abstract

Recent years have seen a significant increase in the number of computational studies that adopted network models for investigating biomolecular systems dynamics and interactions. In particular, elastic network models have proven useful in elucidating the dynamics and allosteric signaling mechanisms of proteins and their complexes. Here we present an overview of two most widely used elastic network models, the Gaussian Network Model (GNM) and Anisotropic Network Model (ANM). We illustrate their use in (i) explaining the anisotropic response of proteins observed in external pulling experiments, (ii) identifying residues that possess high allosteric potentials, and demonstrating in this context the propensity of catalytic sites and metal-binding sites for enabling efficient signal transduction, and (iii) assisting in structure refinement, molecular replacement and comparative modeling of ligand-bound forms via efficient sampling of energetically favored conformers.

INTRODUCTION

Most proteins are molecular machines. They achieve their function because they possess the ability to undergo the structural changes required for their function. These structural changes may vary over a broad range of scales, from atomic fluctuations and side chain rotations to collective domain or subunit movements. Yet, even the large-scale movements do not, in principle, alter the native ‘fold’; the packing of secondary structural elements and/or the distribution of tertiary and quaternary contacts between residues remain unchanged for the most part. The collective motions allow for cooperative rearrangements of domains with respect to each other, or loop motions, which maintain the overall architecture/fold, or allow the protein to restore its original conformation, similar to an elastic material. Here, cooperative motions refer to conformational changes that collectively engage large portions of the structure and usually lie at the lowest frequency end of the spectrum of modes accessible to the protein under physiological conditions. Not surprisingly, elastic network models (ENMs) have been broadly exploited in unraveling protein dynamics, based on the premise that proteins have ‘intrinsic’ abilities, uniquely encoded by their three-dimensional (3D) fold, to sample functional fluctuations near their native state.^1,2

From a statistical thermodynamics perspective, the accessible conformations result from the equilibrium fluctuations near the global free energy minimum. Some directions of fluctuations are more probable than others. These are the ‘soft modes’ of motions; they evolve along a direction, on the multidimensional energy landscape, which by definition involves a relatively small energy ascent for a given deformation. These same modes are also expected to be most frequently recruited to achieve function, following the hypothesis that structures may have evolved to access most easily their functional movements. This hypothesis motivated a large body of studies aiming at characterizing the soft modes and exploring their relevance to function. A popular approach has been to extract the soft modes from the normal mode analysis (NMA) of ENMs. In parallel, simplified models such as the Gaussian network model (GNM),^3,4 rooted in the statistical thermodynamics of polymer networks,⁵ have been broadly used in the last decade. Theory and Methods section provides an overview of the theory and assumptions underlying these approaches.

ENM–NMAs and GNM analyses are now providing us with a better understanding of the cooperative machinery and design principles of biomolecular systems, as will be illustrated for a few cases in the section Learning from Network Models: Cooperative Responses and Communication. First, the soft modes are highly cooperative as may be quantified by their degree of collectivity,⁶ i.e., they cooperatively entail a large part of the molecule, if not the entire molecule. They are also very robust, as indicated by the following two features: (i) detailed atomic coordinates or energetics have negligible effect on these modes, as originally demonstrated by Tirion,⁷ and confirmed in many studies since then. This is presumably due to the fact that they are collectively defined by all the 3N-6 internal degrees of freedom for a structure of N interaction sites (atoms or pseudoatoms); and (ii) the intrinsic, structure-encoded fluctuations in conformations undergone by enzymes (in the absence of ligand binding) are in close accord with the changes observed in ligand-bound forms, suggesting that enzymes are predisposed to make the conformational rearrangements required for ligand binding.^8,9 A similar behavior is exhibited by antibodies when binding their antigens^10,11 or by allosteric proteins in general.¹ It should be noted that predisposition of the enzyme means the accessibility of the structural transition path, or a given mode of motion, rather than the coexistence of the alternative state. As such, predisposition does not exclude the adaptation of a given protein upon binding its ligand, but implies that the directions of structural change are selected from among those intrinsically accessible prior to deformation.

Second, the accessible modes provide a complete orthonormal basis set for describing the equilibrium motions in the 3N-6 dimensional space of internal coordinates. Each mode may be viewed as a mechanism of relaxation, or dissipation of energy, if the structure is subjected to a perturbation from the environment. Low-frequency (or soft) modes evidently constitute the most favorable paths of energy dissipation, as they incur the lowest ascent on the energy surface for a given deformation. Or, the accommodation of a given external stress by a soft mode would be expected to entail a lower internal resistance; therefore, soft modes are naturally activated in response to perturbations. The effective forces measured for exerting uniaxial tensions along different directions can indeed be explained by the selective recruitment of the modes that comply with the extension.^12,13 This concept will be elaborated in the section Anisotropic Response to Mechanical Stress: Selection of Suitable Modes.

Third, biomolecular structures need to be optimally ‘wired’ to efficiently transmit signals, to couple or exchange their chemical and mechanical energies, or induce allosteric responses. ENM representation of proteins permits us to utilize graph theory, along with information theoretic approaches and spectral clustering techniques to identify the sites that play a critical role in the flow of information across the ‘network’ of amino acids in the folded state. The collective fluctuations predicted by the GNM also define signal propagation mechanisms, as derived using a Markovian model in a recent study.¹⁴ Certain ‘nodes’ are distinguished by their effective signal transmission, or allosteric communication, properties. Examination of the identity of such key sites reveals a striking preponderance of active sites (e.g., catalytic residues and metal-binding sites), suggesting that efficient transmission of signals is an inherent, structure-encoded property of active sites. Conceivably, active sites of proteins evolved to be positioned at sites that lend themselves to efficient communication. Examples will be presented in the section Reconciling Equilibrium Dynamics and Signal Propagation Stochastics.

A practical utility of ENM–NMA of proteins is the predictions of collective changes of structures that are expected to be most readily accessible or to generate alternative conformations that satisfy certain requirements, e.g., optimal binding of a substrate.^8,10,15 Conformational changes along the soft modes have indeed been the focus of essential dynamics analysis of molecular dynamics (MD) simulations trajectories¹⁶ and principal component analysis of ensembles of structures.⁸ The soft modes are advantageously exploited for deforming high-resolution structures to fit cryo-electron microscopy (EM) images,^17–19 for structural refinement, and for generating alternative conformations that would suitably account for structural changes stabilized in various complexes/assemblies (e.g., upon binding substrate proteins or ligands). NMA in Structural Refinement section will summarize recent developments in that direction and illustrate the utility of ENM–NMA in refining homology models.

THEORY AND METHODS

Normal Mode Analysis

Classical NMA originated from spectroscopic analyses of molecules, in which the absorption in the vibrational spectra is given by normal modes. Its first application to proteins dates back to early 1980s.^20–22 Renewed interest in the last decade stems from the fact that the low-frequency modes can be robustly and efficiently derived using simplified models such as ENMs, and despite such simplifications, the global modes accessible to biomolecular systems are robustly determined and they usually relate to functional motions.^23,24

The potential energy V(q) of a molecular system of n degrees of freedom (e.g., atomic coordinates) may be approximated to the second order of the series expansion around the equilibrium state q⁰ = [q₁ ⁰ q₂ ⁰1 2q₃ ⁰₃ … q_n ⁰]^T as:

$$\begin{gathered} V(q)=\frac{1}{2}\sum _{i,j}\left(q_i-q_i^0\right){\left[\frac{{\partial }^{2}V}{\partial q_i{q}_j}\right]}^0\left(q_j-q_j^0\right) \\ =\frac{1}{2}\Delta q^{\text{T}}K\Delta q, \end{gathered}$$ (1)

where q is the 3n-dimensional vector of the instantaneous fluctuations, the superscript T designates its transpose, and K is the positive semidefinite matrix of second derivatives of the potential with respect to atomic coordinates. The ijth element of K is K_ij = [∂²V/∂q_i ∂q_j]⁰

$$M\frac{d^2\text{Δ}q}{d{t}^2}+K\text{\hspace{0.17em}Δ}q=0,$$ (2)

where M is a diagonal matrix composed of n superelements m_i I₃ along the diagonal, where m_i is the mass of the ith atom and I₃ is the identity matrix of order 3. The general solution to Eq. (2) is a 3n-dimensional vector of the form q(t) = ae^iωt, which, upon substitution into Eq. (2), leads to

$$\left(-{\omega }^{2}M+K\right)a=0.$$ (3)

Premultiplication of Eq. (3) by M^−1/2 yields ω²M ^1/2 a = M^−1/2 Ka = M^−1/2 K[M^−1/2 M^1/2]a, which, upon the change of variables, u = M^1/2 a, λ ω², and H=M^−1/2 KM^−1/2, leads to the eigenvalue equation

$$\lambda u=Hu.$$ (4)

NMA is the solution of this equation to obtain the 3n-6 nonzero eigenvectors u^(k) of the Hessian H, along with the corresponding eigenvalues, λ_k. The eigenvectors are 3n-dimensional vectors, the elements of which are organized in 3D vectors that represent the displacements u₁ ^(k), u₂ ^(k) (1 2 , … u_n k) n of the n atoms away from their equilibrium positions as the structure reconfigures along a given mode (e.g., mode k); and the eigenvalue λ_k is the corresponding squared frequency. λ_k scales with the curvature of the energy landscape along mode k. Thus, the lower frequency modes have a smaller curvature/stiffness and they undergo larger excursions from the energy minimum for a given energy increase, hence their ‘soft modes’ attribute.

One clear limitation of this method is its applicability to near-native conditions only, because it implicitly assumes linear dynamics, all interactions being approximated by harmonic potentials. This assumption is strictly valid in the immediate neighborhood of the global energy minimum. Proteins are subject, however, to anharmonic potentials and nonlinear dynamics, which are manifested by the ruggedness of the energy landscape and multiple minima/barriers. Even side-chain bond rotations exhibit two or three isomeric states often approximated by cosine functions. Furthermore, solvent damping effect is not accounted for by conventional NMA. The results from NMA should therefore be interpreted in the context of these approximations. As discussed below, coarse graining presents, in a sense, the advantage of eliminating certain degrees of freedom and resulting in a ‘smoother’ energy landscape where local minima are overlooked (or overcome) during collective motions, providing access to substates separated by low-energy barriers, but this comes at the cost of loosing atomic level accuracy.

GNM and Anisotropic Network Model

The use of ENMs to represent native proteins has the following two computational advantages: (i) there is no need for energy minimization and the Protein Data Bank (PDB)²⁵ structure is assumed to represent a global energy minimum, and (ii) a coarse-grained model is adopted for structure and energetics; typically, each node represents a residue and the pairs of nodes within a certain cutoff distance (R_c) are connected by springs of uniform force constant γ, which significantly reduce the size and complexity of H. Two ENMs, the GNM^3,4 and the anisotropic network model (ANM),^26–28 have found wide use in the last decade.

Gaussian Network Model

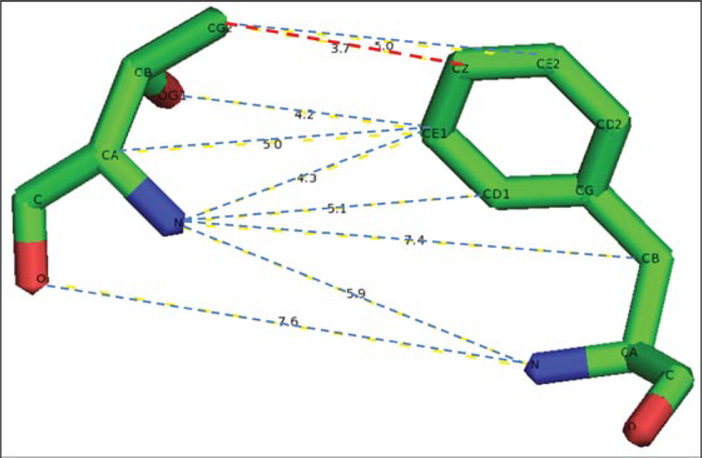
Following the original statistical thermodynamics theory of random polymer networks,⁵ the network nodes are assumed to undergo Gaussian fluctuations ΔR_i (1 ≤ i ≤ N) about their mean positions. Likewise, the distance vectors between nodes undergo Gaussianly distributed fluctuations ΔR_ij = R_ij −R_ij⁰ = ΔR_j −Δ R_i (Figure 1). The coordinates of= α-carbons− are used to define the spatial position of the nodes. The GNM potential is given in terms of the fluctuations ΔR_i= R_i −R_i⁰ in the position vectors of the nodes as³

$$\begin{gathered} V_{\text{GNM}}=\frac{\gamma }{2}\left[\sum _i\sum _{j,j>i}\left(-{\mathrm{\Gamma }}_{ij}\right){\left[\Delta R_j-\Delta R_i\right]}^2\right] \\ =\frac{\gamma }{2}\left[\Delta X^T\Gamma \Delta X+\Delta Y^{\text{T}}\Gamma \Delta Y+\Delta Z^{\text{T}}\Gamma \Delta Z\right], \end{gathered}$$ (5)

where Γ is the Kirchhoff (or connectivity) matrix, the off-diagonal elements of which are defined as Γ_ij=−1 if |R_ij|≤ R_c and zero and otherwise, and the diagonal elements are evaluated from the summation Γ_ii=−Σ_j Γ_ij over all off-diagonal elements in the ith row(or column);ΔX, ΔY, and ΔZ are the N-dimensional vectors of the respective X-, Y-, and Z-components of the fluctuation vectors ΔR₁, ΔR₂, … , and ΔR_N corresponding to the N residues.

FIGURE 1 |.

Schematic representation of equilibrium fluctuations. A portion of the protein backbone is displayed by the dotted curve. Filled dots refer to interaction sites (e.g., C^α-atoms) that are adopted as the network nodes. R_i⁰ and R_j⁰ designate the equilibrium positions of residues i and j; R_i and R_j are their instantaneous position vectors. The original and instantaneous separations are indicated by the solid line and dashed line, respectively. The fluctuations in the position vectors are given by ΔR_j and ΔR_i. R_ij⁰ and R_ij designate the equilibrium and instantaneous distance vectors between residues i and j. The change in the interresidue distance vector is related to the fluctuations in residue positions as ΔR_ij = R_ij − R_ij⁰ = ΔR_j − ΔR_i, and may be expressed as a weighted sum over the contributions ΔR_ij^(k) of individual modes.

The cross-correlations between the fluctuations of residues i and j are found from the statistical mechanical average³

$$\langle \text{Δ}{R}_i\cdot \text{Δ}{R}_j\rangle =\int \left(\text{Δ}{R}_i\cdot \text{Δ}{R}_j\right)\text{exp}\left(-V/k_{B}T\right)d\left\{\text{Δ}R\right\}/\times \int \text{exp}\left(-V/k_{B}T\right)d\left\{\text{Δ}R\right\}=\frac{3k_{B}T}{\gamma }{\left[{\Gamma }^{-1}\right]}_{ii},$$ (6)

where [Γ⁻¹]_ij is the ijth element of Γ⁻¹, k_B is the Boltzmann constant, and T is the absolute temperature. Note the determinant of Γ is 0, i.e., Γ cannot be inverted. Instead, its pseudoinverse is calculated using the N − 1 nonzero eigenvalues σk and eigenvectorsv^(k) of Γ. In compact notation,

$$C^{(N)}=\frac{3k_{\text{B}}T}{\gamma }{\Gamma }^{-1}=\frac{3k_{B}T}{\gamma }\sum _{k=1}^{N-1}\left[{\sigma }_k^{-1}{\mathit{\upsilon }}^{(k)}{\mathit{\upsilon }}^{(k)T}\right],$$ (7)

where C^(N) is the N × N covariance matrix; its ijth element is C_ij^(N) = < ΔR_i ΔR_j>, and the ith diagonal element C _ii ^(N) is simply the mean-square fluctuations <(ΔR_i )² > of residue i. The contribution of any subset of modes to the cross-correlations or mean-square fluctuations may be evaluated by performing the summation in Eq. (8) over this particular subset. Note that the soft modes (smallest eigenvalues) make the largest contribution to the covariance. The eigenvectors are normalized such that the plot of [v^(k) v^(k)T]_ii as a function of residue i represents the probability distribution of residue fluctuations in mode k, also called the kth mode profile.

Anisotropic Network Model

The ANM potential, V_ANM, is similar in form to V_GNM, except for the replacement of the scalar product [ΔRj − ΔR_i]² ≡ [(R_ij − R _ij⁰)•(R_ij – R_ij⁰)] in Eq. (6) by [|R_ij| − |R _ij ⁰|]² where |R_ij| designates• the magnitude of R_ij. Thus, V_GNM penalizes the change in the orientation of ΔR_ij even if the magnitude of the distance vectors is maintained, whereas V_ANM is exclusively based on distance changes. The second derivative of V_ANM leads to expressions of the form²⁶

$$\begin{gathered} {\partial }^2{V}_{\text{ANM}}/\partial X_i\partial Y_j{|}_{\text{R}0} \\ =-\gamma {\mathrm{\Gamma }}_{ij}\left(X_j^0-X_i^0\right)\left(Y_j^0-Y_i^0\right)/{\left(R_{ij}^{\text{c}}\right)}^2 \\ =-\gamma {\mathrm{\Gamma }}_{ij}\left(X_{ij}^0{Y}_{ij}^0\right)/{\left(R_{ij}^0\right)}^2 \end{gathered}$$ (8)

in terms of the components X_i⁰, Y_i⁰, and Z_i⁰ of R_i⁰. This permits us to express the elements of ANM Hessian H in closed form, and easily evaluate the ANM eigenvector u^(k) and eigenvalue λ_k, (1≤ k ≤ 3N-6), which provide information on the shape and frequencies of normal modes subject to V_ANMu ^(k), is a 3N-dimensional vector, composed of 3D vectors u₁^(k), u₂^(k), … u _N(k), that describe the displacements of all N residues in mode k. The change in interresidue distance induced by mode k is given in terms of the elements of u^(k) as

$$\text{Δ}{R}_{ij}^{(k)}=R_{ij}^{(k)}-R_{ij}{}^0={\left(k_{\text{B}}T/{\lambda }_k\right)}^{1/2}[u_i^{(k)}-\left[u_i^{(k)}\right].$$ (9)

Likewise, a 3N × 3N covariance matrix, C^(3N), composed of blocks of size 3 × 3 associated with the three components of each fluctuation vector ΔR_j replaces C^(N). C^(3N) scales with the inverse of the Hessian as

$$C^{(3N)}=k_{B}T{H}^{-1}=k_{B}T\sum _{k=1}^{3N-6}\left[{\lambda }_k^{-1}{u}^{(k)}{u}^{(k)T}\right].$$ (10)

The GNM/ANM results depend on the overall ‘fold’ rather than specific interactions or detailed atomic coordinates. As such, they provide information on the global dynamics favored by the particular fold/architecture, rather than local changes in structure and interactions. The main utility of GNM/ ANM is indeed the ability to efficiently explore global dynamics (collective motions in the low-frequency regime), which have been demonstrated in multiple studies to be insensitive to structural details or detailed force fields. Results on the high-frequency modes have limited utility: they permit us to identify potentially conserved sites and folding nuclei, but provide no information on the mechanisms of local motions.^29–32 It should also be noted that protein conformers used as input in, or generated as outputs from, ENM–NMA are not energy minimized with a molecular mechanics force field and hence may not be directly utilized in docking studies that require atomic level precision. Efforts are underway for designing hybrid methodologies that combine the information on global dynamics from ENMs and local motions from MD simulations³³ to efficiently explore multiscale processes. Also, sequence information is not included in ENMs and hence single mutations that result in loss of function are not captured by ENM analysis of the mutant, unless there are structural data for the mutant, which differ from that of the wild-type protein. Clearly, NMAs with ENMs also suffer from the same limitations (e.g., inadequate description of nonlinear effects, solvent effect, etc.) as atomic NMA. Yet, the coarse-graining of the structure and interactions allows for efficient sampling of domain rearrangements and cooperative movements near native state conditions. These motions could be hardly accessible (due to local energy barriers) should a detailed, full atomic description of the structure and dynamics be implemented.

Markovian Propagation of Allosteric Signals

Network models provide a useful tool for investigating the communication and signaling properties of complex systems. A widely used approach is model signal transduction as a Markovian stochastic process. We recently explored the possibility of probing the stochastics of signal propagation in proteins using a discrete time, discrete state Markov model.¹⁴ The strength of interactions (or weight of edges) in this network model (or the nonzero elements of Γ) could be assumed to be uniform (as in the GNM) as a first approximation. A slightly refined model, however, is to take account of residue specificity at a coarse-grained scale. To this aim, we define affinities a_ij = N_ij/√ (N_iN_j) as the weights of the edges, where N_ij is the total number of heavy atom contacts between residues i and j with the denominator correcting for bias due to size (Figure 2). The degree d_j of each node is given byƩ_i a_ij. The Kirchhoff matrix corresponding to this model is then Γ = D – A, where D is the diagonal matrix of the degrees and Ais the matrix of affinities. The conditional probability of transmitting a signal from residue j to residue i in one time step is simply m_ij = d_j⁻¹a_ij (where m_ij is the ijth element of the Markov transition matrix M).¹⁴

FIGURE 2 |.

Schematic description of the evaluation of affinity matrix elements. Two residues within interaction range are displayed, composed of Ni = 7 and Nj = 11 atoms. The affinity is evaluated based on atom–atom contacts that are closer than a cutoff separation, e.g., 4.0 Å. In the present case, there is only one pair of atom within this interaction rage, such that Nij = 1, and the affinity between this pair becomes aij = Nij /√ (NiNj) = 1/(77)^1/2 (see Markovian Propagation of Allosteric Signals section).

A metric of efficiency of signal transmission in network models is the hit time, which is the average number of steps it takes to transmit information from broadcaster i to receiver j. This is described by enumerating all possible ways to get from residue i to residue j, weighted by the transition/conditional probability of signal flow. The recursive equation to evaluate the average hit time between nodes i and j is given by:

$$\begin{gathered} H\text{(}j\text{,}i\text{)}=\sum _n^{k=1}\text{[1 + }H\text{(}j\text{,}k\text{)]}{m}_{ki} \\ =\sum _{k=1}^n{m}_{ki}+\sum _{k=1,k\ne j}^{n}H(j,k)m_{ki} \\ =1+\sum _{k=1,k\ne j}^{n}H(j,k)m_{ki}. \end{gathered}$$ (11)

Substituting M = DA⁻¹ and Γ= D − A, H(j,i) can be expressed in terms of the elements= of− Γ⁻¹ as¹⁴

$$H(j,i)=\sum _{k=1}^N\left\{{\left[{\Gamma }^{-1}\right]}_{ki}-{\left[{\Gamma }^{-1}\right]}_{ji}-{\left[{\Gamma }^{-1}\right]}_{kj}+{\left[{\Gamma }^{-1}\right]}_{ij}\}\right\}{d}_k,$$ (12)

or, using Eq. (6),

$$H(j,i)={\left(3k_{\text{B}}T/\gamma \right)}^{-1}\sum _N^{k=1}\left[\langle \text{Δ}{R}_k.\text{Δ}{R}_i\rangle -\langle \text{Δ}{R}_j.\text{Δ}{R}_i\rangle -\langle \text{Δ}{R}_k.\text{Δ}{R}_j\rangle +\langle \text{Δ}{R}_j.\text{Δ}{R}_j\rangle \right]{\text{d}}_k.$$ (13)

H(j,i) depends on the direction of signal transmission, i.e., H(j,i) ≠ H(i, j).

Commute time, τ (i, j) ≡ H(j,i) + H(i, j), is another metric, which has no directionality.¹⁴ τ (i, j) scales with the fluctuations in the distance vector ΔR_ij as

$$\begin{gathered} \tau (i,j)\propto \left\{{\left[{\Gamma }^{-1}\right]}_{ii}+{\left[{\Gamma }^{-1}\right]}_{jj}-2{\left[{\Gamma }^{-1}\right]}_{ij}\right\} \\ =\langle \text{Δ}{R}_{ij}\cdot \text{Δ}{R}_{ij}\rangle , \end{gathered}$$ (14)

where the proportionality constant is (3k_BT/γ)⁻¹ Σ_kd_k. Eq. (14) is readily obtained using Eq. (13) twice, for H(j,i) and H(i, j). Eqs (13) and (14) permit us to bridge between statistical physical quantities such as mean-square fluctuations or cross-correlations with graph-theoretic concepts such as hitting or commute times. We will illustrate the utility of these concepts for analyzing signal transduction behavior of proteins by way of application to two cases in the section Reconciling Equilibrium Dynamics and Signal Propagation Stochastics.

LEARNING FROM NETWORK MODELS: COOPERATIVE RESPONSES AND COMMUNICATION

Anisotropic Response to Mechanical Stress: Selection of Suitable Modes

Biomolecules are often subjected to mechanical pressures—e.g., within muscle fibers and micro- tubules. This, together with recent advances in single-molecule manipulation techniques, led to increased interest in the mechanical response of proteins to external pulling forces applied at specific positions.³⁴ A database of results from such experiments has been recently constructed.^34,35

Theoretical studies for elucidating the relationship between mechanical stability and biological function have been traditionally performed using steered MD.^36–40 More recently, network models and analytical treatments have been utilized. One example is the ANM analysis of the anisotropic response to deformations in different pulling directions,¹² presented below in some detail. Although this approach assumes that the unfolding path correlates with the ‘weak/soft directions’ near the native state, other studies went on to longer and more detailed simulations of the process and demonstrated explicitly the relation between normal modes and the unfolding process by interactively considering the specific interactions being broken. An example is the work of Dietz and Reif⁴¹ wherein the fractional force that each ‘bond’ experiences so as to withstand a uniaxial tension was evaluated, which also yielded good agreement with experimental data on green fluorescent protein (GFP). In another study, snapshots from stochastic simulations of stretching have been analyzed.⁴² ENMs also assist in identifying folding nuclei^32,43 and exploring the order of events in thermal unfolding. A recent application of GNM wherein native contacts are iteratively broken to simulate unfolding yielded results in accord with those observed in MD and Monte Carlo simulations.⁴³

The ANM permits us to calculate an effective force constant <κ_ij> for the stiffness/resistance of the molecule against deformation under uniaxial tension applied to residues i and j.¹² The idea is simple: if these residues already undergo long distance fluctuations by virtue of intrinsically accessible slow modes, the molecule is more ‘yielding’. <κ_ij> is the ‘average force constant’ evaluated using¹²

$$\langle {\kappa }_{ij}\rangle =\sum _k{d}_{ij}{}^{(\kappa )}{\lambda }_k/\sum _k{d}_{ij}{}^{(\kappa )},$$ (15)

where d_ij^(κ) represents the contribution of mode k to extension of the interresidue distance R_ij, given by the projection of ΔR_ij ^(k) onto R _ij⁰, i.e., d_ij^(k) = ΔR_ij^(k) cos (R_ij⁰,Δ R_ij^(k)).

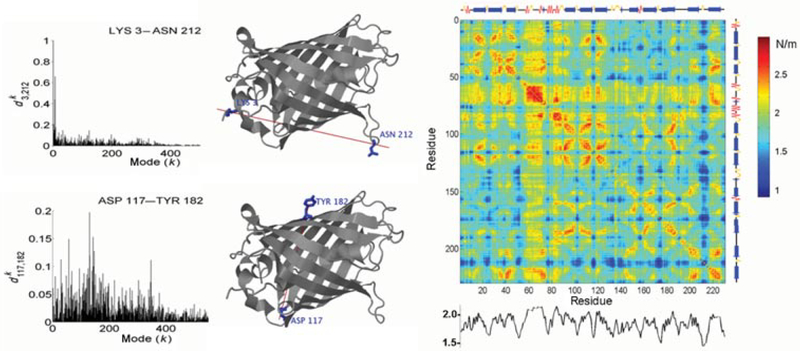
We recently analyzed¹² the mechanical behavior observed by single-molecule atomic force microscopy a series of proteins.^44–46 Figure 3 illustrates the results obtained for GFP. The bars represent the computed contributions d_ij^(k) of different modes to extensions along the pairs Lys3–Asn212 (top) and Asp117–Tyr182 (bottom). In the former case, the low-frequency modes make a larger contribution (e.g., d₃₋₂₁₂^(k) > 0.6 for k = 1), consistent with the relatively low (~115 pN) pulling force observed in experiments.⁴⁶ In the latter case, on the contrary, d_117−182^(k) values are more uniformly distributed over a broader range of modes, including higher frequency modes, which are energetically expensive. Consistent with these predictions, the GFP is destabilized at 548 pN upon pulling these two residues.⁴⁶ Similar calculations performed for all residue pairs led to the resistance map (<κ_ij> values) displayed in Figure 3. The lower profile is the average over all entries in each column, thus providing a measure of mechanical resistance for each individual amino acid. Similar calculations performed for various pulling directions and various proteins yielded results in good agreement with experiments despite the simplicity of the theory and the differences in various experimental conditions.¹²

FIGURE 3 |.

(a) Comparison of mechanical stress (uniaxial tension) experiments with anisotropic network model (ANM) predictions for green fluorescent protein (GFP). The plots on the left display the normalized contributions d_ij^(k) of ANM modes k 1, 3N-6 (abscissa) to the deformation of the molecule in response to uniaxial tension exerted at residues (i, j) = (K3, N212) (top) and (D117,Y182) (bottom). When pulling apart the residues Lys3–Asn212 (upper diagram), the deformation is largely accommodated one soft mode (note the peak at mode 1). In the case of Asp117–Tyr182 (lower diagram), the response is distributed over a broader range of modes, including high-frequency modes that entail high energy cost. The force required to unfold the molecule by stretching in the Lys3–Asn112 direction was reported⁴⁶ to be five times weaker than that needed in the Asp117–Tyr182 direction, consistent with the mode distributions. (b) Complete mechanical resistance map generated for GFP by ANM. The entries in the map represent the effective force constants <κ_ij> (Eq. 15) in response to uniaxial tensions exerted at each of pair of residues. The secondary structure of the protein is shown along the upper abscissa and on the right (blue arrows, β-strand; zigzag line, α-helix). The profile at the lower part of the map displays the mean resistance per residue, averaged over all values in a given column. See our study¹² for more details.

In principle, the forces predicted by the ANM refer to behavior in the immediate neighborhood of the global energy minimum or to the resistance to initiating a motion in a particular direction. Experiments, on the contrary, probe the unfolding behavior. The consistency between theory and experiments points to a correlation between the original stiffness/resistance to exiting from the folded state and the effective cost of unfolding. The approach of Dietz and Reif,⁴¹ on the contrary, assumes that a single bond breakage is equivalent to complete unfolding. Both theoretical approaches are based on native contact topology and cannot be used for unfolding processes wherein the transition state is far from the native state. They yield relative forces for different residue pairs, rather than absolute values; and they lack sequence information. Thus due to calibrations that depend on the protein and on experimental conditions alike, these models cannot compare values obtained for different proteins or mutants. Despite such limitations, coarse-grained (CG) models^42,47 and in particular ENM-based approaches^12,13,41,42 appear as useful tools for estimating the anisotropic response of proteins to external stress, and may assist in designing or interpreting single-molecule experiments at a very low computing time and memory cost.

Reconciling Equilibrium Dynamics and Signal Propagation Stochastics

Equations (13) and (14) establish the connection between information theoretic concepts (hit and commute times) and physics-based equilibrium dynamics (e.g., mean-square fluctuations in interresidue distances). Previous work demonstrated that hit times are relatively small when targeting catalytic residues, consistent with the efficient communication requirements of active sites.¹⁴ A more recent study also shows that metal-binding residues follow the same trend.⁴⁸

Figure 4 illustrates these concepts for two example cases. Panels (a)–(c) display the results for a xylose isomerase that binds a cobalt ion. Panel (a) shows the hit time map of the metal-binding protein. It can be seen that signal propagation properties essentially depend on the target site (abscissa). For a clearer understanding of the signaling properties of individual residues, we define two single-body properties: mean hitting times and mean commute times, <H_r(j)> = Ʃ_i H(j,i)/N and <τ(j)> = Ʃ_i τ(j,i)/N for each residue. These properties provide a measure of the allosteric potential of residues. Panel (b) displays the mean hitting times for xylose isomerase. Metal-binding residues are E267, E231, D338, and D295 in this case. The hitting time profile shows that all these residues (indicated by red dots) are located at minima, i.e., they communicate efficiently with all other residues or they are very sensitive to signals conveyed by other residues. Panel (c) shows that in addition to having small <H_r(j)> values (abscissa), their variances in H(j,i) (for 1 ≤ i ≤ N) are small, suggesting that these residues are not only fast but also precise in their communication with other residues.

FIGURE 4 |.

Efficient signal propagation properties of active sites illustrated for a metal-binding protein (a–c) and an enzyme (a^´–c^´). Hit time maps for cobalt-binding xylose isomerase [Protein Data Bank (PDB) code: 1a0c] and for human carbonic anhydrase II (PDB code: 1a42) are displayed in the respective panels (a) and (a^´). Average hit time profiles as a function of residue number are shown in panels (b) and (b^´) with metal-binding and catalytic residues labeled by the red dots in the two respective cases. Panels (c) and (c^´) display the average hit time versus standard deviation for each residue for the two cases. The residues that participate in metal binding (b) and catalysis (b^´) (shown in red markers) exhibit small average hit time and small-to-moderate standard deviation, indicative of their fast and precise communication properties.

Panels (a^′)–(c^′), on the contrary, present the results for an enzyme, human carbonic anhydrase II, with respect to its catalytic residues H64, Q92, H94, H96, and H119. Again, the active residues appear to be highly predisposed to efficient communication with the rest of the protein, in addition to be precisely tuned (i.e., have minimal variance in hitting times).

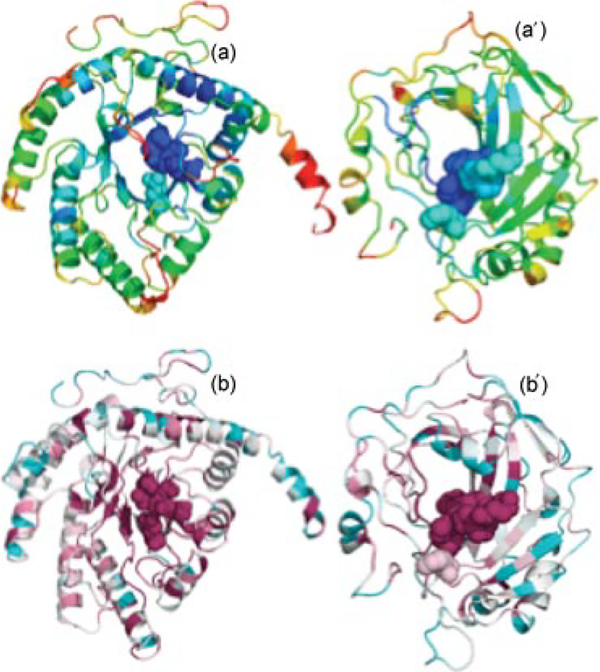
These results suggest that the positions of the active residues in the 3D structure may have been evolutionarily optimized to ensure efficient communication. In order to examine to which extent the sites with high allosteric potential (or enhanced communication properties) are evolutionarily conserved, we compared in Figure 5 the color-coded diagrams based on communication properties (panels a and a^′) and conservation properties (panels b and b^′). Conservation scores were obtained using the ConSurf server.⁴⁹ The comparisons of panels (a) and (b), and panels (a^′) and (b^′) clearly demonstrates the correlation between conservation patterns and efficient communication propensities, i.e., those residues distinguished by their efficient signaling properties are also evolutionarily conserved presumably due to their functional role.

FIGURE 5 |.

Correlation between signaling efficiency and evolutionary conservation. Panels (a; 1a0c) and (a^´; 1a42) show the ribbon diagrams color coded by the distance of residues from the origin in Figure 4 (c) and (c^´). The regions colored blue refer to the fastest and most precise communication sites. Panels (b) and (b^´) are color coded by conservation score of each residue as obtained from the Consurf server, the most conserved sites being colored purple. The metal-binding and catalytic sites are shown in space-filling representation.

There are currently several studies that unravel the structural origins of molecular signaling processes using NMA. A recent study by Beratan and coworkers⁵⁰ demonstrated, e.g., that local structural changes triggered by ligand binding can translate into signaling responses at remote allosteric sites and different motions mediate different signaling pathways. The connection between signaling pathways and collective motions predicted by ENM–NMA has been also demonstrated in an extensive study of GroEL–GroES machinery.⁵¹ Such analyses could be particularly useful in structure-based design of inhibitors/regulators of allosteric proteins.

NMA in Structural Refinement

Soon after the pioneering articles in the 1980s^20–22 that demonstrated the utility of NMA for investigating the equilibrium dynamics of proteins, it was suggested that the new methodology could assist in refining X-ray structures.^52–55 The refinement of B-factors, previously based on a single fitted parameter per atom, was replaced by a summation of the anisotropic fluctuations over a selected set of low-frequency normal modes. The main conceptual advantage of a NMA-based refinement over traditional refinements is that it takes account of intrinsic motions and correlations. The essence of the refinement procedure is to minimize the difference (R-factor) between observed structure factors and those calculated based on model parameters. In a typical NMA-based refinement, the model is evaluated using the position vectors, R⁰ +Σ_k c_ku_k, perturbed along normal modes (k), where c_k is the contribution of mode k to be fitted. As low-frequency modes induce the largest displacements, a subset of slow modes is usually sufficient, and thus the number of fitting parameters is usually significantly smaller than the number of atoms. NMA-based fitting with a small number of parameters may outperform standard refinements with many more parameters^52,54,56 while avoiding overfitting. NMA refinement also allows for large movements beyond the capability of other refinement methods⁵⁷ and is of particular utility for large structures and complexes that are inherently flexible.^58–60 In an application to the potassium channel KcsA, e.g., Chen et al.⁵⁶ were able to resolve residues that were originally missing and obtain anisotropic displacement parameters related to functional motions.

An additional advantage of NMA refinement is that it inherently decomposes the atomic fluctuations into their internal and external components. The internal component refers to the collective vibrational motions of the molecule (corresponding to the nonzero eigenvalues), which are usually of interest for assessing functional mechanisms. The external component, on the contrary, reflects the static disorder and rigid body motion in the crystal as well as uniform thermal noise and inaccuracies in the experiments. By separating the two components, it has been demonstrated^{55,56,58–61} that rigid body motions make a significant contribution to the B-factors observed in X-ray crystallographic structures.

In recent years, it has been shown⁶² that NMA can assist in molecular replacement (MR), the most popular and rapid method for solving structures by X-ray crystallography. The method is based on using a structural template. The authors showed for three different examples (metallodextrin-binding protein, glutamine-binding protein, and HIV-1-protease) that perturbing the template structures along one or two low-frequency modes yields new conformers that allow for successful MR, whereas the original structures fail to do so. This suggests that many structures that cannot be resolved currently using MR—despite the existence of apparently suitable templates—will be resolved upon NMA-based perturbations of their templates. This will save effort, time, and resources, setting the stage for application of NMA-based approaches.

With the advances in cryo-EM techniques, there is a great interest in refining the low-resolution (sometimes in the order of 15–25 Å) data. A useful strategy to this aim is to dock known higher resolution structures (or substructures) onto EM density maps, but often the dynamic nature of the molecules is overlooked. There is a need for tools that consider the flexibility of the molecule during refinement, and NMA has been naturally employed for this purpose.^17,19,63,64 The objective function to be minimized is the difference between computed and measured electron densities, using NMA soft modes as search directions. Applications of this methodology confirmed that large conformational changes need to be accounted for in order to have a good fit to EM density maps. An important contribution was the development of Quantized Elastic Deformational Model,^65,66 wherein the protein is treated as an elastic object with mass distribution taken from the density maps. An elegant application to fatty acid synthase⁶⁷ demonstrated that structures along electron density maps conform to the first two softest modes. This study highlighted the strength of combining NMA with multiple model refinement for highly flexible proteins, as well as the ability to improve the resolution of the final EM reconstructions.

Chacon et al.⁶⁸ showed that alternative conformations for several important well-studied systems (bacterial RNA polymerase, the 30S and 50S subunits of the ribosome, and chaperonin) could be detected within single low-resolution EM structures, consistent with major conformational changes predicted by normal modes. These experimental results validate what coarse-grained NMA models taught us long ago—large-scale motions are insensitive to detailed atomic interactions. A number of excellent tools, such as NOMAD,⁶⁹ NORMA,¹⁸ and NMFF,⁷⁰ are now available to make it easy and straightforward to apply NMA for interpreting EM density maps.

NMA in Modeling Structures, Ligand-bound Forms, and Complexes

NMA approaches can assist not only in the refinement of experimental structures but also for theoretical modeling. We are currently in a position to improve the quality of homology models by refining the template structures using ENM–NMA. The idea is to restrict the search space to a subspace spanned by a few lower frequency normal modes.^71,72 When the scoring function is put aside, by taking it to be ideal, it has been recently shown that the normal modes perform better than short MD refinement or coarse-grained Monte Carlo sampling for moderate difficulty template refinement.⁷³ Baker and coworkers⁷⁴ have shown, e.g., that a search along dominant principal components of ensembles of structures in a given family assists in improving the accuracy in comparative modeling. The idea is to determine the dominant directions of structural variance upon optimal superimposition of multiple structures (for a given protein or a family of proteins that share similar fold) and evaluate the covariances in the departures of residue/atom coordinates from their mean values, which are organized in a covariance matrix (Eqs. 7 and 10). Eigenvalue decomposition of the latter following Eqs (7) and (10) yields the principal axes (as eigenvectors) of structural deviations. Given that the principal components from experimental structures correlate well with normal modes,^8,71,75 it should be possible to use normal modes instead of principal components for this purpose, and thus to expand the utility of this approach. For more about PCA and the relation between NMA and PCA, the reader is referred to previous work.^8,24,71,75

The advantage of normal modes is that they can be calculated based on individual template structures and are not dependent on the availability of numerous family representatives that are needed for PCA. Figure 6 demonstrates the potential of this approach for two ferric ion-binding proteins from bacteria that share only 37% sequence identity. It can be seen that movements along the four softest modes starting from a given structure (‘template’) permit to attain structures significantly closer to the ‘target’ structure. When combining the first four modes, the root-mean-square deviation (RMSD) may be reduced from 3.2 to 2.1 Å. The use of higher order modes has a marginal effect, if any.

FIGURE 6 |.

Structural refinement of the bacteria ferric ion-binding protein by deforming a template protein along its normal modes. (a) Superposition of the target and template proteins [Protein Data Bank codes 1xvy (red) and 1qvs (blue), respectively]. The proteins share 37% sequence identity. The root-mean-square deviation (RMSD) between the structures is 3.21 Å. (b) Reduction of the RMSD by reconfigurations of the template along the first 30 normal modes accessible to the template structure, calculated using the anisotropic network model. The red dotted line shows the RMSD between the two structures prior to refinement.

Recently, a combined method that utilizes principal components and normal modes was developed.⁷⁶ A recent nice application of a similar methodology is the prediction of open and close conformations of rat heme-free oxygenase,⁷⁷ starting from a unique heme-bound X-ray structure, and using templates corresponding to a human and incomplete rat heme-free structures.

CONCLUSION

Here, we present an overview of the foundations, basic approximations, and utility of network models used for delineating protein dynamics. GNM and ANM are physics-based models, whereas the Markov model is information theoretic. The two approaches provide information on different properties: motions in the former case and pathways of communication in the latter. Yet, the average properties predicted by the former such as the mean-square fluctuations in interresidue distances and cross-correlations between residue fluctuations also define information theoretic quantities such as hitting and/or commute times computed for different residue pairs (Eqs. 13 and 14). In a sense, graph/network representation allows us to bridge between dynamic and allosteric signaling properties. In either case, the native contact topology defines the most cooperative modes of motions, which in turn define the effective resistance to deformation, the efficient communication mechanisms, and the potential structural changes in different forms or environments, as illustrated in three different applications (Figures 2–6).

We would like to emphasize in particular the practical utility of NMA–ENM for gaining a deeper understanding of the conformational space/ensemble accessible to each protein. The advantage of NMA–ENM analyses is that they can be performed based on individual structures and do not depend on the availability of numerous family representatives (that are needed for principal components analyses, for example). This endows these approaches with a significant advantage in filling the gaps in the sequence- structure space in the absence of sufficiently broad structural data for a given family. We anticipate these features of ENM–NMA to be increasingly exploited, especially in the characterization of supramolecular structures and assemblies.