Bayesian Inference on Changes in Response Densities over Predictor Clusters

Abstract

In epidemiology, it is often of interest to assess how individuals with different trajectories over time in an environmental exposure or biomarker differ with respect to a continuous response. For ease in interpretation and presentation of results, epidemiologists typically categorize predictors prior to analysis. To extend this approach to time-varying predictors, one can cluster individuals by their predictor trajectory, with the cluster index included as a predictor in a regression model for the response. This article develops a semiparametric Bayes approach, which avoids assuming a pre-specified number of clusters and allows the response to vary nonparametrically over predictor clusters. This methodology is motivated by interest in relating trajectories in weight gain during pregnancy to the distribution of birth weight adjusted for gestational age at delivery. In this setting, the proposed approach allows the tails of the birth weight density to vary flexibly over weight gain clusters.

1. Introduction

1.1. Weight Gain During Pregnancy and Birth Weight

The National Research Council and Institute of Medicine (2007) recently published a report on the influence of pregnancy weight on maternal and child health. One goal of the report was to assess whether Institute of Medicine (IOM) pregnancy weight gain guidelines (1990) need to be reexamined due to recent health trends and increasing obesity. Several studies have examined the pattern of pregnancy weight gain in light of the IOM recommendations and show that most women do not follow the recommendations (Siega-Riz et al., 1994; Carmichael et al., 1997, Dietz et al., 2006).

In providing clinical guidelines, simplicity is of paramount importance. For this reason, epidemiologists typically categorize continuous predictors prior to analysis. For example, in assessing health effects of body mass index (BMI), individuals are categorized into low weight, normal weight, overweight and obese groups instead of including BMI as a continuous predictor in a flexible regression model for the health response. One can then present simple tabular summaries of changes in the response between different BMI categories, so that one set of recommendations can be made for all individuals in a category. For a time-varying predictor, such as pregnancy weight gain, it is not straightforward to pre-define categories. However, one can use methods of functional clustering to group women into weight gain trajectory clusters, with the cluster IDs then providing a predictor of pregnancy outcomes and child health. Then, clinicians can make recommendations based on simply examining a summary of changes in outcomes across weight gain clusters.

The goal of this article is to develop an approach for assessing changes in infant birth weight across maternal weight gain clusters. For simplicity, we focus on data for N=1888 mothers with normal pre-pregnancy weight (pregravid body mass index between 19.8 and 26) and giving birth to singleton infants. In making weight gain recommendations to pregnant women, physicians are primarily concerned with inadequate and excessive weight gain. A women gaining too little weight may not provide adequate nutrition for the developing fetus, resulting in a small for gestational age baby, and potentially in long term developmental problems. At the other extreme, women gaining too much weight may provide too much nutrition to the baby, resulting in a large for gestational age child, and perhaps in a long term risk of obesity. Hence, the primary interest is in how the tails of the birth weight density change across weight gain clusters. With this focus, we propose a Bayesian semiparametric approach, which allows a response density to change nonparametrically over predictor clusters.

1.2. Relevant Statistical Literature

There is an increasingly rich literature on model-based approaches for clustering through the use of finite mixture models. Finite mixture models for functional data are commonly referred to as latent class trajectory models. For example, the approach of Jones, Nagin and Roeder (2001) characterizes functional data using a polynomial curve, with subjects having identical regression coefficients grouped into clusters. This approach can be implemented in SAS using PROC TRAJ (Jones and Nagin, 2007). Muthén (2004) proposes an alternative approach, which allows variability in trajectories among subjects in a trajectory cluster. James and Sugar (2003) instead characterize curves as linear combinations of basis functions, with subjects having similar basis coefficients clustered together. These methods can be used for joint modeling of functional predictors with a response by including the latent trajectory cluster index as a categorical predictor in the response model (Jones and Nagin, 2007). To select the number of latent trajectory classes, the BIC is commonly used.

Considering the application of such an approach to pregnancy weight gain and birth weight data, clusters in the weight gain trajectories could be estimated, with the cluster IDs then included as categorical predictors in a linear regression model for the birth weight outcome. One could adjust for gestational age at delivery and maternal covariates within this model, while accommodating a heavy-tailed residual distribution to better characterize the birth weight density. However, such an approach would only allow the mean of the birth weight distribution to vary across weight gain clusters, so does not address our interest in studying changes in the tails of the distribution. One could modify the approach to allow the variance to also differ across the weight gain clusters, but the model still would not allow different shaped distributions. Given that our primary interest is in assessing how pregnancy weight gain trajectories relate to risk of small and large babies, it seems critical to allow the birth weight densities to change flexibly over the trajectory clusters.

For recent articles on Bayesian functional clustering, refer to Ray and Mallick (2006) and Heard et al. (2006). Related to the method of Ray and Mallick (2006), Bigelow and Dunson (2005) proposed to express the curves using a spline basis, with subject-specific basis coefficients assigned a Dirichlet process (DP) prior (Ferguson, 1973; 1974). This approach automatically groups the subjects into an unknown number of trajectory clusters, while allowing for uncertainty in the clustering process. For joint modeling, one can instead assign a DP prior to the joint distribution of the basis coefficients and a location parameter in the response model. The result is a semiparametric Bayes version of the latent class trajectory methods cited above. Unfortunately, such an approach still assumes that the trajectory cluster-specific response distribution follows a parametric form, with only a location parameter varying.

A primary limitation of such methods is the restriction that predictor (trajectory) and response clusters are fundamentally the same entity, so that a subject assigned to a particular predictor cluster is automatically assigned to the corresponding response cluster. We propose an enriched formulation in which predictor and response clusters are separate, with a subject’s allocation to a given predictor cluster informing, but not constraining, that subject’s assignment to a response cluster. We develop this approach by starting with a semiparametric Bayes hierarchical model, which induces a dependent bivariate clustering structure. Posterior computation relies on a combined sequential updating and greedy search (SUGS) (Wang and Dunson, 2007) and Gibbs sampling algorithm.

Section 2 proposes the nonparametric joint clustering model. Section 3 describes the algorithm for posterior computation and inferences. Section 4 applies the methods to the weight gain and birth weight data. Section 5 discusses the results.

2. Joint Modeling of Predictor Clusters and Response Densities

2.1. Dirichlet process clustering

For ease in presentation, we focus on the pregnancy weight gain and infant birth weight application in describing the methodology, though the approach can certainly be used in other settings. Let f_i denote a smooth measurement error-corrected weight gain trajectory over time for woman i, for i = 1, … , n, and let y_i denote the birth weight of her infant. In the measurement error component, we include not only true measurement errors in weighing the woman arising from scale and recording inaccuracies but also short term fluctuations in body weight that can occur during pregnancy due to water retention and other factors. We are viewing f_i as a smooth function that is close (in a clinical/biological sense) to the true weight trajectory for woman i. Our goal is then to define clusters in the f_i’s and to assess how the birth weight density varies over these clusters.

The actual data collected for woman i are ${\left\{x_i,y_i\right\}}_{i=1}^n$, where x_i = (x_i1, … , x_i,ni)′ and x_ij is the recorded weight at time t_ij, for j = 1, … , n_i. The measurement times may vary somewhat for the different women under study. As a simple measurement model, we assume

$$x_{ij}~N\left(f_i\left(t_{ij}\right),{\tau }_x^{-1}\right),j=1,\dots ,n_i,i=1,\dots ,n,$$ (1)

where τ_x is a fixed measurement error precision (1/variance). In addition, we assume that each of the weight gain trajectories, f_i, can be characterized as a linear combination of pre-specified basis functions ${\left\{b_h\right\}}_{h=1}^p$ as follows:

$$f_i(t)=\sum _{m=1}^p{\beta }_{im}{b}_m(t),\forall t\in \mathcal{T},$$ (2)

where β_i = (β_i1, … , β_ip)′ are subject-specific basis coefficients.

Hence, variability in the weight gain trajectories is controlled by variability in the basis coefficients. For functional clustering, we assume that the basis coefficients have a discrete distribution by letting

$${\beta }_i\stackrel{\mathit{\text{iid}}}{~}{P}_1=\sum _{h=1}^K{\pi }_h{\delta }_{{\beta }_h^{*}},$$ (3)

where K is an upper bound on the number of clusters, π_h is the probability weight on cluster h, δ_θ is a distribution concentrated at θ, and ${\beta }_h^{*}$ are the basis coefficients characterizing the function in cluster h, for h = 1, … , K. It is important to note that the number of clusters among the n women in the sample, denoted by k, is treated as unknown and K just provides an upper bound on this number. By letting π = (π₁, … , π_K)′ ~ Diri(α/K, … , α/K) and ${\beta }_h^{*}\stackrel{\mathit{\text{iid}}}{~}{P}_{01}$, we obtain an accurate finite approximation to a Dirichlet process (DP) prior, P₁ ~ DP(αP₀₁), for the distribution of the basis coefficients (Ishwaran and Zarepour, 2002). The accuracy of this approximation improves as α decreases, favoring a smaller value of k, and K increases.

If we were only interested in clustering the weight gain trajectories, then models (1) – (3) would be sufficient, providing an accurate finite approximation to a DP mixture model. Such an approach is closely related to work by Ray and Mallick (2006) and Bigelow and Dunson (2005). However, our goal is instead to assess changes in the density of birth weight across weight gain clusters, so that is becomes necessary to extend the specification to include y_i. If birth weight did not depend on pregnancy weight gain, then we could flexibly model the birth weight density using a DP mixture (DPM) of normals model:

$$f(y)=\int N\left(y;\mu ,{\sigma }^2\right)dP(\mu ),$$ (4)

where P ~ DP(λP₀₂), with λ a precision parameter and P₀₂ a parametric guess at the mixture distribution (e.g., normal) (Lo, 1984; Escobar and West, 1995). Again using the Ishwaran and Zarepour (2002) finite approximation to the DP, we could then obtain

$$f(y)=\sum _{l=1}^L{\nu }_{l}N\left(y;{\mu }_l^{*},{\sigma }^2\right),\mathit{\nu }~\text{Diri}(\lambda /L,\dots ,\lambda /L),{\mu }_l^{*}\stackrel{\mathit{\text{iid}}}{~}{P}_{02},$$ (5)

where L is an upper bound on the number of birth weight mixture components occupied by the n women in the sample.

2.2. Joint modeling

In addressing our goal of allowing the birth weight density to vary flexibly over the pregnancy weight gain clusters, it is necessary to link the functional clustering component, defined in (1) – (3), with the response component, defined in (5). A simple way to accomplish this is to choose a DP prior for the joint distribution of the basis coefficients, β_i, and the response mean, μ_i, assuming $y_i~N\left({\mu }_i,{\tau }_y^{-1}\right)$, with τ_y a precision parameter. Such an approach will automatically allocate the n women into k clusters, with each cluster having a unique weight gain trajectory and normal distribution for birth weight. Unfortunately, one would then only allow shifts in the mean birth weight between weight gain clusters, which is counter to our interest in studying shifts in the left and right tails of the birth weight distribution.

Hence, we instead propose a novel bivariate partitioning approach, which allows separate predictor and response clusters, while allowing dependent allocation to the two components. In particular, woman i’s chance of falling into the lth birth weight cluster will depend on her pregnancy weight gain cluster. To formalize the dependence structure, we first let γ_i ∈ {1, … , K} represent the weight gain cluster index for woman i under models (1) – (3), so that ${\beta }_i={\beta }_{{\gamma }_i}^{*}$ and $f_i(t)=b{(t)}^{\prime }{\beta }_{{\gamma }_i}^{*}$, where b(t) = [b₁(t), … , b_p(t)]′. We then characterize the birth weight density for women having γ_i = h as

$$f_h(y)=\int N\left(y;\mu ,{\sigma }^2\right)d{P}_h(\mu ),$$ (6)

where P_h is a mixture distribution specific to predictor (pregnancy weight gain) cluster h.

The joint DP approach mentioned above would let $P_h={\delta }_{{\mu }_h^{*}}$, with the ${\mu }_h^{*}$ sampled independently for h = 1, … , K, resulting in $f_h(y)=N\left(y;{\mu }_h^{*},{\sigma }^2\right)$ as the birth weight density for women in weight gain cluster h. To instead allow the birth weight density to be a flexible mixture of normals within each weight gain cluster, while borrowing information, we let

$$P_h=(1-\psi )P_{20}^{*}+\psi P_{2h}^{*},$$ (7)

where $P_{20}^{*}={\sum }_{l=1}^{L_0}{\omega }_{0l}{\delta }_{{\mu }_{0l}^{*}}$ is a global component shared by all predictor clusters, 0 ≤ ψ ≤ 1 is a weight on the global component, and $P_{2h}^{*}={\sum }_{l=1}^{L_0}{\omega }_{hl}{\delta }_{{\mu }_{hl}^{*}}$ is a local component specific to predictor cluster h, for h = 1, … , K. We assume that ω_h = (ω_h1, … , ω_h,L0) ~ Diri(λ/L₀, … , λ/L₀) and ${\mu }_{hl}^{*}\stackrel{\mathit{\text{iid}}}{~}{P}_{02}$, l = 1, … , L₀, h = 0, 1, … , K, which implies that $P_{2h}^{*}$ is assigned a finite approximation to a DP(λP₀₂) prior, independently for h = 0, 1, … , K. The L₀ → ∞ limiting case of (7) is equivalent to the specification Müller, Quintana and Rosner (2004) used for borrowing information from related studies. However, in their setting γ_i was a known study index instead of an unknown cluster index.

Our prior specification for the mixture distribution P_h further implies that

$$P_h=\sum _{l=1}^L{\nu }_{hl}{\delta }_{{\mu }_l}^{*},{\mu }_l^{*}\stackrel{iid}{~}{P}_{02},$$ (8)

where L = (K + 1)L₀, ${\mu }_l^{*}$ is the lth element of ${\mu }^{*}={\left({\mu }_0^{*\prime },{\mu }_1^{*\prime },\dots ,{\mu }_K^{*\prime }\right)}^{\prime }$, ν_hl = (1 − ψ)ω_0l for l = 1, … , L₀, ν_hl = 0 for l ∈ {L₀ + 1, … , (h − 1)L₀, hL₀ + 1, … , L} and ν_hl = ψω_hm for m = 1, … , L₀, l = m+(h−1)L₀. Hence, there are at most L response (birth weight) clusters, with the first L₀ corresponding to global clusters that can occur in any of the K predictor clusters. Let ϕ_i = l if ${\mu }_i={\mu }_l^{*}$ denote that woman i is allocated to the lth response cluster. Then, L represents an upper bound on the number of clusters, as $\sum _{i=1}^{n}1\left({\varphi }_i=l\right)$ often equals zero for many l ∈ {1, … , L}, particularly if L is large. Note that ψ is a key hyperparameter controlling the weight assigned to the global component and hence the degree of similarity in the birth weight distributions across the pregnancy weight gain clusters. To allow the data to inform more strongly, we assign a beta hyperprior to ψ.

2.3. Properties of clustering process

Our interest is in assessing changes in the birth weight density across pregnancy weight gain clusters and not in birth weight clustering. Hence, allowing different birth weight clusters in this application is simply a convenient tool for allowing flexible changes in the density. However, it is still of interest to characterize the process for allocating women to response components in a predictor cluster-dependent manner. This process is not intuitive from the model specification in Section 2.2 without further derivations.

Introducing some additional notation, let ${\beta }^{*(i-1)}={\left\{{\beta }_h^{*}\right\}}_{h=1}^{r_{i-1}}$ denote the r_i−1 unique values of β₁, … , β_i−1 in the order that they appear, and similarly let ${\mu }^{*(i-1)}={\left\{{\mu }_l^{*}\right\}}_{l=1}^{s_{i-1}}$ denote the s_i−1 unique values of μ₁, … , μ_i−1 in order of appearance. Let γ_i = h if ${\beta }_i={\beta }_h^{*}$ index membership of subject i in predictor cluster h, ϕ_i = l if ${\mu }_i={\mu }_l^{*}$ index membership in response cluster l, and ${\mathcal{S}}_l=h$ denote that ${\mu }_l^{*}$ is an component from $P_{2h}^{*}$. Two subjects i and i′ having γ_i ≠ γ_i′ can have ϕ_i = ϕ_i′ if both subjects are assigned to the same cluster within the global component $P_{20}^{*}$. Let $w_h^{(i-1)}=\sum _{j=1}^{i-1}{1}_{\left({\gamma }_i=h\right)}$ denote the number of subjects among {1, … , i−1} in predictor cluster h, and $n_l^{(i-1)}=\sum _{j=1}^{i-1}{1}_{\left({\varphi }_i=l\right)}$ denote the number of subjects among {1, … , i − 1} in response cluster l.

Theorem 1. Assuming (3) and (8), we obtain the conditional distribution

$$\left({\beta }_i|{\beta }^{*(i-1)},{\gamma }^{(i-1)}\right)~\left(\frac{\alpha \left(1-r_{i-1}/K\right)}{\alpha +i-1}\right)P_{01}+\sum _{h=1}^{r_{i-1}}\left(\frac{\alpha /K+w_h^{(i-1)}}{\alpha +i-1}\right){\delta }_{{\beta }_h^{*}}$$ (9)

noting that β_i is conditionally independent of S⁽ⁱ⁻¹⁾, μ*⁽ⁱ⁻¹⁾, ϕ⁽ⁱ⁻¹⁾. In addition,

$$\begin{gathered} \left({\mu }_i|S^{(i-1)},{\mu }^{*(i-1)},{\mathit{\varphi }}^{(i-1)},{\gamma }^{(i)},{\beta }^{*(i)}\right) \\ ~\left\{\frac{(1-\psi )\lambda \left(L-{\sum }_{l=1}^{s_{i-1}}{1}_{\left(S_l=0\right)}\right)/L}{\lambda +{\sum }_{l=1}^{s_{i-1}}{1}_{\left(S_l=0\right)}{n}_l^{(i-1)}}+\frac{\psi \lambda \left(L-{\sum }_{l=1}^{s_{i-1}}{1}_{S_i={\gamma }_i}\right)/L}{\lambda +{\sum }_{l=1}^{s_{i-1}}{1}_{\left(S_l={\gamma }_i\right)}{n}_l^{(i-1)}}\right\}{P}_{02} \\ +\sum _{l=1}^{s_{i-1}}\left\{\frac{(1-\psi )1_{\left(S_l=0\right)}\left(\lambda /L+n_l^{(i-1)}\right)}{\lambda +{\sum }_{t=1}^{s_{i-1}}{1}_{\left(S_t=0\right)}{n}_t^{(i-1)}}+\frac{\psi 1_{\left(S_l={\gamma }_i\right)}\left(\lambda /L+n_t^{(i-1)}\right)}{\lambda +{\sum }_{t=1}^{s_{i-1}}{1}_{\left(S_l={\gamma }_i\right)}{n}_t^{(i-1)}}\right\}{\delta }_{{\mu }_l^{*}}. \end{gathered}$$ (10)

Expression (9) is a straightforward consequence of model (3) and properties of the Dirichlet distribution. Closely related forms are well known. Expression (10) follows from expression (8) using a similar approach to that used in deriving (9), taking care to keep track of the component from which each atom is drawn.

Note that in the limiting case as K → ∞, expression (9) simplifies to the Blackwell and MacQueen (1973) Polya urn scheme, while for L → ∞ (10) becomes

$$\begin{gathered} \left({\mu }_i|S^{(i-1)},{\mu }^{*(i-1)},{\mathit{\varphi }}^{(i-1)},{\gamma }^{(i)},{\beta }^{*(i)}\right) \\ ~\left\{\frac{(1-\psi )\lambda }{\lambda +{\sum }_{l=1}^{s_{i-1}}{1}_{\left(S_l=0\right)}{n}_l^{(i-1)}}+\frac{\psi \lambda }{\lambda +{\sum }_{l=1}^{si-1}{1}_{\left(S_l={\gamma }_i\right)}{n}_l^{(i-1)}}\right\}{P}_{02} \\ +\sum _{l=1}^{s_{i-1}}\left\{\frac{(1-\psi )1_{\left(S_l=0\right)}{n}_l^{(i-1)}}{\lambda +{\sum }_{t=1}^{s_{i-1}}{1}_{\left(S_t=0\right)}{n}_t^{(i-1)}}+\frac{\psi 1_{\left(S_l={\gamma }_i\right)}+n_t^{(i-1)}}{\lambda +{\sum }_{t=1}^{s_{i-1}}{1}_{\left(S_l={\gamma }_i\right)}{n}_t^{(i-1)}}\right\}{\delta }_{{\mu }_l^{*}}. \end{gathered}$$ (11)

The conditional distributions (9)–(10) provide insight into the joint clustering process for predictors and response. Due to exchangeability of the subjects, we can obtain a simple form for the conditional and unconditional probabilities of allocating subjects i and j to the same response component given their predictor allocation. The conditional prior probability of response clustering for i and j is

$$\text{Pr}\left({\mu }_i={\mu }_j|{\gamma }_i,{\gamma }_j\right)=\frac{\lambda /L+1}{\lambda +1}\left\{{\psi }^2{1}_{\left({\gamma }_i={\gamma }_j\right)}+{(1-\psi )}^2\right\},$$ (12)

while the marginal prior probability is

$$\text{Pr}\left({\mu }_i={\mu }_j\right)=\frac{\lambda /L+1}{\lambda +1}\left\{\frac{{\psi }^2(\alpha /K+1)}{\alpha +1}+{(1-\psi )}^2\right\}.$$ (13)

Hence, in the limit as ψ → 0, Pr(μ_i = μ_j) = (λ/L + 1)/(λ + 1) and predictor and response clustering occur independently. In the limit as ψ → 1, Pr(μ_i = μ_j) = 0 if subjects i and j are not in same predictor cluster, and otherwise Pr(μ_i = μ_j) = (λ/L + 1)/(1 + λ). In the limiting case as ψ → 1 and λ → 0, one obtains the same clusters of subjects for the predictor and response component. Taking ψ → 1, λ → 0, K → ∞, we obtain the joint DP approach described in the beginning of Section 2.1.

2.4. Chinese restaurants for families

A Chinese restaurant metaphor is often used as an aid in understanding DP clustering. Under the Chinese restaurant process (CRP) (Aldous, 1985; Pitman, 1996), customers arrive sequentially at a restaurant with infinitely many tables, each of which can seat infinitely many individuals. The first customer is seated at the first table, and as additional customers arrive, they are either assigned to an occupied table or to an empty table. For the ith customer, the probability of assignment to an empty table is α/(α + i − 1), while the probability of assignment to the jth occupied table is n_ij/(α + i − 1), with n_ij denoting the number of customers at table j when individual i arrives. The CRP allocates customers to tables according to the DP(αP₀) Polya urn scheme, with the individuals at table j sharing a dish ${\theta }_j^{*}$ sampled from P₀.

This metaphor can be generalized to describe the process of Sections 2.1–2.2 in the limiting case as K, L → ∞. Suppose families arrive at a Chinese restaurant sequentially and are assigned to tables by a typical CRP with parameter α, with parents at table j sharing a dish ${\beta }_j^{*}$ sampled from P₀₁. Now, suppose that there are bags containing infinitely many games at the front of the restaurant and at each of the tables. When a family arrives, the children choose a game to share, either from the bag at the front (with probability 1 − ψ) or the bag at their table (with probability ψ). The first group of siblings to sample from a bag is given the first game in the bag, while the ith group of siblings to sample from a bag is given a new game with probability λ/(λ + i − 1) and otherwise joins a game already drawn from the bag with probability m_ij/(λ + i−1), with m_ij the number of earlier children assigned to the same game. Games are generated independently from P₀₂.

In our metaphor, the predictors are represented by the parents, with the predictor clusters the tables, and the dishes the parameter values specific to a predictor cluster. In addition, the responses are represented by the children, with children assigned to the same game belonging to the same response cluster.

3. Posterior Computation

For ease in interpretation, to more rapidly analyze the large data set we are faced with, and to address the label switching problem (Stephens, 2000), we avoided a full MCMC analysis of the model proposed in Section 2. Instead, we rely on a combined sequential updating with greedy search (SUGS) (Wang and Dunson, 2007) and Gibbs sampling algorithm. The SUGS algorithm sequentially updates the prior by adding subjects one at a time, selecting the cluster that maximizes the conditional posterior model probability. This results in a greedy stepwise search for a good partition of subjects into clusters, while only requiring a single cycle of computation for each subject.

We propose to use SUGS to choose the partition of subjects into functional predictor clusters and Gibbs sampling for posterior computation of the predictor cluster-specific response densities. We start by introducing an infinite sequence of predictor clusters, ${\left\{{\beta }_h^{*}\right\}}_{h=1}^{\infty }$. The posterior distribution of the parameters in predictor cluster h, conditionally on the data for subjects 1, … , i and on predictor cluster allocation γ⁽ⁱ⁾ = (γ₁, … , γ_i−1)′, is

$$\left({\beta }_h^{*}|X^{(i)},{\gamma }^{(i)}\right)\propto P_{01}\left({\beta }_h^{*}\right)\prod _{j=1}^i{\left\{\prod _{l=1}^{n_i}N\left(x_{jl};b_{jl}^{\prime }{\beta }_h^{*},{\tau }_x^{-1}\right)\right\}}^{1_{\left({\gamma }_j=h\right)}},$$ (14)

which is simply P₀₁ updated with the likelihood for those subjects in predictor cluster h among subjects {1, … , i}. Using the updating equations in the Appendix, (14) is available in closed form for conjugate P₀₁.

Due to the well known label ambiguity problem (Stephens, 2000), the index values in γ are inherently arbitrary, and the important information is simply which subjects are grouped together. For example, γ = 1 could be a cluster of women with rapid weight gain and γ = 2 could be a cluster with no weight gain in the first trimester followed by slow weight gain. The label γ = 1 for the rapid weight gain cluster is arbitrary, and one could obtain an identical marginal likelihood switching the labels to let γ = 2 for the women in the rapid weight gain cluster and γ = 1 for the women in the slow weight gain cluster. Hence, without restriction we let γ₁ = 1 to assign subject i = 1 to the first predictor cluster. The SUGS algorithm proceeds as follows:

1. Let γ₁ = 1 and calculate $\left({\beta }_1^{*}|x_1,{\gamma }_1=1\right)$ using (14).

2. For i = 2,… , n, letting $m_{i-1}^{\gamma }=\text{max}\left\{{\gamma }_1,\dots ,{\gamma }_{i-1}\right\}$,

   1. Choose ${\gamma }_i\in \left\{1,\dots ,m_{i-1}^{\gamma }+1\right\}$ to maximize the conditional posterior probability of γ_i = h:

      $$\text{Pr}\left({\gamma }_i=h|X^{(i)},y^{(i-1)},{\gamma }^{(i-1)},{\mathit{\varphi }}^{(i-1)},{\tau }_x\right)=\frac{u_{ih}\int {\prod }_{j=1}^{n_i}\text{N}\left(x_{ij};b_{ij}^{\prime }{\beta }_h^{*},{\tau }_x^{-1}\right)d\left({\beta }_h^{*}|X^{(i-1)},{\gamma }^{(i-1)}\right)}{{\sum }_{l=1}^{m_{i-1}^{\gamma }+1}{u}_{il}\int {\prod }_{j=1}^{n_i}\text{N}\left(x_{ij};b_{ij}^{\prime }{\beta }_l^{*},{\tau }_x^{-1}\right)d\left({\beta }_l^{*}|X^{(i-1)},{\gamma }^{(i-1)}\right)},$$

      for h = 1, … , r_i−1 + 1, $u_{ih}=\left(\alpha /K+w_h^{(i-1)}\right)/(\alpha +i-1)$, for h = 1, … , r_i−1, and u_ih = α(r_i−1/K − 1)/(α + i − 1) for h = r_i−1 + 1.
   2. Compute $\left({\beta }_{{\gamma }_i}^{*}|X^{(i-1)},{\gamma }^{(i-1)}\right)$ using the data x_i for subject i.

Note that the conditional probability of allocating subject i to predictor cluster h in step 2 (a) does not depend on unknowns in the response component model, so the allocation of subjects to predictor clusters can proceed via this fast sequential updating algorithm in a first stage. No approximations are needed in the sequential updating for conjugate P₀₁. The procedure selects a single partition, γ, instead of model averaging across possible partitions. Model averaging is appealing for prediction, but does not address our interest in inference on changes in the response distribution as the functional predictor changes or in obtaining results that are easily interpretable to a subject matter audience.

In the second stage, we apply a Gibbs sampling algorithm with the steps:

1. Update the allocation of subjects to response clusters, ϕ, by sampling from the multinomial full conditional posterior distribution of ϕ_i given y, X, γ, ψ, ν*, μ* and τ_y, for i = 1, … , n.

2. Update ${\nu }_h^{*}$, for h = 0,1, … , K, by sampling from the conjugate Dirichlet conditional posterior distribution.

3. Update the cluster-specific means μ* from their normal full conditional posterior distribution.

4. Update the precision parameter τ_y from its gamma full conditional.

5. Update ψ from its beta full conditional posterior distribution.

Each of these steps is simple to implement rapidly, involving direct sampling from standard distributions. In cases we have considered, the algorithm is quite efficient, with rapid apparent convergence and good rates of mixing. Note that, unlike for the predictor component, we are model averaging across partitions ϕ of subjects into response clusters. This results in more realistic measures of uncertainty in estimates of the conditional response densities, without leading to any difficulties in interpretation, as we illustrate in Section 4.

4. Weight Gain During Pregnancy and Birth Weight

4.1. Description of data and scientific problem

There is considerable interest in assessing the relationship between maternal weight gain during pregnancy and health outcomes. Inadequate or excessive weight gain during critical stages of pregnancy may indicate or even contribute to problems of both the developing child and the mother. For normal weight women, the Institute of Medicine (IOM) recommends gaining 4–6 lbs in the first trimester and 1lb/week during the 2nd to 3rd trimester, a recommendation motivated by the desire to avoid low birth weight.

Using data from the Pregnancy, Infection and Nutrition (PIN) study (Savitz et al., 1999), our goal is to relate trajectories in weight gain during pregnancy to the distribution of gestational age at delivery-adjusted birth weight. The PIN study enrolled women during the second trimester of the pregnancy. The woman’s height was measured, she was asked her weight prior to pregnancy at the first prenatal visit or the time of recruitment, and weight was collected from each clinic visit during pregnancy. There were n = 1,888 women having a baseline BMI in the [19.8, 26] range, corresponding to normal weight in the IOM guidelines. The number of weight measurements per woman ranged from 1 to 29 with a mean of 10.9, discarding weights that were clearly misrecorded.

To characterize the weight gain trajectories, we used a cubic spline model with knots at the trimesters, motivated by recommendations for weight gain, which are trimester-specific:

$$f_i(t)={\beta }_{i1}t+{\beta }_{i2}{t}^2+{\beta }_{i3}{t}^3+{\beta }_{i4}{(t-13)}_{+}^3+{\beta }_{i5}{(t-26)}_{+}^3,$$

where t is time of gestation in weeks with t = 0 at the time of the last menstrual period. As upper bounds on the number of clusters per component, we let K = 5 and L = 4. This value of K was motivated by interpretability and computational efficiency. Repeating the analysis for K = 25, we obtained essentially the same five common trajectory clusters, but with several additional outlying trajectory clusters containing less than 3% of the subjects. The Jones and Nagin (2007) approach selected K = 5 as the number of trajectory clusters based on the BIC criterion. The value of L = 4 was motivated by the observation that a mixture of 4 normal densities is sufficiently flexible to capture a broad variety of densities. In addition, very similar results were obtained for larger values of L.

To complete a Bayesian specification, we choose P₀₁ as $N\left({\beta }_i;{\beta }_0,\mathrm{\Psi }{\tau }_x^{-1}\right)G\left({\tau }_x;a_x,b_x\right)$ and P₀₂ as $N\left({\mu }_i;\kappa {\tau }_y^{-1}\right)G\left({\tau }_y;a_y,b_y\right)$, with G(a, b) the gamma distribution having mean a/b and variance a/b². We use a default specification with β₀ = (b′b)⁻¹b′x (global least squares estimate of the basis coefficients), Ψ = n(b′b)⁻¹ (a unit information prior covariance), ${\mu }_0=\overline{y}$ (global mean of y), κ = 1 (unit information), α = λ = 1 (a widely used default value for the DP precision), a_x = 2, $b_x=2\text{var}\left(x_{ij}-b_{ij}^{\prime }{\beta }_0\right)$, a_y = 2 and b_y = 2var(y_i). In addition, we choose a uniform(0,1) hyperprior for ψ. Results were robust to local changes in the hyperparameter values, and we obtained very similar results for a variety of alternative specifications. For example, we tried normalizing the data, and then letting β₀ = 0, Ψ=identity, μ₀ = 0, a_x = b_x = a_y = b_y = 1. In addition, we modified the hyperparameters in the initial specification by a factor of 2.

4.2. Analysis and results

We applied the combined sequential updating and Gibbs sampling algorithm proposed in Section 3, taking 50,000 Gibbs samples. In order to assess convergence and mixing of the Gibbs sampler, we monitored values of the birth weight density within different pregnancy weight gain clusters and for a variety of birth weight values, including values in the tails and center of the distribution. Based on examination of trace plots and application of standard diagnostic tests, we found no evidence of lack and convergence and mixing was good. Note that the meaning of the labels for the response (birth weight) clusters will vary over the Gibbs iterations, but this does not present a problem in estimating posterior summaries of the pregnancy weight gain cluster-specific birth weight densities.

The 1,888 women were clustered into 5 weight gain trajectory clusters, which we order according to total weight gain, with the following number (%) in each cluster: (lowest weight gain, magenta) 98 (5.2%), (blue) 617 (32.7%), (black) 774 (41.0%), (cyan) 175 (9.3%), and (green) 224 (11.9%). Figure 1 shows the estimated weight gain trajectory clusters and corresponding pointwise 95% credible intervals. These trajectories are scientifically reasonable, with most women having a slower rate of weight gain in the first trimester (or even small amounts of weight loss, common in women with nausea and vomiting associated with pregnancy-related hormonal changes), followed by an approximately linear rate of gain during the second and third trimesters. The blue cluster, which closely corresponds to the IOM recommendations and has an average gain of 30 pounds, contains approximately 1/3 of the women. Most of the remaining women are in the black cluster, with an average gain of just over 40 pounds, exceeding the IOM recommendation. Twenty percent of women have even higher weight gain, with women in the cyan and green clusters gaining an average of 50 and 60 pounds, respectively, while 5% are in the lowest weight gain (magenta) cluster corresponding to an average weight gain around 15 pounds. Repeating the analysis for a random reordering of women in the data set, we obtained similar results. To illustrate the extent to which the real data mimic these estimated trajectories, we plot the raw data for 25 randomly selected women in each cluster in Figure 2.

Figure 1.

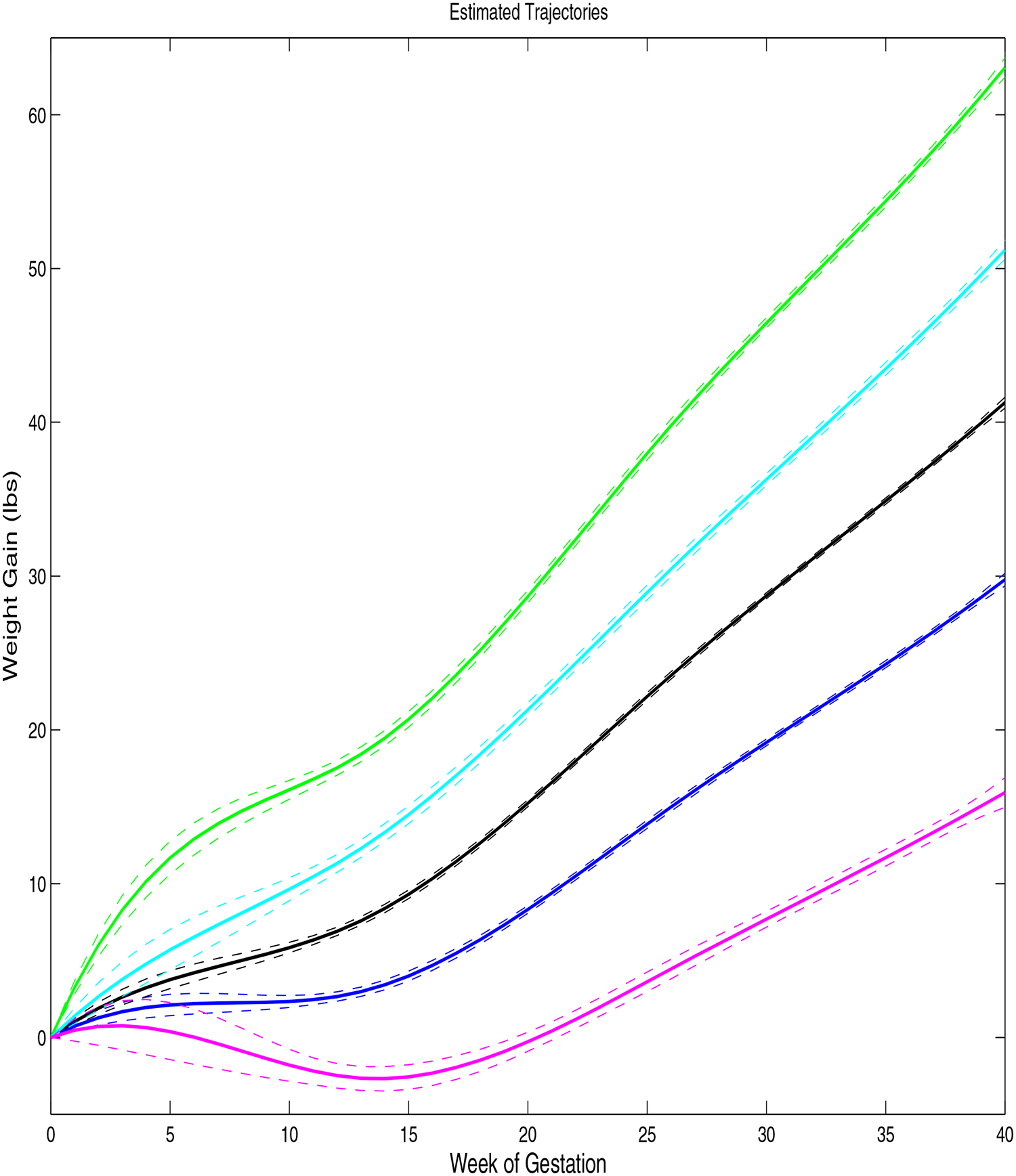
Estimated weight gain trajectory clusters (solid lines) and 95% credible intervals (dashed lines). The proportions of women in each cluster were: (1, blue) 32.7%, (2, black) 41.0%, (3, green) 11.9%, (4, magenta) 5.2%, and (5, cyan) 9.3%.

Figure 2.

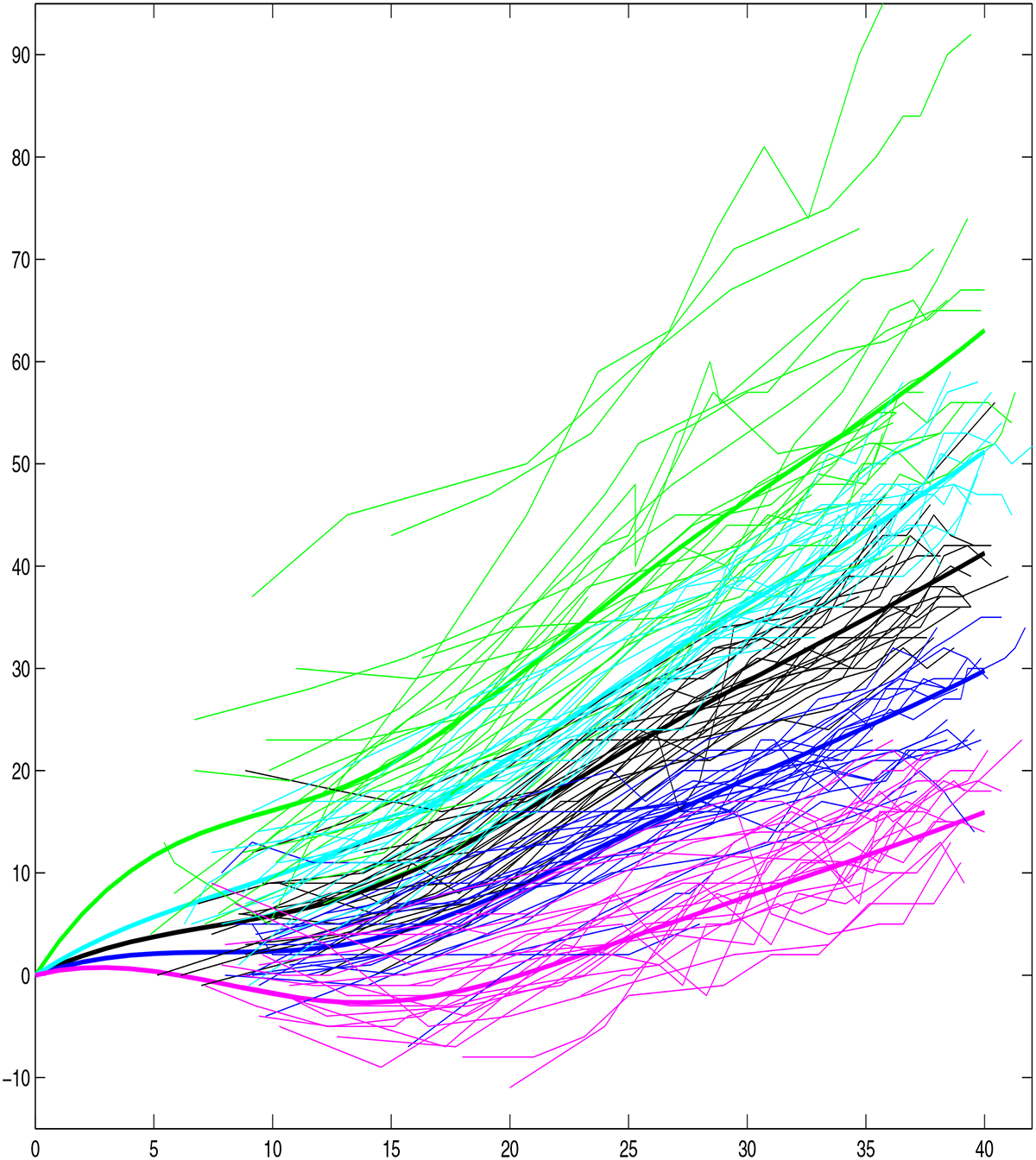
Raw data for 25 randomly selected women in each identified trajectory cluster.

Figure 3 shows the estimated birth weight densities and cumulative distribution functions (adjusted linearly for gestational age at delivery) for women in each weight gain trajectory cluster. Women in the lowest weight gain (magenta) cluster, who had a dip in weight in early pregnancy, had significantly lighter babies than women in the other clusters. The women in the cluster corresponding to the IOM recommendation (blue), had significantly lighter babies than women in the three higher weight gain clusters. Although the estimated birth weight distributions are unimodal, there is clear evidence of non-normality, with heavy tails and a tendency towards a left skew. Figure 4 plots estimated posterior densities for different percentiles of the birth weight distribution, specific to each trajectory cluster. Interestingly, although there were significantly more low birth weight babies in the lowest weight gain trajectory cluster, the difference between the cluster most closely corresponding to the IOM recommendations and the three higher weight gain clusters was more apparent for normal and high birth weight babies. Table 1 provides posterior probabilities for quantile-specific contrasts. Using a standard cutpoint for low birth weight babies (< 2500g), women in the lowest weight gain cluster had significantly more low birth weight babies (17.2%) than women in the higher weight gain clusters (9.3, 6.8, 6.6, and 6.8%, respectively), which is of considerable concern given that low birth weight babies are at increased risk for morbidity and mortality.

Figure 3.

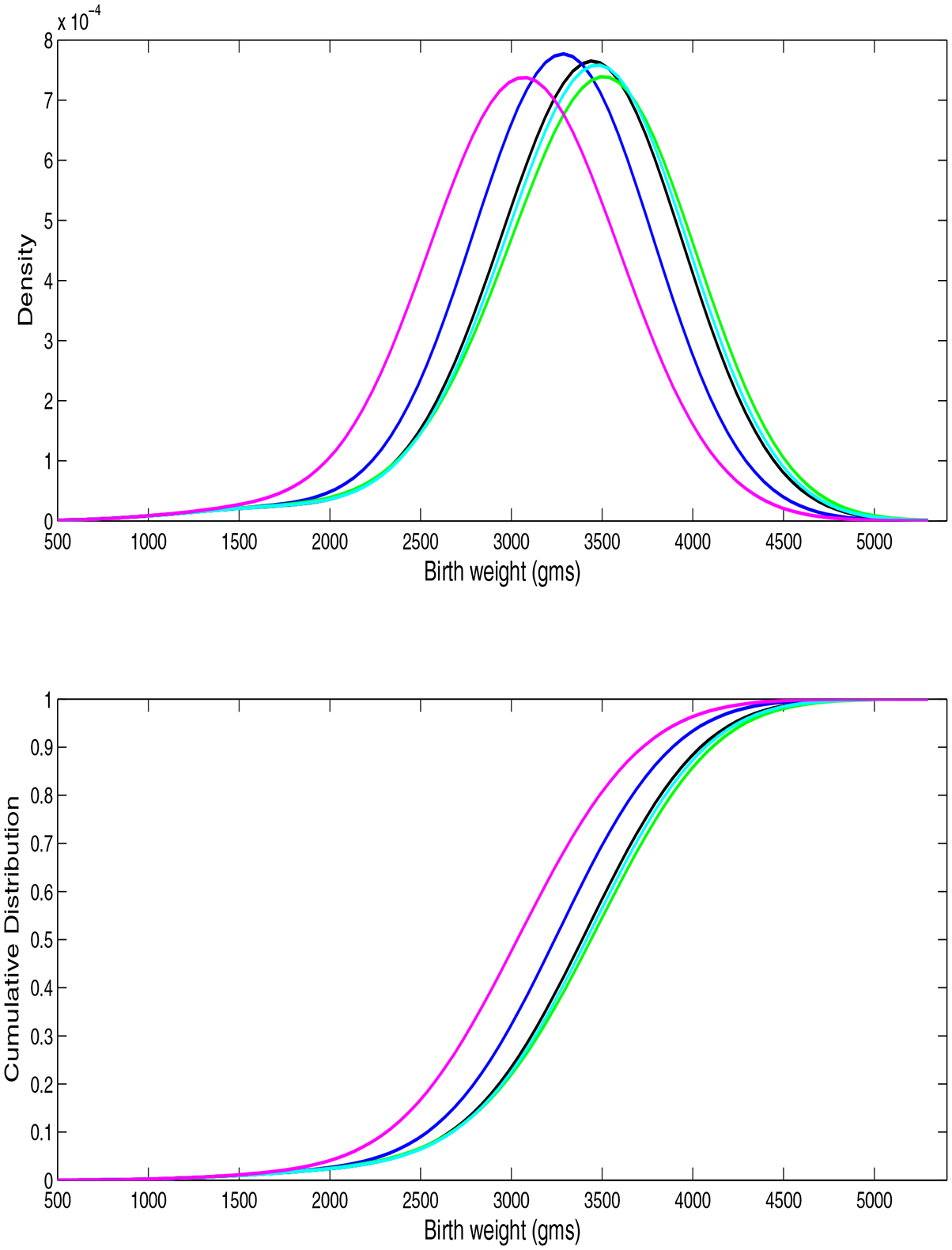
Estimated density and cumulative distribution function for birth weight at 40 weeks for women in each weight gain trajectory cluster.

Figure 4.

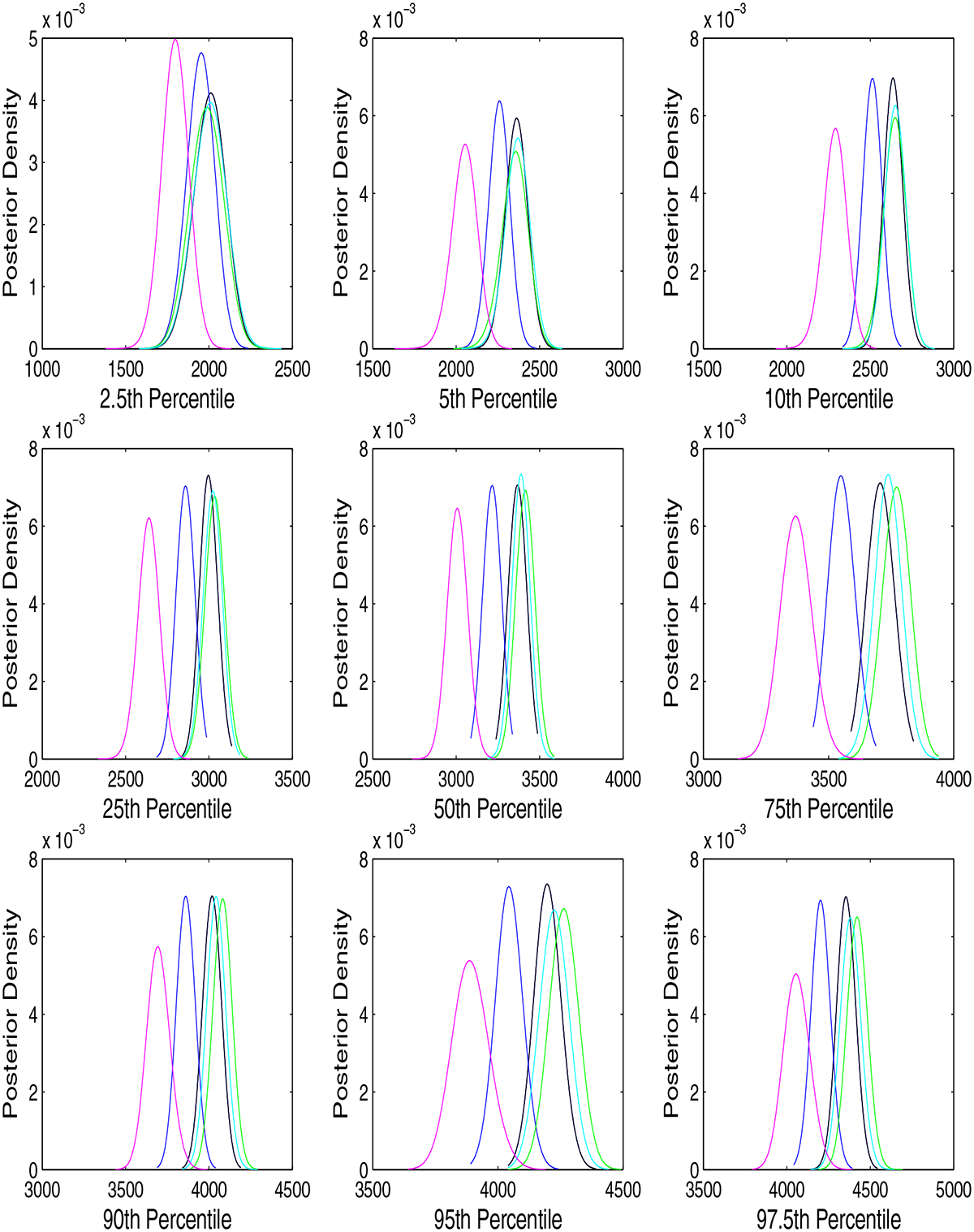
Estimated posterior densities of selected percentiles of the birth weight distribution within each weight gain trajectory cluster.

Table 1.

Posterior probabilities of orderings in selected quantiles of the birth weight distribution between weight gain trajectory clusters.

	Percentile of distribution
Contrast	2.5th	5th	10th	25th	50th	75th	90th	95th	97.5th
magenta < blue	0.998	> 0.999	1.000	1.000	1.000	0.999	0.995	0.988	0.976
blue < black	0.815	0.992	> 0.999	1.000	1.000	1.000	1.000	1.000	> 0.999
black < cyan	0.185	0.309	0.370	0.505	0.444	0.579	0.497	0.518	0.501
black < green	0.127	0.271	0.394	0.648	0.732	0.859	0.875	0.901	0.875
cyan < green	0.141	0.231	0.292	0.365	0.507	0.607	0.650	0.644	0.650

Applying the Jones and Nagin (2007) approach in SAS, we obtained similar trajectories to those shown in Figure 1, though the Jones and Nagin estimates were less smooth early and late in gestation due to edge effects. As in our analysis, the Jones and Nagin approach concluded that women in the two lowest weight gain trajectory clusters had babies with significantly lower birth weight adjusting for gestational age at delivery. However, by assuming normality of the birth weight distribution for women within a trajectory cluster, with only the means varying across trajectory clusters, the Jones and Nagin approach does not allow separate inferences on different quantiles of the birth weight distribution. Such inferences are of primary importance in assessing effects of maternal weight gain on risk of small and large for gestational age babies.

A simple alternative is to use frequentist kernel smoothing to obtain estimated birth weight densities within each trajectory class produced by the Jones and Nagin approach. Such an analysis produces similar, but less smooth, estimates to those shown in Figure 3. Our proposed approach has the advantage of borrowing information across the latent classes in performing density estimation. In addition, our approach automatically produces measures of uncertainty, while also allowing calculation of posterior probabilities for quantile contrasts.

5. Discussion

This article proposes a method for assessing changes in a response density across clusters in a functional predictor. We applied this approach to a rich data set containing detailed records of weight gain during pregnancy, gestational age at delivery and birth weight for a large (by typical reproductive epidemiology standards) sample of woman. We found that women in a low pregnancy weight gain cluster had significantly more low birth weight babies, adjusting for gestational age at delivery. In addition, we found that there was a highly significant increase in the risk of large for gestational age babies among women gaining more than the current clinical recommendations. These results are of substantial clinical and public health interest, given that the majority of women gain more than recommended.

Motivated by label ambiguity problems and difficulties in performing efficient computation, we allocate subjects into predictor clusters using a fast sequential updating and greedy search procedure, with Gibbs sampling used to obtain samples from the conditional posterior for the predictor cluster-specific response densities. Our view is that clustering of the predictor data is useful as a dimensionality reduction technique and as an aid in interpretation of the complex relationship between a high dimensional predictor and a response having an unknown distribution. However, we do not in general recommend interpreting such clusters as corresponding to biologically or clinically distinct groups of individuals, because the formation of clusters is necessarily dependent on parametric assumptions.

Following Quintana (2006) we view partitioning as a model selection problem. From this viewpoint, our sequential updating and greedy search algorithm is a type of stepwise selection procedure to rapidly partition the subjects into clusters. Our proposed joint clustering prior should be useful in other applications in which allocation of a subject to a cluster for one task predicts cluster allocation for another distinct task. In addition, even when clustering is not of interest, the method can be used to generate flexible joint partition models. Joint partitioning extends current Bayesian partition models (Barry and Hartigan, 1992; Quintana and Iglesias, 2003; Holmes et al., 2005; Quintana 2006) to allow flexible joint modeling of data from different sources. Related problems have been considered in the machine learning literature from a different perspective (Barnard et al., 2003).

Appendix A: Posterior Updating

A.1. Predictor component

Assuming $\left(\beta |{\tau }_x\right)~N_p\left({\beta }_0,\mathrm{\Psi }{\tau }_x^{-1}\right)$ and τ_x ~ G(a_x, b_x) and updating with the likelihood $\prod _{j=1}^{n_i}N\left(x_{ij};b_{ij}^{\prime }\beta ,{\tau }_x^{-1}\right)$, we obtain $\left(\beta |{\tau }_x,x_i\right)~N_p\left(\widehat{\beta },\widehat{\mathrm{\Psi }}{\tau }_x^{-1}\right)$ and $\left({\tau }_x|x_i\right)~G\left({\widehat{a}}_x,{\widehat{b}}_x\right)$, where $\widehat{\mathrm{\Psi }}={\left({\mathrm{\Psi }}^{-1}+\sum _{j=1}^{n_i}{b}_{ij}{b}_{ij}^{\prime }\right)}^{-1}$, $\widehat{\beta }=\widehat{\mathrm{\Psi }}\left({\mathrm{\Psi }}^{-1}{\beta }_0+\sum _{j=1}^{n_i}{b}_{ij}{x}_{ij}\right)$, ${\widehat{a}}_x=a_x+n_i/2$ and

$${\widehat{b}}_x=b_x+\frac{1}{2}\left\{{\beta }_0^{\prime }{\mathrm{\Psi }}^{-1}{\beta }_0+\sum _{j=1}^{n_i}{x}_{ij}^2-{\widehat{\beta }}^{\prime }{\widehat{\mathrm{\Psi }}}^{-1}\widehat{\beta }\right\}.$$

In addition, the marginal likelihood of x_i obtained in integrating out (β, τ_x) is

$$f\left(x_i\right)=\frac{\mathrm{\Gamma }\left(\left(\nu +n_i\right)/2\right)}{{(\pi \nu )}^{n_i/2}{\left|{\sigma }^2\mathbf{\Sigma }\right|}^{1/2}\mathrm{\Gamma }(\nu /2)}{\left(1+\frac{{\left(x_i-{\mu }_x\right)}^{\prime }{\mathbf{\Sigma }}^{-1}\left(x_i-{\mu }_x\right)}{{\sigma }^2\nu }\right)}^{-\left(\nu +n_i\right)/2},$$

where v = 2a_x, $\mathbf{\Sigma }={\left(I_{n_i}-b_i\widehat{\mathrm{\Psi }}{b}_i^{\prime }\right)}^{-1}$, ${\mu }_x=\mathbf{\Sigma }\left(b_i\widehat{\mathrm{\Psi }}{\mathrm{\Psi }}^{-1}{\beta }_0\right)$, $b_i={\left(b_{i1},\dots ,b_{i{n}_i}\right)}^{\prime }$ and

$${\sigma }^2=\frac{1}{\nu }\left(2b_x+{\beta }_0^{\prime }\left({\mathrm{\Psi }}^{-1}-{\mathrm{\Psi }}^{-1}\widehat{\mathrm{\Psi }}{\mathrm{\Psi }}^{-1}\right){\beta }_0-{\mu }_x^{\prime }{\mathbf{\Sigma }}^{-1}{\mu }_x\right).$$

A.2. Response component

Assuming $\left(\mu |{\tau }_y\right)~N\left({\mu }_0,\kappa {\tau }_y^{-1}\right)$ and τ_y ~ G(a_y, b_y) and updating with the likelihood $N\left(y_i;\mu ,{\tau }_y^{-1}\right)$, we obtain $\left(\mu |{\tau }_y,y_i\right)~N\left(\widehat{\mu },\widehat{\kappa }{\tau }_y^{-1}\right)$ and $\left({\tau }_y|y_i\right)~G\left({\widehat{a}}_y,{\widehat{b}}_y\right)$, where $\widehat{\kappa }={\left({\kappa }^{-1}+1\right)}^{-1}$, $\widehat{\mu }=\widehat{\kappa }\left({\kappa }^{-1}{\mu }_0+y_i\right)$, ${\widehat{a}}_y=a_y+1/2$ and ${\widehat{b}}_y=b_y+1/2\left({\kappa }^{-1}{\mu }_0^2+y_i^2-{\widehat{\kappa }}^{-1}{\widehat{\mu }}^2\right)$. In addition, the marginal likelihood of y_i obtained in integrating out (μ, τ_y) is

$$f\left(y_i\right)=\frac{\mathrm{\Gamma }((\nu +1)/2)}{{(\pi \nu )}^{1/2}\sigma \mathrm{\Gamma }(\nu /2)}{\left(1+\frac{{\left(y_i-{\mu }_y\right)}^2}{{\sigma }^2\nu }\right)}^{-(\nu +1)/2},$$

where ν = 2a_y, μ_y = μ₀ and σ² = 2b_y(1 + κ)/ν.