One-dimensional hexagonal boron nitride conducting channel

The 6′6′ twin boundary of two-dimensional hexagonal boron nitride is an ultimate one-dimensional conducting channel.

Abstract

Hexagonal boron nitride (hBN) is an insulating two-dimensional (2D) material with a large bandgap. Although known for its interfacing with other 2D materials and structural similarities to graphene, the potential use of hBN in 2D electronics is limited by its insulating nature. Here, we report atomically sharp twin boundaries at AA′/AB stacking boundaries in chemical vapor deposition–synthesized few-layer hBN. We find that the twin boundary is composed of a 6′6′ configuration, showing conducting feature with a zero bandgap. Furthermore, the formation mechanism of the atomically sharp twin boundaries is suggested by an analogy with stacking combinations of AA′/AB based on the observations of extended Klein edges at the layer boundaries of AB-stacked hBN. The atomically sharp AA′/AB stacking boundary is promising as an ultimate 1D electron channel embedded in insulating pristine hBN. This study will provide insights into the fabrication of single-hBN electronic devices.

INTRODUCTION

Hexagonal boron nitride (hBN), analogous to graphene, is a bielemental compound comprising alternating boron and nitrogen atoms. In contrast to the wide spectrum of proposed applications for graphene as an active component in nanodevices, hBN is often regarded as a passive material where the range of applications is largely confined to substrates or electron barriers for two-dimensional (2D) material–based devices due to its electrically insulating feature with a large bandgap of ~5 eV (1). Many attempts to lower the bandgap of hBN by substitutional doping (e.g., with carbon or oxygen atoms) have been mostly ineffective because of the strong covalent BN bonds and chemical inertness (2–4), while hBNC, in-planar compound of graphene and hBN synthesized by Gong et al. (5), showed semiconducting property with tunable bandgap.

Stacking boundaries or phase boundaries of few-layer 2D materials were shown to have unique properties that open new ways to control the performance of a material (6–10). For example, AB/BA stacking boundary with broad range in bilayer graphene showed insulating-like characteristics and reversible transport regimes (6), and 558 line defect formed at a stacking boundary in graphene was reported to act as a metallic wire (7). 1D twin boundaries found in molybdenum diselenide (8) also revealed bandgap changes. In the meantime, Li et al. (11) reported that grain boundaries in hBN such as the 5|7 and 4|8 configurations reduce its bandgap to ~3.4 and ~4.3 eV, respectively. However, there is no further report on few-layer hBN stacking boundaries. Although the most stable stacking structure in bulk hBN is AA′ stacking (12, 13), few-layer hBN can also exist as AB stacked, which is the next most stable configuration according to theoretical calculations (14) and has been experimentally observed in both chemically exfoliated (15) and synthesized hBN (16, 17).

Here, we report atomically sharp AA′/AB stacking boundaries of few-layer hBN grown by chemical vapor deposition (CVD). The configurations, structural stabilities, and electric properties of twin boundaries are investigated systematically by combination of transmission electron microscopy (TEM), image simulations, density functional theory (DFT) calculations, and ab initio molecular dynamics (AIMD) simulations. In addition, the formation mechanism of atomically sharp stacking boundaries is deduced on the basis of the observations of extended Klein (EK) edges at the layer boundary of hBN.

RESULTS AND DISCUSSION

Synthesized few-layer films of hBN with AA′ and AB stacking structures

We synthesized few-layer hBN films on a copper substrate using CVD and transferred them onto TEM grids (see Materials and Methods for details) (18, 19). First, we performed dark-field (DF)–TEM imaging on oriented, few-layer hBN films to determine their structural characteristics. Here, we use the symbols [BN] and [NB] to represent the two different orientations of hBN and differentiate AB and AC stacking orders to classify the configurations of the stacking boundaries and the corresponding stacking structures for AA′- and AB-stacked hBN (see fig. S1 for details about the classification of high-symmetry stacking structures of hBN). Figure 1 (A and B) is DF-TEM images obtained using a second-order (Φ2) and Φ1 spot from a selected area electron diffraction pattern (inset of Fig. 1A). Triangular, multilayered hBN islands are grown on continuous monolayer hBN film with the same orientation. As explained in detail in section S2, the intensities of the islands acquired from Φ2 diffraction spot increase with the number of layers, regardless the AA′ or AB stacking structure (Fig. 1A). However, the intensity obtained from Φ1 diffraction spot is determined by the stacking structure (Fig. 1B). In Fig. 1B, some regions show brighter contrast with the increasing number of layers, indicating that they have the AA′ stacking structure, while the darker regions despite having the same number of layers as the AA′-stacked region have the AB stacking structure. The darkest region outlined with white solid line represents an ABC-stacked region because all the diffracted waves interfere destructively and cancel out each other for this region. However, DF-TEM hardly verifies that an AA′-stacked region is not AA-stacked or that an AB-stacked (AC-stacked) region is not an AB′-stacked (AC′-stacked) region since those images have similar diffraction conditions (16). Hence, the stacking structures were confirmed directly using high-resolution (HR)–TEM images (Fig. 1, C to E). In Fig. 1C, the AA′-stacked bilayer region shows the same hexagonal lattice contrast but brighter than the monolayer region, while the AB-stacked bilayer region reveals a triangular shape with alternating contrast (20, 21). The AA′ and AB stacking structures were further confirmed by the relation of orientation of the triangular defects in two different layers. Triangular hole created by 80-kV electron-beam irradiation always shows N-terminated edges (22–24). Thus, triangular defects in adjoined layers have the same orientations in AB stacking ([BN]/[BN]) (Fig. 1D), while those in AA′ stacking ([BN]/[NB]) point in opposite directions (Fig. 1E). Therefore, a combination of DF-TEM and HR-TEM clearly proves that AA′- and AB-stacked, few-layer hBN films have been grown in our CVD system.

Fig. 1. TEM images of few-layer AA′- and AB-stacked hBN films.

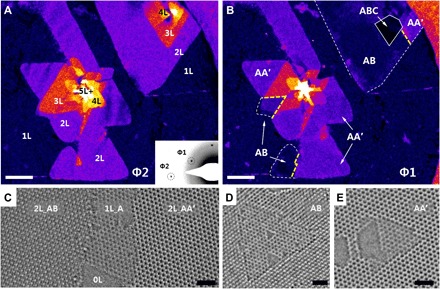
(A and B) False-color DF-TEM images of triangular, few-layer hBN islands from (A) a Φ2 diffraction spot [inset of (A)] and (B) a Φ1 diffraction spot [inset of (A)]. In (A), the number of layers (1L to 5L+) is identified, while different stacking structures (AA′, AB, and ABC) are shown in (B). (C to E) HR-TEM images of AA′- and AB-stacked hBN. Triangular defects grow in the same orientation in AB-stacked hBN (C) and in the opposite direction in AA′-stacked hBN (E). Scale bars, 0.1 μm (A and B) and 1 nm (C to E).

Recent experimental works have suggested the possibility of AB-stacked hBN (15–17), but none report the coexistence of AA′- and AB-stacked hBN in one continuous island. Note that coexistence and even perfect stitching of AA′ and AB stacking structures of the hBN islands are shown in the upper right part of Fig. 1B. Many studies have reported the existence of transition regions without high-symmetry structures between different phases or stacking structures (25–27).

Transition regions that lost high-symmetry stacking structure (neither AA′ nor AB) appear dark in DF-TEM images acquired from the Φ2 diffraction spot (refer to section S3), but unexpectedly, no dark line was detected between the AA′ and AB stacking structures in our DF-TEM image in Fig. 1A (yellow dashed-line regions in Fig. 1B). This represents an abrupt change of stacking structure without any transition region between AA′ and AB stacking. We therefore studied further the stacking boundary under high magnification. Conditions on whether it forms the atomically sharp stacking boundary or broad transition region will be discussed later in the section ‘Formation mechanism of atomically sharp twin boundaries and EK edges’.

Twin boundary at the AA′ and AB stacking boundaries

Figure 2A is an HR-TEM image taken from the white-boxed area in the false-color DF-TEM image in Fig. 2B, which has no dark line between islands having different stacking structures. The magnified atomic images on each side of the insets in Fig. 2A clearly show the AA′ and AB stacking structures on the left and right sides of the figure. Both sides contain three layers, as confirmed by counting the etched layers after prolonged electron-beam irradiation (fig. S3, A and B). In addition, the “ABA” stacking structure on the right side instead of an “ABC” structure is proved by the contrast difference in the TEM image simulation (fig. S3, C to E). Hence, the trilayers of AA′A- and ABA-stacked hBN are stitched together perfectly, forming an atomically sharp stacking boundary along zigzag direction. Figure 2C shows the stacking boundary in a false-color image of the black-boxed region in Fig. 2A.

Fig. 2. Atomically sharp AA′/AB stacking boundary.

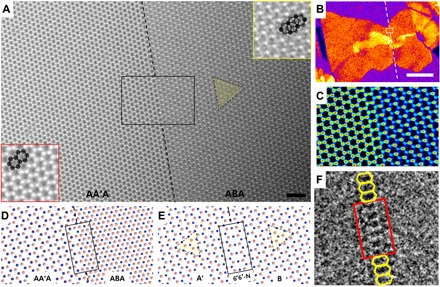
(A) HR-TEM image of the stacking boundary of a trilayer ABA/AA′A-stacked hBN film, from the white-boxed region in (B). (B) False-color DF-TEM image. (C) False-color image of the black-boxed region in (A). (D and E) Atomic models of the stacking boundary of AA′A/ABA-stacked hBN (D) and of the middle layer A′/B (E) after removing two “A” layers each from the top and bottom. Boron and nitrogen atoms are represented by pink and blue spheres, respectively. (F) Inverse fast Fourier transform (IFFT) image displays the 6′6′ configuration at the boundary. Scale bars, 1 nm (A) and 0.1 μm (B).

To determine the atomic configuration at this boundary, we made a corresponding atomic model (Fig. 2D) and subtracted two “A” layers, one each from the top and bottom, leaving only the middle A′ and B layers (Fig. 2E). This shows that the boundary acts as a mirror plane for the A′ and B regions, i.e., a twin boundary. The deduction of the atomic configurations in Fig. 2 (D and E) starts from the four possible structures of AA′A/ABA stacking boundary along a zigzag direction (fig. S4). The corresponding four twin boundaries are denoted by (i) 6′6′-N, (ii) 44-B, (iii) 6′6′-B, and (iv) 44-N, where 6′6′ (44) represents an oblong hexagonal (rhombal) ring and -N(-B) denotes the N(B) mirror plane at the twin boundary. Two verification steps (see section S4 and figs. S4 and S5) prove that the 6′6′-N structure matches the experimental result shown in Fig. 2A. Therefore, an atomically sharp twin boundary, with N atoms as the mirror plane and oblong hexagons (6′6′), is formed at the middle layer of the AA′A/ABA stacking boundary (Fig. 2E). Inverse fast Fourier transform (IFFT) image (Fig. 2F), obtained by inversing the filtered FFT after removing the typical hBN lattice information, also shows the 6′6′ configuration.

6′6′ versus 558 configurations

The N atoms at the mirror plane of the 6′6′-N structure are doubly coordinated with one dangling bond, as expected from Fig. 2. This obviously raises a question about the stability of the structure. Using DFT calculations, we have tested the stabilities of the four possible atomic configurations at the twin boundary (Fig. 3, A to G): (i) 6′6′-N, (ii) 44-B, (iii) 6′6′-B, and (iv) 44-N. As a result, the 6′6′-N configuration changes into 558-N (two pentagons and one octagon), a fully coordinated, stable structure, with the uncoordinated N atoms bonding together (Fig. 3, A and C). There is no shift in the positions of the atoms on the left and right, except for a slight in-plane movement (<1 Å) of the uncoordinated N atoms in the middle layer. The 44-B structure (Fig. 3B) also changes to 558-N by shifting all atoms on the right side of the boundary, as indicated by the red arrow marked in Fig. 3C. Similarly, the stable form of 6′6′-B (Fig. 3D) becomes 558-B (Fig. 3F), with the uncoordinated B atoms at the mirror plane saturating each other. The structure 44-N (Fig. 3E) could not retain the original bonding because of large distortions, with the atoms kicked from the plane. The 558 structure is more stable than 6′6′ for the monolayer, bilayer, and trilayer cases.

Fig. 3. Illustration of the atomic configurations at a twin boundary: 6′6′ versus 558.

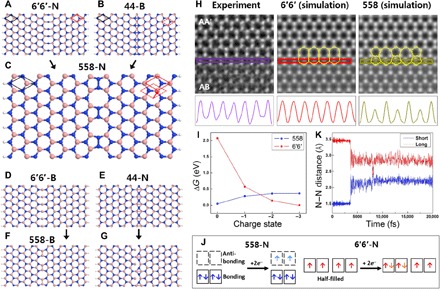
(A to G) A summary of the DFT calculations. The optimized structures (C, F, and G) of the initial four possible structures at the stacking boundary (A, B, D, and E) show the construction of the 558 configurations as a twin boundary. The symbols -B(-N) stand for B(N) atoms in the mirror plane at the twin boundary. Boron and nitrogen atoms are represented by pink and blue, respectively. (H) Intensity profiles along lines at the stacking boundary in the experimental images (purple), simulated images of the 6′6′ (red), and 558 (olive) configurations. (I) Change of free energy with respect to charge state. Free energy of a hBN nanoribbon with 6′6′-N configuration (red) become lower than that with 558 (blue) after addition of two electrons in the system. (J) Highest occupied and lowest unoccupied molecular orbital states for 558-N nanoribbon and singly occupied molecular orbital states for 6′6′-N nanoribbon in 0 and −2 charge state. (K) The result of AIMD simulations showing N─N distance of the 558 configuration with short and long distance through pentagon (1.5 Å; blue-colored) and octagon (3.5 Å; red-colored) changes to distance within the range of hexagons (2.0 to 3.0 Å).

Nevertheless, the intensity profiles along the lines at the AA′A/ABA stacking boundary in the experimental (purple), simulated 6′6′ (red), and simulated 558 (olive) images indicate that the structure observed by TEM is more likely 6′6′ configuration than 558 (Fig. 3H). There are distinctive height differences between the peaks in the experimental and simulated 558 image, whereas there is a little difference between the experimental and simulated 6′6′ images. The height differences of the peaks in the 558 configuration are thought to be due to differences in the electron densities in the pentagon and octagon regions. We performed the same analysis but in the opposite defocus, which shows that the tendency of line profile is consistent with defocus conditions.

To explain the discrepancy between the results of the DFT calculations and the experimental observations, we introduced additional external factors in DFT calculations fostering similar conditions to the TEM operating system. Applying the external electric field and/or thermal effect did not change the preference of 558 configuration to 6′6′ configuration in energetic stability. However, injecting additional electrons in hBN nanoribbon systems, which could happen under high transmitting electron beam, made a reversal of preference of 558 and 6′6′ configurations. As shown in Fig. 3I, the additional electrons in the 6′6′-N nanoribbon make the free energy of the system decreased, while the free energy of the 558-N nanoribbon increases (see Materials and Methods). This is because additional electrons in the 558-N nanoribbon structure fill antibonding states weakening the N─N bonds of a five-membered ring at the twin boundary, while additional electrons in the 6′6′-N nanoribbon structure fill singly occupied molecular orbital states (Fig. 3J). When two or more electrons are added in the system, 6′6′ configuration becomes energetically stable than 558 configuration. The result of energy barrier calculations (fig. S6A) shows that 558 configuration easily transforms to 6′6′ configuration once it overcomes a small energy barrier of ~0.2 eV with two additional electrons in the hBN nanoribbon. We further performed AIMD simulations to directly present the transformation of 558 configuration to 6′6′ configuration. Figure 3K shows the result of AIMD simulations in N─N distance of the five-membered ring (short) and the eight-membered ring (long) along the twin boundary of the 558-N nanoribbon structure with two additional electrons at 400 K. After a few picoseconds, 558-N configuration changes to 6′6′-N configuration and maintains it with a little oscillations (see movie S1). Experimental results of IFFT images at twin boundary also show a little oscillations of 6′6′ configurations over time along the twin boundary (fig. S6, B and C). Note that the time needed for the transformation is different with temperatures (room temperature to 500 K) but the hBN nanoribbon structure always ends up with 6′6′ configuration in AIMD simulations. Therefore, we conclude that the negatively charged TEM operating system makes twin boundaries have 6′6′ configurations.

1D hBN conducting channel

There is little structural difference between the 558 and 6′6′ configurations. However, there is a notable difference in electrical properties due to the presence of free electrons (dangling bonds). Figure 4 (A and B) shows the electronic band structures calculated for both the 558-N and 6′6′-N hBN nanoribbons. The bandgap of the 558-N configuration is 3.44 eV, while the bandgap of the 6′6′-N configuration is 0 eV. N atoms along the twin boundary are fixed, the other atoms are fully relaxed through the structure, and both edges are passivated by hydrogens for the calculation of bandgap (see Materials and Methods for details). The red circles in the band structures indicate the contribution of N atoms at the twin boundary, which signifies that the nitrogen atoms at the twin boundary cause the reduction of bandgap even to 0 eV.

Fig. 4. Bandgap of hBN at twin boundary.

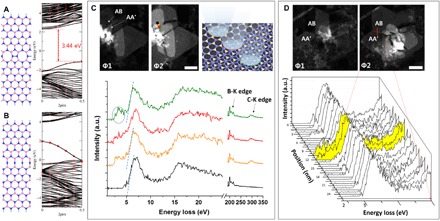
(A and B) The atomic model and corresponding band structure for the 558-N (A) and 6′6′-N (B) configurations, respectively. The red circles in the band structures represent the contribution of N atoms at twin boundary. Boron, nitrogen, and hydrogen atoms are represented by pink, blue, and cyan spheres, respectively. (C) Bandgap measurement at and near the atomically sharp AA′/AB stacking boundary. Four EEL spectra are deconvoluted by the subtraction of ZLP and plural scattering from the original spectra. The black-colored EEL spectrum is from clean hBN, orange- and green-colored EEL spectra are from hBN with hydrocarbon adsorbates on surface, and the red-colored EEL spectrum is from the twin boundary of hBN. The extrapolated lines meet at the x intercept around 5 eV, from the black-, orange-, and green-colored spectrum representing the bandgap of hBN. a.u., arbitrary units. (D) EELS line profile across atomically sharp AA′/AB stacking boundary. Space of each scan is 1.5 nm. Scale bars, 50 nm.

Furthermore, the bandgap at twin boundaries are experimentally assessed using electron energy-loss spectroscopy (EELS) to support the calculation results. Considering the scale of the twin boundary in one-atom width and ~50-nm length, photoluminescence spectroscopy typically used for the bandgap measurement has an insufficient spatial resolution for this sample. In addition, scanning tunneling microscopy that has both high spatial and energy resolution is only applicable when the twin boundary is exposed on the surface. Meanwhile, monochromated EELS can examine the bandgap at the exact twin boundary regions combined with DF-TEM, by reading the cross point between the extrapolated line and the bottom line from the first peak after zero-loss peak (ZLP) in EELS (see Materials and Methods for details) (28). Although monochromated EELS also has the limitation that the first few electron volts should be subtracted because of the tail of ZLP, the bandgap can be assessed by the extrapolation line from the first peak after ZLP (28).

Figure 4C shows four EEL spectra acquired from near atomically sharp AA′/AB stacking boundary. The black EEL spectrum is from clean and pristine hBN, orange and green EEL spectra are from pristine hBN covered with hydrocarbon adsorbates on the surface, and red EEL spectrum is from the atomically sharp stacking boundary of hBN. The cross points where the extrapolated lines (blue dashed lines) meet with the bottom lines at the black, orange, and green spectra are all around 5 eV, which represent the bandgap of pristine hBN. However, the red EEL spectrum acquired from the atomically sharp stacking boundary shows a gradual decrease in the intensity of the front edge without steep falling to x axis of 2 eV. Small intensity around 2 to 4 eV turning up at the orange and green EEL spectra (blue circled region) is due to the unavoidable amorphous hydrocarbon on the surface of hBN, which can be judged by the appearance of C-K edge around 300 eV at high–energy loss region. To prevent misinterpretation of EELS signal in front of 5 eV, we carefully selected areas with small amount of hydrocarbon (see Materials and Methods for details). The signals from 2 to 4 eV in the orange and green EEL spectra are distinctive, but still, the falling slopes are not changed, and the cross points to the x intercept are 5 eV, even with the higher amount of hydrocarbon compared to that detected at the stacking boundary, which can be evaluated by the peak intensity ratio of B-K edge (~200 eV) to C-K edge (~300 eV). In contrast, the red EEL spectrum acquired at the stacking boundary shows a lower slope with gradual decrease to 2 eV. Another example of EELS line profile across atomically sharp AA′/AB stacking boundary (Fig. 4D) also shows the front of EELS edges from the twin boundary (highlighted in yellow) gradually decrease to zero-loss region from the peak of ~6 eV with a lower slope on the contrary to the other EELS edges that are steep to meet the x intercept around 5 eV.

The EELS results at the stacking boundaries could be from the 6′6′-N configurations with the bandgap of 0 eV or mixed 6′6′ and 558 configurations that are not fully charged with additional electrons. Since ZLP has been subtracted to 2 eV, the exact onset of the signal where the delayed front edge starts before 2 eV is not read. However, at least, the reduced bandgap at the atomically sharp stacking boundary was experimentally detected by EELS.

Considering that a pure hBN nanoribbon has a wide bandgap of ~5 eV, the twin boundary can act as an atomically thin electronic channel. The present observations of 6′6′ configuration at twin boundaries open a new possibility for single-hBN nanoelectronic devices. Lahiri et al. (7) have reported that this type of grain boundary in graphene can act as a metallic wire. Similarly, the AA′A/ABA twin boundary in hBN can be a 1D conducting channel embedded in the original insulating hBN, which is expected to be much more effective than a metallic wire in a conductive graphene sheet. In addition, note that trilayer AA′A/ABA stacking structure, where a twin boundary is protected by the top and bottom layers, is very stable compared to bilayer AA′/AB stacking structure, wherein a twin boundary is exposed to ambient conditions (fig. S7).

Formation mechanism of atomically sharp twin boundaries and EK edges

Atomically sharp stacking boundaries are commonly found in our hBN samples, but not always as shown in fig. S2, which has a wide transition region in an AA′/AB stacking boundary. The probability of finding stacking boundary with an abrupt change or with a transition region was about half and half (fig. S8). We elicit that the formation of atomically sharp stacking boundaries is determined by certain combinations of AA′ and AB stacking during crystal growth from observations of EK edges at monolayer/bilayer boundaries of an AB-stacked region, as shown in Fig. 5.

Fig. 5. EK edge at a 1|2-layer boundary in AB-stacked hBN.

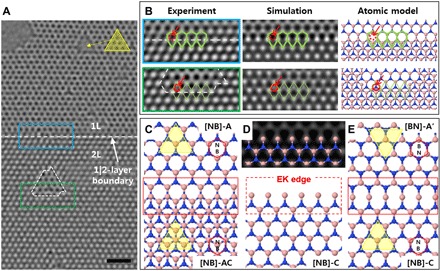
(A) HR-TEM image of monolayer and bilayer hBN with an AB stacking structure. The white arrow points to the 1|2-layer boundary. Scale bar, 1 nm. (B) Experimental images from the blue-boxed area (1|2-layer boundary) and green-boxed area (a triangular defect) inside (A), as well as the corresponding simulation image and atomic model. (C to E) Formation mechanism of a twin boundary from observations of an EK edge. Boron and nitrogen atoms are represented in pink and blue, respectively. Also see movie S2.

Figure 5A is an HR-TEM image of the hBN monolayer and bilayers with the layer boundary (1|2-layer boundary). The atomic configurations of the blue-boxed area containing the 1|2-layer boundary and the green-boxed area ([NB]-AC bilayer containing one edge of a triangular defect) are closely analyzed in Fig. 5B to confirm the edge configuration (see section S6 and fig. S9). There is no contrast in the area marked by red dotted circles at the 1|2-layer boundary, whereas the white contrast is obvious where the N atoms exist at the edges of the triangular defect. The atomic model of the 1|2-layer boundary in Fig. 5B is shown with the stacking notation (Fig. 5C), and the first layer ([NB]-A) is removed (Fig. 5D). The result shows that the edge of the second layer ([NB]-C) is not terminated by N atoms, which is also known as an EK edge (29). The EK edge was predicted as the fourth type of periodic edge, after the zigzag, reconstructed pentagon-heptagon pair, and armchair edge for graphene (30), but there has been no report of EK edge for hBN. Now, suppose that a second layer of [BN]-A′ is grown on top of the monolayer region with AA′ stacking (Fig. 5E, top). If it meets the EK edge of the second layer of [NB]-C (Fig. 5E, bottom), then a 6′6′-B twin boundary is created (see movie S2).

Note that a 6′6′-B twin boundary is formed only for the combination of AA′ and [NB]-AC stacking, as described in Fig. 6. hBN has two types of EK edges: a B-atom EK edge for [NB]-oriented hBN and an N-atom EK edge for [BN]-oriented hBN (Fig. 6, A and D). The B-atom EK edge sits on the N atoms below when the structure has [NB]-AC stacking (Fig. 6B, left), while it terminates at the hollow sites of the hexagonal lattice of the first layer when it has [NB]-AB stacking (Fig. 6C, left). If the B-atom EK edge of the second layer meets the second layer of AA′-stacked hBN, then [NB]-AC forms an atomically sharp 6′6′-B twin boundary (Fig. 6B). However, the [NB]-AB configuration makes 44-N, which cannot maintain its structure, thus expected to form a transition region at the stacking boundary (Fig. 6C). Likewise, an N-atom EK edge of [BN]-AB creates an atomically sharp 6′6′-N twin boundary, while that of [BN]-AC forms a 44-B configuration. As previously explained in Fig. 3 (B and C), transformation of 44-B to 558-N requires overall shift of all atoms of the half system as shown by red arrow in Fig. 3C by overcoming the van der Waals (vdW) force. In addition, it causes a change in the stacking order, which convinces a creation of transition region. Notably, all four pairs of stacking structures for the EK edges and the consequential 6′6′ or 44 twin boundaries coincide with the structures in fig. S4. Therefore, we conclude that atomically sharp stacking boundaries are formed only when AA′- and AB-stacked hBN meet with the certain combinations such as Fig. 6 (B and E) during crystal growth. We suggest that it may open the way to synthesis of one atomic-wide electronic channel by controlled manipulation of stacking structures.

Fig. 6. Two types of EK edges and the formation of different stacking boundaries depending upon the positions of atoms at the EK edges.

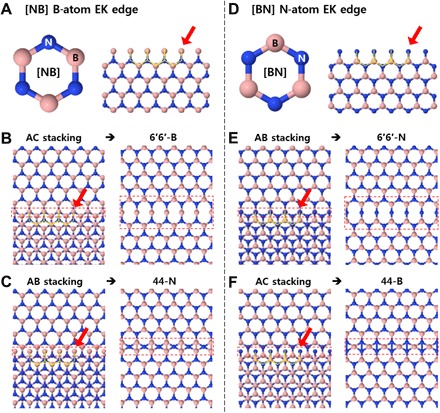
(A to C) B-atom EK edge of [NB]-AC creates an atomically sharp 6′6′-B twin boundary, while that of [NB]-AB forms a 44-N configuration. (D to F) N-atom EK edge of [BN]-AB creates an atomically sharp 6′6′-N twin boundary, while that of [BN]-AC forms a 44-B configuration. The atomic model to the left in each of (B), (C), (E), and (F) shows an hBN structure with an EK edge at the 1|2-layer boundary, while the panels to the right depict an AA′/AB stacking boundary configuration for the second layer, provided that it grows above the upper part of the first layer with the AA′ stacking structure and knits with the EK edge at the 1|2-layer boundary.

CONCLUSION

We observed the coexistence of AA′ and AB stacking structures in CVD-grown few-layer hBN islands using atomic-resolution TEM. We found atomically sharp twin boundaries with 6′6′ configurations along a zigzag direction at the AA′/AB stacking boundaries. The results of DFT calculations suggest 558 configuration for the twin boundary structure, but injection of additional electrons in the hBN nanoribbon explains the transformation of 558 to 6′6′ configuration. While 558-N has a reduced bandgap of 3.44 eV compared to ~5 eV of pristine hBN, 6′6′-N shows a conducting feature with zero bandgap. The reduced bandgap at stacking boundaries was also experimentally detected using EELS. Furthermore, we postulate that atomically sharp stacking boundaries are created from given stacking combinations of AA′/AB, which is inferred from the EK edges of hBN layer boundaries. This gives an insight for the fabrication of atomic-wide electronic channels. Ultimately, the twin boundary of AA′/AB-stacked hBN is promising as a 1D conducting channel embedded in the original insulating hBN sheet, i.e., single-hBN electronic device.

MATERIALS AND METHODS

Synthesis and transfer of hBN films

We used Cu foils (25 μm in thickness; product no. 13382, Alfa Aesar) as growth substrates for the hBN films. The Cu foil was first dipped into dilute nitric acid for a few seconds and then rinsed with deionized water. It was next loaded into a 1 inch quartz tube and placed within the heating zone of the furnace. The furnace was heated to 1050°C for 40 min and kept constant for 2 hours to anneal Cu and remove the surface oxide under a constant Ar/H₂ flow of 200:20 sccm. After annealing the sample, we placed 8 mg of an ammonia borane complex (97%; product no. 682098, Sigma-Aldrich) in a ceramic boat upstream from the quartz tube, outside the heating zone, and heated this compound at 85°C to begin hBN growth. The typical growth time needed to achieve a complete hBN film over the entire Cu substrate was 30 min. After the growth of the film was complete, the lid of the furnace was lifted to allow rapid cooling. The hBN was then transferred onto the TEM grid using the direct transfer method (31). That is, the hBN/Cu was directly transferred onto a quantifoil TEM grid without poly(methyl methacrylate) by sticking them by isopropyl alcohol, and then, Cu was etched out in sodium persulfate overnight. The hBN transferred onto the TEM grid was rinsed and dried under ambient conditions.

TEM analysis

All TEM work was performed using an aberration-corrected FEI Titan Cube TEM (FEI Titan³ G2 60-300). The microscope provides sub-angstrom resolution at 80 kV with a monochromator and −21 ± 0.5 μm of spherical aberration (C_s). The DF-TEM images were taken from Φ1 and Φ2 diffraction spots of the hexagonal lattice of hBN using an objective aperture of 1.28 nm⁻¹ for 10 s of acquisition time. The HR-TEM images were obtained in 0.2 s of exposure time at electron beam densities around 5 × 10⁵ e⁻ nm⁻². Individual atoms are imaged in white to get the actual atomic positions for direct interpretations of the atomic configurations, except for the image in fig. S10. The scanning transmission electron microscopy–EEL spectra were obtained in the same TEM system (FEI Titan³ G2 60-300) with Gatan Quantum 965 dual EELS system at 80 kV. The energy spread of a monochromated ZLP was 0.15 eV in full width at half maximum at 0.01 eV/ch energy dispersion. The convergence angle was 26.6 mrad. ZLPs were subtracted to 2 eV because of the tails, and plural scattering is removed using Fourier-log method using Gatan DigitalMicrograph software. To prevent misinterpretation of EELS signal in front of 5 eV, areas with small amount of hydrocarbon were carefully selected. The sample was heated up at 200°C for a few hours and vacuumed overnight in ultrahigh vacuum TEM system. In addition, EEL spectra were acquired for the minimal time of 0.00053 s per one position to minimize the deposition of hydrocarbon on the surface by intense electron beam, and overlap of the positions was avoided.

Image processing and simulations

Some TEM images presented in this study were processed to emphasize interesting features as described below. We applied false color for better visualization using a color look-up table (Fig. 2, B and C, and fig. S3) and performed band-pass filtering with 40- and 3-pixel filtering for large and small structures, respectively, to make the image contrast even. Contrast and brightness were adjusted using the ImageJ software. We used a Fourier filter built in Gatan DigitalMicrograph for Fig. 5 to confirm the edge configuration. We obtained an IFFT image (Fig. 2F and fig. S6) from the filtered FFT image after negatively masking all the hexagonal spots representing the hBN lattice in real space. The TEM image simulations were performed using MacTempasX under our experimental TEM imaging condition.

Computational methods

To explain the atomic and electronic structure of twin boundary of BN nanoribbons, we performed the DFT calculation within generalized gradient approximation (GGA) using the Vienna ab initio simulation package (VASP) (32, 33). The projector augmented wave potentials, as implemented in the VASP, were used to describe the potentials from atom centers. The energy cutoff for the plane-wave basis was set to 400 eV in GGA. Geometries were optimized until the Hellman-Feynman forces acting on the atoms became smaller than 0.01 eV/Å. To include weak vdW interactions among them, we adopt the Grimme’s DFT-D2 vdW correction based on a semiempirical GGA-type theory (34). For the Brillouin zone interaction, we used a (9 × 1 × 1) and (20 × 1 × 1) grid for atomic relaxation and band states calculation in Γ-centered special k-point scheme, respectively. The super cell of 558, 44, and 6′6′ configuration consists of 26 boron, 28 nitrogen, and 4 hydrogen atoms.

To simulate the AIMD simulations, we used the aforementioned VASP package with same potentials and cutoff. We calculated the AIMD simulation in the canonical ensemble, or NVT (constant number of particles, volume, and temperature) ensemble at the 400 K and the MD model structures consist with 1 × 2 × 1 supercell, 56 boron, and 60 nitrogen atoms, with the restricted movements at the one-side edge atoms to prevent the translation and rotation dynamics. We added two electrons per unit cell to assume the situation in the TEM operating system. For the AIMD simulations, the energy and force criteria were reduced to 1 × 10^–4 eV and 0.05 eV/Å, respectively. We used the Nose thermostat (35, 36) to control the temperature and rescale the velocity of atoms, and the time step was set to 3 fs.

SUPPLEMENTARY MATERIALS

Supplementary material for this article is available at http://advances.sciencemag.org/cgi/content/full/6/10/eaay4958/DC1

Section S1. The stacking structures of hBN

Section S2. Identification of the stacking structure and the number of layers of hBN using DF-TEM

Section S3. A transition region at AA′/AB stacking boundary

Section S4. Deduction of atomic configuration of AA′A/ABA stacking boundary

Section S5. Stability of exposed and sandwiched 6′6′ twin boundary

Section S6. Identification of [NB]-AC stacking for bilayer hBN from the 1|2-layer boundary

Fig. S1. Stacking structures of hBN.

Fig. S2. Transition region at AA′/AB stacking boundary.

Fig. S3. AA′A- and ABA-stacked trilayer hBN.

Fig. S4. Atomic structures of the four possible stacking boundaries.

Fig. S5. Intensity profiles across the AA′/AB stacking boundary.

Fig. S6. The energy barrier for 558 configuration changing to 6′6′ configuration and IFFT images showing oscillation of 6′6′ configurations.

Fig. S7. Atomically sharp stacking boundary at a trilayer and a bilayer hBN.

Fig. S8. Probability of finding stacking boundary with an abrupt change or with a transition region.

Fig. S9. Comparison of experimental HR-TEM image with simulated images of open- and closed-edge conformations at the 1|2-layer boundary of AB-stacked hBN.

Movie S1. Transformation of 558-N to 6′6′-N configuration.

Movie S2. Formation of atomically sharp twin boundary at EK edge.

References (37–40)