Spatial mapping of tissue properties in vivo reveals a 3D stiffness gradient in the mouse limb bud

Significance

Many biological processes are inherently physical in nature. Increasingly, biologists are proposing that the mechanical properties of tissues are critical for processes such as embryonic development and the progression of diseases including cancer and chronic inflammation. However, currently available methods are insufficient to quantitatively test hypotheses that concern the physical properties of living tissues. We introduce a method of three-dimensionally mapping the absolute stiffness and viscosity of tissue in a nontoxic fashion using a multipole magnetic device. By applying our method to the embryonic mouse limb bud, we show how a previously unrecognized distribution of physical properties leads to an important hypothesis, namely that cells move up a stiffness gradient to shape tissue during embryonic development.

Abstract

Numerous hypotheses invoke tissue stiffness as a key parameter that regulates morphogenesis and disease progression. However, current methods are insufficient to test hypotheses that concern physical properties deep in living tissues. Here we introduce, validate, and apply a magnetic device that generates a uniform magnetic field gradient within a space that is sufficient to accommodate an organ-stage mouse embryo under live conditions. The method allows rapid, nontoxic measurement of the three-dimensional (3D) spatial distribution of viscoelastic properties within mesenchyme and epithelia. Using the device, we identify an anteriorly biased mesodermal stiffness gradient along which cells move to shape the early limb bud. The stiffness gradient corresponds to a Wnt5a-dependent domain of fibronectin expression, raising the possibility that durotaxis underlies cell movements. Three-dimensional stiffness mapping enables the generation of hypotheses and potentially the rigorous testing of mechanisms of development and disease.

Morphogenesis results from the interrelated effects of tissue-scale properties and cellular processes such as neighbor exchange, migration, and proliferation. Among epithelia, tissue-scale anisotropic stress orients intercellular rearrangements among invertebrates and vertebrates (1–3). Far less is understood about mechanisms by which bulk mesenchymal tissues, such as the limb bud, are shaped.

Early limb development represents an accessible model of bulk tissue morphogenesis, and multiple biophysical mechanisms potentially underlie how the limb grows outward from the lateral plate and acquires its particular shape (4). During early budding of the limb, mesodermal cells move collectively into the limb field from the lateral plate in a Wnt5a-dependent manner (5–7). Based on the movement of mesodermal tissue toward WNT5A-soaked beads that were embedded in the chicken embryo, we previously postulated that Wnt5a might orient mesodermal cell movements by chemotaxis (5). However, it remains unclear whether chemotaxis can orient long-range cell movements in vivo. In vitro, it has long been recognized that cells migrate toward a relatively stiff region of substrate composed of extracellular matrix (ECM) components such as fibronectin, a phenomenon termed durotaxis or mechanotaxis (8–10). Interestingly, increased mesodermal cohesion (11) coincides with the movement of mesodermal cells into the bud, raising the possibility that tissue properties influence cellular behaviors. However, mechanisms that link these spatial scales have not been sufficiently explored in vivo, owing largely to the lack of appropriate tools to map tissue stiffness in three dimensions within bulk tissues.

Stiffness represents the extent to which an object resists deformation in response to an applied force. Elastic modulus, a measure of tissue stiffness, varies from a few hundred pascals in the brain to a few gigapascals in cortical bone and is determined by both ECM composition and cellular properties (12). Several techniques have been employed to measure forces and stresses in living tissues (13). Although mechanical properties can be derived from the stress–strain curves obtained by those methods, only a few methods have been employed to directly measure stiffness. Those include atomic force microscopy (AFM) indentation, which has been used most extensively to map the surface or epithelial mechanical properties of developing plant and animal tissues (1, 14–16). To measure deeper tissues such as mesoderm by AFM, the surface layers may be surgically removed, as has been done in Xenopus embryos (14, 15), although doing so may alter the properties of the underlying tissue. Optical tweezers and existing single-pole and multipole magnetic tweezer devices have been employed primarily to measure cellular (17–20) and intracellular (21, 22) mechanical properties in vitro. Optical tweezers typically have a low force output (e.g., tens of piconewtons) and the power dissipation of the laser can cause cell or tissue damage (23). As such, the only in vivo context in which optical tweezers were employed was to measure properties of the surface epithelial layer of Drosophila embryos (24).

Magnetic force has been employed to displace and to deform microinjected ferrofluid droplets to measure the viscoelastic properties of epithelial and mesenchymal tissues in Drosophila (25) and zebrafish embryos (26, 27), respectively. In each case, a single droplet was injected per embryo, thereby limiting the spatial resolution and generating two-dimensional (2D) data across multiple embryos. In the mesenchymal application, an array of permanent magnets was used to deform the ferrofluid droplet for several minutes to exert sufficient force to cause tissue deformation (26, 27). The slow dynamic response of ferrofluid droplets is advantageous if one wishes to measure the combined influence of material properties and of dissipative processes such as intercellular rearrangements upon viscoelastic properties. However, measurement of material tissue properties and their three-dimensional (3D) spatial distribution remains a challenge despite these advances.

Magnetic tweezers have been employed in unipolar and multipolar configurations in the drosophila embryo (28) and within the blastocyst cavity of the mouse embryo (29, 30), respectively, to measure the material properties of cells and tissues. However, existing magnetic tweezer devices have not been employed to map the spatial distribution of viscoelastic properties in living tissues due to their traditionally low and nonuniform force generation and limited workspace.

To overcome limitations of existing approaches, we developed a 3D magnetic device that generates a uniform magnetic field gradient within a workspace that is large enough to accommodate a mouse embryo up to embryonic day (E)10.5. The magnetic force generated by the device is sufficient to displace multiple magnetic beads simultaneously to quantify the spatial stiffness distribution in tens of loci inside a single embryo. By applying this device to the mouse embryonic limb bud, we identified a mesodermal stiffness gradient that matches the pattern of cell movements in 3D as observed by live light sheet microscopy. The expression domain of fibronectin within the early limb field mirrors the stiffness gradient that we measured and is mediated by Wnt5a. These data raise the possibility that durotaxis, rather than chemotaxis, guides the movement of mesodermal cells in the early mouse limb bud.

Results

Three-Dimensional Magnetic Device for In Vivo Tissue Stiffness Mapping.

Our device design objective was to generate a uniform magnetic field gradient within a large workspace for stiffness mapping in deep tissue. The magnetic force exerted on a bead within a uniform magnetic field gradient is independent of the distance between the bead and the poles, is identical upon all magnetic beads throughout the field, and does not change as beads move. Other design features of our device include a workspace large enough to accommodate an organ-stage mouse embryo and the capacity to generate no force perpendicular to the focal plane, thereby ensuring accurate measurement of bead displacements.

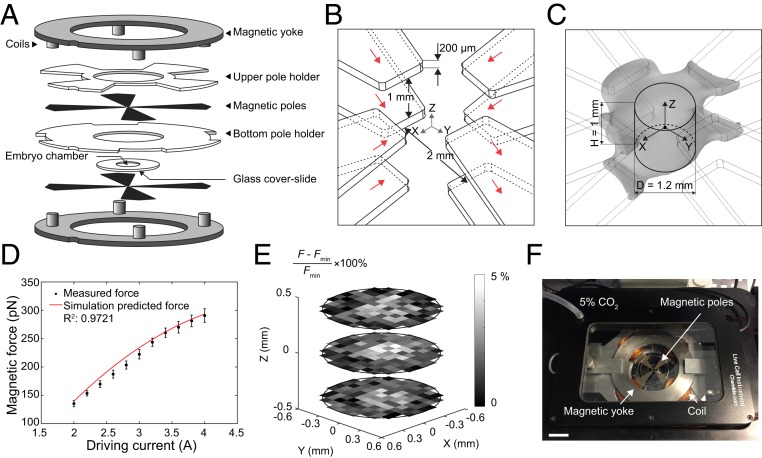
The system we created consists of eight magnetic poles with two magnetic yokes and eight coils (Fig. 1A). To achieve a uniform magnetic field gradient, the eight poles were arranged into two layers. By vertically aligning the two layers of the poles, a uniform magnetic field gradient can be generated between them (24, 25). The pole-to-pole separation in each layer and the vertical separation of the two layers were carefully chosen to achieve high magnetic field generation and a large workspace to accommodate an entire mouse embryo. The ratio between the vertical separation of the two layers and the pole-to-pole separation was determined by numerical simulation using COMSOL Multiphysics. Among the ratios evaluated (1:0.25, 1:0.5, 1:1, and 1:2), the ratio of 1:0.5 resulted in minimal loss of field strength and field deterioration. The final pole configuration is shown in Fig. 1B. The simulated magnetic field of the magnetic device under 2-A driving current is shown in SI Appendix, Fig. S1A. The simulation-predicted uniform magnetic field gradient space (Fig. 1C) can be approximated as a column with a diameter of 1.2 mm and a height of 1 mm, within which the nonuniformity of the magnetic field gradient is less than 3% (SI Appendix, Fig. S1B).

Fig. 1.

Three-dimensional magnetic tweezer system. (A) Structures of the device. (B) Configuration of magnetic poles. Red arrow indicates magnetic flux direction along each pole. (C) Gray space shows the uniform magnetic field gradient (3% error) predicted by simulation. The volume in which the magnetic field gradient is uniform is approximated as a column (diameter: 1.2 mm, height: 1 mm). (D) Magnetic force-driving current calibration result. Red line shows simulated force prediction. Error bars represent SD. (E) Calibrated force error in three different planes (0.4-mm interval) within the workspace. Each grid represents an 100- × 100-µm area. (F) Experimental setup of the magnetic device on a spinning-disk confocal stage with live imaging chamber. (Scale bar: 2 cm.)

We conducted experimental calibration by dispersing 2.8-μm magnetic beads in silicone oils with known viscosities and actuated the magnetic beads to move. The magnetic force was calculated by Stoke’s equation $F_{drag}=3\pi d\eta \upsilon$, where d is the diameter of the bead, $\eta$ is the dynamic viscosity of the silicone oil, and $\upsilon$ is the velocity of the beads. To ensure the magnetic force exerted on the bead was identical throughout the workspace, each magnetic bead was saturated, according to $F=M{V}_{bead}\nabla B$, where M is magnetization and is independent of magnetic field B when saturated, $V_{bead}$ is the volume of the bead, and $\nabla B$ is the magnetic field gradient. For the magnetic beads selected for use in this work (Dynabead M-280; Invitrogen), the magnetic field needed to saturate the beads must be larger than 0.1 T, which was generated by applying a driving current of at least 2 A as guided by magnetic field simulations (SI Appendix, Fig. S1A). The experimentally measured forces agreed well with the simulation-predicted values (Fig. 1D). The device is capable of exerting up to 300-pN forces on 2.8-μm magnetic beads with a force resolution of ∼10 pN. The difference of experimentally calibrated forces throughout the workspace was less than 5%, further confirming the uniformity of magnetic field gradient (Fig. 1E). We also measured heat generation of our device using a thermocouple probe. Under 10-s continuous actuation with 2-A and 4-A driving currents, the measured temperature change in the workspace center was less than 0.6 and 1.3 °C, respectively (SI Appendix, Fig. S1C). The experimentally measured thermal dose under 4-A actuation was 0.01 cumulative equivalent minutes at 43 °C, far below the threshold value of 1 min for potential thermal damage to tissue (26). The device was integrated with an incubation chamber and mounted on a spinning-disk confocal microscope (Fig. 1F).

For validation of our magnetic device, we performed AFM indentation and magnetic measurement of polyacrylamide (PA) gels that were prepared with three different elastic modulus values by varying the concentration of acrylamide and bis-acrylamide in deionized water that also contained a low concentration of magnetic beads (SI Appendix, Fig. S1D). AFM indentation tests, using a spherical tip with a diameter of 35 µm (SI Appendix, Fig. S1E), were performed at multiple locations that were sufficiently apart (>100 µm) on the gel samples in phosphate-buffered saline (PBS). The same gel samples were measured by our 3D magnetic device by actuating magnetic beads inside the gels. The deviation of the elastic modulus values for each gel from both AFM and magnetic measurements was small (SI Appendix, Fig. S1 F and G) due to the homogeneity of the gels. The average errors between the AFM indentation results and our magnetic device results were within 5% for all tested gel samples (SI Appendix, Fig. S1 H–J), indicating the magnetic device is capable of accurate mechanical measurement.

To enable manufacture of this magnetic device, detailed design files are available for download at https://github.com/MinZhuUOTSickKids/3D-tissue-stiffness-mapping (31) (also see SI Appendix, Fig. S2 A–F).

Spatial Distribution of Limb Bud Stiffness.

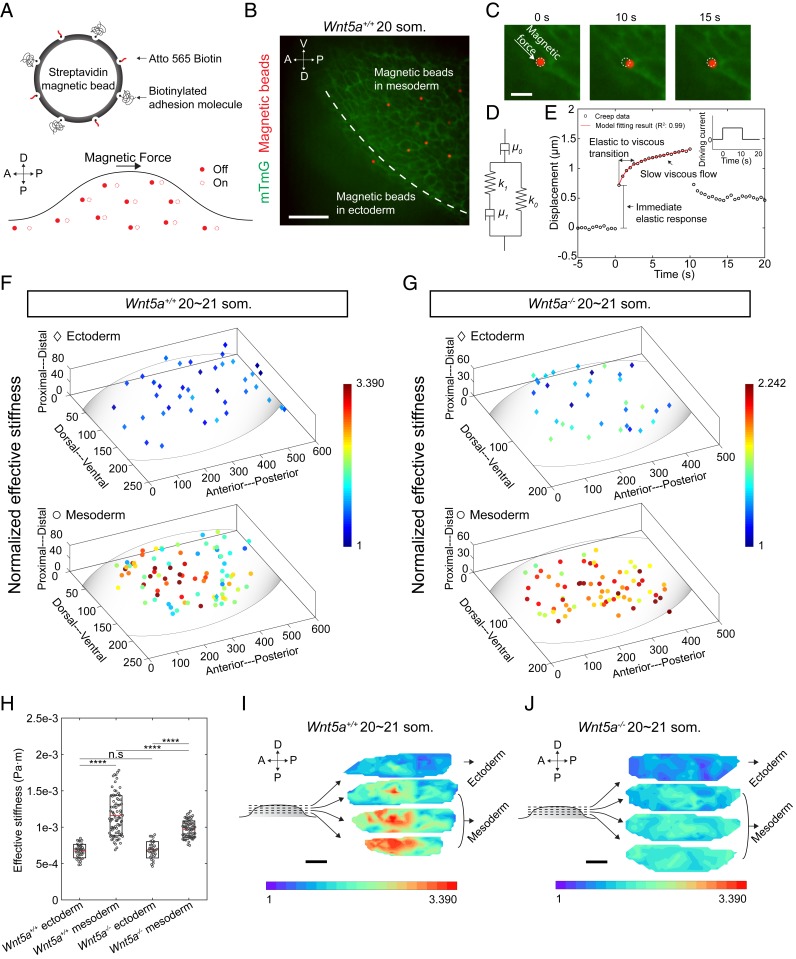
For visualization under confocal microscopy, the magnetic beads were fluorescently labeled via the streptavidin–biotin reaction. Cell membrane-adhesion molecules were coupled onto the fluorescent magnetic beads to ensure that the beads deform cell membranes instead of moving freely within tissue (Fig. 2A). Biotinylated fibronectin and biotinylated poly-l-lysine equally prevented unwanted movement of beads upon membranes, and poly-l-lysine was chosen for experiments. Poly-l-lysine supports the binding of magnetic beads with cell membranes by enhancing electrostatic interaction with no selectivity on specific proteins (27). The functionalized magnetic beads were microinjected into the limb bud region of mouse embryos that expressed a transgenic membrane marker mTmG (membrane-localized tdTomato, membrane EGFP [enhanced green fluorescent protein]) which was activated to label all cell membranes in the early embryo green using pCX-NLS:Cre (28). Beads in a maximum volume of 0.5 nL DMEM (Dulbecco’s modified Eagle’s medium) were deposited at different depths within the 20 to 21 somite stage (som., ∼E9.25) mouse limb bud using stepwise microinjection during withdrawal of a glass needle from mesoderm (SI Appendix, Fig. S3A). Throughout the stiffness mapping period (∼15 min), the functionalized magnetic beads stayed in their as-deposited locations without observable dispersion.

Fig. 2.

Three-dimensional tissue stiffness mapping using magnetic device. (A) Schematic describing magnetic bead functionalization and actuation during tissue stiffness mapping. (B) A representative image showing multiple magnetic beads within tissue. The beads were deposited by stepwise microinjection. (C) Higher-magnification views of bead displacement during one actuation cycle. (D) Sketch of the Zener model with a serial dashpot diagram characterized by viscous (μ₀ and μ₁) and elastic components (k₀ and k₁). (E) Representative bead displacement of one actuation cycle characterized by an immediate elastic response followed by a slow viscous flow. Red line shows the model fitting result. (Inset) The driving current during actuation. (F and G) Stiffness maps of 20∼21 som. stage WT (n = 5 embryos) and Wnt5a^−/− (n = 4 embryos) limb buds. (H) Absolute effective stiffness values of data shown in F and G (two-tailed t test, ****P < 0.0001) n.s, not significant. (I and J) Three-dimensional rendering of the stiffness maps in F and G. For comparison, normalization was performed against lower boundary ectodermal values which were similar in both conditions. (Scale bars: 50 µm in B, 10 µm in C, and 100 µm in I and J.)

Microinjection and magnetic actuation of multiple beads did not result in detectable tissue morphological change at confocal resolution, nor in apoptosis following actuation as assessed by immunostaining against caspase 3, an early marker of apoptosis (29) (SI Appendix, Fig. S3B). Immunostaining against phospho-histone H3 (pHH3) confirmed that microinjection and magnetic actuation of multiple beads did not cause a change in either ectodermal or mesodermal cell proliferation (SI Appendix, Fig. S3 C–E). The majority of the deposited beads (∼93%) successfully adhered to cell membranes (Fig. 2B), and only those beads sufficiently away (>20 µm) from others, such that interference with magnetic force or the strain field was not possible, were analyzed. Situations in which a bead did not adhere to a cell membrane and where multiple beads adhered to the membrane of the same cell (SI Appendix, Fig. S3 F–H) were excluded from stiffness analysis.

We examined the stiffness distribution within the 20 to 21 som. mouse limb bud by actuating the 2.8-μm magnetic beads inside the tissue for 10 s (Fig. 2C). Based on the reported speed of mouse limb bud cell migration (5), cell movement within 10 s is ∼40 nm, and cell rearrangements take place on substantially longer time scales (1). Therefore, the effect of morphogenetic movements can be neglected from these stiffness measurements. Stiffness mapping of one embryo took less than 15 min, during which no tissue morphological change was observed. The beads were controlled to deform cell membranes by up to ∼1.5 µm, and bead displacement was continuously measured in the direction of the applied force (Fig. 2C) with an image tracking resolution of 0.2 pixel (Materials and Methods).

We employed a viscoelastic Zener model with a serial dashpot (Fig. 2D, SI Appendix, Fig. S3 I and J, and Materials and Methods) to fit the bead displacements (R²: 0.99). Elastic and viscous components were extracted using this model. Upon actuation, the local tissue exhibited an immediate elastic response followed by a slow viscous flow (Fig. 2E). After the force was removed, the bead retracted partially because of the viscoelastic nature of the tissue. The creep response we captured reflected primary creep (indicated by the continued deformation shown in Fig. 2E). The relaxation time reflected the elastic and viscous transition time (a few seconds), which is in good agreement with previous tissue viscoelastic properties measurements (30, 32). Since there is an approximately one-somite (∼2 h of development) margin of error in staging mouse embryos, we excluded the stiffness differences between embryos by normalizing results to the maximum value for each embryo.

To test whether the 2.8-μm beads measure tissue-scale properties, we separately calibrated (as described above) and employed larger magnetic beads (SI Appendix, Fig. S3 K and L). To minimize tissue damage, only one 9.3-μm or 32-μm bead was injected per embryo, and the 3D coordinates of those beads were matched with those of 2.8-μm beads in other, stage-matched embryos to compare measurements. There was little difference between stiffness values using different sized beads (SI Appendix, Fig. S3M and Table S1), supporting the tissue-scale nature of measurements using the smaller beads. We therefore performed experiments using the smaller beads that allow for greater spatial resolution with minimal tissue damage.

Stiffness mapping revealed that mesoderm of the 20 to 21 som. wild-type (WT) limb bud exhibits an anteriorly and proximally biased region of high stiffness that diminishes away from that location. In comparison, the spatial distribution of mesodermal stiffness of 20 to 21 som. Wnt5a^−/− mutant embryos was relatively uniform. No stiffness gradient was observed in the ectoderm of WT or Wnt5a mutant embryos (Fig. 2 F–J and Movies S1–S3). WT mesoderm exhibited a broader range of absolute values and a higher mean effective stiffness compared to those of the Wnt5a mutant (Fig. 2H; note the color legends in Fig. 2 F and G are normalized within each genotype and do not reflect absolute differences between WT and mutant tissues. In Fig. 2 I and J, effective stiffness values were also normalized between genotypes to faciliate visual comparison). The absolute effective stiffness map for individual embryos is shown in SI Appendix, Fig. S4 A–E, and the spatial distribution of viscosity closely matched that of stiffness (SI Appendix, Fig. S5 A–C). Our observation that a stiffness gradient is dependent upon Wnt5a, a regulator of limb bud morphology (5, 33), raises the possibility that cell movements are influenced by tissue properties.

Mesodermal Cell Movement Pattern Corresponds to the Distribution of Tissue Stiffness.

We previously showed that mesodermal cells enter the early mouse limb field in an anteriorly biased fashion based on live, confocal imaging (5), suggesting that cell movements may correspond to the spatial distribution of mesodermal stiffness we measured here. Analysis of whole tissue avoids the potential for the edge effect of cell spreading in cultured tissue sections to influence cell movement patterns (34). We therefore performed live light sheet microscopy of intact CAG::H2B-GFP reporter embryos to follow the displacement of cell nuclei in 3D over time. Fluorescent beads were embedded together with the embryo into an agarose gel column that was suspended in media to compensate for positional drift over the course of 3-h imaging sessions similar to a method we employed to live image the mandibular arch (35) (Movie S4). Since the limb bud has not been imaged previously by light sheet microscopy, we examined the viability of limb bud cells by LysoTracker staining of embryos for 3 h. Embryos were either free in culture medium or were embedded in 1% low-melting agarose. We detected virtually no apoptosis in either case (SI Appendix, Fig. S6 A and B). We also quantified the number of metaphase-to-telophase transitions in the limb bud field during 3 h of live imaging and found there was no obvious change in the mitotic cell number over the 3-h period (SI Appendix, Fig. S6 C and D).

Cells were tracked using an autoregressive motion algorithm in Imaris, and drift compensation was performed in MATLAB based upon the positions of fluorescent beads embedded alongside the embryo in agarose. Since limb buds exhibit oriented cell division (5, 33), we eliminated potential bias due to the displacement of daughter cells by excluding cells undergoing mitosis from cell movement analysis.

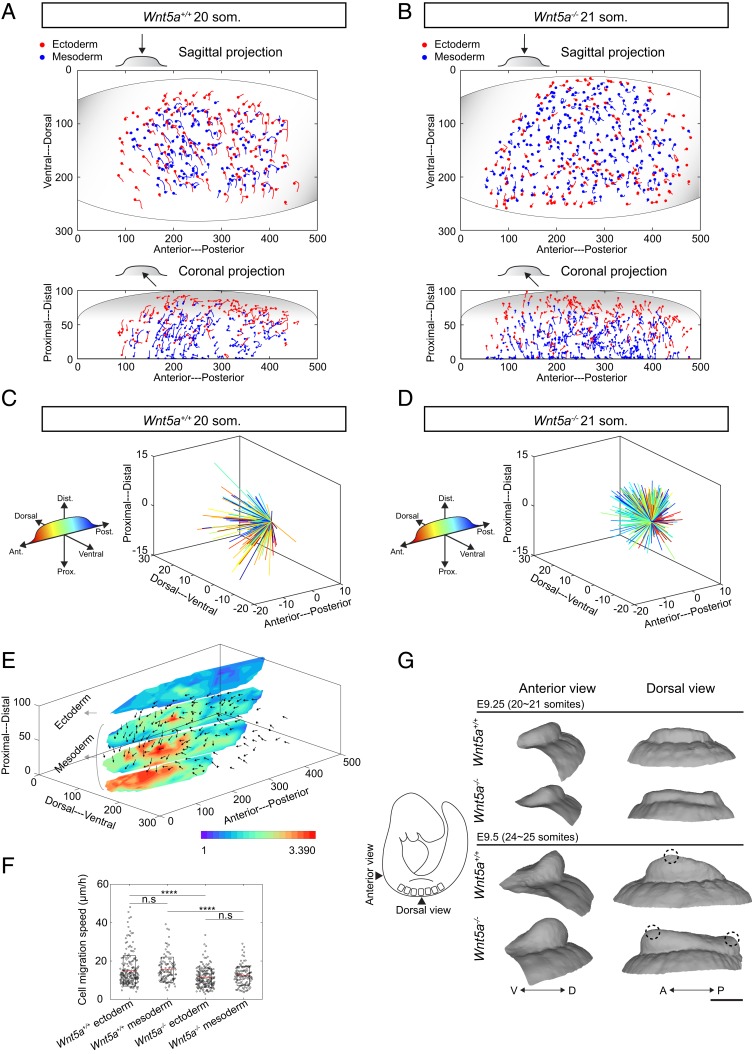
In the WT embryo, cells from lateral plate mesoderm moved into the early limb bud, and ectodermal cells moved toward the midline from dorsal and ventral sides, as expected based on previous confocal time-lapse imaging (1, 5). The 3D nature of the current cell-tracking method revealed a previously unrecognized vector of mesodermal and ectodermal cell movement toward an anterior and proximal region of the limb field (Fig. 3 A–C, SI Appendix, Fig. S6E, and Movies S4–S6). We also performed live imaging using a far-red CAG::H2B-miRFP703 reporter (36) to more clearly visualize the deep anteroproximal cell migration pattern (Movie S5). In the Wnt5a mutant, mesodermal and ectodermal cells lacked this convergent pattern of cell movement and were displaced in a relatively uniform, expansile pattern toward both the anterior and posterior poles of the limb field (Fig. 3 B–D, SI Appendix, Fig. S6F, and Movies S7 and S8). This pattern combined with lower cell migration speeds (Fig. 3F) suggests that mutant cell movements may reflect tissue growth rather than collective migration. Together, these findings show that coordinated cell movements correspond to a gradient of tissue stiffness (Fig. 3E).

Fig. 3.

Collective cell migration contributes to early limb bud shape change. (A and B) Three-dimensional cell movement trajectories (projected in sagittal and coronal planes) within 20∼21 som. stage WT and Wnt5a^−/− limb buds tracked by light sheet live imaging (unit: micrometers, duration: 2 h). Each dot denotes the last time point of tracking. (C and D) Three-dimensional dandelion plot of spatially color-coded trajectories of mesodermal cells at the start and end of 20∼21 som. stage WT and Wnt5a^−/− limb buds (unit: micrometers, duration: 2 h). WT mesodermal cells move anteroproximally while the Wnt5a^−/− mesodermal cell migration pattern has no directional bias. (E) The 20∼21 som. stage WT 3D cell movement pattern (unit: micrometers, duration: 2 h) overlaid with the tissue’s stiffness map. (F) Cell migration speeds within 20∼21 som. WT and Wnt5a^−/− limb buds (two-tailed t test, ****P < 0.0001, n = 3 embryos for each condition). n.s, not significant. (G) Limb bud shape change from 20 to 25 som. stage reconstructed from optical projection tomography. Dashed circles indicate the location of distally based peaks of the limb buds. (Scale bar: 200 µm.)

The correlation above could be explained by the movement of cells toward a relatively stiff region or by tissue stiffening in response to the biased accumulation of cells. Our live, membrane-labeled images of the limb field in this study (Fig. 2 B and C and SI Appendix, Fig. S3G) and in previous studies (1, 37) show that cells are confluent at the resolution afforded by light microscopy. Therefore, cell packing density (i.e., number of cells per unit volume) can be changed if cell volume is reduced. We quantified the cell packing density of 20 to 21 som. WT limb buds using CAG::H2B-GFP reporter. Cell packing density in the relatively stiff region of the limb bud was similar to the relatively soft region (P > 0.2 for pairwise comparisons) (SI Appendix, Fig. S6 G and H), indicating that cell packing does not account for increased anteroproximal stiffness.

To investigate whether tissue is shaped by the morphogenetic cell movements we observed, we performed optical projection tomography. The WT limb bud acquired an anteriorly biased prominence between 20/21 and 24/25 som. stages (∼E9.25 to E9.5). In contrast, the Wnt5a mutant limb bud developed a shallow saddle shape with anterior and posterior prominences (Fig. 3G). Our previous work suggested that a saddle-shaped early limb bud is partly attributable to a lack of dorsal and ventral ectodermal convergence (1), which helps to explain why the early Wnt5a mutant bud is not simply bulbous. Of note, immunostaining against pHH3 and LysoTracker staining suggested that these limb bud shape changes were independent of cell proliferation and apoptosis (SI Appendix, Fig. S6 I–O). Therefore, in both the WT and mutant cases, tissue shape corresponded to the observed pattern of cell movements.

Fibronectin Distribution in the Limb Bud Corresponds to the Stiffness Gradient.

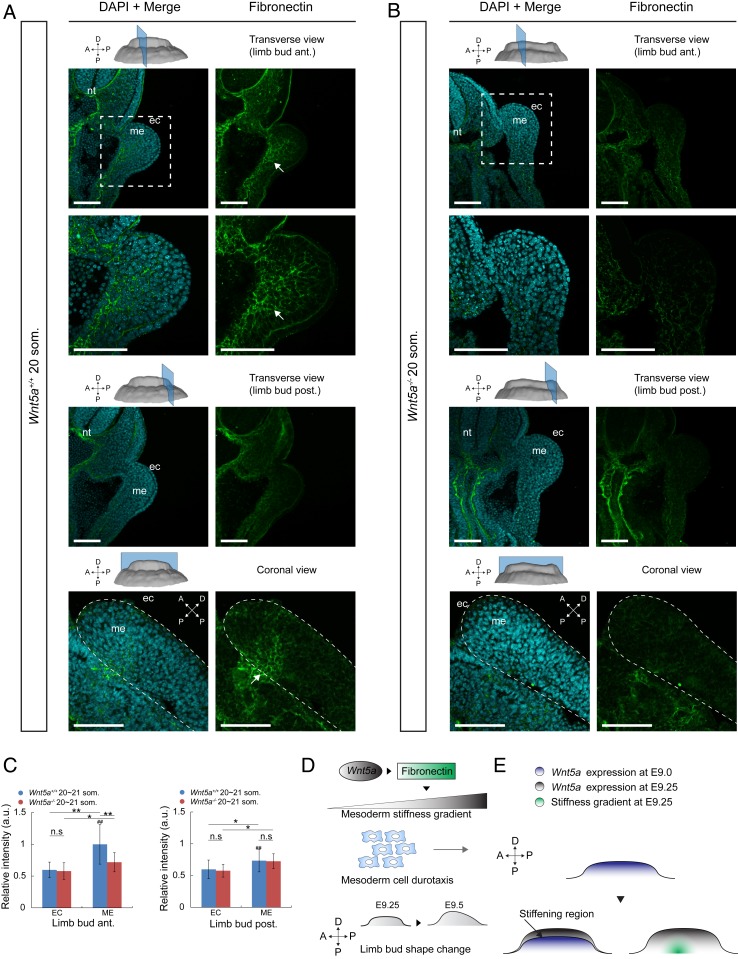
Wnt5a has been implicated as a directional cue and chemoattractant in the limb bud and other contexts (5, 33, 38). Unexpectedly, the vectors of WT cell movements that we observed were not oriented toward the peripherally biased domain of Wnt5a expression (39, 40) (SI Appendix, Fig. S6P) but rather along a stiffness gradient deeper within tissue. Since the stiffness gradient is dependent upon Wnt5a, downstream factors may play a role in establishing that gradient. Recent in vitro work demonstrated that movement of cells along a stiffness gradient depends upon the composition of ECM: Cells migrate toward fibronectin-coated, but not laminin-coated, substrate (10). We examined the spatial distributions of fibronectin and laminin, of cytoskeletal proteins F-actin and vimentin, and of cell–cell adhesion and junctional proteins β-catenin and N-cadherin. Among these candidates, only the expression domain of fibronectin was spatially biased and dependent upon Wnt5a (Fig. 4 A–C and SI Appendix, Fig. S7 A–M). Immunostaining intensity of fibronectin was strongest in the anteroproximal region that we identified as the stiffest in the 20/21 som. WT limb bud. Away from that region, fibronectin intensity was attenuated and very weak in the ectoderm and lateral plate. In the absence of Wnt5a mesodermal fibronectin was lacking (Fig. 4 A–C), consistent with findings in the lung where fibronectin is a major target of Wnt5a signaling (41). To examine the progression of fibronectin expression, we performed immunostaining on later E9.5 embryos. Among E9.5 WT limb buds, the anterior fibronectin-rich domain was more central along the proximodistal axis than in E9.25 embryos, and Wnt5a mutant limb buds still lacked mesodermal fibronectin (SI Appendix, Fig. S8). These results suggest fibronectin establishes a stiffness gradient in a direct or indirect Wnt5a-dependent fashion that corresponds to cell movements (Fig. 4D). The spatial discrepancy between the fibronectin domain and the progressively distal Wnt5a domain may be attributable to the time it takes for fibronectin to be synthesized and secreted (Fig. 4E), and anterior bias of the initial fibronectin domain may be due to the early anterior-lateral bias of mesodermal Wnt5a expression (39, 40).

Fig. 4.

Fibronectin expression domain spatially mirrors the stiffness gradient within the limb bud. (A and B) Transverse and coronal sections of 20 som. WT (A) and Wnt5a^−/− (B) embryos at forelimb anterior and posterior regions. Sections were stained with DAPI (cyan) and antifibronectin antibody (green). Arrows indicate the anteriorly biased region of early fibronectin expression. nt: neural tube; me: mesoderm; ec: ectoderm. (Scale bars: 100 µm.) (C) Relative fibronectin fluorescence intensity of 20 to 21 som. WT (n = 3) and Wnt5a^−/− (n = 3) embryos (two-tailed t test, *P < 0.05, **P < 0.01). n.s, not significant. (D) Schematic model representing Wnt5a up-regulation of fibronectin to generate a stiffness gradient which guides mesodermal cell movements and drives limb bud shape change. (E) Graphical description of the potential mechanism by which the stiffness gradient is localized. Error bars indicate SEM.

Stiffness Gradient Is Formed between E9.0 and E9.25.

To further examine the putative relationship between fibronectin expression and establishment of a stiffness gradient, we conducted stiffness mapping of 17/18 som. (∼E9.0) embryos when the limb bud first emerges from the lateral plate. At that stage, no stiffness gradient was observed in either WT or Wnt5a mutant limb fields (SI Appendix, Fig. S9 A–D and Movies S9 and S10), and average mesodermal stiffness was lower compared to that of 20/21 som. embryos, particularly in the WT background. Average ectodermal stiffness was not significantly different in either genetic background (SI Appendix, Fig. S9E). Corresponding with mesodermal stiffness measurements, fibronectin intensity was spatially uniform and significantly lower than in the 20/21 som. WT embryo (SI Appendix, Fig. S9 F and G), and collective cell migration was largely absent (SI Appendix, Fig. S9 H–J and Movies S11–S14). These findings suggest that tissue stiffness increases following epithelial to mesenchymal transition of coelomic epithelial cells that precipitates limb bud initiation (6). Overall, comparison of data between 17/18 and 20/21 som. stages confirms strong correlation between fibronectin expression, tissue stiffness, collective cell movements, and tissue shape.

Discussion

The resurgence of physical approaches to morphogenesis (42) has been fueled by progressively sophisticated empirical evaluations of mechanical hypotheses. Numerous contemporary proposals in the field invoke feedback between active cell behaviors and tissue-scale properties that underlie tissue shape and organization (2–4, 14, 30, 43, 44). Most of these proposals concern 2D flat or curved tissues for which currently available tools such as microscopic evaluation of cell shape and cytoskeletal organization, micropipette aspiration, AFM, laser ablation, and ferrofluid droplets have been shown to be sufficient to generate relative or absolute measurements of elastic modulus, viscosity, cortical tension, or stress. However, these tools are not sufficient to assess absolute material properties and their spatial variations within bulk 3D tissues. Emerging concepts concerning morphogenetic phenomena, such as the influence of tissue stiffness upon the collective migration of neural crest cells (14), that a stiffness gradient guides axonal growth (15), and that a viscoelastic gradient contributes to tail bud elongation in zebrafish (22), have been evaluated using methods that are arguably suboptimal for measuring bulk tissue properties. These include AFM indentation after the removal of surface tissue layer (14, 15) that potentially alters underlying tissue properties and the ferrofluid approach, which requires prolonged periods to assess droplet deformation and delivers limited spatial resolution (22). The magnetic device we introduce fills an important void for measurement by generating a uniform magnetic field gradient within a volume sufficient to accommodate an embryo. It is capable of rapidly measuring material properties that are not influenced by morphogenetic cell behaviors such as cell shape changes and rearrangements. Devices similar to the one we introduce may have increasing utility as studies of bulk tissues become more common.

Our application of the magnetic device-generated correlations between a stiffness gradient and mesodermal cell migration pattern that can be explained in one of two ways: Either morphogenetic cell movements are guided by tissue stiffness gradient (i.e., durotaxis) or biased cell movements themselves stiffen tissue. Since our data show that cell density is not different in the stiffer region, the latter scenario is less likely to explain our observations. Surface ectodermal cell movements mirror those of deeper cells, suggesting they are either mechanically linked with mesodermal cells or respond to the same cues. With regard to the possibility that durotaxis guides cell movements, it will be important to precisely manipulate tissue stiffness. It is not clear how cells sense a stiffness gradient in vivo and potentially titrate active forces to coordinate cell movements. In vitro, cells can discern stiffness between 1 Pa/µm (45) and 400 Pa/µm (46). The stiffness gradient we measured is ∼0.5 Pa/µm and may reflect finer stiffness sensing ability of cell neighborhoods in vivo. In principle, durotaxis would require the differential binding and unbinding of integrins to specific ECM proteins such as fibronectin. Integrins would engage focal adhesion proteins, such as talin and vinculin, that bind to actomyosin to achieve directional migration toward a stiffer region (47, 48). This process can be mediated by signaling pathways such as noncanonical Wnt5a signaling by activating a RhoA-ROCK cascade (49). Alternatively, cellular forces may also be derived from the differential opening of mechanosensitive ion channels. For example, it has been shown that PIEZO1 can be activated in a stiff environment and inactivated under soft conditions (15, 50). Experiments to test whether different mechanosensing mechanisms are independent or work cooperatively will be useful.

It has been shown that both canonical (41, 51) and noncanonical (52, 53) Wnts can drive fibronectin expression and assembly. In the early limb bud, the Wnt5a and fibronectin expression domains are spatially exclusive. However, the Wnt5a domain dynamically becomes biased distally over time, and the initial fibronectin domain seems to be within an earlier Wnt5a domain. Therefore, one possibility is that WNT5A signaling directly induces fibronectin expression and assembly with a delay. An alternative possibility is that downstream factors or coregulators of Wnt5a indirectly regulate fibronectin (52, 53). Wnt5a may also work cooperatively with canonical Wnts (41, 51) to generate the fibronectin expression domain. Identifying and manipulating regulators of fibronectin will be important for evaluating its role in guiding cell movements.

Our technique is readily applicable to other animal models such as zebrafish and Xenopus laevis. Beyond developmental biology, the method will also help us to understand the role of stiffness in various diseases processes such as the relationship between tumor stiffness heterogeneity and metastasis and how increased stiffness is associated with organ dysfunction. In addition to the evaluation of tissue-scale properties, modification of the methodology we have employed will be applicable to unraveling cellular processes such as mechanotransduction. Combining precise physical property measurements with computational simulations of various biological processes will help to generate and test biologically fundamental hypotheses and accelerate discovery.

Materials and Methods

Mouse Strains.

Analysis was performed using the following mouse strains: CAG::H2B-GFP (54) [The Jackson Laboratory: B6.CgTg(HIST1H2BB/EGFP1Pa/J)], mTmG (55) [The Jackson Laboratory: Gt(ROSA)26Sortm4(ACTB-tdTomato-EGFP)Luo/J)], pCX-NLS:Cre (28) [The Jackson Laboratory: NMRI.Cg-Tg(CAG-cre)1Nagy/Cnbc)], Wnt5a^+/− (40), and CAG::H2B-miRFP703 (36). All strains were outbred to CD1, and all animal experiments were performed in accordance with protocols approved by the Animal Care Committee of the Hospital for Sick Children Research Institute.

Magnetic Device.

The uniform magnetic field gradient was generated by an octuple-pole magnetic device. In order to generate a large magnetic field gradient, the magnetic poles were made of silicon iron (MµShield), which has high permeability at high induction and high saturation. Each pole piece was fabricated from a silicon iron sheet 200 µm thick by electrical discharge machining. The magnetic yoke and the stage were machined by computer numerical control from low-carbon steel 1018 and aluminum, respectively. Each core was wound 100 times with US wire gauge 24 copper wire. Holders for the magnetic poles and customized imaging chamber were cut from an acrylic sheet 1 mm thick by laser machining. The SolidWorks design files of stage, yoke, magnetic poles, acrylic holders, and imaging chamber are available for download at https://github.com/MinZhuUOTSickKids/3D-tissue-stiffness-mapping. Magnetic poles were aligned under the microscope using a calibration slide (MR400; AmScope). The magnetic device is powered using a laboratory bench direct-current power supply (9123A; BK Precision). The eight coils were series-connected with four standard double-pole double-throw switches to control current direction. The magnetic device was mounted on a Quorum Wave FX-X1 spinning-disk confocal system (Quorum Technologies Inc.) that supports a live imaging chamber.

Magnetic Field Simulation.

Magnetic field simulation of the device was performed in COMSOL Mutiphysics 5.3 (COMSOL Inc.). The HB (magnetization) curves of silicon iron and low-carbon steel 1018 were imported into the software and assigned to pole and yoke, respectively. A sweep function (from 2 A to 4 A with 0.2-A step size) was incorporated in the simulation to derive the magnetic field under different driving currents. Partial differential equations were applied to calculate the spatial derivative of the magnetic field (i.e., magnetic field gradient). Within the workspace, simulation predicted that the nonuniformity of the magnetic field gradient was less than 3%.

Magnetic Force Calibration.

To calibrate the magnetic force generated by our magnetic device, magnetic beads (Dynabead M-280; Invitrogen) were dispersed in silicone oil (Sigma-Aldrich) of known viscosity. In detail, 5 µL of beads and 1 mL of silicone oil were placed in an Eppendorf tube. To avoid bead aggregation, ultrasound (model 60; Fisher Scientific) was used to fully mix the solution. The bead–silicone oil solution was placed in the imaging chamber. After a few minutes when all flows in the solution were settled, the device was activated and the bead movements were recorded (12 frames per second). Bead velocities were calculated in ImageJ using the Particle Detector & Tracker plug-in. Force exerted on the beads was calculated using the Stokes drag equation $F=3\pi d\eta \upsilon$.

Subpixel Tracking.

To capture bead displacement with a subpixel resolution, the centroid of the bead was determined first by applying a subpixel edge detector (56) on the grayscale image. Based on the detected edge, the bead centroid was defined. This detector (56) was chosen because of its higher accuracy and robustness in overcoming image noise compared to other detectors such as moment-based (57), least square error-based (58), and interpolation-based detectors (59). Briefly, the intensity F_i,j of a pixel (x,y) on the edge is

$$F_{i,j}=\frac{A{S}_A+B{S}_B}{S_A+S_B},$$

where A and B are the intensities at the two sides of the edge and S_A and S_B are the areas of that pixel covered by intensities A and B, respectively. The edge is approximated by a second-order curve y = a + bx + cx (2). The subpixel position of the edge is obtained from the coefficients a, b, and c, which are solved by considering the intensities of neighboring pixels. The algorithm achieved an accuracy of 0.2 pixel (pixel size: 0.23 µm) as benchmarked to synthetic test images with artificially generated circles. This technique was used to accurately track the displacement of the beads.

PA Gel Verification Experiment.

PA gels with different elastic moduli were fabricated. Briefly, PA gel solutions were prepared by varying the concentration of acrylamide (3 to 5%; Bio-Rad) and bis-acrylamide (0.01 to 0.03%; Bio-Rad) in deionized water. Polymerization was initiated with 0.05% ammonium persulfate (Sigma) and 0.1% N,N,N′,N′-Tetramethylethylenediamine (TEMED; Sigma). Five microliters of magnetic beads in deionized water (1:100) were added to 150 μL PA gel solution. Fifty microliters of final solution were added to each imaging chamber submerged in PBS. The elastic modulus of the PA gel was examined by AFM (BioScope Catalyst; Bruker) mounted on an inverted microscope (Nikon Eclipse-Ti) and by our magnetic device. AFM indentation tests were performed on locations that were sufficiently apart (>100 µm) using a spherical tip (diameter: 35 µm) (SI Appendix, Fig. S1E). Spherical tips were made by assembling a borosilicate glass microsphere onto a tipless AFM cantilever using epoxy glue. The cantilever spring constant was calibrated each time before experimentation by measuring the power spectral density of thermal noise fluctuation of the cantilever under no load. To determine the elastic modulus of the PA gel, a trigger force of 5 nN (SI Appendix, Fig. S1F) was consistently applied, resulting in an indentation depth less than 2 µm. Since the PA gel thickness was ∼1 mm, the substrate effect can be neglected according to the empirical 10% rule. The Hertz model for the spherical tip was used to calculate elastic modulus from the experimental indentation data. The elastic moduli of PA gels were further examined using our 3D magnetic device by actuating magnetic beads (SI Appendix, Fig. S1G).

The bead displacement (in the direction of the magnetic force) was tracked with subpixel resolution. In order to extract the elastic modulus of PA gels from the experimental data in SI Appendix, Fig. S1G, the conversion factor, C_e, needs to be obtained:

$$E=C_e\frac{x}{F},$$

where C_e is defined as the elastic modulus conversion factor, x is the displacement in the linear elastic response, and the F is the applied force. C_e is a function of bead diameter d (which describes the contact dimension during the actuation), Poisson’s ratio v (which describes the compressibility of the material), and bead displacement x (which describes the extent of the material being compressed):

$$C_e=f\left(d,\nu ,x\right).$$

To accurately obtain C_e, we performed finite-element simulation, as shown in SI Appendix, Fig. S1H. In simulation, the bead diameter was set to be 2.8 µm, the same as the bead diameter used in our PA gel experiments. The Poisson’s ratio of PA gel was set as 0.45 (60). The bead displacement was varied in simulation from 0.01 to 1.2 µm to cover our experimental bead displacement range. We performed the simulation on PA gels of three different elastic modulus values, as conducted in experiments (109.15 Pa, 471.97 Pa, and 906.95 Pa). Simulation with these three different moduli resulted in largely identical conversion factor C_e values (SI Appendix, Fig. S1I). C_e varies with displacement and theoretically should not vary with different elastic modulus values, as confirmed by the results shown in SI Appendix, Fig. S1I.

Magnetic Bead Functionalization and Microinjection.

The streptavidin-coated Dynabead M-280 (diameter: 2.8 µm), Spherotech SVM-80-5 (diameter: 9.3 µm), and SVMH-400-4 (diameter: 32 µm) superparamagnetic beads were coupled with Atto565 biotin (Sigma-Aldrich) and biotinylated adhesion molecules through the streptavidin–biotin reaction. We placed 5 μL streptavidin-coated magnetic bead solution into an Eppendorf tube. The bead solution was washed three times with PBS to remove preservatives. A permanent magnet was placed under the tube to collect the magnetic beads (i.e., magnetic separation). The beads were then collected by a micropipette and resuspended in 90 μL of Milli-Q. Atto565 biotin (1 mg) was diluted in 200 μL of ethanol. Five microliters of this dilution and 5 μL of the biotinylated adhesion molecule solution (1:1,000 in PBS) were mixed with 90 μL of the magnetic bead suspension for 30 min. Finally, the solution was washed with PBS five times to remove the biotin surplus through magnetic separation, and the supernatant was collected using a micropipette.

For microinjection of 2.8-µm beads, 5 μL of functionalized magnetic bead solution was suspended in 100 μL DMEM. The solution was then loaded into a microneedle pulled from a glass capillary tube using a micropipette laser puller. A microinjector (CellTram 4r Oil; Eppendorf) was used to inject magnetic beads into the limb bud at anterior, middle, and posterior regions. Multiple depositions were made during one penetration and withdrawal of the needle to distribute the magnetic beads at different depths within the limb bud. For 9.3-µm and 32-µm bead sizes, individual beads were aspirated into the microneedle and only one bead per embryo was injected to minimize tissue damage.

Stiffness Mapping In Vivo.

The embryo with magnetic beads injected was placed into the customized imaging chamber and immobilized by DMEM without phenol red containing 12.5% rat serum and 1% low-melt agarose (Invitrogen). The temperature of the imaging chamber was maintained at 37 °C with 5% CO₂. Prior to stiffness mapping, a Z scan was taken to record the bead locations within the limb bud. Magnetic beads were then actuated by the magnetic device and bead displacements were recorded by spinning-disk confocal microscopy at the highest frame rate. The bead displacement (in the direction of the magnetic force) was tracked with subpixel resolution and fitted using a viscoelastic model in MATLAB to extract the elastic and viscous components.

As shown in Fig. 2E, the experimental data reveal an immediate elastic response followed by a slow viscous flow. Among existing viscoelastic models (SI Appendix, Fig. S3I), the Zener model (also known as standard linear solid) with a serial dashpot (22, 61) properly describes both the elastic and slow viscous behaviors revealed in our experimental data. Other models, including the power law model (44), modified generalized Maxwell fluid model (32), and Kelvin–Voigt model with a serial dashpot (62), do not capture the elastic response. The generalized Maxwell solid model (30) and the Zener model without a serial dashpot demonstrate a plateau during displacement in the viscous stage, which does not properly represent our experimental situation.

The extraction of the viscoelastic parameters from the experimental data is illustrated in SI Appendix, Fig. S3J. In brief, The displacement/force–time relationship of the Zener model with a serial dashpot is (22, 61)

$$\frac{x\left(t\right)}{F}=\frac{1}{k_0}\left(1-\frac{k_1}{k_0+k_1}{e}^{-\frac{t}{\tau }}\right)+\frac{t}{{\mu }_0}$$

$$\tau =\frac{{\mu }_1\left(k_0+k_1\right)}{k_0{k}_1},$$

where x(t) is the displacement of the bead at time t, F is the applied force, k₀ and k₁ are the two elastic constants, μ₀ is the effective viscosity, and τ is the relaxation time. The effective stiffness k (unit: pascals·meter), $k=k_0+k_1$, can be calculated from the immediate elastic response [segment (1) in SI Appendix, Fig. S3J] as follows:

$$k=\frac{1}{height\hspace{0.17em}of\hspace{0.17em}the\hspace{0.17em}elastic\hspace{0.17em}response}.$$

The effective viscosity μ₀ can be extracted by fitting the slope of the slow viscous flow [segment (3) in SI Appendix, Fig. S3J] as

$${\mu }_0=\frac{1}{\tan \alpha }.$$

Additionally, relaxation time τ can be extracted by curve fitting of segment (2) in SI Appendix, Fig. S3J (i.e., elastic to viscous transition).

The stiffness map was a set of points in 3D, each mapped to their corresponding normalized effective stiffness. Using a standard Delaunay triangulation technique, a set of tetrahedrons was obtained with these points positioned at the vertices. The value of the effective stiffness was approximated inside each tetrahedron by calculating the barycentric coordinates. The result was a continuous field for normalized effective stiffness. Section cuts were made perpendicular to the proximal-distal axis at 80%, 60%, 40%, and 20% of the total length as depicted in Fig. 2 H and I and SI Appendix, Fig. S9 C and D.

Live, Time-Lapse Light Sheet Microscopy.

Three-dimensional time-lapse microscopy was performed on a Zeiss Lightsheet Z.1 microscope. Embryos were suspended in a solution of DMEM without phenol red containing 12.5% filtered rat serum, 1% low-melt agarose (Invitrogen), and 2% fluorescent beads (1:500, diameter: 500 nm ; Sigma-Aldrich) that were used for drift-compensation in a glass capillary tube. Once the agarose solidified, the capillary was submerged into an imaging chamber containing DMEM without phenol red, and the agarose plug was partially extruded from the glass capillary tube until the portion containing the embryo was completely outside of the capillary. The temperature of the imaging chamber was maintained at 37 °C with 5% CO₂. Images were acquired using a 20×/0.7 objective with dual-side illumination, and a z-interval of 0.5 µm. Images were acquired for 2 to 3 h with 10-min intervals.

In Vivo Drift-Compensated Cell Tracking.

The light sheet time-lapse image was first rendered in Imaris (Bitplane). The positions of cell nuclei were tracked over time using an autoregressive motion algorithm. Ectodermal and mesodermal cells were separated based on mean thresholding of fluorescence intensity. Cells undergoing division (based on the morphology of the cell nuclei) were excluded from cell migration tracking. The tracking data were then imported into R2017b MATLAB (MathWorks) for drift compensation using a customized program.

Optical Projection Tomography.

Mouse embryos were harvested and fixed in 4% paraformaldehyde overnight at 4 °C. Optical projection tomography was performed using a system that was custom-built and is fully described elsewhere (63). Three-dimensional datasets were reconstructed from autofluorescence projection images acquired during a 25-min scan period at an isotropic voxel size of 4.5 µm. The limb bud structure was segmented from the embryo and rendered in MeshLab.

Immunofluorescence.

Dissected mouse embryos were fixed overnight in 4% paraformaldehyde in PBS followed by three washes in PBS. Fixed embryos were embedded in 7.5% gelatin/15% sucrose and sectioned into 10-µm slices using a Leica CM1800 cryostat. Sections were washed twice for 5 min in Milli-Q and once for 5 min in PBS, permeabilized in 0.1% Triton X-100 in PBS for 20 min, and blocked in 5% normal donkey serum (in 0.05% Triton X-100 in PBS) for 1 h. Sections were incubated in primary antibody overnight at 4 °C followed by four 10-min washes in 0.05% Triton X-100 in PBS, then incubated in secondary antibody (1:1,000) for 1 h at room temperature. Finally, sections were washed three times for 5 min in 0.05% Triton X-100 in PBS and twice for 5 min in PBS. Images were acquired using a Nikon A1R Si Point Scanning Confocal microscope at 10×, 20×, or 40× magnification, and analysis was performed using ImageJ.

Cell Apoptosis Detection.

Lyso Tracker Red DND-99 (Thermo Fisher) was diluted to 2 µM in DMEM containing 50% rat serum. Embryos were placed in the medium and incubated in a roller culture apparatus for 1 h. The temperature was maintained at 37 °C with 5% CO₂. Embryos were washed three times with PBS after staining to remove Lyso Tracker surplus then fixed overnight in 4% paraformaldehyde in PBS followed by three washes in PBS. Images were acquired using a Nikon A1R Si Point Scanning Confocal microscope at 20× magnification, and analysis was performed using ImageJ.

Antibodies.

Primary antibodies included laminin (1:100; Sigma), fibronectin (1:100; Abcam), vimentin (1:500; Sigma), N-cadherin (1:250; BD Bioscience), β-catenin (1:1,000; BD Bioscience), pHH3 (1:250; Cell Signaling), caspase 3 (1:200; Cell Signaling), and rhodamine phalloidin (1:1,000; Invitrogen). All secondary antibodies were purchased from Jackson Immunoresearch and used at 1:1,000 dilutions.

Software and Code.

Data collection.

Volocity was used to collect spinning-disk confocal images. Zeiss Zen was used to collect light sheet confocal images. NIS-Elements was used to collect laser scanning confocal images.

Data analysis.

ImageJ 1.51k was used to process spinning-disk and laser scanning confocal images. Imaris 9.0 (Bitplane) was used to process light sheet confocal images. COMSOL Mutiphysics 5.3 (COMSOL Inc.) was used to perform magnetic field simulation. Custom MATLAB R2017b (MathWorks) code was used to track displacement and perform curve fitting on magnetic bead actuation and AFM indentation data. Custom Python 3.7.0 code was used to render the 3D stiffness map. Custom MATLAB R2017b (MathWorks) code was used to perform drift compensation for four-dimensional cell tracking. MeshLab 2016 was used to process optical projection tomography data. Adobe Illustrator cc was used to create figures.

Data Availability.

The data that support the findings of this study are included in the paper and SI Appendix. Further queries are welcomed by the authors.

Code Availability.

All custom codes used in this paper are available at https://github.com/MinZhuUOTSickKids/3D-tissue-stiffness-mapping.