Abstract
Dynamic functional connectivity (dFC) analysis is an effective way to capture the networks that are functionally associated and continuously changing over the scanning period. However, these methods mostly analyze the dynamic associations across the activation patterns of the spatial networks while assuming that the spatial networks are stationary. Hence, a model that allows for the variability in both domains and reduces the assumptions imposed on the data provides an effective way for extracting spatio-temporal networks. Independent vector analysis is a joint blind source separation technique that allows for estimation of spatial and temporal features while successfully preserving variability. However, its performance is affected for higher number of datasets. Hence, we develop an effective two-stage method to extract time-varying spatial and temporal features using IVA, mitigating the problems with higher number of datasets while preserving the variability across subjects and time. The first stage is used to extract reference signals using group independent component analysis (GICA) that are used in a parameter-tuned constrained IVA (pt-cIVA) framework to estimate time-varying representations of these signals by preserving the variability through tuning the constraint parameter. This approach effectively captures variability across time from a large-scale resting-state fMRI data acquired from healthy controls and patients with schizophrenia and identifies more functionally relevant connections that are significantly different among healthy controls and patients with schizophrenia, compared with the widely used GICA method alone.
Keywords: Blind source separation, connectivity analysis, dimensionality reduction, fMRI analysis
I. Introduction
DYNAMIC functional connectivity (dFC) analysis has emerged due to evidence that the human brain exhibits changes in functional patterns over the scanning period [1]. A number of studies have shown the presence of multiple structured patterns corresponding to different functional connectivity in task-related and resting-state functional magnetic resonance imaging (fMRI) data, see e.g., [2], [3], [4], [5], [6]. Analyzing these connectivity patterns in resting-state data has enabled the identification of distinct biomarkers in a variety of disorders such as schizophrenia [7], bipolar disorder [8], autism [9], [10], post-traumatic stress [11], generalized anxiety disorder [12],attention deficit hyperactivity disorder [13] and mild cognitive impairment [14]. Studies have also shown changes in functional connectivity patterns in different stages of development [15] and due to hallucinations [16].
Most dFC analysis techniques examine time-varying associations among the activation patterns of spatial networks while assuming that the spatial evolution of the networks is stationary. However, studies have shown that changes in functional connectivity patterns imply changes in the spatial networks [17], [18], [19]. Region of interest (ROI)-based analyses on resting-state networks (RSNs) have shown better classification of subjects when variability in both spatial and temporal domains is considered compared with variability assumed in either spatial or temporal domain [17], [18]. Dynamic mode decomposition (DMD), a spatio-temporal modal decomposition technique, has demonstrated changes in the temporal activation of RSNs [19]. Although these techniques provide interesting results, the use of pre-defined RSNs causes the estimated functional connectivity to be sensitive to network selection whereas DMD requires significant dimension reduction that may restrict the method to estimation of few spatial components. Hence a more flexible model that simultaneously captures both time-varying patterns and spatial networks of the whole brain is desirable. Joint blind source separation techniques such as group independent component analysis (GICA) attempt to find a common spatial subspace whereas techniques such as joint ICA assumes a common temporal subspace. Independent vector analysis (IVA) relaxes these assumptions and estimates demixing matrices in order to decompose the data into dataset-specific time courses and spatial maps, providing an attractive approach for capturing spatially varying networks. IVA has been successfully applied to fMRI data to captue variability in spatial networks of patients with schizophrenia and healthy controls [20]. The method proposed in [20] divides each subject’s data into overlapping windows and performs IVA on this setup treating each window as a dataset. While this approach successfully captures the dynamics in the spatial networks, it was limited to a small number of subjects (20 in the given case) due to curse of dimensionality to which IVA is susceptible. The flexibility of IVA comes at a cost that for a fixed number of samples, its performance degrades with the increase in number of datasets and number of sources since it requires estimation of high-dimensional probability density functions in addition to the increase in number of estimation parameters for the demixing matrices.
Analysis of fMRI data on a large number of subjects is common in order to obtain reliable results that can be used to make robust inferences. We develop a two-stage procedure while addressing two important points: (1) use of a flexible model, like IVA, that captures variability in both spatial and temporal domain, and (2) address the performance degradation with high dimensionality in IVA, while preserving the variability in both domains for application to large scale fMRI data. One way to reduce the effect of high dimensionality in IVA is through the use of reference signals to limit the size of the solution space. Constrained IVA (cIVA) is a semi-blind source separation technique that incorporates information regarding reference signals [21]. However, it requires a user-defined constraint parameter that controls the influence of the reference signals on the source estimates. A higher value might constrain the source estimate more than necessary, thus affecting the model’s ability to capture variability. Hence, we propose a new technique, parameter-tuned cIVA (pt-cIVA), to adaptively tune the constraint parameter to effectively capture the variability of these reference signals across time points. The two-stage procedure that includes extraction of reference signals through a data-driven approach and their use in pt-cIVA, enables us to capture time-varying features in the temporal and spatial domain while preserving variability across time windows and reduce the undesirable effects of high dimensionality by enabling analysis of each subject at a time.
The remainder of this paper is organized as follows: Section II introduces IVA and relevant IVA algorithms, followed by an overview of cIVA. It talks about an algorithm that jointly accounts higher order statistics (HOS) and second order statistics (SOS), namely, IVA-L-SOS, that provides a more suitable model for fMRI data and introduces the adaptive parameter tuning technique for cIVA. The proposed method to obtain spatio-temporal dynamics is described in Section III, Section IV and Section V shows the results on simulated and resting-state fMRI data.
II. Methods
IVA is an extension of ICA to multiple datasets and estimates source components that are as statistically independent as possible within each dataset while accounting for dependence across datasets. Given M datasets, each comprised of L components, we have, where is the mixing matrix. Given a set of observations, the IVA model can be written as the rows of are latent sources and V is the number of samples/voxel. IVA estimates M demixing matrices, W[m], to compute the source estimates, by minimizing the cost function given as [22], [23],
| (1) |
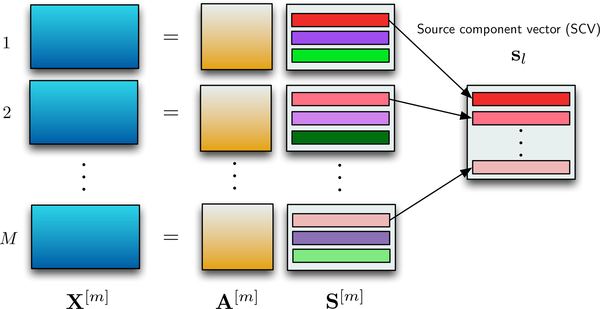
Where denotes the entropy of the source estimate for the dataset, and denotes the mutual information of the source component vector (SCV), The optimization of the cost function jointly weighs the independence within the dataset through the entropy term along with the log determinant term and dependence across the datasets through the mutual information term. SCV takes into account the dependence across the datasets and the SCV is formed by concatenating the component from all the M datasets as shown in Figure 1. For multisubject fMRI analysis, the M datasets corresponds to M subjects, forming an SCV of a similar brain region from M subjects. In this paper, the M datasets correspond to M time windows obtained using a sliding-window on a single subject’s data, yielding an SCV that gives the time-evolution of a brain region and the corresponding columns of the mixing matrix are the time courses.
Fig. 1.
Given a set of observations, the IVA model is given as where A[m] is the mixing matrix and the rows in S[m], are the latent sources that are dependent across datasets. These dependent sources are concatenated together to form an SCV.
A. Choice of IVA algorithm
The assumption of a different model for the latent source distribution has led to the development of different IVA algorithms. IVA-Gaussian (IVA-G) assumes that the underlying SCVs are multivariate Gaussian [23], and thus only takes SOS into account and estimates the covariance matrix for each SCV, IVA-Laplacian (IVA-L) assumes the sources are multivariate Laplacian distributed [24] and takes only HOS into account. It assumes there is no second-order correlation within each SCV, i.e., the covariance matrix is an identity matrix for all SCVs. Although the assumption of no second-order correlation favors some applications, in many others, such as fMRI, it degrades the estimation performance since fMRI sources exhibit a significant level of correlation across windows [25], [26]. IVA-GL, another implementation of IVA that performs IVA-L initialized to the result of IVA-G, is a popular method for fMRI analysis since it has shown more robust performance than using IVA-G or IVA-L alone [23] and since it benefits from the advantages of both algorithms, although sequentially [26]. Since the SCVs for fMRI applications correspond to brain regions that have multivariate heavytailed distributions, like the multivariate Laplacian distribution, with a significant level of correlation across subjects/time windows, an algorithm that simulateneously exploit the benefits of these algorithms is preferable. In this paper, we use an IVA algorithm, IVA-L-SOS, that assumes the sources are multivariate Laplacian distributed, like IVA-L, but also takes second-order correlation of the SCVs into account, like IVA-G, for full statistical characterization of a Laplacian multivariate random vector.
1). IVA-L-SOS algorithm:
The multivariate generalized Gaussian distribution (MGGD) covers a wide range of unimodal distributions by controlling the shape parameter, β, such as super-Gaussian (β < 1), normal (β = 1) and sub-Gaussian (β > 1), and assumes second-order correlation within an SCV [27]. The MGGD is given by,
| (2) |
where ∑ is a positive definite scatter matrix and Γ(·) is the Gamma function. By setting the shape parameter β to 0.5, the MGGD distribution is equivalent to a multivariate Laplacian distribution that accounts for second-order correlation through ∑ and is expressed as,
| (3) |
where ∑ estimated at each iteration. Since fMRI sources are in general expected to have a super-Gaussian distribution, like Laplacian [26], and are dependent across subjects/windows, the IVA-L-SOS model is a good match for fMRI data.
Derivative of (1) with respect to is given by,
| (4) |
where is a vector such that is formed by removing the lth row of W[m]. The last term in (1) can be written as [28], [23], where is independent of The score function, for the IVA-GGD algorithm is given by,
| (5) |
where the Gamma functions, grow at a rate faster than the exponential function towards infinity as M increases, leading the score function to be undefined. Since β = 0.5 provides a better match for fMRI sources [26], by direct substitution of β = 0.5, which corresponds to multivariate Laplacian distribution, in (5), we obtain
which also reduces the effect of high dimensionality and enables a stable version for large M. However, there are other factors that affect the performance of IVA when the number of datasets is high. We discuss these factors in the next section.
2). IVA: Negative effect of high dimensionality:
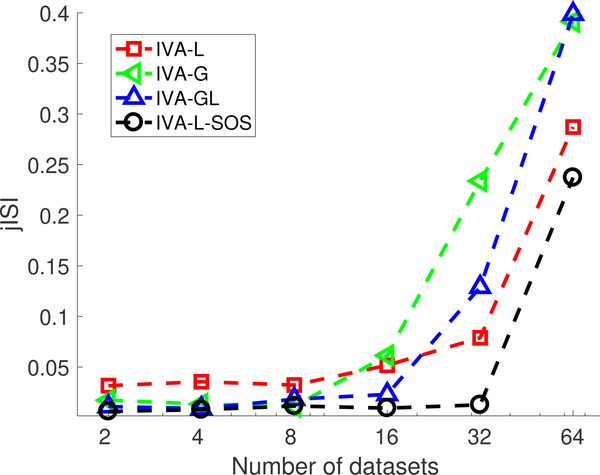
Although IVA provides a desirable framework for capturing time-varying spatial maps and time courses, and IVA-L-SOS mitigates the negative effects of large M, IVA requires the estimation of high-dimensional probability density functions (of dimension M) for the SCVs and with increasing number of datasets, M, and number of sources, L, its performance degrades. It estimates M demixing matrices of dimension L × L yielding a total of ML2 parameters. Algorithms such as IVA-G and IVAL-SOS exploit second-order correlation and require the estimation of the scatter matrix, yielding L × M(M − 1)/2 parameters to be estimated. Thus, the number of parameters to be estimated increases linearly for and quadratically for with respect to the increase in M and L. Hence, for a fixed number of samples the performance of IVA degrades when a large number of sources and datasets is considered. To demonstrate this effect on IVA, we generate M datasets with L = 3 sources generated from a multivariate Laplacian distribution with V = 104 samples. The observations, , are obtained using where is generated randomly from a uniform distribution. We obtain 10 estimates of the demixing matrices, W[m], using four IVA algorithms: IVA-L, IVA-G, IVA-GL and IVA-L-SOS. The performance is measured in terms of joint inter-symbol interference (jISI) [23]. The jISI metric measures the ability of the algorithm to separate the sources where 0 indicates better separation of underlying SCVs, i.e., The average of the jISI metric measured over 50 runs for each algorithm is shown in Fig. 2. IVA-GL and IVA-LSOS both have similar performance for a lower number of datasets since both exploit signal properties that match the underlying source distribution: HOS and SOS. However, for IVA-G, IVA-GL and IVA-L the performance degrades at a faster rate for a large number of datasets as compared with IVA-L-SOS. The increase in jISI value for IVA-G algorithm with increase in number of datasets indicates that even for algorithms that have a convex cost function, as for IVA-G [23], the performance is affected due to increase in number of datasets. This indicates that the performance of IVA starts degrading as the number of samples available to estimate parameters is approximately less than 5Q, hence degrading the estimation of the underlying sources. The method proposed in [20] performs IVA-GL on the windowed datasets from all 20 subjects, i.e., a total of 140 datasets, and thus cannot be directly used for large number of subjects. Hence, we develop a two-stage procedure to reduce the effect of high dimensionality of IVA by performing pt-cIVA on windowed datasets of each subject. Before discussing the pt-cIVA technique, we first introduce the regular cIVA model in the next section.
Fig. 2.
Performance of four IVA algorithms, namely, IVA-L, IVA-G, IVA-GL and IVA-L-SOS, with respect to number of datasets in terms of jISI. Performance of IVA degrades after a certain number of datasets for a fixed number of samples and hence cannot be used for large number of datasets with fixed number of samples.
B. Constrained IVA with fixed constraint parameter
Data-driven dFC analysis techniques, such as IVA, minimize the assumptions imposed on the data whereas model-driven dFC analysis techniques, such as ROI-based methods, make strong assumptions about the data making them robust to noise and other artifacts. However, the use of pre-defined RSNs limits the exploration of possible individual dynamic characteristics. Semi-blind source separation techniques, such as cIVA [21], [29], take advantage of the benefits of both techniques to efficiently capture individual-specific variability of the features extracted from the group of subjects. The cIVA method incorporates prior information about the sources into the IVA model [21] and limits size of the solution space, also addressing the high dimensionality issue. The cost function for cIVA is given as,
| (6) |
where is the regularization parameter, is the penalty parameter and is the inequality constraint function given as,
| (7) |
where is the estimated component, denotes the reference vector for the lth SCV, is a function that defines the measure of similarity between the estimated SCV and reference signal, and ρl is the constraint parameter. One can also constrain the columns of the mixing matrix and the interested reader can refer to [21] for the procedure. The definition of the constraint function as in (7) allows for the use of different dissimilarity functions such as the inner product, mean square error, mutual information and correlation. In this paper, we use the absolute value of Pearson’s correlation coefficient given by,
The absolute value of Pearson’s correlation coefficient as a similarity measure restricts to be between 0 and 1, steering ρl ≤ 1. Thus, a higher value of enforces the estimated source to be exactly similar to the reference signal, not allowing the reference component to vary across datasets, whereas a lower value results in the estimated component to deviate from the reference signal making it to be prone to noise and other artifacts. Hence, the selection of plays a crucial role in the performance of the cIVA algorithm. In this paper we propose an adaptive technique to select the constraint parameter, namely, pt-cIVA, which we introduce in the next section.
C. Parameter-tuned constrained IVA (pt-cIVA)
The use of reference signals provides an effective way to address the high dimensionality issue, however, use of a fixed value for the constraint parameter does not allow the model to efficiently capture the variability. We introduce pt-cIVA method such that it controls the amount of correspondence between the estimated source and the reference signal. In this case, the reference signals are the group components estimated using GICA and exhibit variability across time windows [17], [18], [19]. Using a fixed constraint parameter controls the amount of correspondance between the reference signal and estimated source, and constrains the variability of the reference signals across time windows. Hence, we adaptively tune the constraint parameter during the optimization of cIVA. We define N as the number of constraints, ρn the constraint parameter corresponding to the nth constraint and dn, n = 1,...,N, as the reference signal used to constrain a single source among the L sources. The adaptive ρ-tuning method selects a value for ρn from a set of possible values for ρn, denoted as We randomly initialize the demixing matrices, to a positive scalar value. At each iteration, we obtain an estimate of the sources, and select the first SCV to be the constrained component followed by an estimation of as given in line 8 and 9 of Algorithm 1, respectively. The update given in line 9 in Algorithm 1 identifies the highest value of ρn from set that satisfies the condition in (7) for all M datasets. Hence the distance of the estimated correlation, is computed from all possible values of ρn from set across all datasets, and the value of ρn with least distance is selected. The new value of the constraint parameter, , is then used to compute the gradient, and update the demixing matrix as in line 9 followed by obtaining a new estimate of the sources. The process is repeated until the convergence criterion, following the one proposed in [21], is met. Algorithm 1 describes the ptcIVA technique. The parameter tuning technique improves the estimation of the constraint source at every iteration providing a better solution as compared with using a fixed ρn at every iteration.
III. Implementation
In this section, we present the methodology to capture time-varying spatial and temporal components using pt-cIVA. This method extracts steady-state representation of functionally
Algorithm 1.
pt-cIVA
| Define set as possible values for ρn | |
| 2: | for n = 1,...,N do |
| Randomly initialize demixing matrices, and set to be a positive scalar value | |
| 4: | Compute |
| for l = 1,...,L do | |
| 6: | for m = 1,...,M do |
| if l == 1 then | |
| 8: | |
| 10: | |
| else | |
| 12: | (4) |
| 14: | Repeat 3 to 13 until convergence |
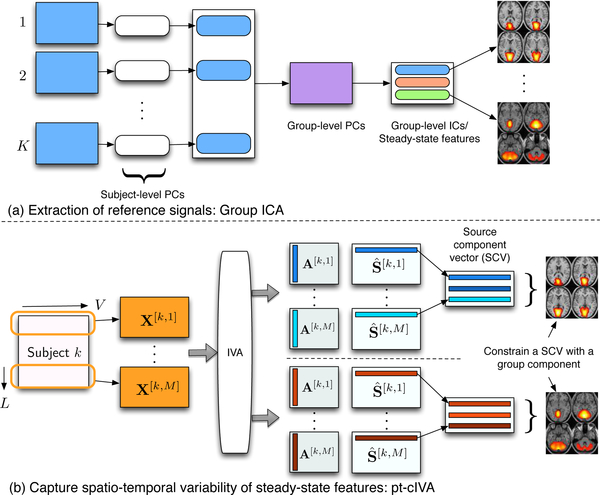
relevant components from all subjects using GICA followed by performing pt-cIVA on each subject to obtain the time-varying representations of these components as shown in Figure 3.
Fig. 3.
The two-stage method for obtaining time-varying spatial networks and corresponding time courses. (a) Reference signals are obtained using group ICA from all subjects. (b) Each subject data is divided into windows and pt-cIVA is applied on the windowed datasets with features extracted from GICA used as reference.
A. Extraction of reference signals
GICA is one of the widely used, data-driven techniques used to extract components that are common across multiple subjects [30], [25]. Given datasets from K subjects, GICA first performs subject-level principal component analysis (PCA) in order to obtain a lower-dimensional signal subspace. PCA estimates uncorrelated features in the order of highest variance, hence the signal subspace corresponds to features that capture most of the variability across time points and can be referred to as the steady-state representation of the time-varying spatial networks. GICA then vertically stacks the subject-level components from all subjects and performs a second group-level PCA on this matrix to obtain group-level principal components, which represent the components that account for most variability across subjects, i.e., a common signal subspace. Since PCA estimates uncorrelated components that separates components using only second-order statistics, ICA is performed on the group-level principal components in order to obtain statistically independent spatial features. Among the estimated independent components (ICs), N functionally relevant group components, denoted as dn, n = 1,...,N, are selected for further analysis. The N features are used as reference signals to obtain the variability of these components across windows by incorporating them into a sliding window pt-cIVA framework.
B. Parameter-tuned cIVA
In the second stage, we divide each subject’s data into M windows of length L with an 50% overlap yielding a total of MK windows. Considering all the MK windows in the analysis results in IVA to model MK-dimensional SCVs resulting in MKL2 and LMK (MK − 1)/2 parameters that need to be estimated from the fixed V samples. However, as discussed, the performance of IVA degrades with a large number of datasets and sources for a fixed number of samples. Thus, we perform a subject-level analysis to mitigate the high dimensionality issue by modeling a M-dimensional SCV instead of a MK-dimensional SCV by performing a subject-level IVA, where the windowed data from each subject defines a dataset. Using this setup, IVA also takes advantage of source dependence across windows since the spatial maps are expected to change smoothly across windows, thus aligning the components across windows. The N reference signals, dn, n = 1,...,N, obtained from GICA are used as constraints in pt-cIVA to constrain the first SCVs for each subject. The pt-cIVA technique we introduced in Section II-C enables since each window to have a different level of correlation with the constraint and setting a fixed value for the constraint parameter can deteriorate the estimation of the SCVs as shown in the simulation examples in Section IV.
IV. Simulation results
We generate M = 5 datasets such that x[m] = A[m]s[m], m = 1,...,M, where the mixing matrix for each dataset, is randomly generated with elements drawn from a normal distribution with zero mean and unit variance. The L =10 SCVs are formed from M-dimensional SCVs of V = 104 samples. Each SCV is generated from a multivariate Laplacian distribution where the scatter matrix, Σ, has a AR-type correlation structure given as,
| (8) |
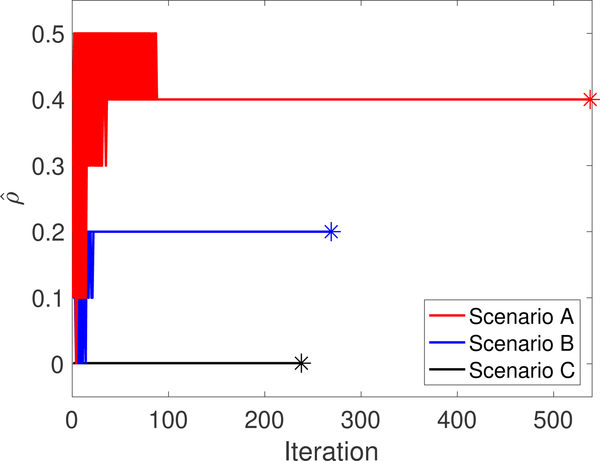
Among the 10 SCVs, first five are generated with medium to high second-order correlation, and the remaining five with lower second-order correlation, A value of between [0.8,0.9] models the components that have low variability across datasets, while a value of between [0.5,0.8] models the components that have high variability. A value of below 0.5 models the artifactual components. A reference signal is generated such that it has ρtrue correlation with the average component of the constrained SCV. We consider three scenarios to test the performance of our method to cover the range of possibilities: Scenario A: ρtrue = 0.6; Scenario B: ρtrue = 0.3; and Scenario C: ρtrue = 0. For each scenario, pt-clVA is applied with the set defined as 0.001,...,0.9, and cIVA with fixed constraint parameter for 50 runs using the IVA-L-SOS algorithm. We tested the performance of the pt-cIVA approach using different values of between 1 and 1000, and observed no change in the performance. In this work, we set following [21]. For cIVA with a fixed constraint parameter, we vary ρ from 0.001 to 0.9, where ρ = 0.9 corresponds to stronger influence of the constraint and ρ = 0.001 corresponds to weaker influence.
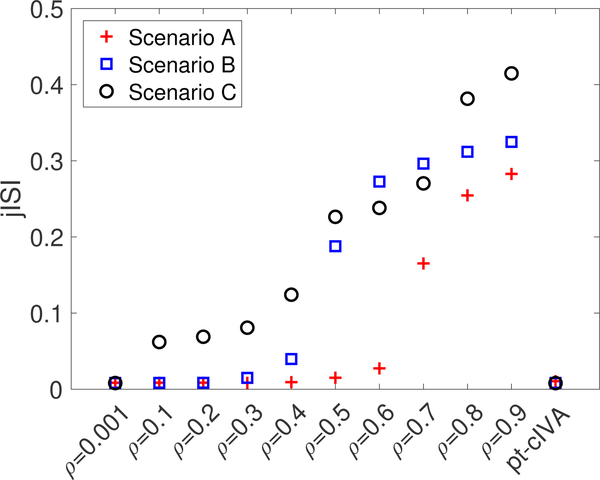
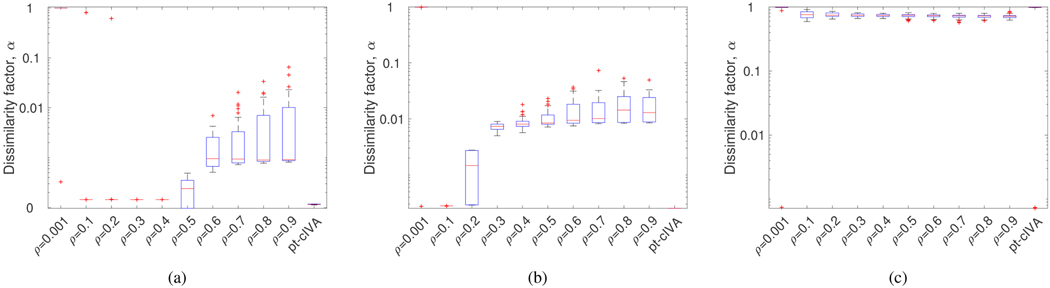
We measure the performance of the methods in terms of jISI, and dissimilarity between the constrained estimated source and ground truth. The average of the jISI metric computed over 50 runs for each method is shown in Figure. 4. For each scenario in Figure. 4, jISI obtained using regular cIVA increases when the constraint parameter is fixed to a value above the true parameter value indicating poor separation of the sources. On the other hand, pt-cIVA demonstrates lower jISI for all three scenarios indicating good separation performance. The constraint parameter selected at each IVA iteration for the three scenarios for all 50 runs is shown in Figure 5. We can see that the parameter converges to the true value (indicated by ‘*’) for all the scenarios. The true value is computed by plugging in the true constrained sources, , into the equation in line 9 of Algorithm 1. Hence, it is lower than ρtrue for scenarios A and B. In order to verify if the proposed method accurately estimates the constrained source across time windows, we measure the dissimilarity factor, α, between the constrained estimated source, and corresponding ground truth, computed as, A higher value of this metric indicates poor estimation of the sources. Figure. 6 shows the dissimilarity factor obtained using regular cIVA and pt-cIVA for the three scenarios. The estimation of the constrained component degrades using regular cIVA when a higher constraint parameter is used whereas the proposed method has low dissimilarity factor for scenarios A and B. Noting the lower jISI and dissimilarity factor metric for lower values of ρ in regular cIVA, it might be initially thought that cIVA might be preferable rather than pt-cIVA. However, since in real world applications, one does not know the true value of the constraint parameter and whether the constraint is present or not, setting a lower value for ρ might adversely affect the performance of the estimation. For scenario C, i.e., when the constraint is not present, pt-cIVA demonstrates better performance than regular cIVA for lower values of ρ. At ρ = 0.001, which is equivalent to performing unconstrained IVA, the jISI value is similar to that of pt-cIVA, however the dissimilarity factor is high for all scenarios, indicating a weaker influence of the constraints on the source. For scenario C the estimated constraint parameter, imposing a weaker constraint on the IVA decomposition. This is equivalent to performing regular IVA that holds permutation ambiguity. Thus the dissimilarity factor between the estimated source and constraint source is high even though the jISI value is low.
Fig. 4.
Performance of cIVA with fixed constraint parameter varied from ρ = 0.001,...,0.9 and pt-cIVA with in terms of jISI for the three scenarios. The performance of cIVA with fixed constraint parameter degrades if the parameter is fixed to value higher than the true constraint parameter whereas pt-cIVA has low jISI for all three scenarios.
Fig. 5.
Constraint parameter selected at every IVA iteration for all 50 runs for scenarios A, B and C. The marker ‘*’ indicates the corresponding true value of ρ. The estimated constraint parameter using pt-cIVA converges to the true value for all scenarios.
Fig. 6.
Performance of cIVA with fixed constraint parameter varied from ρ = 0.001,...,0.9 and pt-cIVA with in terms of dissimilarity factor for (a) Scenario A, (b) Scenario B and (c) Scenario C. For each box, the horizontal red line indicates the median, the top and bottom edges indicate the 75th and 25th percentiles, respectively, the whiskers show the extreme points not considered as outliers and the ‘+’ symbol indicate outliers. The dissimilarity factor of the constrained component is low for pt-cIVA whereas it increases using regular cIVA when a higher constraint parameter is used.
V. Identification of resting-state dynamics
We use a large-scale resting-state fMRI data obtained from the Center for Biomedical Research Excellence (CO-BRE), which is available on the collaborative informatics and neuroimaging suite data exchange repository (http://coins.mrn.org/dx) [31], to capture the variability using the proposed pipeline. This resting-state fMRI data includes K = 179 subjects: 91 healthy controls (HCs) (average age: 38 ± 12) and 88 patients with schizophrenia (SZs) (average age: 37 ± 14). For this study, the participants were asked to keep their eyes open during the entire scanning period. The resting fMRI data were obtained using a 3-Tesla TIM Trio Siemens scanner with TE = 29 ms, TR = 2 s, flip angle = 75°, slice thickness = 3.5 mm, voxel size = 3.75 × 3.75 × 4.55 mm3 and slice gap = 1.05 mm. Image scans were obtained over five minutes with a sampling period of 2 seconds yielding 150 timepoints per subject. We removed the first 6 timepoints to address T1-effect and each subject’s image data was preprocessed including motion correction, slice-time correction, spatial normalization and slightly re-sampled to 3 × 3 × 3mm3 yielding 53 × 63 × 46 voxels. We perform masking on each image volume to remove the non-brain voxels and flatten the result to form an observation vector of V = 58604 voxels, giving T = 144 time evolving observations for each subject. Each subject’s data is normalized to zero mean per time point and whitened.
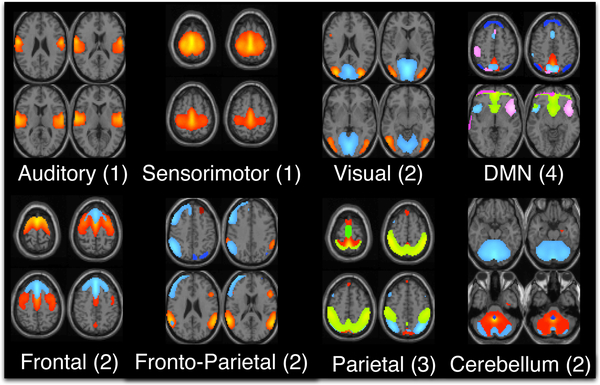
In order to extract the reference signals using a data-driven approach, we perform GICA using the Group ICA for fMRI (GIFT) toolbox (http://mialab.mrn.org/software/gift) on the resting-state fMRI data. The number of group components are estimated using a modified minimum description length criterion that accounts for sample dependence [32], for each subject’s data and the mean (30) plus one standard deviation (5) across subjects is used as the final number of estimated group components. ICA using the entropy rate bound minimization algorithm [33], [34] is used to estimate 35 components/networks. Of these, N = 17 functionally relevant networks are selected based on visual inspection. These networks are categorized into 8 domains: auditory, sensorimotor (SM), frontal, fronto-parietal (FP), parietal (PAR), default mode network (DMN), visual (VIS) and cerebellum. The DMN domain also consists of voxels corresponding to anterior DMN (ADMN) and insular (INS) regions. The frontal, parietal and fronto-parietal networks comprise the cognitive control domain. The FRO domain consists of two networks: FRO1 and FRO2 corresponding to their peak activation in the frontal cortex situated anterior to the premotor cortex and dorsolateral prefrontal cortex, respectively. The PAR domain consists of three networks: PAR1, PAR2 and PAR3, corresponding to their peak activation in the primary somatosensory cortex, supramarginal gyrus and somatosensory association cortex, respectively. The VIS domain consists of two networks: VIS1 and VIS2, corresponding to their peak activation in the lateral and medial visual cortex, respectively. The components in each domain and the corresponding number of components are shown in Figure. 7.
Fig. 7.
17 features are selected from GICA as constraints for pt-cIVA. The features are categorized into 8 domains: auditory (AUD), sensorimotor (SM), frontal (FRO), fronto-parietal (FP), parietal (PAR), default mode network (DMN), visual (VIS) and cerebellum (CB).
Each of these N = 17 components is used as a reference signal in the pt-cIVA model in order to capture their variation in both the spatial and temporal domain. For the pt-cIVA model, we divide each subject’s data into M = 17 windows of length L = 16 with a 50% overlap, resulting in a total of MK = 3043 windows. By performing pt-cIVA on each subject’s data, we reduce the dimensionality of the SCV from 3043 to 17. The first SCV is constrained to be correlated with one of the 17 group components. The pt-cIVA method using IVA-L-SOS algorithm, with the set defined as 0.001,..., 0.9 and is applied on the windowed datasets of each subject to estimate 10 solutions. Since IVA is an iterative algorithm, optimization of IVA results in different solutions depending on the initialization. Hence, in order to select the most representative run, we perform the method in [35] to select the most consistent run across multiple runs with different initializations. This method computes the distance between solutions obtained for each pair of runs and selects the runs that has the least average distance. Along with addressing the issue of high dimensionality by limiting the size of the solution space, the use of references in IVA also results in components that are ordered across multiple subject-level IVA decompositions, thus yielding SCVs that are aligned across subjects. In order to verify that the estimated constrained SCVs are ordered across subjects, we visually inspected the estimated components and observed that these components were similar to the reference signal. We also inspected the final constraint parameter for all reference signals and for all subjects and the range of these values was between 0.4 to 0.9, indicating that the components are ordered as per the reference signal. The estimated source corresponding to nth constraint for the kth subject at mth window from the consistent run is denoted as The corresponding time courses at each window are further processed to correct for quadratic, linear and cubic trends, and low-pass filtered with a cutoff of 0.15Hz [6]. We obtain M graphs for each subject, using N nodes and N(N − 1) edges, denoted as The N nodes represent spatial maps or time courses and an edge defines the Pearson’s correlation coefficient between the n1th and n2th nodes, n1, n2 = 1,...,N. Thus, we obtain M temporal dFC (tdFC) and spatial dFC (sdFC) graphs of dimension N × N from time courses and spatial nodes respectively for each subject.
Quantification of dynamics
A number of studies have focused on identifying biomarkers that show differences in the HC and SZ groups [36], [37], [38]. We were interested in determining if any of the estimated spatio-temporal component features would be sensitive to mental illness. One feature that is of interest is variability of functional connectivity and spatial maps [39], [20]. In this paper, we define two metrics: component similarity and functional connectivity fluctuation, to identify the spatial components and functional connections that are variable. To evaluate differences between the HC and SZ groups, we perform a permutation test on each metric, that is, a non-parametric statistical test which controls the false alarm rate under the null hypothesis [40], [41]. The idea of a permutation test is to determine whether the difference between the two groups is large enough to reject the null hypothesis that two groups have identical distributions. The test first obtains the observed difference between the two groups using the true labels of the subjects. The labels for the subjects from the two groups are randomly pooled and a difference statistic using the new labels is obtained for every permutation of the labels. A distribution of the calculated differences is the exact distribution of possible differences under the null hypothesis. If the observed difference is within 95% of the exact distribution, then we do not reject the null hypothesis. This test hence assumes that there are no differences between the two groups and tests if this hypothesis is true or not. We use the t-statistic obtained from a two-sample t-test to measure the difference between the two groups and identify whether a particular group has higher intensity using the sign of the t-statistic
A. Functional connectivity fluctuation
The functional connectivity fluctuation, for each subject using tdFC and sdFC graphs is computed as follows,
| (9) |
where is the mean of the connectivity metric, computed across M windows for nodes n1 and n2, and denotes the Pearson’s correlation coefficient between the nodes n1 and n2. Each node represents a spatial map/time course obtained using pt-cIVA. We also compute this metric on the tdFC graphs obtained from GICA, which estimates time courses while assuming the spatial networks are stationary. The estimated reference signals are back-reconstructed to estimate subject specific time courses, and a sliding window of length L = 16 is applied with a 50% overlap yielding M = 17 windows. For each subject, tdFC graphs are obtained as mentioned above. The mean and standard deviation of functional connectivity fluctuation metric across the HC and SZ group are obtained for tdFC graphs from GICA and proposed approach, and sdFC graphs, and are provided as supplementary material1.
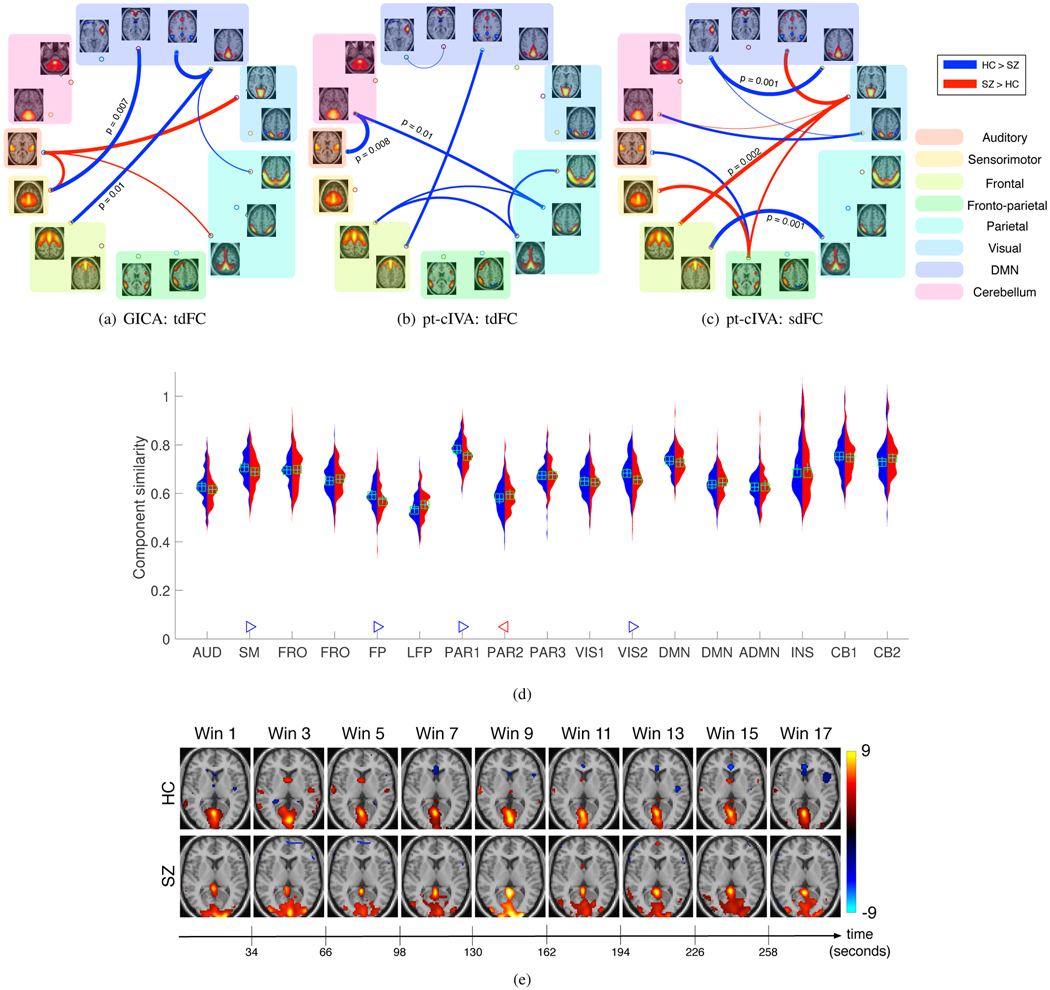
The permutation test results on the functional connectivity fluctuation metric identified a number of distinct and relevant connections. These also showed lower p-values using the proposed method as compared with GICA. Figure. 8 shows the connections identified as significantly different using tdFC: GICA (Figure. 8(a)), tdFC: pt-cIVA (Figure. 8(b)) and sdFC: pt-cIVA (Figure. 8(c)). The combined result using tdFC and sdFC graphs computed from our method suggests lower variability within the cognitive control network and within the default mode network for the SZ group. Studies have reported descreased hemodynamic response in the insula region in the SZ group causing low variability in this region [42]. Higher variability is observed across components in different clusters, namely, the visual and cognitive control cluster, visual and DMN cluster, visual and frontal component, and frontoparietal and sensorimotor component for the SZ group. This variability across brain regions may be due to dysfunction in the working memory, attention and visual learning [43] and the tendency of patients with schizophrenia to engage more brain regions than healthy controls [44]. However, GICA results identifies higher temporal variability in HC group between DMN and the frontal component of the cognitive network and higher variability in the SZ group between visual and auditory component, and between auditory and sensorimotor component. These results suggest that the use of tdFC graphs alone does not fully characterize the dynamic functional connectivity and assuming variability in both spatial and temporal domains results in identification of more distinct biomarkers.
Fig. 8.
(a-c) Associations that demonstrate significant difference (p < 0.05, corrected) between HC and SZ group. Blue connections indicate higher measures in controls whereas red indicates higher measure in patients. Thickness of the connection indicates a more significant difference (lower p-value) between HCs and SZs. More group differentiating and relevant connections with significantly lower p-values are obtained using the proposed method as compared with GICA. (d) Component similarity of all components. Red indicates the distribution of this metric for the SZ group and blue indicates the distribution of this metric across HC group. Components that demonstrate significant difference (p < 0.05, corrected) between HC and SZ group are indicated by a triangle. A blue ’▷’ denotes the corresponding component is less variable in the HC group whereas a red ‘◁‘ denotes the corresponding component is less variable in the SZ group. The results indicate that SM, FP, PAR1, and VIS components are less variable in HC whereas PAR2 is less variable in SZ group. (e) Changes in the visual component (VIS1) for one subject corresponding to lowest variability within the HC group and SZ group. The visual component shows disrupted activation pattern for the SZ subject as compared with the HC subject.
B. Component similarity
In order to quantify the variability of the nth feature for each subject k, we compute the absolute value of the Pearson’s correlation coefficient between the nth component at window and the nth component at window Component similarity is then obtained by computing the mean across all adjacent windows. A higher value of this metric suggests that the spatial network is less variable. Figure. 8(e) shows the results for the components that demonstrated significant differences (p < 0.05, corrected) using a permutation test between healthy controls and schizophrenia patients. The VIS, SM, FP and PAR1 components exhibited less variability within the HC group whereas the PAR2 component exhibited less variability in schizophrenia. These components were also identified as less variable among healthy individuals in a previous dynamic study [20]. Deficits in visual perception, attention and motor regions have been previously shown in schizophrenia, which may lead to variability in these components. Figure. 8(f) shows an example of the changes in the visual component of one subject for whom the stationarity is estimated as the highest within the HC and SZ groups. The activated voxels corresponding to the visual component also shows disrupted activation patterns across time for the SZ subject. This is consistent with previous work showing disruptions in the perceptual functions in SZ subjects including abnormalities of smooth pursuit in this group of subjects [45].
VI. Discussion
In recent years, extracting time-varying spatial and temporal features has become of interest in neuroimaging studies. IVA provides a simple linear formulation with minimum assumptions and allows for estimation of spatio-temporal features. However, due to the effect of high dimensionality in IVA, it has been applied to a small number of subjects. We develop a technique that reduces the effect of high dimensionality and extracts time-varying features in both spatial and temporal domain for a large number of subjects. This method extracts reference signals using GICA followed by pt-cIVA to extract their variability across time windows through tuning the constraint parameter. The tuning method effectively captures the variability of the components across time windows using simulated data as compared with using regular cIVA. It also identifies functional connections that differentiate healthy controls and patients with schizophrenia from a large-scale fMRI data.
The two-stage procedure allows for flexibility in the use of different methods for extraction of reference signals. Methods such as dictionary learning [46] and sparse ICA [47] can be used to exploit sparsity of the components. Matrix decomposition techniques such as multiset canonical correlation analysis (MCCA) [48], population value decomposition [49], shared dictionary learning [50], joint and individual variation explained (JIVE) [51] and common orthogonal basis extraction (COBE) [52] can be used to extract common and individual features from subjects and used as reference signals for the second stage.
The success of the proposed method leads to a number of future directions. Identification of spatial connectivity states and studying potential gains from analyzing them is of interest. Studying the ability of the spatial features to classify subjects can provide a quantification to study the effectiveness of spatial features. Graph theorotical metrics such as dynamic connectivity strength, clustering coefficient and centrality measures can be used to summarize the dynamic spatial networks [53]. Along with capturing variability of the features across time windows, the pt-cIVA technique can be used for applications where the effect of prior information is unknown. In seed-based analysis, selection of ‘seeds’ is crucial to the analysis of fMRI data, i.e., incorrect selection of ‘seeds’ may lead to incorrect detection of connectivity. In analysis of EEG data, prior information regarding target frequencies is imposed on all subjects without any knowledge about the presence of these frequencies for each subject. The use of pt-cIVA model would automatically weigh the influence of incorrect reference selection.
Supplementary Material
Acknowledgments
This work is supported in parts by the National Institute of Biomedical Imaging and Bioengineering under Grant R01 EB 020407, National Science Foundation under Grant 1631838 and National Science Foundation-Computing and Communication Foundations under Grant 1618551.
Footnotes
Supplementary materials are available in the supporting documents/multimedia tab.
Contributor Information
Suchita Bhinge, Department of Electrical and Computer Engineering, University of Maryland, Baltimore County, Baltimore, MD 21250 USA..
Rami Mowakeaa, Department of Electrical and Computer Engineering, University of Maryland, Baltimore County, Baltimore, MD 21250 USA..
Vince D. Calhoun, The Mind Research Network, Albuquerque, NM 87106 USA Department of Electrical and Computer Engineering, University of New Mexico, Albuquerque, NM 87131 USA..
Tülay Adalı, Department of Electrical and Computer Engineering, University of Maryland, Baltimore County, Baltimore, MD 21250 USA..
References
- [1].Hutchison RM, Womelsdorf T, Gati JS, Everling S, and Menon RS, “Resting-state networks show dynamic functional connectivity in awake humans and anesthetized macaques,” Human Brain Mapping, vol. 34, no. 9, pp. 2154–2177, 2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [2].Sakoğlu Ü, Pearlson GD, Kiehl KA, Wang YM, Michael AM, and Calhoun VD, “A method for evaluating dynamic functional network connectivity and task-modulation: Application to schizophrenia,” Magnetic Resonance Materials in Physics, Biology and Medicine, vol. 23, no. 5–6, pp. 351–366, 2010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [3].Kucyi A and Davis KD, “Dynamic functional connectivity of the default mode network tracks daydreaming,” NeuroImage, vol. 100, pp. 471–480, 2014. [DOI] [PubMed] [Google Scholar]
- [4].Wang L, Yu C, Chen H, Qin W, He Y, Fan F, Zhang Y, Wang M, Li K, Zang Y et al. , “Dynamic functional reorganization of the motor execution network after stroke,” Brain, vol. 133, no. 4, pp. 1224–1238, 2010. [DOI] [PubMed] [Google Scholar]
- [5].Calhoun VD, Miller R, Pearlson G, and Adali T, “The chronnectome: Time-varying connectivity networks as the next frontier in fMRI data discovery,” Neuron, vol. 84, no. 2, pp. 262–274, 2014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [6].Allen EA, Damaraju E, Plis SM, Erhardt EB, Eichele T, and Calhoun VD, “Tracking whole-brain connectivity dynamics in the resting state,” Cerebral Cortex, vol. 24, no. 3, pp. 663–676, 2014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [7].Damaraju E, Allen EA, Belger A, Ford J, McEwen S, Mathalon D, Mueller B, Pearlson G, Potkin S, Preda A et al. , “Dynamic functional connectivity analysis reveals transient states of dysconnectivity in schizophrenia,” NeuroImage: Clinical, vol. 5, pp. 298–308, 2014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [8].Rashid B, Damaraju E, Pearlson GD, and Calhoun VD, “Dynamic connectivity states estimated from resting fMRI identify differences among schizophrenia, bipolar disorder, and healthy control subjects,” Frontiers in Human Neuroscience, vol. 8, p. 897, 2014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [9].Assaf M, Jagannathan K, Calhoun VD, Miller L, Stevens MC, Sahl R, O’Boyle JG, Schultz RT, and Pearlson GD, “Abnormal functional connectivity of default mode sub-networks in autism spectrum disorder patients,” NeuroImage, vol. 53, no. 1, pp. 247–256, 2010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [10].Fu Z, Tu Y, Di X, Du Y, Sui J, Biswal BB, Zhang Z, de Lacy N, and Calhoun VD, “Transient increased thalamic-sensory connectivity and decreased whole-brain dynamism in autism,” NeuroImage, 2018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [11].Bluhm RL, Williamson PC, Osuch EA, Frewen PA, Stevens TK, Boksman K, Neufeld RW, Theberge J, and Lanius RA, “Alterations in default network connectivity in post-traumatic stress disorder related to early-life trauma,” Journal of Psychiatry & Neuroscience: JPN, vol. 34, no. 3, p. 187, 2009. [PMC free article] [PubMed] [Google Scholar]
- [12].Etkin A, Prater E, Schatzberg AF, Menon V, and Greicius MD, “Disrupted amygdalar subregion functional connectivity and evidence of a compensatory network in generalized anxiety disorder,” Archives of General Psychiatry, vol. 66, no. 12, pp. 1361–1372, 2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [13].de Lacy N and Calhoun VD, “Dynamic connectivity and the effects of maturation in youth with attention deficit hyperactivity disorder,” Network Neuroscience, no. Just Accepted, pp. 1–41, 2018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [14].Chen X, Zhang H, Gao Y, Wee C-Y, Li G, Shen D, and Initiative ADN, “High-order resting-state functional connectivity network for MCI classification,” Human Brain Mapping, vol. 37, no. 9, pp. 3282–3296, 2016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [15].Uddin LQ, Supekar KS, Ryali S, and Menon V, “Dynamic reconfiguration of structural and functional connectivity across core neurocognitive brain networks with development,” Journal of Neuroscience, vol. 31, no. 50, pp. 18578–18589, 2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [16].Lefebvre S, Demeulemeester M, Leroy A, Delmaire C, Lopes R, Pins D, Thomas P, and Jardri R, “Network dynamics during the different stages of hallucinations in schizophrenia,” Human Brain Mapping, vol. 37, no. 7, pp. 2571–2586, 2016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [17].Jie B, Liu M, and Shen D, “Integration of temporal and spatial properties of dynamic connectivity networks for automatic diagnosis of brain disease,” Medical Image Analysis, vol. 47, pp. 81–94, 2018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [18].Kottaram A, Johnston L, Ganella E, Pantelis C, Kotagiri R, and Zalesky A, “Spatio-temporal dynamics of resting-state brain networks improve single-subject prediction of schizophrenia diagnosis,” Human Brain Mapping, 2018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [19].Kunert-Graf JM, Eschenburg KM, Galas DJ, Kutz JN, Rane SD, and Brunton BW, “Extracting reproducible time-resolved resting state networks using dynamic mode decomposition,” bioRxiv, p. 343061, 2018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [20].Ma S, Calhoun VD, Phlypo R, and Adali T, “Dynamic changes of spatial functional network connectivity in healthy individuals and schizophrenia patients using independent vector analysis,” NeuroImage, vol. 90, pp. 196–206, 2014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [21].Bhinge S, Long Q, Levin-Schwartz Y, Boukouvalas Z, Calhoun VD, and Adali T, “Non-orthogonal constrained independent vector analysis: Application to data fusion,” in International Conference on Acoustics, Speech and Signal Processing (ICASSP), March 2017, pp. 2666–2670. [Google Scholar]
- [22].Adali T, Anderson M, and Fu G-S, “Diversity in independent component and vector analyses: Identifiability, algorithms, and applications in medical imaging,” IEEE Signal Processing Magazine, vol. 31, no. 3, pp. 18–33, 2014. [Google Scholar]
- [23].Anderson M, Adali T, and Li X-L, “Joint blind source separation with multivariate Gaussian model: Algorithms and performance analysis,” IEEE Transactions on Signal Processing, vol. 60, no. 4, pp. 1672–1683, 2012. [Google Scholar]
- [24].Kim T, Eltoft T, and Lee T-W, “Independent vector analysis: An extension of ICA to multivariate components,” in International Conference on Independent Component Analysis and Signal Separation. Springer, 2006, pp. 165–172. [Google Scholar]
- [25].Calhoun VD, Adali T, Pearlson GD, and Pekar J, “A method for making group inferences from functional MRI data using independent component analysis,” Human Brain Mapping, vol. 14, no. 3, pp. 140–151, 2001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [26].Calhoun VD and Adali T, “Multisubject independent component analysis of fMRI: A decade of intrinsic networks, default mode, and neurodiagnostic discovery,” IEEE Reviews in Biomedical Engineering, vol. 5, pp. 60–73, 2012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [27].Gómez E, Gomez-Viilegas M, and Marin J, “A multivariate generalization of the power exponential family of distributions,” Communications in Statistics-Theory and Methods, vol. 27, no. 3, pp. 589–600, 1998. [Google Scholar]
- [28].Li X-L and Zhang X-D, “Nonorthogonal joint diagonalization free of degenerate solution,” IEEE Transactions on Signal Processing, vol. 55, no. 5, pp. 1803–1814, 2007. [Google Scholar]
- [29].Khan AH, Taseska M, and Habets EA, “A geometrically constrained independent vector analysis algorithm for online source extraction,” in International Conference on Latent Variable Analysis and Signal Separation. Springer, 2015, pp. 396–403. [Google Scholar]
- [30].Calhoun V, Adali T, Pearlson G, and Pekar J, “Group ICA of functional MRI data: Separability, stationarity, and inference,” in Proc. Int. Conf. on ICA and BSS; San Diego, CA: p, vol. 155, 2001. [Google Scholar]
- [31].Scott A, Courtney W, Wood D, De la Garza R, Lane S, Wang R, King M, Roberts J, Turner JA, and Calhoun VD, “COINS: An innovative informatics and neuroimaging tool suite built for large heterogeneous datasets,” Frontiers in NeuroInformatics, vol. 5, p. 33, 2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [32].Li Y-O, Adali T, and Calhoun VD, “Estimating the number of independent components for functional magnetic resonance imaging data,” Human Brain Mapping, vol. 28, no. 11, pp. 1251–1266, 2007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [33].Li X-L and Adali T, “Blind spatiotemporal separation of second and/or higher-order correlated sources by entropy rate minimization,” in International Conference on Acoustics Speech and Signal Processing (ICASSP). IEEE, 2010, pp. 1934–1937. [Google Scholar]
- [34].Fu G-S, Phlypo R, Anderson M, Li X-L et al. , “Blind source separation by entropy rate minimization,” IEEE Transactions on Signal Processing, vol. 62, no. 16, pp. 4245–4255, 2014. [Google Scholar]
- [35].Long Q, Jia C, Boukouvalas Z, Gabrielson B, Emge D, and Adali T, “Consistent run selection for independent component analysis: Application to fMRI analysis,” in International Conference on Acoustics, Speech and Signal Processing (ICASSP). IEEE, 2018, pp. 2581–2585. [Google Scholar]
- [36].Du Y, Pearlson GD, Lin D, Sui J, Chen J, Salman M, Tamminga CA, Ivleva EI, Sweeney JA, Keshavan MS et al. , “Identifying dynamic functional connectivity biomarkers using GIG-ICA: Application to schizophrenia, schizoaffective disorder, and psychotic bipolar disorder,” Human Brain Mapping, vol. 38, no. 5, pp. 2683–2708, 2017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [37].Du Y, Fu Z, and Calhoun VD, “Classification and prediction of brain disorders using functional connectivity: Promising but challenging,” Frontiers in Neuroscience, vol. 12, 2018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [38].Salman MS, Du Y, Lin D, Fu Z, Damaraju E, Sui J, Chen J, Yu Q, Mayer AR, Posse S et al. , “Group ICA for identifying biomarkers in schizophrenia: ‘adaptive’ networks via spatially constrained ICA show more sensitivity to group differences than spatio-temporal regression,” bioRxiv, p. 429837, 2018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [39].Zalesky A, Fornito A, Cocchi L, Gollo LL, and Breakspear M, “Time-resolved resting-state brain networks,” Proceedings of the National Academy of Sciences, p. 201400181, 2014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [40].Zalesky A, Fornito A, and Bullmore ET, “Network-based statistic: Identifying differences in brain networks,” NeuroImage, vol. 53, no. 4, pp. 1197–1207, 2010. [DOI] [PubMed] [Google Scholar]
- [41].Maris E and Oostenveld R, “Nonparametric statistical testing of EEG- and MEG-data,” Journal of Neuroscience Methods, vol. 164, no. 1, pp. 177–190, 2007. [DOI] [PubMed] [Google Scholar]
- [42].Wylie KP and Tregellas JR, “The role of the insula in schizophrenia,” Schizophrenia research, vol. 123, no. 2–3, pp. 93–104, 2010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [43].Heinrichs RW and Zakzanis KK, “Neurocognitive deficit in schizophrenia: a quantitative review of the evidence.” Neuropsychology, vol. 12, no. 3, p. 426, 1998. [DOI] [PubMed] [Google Scholar]
- [44].Ma S, Eichele T, Correa NM, Calhoun VD, and Adali T, “Hierarchical and graphical analysis of fMRI network connectivity in healthy and schizophrenic groups,” in IEEE International Symposium on Biomedical Imaging: From Nano to Macro. IEEE, 2011, pp. 1031–1034. [Google Scholar]
- [45].Abel L, Levin S, and Holzman P, “Abnormalities of smooth pursuit and saccadic control in schizophrenia and affective disorders,” Vision Research, vol. 32, no. 6, pp. 1009–1014, 1992. [DOI] [PubMed] [Google Scholar]
- [46].Varoquaux G, Gramfort A, Pedregosa F, Michel V, and Thirion B, “Multi-subject dictionary learning to segment an atlas of brain spontaneous activity,” in Biennial International Conference on Information Processing in Medical Imaging. Springer, 2011, pp. 562–573. [DOI] [PubMed] [Google Scholar]
- [47].Boukouvalas Z, Levin-Schwartz Y, and Adali T, “Enhancing ICA performance by exploiting sparsity: Application to FMRI analysis,” in IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP),. IEEE, 2017, pp. 2532–2536. [Google Scholar]
- [48].Li Y-O, Adali T, Wang W, and Calhoun VD, “Joint blind source separation by multiset canonical correlation analysis,” IEEE Transactions on Signal Processing, vol. 57, no. 10, pp. 3918–3929, 2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [49].Crainiceanu CM, Caffo BS, Luo S, Zipunnikov VM, and Punjabi NM, “Population value decomposition, a framework for the analysis of image populations,” Journal of the American Statistical Association, vol. 106, no. 495, pp. 775–790, 2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [50].Vu TH and Monga V, “Fast low-rank shared dictionary learning for image classification,” IEEE Transactions on Image Processing, vol. 26, no. 11, pp. 5160–5175, 2017. [DOI] [PubMed] [Google Scholar]
- [51].Lock EF, Hoadley KA, Marron JS, and Nobel AB, “Joint and individual variation explained (JIVE) for integrated analysis of multiple data types,” The Annals of Applied Statistics, vol. 7, no. 1, p. 523, 2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [52].Zhou G, Cichocki A, Zhang Y, and Mandic DP, “Group component analysis for multiblock data: Common and individual feature extraction,” IEEE Transactions on neural networks and learning systems, vol. 27, no. 11, pp. 2426–2439, 2016. [DOI] [PubMed] [Google Scholar]
- [53].Sizemore AE and Bassett DS, “Dynamic graph metrics: Tutorial, toolbox, and tale,” NeuroImage, 2017. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.