An Online Calculator for the Prediction of Survival in Glioblastoma Patients Using Classical Statistics and Machine Learning

Abstract

BACKGROUND

Although survival statistics in patients with glioblastoma multiforme (GBM) are well-defined at the group level, predicting individual patient survival remains challenging because of significant variation within strata.

OBJECTIVE

To compare statistical and machine learning algorithms in their ability to predict survival in GBM patients and deploy the best performing model as an online survival calculator.

METHODS

Patients undergoing an operation for a histopathologically confirmed GBM were extracted from the Surveillance Epidemiology and End Results (SEER) database (2005-2015) and split into a training and hold-out test set in an 80/20 ratio. Fifteen statistical and machine learning algorithms were trained based on 13 demographic, socioeconomic, clinical, and radiographic features to predict overall survival, 1-yr survival status, and compute personalized survival curves.

RESULTS

In total, 20 821 patients met our inclusion criteria. The accelerated failure time model demonstrated superior performance in terms of discrimination (concordance index = 0.70), calibration, interpretability, predictive applicability, and computational efficiency compared to Cox proportional hazards regression and other machine learning algorithms. This model was deployed through a free, publicly available software interface (https://cnoc-bwh.shinyapps.io/gbmsurvivalpredictor/).

CONCLUSION

The development and deployment of survival prediction tools require a multimodal assessment rather than a single metric comparison. This study provides a framework for the development of prediction tools in cancer patients, as well as an online survival calculator for patients with GBM. Future efforts should improve the interpretability, predictive applicability, and computational efficiency of existing machine learning algorithms, increase the granularity of population-based registries, and externally validate the proposed prediction tool.

ABBREVIATIONS

AFT

accelerated failure time

CI

confidence interval

CPHR

Cox proportional hazards regression

GBM

glioblastoma multiforme

IDH1

isocitrate dehydrogenase 1

KPS

Karnofsky performance status

MGMT

O6-methylguanine-DNA methyltransferase

MMSE

mini-mental state examination

SEER

Surveillance Epidemiology and End Result

Glioblastoma multiforme (GBM) is the most common primary malignant brain tumor with almost 12 000 new cases per year in the United States and a median survival of only a year after diagnosis.¹ Adequate survival prognostication is essential for informing clinical and personal decision-making. Although survival statistics are well-defined at the group level, predicting individual patient survival remains challenging because of the heterogenous nature of the disease and significant variation in survival within strata.

In recent years, numerous statistical and machine learning algorithms have emerged that

can learn from examples to make patient-level predictions of survival. These algorithms can be particularly useful for tailoring clinical care to the needs of the individual GBM patient.

This study aims to compare the most commonly used statistical and machine learning algorithms in their ability to predict individual patient survival in GBM patients. In order to promote the reproducibility of the current study and facilitate external validation and implementation of the developed models, we deployed the best performing model as an online calculator that provides interactive, online, and graphical representations of personalized survival estimates.

METHODS

Data and Study Population

The transparent reporting of a multivariable prediction model for Individual Prognosis or Diagnosis (TRIPOD) statement was used for the reporting of this study.² Data were extracted from the Surveillance Epidemiology and End Results (SEER) database (2005-2015).³ The SEER registry compiles cancer incidence and survival data of 18 registries and covers 28% of the United States population from academic and nonacademic hospitals and, as such, is broadly representative of the United States population as a whole.⁴ Patients who underwent surgery for a histopathologically confirmed diagnosis of a GBM (International Classification of Diseases for Oncology-Third Edition [ICD-O-3] codes 9440, 9441, and 9442) were included in the analysis. Patients were excluded from the analysis if they died in the direct postoperative period (≤30 d after surgery). Our institutional review board has exempted the SEER database from review and waived the need for informed consent because of the retrospective nature of this study.

Outcome and Input Features

Although machine learning provides a variety of predictive algorithms, most of them are developed to accommodate binary or continuous outcomes instead of censored survival outcomes (ie, time-to-event data). To facilitate a vis-à-vis comparison between traditional statistical and novel machine learning algorithms, we compared all algorithms in their ability to predict one or more of the following survival outcomes: (i) continuous: overall survival from diagnosis to death in months; (ii) binary: 1-yr survival probability; and (iii) censored: subject-level Kaplan-Meier survival curves. All demographic, socioeconomic, radiographical, and therapeutic characteristics available at individual patient-level in the SEER registry were included as input features. Continuous variables included age at diagnosis (years) and maximal enhancing tumor diameter in any dimension (millimeters). Categorical variables included sex, race (White; Black; Asian; Other), ethnicity (Hispanic; non-Hispanic), marital status (married; nonmarried), insurance status (insured; uninsured/Medicaid), tumor laterality (left; right; midline), tumor location (frontal; temporal; parietal; occipital; cerebellum; brainstem; ventricles; overlapping lesion), tumor extension (confined to primary location; ventricle involvement; midline crossing), surgery type (biopsy; subtotal resection; gross-total resection), and administration of any form of postoperative chemotherapy and/or radiotherapy. Data on input features and survival outcomes were collected by independent, trained data collectors.

Statistical Analysis

Missing data were multiple imputed by means of a random forest algorithm.⁵ The total cohort was randomly split into a training and hold-out test set based on an 80/20 ratio.

The Cox proportional hazards regression (CPHR) and the accelerated failure time (AFT) algorithms allow for inferential analysis on censored survival data. Therefore, both approaches were also utilized to provide insight into the independent association between covariates and survival. Interactions between age, sex, surgery type, radiotherapy, and chemotherapy were modeled in both approaches. The Benjamini-Hochberg procedure based on 41 comparisons (26 parameters plus 15 two-way interactions) was used to adjust for multiple testing. The proportional hazards assumption of the CPHR model was assessed by means of the Schoenfeld Residuals Test, and the distribution assumption of the AFT by means of a quantile-quantile plot. All covariates that were statistically significantly associated with survival in the inferential analysis were included in the predictive analysis.

For the predictive analysis, 15 machine learning and statistical algorithms were trained including AFT, bagged decision trees, boosted decision trees, boosted decision trees survival, CPHR, extreme boosted decision trees, k-nearest neighbors, generalized linear models, lasso and elastic-net regularized generalized linear models, multilayer perceptron, naïve Bayes, random forests, random forest survival, recursive partitioning, and support vector machines.^6-8 Among these, only the AFT, boosted decision trees survival, CPHR, random forest survival, and recursive partitioning algorithms were capable of modeling time-to-event data. Five-fold cross-validation was used on the training set for preprocessing optimization and hyperparameter tuning. Hyperparameters were model specific, such as the number of trees in a random forest model and the number of layers or nodes per layer in a neural network. The algorithms were subsequently trained with optimized hyperparameter settings on the full training set and evaluated on the hold-out test set, which has not been used for preprocessing and hyperparameter tuning in any form.

Metrics of Predictive Performance

Discrimination and calibration were used as metrics for prediction performance. Discrimination reflects the ability of a model to separate observations, whereas calibration measures the agreement between the observed and predicted outcomes.⁹ Discrimination was quantified according to the concordance index (C-index). The C-index represents the probability that for any 2 patients chosen at random, the patient who had the event first is rated as being more at risk of the event according to the model. Therefore, the C-index takes into account the occurrence of the event, as well as the length of follow-up, and is particularly well-suited for right-censored survival analysis.¹⁰ For the subject-level survival curves produced by time-to-event models, the C-index was evaluated per time point weighted according to the survival distribution in the test set and integrated over time. The relationship between predicted 1-yr survival probability and observed survival rate was graphically assessed in a calibration plot.

Secondary Metrics

In addition to prediction performance, we evaluated additional metrics that pose significant pragmatic challenges to the deployment and implementation of prediction models in clinical care. These metrics include model interpretability, predictive applicability, and computational efficiency. Lack of interpretability is an important concern for the implementation of many machine learning models, which are typically referred to as “black-boxes” and sometimes cited as a weakness compared to classical statistical methods. Inferential utility is a traditional hallmark of model interpretability and therefore included as a model assessment measure. Predictive applicability refers to the type of outcome classes to be predicted (binary, continuous, or time-to-event), as well as the generated output of the fitted models (class probability, numeric estimate, or subject-level survival curve, respectively). Computational efficiency was measured in terms of model size, loading time, and computation time to produce a prediction. For models that do not provide natural prediction CI, model predictions were bootstrapped 100 times with replacement to provide such estimates.

We also developed an online, interactive, and graphical tool based on the overall best performing model. Statistical analyses were conducted using R (version 3.5.1, R Core Team, Vienna, Austria).¹¹ All machine learning modeling was performed using the Caret package,¹² and the application was built and deployed using the Shiny package and server.¹³

RESULTS

Patient Demographics and Clinical Characteristics

In total, 20 821 patients met our inclusion criteria. Missing data were multiply imputed for insurance status (16.7% missingness), tumor size (14.3%), tumor laterality (12.0%), tumor location (6.6%), marital status (3.8%), tumor extension (1.6%), surgery type (1.3%), and race (0.2%). Survival time was censored for 3745 patients (18.0%). The estimated median survival time in the total cohort was 13 mo (95%CI 12-13 mo). The total cohort was split into a training and hold-out test set of 16 656 and 4165 patients, respectively (Table, Supplemental Digital Content 1).

Inferential Analysis

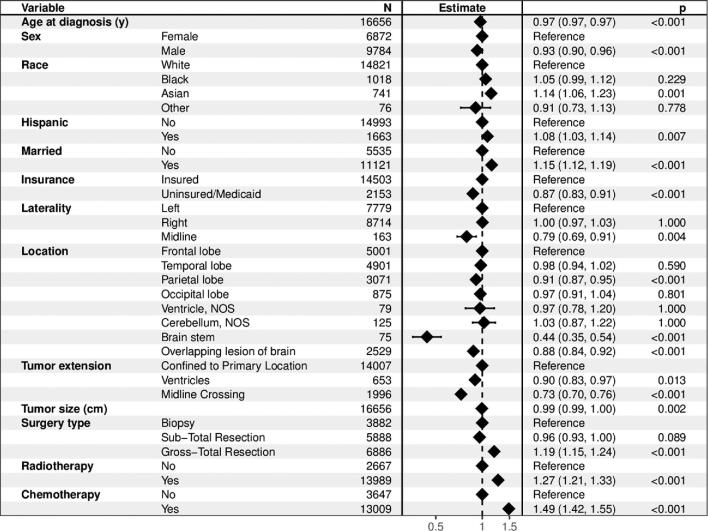
The Schoenfeld residuals test demonstrated that the assumption of proportionality was violated for all variables except sex and ethnicity in the CPHR model (all P < .006 and global test P < .001; Table, Supplemental Digital Content 2). The quantile-quantile plot demonstrated a valid log-logistic distribution assumption for the (AFT) model (Figure, Supplemental Digital Content 4). For these reasons, we present the inferential results of the AFT model. The AFT allows for uncomplicated interpretation, as it provides acceleration factors (γ), which represent the relative survival duration of a strata compared to the reference group. For example, a γ of 1.5 reflects an expected survival duration that is 50% longer compared to the reference group. Multivariable AFT analysis identified older age (γ = 0.75 per 10 yr increase, P < .001), male sex (γ = 0.93, P < .001), uninsured insurance status or insurance by Medicaid (γ = 0.87, P < .001), midline tumors (γ = 0.79, P = .004), tumors primarily located in the parietal lobe (γ = 0.91, P < .001), brain stem (γ = 0.44, P < .001) or multiple lobes (γ = 0.88, P < .001), tumors extending to the ventricles (γ = 0.90, P < .001) or across the midline (γ = 0.73, P < .001), and larger sized tumors (γ = 0.99 per cm, P < .001) as independent predictors of shorter survival (Figure 1). Asian race (γ = 1.14, P = .001), Hispanic ethnicity (γ = 1.08, P = .007), married marital status (γ = 1.15, P < .001), gross-total resection (γ = 1.19, P < .001), radiotherapy (γ = 1.27, P < .001), and chemotherapy (γ = 1.49, P < .001) were identified as independent predictors of longer survival.

FIGURE 1.

Forest plot for the accelerated failure time model characterizing the association between the individual predictors and survival. In the inferential analysis, the estimates for age and tumor size were presented per 10-yr and 10-mm increase, respectively, to reflect the incremental relative survival duration of clinically meaningful intervals. The P value was corrected for multiple testing by means of the Benjamini-Hochberg procedure.

The AFT model with interaction terms demonstrated that age interacted with extent of resection (γ > 1.03 per 10 yr increase, P < .02) as well as radiotherapy (γ = 1.04 per 10 yr increase, P = .03) (Table, Supplemental Digital Content 3).

Predictive Analysis

The discriminatory performance on the hold-out test set as measured by the C-index set ranged between 0.66 and 0.70 and between 0.67 and 0.70 across all models for predicting overall survival and 1-yr survival status, respectively (Table 1). Among the time-to-event models, the integrated C-index ranged between 0.68 and 0.70 for predicting subject-level Kaplan-Meier survival curves. The AFT model based on a log-logistic distribution demonstrated the highest discriminatory performance for computing personalized survival curves. Compared to all continuous and binary models, the AFT model demonstrated similar or better discrimination for predicting overall survival and 1-yr survival probability, respectively. Model calibration varied significantly across all models (Figure, Supplemental Digital Content 4). The traditional CPHR model systematically underestimated survival in the 1-yr survival probability range of 0.5 to 0.75, whereas the AFT model showed better calibration, particularly in this clinically relevant interval (Figure 2 and Figure, Supplemental Digital Content 5).

TABLE 1.

Discriminatory Performance for All Time-to-Event, Continuous, and Binary Survival Models According to the (Integrated) Concordance Index

	C-index (95%CI)
	Overall survival	1 yr survival status	Integrated C-index
Time-to-Event Models
Accelerated failure time	0.70 (0.70-0.70)	0.70 (0.70-0.70)	0.70 (0.70-0.70)
Cox proportional hazards regression	0.69 (0.69-0.70)	0.69 (0.69-0.70)	0.69 (0.69-0.70)
Boosted decision trees survival	0.69 (0.69-0.70)	0.69 (0.69-0.70)	0.69 (0.69-0.70)
Random forest survival	0.68 (0.68-0.68)	0.69 (0.69-0.69)	0.68 (0.68-0.68)
Recursive partitioning	0.68 (0.68-0.68)	0.68 (0.68-0.68)	0.68 (0.68-0.68)
Continuous and Binary Models
Boosted decision trees	0.70 (0.70-0.70)	0.70 (0.70-0.70)	NA
Regularized generalized linear models	0.70 (0.70-0.70)	0.70 (0.70-0.70)	NA
Generalized linear models	0.70 (0.70-0.70)	0.70 (0.70-0.70)	NA
Support vector machines	0.70 (0.70-0.70)	0.69 (0.69-0.69)	NA
Multilayer perceptron	0.61 (0.61-0.61)	0.69 (0.69-0.69)	NA
Naïve Bayesa	NA	0.69 (0.69-0.69)	NA
Random forest	0.69 (0.69-0.69)	0.69 (0.69-0.69)	NA
Extreme boosted decision trees	0.68 (0.68-0.68)	0.68 (0.68-0.68)	NA
K-nearest neighbors	0.67 (0.67-0.67)	0.68 (0.67-0.68)	NA
Bagged decision trees	0.67 (0.66-0.67)	0.66 (0.66-0.66)	NA

Abbreviations: 1 yr, one year; C-index, concordance index; not available.

^aNaïve Bayes fits to categorical data only.

FIGURE 2.

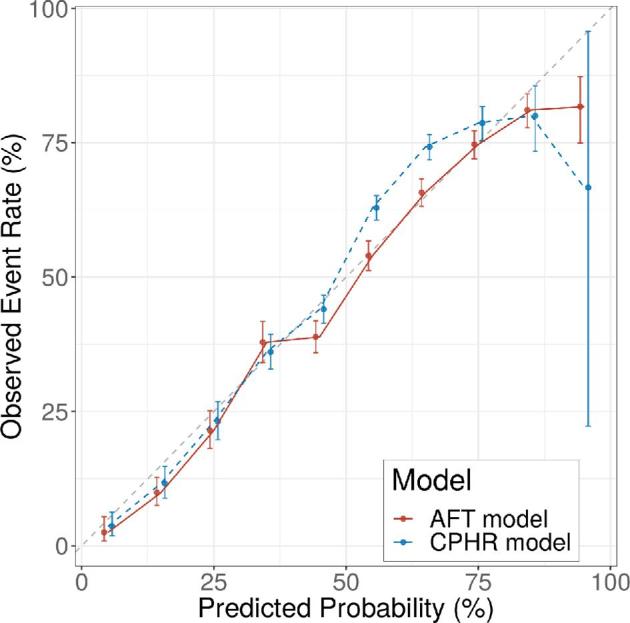
Calibration plot demonstrating a systematic underestimation of survival by the Cox proportional hazards regression model in the 1-yr survival probability range of 0.5 to 0.75 and a well-calibrated accelerated failure time model. Abbreviations: AFT, accelerated failure time; CPHR, Cox proportional hazards regression.

Secondary Metrics

Secondary metrics related to model deployment and clinical implementation varied across all models (Table 2). AFT, CPHR, and (regularized) generalized linear models were the only models with inferential utility. AFT, CPHR, boosted decision trees survival, recursive partitioning, and random forest survival were the only models that can analyze time-to-event data and thus compute subject-level survival curves. The application loading time varied between 0.2 s and 45 min. The 100-fold bootstrapped prediction time varied between 1.9 s and 4 min on a single central processing unit.

TABLE 2.

Secondary Metrics for Model Performance and Deployment

	Interpretability		Predictive applicability			Computational efficiencya
Model	Inference	Prediction	Binary	Continuous	Survival curves	Size (Mb)	Load time (s)	Prediction time (s)
AFT	X	X	X	X	X	20	0.9	1.9
Bagged decision trees	–	X	X	X	–	16 380	1335	31.8
Boosted decision trees	–	X	X	X	–	300	8.2	2.1
BDTS	–	X	X	X	X	36 790	2455	234.3
CPHR	X	X	X	X	X	37	1.7	7.5
GLM	X	X	X	X	–	1	0.2	1.7
GLMnet	X	X	X	X	–	109	6.7	2.3
K-nearest neighbors	–	X	X	X	–	91	5.6	1.9
Multilayer perceptron	–	X	X	X	–	45	1.4	17.4
Naïve Bayes	–	X	X	–	–	82	2.9	13.0
Random forest	–	X	X	X	–	1100	41.4	10.1
Random forest survival	–	X	X	X	X	6350	65.7	139.0
Recursive partitioning	–	X	X	X	X	490	52.1	3.4
Support vector machine	–	X	X	X	–	111	4.8	4.4
X-boosted decision trees	–	X	X	X	–	92	2.4	1.5

Abbreviations: AFT, accelerated failure time; BDTS, boosted decision trees survival; CPHR, Cox proportional hazards regression; GLM(net), (Lasso and elastic-net regularized) generalized linear models; Mb, megabyte; s, seconds; TTE, time to event; X, extreme.

^aBased on a 100-fold bootstrapped model.

Deployment

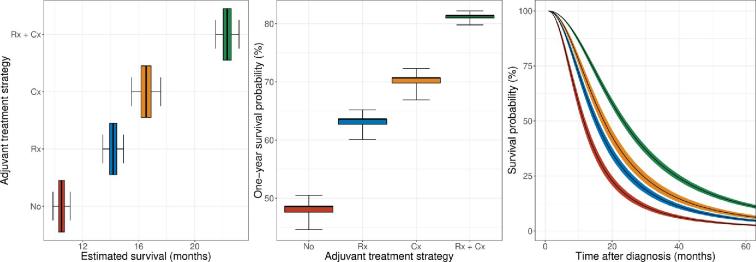
Although the AFT model demonstrated similar to superior performance in terms of discrimination and calibration, it outperformed competing statistical and machine learning algorithms in terms of interpretability, predictive applicability, and computational efficiency. Therefore, it was selected as backend for the online survival prediction tool (https://cnoc-bwh.shinyapps.io/gbmsurvivalpredictor/). The estimated survival profile for a hypothetical patient is shown in Figure 3.

FIGURE 3.

Estimated survival profile of a hypothetical patient (male, 50-yr old, white, non-Hispanic, married, insured, left-sided, frontal lobe, confined to its primary location, 50 mm in size, gross-total resection), plotted per adjuvant treatment strategy. Personalized estimates of overall survival in months (left), 1-yr survival probability (middle), and 5-yr survival curves (right) as predicted by the accelerated failure time model. The boxes and whiskers in the boxplots represent the 50% and 95% CI, respectively. The ribbons in the survival curves represent the 95% CI. Abbreviations: Rx, radiotherapy; Cx, chemotherapy.

DISCUSSION

This manuscript and the accompanying online prediction tool provide a framework for individualized survival modeling in patients with GBM that is generalizable to other cancer and neurosurgical patients. Although prior investigation in this area tends to focus on metrics of prediction performance, we advocate a multimodal assessment when constructing and implementing clinical prediction models. The online prediction tool provides interactive, online, and graphical representations of expected survival in GBM patients.

Few other groups have developed an online survival prediction tool for GBM patients.^14-16 Gorlia et al¹⁴ developed multiple nomograms based on a secondary analysis of trial data using age at diagnosis, World Health Organization Performance Status (WPS), extent of resection, Mini-Mental State Examination (MMSE) score, and O6-methylguanine-DNA methyltransferase (MGMT) methylation status as input features, thereby achieving a maximum C-index of 0.66. Gittleman et al¹⁵ developed similar nomograms including sex as an input feature and Karnofsky Performance Status (KPS) score as a measure of functional status. However, model discrimination remained similar (C-index 0.66). Marko et al¹⁶ developed a model in which extent of resection was modeled as a continuous covariate. This group also utilized an AFT model to account for the violated proportional hazards assumption and achieved a C-index of 0.69. Higher discriminatory performance (C-index 0.63-0.77) was achieved in studies that used machine learning algorithms to analyze complex, high-dimensional data structures, such as genomic, imaging, and health-related quality of life data.^17-25 Although many machine learning algorithms are ideally suited for superior prediction performance by utilizing these high-dimensional data structures, increasing model complexity may incur other costs in terms of interpretability, ease of use, computation speed, and external generalizability.

Limitations

Due to the retrospective nature of the data acquisition, it cannot be excluded that adjuvant therapy was administered at outside hospitals and not corresponded back to the reporting hospital. However, because of the short survival period in this patient population, the percentage of patients with complete survival follow-up is exceptionally high. Although clinically essential features were included to mitigate the risk of confounding, the possibility of influence from unmeasured confounders cannot be excluded. Randomized data would be ideal; however, it is practically and financially infeasible to establish a cohort on this scale, and it has become ethically unjustifiable to randomize newly diagnosed patients to a placebo arm now that a proven, effective adjuvant treatment for GBM has emerged.²⁶ Predictive modeling on this scale remains therefore bound to observational data, thereby highlighting the need for exploring analytical approaches to mitigate confounding.

On average, 3.3% of all data points were missing in the total data set, which was multiply imputed by means of a random forest algorithm to mitigate the risk of systematic bias associated with a complete-case analysis. Nonetheless, survival performance in the current study is limited by the type and number of features included in the SEER registry. As a result, KPS score, isocitrate dehydrogenase 1 (IDH1) mutation, 1p/19q codeletion, and MGMT methylation status were not included in the current iteration of the prediction model. Despite these limitations, the performance of the current proposed prediction tool exceeds that of the currently available prediction tools and even approximates the performance of many complex radiogenomic models,^17-25 yet with the ease, speed, accessibility, interpretability, and generalizability of clinical prediction tools. Furthermore, this study presents a framework that can be updated and reiterated when novel variables are added to the SEER registry or when novel large-scale multicenter glioblastoma registries are assembled. Because these models are trained on data from thousands of patients from numerous hospitals across the U.S., we expect the fitted models to be less prone to overfitting of data from a single institution and plausibly more generalizable to patients from diverse geographic regions undergoing a variety of clinical treatments.

Implications

Survival prognostication is critical for clinical and personal decision-making in GBM patients. Although our current prediction tool provides an interactive interface for survival modeling with potential clinical utility, it is designed as a research tool and should not be implemented in clinical practice prior to prospective validation on multiple heterogenous cohorts. Using a population-based registry might be more representative of the typical glioblastoma patient in the United States; however, testing the current model on single institutional or multicenter data might be essential to confirm its prognostic value at point of care. Furthermore, predictive models should inform rather than direct clinical decision-making. We advocate a multidimensional approach for survival prognostication, in which model predictions are adjusted and balanced against complementary information that is available including clinical experience, neuropsychological testing, imaging data, and genomic information.

Many statistical and machine learning algorithms allow for the analysis of historical patient cohorts to predict survival in new patients. However, prediction performance, interpretability, clinical utility, computational efficiency, and their associated limitations vary widely across different models because of their mathematical underpinnings. CPHR has emerged as the cornerstone of survival analysis but is limited by the assumption of proportionality, which assumes that the relationship between covariate and outcome is constant over time. In the real world, this association is often dynamic, and the assumption of proportionality is effectively violated. The AFT model does allow for increasing or decreasing covariate risk contribution over time, which is particularly useful in individualizing survival predictions. The AFT model has been shown to be a valuable alternative to CPHR in simulation studies,²⁷ as well as survival studies on GBM patients.¹⁶

Molecular markers (eg, IDH1 mutation, 1p19q codeletion, and MGMT methylation status), as well as functional status (eg, KPS and MMSE), have been demonstrated to impact survival in glioblastoma patients and are commonly used for stratifying patient cohorts in clinical decision-making. However, they have not yet been included in large-scale, multicenter registries. Their eventual inclusion could improve individual patient survival modeling. Furthermore, granular information with regards to the healthcare setting (eg, academic vs nonacademic) and provided clinical care (eg, volumetric measurements of tumor size and extent of resection, as well as the timing, type, dose, and sequence of adjuvant treatment) would be valuable to further improve model performance. If addition of any of these variables improves model performance only slightly, however, it may be preferable to exclude some predictors for ease of use at the point of care. Another method to overcome the lack of large-scale granular datasets could be to explore the concept of transfer learning, a common machine learning approach of updating a pretrained model on novel data sources or even different outcomes.²⁸ In the context of glioblastoma survival prediction, this could mean developing a base model on population-based data, which is further trained on institutional data to fit institutional patterns and include relevant institutional parameters not available in population-based registries.

Although many machine learning algorithms show great predictive performance, their utility is often limited to continuous and binary models, which merely provide point estimates of overall survival and 1-yr survival probability at a given point in time, respectively. Transferring the predictive power of these algorithms to time-to-event models allows for the computation of subject-level survival curves, thereby enabling more granular insight into expected survival. Furthermore, time-to-event models can be trained on patients with either complete or incomplete follow-up, which mitigates the systematic bias associated with exclusion of the latter group. Although many machine learning models demonstrate high performance in the academic realm,²⁹ lack of interpretability and computational inefficiency hinders their deployment in the clinical realm. When evaluating models for clinical deployment, we recommend evaluating fitted models on several criteria rather than a singular focus on prediction performance because factors unrelated to prediction performance (such as interpretability or applicability) can exclude high-performing models from clinical deployment. Although the AFT model was selected because of its high overall performance, the difference in prediction performance was not always clinically meaningful, thereby emphasizing the importance of taking into account these secondary metrics as well. Furthermore, the prediction performance can change as the number and nature of the input features change. For example, the assembly of multimodal data including radiogenomics data might call for alternative analytical approaches in the near future.

Prognostication is and always has been aimed at a moving target and future factors impacting clinical course cannot be modeled, most importantly advances in clinical care. Prediction performance therefore remains an asymptotic ideal for which perfection will never be reached. Future research should focus on developing clinically meaningful and interpretable prediction tools. Improving the end-user transparency regarding the underlying predictive mechanisms and the inherent limitations allows for a safe and reliable implementation of survival prediction tools in clinical care.

CONCLUSION

This study provides a framework for the development of survival prediction tools in cancer patients, as well as an online calculator for predicting survival in GBM patients. Future efforts should focus on developing additional algorithms that can train on right-censored survival data, improve the granularity of population-based registries, and externally validate the proposed prediction tool.

Disclosures

Funding was received from a National Institutes of Health (NIH) P41EB015898 (to Mr Mehrtash) and Training Grant T32 CA 009001 (to Mr Cote). The authors have no personal, financial, or institutional interest in any of the drugs, materials, or devices described in this article.

Supplemental Digital Content 1. Table. Baseline characteristics for the training and hold-out test set.

Supplemental Digital Content 2. Table. Schoenfield residuals test for the proportional hazards assumption of the Cox proportional hazards model.

Supplemental Digital Content 3. Table. Accelerated failure time model demonstrating the association between the predictors and survival with inclusion of interactions terms.

Supplemental Digital Content 4. Figure. Distribution plots. The quantile-quantile (QQ) plots based on the log-logistic distribution approximate linearity and demonstrate excellent parallelism across different treatment strata suggesting a valid log-logistic distribution assumption of the accelerated failure time model.

Supplemental Digital Content 5. Figure. Calibration plots for all models.

COMMENTS

The authors have performed a comprehensive survival modeling study using statistical and machine learning algorithms from a larger population database (SEER) to predict survival in GBM patients using solid and valid statistical methods. Additionally, they present an online prediction tool that provides interactive and graphical representation of survival in these patients with an easy to use interface. For the analysis they have incorporated variables such as socioeconomics, clinical and radiographic features with a total of 20 281 patients meeting the inclusion criteria. The current work provides a framework for the development of a prediction tool that could potentially be utilized in clinical practice to predict survival not only in GBM but also in other cancer types. Such tool could potentially be incorporated into a mobile app to further facilitate its use. There are obvious and inherent limitations of the proposed predictive model (data obtained from a public database) related to the lack of factors that may improve the survival modeling such as molecular markers, IDH mutations, MGMT methylation, facility type, accurate extent of resection, KPS, etc. Despite these limitations, the current study provides a model to be further tested in single or multicenter institutional databases to further validate and implement its use in the clinical setting.

Yoshua Esquenazi

Yoshua Esquenazi

This is a very interesting and timely article. The online calculator described will be useful for individual patient prognostication. As with any machine learning process the most important step is data acquisition. The quality and quantity of this data is the determinant of how good any predictive model can be. The model uses SEER data from 2005–2015, just at the time of emergence of the Stupp protocol until WHO 2016.

This area of AI may well provide the basis for future endeavor in this area and also provide a useful means to assess the impact of new and emerging therapies for GBM. I agree that the AFT model is a good choice for predicting survival however it may be inferior with interpreting hazard ratios.

The authors acknowledge several limitations with their study in that KPS, IDH1 mutation, 1p/19q co-deletion, and MGMT methylation status were not included in the current iteration of the prediction model. The authors have shared their insights into developing a more useful and accurate model for the future and call for the development new large-scale multicenter GBM registries.

The online calculator described will hopefully be (in the future when fully developed to include KPS score and molecular data) useful for individual patient prognostication.

Cormac G. Gavin

London, United Kingdom