Traction force microscopy for understanding cellular mechanotransduction

Abstract

Under physiological and pathological conditions, mechanical forces generated from cells themselves or transmitted from extracellular matrix (ECM) through focal adhesions (FAs) and adherens junctions (AJs) are known to play a significant role in regulating various cell behaviors. Substantial progresses have been made in the field of mechanobiology towards novel methods to understand how cells are able to sense and adapt to these mechanical forces over the years. To address these issues, this review will discuss recent advancements of traction force microscopy (TFM), intracellular force microscopy (IFM), and monolayer stress microscopy (MSM) to measure multiple aspects of cellular forces exerted by cells at cell-ECM and cell-cell junctional intracellular interfaces. We will also highlight how these methods can elucidate the roles of mechanical forces at interfaces of cell-cell/cell-ECM in regulating various cellular functions.

INTRODUCTION

It is well established that mechanical forces around cells and cellular functions are closely related to each other under both physiological and pathological conditions (1, 2). These cellular forces are either generated from cells and then transmitted through actin stress fibers referred to as endogenous forces or transmitted from outside cells referred to as external forces (3). Advancements in the field of mechanobiology have provided much evidence that cells are able to sense and adapt to these mechanical forces around their microenvironment (4). It has been shown that mechanotransduction through cell-extracellular matrix (ECM) adhesions (5), cell-cell junctions (6), plasma membrane (7), glycocalyx (8), and nucleus (9) can modulate various cell behaviors such as cell spreading (10), proliferation (11), differentiation (12-14), migration (15, 16), morphogenesis (7), cancer progression (17), and ECM remodeling (18, 19). Therefore, developing novel tools to discover how cells could dynamically sense and respond to these mechanical forces would be of great importance to understand the physiology and pathology in life science and bioengineering fields.

Over the years, studies on mechanical forces have extensively exploited functions of integrin-mediated FAs that can act as mechanotransducers between actomyosin stress fibers and ECMs-/polymer-based cell culture substrates with varying stiffness (13, 20). Moreover, it has been well established that the interplay among focal adhesions, cell surface integrins, and the stiffness of ECMs could play a significant role in regulating cell adhesion and spreading (21-23). For examples, it has been reported that the density of ECM ligands could control the spreading behavior of cells through focal adhesion (FA) assembly and that subsequent degree of cell spreading could regulate cellular functions through changes in cell shape, cytoskeletal tension, and Ras homolog family member A (RhoA) mediation (10, 24). In addition, seminal studies pioneered by Discher and Engler have reported that the stiffness of PAA-based hydrogels as cell culture substrates with tunable mechanical properties could determine the fate of human mesenchymal stem cells (hMSCs) by remodeling focal adhesion and cytoskeleton (12, 25). These hMSCs adhered onto either “soft” or “stiff” matrix could sense biophysical and mechanical cues of the matrix having a native tissue-like stiffness, resulting in undergoing lineage-specific differentiation of hMSCs into various cell types depending on tissue-like elasticity. They also further reported that mechanotransduction for regulating stem cell fates could be primarily determined by matrix stiffness, not by ECM tethering or porosity of substrates (12, 26). Indeed, a comprehensive understanding of mechanobiology requires novel tools to measure the forces between cells and ECMs, which are termed as traction forces and the methods to quantify these forces using microscopy-based techniques are known as traction force microscopy (TFM) (27). Therefore, in this review, we will highlight recent advancements in TFM-based methods for understanding multiple aspects of cellular forces exerted by cells at cell-ECM interfaces as well as at junctional intracellular domains within cellular microenvironment. Specifically, we will also discuss how the TFM-based methods can further elucidate the roles of mechanical forces at interfaces of cell-cell/cell-ECM in controlling various cellular functions. The different approaches and methods introduced in this review are summarized in Table 1 and 2.

Table 1.

Summary of each TFM-based cellular force measurement analysis

TFM Methods	Target Forces	Dimension & Image acquisition	Substrate Materials	Advantages	Disadvantages	Refs
Deformable material-based 2D TFM	Cell-ECM	Cells on 2D substrates Force measurement in 2D Epifluorescence microscopy	PAA, PDMS, PEG	Simple experimental setups to prepare cell culture substrate Tunable substrate stiffness with wide ranges by concentration of monomers and cross-linking agents Scalable and economic Showing flat physiological surface Most popular and well verified method	Essential to have reference image without force for force analysis Required intensive image processing and stress computation steps Unable to measure normal (out-of-plane) forces	(27, 31, 32, 34)
Micropost-based 2D TFM	Cell-ECM	Essential to have reference image without force for force analysis Force measurement in 2D Epifluorescence microscopy	PDMS (microposts)	Tunable stiffness by geometrical parameters of microposts, such as diameters and heights Simple process for force analysis due to no need for reference image without force Higher degree of force sensitivity detected by bending of microposts	Required sophisticated photolithography techniques for substrate preparation Narrow range of stiffness Having discrete substrate morphology and less physiological surface due to the distribution of adhesion molecules Unable to measure normal (out-of-plane) forces	(36, 37)
Deformable material-based 3D (2.5D) TFM	Cell-ECM	Cells on 2D substrates Force measurement in 3D Confocal microscopy	PAA, PEG	Enable to measure normal (out-of-plane) forces, allowing to understand cell behaviors in 3D Simple experimental setups to prepare cell culture substrate Tunable substrate stiffness with wide ranges by concentration of monomers and cross-linking agents Flat physiological surface	Required highly intensive image processing and stress computation steps compared to 2D TFM methods Essential to have reference image without force for force analysis	(33, 41)
Deformable material-based 3D TFM	Cell-ECM	Cells embedded in 3D matrix Force measurement in 3D Confocal microscopy	PEG, type I collagen	Suitable to mimic in-vivo environment due to the 3D cell encapsulation Enable to measure normal (out-of-plane) forces, allowing to understand cell behaviors of 3D organoids in 3D Tunable substrate stiffness with wide ranges by concentration of monomers and cross-linking agents	Required the most intensive image processing and stress computation steps Essential to have reference image without force for force analysis, but it is difficult to acquire due to technical inability to remove cells within 3D substrate Complex force analyses due to the non-linear material properties (type I collagen)	(42, 43)

Table 2.

Summary of each IFM- or MNM-based cellular force measurement analysis

IFM & MSN Methods	Target Forces	Dimension & Image acquisition	Basic method for IFM & MSN	Advantages#	Disadvantages#	Refs
Deformable material-based 2D IFM	Cell-cell Intracellular	Cells on 2D substrate Force measurement in 2D Epifluorescence microscopy	Deformable material-based 2D TFM	Enable to quantify forces on cell-cell junction and intracellular organelles, such as adherens junctions and nucleus	Intracellular tension is measured as an average value in 1D, and therefore, 2D mapping is not possible	(46, 52)
Micropost-based 2D IFM	Cell-cell Intracellular	Cells on 2D substrate Force measurement in 2D Epifluorescence microscopy	Micropost-based 2D TFM	Enable to quantify forces on cell-cell junction and intracellular organelles, such as adherens junctions and nucleus	Intracellular tension is measured as an average value in 1D, and therefore, 2D mapping is not possible	(51)
Deformable material-based 3D IFM	Cell-cell Intracellular	Cells on 2D substrate Force measurement in 3D Confocal microscopy	Deformable material-based 3D (2.5D) TFM	Enable to measure normal (out-of-plane) forces, allowing to understand cell behaviors in 3D Enable to quantify forces on cell-cell junction and intracellular organelles, such as adherens junctions and nucleus	Intracellular tension is measured as an average value in 1D, and therefore, 2D mapping is not possible	(47)
Deformable material-based 2D MSM	Cell-cell Intracellular	Cells on 2D substrate Force measurement in 2D Epifluorescence microscopy	TFM 2D Micropost-based	Enable to quantify forces on cell-cell junction and intracellular organelles, such as adherens junctions and nucleus Enable to measure intracellular stress map in 2D, resulting in higher degree of spatial resolution	Need to have heavy assumption that mechanical properties of intracellular components, including nucleus, plasma membrane, etc., are the same Ignoring normal (out-of-plane) forces (no bending component)	(53, 54)
Deformable material-based 3D MSM	Cell-cell Intracellular	Cells on 2D substrate Force measurement in 3D Confocal microscopy	Deformable material-based 3D (2.5D) TFM	Enable to measure bending stresses, allowing to understand inter-/intracellular behaviors in 3D Enable to quantify forces on cell-cell junction and intracellular organelles, such as adherens junctions and nucleus Enable to measure intracellular stress map in 3D	Need to have heavy assumption that mechanical properties of intracellular components, including nucleus, plasma membrane, etc., are the same	(55)

^#IFM and MSN analyses are proceeded using the basic information acquired from TFM, therefore IFM and MSN inherit advantages and disadvantages of TFM-based force measurement analysis.

ENGINEERING TOOLS TO MEASURE CELL-ECM FORCES

Deformable material-based TFM

The first approach to determine cellular traction force using TFM was reported by Harris et al. (28). Since then, TFM has become one of the most successful techniques to quantify cell-ECM forces. Recent fundamental and technological advancements in TFM have significantly enlightened our understanding of mechanobiological parameters in controlling biochemical response and cellular mechanotransduction at cell-matrix interfaces (29). To investigate these parameters, various engineering tools have been developed to measure traction forces exerted by adhered cells onto deformable substrates such as polyacrylamide (PAA), polyethylene glycol (PEG), and polydimethylsiloxane (PDMS) known to have linearly elastic and isotropic properties in response to external force (27, 30, 31). Among these materials, the most extensively used substrates in TFM thus far is a PAA-based elastic substrate firstly introduced by Dembo and his colleagues (27). Generally, in this approach, adhered cell-driven subtle deformation of a substrate less than submicron scale is measured by tracking the displacement of embedded fluorescent beads within PAA hydrogels while adhered cells undergo cell spreading or migration (Fig. 1A) (32). Subsequently, traction forces are calculated using constitutive equations by computational engineering analyses such as standard finite element method (FEM) (33) and Fast Fourier Transform (FFT) (34).

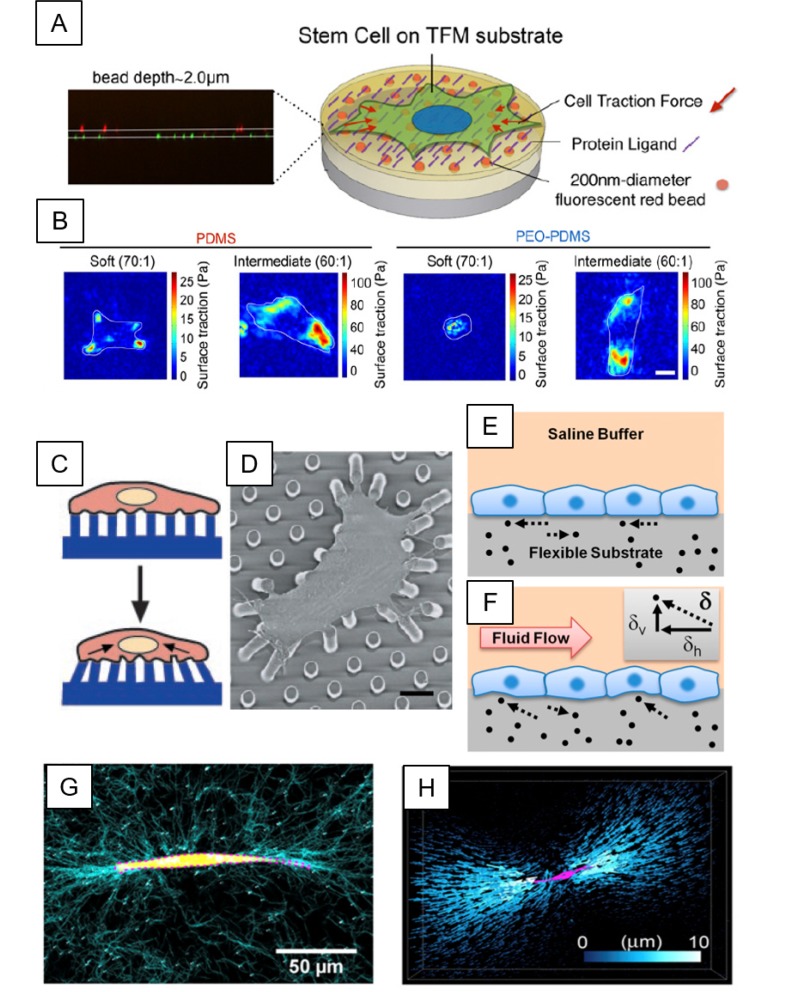
Fig. 1.

Traction force microscopy (TFM)-based cell-ECM force quantification. (A) Schematic diagram for typical TFM platform using deformable substrates, where fluorescence beads (orange dots) are embedded. Cells can adhere to the substrate through surface-conjugated ECMs or protein ligands (purple line). Traction forces (indicated by red arrows) exerted by cells can cause subtle deformation of a substrate, where traction forces can be measured by tracking the displacement of fluorescent beads within the substrate. (B) Traction force stress map showing human bone marrow-derived mesenchymal stem cells adhered onto hydrophobic-polydimethylsiloxane (PDMS) and hydrophilic-PDMS with polyethyleneoxide (PEO) (PEO-PDMS), with varying stiffness ranging from 0.2-0.3 kPa (soft, 70:1) to 5-6 kPa (intermediate, 60:1). (C, D) Schematic and scanning electron microscopy (SEM) image of 2D TFM by micropillars. Vertical arrays of PDMS microposts are fabricated by a photolithography technique. Cell spreads across multiple post beds on which ECMs are pre-coated. Adhered cells can exert traction forces. Traction forces are calculated from the deflection and material property (spring constant) of microposts. (E, F) Schematic representations of traditional 2D TFM method (E) and novel 3D TFM method (F). 3D TFM determines both horizontal (dh) and vertical (dv) components of the displacement vector (d), allowing the calculation of a 3D traction force vector. (G) A breast tumor cell (yellow, MDA-MB-231 cell line) is embedded in 3D type I collagen matrix, visualized by reflective confocal images (cyan). (H) 3D rendering images of bead displacements (blue) and cells (magenta) in 3D collagen matrix. *Figures adapted with permission from; Fig. 1A, B: ref. (32, Fig. 1C, D: ref. (36, Fig. 1E, F: ref. (40, Fig. 1G, H: ref. (44).

Very recently, Razafiarison et al. (32, 35) utilized the aforementioned PAA hydrogel-based TFM method to unveil the relationship of mechanosensitivity of hMSCs to matrix stiffness with supramolecular self-assembly and topology of ECM ligands on biomaterial surfaces with respect to surface energy. The contribution of such relationship to stem cell lineage commitment was evaluated by TFM (32, 35). To validate the hypothesis that surface energy-driven ligand topology could regulate stem cell fates, they introduced hydrophobic-polydimethylsiloxane (PDMS) and its counterpart-hydrophilic-PDMS with polyethyleneoxide (PEO) (PEO-PDMS). Their stiffness varied from 0.2-0.3 kPa (soft, 70:1) to 5-6 kPa (intermediate, 60:1). Surfaces of these substrates were coated with type I collagen (Fig. 1B). Their results indicated that both incorporation of collagen and the increase of matrix stiffness could escalade traction forces on both hydrophobic PDMS and hydrophilic PDMS. In addition, adhered cells on both matrices having intermediated stiffness (5-6 kPa) showed a spreading morphology, resulting in osteogenic lineage commitment. On the other hand, addition of hydrophilic moiety (PEO) to PDMS in a soft rigidity (0.2-0.3 kPa) decreased traction forces. More importantly, cell spreading was inhibited through surface energy-driven collagen assembly, thus promoting adipogenesis of hMSCs rather than osteogensis. Taken together, these studies suggest that matrix stiffness alone could enable stem cells to differentiate into a certain lineage based on their native microenvironment having a tissue-elasticity. These studies also suggest that TFM can offer better understanding of how these stem cells sense matrix stiffness and their subsequent cell spreading and differentiation.

Micropost-based TFM

As an alternative to TFM using PAA hydrogel-based flat and continuous substrates, Chen and his colleagues have developed microfabricated post-array-detectors (mPADs) to manipulate spatial characteristics of substrates with tunable mechanical compliance (Fig. 1C and 1D). Subcellular traction force was calculated based on one-dimensional (1D) Hooke's law by measured deflection and spring constant of deformable posts (36). Very importantly, this study firstly suggested the possibility of tunable mechanical properties of micropost-based substrates by varying heights of deformable posts without changing their surface chemistry. In their follow-up studies using mPADs, Fu et al. (37) have investigated effects of micropost stiffness on cell morphology, cell traction force, and stem cell lineage commitment. As we discussed earlier regarding roles of matrix stiffness in stem cell differentiation, results also showed that cell surface areas, focal adhesions, and traction forces were all increased when the micropost became stiffer. Furthermore, they found a strong correlation between the traction force and stem cell lineage commitment into either osteogenic or adipogenic fate.

In another study, Kiran et al. (36) have elucidated roles of cytoskeletal tension in regulation of RhoA activity known to regulate actin stress fiber formation and actomyosin contractility using pulmonary artery endothelial cells. They utilized micropost-based TFM to confirm that cytoskeletal tension-mediated traction forces were critical to activate GTP-bound RhoA and its downstream effector, Rho-associated protein kinase (ROCK), which was validated by suppressing actin cytoskeletal tension of cells using blebbistatin and cytochalasin D.

Similar approaches have been applied to understand how traction forces could mediate cell shape changes such as cell spreading and flatting of human mesenchymal stem cells (hMSCs) and their differentiation into osteogenic lineage through RhoA/ROCK activation and cytoskeletal tension (38). In that study, Wang et al. (38) utilized mPADs with microcontact printing of fibronectin (FN) into substrates to restrict the cell shape according to FN-patterned island size ranging from 625 to 10000 µm². They demonstrated that the degree of cell spreading was significantly higher in case of cells adhered to FN-coated substrate with larger sizes and that these cells could become highly stretched, resulting in increased actin stress fiber formation and traction forces. These results suggest that cell spreading could induce RhoA/ROCK signaling pathway-dependent cytoskeletal traction force and eventually promote osteogenic differentiation of hMSCs.

In combination, these diverse reports indicate that there is a strong correlation between matrix stiffness and adhered cell-induced traction forces. The degree of traction forces could become one of the determinants for switching stem cell fates through cell spreading.

Recent advancements on measuring three-dimensional (3D) TFM (3D TFM)

Cellular forces are known to predominantly occur in tangential (in-plane) directions (X, Y) with an assumption that there are no normal (out-of-plane) forces to the substrates beneath cells (Fig. 1E) (4). Therefore, TFM has been extensively used to calculate two-dimensional (2D) traction forces generated by adhered cells onto 2D substrates. More recently, however, several studies have reported 3D TFM methods to quantify both tangential and normal forces against 3D ECM by utilizing z-stacked 3D images obtained from confocal microscopy (33, 39, 40). For example, Hur et al. (28) reported 3D TFM techniques to quantify 3D forces exerted by cells on 2D substrates, thus often called as 2.5D, in both tangential and normal directions. They were able to visualize 3D traction forces particularly at the cell-cell junctional and intracellular tensions in monolayers of vascular endothelial cells (Fig. 1F) (4, 33). This method enabled embedded cells to penetrate, stretch, and become physiologically similar cell shapes within 3D hydrogels. Furthermore, they clearly explained that FAs were experiencing various out-of-plane rotational moments at different regions of either migrating or spreading cells (41).

Although mapping multi-dimensional traction forces with spatiotemporal manners is highly demanded, much less is known about how to quantify 3D traction forces exerted by cells within 3D microenvironments. To solve these issues, novel approaches have been reported to quantify the spatiotemporal nature of 3D traction forces exerted by cells within 3D hydrogels, exhibiting linear elastic properties (41, 42). Legant et al. (43) firstly reported the most sophisticated 3D TFM methods by encapsulating GFP-expressing fibroblasts into enzymatically degradable but linear elastic polyethylene glycol (PEG) hydrogels, rather than highly non-linear 3D biopolymers such as collagen, fibrin, and mixture of ECMs.

As an alternative approach to measure 3D traction forces in native nonlinear and viscoelastic connective tissue-like microenvironments, Steinwachs et al. (43) have utilized collagen-based 3D matrices as physiologically equivalent platforms. Their results showed that MDA-MB-231 breast carcinoma cells embedded in 3D collagen gels produced almost constant forces irrespective of the concentration or stiffness of collagen (43). Similarly, Hall et al. (44) have investigated mechanical interactions between encapsulated MDA-MB-231 breast carcinoma cells and fibrous 3D collagen networks using 3D single cell TFM methods. In that study, they established breast tumor-like microenvironments with varying microstructures and densities of 3D fibrous collagen networks exhibiting nonlinear elasticity. Their results revealed a positive mechanical feedback loop. They indicated that cells could locally induce collagen fiber alignment, reinforce the collagen network, and then mechanically reinforce 3D collagen networks, which in return could create greater cellular traction forces evident by significantly long range of displacement propagation (Fig. 1G and 1H). Altogether, these studies highlight the great potential of 3D TFM methods to probe cell-induced multi-dimensional traction forces associated with FAs, actin cytoskeleton, and ECM remodeling.

NOVEL METHODS TO UNDERSTAND JUNCTIONAL OR INTRACELLUAR FORCES

Intracellular force microscopy (IFM)

Soon after substantial progresses have been made in analyzing cellular traction forces via TFM, it has been suggested that the same principle as TFM could be extended to interpret average cell-cell junctional or intracellular forces by applying the same force balance principle. These methods are known as intracellular force microscopy (IFM) and monolayer stress microscopy (MSM) (45-47). Emerging evidences have suggested that adherent cells could exert normal forces to beneath substrates and that these forces are no longer ignorable. Thus, there have been numerous attempts to decipher spatiotemporal regulations of 3D forces around cells (33, 48). Furthermore, recent advances in IFM have unraveled important attributes of force transmission through cell-ECM and cell-cell adhesions or intercellular junctions-mediated force transmission to the ECM (49, 50). In addition, these IFM methods offer new opportunities to assess intracellular and intercellular forces in a group of cells such as cell-cell doublets (46, 51) and monolayers of cells.

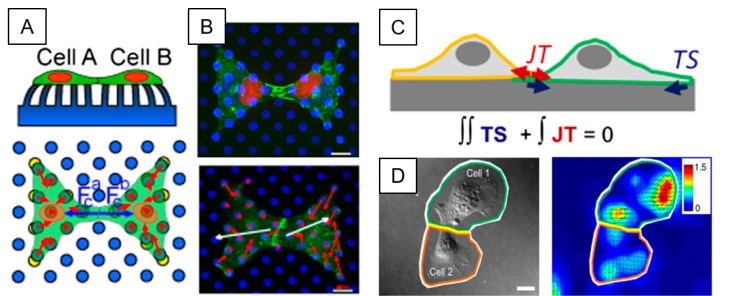
For example, to better understand endogenous intracellular forces, cell-cell tugging junctional forces between pairs of ECs, Liu et al. (51) enabled 2D IFM by utilizing microfabricated arrays of microneedles to evaluate intercellular tugging forces at cell-cell adherens junctions. Their study uncovered that intercellular forces could alter the size of AJs of ECs. They also found close correlations between adherens junction sizes and subsequent forces (Fig. 2A and 2B). Similarly, Chien and his colleagues (47) have expanded this idea into developing novel 3D IFM methods to quantify 3D cell-cell junctional and intracellular forces of monolayers of ECs under static and dynamic shear flow conditions (Fig. 2C and 2D) (47). They investigated how fluid shear stresses could interplay with 3D cell-ECM, cell-cell, and intracellular forces of partially confluent or confluent monolayers of ECs, exhibiting both normal and tangential stresses exerted by monolayers of ECs. These results suggested that intracellular tension could be highly associated with chemo-mechanical feedbacks of ECs under the flow shear, allowing localization and growth of adherens junctions at cell-cell adherens junctions.

Fig. 2.

Intercellular junctional force quantification by IFM. (A) Schematic diagram 2D IFM by micropillars for a pair of endothelial cells at cell-cell junctional interfaces. For a doublet of contacting cells, the net force encompasses both traction force Ti (red arrows) and the intercellular force Fc, (blue arrows). Cell-cell junction or intracellular force Fc plotted over cell A is defined as the net tugging force that cell A is exerting on cell B at the cell-cell junctional interface. Cell B is expected to pull on cell A with an equal amount of opposite force. (B) Cells adhered onto microposts are constricted to have a shape of a bowtie pattern by micropatterned of fibronectin (Cyan) (top). Arrows present the force vectors with direction and magnitude (bottom). Red arrows show individual traction forces and white arrows exhibit tugging force between two cells. (C) 3D IFM by a deformable substrate. Schematic of two cells on a substrate with traction stress TS (blue arrows) and cell-cell tension JT (red arrows). Cell-cell and intracellular forces are determined in 3D by the force balance on the ground of Newton's first law. (D) A phase contrast image of a pair of endothelial cells in contact (left) and corresponding contour and vector map of displacement of two endothelial cells (right). *Figures adapted with permission from ref. (51) for Fig. 2A, B and from ref. (47) for Fig. 2C, 2D.

In a similar approach using IFM-based methods, Ng et al. (52) have demonstrated the dynamics of E-cadherin-associated basal force fluctuations at intercellular adherens junctions of epithelial cells and quantified the force transmission at the cell-cell adherens junctions during spontaneous epithelial cluster formation. In that study, they revealed that at the multi-cellular level intercellular forces, the following transfer through cells required orchestrated changes in cell-matrix adhesions and actomyocin contraction within cells and their neighbors. Furthermore, they revealed that intercellular forces and force exchanges among neighboring cells were increased by recruitment of E-cadherin at cell-cell adherens junctions evident by IFM. Altogether, these results indicate that formation of cell-cell adhesion junctions plays an important role in the exchange of forces among cells within clusters or monolayers of cells.

Monolayer stress microscopy (MSM)

It has been shown that IFM-based methods have great advantages with little assumptions required for mechanical properties of cellular materials such as nuclei, plasma membranes, actin cytoskeletons, and cell-cell junctions to calculate intercellular or intracellular forces at adherens junctions. However, intercellular or intracellular tensions measured by IFM-based methods are averaged in-plane (in 2D) and mapped linearly (in 1D). Therefore, stresses could not be mapped on a 2D plane (53, 54). To resolve these challenges, Tambe et al. (53, 54) have developed a novel method, monolayer stress microscopy (MSM), to quantify forces within and between cell sheets. It can analyze forces based on an assumption that cells are made of one large sheet with one stiffness or Young's modulus. By employing MSM-based method, collective migration behaviors of endothelial and epithelial monolayers could be visible. Their results confirmed that collective migration of neighboring cells had to join forces together to transfer detectable stresses through cell-cell adherens junctions.

Very recently, Serrano et al. (55) have developed a new 3D MSM method to quantify the collective generation and transmission of intracellular stresses within monolayers of ECs in micropatterned islands with varying sizes and shapes, where cell monolayers undergo bending stresses and lateral deformations. Their results revealed that these lateral deformations to cell monolayers could develop over long distances, whereas bending-associated stresses at cell-cell adhesions were predominantly localized within a few cell lengths. Taken together, these studies suggest that novel approaches using MSM-based methods offer the possibility to understand collective migration behaviors of cell sheets and cell-cell adherens junctional forces.

CONCLUDING REMARKS

The past two decades have seen the development of a variety of methods to measure cell-generated forces on FAs, AJs, and intracellular organelles via actin stress fibers. These methods have elucidated many aspects of mechanisms through which cells migrate, proliferate, differentiate, remodel, and mechanosense their microenvironment. In this review, we provided an overview of recent advancements of TFM quantifying cell-ECM forces (or traction forces) exerted on integrin-based focal adhesions and IFM and MSN quantifying cell-cell and intracellular forces applied through E-cadherin-based adherens junctions. As mechanobiology becomes more important in life science and engineering, TFM and IFM will play a fundamental role in elucidating cell functions related to mechanical force responses in biological research field. There is no doubt that these TFM-/IFM-based novel methods for understanding roles of biomechanical forces at interfaces of cell-cell/cell-ECM will open doors to breakthrough technologies for revolutionizing regenerative medicine, disease modelling, and drug discovery.