Abstract
Cetaceans convert dorsoventral body oscillations into forward velocity with a complex interplay between their morphological and kinematic features and the fluid environment. However, it is unknown to what extent morpho-kinematic features of cetaceans are intertwined to maximize their efficiency. By interchanging the shape and kinematic variables of five cetacean species, the interplay of their flukes morpho-kinematic features is examined by characterizing their thrust, power and propulsive efficiency. It is determined that the shape and kinematics of the flukes have considerable influence on force production and power consumption. Three-dimensional heaving and pitching scaling laws are developed by considering both added mass and circulatory-based forces, which are shown to closely model the numerical data. Using the scaling relations as a guide, it is determined that the added mass forces are important in predicting the trend between the efficiency and aspect ratio, however, the thrust and power are driven predominately by the circulatory forces. The scaling laws also reveal that there is an optimal dimensionless heave-to-pitch ratio h* that maximizes the efficiency. Moreover, the optimal h* varies with the aspect ratio, the amplitude-to-chord ratio and the Lighthill number. This indicates that the shape and kinematics of propulsors are intertwined, that is, there are specific kinematics that are tailored to the shape of a propulsor in order to maximize its propulsive efficiency.
Keywords: swimming, bio-propulsion, biological fluid dynamics, scaling laws
1. Introduction
Evolution has created a wide range of morphological and kinematical examples of swimmers that often serve as inspiration for engineering devices [1]. Observations of these swimmers have suggested that there are biologically beneficial morpho-kinematic combinations since specific kinematics are often associated with typical morphological characteristics [2]. Cetaceans such as dolphins, whales and porpoises are some of the examples of aquatic animals that display a wide variety of beneficial morpho-kinematic combinations associated with their biological role, evolutionary history and their aquatic environment. They oscillate their moderate to high aspect ratio flukes in a combined heaving and pitching motion in order to generate propulsive forces through circulatory-based mechanisms [3]. Circulatory-based propulsion has been shown to lead to high-speed, efficiency and manoeuvrability during swimming [4–8], which has motivated numerous theoretical and numerical studies of cetacean swimming [9–16]. However, our understanding of the hydrodynamic interplay between the morphology and the kinematics of the swimmer is still lacking.
The theory of unsteady lift production by combined heaving and pitching foils has a long history. It was first developed by Theodorsen [17] for a two-dimensional aerofoil in a potential flow. This theoretical model was then extended by Garrick [18] to also determine the thrust force and power consumption produced by such motions, which has led to new insights into animal swimming in recent years [19–23]. Later in the 1960s, Lighthill [4] and Wu [11,12] discussed the hydrodynamic analysis of fish and cetacean swimming. Their theories estimated the unsteady force production in a potential flow in the context of elongated body theory [4] and waving plate theory [11,12]. Lighthill further extended his theory to large-amplitude motions [24], however, only added mass forces were considered in the latter work. Chopra [25] and Chopra & Kambe [26] extended Lighthill's theory [27] to three-dimensional flows by incorporating lifting-line theory. Following previous work [25,26], Karpouzian [9] developed an asymptotic theory for high aspect ratio tails and flukes. He compared the performance of fins with varying aspect ratio and sweep, and both variables were found to have a significant impact on thrust and efficiency. Liu & Bose [13] applied a similar lifting surface theory to Chopra & Kambe's [26] study to examine the performance of three cetacean fluke shapes. They used a quasi-vortex-lattice numerical method. By varying pitch and heave amplitude, it was found that the tail shape significantly altered the conditions for maximum efficiency.
Boundary element method numerical simulations helped identify the effects of morpho-kinematic combinations of three-dimensional swimmers [14,28–31] moving at a constant velocity with non-deforming [14,28,29] and deforming wakes [30,31] in terms of thrust production and efficiency. Moored et al. [32] later extended the boundary element method to examine the self-propelled swimming of bioinspired undulatory fins as well as the self-propelled performance of the manta ray [33]. Beyond inviscid methods, Tytell et al. [15] emphasized the close interplay between shape and kinematics as quantified in terms of speed and efficiency. However, these studies have not examined the interdependence between the three-dimensional shape, the unsteady kinematics and the performance of cetacean-like flukes during self-propelled swimming. Also, in many of these studies, morpho-kinematic variations are not decoupled from each other, which means that alteration of one variable may affect the others and cause entangled performance variations.
Scaling laws have provided an additional route to derive insight into the performance of unsteady propulsors and swimmers. Gazzola et al. [34] developed scaling laws to connect basic morpho-kinematic variables such as body length, tail beat amplitude and frequency to the swimming speed of aquatic animals. Floryan et al. [35] and Van Buren et al. [36] considered both circulatory and added mass forces to develop scaling relations that described the mean forces generated by two-dimensional heaving, pitching, and combined heaving and pitching hydrofoils. Concurrently, Moored & Quinn [22] introduced new scaling laws with a different approach than other studies [35,36], by modifying Garrick's linear theory with additional nonlinear terms caused by large-amplitude motion and non-planar, deforming wakes that are not accounted for in classical theory. These new scaling laws were valid for two-dimensional fixed-velocity or self-propelled pitching hydrofoils. Later, Ayancik et al. [37] extended Moored and Quinn's scaling laws to consider three-dimensional effects for varying aspect ratio hydrofoils. They accounted for the added mass of a finite-span propulsor, the downwash/upwash effects from the trailing vortex system, and the elliptical topology of shedding vortices. In the current study, we consider the scaling laws for three-dimensional, combined heaving and pitching hydrofoils by following the framework of Moored & Quinn [22] to modify Garrick's theory for combined heaving and pitching motions with the three-dimensional corrections determined by Ayancik et al. [37].
Motivated by these observations, the present study advances our understanding of cetacean swimming by addressing three driving research questions: how do variations in the shape and kinematics of a self-propelled cetacean fluke alter its performance? In order to maximize the propulsive efficiency, is the specific shape of a cetacean fluke tailored to specific swimming kinematics? How do the forces and energetics scale with the kinematic and shape variables? To answer these questions, the paper is structured in the following manner. Section 2 describes the scope of the problem definition and the approach taken. Section 3 describes the numerical methodology employed. Section 4 details the results of the cetacean simulations. Section 5 presents new scaling laws and verifies their efficacy. Section 6 uses the developed scaling laws to provide deeper insight into cetacean swimming. Finally, section 7 describes the conclusions of the study.
2. Problem definition and approach
2.1. Fluke shape definition
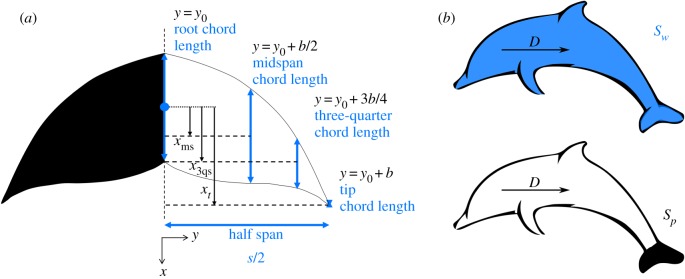
The fluke shape from five species of cetaceans is examined. These species include the beluga whale (Delphinapterus leucas), bottlenose dolphin (Tursiops truncatus), killer whale (Orcinus orca), spotted dolphin (Stenella plagiodon) and the false killer whale (Pseudorca crassidens). Images of the flukes are from live animals in the collection at Sea World. There is extensive inter- and intra-species fluke shape variation among cetaceans that can be quantified by the aspect ratio, sweep angle, curvature and planform area [3]. In this study, we quantitatively characterize a fluke shape with a parametric geometry function developed with coefficients that are fit to a given species. This function measures distances of chord length, c, and the x-position of the chord length at the root, midspan, three-quarter midspan and tip locations on the flukes to define the mid-chord line and the chord distribution by using fourth- and second-order polynomials, respectively.
The parametric geometry functions are NACA-inspired equations in that a chord distribution is wrapped around the mid-chord line just like the thickness distribution is wrapped around the camberline of NACA aerofoils. The measurement locations on the flukes are shown in figure 1a and the polynomial functions are indicated by equations (2.1) and (2.2) for the mid-chord line and chord distribution, respectively. The coefficients in these equations, presented in table 1 for different species, are solved with the help of boundary conditions indicated in figure 1a.
| 2.1 |
and
| 2.2 |
Figure 1.
(a) Demonstration of the characterization of a cetacean fluke planform. (b) Illustration of an idealized swimmer as a combination of a virtual body with drag D and propulsor, and the representation of the wetted surface area, Sw and propulsor planform area, Sp.
Table 1.
Coefficients of mid-chord line and chord distribution equations based on the five cetacean species. The photographs for analysis were from animals in the collections at Sea World.
| species name | A1 | A2 | A3 | A4 | F1 | F2 | F3 |
|---|---|---|---|---|---|---|---|
| Delphinapterus leucas | −0.8471 | 1.0010 | −0.8114 | −0.3708 | −1.2522 | 0.3292 | 0.7415 |
| Tursiops truncatus | −0.5065 | 0.3549 | −0.5429 | −0.3838 | −0.7435 | −0.0356 | 0.7677 |
| Orcinus orca | 0.0172 | 0.0333 | −0.3204 | −0.3385 | −0.7330 | 0.1297 | 0.6771 |
| Stenella plagiodon | −0.5791 | 0.4845 | −0.4384 | −0.3313 | −0.7703 | 0.1985 | 0.6626 |
| Pseudorca crassidens | −0.2670 | 0.1980 | −0.3373 | −0.3461 | −0.3048 | −0.2185 | 0.6923 |
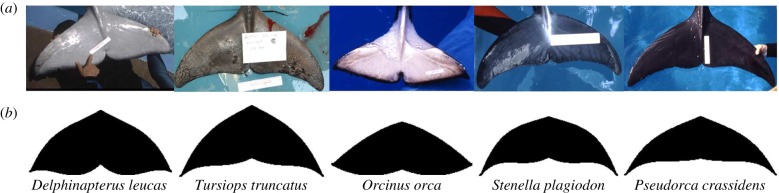
Figure 2 presents a comparison between the biological fluke shapes and the idealized fluke shapes obtained from the parametric geometry function. The parametric geometry function, with its limited number of terms, shows good agreement with biology. However, it is notable that the shapes deviate from the biological flukes at its tips.
Figure 2.
Real fluke images (a) and output images of parametric geometry function (b). The photographs were from animals in the collections at Sea World.
The aspect ratio of the flukes is defined as AR = s2/Sp, where s is the span length and Sp is the planform area. The various species aspect ratios are presented in table 2. The thickness distribution is described by the equations for a NACA 0018 aerofoil as used previously to describe the cross-sectional fluke design [38,39].
Table 2.
Shape and kinematic variables of the five cetacean species.
| species name | AR | h0/c | θ0 (deg) | h* | A* | f (Hz) | Li | m (kg) | Sp [m2] |
|---|---|---|---|---|---|---|---|---|---|
| Delphinapterus leucas | 3.30 | 2.45 | 35.44 | 0.940 | 5.05 | 2 | 0.207 | 433 | 0.2 |
| Tursiops truncatus | 3.90 | 2.51 | 28.85 | 0.960 | 5.12 | 2 | 0.254 | 205 | 0.1 |
| Orcinus orca | 4.40 | 2.50 | 23.61 | 0.974 | 5.07 | 2 | 0.270 | 102 | 0.06 |
| Stenella plagiodon | 4.50 | 3.75 | 21.53 | 0.990 | 7.53 | 2 | 0.178 | 483 | 0.25 |
| Pseudorca crassidens | 5.60 | 2.85 | 29.03 | 0.970 | 5.79 | 2 | 0.201 | 415 | 0.2 |
| interpolated artificial kinematics | 3.30–5.60 | 2.60–3.30 | 27.00 | 0.96–0.98 | 5.28–6.67 | 2 |
2.2. Idealized swimmer
Cetaceans propel themselves by producing their principal thrust from the dorsoventral oscillations of their flukes in a combined heaving and pitching motion. In this case, the cetacean body is considered to be the main source of drag while the flukes are considered to be the main source of thrust [40,41]. As a first-order approximation, the presence of a body can be modelled with a virtual body that is not present in the computational domain but acts as a drag source applied to a self-propelled fluke (figure 1b). This approximation assumes there is no body/fluke interaction. While this is a reasonable first-order approximation, it does not fully account for the flow physics of a self-propelled swimmer [42]. The drag, D, from the virtual body is defined as the following:
| 2.3 |
where ρ is the density of the fluid, CD is the coefficient of drag, Sw is the wetted surface area of the body and flukes, and U is the time-varying swimming speed of the virtual body–fluke combination. Identical virtual body parameters are used in combination with each fluke shape in order to isolate the effects of the fluke shape and its kinematics on the swimming performance. The drag coefficient and the wetted area to propulsor planform area ratio are chosen as CD = 0.01 and Swp = Sw/Sp = 30 m2, respectively, which are typical values for cetaceans [43,44]. The propulsor area, Sp and Sw are kept constant to maintain Swp and defined as Sp = 1 m2 and Sw = 30 m2. The virtual body is given a mass of 9000 kg, which is calculated based on wetted surface area of an idealized swimmer with the help of a correlation given in the study of Fish [43] and kept constant for all the species' fluke shapes examined.
2.3. Input variables and parameters
In self-propelled swimming, the swimmer reaches a cycle-averaged steady state where the time-averaged thrust and drag of a swimmer are balanced. The drag coefficient of the body, CD, and the wetted area to propulsor planform area ratio, Swp, both affect how thrust and drag are balanced on a swimmer and their combination is represented by the Lighthill number
| 2.4 |
The Lighthill number also represents the propulsor loading during self-propelled swimming. When Li is low there is low propulsor loading and vice versa. Low Li swimmers will swim faster than high Li swimmers for given constant kinematics and propulsor geometries. In the current study, the Lighthill number is fixed to Li = 0.3, which is in a range typical of animal locomotion [45].
A combined heaving and pitching motion with a fixed phase delay between pitching and heaving of ψ = 270° is defined as
| 2.5 |
and
| 2.6 |
Here, h0, θ0 and f correspond to the heave amplitude, pitch amplitude and the oscillation frequency, respectively. A constant frequency of f = 2 Hz is used throughout the simulations as an average frequency used by cetaceans [43]. For the combined heaving and pitching motion of the flukes, the peak-to-peak amplitude is defined as A = 2h(t*) + c sin[θ(t*)], where t* represents the time when the maximum amplitude is reached. The peak-to-peak amplitude is non-dimensionalized by the chord length as A* = A/c and reported for the studied species in table 2. The heaving and pitching amplitudes, at the time when the maximum amplitude is reached, can then be non-dimensionalized by the peak-to-peak amplitude as
| 2.7 |
Here, h* and θ* represent the dimensionless heave-to-pitch and pitch-to-heave ratios, respectively. These terms identify what proportion of the total amplitude is due to heaving and pitching motions. For instance, h* = 0, h* = 0.5 and h* = 1 represent a pure pitching motion, a combined heaving and pitching motion with equal parts heaving and pitching, and a pure heaving motion, respectively. The dimensionless heave-to-pitch and pitch-to-heave ratios are related by h* + θ* = 1, which highlights the redundancy between the two variables [46]. As such, only the dimensionless heave-to-pitch ratio will be used in this study, which is reported for the examined species in table 2.
2.4. Output variables
The output variables used in the current study are based on the mean values of quantities that are time-averaged over an oscillation cycle and are denoted with an overline such as (). Mean values are acquired once a self-propelled swimmer has reached the steady state of its cycle-averaged speed. Steady-state conditions occur when , where is the net thrust coefficient and T is the thrust force, calculated by integrating of the pressure forces acting on the fluke projected in the x-direction. Also, the dimensionless swimming speed is non-dimensionalized by the frequency of motion and the length of the swimmer, L, as
| 2.8 |
Here, U* can be described as the dimensionless stride length since it is a measure of the number of body lengths travelled in one cycle of motion. Additionally, the characteristic length was chosen to be L = 30 m for all of the fluke shapes tested based on the correlation used in the study of Fish [43].
In self-propelled swimming, the reduced frequency (k) and the Strouhal number (St) become outputs, since the swimming speed is unknown a priori and they are defined as
| 2.9 |
Furthermore, the time-averaged thrust (CT) and power (CP) coefficients are non-dimensionalized by a characteristic added mass force and a characteristic added mass power as defined in Garrick's theory [18],
| 2.10 |
Here, the power (P) is calculated as the negative inner product of the force vector (Fele) and velocity vector (uele) of each boundary element, that is, where is the body surface. The mean thrust and power may be represented as the thrust and power coefficients by normalizing with the dynamic pressure as
| 2.11 |
These two normalizations are related by the simple transformations of and . The propulsive efficiency (η) is then the ratio of the thrust and power coefficients regardless of the chosen normalization
| 2.12 |
The cost of transport, CoT, will also be reported in this study to measure the energy consumption per unit distance per unit mass (m) defined as
| 2.13 |
The CoT can be connected to the efficiency as for self-propelled swimming [22] where the time-averaged thrust and drag balance each other as . The CoT can then be rearranged by substituting the drag law of equation (2.3) into equation (2.13)
| 2.14 |
The parameters within the parentheses in equation (2.14) are constants throughout the current study. This means that the following proportionality will connect the dimensionless stride length, efficiency and cost of transport:
| 2.15 |
2.5. Approach
First, biological morpho-kinematic features of five cetacean species are identified. To be used as a reference case, numerical simulations are performed for each species by using their corresponding variables including mass, Li number, planform area, fluke shape and kinematics (table 2), and the results are discussed.
However, to be able to directly probe the connection between the fluke shape and swimming, in the second part of the study, a single virtual body with a fixed mass and Li number is used in conjunction with all of the fluke shapes and kinematics. Then, the fluke shapes of five cetacean species and their corresponding kinematics are interchanged creating 25 shape and kinematic permutations. Then the thrust, power and efficiency of swimming in relation to the produced wake structures are examined. Artificial kinematics that do not correspond to known species are also considered in order to more evenly resolve the variable space. Table 2 also shows the range of interpolated artificial kinematic variables used in this study.
3. Numerical methods
To model the forces acting on self-propelled flukes, we use an unsteady three-dimensional boundary element method for potential flow, that is, irrotational, incompressible and inviscid flow governed by Laplace's equation. There is a general solution to the governing equation that reduces the problem to finding a distribution of doublet and source elements on the propulsor's surface and wake that satisfy the no-flux boundary condition on the fluke's surface. An internal Dirichlet boundary condition is imposed in order to enforce this condition at each time step. The far-field boundary condition, which is that flow perturbations must decay with distance from the propulsor, is implicitly satisfied by the doublet and source elements. The propulsor and wake surface are discretized by a finite number of quadrilateral boundary elements. Each element on the body surface has an associated collocation point located at the element's centre just inside the body where the Dirichlet condition is enforced. An explicit Kutta condition is enforced at the trailing edge, and at each time step a wake doublet element is shed with a strength that satisfies Kelvin's circulation theorem. The wake elements are advected with the local velocity field by applying the desingularized Biot–Savart Law [47] leading to wake deformation and roll up. The tangential perturbation velocity over the body is found by a local differentiation of the perturbation potential. The unsteady Bernoulli equation is then used to calculate the pressure field acting on the body. Finally, the self-propelled body dynamics are calculated when the streamwise translational degree of freedom is unconstrained. The body velocity and position are determined at the current time step through forward differencing and the trapezoidal rule, respectively.
| 3.1 |
and
| 3.2 |
where is the net force acting on the foil in the streamwise direction at the nth timestep, xb is the body position of the foil and Δt is the time step. Further details of the method and extensive validations of the solver can be found in [32]. Further validations and applications of the solver can be found in [21,23,33,37,48].
4. Swimming performance
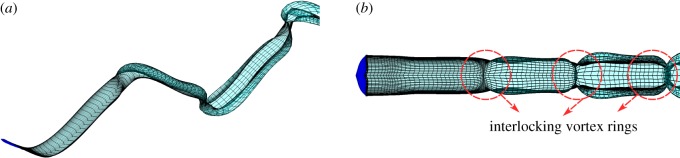
Figure 3a presents an isometric view and (b) a top view of the typical deforming wake elements shed from the self-propelled flukes. By examining the roll-up of the wake elements, it is evident that the wake structure consists of a series of interlocked and elongated vortex ring structures. The rings take on a rectangular-like or elliptical-like shape.
Figure 3.
Compilation of (a) an isometric and (b) a top view of the deforming wake elements from a typical case.
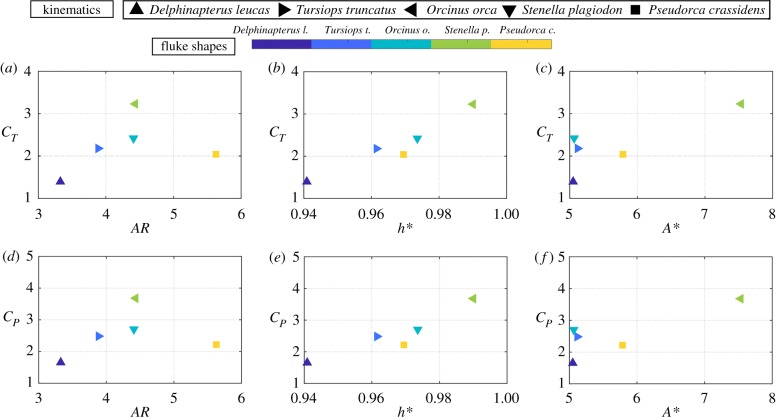
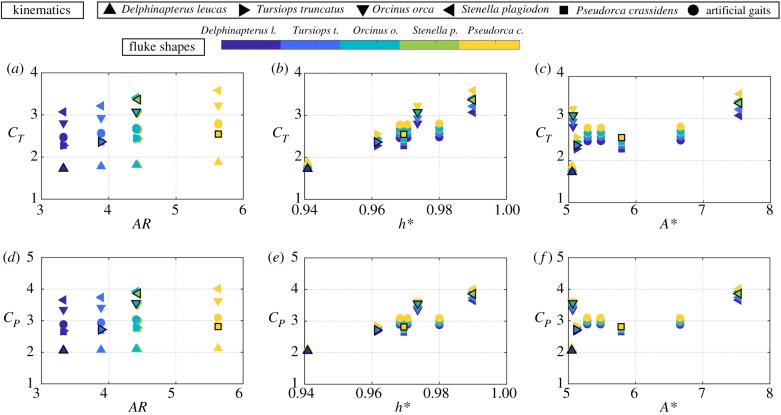
Figure 4 presents the thrust and power coefficients as a function of the aspect ratio, dimensionless heave-to-pitch ratio, and amplitude-to-chord ratio for the five cetacean species using their specific biological variables as indicated in table 2.
Figure 4.
Self-propelled thrust and power coefficients as a function of (a,d) aspect ratio, (b,e) the dimensionless heave-to-pitch ratio, and (b,e) amplitude-to-chord-ratio for the five species with their own biological variables.
The marker colours represent the fluke shapes as indicated in the colour bar above the figure, while the marker style denotes the kinematics of the species. Stenella plagiodon has the highest thrust and power coefficients, which seems to be generally correlated to its high h* value and lower Li. The thrust and power coefficients show a generally increasing trend for increasing h*, although not a monotonic trend, while they show no clear trends with A* or AR. This highlights the difficulty in deciphering trends in the performance data of various species, and consequently, the physical nature of their force production and energetics when their body properties, fluke shape and kinematics are all allowed to vary. Now, we reduce the number of variables by fixing the body properties to a mass of m = 9000 kg and a Lighthill number of Li = 0.3, and only allow the fluke shape and kinematics to vary.
Figure 5 presents the thrust and power coefficients as functions of the aspect ratio, dimensionless heave-to-pitch ratio and amplitude-to-chord ratio for the various fluke shape and kinematic permutations when the mass and Li number are kept constant for all species. The marker colours and shapes are the same as represented above in figure 4. The black outlined markers in the figure represent the species swimming with their corresponding kinematics. In contrast to figure 4, in figure 5a,d, the thrust and power coefficients increase monotonically with increasing aspect ratio. When the aspect ratio is fixed, the thrust and power coefficients show a wide range of variation due to the varying kinematics. By using fixed body properties, a clear trend emerges for variations in the aspect ratio. However, the thrust and power coefficients show the same trends as seen in the figure 4, for increasing h* and A*.
Figure 5.
Self-propelled thrust and power coefficients as a function of (a,d) aspect ratio, (b,e) the dimensionless heave-to-pitch ratio, and (c,f) amplitude-to-chord-ratio. The black outlined markers in the figure represent the species swimming with their corresponding kinematics.
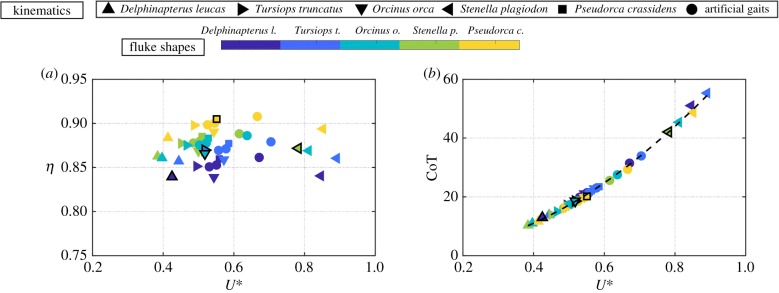
Figure 6 presents the propulsive efficiency and cost of transport as a function of the dimensionless stride length. High propulsive efficiency for the cetaceans is observed in the range of 83–92%, which is in accordance with previous findings [44,49]. For constant kinematic variables, the Pseudorca crassidens shape always has the highest efficiency. Similarly, for constant shape variables the Delphinapterus leucas kinematics always have the highest efficiency. In fact, the efficiency data show that the fluke shape and its kinematics are not tailored to each other, at least for the range of h* examined. Viewed in another way, there is one shape that maximizes the propulsive efficiency regardless of the kinematics and vice versa. However, this result is counterintuitive and, in fact, through the use of scaling laws (§6) it will be shown that in general the shape and kinematics that maximize the efficiency are interdependent.
Figure 6.
Self-propelled efficiency and cost of transport as a function of the dimensionless stride length U∗=U/Lf, where L is the body length of the swimmer.
It is also interesting the note the performance comparison of species with their own shape and kinematics. In order from the highest to lowest efficiency, the species are Pseudorca crassidens, Stenella plagiodon, Orcinus orca, Tursiops truncatus and Delphinapterus leucas. In order from the highest to lowest dimensionless stride length (a normalized measure of swimming speed), the species are Stenella plagiodon, Pseudorca crassidens, Orcinus orca, Tursiops truncatus and Delphinapterus leucas. These results confirm the performance comparison shown in Fish [44].
The CoT is another energetic metric commonly used in biological literature since it is easier to measure than propulsive efficiency. The CoT is observed to have an increasing trend for increasing values of the dimensionless stride length. At first, it is surprising that all of the data collapses to a curve, however, equation (2.15) reveals the scaling trend. The proportionality relation predicts that the CoT will vary quadratically with U* and inversely with η, however, η varies over a small range leading to the predominant scaling with the non-dimensional stride length. In fact, the parameters in equation (2.14) are substituted along with the average efficiency of η = 0.87 and the cost of transport as a function of the non-dimensional stride length is determined and plotted in figure 6 as the dashed line. The dashed line shows good agreement with the data suggesting that it properly captures the scaling trends. Note that at the high U* values, the CoT are underpredicted by the dashed line. This occurs since the efficiency at the high U* values is lower than the average of η = 0.87. The increasing trend in the CoT with dimensionless stride length indicates that even though the efficiency is only changing slightly across the range of U*, the amount of power expended to swim faster is increasing by a factor of 4 across the same range of U*.
5. Scaling approach
For the readers not interested in the development of the scaling laws, they can go directly to §6 to understand the physical insights derived from the scaling laws. In this section, to gain deeper insight into the physics of cetacean locomotion and more precise models of the force production and energetics, scaling laws are sought. We begin our scaling analysis with Garrick's solution [18] for the thrust and power coefficients of a combined heaving and pitching foil where the pitch axis is about the leading edge
| 5.1 |
| 5.2 |
Here, F and G are the real and imaginary parts of Theodorsen's lift deficiency function, respectively [17]. The thrust and power are decomposed into their purely pitching, purely heaving and combined heaving and pitching terms as denoted by the underbrackets. The coefficients have exact values from theory of and . Garrick's theory makes further assumptions that the motion is of small amplitude, and that the wake is non-deforming and planar. However, the simulations in this study use large-amplitude motions and deforming wakes. Therefore, in order to more accurately produce a scaling model relevant to the current data, the exact theoretical coefficients are relaxed and left to be determined. Now, equations (5.1) and (5.2) can be written in a more compact form and the approximations , 4ch0θ0/A2 ≈ h*θ*, and can be substituted
| 5.3 |
and
| 5.4 |
The approximations that were substituted become equalities in the limit of small amplitude motions [46], however, the current study examines large-amplitude motions thus necessitating the use of the approximation symbol. In this study, h* varies over a small range of 0.94 ≤ h* ≤ 0.99. This indicates that cetaceans are swimming with heave dominated motions. Since θ* = 1 − h* and h* is close to one, the purely pitching term, which is proportional to θ*2 is small and can be neglected. The combined heaving and pitching term, which is proportional to h*θ* is small, but not negligible. Consequently, we neglect the purely pitching terms in the thrust and power relations thereby reducing the equations to
| 5.5 |
| 5.6 |
Importantly, it should be noted that neglecting the purely pitching term also eliminated the added mass thrust and power terms from the equations. Now, the reduced relations valid for high h* cases are only composed of circulatory terms as indicated by the presence of Theodorsen's lift deficiency function in each term. Even with the coefficients left to be determined, the reduced relations still do not account for the three-dimensional nature of cetacean flukes. To extend the scaling relations to three dimensions, we will only consider modifications that account for variations in aspect ratio and we will assume that the effects of variations in sweep and curvature are small. Following our previous work on scaling laws for three-dimensional pitching propulsors [37], we will apply circulatory corrections to capture the effects of upwash and downwash from the trailing vortex system. Based on classical finite wing theory [50], the circulatory forces should scale with the aspect ratio as AR/(AR + 2). By applying this correction to the two-dimensional relations, the final three-dimensional scaling relations can be obtained
| 5.7 |
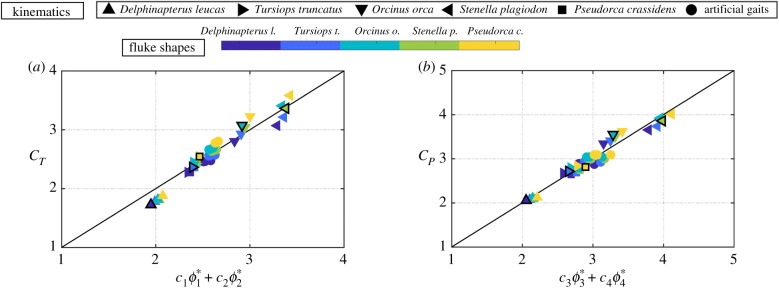
Figure 7a,b presents the thrust and power coefficients for all of the cases as a function of the scaling relations. The coefficients are determined by minimizing the squared residuals and are found to be c1 = 18.11, c2 = 22.80, c3 = 15.74 and c4 = −7.65. We see the expected linear relationship between the thrust and power scaling models and the corresponding numerical data. For both power and thrust, there is a collapse of the data to within ± 10% of the full-scale value. This indicates that our simplified scaling model closely describes the propulsive performance of cetacean swimming. The discrepancies between the scaling model and the simulated data may be due to shape variations that were not accounted for in the model, such as variations in sweep angle and/or curvature, and nonlinearities not accounted for in Garrick's theory, such as large-amplitude motion and/or a deforming wake. To make the scaling relations collapse to the line, we need to add terms to account for these shape effects and nonlinearities, however, that is beyond the scope of the current analysis.
Figure 7.
Scaling of the (a) time-averaged thrust and (b) power coefficients for all motion amplitudes and aspect ratios tested.
6. Discussion and physical insight derived from the scaling laws
The scaling laws are now used as a guide to more deeply understand the effects of shape and kinematics on the efficiency. As shown in the previous section, the scaling laws accurately capture both the thrust and power of cetacean swimmers. This leads to the conclusion that cetacean propulsion is driven by circulatory force production, which is in-line with the proposition that cetaceans use the so-called ‘lift-based’ forces for propulsion [8]. However, the scaling laws reveal a new insight into cetacean swimming. If we take the ratio of the thrust and power coefficients as stated from the scaling laws, then the scaling law for the propulsive efficiency is
| 6.1 |
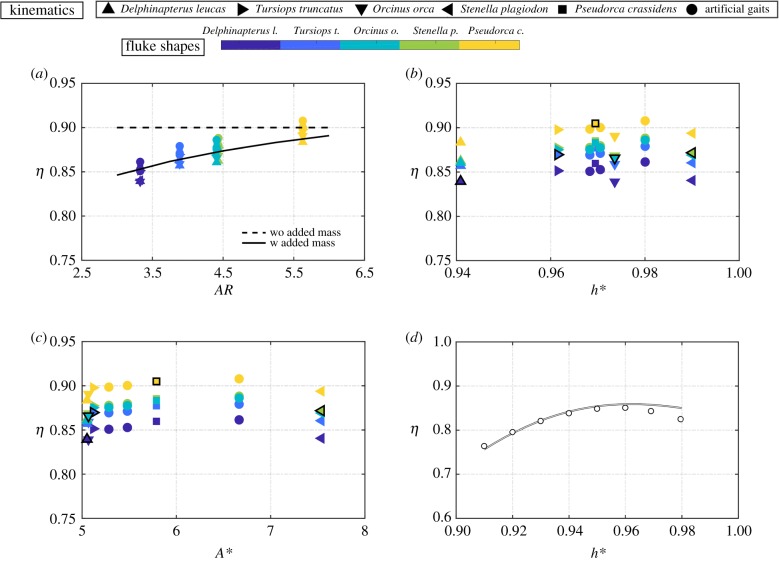
Notice that the circulatory force reduction of AR/(AR + 2) due to the upwash/downwash of the trailing vortex system is in each term of the thrust and power coefficients and therefore cancels in the calculation of efficiency. However, figure 8a presents the efficiency as a function of the aspect ratio for the cetacean simulations and the scaling law (dashed line) applied to the kinematics of Orcinus orca (down triangle). It can be clearly observed that the efficiency increases for higher aspect ratio flukes, however, it is also clear that the scaling law does not capture this trend when only circulatory forces are considered. This motivated us to reconsider the neglected added mass terms due to pitching, which have a different aspect ratio correction than circulatory terms of AR/(AR + 1) as determined in our previous work [37]. The new scaling relations will then be
| 6.2 |
By minimizing the squared residuals, the coefficients are determined to be c1 = 18.107, c2 = 22.804, c3 = 6.749 × 10−6, c4 = 17.527, c5 = −9.284 and c6 = 7.489. The uncertainty between the scaling law prediction and simulation data slightly improves to be within 8.1% and 6.6% of the thrust and power data. Interestingly, the c3 coefficient on the added mass thrust term is effectively zero and that term may be neglected without a loss in accuracy in the scaling. Yet, the added mass power term (with c6 coefficient) is crucial to the improved accuracy in the efficiency scaling law. When the scaling laws with the re-introduced added mass terms are graphed in figure 8a (solid line) for the kinematics of Orcinus orca as a function of the aspect ratio it is seen that the proper trend with aspect ratio is now recovered. Since adding the added mass terms made little improvement to the prediction of thrust and power, but revealed the correct trend in the efficiency we can conclude that the thrust production and power consumption are indeed driven by circulatory force production, however, the efficiency is driven by a combination of circulatory and added mass forces. If only circulatory forces are considered or only added mass forces are considered, then there is no predicted trend in the efficiency with aspect ratio. Only by including both types of terms does the proper trend emerge. Both trends show a monotonic increase with aspect ratio, however they have different rates of increase and they likely asymptote to different values as expected. The agreement between the rates of increase may be improved by considering the terms in the scaling laws that have been neglected.
Figure 8.
The cetacean simulation efficiency as a function of (a) aspect ratio, (b) dimensionless heave-to-pitch ratio, and (c) dimensionless amplitude. The dashed line in (a) represents the scaling laws (5.7) without added mass forces included with varying aspect ratio and all other kinematic/shape variables the same as Orcinus orca. The solid line in (a) represents the scaling laws (6.2) with added mass forces included. Additional simulations using the kinematic/shape variables of Delphinapterus leucas are reported in (d) in terms of the efficiency as a function of the dimensionless heave-to-pitch ratio. The solid line in (d) is the prediction from the scaling laws (6.2) with added mass forces included.
Figure 8b,c shows the efficiency as a function of h* and A* for the simulations. The efficiency is increasing with increasing h* and A* until it reaches to a peak point, then starts to decrease with increasing h* and A* values. This suggests that there may be an optimal h* and/or A* value within the range of h* examined here. However, without independently varying h* and A* it is unclear which variable has an optimal condition. Moreover, the range of h* used in the simulations is rather narrow, and the peak in efficiency may just be a local peak. Therefore, the accuracy of the efficiency scaling law must be assessed for lower h* values beyond the range of h* used in the simulations.
In figure 8d, the scaling law (solid line) was first used to predict the trend in efficiency with a variation in h* when all other variables were held constant as those of the Delphinapterus leucas kinematics and shape. To be clear, the reduced frequency used in the efficiency scaling is determined from the self-propelled equations of motion as outlined in [22]. Specifically, the reduced frequency can be directly determined by using eqn (33) in that study once Li and A* are specified.
The scaling laws predict that indeed when h* is varied independently, there is an optimal heave-to-pitch ratio that maximizes the efficiency (), which is inside the examined range of the cetacean simulations. To verify that this is not just an artefact of the scaling relations, additional simulations were run (circles) where Delphinapterus leucas kinematic/shape variables were used with the exception of h*. Indeed, the scaling prediction of an optimal condition for h* is validated, though the simulations calculate a slightly different value of . The scaling laws also somewhat overpredict the efficiency of the simulations for the highest h* values. Yet, these results provide confidence that the scaling laws can be used in the vicinity, but outside of their validation range to predict the broad trends in the data.
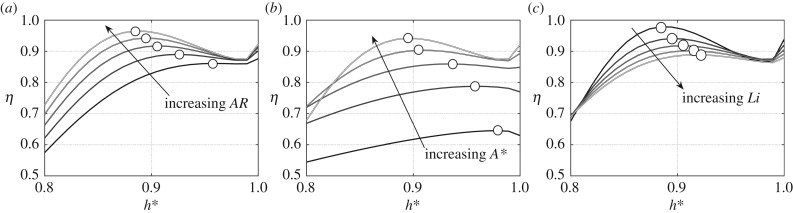
Next we use the scaling laws to examine the trends in efficiency when the AR, A*, Li and h* are all varied independently. As a baseline case, the shape and kinematics of Delphinapterus leucas are chosen since it is approximately at the average efficiency of the dataset. The shape and kinematic variables that define its performance are h* = 0.94, A* = 5.05, and AR = 3.3. Figure 9a presents the efficiency as functions of h* and AR while A* = 5.05, figure 9b presents the efficiency as functions of h* and A* while AR = 3.3, and figure 9c presents the efficiency as functions of h* and Li while A* = 5.05 and AR = 3.3. All figures show that there is an optimal h* that maximizes the efficiency.
Figure 9.
Efficiency as a function of h* for (a) A*=5.05, 1 ≤ AR ≤ 5 and Li = 0.3, (b) AR = 3.3, 1 ≤ A* ≤ 6 and Li = 0.3, (c) A* = 5.05, AR = 3.3 and 0.2 ≤ Li ≤ 0.6. Colours from black to white correspond to small to large values, respectively, for AR, A* and Li.
Surprisingly, as the aspect ratio is increased the optimal h* decreases. This indicates that actually the shape and kinematics of cetaceans are interdependent, as originally hypothesized, instead of independent as was observed with only a narrow range of h*. To be clear, the cetacean simulations and the scaling laws do not contradict each other. In the h* range of the cetacean simulations both the scaling laws and the simulations produce the same result that one shape and one set of kinematics maximizes the efficiency performance independently. However, by using the scaling laws to probe a wider range of h*, it is observed that, in fact, the shape and kinematics are interdependent. Additionally, as A* increases the optimal h* decreases slightly, and the peak efficiency is increased when AR and A* increase. By contrast, it is observed that the optimal h* value increases and the efficiency decreases with increasing Li. This result is a consequence of a chain of effects that an increase in Li leads to a higher drag producing body, lower swimming speed, higher reduced frequency, and therefore lower efficiency for heavy-dominated motions [18,22].
Future work should extend these scaling laws to apply to a wide range of variables by generating a larger data range of h* and including the nonlinear terms that are known to be important for low h* cases [37]. Moreover, the scaling laws should be further extended to cover a broader range of propulsor shapes that go beyond those shapes that have evolved for cetaceans.
7. Conclusion
The connection between the fluke shape and the swimming kinematics of cetaceans were examined by exchanging the shape and kinematic variables of different species. When the fluke aspect ratio and dimensionless heave-to-pitch ratio are increased, the thrust production and power consumption also increase. Cetacean efficiencies are found to range between 83 and 92% with the peak efficiency occurring for the Pseudorca crassidens shape with the Delphinapterus leucas kinematics. When considering the performance of a species own fluke shape and kinematics, the most efficient swimmer is Pseudorca crassidens and the swimmer with the fastest relative speed (dimensionless stride length) is Stenella plagiodon. Within the narrow range of dimensionless heave-to-pitch ratio of 0.94 ≤ h* ≤ 0.99, the shape and kinematics of cetacean flukes are found to have independent effects on the swimming efficiency, where one shape is always the most efficient regardless of the kinematics and vice versa. New scaling laws for the thrust production and power consumption of three-dimensional combined heaving and pitching flukes are developed by using Garrick's linear theory [18] and Ayancik's et al. [37] three-dimensional corrections to account for variations in the aspect ratio of propulsors. The scaling laws reveal that the thrust and power production of cetaceans are driven by circulatory forces, however, the trends in the efficiency emerge from both the circulatory and added mass forces acting on the flukes. The scaling laws further indicate that there is an optimal h* that maximizes the efficiency and it is dependent upon the aspect ratio, amplitude to-chord ratio and the Lighthill number. This leads to the conclusion that in fact during peak efficiency swimming, the shape and kinematics of a cetacean propulsor are tailored to each other.
Data accessibility
This article does not contain any additional data.
Authors' contributions
F.A. and K.W.M. conceived the study. F.A. designed and performed the numerical simulations and developed scaling relations. F.E.F. collected biological data. F.A., F.E.F. and K.W.M. analysed results. F.A. and K.W.M. wrote the paper and all co-authors revised the manuscript.
Competing interests
We declare we have no competing interests.
Funding
This work was supported by the Office of Naval Research (ONR) under Multidisciplinary University Research Initiative (MURI) programme (grant no. N00014-14-1-0533).
References
- 1.Van Rees W, Gazzola M, Koumoutsakos P. 2015. Optimal morphokinematics for undulatory swimmers at intermediate Reynolds numbers. J. Fluid Mech. 775, 178–188. ( 10.1017/jfm.2015.283) [DOI] [Google Scholar]
- 2.Webb PW. 1984. Body form, locomotion and foraging in aquatic vertebrates. Am. Zool. 24, 107–120. ( 10.1093/icb/24.1.107) [DOI] [Google Scholar]
- 3.Fish FE, Rohr JJ. 1999. Review of dolphin hydrodynamics and swimming performance. Technical report San Diego, CA: Space and Naval Warfare (SPAWAR) Systems Center. [Google Scholar]
- 4.Lighthill MJ. 1969. Hydromechanics of aquatic animal propulsion. Annu. Rev. Fluid Mech. 1, 413–446. ( 10.1146/annurev.fl.01.010169.002213) [DOI] [Google Scholar]
- 5.McNeil AR. 1983. Animal mechanics. Oxford, UK: Blackwell Science. [Google Scholar]
- 6.Daniel TL. 1984. Unsteady aspects of aquatic locomotion. Am. Zool. 24, 121–134. ( 10.1093/icb/24.1.121) [DOI] [Google Scholar]
- 7.Webb PW. 1988. Simple physical principles and vertebrate aquatic locomotion. Am. Zool. 28, 709–725. ( 10.1093/icb/28.2.709) [DOI] [Google Scholar]
- 8.Fish FE. 1996. Transitions from drag-based to lift-based propulsion in mammalian swimming. Am. Zool. 36, 628–641. ( 10.1093/icb/36.6.628) [DOI] [Google Scholar]
- 9.Karpouzian G, Spedding G, Cheng HK. 1990. Lunate-tail swimming propulsion. Part 2. Performance analysis. J. Fluid Mech. 210, 329–351. ( 10.1017/S0022112090001318) [DOI] [Google Scholar]
- 10.Cheng HK, Murillo LE. 1984. Lunate-tail swimming propulsion as a problem of curved lifting line in unsteady flow. Part 1. Asymptotic theory. J. Fluid Mech. 143, 327–350. ( 10.1017/S0022112084001373) [DOI] [Google Scholar]
- 11.Wu TY. 1961. Swimming of a waving plate. J. Fluid Mech. 10, 321–344. ( 10.1017/S0022112061000949) [DOI] [Google Scholar]
- 12.Wu TY. 1971. Hydromechanics of swimming propulsion. Part 1. Swimming of a two-dimensional flexible plate at variable forward speeds in an inviscid fluid. J. Fluid Mech. 46, 337–355. ( 10.1017/S0022112071000570) [DOI] [Google Scholar]
- 13.Liu P, Bose N. 1993. Propulsive performance of three naturally occurring oscillating propeller planforms. Ocean Eng. 20, 57–75. ( 10.1016/0029-8018(93)90046-K) [DOI] [Google Scholar]
- 14.Liu P, Bose N. 1997. Propulsive performance from oscillating propulsors with spanwise flexibility. Proc. R. Soc. Lond. A 453, 1763–1770. ( 10.1098/rspa.1997.0095) [DOI] [Google Scholar]
- 15.Tytell ED, Borazjani I, Sotiropoulos F, Baker TV, Anderson EJ, Lauder GV. 2010. Disentangling the functional roles of morphology and motion in the swimming of fish. Integr. Comp. Biol. 50, 1140–1154. ( 10.1093/icb/icq057) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Borazjani I, Sotiropoulos F. 2010. On the role of form and kinematics on the hydrodynamics of self-propelled body/caudal fin swimming. J. Exp. Biol. 213, 89–107. ( 10.1242/jeb.030932) [DOI] [PubMed] [Google Scholar]
- 17.Theodorsen T. 1935. General theory of aerodynamic instability and the mechanism of flutter. NACARep 496, 7. [Google Scholar]
- 18.Garrick IE. 1937. Propulsion of a flapping and oscillating airfoil. NACARep 567, 1–14. [Google Scholar]
- 19.Anderson JM, Streitlien K, Barrett DS, Triantafyllou MS. 1998. Oscillating foils of high propulsive efficiency. J. Fluid Mech. 360, 41–72. ( 10.1017/S0022112097008392) [DOI] [Google Scholar]
- 20.Dewey PA, Boschitsch BM, Moored KW, Stone HA, Smits AJ. 2013. Scaling laws for the thrust production of flexible pitching panels. J. Fluid Mech. 732, 29–46. ( 10.1017/jfm.2013.384) [DOI] [Google Scholar]
- 21.Quinn DB, Moored KW, Dewey PA, Smits AJ. 2014. Unsteady propulsion near a solid boundary. J. Fluid Mech. 742, 152–170. ( 10.1017/jfm.2013.659) [DOI] [Google Scholar]
- 22.Moored KW, Quinn DB. 2019. Inviscid scaling laws of a self-propelled pitching airfoil. AIAA J 57, 3686–3700. [Google Scholar]
- 23.Akoz E, Moored KW. 2018. Unsteady propulsion by an intermittent swimming gait. J. Fluid Mech. 834, 149–172. ( 10.1017/jfm.2017.731) [DOI] [Google Scholar]
- 24.Lighthill MJ. 1971. Large-amplitude elongated-body theory of fish locomotion. Proc. R. Soc. Lond. B 179, 125–138. ( 10.1098/rspb.1971.0085) [DOI] [Google Scholar]
- 25.Chopra MG. 1976. Large amplitude lunate-tail theory of fish locomotion. J. Fluid Mech. 74, 161–182. ( 10.1017/S0022112076001742) [DOI] [Google Scholar]
- 26.Chopra MG, Kambe T. 1977. Hydromechanics of lunate-tail swimming propulsion. Part 2. J. Fluid Mech. 79, 49–69. ( 10.1017/S0022112077000032) [DOI] [Google Scholar]
- 27.Lighthill J, Blake R. 1990. Biofluiddynamics of balistiform and gymnotiform locomotion. Part 1. Biological background, and analysis by elongated-body theory. J. Fluid Mech. 212, 183–207. ( 10.1017/S0022112090001926) [DOI] [Google Scholar]
- 28.Bose N. 1995. Performance of chordwise flexible oscillating propulsors using a time-domain panel method. Int. Shipbuilding Progress 42, 281–294. [Google Scholar]
- 29.Liu P. 1996. A time-domain panel method for oscillating propulsors with both chordwise and spanwise flexibility. PhD thesis, Memorial University of Newfoundland. [Google Scholar]
- 30.Wolfgang MJ, Triantafyllou MS, Yue DKP. 1999. Visualization of complex near-body transport processes in flexible-body propulsion. J. Visual. 2, 143–151. ( 10.1007/BF03181517) [DOI] [Google Scholar]
- 31.Zhu Q, Wolfgang MJ, Yue DKP, Triantafyllou MS. 2002. Three-dimensional flow structures and vorticity control in fish-like swimming. J. Fluid Mech. 468, 1–28. ( 10.1017/S002211200200143X) [DOI] [Google Scholar]
- 32.Moored KW. 2018. Unsteady three-dimensional boundary element method for self-propelled bio-inspired locomotion. Comput. Fluids 167, 324–340. ( 10.1016/j.compfluid.2018.03.045) [DOI] [Google Scholar]
- 33.Fish FE, Schreiber CM, Moored KW, Liu G, Dong H, Bart-Smith H. 2016. Hydrodynamic performance of aquatic flapping: efficiency of underwater flight in the manta. Aerospace 3, 20 ( 10.3390/aerospace3030020) [DOI] [Google Scholar]
- 34.Gazzola M, Argentina M, Mahadevan L. 2014. Scaling macroscopic aquatic locomotion. Nat. Phys. 10, 758–761. ( 10.1038/nphys3078) [DOI] [Google Scholar]
- 35.Floryan D, Van Buren T, Rowley CW, Smits AJ. 2017. Scaling the propulsive performance of heaving and pitching foils. J. Fluid Mech. 822, 386–397. ( 10.1017/jfm.2017.302) [DOI] [Google Scholar]
- 36.Van Buren T, Floryan D, Smits AJ. 2019. Scaling and performance of simultaneously heaving and pitching foils. AIAA J 57, 3666–3677. [Google Scholar]
- 37.Ayancik F, Zhong Q, Quinn DB, Brandes A, Bart-Smith H, Moored KW. 2019. Scaling laws for the propulsive performance of three-dimensional pitching propulsors. J. Fluid Mech. 871, 1117–1138. ( 10.1017/jfm.2019.334) [DOI] [Google Scholar]
- 38.Kayan V. 1979. The hydrodynamic characteristics of the caudal fin of the dolphin. Bionika 13, 9–15. [Google Scholar]
- 39.Hertel H. 1969. Hydrodynamics of swimming and wave-riding dolphins. In The biology of marine mammals (ed. Anderson HT.), pp. 31–63. New York, NY: Academic Press. [Google Scholar]
- 40.Saadat M, Fish FE, Domel AG, Di Santo V, Lauder GV, Haj-Hariri H. 2017. On the rules for aquatic locomotion. Phys. Rev. Fluids 2, 1–12. ( 10.1103/PhysRevFluids.2.083102) [DOI] [Google Scholar]
- 41.Fish FE. 1998. Biomechanical perspective on the origin of cetacean flukes. In The emergence of whales, pp. 303–324. Berlin, Germany: Springer. [Google Scholar]
- 42.Liu G, Ren Y, Dong H, Akanyeti O, Liao JC, Lauder GV. 2017. Computational analysis of vortex dynamics and performance enhancement due to body–fin and fin–fin interactions in fish-like locomotion. J. Fluid Mech. 829, 65–88. ( 10.1017/jfm.2017.533) [DOI] [Google Scholar]
- 43.Fish FE. 1993. Power output and propulsive efficiency of swimming bottlenose dolphins (Tursiops truncatus). J. Exp. Biol. 185, 179–193. [Google Scholar]
- 44.Fish FE. 1998. Comparative kinematics and hydrodynamics of odontocete cetaceans: morphological and ecological correlates with swimming performance. J. Exp. Biol. 201, 2867–2877. [PubMed] [Google Scholar]
- 45.Eloy C. 2013. On the best design for undulatory swimming. J. Fluid Mech. 717, 48–89. ( 10.1017/jfm.2012.561) [DOI] [Google Scholar]
- 46.Floryan D, Van Buren T, Smits AJ. 2018. Efficient cruising for swimming and flying animals is dictated by fluid drag. Proc. Natl Acad. Sci. USA 115, 8116–8118. ( 10.1073/pnas.1805941115) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Krasny R. 1986. Desingularization of periodic vortex sheet roll-up. J. Comput. Phys. 65, 292–313. ( 10.1016/0021-9991(86)90210-X) [DOI] [Google Scholar]
- 48.Akoz E, Han P, Liu G, Dong H, Moored KW. 2019. Large-amplitude intermittent swimming in viscous and inviscid flows. AIAA J 57, 3678–3685. [Google Scholar]
- 49.Fish FE, Nusbaum MK, Beneski JT, Ketten DR. 2006. Passive cambering and flexible propulsors: cetacean flukes. Bioinspir. Biomim. 1, S42–S48. ( 10.1088/1748-3182/1/4/S06) [DOI] [PubMed] [Google Scholar]
- 50.Prandtl L. 1920. Theory of lifting surfaces. NACA Tech. Rep. 9, 1–11. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
This article does not contain any additional data.