Mathematical modelling of fluid flow and solute transport to define operating parameters for in vitro perfusion cell culture systems

Abstract

In recent years, there has been a move away from the use of static in vitro two-dimensional cell culture models for testing the chemical safety and efficacy of drugs. Such models are increasingly being replaced by more physiologically relevant cell culture systems featuring dynamic flow and/or three-dimensional structures of cells. While it is acknowledged that such systems provide a more realistic environment within which to test drugs, progress is being hindered by a lack of understanding of the physical and chemical environment that the cells are exposed to. Mathematical and computational modelling may be exploited in this regard to unravel the dependency of the cell response on spatio-temporal differences in chemical and mechanical cues, thereby assisting with the understanding and design of these systems. In this paper, we present a mathematical modelling framework that characterizes the fluid flow and solute transport in perfusion bioreactors featuring an inlet and an outlet. To demonstrate the utility of our model, we simulated the fluid dynamics and solute concentration profiles for a variety of different flow rates, inlet solute concentrations and cell types within a specific commercial bioreactor chamber. Our subsequent analysis has elucidated the basic relationship between inlet flow rate and cell surface flow speed, shear stress and solute concentrations, allowing us to derive simple but useful relationships that enable prediction of the behaviour of the system under a variety of experimental conditions, prior to experimentation. We describe how the model may used by experimentalists to define operating parameters for their particular perfusion cell culture systems and highlight some operating conditions that should be avoided. Finally, we critically comment on the limitations of mathematical and computational modelling in this field, and the challenges associated with the adoption of such methods.

1. Introduction

Drug discovery is a long and expensive process, with the development of a single drug taking many years to complete and the cost increasing significantly at each stage of testing [1,2]. In addition, regulation states that animal usage in drug testing must be minimized or avoided [3]. Therefore, it is critical that the drug discovery process is as efficient as possible in order to develop drugs quickly while lowering costs and reducing the use of animals.

The first stage of drug development is to identify and optimize lead compounds to create potential drug molecules. Properties such as absorption, metabolism and toxicity are tested in preclinical studies (in vitro cell-based and in vivo animal-based experiments) before human clinical trials take place prior to marketing and approval of the drug. In order to maximize the efficiency of the screening process, drugs which are likely to fail need to be eliminated as early as possible. In vitro experiments conducted at the initial stages of testing are often poorly representative of the in vivo environment since cells are typically cultured under static conditions in a two-dimensional (2D) array, whereas in reality, cells in three-dimensional (3D) configurations are able to communicate with other cells while being exposed to flow. Animal studies are unethical, costly and often poorly predictive of the human response due to species differences. Thus, it is essential that new drug-testing systems are developed which do not involve (or limit the use of) animals and which reflect the physiological environment so that drugs likely to fail will be eliminated earlier in the screening process [1,2].

Mathematical modelling can be useful in the design and optimization of novel drug testing systems. For example, prototypes of new devices can be built virtually and features such as geometry can be easily modified allowing the ‘best’ design to be chosen prior to fabrication of the device. Despite the fact that experiments are usually run with constant inlet solute concentrations (e.g. oxygen (O₂), drug, nutrients) and flow rates, spatial gradients and time-dependencies in solute concentrations and fluid forces (shear stress) often emerge, meaning that cells are not exposed to a homogeneous environment. Mathematical and computational modelling may be exploited in this regard to unravel the dependency of the cellular response on spatio-temporal differences in chemical and mechanical cues, thereby assisting with the understanding and design of these systems. A range of suitable operating parameters can then be established depending on the desired experimental outcome, allowing for the accurate configuration of devices with less reliance on a ‘trial and error’ approach.

Perfusion bioreactors are dynamic cell culture systems which have been gaining much attention in recent years. These systems allow cells to be cultured in 2D and 3D configurations while being exposed to flow. Improved cell viability and metabolic function has been observed under cell culture conditions provided by bioreactors: the presence of flow provides a supply of nutrients to the cells, co-culture promotes cell–cell interactions and cells cultured in 3D configurations are able to retain their physiological morphology [4].

There are a number of existing studies in the literature which use mathematical modelling to characterize certain perfusion bioreactors. For example, models of fluid flow and solute transport have been employed to optimize chamber design [5], design a gradient generator for drug toxicity testing [6], predict concentration gradients [7] and maximize mass transfer while controlling shear stress levels [8]. Other studies have adopted multiphase approaches to investigate the effect of flow on tissue growth [9] and elucidate the relationship between shear stress and cell yield and distribution within hollow-fibre bioreactors [10]. A comprehensive review of continuum modelling approaches in artificial scaffolds and bioreactors more generally, covering cell population dynamics, the cell’s mechanical environment and cell–environment interactions, within a multiphase framework, may be found in [11]. Most relevant to this study, a model was developed to optimize the design of a modular bioreactor chamber [12] and to assess if the O₂ delivery and shear stress levels would be acceptable for the culture of hepatocytes within a hydrogel layer [13]. More recently, models were developed to predict flow patterns, O₂ transport and test compound distribution within three different bioreactors to identify which of the systems would be most suitable for long-term culture of hepatocytes within alginate beads [14]. A key limitation of these existing models is that they account for very specific experiments and cell types (e.g. culturing hepatocytes within a hydrogel layer or alginate beads). Since perfusion bioreactors are increasingly being used for a variety of applications incorporating different cell types and solutes with different mechanisms of action, it is important to consider potential differences in the environment and operating conditions.

The primary purpose of this paper is to provide mathematical and computational models and results that can assist with the design and operation of advanced cell culture systems. In addition, we aim to highlight potential barriers to the adoption of in silico models in this field. We present a more general modelling framework that characterizes the fluid flow and solute transport in perfusion bioreactors featuring an inlet and an outlet. We start by presenting the model equations, as well as initial and boundary conditions that describe the environment within an arbitrary bioreactor chamber. We consider two common types of solute reaction with the cells—nonlinear saturable binding and Michaelis–Menten (M–M) kinetics—and we use mathematical arguments to justify simplifications of the underlying equations in certain cases. We then provide simple relationships which allow for the rapid prediction of cell surface solute concentration profiles in single and connected chambers, prior to experimentation. To demonstrate the utility of our model, we simulate the fluid dynamics and solute concentration profiles for a variety of input flow rates, inlet concentrations and cell types within a specific bioreactor chamber: the Kirkstall QV900. For single and connected chambers, we examine the relationships between input flow rate and cell surface flow speeds, shear stress levels and solute concentrations and investigate the effect of varying cell-specific parameters on solute concentration profiles at the cell surface. Finally, we critically comment on the limitations of mathematical and computational modelling in this field, and the challenges associated with the adoption of such methods.

2. Mathematical and computational methods

We begin by considering an arbitrary geometry to represent a bioreactor chamber featuring an inlet and an outlet, assuming that cells are cultured at the base of the chamber either in a 3D region or within a monolayer. We note that the model is applicable to any chamber geometry with these properties. Figure 1 illustrates how we set up the model equations to describe fluid flow and solute transport and this will be discussed in detail in the following text.

Figure 1.

Schematic drawing of an arbitrary bioreactor geometry featuring an inlet and an outlet with cells cultured at the base of the chamber to illustrate the model set-up. For full details of the equations, the reader is referred to the text.

2.1. Fluid dynamics in the chamber

Assuming we have an incompressible Newtonian fluid, the flow velocity and pressure are described using the continuity and Navier–Stokes equations

$$\mathrm{\nabla }\cdot \mathbf{u}=0,$$ 2.1

and

$$\rho \frac{\mathrm{\partial }\mathbf{u}}{\mathrm{\partial }t}+\rho (\mathbf{u}\cdot \mathrm{\nabla })\mathbf{u}=-\mathrm{\nabla }p+\mu {\mathrm{\nabla }}^2\mathbf{u},$$ 2.2

where u ($\text{m}\hspace{0.17em}{\text{s}}^{-1}$) is the velocity field, p (Pa) is the pressure, ρ (${\text{kg m}}^{-3}$) is the fluid density and μ ($\text{Pa s}$) is the dynamic viscosity. Initially, the fluid velocity is zero (u = 0) in the chamber. At the inlet, we assume a normal inflow parabolic velocity profile with magnitude derived from the volumetric flow rate, Q, which can be controlled in experiments (see electronic supplementary material). We assume zero pressure (p = 0) at the outlet and no-slip and no penetration conditions (u = 0) are imposed on all interior walls.

2.2. Solute transport in the chamber

The transport of each solute through the fluid is described using an advection–diffusion equation:

$$\frac{\mathrm{\partial }{c}_j}{\mathrm{\partial }t}+(\mathbf{u}\cdot \mathrm{\nabla })c_j=D_j{\mathrm{\nabla }}^2{c}_j,$$ 2.3

where c_j (${\text{mol m}}^{-3}$) is the concentration of solute j and D_j (m² s⁻¹) is the diffusion coefficient associated with solute j. We assume that each solute is present at a sufficiently low concentration such that the presence of one solute has no impact on the transport of another (dilute assumption). We further assume no binding of solute j to components of the fluid (e.g. proteins) but note that D_j may be adjusted to account for this process [15]. Initially, the solute concentration is zero (c_j = 0) in the chamber. A constant supply of each solute ($c_{\hspace{0.17em}j}=c_{\hspace{0.17em}j}^{\mathrm{in}}$) is prescribed at the inlet and a convective flux ($-\mathbf{n}\cdot D_{\hspace{0.17em}j}\mathrm{\nabla }{c}_{\hspace{0.17em}j}=0$, where n is an outward facing normal) is imposed at the outlet. We assume the walls of the chamber are impermeable and impose a zero flux condition of the form $\mathbf{n}\cdot (-D_{\hspace{0.17em}j}\mathrm{\nabla }{c}_{\hspace{0.17em}j}+\mathbf{u}{c}_{\hspace{0.17em}j})=0$ on all interior walls.

2.3. Solute reaction with the cells

We assume the cells are cultured at the base of the chamber either (i) within a 3D region of thickness h_c or (ii) as a monolayer. We further assume that the cells reside within media that does not facilitate proliferation, which is common in many applications. For cases where cell proliferation is important, this may be incorporated following existing approaches in the literature (e.g. [9–11]). To demonstrate how we may characterize different types of reaction between the solute and the cells, we present two common reaction mechanisms. First, we consider a reaction governed by nonlinear saturable binding kinetics, suitable for describing the effect of a wide range of drugs whose mode of action is governed by ligand–receptor interactions. Then, we consider a reaction governed by M–M kinetics, commonly used in the literature to describe O₂ consumption [5,7,8,12–14] and paracetamol (APAP) metabolism [16,17].

2.3.1. Reaction within a 3D cell region.

Within the 3D cell region, there will be fluid flow in the interstitium between cells. This may be modelled by considering the cell region as a porous medium and using Darcy’s Law to calculate the flow field. However, the thinness of the cell region and the relatively low lateral pressure differences and low permeability of the cell region, suggest that flow in the cell region will be negligible. In instances in which interstitial flow is important, the reader is directed to [11] for models that include this effect. We, therefore, describe solute transport using a reaction–diffusion equation:

$$\frac{\mathrm{\partial }{c}_{\hspace{0.17em}j}}{\mathrm{\partial }t}=\mathrm{\nabla }\cdot ({\mathit{D}}_{\hspace{0.17em}j}^{\mathrm{cell}}\mathrm{\nabla }{c}_{\hspace{0.17em}j})-R_{\hspace{0.17em}j}^{3D},$$ 2.4

where ${\mathit{D}}_{\hspace{0.17em}j}^{\mathrm{cell}}$ (m² s⁻¹), the diffusivity tensor associated with solute j, is assumed to capture any heterogeneity in cell distribution within the 3D region and, here, $R_{\hspace{0.17em}j}^{3D}$ (${\text{mol m}}^{-3}\hspace{0.17em}{\text{s}}^{-1}$) describes the bulk reaction between solute j and the cells. Initially, the solute concentration is zero (c_j = 0) in the cell region and we assume continuity of concentration and flux across the boundary.

2.3.2. Reaction within a monolayer

If we are interested in estimating only cell surface solute concentration profiles of a monolayer, we may replace the 3D cell region with a flux boundary condition of the following form:

$$\mathbf{n}\cdot (-D_{\hspace{0.17em}j}\mathrm{\nabla }{c}_{\hspace{0.17em}j}+\mathbf{u}{c}_{\hspace{0.17em}j})=R_{\hspace{0.17em}j}^{2\mathrm{D}},$$ 2.5

where, here, $R_{\hspace{0.17em}j}^{2\mathrm{D}}$ (${\text{mol m}}^{-2}\hspace{0.17em}{\text{s}}^{-1}$) describes the surface reaction between solute j and the cells. We note that (2.5) may also be used if we are interested in estimating solute concentrations on the surface of a 3D region of cells (as in §2.3.1) in the special case of isotropic diffusion within a sufficiently thin cell region.

2.3.3. Reaction governed by nonlinear saturable binding kinetics

We describe the first type of reaction by nonlinear saturable binding:

$$R_{\hspace{0.17em}j}^{3D}=k_{\hspace{0.17em}j}^{\hspace{0.17em}f}{c}_{\hspace{0.17em}j}(B_{\hspace{0.17em}j}-b_{\hspace{0.17em}j})-k_{\hspace{0.17em}j}^r{b}_{\hspace{0.17em}j},$$ 2.6

where c_j (${\text{mol m}}^{-3}$) is the concentration of free drug, B_j (${\text{mol m}}^{-3}$) is the local density of binding sites and $k_{\hspace{0.17em}j}^{\hspace{0.17em}f}$ (mol⁻¹ m³ s⁻¹) and $k_{\hspace{0.17em}j}^r$ (s⁻¹) are the forward and reverse reaction rates, respectively. Here, we require an additional equation to track the concentration of bound drug, b_j (${\text{mol m}}^{-3}$), in the 3D cell region:

$$\frac{\mathrm{\partial }{b}_{\hspace{0.17em}j}}{\mathrm{\partial }t}=k_{\hspace{0.17em}j}^{\hspace{0.17em}f}{c}_{\hspace{0.17em}j}(B_{\hspace{0.17em}j}-b_{\hspace{0.17em}j})-k_{\hspace{0.17em}j}^r{b}_{\hspace{0.17em}j}.$$ 2.7

We remark that nonlinear saturable irreversible binding and linear binding kinetics may be recovered as special cases of (2.7) through appropriate choice of the model parameters. We also note that although we have chosen to model the binding process within a 3D cell region, these equations may be easily adapted to describe the binding process via a flux boundary condition, as in (2.5), by defining b_j in units of ${\text{mol m}}^{-2}$ and employing an appropriate mass conservation condition.

2.3.4. Reaction governed by Michaelis–Menten kinetics

We describe the second type of solute reaction by M–M kinetics. These kinetics describe the relationship between the concentration of solute and speed of a reaction: as solute concentration increases, the reaction rate increases before approaching a maximum for higher solute concentrations [18,19]. In this case, we have chosen to model the metabolic process using a flux boundary condition but, again, these equations may be easily adapted to describe the metabolic process within a 3D cell region by suitably adjusting the units of the model parameters. A general M–M reaction term has the following form:

$$R_{\hspace{0.17em}j}^{2\mathrm{D}}=\sum _{i=1}^m\frac{V_{\hspace{0.17em}j}^i{c}_{\hspace{0.17em}j}}{K_{\hspace{0.17em}j}^i+c_{\hspace{0.17em}j}},$$ 2.8

where m is the number of metabolic pathways involved in the reaction, $K_{\hspace{0.17em}j}^i$ (${\text{mol m}}^{-3}$) is the M–M constant for solute j and pathway i and $V_{\hspace{0.17em}j}^i$ (${\text{mol m}}^{-2}\hspace{0.17em}{\text{s}}^{-1}$) is the maximum reaction rate for solute j and pathway i. It may be readily shown that

$$R_{\hspace{0.17em}j}^{2\mathrm{D}}\approx \{\begin{array}{cc}\sum _{i=1}^m{V}_{\hspace{0.17em}j}^i& \text{when}\hspace{0.17em}\frac{K_{\hspace{0.17em}j}^i}{c_{\hspace{0.17em}j}}\ll 1\\ \sum _{i=1}^m\frac{V_{\hspace{0.17em}j}^i{c}_{\hspace{0.17em}j}}{K_{\hspace{0.17em}j}^i},& \text{when}\hspace{0.17em}\frac{K_{\hspace{0.17em}j}^i}{c_{\hspace{0.17em}j}}\gg 1\end{array},$$ 2.9

so that when the ratio of $K_{\hspace{0.17em}j}^i$ to c_j satisfies the above criteria, we can reasonably replace the full M–M kinetics (2.8) by the approximate expressions (2.9).

2.4. Derivation of relationships to inform experimental operating conditions

For each type of reaction mechanism, we provide simple relationships which allow for the rapid prediction of steady-state solute concentrations, prior to experimentation.

2.4.1. Predicting steady-state solute concentrations when reaction is governed by nonlinear saturable binding kinetics

Within the cell region, drug dynamics are typically characterized by a reaction rate considerably faster than the timescale associated with diffusion [20], meaning that binding is usually diffusion-limited. The implication is that bound and free drug coexist in a quasi-equilibrium with bound drug concentrations given by

$$b_{\hspace{0.17em}j}\approx \frac{B_{\hspace{0.17em}j}{c}_{\hspace{0.17em}j}}{k_{\hspace{0.17em}j}^d+c_{\hspace{0.17em}j}}.$$ 2.10

In such cases of rapid binding, it may readily be shown (see electronic supplementary material) that in the case of isotropic diffusion, we are able to reduce the nonlinear saturable binding model by combining (2.4) and (2.7) to obtain an equation for the total drug concentration (T_j = c_j + b_j)

$$\frac{\mathrm{\partial }{T}_{\hspace{0.17em}j}}{\mathrm{\partial }t}=\mathrm{\nabla }\cdot (D_{\hspace{0.17em}j}^{\ast }\mathrm{\nabla }{T}_{\hspace{0.17em}j})\text{and}{D}_{\hspace{0.17em}j}^{\ast }\approx \frac{D_{\hspace{0.17em}j}^{\mathrm{cell}}}{1+(B_{\hspace{0.17em}j}{k}_{\hspace{0.17em}j}^d/{(k_{\hspace{0.17em}j}^d+c_{\hspace{0.17em}j})}^2)},$$ 2.11

where D_j* is an effective concentration-dependent diffusion coefficient, $k_{\hspace{0.17em}j}^d=k_{\hspace{0.17em}j}^r/k_{\hspace{0.17em}j}^{\hspace{0.17em}f}$ is the equilibrium dissociation constant and

$$c_{\hspace{0.17em}j}=-\frac{1}{2}(k_{\hspace{0.17em}j}^d+B_{\hspace{0.17em}j}-T_{\hspace{0.17em}j})\pm \frac{1}{2}\sqrt{{(k_{\hspace{0.17em}j}^d+B_{\hspace{0.17em}j}-T_{\hspace{0.17em}j})}^2+4k_{\hspace{0.17em}j}^d{T}_{\hspace{0.17em}j}}.$$ 2.12

For physically meaningful results, we require c_j ≥ 0 so we consider only the positive root. It is clear that the role of binding is accounted for through a reduced diffusion coefficient. In the limit of rapid binding, the coupled time-dependent equations (2.4) and (2.7) may then be replaced with the single partial differential equation (2.11) with b_j obtained through the algebraic expression (2.10). Expressing the model in terms of total drug concentration is often useful, since experimental researchers often measure total drug concentrations (for reasons of convenience or due to limitations of measurement protocols). Since no drug is lost from the system in this model (it is either bound or unbound), at steady state the free drug concentration should be equal to the inlet concentration, i.e. $c_{\hspace{0.17em}j}=c_{\hspace{0.17em}j}^{\mathrm{in}}$, and thus we may use (2.10) to calculate the partitioning of drug between c_j and b_j prior to experimentation. Note that since these expressions rely only on the parameters $k_{\hspace{0.17em}j}^d$ and B_j, they may be used to calculate the steady-state concentrations for any drug whose interaction with the cells is governed by nonlinear saturable binding kinetics, given that the drug is supplied as a constant source and diffusion of drug within the cell region is isotropic.

2.4.2. Predicting steady-state cell surface solute concentrations when reaction is governed by Michaelis–Menten kinetics

Since experiments can span over many days and it is often possible to connect multiple bioreactor chambers together for high throughput testing, it would be useful to establish relationships between the inlet and cell surface concentrations in single and connected chambers so that cell surface solute concentration profiles may be predicted a priori. When the solute reaction is governed by M–M kinetics, the rate of metabolism is dependent on the solute concentration at the cell surface, i.e. metabolism is variable unless the cell surface solute concentration is uniform. However, if the solute concentration is high enough ($c_{\hspace{0.17em}j}\gg K_{\hspace{0.17em}j}^i$), then from (2.9) the rate of metabolism is approximately constant. In this case, if we vary only the inlet concentration, $c_{\hspace{0.17em}j}^{\mathrm{in}}$, then the shape of the cell surface solute concentration profile will stay approximately the same since the fluid dynamics are unchanged and approximately the same amount of solute is metabolized across the entire cell surface; however, the magnitude of the cell surface solute concentration will vary according to the change in the inlet concentration. Thus, provided that $R_{\hspace{0.17em}j}\approx \sum _{i=1}^m{V}_{\hspace{0.17em}j}^i$, if the cell surface concentration profile is known for a given $c_{\hspace{0.17em}j}^{\mathrm{in}}$, we may predict the cell surface concentration profile for any $c_{\hspace{0.17em}j}^{{\mathrm{in}}^{\ast }}$ via the following equation:

$$c_{\hspace{0.17em}j}^{\ast }(y)\approx c_{\hspace{0.17em}j}(y)+\mathrm{\Delta }{c}_{\hspace{0.17em}j}^{\mathrm{in}}\text{and}\mathrm{\Delta }{c}_{\hspace{0.17em}j}^{\mathrm{in}}=c_{\hspace{0.17em}j}^{\mathrm{i}{\mathrm{n}}^{\ast }}-c_{\hspace{0.17em}j}^{\mathrm{in}},$$ 2.13

where y is the axis through the centre of the cell surface from the inlet side to the outlet side of the chamber. Here, $c_{\hspace{0.17em}j}^{\ast }(y)$ and c_j(y) are the concentration profiles across the centre of the cell surface corresponding to inlet concentrations of $c_{\hspace{0.17em}j}^{{\mathrm{in}}^{\ast }}$ and $c_{\hspace{0.17em}j}^{\mathrm{in}}$, respectively. Note we have verified that this equation may be generalized to predict the concentration profile across the entire surface of the cells, but for simplicity, we consider only the profile across the centre of the cell surface.

We can extend this idea to chambers connected in series: clearly, the solute concentration will decrease from the first to the last chamber due to metabolism so it would be useful to establish a relationship between the cell surface solute concentration profiles in the first chamber and in subsequent chambers. This would enable the prediction of the cell surface solute concentration profile in chamber n based only on knowledge of the profile in chamber 1. Similarly to (2.13), we have

$$c_{\hspace{0.17em}j}^n(y)\approx c_{\hspace{0.17em}j}^1(y)+\mathrm{\Delta }{c}_{\hspace{0.17em}j}^{\mathrm{in}}\text{and}\mathrm{\Delta }{c}_{\hspace{0.17em}j}^{\mathrm{in}}=c_{\hspace{0.17em}j}^{\mathrm{i}{\mathrm{n}}^{\mathit{n}}}-c_{\hspace{0.17em}j}^{\mathrm{i}{\mathrm{n}}^1},$$

where $c_{\hspace{0.17em}j}^n(y)$ is the unknown concentration profile across the centre of the cell surface in chamber n, $c_{\hspace{0.17em}j}^1(y)$ is the known concentration profile across the centre of the cell surface in chamber 1 and $\mathrm{\Delta }{c}_{\hspace{0.17em}j}^{\mathrm{in}}$ is the difference between the unknown inlet concentration in chamber n and the known inlet concentration in chamber 1. Thus, in order to make use of this equation, we need to be able to estimate $c_{\hspace{0.17em}j}^{{\mathrm{in}}^n}$.

Let us first consider the concentration flux (${\text{mol s}}^{-1}$) entering and leaving chamber 1. At steady state, the concentration flux leaving the chamber via the outlet must be equal to the concentration flux entering the chamber via the inlet minus the concentration flux at the cell surface due to metabolism, i.e.

$$\begin{array}{rl}\hspace{0.17em}& {\int }_{A_{\mathrm{out}}}\mathbf{n}\cdot (-D_{\hspace{0.17em}j}\mathrm{\nabla }{c}_{\mathrm{out}}^1+{\mathbf{u}}_{\mathrm{out}}^1{c}_{\mathrm{out}}^1)\hspace{0.17em}\text{d}{A}_{\mathrm{out}}\\ \hspace{0.17em}& ={\int }_{A_{\mathrm{in}}}\mathbf{n}\cdot (-D_{\hspace{0.17em}j}\mathrm{\nabla }{c}_{\mathrm{in}}^1+{\mathbf{u}}_{\mathrm{in}}^1{c}_{\mathrm{in}}^1)\hspace{0.17em}\text{d}{A}_{\mathrm{in}}\\ \hspace{0.17em}& -{\int }_{A_{\mathrm{cells}}}\sum _{i=1}^m{V}_{\hspace{0.17em}j}^i\hspace{0.17em}\text{d}{A}_{\mathrm{cells}},\end{array}$$ 2.14

where $c_{\mathrm{out}}^1$ and $c_{\mathrm{in}}^1$ (${\text{mol m}}^{-3}$) are the concentrations at the outlet and the inlet faces of chamber 1, respectively, and A_out, A_in and A_cells are the areas of the outlet face, the inlet face and the cell surface, respectively. Note that again we assume metabolism is approximately constant and for convenience we define $\alpha ={\int }_{A_{\mathrm{cells}}}\sum _{i=1}^m{V}_{\hspace{0.17em}j}^i\hspace{0.17em}\text{d}{A}_{\mathrm{cells}}$.

Also at steady state, the concentration flux leaving chamber 1 via the outlet must be equal to the concentration flux entering chamber 2 via the inlet, i.e.

$${\int }_{A_{\mathrm{out}}}\mathbf{n}\cdot (-D_{\hspace{0.17em}j}\mathrm{\nabla }{c}_{\mathrm{out}}^1+{\mathbf{u}}_{\mathrm{out}}^1{c}_{\mathrm{out}}^1)\hspace{0.17em}\text{d}{A}_{\mathrm{out}}={\int }_{A_{\mathrm{in}}}\mathbf{n}\cdot (-D_{\hspace{0.17em}j}\mathrm{\nabla }{c}_{\mathrm{in}}^2+{\mathbf{u}}_{\mathrm{in}}^2{c}_{\mathrm{in}}^2)\hspace{0.17em}\text{d}{A}_{\mathrm{in}},$$ 2.15

and combining (2.15) with (2.14) gives

$${\int }_{A_{\mathrm{in}}}\mathbf{n}\cdot (-D_{\hspace{0.17em}j}\mathrm{\nabla }{c}_{\mathrm{in}}^2+{\mathbf{u}}_{\mathrm{in}}^2{c}_{\mathrm{in}}^2)\hspace{0.17em}\text{d}{A}_{\mathrm{in}}={\int }_{A_{\mathrm{in}}}\mathbf{n}\cdot (-D_{\hspace{0.17em}j}\mathrm{\nabla }{c}_{\mathrm{in}}^1+{\mathbf{u}}_{\mathrm{in}}^1{c}_{\mathrm{in}}^1)\hspace{0.17em}\text{d}{A}_{\mathrm{in}}-\alpha .$$ 2.16

We know that $c_{\mathrm{in}}^1$ is constant across A_in and if we also assume that $c_{\mathrm{in}}^2$ is constant then we have

$$-D_{\hspace{0.17em}j}\mathrm{\nabla }{c}_{\mathrm{in}}^2=-D_{\hspace{0.17em}j}\mathrm{\nabla }{c}_{\mathrm{in}}^1=0.$$

We therefore neglect the diffusive flux at the inlets and this assumption will always be appropriate when the system is convection-dominated. Then, from (2.16) we have

$$c_{\mathrm{in}}^2{\int }_{A_{\mathrm{in}}}{\mathbf{u}}_{\mathrm{in}}^2\cdot \mathbf{n}\hspace{0.17em}\text{d}{A}_{\mathrm{in}}=c_{\mathrm{in}}^1{\int }_{A_{\mathrm{in}}}{\mathbf{u}}_{\mathrm{in}}^1\cdot \mathbf{n}\hspace{0.17em}\text{d}{A}_{\mathrm{in}}-\alpha ,$$

and if we assume that the velocity profiles at the inlet to each chamber are identical then we obtain:

$$\begin{array}{rl}{c}_{\mathrm{in}}^2{\int }_{A_{\mathrm{in}}}{\mathbf{u}}_{\mathrm{in}}^1\cdot \mathbf{n}\hspace{0.17em}\text{d}{A}_{\mathrm{in}}& =c_{\mathrm{in}}^1{\int }_{A_{\mathrm{in}}}{\mathbf{u}}_{\mathrm{in}}^1\cdot \mathbf{n}\hspace{0.17em}\text{d}{A}_{\mathrm{in}}-\alpha \hspace{0.17em}\\ ⟹\hspace{0.17em}\hspace{0.17em}⟹\hspace{0.17em}{c}_{\mathrm{in}}^2& =\hspace{0.17em}{c}_{\mathrm{in}}^1-\frac{\alpha }{{\int }_{A_{\mathrm{in}}}{\mathbf{u}}_{\mathrm{in}}^1\cdot \mathbf{n}\hspace{0.17em}\text{d}{A}_{\mathrm{in}}}=c_{\mathrm{in}}^1-\frac{\alpha }{Q},\end{array}$$

where Q (m³ s⁻¹) is the input flow rate. Similarly, we have

$$c_{\mathrm{in}}^3=c_{\mathrm{in}}^2-\frac{\alpha }{Q}=c_{\mathrm{in}}^1-\frac{2\alpha }{Q},$$

and for n chambers we obtain

$$c_{\mathrm{in}}^n=c_{\mathrm{in}}^1-\frac{(n-1)\alpha }{Q}.$$

Thus, provided that $R_{\hspace{0.17em}j}\approx \sum _{i=1}^m{V}_{\hspace{0.17em}j}^i$, the cell surface concentration profile in chamber 1 is known, the inlet concentrations are constant and the velocity profile at all inlets are the same, we may predict the cell surface concentration profile in chamber n via the following equation:

$$c_{\hspace{0.17em}j}^n(y)\approx c_{\hspace{0.17em}j}^1(y)-\frac{(n-1)\alpha }{Q}.$$ 2.17

As before, we have verified that this equation may be generalized to predict the concentration profile across the entire surface of the cells, but for simplicity we consider only the profile across the centre of the cell surface.

2.5. Computational geometry

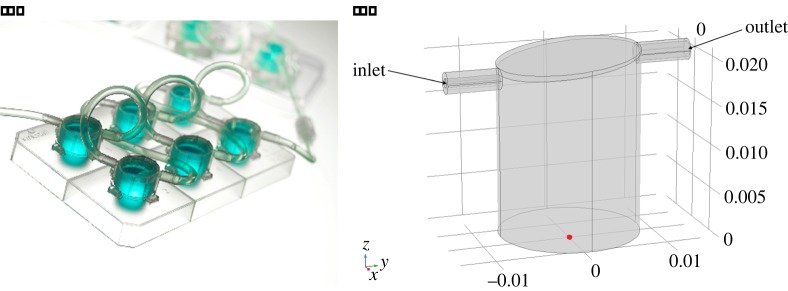
In order to demonstrate the utility of our model, we choose the geometry of a specific commercial perfusion cell culture system which is gaining popularity: the QV900 (figure 2a) manufactured by Kirkstall Ltd (York, UK). The QV900 is a modular system comprising six cell culture chambers that can be connected together in any combination. This allows experiments to be performed either in parallel or in series, providing a high degree of flexibility as well as the potential to culture cells over a defined set of conditions.

Figure 2.

(a) The QV900. (www.kirkstall.org). (b) Idealized 3D geometry of a single QV900 chamber, showing the orientation of the x-, y- and z-axes where the origin is located at the centre of the base (indicated by the red dot). Note that length scales are in metres.

Initially, a computational 3D representation of a single chamber (figure 2b) was constructed. The overall height of a single chamber ranges from 18.6 mm at the inlet side to 20.7 mm at the outlet side. The diameter of the chamber is taken to be 16.0 mm, while the inner diameter of the inlet and the outlet is 1.0 mm and 1.8 mm, respectively. The cells are assumed to be cultured at the base of the chamber in either a 3D region of height h_c or a monolayer.

We subsequently created a geometry to represent six chambers connected in series. Each chamber is connected by a cylindrical tube of length 100 mm and diameter 2.4 mm. This is representative of a typical connecting tube, although it is noted that there is a choice of various tube lengths; however, we have verified that this feature does not significantly influence the results since employing various tube lengths from 5 to 100 mm alters the results by approximately 1% or less.

2.6. Parameter values

There are a number of parameters in the model that can be adjusted to represent different cell culture conditions. Variable parameters such as input flow rate and inlet concentration are specified for each set of results and table 1 presents the remaining parameters. For simplicity, the values of ρ and μ are chosen under the assumption that the fluid is water; however, it is recognized that these parameters may vary depending on the specific fluid used. Also note that for this study we assume isotropic diffusion of solute within the 3D cell region and choose $D_{\hspace{0.17em}j}^{\mathrm{cell}}=D_{\hspace{0.17em}j}$, but we acknowledge that in reality these parameters may differ. To illustrate the results of our model, we choose representative parameters for three different solutes. For the reaction governed by nonlinear saturable binding, we describe the action of sirolimus (a drug with potent anti-proliferative and immunosuppressive properties commonly used to coat arterial stents) on smooth muscle cells. For the reaction governed by M–M kinetics, we describe O₂ consumption for four different cell types (rat cardiomyocytes, human cardiomyocytes, rat hepatocytes and HepG2 cells) and we describe APAP metabolism using parameters obtained from a study performed in vivo in humans. Note that the maximum reaction rate for M–M kinetics is often provided in varying units for different solutes; in order to balance the equations, we need to either multiply this parameter by the cell density or divide this parameter by the cell area for O₂ and APAP, respectively.

Table 1.

Parameter values.

parameter description	value	reference
fluid parameters
density (ρ)	$9.94\times {10}^2\hspace{0.17em}{\text{kg m}}^{-3}$	[21]
dynamic viscosity (μ)	$6.89\times {10}^{-4}\hspace{0.17em}\text{Pa s}$	[21]
diffusion coefficients
sirolimus (DS)	2.50 × 10−10 m2 s−1	[22]
O2 ($D_{{\mathrm{O}}_2}$)	3.00 × 10−9 m2 s−1	[12]
APAP (DAPAP)	6.00 × 10−10 m2 s−1	[23]
binding parameters for sirolimus
forward reaction rate ($k_S^{\hspace{0.17em}f}$)	2.00 mol−1 m3 s−1	[22]
reverse reaction rate ($k_S^r$)	5.20 × 10−3 s−1	[22]
local density of binding sites (BS)	$3.63\times {10}^{-1}\hspace{0.17em}{\text{mol m}}^{-3}$	[22]
Michaelis–Menten constants
O2 ($K_{{\mathrm{O}}_2}$)	$6.60\times {10}^{-4}\hspace{0.17em}{\text{mol m}}^{-3}$	[12]
glucuronidation ($K_{\mathrm{APAP}}^1$)	$6.89\hspace{0.17em}{\text{mol m}}^{-3}$	[17]
sulphation ($K_{\mathrm{APAP}}^2$)	$9.70\times {10}^{-2}\hspace{0.17em}{\text{mol m}}^{-3}$	[17]
oxidation ($K_{\mathrm{APAP}}^3$)	$3.03\times {10}^{-1}\hspace{0.17em}{\text{mol m}}^{-3}$	[17]
maximum O2 consumption rates
rat cardiomyocytes ($V_{{\mathrm{O}}_2}$)	$4.01\times {10}^{-8}\hspace{0.17em}{\text{mol m}}^{-2}\hspace{0.17em}{\text{s}}^{-1}$	[24]
human cardiomyocytes ($V_{{\mathrm{O}}_2}$)	$9.81\times {10}^{-8}\hspace{0.17em}{\text{mol m}}^{-2}\hspace{0.17em}{\text{s}}^{-1}$	[24]
rat hepatocytes ($V_{{\mathrm{O}}_2}$)	$2.39\times {10}^{-8}\hspace{0.17em}{\text{mol m}}^{-2}\hspace{0.17em}{\text{s}}^{-1}$	[25]
HepG2 cells ($V_{{\mathrm{O}}_2}$)	$1.17\times {10}^{-8}\hspace{0.17em}{\text{mol m}}^{-2}\hspace{0.17em}{\text{s}}^{-1}$	[25]
maximum APAP metabolic rates
glucuronidation ($V_{\mathrm{APAP}}^1$)	$8.86\times {10}^{-2}\hspace{0.17em}{\text{mol m}}^{-2}\hspace{0.17em}{\text{s}}^{-1}$	[17]
sulphation ($V_{\mathrm{APAP}}^2$)	$1.02\times {10}^{-3}\hspace{0.17em}{\text{mol m}}^{-2}\hspace{0.17em}{\text{s}}^{-1}$	[17]
oxidation ($V_{\mathrm{APAP}}^3$)	$3.41\times {10}^{-4}\hspace{0.17em}{\text{mol m}}^{-2}\hspace{0.17em}{\text{s}}^{-1}$	[17]
general parameters
total number of cells (N)	1.00 × 105	this study
volume of a smooth muscle cell (Vcell)	1.50 × 10−14 m3	[26]
area covered by the cells (A)	2.01 × 10−4 m2	this study
thickness of 3D cell region (hc = NVcell/A)	7.46 × 10−6 m	this study
cell density (d = N/A)	$4.97\times {10}^8\hspace{0.17em}{\text{cells m}}^{-2}$	this study

2.7. Numerical implementation

Since the equations describing fluid flow are independent of solute concentration, we first solved the fluid equations and then used this solution to subsequently solve the transport equations. The computational geometry was constructed and the finite-element method was implemented in COMSOL Multiphysics^®, 5.3 (Stockholm, Sweden). We note that a number of alternative finite element codes may also be used to solve the model equations and boundary conditions as detailed in §2. Since preliminary simulations showed that the solution to the problem is symmetric about the y, z plane passing through the origin, we used symmetry of the geometry to reduce the computational cost of the model so that only half of the problem was solved numerically. The computational mesh was generated using the physics-controlled ‘extremely fine’ setting. This choice was made based on a mesh sensitivity study where we established that refinement of the mesh from the ‘extra fine’ setting to the ‘extremely fine’ setting resulted in less than $1\text{\%}$ change in the quantities of interest (mass conservation, shear stress and solute concentration at the cell surface). This indicates that further refinement would have a negligible effect on the results. The final mesh consisted of 2 152 947 tetrahedral elements with size ranging from 0.03 to 0.46 mm and, where we modelled the cells as a 3D region, we generated a swept triangular prism mesh in this domain. Note that we consider only the steady-state results since our time-dependent simulations show that equilibrium is established relatively quickly. Specifically, the flow reaches steady state rapidly for all flow rates considered (within 50 s) while the time to steady state is more variable when solute transport is considered, ranging from 5 to 20 h between the lowest and highest flow rates considered. The time to steady state was assessed by quantitative comparison of fluid flow patterns, cell surface shear stresses, patterns of solute concentrations and cell surface solute concentrations at different times. The model may, of course, be used to generate time-dependent solutions if required.

3. Results

3.1. Fluid dynamics

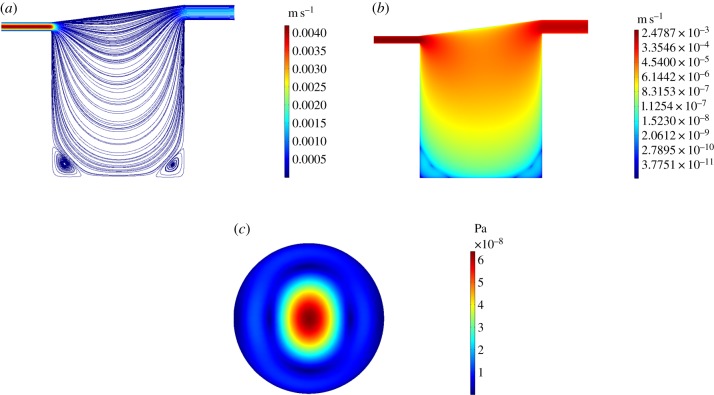
We describe the velocity profile and cell surface shear stress in a single chamber for $Q=100\text{–}1000\hspace{0.17em}\mu {\text{l min}}^{-1}$, covering a realistic range of operating flow rates. As an example, we display only the results for $Q=100\hspace{0.17em}\mu {\text{l min}}^{-1}$ (figure 3) and the corresponding results for the remaining flow rates can be found in the electronic supplementary material. In this case, some small zones of recirculation arise around the periphery at the base of the chamber and the peak flow speed ($4.20\times {10}^{-3}\hspace{0.17em}{\text{m s}}^{-1}$) is located at the inlet. Given the considerable decrease in flow speed with chamber depth, in figure 3b, we use a log scale to plot the velocity magnitude in order to better emphasize the variation in flow speed throughout the chamber. The magnitude of the cell surface shear stress is of the order of 10⁻⁸ Pa and rises from all sides of the chamber towards the peak (6.39 × 10⁻⁸ Pa) located at the centre. As input flow rate is increased, the recirculation zones increase in size and eventually merge to form one large zone which takes up the majority of the chamber. The cell surface shear stress rises in magnitude with increasing input flow rate and the profile changes most substantially between $Q=200\hspace{0.17em}\mu {\text{l min}}^{-1}$ and $Q=500\hspace{0.17em}\mu {\text{l min}}^{-1}$, where the flow pattern transforms dramatically. We note that for chambers connected in series there is no significant difference in the fluid dynamics in downstream chambers (not shown).

Figure 3.

Simulation results for $Q=100\hspace{0.17em}\mu {\text{l min}}^{-1}$. (a) Streamlines and magnitude of velocity through the centre of the chamber on the y, z plane. (b) Magnitude of velocity through the centre of the chamber on the y, z plane using a log scale. (c) Magnitude of shear stress at the cell surface on the x, y plane.

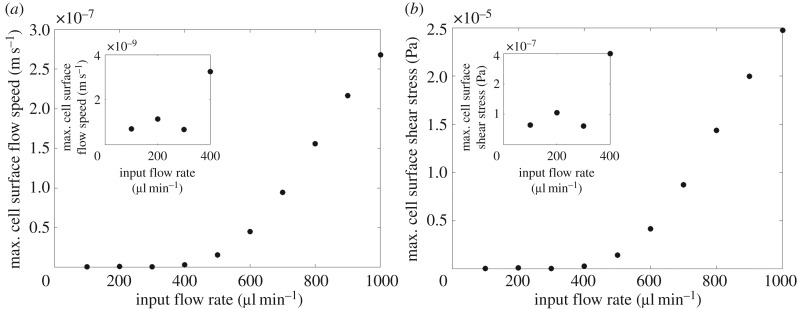
The peak cell surface flow speed and shear stress increase with input flow rate in a nonlinear manner (figure 4). As input flow rate increases, the peak cell surface flow speed and shear stress increase until around $Q=200\hspace{0.17em}\mu {\text{l min}}^{-1}$ after which the profiles dip, reaching a minimum at around $Q=300\hspace{0.17em}\mu {\text{l min}}^{-1}$. After $Q=400\hspace{0.17em}\mu {\text{l min}}^{-1}$ the peak cell surface flow speed and shear stress increase rapidly with increasing input flow rate. We deduced that a significant change in the pattern of flow is responsible for the dip: up to $Q=200\hspace{0.17em}\mu {\text{l min}}^{-1}$ and after $Q=500\hspace{0.17em}\mu {\text{l min}}^{-1}$ the behaviour of the flow is relatively unchanging, whereas in between we observe substantial differences in the appearance of the streamlines (most noticeably in the merging of the recirculation zones) and cell surface shear stress profiles (see electronic supplementary material).

Figure 4.

Relationship between input flow rate and peak cell surface flow speed (a) and shear stress (b) with the inset plots illustrating each relationship up to $Q=400\hspace{0.17em}\mu {\text{l min}}^{-1}$. Note that since the velocity is equal to zero on the cell surface, we evaluate the ‘cell surface’ flow speed just above the cell surface at z = h_c.

3.2. Reaction governed by nonlinear saturable binding kinetics

We examine drug concentration profiles in the chamber for an input flow rate of $Q=100\hspace{0.17em}\mu {\text{l min}}^{-1}$ and a nominal inlet sirolimus concentration of $c_S^{\mathrm{in}}=5.00\times {10}^{-3}\hspace{0.17em}{\text{mol m}}^{-3}$. Our simulations confirm (not shown) that at steady state the free drug concentration profiles are uniform in the chamber in line with our rationale described in §2.4.1. Furthermore, the bound drug concentration within the cell layer takes the constant value $b_S=0.2388\hspace{0.17em}{\text{mol m}}^{-3}$, as predicted from (2.10). The significance of this result is that since the steady-state concentration profiles are uniform throughout, this implies the binding model is effectively a 1D problem which suggests the geometry of the chamber and the flow profile within the chamber are irrelevant features. To confirm this, we compared results between identical simulations using: (i) the QV900 geometry versus a simple cylindrical geometry, and (ii) flow versus no flow. The results were identical (data not shown).

3.3. Reaction governed by Michaelis–Menten kinetics

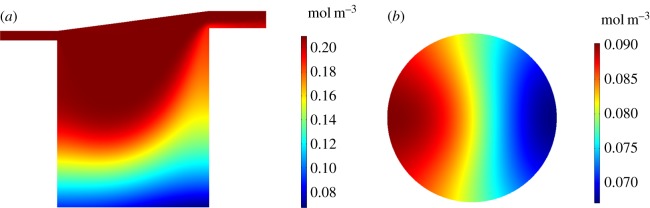
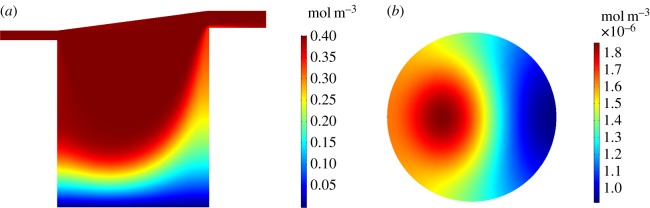
We examine solute concentration profiles in the chamber and at the cell surface for an input flow rate of $Q=100\hspace{0.17em}\mu {\text{l min}}^{-1}$. For the O₂ profiles (figure 5), we show results for rat cardiomyocytes as an example and we set $c_{{\mathrm{O}}_2}^{\mathrm{in}}=0.21\hspace{0.17em}{\text{mol m}}^{-3}$ to represent atmospheric O₂ levels [12]. Corresponding results for the remaining cell types are detailed in the electronic supplementary material. The O₂ concentration decreases from $c_{{\mathrm{O}}_2}^{\mathrm{in}}=0.21\hspace{0.17em}{\text{mol m}}^{-3}$ at the top of the chamber to approximately $0.07\hspace{0.17em}{\text{mol m}}^{-3}$ at the base of the chamber. The cell surface O₂ concentration ranges from approximately 0.07 to $0.09\hspace{0.17em}{\text{mol m}}^{-3}$.

Figure 5.

Simulation results for rat cardiomyocytes with $Q=100\hspace{0.17em}\mu {\text{l min}}^{-1}$ and $c_{{\mathrm{O}}_2}^{\mathrm{in}}=0.21\hspace{0.17em}{\text{mol m}}^{-3}$. (a) O₂ concentration profile through the centre of the chamber on the y, z plane. (b) O₂ concentration at the cell surface on the x, y plane.

Similar trends are observed for the APAP profiles (figure 6). Here, we show the results for human liver cells with an inlet concentration of $c_{\mathrm{APAP}}^{\mathrm{in}}=0.4\hspace{0.17em}{\text{mol m}}^{-3}$ to represent a dose of 60 mg kg⁻¹ [17]. The APAP concentration decreases from $c_{\mathrm{APAP}}^{\mathrm{in}}=0.4\hspace{0.17em}{\text{mol m}}^{-3}$ at the top of the chamber to approximately $9.15\times {10}^{-7}\hspace{0.17em}{\text{mol m}}^{-3}$ at the base of the chamber. The APAP concentrations are very low at the cell surface, ranging from approximately 9.15 × 10⁻⁷ to $1.86\times {10}^{-6}\hspace{0.17em}{\text{mol m}}^{-3}$, suggesting that the majority of the APAP is metabolized by the cells.

Figure 6.

Simulation results for human liver cells with $Q=100\hspace{0.17em}\mu {\text{l min}}^{-1}$ and $c_{\mathrm{APAP}}^{\mathrm{in}}=0.4\hspace{0.17em}{\text{mol m}}^{-3}$. (a) APAP concentration profile through the centre of the chamber on the y, z plane. (b) APAP concentration at the cell surface on the x, y plane.

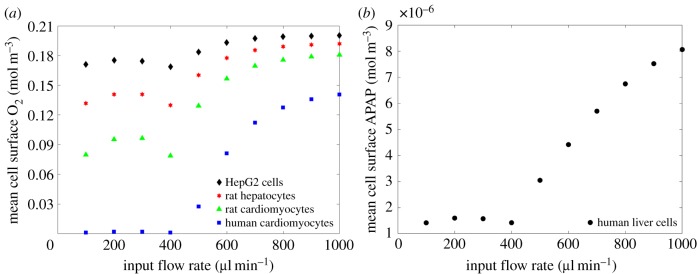
In figure 7, we plot the average cell surface concentration versus flow rate for both O₂ and APAP. In the case of oxygen consumption, we consider four cell types (rat cardiomyocytes, human cardiomyocytes, rat hepatocytes and HepG2 cells), while for APAP, we consider only human liver cells due to the available data. The results of the simulations show that the average cell surface concentration tends to increase as input flow rate increases across all cell types. As with the profiles for the peak cell surface flow speed and shear stress, we observe a dip in average cell surface concentration between $Q=200\hspace{0.17em}\mu {\text{l min}}^{-1}$ and $Q=500\hspace{0.17em}\mu {\text{l min}}^{-1}$ which is explained by changes in the flow pattern.

Figure 7.

Relationship between input flow rate and average cell surface O₂ (a) and APAP (b). These results correspond to input solute concentrations of $c_{{\mathrm{O}}_2}^{\mathrm{in}}=0.21\hspace{0.17em}{\text{mol m}}^{-3}$ and $c_{\mathrm{APAP}}^{\mathrm{in}}=0.4\hspace{0.17em}{\text{mol m}}^{-3}$, respectively.

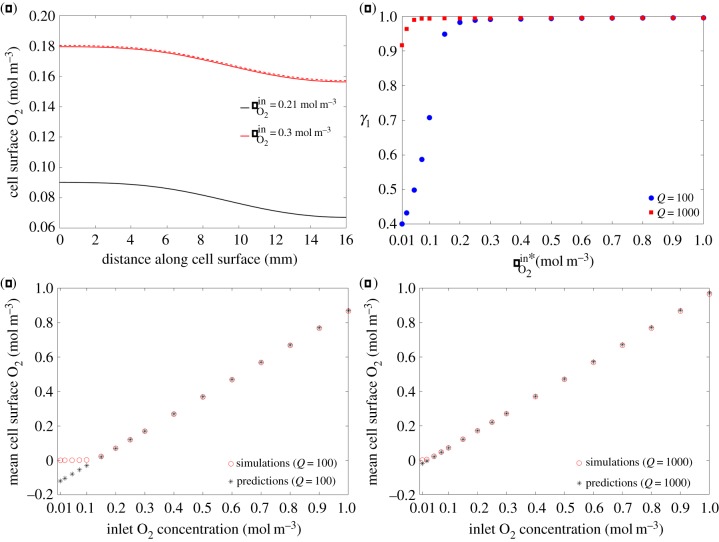
Next, we test our hypotheses (2.13) and (2.17) which should allow for the prediction of the solute concentration profiles at the cell surface in single and connected chambers, respectively. Recall that these relationships inherently assume that the rate of metabolism is constant and so only hold true for $c_{\hspace{0.17em}j}\gg K_{\hspace{0.17em}j}^i$. For the parameters in table 1, this criteria is not satisfied by APAP and so we consider O₂ as an example and illustrate the results for rat cardiomyocytes. In figure 8a, we compare our prediction of the cell surface O₂ concentration profile from (2.13) to the results of the simulation when we increase the inlet concentration from $c_{{\mathrm{O}}_2}^{\mathrm{in}}=0.21\hspace{0.17em}{\text{mol m}}^{-3}$ to $c_{{\mathrm{O}}_2}^{\mathrm{in}}=0.3\hspace{0.17em}{\text{mol m}}^{-3}$, and excellent agreement is found. Integrating (2.13) with respect to y over the diameter of the cell surface (−r < y < r) and rearranging gives

$${\gamma }_1=\frac{{\int }_{-r}^r{c}_{\hspace{0.17em}j}^{\ast }(y)\hspace{0.17em}\text{d}y-{\int }_{-r}^r{c}_{\hspace{0.17em}j}(y)\hspace{0.17em}\text{d}y}{2r\mathrm{\Delta }{c}_{\hspace{0.17em}j}^{\mathrm{in}}}\approx 1,$$ 3.1

where we have defined γ₁ as a measure of how good the approximation (2.13) is. Therefore, to test the validity of our hypothesis for predicting the cell surface solute concentration profile in a single chamber when the inlet concentration is varied, we evaluated (3.1) for $Q=100\hspace{0.17em}\mu {\text{l min}}^{-1}$ and $Q=1000\hspace{0.17em}\mu {\text{l min}}^{-1}$ with $c_{{\mathrm{O}}_2}^{\mathrm{in}}=0.21\hspace{0.17em}{\text{mol m}}^{-3}$. Figure 8b demonstrates that γ₁ ≈ 1 for the majority of these cases, with the prediction improving for higher inlet concentrations where $c_{{\mathrm{O}}_2}\gg K_{{\mathrm{O}}_2}$ and metabolism is approximately constant. The approximation is weakest for the lowest values of $c_{{\mathrm{O}}_2}^{\mathrm{in}}$ where this criteria is not satisfied. Note that the prediction is better for the higher flow rate: increasing input flow rate gives rise to higher cell surface concentrations and so the assumption of $c_{{\mathrm{O}}_2}\gg K_{{\mathrm{O}}_2}$ is more accurate in this case.

Figure 8.

Single chamber predictions. (a) Comparison between our prediction using (2.13) (dashed line) and the simulation (solid line) when we increase the inlet concentration from $c_{{\mathrm{O}}_2}^{\mathrm{in}}=0.21\hspace{0.17em}{\text{mol m}}^{-3}$ to $c_{{\mathrm{O}}_2}^{\mathrm{in}}=0.3\hspace{0.17em}\mathrm{mol}\hspace{0.17em}{\mathrm{m}}^{-3}$. (b) Calculated γ₁ values for Q = 100 and $1000\hspace{0.17em}\mu {\text{l min}}^{-1}$ with $c_{{\mathrm{O}}_2}^{\mathrm{in}}=0.21\hspace{0.17em}{\text{mol m}}^{-3}$. (c) Relationship between inlet O₂ concentration and mean cell surface O₂ concentration for $Q=100\hspace{0.17em}\mu {\text{l min}}^{-1}$. (d) Relationship between inlet O₂ concentration and mean cell surface O₂ concentration for $Q=1000\hspace{0.17em}\mu {\text{l min}}^{-1}$.

In certain cases, it may be that the quantity of interest is the mean cell surface concentration, rather than spatial profiles. We have demonstrated that our formula (2.13) extends to the case of predicting mean concentrations (figure 8c,d). Moreover, we have established that there is a linear relationship between the inlet O₂ concentration and the mean cell surface O₂ concentration for the majority of inlet O₂ concentrations considered: the linear relationship breaks down when cell surface O₂ concentrations are sufficiently low that our approximation $c_{{\mathrm{O}}_2}\gg K_{{\mathrm{O}}_2}$ is no longer valid. We note from figure 8c,d that the approximation breaks down at higher inlet O₂ concentrations for the lower flow rate.

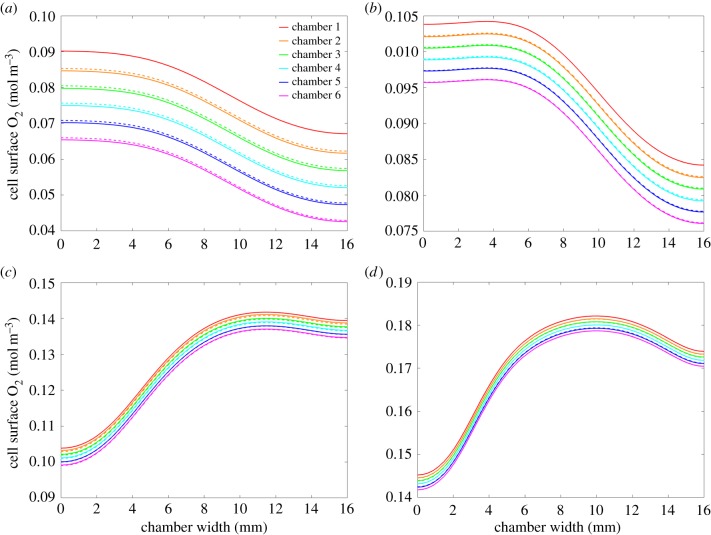
To test the validity of our hypothesis for predicting the cell surface solute concentration profile in chamber n given that the profile is known in chamber 1, we simulated the environment in six connected chambers for $Q=100\hspace{0.17em}\mu {\text{l min}}^{-1}$ and $c_{{\mathrm{O}}_2}^{\mathrm{in}}=0.21\hspace{0.17em}{\text{mol m}}^{-3}$. We then used (2.17) to predict $c_{\hspace{0.17em}j}^n(y)$. Figure 9 compares the predictions (dashed lines) with the results obtained from simulations (solid lines) for various input flow rates. The plots show that the predictions improve with increasing input flow rate, since the assumption of constant metabolism is more accurate. The deviation of the predicted values from the simulated concentrations is a combination of numerical error and the small errors associated with the assumptions that have been made in deriving (2.17). We note that the difference between the predicted values and the simulated concentrations in each chamber is less than 1% and this small deviation is, therefore, considered to be acceptable. As with the single chamber predictions, our formula holds also for mean cell surface concentrations and there is a linear relationship between mean cell surface O₂ concentration and chamber number, provided that $c_{{\mathrm{O}}_2}\gg K_{{\mathrm{O}}_2}$.

Figure 9.

Connected chamber predictions for $c_{{\mathrm{O}}_2}^{\mathrm{in}}=0.21\hspace{0.17em}{\text{mol m}}^{-3}$, showing simulated (solid lines) versus predicted (dashed lines) cell surface O₂ concentration profiles for (a) $Q=100\hspace{0.17em}\mu {\text{l min}}^{-1}$, (b) $Q=300\hspace{0.17em}\mu {\text{l min}}^{-1}$, (c) $Q=500\hspace{0.17em}\mu {\text{l min}}^{-1}$ and (d) $Q=700\hspace{0.17em}\mu {\text{l min}}^{-1}$.

4. Discussion

Our findings have a number of important implications that should be considered carefully when deciding on the operating conditions of perfusion cell culture systems.

4.1. Cell surface flow speed and shear stress critically depend on the choice of input flow rate

Varying the input flow rate over a realistic range of operating flow rates gives rise to qualitatively different fluid dynamics within the chamber and strongly influences the cell surface flow speed and shear stress levels. This means not only that the choice of flow rate is critical but also that different flow rates should be chosen for different applications. For example, if one wishes to test the response of cells to a drug where it is known that the cells are exposed to flow in vivo, then the model presented here may be used to calculate the input flow rate that gives rise to the desired cell surface flow speed. For some applications, it may be that the cells should be exposed to slow-flow, while for other cell types it may be that higher flow speeds at the cell surface are desired. Similarly, if it is known that a given cell type is capable of tolerating a known level of shear stress, then again the model may be used to select a sensible flow rate that ensures cell surface shear stress is kept within the desired range.

4.2. Spatial placement of cells influences the flow speed and shear stress that they experience

Figure 3c shows clearly that there is a spatial distribution of shear stress at the cell surface. This means that the choice of where cells are placed has an impact on the level of shear stress they will experience. For example, in the case figure 3c, depending on the application, it may be wise not to culture cells in the centre of the chamber, due to the peak in shear stress that occurs there. The spatial distribution of shear stress changes with input flow rate (see electronic supplementary material), most substantially between $Q=200\text{–}500\hspace{0.17em}\mu {\text{l min}}^{-1}$ as a result of the merging recirculation zones. We remark that the non-monotonic behaviour of the flow speed and shear stress with increasing input flow rate is not at all obvious and has only been identifiable through the simulation approach considered here. For flow rates outside of this range the peak cell surface shear stress is observed at the centre, whereas for flow rates within this range the pattern is less predictable. Therefore, depending on the application it may well be wise to avoid these flow rates. It is also important to note that the flow speed (and consequently the magnitude of the shear stress) decreases as we move down the chamber (figure 3b). Therefore, one may also change the flow environment the cells are exposed to by raising the position of the cells in the chamber. The model presented here may, therefore, be used to optimize the spatial placement of cells within the chamber.

4.3. Flow rate and Michaelis–Menten parameters dictate cell surface solute concentrations

Figure 7 highlights that the cell surface solute concentration is strongly influenced by both flow rate and the cell-specific M–M parameters. With the exception of the dip between $Q=200\text{–}500\hspace{0.17em}\mu {\text{l min}}^{-1}$ (due to the change in fluid dynamics as described earlier), increasing the flow rate corresponds to increasing the solute concentration that arrives at the cell surface and is available for reaction. The variation in cell surface solute concentration across the different cell types confirms that the M–M reaction at the cell surface also has an important influence on the cell surface solute concentration. Relationships derived from the model, such as those in figure 7, can, therefore, be used when configuring the input flow rate for experiments in which the desired cell surface concentration is known.

4.4. Steady-state solute concentrations may be predicted a priori

In the case of reaction governed by nonlinear saturable binding kinetics, steady-state free and bound solute concentrations within the cells may be calculated a priori using (2.10)–(2.12). Since (2.10)–(2.12) rely only on the parameters $k_{\hspace{0.17em}j}^d$ and B_j, they may be used to calculate the steady-state concentrations for any drug whose interaction with the cells is governed by nonlinear saturable binding kinetics, given that the drug is supplied as a constant source and diffusion of drug within the cell region is isotropic. In the case of reaction governed by M–M kinetics, we have uncovered simple relationships between inlet solute concentrations and cell surface concentration in single and connected chambers, provided that c_j ≫ K_j (figures 8 and 9). Our simple formula (2.13) may be used to predict changes in cell surface solute concentrations when the inlet solute concentration is altered, while (2.17) may be used to predict cell surface concentrations in downstream chambers. These relationships could be extremely useful to help determine the inlet concentration required to achieve a desired cell surface concentration, and moreover to decide on a suitable number of chambers to connect before concentrations fall below some desired level. Where possible, it is advisable to stay within the regime c_j ≫ K_j so that the results remain predictable.

We feel it appropriate to reiterate that a number of assumptions have been made in this work, as outlined in the preceding text. While the overall conclusions above are generally true, the quantitative results provided in §3 are specific to the particular bioreactor that we have simulated and must be interpreted within the context of the assumptions made. In particular, we present results only for steady state. Depending on the specific cell type and application, it may be more appropriate to consider time-dependent solutions, for example, if the quantities of interest need to be known in the very early stages of culture under flow. Our results are most applicable when the steady state (or ‘equilibrium’) conditions are of most interest.

5. Challenges

The focus of this paper has been on using modelling and simulation to help inform experimental operating parameters. However, these two endeavours are, of course, intrinsically linked. Mathematical and computational models require physical parameters (e.g. diffusion coefficients and metabolism rates) and these are not always known to a great degree of accuracy. It is particularly common for parameters to be gleaned from a variety of datasets, where experiments may not have been performed consistently, nor on the same type of cells or species. Sensitivity analysis may be used where there is some uncertainty over parameter values, but this has limitations, especially when the model results are highly sensitive to changes in the unknown parameters. Models, such as the one presented here, are most valuable when used in a predictive sense. However, before one may gain confidence in the model predictions, it is crucial that the model is validated. Therefore, it is critical that in silico tools are compared with experimental data, even if such data is limited. This can be challenging for a number of reasons. For example, it may not be easy (or possible) to take non-destructive measurements (e.g. cellular drug concentrations, O₂ concentrations at the cell surface, spatially varying flow speeds) within certain in vitro perfusion systems. Advanced imaging methods can help in this regard, but these may be limited by the optical properties of the system at hand. Oxygen probes are available, but again, these cannot easily be used without disrupting the experiments. We therefore strongly encourage the development of methods to acquire such data to facilitate model validation. While the difficulty of providing validation may be viewed as a disadvantage of modelling, it could also be seen as an advantage, i.e. modelling can allow us to obtain insight into quantities that we cannot easily measure experimentally.

The real value in modelling lies in the ability to reduce the number of experiments that have to be performed. For example, even if a system has been experimentally characterized under a given set of operating parameters, it may not be obvious how the environment changes when these operating parameters are altered. In this respect, a validated model can be invaluable, even if the validation is performed over a limited set of conditions.

The issue of model verification is also highly pertinent in this field, i.e. ensuring the numerical implementation of the model is correct. It is tempting to ‘believe’ results produced from computational software. However, great care must be taken to ensure the correctness and accuracy of the results. In this sense, mesh sensitivity studies and common-sense checks are both an integral part of computational modelling. However, these aspects are perhaps less familiar to non-experts, underlining the critical role of computational modellers.

These challenges only emphasize the importance of interdisciplinarity in this exciting field and that modelling and experimentation should go hand-in-hand, each complementing the other.

Data accessibility

This article has no additional data.

Authors' contributions

Conceived and designed the study: S.Mc.G., N.J.M., S.Mc.K., S.D.W. and B.S. Development of mathematical model: L.H., S.Mc.G., N.J.M., S.Mc.K. and S.D.W. Computational implementation of model: L.H. First draft: L.H. Review and editing: S.Mc.G., N.J.M., S.Mc.K., S.D.W. and B.S.

Competing interests

S.Mc.G. and L.H. gratefully acknowledge a financial donation from Kirkstall Ltd. B.S. is employed by Kirkstall Ltd.

Funding

The authors gratefully acknowledge funding provided by EPSRC (EP/M506539/1 and EP/M508056/1), a financial donation from Kirkstall Ltd and the award of an Alan & Kathie Stross Summer Fellowship by the Dr Hadwen Trust.