In vitro and computational modelling of drug delivery across the outer blood–retinal barrier

Abstract

The ability to produce rapid, cost-effective and human-relevant data has the potential to accelerate the development of new drug delivery systems. Intraocular drug delivery is an area undergoing rapid expansion, due to the increase in sight-threatening diseases linked to increasing age and lifestyle factors. The outer blood–retinal barrier (OBRB) is important in this area of drug delivery, as it separates the eye from the systemic blood flow. This study reports the development of complementary in vitro and in silico models to study drug transport from silicone oil across the OBRB. Monolayer cultures of a human retinal pigmented epithelium cell line, ARPE-19, were added to chambers and exposed to a controlled flow to simulate drug clearance across the OBRB. Movement of dextran molecules and release of ibuprofen from silicone oil in this model were measured. Corresponding simulations were developed using COMSOL Multiphysics computational fluid dynamics software and validated using independent in vitro datasets. Computational simulations were able to predict dextran movement and ibuprofen release, with all of the features of the experimental release profiles being observed in the simulated data. Simulated values for peak concentrations of permeated dextran and ibuprofen released from silicone oil were within 18% of the in vitro results. This model could be used as a predictive tool for drug transport across this important tissue.

1. Introduction

The ability to produce models that mimic tissue biology and physiology is crucial in the development of drug delivery systems. Currently, much of the pre-clinical work is conducted in animals, the limitations of which are well reported and which may be the cause of the 86% of drugs that fail in clinical testing [1]. The use of in vitro models means that human tissue can be used, minimizing species differences as well as ethical concerns. Although lacking the complex environment of a living body, they can be used to generate reliable data on drug transport and toxicology [2–4]. Computer science and simulation of pharmacokinetic behaviour are becoming an integral part of pharmaceutical research and development due to the significant reductions in cost and time they can offer. In silico tools can, in conjunction with complementary empirical measurements, contribute to the optimization of novel drug delivery systems, and ever-increasing computing power has allowed more sophisticated models to be developed. The combination of accurate, validated in vitro and in silico models has the potential to revolutionize the development of drug delivery technologies by providing rapid, reproducible and human-relevant data [5].

Epithelial barriers are particularly important in drug delivery, as one of the primary functions of epithelium is to act as a barrier, and certain drugs must cross the barrier to reach the target tissue. Tissues such as skin [6], intestinal [7] and pulmonary epithelium [8] have all been studied in the development of drugs and chemicals, and the complexity of the models of these barriers has improved dramatically in the last few decades, from simple two-dimensional, multi-well plate cultures to intricate microfluidic culture chips. Many epithelial barrier models, such as those for skin, are based on an air–liquid interface. In the case of fluid–fluid interfaces, many are designed as static culture systems. These static culture systems allow the determination of parameters such as barrier permeability and diffusion coefficients, which are of crucial importance when studying the movement of potential therapeutic treatments across epithelial tissues. They do not, however, provide realistic, time-dependant development of concentration gradients across the model as they do not mimic the many dynamic factors associated with these physiological barriers. With the rapid rise in microfluidic technologies for cell culture that has occurred over recent years, the creation of dynamic in vitro models has become more accessible [9].

There are many eye diseases that require treatment with pharmacological agents. In contrast to the front of the eye, where drug delivery can often be achieved by topical application of eye drops and ointments, many eye diseases of the posterior segment of the eye require the delivery of drugs directly into the vitreous. The drugs may be required to treat acute infection or inflammation, or to treat a chronic condition such as age-related macular degeneration or diabetic retinopathy. In the latter case, repeated intravitreal injection or use of implantable drug delivery devices are the preferred methods to achieve therapeutic levels of the drug over the extended periods required. Owing to the cost and invasive nature associated with repeated intravitreal injection, as well as the potential for sight-threatening complications, much effort has been directed towards developing implants that can deliver drugs over extended periods [10]. We have recently developed technology to achieve extended release of drugs from silicone oil tamponades [11,12]. Silicone oil and gas tamponades are used to replace the native vitreous humour in the treatment of sight-threatening retinal detachments. They inhibit the flow of aqueous fluids into the subretinal space, exclude inflammatory factors, and support the retina as tears heal [13,14]. Silicone oils are the only medical devices licensed for long-term use as tamponades. Drug release from silicone oil tamponades would release pharmacological adjuncts to the surgical treatment with the aim of reducing complications caused by scarring conditions, such as proliferative vitreoretinopathy and proliferative diabetic retinopathy. The ability to predict the release of drugs from such devices, as well as understand factors that influence clearance from the posterior cavity, is crucial if over- and under-dosing is to be avoided.

Drugs administered intravitreally, whether via injection or an implant, are cleared via two routes, either anteriorly or posteriorly (figure 1a). Nearly all compounds can be eliminated via the anterior route. Anteriorly, once the drug has diffused across the vitreous, it enters the aqueous of the posterior chamber where it is transported into the anterior chamber and cleared, either through Schlemm's canal or into the uveal blood flow [15]. Alternatively, posterior elimination occurs through permeation across the posterior blood–ocular barriers such as the outer and inner blood–retinal barrier (BRB). This route requires either adequate passive permeability of agents, which is generally only applicable to very low molecular weight or lipophilic substances, or active transport of molecules by the cells present in the barrier. For this reason, larger or hydrophilic molecules generally have longer half-lives in the vitreous as they are not able to move as freely through the vitreous or pass across the retina [16].

Figure 1.

Clearance mechanisms in the eye and comparison to Kirkstall QV600 system. (a) Key structures in the anterior and posterior drug clearance routes. Created with BioRender. The OBRB is the structure of interest in this study. (b, top) Schematic of Kirkstall QV600 set-up showing analogous OBRB structures (created with BioRender), (middle) dimensions of the QV600 chamber, (bottom) three-dimensional composite of QV600 chamber. (c) Single-pass experimental set-up. Dotted line represents dynamic flow. (a) Fresh media reservoir, (b) QV600 chamber, (c) peristaltic pump and (d) waste collection reservoir.

In vitro models have often been used to investigate the permeability of drugs and compounds across the retinal pigmented epithelium (RPE) or to model diseases of the outer blood–retinal barrier (OBRB). In order to obtain a physically accurate model of the OBRB, the main anatomical structures (retinal pigment epithelium, Bruch's membrane and choroid), as well as physiological conditions, such as flow, need to be incorporated. Although many of the in vitro models of the OBRB that have been reported include the main anatomical structures within the tissue [17–20], few include a flow mechanism to model the blood flow within the choroid and to avoid the formation of an unstirred water layer [21]. This flow mechanism is particularly important when investigating the clearance of drugs across the BRB, as it causes systemic removal of drugs. Yeste et al. describe a system which comprises the co-culture of human retinal endothelial cells and ARPE-19 (a widely used RPE cell line [22,23]) in a microfluidic culture system [24]. This system compartmentalizes the cells and, therefore, does not create a single construct. The transepithelial electrical resistance of each of the cell layers was measured independently; this does not represent the true barrier functionality of the tissue as it investigates each component of the barrier in separate parts. Additionally, no investigations of drug transport across the barrier were conducted. Another microfluidic chip device was reported by Chen et al. who investigated the co-culture of ARPE-19s and human vascular endothelial cells in a microfluidic model of choroidal angiogenesis [25]. Within this model, glucose was transported to the cells within the flow of the media but the movement of the molecules was not studied. The lack of studies regarding in vitro modelling of the effects of posterior systemic clearance of drugs in the eye by, for example, incorporating flow, leaves scope for this to be investigated further.

The Kirkstall QV600 cell culture chamber is a novel system which has been designed to allow cells to be cultured in an air–liquid interface environment in vivo, for example, skin, respiratory epithelium or corneal cells. It can also be modified to co-culture cells at a fluid–fluid interface and expose each surface to independently controlled flow. The availability of published data from studies using this system is limited. The QV600 has been used to study the permeability of fluorescein across a cell culture model of gut epithelium [26], demonstrating that the application of flow resulted in increased permeability, as well as increased barrier function of the cells. It has also been used to build a human bronchial or small airway epithelial model, using the combination of the air–liquid interface and flow to improve and accelerate cell differentiation [27]. To the best of our knowledge, there are no reports of this chamber being used to build a model of the OBRB. For the purposes of investigating drug permeability across the OBRB, this system provides many of the necessary properties for a representative model, i.e. the ability to mimic clearance by choroidal flow and to incorporate drug delivery devices that work in aqueous and non-aqueous environments (figure 1b).

There have been several studies carried out that specifically use computational techniques to model drug delivery and kinetics in the posterior segment of the eye, including systemic delivery methods, intravitreal injection and ocular implants [28–30]. These models all simulate drug delivery within computer-built geometries of the eye and although they can provide useful information regarding the drug kinetics in the eye, experimentally these results cannot be validated in vivo due to the invasive nature of the techniques that would be required to do so. Much of the work carried out is based on experimental work conducted almost four decades ago by Palestine & Brubaker [31], who investigated the kinetics of fluorescein in the human eye. Other published pharmacokinetic data are predominantly from animal models, which bring a series of well-reported problems, including the use of different animal models, differences between animal and human anatomy and vitreous composition and different experimental set-ups [32]. In order for the sophistication of these models of drug delivery in the eye to be improved, more experimental data are required to provide a greater database for finite-element analysis validation. Furthermore, very little data on the release of drugs from silicone oil tamponades are available. For this reason, it could be useful to build predictive models of in vitro devices used in the development of novel drug delivery devices as they are able to be validated using data from benchtop experiments. Although these models may not provide an approximation of what will occur once the device is administered in the eye, it may make the development process more efficient. In addition, an accurate model of drug transport across the OBRB may be able to help predict systemic effects from ocular delivery, or design drugs that could be delivered systemically and cross the BRB [33]. In this study, we used a combinatory approach of in vitro and in silico modelling to investigate drug transport and clearance through the posterior drug elimination pathway with the aim of producing validated tools for the optimization of intravitreal drug delivery devices.

2. Material and methods

2.1. In vitro model

2.1.1. Materials

Fluorescein isothiocynate conjugated dextran (FD) was purchased from Sigma-Aldrich (FD-4, MW 4 kDa) and diluted to 50 µg ml⁻¹ in phosphate-buffered saline (PBS) solution. Ibuprofen (2-(4-isobutylphenyl)propionic acid, C₁₃H₁₈O₂, MW 206.29) was purchased from Tokyo Chemical Industry UK (I0415) and 1 mg ml⁻¹ was dissolved in technical grade 1000 cSt silicone oil (SIO) obtained from Fluoron GmbH. PBS tablets were purchased from Thermo Scientific (Oxoid BR0014G) and used as instructed, 1 tablet per 100 ml distilled water. Expanded-polytetrafluoroethylene (ePTFE_M) cell culture membrane inserts were purchased from Merck Millipore (PICM02150, 0.4 µm pore size). The microfluidic chambers and associated silicone tubing were QV600 cell culture kits purchased from Kirkstall Ltd (Rotherham, UK) and the peristaltic pump (Parker, PF22X0103) used to generate the fluid flow was also purchased from Kirkstall Ltd. Fluorescence measurements were performed using a microplate reader (FLUOstar OPTIMA, BMG LABTECH). UV–visible spectroscopy (UV–vis) measurements were performed in UV transparent, plastic cuvettes (Merck Z605050) using a spectrometer (SPECTROstar nano, BMG LABTECH).

2.2. Methods

2.2.1. Cell culture

ARPE-19 cells (ATCC^® Number: CRL-2302™) between passage 23 and 30 were cultured in Dulbecco's Modified Eagle Medium/Ham's Nutrient Mixture F-12 Formulation (1 : 1 mix) with l-glutamine, 15 mM HEPES and sodium bicarbonate (DMEM-F12) (Sigma, D8437) supplemented with 10% fetal bovine serum (BioSera, S1900) and 1% penicillin/streptomycin (Sigma, P0781). Following seeding, cells were maintained in 2% serum. Cells were seeded on ammonia plasma-treated ePTFE_M cell culture insert membranes (NH3_ePTFE_M). These are ePTFE membranes that have been subjected to a proprietary treatment by the manufacturer, designated ePTFE_M, and ammonia gas plasma treated to improve the hydrophilicity of the membrane as described previously [34,35] designated NH3_ePTFE_M. Following seeding cells were cultured for 10 days at 37°C in a humidified incubator with 5% CO₂.

2.2.2. Determination of apparent permeability coefficient

Permeability experiments were performed in a classic two-compartment, zero-flow, model system. NH3_ePTFE_M cell culture inserts were placed in a 24-well plate and 400 µl of tracer molecule solution (50 µg ml⁻¹ FITC-dextran; MW: 4 kDa) was added to the donor compartment with 600 µl of PBS solution in the receptor compartment. In static conditions, transmembrane flux (J_d) is predominantly determined by diffusive forces and can thus be calculated using the permeability (P_s) and concentration gradient (ΔC):

$$J_{\mathrm{d}}=P_{\mathrm{s}}\mathrm{\Delta }C.$$

At time intervals of 1, 3, 8 and 24 h, 50 µl samples were taken from the receptor compartment and replaced with fresh PBS solution. Samples were stored at 4°C and protected from light until the time points had been completed, and the fluorescence intensity of the samples was read in a microplate reader at λ_ex (excitation wavelength): 485 nm, λ_em (emission wavelength): 535 nm. Flux was determined from the slope of the linear portion of the curve. Calibration curves (R² ≥ 0.997) for each molecule were made using a serial dilution of 50 µg ml⁻¹ dextran solution. Average measurements for blanks (0 µg ml⁻¹ of dextran) were subtracted from the standards and the unknown samples. Concentrations of the unknown samples were determined from the calibration curves and each sample was repeated in triplicate (n = 3).

2.2.3. Measurement of drug release

An experimental concentration of 1 mg of ibuprofen (ibu) in 1 ml of 1000cSt silicone oil (Fluoron GmbH) was used. The ibu-SiO was stirred for 72 h in a sealed flask and then filtered in a Class II biological safety hood to sterilize. In a 24-well plate, 1 ml of ibu-SiO was syringed on top of 500 µl of PBS. At defined time points, 100 µl samples were taken from the PBS, transferred to UV transparent cuvettes (UVette, Eppendorf) and the time-dependent increase in ibuprofen concentration measured by UV–vis spectroscopy (n = 3).

2.2.4. Determination of diffusion coefficients

The diffusion coefficients (D) were calculated using the Stokes–Einstein equation, using the appropriate solvent viscosity for either DMEM-F12, PBS, water or SiO (μ), the apparent radius (r) of either the dextran or ibuprofen molecule [36], temperature (T) and Boltzmann constant (k):

$$D=\frac{kT}{6\pi \mu r}.$$

2.2.5. Drug clearance study

The Kirkstall QV600 system was arranged in a single-pass series fluid circuit using a peristaltic pump to control the fluid flow inlet rate (figure 1c). Either acellular or cell-seeded cell culture inserts containing 400 µl of tracer solution were inserted into the QV600 chamber to allow flow across the receptor side of the membrane. The cell culture inserts have a smaller diameter than the QV600 chamber. In order to create a seal between the donor and receptor compartments, a silicone O-ring was placed around the exterior wall of the insert before it was placed in the chamber. The system was incubated at 37°C and PBS solution was perfused through the receptor chamber at a constant flow rate for 24 h (8 h for 2 ml min⁻¹ experiments). The flow rates used were 20 µl min⁻¹, 200 µl min⁻¹, 400 µl min⁻¹.

FITC-conjugated dextran (4 kDa) was dissolved in DMEM-F-12 supplemented with 10% fetal calf serum to 50 µg ml⁻¹ in the donor chamber. The systems were set up and perfused for 1 h, after which the flow was stopped and the tubes were clamped. The solution in the receptor chamber was completely removed and homogenized, and 50 µl samples were taken. The systems were cleaned and reset, and the protocol was repeated for increasing periods of time (1 h time increments). The fluorescence intensity of the samples was read in a microplate reader at λ_ex: 485 nm, λ_em: 535 nm. Concentration of the unknown samples was determined from the calibration curves and each sample was repeated in triplicate (n = 3).

2.2.6. Measurement of ibuprofen release from silicone oil under flow conditions

The QV600 chamber and peristaltic pump were assembled as described previously. The system was primed with 30 ml of sterile PBS. In total, 2 ml of 1 mg ml⁻¹ ibu-SiO was added directly on top of the PBS. The system was incubated at 37°C and PBS was perfused through the receptor chamber at a constant flow rate for 24 h (8 h for 2 ml min⁻¹ experiments). The flow rates used were 20 µl min⁻¹, 200 µl min⁻¹ and 2 ml min⁻¹. At set time intervals, the ports were clamped shut and the volume of PBS beneath the ibu-SiO removed using a 25-gauge needle. A 25G needle allows the PBS to be removed but the viscosity of the oil prevents its withdrawal through the needle. The solution was homogenized and 50 µl samples taken. UV–vis was used to determine the ibuprofen concentration in the samples as previously described.

2.3. Computer model

2.3.1. Geometry of the QV600 chamber and grid generation

Figure 2 shows the two-dimensional geometrical models used. Key dimensions are based on dimensions obtained from the technical drawing from the QV600 chamber. Differences in the donor compartment domain take into account the differences in geometry between the cell culture inserts (figure 2a–d) and the silicone oil tamponade (figure 2e,f). The cell culture inserts have a smaller diameter than the chamber, therefore the width of this domain is reduced. Additionally, the geometry used in the dextran transport studies included a third domain representative of the ePTFE/cell membrane. The dimensions of this domain were dependent on whether a representative cell monolayer was included.

Figure 2.

Input geometry and mesh generation of each model by COMSOL Multiphysics. (a) Input geometry for Kirkstall QV600 dextran simulations. Red dots indicate points 1 and 2 in grid independence study. (b) Mesh generated for Kirkstall QV600 chamber used in dextran transport simulations. This mesh comprised 38 267 free triangular elements. (c,d) Geometry and mesh zoomed to membrane domain. (e) Input geometry; red dots indicate points 1 and 2 for grid independence study. (f) Mesh generated for Kirkstall QV600 chamber used in ibuprofen release simulations. This mesh comprised 2258 free triangular elements. (g) Percentage difference in velocity at two points in the centre of the chamber compared with the finest mesh for dextran transport (finest mesh: 108 814 elements). (h) Percentage difference in velocity at two points in the centre of the chamber compared with the finest mesh ibuprofen release (finest mesh: 3481 elements). An acceptable mesh density was deemed to produce less than 5% error.

The mesh was generated using the commercial software COMSOL Multiphysics. For the single-phase, dextran transport studies, the mesh comprised free triangular elements with boundary layers at the no-slip walls. The total number of elements in the mesh was 38 267. For the ibuprofen release studies, the mesh consisted of 2258 free triangular elements in a moving mesh system to model the flow of two immiscible liquids.

2.3.2. Governing equations

The incompressible Navier–Stokes equations along with a species transport equation were solved in order to obtain the velocity and concentration fields across the models.

Momentum equation:

$$\rho \left(\frac{\mathrm{\partial }\mathit{u}}{\mathrm{\partial }t}+\mathit{u}\hspace{0.17em}.\hspace{0.17em}\mathrm{\nabla }\mathit{u}\right)=-\mathrm{\nabla }p+\mathrm{\nabla }\hspace{0.17em}.\hspace{0.17em}\mathbf{T}+\mathbf{f}.$$

The left-hand side of the equation describes the product of the density of the fluid, ρ, and the acceleration that is experienced by the particles within the fluid where u is the velocity vector. The right-hand side of the equation incorporates the forces which are responsible for the particle acceleration, the pressure, p; the viscous shear stresses, T; and volume forces, f, which is equal to the product of the gravity constant, g, and the density of the fluid.

Continuity equation:

$$\mathrm{\nabla }\hspace{0.17em}.\hspace{0.17em}\mathit{u}=0.$$

Species transport equation:

$$\frac{\mathrm{\partial }{c}_i}{\mathrm{\partial }t}+\mathrm{\nabla }\hspace{0.17em}.\hspace{0.17em}(-D\mathrm{\nabla }{c}_i)+\mathit{u}\hspace{0.17em}.\hspace{0.17em}\mathrm{\nabla }{c}_i=0.$$

This equation solves the mass conservation equation for the concentration of one or more chemical species, c_i. The diffusion coefficient, D, which was determined from the in vitro studies, is specific to each species. These are presented in table 1. As the drugs used in this study are not reacting with the cells and the cell layer acts only as a barrier, the right-hand side of the equation is zero.

Table 1.

Input parameters for dextran transport studies.

parameter	value
diffusion coefficient of FD in water	2.39 × 10−11 m2 s−1
diffusion coefficient of FD across ePTFE	1.2 × 10−6 m2 s−1
diffusion coefficient of FD across ePTFE ARPE-19 complex	1.1 × 10−7 m2 s−1
initial concentration of FD in donor domain	50 µg ml−1
initial concentration of FD in membrane domain	0 µg ml−1
initial concentration of FD in receptor domain	0 µg ml−1
flow rate	20, 200, 400, 2000 µl min−1
permeability coefficient of ePTFE	1.4 × 10−5 cm s−1
permeability coefficient of ePTFE ARPE-19 complex	8.8 × 10−6 cm s−1
porosity of ePTFE membrane	0.3 (from manufacturer)
permeability of water across ePTFE	1 × 10−6 cm2
density of water at 37°C	994.12 kg m−3
dynamic viscosity of water at 37°C	0.691 mPa s

Two models were investigated in this study: one to study the passage of dextran molecules across the NH3_ePTFE_M membrane and the other to study the release of ibuprofen from silicone oil. These two models are described separately below.

2.3.3. Dextran transport model

The model itself consists of two parts: a laminar flow interface to compute the velocity flow and pressure fields of the single-phase fluid flow, and a transport of diluted species interface. COMSOL provides this interface to calculate the concentration field of a dilute solute in a solvent, i.e. the fluorescently labelled dextran solutions diluted in culture medium. The model was run to simulate both the absence and presence of cells using alterations in both the geometry and permeability boundary conditions that are described below.

An additional physics node was included to model the transport of FD through the membrane into basolateral medium flow. This model accounts for the dissipation of kinetic energy experienced by the fluid moving through a porous matrix through means of viscous shear. In COMSOL, this is implemented using the fluid and matrix properties node which uses the Brinkman equations:

$$-\frac{\mu }{\kappa }\mathit{u}+\hspace{0.17em}\frac{\mu }{{\epsilon }_p}{\mathrm{\nabla }}^2\mathit{u}=\mathrm{\nabla }p,$$

where κ is the permeability of the membrane to the fluid and ε_p is the porosity (table 1). This node was only applicable to the membrane part of the model and was therefore only applied to that domain.

2.4. Boundary conditions

A no-slip boundary condition was applied to the walls of the geometry:

$$\mathit{v}=0.$$

The inlet was applied to the left-hand wall of the inlet tube. The velocity field, v, for the inlet was defined by

$$\mathit{v}=\frac{Q}{A},$$

where Q is the flow rate and A is the cross-sectional area of the inlet tube. A range of inlet flow rates was investigated to coincide with the flow rates used in the in vitro experiments: 20 µl min⁻¹, 200 µl min⁻¹, 400 µl min⁻¹ and 2 ml min⁻¹. The outlet was applied to the right-hand wall of the outlet tube. The outlet condition was a zero pressure (p) condition:

$$p=0.$$

Two transport of diluted species nodes were used in the transport of dextran simulations: one for the donor and receptor domains, and one for the membrane domain. This separate node for the membrane domain allowed the difference in diffusion in that domain to be accounted for.

For the donor and receptor domains, a no-flux boundary condition was applied to the exterior boundaries of the geometry on the same edges as the no-slip conditions for laminar flow. An outflow condition was applied to the outlet to account for transport of FD out of the domain by the fluid motion. At the boundaries where the two domains meet the membrane domain, a pointwise constraint was applied to compute the transfer of mass across the membrane out of the donor domain into the receptor domain. The pointwise constraint was a function of the two concentrations at the boundaries which were defined by the diffusive and convective movements of the FD through the domains. The flux (J_d) across the boundaries was computed based on the concentration of FD (c_i) and the diffusion coefficient (D) for each domain.

$$J_d=-D\mathrm{\nabla }{c}_i+\mathit{u}{c}_i.$$

The second transport of diluted species node applied similar boundary conditions as above but across the membrane domain, therefore accounting for the difference in diffusion. A no-flux condition was applied on the exterior wall boundaries of the membrane. The same function for the pointwise constraint was applied to the boundaries that were shared with the other two domains. The dimensions of the membrane domain were altered depending on whether the presence of the cells was being modelled or not. In the presence of cells, the membrane domain was 70 µm in height and the appropriate diffusion coefficient of the domain was used, as described in table 1. In the absence of the cells, the domain was reduced to 50 µm and the diffusion coefficient was altered to account for their absence.

2.5. Ibuprofen release model

The second model explored ibuprofen release from SiO. With the differences that the ibuprofen release studies required, the model was altered to simulate the interaction of two immiscible fluid phases: the aqueous PBS phase and the 1000 cSt silicone oil phase. This model also removes the membrane domain as the movement of drug was directly from the oil into PBS.

To model the two-phase nature of the model, an additional moving mesh mechanism was used. The laminar flow moving mesh physics node in COMSOL solves the same equations for velocity and pressure fields, but also tracks the movement of the interface between two immiscible fluids by allowing deformation of the mesh during the solution. A free mesh deformation was prescribed to the domains either side of the interface. The inlet and outlet tubes of the geometry were prescribed a fixed mesh as only one of the fluid phases moved through these regions. The mesh is also prescribed zero displacement at the exterior boundary walls to prevent collapsing of the solid wall boundaries. The walls that were in contact with the fluid–fluid interface were prescribed free deformation of the mesh parallel to the exterior wall boundaries, but with zero perpendicular displacement, again to prevent collapse of the solid exterior walls.

The additional equation solved for in the laminar flow moving mesh interface was the Navier slip equation. This condition was applied to the boundaries that were in contact with the fluid–fluid interface, and is appropriate for the two-phase flow model. This condition adds a frictional force, F_fr , at a stationary wall, which allows the interface to move against the wall:

$${\mathit{F}}_{\mathrm{fr}}=-\frac{\mu }{\beta }\mathit{u},$$

where β is the slip length, which was a function of the element size of the mesh, μ is viscosity and u is the velocity vector. The fluid–fluid interface node also takes into account the interfacial tension of the two fluids, σ = 50 mN m⁻¹ [37], and the contact angle between the wall and the fluids, θ_w = 1.3 rad [38].

Owing to the nature of the two-phase model, a stationary solution for the velocity field could not be solved because of the movement at the interface; therefore a time-dependent solution was obtained over 9 s, at which point the flow stabilized. This stabilized flow was used as the velocity field input for the transport of diluted species solutions.

The solution for the transport is simpler for the release of ibuprofen because the concentration species only moves through two domains and not the fluid matrix domain; therefore the movement is purely diffusion and convection in the two different fluids. An additional expression for the partition coefficient (P_p) is included in the mass transport between the two phases:

$$J_d=-P_s(P_p{c}_d-c_r),$$

where J_d is flux, P_s is permeability and c_d and c_r represent the concentration in the donor and receptor domain, respectively.

2.6. Boundary conditions

A no-slip condition was applied to the exterior boundary walls. The walls in contact with the fluid–fluid interface were assigned a Navier slip condition. This condition allows the fluid–fluid interface to move along the wall. Additionally, the top boundary of the oil phase, parallel to the fluid–fluid interface, was assigned a slip condition. This slip condition allows the deformation of the mesh to continue throughout the phase while still applying a no penetration condition, meaning the model allows the movement of the mesh without fluid leaving that domain.

The inlet and outlet conditions were as described previously and the same flow rates were investigated as with the dextran transport studies (20 µl min⁻¹, 200 µl min⁻¹, 400 µl min⁻¹ and 2 ml min⁻¹). A volume force was also implemented across the entire geometry to account for gravity in the system.

Two transport of diluted species nodes were used to investigate the release of ibuprofen from the silicone oil: one for the oil phase and one for the aqueous phase. The appropriate diffusion coefficients (table 1) were applied to each fluid domain and a pointwise constraint was applied at the fluid–fluid interface. This pointwise constraint takes into account the concentration at the interfaces and solves for the mass flux across that boundary using a function of the concentration gradient and the partition coefficient. The accepted error between the computer models and experimental data was set by two boundaries: less than 10% was considered to be good agreement and less than 20% was considered to be acceptable agreement.

2.7. Material properties

1000 cSt silicone oil is often used by surgeons because its viscosity makes it easily injectable, a motivation for its use in this study. SiO has a lower density than water, and therefore floats on it, but this oil has a higher viscosity. These properties are shown in table 2. Rheological evaluation of water, PBS and silicone oil was done using a Rheosense µVISC rheometer (Rheosense Inc., USA) with a 100 N load cell. The results showed negligible differences between water and PBS in terms of viscosity and density; therefore water was used as the aqueous fluid of interest in the computer model. A handheld density meter (Anton Parr) was used to measure the density of the fluids at 37°C.

Table 2.

Input parameters for ibuprofen release studies.

parameter	value
diffusion coefficient of ibuprofen in 1000 cSt silicone oil	3.35 × 10−11 m2 s−1
diffusion coefficient of ibuprofen in water	2.27 × 10−13 m2 s−1
partition coefficient of ibuprofen	2.2 [39]
initial concentration of ibuprofen in oil phase	1 mg ml−1
initial concentration of ibuprofen in aqueous phase	0 µg ml−1
flow rate	20, 200, 2000 µl min−1
interfacial tension of 1000 cSt silicone oil/PBS	50 mN m−1 [37]
wall contact angle of fluid interface	1.3 rad [38]
density of water at 37°C	994.12 kg m−3
dynamic viscosity of water at 37°C	0.691 mPa s
density of silicone oil at 37°C	967 kg m−3
dynamic viscosity of silicone oil at 37°C	790 mPa s

3. Results and discussion

3.1. Grid independence studies

To demonstrate grid independence, simulations were run with varying degrees of mesh refinement (dextran model between 18 000 and 108 814 elements, ibuprofen model between 300 and 4000 elements). The velocity at two points in the geometry was measured (figure 2a,e) and compared as the mesh was refined. The number of elements used in each model was justified by using the mesh refined to within 5% agreement between both points and the highest resolved mesh (figure 2g,h). This was chosen as an acceptable error limit that reduced the computational time while maintaining sufficient accuracy. For the dextran model, this was 38 267 elements. For the ibuprofen model, this was 2258 elements.

3.2. Dextran transport studies

For predicted velocity profiles within the Kirkstall QV600 for flow rates 20, 200 and 400 µl min⁻¹, the velocity fields produce similar patterns (figure 3): a parabolic flow out of the inlet tube and in to the outlet tube with considerably lower velocities in the main wall of the chamber. Each flow rate shows areas of recirculating flow trapped in the corners of the receptor compartment on the inlet side, which increase in size as the inlet flow rate is increased. The streamlines show that, at the lowest flow rate (20 µl min⁻¹), the flow in the main chamber has little effect on the velocity field in the donor compartment of the chamber. As the flow rate increases, the flow profile of the donor compartment becomes more uniform as fluid from the main wall penetrates through the membrane and causes fluid flow in the donor compartment. This phenomenon is most obvious at the highest flow rate (2 ml min⁻¹). In the donor compartment of this simulation, a complex flow regime is observed. The velocities in the main wall of the chamber are also considerably higher than in comparison with lower inlet flow rates. Another feature of this high flow rate is the development of a dominating stream of fluid from the inlet tube to the outlet port and large area of recirculating fluid beneath this stream which occurs in the majority of the chamber volume. Previous studies have reported the flow rate within the choriocapillaris in vivo to be 9.45 ml h⁻¹ or 160 µl min⁻¹ [40], and disruptions or alterations in the flow have been attributed to problems with homeostasis within the RPE [41,42]. Here, we wanted to investigate a range of flow rates, including one which was biologically relevant, in order to prove the reliability of the computer model. For this reason, flow rates which were experimentally achievable were used. Although 2 ml min⁻¹ was tested in the computer model and produced interesting flow patterns, this flow rate was found to be too high to maintain the survival of the ARPE-19 cells; therefore, no further studies were conducted using this flow rate.

Figure 3.

Steady-state velocity fields for different inlet flow rates used in the Kirkstall QV600 chamber geometry for dextran transport studies. Inlet flow rates: (a) 20 µl min⁻¹, (b) 200 µl min⁻¹, (c) 400 µl min⁻¹ and (d) 2 ml min⁻¹. Colour scale bar indicates velocity (m s⁻¹). Streamlines show velocity field. Each flow rate shows areas of recirculating flow trapped in the corners of the receptor compartment on the inlet side which increase in size as the inlet flow rate is increased. The flow profile of the donor compartment becomes more uniform with increased flow rate.

To validate the numerical model, the results for the concentration of dextran on the receptor compartment side of the membrane were compared with experimental data. Permeability and diffusion coefficients were determined in simple static experiments and implemented in the numerical model. The resulting coefficients (table 1) were comparable with those seen in a similar experiment by Mannermaa et al. [19]. In that study, the authors compared the transport of drugs through a static, ARPE-19-based model and bovine RPE tissue, finding similar transport trends. The simulation shows the concentration gradient of dextran in the donor compartment to decrease with increasing flow rate after 24 h. As expected, dextran is less readily cleared across the barrier when the presence of cells is included in the simulation (figure 4). The results of the model were then validated using data from complementary in vitro experiments. The numerical model shows agreement with the in vitro data in both the acellular and cell-seeded experiments (figure 5). At the higher flow rates, the simulated results are able to mirror the change in release exhibited in vitro, which shows a shift to a burst release response followed by an exponential decay in concentration over time, and there appears to be no correlation between flow rate and simulation accuracy [43]. The simulation of dextran transport was able to predict the maximum concentration (C_max) observed in that chamber to within 5% of the acellular experimental data. The introduction of cells to the system increased the error observed in C_max but still to within 18% of the experimental data. Similar studies, which simulated permeability of different molecular weight FITC-dextrans in a static set-up and across collagen or agarose gel, showed an increase in error (between approx. 4% and 46%) between their simulated and experimental results with increasing molecular weight [44]. Here, we have only presented data for the transport of 4 kDa FITC-dextran; other sizes were also investigated (40 kDa and 70 kDa FITC-dextran) with 4 kDa and 40 kDa producing similar errors, but 70 kDa showed increased error in comparison. The simulation does not take into consideration the biological effects of culturing cells under flow might have on the barrier functionality of the ARPE-19 cell monolayer. There are studies which have investigated biological effects on epithelial tissues in computer simulations, for example, modelling inflammatory effects on intestinal epithelium in necrotizing enterocolitis [45], and investigating links between epithelial morphogenesis and cancer mutations [46]. A combination of computational fluid dynamics modelling such as in this study and a more computational biology approach to investigate cell-dependent changes in transport and clearance of molecules could further improve the agreement between the experimental and simulated data in cell-seeded simulations.

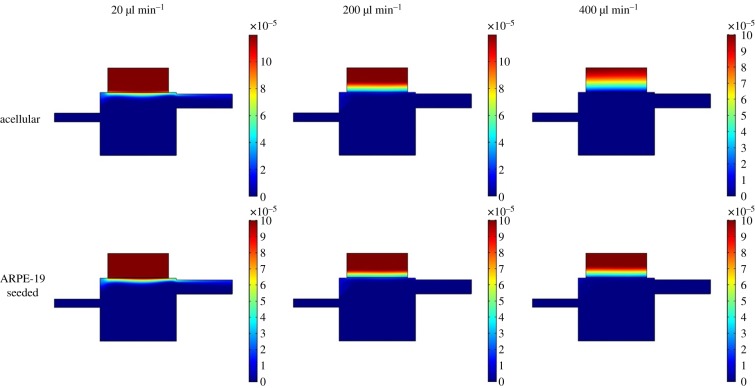
Figure 4.

Concentration fields for different inlet flow rates used in the Kirkstall QV600 chamber geometry for dextran transport studies across acellular and seeded membranes at 1 h. Colour scale bar indicates concentration (mol m⁻³). As expected, the drug is cleared from the donor chamber more rapidly as flow rate increases, but is impeded by the presence of cells.

Figure 5.

Experimental versus simulated average concentration profiles in the receptor compartment of the Kirkstall QV600 chamber for dextran transport studies across acellular and seeded membranes. Experimental data presented as mean concentration ± 1 s.d., n = 3. There is good agreement with respect to the concentration at all flow rates, including the change of behaviours from burst release to exponential decay, with differences within 5% for acellular and 18% for cellular experiments.

3.3. Ibuprofen release studies

Tracking the fluid–fluid interface is important when considering the concentration distribution of drugs across the two fluids. An adaptive mesh was used to simulate the interaction between the silicone oil phase and the aqueous (PBS) phase. Based on the interfacial tension and wall contact angle of the two fluids, the simulation shows that a meniscus is formed between the two phases over time until a steady state is reached at approximately 1.4 s (figure 6).

Figure 6.

Deformation of the mesh. A steady-state solution is reached indicated by the meniscus formation at the fluid–fluid interface boundary of the two phases (green boundary).

In the two-phase system (oil and aqueous), the simulation shows two distinct flow fields within each phase (figure 7). The flow field in the oil phase, however, does appear to be influenced by the flow rate of the aqueous phase. The flow fields formed at 20 µl min⁻¹, 200 µl min⁻¹ and 400 µl min⁻¹ show similarities to those formed in the single-phase, membrane system. At 20 µl min⁻¹, however, the low flow rate inlet stream within the aqueous phase appears to bounce off the oil phase and creates a ripple within the primary flow stream. The interaction between the main flow stream and the oil phase also creates two recirculating streams within the oil domain itself. This phenomenon is observed for each of the flow rates studied, with the split in the two streams shifting towards the inlet as the inlet flow rate increased. Unlike the 2 ml min⁻¹ flow field in the single-phase system, the 2 ml min⁻¹ flow profile for the two-phase model did not develop large regions of recirculating flow and maintained a single dominating fluid stream from inlet to outlet.

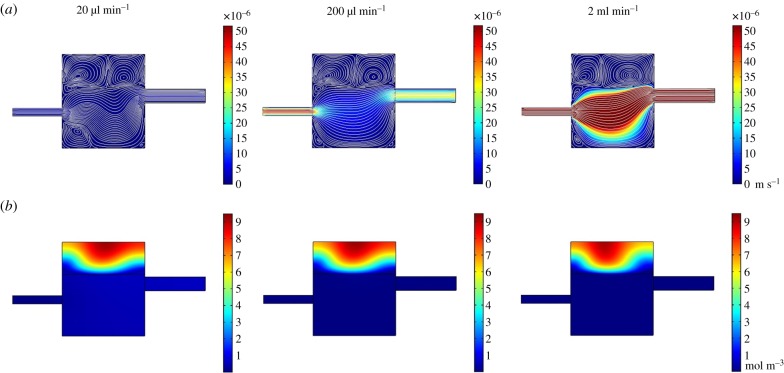
Figure 7.

Stead-state velocity (a) and concentration at 1 h (b) fields for different inlet flow rates used in the Kirkstall QV600 chamber geometry for ibuprofen release studies. Inlet flow rates: 20 µl min⁻¹, 200 µl min⁻¹ and 2 ml min⁻¹. (a) Colour scale bar indicates velocity (m s⁻¹), streamlines show velocity field. (b) Colour scale bar indicates concentration (mol m⁻³). The velocity simulation shows two distinct flow fields within each phase, with velocity within the oil phase being influenced by the flow in the fluid phase. This is accompanied by concentration contours that indicate that the fluid phase is influencing the concentration gradient in the oil phase.

The concentration fields within the oil domain showed little difference as the flow rate increased, other than to shift the centre of diffusion towards the inlet at 2 ml min⁻¹. For each flow rate, the ibuprofen was never completely cleared from the oil domain by the final 72 h time point. The simulation predicted that a small region of oil at the top of the domain, in contact with the exterior wall of the chamber through to the centre of the domain, maintained a low concentration of ibuprofen.

To model the release of ibuprofen from SiO, the physics controls of the computer model were redesigned to allow the interaction of two immiscible fluid phases within the QV600 chamber. For this ibu-SiO model, the moving mesh method was applied. COMSOL Multiphysics reports that this method provides the best results when tracking the interface between the phases is important, and also allows mass transport across the interface, which is difficult to implement using other methods [47]. At 20 µl min⁻¹, the flow entering the main chamber bounces off the bottom of the meniscus formed by the oil phase and creates a ripple in the main stream of flow. The interaction of the main stream of flow with the oil domain also creates very low-velocity recirculating flow patterns within the oil which are separate from the main flow stream. The movement within the oil could be expected to have implications on the distribution of ibuprofen within the oil phase but it appears that, because the velocities are so low, the diffusion of the ibuprofen from the oil still occurs symmetrically, starting from the centre of the domain. As the inlet velocity increases, more asymmetrical diffusion patterns appear, but the recirculation velocities within the oil remain very low in comparison with the velocity observed in the main stream of flow, and so the distribution of ibuprofen in the oil domain appears to be controlled by the concentration gradient between the two phases. This is, in turn, controlled by the convection of ibuprofen away from the interface by the fluid flow. The flow profiles in the aqueous phase of the two-phase model were not comparable with those seen in the dextran transport model. In that model, the membrane was modelled as a fluid matrix domain, whereby the fluid can move through the domain at a retarded rate based on the porosity and permeability of the membrane. For this reason, only a small percentage of fluid actually passes through the membrane and interacts with the donor domain. The majority of the flowing fluid sees this as a walled domain and so this reduces the height of the chamber, which is the reason for recirculating flows to develop instabilities. In the two-phase, oil/PBS model, the force of the aqueous flow is partially absorbed by the oil, which causes the recirculation within the oil, but also reduces the velocity of the aqueous flow in comparison with the single-phase model. This reduction in velocity also removes the secondary recirculating streams which occur in the single-phase model.

As with the dextran transport simulations, the concentration of ibuprofen in the receptor domain was measured over time to validate the computer model of the ibu-SiO device within the QV600 chamber. The accuracy to which the model was able to predict the concentration of ibuprofen varied with the inlet flow rate. There is strong agreement in the trends between the experimental and simulated data (figure 8), with the simulation able to predict the concentration of the ibuprofen in the receptor chamber over a period of 24 h. There are small discrepancies in the values of C_max at each flow rate, but the simulation is able to predict the total exposure of the ibuprofen in the bottom chamber to within 10%. At the highest flow rate, which is unrealistic in comparison with the in vivo environment, C_max was underestimated by the simulation, although the values for concentration under these conditions were at the very lower detection limit of the UV spectrophotometer. Furthermore, the differences in absolute value of C_max were negligible in comparison to the 1 mg ml⁻¹ initial concentration present in the SiO.

Figure 8.

Experimental versus simulated average concentration profiles of ibuprofen in receptor compartment of Kirkstall QV600 chamber. Experimental data presented as mean concentration ± 1 s.d., n = 3. There is good agreement with respect to the concentration at all flow rates, including the change of behaviours from burst release to exponential decay, with differences within 10%.

Computational models, such as the ones incorporating fluid dynamics, present the advantage of accurately describing the system behaviours when the constitutive parameters are varied. Unlike the traditional, benchtop experiments, after thorough validation and benchmarking, these models can be used to describe complex systems in a fast, inexpensive, accurate and reliable manner. Moreover, a vast parameter field can be tested and considered, enabling the analysis and comparison of different physical processes such as fluid flow or drug transport and diffusion.

The fluid flow set-up used in this study was designed to emulate the mechanism of elimination of molecules via convectional clearance analogous to the systemic circulation present in choroidal tissue in vivo. To validate the computer model, comparisons of the average concentration in the receptor compartment of the Kirkstall QV600 chamber were made between predicted and experimental data. It is important to note that previous studies have used computer models to study drug delivery and distribution in the posterior segment of the eye [29,48,49]; these studies, however, are mostly theoretical or based on experimental data published by Palestine & Brubaker [31], who investigated the pharmacokinetics of fluorescein in the vitreous of humans. Our study looked to create an in silico model that could predict drug distributions in an in vitro model and that could be used in the development of a novel SiO-based drug delivery device.

As robust and mathematically stringent as computer models may be, they will never be able to provide a fully accurate representation of a biological environment due to the variability and continually dynamic environment of nature. What they are able to do is provide predictions of results across a vast number of parameters in a fast and inexpensive manner. In terms of developing drug delivery devices such as the ibu-SiO described here, it allows variations in conditions such as initial concentration, drug permeability and material properties, and produces estimations which can narrow the range of expensive and time-consuming experimental work that would otherwise need to be conducted. Ultimately, it would be of interest to apply the knowledge and understanding of drug release from SiO gained from these complementary in silico and in vitro models to build a computational model of the eye which could help us predict how this system might work in vivo in a human eye.

4. Conclusion

The ability to model drug transport across epithelial tissues such as the BRB could lead to the development of more effective treatments. The data presented here demonstrate the ability of in silico models to predict in vitro behaviour in complex environments. When used together, these complementary in vitro and in silico models could help make the design of drug delivery devices more efficient, as well as having potential benefits to the drug discovery community. Ophthalmologists and other researchers should be cautious when interpreting data from any model. No model will fully recapitulate the complex environment of the human eye, but more sophisticated designs that can reproduce features such as choroidal flow can help move experimental data closer to clinical behaviour.

Data accessibility

Data are available at: https://doi.org/10.17638/datacat.liverpool.ac.uk/908 [43].

Authors' contributions

A.E.D. carried out laboratory work, computational modelling, data analysis and drafted the manuscript. R.L.W. participated in the design of the study and critically revised the manuscript. G.L. critically revised the manuscript. S.R.P. participated in computer model design, data analysis and critically revised the manuscript. V.R.K. conceived the study, designed the study, coordinated the study and helped draft the manuscript. All authors gave final approval for publication and agree to be accountable for the work performed therein.

Competing interests

A.E.D. was employed by Kirkstall Ltd until September 2012. V.R.K. has held several grants on which Kirkstall Ltd has been a collaborator.

Funding

This work was supported by the Crossley Barnes Bequest and the EPSRC (grant nos. EP/l000458/1, EP/R024839/1 and EP/M002209/1). Silicone oil was donated by Fluoron GmbH.