Evolving complexity: how tinkering shapes cells, software and ecological networks

Abstract

A common trait of complex systems is that they can be represented by means of a network of interacting parts. It is, in fact, the network organization (more than the parts) that largely conditions most higher-level properties, which are not reducible to the properties of the individual parts. Can the topological organization of these webs provide some insight into their evolutionary origins? Both biological and artificial networks share some common architectural traits. They are often heterogeneous and sparse, and most exhibit different types of correlations, such as nestedness, modularity or hierarchical patterns. These properties have often been attributed to the selection of functionally meaningful traits. However, a proper formulation of generative network models suggests a rather different picture. Against the standard selection–optimization argument, some networks reveal the inevitable generation of complex patterns resulting from reuse and can be modelled using duplication–rewiring rules lacking functionality. These give rise to the observed heterogeneous, scale-free and modular architectures. Here, we examine the evidence for tinkering in cellular, technological and ecological webs and its impact in shaping their architecture. Our analysis suggests a serious consideration of the role played by selection as the origin of network topology. Instead, we suggest that the amplification processes associated with reuse might shape these graphs at the topological level. In biological systems, selection forces would take advantage of emergent patterns.

This article is part of the theme issue ‘Unifying the essential concepts of biological networks: biological insights and philosophical foundations’.

1. Introduction

The fabric of complexity is made of networks. The presence of collective-level, system properties necessarily requires a description grounded in a map of connections between individual parts. Such a view has been around for much longer than is usually acknowledged within the field of Network Science. Long before small worlds and scale-free structures were identified, the importance of interactions and their embodiment within graphs were already in place in ecology and neuroscience. Classic studies on trophic webs and their stability had an enormous impact on our understanding of communities [1–6]. Similarly, since Ramon y Cajal [7] the realization that cognition was associated with complex webs has been percolating through the entire field [8,9].

Why to care about interactions among the units? Why is the network level relevant in seeking explanations for the origins of complexity? A main avenue that largely precluded the rise of Network Science early provided the answers. It was the field of phase transitions [10–13]. Phase transitions are a common phenomenon that we know well: water freezes or boils and completely different, homogeneous macroscopic properties can be seen in each phase (liquid, solid and gas) separated by characteristic transition temperatures. But how do these phase transitions happen? How can we use a microscopic theory that incorporates the properties and interactions among components and explain the completely different qualitative properties displayed by each phase? In searching for theories, physicists found that very simple models, incorporating a toy description of the interactions (and paying very little attention to the structure of the components) can fully explain them. The nature of the interactions, and not the components, is what matters.

The insignificant role played by the details of the units is deeply tied to the presence of emergent patterns arising on the larger scale [2,14,15] and the failure of the reductionist programme [16,17]. Emergence became a central concept and the cornerstone of a view of systems where system-level properties could not be reduced to the properties of their component units. One particularly interesting problem that received considerable attention (and that will be relevant here) was the phenomenon of percolation [18]: the sudden shift from a disconnected to a connected system that is experienced by a set of N elements that are connected with pairwise threads with a given probability p. If 〈k〉 indicates the average number of connections displayed by a randomly chosen element of this system, for a random connection rule we have 〈k〉 = pN and it can be shown that the critical condition 〈k〉_c = 1 defines an abrupt (topological) phase transition [19]. It provides a powerful illustration of emergence and had a tremendous impact in very diverse domains, from molecular biology to social dynamics [19–24].

With the turn of this century, the combination of available datasets associated with social, technological and biological systems and a new generation of theoretical models triggered a revolution that spread across all disciplines. Network Science became the basis for both new concepts and statistical methods. Classical graph theory [25] had been mainly associated with the study of homogeneous webs, including in particular all kinds of lattices, trees and random graphs. Because of the lack of knowledge about the architecture of real networks, most early models of genetic, neural and ecological systems used homogeneous graphs. Everything changed once the mapping of Internet, social webs or -omic data provided the first solid picture of real networks. They confirmed an old sociological study [26] indicating that the number of degrees of separation between two randomly chosen individuals is very low, providing a very elegant mathematical framework to explain the phenomenon [27]. Second, an unexpectedly general finding was the realization that real networks are heterogeneous. Instead of previously assumed regular, Gaussian or exponential distributions of connections, long-tailed ones were found to be the rule: most elements are connected with a few others, whereas a small number of them include units connected to many others (the hubs).

It has been suggested [28] that inspecting the organization of complex networks can reveal the evolutionary design or evolutionary principles that shaped them. In a nutshell, identifying the generative rules responsible for their topology could be used to find their origins and the contributions of randomness, architectural constraints or self-organization. In other words, the paths followed by each system (either through evolutionary dynamics, developmental processes or technological design protocols) can be deeply limited by fundamental principles of a mathematical nature. Very often, this reveals the failure of some standard assumptions and explanations involving selection or optimization.

In this paper, we will review the existing evidence for tinkering and its deep implications for our understanding of network complexity. This includes: (1) the presence of mechanisms of network growth that are dominated by extensive reuse of extant components. (2) Structural constraints limit the repertoire of potential forms of network complexity that can be found. (3) Some particular structures (at different scales) display robust statistical patterns that could be attributed to optimal or efficient design principles: they are by-products of the heterogeneities created by generative rules. These results have to be taken as one aspect of network complexity, namely the topological patterns emerging from simple growth rules. Such choice does not rule out other components of evolutionary change nor other alternative models, including those used in modelling coevolutionary networks [29,30].

The importance of reuse or ‘tinkering’ was early suggested by the French biologist Francois Jacob and has enormous importance in evolution. As discussed in [31], there is a major difference between the ways that an engineer and evolutionary processes work. The first has a goal and thus foresees what needs to be designed. To do so, the engineer can completely replace previous components and ignore previous protocols to build an artefact. In this way, novelties can emerge as a result, for example, of adopting a new material (such as liquid crystal). In stark contrast, evolution does not foresee what solution is required for a given problem. Moreover, there is no way that evolutionary processes ignore those components and structures that are already in place: reuse of previous parts is crucial. Surprisingly, as discussed in this paper, reuse leads to network heterogeneities that strongly constrain the local and global properties of the resulting graphs.

2. Evolutionary tinkering in cellular networks

An example of the implications of tinkering rules can be found in models of protein interaction networks. As with other non-directed graphs, we define a network Ω as a pair (V, E). Here V stands now for the set of nodes and E the matrix of interactions between pairs of nodes. If we take a given protein v_j ∈ V it will have a given number of links with other proteins in our graph. These networks are characterized by the presence of degree distributions following a truncated power law shape, i.e.

$$P(k)\sim {(k+k_0)}^{-\gamma }\hspace{0.17em}{\text{e}}^{-k/k_c},$$ 2.1

where P(k) is the probability distribution of having a protein interacting with k other proteins with an exponent γ ≈ 2.5 [32–34]. Here k_c is a cut-off (indicating some intrinsic limit to the maximum number of links of a given protein).

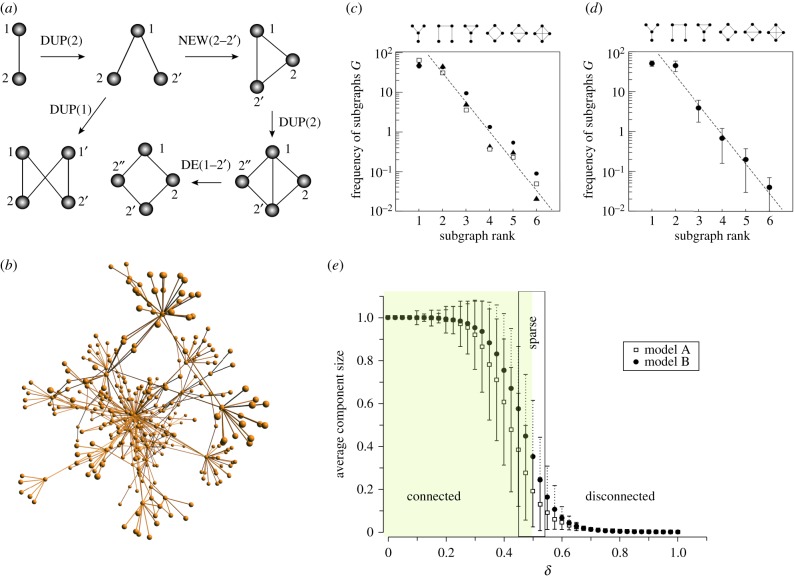
Consider the following model from Solé and co-workers [28,35]. The protein network is now reduced to a graph defined by a collection of vertices V = {v_k} and a matrix of connections provided by the adjacency matrix A = (a_ij), where a_ij = 1 if the two proteins interact and zero otherwise. Let us indicate by |V| the size of the network at a given step. We start from a set m₀ of connected nodes, and at each time step we perform the following operations (figure 1a): (i) one node of the graph is selected at random and duplicated; (ii) the links emanating from the newly generated node are removed with probability δ; and (iii) new links (not previously present after the duplication step) are created between the new node and any other node with probability α. Although available data indicate that new interactions are more likely between more connected proteins, we ignore this constraint.

Figure 1.

Modelling tinkered evolution in complex cellular networks. Simple rules of reuse (a) generate heterogeneous networks closely similar to those found in cells, such as the human transcription factor network shown in (b), described in [36]. DUP, duplication; DE, deletion; NEW, addition. Here hubs include key transcription factors (TFs) (such as the tumour supressor P53) associated with proliferation diseases. Most measurable network properties found in proteomes can be replicated, such as the distribution of network motifs. In (c), we display the observed frequencies (ordered from or three different protein networks), namely the human interactome (HI, filled triangles), yeast proteome (YP, filled circles) and the subset of human transcription factors (HTF, open squares). For comparison we display the predicted subgraph census from the duplication–rewiring model (d, [37]). By tuning the removal rate of links associated with divergence, it can be shown that a transition from connected to disconnected occurs close to a critical value δ_c = 1/2, as shown, for example, from the estimation of the average network size against δ (e). Here, two different models [28,38] have been used, indicated as A and B, respectively. (Online version in colour.)

Step (i) implements gene duplication (the tinkering component) in which both the original and the replicated proteins retain the same set of interactions. The rewiring steps (ii) and (iii) implement mutations that translate into the deletion or addition of interactions with different proteins. The process is repeated until N proteins have been obtained. An example of a network obtained from this process is shown in (figure 1b), closely resembling the protein maps found in cells. This network fits the heterogeneous degree distributions very well, with a robust γ ≈ 2.5 exponent, but it also fits other distributions associated to correlation profiles [39]. Concerning small-scale patterns, such as the abundance of three- and four-component (figure 1c) network motifs [40] that naturally result from our tinkering process, the model correctly reproduces the observed data (figure 1d).

In general, this model (indicated as A in figure 1e) and the work by Vespignani (indicated as B in figure 1e) and co-workers [32,38,41] provide very similar results. In the latter, duplication is also followed by two probabilistic rules that operate independently. For each of the nodes v_j linked to the duplicated node and its duplicate, we choose randomly one of the two redundant links and remove it with probability δ. Additionally, a new interaction connecting the two proteins (the parent and the duplicated) is introduced with probability ρ. The last rule will naturally increase the number of triangles in the system and thus provide a source of high clustering. The same results are gathered from duplication models involving gene regulation [42]. Sole’s model in particular successfully explains the architecture of protein maps [43,44].

The network shown in figure 1b is sparse, but the model described above can give highly connected or even totally disconnected graphs. Deletion rate in particular needs to be tuned. What can the model say about this? It is not difficult to show [35] that the rate of link removal defines two phases separated by a critical value δ_c. This is obtained from an average (mean field) description that gives a dynamical equation for the average degree:

$$\frac{d_K(n)}{\text{d}n}=\frac{2\alpha }{n}+\frac{1-2\delta \alpha }{n}K(n),$$ 2.2

where n is the proteome size (acting as a time scale). By solving this equation, a steady-state K* is obtained, namely:

$$K^{\ast }=\underset{n\to \mathrm{\infty }}{lim}K(n)=\frac{2\alpha }{2\delta -1}.$$ 2.3

One phase, associated with deletion rates δ > δ_c, involves a disconnected proteome (fragmented into different parts), and there is another phase where it becomes rapidly hyperconnected. At the critical point separating these two phases (figure 1e), we see the emergence of a sparse, but connected graph associated with a percolation transition. In other words, there is a point where the protein interaction network becomes a true system (with paths connecting all elements) at a low cost. This is the region where the model fits the data in the two main models of duplication and divergence very well.

Perhaps more surprising, the networks resulting from tinkering also display modularity: they appear organized in subsets whose elements are more connected among themselves than with the rest of the web [37]. This was unexpected, since modularity is considered one of the most important patterns associated with adaptive, functional traits of biological complexity [45–47]. Multiple cellular functions are carried by subsets of proteins, including developmental modules. In general, biological modularity provides the right trade-off between specialization and integration [48–50]. Against that intuition, it was shown that modularity can emerge for free. As it occurs with other network patterns to be discussed below, it might be the inevitable outcome of reuse. Similarly, a common statistical pattern is also found at the level of the so-called network motifs [40], which were already known from early work on social and ecological webs [51]. Importantly, since modularity is considered an important component of evolvability, the topological modularity emerging from the tinkered dynamics would have an immediate impact on adaptability.

The topological structure of protein nets, as discussed above, might be largely a by-product of the network construction process. Tinkering is an inevitable constraint in the process of increasing complexity through genome expansion. This is of course one part of the whole range of possible changes affecting evolving genomes. Other processes such as de novo gene formation or whole-genome duplications would influence the outcome [52], but the main driver shaping the interaction network is tinkering [53].

There is an important consequence of these results within the context of evolutionary theory. The observed patterns, as mentioned above, describe a set of correlations that require an explanation. The network organization found in these graphs includes structural traits that could be interpreted as resulting from selective pressures. But sometimes structural patterns have no adaptive meaning [1]. They are actually examples of what Stephen Jay Gould and Richard Lewontin called spandrels [54]. The term spandrel, borrowed from the vocabulary of architecture by these authors, defines the space between two arches or between an arch and a rectangular enclosure. In evolutionary biology, a spandrel is a phenotypic characteristic that evolved as a side effect of a true adaptation [55].

The defining traits of evolutionary spandrels can be summarized as follows. (a) They are the by-product of building rules. They have intrinsic, well-defined, non-random features. (b) Their structure reveals some of the underlying rules of the system’s construction. This is also consistent with previous studies [56] showing that stochastic fluctuations in random graphs can display statistically significant modularity, even when no preferential attachment rules are involved. Evolutionary models (involving very small neural or genetic networks with feed-forward discrete dynamics) have shown that modularity can result from selection pressures [57]. The scale of the networks considered here (the protein maps) is much larger and purely topological. Future models of proteome evolution should contain a dynamical description in order to properly weight the potential roles played by reuse versus functionality.

The findings described above support the idea that the proteome map contains a considerable number of independent (or early-independent) statistical correlations that can be explained by the duplication–rewiring model. Although an alternative model including growth (an inevitable part of genome growth) along with functional traits would also fit all these topological trends, it is important to realize that it would necessarily require a more sophisticated description. We believe that an important implication is that the specific values of the network measures, along with the presence of modularity or non-random distributions of motifs, do not require selection. This finding, as shown below, is far from accidental.

3. Software networks: human tinkering

Technology, as we mentioned above, is different from biology in a fundamental way. Jacob’s conjecture about this seems very well established. There is no intentional design in evolution, but it turns out that the limitations imposed by technological complexity impose an effective design barrier to engineers. To illustrate this idea, we will use the field of software engineering. The reason for this choice is twofold. On the one hand, software projects allow the extraction of a network of interactions among different parts in a meaningful way, Second, software has become increasingly relevant since its inception in the 1950s and has become, even more than the Internet and the power grid, the most important (but largely invisible) technology [58–62].

Like many technologies, a software system consists of a large number of elements interacting with each other. Software is similar to a collection of linked pages in a website, but instead of being readable by humans, it is written in a programming language meant for computer processors [63]. Consider the so-called dependency graph G = (V, E), where a vertex v_i ∈ V is a program file (e.g. written in a programming language like Java, C or C++). The links between files are described by a (directed) edge e_ij ∈ E, indicating a code dependency between source files v_i and v_j, which is encoded with the reserved keyword include [64]. No other information is considered by the network reconstruction algorithm, which means that we are not including any further information, such as functionality. We keep ourselves in the purely topological level. Figure 2b shows an example of a real software graph. Using this network reconstruction, it was shown that different large-scale software graphs shared a surprisingly universal set of traits.

Figure 2.

Modelling tinkered evolution in software dependency graphs. (a) A simple growth model simulates tinkering in software development processes. A programmer creates a new file by inheriting source code (and their dependencies) from other, existing m source code files or targets (each target file is referred with probability p). Afterwards, code editing removes some dependencies from the new node with probability q. Our model generates networks that look like real dependency graphs. For example, in (b) the software architecture of XFree86 (a very popular Unix package developed since 1992) displays scale-free behaviour. In (c), the cumulative distributions associated with P_i(k) and P_o > (k) are shown. The power-law fit of the cumulative in-degree distribution follows a power law with ${\gamma }_i^c\approx 1$, while the out-degree distribution is exponential. (d) From left to right, we show the temporal evolution of a software network generated with tinkering rules. In spite of not assuming any kind of function, duplication and rewiring rules predict the heterogeneity of real dependency graphs, the emergence of clusters of source code files and even the temporal evolution of the average connectivity. (Online version in colour.)

One in particular is the marked difference and statistical nature of the in- and out-degree distributions [59,60]. These distributions, to be indicated as P_i(k) and P_o(k), respectively, indicate the probability of having k links coming to or leaving the node, respectively. They are very different: the first follows a power law, i.e. $P_{>}(k)\sim k_i^{-{\gamma }_i}$, whereas the second follows an exponential decay, as displayed in figure 2c with the cumulative distributions. In order to compute them, we just need to integrate the degree distribution P(k), i.e.

$$P_{>}(k)={\int }_k^{K_m}P(k^{\prime })\hspace{0.17em}\text{d}{k}^{\prime },$$ 3.1

where K_m is the largest degree value. If the original distribution is already a power law, i.e. P(k) = k^−γ, it is easy to show that

$$P_{>}(k)=\frac{1}{\gamma -1}(k^{\gamma -1}-K_m^{\gamma -1})\sim \frac{k^{\gamma -1}}{\gamma -1},$$ 3.2

where the last approximation is valid for K_m ≫ 1. The fit to the exponent is particularly good for these fat-tailed distributions using the accumulated form. For the software graphs discussed here, the in-degree distribution has a characteristic value very close to γ ≈ 2 in all the analysed systems [60]. This is consistent with the pervasiveness of scaling laws in software graphs, which seems largely independent of the choice of programming languages and/or specific functional traits [58,65–67].

What is the origin of these patterns? Why are they so close, despite the obvious dissimilarities to be expected from different engineering projects? The response is provided through two arguments. One is the known fact that software projects, as much as they are planned and serve to a given objective, are developed by engineers who create a system that grows over time. Diverse parts of the system are created by programmers with a good picture of the global organization and the different parts that need to be assembled, in principle, following well-defined principles [68]. But, as the network grows, that knowledge becomes less detailed and interactions among components are more unpredictable, leading to conflicts between subparts. A common strategy is to reuse extant parts of the network and use them as the starting point for a new component.

Code duplication in software projects is much more common than one would expect. Reuse is a natural process during development of complex software, where new code shares common traits with previously created elements. Duplicate code is reused at different scales, including large blocks containing millions of lines of code. Useful blocks deal with specific tasks and they are often encapsulated in well-defined software modules. Internally, these modules comprise sets of densely interconnected software elements [69,70]. Since they are sophisticated structures, once a block has been created, a large part of its structure is more likely to be reused in the future. As the system becomes more complex, programmers rely more frequently on duplication (also known as cloning), since they know from experience that these structures are quite stable and behave well. Empirical analysis of software evolution confirms that duplicate codes are more stable than non-duplicated codes [71]. In this way, the software dependency network grows in an increasingly complex and integrated way, and their interdependencies naturally lead to reuse (figure 2a).

The universal class of structural patterns obtained by duplication rules is consistent with the hierarchical architecture of software networks. Although human minds take part in the manufacturing of software technology (instead of the blind watchmaker) and software systems cannot repair themselves [72], tinkering appears to be the main driver for the large-scale software structure. In addition, software design principles include fault-tolerance and extensibility, and the latter is closely related to the capability of software to evolve. The fact that a simple growth model (figure 2d) is able to explain most of the statistical properties of software graphs [60] is an unexpected turn to Jacob’s views: even the engineer, who consciously plans for the future, cannot avoid tinkering when preserving software stability.

A simple model, known as the Growing Network with Copying [73], explains the asymmetric nature of the two degree distributions and the robust scaling exponents. The rules are summarized in figure 2a and include directed links. The network grows by introducing a single node at a time. This new node links to m randomly selected target node(s) with probability p, as well as to all ancestor nodes of each target, with probability q. Specifically, if we label each node with a number indicating its age (number one is the oldest), a new node (number 6) attaches to target node 4 with probability p. This new node inherits every link from the target node (dashed links), with probability q. The corresponding mathematical model for the average number of links L(n) is now

$$\frac{\text{d}L(n)}{\text{d}n}=mp+mq\frac{L}{n}.$$ 3.3

Once solved, it gives us the average degree 〈K_n〉 = L(n)/n. Interestingly, the solution to this equation gives three main regimes: (a) a constant average degree

$$⟨K_n⟩\sim \frac{mp}{1-mq},$$

when mq < 1, (b) a rapidly growing phase with accelerated increase

$$⟨K_n⟩\sim N^{mq-1}$$

(ending up in a fully connected web) when mq > 1 and (c) a marginal state given by mq = 1 that displays a logarithmic growth, i.e.

$$⟨K_n⟩\sim LnN.$$

Interestingly, software graphs seem to grow right at this critical point [59,60] separating no increase in the number of dependencies from a super-connected system. As shown by Kaprivski and Redner [73], the model predicts the previously described distributions at the marginal point, i.e. P_i(k) ∼ k⁻² and an exponential decay for P_o(k).

The universal class of structural patterns obtained by duplication rules is consistent with the hierarchical architecture of software networks. Although human minds take part in the manufacturing of software technology (instead of the blind watchmaker) and software systems cannot repair themselves [72], tinkering appears to be the main driver for the large-scale software structure. In addition, software design principles include fault-tolerance and extensibility, and the latter is closely related to the capability of software to evolve. The fact that a simple growth model is able to explain most of the statistical properties of software graphs [59,60] is an unexpected turn to Jacob’s views: even the engineer who consciously plans for the future cannot avoid tinkering when preserving software stability.

We can find common signatures of tinkering in the statistics of software subgraphs. As happened with network motifs for cellular networks, here too the distribution of motifs in dependency graphs is essentially a by-product of tinkering. Given a (sparse) subgraph motif Ω, the average number of occurrences 〈G〉 of this motif in an uncorrelated scale-free network scales with the subgraph size and the exponent of the in-degree distribution [74]:

$$⟨G⟩\sim N^{n-g+s-{\gamma }_i+1},$$ 3.4

where s is the maximum in-degree in the motif and n and g are the numbers of nodes and links in the motif, respectively. This scaling is actually valid for 2 < γ_i < s + 1. Interestingly, this prediction is in very good agreement with the number of appearances of motifs in software networks [60].

It has been proposed that network features (e.g. motif abundances) reveal functions [40]. However, software and proteome networks display very similar structural features, including scaling exponents, motif distribution and modularity, which can be readily explained using duplication–rewiring mechanisms. The remarkable convergence between natural and artificial networks suggests that the origin of motif abundances is neutral to selection. Assigning specific functions to motifs does not take into account the plasticity of complex systems. Indeed, the same network motif can perform many different functions depending on global requirements [75]. In this context, the origin of universal network patterns might be largely independent of specific selection pressures, but this does not mean that they are not advantageous.

Many other relevant findings emerged from the first study of software maps [76]. One of them was the concept of breakdown of modularity [77]: because of a tendency of software projects to become more disordered (in terms of the pattern of dependencies), modules can become more interconnected. Because of this, changes propagate [78]. Within the context of software engineering, shortcuts among modules would allow changes made in one module to other, apparently distant parts. These kinds of phenomena were afterwards described within the context of brain networks, where nowadays the concept of disconnection disease has become a central concept. It would be key to understand faulty intermodule communication in, for example, Alzheimer’s disease or schizophrenia [79–83].

4. Evolution of ecological tinkered networks

On a much larger scale, consider the large-scale organization of ecological systems, as described in terms of complex networks. There is a long tradition within ecology where networks of some kind have been studied. The reason is obvious when we realize that ecology has always been a systems science, with ecological interactions placed at the centre of any meaningful description of communities and their environments. However, the rise of Network Science provided a novel view of the fabric of nature. The early papers on ecological networks [84–87] soon indicated that they shared the complexity–fragility trade-offs with other complex systems. A very important implication of that was the existence of network co-extinctions and cascades promoted by the propagation of species losses through the trophic structure [87]. Some simple, elegant models revealed, here too, that simple rules could help the understanding of the origins of food web graphs [88–90].

Along with predator–prey interactions, which include carnivorous interactions that benefit one organism (predator) to the detriment of another (prey), another important class of exchanges deals with cooperative interactions. This is the case of mutualistic webs, which are associated with pairwise relations where the two species help each other [91,92]. This can occur through a diverse number of ways, including pollination (transfer of pollen from a male plant to a female plant by another agent, including animals, insects and birds) or through frugivory (dispersal of seeds along with the fruits consumed by an agent). In both cases, it is assumed that a long-term coevolutionary dynamics has been shaping these interactions. Some examples that are often mentioned illustrate this coevolutionary path with specialized pairs. But a more appropriate picture tells us that there is a range of possible patterns of interaction where generalists also abound.

The architecture of mutualistic webs has been shown to display well-defined, common structural regularities already discussed above. In contrast with previous examples, a bipartite organization is present: there are two distinct classes of organisms (such as plants and their pollinators). They are small worlds [27,85,93] and the distribution of connections is known to follow a truncated power-law shape:

$$P(k)\sim k^{-\gamma }\exp (-\frac{k}{k_c}),$$ 4.1

where the exponent γ for this distribution has a value close to one. Moreover, several additional structural patterns have also been found. These include a highly asymmetric matrix of interactions [94] and, more importantly, the presence of nestedness [95]. In a nested network, both generalists and specialists are more likely to interact with generalists while interactions among specialists are rare. Nestedness has been shown to correlate positively with biodiversity [92,96].

We ask whether speciation and divergence rules alone can explain structural regularities of mutualistic networks. This approach makes strong assumptions. First, we assume that species are present or absent and their abundances (and other species-specific traits) do not play any part. Second, weighted links represent quantitative interactions among species. The strength of interactions evolves in time following a simple structural approach. The large-scale network structure is the combination of two processes taking place at evolutionary time scales: (a) new species are engendered from old ones through speciation and (b) environmental or stochastic factors vary the presence and the strength of species–species interactions.

Unlike our two previous examples involving unimodal networks, our model addresses bipartite graphs G = (A, P, E) now including two subsets A(t) and P(t) that correspond to different species. The time t needs to be understood as an evolutionary time step t. Bipartite networks only have links between species of different kinds, that is, when there is a mutualistic relationship. The quantitative impact of animals on plants is weighted through the matrix ω_ij = ω(A_i → P_j), which gives the strength of interaction between animal species A_i and plant species P_j. The quantitative approach leads to the use of spectral radius ρ(ω), which is a more rigorous assessment of nestedness than previous studies [97,98]. From this weighted network, we can also limit ourselves to the topological network, where ω_ij = ω_ji = 1 when a positive interaction exists and zero otherwise.

A schematic in figure 3a illustrates the simple set of neutral rules used to evolve mutualistic networks [99]. During speciation events (denoted by S), a new animal species A_k inherits all the mutualistic interactions from its parent species, ω_kj = ω_ij for all j = 1, …, |P| (see left branch in figure 3a). A similar speciation event takes place for plant species (see right branch in figure 3a). This splitting process derives two new species from their common ancestor. In the long term, the lineages diverge owing to the random redistribution of link weights between parent and daughter species. Link mutations (denoted by D) satisfy two additional requirements. First, there is a maximum value for the sum of weights attached to any species, i.e. $\sum _j{\omega }_{\hspace{0.17em}ji}\le 1$. And second, links whose weight falls below a minimal threshold are always removed, which can lead to the eventual extinction of whole species, i.e. if $\sum _j{\omega }_{\hspace{0.17em}ji}=0$. This combination of rules represents natural resource constraints, e.g. too many animals feeding on the same plant would rapidly deplete it.

Figure 3.

Modelling tinkering evolution in ecological networks. On a large scale, involving whole ecosystems, rules of tinkering can be understood in terms of species-level evolutionary events. (a) In particular, the large-scale organization of mutualistic webs can be obtained from a simple model where speciation (S) of extant species is the equivalent to duplication events, whereas species divergence (D) is here related to link weight redistribution over evolutionary time. Using this model, the resulting webs (b) display truncated power laws (c) fully consistent (in average and diversity) with observable ones. (d) The spectral radius ρ(ω) (a quantitative measure of nestedness) is plotted against the network size (S) for a large sample of random networks evolved by duplication and divergence (node colour represents the statistical significance of the measured nestedness; higher values are more significant). Open circles correspond to real networks, including the one displayed in panel (b), while the black line defines the analytical prediction for the random model. (Online version in colour.)

Speciation divergence reproduces the observed patterns of network architecture, and without assuming any kind of adaptive mechanism. To validate our predictions, a database (IWDB) of n = 25 weighted mutualistic webs (figure 3b is an example of real network) is compared against a large set of simulated bipartite networks randomly sampled from the full parameter space. The predicted degree distribution follows the truncated power-law found in empirical data (figure 3c) and analytical models. Not only degree heterogeneity emerges from the neutral model, but all other measurable network attributes, including among them nestedness (figure 3d). But nestedness has been shown to be a by-product of the heterogeneity [100]. Given the lack of a fitness function driving selection, the agreement between theory and data supports the non-adaptive nature of the observed architecture [99]. Macroevolutionary patterns shape the global architecture of mutualistic networks, while adaptation and selection work on top of universal features derived from general principles of network growth. Recent work further supports the importance of ecological spandrels in community assembly [101].

As a final point, let us mention that the model discussed above does not stand alone here. In [102], the authors show that nestedness and heterogeneous degree distributions (but not other features) can emerge from an optimization principle that maximizes species abundances. Their model, however, works over ecological time scales, whereas the question we pose here is to what extent simple evolutionary models can account for observed structural patterns. In this respect, [103] developed a quantitative genetic model that allows inference of network structure over evolutionary time. Their model is far more complex that the one presented here and matches some observations under much more restrictive conditions. A possible extension of our model, using some class of digital genome species description, could help to discover whether some coevolutionary patterns found in plant–pollinator webs [91] can be reproduced under our framework.

5. Discussion: tinkering and beyond

One specially important consequence of our proposal is that null models are fundamental in order to discard potential explanations to given phenomena based on optimization or selection. Too often, the observation of some particular pattern is interpreted in terms of optimal design or at least as evidence of some kind of adaptive trait. This is a traditional tendency among biologists while looking for explanations under the absence of solid arguments (the same can be said about many physicists with a limited understanding of biology and evolution). Instead, we suggest that the fundamental constraints imposed by extensive reuse pervades the presence of most network-level structures. However, they have to be interpreted as byproducts of the amplification process with no adaptive a priori functional meaning, i.e. they are spandrels. Heterogeneity, small-world patterns, nestedness, asymmetries and even modularity are instances of these non-adaptive features.

In this paper, we have reviewed three relevant examples illustrating this conceptual framework that show how duplication and rewiring inevitably occur either as evolutionary tinkering or as a consequence of a complexity design horizon. The latter provides an unexpected twist to Jacob’s proposal: the engineer can sometimes act as a tinkerer. This is a somewhat paradoxical situation: as a software project keeps growing, complexity also grows in a nonlinear fashion and individual understanding of the system decreases. However, emergent patterns also appear, such as scale-freeness or a well-defined distribution of motifs. Because of the inevitable tendency towards heterogeneous distributions of links resulting from the amplification process, several desirable properties emerge for free: the efficient connectivity associated with the presence of hubs, along with the sparse connectivity (and thus low-cost in terms of connections) guarantees efficient propagation of information among subparts. The modular or nested organization facilitates the development of specialized (but integrated) subparts. Here too, division of labour can be selected on top of the incipient modular structure. The tinkering scenario thus enhances the chances for natural selection to exploit an advantageous network topology. This idea is somewhat related to Kauffman’s concept of order for free [15] where dynamical attractors in randomly connected networks exhibit remarkable stability and robustness properties when average connectivity is tuned. Selection would take advantage of such favourable dynamical states. Both in our topological framework and in the Boolean network scenario, there is no need to use selective forces to explain the emergent phenomena, nor is selection irrelevant. But the latter would be operating on top of the emergent patterns, instead of generating them.

The architecture of these complex networks and our knowledge of the microscopic rules operating in each case study provide the basis for identifying the origins of web complexity. What about other systems, where tinkering might be less relevant? Optimality can certainly work in some cases, particularly in relation with tree-like structures where global optima can be reached through evolutionary search or energy minimization principles [104]. Most evolutionary paths towards optimality in networks, particularly spatial ones, require consideration of a conflict between efficient communication and wiring costs ([105–107] and references therein) or conflicts between different subparts [108–110]. In most cases, percolation and geometry constraints (along with graph heterogeneity) can play a crucial role in limiting the space of possible networks that can exist [111,112].

Optimization and emergence seem to belong to totally different domains. They are not when dealing with evolved biological nets, optimization processes involving a conflict between two (or more) constraints can lead to phase transitions where the conflict is resolved along with the emergence of some inevitable network organization features. An example is provided by an information theory model of emergence of language [106,113,114]. Language has been a great challenge to scholars from very different disciplines and remains one of the most difficult to explain as a major evolutionary transition [115]. Interestingly, here too a set of components (words) interact in complex ways and some striking statistical patterns seem to be universal. This is the case of the so-called Zipf’s Law. Imagine we count all words that appear within a text and rank them from the most to the least frequent. Zipf’s Law is a scaling law, common to all known languages, and says that the frequency of a word within a given (long) text decays with the inverse of its rank. In this way, most words are rare while a small number are very common. How is this connected with the way words interact?

One of the most successful examples of application of network science is the study of language as a web of connected words. Specifically, using diverse ways of relating words by their appearance within sentences [116], semantic relations [117–119] or syntax [106,120], it was early shown that the resulting graphs shed light on the the functional and evolutionary aspects of their global organization [121]. A very simple illustration is provided by co-occurrence graphs obtained from written texts (figure 4a) from which two words are considered to be linked if they appear one after the other within (at least) one sentence (figure 4b). By using this definition, a scale-free network is obtained (figure 4c). Specifically, the frequency distribution of words having k co-occurrences with others was shown to scale as $P(k)\sim k^{-\gamma }$. Several interesting properties can be detected—among others, very short path lengths, high clustering and the lack of links between prepositions and other words acting as hubs.

Figure 4.

Language networks exhibit scale-free structure and several kinds of correlations. A simple way of generating a web of words is the use of co-occurrence links. Here, two words from a given text (a) are connected if they appear one after the other (at least once) within a given sentence (b). In (c), we display a zoom to the co-occurrence (purely topological) network obtained from the first paragraphs of Augie Wren's Xmas Tale by Paul Auster. The resulting web has some marked features, such as the lack of connections between hubs (disassortativity) and very short path lengths. (Online version in colour.)

It can be shown that some of these properties emerge for free from a simple model based on a conflict between cognitive efforts [106]. In a nutshell, language complexity would be the result of simultaneously reducing the cost of both speaker and hearer [122] by minimizing the error on both sides of the communication channel. Using two well-defined quantities from information theory as measures of efforts, it was shown that a phase transition takes place when both efforts are equal. At that point, Zipf’s Law emerges as a universal pattern and the underlying network of word–word interactions also displays robust properties shared with real language nets even at the syntax level [120,123–126].

Tinkering processes are one major driving force in the historical and evolutionary dynamics of complex networks. If duplication-divergence rules are responsible for network growth, they deeply constrain the structural outcome, creating graph correlations that are measurable and largely universal. As a consequence, order comes for free: observable regularities are the expected result of amplification processes. Two important lessons are of relevance to evolutionary dynamics. The first is that convergent patterns found at the network level can be largely explained by the mathematics of network growth under reuse of parts. Second, a considerable amount of topological precursors required to develop adaptive traits and robustness are in place with no active selection.

These lessons can be extended to technological systems, where network organization has been shown to be irreducible to the individual-level decisions based on rational engineering practices [127,128]. This irreducible complexity is at the core of the structuralist view of evolution [1,129] that has been particularly relevant within the context of development. Structuralism holds the view that self-organization and constraints play a leading role in defining the space of the possible, sometimes as a consequence of physical constraints [130,131]. Our view is that topological constraints play a similar role in the context of network complexity.

Data accessibility

This article has no additional data.

Authors' contributions

Both authors wrote the paper.

Competing interests

We declare we have no competing interests.

Funding

This work has been supported by the Botín Foundation by Banco Santander through its Santander Universities Global Division, a MINECO FIS2015-67616 fellowship and the Santa Fe Institute (RS) and by the Spanish Ministry of Economy and Competitiveness, grant no. FIS2016-77447-R MINECO/AEI/ FEDER and European Union (to S.V.). This work has also been supported by Secretaria d’Universitats i Recerca del Departament d’Economia i Coneixement de la Generalitat de Catalunya and by the ‘María de Maeztu’ Programme for Units of Excellence in R&D (MDM- 2014-0445), and the CERCA Programme of the Generalitat de Catalunya (R.S. and S.V.).