Estimating Urine Albumin-to-Creatinine Ratio from Protein-to-Creatinine Ratio: Development of Equations using Same-Day Measurements

Significance Statement

The urine albumin-to-creatinine ratio (ACR) is the preferred metric for quantifying albuminuria, and it also has been incorporated into equations to predict risk of kidney failure. However, often only the protein-to-creatinine ratio (PCR) is available. Previous studies have described the association between ACR and PCR, although none have provided a method to estimate ACR from PCR that accounts for the nonlinear association or the effect of covariates other than sex. The authors used same-sample urine ACR/PCR measurement pairs from a population-based cohort of 47,714 adults to derive equations to estimate ACR from PCR, taking into account nonlinearity and modification by several clinical characteristics. These equations may be useful in specific retrospective applications where an estimate of ACR is desired but only PCR is available.

Visual Abstract

Abstract

Background

Urine albumin-to-creatinine ratio (ACR) and protein-to-creatinine ratio (PCR) are used to measure urine protein. Recent guidelines endorse ACR use, and equations have been developed incorporating ACR to predict risk of kidney failure. For situations in which PCR only is available, having a method to estimate ACR from PCR as accurately as possible would be useful.

Methods

We used data from a population-based cohort of 47,714 adults in Alberta, Canada, who had simultaneous assessments of urine ACR and PCR. After log-transforming ACR and PCR, we used cubic splines and quantile regression to estimate the median ACR from a PCR, allowing for modification by specified covariates. On the basis of the cubic splines, we created models using linear splines to develop equations to estimate ACR from PCR. In a subcohort with eGFR<60 ml/min per 1.73 m², we then used the kidney failure risk equation to compare kidney failure risk using measured ACR as well as estimated ACR that had been derived from PCR.

Results

We found a nonlinear association between log(ACR) and log(PCR), with the implied albumin-to-protein ratio increasing from <30% in normal to mild proteinuria to about 70% in severe proteinuria, and with wider prediction intervals at lower levels. Sex was the most important modifier of the relationship between ACR and PCR, with men generally having a higher albumin-to-protein ratio. Estimates of kidney failure risk were similar using measured ACR and ACR estimated from PCR.

Conclusions

We developed equations to estimate the median ACR from a PCR, optionally including specified covariates. These equations may prove useful in certain retrospective clinical or research applications where only PCR is available.

Over the past decade the prognostic significance of albuminuria has been demonstrated in predicting risk of CKD progression and other outcomes such as cardiovascular events.^1–3 Consequently, albuminuria has been incorporated into the CKD staging system as well as risk scores to predict the development of kidney failure.^4,5 The albumin-to-creatinine ratio (ACR) is recommended by guidelines^6,7 as the preferred test for quantifying albuminuria/proteinuria for several reasons. Assays for measurement of albuminuria are typically susceptible to less analytical imprecision than total protein, particularly at lower levels of proteinuria. Further, albumin is the predominant urinary protein in the majority of kidney diseases, and it is possible to accurately measure urine albumin at levels in the physiologic range.⁸ Finally, ACR is more sensitive than protein-to-creatinine ratio (PCR) in detecting the onset of diabetic nephropathy.^6,7 Despite these benefits of ACR, in many instances, particularly when using secondary data for research, PCR but not ACR is available. To capitalize on the prognostic power of albuminuria from existing data sets, it would be useful to estimate ACR from PCR as accurately as possible.

Prior studies have investigated the relationship between ACR and PCR measurements and noted their nonlinear association.^9–12 Specifically, the ACR/PCR ratio varies with the level of proteinuria, with the proportion of total protein that is albumin varying from 20% to 30% at normal levels of proteinuria and rising to approximately 70% at higher levels.^9,13 There is also weaker correlation between ACR and PCR at lower proteinuria levels than at higher.^8,9,14 Patient characteristics such as age, sex, GFR, diabetes, and race may also affect the relationship between ACR and PCR,^9,10,12 whereas the laboratory methods used, particularly for measuring urine protein, may also be important.^8,15 However, a method to estimate ACR from PCR that addresses the nonlinearity or includes the effect of covariates other than sex has not been developed, potentially limiting current approaches for estimating the former from the latter. In addition, findings regarding the effect of sex on the relationship between ACR and PCR have been contradictory.^10,16

We therefore sought to develop equations to estimate ACR from PCR, taking into account potential modification by patient characteristics, using a population-based cohort with pairs of ACR/PCR measurements conducted on the same day in the same patient. We examined the influence of several clinically relevant covariates, using a flexible approach to allow for a nonlinear association.

Methods

Data Sources, Study Population, and Covariates

We used population-level laboratory and administrative data from Alberta, Canada.¹⁷ The study population included all adults in Alberta (population of 4.3 million as of 2017) aged ≥18 years who had outpatient urine ACR and PCR measurements on the same day (presumably from the same urine sample) between May 2002 and December 2016. As we were interested in potential modification by eGFR category, we included only ACR/PCR pairs where there was a serum creatinine measurement on the same day. For patients who had multiple ACR/PCR pairs, we randomly chose one. We established the commencement date of RRT by linking to our provincial renal program database, and excluded patients with a prior kidney transplant or receiving maintenance dialysis. We linked to demographic data to establish sex and age, and defined diabetes and hypertension from hospitalization and physician claims data, using validated algorithms.^18,19 We calculated eGFR using the CKD Epidemiology Collaboration equation.²⁰ We also identified the analyzers and methods used for measuring ACR and PCR in the largest cities in Alberta (Calgary and Edmonton) during most of the study timeframe, although we were unable to obtain this information for laboratories in other parts of the province.

Statistical Analyses

Model Development: Primary Approach

Because the distribution of ACR and PCR are known to be highly skewed, we analyzed the relationship between log(ACR) and log(PCR). Anticipating residual skewness, we conducted median rather than mean regression because it does not assume conditional normality²¹ and provides an estimate of a measure of central tendency that is more meaningful in a skewed distribution. Median regression (a special case of quantile regression) uses nonparametric methods to fit models with coefficients that can be interpreted similarly to those from least squares regression. An additional advantage of median regression is that the median value is unaffected by the log transformation, i.e., the log of the median is the same as the median of the log, which is not true of the mean. We addressed the nonlinearity of the relationship between log(ACR) and log(PCR) by transforming log(PCR) with a restricted cubic spline, a recommended approach for modeling a nonlinear association²² using five knots placed at standard locations.²³ We assessed for potential modification by age, sex, hypertension, diabetes, eGFR category, and laboratory location (a proxy for analyzer and method used), adding each covariate to the model by including the categorical variable and interaction terms between the covariate and each of the four spline variables, to allow for effects that varied with PCR. We estimated standard errors using bootstrapping, recommended if the conditional distribution of the dependent variable is heteroscedastic [i.e., variation in log(ACR) changes with log(PCR)].²⁴ Through this process we created models for median log(ACR) with no covariates, specified covariates, and all covariates. In addition, to better describe the prediction interval for estimated log(ACR), we fit quantile regression models for the 25th and 75th percentiles. Because the coefficients from models with cubic splines with interactions are difficult to interpret, we assessed the effect of each covariate graphically by plotting the predicted median ACR versus the measured PCR, including 95% confidence intervals (95% CIs), for each covariate value using models that contained the spline, the covariate, and interactions. We also tested the statistical significance of each covariate in a full model by using a Wald test for the groups of variables that corresponded to each covariate.

Alternative Approaches

Because models incorporating restricted cubic splines do not easily allow the estimation of predicted values from the coefficients alone, we created models with log(PCR) transformed with a linear spline, with knots on the basis of inflections of the cubic spline. We created four models: one with only the linear spline of log(PCR); one with sex and linear spline interactions added; one with age, sex, diabetes, hypertension, GFR category, and linear spline interactions added; and one with all covariates, including laboratory location.

Assessment of Model Performance

To visually assess the overall performance of the full cubic spline model for median ACR across a wide range of PCR values, we created a scatterplot of measured ACR versus predicted ACR. We compared this with scatterplots applying other equations^13,16 that have been developed to estimate ACR from PCR.

Comparison with Albuminuria and Proteinuria Category Thresholds

We used cubic splines to estimate the median, 25th and 75th percentiles of ACR at the Kidney Disease Improving Global Outcomes (KDIGO) PCR category thresholds of 150 and 500 mg/g,⁶ first in an unadjusted model and then in models containing one covariate. We also estimated the PCR value that would be equivalent to a predicted ACR at the KDIGO ACR category thresholds. We then compared the sensitivity, specificity, positive predictive value (PPV), negative predictive value (NPV), and overall correct classification for the measured ACR category versus measured PCR category, and for the measured ACR category versus predicted ACR category, with respect to KDIGO category thresholds, using measured ACR category as the reference. We also calculated C-statistics for the models, using these thresholds.

Predictive Performance using the Kidney Failure Risk Equation

We selected patients with eGFR<60 ml/min per 1.73 m² and at least 2 years of follow-up for commencement of RRT, and compared observed cases of RRT within 2 years with the number expected from applying the four-variable kidney failure risk equation (KFRE), which uses log(ACR), eGFR, age, and sex.^5,16 We performed this comparison using measured ACR, then ACR estimated from PCR. We also calculated sensitivity, specificity, PPV, NPV, and correct classification for observed RRT versus >10% calculated risk.

Assessment of Within-Person Correlation of ACR/PCR Ratio

Finally, we investigated within-person correlation of the ACR/PCR ratio in a data set comprising individuals with more than one ACR/PCR pair by estimating the intraclass correlation coefficient in a mixed linear regression model to estimate mean log(ACR), using cubic spline terms of log(PCR), covariates, and interactions as before, with between-person variability modeled with a random intercept.

This study was approved by the University of Calgary’s Conjoint Health Research Ethics Board. Analysis was conducted using Stata MP version 14.2.

Results

We identified 120,564 pairs of outpatient same-day/same-person ACR and PCR measurements; these represented 4.4% of outpatient ACR measurements and 21.1% of outpatient PCR measurements, proportions that were fairly consistent throughout the study period. In 106,948 cases (88.7%) there was also a serum creatinine measurement on the same day. After excluding 1606 who had previously initiated RRT, there were 105,342 eligible pairs of ACR and PCR measurements from 47,714 individuals; the final cohort consisted of a random pair chosen from each person. Measurements were well distributed across albuminuria/proteinuria categories, from patients with a wide range of demographic and clinical characteristics (Table 1).

Table 1.

Patient characteristics in the full cohort, the subcohort used for application of the KFRE, and the subcohort used for the repeated measures analysis

Characteristic	% of Patientsa
	Full Cohort (N=47,714)	Subcohort for Application of the KFRE (n=9998)	Subcohort for Repeated Measures Analysis (n=17,259) (74,341 Pairs)b
Age in yr, median (IQR)	59.3 (47.2–70.4)	71.3 (61.9–79.1)	58.9 (49.0–70.1)
Age category, yr
18–49	29.8	8.3	26.9
50–69	44.5	37.6	47.9
≥70	25.7	54.1	25.2
Women	46.6	46.4	43.9
KDIGO CKD PCR category, mg/gc
A1: <150 (normal/mild)	65.8	45.3	59.4
A2: 150–500 (moderate)	19.0	25.4	20.9
A3: >500 (severe)	15.2	29.3	19.7
KDIGO CKD ACR category, mg/gc
A1: <30 (normal/mild)	61.9	42.4	54.7
A2: 30–300 (moderate)	23.8	31.0	26.4
A3: >300 (severe)	14.3	26.6	18.9
KDIGO CKD eGFR category, ml/min per 1.73 m2
G1: eGFR≥90	35.0	—	32.1
G2: eGFR=60–89	33.3	—	33.4
G3A: eGFR=45–59	12.3	38.9	13.2
G3B: eGFR=30–44	11.1	34.5	13.5
G4: eGFR=15–29	7.1	22.9	7.1
G5: eGFR<15	1.1	3.7	0.7
Hypertension	62.4	87.7	66.8
Diabetes	47.1	56.7	54.9
Year of ACR/PCR test pair
2002–2006	11.9	16.0	16.2
2007–2011	29.3	40.4	39.8
2012–2016	58.8	43.6	44.0
Laboratory locationd
Edmonton	66.5	62.7	67.5
Calgary	17.8	24.9	16.4
Other	15.8	12.4	16.1

^aUnless otherwise indicated.

^bPercents in this column are calculated on the basis of the number of patients, using characteristics on the date of the earliest pair.

^cTo convert ACR or PCR from milligrams per gram to milligrams per millimole, multiply by 0.113.

^dIn Edmonton, most urine albumin measurements were made using a Siemens Advia 1800 analyzer, with an immunoturbidimetric method. Urine protein was measured using a colorimetric method (pyrogallol red) on a Protein Pointe Scientific analyzer (from September 2013 to December 2016), a Wako analyzer (July 2011 to September 2013), and a Genzyme analyzer (before July 2011). In Calgary, most measurements were made with a Roche Integra analyzer, with albumin measured with an immunoturbidimetric method and protein with a turbidimetric method (benzethonium chloride). Testing at other sites was done using various analyzers and methods, which we were unable to determine in all cases.

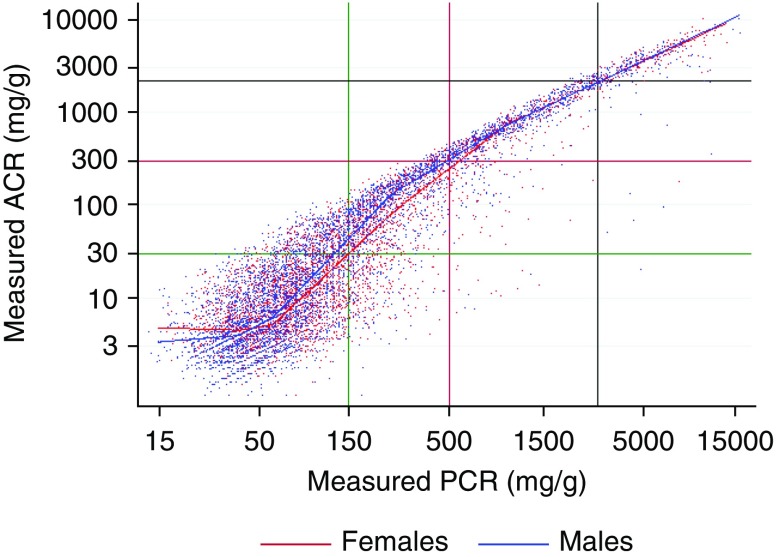
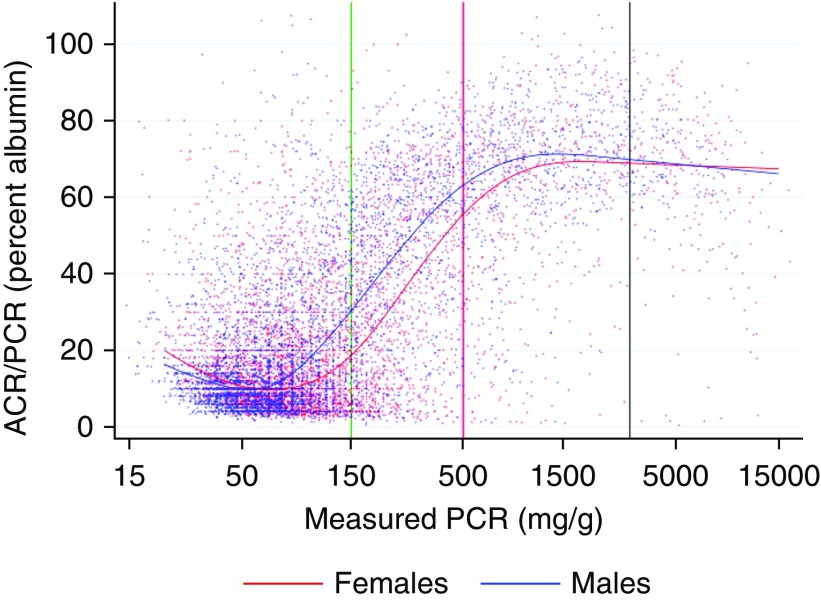
Figure 1 shows a scatterplot of ACR versus PCR on a log scale for a 20% random sample (for clarity) of ACR/PCR pairs. A curvilinear relationship at lower levels of ACR and PCR shows the nonlinearity of the log(ACR) versus log(PCR) relationship, whereas the greater dispersion demonstrates the poorer correlation between ACR and PCR at lower levels of proteinuria. Although the log transformation reduced the skewness of the conditional distribution of log(ACR), we noted that some remained and varied according to PCR (negatively skewed at higher ranges; near normal or slightly positively skewed at lower ranges). Figure 2 shows a scatterplot of the ACR/PCR ratio versus PCR for the same random sample.

Figure 1.

This scatterplot (on log/log scale) of measured ACR versus measured PCR shows the non-linearity of the log(ACR) versus log(PCR) relationship, and the weaker correlation between ACR and PCR at lower proteinuria levels. Cohort size is 47,714 pairs; the graph includes a 20% random sample of 9466 pairs. The green, red, and black lines show the thresholds for A1 versus A2, A2 versus A3, and A3 versus nephrotic range, respectively. The blue dots represent men and the red dots represent women. The blue and red lines show the values predicted by one of the linear spline models for median ACR (model L2), for men (blue) and women (red). To convert ACR or PCR from milligrams per gram to milligrams per millimole, multiply by 0.113.

Figure 2.

This scatterplot of the ratio of measured ACR/measured PCR versus measured PCR for a 20% random sample of ACR/PCR pairs shows the variation in the albumin-to-protein with proteinuria level. Measured PCR is shown on a log scale, whereas measured ACR/measured PCR is shown as a percent. The green, red, and black vertical lines show the thresholds for A1 versus A2, A2 versus A3, and A3 versus nephrotic range of PCR, respectively. The blue dots represent men and the red dots represent women, whereas the curved blue and red lines show the values predicted by one of the cubic spline models for median ACR (model C2), for men (blue) and women (red).

Regression Modeling

In quantile regression models of log(PCR) transformed with a restricted cubic spline, we found that the implied median albumin-to-protein percent rose from <30% in A1 proteinuria (ACR<30 mg/g) to >60% in A3 proteinuria (ACR>300 mg/g) (Supplemental Figure 1), and that the association between ACR and PCR became more linear, with relatively less dispersion, in A3 proteinuria (Supplemental Figure 2). We also found that sex, hypertension, diabetes, age category, eGFR category, and laboratory location all significantly modified the log(ACR) versus log(PCR) relationship (all P<0.001). Supplemental Figures 3–21 illustrate the effect of these covariates on the ACR-PCR relationship. For each covariate we include three figures: the predicted median ACR versus PCR for the entire range (log scale), the predicted median ACR versus PCR for the lower range, and the implied median albumin-to-protein percent versus PCR for the lower range. In addition, for the model with sex, Supplemental Figure 4 shows the predicted median and 25th and 75th percentiles of ACR for men and women separately.

Table 2 shows summary statistics for the cubic and linear spline models with specified combinations of covariates. The correlation coefficients show the close correspondence between the cubic and linear spline models, which is confirmed in Supplemental Figure 22. Table 3 provides equations to estimate the median ACR and the interquartile range (IQR) from a PCR, on the basis of the linear spline model with no covariates, whereas Supplemental Table 1 provides equations on the basis of a model containing the linear spline and sex. Regression coefficients for the four linear spline models included in Table 2 are provided in Supplemental Table 2.

Table 2.

Summary statistics for selected median regression models on the basis of cubic and linear splines, and specified covariates

Variables included	Models with Log(PCR) Transformed with a Five-Knot Restricted Cubic Spline			Models with Log(PCR) Transformed with a Four-Knot Linear Spline			Correlation Coefficient between Estimates from Model Pairs
	Model	No. of Coefficients	Pseudo R2	Model	No. of Coefficients	Pseudo R2
Spline of log(PCR) only	C1	5	0.624	L1	6	0.623	>0.99
Spline of log(PCR), sex, and interactions	C2	10	0.629	L2	12	0.628	>0.99
Spline of log(PCR), sex, age, diabetes, hypertension and eGFR category, and interactions	C3	40	0.637	L3	48	0.635	>0.99
Spline of log(PCR) sex, age, diabetes, hypertension, eGFR category, laboratory location, and interactions	C4	50	0.642	L4	60	0.641	>0.99

The knots for the restricted cubic spline were at percentiles 5, 27.5, 50, 72.5, and 95 of log(PCR) (3.4668, 4.0625, 4.5664, 5.3992, and 7.7333, corresponding to PCR values of 32.0, 58.1, 96.2, 221, and 2283 mg/g). Knots for the linear spline were at values of log(PCR) of 3.689, 4.094, 5.521, and 6.908, corresponding to PCR values of 40, 60, 250, and 1000 mg/g. The number of coefficients includes the constant. The interactions are between the covariate and the spline terms. Pseudo R² is the proportion of the sum of absolute deviations from the median that is explained by the model.

Table 3.

Equations to estimate median and 25th and 75th percentiles of ACR from a PCR measurement, on the basis of quantile regression models for log(ACR) containing only the linear spline terms for log(PCR)

Range of PCR, mg/g	Equation to Estimate Median Log(ACR)	Equation to Estimate 25th Percentile Log(ACR)	Equation to Estimate 75th Percentile Log(ACR)
PCR<40	0.9518+0.1264×log(PCR)	0.5528+0.1297×log(PCR)	1.4520+0.1074×log(PCR)
PCR 40 to <60	−1.2568+0.7251×log(PCR)	−0.1416+0.3179×log(PCR)	−3.7193+1.5092×log(PCR)
PCR 60 to <250	−6.7837+2.0751×log(PCR)	−6.2467+1.8092×log(PCR)	−4.9571+1.8116×log(PCR)
PCR 250 to <1000	−2.9649+1.3834×log(PCR)	−7.1833+1.9788×log(PCR)	−1.4477+1.1760×log(PCR)
PCR≥1000	−0.0239+0.9577×log(PCR)	−0.0867+0.9264×log(PCR)	−0.1902+0.9939×log(PCR)

Log refers to the natural logarithm, so ACR=exp[log(ACR)]=2.71828^log(ACR). Median predicted ACR=exp[median of predicted log(ACR)]. ACR and PCR are in milligrams per gram.

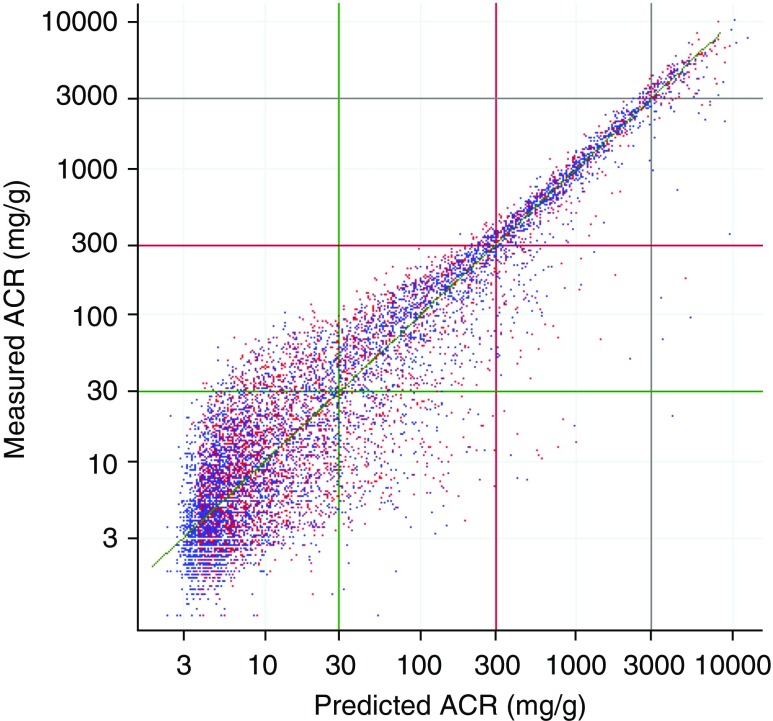
Overall Performance of the Models

Figure 3 shows a scatterplot of measured ACR versus predicted median ACR from the full cubic spline model, whereas Supplemental Figure 23 shows a similar plot using the linear spline model with only sex. In both plots, the points are distributed fairly symmetrically about the line of identity throughout the entire range, with greater scatter at lower ACR values. Scatterplots on the basis of two equations developed by others to estimate PCR from ACR show less linearity and symmetry with respect to the line of identity (Supplemental Figures 24 and 25).

Figure 3.

This scatterplot of measured ACR versus predicted median ACR from the full cubic spline model (C4), for a 20% random sample shows a relatively symmetrical distribution around the line of identity (the diagonal line) indicating unbiased prediction. The blue dots represent men and the red dots represent women. To convert ACR or PCR from milligrams per gram to milligrams per millimole, multiply by 0.113.

Estimates of ACR at KDIGO PCR Category Thresholds

Figure 4 shows the estimated median and 95% CIs of predicted ACR at the KDIGO PCR category thresholds for the overall cohort and for groups defined by specified covariates, on the basis of cubic spline quantile regression models for the 50th percentile. Supplemental Figure 26 shows the estimated median and IQR on the basis of models for the 25th, 50th, and 75th percentiles, whereas the estimates themselves are shown in Supplemental Table 3. Overall, the median ACR corresponding to a PCR of 150 mg/g was 35.5 mg/g (95% CI, 34.9 to 36.1), with an IQR of 16.0–65.8 mg/g, whereas the median ACR corresponding to a PCR of 500 mg/g was 301 mg/g (95% CI, 298 to 304), with an IQR of 213–357 mg/g. Being a man, younger, and having higher eGFR were associated with a higher median ACR for a PCR of 150 and 500 mg/g, whereas diabetes and hypertension were associated with a higher median ACR only for a PCR of 150 mg/g. Laboratory testing in Calgary was associated with a higher median ACR for a PCR of 500 mg/g, but with a lower median ACR for a PCR of 150 mg/g, compared with laboratory testing in Edmonton. Supplemental Table 3 also provides the estimated PCR corresponding to the KDIGO ACR category thresholds of 30 and 300 mg/g. For example, the PCR associated with a predicted median ACR of 30 mg/g was 139 mg/g (123 mg/g for men and 155 mg/g for women).

Figure 4.

The estimated median and 95% CIs of ACR at the KDIGO A1/A2 and A2/A3 PCR thresholds of 150 and 500 mg/g, vary by covariate. To convert ACR or PCR from milligrams per gram to milligrams per millimole, multiply by 0.113. Age is in years and eGFR is in ml/min per 1.73 m², The estimates are on the basis of quantile regression models for the 50th percentile of log (ACR), with log(PCR) transformed with a restricted cubic spline, and with each model containing only the specified covariate, the spline terms, and the interactions between the specified covariate and the spline terms.

ACR Classification Accuracy from PCR

The sensitivity, specificity, PPV, NPV, and overall agreement for measured ACR category versus measured PCR category, and measured ACR category versus ACR category estimated from PCR using the full cubic spline model are provided in Table 4 for the A1/A2 and A2/A3 thresholds. The sensitivity for identifying A2 versus A1 albuminuria improved when using the ACR category imputed from the full model compared with using the measured PCR category (from 79.1% to 83.2%), but at the loss of some specificity. The overall agreement using the ACR category imputed from the model was slightly higher than it was using the PCR category at the A1/A2 threshold (88.8% versus 87.9%) and marginally higher at the A2/A3 threshold (97.8% versus 97.6%).

Table 4.

Sensitivity, specificity, PPVs, NPVs, and overall agreement for measured PCR category, and ACR category imputed from PCR using model C4, at KDIGO category thresholds (reference standard: KDIGO category of measured ACR)

KDIGO Category Threshold	Comparison with Category of Measured ACR	Sensitivity (95% CI)	Specificity (95% CI)	PPV (95% CI)	NPV (95% CI)	% Overall Agreement (95% CI)	ROC C-Statistic (95% CI)
A1/A2	KDIGO category of measured PCR	79.1 (78.5 to 79.7)	93.3 (93.1 to 93.6)	88.0 (87.4 to 88.4)	87.9 (87.5 to 88.3)	87.9 (87.6 to 88.2)	0.86 (0.86 to 0.87)
	ACR category imputed from PCR using model with cubic spline and all covariates (C4)	83.2 (82.6 to 83.7)	92.3 (92.0 to 92.6)	86.9 (86.4 to 87.4)	89.9 (89.6 to 90.3)	88.8 (88.5 to 89.1)	0.95 (0.95 to 0.96)
A2/A3	KDIGO category of measured PCR	94.7 (94.1 to 95.2)	98.0 (97.9 to 98.2)	89.0 (88.3 to 89.7)	99.1 (99.0 to 99.2)	97.6 (97.4 to 97.7)	0.96 (0.96 to 0.97)
	ACR category imputed from model with cubic spline and all covariates (C4)	95.4 (94.8 to 95.8)	98.2 (98.0 to 98.3)	89.7 (89.0 to 90.4)	99.2 (99.1 to 99.3)	97.8 (97.6 to 97.9)	>0.99 (>0.99 to >0.99)

Values except ROC statistic are reported in percent. A1/A2 threshold: ACR=30 mg/g, PCR=150 mg/g. A2/A3 threshold: ACR=300 mg/g, PCR=500 mg/g. Positive cases are above the threshold. ROC, receiver operator characteristic.

Application of the Kidney Failure Risk Equation

We identified 9998 patients with eGFR<60 ml/min per 1.73 m² and 2 years of follow-up to estimate the risk of kidney failure using the KFRE (for baseline characteristics see Table 1). Among these, 484 (4.8%; 95% CI, 4.4 to 5.3) were observed to commence RRT within 2 years; using predictions on the basis of the KFRE, the corresponding estimates were 665 patients (6.7%; 95% CI, 6.2 to 7.2) using measured ACR, 694 patients (6.9%; 95% CI, 6.5 to 7.5) using the full cubic spline model, and 705 patients (7.1%; 95% CI, 6.6 to 7.6) using the model with the linear spline and sex (Table 5). For 10% 2-year risk of RRT, sensitivity was slightly higher but specificity slightly lower for predictions on the basis of PCR; the overall correct classification was similar using measured ACR (87.7%; 95% CI, 87.0 to 88.3) versus ACR predicted from the full cubic spline model (87.2%; 95% CI, 86.6 to 87.9) and ACR predicted from the model with the linear spline and sex (87.0%; 95% CI, 86.3 to 87.7). C-statistics were almost identical.

Table 5.

Comparisons of predicted versus observed cases of RRT commencement within 2 years among those with eGFR<60 ml/min per 1.73 m², on the basis of the KFRE, and estimates of classification accuracy at 10% risk, using measured ACR versus ACR estimated from the PCR

RRT Cases	Prediction using Measured ACR (95% CI)a	Prediction using Median ACR Estimated from PCR with Model C4 (95% CI)a	Prediction using Median ACR Estimated from PCR with Model L2 (95% CI)a	Observed RRT within 2 yr (95% CI)
Cohort for comparing predicted vs. observed cases requiring RRT
Overall cohort (n=9998)	6.7 (6.2 to 7.2)	6.9 (6.5 to 7.5)	7.1 (6.6 to 7.6)	4.8 (4.4 to 5.3)
ACR <30 mg/g (n=4237)	0.7 (0.5 to 1.0)	0.9 (0.6 to 1.2)	0.9 (0.6 to 1.2)	0.3 (0.2 to 0.5)
ACR 30–300 mg/g (n=3104)	3.8 (3.1 to 4.5)	4.2 (3.5 to 5.0)	4.4 (3.7 to 5.2)	2.1 (1.6 to 2.7)
ACR >300 mg/g (n=2657)	19.5 (18.0 to 21.1)	19.8 (18.3 to 21.3)	20.0 (18.5 to 21.6)	15.3 (13.9 to 16.7)
Estimates of classification accuracy for 10% 2 yr risk of RRT versus observed RRT in 2 yr
Sensitivity	87.8 (84.6 to 90.4)	89.3 (86.2 to 91.7)	89.3 (86.2 to 91.7)
Specificity	87.7 (87.0 to 88.3)	87.1 (86.5 to 87.8)	86.9 (86.2 to 87.6)
PPV	26.6 (24.5 to 28.9)	26.1 (24.0 to 28.3)	25.7 (23.7 to 27.9)
NPV	99.3 (99.1 to 99.5)	99.4 (99.2 to 99.5)	99.4 (99.2 to 99.5)
Overall correct classification	87.7 (87.0 to 88.3)	87.2 (86.6 to 87.9)	87.0 (86.3 to 87.7)
ROC C-statistic	0.94 (0.94 to 9.96)	0.95 (0.94 to 0.96)	0.95 (0.94 to 0.96)

Data are shown as percent, unless otherwise indicated. Values reported in percent except for the ROC C-statistic. Model C4 is the full cubic spline median regression model; L2 is the linear spline median regression model containing only the linear spline, sex, and interactions between the spline and sex. All classification into ACR categories is on the basis of measured ACR. ROC, receiver operator characteristic.

^aCalculated using log(ACR), eGFR, age, and sex according to the equation given in Tangri et al.¹⁶

Assessment of Within-Person Correlation of ACR/PCR Ratio

Finally, in a cohort including 74,341 ACR/PCR pairs for 17,259 individuals, we fit a mixed linear regression model for log(ACR) and found the intraclass correlation coefficient to be 0.64, indicating that 64% of the variance that was not explained by the fixed effects was explained by between-person variability, and that there was moderately strong within-person correlation of the ACR/PCR ratio.

Discussion

We used a large, population-based cohort of same-day urine ACR/PCR pairs to examine the relationship between the ACR and PCR for a wide range of proteinuria levels and clinically relevant covariates. Consistent with prior research, we found substantial variation in the median albumin-to-protein ratio with the level of proteinuria, with the median ratio approaching 70% in severe (A3) proteinuria, but dropping to below 30% in normal/mild (A1) proteinuria. Using splines to represent PCR measurements, we developed equations to allow the estimation of ACR from PCR, accounting for the nonlinear association between ACR and PCR measurements. These equations allow the accurate estimation of the median expected ACR from a PCR measurement, for a wide range of PCR values. To describe the range of probable ACR values corresponding to a PCR measurement, we also developed equations to estimate the 25th and 75th percentiles of the expected ACR. Although we used advanced methods, the final equations are relatively simple to use.

All covariates significantly modified the ACR–PCR association; however, the effect of these covariates on predicted median PCR was small compared with the IQR for predicted PCR. Sex was the most important modifier of the relationship between ACR and PCR, with men generally having a higher albumin-to-protein ratio than women. The sex difference in the median albumin-to-protein ratio varied substantially by level of proteinuria, with the greatest difference occurring from 100 to 200 mg/g, where the median proportion for women was 0.6 times that for men (e.g., for PCR of 150 mg/g, the median proportion was 30% for men and 18% for women; median predicted ACR was 45 mg/g for men and 28 mg/g for women). At higher ranges, the difference was attenuated (e.g., female/male ratio of 0.87 at PCR of 500 mg/g), and for PCR<45 mg/g the proportion was slightly higher for women than men. Our findings were generally consistent with those of Fisher et al.,¹⁰ who used urine samples from 3481 patients and fit a multivariable regression equation for the log(ACR)/log(PCR) ratio. They found a female/male ratio of 0.75, with no allowance for variation with level of proteinuria, and excluding the highest 2.5% of ACR measurements. Our findings are also consistent with studies that found higher rates of albuminuria among men than women, but higher rates of nonalbumin proteinuria among women than men.^15,25,26 Our results contradict, however, the method used by Tangri et al.¹⁶ to convert PCR to ACR, which implies a constant albumin/protein ratio of 38% for men and 57% for women (i.e., female/male ratio of 1.5).

Laboratory location was also an important modifier. In Calgary and Edmonton, urine albumin was measured by an immunoturbidimetric method. However, urine protein was measured by a turbidimetric method (benzethonium chloride) in Calgary but by a colorimetric method (pyrogallol red) in Edmonton. Given that urine protein measurement is known to vary by method, it is likely that the differences between the sites were largely related to differences in protein measurement. McTaggart et al.¹⁵ found that the pyrogallol red method gave significantly lower protein measurements than the benzethonium chloride method (i.e., higher apparent albumin-to-protein ratios). We also noted a higher albumin-to-protein ratio for pyrogallol red, but only for PCR under approximately 300 mg/g; above this range, measurement with pyrogallol red was associated with a lower albumin-to-protein ratio.

Age, eGFR category, diabetes, and hypertension were also important modifiers. Younger age and higher eGFR were associated with a higher median albumin-to-protein ratio across all proteinuria ranges. At PCR under approximately 400 mg/g, patients with diabetes and those with hypertension had a higher median albumin-to-protein ratio than those who did not (e.g., at PCR of 150 mg/g, 26% for diabetes versus 20% for no diabetes, and 25% versus 21% for hypertension versus no hypertension), but at higher PCR levels there was little difference. Others have noted the association of younger age,^10,25 higher eGFR,¹⁰ and diabetes¹⁰ with higher albumin-to-protein ratio. Estimates of the effect of low eGFR were less accurate because of the smaller group sizes (particularly eGFR<15 ml/min per 1.73 m²), so they should be interpreted with caution.

Our results are in general agreement with the equivalence implied by the KDIGO ACR/PCR category thresholds of 30/150 and 300/500 mg/g. However, the modification of the albumin-to-protein ratio by covariates suggests that the thresholds could be refined by inclusion of covariates to optimize classification (Figures 3 and 4, Supplemental Table 3). For example, the PCR corresponding to a median ACR of 30 mg/g was 139 mg/g overall, but was 155 mg/g among women and 123 mg/g among men. The full model resulted in only slight improvement in classification into KDIGO categories (from 87.9% to 88.8% at the A1/A2 threshold; from 97.6% to 97.8% at the A2/A3 threshold). However, the denominator in these calculations was the entire cohort, which understates the benefit of the model, as classification could only be improved for cases near the thresholds; among these, the improvement would have been larger. Any increases in accuracy resulting from inclusion of covariates should be balanced against the implementation challenges resulting from increased complexity. In most cases, using either the model with only the linear spline of PCR, or the linear spline and sex, will provide an adequate estimate of ACR. For example, if retrospective estimation of ACR or retrospective classification into albuminuria categories is required for a large number of patients with only PCR, then the effort in estimating median ACR from PCR and covariates on the basis of additional coefficients in Supplemental Table 2 could be justified by improved estimation; in other applications this may not be the case.

Although the models provide precise estimates of the expected median ACR (narrow 95% CIs), there was substantial unexplained variability in the ACR–PCR relationship, especially at lower levels of proteinuria, resulting in wide prediction intervals (Supplemental Figure 2). The greater variability at lower ranges of PCR was likely partly related to greater individual variability in disease states at lower ranges, as the albumin-to-protein ratio is associated with the location of kidney damage.^6,27 This is supported by the moderately strong within-person correlation of the ACR/PCR ratio, seen in the mixed model. It was also likely related to greater variability in the reactivity of different total protein assays at these levels.⁸

The use of the KFRE to compare 2-year expected and observed RRT found little difference between using measured ACR and ACR estimated from PCR. In our cohort, both measured ACR and ACR predicted from PCR overestimated the risk of kidney failure by a small but similar amount. However, most cases of RRT (both expected and observed) were in people with A3 albuminuria, and the ACR-to-PCR conversion is more accurate in this range; very few had A1 albuminuria, where the conversion is less accurate. Its use with the KFRE in people with A1 albuminuria has therefore not been adequately tested.

Because of the wide prediction intervals for ACR, particularly at lower levels, the equations should only be used in specific situations. Table 6 summarizes potential clinical and research applications, whether they are recommended, and associated limitations. We emphasize that the equations should not be used in clinical care to justify measuring PCR rather than ACR; ACR is the recommended test for albuminuria.⁶ The equations are most suited for retrospective applications (clinical or research) where PCR results are available but not ACR. We recommend estimating 25th and 75th percentiles of ACR in addition to the median, to estimate an approximate range of ACR.

Table 6.

Potential applications for PCR to ACR conversion equations, with recommendations and limitations

Potential Application	Recommendation and Limitations
Clinical: Current use (e.g., is it acceptable to test with a PCR and use the equations to estimate ACR for CKD staging or kidney failure risk prediction?)	Not recommended. ACR is the preferred test to assess albuminuria.6
Clinical: Retrospective/historical use (e.g., when there is a prior PCR result but no ACR is available)	Obtain an ACR when possible. If not feasible, one can use the equations to calculate the median, 25th and 75th percentiles of ACR, to estimate the likely range. Estimation is more accurate in A3 proteinuria (>500 mg/g).
Research: Prospective use (e.g., collect data on PCR and convert to ACR)	Not recommended. ACR is the preferred test to assess albuminuria.6
Research: Retrospective use (e.g., to estimate ACR from historical PCR data when no ACR available)	One can use the PCR and available covariates to estimate the median expected ACR. One can also estimate the 25th and 75th percentiles of ACR to estimate the likely range. Estimation is more accurate in A3 proteinuria (>500 mg/g).

Our study’s strengths include the large number of same-day ACR/PCR pairs, and linkage with other sources of data to define relevant covariates. Importantly, our regression models included methods that addressed the nonlinear relationship between ACR and PCR, their skewed distributions, heteroscedasticity, and covariate effects that varied with PCR.

The study also had limitations. Our results may have been influenced by the type of patients who were tested with both ACR and PCR, although by adjusting for several patient characteristics we believe we substantially addressed this. We were not, however, able to account for the underlying cause of CKD or race as potential modifiers. Additionally, we were unable to identify the analyzers and methods used in approximately 20% of tests, and the overall results reflect the particular combination of analyzers and methods in use in Alberta during the study period. However, the results presented here are appropriate for the primary intended purpose of estimating ACR from PCR in large samples where several analyzers/methods may have been used. Finally, the equations presented here should be validated in other cohorts.

Our findings provide an improved method to estimate ACR from PCR, which can be used in specific retrospective clinical or research applications, where ACR is unavailable.

Disclosures

Dr. James and Dr. Hemmelgarn report grants from Amgen Canada, outside the submitted work. Dr. Jun reports grants from VentureWise (a wholly owned commercial subsidiary of NPS MedicineWise) to conduct a commissioned project funded by AstraZeneca, outside the submitted work. Dr. Tonelli reports personal fees from B. Braun and grants from Merck, outside the submitted work. All of the remaining authors have nothing to disclose.

Funding

The study received funding from the Interdisciplinary Chronic Disease Collaboration (ICDC); the ICDC is funded through an Alberta Innovates Collaborative Research & Innovation Opportunity Team Grant. Dr. Hemmelgarn, Dr. James, Dr. Manns, Dr. Quinn, Dr. Ravani, and Dr. Tonelli are supported by grants from the Canadian Institutes of Health Research. Dr. Tonelli was supported by the David Freeze Chair in Health Services Research, Dr. Manns was supported by the Svare Chair in Health Economics, and Dr. Hemmelgarn was supported by the Roy and Vi Baay Chair in Kidney Disease, all at the University of Calgary. The funding agencies had no role in the design and conduct of the study; in the collection, analysis, and interpretation of the data; or in the preparation, review, or approval of the manuscript.

Supplemental Material

This article contains the following supplemental material online at http://jasn.asnjournals.org/lookup/suppl/doi:10.1681/ASN.2019060605/-/DCSupplemental.

Supplemental Table 1. Equations to estimate the median and 25th and 75th percentiles of ACR from a PCR measurement, by sex.

Supplemental Table 2. Regression coefficients for four models for median log (ACR), with log (PCR) represented by a four-knot linear spline.

Supplemental Table 3. Estimated median and IQR for ACR, at the KDIGO PCR category thresholds of 150 and 500 mg/g, for the overall cohort and for groups specified by covariates, and estimated PCR giving predicted median ACR at KDIGO ACR category thresholds.

Supplemental Figure 1. Median and 25th and 75th percentiles of predicted albumin-to-protein percent, by PCR value.

Supplemental Figure 2. Median and 25th and 75th percentiles of predicted ACR by PCR value.

Supplemental Figure 3. Effect of sex on predicted median ACR, log scale.

Supplemental Figure 4. Predicted median and 25th and 75th percentiles of ACR for men and women, by PCR value.

Supplemental Figure 5. Effect of sex on predicted median ACR, linear scale, PCR<600 mg/g.

Supplemental Figure 6. Effect of sex on predicted median albumin-to-protein percent.

Supplemental Figure 7. Effect of age on predicted median ACR, log scale.

Supplemental Figure 8. Effect of age on predicted median ACR, linear scale.

Supplemental Figure 9. Effect of age on predicted median albumin-to-protein percent.

Supplemental Figure 10. Effect of eGFR category on predicted median ACR, log scale.

Supplemental Figure 11. Effect of eGFR category on predicted median ACR, linear scale.

Supplemental Figure 12. Effect of eGFR category on predicted median albumin-to-protein percent.

Supplemental Figure 13. Effect of diabetes on median ACR, log scale.

Supplemental Figure 14. Effect of diabetes on median ACR, linear scale.

Supplemental Figure 15. Effect of diabetes on albumin-to-protein percent.

Supplemental Figure 16. Effect of hypertension on median ACR, log scale.

Supplemental Figure 17. Effect of hypertension on median ACR, linear scale.

Supplemental Figure 18. Effect of hypertension on albumin-to-protein percent.

Supplemental Figure 19. Effect of laboratory location (proxy for analyzer and method) on median ACR, log scale.

Supplemental Figure 20. Effect of laboratory location (proxy for analyzer and method) on median ACR, linear scale.

Supplemental Figure 21. Effect of laboratory location (proxy for analyzer and method) on albumin-to-protein percent.

Supplemental Figure 22. Comparison of predicted median ACR on the basis of models with PCR transformed with a restricted cubic spline (C1), and with PCR transformed with a linear spline (L1).

Supplemental Figure 23. Scatterplot of measured ACR and median ACR predicted from the linear spline model (L2).

Supplemental Figure 24. Scatterplot of measured ACR versus ACR estimated from PCR measurements using the equations of Tangri et al.¹⁶

Supplemental Figure 25. Scatterplot showing measured ACR versus ACR estimated from PCR measurements using the equation of Collier et al.¹³

Supplemental Figure 26. Estimated median, 25th and 75th percentiles of ACR at the KDIGO A1/A2 and A2/A3 PCR thresholds of 150 and 500 mg/g, overall and by specified covariate.