Achievable Rates for Pattern Recognition

Abstract

Biological and machine pattern recognition systems face a common challenge: Given sensory data about an unknown pattern, classify the pattern by searching for the best match within a library of representations stored in memory. In many cases, the number of patterns to be discriminated and the richness of the raw data force recognition systems to internally represent memory and sensory information in a compressed format. However, these representations must preserve enough information to accommodate the variability and complexity of the environment, otherwise recognition will be unreliable. Thus, there is an intrinsic tradeoff between the amount of resources devoted to data representation and the complexity of the environment in which a recognition system may reliably operate.

In this paper, we describe a mathematical model for pattern recognition systems subject to resource constraints, and show how the aforementioned resource–complexity tradeoff can be characterized in terms of three rates related to the number of bits available for representing memory and sensory data, and the number of patterns populating a given statistical environment. We prove single-letter information-theoretic bounds governing the achievable rates, and investigate in detail two illustrative cases where the pattern data is either binary or Gaussian.

I. Introduction

PATTERN recognition is the problem of inferring the state of an environment from incoming and previously stored data. In real-world operating environments, the volume of raw data available often exceeds a recognition system’s resources for data storage and representation. Consequently, data stored in memory only partially summarizes the properties of patterns, and internal representations of incoming sensory data are likewise imperfect approximations. In other words, pattern recognition is frequently a problem of inference from compressed data. However, excessive compression precludes reliable recognition. This apparent tradeoff raises a fundamental question: In a given environment, what are the least amounts of memory data and sensory data consistent with reliable pattern recognition?

The paper is organized as follows. In Section II, we introduce the general problem informally. Relationships between the present work and other pattern recognition research is briefly described in Section III. In Section IV, we formalize our problem as that of determining which combinations of three key rates are achievable, that is, determining which rate combinations allow the theoretical possibility of reliable pattern recognition. These rates quantify the information available for representing memory and sensory data, and the number of distinct patterns which the recognition system can discriminate. Our main results are single-letter formulas providing inner and outer bounds on the set of achievable rates, presented in Section V. In Section VI, we consider some instructive special cases of the main results, and compare our results to those for the related problem of distributed source coding. In Section VII, we explore explicit formulas for the bounds in two special binary and Gaussian cases. Section VIII contains concluding remarks. Proofs for most of the results are placed in the Appendices. The entire discussion is organized around the block diagram in Fig. 1.

Fig. 1.

Pattern recognition subject to data compression.

II. Informal Problem Statement

In this section, we use an imagined example to motivate the mathematical model studied in the later technical sections. Suppose that our pattern recognition system consists of a homunculus living inside the head of some animal. The homunculus has access to a video monitor which displays data captured by the animal’s retinas, and a set of index cards for storing information about the patterns in the environment relevant to survival, constituting a “memory.” The homunculus must identify each pattern by comparing viewed images with information stored in memory. These identifications are then used to guide the animal’s behavior. Let us consider which factors govern the difficulty of our homunculus’ task.

A. Pattern Rate

First, the number of patterns that must be discriminated, M_c, obviously cannot exceed the number of images registerable on the animal’s retinas, which depends in turn on the number of retinal photoreceptors and the number of distinct signaling states of each photoreceptor. Denoting the state of the retinas as Y = (Y₁, Y₂, …, Y_n), where each Y_i takes values in a finite alphabet $\mathcal{Y}$, the number of possible retinal images is $|\mathcal{Y}{|}^n$. In a very simple animal with n = 8 photoreceptors, each able only to distinguish “bright” (Y = 1) from “dark” (Y = 0) (so $\mathcal{Y}\in \left\{0,1\right\}$), the absolute upper limit on M_c would be $|\mathcal{Y}{|}^n=2^8=256$.

With higher resolution eyes (larger n) an exponential explosion in the number of possible images rapidly overwhelms memory and computational resources. In humans, for whom $\left|\mathcal{Y}\right|\approx 256$, and n ≈ 2 × 10⁶ [1], [2], $|\mathcal{Y}{|}^n~{10}^{2,408,200}$, far exceeding estimates of the number of particles in the universe [3]. Fortunately, two features of real-world pattern recognition intervene: First, sensory data exhibits strong statistical structure, p(y), so that the vast majority of the $|\mathcal{Y}{|}^n$ possible images are never experienced.¹ Second, much of the animal’s visual experience can be filtered out as irrelevant to survival. Thus, we express the number of patterns our homunculus must discriminate as $M_c=|\mathcal{Y}{|}^{n{R}_c^{\prime }}$, where $R_c^{\prime }$ is called the pattern rate, $0<R_c^{\prime }<1$, and generally $M_c\ll |\mathcal{Y}{|}^n$. Equivalently, we can express M_c in binary units, as $M_c=2^{n{R}_c}$, in which case $R_c=R_c^{\prime }{\text{log}}_2\left|\mathcal{Y}\right|$.

B. Sensory Data Compression Rate

Our homunculus accesses sensory data indirectly through a video monitor that has limited display capacity. That is, whereas the retinas can be in up to $|\mathcal{Y}{|}^n$ distinct signaling states, the homunculus’ internal monitor can display at most $M_y=2^{n{R}_y}\ll |\mathcal{Y}{|}^n$, where R_y is thus the sensory data compression rate. Analogous data reductions arise in real recognition problems for various reasons, both computational (e.g., dimensionality reduction, sparsification, regularization, or other “feature extraction” operations), and economic (e.g., energy constraints, processing time constraints, storage limitations). We represent the transformation from retinal data Y to video data J by the action of an encoder ϕ, resulting in the displayed data J = ϕ(Y).

This sensory data compression step places another restriction on the number of discriminable patterns, so that, in general, $M_c\ll M_y\ll |\mathcal{Y}{|}^n$; or $R_c\le R_y\le {\text{log}}_2\left|\mathcal{Y}\right|$.

C. Memory Data Compression Rate

The job of our homunculus is to recognize patterns. More formally, the homunculus must assign to each viewed image Y one of M_c class labels, which we take to be integers ${\mathcal{M}}_c=\left\{1,2,\dots ,M_c\right\}$. As pre-job training, we imagine the homunculus studies a set of labeled class prototypes or “templates,” T(w) = (X(w), w), $w=\left\{1,2,\dots ,M_c\right\}={\mathcal{M}}_c$, each drawn from a distribution p(x), where each template has dimensionality identical to that of the sensory data, X(w) = (X₁(w), …, X_n(w)).

The homunculus creates index cards, on which it writes the class labels and descriptive information about each class template. However, the number of cards and the amount of information per card are limited, allowing only a compressed summary of the available data. We represent the information memorized about a class M(w) as the output of an encoder f, i.e., M(w) = (I(w), w) = f(T(w)), where I(w) is the compressed description of X(w) and w is the memorized class label. The degree of compression is quantified by specifying either the number of index cards comprising the memory, M_x, or by a compression rate (given in bits) $R_x=\frac{1}{n}\text{log}{M}_x$.

As above, memory data compression restricts the number of discriminable patterns M_c, so that $M_c\ll M_x\ll |\mathcal{X}{|}^n$; or, in terms of rates, $R_c\le R_x\le {\text{log}}_2\left|\mathcal{X}\right|$.

D. Image Formation and Testing

The “testing” phase of our homunculus-driven pattern recognition system involves two processes:, image formation and recognition.

Image formation proceeds as follows. Nature selects a pattern class $W\in {\mathcal{M}}_c$ at random, then generates an image Y which is registered on the animal’s retinas. (The class label W is not observable by the homunculus.) We model the image formation process as the transmission of the class template X(w) through a random channel p(y|x). The retinal image Y thus represents a “signature” of the underlying pattern X(w), and the channel p(y|x) represents two types of difficulties intrinsic to most real-world pattern recognition problems: signature variation (differences in the sensory data generated on repeated viewings of the same underlying pattern); and signature ambiguities (distinct patterns may produce similar signatures).²

The homunculus receives the compressed sensory data J = ϕ(Y), compares it with the memory data ${\mathcal{C}}_u=\left\{M(1),\dots ,M\left(M_c\right)\right\}$, and finally reports the class label of the best match, Ŵ. The inference procedure used to make these comparisons can reflect knowledge of the pattern source p(x) and image formation process p(y|x), but at the time of testing, it must be specified so as to depend only on the available data, i.e., g must be function only of ${\mathcal{C}}_u$ and J, $\widehat{W}=g\left(J,{\mathcal{C}}_u\right)$. We judge the homunculus’ performance by the probability of error P_e. We will consider the system reliable if for some acceptable ϵ it achieves P_e ≤ ϵ.

E. Interpretations of the Problem Formulation

We have now introduced the basic elements of our problem, which is to determine the rate combinations (R_x, R_y, R_c) compatible with the possibility of reliable pattern recognition systems, where a “reliable” system is one for which the probability of recognition error can be made arbitrarily small. To summarize, these basic elements are 1) a model for the underlying patterns, consisting of the number of patterns $M_c=2^{n{R}_c}$, a set of class labels w ∈ {1, …, M_c}, and the class prototypes X(w) together with their generative model p(x); 2) a model of the channel connecting class prototypes to the sensory data p(y|x); and 3) budgets specifying the number of bits allowed for representing sensory data R_y and memory data R_x inside the system.

We pause here to consider a few different possible perspectives on the problem under study.

Optimization views.

From an optimization point of view, we can ask our central question in two different but equivalent ways: Given the pattern rate R_c, what are the least amounts of sensory and memory data R_y and R_x, needed for reliable pattern recognition? Alternatively, given fixed information budgets for memory and sensory data representation R_x and R_y, what is the maximum achievable pattern recognition rate R_c?

Regarding “n.”

Second, the problem has a different “feel” depending on whether one views the data dimensionality n either as a fixed or an increasing parameter. In the preceding discussion, we have primarily taken the static view, in which there are a fixed number $M_c=2^{n{R}_c}$ of patterns, or “states of nature” of interest, and the problem is to investigate how many memory states M_x and sensory states M_y are needed to recognize them reliably. Alternatively, we may regard n as a dynamic, increasing parameter. Biologically, allowing n to increase might correspond to studying a series of animals with increasingly better eyes and memory organs. In engineering applications, the increase might correspond to building a sequence of machines with progressively higher camera resolution and data storage capacities [6]. Obviously, if while increasing n we hold the bit-budgets R_x and R_y fixed, then the number of memory and sensory states available for data representation grows exponentially, $M_x=2^{n{R}_x}$, $M_y=2^{n{R}_y}$. Less obviously, the maximum number of discriminable patterns also grows exponentially,³ with a constant rate R_c, i.e., $M_c=2^{n{R}_c}$. The “fixed n” and “increasing n” perspectives correspond to the familiar, complementary mathematical methods of proving a given inequality, respectively, either by the “adversarial” approach (given any ϵ, choose n large enough…); or the “asymptotic approach” (take the limit as n → ∞…).

An important final point regarding n is that, like many results in information theory, our results rely on asymptotic arguments. Thus, we only prove the results valid only for “sufficiently large n,” depending in turn on an ϵ corresponding to the tolerable error rate. The needed magnitude of n for a given ϵ (i.e., the issue of error exponents) will depend on the application, and is an important open problem.

III. Related Work

A. Machine Learning Approaches

Pattern recognition is a central topic in machine learning [7]–[10]. The machine learning approach to pattern recognition centers around the following problem: Given a set of labeled sensory data $\mathcal{D}=\left\{Y(i),w(i),i=1\dots N\right\}$, we wish to find a rule g that predicts the labels for future sensory data, i.e., if Y is in fact a signature of pattern class w ∈ {1, 2, …, M_c}, we want Pr(g(Y) ≠ W) ≤ ϵ for some acceptable ϵ > 0. Broadly speaking, two competing approaches dominate the literature. In the “generative modeling” approach, one attempts to estimate the distribution underlying the data p(w, y), and then to use the conditional distribution p(w, y) to infer w from Y, i.e., $\widehat{w}=g(Y)=\text{arg}{\text{max}}_{w\in M_c}p(w|Y)$. Alternatively, in the “discriminative” approach, one attempts to learn the optimal decision region boundaries directly, without estimating p(w, y).

Our problem formulation resonates with the “generative modeling” approach, in that we allow the homunculus access to p(w, y).⁴ Informally, such knowledge might come from allowing a very large volume of training data. Nevertheless, the distinction between generative and discriminative approaches then may become practically unimportant, as in many instances either approach can achieve asymptotically optimal performance.

In any case, in the present work we are not directly concerned with the problem of classifier learning. Rather, we investigate the conditions under which reliable classifiers can exist at all, regardless of how they are deigned or learned; we describe performance bounds to which all pattern recognition systems are subject.

It is also worth pointing out the distinction between the machine learning concept of “Vapnik–Chervonenkis (VC) dimension” and M_c in the present work. Informally, the VC dimension is the number of distinct patterns that can be shattered by a given family of classifiers (see [10], [12] for a detailed description). As such, VC dimension is a measure of the complexity of the decision boundaries that can be fit with a given family of classifiers. In contrast, M_c in our work is the number of patterns or pattern classes that can be distinguished, with no constraints on the family of classifiers.

B. Related Work in Combined Data Compression and Inference

Neuroscientist Horace Barlow has argued for more than four decades that data compression is an essential principle underlying learning and intelligent behavior in animal brains (see, e.g., [13]–[17]). Barlow and many others have amassed substantial experimental evidence showing efficient data coding mechanisms at work in the sensory systems of diverse animals, including monkeys, cats, frogs, crickets, and flies [18]. More recently, data compression is gaining appreciation as a mechanism for managing metabolic energy costs in neural systems [19].

In the engineering pattern recognition literature, data compression usually arises indirectly in the context of feature extraction, i.e., techniques for transforming raw data such that “irrelevant” data is discarded and the residual data is rendered into some advantageous format which facilitates storage and comparison, and is robust (“invariant”) with respect to signature variations [20], [21]. In the information theory literature, probably the first direct investigation of the interplay between data compression and statistical inference is due to Ahlswede and Csiszár [22]. In [23] Han and Amari reviewed work up through 1998 on rate-constrained inference problems, including hypothesis testing, pattern recognition, and parameter estimation. Recently, Ishwar et al. have studied the problem of joint classification and reconstruction of sensory data subject to a fidelity constraint, in the context of video coding [24], [25]. In contrast to the problem studied in this paper, in that work there is no data compression constraint on memory data. Work on practical algorithms for joint classification and data compression includes [26]–[28].

IV. Problem Statement

We now proceed to the formal presentation of the main results.

A. Notation

We adopt the following notational conventions. Random variables are denoted by capital letters (e.g., U), their values by lowercase letters (e.g., u), their alphabets by script capital letters (e.g., $\mathcal{U}$). Sequences of symbols are denoted either by boldface letters or with a superscript, e.g., u = uⁿ = (u₁, u₂, …, u_n). The probability distribution for a random variable $U\in \mathcal{U}$ is denoted by pU(u), or p(u) simply when the implied subscript is clear from the context. Entropy, mutual information, and conditional mutual information are denoted in the usual ways, e.g., for random variables U, V, W, we write H(U), I(U; V), and I(U; V|W), respectively. All logarithms are understood to be base two, i.e., log = log₂. Finally, to express statements such as “X and Z are conditionally independent given Y,” i.e., p(x, y, z) = p(y) p(x | y)p(z | y), we write “X – Y – Z form a Markov chain,” or simply X −.Y – Z.

B. Definitions and Assumptions

Definition 1: The environment $\mathcal{E}$ for a pattern recognition system is a set of eight objects

$$\mathcal{E}=\left\{{\mathcal{M}}_c,\mathcal{X},\mathcal{Y},p(x),p(y|x),p(w),{\mathcal{C}}_x,\mathrm{\Phi }\right\}$$

where

• ${\mathcal{M}}_c$, $\mathcal{X}$, $\mathcal{Y}$ are finite alphabets;

• p(w), p(xy) = p(x)p(y|x), are probability distributions over ${\mathcal{M}}_c$, and ${\mathcal{X}}^n\times {\mathcal{Y}}^n$, respectively;

• ${\mathcal{C}}_x=\left\{T(1),\dots T\left(M_c\right)\right\}$ is a set of pairs T(w) = (X(w), w) of random vectors X(w) drawn independent and identically distributed (i.i.d.) ~p(x), labeled by $w\in \left\{1,2,\dots ,M_c\right\}={\mathcal{M}}_c$;

• Φ is a mapping from labels ${\mathcal{M}}_c$ to vectors in ${\mathcal{C}}_x$, $\mathrm{\Phi }:{\mathcal{M}}_c\to {\mathcal{C}}_x$, Φ(w) = X(w).

We make the following simplifications:

• the distribution over class labels is uniform, $p\left(w\right)=1/\left|{\mathcal{M}}_c\right|$ for all $w\in {\mathcal{M}}_c$;

• the pattern components are i.i.d., $p(x)={\prod }_{i=1}^{n}p\left(x_i\right)$;

• the observation channel is memoryless, $p(y|x)={\prod }_{i=1}^{n}p\left(y_i|x_i\right)$.

Definition 2: An (M_c, M_x, M_y, n) pattern recognition code for an environment $\mathcal{E}$ consists of three sets of integers

$${\mathcal{M}}_c=\left\{1\dots M_c\right\},{\mathcal{M}}_x=\left\{1\dots M_x\right\},{\mathcal{M}}_y=\left\{1\dots M_y\right\}$$

and three mappings

$$\begin{gathered} f:{\mathcal{X}}^n\times {\mathcal{M}}_c\to {\mathcal{M}}_x\times {\mathcal{M}}_c,f(t(w))=f(x,w)=(i,w)\triangleq m(w) \\ \varphi :{\mathcal{Y}}^n\to {\mathcal{M}}_y,\varphi (y)=j \\ g:{\mathcal{M}}_y\times {\left({\mathcal{M}}_x\right)}^{M_c}\to {\mathcal{M}}_c,g\left(j,{\mathcal{C}}_u\right)=\widehat{w} \end{gathered}$$

where ${\mathcal{C}}_u$ denotes the result of applying f to the entries of ${\mathcal{C}}_x$

$${\mathcal{C}}_u=\left\{f(T(1)),\dots ,f\left(T\left(M_c\right)\right)\right\}=\{m(1),\dots ,m\left(M_c\right)).$$

We call ${\mathcal{C}}_x$ the pattern templates; f, the memory encoder; ${\mathcal{C}}_u$, the memorized data; ϕ, the sensory encoder; and g, the recognition function or classifier.

Definition 3: The operation of a pattern recognition system (“agent”) implementing a given (M_c, M_x, M_y, n) pattern recognition code (f, ϕ, g) for an environment $\mathcal{E}$ is defined in terms of the following events.

Memorization phase:

• The agent observes ${\mathcal{C}}_x$, and uses f to compute the memory data ${\mathcal{C}}_u$.

• Access to ${\mathcal{C}}_x$ is taken away, and thereafter the agent knows of ${\mathcal{C}}_x$ only what is retained in ${\mathcal{C}}_u$.

Testing phase

• Nature selects an index W ~ p(w).

• Nature encodes the pattern according to X(W) = Φ(W).

• The pattern X(W)passes through the channel p(y|x), giving rise to an observable signal Y.

• The agent computes J = ϕ(Y).

• The agent infers W by computing $\widehat{W}=g\left(J,{\mathcal{C}}_u\right)$.

With respect to the events just described, the probability of error for a code (f, ϕ, g) in $\mathcal{E}$ is

$$P_e^n(w)=\text{Pr}(\widehat{W}\ne w|W=w)$$

and the average probability of error of the code is

$$\begin{gathered} P_e^n=\sum _{w\in {\mathcal{M}}_c}p(w)\text{Pr}(\widehat{W}\ne w|W=w) \\ =\frac{1}{M_c}\sum _{w\in {\mathcal{M}}_c}{P}_e^n(w). \end{gathered}$$

Definition 4: The rate R = (R_c, R_x, R_y) of an (M_c, M_x, M_y, n) code is

$$R_c=\frac{1}{n}{\text{log}}_2{M}_c,R_x=\frac{1}{n}{\text{log}}_2{M}_x,R_y=\frac{1}{n}{\text{log}}_2{M}_y$$

where the units are bits-per-symbol.

Definition 5: A rate R = (R_c, R_x, R_y) is achievable in a recognition environment $\mathcal{E}$ if for any ϵ > 0 and for n sufficiently large, there exists an (M_c, M_x, M_y, n) code (f, ϕ, g) with rates

$$R_c^{\prime }=\frac{1}{n}\text{log}{M}_c,R_x^{\prime }=\frac{1}{n}\text{log}{M}_x,R_y^{\prime }=\frac{1}{n}\text{log}{M}_y$$

such that $R_c^{\prime }\ge R_c$, $R_x^{\prime }\le R_x$, $R_y^{\prime }\le R_y$ and $P_e^n<ϵ$.

Definition 6: The achievable rate region $\mathcal{R}$ for a recognition environment $\mathcal{E}$ is the set of all achievable rates R = (R_c, R_x, R_y).

Our ultimate goal in an information-theoretic analysis of this problem is to characterize the achievable rate region $\mathcal{R}$ in a way that does not involve the unbounded parameter n, that is, to exhibit a single-letter characterization of $\mathcal{R}$.

V. Main results

In this section, we present inner and outer bounds on the achievable rate region $\mathcal{R}$. The bounds are expressed in terms of sets of “auxiliary” random variable pairs UV, defined below. In these definitions, U and V are assumed to take values in finite alphabets $\mathcal{U}$ and $\mathcal{V}$ and have a well-defined joint distribution with the “given” random variables XY. To each such pair of auxiliary random variables UV we associate a set of rates

$${\mathcal{R}}_{UV}=\left\{R:R_x\ge I(U;X)R_y\ge I(V;Y)R_c\le R_x+R_y-I(XY;UV)\right\}.$$

Next, define two sets of random variable pairs

$${\mathcal{P}}_{\text{in }}=\left\{UV:U-X-Y,X-Y-V,U-\text{(}X\text{, }Y\text{)}-V\right\},$$

and

$${\mathcal{P}}_{\text{out}}=\left\{UV:U-X-Y,X-Y-V\right\}.$$

We will also sometimes summarize the independence constraints in ${\mathcal{P}}_{\text{in}}$ as a single “long” Markov chain U – X − Y − V.

Next, define two additional sets of rates

$$\begin{gathered} {\mathcal{R}}_{\text{in}}=\left\{R:R\in {\mathcal{R}}_{UV}\text{ for some }UV\in {\mathcal{P}}_{\text{in}}\right\} \\ {\mathcal{R}}_{\text{out }}=\left\{R:R\in {\mathcal{R}}_{UV}\text{ for some }UV\in {\mathcal{P}}_{\text{out}}\right\} \end{gathered}$$

and denote the convex hull of ${\mathcal{R}}_{\text{in}}$ by ${\overline{\mathcal{R}}}_{\text{in}}$.

Our main results are the following.

Theorem 1 (Inner Bound):

$${\mathcal{R}}_{\text{in}}\subseteq \mathcal{R}.$$

That is, every rate $R\in {\mathcal{R}}_{\text{in}}$ is achievable.

Theorem 2 (Better Inner Bound):

$${\overline{\mathcal{R}}}_{\text{in}}\subseteq \mathcal{R}$$

That is, every rate $R\in {\overline{\mathcal{R}}}_{\text{in}}$ is achievable.

Theorem 3 (Outer Bound):

$${\mathcal{R}}_{\text{out}}\supseteq \mathcal{R}.$$

That is, no rate $R\notin {\mathcal{R}}_{\text{out}}$ is achievable.

Finally, to ensure computability, we include a cardinality bound.

Theorem 4: Regions ${\mathcal{R}}_{\text{in}}$ and ${\mathcal{R}}_{\text{out}}$ are unchanged if we restrict the cardinality of $\mathcal{U}\mathcal{V}$ to

$$\left|\mathcal{U}\right|\left|\mathcal{V}\right|\le \left|\mathcal{X}\right|\left|\mathcal{Y}\right|+2.$$

Theorem 4 is a simple consequence of the Support Lemma [29 (p. 310)]: we must have $\left|\mathcal{X}\Vert \mathcal{Y}\right|-1$ letters to ensure preservation of p(xy|uv), and three additional letters to satisfy the constraints on I(X; U), I(Y; V) and I(XY; UV).

Remark 1: If either X = U or Y = V, or both, then the outer bound collapses to the inner bound, since in this case the extra Markov condition U – (X, Y) – V in the definition of ${\mathcal{P}}_{\text{in}}$ is extraneous. For example, if U = X, then the condition is equivalent to I(U; V | XY) = I(X; V | XY) = 0, which is obviously true. Similar comments apply if U and V are any deterministic functions of X and Y, e.g., if V = γ(Y), then I(U; V | XY) = I(U; γ(Y)|XY) = 0.

Remark 2: The bounds ${\mathcal{R}}_{\text{in}}$ and ${\mathcal{R}}_{\text{out}}$ can be expressed in various ways. For example, it is not difficult to show that the following replacements for ${\mathcal{R}}_{UV}$ lead to the same sets of rates ${\mathcal{R}}_{\text{in}}$ and ${\mathcal{R}}_{\text{out}}$:

$${\mathcal{R}}_{UV}^{\prime }=\left\{R:R_x\ge I(U;X)R_y\ge I(V;Y)R_c\le I(U;V)-I(U;V|XY)\right\}$$ (1)

$${\mathcal{R}}_{UV}^{″}=\left\{R:R_c\le I(U;V)-I(U;V\left|XY)R_x\ge I(XY;U\right|V)+R_c{R}_y\ge I(XY;V|U)+R_c{R}_x+R_y\ge I(XY;UV)+R_c\right\}.$$ (2)

That is, if we define

$$\begin{gathered} {\mathcal{R}}_{*}^{\prime }=\left\{R:R\in {\mathcal{R}}_{UV}^{\prime }\text{ for some }UV\in {\mathcal{P}}_{*}\right\} \\ {\mathcal{R}}_{*}^{″}=\left\{\mathit{R}:\mathit{R}\in {\mathcal{R}}_{UV}^{″}\text{ for some }UV\in {\mathcal{P}}_{*}\right\} \end{gathered}$$

where * stands for either “in” or “out,” then ${\mathcal{R}}_{\text{in}}={\mathcal{R}}_{\text{in}}^{\prime }={\mathcal{R}}_{\text{in}}^{″}$, and ${\mathcal{R}}_{\text{out}}={\mathcal{R}}_{\text{out}}^{\prime }={\mathcal{R}}_{\text{out}}^{″}$. These equivalencies are proved in Appendix E, and are used in Sections VI-B and VII.

Remark 3: In general, ${\mathcal{R}}_{\text{in}}$ is not a convex set, as evidenced by the examples studied in Section VIII. Thus, ${\overline{\mathcal{R}}}_{\text{in}}$ is in fact an improvement on ${\mathcal{R}}_{\text{in}}$. ${\mathcal{R}}_{\text{out}}$ is a convex set, as shown in Appendix C.

The proofs for Theorems 2 and 3 appear in Appendices A and B. Theorem 1 follows immediately from Theorem 2. In sketch-form, the method we use to prove achievability (the inner bound), based on ${\mathcal{R}}^{\prime }UV$ (1), is as follows. We represent the memory and sensory data using codewords U(i), $i\in \left\{1\dots 2^{n{R}_x}\right\}$ and V(i), $j\in \left\{1\dots 2^{n{R}_y}\right\}$ that are typical according to p(u) and p(v), respectively, and the recognition system stores a list of these codewords. Making R_x ≥ I(X; U) and R_y ≥ I(Y; V) provides enough U’s and V’s to “cover” ${\mathcal{X}}^n$ and ${\mathcal{Y}}^n$. During pretesting, the system matches each of the labeled template patterns (X(w), w), w = 1, …, M_c presented to it with a unique memory codeword, and attaches to this codeword the corresponding class label (with matching defined in the sense of joint typicality according to p(xu)). The resulting set of M_c “active,” labeled codewords constitutes the system’s memory. During subsequent testing, suppose Nature selects class w, generating sensory data Y ~ p(y|X(w)). The system receives the index J of the codeword for Y, and uses it to retrieve the sensory codeword V(J). The system can then narrow down the list of M_c active memory codewords by a factor of 2^{−nI(U; V)} using knowledge of p(uv).⁵ Thus, the correct memory vector U(w) can be uniquely identified so long as $M_c=2^{n{R}_c}\le 2^{nI(U;V)}$, i.e., if R_c ≤ I(U; V).

It is also possible to prove the achievability result using a binning argument, which induces the set ${\mathcal{R}}_{UV}^{″}$ (2): Generate 2^{nI(X; V)} U’s and 2^{nI(Y; V)}V’s, and divide these equally among roughly $2^{n{R}_x}$ and $2^{n{R}_y}$ bins each, respectively. A pattern X(w) is encoded in memory by searching for a bin containing a matching (jointly typical) codeword U(X), and the $M_c=2^{n{R}_c}$ bins thus selected are each assigned the class label w of the pattern stored therein. Sensory data Y is encoded as the bin index of a matching codeword V(Y). This number of U’s and V’s is sufficient to ensure that any given pair X and Y will have a matching (jointly typical) U(X), and V(Y), and the Markov lemma ensures joint typicality of the quadruple (U(X), X, Y, V(Y)). Given encoded sensory data J = ϕ(Y), recognition is done by comparing the roughly $2^{nI(Y;V)}/2^{n{R}_y}$ sensory codewords in bin J with the $2^{nI(X;U)}/2^{n{R}_x}$ memory codewords in each of the $2^{n{R}_c}$ memory bins, then reporting the class label $\widehat{w}$ assigned to the bin containing the matching memory codeword. No matches other than the correct one, (U(X), V(Y)), will be found provided the number of (U, V) comparisons grows exponentially with n at a rate less than I(U; V), that is, provided I(Y; V) − R_y + I(X; U) – R_x + R_c ≤ I(U; V), which simplifies to the rate–sum constraint R_x + R_y ≥ I(XY; UV) + R_c. The “side” constraints R_x ≥ I(XY; U|V) + R_c and R_y ≥ I(XY; V|U) + R_c then follow from requiring that each bin contain at least one codeword. The final inequality R_c ≤ I(U; V) follows from the first three.

VI. Discussion of the Main Results

A. The Gap Between Bounds

In general, there is a gap between ${\mathcal{R}}_{\text{in}}$ and ${\mathcal{R}}_{\text{out}}$, so that ${\mathcal{R}}_{\text{in }}⊊\mathcal{R}⊊{\mathcal{R}}_{\text{out }}$. This gap is due to the different constraints in the definitions of ${\mathcal{P}}_{\text{in}}$ and ${\mathcal{P}}_{\text{out}}$: Whereas distributions in satisfy three independence constraints U – X – Y, X – Y – V, and U – (X, Y) – V (equivalently, the single “long chain” constraint U – X – Y – V), distributions in ${\mathcal{P}}_{\text{out}}$ only need satisfy the first two “short chain” constraints.

Further insight into the nature of the gap can be gained by attempting to construct ${\mathcal{P}}_{\text{out}}$ by combining distributions from ${\mathcal{P}}_{\text{in}}$ in various ways, and then considering whether the resulting distributions can be used to expand the achievable rate region.⁶ We consider two such constructions. In both, let $Q\in \mathcal{Q}$ be a finite random variable, independent of X and Y. Holding p(xy) fixed, to describe a pair of auxiliary random variables $U\in \mathcal{U}$, $V\in \mathcal{V}$ with joint distribution p(xyuv), we need only to specify the marginal distribution p(uv | xy). Consider the following two sets:

$${\mathcal{P}}_{\text{mix}}=\left\{UV:p(uv|xy)=\sum _{q\in \mathcal{Q}}p(q)p(u\left|xq)p(v\right|yq)\right\}$$ (3)

$${\mathcal{P}}_{\text{conv}}=\left\{UV:U=\left(U_Q,Q\right),V=\left(V_Q,Q\right),U_q{V}_q\in {\mathcal{P}}_{\text{in }}\forall q\in \mathcal{Q}\right\}.$$ (4)

In words, ${\mathcal{P}}_{\text{mix}}$ is the set of UV whose distributions p(uv | xy) can be constructed as “mixtures” of product marginals; and ${\mathcal{P}}_{\text{conv}}$ is the set of “convexifying” random variables (this terminology is explained below).⁷ In both of these sets it is possible to have dependencies between U and V given XY; i.e., in general p(uv | xy) ≠ p(u | x) p(v | y), hence, in general, ${\mathcal{P}}_{\text{mix}}$, ${\mathcal{P}}_{\text{conv}}⊋{\mathcal{P}}_{\text{in}}$.

There is a gap similar to the one under discussion between the best known bounds for the distributed source coding problem (DSC), established by Berger and Tung (see Section VI-B). In both problems, the bounds are given in terms of sets with independence (Markov) constraints identical to those in ${\mathcal{P}}_{\text{in}}$ and ${\mathcal{P}}_{\text{out}}$.⁸ Berger has suggested that in the DSC problem the gap is due to the fact that ${\mathcal{P}}_{\text{out}}$ admits convex mixtures of product marginal distributions, whereas ${\mathcal{P}}_{\text{in}}$ does not; i.e., in our notation, ${\mathcal{P}}_{\text{in}}⊊{\mathcal{P}}_{\text{mix}}\subseteq {\mathcal{P}}_{\text{out}}$ [31]. The inclusion ${\mathcal{P}}_{\text{mix}}\subseteq {\mathcal{P}}_{\text{out}}$ is verified by checking U – X – Y and X – Y – V: Write

$$\begin{gathered} p(u|xy)=\sum _{v}p(uv|xy) \\ =\sum _{q}p(q)p(u|xq)\sum _{v}p(v|yq) \\ =\sum _{q}p(q)p(u|xq) \\ \triangleq p(u|x) \end{gathered}$$

hence, U – X – Y; and a symmetric calculation shows X – Y – V. While clearly ${\mathcal{P}}_{\text{mix}}$ is a larger set than ${\mathcal{P}}_{\text{in}}$, it is unclear whether the admission of mixtures can account for all of the gap between ${\mathcal{P}}_{\text{in}}$ and ${\mathcal{P}}_{\text{out}}$. That is, we know of no proof that ${\mathcal{P}}_{\text{mix}}={\mathcal{P}}_{\text{out}}$. Moreover, we know of no way to use auxiliary random variables from ${\mathcal{P}}_{\text{mix}}$ in achievability arguments.

It is also straightforward to verify that the second set ${\mathcal{P}}_{\text{conv}}$ is contained in ${\mathcal{P}}_{\text{out}}$

$$\begin{gathered} I(U;Y|X)=I\left(U_Q,Q;Y|X\right) \\ =I(Q;Y|X)+I\left(U_Q;Y|X,Q\right) \\ \stackrel{(\text{a})}{=}0+\sum _{q}p(q)I\left(U_q;Y|X,Q=q\right) \\ \stackrel{(\text{b})}{=}0 \end{gathered}$$

(where the reasons are: (a) Q is independent of X and Y, and (b) $U_q{V}_q\in {\mathcal{P}}_{\text{in}}$; hence, U – X – Y; and a symmetric calculation shows X − Y − V. ${\mathcal{P}}_{\text{conv}}$ has a form sometimes introduced in time-sharing arguments, as a means to convexify a given rate region. For example, for $UV\in {\mathcal{P}}_{\text{conv}}$, we have

$$\begin{gathered} I(XY;UV)=I\left(XY;U_Q,V_Q,Q\right) \\ =I(XY;Q)+I\left(XY;U_Q;V_Q|Q\right) \\ \stackrel{(\text{a})}{=}\sum _{q}p(q)I\left(XY;U_q{V}_q|Q=q\right) \\ \triangleq \sum _{q}p(q)I\left(XY;U_q{V}_q\right) \end{gathered}$$

(where (a) is because Q is independent of X and Y) and similarly I(X; U) = Σ_qp(q)I(X; U_q), and I(Y; V) = Σ_qp(q)I(Y; V_q). It follows that the convex hull of ${\mathcal{R}}_{\text{in}}$ may be represented as

$${\overline{\mathcal{R}}}_{\text{in}}=\left\{R:R\in {\mathcal{R}}_{UV}\text{ for some }UV\in {\mathcal{P}}_{\text{conv}}\right\}.$$ (5)

In contrast to ${\mathcal{P}}_{\text{mix}}$, auxiliary variables from ${\mathcal{P}}_{\text{conv}}$ can be used as the basis for standard achievability arguments, as we have done in the proof of Theorem 2 (see Appendix A). From this, we have the following logical statement:

$$\begin{gathered} \text{If }{\mathcal{P}}_{\text{out }}={\mathcal{P}}_{\text{conv}} \\ \text{then }{\mathcal{R}}_{\text{out}}={\overline{\mathcal{R}}}_{\text{in}}. \end{gathered}$$ (6)

Unfortunately, we have no proof that ${\mathcal{P}}_{\text{out}}={\mathcal{P}}_{\text{conv}}$. Notwithstanding, in Subsection VII-A, we examine one case where it appears that ${\mathcal{R}}_{\text{out}}={\overline{\mathcal{R}}}_{\text{in}}$ does hold, giving grounds to conjecture that this equality may hold at least under special conditions.

B. Relationship With Distributed Source Coding

There are interesting connections between the results of Tung and Berger [32], [33] for the DSC problem and our results in Theorems 1 and 3. Briefly, the situation treated in the DSC problem is as follows (see Fig. 2). Two correlated sequences, X and Y, are encoded separately as i = f(X), j = ϕ(Y) and the decoder g must reproduce the original sequences subject to a fidelity constraint $\left(E{d}_x(\widehat{X},X),E{d}_y(\widehat{Y},Y)\right)\le D$, where D = (D_x, D_y). The problem is to characterize, for any given distortion D, the set of achievable rates $\tilde{\mathcal{R}}(D)$.

Fig. 2.

The distributed source coding problem.

The best known inner and outer bounds for the DSC problem can be expressed as follows.⁹ Let ${\mathcal{P}}_{\text{in}}$ and ${\mathcal{P}}_{\text{out}}$ be defined as above, and define two new sets incorporating the distortion constraint

$$\begin{gathered} {\mathcal{P}}_{\text{in }}(D)={\mathcal{P}}_{\text{in }}\cap {\mathcal{P}}_{UV}(D) \\ {\mathcal{P}}_{\text{out }}(D)={\mathcal{P}}_{\text{out }}\cap {\mathcal{P}}_{UV}(D) \end{gathered}$$

where

$${\mathcal{P}}_{UV}(D)=\left\{UV:\exists \widehat{X}(U,V),\widehat{Y}(U,V)\text{ s.t.}\left(E{d}_x(\widehat{X},X),E{d}_y(\widehat{Y},Y)\right)\le D\right\}.$$

Parallelling (1), also define the sets of rates

$${\tilde{\mathcal{R}}}_{UV}=\left\{R:R_x\ge I(XY;U|V)R_y\ge I(XY;V|U)R_x+R_y\ge I(XY;UV)\right\}$$ (7)

and

$$\begin{gathered} {\tilde{\mathcal{R}}}_{\text{in }}(D)=\left\{R:R\in {\tilde{\mathcal{R}}}_{UV}\text{ for some }UV\in {\mathcal{P}}_{\text{in }}(D)\right\} \\ {\tilde{\mathcal{R}}}_{\text{out }}(D)=\left\{R:R\in {\tilde{\mathcal{R}}}_{UV}\text{ for some }UV\in {\mathcal{P}}_{\text{out }}(D)\right\}. \end{gathered}$$

Then the Berger–Tung bounds for the DSC problem are ${\tilde{\mathcal{R}}}_{\text{in }}(D)\subseteq \tilde{\mathcal{R}}(D)$ and ${\tilde{\mathcal{R}}}_{\text{out}}(D)\supseteq \tilde{\mathcal{R}}(D)$.

There are strong formal similarities between our bounds and the DSC bounds. Most importantly, the gap between bounds for both problems is due to the difference between the length-four constraint U − X − Y − V and the less stringent length-three constraints U − X – Y, X − Y − V. Further, note the formal similarity between the sets ${\tilde{\mathcal{R}}}_{UV}$ (7) and ${\mathcal{R}}_{UV}^{\prime \prime }$. To carry this comparison further, suppose in the problem under study that, in addition to recognizing patterns, we also wish to reproduce an estimate of the original signals subject to a fidelity constraint, as in the DSC problem.¹⁰ Denote the achievable rate region for this “joint recognition and recovery” problem by $\mathcal{R}(D)$. Making this addition in fact adds little technical difficulty, and the resulting bounds can be expressed, not surprisingly, as ${\mathcal{R}}_{\text{in}}(D)\subseteq \mathcal{R}(D)$ and ${\mathcal{R}}_{\text{out}}(D)\supseteq \mathcal{R}(D)$, where

$$\begin{gathered} {\mathcal{R}}_{\text{in}}(D)=\left\{R:R\in {\mathcal{R}}_{UV}\text{ for some }UV\in {\mathcal{P}}_{\text{in}}(D)\right\} \\ {\mathcal{R}}_{\text{out}}(D)=\left\{R:R\in {\mathcal{R}}_{UV}\text{ for some }UV\in {\mathcal{P}}_{\text{out}}(D)\right\}. \end{gathered}$$

Apparently, the pattern recognition problem can be construed as a kind of generalization of the DSC problem, with the added complication that the “decoder” receives with Y not one sequence X but $M_c=2^{n{R}_c}$ such sequences X(1),…,X(M_c) and must first determine which is the appropriate one with which to jointly decode Y. This extra discrimination evidently requires that extra information be included at the encoders. This “rate excess” is the difference between the minimum encoding rates required for the DSC and pattern recognition problems.¹¹ Comparing ${\mathcal{R}}_{UV}^{\prime \prime }$ (7) with ${\tilde{\mathcal{R}}}_{UV}$ (7), this rate excess is the same at both decoders, and is equal to R_c. Thus, R_c can be interpreted as the number of extra bits needed at both encoders to decide which of the possible $M_c=2^{n{R}_c}$ patterns X(w) the sensory data Y represents, beyond the information required to simply reproduce the pair Y, X(w) within the allowed distortion limits.

C. Degenerate Cases

We now briefly examine the degenerate cases where either X = U, or Y = V, or both. In these cases, I(U; V | XY) = 0. Hence, using (1), we see that both inner and outer bounds on $\mathcal{R}$ both reduce to the three inequalities R_x ≥ I(U; X), R_y ≥ I(V; Y), R_c ≤ I(U; V)}. Clearly, in these cases the bounds are tight, in that the inner and outer bounds are equal; there is no gap (see Remark 1). These degenerate cases have simple interpretations and are thus useful for building intuition about Theorems 1–3.

Sharp memory, sharp eyesight.

First, consider a system in which the budgets for memory and sensory representations are unrestricted, i.e., no compression is required. In this case, we can effectively treat the memories and sensory representations as veridical; i.e., we can set U = X and V = Y. The theorem constraints then become R_x ≥ I(X; X) = H(X), R_y ≥ I(Y; Y) = H(Y), and

$$R_c\le I(U;V)=I(X;Y).$$ (8)

This result indicates that, in the absence of compression, the recognition problem is formally equivalent to the following classical communication problem: Transmit one of $M_c=2^{n{R}_c}$ possible messages (patterns) to a receiver (the recognition module) [6]. In this case, the patterns can be thought of as random codewords stored without compression and available to the decoder; Shannon’s random coding for communication [30], [34] applies, yielding the mutual information I(X; Y) (see (8)) as the bound on R_c.

Sharp memory, poor eyesight.

Next, suppose that memory is effectively unlimited, so that we can put U = X, but sensory data may be compressed. In this case, we can readily rewrite the condition on R_c as

$$R_c\le I(X;Y)-I(X;Y|V)=I(X;V).$$ (9)

We check the extreme cases: If V is fully informative about Y, Y = ϕ⁻¹(V), then I(X; Y | V) = H(Y | V)−H(Y | X, V) = 0, and we recover the case discussed above, R_c ≤ I(X; Y). For intermediate cases, where V is partially informative, the effect of V is to degrade the achievable performance of the system below that possible with “perfect senses,” and the reduction incurred is I(X; Y | V). In the extreme case that V is utterly uninformative (e.g., a constant V = 0, or otherwise independent of Y), I(X; Y | V) = I(X; Y), and we get R_c = 0, or $M_c\le 2^{n{R}_c}=1$; hence, the system is useless.

Poor memory, sharp eyesight.

In the case of limited memory but unrestricted resources for sensory data representation (V = Y), we get an expression symmetric with the previous case

$$R_c\le I(X;Y)-I(X;Y|U)=I(U;Y).$$ (10)

As before, if the memory is perfect (U = X), we get I(X; Y | U) = I(X; Y | X) = 0, recovering the channel coding constraint R_c ≤ I(X; Y); assuming useless memories (U = 0) yields R_c ≤ I(X; Y) − I(X; Y) = 0; and intermediate cases place the system between these extremes.

VII. Examples

In this section, we investigate the achievable rate regions for binary and Gaussian versions of our problem. For this purpose, it will be convenient to characterize the sets $\mathcal{R}$, ${\mathcal{R}}_{\text{in}}$ and ${\mathcal{R}}_{\text{out}}$ by their surfaces in the positive orthant ${ℝ}_{+}^3$. The surface of $\mathcal{R}$ can be expressed as

$$\begin{gathered} r\left(r_x,r_y\right)=\underset{R\in \mathcal{C}\left(r_x,r_y\right)}{\text{max}}{R}_c \\ \mathcal{C}\left(r_x,r_y\right)=\left\{R:R\in \mathcal{R},R_x=r_x,R_y=r_y\right\}. \end{gathered}$$

Similarly, by direct extension of Theorems 1 and 3, and using the representation of ${\mathcal{R}}_{\text{in}}$ and ${\mathcal{R}}_{\text{out}}$ based on ${\mathcal{R}}_{UV}^{\prime }$ (1), the surfaces of ${\mathcal{R}}_{\text{in}}$ and ${\mathcal{R}}_{\text{out}}$ are

$$r_{\text{in}}\left(r_x,r_y\right)=\underset{UV\in {\mathcal{C}}_{\text{in }}\left(r_x,r_y\right)}{\text{max}}I(U;V)-I(U;V|XY)$$ (11)

$$r_{\text{out}}\left(r_x,r_y\right)=\underset{UV\in {\mathcal{C}}_{\text{out }}\left(r_x,r_y\right)}{\text{max}}I(U;V)-I(U;V|XY)$$ (12)

where

$$\begin{gathered} {\mathcal{C}}_{\text{in}}\left(r_x,r_y\right)=\left\{UV\in {\mathcal{P}}_{\text{in}}:I(U;X)=r_x,I(V;Y)=r_y\right\} \\ {\mathcal{C}}_{\text{out}}\left(r_x,r_y\right)=\left\{UV\in {\mathcal{P}}_{\text{out}}:I(U;X)=r_x,I(V;Y)=r_y\right\} \end{gathered}$$

The expression for the inner bound surface (11) reduces to

$$r_{\text{in}}=\underset{UV\in {\mathcal{C}}_{\text{in}}\left(r_x,r_y\right)}{\text{max}}I(U;V).$$

An alternative expression for the outer bound surface which will be used in Subsection VII-B, based on R_UV (1), is

$$r_{\text{in}}=r_x+r_y-\underset{UV\in {\mathcal{C}}_{\text{in}}\left(r_x,r_y\right)}{\text{min}}I(XY;UV).$$ (13)

Finally, denote the convex hull of the inner and outer bound surfaces $\overline{r_{\text{in}}}\left(r_x,r_y\right)$, $\overline{r_{\text{out }}}\left(r_x,r_y\right)$.

In the specific cases studied in the following examples we seek to convert these implicit characterizations into explicit formulas not involving the optimization over ${\mathcal{C}}_{\text{in}}\left(r_x,r_y\right)$ and ${\mathcal{C}}_{\text{out}}\left(r_x,r_y\right)$.

A. Binary Case

We first investigate the inner and outer bound surfaces for a case in which the template patterns and sensory data alphabets are binary, $\mathcal{X}=\mathcal{Y}=\left\{0,1\right\}$. Let the template patterns X = (X₁,…,X_n) consist of n independent drawings from a uniform Bernoulli distribution X_i ~ B(1/2), i = 1…n, and let the sensory data Y = (Y₁,…,Y_n) be the output of a binary-symmetric channel with crossover probability q, $p(y|x)=q^{\overline{\delta }(x,y)}{\overline{q}}^{\delta (x,y)}$ where $\overline{q}=1-q;\overline{\delta }(x,y)=1-\delta (x,y)$; and δ(x, y) = 1 if x = y, and otherwise δ(x, y) = 0. Equivalently, we can represent Y as Y = X ⊕ W, where W ~ B(q) and is independent of X.

1). Numerical Results:

We have taken two approaches to studying the surfaces of ${\mathcal{R}}_{\text{in}}$ and ${\mathcal{R}}_{\text{out}}$ for this binary case. First, we carried out the optimizations in (11) and (12) numerically. This calculation was via a Monte Carlo method which executed a dense random sampling of the set of probability distributions p(uv | xy) associated with ${\mathcal{P}}_{\text{in}}$ and ${\mathcal{P}}_{\text{out}}$.¹² For each sample p(uv | xy), we calculated I(X; U), I(Y; V) and I(XY; UV); then, for each value of r_x, r_y ∈ [0,1] the numerical estimate of r_in(r_x, r_y) or r_out(r_x, r_y) was the largest sample value found by the Monte Carlo search for r_x + r_y – I(XY; UV). From here on, we denote the numerical surface estimates by $\widehat{r_{\text{in}}}\left(r_x,r_y\right)$ and $\widehat{r_{\text{out }}}\left(r_x,r_y\right)$.

The cardinality bound in Theorem 4 is not necessarily tight. Therefore, to assess the alphabet sizes required of $\mathcal{U}$ and $\mathcal{V}$ for the binary case, we performed our numerical experiments for increasing values of $\left|\mathcal{U}\right|$ and $\left|\mathcal{V}\right|$. For the inner bound surface, we found $\left|\mathcal{U}\right|=\left|\mathcal{V}\right|=2$ was sufficient: no further increase in $\widehat{r_{\text{in}}}\left(r_x,r_y\right)$ was afforded by allowing $\left|\mathcal{U}\right|$, $\left|\mathcal{V}\right|=3$, 4. For the outer bound surface, $\left|\mathcal{U}\right|=\left|\mathcal{V}\right|=3$ was sufficient.

The surface plots from our numerical experiments are shown in Fig. 3. Fig. 4 shows representations of the distributions p(uv | xy) underlying 25 different points (r_x, r_y) for Fig. 3 (a) the inner and Fig. 3 (b) the outer bounds, in which probabilities are represented by the area of white squares.^{13, 14} The row–column format of the matrix p(uv | xy) is xy = 00, 01, 10, 11 moving down rows; moving across columns, for the inner bound with $\mathcal{U},\mathcal{V}=\left\{0,1\right\}$ the format is uv = 00, 01, 10, 11, whereas for the outer bound with $\mathcal{U},\mathcal{V}=\left\{0,1,e\right\}$, the column format is uv = 00, 01, 1e, 10, 1e, e0, e1, ee. (The choice of for the third letter of $\mathcal{U}$ and $\mathcal{V}$ is explained below.)

Fig. 3.

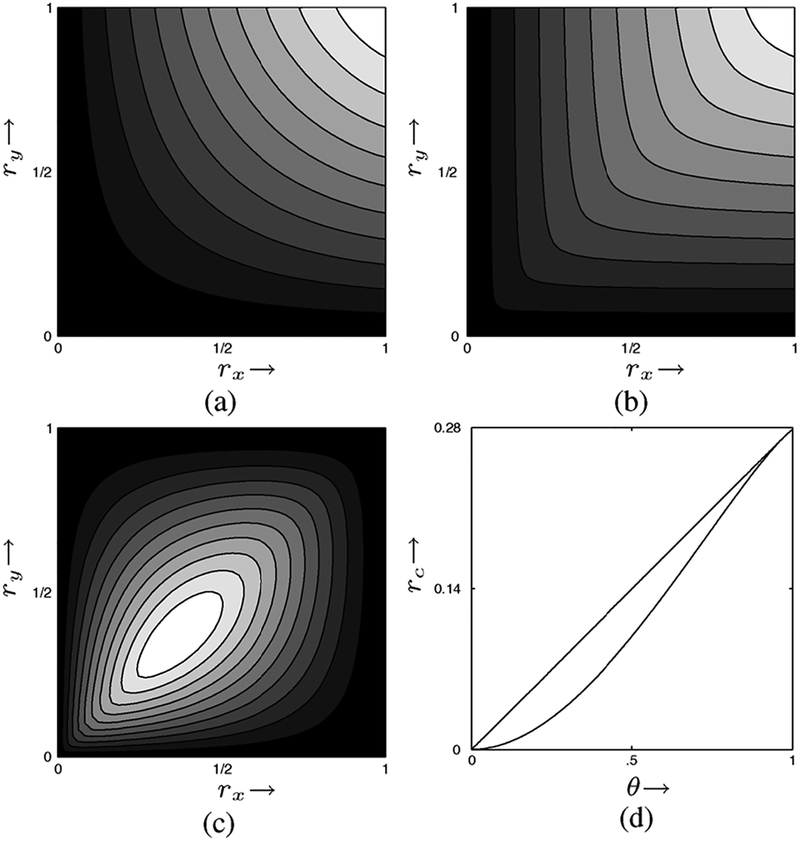
Contour plots of the binary inner bound surface (a); outer bound surface (b); differences between the outer bound and inner bounds (c); and plot of inner and outer bound surfaces along a diagonal cut, (r_x(θ), r_y(θ)) = θ(1, 1), θ ∈ [0, 1]. In these plots q = 0.2.

Fig. 4.

Hinton diagrams of the maximizing probability distributions p(uv | xy) for 25 values of (r_x, r_y). (a) Distributions for ${\mathcal{R}}_{\text{in}}$. (b) Distributions for ${\mathcal{R}}_{\text{out}}$.

2). Conjectured Formulas:

Second, we guessed formulas for the inner and outer bound surfaces, which turned out to fit the numerical results just described. We first present the formulas, then discuss the motivations behind them.

Our formulas involve the following two functions. First, define

$$s\left(r_x,r_y\right)=1-h\left(q_x*q*q_y\right),$$

where

$$\begin{gathered} q_x=h^{-1}\left(1-r_x\right), \\ {q}_y=h^{-1}\left(1-r_y\right); \end{gathered}$$

h(·) is the binary entropy function

$$h(x)=-x\text{log}(x)-(1-x)\text{log}(1-x);$$

“*” denotes binary convolution

$$x*y=x\left(1-y\right)+y\left(1-x\right);$$

and q_x, q_y ∈ [0, 1/2] to ensure that h(·) is invertible. Next, let s*(r_x, r_y) denote the upper concave envelope of s(r_x, r_y)

$$s^{*}\left(r_x,r_y\right)=\text{sup}\theta s\left(r_{x_1},r_{y_1}\right)+\overline{\theta }s\left(r_{x_2},r_{y_2}\right)$$

where $\overline{\theta }=1-\theta$; and the supremum is over all combinations (θ, r_x1, r_y1, r_x2, r_y2) such that

$$\left(r_x,r_y\right)=\theta \left(r_{x_1},r_{y_1}\right)+\overline{\theta }\left(r_{x_2},r_{y_2}\right)$$

and each variable in the optimization is restricted to the unit interval [0, 1]. As explained in Appendix F, in both this case and for the corresponding Gaussian formulas in the next section, the expression for this convex hull simplifies to

$$s^{*}\left(r_x,r_y\right)=\text{sup}\theta s\left(r_{x^{\prime }}^{\prime }{r}_y^{\prime }\right)$$

with the supremum over all combinations $\left(\theta ,r_x^{\prime },r_y^{\prime }\right)$ such that

$$\left(r_x,r_y\right)=\theta \left(r_x^{\prime },r_y^{\prime }\right).$$

Conjecture 1: For the binary case the surfaces of ${\mathcal{R}}_{\text{in}}$ and ${\mathcal{R}}_{\text{out}}$ are

$$r_{\text{in}}\left(r_x,r_y\right)=s\left(r_{x,}{r}_y\right)$$ (14)

$$r_{\text{out}}\left(r_x,r_y\right)=s^{*}\left(r_x,r_y\right)$$ (15)

and the surface of the achievable rate region $\mathcal{R}$ is

$$r\left(r_x,r_y\right)=\overline{r_{\text{in}}}\left(r_x,r_y\right)=r_{\text{out}}\left(r_x,r_y\right).$$ (16)

3). Rationale for the Inner Bound (14):

The surfaces r_in(r_x, r_y), r_out(r_x, r_y) are specified in terms of probability distributions p(xyuv) = p(xy)p(uv | xy) that maximize (11) and (12). For r_in(r_x, r_y), the distribution factorizes as p(uv | xy) = p(u | x)p(v | y), and a natural guess is that in the maximizing distribution both p(u | x) and p(v | y) are binary symmetric channels

$$p(u|x)=q_x^{\overline{\delta }(x,u)}{\overline{q}}_x^{\delta (x,u)},p(v|y)=q_y^{\overline{\delta }(y,v)}{\overline{q}}_y^{\delta (y,v)};$$

or, equivalently, U = X ⊕ W_x, V = Y ⊕ W_y, where W_x ~ B(q_x), W_x ~ B(q_y), and q_x, $q_y\in \left[0,\frac{1}{2}\right]$; see Fig. 5(a). For this choice of U and V we calculate

$$\begin{gathered} r_x=I\left(X;U\right) \\ =H\left(X\right)-H\left(X|U\right) \\ =1-H\left(U\oplus W_x|U\right) \\ =1-H\left(W_x\right) \\ =1-h\left(q_x\right) \end{gathered}$$

and likewise r_y = 1 − h(q_y). Then

$$\begin{gathered} I\left(U;V\right)=H\left(V\right)-H\left(V|U\right) \\ =1-H\left(U\oplus W_x\oplus W\oplus W_y|U\right) \\ =1-h\left(q_x\ast q\ast q_y\right) \\ =s\left(r_x,r_y\right). \end{gathered}$$

Clearly, s(r_x, r_y) is a lower bound on r_in(r_x, r_y), since: 1) U – Y − V, hence $UV\in {\mathcal{P}}_{\text{in}}$; 2) $UV\in \mathcal{C}\left(r_x,r_y\right)$; and 3)

$$\begin{gathered} r_{\text{in}}\left(r_x,r_y\right)=\underset{UV\in \mathcal{C}\left(r_x,r_y\right)}{\text{max}}I(U;V)\ge 1-h\left(q*q_x*q_y\right) \\ =s\left(r_x,r_y\right). \end{gathered}$$

The converse, r_in(r_x, r_y), ≤ s(r_x, r_y) is unproven, so the identification of r_in(r_x, r_y) with s(r_x, r_y) remains a conjecture. Nevertheless, in our numerical optimization we found no points outside of this region for any choice of (r_x, r_y), and the distributions which emerge from our computer experiments (Fig. 4(a)) closely resemble the long binary-symmetric channel in the calculation of s(r_x, r_y). This provides strong experimental evidence supporting (14) in Conjecture 1.

Fig. 5.

Binary-symmetric channel models for the inner and outer bounds. (a) Model for r_in(r_x, r_y) with $\left|\mathcal{U}\right|=\left|\mathcal{V}\right|=2$. (b) Model for r_out(r_x, r_y) with $\left|\mathcal{U}\right|=\left|\mathcal{V}\right|=3$. See text for explanation.

4). Rationale for the Outer Bound (15):

Clearly, s*(r_x, r_y) is a lower bound on r_out, since, for all r_x, r_y ∈ [0, 1]

• $r_{\text{out }}\left(r_x,r_y\right)\ge r_{\text{in }}\left(r_x,r_y\right)\Rightarrow \overline{r_{\text{out }}}\left(r_x,r_y\right)\ge \overline{r_{\text{in }}}\left(r_x,r_y\right)$;

• ${\mathcal{R}}_{\text{out}}$ is convex, ⇒ $\overline{r_{\text{out }}}\left(r_x,r_y\right)=r_{\text{out }}\left(r_x,r_y\right)$;

• $r_{\text{in }}\left(r_x,r_y\right)\ge s\left(r_x,r_y\right)\Rightarrow \overline{r_{\text{in}}}\left(r_x,r_y\right)\ge \overline{s}\left(r_x,r_y\right)=s^{*}\left(r_x,r_y\right)$;

and together these imply r_out(r_x, r_y) ≥ s*(r_x, r_y). Unfortunately, we do not have a proof of the converse, r_out(r_x, r_y) ≤ s*(r_x, r_y), so the identification of r_out(r_x, r_y) with s*(r_x, r_y) remains a conjecture. Nevertheless, empirically (i.e., according to our numerical experiments) the outer bound surface is identical to the convex hull of the inner bound surface. Moreover, empirically, the cardinalities required to construct the outer bound are $\left|\mathcal{U}\right|=\left|\mathcal{V}\right|=3$.

We can provide an explicit construction of the conjectured outer bound surface and the probability distributions that achieve it as follows. The distributions in this construction also agree with those found empirically, shown in Fig. 4(b). Let $\mathcal{U}=\mathcal{V}=\left\{0,1,e\right\}$. Consider the channel diagrammed in Fig. 5(b), which could be called a “synchronous erasure channel.” Here, U and V are generated by first passing X and Y through binary-symmetric channels, followed by an “erasure” E ∈ {0, 1} event in which both channel outputs are preserved with probability θ = Pr(E = 0), or both are erased (UV = ee) with probability $\overline{\theta }=1-\theta =\text{Pr}(E=1)$. An explicit formula for this channel is

$$\begin{gathered} p(uv|xy) \\ ={\theta }^{{\overline{\delta }}_e}(u,v){\overline{\theta }}^{{\delta }_e(u,v)} \\ {\left(q_x^{\overline{\delta }(x,u)}{\overline{q}}_x^{\delta (x,u)}{q}_y^{\overline{\delta }(y,v)}{\overline{q}}_y^{\delta (y,v)}\right)}^{{\overline{\delta }}_e(u,v)}{\text{Δ}}_e(u,v) \end{gathered}$$

where

$$\begin{gathered} \delta (\alpha ,\beta )=\{\begin{array}{ll}1,\hfill & \text{ if }\alpha =\beta \hfill \\ 0,\hfill & \text{ if }\alpha \ne \beta \hfill \end{array} \\ {\delta }_e(\alpha ,\beta )=\{\begin{array}{ll}1,\hfill & \text{ if }(\alpha ,\beta )=(e,e)\hfill \\ 0,\hfill & \text{ if }(\alpha ,\beta )\ne (e,e)\hfill \end{array} \\ {\mathrm{\Delta }}_e(\alpha ,\beta )=\{\begin{array}{ll}0,\hfill & \text{ if }\alpha =e,\beta \ne e\hfill \\ 0,\hfill & \text{ if }\alpha \ne e,\beta =e\hfill \\ 1,\hfill & \text{ otherwise }\hfill \end{array} \end{gathered}$$

and

$$\overline{\delta }(\alpha ,\beta )=1-\delta (\alpha ,\beta ),{\overline{\delta }}_e(\alpha ,\beta )=1-{\delta }_e(\alpha ,\beta ).$$

Equivalently, we can represent U and V as follows. Let W ~ B(q), W_x ~ B(q_x), W_y ~ B(q_y), E ~ B(θ) be Bernoulli random variables that are independent of each other and independent of X and Y, and define

$$\begin{gathered} Y=X\oplus W \\ U=\left(X\oplus W_x\right)\otimes E \\ V=\left(Y\oplus W_y\right)\otimes E \end{gathered}$$

where the multiplication by E is defined by

$$\alpha \otimes E=\{\begin{array}{ll}\alpha ,\hfill & \text{if }E=0\hfill \\ e,\hfill & \text{if }E=1.\hfill \end{array}$$

It is straightforward to verify $UV\in {\mathcal{P}}_{\text{out}}$. To check U – X − Y, write

$$\begin{gathered} I(U;Y|X)=I\left(\left(X\oplus W_x\right)\otimes E;X\oplus W|X\right) \\ =I\left(W_x\otimes E;W|X\right) \\ \text{=}\text{0} \end{gathered}$$

where the last line follows from the independence of W, W_x and E from each other and X. A similar calculation shows X – Y – V. Finally, calculating the rate region surface associated with this choice of UV we get, first

$$\begin{gathered} r_x=I\left(X;U\right) \\ =I\left(X;\left(X\oplus W_x\right)\otimes E,E\right) \\ =I(X;E)+I\left(X;\left(X\oplus W_x\right)\otimes E|E\right) \\ =0+\overline{\theta }I(X;E|E=1)+\theta I\left(X;X\oplus W_x|E=0\right) \\ =0+0+\theta \left(1-h\left(q_x\right)\right) \end{gathered}$$

where the last step follows from the previous calculations for the inner bound; and a similar calculation shows r_y = θ(1 – h(q_y)). Then, using U – X – Y, X – Y – V to write

$$\begin{gathered} I(U;V)-I(U;V|XY) \\ =I(X;U)+I(Y;V)-I(XY;UV) \\ =I(X;U)+I(Y;V)-\left[H(U)+H(U\left|V)-H(UV\right|XY)\right] \end{gathered}$$

we have (suppressing some detail)

$$\begin{gathered} H\left(U\right)=H\left(U,E\right) \\ =H\left(E\right)+H\left(U|E\right) \\ =h(\theta )+\theta H(U\left|E=0)+\overline{\theta }H(U\right|E=1) \\ =h(\theta )+\theta +0 \end{gathered}$$

$$\begin{gathered} H\left(U|V\right)=H\left(U|V,E\right) \\ =\theta H(U|V,E=0)+\overline{\theta }H(U|V,E=1) \\ =\theta h\left(q_x\ast q\ast q_y\right) \end{gathered}$$

$$\begin{gathered} H\left(UV|XY\right)=H\left(E|XY\right)+H\left(UV|XY,E\right) \\ =h(\theta )+\theta \left[H(U|X,E=0)+H\left(V|Y,E=1\right)\right] \\ =h(\theta )+\theta \left[h\left(q_x\right)+h\left(q_y\right)\right]. \end{gathered}$$

Putting these together and canceling terms

$$\begin{gathered} I(U;V)-I(U;V|XY)=\theta \left(1-h\left(q_x\ast q\ast q_y\right)\right) \\ =s^{*}\left(r_x,r_y\right). \end{gathered}$$

Thus, we have constructed an explicit example which achieves s*(r_x, r_y) with $\left|\mathcal{U}\right|=\left|\mathcal{V}\right|=3$.

B. Gaussian Case

We now consider a Gaussian version of our problem. Let X and Y be zero-mean Gaussian random variables with correlation coefficient ρ_xy. We propose explicit formulas for the surfaces of ${\mathcal{R}}_{\text{in}}$ and ${\mathcal{R}}_{\text{out}}$ for the Gaussian case, in terms of the following two functions. In both formulas, put

$$\begin{gathered} r_x=-\frac{1}{2}\text{log}\left(1-{\rho }_{xu}^2\right) \\ {r}_y=-\frac{1}{2}\text{log}\left(1-{\rho }_{yv}^2\right). \end{gathered}$$

Note that these expressions determine the correlation coefficients ρ_xu and ρ_yv. Define

$$S\left(r_x,r_y\right)=-\frac{1}{2}\text{log}\left(1-{\rho }_{xy}^2{\rho }_{yv}^2{\rho }_{xu}^2\right)$$ (17)

and

$$S^{*}\left(r_x,r_y\right)=r_x+r_y+\frac{1}{2}\text{log}\left[1+\frac{2\rho \gamma -\beta }{1-{\rho }^2}\right]$$ (18)

where

$$\begin{gathered} \gamma ={\rho }_{xy}{\rho }_{xu}{\rho }_{yv} \\ \beta ={\rho }_{xu}^2+{\rho }_{yv}^2-\left(1-{\rho }_{xy}^2\right){\rho }_{xu}^2{\rho }_{yv}^2, \\ \rho =\frac{\beta }{2\gamma }-\sqrt{{\left(\frac{\beta }{2\gamma }\right)}^2-1}. \end{gathered}$$ (19)

Conjecture 2: In the Gaussian case, the surfaces of ${\mathcal{R}}_{\text{in}}$ and ${\mathcal{R}}_{\text{out}}$ are

$$r_{\text{in}}\left(r_x,r_y\right)=S\left(r_x,r_y\right)$$ (20)

$$r_{\text{out}}\left(r_x,r_y\right)=S^{*}\left(r_x,r_y\right).$$ (21)

Fig. 6 shows plots of the inner and outer bounds and their difference, as well as the difference between the outer bound and the convex hull of the inner bound. Interestingly, unlike the binary case, for the Gaussian case the outer bound is not equal to the convex hull of the inner bound.

Fig. 6.

Contour plots of (a) the binary inner bound surface; (b) outer bound surface; (c) difference between the outer bound and inner bounds; and (d) plot of surfaces for the inner bound, its convex hull, and the outer bound along a diagonal cut, (r_x(θ), r_y(θ)) = θ(1, 1), θ ∈ [0, 1]. In these plots ρ_xy = 0.8.

The following proof relies on some basic properties of the mutual information between Gaussian random variables, given as lemmas in Appendix G.

In the analysis that follows, we assume that the maximizing distributions are Gaussian. Under this assumption, we solve the inner and outer bounds. Except for this unproved assumption, the proof of the conjecture is complete.

Proof: (Conjecture 2, eq. (20)) As noted in Appendix G, mutual informations between jointly Gaussian random variables are completely determined by their correlation coefficients. For a length-4 Markov chain U – X – Y – V of jointly Gaussian random variables I(U; V | XY) = 0 and, applying Lemma 9 from Appendix G we have ρ_uv = ρ_xuρ_xyρ_yv, hence

$$I(U;V)-I(U;V|XY)=-\frac{1}{2}\text{log}\left(1-{\rho }_{xu}^2{\rho }_{xy}^2{\rho }_{yv}^2\right).$$

This mutual information is maximized when the constraints I(X; U) ≤ r_x, I(Y; V) ≤ r_y are satisfied with equality, hence when ρ_xu and ρ_yv satisfy $r_x=-\frac{1}{2}\text{log}\left(1-{\rho }_{xu}^2\right)$ and $r_y=-\frac{1}{2}\text{log}\left(1-{\rho }_{yv}^2\right)$.

The following proof for the surface of the outer bound region uses the form of r_out(r_x, r_y) given by (13). In this case, the optimization problem reduces to minimizing I(XY; UV) subject to the length-3 Markov constraints U – X – Y, X – Y – V.

Proof: (Conjecture 2, eq. (21)) Using Lemma 10 from Appendix G, we have

$$C_{xy,uv}=\left[\begin{array}{cc}{\rho }_{xu}& {\rho }_{xv}\\ {\rho }_{yu}& {\rho }_{yv}\end{array}\right]=\left[\begin{array}{cc}1& {\rho }_{xy}\\ {\rho }_{xy}& 1\end{array}\right]\left[\begin{array}{cc}{\rho }_{xu}& 0\\ 0& {\rho }_{yv}\end{array}\right].$$

The left-hand matrix in this decomposition is C_xy,_xy, denoted hereafter simply as C, and we denote the right-hand matrix by D. Then applying Lemma 8 from Appendix G yields

$$\begin{gathered} I(XY;UV) \\ =\frac{1}{2}\text{log}\left|C\right|-\frac{1}{2}\text{log}\left|C-C_{xy,uv}{C}_{uv,uv}^{-1}{C}_{uv,yx}\right| \\ =\frac{1}{2}\text{log}\left|C\right|-\frac{1}{2}\text{log}\left|C-CD{C}_{uv,uv}^{-1}DC\right| \\ =-\frac{1}{2}\text{log}\left|C\right|-\frac{1}{2}\text{log}\left|C^{-1}-D{C}_{uv,uv}^{-1}D\right|. \end{gathered}$$

Substituting for the 2 × 2 matrices in this last expression and rearranging terms yields

$$I(XY;UV)=-\frac{1}{2}\text{log}\left[1+\frac{2{\rho }_{uv}\gamma -\beta }{1-{\rho }_{uv}^2}\right]$$

where γ and β are defined in (19).

By assumption, ρ_xu and ρ_yv are fixed, so we optimize I(XY; UV) only with respect to ρ_uv. Setting ∂I(XY; UV)/∂ρ_uv = 0 and solving, we obtain that, if β > 2γ > 0, then the maximum is achieved at ${\rho }_{uv}^{*}=\rho$, where ρ is defined in (19).

To complete the proof we must show that β > 2γ > 0. Noting that β, γ > 0 and substituting, the desired inequality becomes

$${\rho }_{xu}^2+{\rho }_{yv}^2-{\rho }_{xu}^2{\rho }_{yv}^2>2{\rho }_{xy}{\rho }_{xu}{\rho }_{yv}-{\rho }_{xy}^2{\rho }_{xu}^2{\rho }_{yv}^2.$$

Subtracting from each side and factoring yields the equivalent inequality

$$-\left(1-{\rho }_{xu}^2\right)\left(1-{\rho }_{yv}^2\right)>-{\left(1-{\rho }_{xy}{\rho }_{xu}{\rho }_{yv}\right)}^2.$$

To show that this holds for all ρ_xy, note that the maximum of the right-hand side is achieved by ρ_xy = 1, so that the inequality becomes

$$\left(1-{\rho }_{xu}^2\right)\left(1-{\rho }_{yv}^2\right)-{\left(1-{\rho }_{xu}{\rho }_{yv}\right)}^2<0.$$

This inequality holds, since

$$\begin{gathered} \left(1-{\rho }_{xu}^2\right)\left(1-{\rho }_{yv}^2\right)-{\left(1-{\rho }_{xu}{\rho }_{yv}\right)}^2 \\ =-{\rho }_{xu}^2-{\rho }_{yv}^2+2{\rho }_{xu}{\rho }_{yv} \\ =\left({\rho }_{xu}-{\rho }_{yv}\right)\left({\rho }_{yv}-{\rho }_{xu}\right) \\ =-{\left({\rho }_{xu}-{\rho }_{yv}\right)}^2 \\ \text{<}\text{0}. \end{gathered}$$

VIII. Conclusion

We have presented an information-theoretic analysis of pattern recognition systems subject to data compression constraints. Our main results consist of fundamental bounds characterizing the minimum sensory and memory information budgets required for reliable pattern recognition, or, equivalently, the maximum number of patterns that can be discriminated on given sensory and memory data budgets.

As a starting point, we have focused on the case of unstructured data, in which patterns are representable as vectors with i.i.d. components, and the sensory data observation channel is memoryless. In recent years, there has been much theoretical and experimental work aimed at developing methods to render data into a format with independent (or approximately independent) components (see, e.g., [36]–[39]). Such methods have been especially successful in the study of “natural” signals, e.g., sounds and imagery in naturally occurring environments. Nevertheless, a decomposition into independent components is often impossible or only approximate, and it will be important in future work to extend our results to cover the case of correlated components and channels with memory.

We have focused on “reliable” pattern recognition systems, in the sense that the recognition error rate is able to be made arbitrarily close to zero. Nevertheless, in some applications it is of interest (or unavoidable) to allow less-than-perfect accuracy. This can be partly addressed by recasting the recognition problem as a “coarse-to-fine” search, where the system is given information in several successive stages, and at each stage is required only to partially recognize the pattern, i.e., to identify the pattern as belonging to a particular subclass, postponing definitive identification for the final stage. Extending our results to this successive refinement setting is relatively straightforward; see [40]. The more direct approach of explicitly allowing a strictly positive error rate is an open problem.

Much work remains to be done in designing practical pattern recognition systems that achieve the bounds described herein. One of the most challenging problems in this regard is the design of adequate statistical models of real-world signals. For examples of progress on this exciting front, see [11], [36], [41]–[48]. Another significant challenge is that of learning optimal classifiers from training data. In this connection, it will likely prove fruitful to explore connections between the present results and those established in machine learning theory; see, e.g., [7]–[10]. Another practical challenge is to build systems that make optimal use of time. Donald Geman and colleagues have been developing the theory of systems that reach their pattern recognition decisions with a minimum amount of computation [49]. It will be interesting to explore the relationship of this concept with our results concerning recognition using the minimum amount of information.

Open theoretical problems include the calculation of error exponents and, most importantly, the closing of the gap between our inner and outer bounds. As discussed in Section VI-B, the gap in our problem bears close resemblance to that in the distributed source coding problem. A solution to the distributed source coding problem would likely lead to a solution to ours, and vice versa.¹⁵

Appendix A. Proof of the Inner Bound

In this section we prove the inner bound ${\overline{\mathcal{R}}}_{\text{in }}\subseteq \mathcal{R}$, Theorem 2. The proof relies on standard random coding arguments and properties of strongly jointly typical sets [30]. Given a joint distribution p(xyuv), the strongly jointly δ-typical set is defined by

$${\mathcal{T}}_{\mathit{\text{UVXY}}}^{\delta }=\left\{xyuv:\right|N(\mathit{\text{xyuv}}|xyuv)/n-p(\mathit{\text{xyuv}})|\le \delta \forall \mathit{\text{xyuv}}\in \mathcal{X}\mathcal{Y}\mathcal{U}\mathcal{V}\}$$

where N(xyuv | xyuv) is the number of times the symbol combination xyuv occurs in xyuv. Likewise, we write. e.g., ${\mathcal{T}}_X^{\delta }$, ${\mathcal{T}}_{XY}^{\delta }$, ${\mathcal{T}}_{XYU}^{\delta }$ for singles, pairs, and triples. We will also use conditionally strongly jointly δ-typical sets, for example

$${\mathcal{T}}_{xU}^{\delta }=\left\{u:(xu)\in {\mathcal{T}}_{XU}^{\delta }\right\}.$$

The subscripts are omitted when context allows. We will also need the fact that for any positive numbers δ, ϵ > 0, fixed vector x, and large enough n

$$2^{-n[I(X;Y)+ϵ]}\le \text{Pr}\left(xY\in {\mathcal{T}}_{xY}^{\delta }\right)\le 2^{-n[I(X;Y)-ϵ]}.$$ (22)

Theorem 1: Suppose R is a point in the convex hull of ${\mathcal{R}}_{\text{in}}$, $R\in {\overline{\mathcal{R}}}_{\text{in}}$. That is, $R={\sum }_{q\in \mathcal{Q}}p(q)R_q$, where p(q) is a probability distribution over some finite alphabet $\mathcal{Q}$, and for each $q\in \mathcal{Q}$, $R_q=\left(R_{xq},R_{yq},R_{cq}\right)\in {\mathcal{R}}_{\text{in}}$.

We wish to show that for any ϵ > 0 and large enough n, there exists an (M_c, M_x, M_y, n) code (f, ϕ, g) with rates $R_c^{\prime }=\frac{1}{n}\text{log}{M}_c$, $R_x^{\prime }=\frac{1}{n}\text{log}{M}_x$, $R_y^{\prime }=\frac{1}{n}\text{log}{M}_y$ such that $R_c^{\prime }\ge R_c$, $R_x^{\prime }\le R_x$, $R_y^{\prime }\le R_y$, and $P_e^n\le ϵ$.

By definition, $R_q\in {\mathcal{R}}_{\text{in}}$ implies that for each $q\in \mathcal{Q}$ there exist random variables U_q, V_q such that

$$p_q(\mathit{\text{xyuv}})=p(xy)p_q(u|x)p_q(v|y)$$

and

$$\begin{gathered} R_{xq}=I\left(X;U_q\right)+{\alpha }_{xq} \\ {R}_{yq}=I\left(Y;V_q\right)+{\alpha }_{yq} \\ {R}_{cq}=R_{xq}+R_{yq}-I\left(XY;U_q{V}_q\right)-{\gamma }_q \end{gathered}$$

for some values α_xq, α_yq, γ_q > 0 such that γ_q ≥ α_xq + α_yq.¹⁶ Now let

$$\begin{gathered} R_{xq}^{\prime }=I\left(X;U_q\right)+{\alpha }_{xq}/4,R_x^{\prime }=\sum _{q\in \mathcal{Q}}p(q)R_{xq}^{\prime } \\ {R}_{yq}^{\prime }=I\left(Y;V_q\right)+{\alpha }_{yq}/4,R_y^{\prime }=\sum _{q\in \mathcal{Q}}p(q)R_{yq}^{\prime } \end{gathered}$$

and

$$\begin{gathered} R_{cq}^{\prime }=R_{xq}^{\prime }+R_{yq}^{\prime }-I\left(XY;U_q{V}_q\right)-{\gamma }_q/4 \\ {R}_c^{\prime }=\sum _{q\in \mathcal{Q}}p(q)R_{cq}^{\prime }. \end{gathered}$$

With these choices, we have $R_x^{\prime }\le R_x$, $R_y^{\prime }\le R_y$, $R_c^{\prime }\ge R_c$.

Given

$$X^n~\prod _{i=1}^{n}p\left(x_i\right),Y^n~\prod _{i=1}^{n}p\left(y_i\right)$$

divide the sequences into $|\mathcal{Q}|$ segments with lengths n_q = np(q), denoted $X^{n_q}$, $Y^{n_q}$, i.e.,

$$X^n=\left[X^{n_1}{X}^{n_2}\dots X^{n_{\left|Q\right|}}\right],Y^n=\left[Y^{n_1}{Y}^{n_2}\dots Y^{n_{\left|Q\right|}}\right].$$

Finally, we will use the additional notation: $M_{xq}=2^{n_q{R}_{xq}^{\prime }}$, $M_{yq}=2^{n_q{R}_{yq}^{\prime }}$ and ${\mathcal{M}}_{xq}=\left\{1,\dots ,M_{xq}\right\}$, ${\mathcal{M}}_{yq}=\left\{1,\dots ,M_{yq}\right\}$.

We will construct the desired overall code (f, ϕ, g) with rate $\left(R_c^{\prime },R_x^{\prime },R_y^{\prime }\right)$ by first constructing encoders f_q, ϕ_q with rates $R_{xq}^{\prime }$, $R_{yq}^{\prime }$ for the $|\mathcal{Q}|$ component sequences $X^{n_q}$, $Y^{n_q}$, then constructing a classifier g which acts on the combined outputs of the encoders.

Please refer to Fig. 7 for a summary of the notation introduced below.

Fig. 7.

Mappings for sequences $\left(X^{n_q},Y^{n_q}\right)$, $q\in \mathcal{Q}$ and concatenations (Xⁿ, Yⁿ).

• 1
  Codebooks: For each $q\in \mathcal{Q}$, from p_q(xyuv) compute the marginal distributions p_q(u),p_q(v). To serve as memory codewords, select M_xq length-n_q vectors by sampling with replacement from a uniform distribution over the set ${\mathcal{T}}_U^{\delta }$. Assign each codeword a unique index $i_q\in {\mathcal{M}}_{xq}=\left\{1,2,\dots ,M_{xq}\right\}$. To serve as sensory codewords, similarly select M_yq length-n_q vectors by from ${\mathcal{T}}_V^{\delta }$, and assign each an index $j_q\in {\mathcal{M}}_{yq}=\left\{1,2,\dots ,M_{yq}\right\}$. Denote the codebooks

  $$\begin{gathered} {\mathcal{B}}_u(q)=\left\{u^{n_q}(1),\dots ,u^{n_q}\left(M_{xq}\right)\right\} \\ {\mathcal{B}}_v(q)=\left\{v^{n_q}(1),\dots ,v^{n_q}\left(M_{yq}\right)\right\}. \end{gathered}$$
• 2
  Encoders: We define encoders f_q and ϕ_q in terms of maps

  $$\begin{gathered} {\phi }_{xq}:{\mathcal{X}}^{n_q}\to {\mathcal{U}}^{n_q}{b}_{xq}:{\mathcal{U}}^{n_q}\to {\mathcal{M}}_{xq} \\ {\phi }_{yq}:{\mathcal{Y}}^{n_q}\to {\mathcal{V}}^{n_q}{b}_{yq}:{\mathcal{V}}^{n_q}\to {\mathcal{M}}_{yq} \end{gathered}$$

  as follows. Given any $x^{n_q}\in {\mathcal{X}}^{n_q}$, search the codebook ${\mathcal{B}}_u(q)$ for a codeword $u^{n_q}$ such that $\left(x^{n_q},u^{n_q}\right)\in {\mathcal{T}}_{XU}^{\delta }$. If this search is successful, set ${\phi }_{xq}\left(x^{n_q}\right)=u^{n_q}$, $b_{xq}\left(u^{n_q}\right)=i_q$, $b_{xq}^{-1}\left(i_q\right)=u^{n_q}$, where i_q is the index of $u^{n_q}$ in ${\mathcal{B}}_u(q)$. If the search fails, (arbitrarily) set $u^{n_q}=u^{n_q}(1)$ so that φ_xq and b_xq are defined for all of ${\mathcal{X}}^{n_q}$. In the same way, given any $y^{n_q}\in {\mathcal{Y}}^{n_q}$, search ${\mathcal{B}}_v(q)$ for a codeword $v^{n_q}$ such that $\left(y^{n_q},v^{n_q}\right)\in {\mathcal{T}}_{YV}^{\delta }$. If successful, denote the index of the found codeword j_q, and set ${\phi }_{yq}\left(y^{n_q}\right)=v^{n_q}$, $b_{yq}\left(v^{n_q}\right)=j_q$, $b_{yq}^{-1}\left(j_q\right)=v^{n_q}$. For search failure, set j_q =1, $v^{n_q}=v^{n_q}(1)$ so that φ_yq and b_yq are defined for all of ${\mathcal{Y}}^{n_q}$.

Finally, define

$$\begin{gathered} f_q:{\mathcal{X}}^{n_q}\to {\mathcal{M}}_{xq},f_q\left(x^{n_q}\right)=i_q\triangleq b_{xq}\left({\phi }_{xq}\left(x^{n_q}\right)\right) \\ {\varphi }_q:{\mathcal{Y}}^{n_q}\to {\mathcal{M}}_{yq},{\varphi }_q\left(y^{n_q}\right)=j_q\triangleq b_{yq}\left({\phi }_{yq}\left(y^{n_q}\right)\right). \end{gathered}$$

Now, given vectors $x^n=\left(x^{n_1}\dots x^{n_{|\mathcal{Q}|}}\right)$ and $y^n=\left(y^{n_1}\dots y^{n_{|\mathcal{Q}|}}\right)$, the encoders above each produce $|\mathcal{Q}|$ vectors ${\phi }_{xq}\left(x^{n_q}\right)=u^{n_q}$, ${\phi }_{yq}\left(y^{n_q}\right)=v^{n_q}$, and $|\mathcal{Q}|$ indices $b_{xq}\left(u^{n_q}\right)=i_q$, $b_{yq}\left(y^{n_q}\right)=j_q$. Denote the concatenations of these

Note that the vector of integers i ranges over $M_x={\prod }_{q\in \mathcal{Q}}{M}_{xq}$ different values i(i),i = 1…M_x. Let the map between the vectors i and the corresponding integers i be ℓ_x, i.e., if i = i(i), let ℓ_x(i) = i, and ${\mathcal{l}}_x^{-1}(i)=i$. Similarly, j ranges over $M_y={\prod }_{q\in \mathcal{Q}}{M}_{yq}$ values, j(j),j = 1…M_y and we define ℓ_y such that if j = j(j), then ℓ_y(j) = j and ${\mathcal{l}}_y^{-1}(j)=j$. Then we can specify encoders $f^{\prime }:{\mathcal{X}}^n\to {\mathcal{M}}_x$ and $\varphi :{\mathcal{Y}}^n\to {\mathcal{M}}_y$ for full length-n vectors xⁿ and yⁿ by

$$\begin{gathered} f^{\prime }\left(x^n\right)=i\triangleq {\mathcal{l}}_x(b_x\left({\phi }_x\left(x^n\right)\right) \\ \varphi \left(y^n\right)=j\triangleq {\mathcal{l}}_y(b_y\left({\phi }_y\left(y^n\right)\right). \end{gathered}$$

To finalize the construction of the memory encoder, for any given labeled template pattern t(w) = (xⁿ, w), let $f:{\mathcal{X}}^n\times {\mathcal{M}}_c\to {\mathcal{M}}_x\times {\mathcal{M}}_c$ be defined by

$$f(t(w))=m(w)=(i,w)\triangleq \left(f^{\prime }\left(x^n\right),w\right).$$

The rates of the encoders are $\left(R_x^{\prime },R_y^{\prime }\right)$, as verified by calculating

$$\begin{gathered} \frac{1}{n}\text{log}{M}_x=\frac{1}{n}\text{log}\prod _{q\in \mathcal{Q}}{M}_{xq}=\frac{1}{n}\sum _{q\in \mathcal{Q}}\text{log}{2}^{n_q{R}_{xq}^{\prime }} \\ =\sum _{q\in \mathcal{Q}}p(q)R_{xq}^{\prime }=R_x^{\prime } \\ \frac{1}{n}\text{log}{M}_y=\frac{1}{n}\text{log}\prod _{q\in \mathcal{Q}}{M}_{yq}=\frac{1}{n}\sum _{q\in \mathcal{Q}}\text{log}{2}^{n_q{R}_{yq}^{\prime }} \\ =\sum _{q\in \mathcal{Q}}p(q)R_{yq}^{\prime }=R_y^{\prime }. \end{gathered}$$

• 3Memorization: Given a realization of the template patterns ${\mathcal{C}}_x=\left(\mathit{t}(1)\dots t\left(M_c\right)\right),t(w)=\left(x^n(w),w\right)$ and the encoders defined above f and ϕ, compute the memory data ${\mathcal{C}}_u=f\left(C_x\right)\triangleq \left\{f(t(1)),\dots ,f\left(t\left(M_c\right)\right)\right\}=\left\{m(1),\dots ,m\left(M_c\right)\right\}$.
• 4Recognition Function: Given the stored memory data ${\mathcal{C}}_u$, we proceed to construct the classifier g as follows.

For each $q\in \mathcal{Q}$, given any pair of length n_q vectors $u^{n_q}$, $v^{n_q}$, define a function that tests the pair for strong joint typicality

$${\rho }_q\left(u^{n_q},v^{n_q}\right)=\mathbb{T}\left[\left(u^{n_q},v^{n_q}\right)\in {\mathcal{T}}_{UV}^{\delta }\right]$$

where $\mathbb{T}[\cdot ]$ is the truth-indicator function $\mathbb{T}[A]=1$ if A is true, and $\mathbb{T}[A]=0$ if A is false.

Now, given the sensory data j, compute its vector representation $j=\left[j_1\dots j_{\left|Q\right|}\right]={\mathcal{l}}_y^{-1}(j)$. For each $q\in \mathcal{Q}$, retrieve from ${\mathcal{B}}_v(q)$ the corresponding codeword $v^{n_q}=b_{yq}^{-1}\left(j_q\right)$. Similarly, for each memory $m(w)=(i,w)\in {\mathcal{C}}_u$, compute the corresponding vector $i=\left[i_q\dots i_{\left|\mathcal{Q}\right|}\right]={\mathcal{l}}_x^{-1}(i)$, and from the memory codebook ${\mathcal{B}}_u(q)$ retrieve $u^{n_q}=b_{xq}^{-1}\left(i_q\right)$. Next, define a function $r_w:{\mathcal{M}}_y\to \{0,1\}$ that tests each $v^{n_q}$ in $v^n=\left[v^{n_1}\dots v^{n_{|\mathcal{Q}|}}\right]$ against the corresponding $u^{n_q}$ in $u^n=\left[u^{n_1}\dots u^{n_{|\mathcal{Q}|}}\right]$, reporting a 1 if all compared pairs are jointly typical and zero otherwise

$$r_w(j)=\mathbb{T}\left[{\rho }_1\left(u^{n_1},v^{n_1}\right)\dots {\rho }_{\left|\mathcal{Q}\right|}\left(u^{n_{\left|\mathcal{Q}\right|}},v^{n_{\left|\mathcal{Q}\right|}}\right)=1^{\left|\mathcal{Q}\right|}\right]$$

where $1^{|\mathcal{Q}|}$ denotes the length-$|\mathcal{Q}|$ all-ones vector.

We can now specify the recognition function g as follows. Given the encoded sensory data j, the recognition module searches for a unique $w^{\prime }\in {\mathcal{M}}_c$ such that r_w′ (j) = 1. If this search is successful, set $\widehat{w}=w^{\prime }$. Otherwise, if there is none or more than one such value, declare an error and (arbitrarily) set $\widehat{w}=1$. Thus, we have defined $g:{\mathcal{M}}_y\times {\left({\mathcal{M}}_x\right)}^{M_c}\to {\mathcal{M}}_c$, $g\left(j,{\mathcal{C}}_u\right)=\widehat{w}$, as desired.

A. Performance Analysis

1). Error Events:

We analyze the probability of error for a given W = w, T(w) = (Xⁿ(w), w), Yⁿ. Denote the results of processing these with the components of the code (f, ϕ, g) above by M(w) = (I(w), w) = f(T(w)), J(w) = ϕ(Yⁿ); $U^{n_q}(w)={\phi }_{xq}\left(X^{n_q}\right)$, $V^{n_q}(w)={\phi }_{yq}\left(Y^{n_q}\right)$ for each $q\in \mathcal{Q}$, and R_w = r_w(J(w)). The following is an exhaustive list of possible errors.

First, in words, the possible errors are as follows:

• the sensory data and pattern template are not jointly typical;

• the pattern template is unencodable;

• the sensory data is unencodable;

• the codewords for the memory and sensory data are not jointly typical;

• the sensory data is jointly typical with more than one memory codeword;

• two different patterns are assigned the same memory codeword.

More formally, we express the error events thus: For events E_i, let ${\overline{E}}_k={\left({\cup }_{i=1}^k{E}_i\right)}^c$, where A^c denotes the complement of A. For each $q\in \mathcal{Q}$

• $E_1(q)=\left\{\left(X^{n_q},Y^{n_q}\right)\notin {\mathcal{T}}_{XY}^{\delta }\right\}$;

• $E_2(q)={\overline{E}}_1(q)\cap \left\{\forall U^{n_q}\in {\mathcal{B}}_u(q):\left(X^{n_q},U^{n_q}\right)\notin {\mathcal{T}}_{XU}^{\delta }\right\}$;

• $E_3(q)={\overline{E}}_1(q)\cap \left\{\forall V^{n_q}\in {\mathcal{B}}_v(q):\left(Y^{n_q},V^{n_q}\right)\notin {\mathcal{T}}_{YV}^{\delta }\right\}$;

• $E_4(q)={\overline{E}}_3(q)\cap \left\{\left(U^{n_q}(w),V^{n_q}(w)\right)\notin {\mathcal{T}}_{UV}^{\delta }\right\}$; and letting $E_i\triangleq {\cup }_{q\in \mathcal{Q}}{E}_i(q)$, i = 1…4

• $E_5={\overline{E}}_4\cap \left\{\exists w^{\prime }\in {\mathcal{M}}_c:w^{\prime }\ne w,r_{w^{\prime }}(J(w))=1\right\}$;

• $E_6={\overline{E}}_5\cap \left\{\exists w^{\prime }\in {\mathcal{M}}_c:w^{\prime }\ne w,I\left(w^{\prime }\right)=I(w)\right\}$.

Each of these vanishes as n → ∞, for the following reasons:

• P(E₁(q)) → 0, by the strong asymptotic equipartition property (AEP);

• P(E₂(q)) → 0, because $R_{xq}^{\prime }\ge I\left(X;U_q\right)$;

• P(E₃(q)) → 0, because $R_{yq}^{\prime }\ge I\left(Y;V_q\right)$;

• P(E₄(q)) → 0, because of the factorization p_q(xyuv) = p(xy)p_q(u | x)p_q(v | y) and the Markov lemma.

• Regarding P(E₅) Rewrite E₅ as

  $$\begin{gathered} E_5={\overline{E}}_4\cap \left\{\exists w^{\prime }\in {\mathcal{M}}_c:w^{\prime }\ne w,r_{w^{\prime }}(J(w))=1\right\} \\ ={\overline{E}}_4\cap \left\{\underset{w^{\prime }\in \langle {\mathcal{M}}_c\backslash w\}}{\cup }\{\forall q\in \mathcal{Q},\left(U^{n_q}\left(w^{\prime }\right),V^{n_q}(w)\right)\in {\mathcal{T}}_{UV}^{\delta }\}\right\}. \end{gathered}$$

  Then

  $$\begin{gathered} P\left(E_5\right)\le \left|{\mathcal{C}}_u\right|\prod _{q\in \mathcal{Q}}{2}^{-n_q\left[I\left(U_q;V_q\right)-{ϵ}_q\right]} \\ \le M_c\prod _{q\in \mathcal{Q}}{2}^{-n_q\left[I\left(U_q;V_q\right)-{ϵ}_q\right]} \\ =2^{n{R}_c^{\prime }}{2}^{-n{\sum }_{q\in \mathcal{Q}}p(q)\left[I\left(U_q;V_q\right)+{ϵ}_q\right]} \\ =2^{n\left[R_c^{\prime }-{\sum }_{q\in \mathcal{Q}}p(q)I\left(U_q;V_q\right)-ϵ\right]}. \end{gathered}$$

  So, P(E₅) → 0 as n → ∞ if. $R_c^{\prime }\le {\sum }_{q\in \mathcal{Q}}p(q)I\left(U_q;V_q\right)+ϵ$. This is indeed the case, since

  $$\begin{gathered} R_c^{\prime }=\sum _{q\in \mathcal{Q}}p(q)R_{cq}^{\prime } \\ =\sum _{q\in \mathcal{Q}}p(q)\left[R_{xq}^{\prime }+R_{yq}^{\prime }-I\left(XY;U_q{V}_q\right)-{\gamma }_q\right] \\ =\sum _{q\in \mathcal{Q}}p(q)[I\left(X;U_q\right)+I\left(Y;V_q\right)-I\left(XY;U_q{V}_q\right)+{\alpha }_{xq}+{\alpha }_{yq}-{\gamma }_q] \\ \stackrel{(\text{a})}{\le }\sum _{q\in \mathcal{Q}}p(q)[I\left(X;U_q\right)+I\left(Y;V_q\right)-I\left(XY;U_q{V}_q\right)]+ϵ \\ \stackrel{(\text{b})}{\le }\sum _{q\in \mathcal{Q}}p(q)I\left(U_q;V_q\right)+ϵ \end{gathered}$$

  where (a) is because (γ – α_xq + α_yq); and (b) follows from elementary properties of mutual information and from the factorization. p(q)p(xy)p(u | xq) p(v | yq).
• Regarding P(E₆): Denoting the components of the codeword for each memory $M(w)\in {\mathcal{C}}_u$ by $U^{n_q}(w)$, rewrite event E₆ as

  $$\begin{gathered} E_6={\overline{E}}_5\cap \left\{\exists w^{\prime }\in {\mathcal{M}}_c:w^{\prime }\ne w,I\left(w^{\prime }\right)=I(w)\right\} \\ ={\overline{E}}_5\cap \left\{\exists w^{\prime }\in {\mathcal{M}}_c:w^{\prime }\ne w,\forall q\in \mathcal{Q}:\left(X^{n_q}\left(w^{\prime }\right),U^{n_q}(w)\right)\in {\mathcal{T}}_{XU}^{\delta }\right\}. \end{gathered}$$

  Then

  $$\begin{gathered} P\left(E_6\right)\le M_c\prod _{q\in \mathcal{Q}}{2}^{-n_q\left[I\left(X;U_q\right)-{ϵ}_q\right]} \\ =2^{n\left[R_c^{\prime }-{\sum }_{q\in \mathcal{Q}}p(q)I\left(X;U_q\right)-ϵ\right]}. \end{gathered}$$

  So as if P(E₆) → 0 as n → ∞ if $R_c^{\prime }\le {\sum }_{q\in \mathcal{Q}}p(q)I\left(X;U_q\right)+ϵ]$. This is indeed the case: From our preceding calculation for P(E₅), we have $R_c^{\prime }\le {\sum }_{q\in \mathcal{Q}}p(q)I\left(U_q;V_q\right)+ϵ$; and the assumed factorization of p_q(xyuv) implies that the following is a Markov chain: U_q – X – Y − V_q. Hence, by the data processing inequality

  $$\begin{gathered} R_c\le \sum _{q\in \mathcal{Q}}p(q)I\left(U_q;V_q\right)+ϵ \\ \le \sum _{q\in \mathcal{Q}}p(q)I\left(U_q;X\right)+ϵ. \end{gathered}$$

This concludes the proof of the inner bound.

Appendix B. Proof of the Outer Bound

In this section we prove Theorem 1, which states the outer bound $\mathcal{R}\subseteq {\mathcal{R}}_{\text{out}}$. In the proof let W be the test index, selected from a uniform distribution p(w) over the pattern indices ${\mathcal{M}}_c$; let T = T(W) = (X, W)be the selected test pattern from the set of template patterns ${\mathcal{C}}_x$; let M = M(W) = (I, W) = f(T) be the compressed, memorized form of T; let ${\mathcal{C}}_u=f\left({\mathcal{C}}_x\right)$ be the memorized data; let Y be the sensory data; let J = J(W) = ϕ(Y) be the encoded sensory data, and let $\widehat{W}=g\left(J,{\mathcal{C}}_u\right)$ be the inferred value of W. Note that M, $\widehat{W}$ are random variables through their dependence on X, W, Y, and ${\mathcal{C}}_x$. The mutual informations in the proof are calculated with respect to the joint distribution (and its marginals) over (W, ${\mathcal{C}}_x$, ${\mathcal{C}}_u$, X, Y, M, I, J, $\widehat{W}$). We can verify that this distribution is well defined by writing it out explicitly. Let $\mathbb{T}[\cdot ]$ be the truth-indicator function $\mathbb{T}[A]=1$ if A is true, and $\mathbb{T}[A]=0$ if A is false. Then

$$\begin{gathered} p\left(w,{\mathcal{C}}_x,{\mathcal{C}}_u,x,y,m,j\right) \\ =p(w)p\left({\mathcal{C}}_x\right)p\left({\mathcal{C}}_u|{\mathcal{C}}_x\right)p\left(x|w,{\mathcal{C}}_x\right) \\ p(y|x)p(m|x,w)p(j|y)p\left(\widehat{w}|j,{\mathcal{C}}_u\right) \end{gathered}$$

where

$$\begin{gathered} p(w)=\frac{1}{M_c}\mathbb{T}\left[w\in {\mathcal{M}}_c\right] \\ p\left({\mathcal{C}}_x\right)=\prod _{w=1}^{M_c}\prod _{i=1}^{n}p\left(x_i(w)\right) \\ p\left({\mathcal{C}}_u|{\mathcal{C}}_x\right)=\mathbb{T}\left[{\mathcal{C}}_u=f\left({\mathcal{C}}_x\right)\right] \\ p\left(x|w,{\mathcal{C}}_x\right)=\mathbb{T}\left[x=x(w)\in {\mathcal{C}}_x\right] \\ p(y|x)=\prod _{i=1}^{n}p\left(y_i|x_i\right) \\ p(m|x,w)=\mathbb{T}[m=f(x,w)] \\ p(j|y)=\mathbb{T}[j=\varphi (y)] \\ p\left(\widehat{w}|j,{\mathcal{C}}_u\right)=\mathbb{T}\left[\widehat{w}=g\left(j,{\mathcal{C}}_u\right)\right]. \end{gathered}$$

The independence relationships underlying the structure of this distribution are evident from the block diagram of Fig. 1.

Proof: (Theorem 3) Assume $R=\left(R_x,R_y,R_c\right)\in \mathcal{R}$. Then there exists a sequence of (Mx, M_y, M_c, n) codes (f, ϕ, g), such that for any ϵ > 0

$$\begin{gathered} M_c\ge 2^{n{R}_c} \\ {M}_x\le 2^{n{R}_x} \\ {M}_y\le 2^{n{R}_y} \end{gathered}$$

and $P_e^n=\text{Pr}(\widehat{W}\ne W)\le ϵ$. To show that $R\in {\mathcal{R}}_{\text{out }}$, we must construct a pair of auxiliary random variables UV such that $UV\in {\mathcal{P}}_{\text{out}}$ and $R\in {\mathcal{R}}_{UV}$.

We construct the desired pair UV in three steps: 1) We introduce a set of intermediate random variable pairs U_iV_i, i = 1,2,…,n, individually contained in ${\mathcal{P}}_{\text{out }}$; 2) we derive mutual information inequalities for R_x, R_y, and R_c involving sums of the intermediate variables; 3) we convert the sum-inequalities into inequalities in the desired pair UV.

Step 1:

Let the intermediate auxiliary random variables be

$$\begin{gathered} U_i=\left(M,X^{i-1}\right) \\ {V}_i=\left(J,Y^{i-1}\right) \end{gathered}$$

for i = 1,2,…,n. Each pair is in ${\mathcal{P}}_{\text{out }}$. This is verified for the U_i by calculating

$$\begin{gathered} I\left(U_i;Y_i|X_i\right)=H\left(Y_i|X_i\right)-H\left(Y_i|M,X^{i-1},X_i\right) \\ =H\left(Y_i|X_i\right)-H\left(Y_i|M,X^i\right) \\ \stackrel{(\text{a})}{\le }H\left(Y_i|X_i\right)-H\left(Y_i|M,X^n\right) \\ \stackrel{(\text{b})}{=}H\left(Y_i|X_i\right)-H\left(Y_i|X^n\right) \\ \stackrel{(\text{c})}{=}H\left(Y_i|X_i\right)-H\left(Y_i|X_i\right) \\ =0 \end{gathered}$$

where the reasons for the lettered steps are (a) conditioning does not increase entropy, (b) the Y_i are independent of all other variables given Xⁿ, and (c) the pairs X_iY_i are i.i.d. Hence, U_i − X_i − Y_i is a Markov chain. By a similar argument, X_i − Y_i − V_i is also a Markov chain. Hence, $U_i{V}_i\in {\mathcal{P}}_{\text{out}}$ for each i = 1,2,…,n.

Step 2:

First, for the sensory encoder rate

$$\begin{gathered} n{R}_y\ge H(J) \\ \stackrel{(\text{a})}{=}H(J)-H\left(J|Y^n\right) \\ =\sum _{i=1}^{n}H\left(Y_i\right)-H\left(Y_i|Y^{i-1}J\right) \\ =\sum _{i=1}^{n}H\left(X_i\right)-H\left(X_i|V_i\right) \\ =\sum _{i=1}^{n}I\left(X_i;V_i\right) \end{gathered}$$

where (a) follows from J = ϕ(Yⁿ).

Next, taking account of all M_c memorized patterns, for the memory encoder rate we have

$$\begin{gathered} M_c\left(n{R}_x\right)=M_c\text{log}{M}_x \\ \ge H\left({\mathcal{C}}_u\right) \\ =H\left({\mathcal{C}}_u\right)-H\left({\mathcal{C}}_u|{\mathcal{C}}_x\right) \\ =H\left({\mathcal{C}}_x\right)-H\left({\mathcal{C}}_x|{\mathcal{C}}_u\right) \\ =\sum _{w=1}^{M_c}H(T(w))-H(T(w)|M(w)) \\ \stackrel{(\text{a})}{=}\sum _{w=1}^{M_{\text{c}}}H\left(X^n(W)|W=w\right)-H\left(X^n(W)|I,W=w\right) \\ \stackrel{(\text{b})}{=}\sum _{w=1}^{M_c}H\left(X^n\right)-H\left(X^n|I,W=w\right) \\ \stackrel{(\text{c})}{=}{M}_c\sum _{w=1}^{M_c}p(w)[H\left(X^n\right)-H\left(X^n|I,W=w\right)] \\ \stackrel{(\text{d})}{=}{M}_c\left[H\left(X^n\right)-H\left(X^n|I,W\right)\right] \\ \stackrel{(\text{e})}{=}{M}_c\sum _{i=1}^n\left[H\left(X_i\right)-H\left(X_i|X^{i-1},I,W\right)\right] \\ \stackrel{(\text{f})}{=}{M}_c\sum _{i=1}^n\left[H\left(X_i\right)-H\left(X_i|U_i\right)\right] \\ =M_c\sum _{i=1}^{n}I\left(X_i;U_i\right) \end{gathered}$$

where (a) is simply a matter of variable definitions and notation, (b) follows from the assumption that the Xⁿ(W)’s all have the same distribution and are drawn independently of W, (c) follows from the definition of p(w), (d) follows from the definition of conditional entropy, (e) follows from $p\left(x^n\right)={\prod }_{i=1}^{n}p\left(x_i\right)$ and the telescoping property, and (f) follows from the definition of U_i. Hence, $n{R}_x\ge {\sum }_{i=1}^{n}I\left(X_i;U_i\right)$.

$$\begin{gathered} \text{Finally}n{R}_c\le \text{log}{M}_c \\ =H(W) \\ =I\left(W;{\mathcal{C}}_u,J\right)+H\left(W|{\mathcal{C}}_u,J\right) \\ \stackrel{(a)}{\le }I\left(W;{\mathcal{C}}_u,J\right)+n{ϵ}_n \\ =I\left(W;{\mathcal{C}}_u\right)+I\left(W;J|{\mathcal{C}}_u\right)+n{ϵ}_n \\ \stackrel{(\text{b})}{=}0+I\left(W;J|{\mathcal{C}}_u\right)+n{ϵ}_n \\ =I\left(W,{\mathcal{C}}_u;J\right)-I\left(J;{\mathcal{C}}_u\right)+n{ϵ}_n \\ \le I\left(W,{\mathcal{C}}_u;J\right)+n{ϵ}_n \\ \stackrel{(\text{c})}{=}I(M;J)+n{ϵ}_n \\ \stackrel{(\text{d})}{=}\sum _{i=1}^{n}I\left(X_i;U_i\right)+I\left(Y_i;V_i\right)-I\left(X_i{Y}_i;U_i{V}_i\right)+n{ϵ}_n. \end{gathered}$$

The lettered steps are justified as follows.

1. By assumption, $\text{Pr}(\widehat{w}\ne W)=P_e^n\to 0$, where $\widehat{W}=g\left(J,{\mathcal{C}}_u\right)$. Thus, applying Fano’s inequality yields

   $$H\left(W|{\mathcal{C}}_u,J\right)\le H\left(P_e^n\right)+P_e^n\text{log}\left(M_c-1\right)\le n{ϵ}_n$$

   where ϵ_n → 0.

2. The test index W and patterns ${\mathcal{C}}_x$ are drawn independently, hence, $I\left(W;{\mathcal{C}}_u\right)=I\left(W;f\left({\mathcal{C}}_x\right)\right)=0$.

3. Writing ${\mathcal{C}}_u={\mathcal{C}}_u^{*}\cup M$, ${\mathcal{C}}_u^{*}={\mathcal{C}}_u\backslash M$, we have

   $$\begin{gathered} I\left(W,{\mathcal{C}}_u;J\right)=I\left(W,M,{\mathcal{C}}_u^{*};J\right) \\ =I(M;J)+I\left(W,{\mathcal{C}}_u^{*};J|M\right) \\ =I(M;J)+I\left(W,{\mathcal{C}}_u^{*};J|I,W\right) \\ =I(M;J)+I\left({\mathcal{C}}_u^{*};J|I,W\right) \\ =I(M;J)+0, \end{gathered}$$

   since the M(i) = (I(i), i) are independent of J for i ≠ W.

4. To justify this step, we invoke the following two results, proved in Appendix D. Let A, α, B, β and γ be arbitrary discrete random variables.

Then we get the following.

Lemma 6:

$$I(\alpha ;\beta )\ge I(A;\alpha )+I(B;\beta )-I(AB;\alpha \beta ),$$

with equality if and only if I(Aα; Bβ) = I(A; B).

Lemma 7: Let Z_i = (γ; Aⁱ⁻¹), i =1,2,…,n where the A_i are i.i.d. Then

$$\sum _{i=1}^{n}I\left(A_i;Z_i\right)=I\left(A^n;\gamma \right).$$

To apply Lemma 6, make the substitution (α, β, A, B) → (M, J, Xⁿ, Yⁿ). Then the condition for equality is satisfied

$$\begin{gathered} I\left(X^n,M;Y^n,J\right) \\ =I\left(X^n,I,W;Y^n,J\right) \\ =I\left(X^n,W;Y^n,J\right)+I\left(I;Y^n,J|X^n,W\right) \\ =I\left(X^n,W;Y^n,J\right)+I\left(I,W;Y^n,J|X^n,W\right) \\ \stackrel{(\text{a})}{=}I\left(X^n,W;Y^n,J\right)+0 \\ =I\left(X^n,W;Y^n\right)+I\left(X^n,W;J|Y^n\right) \\ \stackrel{(\text{b})}{=}I\left(X^n,W;Y^n\right)+0 \\ =I\left(X^n;Y^n\right)+I\left(W;Y^n|X^n\right) \\ \stackrel{(\text{c})}{=}I\left(X^n;Y^n\right)+0 \end{gathered}$$

since (a) M = (I, W) = f(Xⁿ, W), (b) J = ϕ(Yⁿ), and (c) Yⁿ only depends on W through Xⁿ = Xⁿ(W), so that H(Yⁿ | Xⁿ, W) = H(Yⁿ | Xⁿ). Thus, we have

$$I(M;J)=I\left(X^n;M\right)+I\left(Y^n;J\right)-I\left(X^n,Y^n;M,J\right).$$ (23)

Next, apply Lemma 7 three times with the substitutions

$$\begin{gathered} \left(Z_i,\gamma ,A^{i-1}\right)\to \left(U_i,M,X^{i-1}\right), \\ \to \left(V_i,J,Y^{i-1}\right), \\ \to \left(U_i{V}_i,MJ,X^{i-1}{Y}^{i-1}\right) \end{gathered}$$

to obtain

$$\begin{gathered} \sum _{i=1}^{n}I\left(X_i;U_i\right)=I\left(X^n;M\right) \\ \sum _{i=1}^{n}I\left(Y_i;V_i\right)=I\left(Y^n;J\right) \\ \sum _{i=1}^{n}I\left(X_i{Y}_i;U_i{V}_i\right)=I\left(X^n{Y}^n;MJ\right). \end{gathered}$$

Adding the first two expressions and subtracting the third yields

$$\begin{gathered} \sum _{i=1}^n\left[I\left(X_i,U_i\right)+I\left(Y_i;V_i\right)-I\left(X_i,Y_i;U_i,V_i\right)\right] \\ =\left[I\left(X^n;M\right)+I\left(Y^n;J\right)-I\left(X^n{Y}^n;MJ\right)\right]. \end{gathered}$$ (24)

Combining (23) and (24) yields

$$I(M;J)=\sum _{i=1}^{n}I\left(X_i;U_i\right)+I\left(Y_i;V_i\right)-I\left(X_i,Y_i;U_i,V_i\right)$$

as claimed.

Step 3:

For this step, we use the following lemma, proved in Appendix C as part of the demonstration that ${\mathcal{R}}_{\text{out }}$ is convex.

Lemma 1: Suppose $U_i{V}_i\in {\mathcal{P}}_{\text{out}}$, i = 1,2,…,n. Then there exists $UV\in {\mathcal{P}}_{\text{out}}$ such that

$$\begin{gathered} \frac{1}{n}\sum _{i=1}^{n}I\left(X_i;U_i\right)=I(X;U) \\ \frac{1}{n}\sum _{i=1}^{n}I\left(Y_i;V_i\right)=I(Y;V) \\ \frac{1}{n}\sum _{i=1}^{n}I\left(X_i{Y}_i;U_i{V}_i\right)=I(XY;UV). \end{gathered}$$

Applying Lemma 1 to the results of Steps 1 and 2, we obtain

$$\begin{gathered} R_x\ge \frac{1}{n}\sum _{i=1}^{n}I\left(X_i;U_i\right)=I(X;U) \\ {R}_y\ge \frac{1}{n}\sum _{i=1}^{n}I\left(Y_i;V_i\right)=I(Y;V) \\ {R}_c\le R_x+R_y-\frac{1}{n}\sum _{i=1}^{n}I\left(X_i{Y}_i;U_i{V}_i\right) \\ =R_x+R_y-I(XY;UV) \end{gathered}$$

where $UV\in {\mathcal{P}}_{\text{out }}$. With respect to this UV, by definition we have $R\in {\mathcal{R}}_{UV}$. Hence, $R\in {\mathcal{R}}_{\text{out }}$, and the proof is complete. □

Appendix C. Convexity of the Outer Bound

In this appendix, we prove a slightly more general version of Lemma 1 from Appendix B, and use this result to show that the outer bound rate region ${\mathcal{R}}_{\text{out }}$ is convex.

In the following, let $\mathcal{Q}$ be any finite alphabet, and assume that we have pairs X_qY_q for all $q\in \mathcal{Q}$ which are i.i.d. ~ p(xy).

Lemma 2: Suppose $U_q{V}_q\in {\mathcal{P}}_{\text{out}}$ for all $q\in \mathcal{Q}$, and let $Q~p(q)$, $q\in \mathcal{Q}$ be any discrete random variable independent of the pairs {X_qY_q}. Then there exists a pair of discrete random variables $UV\in {\mathcal{P}}_{\text{out}}$ such that

$$\begin{gathered} \sum _{q\in \mathcal{Q}}p(q)I\left(X_q;U_q\right)=I(X;U) \\ \sum _{q\in \mathcal{Q}}p(q)I\left(Y_q;V_q\right)=I(Y;V) \\ \sum _{q\in \mathcal{Q}}p(q)\left[I\left(X_q;U_q\right)+I\left(Y_q;V_q\right)-I\left(X_q{Y}_q;U_q{V}_q\right)\right] \\ =I(X;U)+I(Y;V)-I(XY;UV). \end{gathered}$$

Remark 4: Lemma 1 in Appendix B follows immediately from the above Lemma, by choosing $\mathcal{Q}=\{1,2,\dots ,n\}$ and p(q) = 1/n for all $q\in \mathcal{Q}$.

Proof: As a candidate for the pair UV in the lemma, consider $UV\in {\mathcal{P}}_{\text{conv}}$ for the given Q (see (4)), i.e., U = (U_Q,Q) and V = (V_Q,Q). To verify that $UV\in {\mathcal{P}}_{\text{out}}$, we proceed to check that U − X − Y and X − Y − V are Markov chains.

By the assumption $U_q{V}_q\in {\mathcal{P}}_{\text{out}}$ for each $q\in \mathcal{Q}$, we have I(U_q; Y_q | X_q) = 0 and I(V_q; X_q | Y_q) = 0. Hence

$$\begin{gathered} 0=\sum _{q\in \mathcal{Q}}p(q)I\left(U_q;Y_q|X_q\right) \\ =\sum _{q\in \mathcal{Q}}p(q)I\left(U_q;Y_q|X_q,Q=q\right) \\ =I\left(U_Q;Y_Q|X_{Q}Q\right) \\ \stackrel{(\text{a})}{=}I\left(U_Q;Y|X,Q\right) \\ =I\left(U_{Q}Q;Y|X\right)-I(Q;Y|X) \\ \stackrel{(\text{b})}{=}I\left(U_{Q}Q;Y|X\right) \\ =I(U;Y|X) \end{gathered}$$

where in (a) we are able to drop the subscript Q on X_Q and Y_Q because the X_q and Y_q are i.i.d. and independent of Q; and similarly (b) is because I(Q;Y | X) = 0, due to the independence of Q and Y. By an analogous calculation, we also find I(V; X | Y) = 0. Hence, U − X − Y and X − Y − V, and $UV\in {\mathcal{P}}_{\text{out}}$ as desired.

It remains to demonstrate the three equalities in the lemma. For the first, write

$$\begin{gathered} I(X;U)=I\left(X;U_{Q}Q\right) \\ =I\left(X;U_Q|Q\right)+I(X;Q) \\ \stackrel{(\underset{\_}{\text{a}})}{=}I\left(X;U_Q|Q\right) \\ \stackrel{(\text{b})}{=}I\left(X_Q;U_Q|Q\right) \\ =\sum _{q\in \mathcal{Q}}p(q)I\left(X_q;U_q\right) \end{gathered}$$

where, as above, (a) and (b) follow from the fact that the X_q are i.i.d. and independent of Q. Similar calculations yield

$$I(Y;V)=\sum _{q\in \mathcal{Q}}p(q)I\left(Y_q;V_q\right),$$

and

$$I(XY;UV)=\sum _{q\in \mathcal{Q}}p(q)I\left(X_q{Y}_q;U_q{V}_q\right).$$

The convexity of ${\mathcal{R}}_{\text{out}}$ follows readily from the preceding lemma.

Lemma 3: ${\mathcal{R}}_{\text{out}}$ is convex. That is, let R_q be any set of rates such that $R_q\in {\mathcal{R}}_{\text{out}}$ for all $q\in \mathcal{Q}$, where $\mathcal{Q}$ is a finite alphabet, and let p(q) be any probability distribution over $\mathcal{Q}$. Then $R={\sum }_{q\in \mathcal{Q}}p(q)R_q\in {\mathcal{R}}_{\text{out}}$.

Proof: Fix an arbitrary distribution p(q) and rates $R_q\in {\mathcal{R}}_{\text{out}}$ for all $q\in \mathcal{Q}$. By the definition of ${\mathcal{R}}_{\text{out}}$, for each rate R_q, there exists a pair $U_q{V}_q\in {\mathcal{P}}_{\text{out}}$ such that $R_q\in {\mathcal{R}}_{U_q{V}_q}$. Consequently

$$\begin{gathered} R_x=\sum _{q\in \mathcal{Q}}p(q)R_{x,q}\ge \sum _{q\in \mathcal{Q}}p(q)I\left(X_q;U_q\right) \\ {R}_y=\sum _{q\in \mathcal{Q}}p(q)R_{y,q}\ge \sum _{q\in \mathcal{Q}}p(q)I\left(Y_q;V_q\right) \\ {R}_c=\sum _{q\in \mathcal{Q}}p(q)R_{c,q} \\ \le \sum _{q\in \mathcal{Q}}p(q)\left[I\left(X_q;U_q\right)+I\left(Y_q;V_q\right)-I\left(X_q{Y}_q;U_q{V}_q\right)\right]. \end{gathered}$$

As in the proof of Lemma 2, use these pairs to construct a new pair UV, by defining U = (UQ, Q), V = (VQ, Q). From the proof of Lemma 2, we know 1) that $UV\in {\mathcal{P}}_{\text{out}}$, and 2) the sums on the right-hand sides of the inequalities above can be replaced with expressions in U and V, yielding

$$\begin{gathered} R_x\ge I(X;U) \\ {R}_y\ge I(Y;V) \\ {R}_c\le I(X;U)+I(Y;V)-I(XY;UV) \\ \le R_x+R_y-I(XY;UV) \end{gathered}$$

which means that $R\in {\mathcal{R}}_{UV}$ for the given UV. Hence, $R={\sum }_{q\in \mathcal{Q}}p(q)R_q\in {\mathcal{R}}_{\text{out}}$. Since p(q) and $R_q\in {\mathcal{R}}_{\text{out}}$ were arbitrary, we conclude that ${\mathcal{R}}_{\text{out}}$ is convex. □

Appendix D. Mixing Lemmas

In this appendix, we prove Lemmas 6 and 7, which are used in proving the outer bound.

Consider the elementary Shannon inequalities, stated in the following two lemmas. The variables A, B, α, β, γ, δ appearing in the lemmas denote arbitrary discrete random variables.

Lemma 4:

$$I(A;\alpha )=I(A;\alpha ,\gamma )-I(A,\alpha ;\gamma )+I(\alpha ;\gamma ).$$

Proof:

$$\begin{gathered} I(A;\gamma |\alpha )=I(A;\alpha ,\gamma )-I(A;\alpha ) \\ =I(A,\alpha ;\gamma )-I(\gamma ;\alpha ). \end{gathered}$$

Lemma 5:

$$I(A;\alpha )+I(B;\beta )=I(A;B)+I(\alpha ;\beta )-I(A,\alpha ;B,\beta )+I(A,B;\alpha ,\beta ).$$

Proof:

$$\begin{gathered} I(A,\alpha ;B,\beta )-I(A,B;\alpha ,\beta ) \\ =H(A,\alpha )+H(B,\beta )-H(A,B)-H(\alpha ,\beta ) \\ =-I(A;\alpha )-I(B;\beta )+I(A;B)+I(\alpha ;\beta ). \end{gathered}$$

Lemma 6 follows directly from the preceding lemmas.

Lemma 6:

$$I(\alpha ;\beta )\ge I(A;\alpha )+I(B;\beta )-I(A,B;\alpha ,\beta )$$

with equality if and only if I(A, α; B, β) = I(A; B).

Proof: Rearrange Lemma 5 to get

$$I(\alpha ;\beta )=I(A;\alpha )+I(B;\beta )-I(A,B;\alpha ,\beta )+[I(A,\alpha ;B,\beta )-I(A;B)].$$

The lemma now follows readily from the preceding expression: We obtain equality in the lemma if (and only if) the term in brackets is zero. Otherwise, the bracketed term is nonnegative, since

$$\begin{gathered} I(A,\alpha ;B,\beta )-I(A;B) \\ =H(\alpha |A)+H(\beta |B)-H(\alpha ,\beta |A,B) \\ =H(\alpha |A)-H(\alpha |A,B)+H(\beta |B)-H(\beta |A,B,\alpha ) \\ \ge 0, \end{gathered}$$

where the inequality is due to the fact that conditioning does not increase entropy. □

Lemma 7: If U_i = (γ, Aⁱ⁻¹), then

$$I\left(A^n;\gamma \right)=\sum _{i=1}^{n}I\left(A_i;U_i\right)-\sum _{i=2}^{n}I\left(A_i;A^{i-1}\right),$$

Proof: In Lemma 4, put A = A_i, α = Aⁱ⁻¹ Note that U₁ = γ. Hence, substituting and summing from 2 to n yields

$$\begin{gathered} \sum _{i=2}^{n}I\left(A_i;A^{i-1}\right) \\ =\sum _{i=2}^{n}I\left(A_i;U_i\right)-I\left(A^n;\gamma \right)+I\left(A_1;\gamma \right) \\ =\sum _{i=2}^{n}I\left(A_i;U_i\right)-I\left(A^n;\gamma \right)+I\left(A_1;U_1\right) \\ =\sum _{i=1}^{n}I\left(A_i;U_i\right)-I\left(A^n;\gamma \right). \end{gathered}$$

Appendix E. Alternative Representations of ${\mathcal{R}}_{\text{in}}$ and ${\mathcal{R}}_{\text{out}}$

Here we show that the alternative representations of the inner and outer bound surfaces introduced in Remark 2 are in fact equivalent, i.e., ${\mathcal{R}}_{\text{in }}={\mathcal{R}}_{\text{in }}^{\prime }={\mathcal{R}}_{\text{in}}^{\prime \prime }$, ${\mathcal{R}}_{\text{out }}={\mathcal{R}}_{\text{out }}^{\prime }={\mathcal{R}}_{\text{out}}^{\prime \prime }$.

We show first that ${\mathcal{R}}_{\text{out}}^{\prime }={\mathcal{R}}_{\text{out}}^{\prime \prime }$. Suppose $R\in {\mathcal{R}}_{\text{out}}^{\prime }$. Then, using U − X − Y, X − Y − V we have

$$\begin{gathered} R_c\le I(U;V)-I(U;V|XY) \\ =I(X;U)+I(Y;V)-I(XY;UV) \end{gathered}$$ (25)

which implies

$$\begin{gathered} R_x\ge I(X;U) \\ \ge I(XY;UV)-I(Y;V)+R_{\text{c}} \\ =I(XY;U|V)+R_c \end{gathered}$$

and similarly R_y ≥ I(XY; V | U) + R_c; and

$$\begin{gathered} R_x+R_y\ge I(X;U)+I(Y;V) \\ \ge I(XY;UV)+R_c. \end{gathered}$$

We conclude that $R\in {\mathcal{R}}_{\text{out}}^{\prime \prime }$, hence ${\mathcal{R}}_{\text{out }}^{\prime }\subseteq {\mathcal{R}}_{\text{out}}^{\prime \prime }$. A symmetrical argument shows ${\mathcal{R}}_{\text{out }}^{\prime \prime }\subseteq {\mathcal{R}}_{\text{out}}^{\prime }$, proving ${\mathcal{R}}_{\text{out }}^{\prime }={\mathcal{R}}_{\text{out}}^{\prime \prime }$.

Next, we show that ${\mathcal{R}}_{\text{out}}$ and ${\mathcal{R}}_{\text{out}}^{\prime }$ are identical. To this end, note that these sets correspond to regions in the positive orthant ${ℝ}_{+}^3$, and that two such regions are identical if they have the same surfaces. Following the presentation in Section VII, the surfaces of ${\mathcal{R}}_{\text{out}}$ and ${\mathcal{R}}_{\text{out}}^{\prime }$ are

$$\begin{gathered} r_{\text{out}}\left(r_x,r_y\right)=\underset{UV\in {\mathcal{C}}_{\text{out }}\left(r_x,r_y\right)}{\text{max}}{r}_x+r_y-I(XY;UV) \\ {r}_{\text{out }}^{\prime }\left(r_x,r_y\right)=\underset{UV\in C_{\text{out }}\left(r_x,r_y\right)}{\text{max}}I(U;V)-I(U;V|XY) \end{gathered}$$

where

$${\mathcal{C}}_{\text{out}}\left(r_x,r_y\right)=\{UV\in {\mathcal{P}}_{\text{out}}:I(U;X)=r_x,I(V;Y))=r_y\}.$$

$$\begin{gathered} r_{\text{out }}^{\prime }\left(r_{x,}{r}_y\right) \\ =\underset{UV\in {\mathcal{C}}_{\text{out }}\left(r_x,r_y\right)}{\text{max}}I(X;U)+I(Y;V)-I(XY;UV) \\ =\underset{UV\in {\mathcal{C}}_{\text{in}}\left(r_x,r_y\right)}{\text{max}}{r}_x+r_y-I(XY;UV) \\ =r_{\text{out }}\left(r_x,r_y\right). \end{gathered}$$

Thus, the desired equivalence ${\mathcal{R}}_{\text{out}}={\mathcal{R}}_{\text{out}}^{\prime }$ follows simply from the fact that at the surfaces, the inequalities defining each region become equalities.

The same line of argument as above of course also shows ${\mathcal{R}}_{\text{in}}={\mathcal{R}}_{\text{in}}^{\prime }={\mathcal{R}}_{\text{in}}^{\prime \prime }$.

Appendix F. Simplification of Convex Hulls

In this appendix, we argue geometrically that the expressions for the convex hulls of the inner bound regions simplify to just one term in both the binary and Gaussian cases. To discuss both cases simultaneously, let us represent the surface of either inner bound by a positive-valued function $f:\mathcal{D}\to {ℝ}_{+}$. Here, $\mathcal{D}$ is a square region

$$\mathcal{D}=\left\{r=(x,y)\in {ℝ}^2:0\le x\le M,0\le y\le M\right\}$$

and M is a positive constant. In the binary case, f(r) = s(r), and $\mathcal{D}=[0,1]\times [0,1]$; in the Gaussian case, f(r) = S(r) and $\mathcal{D}=[0,\infty )\times [0,\infty )$. Some important properties shared by both cases are that for all $\mathcal{D}=[0,\infty )\times [0,\infty )$

$$\begin{gathered} f(x,y)\ge 0,f(0,y)=f(x,0)=0 \\ {f}_x(r),f_y(r)>0,f_{xx}(r),f_{yy}(r)<0 \end{gathered}$$

where the subscripts denote partial derivatives.

Denote the convex hull of f(r) by c(r). Generically, the boundary of the convex hull is

$$c(r)=\text{max}\theta f\left(r_1\right)+\overline{\theta }f\left(r_2\right)$$

where the maximum is over all triples (θ, r₁, r₂) such that $r\text{=}\theta r_1+\overline{\theta }{r}_2,\theta \in [0,1]$, and $r_1,r_2\in \mathcal{D}$. However, as argued next, for the cases under study this simplifies to

$$c(r)=\text{max}\theta f\left(r^{\prime }\right)$$

where r = θr′.

The convex hull of a surface can be characterized in terms of its tangent planes. Given any point $r^{\prime }=(x,y)\in \mathcal{D}$, if its tangent plane lies entirely above the surface, then (r′, f(r′)) is on the convex hull. If the tangent plane cuts through the surface at one or more other points, or if the tangent plane lies below the surface, then (r, f(r)) is not on the convex hull. If the tangent plane intersects the surface at exactly two points, then both points are on the convex hull.

The tangent plane at an arbitrary point $r^{\prime }=\left(x^{\prime },y^{\prime }\right)\in \mathcal{D}$ is the set of points satisfying

$$z(x,y)=f_x\left(x-x^{\prime }\right)+f_y\left(y-y^{\prime }\right)+z^{\prime }$$

where the partial derivatives are evaluated at r′, i.e., f_x = f_x(r′), f_y = f_y(r′), and z′ = f(r′). The tangent plane intersects the z = 0 plane in a line. Setting z(r) = 0 and solving

$$\begin{gathered} y=mx+b,\text{where} \\ m=-\left(f_x/f_y\right) \\ b=1/f_y\left[x^{\prime }{f}_x+y^{\prime }{f}_y-z^{\prime }\right]. \end{gathered}$$

Since f_x, f_y > 0, the slope m = −(f_x/f_y) is negative. This line intersects the positive orthant whenever the intercept b ≥ 0, in which case the tangent plane cuts through the surface, since f ≥ 0. Thus, the only points on the original surface f(x,y) that can be on the convex hull are those for which b ≤ 0.

Next, consider any path through $\mathcal{D}$ along a line segment y = αx, α > 0, starting from one of the “outer edges” of $\mathcal{D}$, where x = M or y = M, and consider what happens to the tangent plane’s line of intersection ℓ with the z = 0 plane as we move in along the path toward the origin (0, 0). Initially, the tangent planes lie entirely above the surface, and the intercept of ℓ is negative, b < 0. This intercept increases along the path until b = 0, at which point ℓ intersects (0, 0). Here, the tangent plane contains a line segment attached on one end to the point of tangency, and at the other end to the point (r, f(r)) = (0, 0, 0); everywhere else, the tangent plane is above the surface. Continuing toward the origin, all other points along the path have tangent planes such that ℓ has a positive intercept b > 0, hence, these points are excluded from the convex hull.

These considerations imply that the convex hull c(r) is composed entirely of two kinds of points. First, points which coincide with the original surface, c(r), = θf(r) with θ = 1. These points occur at values of r = (x, y) “up and to the right” of (0, 0). Second, points along line segments connecting surface points “up and to the right” (r′, f(r′)) with the point (r, f(r)) = (0, 0, 0), that is $c(r)=\theta f\left(r^{\prime }\right)+\overline{\theta }f(0,0)=\theta f\left(r^{\prime }\right)$, where r = θr′ and θ ∈ [0, 1]. Hence, for all $r\in \mathcal{D}$, c(r) has the desired form.

Two more examples of functions that behave in the same way just described are f(x, y) = (1 − (1 − x)²)(1 − (1 − y)²) and f(x, y) = xy, with $\mathcal{D}=[0,1]\times [0,1]$.

Appendix G. Properties of Gaussian Mutual Information

Our analysis of the Gaussian pattern recognition problem relies on the following well-known results, stated below without proof.

Lemma 8: The mutual information between two Gaussian random vectors X and Y depends only on the matrices of correlation coefficients. Specifically

$$I(X;Y)=\frac{1}{2}\text{log}\left(\text{det}{C}_{x,x}\right)-\frac{1}{2}\text{log}\left(\text{det}{C}_{x,x}|y\right)$$

where

$$C_{x,x|y}=C_{x,x}-C_{x,y}{C}_{y,y}^{-1}{C}_{y,x}.$$

In the special case Y = X + W, where X and W are independent Gaussian random variables with variances P and N, respectively, we have

$$I(X;Y)=\frac{1}{2}\text{log}\left(1+\frac{P}{N}\right)=-\frac{1}{2}\text{log}\left(1-{\rho }_{x,y}^2\right)$$

where the correlation coefficient ${\rho }_{x,y}=\sqrt{P/(P+N)}$.

Lemma 9: If X, Y and Z are zero-mean Gaussian random vectors that form a Markov chain X − Y − Z, then

$$C_{x,z}=C_{x,y}{C}_{y,y}^{-1}{C}_{y,z}.$$

Note that for dimension one, X → Y → Z ρ_x,z = ρ_x,yρ_y,z implies.

Lemma 10: Let X, Y, U, and V be jointly Gaussian random variables such that U − X − Y and X − Y − V are Markov chains. Then the matrix of correlation coefficients C_xy,uv decomposes as

$$C_{xy,uv}=\left[\begin{array}{cc}1& {\rho }_{xy}\\ {\rho }_{xy}& 1\end{array}\right]\left[\begin{array}{cc}{\rho }_{xu}& 0\\ 0& {\rho }_{yv}\end{array}\right].$$

This lemma follows immediately by using Lemma 9 to obtain the substitutions $C_{x,v}=C_{x,y}{C}_{y,y}^{-1}{C}_{y,v}={\rho }_{xy}{\rho }_{yv}$ and $C_{x,y}=C_{u,x}{C}_{x,x}^{-1}{C}_{x,y}={\rho }_{ux}{\rho }_{xy}$.