Abstract
T cell receptor stimulation initiates a cascade of reactions that cause an increase in intracellular calcium (Ca2+) concentration mediated through inositol 1,4,5-trisphosphate (IP3). To understand the basic mechanisms by which the immune response in T cells is activated, it is useful to understand the signaling pathways that contain important targets for drugs in a quantitative fashion. A computational model helps us to understand how the selected elements in the pathways interact with each other, and which component plays the crucial role in systems. We have developed a mathematical model to explore the mechanism for controlling transcription factor activity, which regulates gene expression, by the modulation of calcium signaling triggered during T cell activation. The model simulates the activation and modulation of Ca2+ release-activated Ca2+ (CRAC) channels by mitochondrial dynamics and depletion of endoplasmic reticulum (ER) store, and also includes membrane potential in T-cells. The model simulates the experimental finding that increases in Ca2+ current enhances the activation of transcription factors and the Ca2+ influx through CRAC is also essential for the NFAT and NFκB activation. The model also suggests that plasma membrane Ca2+-ATPase (PMCA) controls a majority of the extrusion of Ca2+ and modulates the activation of CRAC channels. Furthermore, the model simulations explain how the complex interaction of the endoplasmic reticulum, membrane potential, mitochondria, and ion channels such as CRAC channels control T cell activation.
Keywords: Biochemistry, Bioinformatics, Immunology, Mathematical biology, Biophysics, Systems biology, Immune response, Immune system, Calcium signaling, Mathematical modeling, T cell activation, NFAT, JNK, NFkappaB
Biochemistry; Bioinformatics; Immunology; Mathematical Biology; Biophysics; Systems Biology; Immune Response; Immune System; calcium signaling; Mathematical Modeling; T cell activation; NFAT; JNK; NFkappaB
1. Introduction
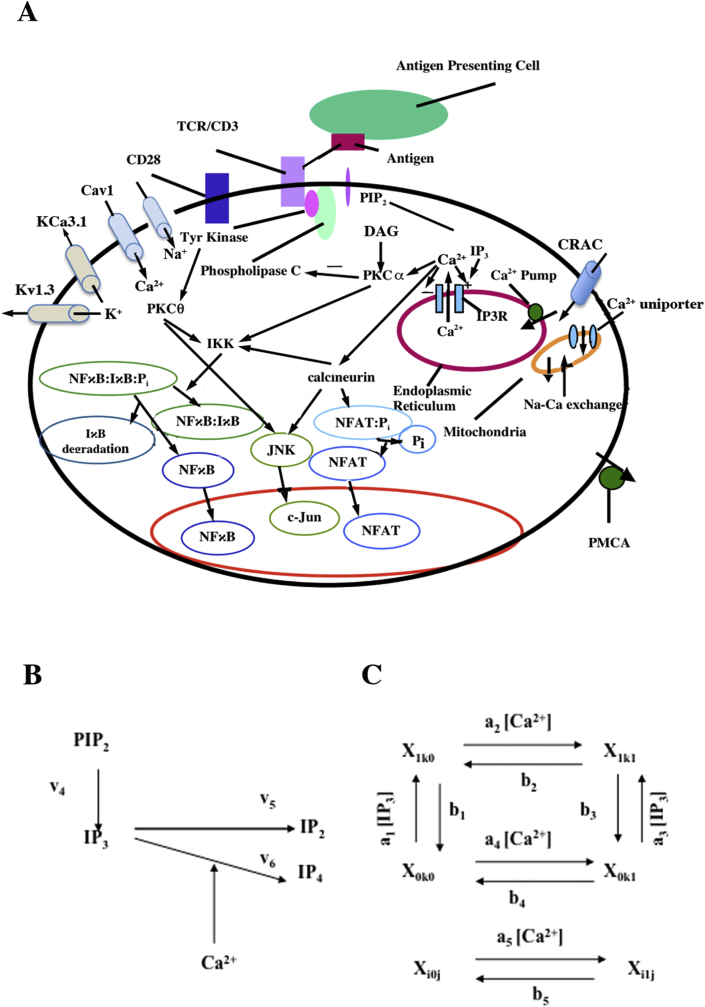
In many cells, the interplay of calcium (Ca2+) uptake and release processes results in oscillations in the intracellular Ca2+ concentration when surface receptors are stimulated by agonist [1]. As diagrammed in Figure 1A, the binding of antigen-MHC (major histocompatibility complex) complexes to the T cell receptor (TCR) results in the activation of a tyrosine kinase that phosphorylates phospholipase C-gamma (PLC-γ) causing its activation. Activated PLC-γ cleaves phosphatidyl inositol (PIP2) in the plasma membrane into two parts, diacylglycerol (DAG) and inositol 1,4,5-triphosphate (IP3). The molecule DAG remains in the plasma membrane and activates protein kinase C (PKC). IP3, in contrast, is a diffusible cytosolic messenger, which binds to the IP3 receptor on the endoplasmic reticulum (ER) and synergistically with Ca2+ causes Ca2+ release from the ER. The ER is refilled by the sarcoplasmic and endoplasmic reticulum Ca2+-ATPases (SERCA) pump [2]. In addition, there are also other membrane ion channels, voltage-dependent calcium (Cav1) and voltage- (Kv1.3) [3,4] and calcium-dependent potassium channels (IK(Ca), KCa3.1) [4, 5, 6], that maintain the membrane potential [7, 8].
Figure 1.
Schematic diagram for T cell activation and mechanism of IP3 activation. (A) Schematic diagram of the mechanism of Ca2+ dynamics in T-cells. (B) IP3 activation pathway. (C) The model of IP3R/channel subunit [78]. Each subunit represents an IP3 binding site, activating and inactivating Ca2+ binding site. Each state is labeled Xikj, where i (IP3 binding site), j (activating Ca2+ binding site) and k (inactivating Ca2+ binding site) are equal to 0 (unoccupied binding site) or 1 (occupied binding site) [78].
Many studies have indicated that Ca2+ release-activated Ca2+ (CRAC) channels are responsible for Ca2+ influx, and that plasma membrane Ca2+-ATPases (PMCA) play a major role in removal of Ca2+ in T cells [9]. In addition, mitochondria can modulate the Ca2+ influx by reducing the Ca2+-dependent inactivation of CRAC channels [10]. The Ca2+ ion is a signaling molecule that binds to and activates the phosphatase calcineurin, which in turn binds to and dephosphorylates NFAT (nuclear factor – activated T cells) [11, 12, 13, 14]. Dephosphorylation exposes nuclear localization signals on NFAT [15], resulting in rapid translocation of the NFAT-calcineurin complex to the nucleus where it can participate in promoting gene transcription [16]. In contrast to NFAT, NFκB is retained in the cytoplasm not by phosphorylation but by association with the inhibitory IκB protein [17]. Increasing Ca2+ and activated PKCθ co-activate Iκ kinase (IKK) and phosphorylates IκB associated with NFκB allowing the IκB to dissociate from NFκB and marking the IκB for subsequent polyubiquitination and degradation by the proteasome [18, 19]. The free NFκB is translocated to the nucleus where it can bind to DNA and promote gene transcription. Moreover, in the related c-Jun NH2-terminal kinase (JNK) pathway, PKCθ mediates the activation of c-Jun (Figure 1A). PKC-θ is induced by co-stimulation of TCR/CD3 and CD28. Several studies show that PKCθ regulates the mitogen-activated protein kinase (MAP kinase) cascade, SEK1/MKK4 that directly phosphorylate JNK [20, 21]. Ca2+ activated calcineurin also activates on SEK1. Integration of these two activities reaches the full activation of JNK [22]. As in result, activated JNK phosphorylates two positive regulatory serine residues in the activation domain of c-Jun. Finally, c-Jun and c-Fos protein together forms the activator-protein 1 (AP-1) transcription factors complex that participate in cell growth [23].
Our previous model simulated the calcium clamp protocol used in the in vitro experiments used by Dolmetsch and co-workers; in vivo, however, the T cell has more complex calcium dynamics [24, 25]. The calcium dynamics model presented here explores how the interplay between Ca2+ influx through CRAC channels, the mitochondria, the plasmalemmal Ca2+-ATPase (PMCA) pump, and ER stores work together to control cytosolic calcium concentration ([Ca2+]cyt) dynamics and how membrane currents affect the calcium dynamics. This novel model includes the following features: 1) a mechanistic description of the cytosolic Ca2+ dynamics that relies on local Ca2+ signaling based on the experimental data of Bautista and co-workers [26]; 2) IP3 production and degradation based on the work of Swillens and Mercan [27]; 3) A novel description of the CRAC channel; 4) a description of the PMCA pump based on the experimental kinetics observed by Bautista and co-workers [26]; 5) a description of the membrane potentials and the ion channels that regulate it 6) a voltage-dependent potassium channel (Kv1.3) based on the experimental data of Dupuis et al. [28]; 7) a calcium-dependent potassium channel based upon the data of Verheugen et al. [29]; 8) a description of the TRPM4 channel by Gaur et al. [30]; 9) a new formulation of the TRPC3 channel based on the experimental data of Rose et al. [31].; 10) the Cl− channel based on data by Feske [8] 11) the L-type Ca2+ channel description by Luo and Rudy [32]; and a Na+ channel description by Luo and Rudy [32].
Defects in the activation of NFAT and expression of IL-2 have been implicated in a number of human diseases and conditions. In several patients, failure to activate NFAT was shown to cause severe combined immunodeficiency disease, SCID [8]. In contrast, a number of studies have suggested that active NFAT from patients infected by human immunodeficiency virus 1 (HIV-1) or human T-cell lymphotropic virus type-1 (HTLV-1) boost the viral infectivity [33]. The NFAT pathway is also an important target for drugs such as FK506 and cyclosporine A, both powerful immunosuppressants that block the activation of calcineurin's phosphatase activity [34, 35, 36]. While these drugs are useful for preventing the rejection of transplanted tissues, immune system suppression can lead to severe side effects, such as secondary tumors and opportunistic infections [37], and progressive loss of renal function and neurotoxicity [38]. In addition, inhibition of transcription factor activation in other types of cells can have unintended and undesirable consequences [39].
A quantitative understanding of the mechanisms of T cell activation would help to predict the underlying mechanisms and suggest possible targets for drug intervention. Therefore, computational models are useful to understand the complex Ca2+ dynamics in transcription factors activation pathways both to find better ways to control the immune system in transplant patients and to find therapies for immunodeficiency viral infections.
2. Results
Using the parameter values in Tables 1, 2, 3, 4, 5, 6, and 7, the model under resting conditions reached steady state variable values shown in Table 8. After 1000 s at rest, the variable stay near the initial values with the membrane potential within the experimental range of 50–60 mV assuming the value of 59.0 mV at rest [7, 8]. Calcium concentrations for cytoplasmic (0.089 μM), endoplasmic (335.8 μM), and mitochondrial (0.00054 μM) calcium also fall within experimental ranges [7, 8, 40].
Table 1.
IP3 and DAG production and degradation parameters.
| Parameters | Definition | Values | Reference |
|---|---|---|---|
| v4 | Maximal rate of IP3 and DAG formation by PLC | 5.0 μM s−1 | Scaled from [27] |
| v5 | Maximal rate of IP3 dephosphorylation | 12.5 μM s−1 | Scaled from [27] |
| v6 | Maximal rate of IP3 phosphorylation | 0.9 μM s−1 | Scaled from [27] |
| K5 | IP3 dissociation constant | 6.0 μM | Scaled from [27] |
| K6 | IP3 dissociation constant | 0.1 μM | Scaled from [27] |
| K7 | Ca2+ dissociation constant | 1.0 μM | Scaled from [27] |
| H | Hill coefficient | 1 | [27] |
| v8 | DAG degradation rate | 1.0 s−1 | Estimated |
Table 2.
Ca2+ Regulatory Mechanism Parameters and Binding Constants of IP3 receptor.
| Parameters | Definition | Values | Reference |
|---|---|---|---|
| v1 | Maximum IP3 receptor flux | 90 s−1 | Rescaled from [78] |
| a1 | IP3 binding constant | 400 μM−1 s−1 | [78] |
| a2 | Ca2+ inhibitory receptor binding constant | 0.2 μM−1 s−1 | [78] |
| a3 | IP3 binding constant | 400 μM−1 s−1 | [78] |
| a4 | Ca2+ Inhibitory receptor binding constant | 0.2 μM−1 s−1 | [78] |
| a5 | Ca2+activation receptor binding constant | 20.0 μM−1 s−1 | [78] |
| d1 | IP3 dissociation constant | 0.13 μM | [78] |
| d2 | Ca2+ Inhibitory receptor dissociation constant | 1.049 μM | [78] |
| d3 | IP3 dissociation constant | 0.9434 μM | [78] |
| d4 | Ca2+ Inhibitory receptor dissociation constant | 0.1445 μM | [78] |
| d5 | Ca2+activation receptor dissociation constant | 82.34 nM | [78] |
| vSERCA | Maximal velocity for SR Ca2+ ATPase | 1.0 μM s−1 | [2, 78] |
| Kserca | Ca2+ dissociation constant for SR Ca2+ ATPase | 0.1 μM | [2, 78] |
| τsscyt | Transfer time constant between subspace and cytosol | 0.5 s | Estimated |
Table 3.
Ca2+ buffering parameters.
| Parameters | Definition | Values | Reference |
|---|---|---|---|
| [Bs]cyt | Total cytosolic stationary buffer concentration | 225.0 μM | [2] |
| [Bs]ss | Total subspace stationary buffer concentration | 5.0 mM | |
| [Bs]ER | Total stationary buffer concentration in the ER | 2.0 mM | [2] |
| [Be]cyt | Total cytoplasmic buffer concentration in the cytosol | 111.0 μM | [2] |
| [Be]SS | Total buffer concentration in the subspace | 111.0 μM | Same as [Be]cyt |
| [Be]ER | Total buffer concentration in the ER | 111.0 μM | Same as [Be]cyt |
| KsER | Stationary buffer dissociation constant in ER | 1.0 μM | [2] |
| Kscyt | Cytosolic stationary buffer dissociation constant for Ca2+ | 0.1 μM | [2] |
| Ksss | Subspace stationary buffer dissociation constant for Ca2+ | 0.1 μM | Same as Kscyt |
| Kecyt | Mobile cytoplasmic buffer dissociation constant for Ca2+ in the cytosol | 0.123 μM | [26] |
| Kess | Mobile buffer dissociation constant for Ca2+ in the subspace | 0.123 μM | Same as Kecyt |
| KeER | Mobile buffer dissociation constant for Ca2+ in the ER | 0.123 μM | Same as Kecyt |
Table 4.
Parameters of mitochondrial dynamics.
| Parameters | Definition | Values | Reference |
|---|---|---|---|
| PUNI | Uniporter Ca2+ permeability | 2.776× 10−14 s−1 | Estimated |
| αm | Mitochondrial Ca2+ activity coefficient | 0.2 | [89] |
| αss | Subspace Ca2+ activity coefficient | 1.0 | Fit to [26] |
| Vnc | Na+-Ca2+ exchanger maximal velocity | 1.836 μM s−1 | Estimated |
| KNa | Na+-Ca2+ exchanger Na + affinity | 8.0 mM | [90] |
| KCa | Na+-Ca2+ exchanger Ca2+ affinity | 8 μM | [90] |
| Ψm | Mitochondrial membrane potential | 160 mV | [91] |
| [Na+]SS | Extramitochondrial Na+ concentration | 5.0 mM | [32] |
| [Na+]m | Mitochondrial Na+ concentration | 5.0 mM | Estimated |
| βCa | Ca2+ buffers in the mitochondria. | 0.01 | [92] |
Table 5.
Parameters of ICRAC channel and PMCA pump.
| Parameters | Definition | Values | Reference |
|---|---|---|---|
| Vu | Unmodulated PMCA velocity | 1.54×106 s−1 | [26] |
| Ku | Dissociation constant for Ca2+ stimulation of unmodulated PMCA | 303.0 nM | [26] |
| Vm | Modulated PMCA velocity | 2.20×106 s−1 | [26] |
| Km | Dissociation constant for Ca2+ stimulation of modulated PMCA | 140.0 nM | [26] |
| Kinact | Dissociation constant for ORAI1 Ca2+ inhibition by CRACR2A | 0.8 μM | Estimated |
| Kcc | Dissociation constant for time constant for ORAI1 inhibition by calmodulin | 2.0 μM | Estimated |
| Kact | Dissociation constant for ER Ca2+ inhibition | 200.0 μM | Estimated |
| τinact | JCRAC inactivation time constant | 40 s | [10] |
| τact | JCRAC activation time constant | 3 s | [93] |
| αSS | Subspace Ca2+ activity coefficient | 1.0 | Fit to [26] |
| αo | Extracellular Ca2+ activity coefficient | 0.341 | Fit to [26] |
| PCRAC | CRAC permeability to Ca2+ | 2.8 × 10−10 cm3/s | Estimated |
Table 6.
General parameters.
| Parameters | Definition | Values | Reference |
|---|---|---|---|
| z | Valence of Ca2+ | 2 | Physical constant |
| F | Faraday's constant | 96484.6 coul (mol e−)−1 | Physical constant |
| R | Ideal gas constant | 8314 mJ mol−1 K−1 | Physical constant |
| T | Absolute temperature | 310 K | Body temp |
| VT | T cell volume | 2 pl | [26] |
| Vcyt | Cytosol volume | 1.1 pl | [94] |
| VSS | Subspace volume | 0.11 pl | [94] |
| VER | ER volume | 0.011 pl | [94] |
| Vmito | Mitochondrial matrix volume | 0.088 pl | [94] |
Table 7.
–Membrane currents parameters.
| Parameters | Definition | Values | Reference |
|---|---|---|---|
| Emax | Maximum conductance for Ca2+-dependent K+ channel | 0.8 nS | [6, 29] |
| Kd | Ca2+ dissociation constant for Ca2+-dependent K+ channel | 0.45 μM | [29] |
| gt | Maximum conductance of the K+ channels | 3.0 nS | [6] |
| EK | Reversal potential of K+ | -84 mV | [6, 95] |
| gCl | Maximum conductance of the background current | 0.07 nS | Estimated |
| ECl | Reversal potential for Cl- | -33.0 mV | [95] |
| gNa | Maximum conductance of the Na + channels | 3.0 nS | Estimated |
| ENa | Reversal potential of K+ | -70 mV | [6, 95] |
| Cm | Membrane capacitance | 2.5e-3 nF | [94] |
| ECa | Reversal potential of Ca2+ | 60 mV | [6, 95] |
| PcaL | L-type Ca2+ channel permeability | 0.3 x 10−7 cm2s−1 | [32] |
| gTRPC3 | Maximum conductance of TRPC3 channels | 0.00195 nS | Estimated |
| KDAG | DAG binding constant for TRPC3 activation | 2.0 μM | Estimated |
| ETRPM4 | TRPM4 reversal potential | 0.2 mV | [30] |
| gTRPM4 | Maximum conductance of TRPM4 channels | 1.2 nS | Estimated |
| τxCa | Hodgkin-Huxley time constant TRPM4 channel | 30 s | [30] |
Table 8.
Steady-state values.
| Variables | Initial values |
|---|---|
| [Ca2+]cyt | 0.089 μM |
| [Ca2+]ER | 335.5 μM |
| [Ca2+]m | 0.00054 μM |
| [Ca2+]ss | 0.33 μM |
| V | -58.1 mV |
| [IP3]cyt | 0.018 μM |
| [DAG] | 0.050 μM |
| X100 | 0.039 |
| X110 | 0.042 |
| X000 | 0.27 |
| X010 | 0.29 |
| X001 | 0.17 |
| X101 | 0.0033 |
| X011 | 0.18 |
| X111 | 0.0035 |
| u | 0.53 |
| m | 0.0898 |
| h | 0.0796 |
| n | 0.04 |
| j | .08 |
| d | 0.00038 |
| f | 0.94 |
| xCa | 0.0497 |
| JNK:PKC:Cn | 0.00398 |
| [NFAT:Pi]c | 0.00957 μM |
| [NFAT:C∗]n | 0.000723 μM |
| [NFκB]n | 49.13 nM |
| [NFκB:IκB]c | 31.69 nM |
| inact | 0.90 |
| proact | 0.081 |
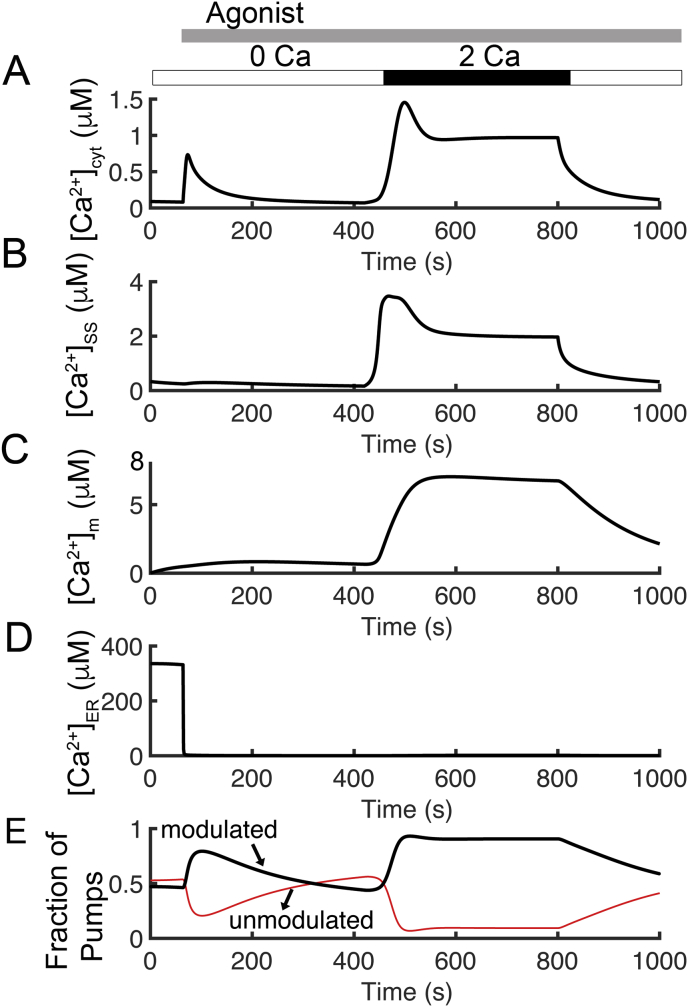
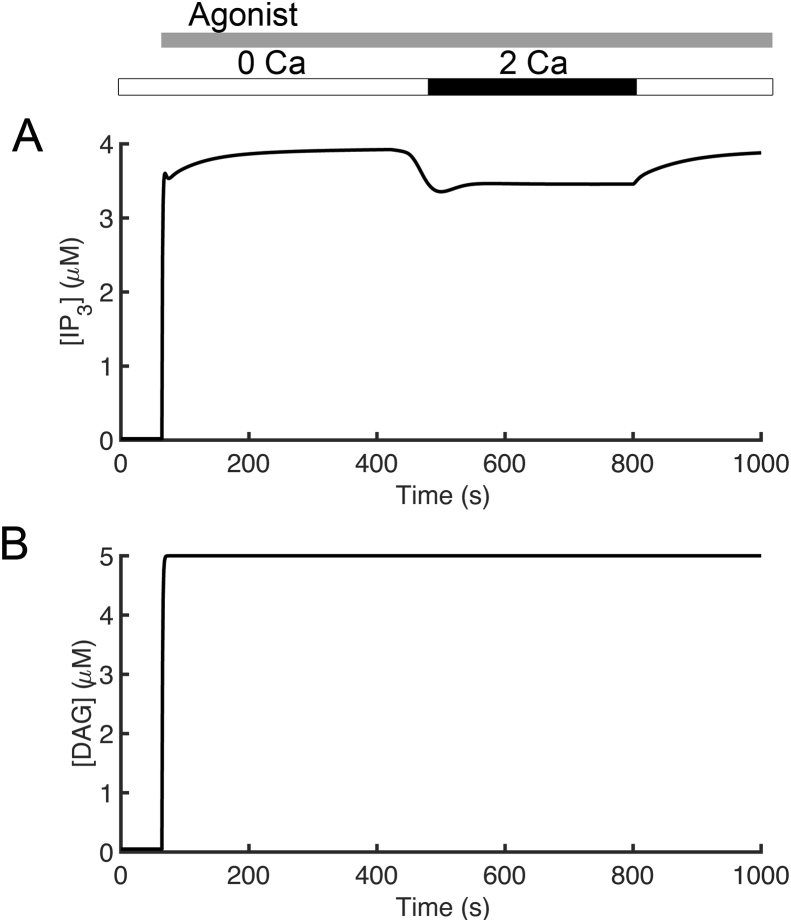
Figure 2 presents simulations of cytosolic and endoplasmic reticulum calcium concentrations and fluxes. In these simulations, the extracellular calcium concentration ([Ca2+]o) was set to 2.0 mM from 420 s to 800 s and 0.0 mM otherwise. Increasing levels of agonist stimulation are assumed to result in increasing PLC activity in accordance with experimental studies on T cell receptor activation and PLC activity [41]. The application of agonist (indicated by the gray bar in Figure 2A) is simulated by increasing the rate of IP3 production (and DAG) from PIP2 by phospholipase C (v4) from 0.05 μM s−1 to 5.0 μM s−1 after 64 s. The simulated traces for cytosolic [IP3] and [DAG] are shown in Figure 3. Simulated cytosolic calcium concentration is shown in Figure 2A. After the simulated application of agonist, there is a transient increase in [Ca2+]cyt.. After the addition of 2.0 mM [Ca2+]o, a larger increase from baseline to a ~1.5 μM, followed by a slow decrease to a plateau of approximately 1.0 μM is observed. These results agree with the results observed by Bautista and co-workers [26]. The time course of [Ca2+]SS is similar to that of [Ca2+]cyt except that the plateau of the second transient is larger in amplitude (Figure 2B). The cytosolic Ca2+ transients are accompanied by mitochondrial Ca2+ transients that are significantly larger in amplitude shown in Figure 2C. Figure 2D shows an initial depletion of [Ca2+]ER as Ca2+ is released from the ER store in response to agonist. During the Ca2+ transients, the model predicts that PMCA switches from the unmodulated (Figure 2E; red line) to the modulated state (Figure 2E; black line) whenever [Ca2+]cyt is elevated above the resting level.
Figure 2.
Simulated Ca2+ transients with [Ca2+]o = 2.0mM from 420s to 800s and agonist application after 60s. (A) The simulated cytosolic calcium concentration. (B) Subspace calcium transients are slightly higher than the cytosolic calcium concentration. (C) Mitochondrial Ca2+ concentration is higher than both [Ca2+]cyt and [Ca2+]ss. (D) Initial intracellular ER store calcium concentration depletion as Ca2+ is released from the ER store, and an additional decrease in [Ca2+]ER after removal of extracellular calcium. (E) A comparison of PMCA states corresponds to Ca2+ transient from unmodulated (red line) to modulated (black line) PMCA with [Ca2+]o set to 2.0 mM from 420 s to 800 s.
Figure 3.
Simulated concentrations in T cell. (A) cytosolic IP3 and (B) DAG concentrations.
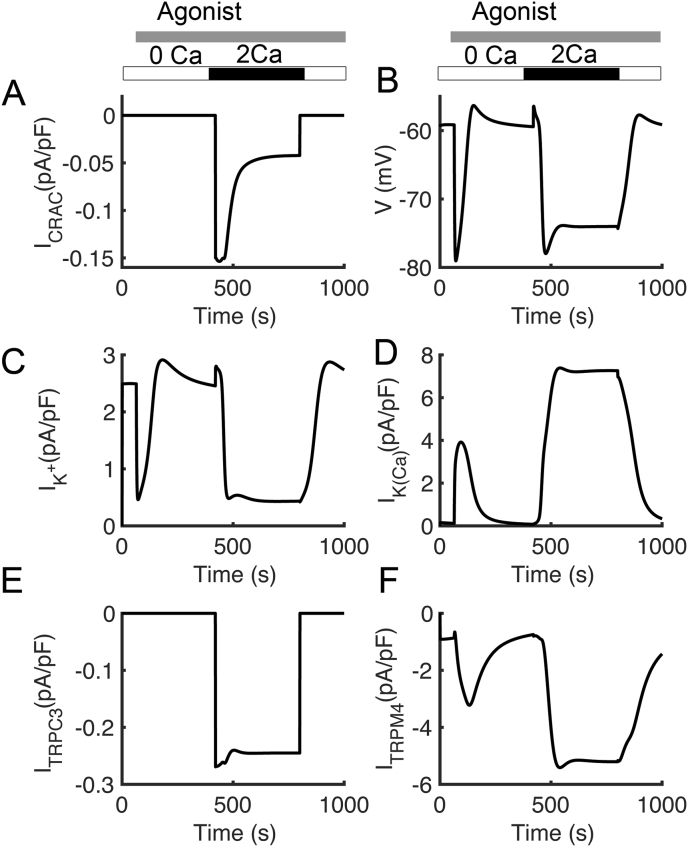
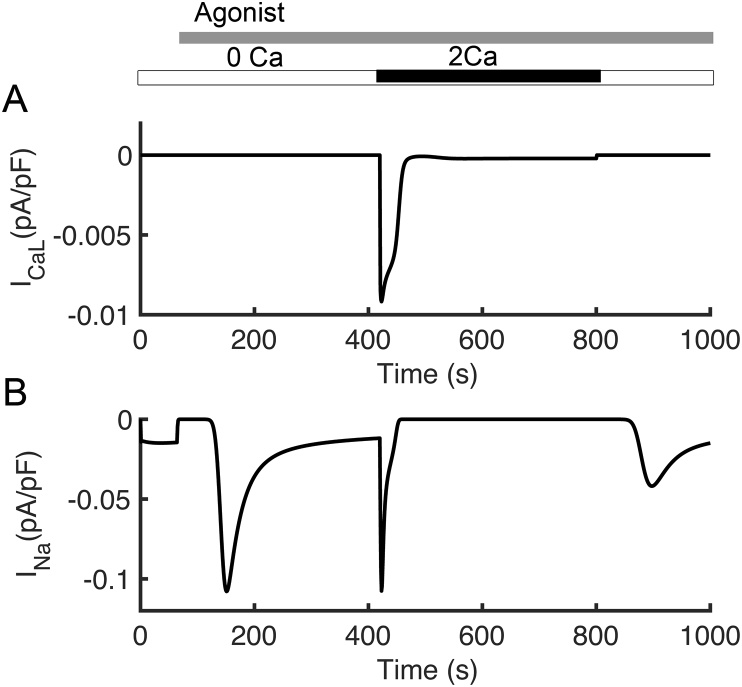
Figure 4 shows plasma membrane current responses in the simulations from Figure 2. As suggested by the Bautista, the model also predicts that the transient rise in cytosolic Ca2+ after the reintroduction of extracellular calcium is due to Ca2+ entry through the CRAC channel (Figure 4A). Ca2+ entry is accompanied by membrane hyperpolarization (Figure 4B), as observed by Tsien and co-workers [42]. The depolarizing influence of the CRAC current is opposed by Ca2+ triggered opening K+ channels (Figure 4C) which contributes to hyperpolarization in Figure 4B, as well as by the opening of voltage-dependent K+ channels (Figure 4D). The TRPC3 channel opens in response to an increase in DAG to allow Ca2+ entry (Figure 4E). The TRPM4 channel conducts Na+ and K+ and is activated by Ca2+ (Figure 4F).
Figure 4.
Simulated T cell membrane potential and major ionic currents. (A) Ca2+ release-activated Ca2+ (CRAC) current. (B) T cell membrane potential (C) Voltage-dependent K+ current (D) Ca2+-activated K+ current.
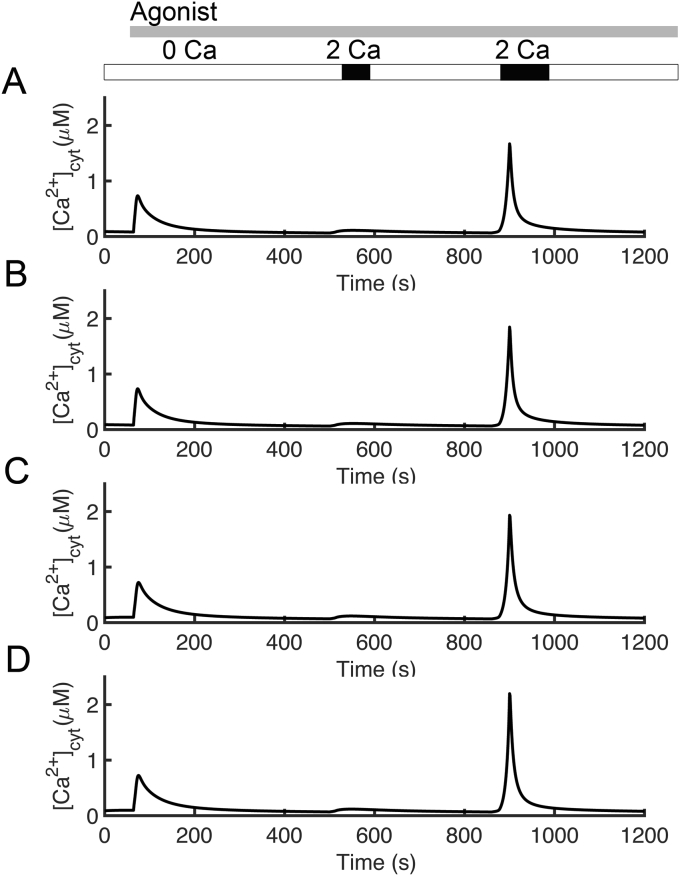
Bautista and colleagues [26] suggested that mechanisms of Ca2+ clearance from the cytosol include the PMCA, mitochondria, and SERCA. To investigate this proposal, four different simulations were performed with the model (Figures 5, 6, and 7). The following protocol used by Bautista and colleagues was used for each of these simulations: [Ca2+]o was set to 2.0 mM for 15 s and 40 s as indicated by the black bars above the graphs and held at 0.0 mM otherwise. Agonist was simulated by increasing the IP3 production rate from 0.01 μM s−1 to 5 μM s−1 after 64 s indicated by the gray bar. In their experiments, oligomycin/antimycin was added to block mitochondrial Ca2+ uptake to test the role of the mitochondria. To test the role of the ER, Ca2+ uptake was blocked by incubation with thapsigargin. Finally, both oligomycin/antimycin and thapsigargin were added to the incubation medium to simulate blocking of both mitochondrial and ER uptake of Ca2+.
Figure 5.
Simulated the effects of mitochondria, PMCA, and SERCA on intracellular calcium clearance. (A) The first spike of Ca2+ was due to release of Ca2+ from the ER resulting mainly from opening of the IP3R, which was induced by the application of agonist. (B) The role of mitochondria is tested by blocking mitochondrial Ca2+ uptake. (C) The effects of the ER on Ca2+ clearance dynamics are determined by simulations with a disabled SERCA pump. (D) Both mitochondrial and ER uptake of Ca2+ are blocked by combining the protocols used in Figures. 4B and 4C.
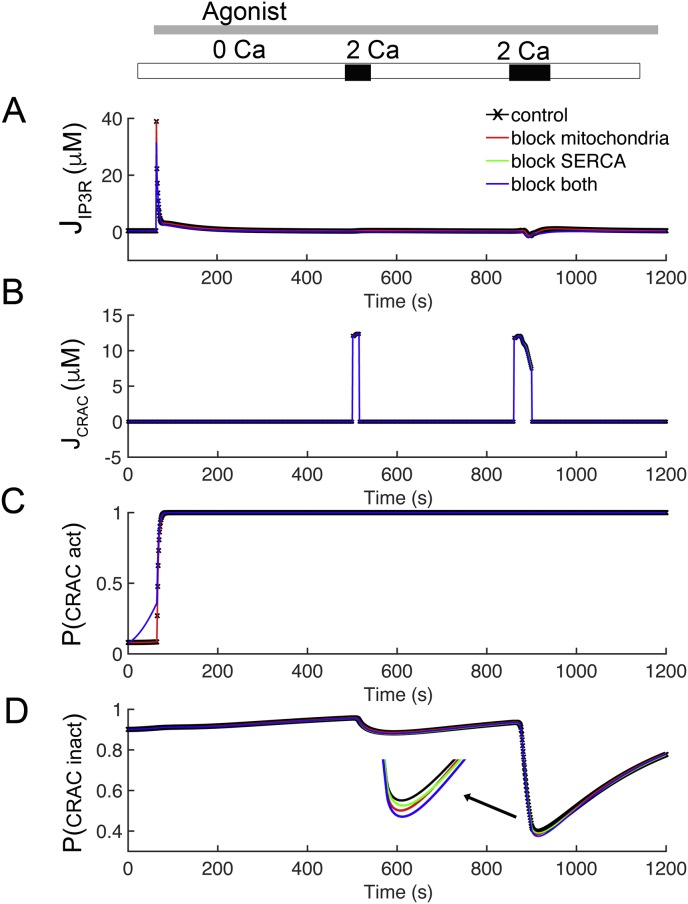
Figure 6.
Investigating the behavior of the Ca2+ fluxes through IP3 receptor and CRAC channel. (A) Ca2+ fluxes through the IP3 receptor from Figure 4: control (black), disabled mitochondrial Ca2+ uptake (red), blocked SERCA pump (green), and disabled mitochondria and SERCA (blue). (B) Ca2+ current for the four cases. (C) The activation of the CRAC channel is controlled by the [Ca2+]ER for the four cases from Figure 4: control (black), disabled mitochondrial Ca2+ uptake (red dashed), blocked SERCA pump (green), and disabled mitochondria and SERCA (blue solid). (D) CRAC inactivation is driven by subspace Ca2+ concentration.
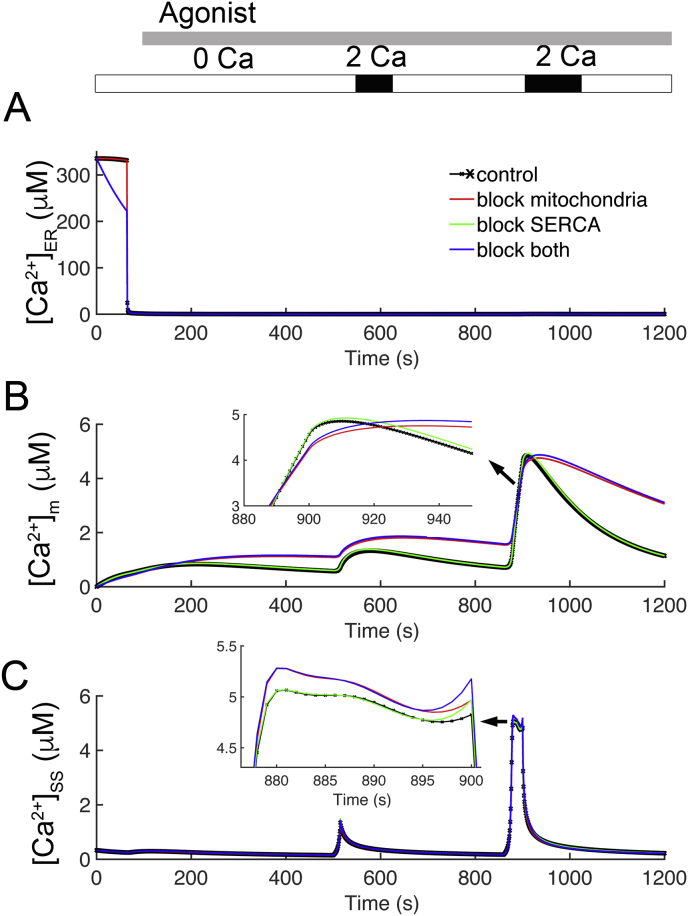
Figure 7.
The model predicts the Ca2+ concentrations in the ER, mitochondria, and subspace. (A) The changes in ER Ca2+ concentration for the four cases from Figure 4: control (black), disabled mitochondrial Ca2+ uptake (red), blocked SERCA pump (green), and disabled mitochondria and SERCA (blue). (B) The mitochondria activity for four cases. (C) The changes in subspace Ca2+ concentrations for all four cases.
The control (Figure 5A) shows that after the addition of agonist there is an initial elevation of [Ca2+]cyt, followed by a second and a third cytosolic Ca2+ transient during the 15 s and 40 s intervals of raised [Ca2+]o. The next set of simulations tests the role of mitochondria by blocking mitochondrial Ca2+ uptake (Figure 5B). To simulate this hypothesis, the fluxes through the Ca2+ uniporter and mitochondrial membrane potential (Ψm) were set to 0. As in the control, Figure 5A, 2.0 mM [Ca2+]o was applied for 15 s and 40 s. In this case (Figure 5B), the first transient elevations of [Ca2+]cyt are slightly higher than control (Figure 5A) and the third transient elevations of [Ca2+]cyt are noticeably higher than control (Figure 5A). To determine the effects of the ER on Ca2+ clearance dynamics, simulations with a disabled SERCA pump (JSERCA = 0) were performed (Figure 5C). In these simulations the initial [Ca2+]cyt transient is mostly abolished and the third transient is slightly larger. Finally, when both mitochondrial and ER uptake of Ca2+ are blocked (Figure 5D) by combining the protocols used in Figures 5B and 5C, the first transient is abolished, and the third transients are higher than the control. These results agree with the experimental observations [26]. In all cases the second transients are slightly bigger than the control, also similar to experiments.
Studies have been shown that the main sources of Ca2+ that produce [Ca2+]cyt transients in T lymphocytes are released from the ER through the IP3 receptor, and Ca2+ influx into the cell through the CRAC channel from the extracellular space [9, 43]. Figure 6A, B shows these Ca2+ currents for the four cases shown in Figure 5: control (black line), disabled mitochondrial Ca2+ uptake (red line), blocked SERCA pump (green line), and disabled both mitochondria and SERCA (blue line). The first transient after application of agonist is due entirely to release from the ER through the IP3 receptor (Figure 6A) for the control case (black solid line) and the case with blocked mitochondria (red). There is attenuated release from the ER in the cases with the SERCA blocked (green and blue lines overlapping). Release through the IP3 receptor contributes significantly to the second and third transient in all cases as the opening of CRAC channels provides Ca2+ to trigger Ca2+ release from the IP3 receptor, which is possible in the presence of IP3. There is a large CRAC current during both the second and third Ca2+ transients (Figure 6B). The behavior of the activation and inactivation “gates” for the CRAC channel which shown in Figure 6C, D. The activation of the CRAC channel is controlled by ER concentrations (Figure 6C). In the control case and case with the mitochondria blocked, the ER is full until application of agonist at which point the [Ca2+]ER declines. When the ER is full the activation gate of the CRAC channel is near 0. When the ER depletes it rises to above 0.5. In the cases with the ER is blocked (green and blue lines), the activation gate of the CRAC channel starts the simulation partially activated and quickly rises for the duration of the simulation (Figure 6C). Note that in all cases for the second and third transients the CRAC activation gates are open, suggesting that activation of the CRAC channel is not responsible for the changes of ICRAC seen in Figure 6B. Figure 6D shows the behavior of the CRAC inactivation by [Ca2+]SS. In all cases and with all transients, the CRAC activation gates are off at the beginning of the simulation (i.e. equal to 1). For the second transients, all cases are similar. However, for the third transients, CRAC currents are prolonged and slowly decrease. The downward deflections are inversely proportional to the transients in [Ca2+]SS. The inactivation gate of CRAC decreased in the four cases (arrow) with the probability described from largest decrease to the smallest decrease block of both SERCA and mitochondria (blue) > being blocked mitochondria (red) > blocked SERCA (green) > control (black). This suggests that the differences in CRAC seen during this protocol are due to differences in CRAC inactivation governed by [Ca2+]SS.
To further understand the mechanisms at play, the model was used to predict the Ca2+ concentrations in the ER, mitochondria, and subspace. Figure 6 shows all four cases with the same labeling scheme as Figure 6. After the application of agonist, the [Ca2+]ER falls from its resting value of 335.5 μM (Figure 7A) for the control (black line) and the case with blocked mitochondria (red line) due to opening of the IP3 receptors (shown previously in Figure 6A). In the cases where the SERCA pump is blocked (Figure 7A – green and blue lines overlapping) there is reduced [Ca2+] in the ER, at the start of the simulation. In these cases, the [Ca2+]ER reaches is nadir of approximately 1 μM. During each of the [Ca2+]cyt transients in the cases with functioning mitochondria (Figure 7B – black solid and green lines) there is a transient rise in [Ca2+]m. When SERCA is blocked (Figure 7B – green line), the [Ca2+]m is smaller in amplitude transient and slightly lower during the first transient but otherwise similar to the control. This can be attributed to the decreased release from the ER seen in Figure 6A. In the cases with the mitochondria Ca2+ uptake blocked there is little notable change in [Ca2+]m. From highest to lowest increases in the third transient, are the cases with both SERCA blocked (green) > control (black) > mitochondria and SERCA blocked (blue) > blocked mitochondrial Ca2+ uptake (red). The changes in [Ca2+]SS are shown in Figure 7C. When the SERCA is unblocked (black and red lines), the first transient is similar to the transients in [Ca2+]cyt. In the second and third transients, in all cases, there are transients in [Ca2+]SS. The difference in the cases is most clear in the third transient where there is prolonged Ca2+ entry through CRAC channels. Here the current, in order from highest to lowest (arrow), are the cases with both mitochondria and SERCA blocked (blue) > blocked mitochondrial Ca2+ uptake (red) > SERCA blocked (green) > control (black) Note that these are opposite the contributions from CRAC inactivation by [Ca2+]SS shown in the third transient in Figure 6D, indicating a possible role of CRAC channels in this observation.
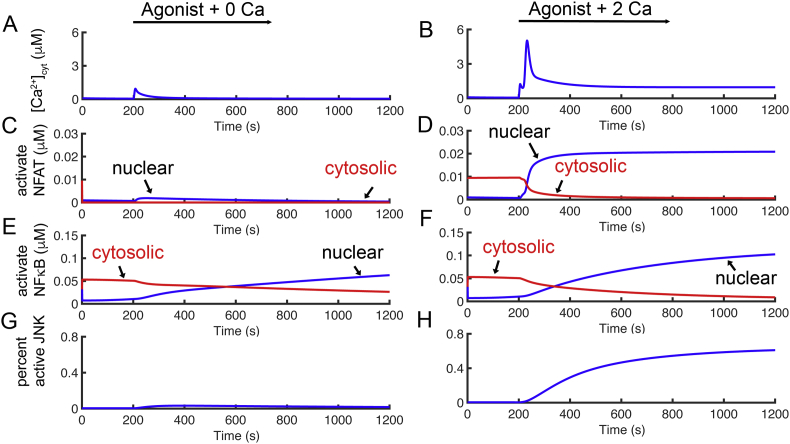
The model was used to study the importance of ICRAC for activation of NFAT, Ca2+ was triggered by the simulated application of agonist in the presence of 0.0 mM [Ca2+]o to eliminate ICRAC (Figure 8A). The result is an initial transient due to Ca2+ release from the ER followed by a return to baseline, and consequently little translocation of NFAT and NFκB (Figures 8C and 8E, respectively) to the nucleus and little JNK activation (Figure 8G). In Figure 8B, [Ca2+]o was set to 2.0 mM for 1000 s, and 0.0 mM after that. Agonist was added after 200 s. The [Ca2+]cyt increases to peak of approximately 5 μM, then slowly decreases to a plateau of 1.0 μM. When [Ca2+]o is reduced to 0.0 mM at 1200 s, the [Ca2+]cyt decline back toward baseline. During the simulation protocol NFAT and NFκB (Figures 8D and 8F, respectively) translocate to the nucleus during calcium transient and decline after the [Ca2+]cyt decreases back to baseline Figure 8H shows the percent active JNK in the cytoplasm raises rapidly when PKCθ is activated and Ca2+ concentration increase. When Ca2+ are fall after 1200 s when agonist stimulation of PLC activation is ended i.e. production of IP3 returns to baseline), the JNK and NFAT levels fall rapidly and the NFκB declines more slowly. The simulated JNK and the experimental results from Leung and co-workers [44] showing the co-activation by PKCθ and Ca2+ is greater than activation by either alone (Figure 9).
Figure 8.
Transcription factors activation corresponds to the Ca2+ transient. (A) Transients in [Ca2+]cyt are induced by agonist activation with 0.0 mM [Ca2+]o. Activation of NFAT from resting state corresponds to the top panel. (B) Simulation of Ca2+ transition in the cytoplasm ([Ca2+]cyt) is induced by agonist and [Ca2+]ot was set to 2.0 mM for 1000 s. (C)–(D). Calculated active NFAT from the resting state corresponds to the Ca2+ transient from the top panels. (E)–(F) Simulated active ΝFκΒ from the resting state corresponds to the Ca2+ transient from the top panels. (G)–(H) Calculated percent active JNK from the resting state corresponds to the Ca2+ transient from the top panels.
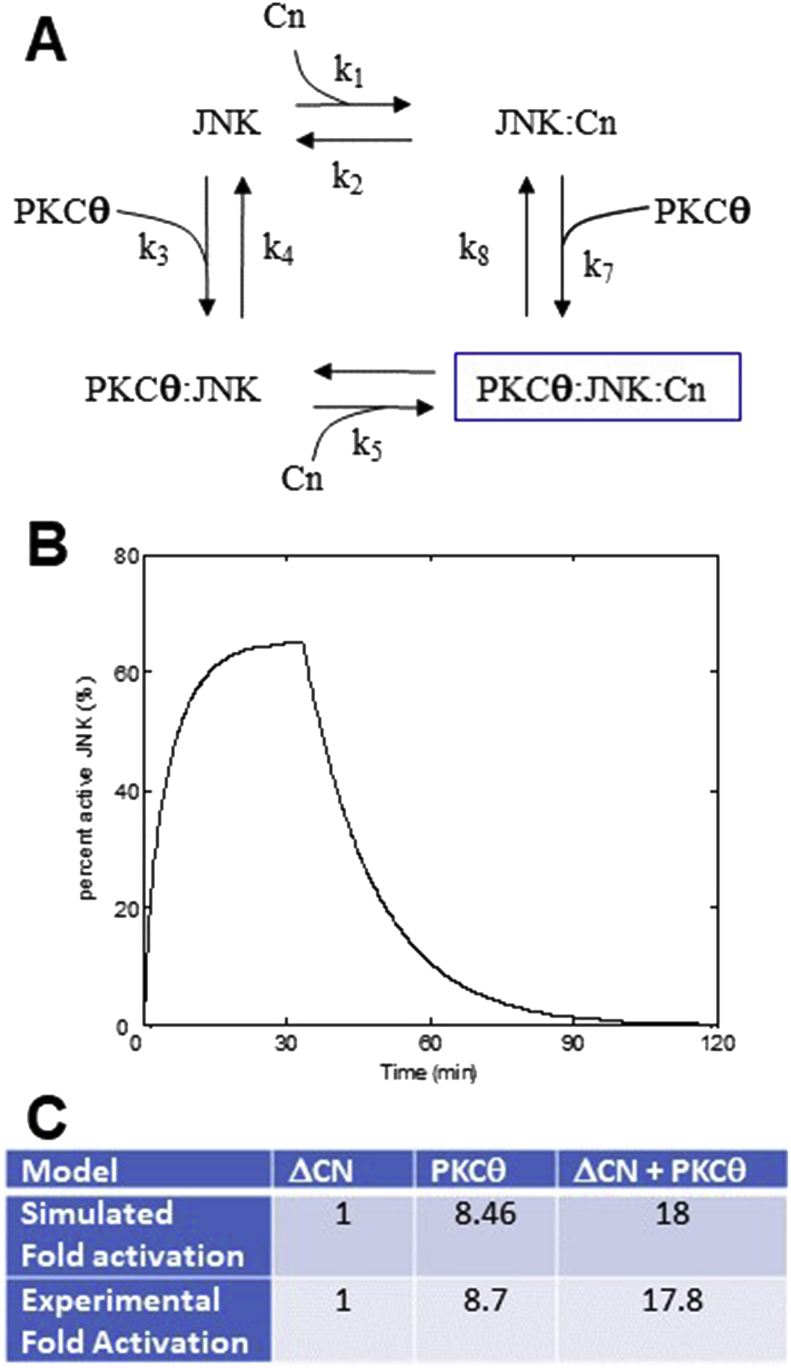
Figure 9.
JNK Model. (A) Reaction dynamics of JNK. (B) Simulated JNK phosphorylation (activation). (C) Fold change of JNK phosphorylation compared to experiment (Avraham et. al., 1998 [20]).
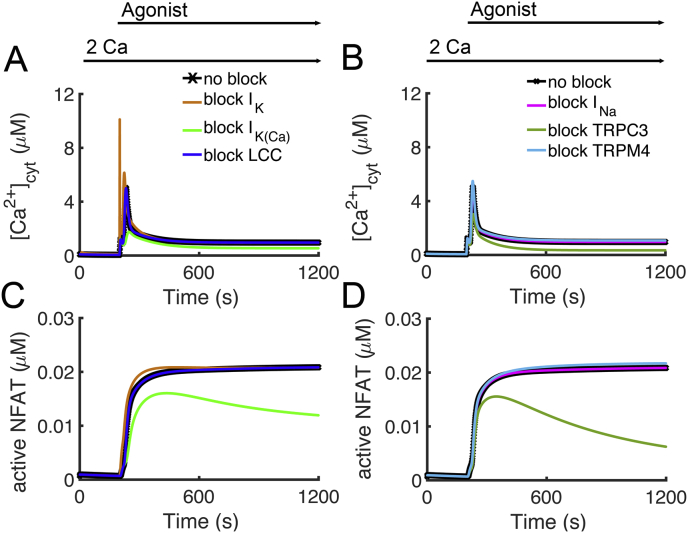
The model was used to explore the role of the membrane currents in T lymphocyte activation. Experiments have shown that block of IK (green)and IK(Ca) (blue) can inhibit T lymphocyte activation [45, 46]. Their expression level differs across different types of T lymphocytes and knockdown experiments have shown that deficiency of IK can be compensated for by IK(Ca) [47, 48]. Figure 8AC shows that block of IK(Ca) attenuates the Ca2+ transient and NFAT translocation to the nucleus. This is due to activation of IK(Ca) during Ca2+ entry through the CRAC channel preventing membrane depolarization thereby maintaining the driving force for Ca2+ entry. Under the current parameter block of IK has little effect on T lymphocyte activation. However, if IK expression was increased so that it played a more significant role in preventing depolarization during Ca2+ entry, it would affect T lymphocyte activation.
In the current parameter set, L-type Ca2+ expression is low resulting in a small current (Figure 10A). As such it plays a small role in T lymphocyte activation as its block does little to alter the Ca2+ transient and NFAT translocation to the nucleus (Figure 11AC - tan). If the L-type current is increased and other currents rebalanced, its block can attenuate T lymphocyte activation. Block of INa shows little effect on T lymphocyte activation (Figure 11BD - pink). This is because INa activated during depolarization and not during the peak period of Ca2+ entry (Figure 10B).
Figure 10.
Simulated T cell major ionic currents. (A) L-type Ca2+ current (B) Na+ current.
Figure 11.
Block of membrane currents can affect T lymphocyte activation. Agonist was applied from 200 s to 1200 s. [Ca2+]o was held at 2,0 mM throughout the simulation. (A) [Ca2+]cyt transients are reduced with block of IK(Ca) (green) compared to control (black). Under the current channel expression levels, block of ICaL (blue) and IK (tan) have little effect on the [Ca2+]cyt transient. (C) NFAT translocation to the nucleus is attenuated with block of IK(Ca) (green) compared to control (black). Block of ICaL (blue) and IK (tan) have only a small effect on NFAT translocation to the nucleus. (B) [Ca2+]cyt transients are reduced with block of ITRPC3 (dark green) compared to control (black). Under the current channel expression levels, block of ITRPM4 (light blue) and INa (fuschia) have little effect on the [Ca2+]cyt transient. Note that increasing ITRPM4 decreases the [Ca2+]cyt transient. (D) NFAT translocation to the nucleus is attenuated with block of ITRPC3 (dark green) compared to control (black). Block of INa (light blue) and ITRPM4 (fuchsia) have only a small effect on NFAT translocation to the nucleus.
In model simulation, block of TRPM4 channels results in a slightly increased Ca2+ transient and increase in NFAT activation while increase expression of the channel results in a decreased Ca2+ transient and decrease in NFAT activation (Figure 11BD – light blue). Increase in TRPM4 results in a decreased Ca2+ transient and NFAT (not shown). Experiments have shown that RNAi inhibition of TRPM4 in T cells results in an increase in the magnitude of the Ca2+ during activation [49]. TRPM4 channels are activated by Ca2+ and the ensuing Na+ entry through open channels depolarizes the membrane reducing the driving force for Ca2+ through other channels such as CRAC [50, 51]. The model confirms this mechanism.
The model was used to explore the role of TRP channels in T lymphocyte activation. Block of TRPC3 attenuates Ca2+ entry, which limits NFAT translocation to the nucleus (Figure 11BD – dark green). In the model, this is due to Ca2+ entry through TRPC3 during periods elevated DAG (Figure 4E and Figure 3). In experiments, TRPC3 mutants that had impaired channel function displayed smaller Ca2+ transients that T cells upon stimulation [52]. Experiments show that TRPC3 channels contribute to Ca2+ entry and are activated by membrane bound DAG [50, 51].
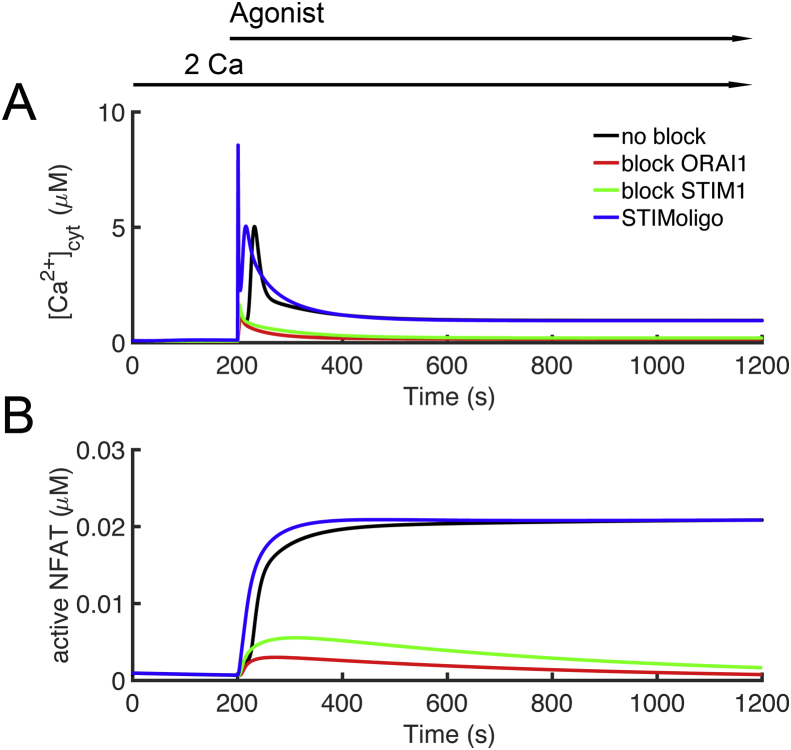
Mutations in CRAC channel proteins have been identified in disease. Immunodeficiency 9 is caused by mutations in the ORAI1 and Immunodeficiency 10 is caused by mutation in STIM1 [53]. Simulations show that block of ORAI1 (Ca2+ conductance set to zero) results greatly attenuates Ca2+ transient (due to block Ca2+ entry) and NFAT translocation to the nucleus (Figure 12AB – red). If the ER Ca2+ sensing function is removed, i.e. in , the Ca2+ transient and NFAT translocation is greatly attenuated as CRAC is not activated (Figure 12AB – green). STIM1 oligomerization is considered to necessary for activation of CRAC because it thought to be a prerequisite for activation of ORAI1. In the model if the oligomerization is removed by setting the Hill coefficient to n = 1 (instead of n = 4.7) in the equation for ER Ca2+ sensing, activation actually occurs earlier as there is a more gradual response (the Hill curve is not as steep) as seen in Figure 12AB – blue. This agrees with the idea that the oligomerization must be a part of the process of ORAI1 activation.
Figure 12.
Blocking STIM1 and ORAI greatly attenuate T lymphocyte activation. Agonist was applied from 200 s to 1200 s. [Ca2+]o was held at 2,0 mM throughout the simulation. (A) Block of the channel conductance of ORAI1 (red) or blocking the Ca2+ sensitivity of STIM1 (green) greatly attenuate the [Ca2+]cyt transient compared to control (black). Blocking the cooperativity of STIM1 (blue) but still allowing monomers to activate ORAI1 has little effect the [Ca2+]cyt transient. (B) Block of the channel conductance of ORAI1 (red) or blocking the Ca2+ sensitivity of STIM1 (green) greatly attenuate NFAT translocation to the nucleus compared to control (black). Blocking the cooperativity of STIM1 (blue) but still allowing monomers to activate ORAI1 has little effect on NFAT translocation to the nucleus.
Experimental studies have suggested that Ca2+ uptake by mitochondria is necessary for CRAC activation and that in the absence of mitochondrial Ca2+ uptake, the CRAC channel inactivates [54]. Experiments have shown that blocking either mitochondrial calcium uptake via the Ca2+ uniport (Juni) or blocking the mitochondrial Na+-Ca2+ exchanger (Jnc) result in reduced Ca2+ entry through CRAC channels [7]. There have been various hypotheses about to the mechanism behind this phenomenon. 1) The mitochondrial uptake Ca2+ preventing Ca2+-inactivation of CRAC [10]; 2) STIM1 oligomerization is considered to necessary for activation of CRAC. Experiments show that if mitochondrial Ca2+ uptake is blocked by either bock of the mitochondrial Ca2+ uniporter or through loss of membrane potential through uncoupling STIM1 oligomerzation is inhibited [55]. 3) Ca2+ bound calmodulin has been show to bind to STIM1 and ORAI1 leading to inactivation of the channel and disassociation of the STIM1 oligomer [56, 57]. 4) Block of Jnc results in mitochondrial Ca2+ overload and excess ROS production which leads to oxidation of ORAI1 inactivating Ca2+ entry through CRAC [58].
Model simulations were performed to explore how different mitochondrial might play a role in inactivation of the CRAC channel. Block of the mitochondrial Ca2+ uniporter results in a larger calcium transient (Figure 13 – red). The model suggests that this increase in Ca2+ due to the loss of the buffering of Ca2+ provided by the mitochondria. The CRAC channel current is inhibited over control (Figure 13C – red vs black). Blocking inactivation of the CRAC channel by Ca2+ results in a large increase in the Ca2+ channel and CRAC current suggesting that this plays a major role in controlling Ca2+ entry (Figure 13 – blue). In our model, this effect is assumed to be conferred by Ca2+ binding to CRACR2A. Calmodulin has also been shown to affect conductance through ORAI1. We modeled this effect as regulating the rate at which the channel inactivated (Figure 13 – green). This also has a large effect on CRAC current. However, none of these resulting in significant inhibition of CRAC current and loss of NFAT translocation to the nucleus. In the model all these processes to inactivate CRAC are reversible. This analysis suggests that there must be an inactivation process, not explicitly modeled from which there is slow return from the inactivated state. When such a process is included, it is possible to get mitochondrial inhibition resulting in a reduction of NFAT activation. However, such a mechanism is not presented as the mechanism is not clear.
Figure 13.
The role of mitochondrial Ca2+ uptake on T lymphocyte activation. Agonist was applied from 200 s to 1200 s. [Ca2+]o was held at 2,0 mM throughout the simulation. (A) Block of the channel conductance of the mitochondrial Ca2+ uniporter (red) slightly increases the [Ca2+]cyt transient compared to control (black). Blocking the Ca2+-dependent inhibition of ORAI1 (blue) or blocking the Ca2+-dependent rate of inhibition (green) result in a large [Ca2+]cyt transient. (B) Block of the channel conductance of the mitochondrial Ca2+ uniporter (red) slightly decreases NFAT translocation to the nucleus compared to control (black). Blocking the Ca2+-dependent inhibition of ORAI1 (blue) or blocking the Ca2+-dependent rate of inhibition (green) increases NFAT translocation to the nucleus. (C) Block of the channel conductance of the mitochondrial Ca2+ uniporter (red) slightly decreases CRAC current compared to control (black). Blocking the Ca2+-dependent inhibition of ORAI1 (blue) or blocking the Ca2+-dependent rate of inhibition (green) result in increased CRAC current.
3. Discussion
We have developed a mathematical model for calcium dynamics in T lymphocytes induced by IP3 to mimic T cell activation by antigen. Our model includes intracellular calcium signaling dynamics, transcription factor signaling, intracellular signaling cascades, and plasma membrane ion channels and pumps. The model reproduces several experimentally observed behaviors of Ca2+ signaling pathways in T cells. The [Ca2+]cyt simulation results closely match the experimental data of Bautista and co-workers [26]. Calcium influx prolongs the calcium transient in the cytoplasm, and the PMCA pump plays the leading role in cytosolic Ca2+ clearance from the cell. This work shows that the SERCA pump and mitochondria together have an impact on the rate of Ca2+ extrusion. The model also explores the contributions of mitochondria dynamics and ICRAC to activation of NFAT. Experimental studies indicated that mitochondria localized close to the cell membrane absorb calcium from ICRAC [9, 10], suggesting that increases in local [Ca2+]cyt leads to inactivation of ICRAC. The model explores this hypothesis and assumes a local subspace contains mitochondria near the CRAC channel. In order to further validate the predictive value of the model, simulation results are compared to experimental data that was not used to constrain the model. In particular, the time course of [Ca2+]SS and [Ca2+]m from Figure 2B, C compares well to the experimental data. The significant rise in [Ca2+]m close to the site of Ca2+ entry is similar to that shown in Schwindling et al (2010) [59]. The model predictions about [Ca2+]SS and plasmalemmal Ca2+ ATPase currents are similar to the experimental results of Quintana et al 2011 [60].
We have also tested the role of the voltage-dependent sodium (Nav1.5) that is only present in a small fraction of cells [61]. To this end, a voltage-dependent sodium channels based on the experimentally verified Luo-Rudy model [32] was also included to test its possible role in T cell activation. The currents generated by this channel were small and sensitivity analysis showed no significant effect of Na+ channel conductance on NFAT translocation into the nucleus.
In this paper, our simulations suggest that NFAT and NFκB activation can be inhibited by decreasing [Ca2+]cyt through termination of Ca2+ release from the ER and thus preventing opening of CRAC channels. This finding suggests that blocking ICRAC might be a possible target for immunosuppression. The exact mechanism of opening of CRAC channels is still not clear. One hypothesis is that ER stores reside close to CRAC channels [9] and there is some sort of physical sensor that transmits ER depletion to the CRAC channel. Many studies showed that Ca2+ influx has a great impact on T-cell activation and proliferation [9, 33]. Our model suggests that Ca2+ entry from CRAC channels is essential for NFAT and NFκB activity. The model can also be used to understand other mutations leading to T lymphocyte dysfunction. Mutations in the Gimap5 gene lead the immune system disorders through T cell dysfunction [62]. Gimap5 inhibits a protein that inactivates GSK3, there the mutation leads to increased GSK3 activity [62]. Our previous studies have shown that GSK3 dephosphorylates nuclear NFAT allowing it to be translocated out of the nucleus [63]. The model predicts that the Gimap5 mutation might lead to immune dysfunction by increasing NFAT export from the nucleus. Mutations in the IP3R can lead to T cell lymphoma with some mutants contributing to increased IP3R Ca2+ release while others lead to increased IP3 sensitivity with no observed change to Ca2+ dynamics [64]. Our previous work in Ca2+ dynamics in cardiac myocytes offers and explanation [65, 66]. With increased IP3R open probability, there is Ca2+ efflux (leak) from the ER. This results in lower ER Ca2+ content reducing the driving force for Ca2+ efflux during IP3R opening. The production of increased open probability and decreased driving force returns the Ca2+ transient to normal levels.
Our model successfully simulates the calcium dynamics and control of NFAT and NFκB activation. However, not every feature present in the T cell could be represented, only selected ones. There are many improvements to the model possible to address important scientific questions, including upstream elements of the signaling pathway, the role mitochondrial function, cytoskeleton, spatial reorganization, and changes in gene expression play in T cell physiology.
Upstream elements of the T cell activation signaling pathway can be added to the model, for example, the activation of DAG and protein kinase C (PKC) on calcium and its feedback on phospholipase C (PLC). The early events in T cell activation show that IP3 induction of Ca2+ release from ER stores follows the cleavage of PIP2 by PLCγ1, and suggest that this time delay in the activation of PLCγ1 could account for the experimentally observed a delay in calcium signaling [67].
Calcium signaling between the mitochondria and ER plays a role in T cell physiological processes such as activation, effector functions, lineage determination, apoptosis, autophagy and mitochondrial bioenergetics [68, 69, 70, 71]. It has been suggest that mitochondrial contact sites are necessary for the reprogramming and stimulation of energy metabolism that occurs during T cell activation [69]. In its current form, the model cannot address these issues. We understand that the role mitochondria play in T cell activation is topic of current research and hope to include that in future work. We have a detailed model of ionic homeostasis and energy metabolism that we developed for the cardiac myocyte that demonstrates activation of energy metabolism. It is clear that increases in mitochondrial Ca2+ can stimulate energy production, but changes in ADP, ATP, and NADH levels can also contribute to meeting the increased energy demands during T cell activation. There is also experimental evidence that NFAT activation triggers signaling cascades that also increase energy production in the T cell [14]. The model currently does not address these issues, but lays the foundations for future modeling. This model described membrane ion channels, calcium dynamics and transcription factor signaling during T cell activation. While we have not modeled apoptosis, and autophagy, there are models that have been developed to describe these processes that might be adapted for this purpose. In future work, we hope to add features to this model for the T cell and explore these issues.
The changes to spatial organization, membrane ultrastucture, and signaling pathways and changes to gene expression are crucial to T cell activation and other physiological processes [72, 73]. This suggests that the development of a spatial model might be helpful in understanding T cell physiology. For example, the STIM1:ORAI1 puncti that form during T cell activation display single channel ORAI responses with complex dynamics. Describing these might require development of a spatial stochastic model [74]. Different types of T cells have different ion channel expression. The model in the future could be used to explore these cell-to-cell differences.
NFAT activation resulting from Ca2+ mobilization is important for the differentiation into T helper 1 (Th1), Th2, Th17, regulatory T (Treg), and follicular helper T cells (Tfh) through interaction with different other transcription factors such as GATA3 and Foxp3 [75]. Another future question that can be addressed by the model is the differentiation of T cells after activation requires activation of different transcription factors. This might arise different patterns of signaling that might arise from cell heterogeneity.
During T cell activation there is a reorganization of cellular structure to form the immunological synapse [76]. These changes rely on the microtubular network and actin cytoskeleton. Movement of the cytoskeleton responds to Ca2+ mobilization [72]. There has been significant computational modeling studies on how the cytoskeleton reorganizes cell structure, for example, in dendritic spines, that can be used in future work to understand these dynamics [77].
4. Materials and methods
4.1. The model
The De Young-Keizer model [78] was revised to include four different Ca2+ compartments, the ER, the cytosol, the mitochondria, and a subspace between the plasma membrane and mitochondria. The model describes the membrane potential and several ion channels that regulate it. The model also includes the Ca2+ release-activated Ca2+ (CRAC) channel (STIM1, ORAI1, and CRACR2A), the plasmalemmal Ca2+-ATPase (PMCA), and the dynamics of IP3 production and degradation. The model consists differential equations describing the time rate of change of the following quantities: (1) the ER Ca2+ concentration ([Ca2+]ER); (2) the cytosolic IP3 concentration ([IP3]cyt); (3) the eight states of IP3R gating; (4) the mitochondrial Ca2+ concentration ([Ca2+]m); (5) the subspace Ca2+ concentration ([Ca2+]SS); (6) the fraction of PMCA channels in the unmodulated state (u); (7) the cytosolic Ca2+ concentration ([Ca2+]cyt); (8) the three gates of the sodium channel (INa); (9) the voltage dependent K+ channel (IK); (10) the calcium activated potassium channel IK(Ca); (11) the L-type Ca2+ current; (12) the TRPM4 current (ITRPM4); (13) the TRPC3 current (ITRPC3); (14) the membrane potential (V). The parameter values and definitions are given in Tables 1, 2, 3, 4, 5, 6, 7, 8, and 9. Changes to the parameters for a particular simulation are stated in the text where the simulations are described. Model Fortran code is included as supplementary material. Sensitivity analysis was also performed to ensure that the model was not overly sensitive to any model parameters (Figure 14).
Table 9.
JNK activation rate constants.
| Rate Constant | Value |
|---|---|
| k1 | 0.016 |
| k2 | 0.00038 |
| k3 | 0.00012 |
| k4 | 0.0075 |
| k5 | 0.00001 |
| k6 | 0.00088 |
| k7 | 0.00001 |
| k8 | 0.00025 |
Figure 14.
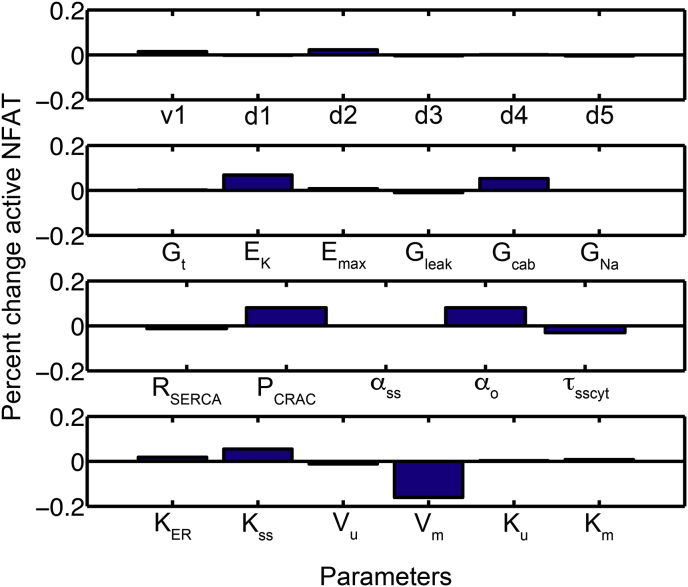
Sensitivity analysis for NFAT activation depended upon model parameters.
The ER store dynamics are governed by four processes: (1) Ca2+ buffering (βER), (2) Ca2+ sequestration in the ER though the sarcoplasmic reticulum calcium ATPase (JSERCA) from the cytosol, and (3) Ca2+ release from the ER through the IP3 receptor (JIP3R). The balance equation for [Ca2+]ER is
| (1) |
where βER represents the fractional buffering of Ca2+ in the ER using the rapid buffering approximation developed by Wagner and Keizer [79] described as follows:
| (2) |
where is the total concentration of stationary buffer in the ER, and other rate constants are defined as shown in Table 3.
The SERCA flux for Ca2+ movement from the cytoplasm into the ER, (JSERCA) is described by
| (3) |
where KSERCA is the binding constant for Ca2+ to the pump.
The flux of Ca2+ through the IP3 receptor (JIP3R) into the cytosol can be described by
| (4) |
where v1 is the maximal Ca2+ flux rate through the IP3R, and X110 is the fraction of IP3R subunits in the open state. The ER and cytosolic Ca2+ concentrations are represented by [Ca2+]ER and [Ca2+]cyt, respectively, and their difference describes the Ca2+ concentration gradient.
The notation X110 comes from the model of the IP3 receptor developed by De Young and Keizer and denotes that IP3 has already bound a channel subunit (1 in the first subscript position), but activating Ca2+ is bound (1 in the second subscript position) but no inactivating Ca2+ is bound (0 in the third subscript position has yet bound so the channel is open) (Figure 1C) [78]. The channel state X110 is cubed to fit the experimental data and suggests that three subunits must be in this state for the channel to conduct Ca2+. The rate constants are defined as shown in Table 2. The equations for activation and inactivation states of cytosolic IP3 receptors by Ca2+ are describing in the following equations:
| (5) |
| (6) |
| (7) |
| (8) |
| (9) |
| (10) |
| (11) |
| (12) |
| (13) |
| (14) |
| (15) |
| (16) |
| (17) |
| (18) |
| (19) |
| (20) |
| (21) |
| (22) |
| (23) |
| (24) |
The IP3 production and degradation dynamics in the cytosol are based on the Swillens-Mercan model [27]. The equation of free cytosolic concentration of IP3 ([IP3]cyt) is given by
| (25) |
where v4 is the rate of formation of IP3 from phosphatidyl inositol (PIP2) by phospholipase C (PLC). In the second term, v5 is the maximal rate of dephosphorylation of IP3 by a 5-phosphatase governed by the binding constant K5. The third term represents the rate of IP3 phosphorylation to inositol 1,3,4,5-tetrakisphosphate by a 3-kinase with maximal rate v6 and binding constant K6 that is increased by Ca2+ with binding constant K7 (Figure 1B) [27]. The rate constants are defined as shown in Table 1.
The production dynamics for diacyl glycerol (DAG) is that same as IP3 as they are both produced by PLC. The dynamics equation of free cytosolic concentration of DAG is
| (26) |
The mitochondrial Ca2+ dynamics are governed by three processes: (1) Ca2+ influx through the Ca2+ uniporter (JUNI), (2) Ca2+ efflux through the Na+-Ca2+ exchanger (JNCLX) and (3) Ca2+ buffering [80, 81]. The Ca2+ influx through uniporter (JUNI) is described as by Nguyen and Jafri [81] using on the Goldman-Hodgkin-Katz (GHK) equation as follows
| (27) |
where PUNI is the permeability of the uniporter, z is the valence of Ca2+, Ψm is the mitochondrial membrane potential, F is Faraday's constant, Vmito is the mitochondrial matrix volume, R is the ideal gas constant, T is the absolute temperature, αm and αSS are the mitochondrial and subspace activity coefficients for Ca2+ at the mouth of the uniporter which is thought to be a channel. The Ca2+ efflux through the Na+-Ca2+ exchanger (JNC) used the formulation by Jafri and Nguyen [81] described by
| (28) |
where KNa is the Na+ binding constant, KCa is the Ca2+ binding constant, VNC is the maximal exchanger velocity, [Na+]ss is the subspace Na+ concentration, and [Na+]m is the mitochondrial Na+ concentration (Table 4). These two fluxes comprise the balance equations for [Ca2+]m
| (29) |
where βCa is a constant describing Ca2+ buffers in the mitochondria.
Mitochondrial Ca2+ uptake dynamics and depletion of the endoplasmic reticulum (ER) trigger prolonged Ca2+ influx through CRAC channels [9, 10, 26, 33, 74]. The Ca2+ influx through CRAC channels (JCRAC) can be described by contributions from three components STIM1, CRACR2A, calmodulin and ORAI1 [82,83]. STIM1 oligomerizes to activate the channel when [Ca2+]ER is depleted and can be described by the Hodgkin-Huxley formalism
| (30) |
where act is the fraction of channels activated, τbb is the time constant, and the steady state probability of the activation gate is
| (31) |
with Kact as the Ca2+ dissociation constant [84, 85]. CRAC2A binding to ORAI1 is required for proper Ca2+ signaling during T-cell activation [83, 86]. CRACR2A disassociates from the ORAI1 protein when it binds Ca2+ leading to inactivation of the channel [87]. Binding of Ca2+/calmodulin to ORAI1 has also been shown to inactivate the channel Ca2+ bound [56, 57]. This inactivation process is described by
| (32) |
where inact is the fraction of channels activated. The time constant
| (33) |
represents the inhibitory action of Ca2+/calmodulin with Kcc as the calcium binding affinity. The steady-state probability the inactivation gate
| (34) |
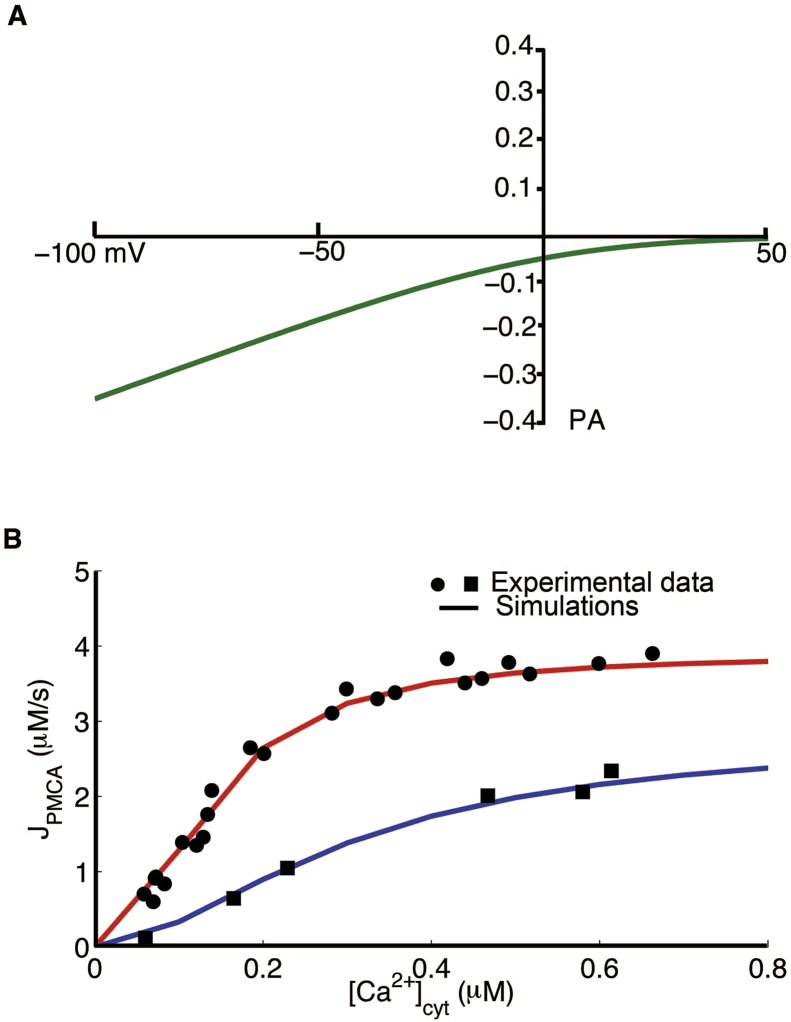
with Kinact as the dissociation constant for Ca2+ binding represents Ca2+ binding to CRACR2A. These are approximations as quantitative data is not yet available. The ICRAC is based on the GHK equation and closely matches the experimental results shown by Bautista et. al., [26], (Figure 15A).
| (35) |
here PCRAC is the permeability of Ca2+, V is the cell membrane potential, and αo is the extracellular activity coefficient for Ca2+ at the mouth of the channel. In this context, αSS is the subspace activity coefficient at the mouth of the ICRAC channel. The rate constants are shown in Table 5. Finally, the Ca2+ is
| (36) |
where VSS is subspace volume.
Figure 15.
Simulated ICRACand JPMCA. (A) Extracellular calcium concentration was set to 2.0 mM to measure ICRAC from -100 mV to +50 mV. (B) JPMCA as function of [Ca2+]cyt is shown for two pump states, modulated and unmodulated.
The final flux that influences the Ca2+ dynamics is the transfer from the subspace into the cytosol (JSScyt)
| (37) |
where τsscyt is transfer time between the subspace and the cytosol. The subspace Ca2+ dynamics can be described in terms of the fluxes described above by
| (38) |
where Vcyt is the cytosolic volume and the volume ratios rescale the fluxes to account for the volume difference between the subspace and the other compartments (Table 6). The factor βss represents the buffering in the subspace and is described by
| (39) |
The total concentrations of stationary (s) and exogenous (e) buffers are represented by [Bj]SS, and (j = s,e) are their dissociation constants for Ca2+ (Table 3).
According to Bautista and co-workers, the plasma-membrane Ca2+-ATPase (PMCA) controls a majority of the extrusion of Ca2+ and is slowly modulated by changes in calcium concentration [26]. They observed altered Michaelis-Menten kinetics that describes Ca2+ removal in the modulated (pre-incubated with high Ca2+) and unmodulated states. A Hodgkin-Huxley type formalism is used here to describe transitions between the two states of PMCA designated U (unmodulated) and M (modulated) (M) PMCA. Transitions to and from the modulated state are represented by the rate constants w1 which depends upon [Ca2+]cyt and w2,
| (40) |
where
| (41) |
and , where p1 = 0.1 μM−1 is the rate constant for activation of the PMCA. These rate constants were estimated to match experimental results. The fraction of the pumps in the unmodulated state (u) can be described by
| (42) |
where
| (43) |
and
| (44) |
The total PMCA (plasma membrane Ca2+-ATPases) flux (JPMCA), including contributions from both the unmodulated and modulated states, is given by
| (45) |
where m is the fraction of pumps in the modulated state (m + u = 1). The parameters vu and vm denote the maximal rate of unmodulated and modulated PMCA fluxes, and Ku and Km are the [Ca2+]cyt for half maximal velocity for Vu and Vm, respectively. These parameters, including the exponents 1.8 and 2.1, are taken to fit the experimental data observed by Bautista and coworkers [26]. Figure 15B shows the changes in JPMCA as a function of [Ca2+]cyt during unmodulated and modulated PMCA. PMCA efflux increases when [Ca2+]cyt increases more in the modulated state (Figure 15B − red line) than in the unmodulated state (Figure 15B − blue line), which are fitted to experimental data of Bautista and co-workers [26].
IPMCA is the total PMCA current is given by
| (46) |
The balance equation for cytosolic calcium concentration is given by
| (47) |
using fluxes described above. In this equation, βcyt is the cytosolic Ca2+ buffering factor,
| (48) |
with the total concentrations of stationary (s) and exogenous (e) buffers represented by [Bj]cyt, and (j = s,e) their dissociation constants for Ca2+. Note that the model assumes that the total buffer concentrations in the subspace and cytosol are equal (Table 3).
The equations of model IK current are defined as follows
| (49) |
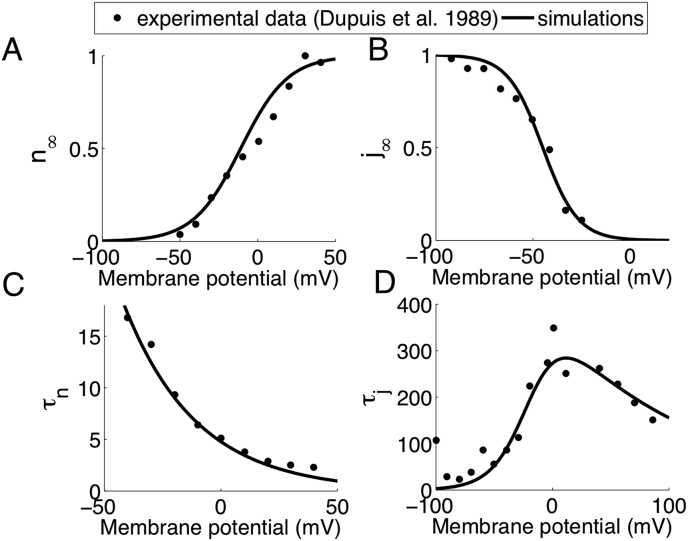
the activation (xn) and inactivation (xj) gating variables are fitted to experimental data of Dupuis and co-workers [28] as shown in Figure 16 and described by the equations
| (50) |
| (51) |
| (52) |
and
| (53) |
Figure 16.
Experimental (symbols) and model optimized (lines) IK current. (A) IK current activation and (B) inactivation curves. (C) n-gate and j-gate (D) time constants.
The IK(Ca) current can be described by
| (54) |
where Emax = 0.8 nS [6] and Kd = 0.45 μM is derived from the experiments of Verheugen and co-workers [29].
The model of the fast Na+ current include activation and inactivation gate is based on the Luo-Rudy model [32]. The formulation is given by
| (55) |
Activation gate m and inactivation gate are described as
For V-40 mV
| (56) |
| (57) |
and
| (58) |
For V-40 mV
| (59) |
and
| (60) |
| (61) |
and
| (62) |
| (63) |
and
| (64) |
L-type voltage gates Ca2+ channels have been found in human T cells [88]. The L-type calcium current also follows the formulation from the Luo-Rudy model given by
| (65) |
where the maximal current , the activation gate d, and inactivation gate f, and Ca2+ inactivation gate fCa are described by
| (66) |
| (67) |
| (68) |
| (69) |
| (70) |
| (71) |
The TRPM4 channel is a non-selective cation channel that is activated by calcium and membrane potential, For this model the formulation developed by Gaur and co-workers was used [30]:
| (72) |
| (73) |
| (74) |
| (75) |
where ETRPM4 is the reversal potential, gTRPM4 is the conductance, and τxCa is the Hodgkin-Huxley time constant.
The TRPC3 channel conducts Ca2+ and is activated by diacyl glycerol (DAG) with a roughly linear I–V relation [31].
| (76) |
where KDAG is the activation constant for DAG binding to the channel.
The chloride current (ICl) is described by
| (77) |
where gCl is the Cl− channel conductance and ECl is the reversal potential for Cl−.
The [DAG] is produced by phospholipase C from the cleavage of PIP2 and thus has the same production rate (v4) as IP3. It is assumed to decay with first order kinetics with rate constant vDAGdeg.
| (78) |
The membrane potential equation is given by
| (79) |
where Cm is the membrane capacitance.
In the simulations used to study NFAT and NFκB activation, we incorporated the NFAT and NFκB activation pathways described by Fisher and co-workers [63] into this cytosolic Ca2+ transients model. The NFAT model has a modification to activation of calmodulin by Ca2+ to represent the 2 high and 2 low affinity binding sites of calmodulin replacing the dependence on in that model by the equation
| (80) |
To study JNK activation, the cytosolic Ca2+ transients generated by this model were used as inputs for the model of JNK activation. Using the law of mass action, the reaction scheme in Figure 9A yields a system of 3 coupled first order differential equations.
| (81) |
| (82) |
| (83) |
The model simulates the JNK activation pathways that are involved in the activation of transcription factor AP-1 in T lymphocytes. AP-1 binds to promoter regions of DNA with transcription factors NFAT and NFκB initiating new gene transcription results in cell proliferation and differentiation [23].
Many studies have shown that PKCs and calcineurin act as co-activators of JNK leading to phosphorylation of c-Jun. Figure 9B shows that the percent active JNK in the cytoplasm falls rapidly when PKCθ concentrations are low, which agrees with the experimental results shown in Leung and co-workers [44]. As in experiment, with activation the phosphorylated JNK reaches a maximum at about 30 min, declines to half maximum at about 45 min and is close to zero after 2 h.
Avraham and colleagues [20] suggest that calcineurin and PKCθ must co-stimulate to reach full activation of JNK. A high calcineurin concentration does not activate JNK. On the other hand, high PKCθ concentration can induce about 50% JNK activation. Figure 9C shows that the fold activation only reached to 1 with calcineurin, and that fold activation is 8.7 with PKCθ, which matches with the experimental data shown [20].
4.2. Sensitivity analysis
A sensitivity analysis was performed to demonstrate how NFAT activation depended upon model parameters (Figure 14). Sensitivity was calculated by:
| (84) |
The parameters controlling CRAC current, K+ currents, and membrane potential show the greatest effect on active NFAT. Upon further exploration, the model suggests CRAC current is essential for the elevation in cytosolic Ca2+ sufficiently to activate NFAT. Hence increasing the Ca2+ entry via CRAC enhances NFAT activation. Reduction of the membrane potential serves to reduce CRAC current making it an important parameter. Therefore, K+ current that help to maintain the membrane potential by opposing depolarization by CRAC are necessary to maintain sufficient driving force for Ca2+ entry to activate NFAT. These studies suggest the important components for T cell activation.
4.3. Numerical methods
The differential equations defining the model were solved using Euler's Method with a fixed time step of 0.01 s. The computer program was written in FORTRAN and run on Linux workstations. Numerical results were visualized using MATLAB 7.0.1 by The MathWorks, Inc.
Model parameters may be loosely divided into three groups: 1) derived from published data, 2) estimated from published data so that model variable value and time course conformed to experimental data, and 3) fitted specific model equations to experimental data.
Declarations
Author contribution statement
Pei-Chi Yang: Conceived and designed the experiments; Performed the experiments; Analyzed and interpreted the data; Wrote the paper.
M. Saleet Jafri: Conceived and designed the experiments; Performed the experiments; Analyzed and interpreted the data; Contributed reagents, materials, analysis tools or data; Wrote the paper.
Funding statement
This work was supported by the National Science Foundation under Grant No. 0443843 (MSJ) and by National Institutes of Health (NIH) grant No. R01HL105239 (MSJ) and U01HL116321 (MSJ).
Competing interest statement
The authors declare no conflict of interest.
Additional information
No additional information is available for this paper.
Acknowledgements
We would like to thank Wayne Fisher for helpful comments and suggestions on the manuscript.
Appendix A. Supplementary data
The following is the supplementary data related to this article:
References
- 1.Berridge M.J., Galione A. Cytosolic calcium oscillators. Faseb. J. 1988;2(15):3074–3082. doi: 10.1096/fasebj.2.15.2847949. PubMed PMID: 2847949. [DOI] [PubMed] [Google Scholar]
- 2.Jafri M.S., Keizer J. On the roles of Ca2+ diffusion, Ca2+ buffers, and the endoplasmic reticulum in IP3-induced Ca2+ waves. Biophys. J. 1995;69(5):2139–2153. doi: 10.1016/S0006-3495(95)80088-3. PubMed PMID: 8580358. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Kalman K., Pennington M.W., Lanigan M.D., Nguyen A., Rauer H., Mahnir V. ShK-Dap22, a potent Kv1.3-specific immunosuppressive polypeptide. J. Biol. Chem. 1998;273(49):32697–32707. doi: 10.1074/jbc.273.49.32697. PubMed PMID: 9830012. [DOI] [PubMed] [Google Scholar]
- 4.Panyi G., Varga Z., Gaspar R. Ion channels and lymphocyte activation. Immunol. Lett. 2004;92(1-2):55–66. doi: 10.1016/j.imlet.2003.11.020. PubMed PMID: 15081528. [DOI] [PubMed] [Google Scholar]
- 5.Srivastava S., Li Z., Ko K., Choudhury P., Albaqumi M., Johnson A.K. Histidine phosphorylation of the potassium channel KCa3.1 by nucleoside diphosphate kinase B is required for activation of KCa3.1 and CD4 T cells. Mol. Cell. 2006;24(5):665–675. doi: 10.1016/j.molcel.2006.11.012. PubMed PMID: 17157250. [DOI] [PubMed] [Google Scholar]
- 6.Grissmer S., Nguyen A.N., Cahalan M.D. Calcium-activated potassium channels in resting and activated human T lymphocytes. Expression levels, calcium dependence, ion selectivity, and pharmacology. J. Gen. Physiol. 1993;102(4):601–630. doi: 10.1085/jgp.102.4.601. PubMed PMID: 7505804. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Trebak M., Kinet J.-P. Calcium signalling in T cells. Nat. Rev. Immunol. 2019;19(3):154–169. doi: 10.1038/s41577-018-0110-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Feske S., Wulff H., Skolnik E.Y. Ion channels in innate and adaptive immunity. Annu. Rev. Immunol. 2015;33:291–353. doi: 10.1146/annurev-immunol-032414-112212. Epub 2015/04/12, PubMed PMID: 25861976; PubMed Central PMCID: PMCPMC4822408. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Lewis R.S. Calcium signaling mechanisms in T lymphocytes. Annu. Rev. Immunol. 2001;19:497–521. doi: 10.1146/annurev.immunol.19.1.497. PubMed PMID: 11244045. [DOI] [PubMed] [Google Scholar]
- 10.Hoth M., Button D.C., Lewis R.S. Mitochondrial control of calcium-channel gating: a mechanism for sustained signaling and transcriptional activation in T lymphocytes. Proc. Natl. Acad. Sci. U. S. A. 2000;97(19):10607–10612. doi: 10.1073/pnas.180143997. PubMed PMID: 10973476. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Loh C., Shaw K.T., Carew J., Viola J.P., Luo C., Perrino B.A. Calcineurin binds the transcription factor NFAT1 and reversibly regulates its activity. J. Biol. Chem. 1996;271(18):10884–10891. doi: 10.1074/jbc.271.18.10884. PubMed PMID: 8631904. [DOI] [PubMed] [Google Scholar]
- 12.Ruff V.A., Leach K.L. Direct demonstration of NFATp dephosphorylation and nuclear localization in activated HT-2 cells using a specific NFATp polyclonal antibody. J. Biol. Chem. 1995;270(38):22602–22607. doi: 10.1074/jbc.270.38.22602. PubMed PMID: 7545680. [DOI] [PubMed] [Google Scholar]
- 13.Wesselborg S., Fruman D.A., Sagoo J.K., Bierer B.E., Burakoff S.J. Identification of a physical interaction between calcineurin and nuclear factor of activated T cells (NFATp) J. Biol. Chem. 1996;271(3):1274–1277. doi: 10.1074/jbc.271.3.1274. PubMed PMID: 8576111. [DOI] [PubMed] [Google Scholar]
- 14.Vaeth M., Feske S. NFAT control of immune function: new frontiers for an abiding trooper. F1000Res. 2018;7:260. doi: 10.12688/f1000research.13426.1. Epub 2018/03/24, PubMed PMID: 29568499; PubMed Central PMCID: PMCPMC5840618. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Beals C.R., Clipstone N.A., Ho S.N., Crabtree G.R. Nuclear localization of NF-ATc by a calcineurin-dependent, cyclosporin-sensitive intramolecular interaction. Genes Dev. 1997;11(7):824–834. doi: 10.1101/gad.11.7.824. PubMed PMID: 9106655. [DOI] [PubMed] [Google Scholar]
- 16.Shaw K.T., Ho A.M., Raghavan A., Kim J., Jain J., Park J. Immunosuppressive drugs prevent a rapid dephosphorylation of transcription factor NFAT1 in stimulated immune cells. Proc. Natl. Acad. Sci. U. S. A. 1995;92(24):11205–11209. doi: 10.1073/pnas.92.24.11205. PubMed PMID: 7479966. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Baeuerle P.A., Baltimore D. I kappa B: a specific inhibitor of the NF-kappa B transcription factor. Science. 1988;242(4878):540–546. doi: 10.1126/science.3140380. PubMed PMID: 3140380. [DOI] [PubMed] [Google Scholar]
- 18.DiDonato J.A., Hayakawa M., Rothwarf D.M., Zandi E., Karin M. A cytokine-responsive IkappaB kinase that activates the transcription factor NF-kappaB. Nature. 1997;388(6642):548–554. doi: 10.1038/41493. PubMed PMID: 9252186. [DOI] [PubMed] [Google Scholar]
- 19.Mercurio F., Zhu H., Murray B.W., Shevchenko A., Bennett B.L., Li J. IKK-1 and IKK-2: cytokine-activated IkappaB kinases essential for NF-kappaB activation. Science. 1997;278(5339):860–866. doi: 10.1126/science.278.5339.860. PubMed PMID: 9346484. [DOI] [PubMed] [Google Scholar]
- 20.Avraham A., Jung S., Samuels Y., Seger R., Ben-Neriah Y. Co-stimulation-dependent activation of a JNK-kinase in T lymphocytes. Eur. J. Immunol. 1998;28(8):2320–2330. doi: 10.1002/(SICI)1521-4141(199808)28:08<2320::AID-IMMU2320>3.0.CO;2-K. PubMed PMID: 9710210. [DOI] [PubMed] [Google Scholar]
- 21.Altman A., Villalba M. Protein kinase C-theta (PKC theta): a key enzyme in T cell life and death. J. Biochem. (Tokyo) 2002;132(6):841–846. doi: 10.1093/oxfordjournals.jbchem.a003295. PubMed PMID: 12473184. [DOI] [PubMed] [Google Scholar]
- 22.Villalba M., Altman A. Protein kinase C-theta (PKCtheta), a potential drug target for therapeutic intervention with human T cell leukemias. Curr. Cancer Drug Targets. 2002;2(2):125–137. doi: 10.2174/1568009023333908. PubMed PMID: 12188914. [DOI] [PubMed] [Google Scholar]
- 23.Janeway C. sixth ed. xxiii. Garland Science; New York: 2005. p. 823. (Immunobiology: the Immune System in Health and Disease). [Google Scholar]
- 24.Dolmetsch R.E., Xu K., Lewis R.S. Calcium oscillations increase the efficiency and specificity of gene expression. Nature. 1998;392(6679):933–936. doi: 10.1038/31960. PubMed PMID: 9582075. [DOI] [PubMed] [Google Scholar]
- 25.Dolmetsch R.E., Lewis R.S. Signaling between intracellular Ca2+ stores and depletion-activated Ca2+ channels generates [Ca2+]i oscillations in T lymphocytes. J. Gen. Physiol. 1994;103(3):365–388. doi: 10.1085/jgp.103.3.365. PubMed PMID: 8195779. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Bautista D.M., Hoth M., Lewis R.S. Enhancement of calcium signalling dynamics and stability by delayed modulation of the plasma-membrane calcium-ATPase in human T cells. J. Physiol. 2002;541(Pt 3):877–894. doi: 10.1113/jphysiol.2001.016154. PubMed PMID: 12068047. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Swillens S., Mercan D. Computer simulation of a cytosolic calcium oscillator. Biochem. J. 1990;271(3):835–838. doi: 10.1042/bj2710835. PubMed PMID: 2244883. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Dupuis G., Heroux J., Payet M.D. Characterization of Ca2+ and K+ currents in the human Jurkat T cell line: effects of phytohaemagglutinin. J. Physiol. 1989;412:135–154. doi: 10.1113/jphysiol.1989.sp017608. PubMed PMID: 2557424. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Verheugen J.A., Vijverberg H.P., Oortgiesen M., Cahalan M.D. Voltage-gated and Ca(2+)-activated K+ channels in intact human T lymphocytes. Noninvasive measurements of membrane currents, membrane potential, and intracellular calcium. J. Gen. Physiol. 1995;105(6):765–794. doi: 10.1085/jgp.105.6.765. PubMed PMID: 7561743. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Gaur N., Hof T., Hassaiguerre M., Vigmond E.J. Propagation failiure by TRPM4 overexpreission. Biophys. J. 2019;116:69–476. doi: 10.1016/j.bpj.2018.11.3137. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Rose R.A., DD B., MM M., WR G. Ca(2+) entry through TRP-C channels regulates fibroblast biology in chronic atrial fibrillation. Circulation. 2012;126(17):2039–2041. doi: 10.1161/CIRCULATIONAHA.112.138065. [DOI] [PubMed] [Google Scholar]
- 32.Luo C.H., Rudy Y. A dynamic model of the cardiac ventricular action potential. I. Simulations of ionic currents and concentration changes. Circ. Res. 1994;74(6):1071–1096. doi: 10.1161/01.res.74.6.1071. Epub 1994/06/01. PubMed PMID: 7514509. [DOI] [PubMed] [Google Scholar]
- 33.Quintana A., Griesemer D., Schwarz E.C., Hoth M. Calcium-dependent activation of T-lymphocytes. Pflügers Archiv. 2005;450(1):1–12. doi: 10.1007/s00424-004-1364-4. PubMed PMID: 15806400. [DOI] [PubMed] [Google Scholar]
- 34.Crabtree G.R. Calcium, calcineurin, and the control of transcription. J. Biol. Chem. 2001;276(4):2313–2316. doi: 10.1074/jbc.R000024200. PubMed PMID: 11096121. [DOI] [PubMed] [Google Scholar]
- 35.Clipstone N.A., Crabtree G.R. Identification of calcineurin as a key signalling enzyme in T-lymphocyte activation. Nature. 1992;357(6380):695–697. doi: 10.1038/357695a0. PubMed PMID: 1377362. [DOI] [PubMed] [Google Scholar]
- 36.O'Keefe S.J., Tamura J., Kincaid R.L., Tocci M.J., O'Neill E.A. FK-506- and CsA-sensitive activation of the interleukin-2 promoter by calcineurin. Nature. 1992;357(6380):692–694. doi: 10.1038/357692a0. PubMed PMID: 1377361. [DOI] [PubMed] [Google Scholar]
- 37.Kiani A., Rao A., Aramburu J. Manipulating immune responses with immunosuppressive agents that target NFAT. Immunity. 2000;12(4):359–372. doi: 10.1016/s1074-7613(00)80188-0. PubMed PMID: 10795734. [DOI] [PubMed] [Google Scholar]
- 38.Aramburu J., Yaffe M.B., Lopez-Rodriguez C., Cantley L.C., Hogan P.G., Rao A. Affinity-driven peptide selection of an NFAT inhibitor more selective than cyclosporin A. Science. 1999;285(5436):2129–2133. doi: 10.1126/science.285.5436.2129. PubMed PMID: 10497131. [DOI] [PubMed] [Google Scholar]
- 39.Abbott K.L., Friday B.B., Thaloor D., Murphy T.J., Pavlath G.K. Activation and cellular localization of the cyclosporine A-sensitive transcription factor NF-AT in skeletal muscle cells. Mol. Biol. Cell. 1998;9(10):2905–2916. doi: 10.1091/mbc.9.10.2905. PubMed PMID: 9763451. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Xu Z., Zhang D., He X., Huang Y., Shao H. Transport of calcium ions into mitochondria. Curr. Genom. 2016;17(3):215–219. doi: 10.2174/1389202917666160202215748. Epub 2016/06/03, PubMed PMID: 27252588; PubMed Central PMCID: PMCPMC4869008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Graber M., Bockenstedt L.K., Weiss A. Signaling via the inositol phospholipid pathway by T cell antigen receptor is limited by receptor number. J. Immunol. 1991;146(9):2935–2943. [PubMed] [Google Scholar]
- 42.Tsien R.Y., Pozzan T., Rink T.J. T-cell mitogens cause early changes in cytoplasmic free Ca2+ and membrane potential in lymphocytes. Nature. 1982;295(5844):68–71. doi: 10.1038/295068a0. PubMed PMID: 6799829. [DOI] [PubMed] [Google Scholar]
- 43.Donnadieu E., Cefai D., Tan Y.P., Paresys G., Bismuth G., Trautmann A. Imaging early steps of human T cell activation by antigen-presenting cells. J. Immunol. 1992;148(9):2643–2653. PubMed PMID: 1349319. [PubMed] [Google Scholar]
- 44.Leung C.Y., Liu L., Wong R.N., Zeng Y.Y., Li M., Zhou H. Saikosaponin-d inhibits T cell activation through the modulation of PKCtheta, JNK, and NF-kappaB transcription factor. Biochem. Biophys. Res. Commun. 2005;338(4):1920–1927. doi: 10.1016/j.bbrc.2005.10.175. PubMed PMID: 16289105. [DOI] [PubMed] [Google Scholar]
- 45.Lam J., Wulff H. The lymphocyte potassium channels Kv1.3 and KCa3.1 as targets for immunosuppression. Drug Dev. Res. 2011;72(7):573–584. doi: 10.1002/ddr.20467. Epub 2012/01/14, PubMed PMID: 22241939; PubMed Central PMCID: PMCPMC3253536. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Zhao N., Dong Q., Fu X.X., Du L.L., Cheng X., Du Y.M. Acacetin blocks kv1.3 channels and inhibits human T cell activation. Cell. Physiol. Biochem. 2014;34(4):1359–1372. doi: 10.1159/000366343. Epub 2014/10/11, PubMed PMID: 25301362. [DOI] [PubMed] [Google Scholar]
- 47.Chiang E.Y., Li T., Jeet S., Peng I., Zhang J., Lee W.P. Potassium channels Kv1.3 and KCa3.1 cooperatively and compensatorily regulate antigen-specific memory T cell functions. Nat. Commun. 2017;8:14644. doi: 10.1038/ncomms14644. https://www.nature.com/articles/ncomms14644#supplementary-information [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Sim J.H., Kim K.S., Park H., Kim K.J., Lin H., Kim T.J. Differentially expressed potassium channels are associated with function of human effector memory CD8(+) T cells. Front. Immunol. 2017;8:859. doi: 10.3389/fimmu.2017.00859. Epub 2017/08/10, PubMed PMID: 28791017; PubMed Central PMCID: PMCPMC5522836. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Launay P., Cheng H., Srivatsan S., Penner R., Fleig A., Kinet J.P. TRPM4 regulates calcium oscillations after T cell activation. Science. 2004;306(5700):1374–1377. doi: 10.1126/science.1098845. Epub 2004/11/20, PubMed PMID: 15550671. [DOI] [PubMed] [Google Scholar]
- 50.Parenti A., De Logu F., Geppetti P., Benemei S. What is the evidence for the role of TRP channels in inflammatory and immune cells? Br. J. Pharmacol. 2016;173(6):953–969. doi: 10.1111/bph.13392. Epub 2015/11/26, PubMed PMID: 26603538; PubMed Central PMCID: PMCPMC5341240. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Bertin S., Raz E. Transient receptor potential (TRP) channels in T cells. Semin. Immunopathol. 2016;38(3):309–319. doi: 10.1007/s00281-015-0535-z. Epub 2015/10/16, PubMed PMID: 26468011; PubMed Central PMCID: PMCPMC4833713. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Philipp S., Strauss B., Hirnet D., Wissenbach U., Mery L., Flockerzi V. TRPC3 mediates T-cell receptor-dependent calcium entry in human T-lymphocytes. J. Biol. Chem. 2003;278(29):26629–26638. doi: 10.1074/jbc.M304044200. Epub 2003/05/09, PubMed PMID: 12736256. [DOI] [PubMed] [Google Scholar]
- 53.Lacruz R.S., Feske S. Diseases caused by mutations in ORAI1 and STIM1. Ann. N. Y. Acad. Sci. 2015;1356:45–79. doi: 10.1111/nyas.12938. Epub 2015/10/16, PubMed PMID: 26469693; PubMed Central PMCID: PMCPMC4692058. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Naghdi S., Waldeck-Weiermair M., Fertschai I., Poteser M., Graier W.F., Malli R. Mitochondrial Ca2+ uptake and not mitochondrial motility is required for STIM1-Orai1-dependent store-operated Ca2+ entry. J. Cell Sci. 2010;123(15):2553–2564. doi: 10.1242/jcs.070151. [DOI] [PubMed] [Google Scholar]
- 55.Deak A.T., Blass S., Khan M.J., Groschner L.N., Waldeck-Weiermair M., Hallstrom S. IP3-mediated STIM1 oligomerization requires intact mitochondrial Ca2+ uptake. J. Cell Sci. 2014;127(Pt 13):2944–2955. doi: 10.1242/jcs.149807. Epub 2014/05/09, PubMed PMID: 24806964; PubMed Central PMCID: PMCPMC4077590. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56.Li X., Wu G., Yang Y., Fu S., Liu X., Kang H. Calmodulin dissociates the STIM1-Orai1 complex and STIM1 oligomers. Nat. Commun. 2017;8(1):1042. doi: 10.1038/s41467-017-01135-w. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57.Mullins F.M., Park C.Y., Dolmetsch R.E., Lewis R.S. STIM1 and calmodulin interact with Orai1 to induce Ca2+-dependent inactivation of CRAC channels. Proc. Natl. Acad. Sci. U. S. A. 2009;106(36):15495–15500. doi: 10.1073/pnas.0906781106. Epub 2009/08/27, PubMed PMID: 19706428; PubMed Central PMCID: PMCPMC2741279. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58.Ben-Kasus Nissim T., Zhang X., Elazar A., Roy S., Stolwijk J.A., Zhou Y. Mitochondria control store-operated Ca(2+) entry through Na(+) and redox signals. EMBO J. 2017;36(6):797–815. doi: 10.15252/embj.201592481. Epub 2017/02/22, PubMed PMID: 28219928; PubMed Central PMCID: PMCPMC5350565. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 59.Schwindling C., Quintana A., Krause E., Hoth M. Mitochondria positioning controls local calcium influx in T cells. J. Immunol. 2010;184(1):184–190. doi: 10.4049/jimmunol.0902872. PubMed PMID: 19949095. [DOI] [PubMed] [Google Scholar]
- 60.Quintana A., Pasche M., Junker C., Al-Ansary D., Rieger H., Kummerow C. Calcium microdomains at the immunological synapse: how ORAI channels, mitochondria and calcium pumps generate local calcium signals for efficient T-cell activation. EMBO J. 2011;30(19):3895–3912. doi: 10.1038/emboj.2011.289. PubMed PMID: 21847095; PubMed Central PMCID: PMCPMC3209779. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 61.Fraser S.P., Diss J.K., Lloyd L.J., Pani F., Chioni A.M., George A.J. T-lymphocyte invasiveness: control by voltage-gated Na+ channel activity. FEBS Lett. 2004;569(1-3):191–194. doi: 10.1016/j.febslet.2004.05.063. Epub 2004/07/01, PubMed PMID: 15225632. [DOI] [PubMed] [Google Scholar]
- 62.Patterson A.R., Endale M., Lampe K., Aksoylar H.I., Flagg A., Woodgett J.R. Gimap5-dependent inactivation of GSK3β is required for CD4+ T cell homeostasis and prevention of immune pathology. Nat. Commun. 2018;9(1):430. doi: 10.1038/s41467-018-02897-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 63.Fisher W.G., Yang P.C., Medikonduri R.K., Jafri M.S. NFAT and NFkappaB activation In T lymphocytes: a model of differential activation of gene expression. Ann. Biomed. Eng. 2006;34(11):1712–1728. doi: 10.1007/s10439-006-9179-4. PubMed PMID: 17031595. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 64.Terry L.E., Alzayady K.J., Furati E., Yule D.I. Inositol 1,4,5-trisphosphate receptor mutations associated with human disease. Messenger (Los Angel) 2018;6(1-2):29–44. Epub 2018/09/11. PubMed PMID: 30197841; PubMed Central PMCID: PMCPMC6128530. [PMC free article] [PubMed] [Google Scholar]
- 65.Rice J.J., Jafri M.S., Winslow R.L. Modeling short-term interval-force relations in cardiac muscle. Am. J. Physiol. Heart Circ. Physiol. 2000;278(3):H913–H931. doi: 10.1152/ajpheart.2000.278.3.H913. Epub 2000/03/10, PubMed PMID: 10710361. [DOI] [PubMed] [Google Scholar]
- 66.Williams G.S., Chikando A.C., Tuan H.T., Sobie E.A., Lederer W.J., Jafri M.S. Dynamics of calcium sparks and calcium leak in the heart. Biophys. J. 2011;101(6):1287–1296. doi: 10.1016/j.bpj.2011.07.021. Epub 2011/09/29, PubMed PMID: 21943409; PubMed Central PMCID: PMCPMC3177068. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 67.Kim S., Patrick S.M., Braunstein N.S., Thomas J.L., Leonard E.F. Modeling of early events in T cell signal transduction after controlled T cell activation by peptide major histocompatibility complex. Ann. Biomed. Eng. 2001;29(5):373–383. doi: 10.1114/1.1366671. PubMed PMID: 11400719. [DOI] [PubMed] [Google Scholar]
- 68.Desdín-Micó G., Soto-Heredero G., Mittelbrunn M. Mitochondrial activity in T cells. Mitochondrion. 2018;41:51–57. doi: 10.1016/j.mito.2017.10.006. [DOI] [PubMed] [Google Scholar]
- 69.Bantug G.R., Fischer M., Grahlert J., Balmer M.L., Unterstab G., Develioglu L. Mitochondria-endoplasmic reticulum contact sites function as immunometabolic hubs that orchestrate the rapid recall response of memory CD8(+) T cells. Immunity. 2018;48(3):542–555 e6. doi: 10.1016/j.immuni.2018.02.012. Epub 2018/03/11, PubMed PMID: 29523440; PubMed Central PMCID: PMCPMC6049611. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 70.Dimeloe S., Burgener A.V., Grahlert J., Hess C. T-cell metabolism governing activation, proliferation and differentiation; a modular view. Immunology. 2017;150(1):35–44. doi: 10.1111/imm.12655. Epub 2016/08/02, PubMed PMID: 27479920; PubMed Central PMCID: PMCPMC5341500. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 71.Ron-Harel N., Sharpe A.H., Haigis M.C. Mitochondrial metabolism in T cell activation and senescence: a mini-review. Gerontology. 2015;61(2):131–138. doi: 10.1159/000362502. Epub 2014/11/18, PubMed PMID: 25402204. [DOI] [PubMed] [Google Scholar]
- 72.Wolf I.M.A., Guse A.H. Ca(2+) microdomains in T-lymphocytes. Front. Oncol. 2017;7:73. doi: 10.3389/fonc.2017.00073. Epub 2017/05/18, PubMed PMID: 28512623; PubMed Central PMCID: PMCPMC5411426. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 73.Pettmann J., Santos A.M., Dushek O., Davis S.J. Membrane ultrastructure and T cell activation. Front. Immunol. 2018;9(2152) doi: 10.3389/fimmu.2018.02152. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 74.Dynes J.L., Amcheslavsky A., Cahalan M.D. Genetically targeted single-channel optical recording reveals multiple Orai1 gating states and oscillations in calcium influx. Proc. Natl. Acad. Sci. U. S. A. 2016;113(2):440–445. doi: 10.1073/pnas.1523410113. Epub 2015/12/30, PubMed PMID: 26712003; PubMed Central PMCID: PMCPMC4720334. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 75.Lee J.U., Kim L.K., Choi J.M. Revisiting the concept of targeting NFAT to control T cell immunity and autoimmune diseases. Front. Immunol. 2018;9:2747. doi: 10.3389/fimmu.2018.02747. Epub 2018/12/13, PubMed PMID: 30538703; PubMed Central PMCID: PMCPMC6277705. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 76.Joseph N., Reicher B., Barda-Saad M. The calcium feedback loop and T cell activation: how cytoskeleton networks control intracellular calcium flux. Biochim. Biophys. Acta. 2014;1838(2):557–568. doi: 10.1016/j.bbamem.2013.07.009. Epub 2013/07/19, PubMed PMID: 23860253. [DOI] [PubMed] [Google Scholar]
- 77.Rangamani P., Levy M.G., Khan S., Oster G. Paradoxical signaling regulates structural plasticity in dendritic spines. Proc. Natl. Acad. Sci. U. S. A. 2016;113(36):E5298–E5307. doi: 10.1073/pnas.1610391113. Epub 2016/08/24, PubMed PMID: 27551076; PubMed Central PMCID: PMCPMC5018790. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 78.De Young G.W., Keizer J. A single-pool inositol 1,4,5-trisphosphate-receptor-based model for agonist-stimulated oscillations in Ca2+ concentration. Proc. Natl. Acad. Sci. U. S. A. 1992;89(20):9895–9899. doi: 10.1073/pnas.89.20.9895. PubMed PMID: 1329108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 79.Wagner J., Keizer J. Effects of rapid buffers on Ca2+ diffusion and Ca2+ oscillations. Biophys. J. 1994;67(1):447–456. doi: 10.1016/S0006-3495(94)80500-4. PubMed PMID: 7919018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 80.Jafri M.S., Kotulska M. Modeling the mechanism of metabolic oscillations in ischemic cardiac myocytes. J. Theor. Biol. 2006;242:801–817. doi: 10.1016/j.jtbi.2006.05.007. [DOI] [PubMed] [Google Scholar]
- 81.Nguyen M.H., Jafri M.S. Mitochondrial calcium signaling and energy metabolism. Ann. N. Y. Acad. Sci. 2005;1047:127–137. doi: 10.1196/annals.1341.012. PubMed PMID: 16093491. [DOI] [PubMed] [Google Scholar]
- 82.Carrasco S., Meyer T. Cracking CRAC. Nat. Cell Biol. 2010;12(5):416–418. doi: 10.1038/ncb0510-416. Epub 2010/05/06, PubMed PMID: 20442700; PubMed Central PMCID: PMCPMC3897201. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 83.Pacheco J., Vaca L. STIM-TRP pathways and microdomain organization: auxiliary proteins of the STIM/orai complex. Adv. Exp. Med. Biol. 2017;993:189–210. doi: 10.1007/978-3-319-57732-6_10. Epub 2017/09/14, PubMed PMID: 28900915. [DOI] [PubMed] [Google Scholar]
- 84.Gudlur A., Zeraik A.E., Hirve N., Rajanikanth V., Bobkov A.A., Ma G. Calcium sensing by the STIM1 ER-luminal domain. Nat. Commun. 2018;9(1):4536. doi: 10.1038/s41467-018-06816-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 85.Luik R.M., Wang B., Prakriya M., Wu M.M., Lewis R.S. Oligomerization of STIM1 couples ER calcium depletion to CRAC channel activation. Nature. 2008;454(7203):538–542. doi: 10.1038/nature07065. Epub 2008/07/04, PubMed PMID: 18596693; PubMed Central PMCID: PMCPMC2712442. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 86.Srikanth S., Kim K.D., Gao Y., Woo J.S., Ghosh S., Calmettes G. A large Rab GTPase encoded by CRACR2A is a component of subsynaptic vesicles that transmit T cell activation signals. Sci. Signal. 2016;9(420):ra31. doi: 10.1126/scisignal.aac9171. Epub 2016/03/27, PubMed PMID: 27016526; PubMed Central PMCID: PMCPMC5013727. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 87.Srikanth S., Jung H.J., Kim K.D., Souda P., Whitelegge J., Gwack Y. A novel EF-hand protein, CRACR2A, is a cytosolic Ca2+ sensor that stabilizes CRAC channels in T cells. Nat. Cell Biol. 2010;12(5):436–446. doi: 10.1038/ncb2045. Epub 2010/04/27, PubMed PMID: 20418871; PubMed Central PMCID: PMCPMC2875865. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 88.Badou A., Jha M.K., Matza D., Flavell R.A. Emerging roles of L-type voltage-gated and other calcium channels in T lymphocytes. Front. Immunol. 2013;4:243. doi: 10.3389/fimmu.2013.00243. Epub 2013/09/07, PubMed PMID: 24009608; PubMed Central PMCID: PMCPMC3757574. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 89.Kirichok Y., Krapivinsky G., Clapham D.E. The mitochondrial calcium uniporter is a highly selective ion channel. Nature. 2004;427(6972):360–364. doi: 10.1038/nature02246. Epub 2004/01/23, PubMed PMID: 14737170. [DOI] [PubMed] [Google Scholar]
- 90.Paucek P., Jaburek M. Kinetics and ion specificity of Na(+)/Ca(2+) exchange mediated by the reconstituted beef heart mitochondrial Na(+)/Ca(2+) antiporter. Biochim. Biophys. Acta. 2004;1659(1):83–91. doi: 10.1016/j.bbabio.2004.03.019. PubMed PMID: 15511530. [DOI] [PubMed] [Google Scholar]
- 91.Skarka L., Ostadal B. Mitochondrial membrane potential in cardiac myocytes. Physiol. Res./Academia Scientiarum Bohemoslovaca. 2002;51(5):425–434. Epub 2002/12/10. PubMed PMID: 12470194. [PubMed] [Google Scholar]
- 92.Corkey B.E., Duszynski J., Rich T.L., Matschinsky B., Williamson J.R. Regulation of free and bound magnesium in rat hepatocytes and isolated mitochondria. J. Biol. Chem. 1986;261(6):2567–2574. [PubMed] [Google Scholar]
- 93.Zweifach A., Lewis R.S. Calcium-dependent potentiation of store-operated calcium channels in T lymphocytes. J. Gen. Physiol. 1996;107(5):597–610. doi: 10.1085/jgp.107.5.597. PubMed PMID: 8740373. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 94.Boesen A.M., Hokland P. Stereological analysis of the ultrastructure in isolated human T and non-T lymphoid cells. I. Description of method and data on normal blood lymphocytes. Virchows Arch. B Cell Pathol. Incl. Mol. Pathol. 1982;39(3):273–284. doi: 10.1007/BF02892854. PubMed PMID: 6126033. [DOI] [PubMed] [Google Scholar]
- 95.Feske S., Draeger R., Peter H.H., Eichmann K., Rao A. The duration of nuclear residence of NFAT determines the pattern of cytokine expression in human SCID T cells. J. Immunol. 2000;165(1):297–305. doi: 10.4049/jimmunol.165.1.297. PubMed PMID: 10861065. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.