Elastic Anisotropy Governs the Range of Cell-Induced Displacements

Abstract

The unique nonlinear mechanics of the fibrous extracellular matrix (ECM) facilitates long-range cell-cell mechanical communications that would be impossible for linear elastic substrates. Past research has described the contribution of two separated effects on the range of force transmission, including ECM elastic nonlinearity and fiber alignment. However, the relation between these different effects is unclear, and how they combine to dictate force transmission range is still elusive. Here, we combine discrete fiber simulations with continuum modeling to study the decay of displacements induced by a contractile cell in fibrous networks. We demonstrate that fiber nonlinearity and fiber reorientation both contribute to the strain-induced elastic anisotropy of the cell’s local environment. This elastic anisotropy is a “lumped” parameter that governs the slow decay of displacements, and it depends on the magnitude of applied strain, either an external tension or an internal contraction, as a model of the cell. Furthermore, we show that accounting for artificially prescribed elastic anisotropy dictates the decay of displacements induced by a contracting cell. Our findings unify previous single effects into a mechanical theory that explains force transmission in fibrous networks. This work may provide insights into biological processes that involve communication of distant cells mediated by the ECM, such as those occurring in morphogenesis, wound healing, angiogenesis, and cancer metastasis. It may also provide design parameters for biomaterials to control force transmission between cells as a way to guide morphogenesis in tissue engineering.

Significance

Tissues are made up of cells embedded in an extracellular matrix (ECM), a complex network of biopolymers. Cells actively alter the ECM structure and mechanics by applying contractile forces, which allow them to sense other distant cells and regulate many tissue functions. We study theoretically the decay of cell-induced displacements in fibrous networks while quantifying the changes in the elastic properties of the cell’s local environment. We demonstrate that cell contraction induces an anisotropic elastic state, i.e., unequal principal stiffnesses, in the ECM that dictates the slow decay of displacements. These observations suggest a, new mechanical mechanism through which cells can mechanically communicate over long distances and may provide design principles of biomaterials to guide morphogenesis in tissue engineering.

Introduction

Cells in tissues are surrounded by a cross-linked network of semiflexible biopolymers, such as collagen and elastin, known as the extracellular matrix (ECM) (1,2). The ECM has complex mechanics, including elastic nonlinearity, viscoelasticity, and plasticity (3,4). Cells actively adhere and are mechanically connected to the ECM, which enables them to sense and respond to their mechanical microenvironment by applying active contractile forces (5). These cellular forces can alter the structure and mechanical properties of the ECM in the proximity of the cell (6). As such, cell-ECM mechanical interactions play important roles at the cellular level such as in migration (7,8), proliferation (8, 9, 10), differentiation (7, 8, 9,11,12), cancer invasion (13, 14, 15), and mineral deposition (16).

When cells contract their microenvironment, they cause substantial displacements and structural changes that can reach a distance of tens of cell diameters away (4,17, 18, 19). Such phenomena support long-range cell-cell mechanical communication, a process that can mechanically couple distant cells and coordinate processes such as capillary sprouting (20) and synchronous beating (21). The long-range transmission of cellular forces is usually attributed to the unique nonlinear mechanics and fibrous nature of the ECM (17, 18, 19,22, 23, 24, 25, 26, 27, 28, 29, 30). It is currently clear that multiple physical effects (29,31) play central roles in enhancing force transmission in the ECM, including fiber stiffening (17,32), buckling (19,23), and collective network responses (e.g., fiber alignment (4,26,32)). Here, we show how these effects that were previously considered separately are interlinked and contribute to a more general mechanical mechanism: elastic anisotropy, i.e., unequal principal stiffnesses.

Specifically, fibrous networks are known to show substantial stiffening under different kinds of tensile loading (31,33, 34, 35, 36), and contracting cells have been shown to stiffen their surrounding environment when embedded in fibrous gels (17,35,37). Stiffening of networks can result either from the stretch stiffening of individual fibers, as described by the semiflexible polymer model (2,38,39), or from collective network alignment due to strain-induced fiber reorientation (24, 25, 26,40). In various biological contexts, it was frequently shown that fibers align in the vicinity of contracting cells and in the matrix between neighboring cells (4,14,15,24,27,28,32,37,41,42). The tendency of the ECM to stiffen and align under tension was shown to facilitate long-range transmission of internal cellular forces (17,29,30,40,43). In particular, Hall et al. (18) demonstrated that cell contractility induces local collagen alignment, which was shown to be highly correlated to enhanced force transmission. Wang et al. (27) devised a continuum model that incorporates the effect of alignment and managed to reproduce the nonlinear properties of collagen networks and the increased force transmission. Importantly, however, the isotropic stiffening alone is not enough to account for far-reaching forces observed in experiments, and other mechanisms must be involved (28). For example, buckling of fibers under compression results in softening of the fibrous network when compressed over some small critical strain (2,31,44, 45, 46). In previous works (19,22,23,27,29), including ours (19,29), fiber buckling was shown to enhance force transmission. Ronceray et al. (23) have shown, for example, that cell contracting in a simulated fibrous network creates a buckled region near the cell where the decay of force is very slow, owing to the loss of transverse stiffness. Indeed, fiber buckling has been observed near contracting cells in both experiments (47,48) and network simulations (23,49), which provide direct evidence for its involvement. Interestingly, in other types of fibrous networks such as in vitro reconstituted actomyosin gels, buckling of actin filaments, as well as folding of actomyosin sheets, has been shown to be related to displacement propagation from the gel edge inwards, which results in efficient contraction of the whole gel (50, 51, 52). Although the effects of buckling and stiffening have been clearly observed, it is still unknown whether they are related phenomena. Taking into account that both buckling (22) and stiffening (17,32) lead to changes in the elastic properties of the fibrous environment, the relationship between them may hint into the underlying mechanism in controlling force transmission.

In addition, different mechanical properties of the network may also arise from network topology and, in particular, its nodal coordination number, i.e., its average connectivity, denoting the mean number of fibers joined at each node. It is well established that networks below a critical connectivity number, known as the isostatic point, lose their rigidity and can deform without stretching of individual fibers. At low strains, bending interactions between fiber segments can stabilize these networks (2,53,54), and at larger strains, the network fibers start to deform by stretching (55). The phase transition at the isostatic critical point, and also its dependence on external strains, has been studied intensively (40,53,55,56). Network connectivity has been shown to be an important parameter affecting the stiffness and nonlinearity of the system (57). In the context of transmitting cell forces, Ronceray et al. (23) have described that in low-connectivity networks, contracting cell forces are transmitted through highly directed force chains, which transmit the forces to long ranges. However, quantitative characterization of the effect of network connectivity on force transmission range is still lacking. Moreover, whereas natural collagen networks are reported to have a connectivity number between 3 and 4 (57,58), many other scaffolds used for cell culturing are more highly cross-linked (59, 60, 61). Therefore, it is important to explore both low- and high-connectivity regimes in computational models.

Despite the understanding of the effects of fiber nonlinearity (buckling, stiffening) and fiber reorientation on force transmission, they were previously considered separately. The manner in which these effects are related and combined to determine the long-range cell-induced displacements has yet to be quantified and is still unclear (29,30). This work combines discrete fiber simulations with continuum modeling to study how the displacements induced by a contracting cell are transmitted in fibrous networks and quantifies how the nonlinear mechanics of individual fibers and collective fiber alignment combine to increase the elastic anisotropy of the cell’s local environment. We demonstrate that when a cell pulls on the network, the stiffness along the radial direction becomes higher than the stiffness along the angular direction, leading to a substantial increase in the elastic anisotropy of the network. This newly established elastic state dictates the decay of displacements in cross-linked fibrous networks. We thus propose a new universal mechanism of strain-induced elastic anisotropy through which cells can maintain long-range mechanical communications with one another in fibrous networks consisting of various types of fibers with different properties. Furthermore, we have also validated this mechanism of anisotropy-facilitated displacement transmission by studying the decay of displacements in intrinsically predesigned anisotropic networks.

We expect our studies on ECM-facilitated long-range force transmission to be most relevant for environments sparse in cells, such as connective tissues and engineered tissue scaffolds. In particular, they would apply to cells in scaffolds in the first few hours after seeding, when cells normally assume a spherical shape and matrix degradation and synthesis are absent (37,62). Our findings provide a new strategy in controlling force transmission in biomaterials by altering the material elastic anisotropy.

Methods

Discrete fiber simulations

We employ discrete fiber simulations to study the response of fiber networks to cell contraction and external uniaxial stretch. We use MATLAB R2018b (The MathWorks, Natick, MA) to create the network geometry and architecture. The MATLAB codes are available as a separate supporting file (Data S1). For all high-connectivity networks (with average connectivities of 5 and 8), we use the finite element software Abaqus/CAE 2017 (Dassault Systèmes Simulia, Johnston, RI) to simulate the network mechanics. For networks with a low connectivity of 3.5, we developed a program in MATLAB R2018b, implementing the conjugate gradient algorithm. The program was tested by applying it to the simulations identical to the ones done in Abaqus and verifying identical results. We perform simulations of a cell contracting isotropically in a network and simulations of rectangular pieces of network in uniaxial tension, as explained in the Results.

Mechanical modeling of the fibers

Each individual fiber segment is modeled as a one-dimensional linear truss element undergoing uniaxial tension or compression. In part of the simulations, we also modeled the fibers as beams, which are elements that resist perpendicular forces and transfer moments, and we show that truss and beam elements support similar effects and conclusions (Supporting Materials and Methods, Section SVII). Four mechanical models for the individual fibers are compared in this work (Fig. 1 B): linear, buckling, stiffening, and stiffening-buckling. All types of fibers have an elastic modulus E^∗ and a radius of r. Linear fibers maintain their stiffness for all strains, whereas buckling fibers buckle at a compressive strain ϵ_b < 0 and soften by a factor ρ, and stiffening fibers stiffen exponentially above a tensile strain ϵ_s > 0. Buckling-stiffening fibers combine both the softening and stiffening of the two last-mentioned material models. The stiffness assigned to an individual fiber that exhibits buckling and stiffening is given by

$$E=\{\begin{array}{ll}\rho E^{\text{∗}}& ϵ<{ϵ}_b\\ E^{\text{∗}}& {ϵ}_b<ϵ<{ϵ}_s\\ E^{\text{∗}}\left(1+\left(ϵ/{ϵ}_0\right)\right)\times exp\left[\left(ϵ-{ϵ}_s\right)/{ϵ}_0\right]& 0<{ϵ}_s<ϵ\end{array}$$ (1)

Figure 1.

Cell contraction simulation. (A) An illustration of a contractile cell, simulated by a circular cavity, embedded in an isotropic, homogeneous fibrous network. Isotropic inward displacements are imposed at the boundary of the cell, and the outer boundary of the network is held to be fixed (data not shown). (B) Force-strain curves for individual fibers used in the simulations. Four different mechanical models are used: linear, stretch stiffening, compression buckling, and nonlinear fibers with both buckling and stiffening. To see this figure in color, go online.

The values used in the model are E^∗ = 11.5 kPa, r = 100 nm, ϵ_b = −2%, ϵ_s = +2%, ϵ₀ = 5%, and ρ = 0.1. This mechanical behavior is largely based on computational models described in previous studies (42,48), and it produces networks that respond to uniaxial tension in a similar manner to previously reported 1.2 mg/ml collagen gels (Supporting Materials and Methods, Section S1; Fig. S1).

When simulating low-connectivity network deformations, we assign an energy cost to bending between fiber segments by defining “hinges” constraining the angle changes between two joint fiber segments. At each node, every fiber segment is hinged to the segment that is closest to being collinear to it, i.e., the segment whose angle is closest to 180°. The energy cost of angle changes between the hinged segments is:

$$\Delta U_b=\frac{2\kappa }{l_{1\_0}+l_{2\_0}}\left(1-\cos \left(\theta -{\theta }_0\right)\right),$$ (2)

where θ − θ₀ is the angle change between neighboring segments with respect to the undeformed network, l_{1_0} and l_{2_0} denote the initial lengths of the two neighboring segments, and $\kappa =\left(\pi /4\right)E^{\ast }{r}^4$ is the bending modulus of the fibers (63). This form of bending energy interaction between segments is a combination of the forms used by Ronceray et al. (23) and Rens et al. (64). Because our fibers are slender—$r\ll l_0$, where l₀ is the mean fiber length—when the network connectivity is larger than 4, fiber stretching becomes dominant, and fiber bending can be safely neglected (40).

Network architecture

We designed the networks to have an isotropic distribution of fiber orientations, a homogenous density, and a controlled connectivity number. We devised a random process to create network geometries, starting by uniformly scattering nodes in a circular domain. An objective function is introduced to control the generation of fiber segments between the nodes: this objective function includes three terms, accounting for fiber lengths, connectivity, and isotropy. Only segments that decrease the objective function can be created, and the process terminates when no segments can be added to the network (more detail in Supporting Materials and Methods, Section SII). Finally, a cell is embedded in the network by removing fibers and nodes in a circular domain in the middle of the network. We choose the radius of the outer boundary of the system to be 50 times the cell radius to make sure the displacements near the cell are not affected by the outer boundary.

Boundary conditions, model variants, and numerical methods

To model cell contraction in fibrous networks, we simulate isotropic contraction of a circular cell to different degrees (Fig. 1 A). We construct networks of very large size (50 times) in comparison to the cell radius, in which case the decay of displacements in the simulated network near the cell is not sensitive to the specific boundary conditions (either free or fixed) set at the outer boundary. We therefore choose to fix the displacements to be zero at the outer boundary of the network.

In most of our work, we study networks of connectivity number around 8, in which we compare the four fiber mechanical models for the individual fibers (as described above). In the Results, Effect of Network Connectivity on Displacement Transmission, we use networks with three different values of connectivity: ∼8, ∼5, and ∼3.5. For this comparison, we only use the linear model for the individual fibers. For all cases, the responses of five networks with different random geometries are averaged to reduce the effects of specific network geometry on the obtained results.

For uniaxial simulations, we measure the stiffness of the network both in the stretch longitudinal direction and in the transverse direction. This is done by stretching the network to some finite strain, then applying an additional small tension in the axis of stretch to measure the longitudinal stiffness and consequently a small tension in the transverse direction to obtain the transverse stiffness (See Supporting Materials and Methods, Section III2).

Results and Discussion

Discrete fiber simulations of a contracting cell in an isotropic network

Using a simplified finite element model of a contracting cell in a two-dimensional (2D) isotropic fibrous network (Fig. 1 A), we explore how the nonlinear mechanical properties of the fibers and the strain-induced fiber alignment affect the decay of cell-induced displacements. The cell is represented by a circular cavity that is isotropically contracting in the fibrous network. The fibrous networks are designed to be isotropic (in fiber orientation) and homogenous (in fiber density) at the scale of a cell. Four fiber models are used to compare different mechanical behaviors of the ECM biopolymers: linear, compression buckling, tension stiffening, and a stiffening-buckling model accounting for both phenomena (Fig. 1 B). In this part, nodes are modeled as freely rotating hinges, and only stretching energy is considered. Here, we focus on networks with a high connectivity around 8, at which the deformations are found to be nearly affine (Supporting Materials and Methods, Section SIII.1; Figs. S3–S5). Note that such high-connectivity networks can represent fibrous biopolymer gels that are more vigorously cross-linked (60,65,66) or combined with synthetic gels (67). We take advantage of the nearly affine deformation in such high-connectivity networks to compare them with continuum models that are based on affine deformation. This comparison allows us to gain deeper insights into the associated mechanisms. To further simplify the system, we perform the simulations in two dimensions, which has been shown to qualitatively capture all of the main mechanical behaviors of fibrous ECM while being substantially simpler computationally (2,23,68).

Two decaying regimes of displacements induced by a contracting cell

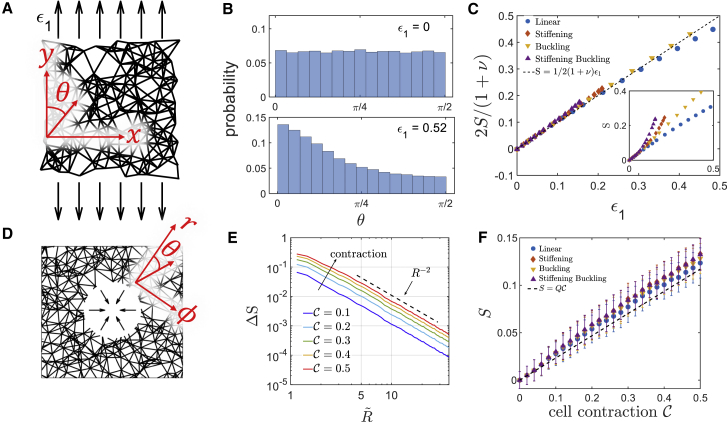
To simulate the decay of network displacements induced by a contracting cell, we embed a cell represented by a circular cavity of radius R_cell in the fibrous network. The cell contracts isotropically by radial displacement U_cell (<0) at its edge (Fig. 1 A). From these simulations, we obtain the network radial displacement U as a function of the distance R from the center of the cell (Fig. 2 A). We consider cell contractions, $\mathcal{C}\equiv$ −U_cell/R_cell, ranging from 2 to 50%. Distances are normalized by R_cell ($\tilde{R}$ = R/R_cell), and displacements are normalized by U_cell (Ũ = U/U_cell).

Figure 2.

Decay of displacements induced by an isotropic cell contraction. (A) A color map of displacements induced by 50% cell contraction. (B) A color map of strains of individual fibers. Radially aligned fibers are stretched (red), whereas angularly aligned fibers are compressed (blue). (C) Normalized displacement Ũ as a function of the normalized distance $\tilde{\text{R}}$ from the cell center is shown for the four fiber models, with 40% cell contraction. Two power-law regimes can be identified. (D) Near-field effective power-law exponent n vs. normalized cell contraction $\mathcal{C}/{\mathcal{C}}_{\text{crit}}$. Inset: n decreases linearly with contraction for linear fibers because of increased fiber alignment. Fiber nonlinearities facilitate the decrease in n. Error bars are standard deviations over five network realizations. (E) Effective cell displacement Ũ_eff vs. normalized cell contraction $\mathcal{C}/{\mathcal{C}}_{\text{crit}}$. Ũ_eff increased linearly with contraction for all fiber models (inset). To see this figure in color, go online.

Because our network is isotropic at the undeformed state, and because all the simulated fiber models behave linearly at small strains, we expect to find Ũ ∼ ${\tilde{R}}^{-1}$ for small strains, as in the linear isotropic elastic continuum (63). We indeed observe this scaling at the far-field $\tilde{R}\gg 1$, where strains are small (Fig. 2 C). In contrast, close to the cell—up to a distance of around 3R_cell—the displacements decay more slowly. In this near-field regime, strains are high such that fiber alignment and fiber nonlinearities (stiffening/buckling) play substantial roles in slowing the decay of displacements. We note that the slow decay of displacements in the near-field regime can be well fitted by an effective power law Ũ ∼ ${\tilde{R}}^{-n}$, with n ≤ 1 for all fiber model types and cell contractions (Fig. 2 C). For the purpose of this fitting, we use the 200 nodes closest to the cell, corresponding to the area up to 2.7 cell radii away from the cell. We note that although this choice is somewhat arbitrary, we have verified that the results are not sensitive to this particular value within a reasonable range (data not shown). We find that as the cell pulls more on the network, the fitted exponent n in the near field decreases, giving rise to longer-range transmission of displacements (Fig. 2 D). Remarkably, even for networks of linear fibers, there is a monotonic decrease of n as the cell contracts. This is in contrast to a linear isotropic continuum, in which we expect a constant n = 1, and the decay of displacement is independent of the cell contraction and the elastic properties of the linear medium (63). The range of displacement transmission is further enhanced (i.e., n decreases more with increasing cell contraction) by introducing fiber buckling and stiffening (inset of Fig. 2 D). Interestingly, the exponents n for all types of fibers fall to a single master curve (Fig. 2 D) when plotted as a function of the normalized cell contraction, $\mathcal{C}/{\mathcal{C}}_{\text{crit}}$. Here, ${\mathcal{C}}_{\text{crit}}$ is the critical cell contraction over which the slow-decay near-field region becomes evident. In our analysis, to be specific, we determine ${\mathcal{C}}_{\text{crit}}$ as the magnitude of cell contraction for which n = 0.9 in the near-field region, as shown by the dashed line in the inset of Fig. 2 D. It can be seen that ${\mathcal{C}}_{\text{crit}}$, as previously introduced by Xu et al. (29), depends sensitively on the mechanics of individual fibers of the network. However, $\mathcal{C}/{\mathcal{C}}_{\text{crit}}$ is a universal parameter that is independent of specific fiber mechanics, as indicated by the single master curve in Fig. 2 D. The magnitude of $\mathcal{C}/{\mathcal{C}}_{\text{crit}}$ measures the degree of nonlinearity in the cell-contracted network. When $\mathcal{C}/{\mathcal{C}}_{\text{crit}}$ ≪ 1, the network behaves like a linear material with n ≈ 1.0. When $\mathcal{C}/{\mathcal{C}}_{\text{crit}}$ increases above 1.0, the network becomes highly nonlinear with n significantly smaller than 1.0, indicating longer-range displacement transmission.

The increase in the range of displacement transmission by the nonlinear near-field region can also be quantified by introducing an effective cell contraction, Ũ_eff, through fitting the far-field displacement by Ũ = Ũ_eff × ${\tilde{R}}^{-1}$ (69). The fit to the far-field regime was done by finding a range of distances (typically 6–25 cell radii away from the cell) in which the fitted power-law exponent is −1 ± 0.01. Ũ_eff reflects the degree of cell contraction that would induce the same magnitude of displacements far from the cell in a linear isotropic elastic continuum (Fig. 2 E). Ũ_eff increases with contraction and is enhanced when nonlinear mechanical properties are introduced. We find that for strong cell contraction, Ũ_eff scales linearly with the normalized cell contraction $\mathcal{C}/{\mathcal{C}}_{\text{crit}}$ for all types of fibers simulated in this work. This unified linear relation for all fiber models is consistent with our theory prediction (see Supporting Materials and Methods, Section SVI.2; Eq. S35) and further justifies the importance of the normalized cell contraction $\mathcal{C}/{\mathcal{C}}_{\text{crit}}$ as an essential “emergent” dimensionless parameter involved in the long-range transmission. Overall, these results indicate that mechanical and geometrical nonlinearities give rise to two power-law regimes with distinct scaling, and nonlinear properties of individual fibers, as well as strain-induced fiber alignment, play important roles mainly in the near-field regime. These findings extend on previous studies in which multiple scaling regimes were identified (23,29) by systematically quantifying the effects of the strength of cell contraction and the mechanical properties of fibers on the identified regimes.

Strain-induced elastic anisotropy: Effects of fiber alignment, stiffening, and buckling

Our next goal is to understand why the near-field regime shows a slower decay of displacements and what mechanism dictates the slope of the decay. We hypothesize that when cells pull on the network, the stiffness along the radial direction becomes much higher than the stiffness along the angular direction (i.e., the network becomes elastically anisotropic), and this new elastic state dictates the slow decay of displacements. Our motivation originates from the established theory of anisotropic continuum: when a circular cavity contracts isotropically in a linear 2D anisotropic elastic continuum (22,70), the displacements decay as Ũ ∼ ${\tilde{R}}^{-\sqrt{E_2/E_1}}$ (Supporting Materials and Methods, Section SVI; (22,70)), where E₁ and E₂ are the stiffnesses in the radial and angular directions, respectively. Recently, Wang et al. (27) have developed a constitutive law of collagen networks that accounts for the anisotropic stiffness ratio and showed that this parameter affects the range of force transmission. Han et al. (35) demonstrated experimentally that stiffness indeed becomes anisotropic near contracting cells, with a higher extent of stiffening in the radial relative to the angular direction. In our simulations, we find that radially aligned fibers are stretched, whereas angularly aligned fibers are typically compressed (Fig. 2 B). In the case of nonlinear elastic fibers, this can clearly lead to elastic anisotropy in the network because radial stretched fibers will become stiffer than the angular compressed fibers.

We first carry out simulations to study how an external strain induces elastic anisotropy in a bulk fibrous network. We generate a rectangular piece of the network and subject it to uniaxial stretch ϵ₁ (Fig. 3 A). Under external stretch, the network assumes an aligned, anisotropic state (Fig. 3 B). We refer to the axis of strain as the longitudinal axis and the axis perpendicular to it as the transverse axis. We apply an additional small longitudinal stretch dϵ₁ and measure the change in stress dσ₁ to obtain the longitudinal stiffness E₁(ϵ₁) = dσ₁(ϵ₁)/dϵ₁. The transverse stiffness E₂ is then measured by applying a small stretch dϵ₂ in the transverse direction and obtaining E₂(ϵ₁) = dσ₂(ϵ₁)/dϵ₂ (Supporting Materials and Methods, Section SIII.2; Fig. S7). We verify that in the absence of uniaxial prestretch, the two stiffnesses are equal, i.e., E₁(ϵ₁ = 0) = E₂(ϵ₁ = 0) $\equiv$ E₀. We also observe that E₀ ≈ E^∗ϕ_f, with E^∗ being the modulus of the fibers and ϕ_f being the fiber volume fraction. This agrees with the prediction of the stiffness of foams in classical cellular solid theory (45,71).

Figure 3.

Elastic anisotropy induced by external uniaxial tension. (A) A schematic illustration of the rectangular network upon external uniaxial stress. (B) Strain color map: the fibers along the axis of strain are stretched (red), whereas transverse fibers are compressed (blue). (C) The ratio of the two principal moduli, E₂/E₁, measuring the elastic anisotropy versus normalized strain, ϵ₁/ϵ_crit. At a given tensile prestrain ϵ₁, additional infinitesimal tensile strains are applied in both directions to measure the respective elastic moduli, E₁ (longitudinal) and E₂ (transverse) (see illustration in A). The modulus ratio E₂/E₁ deviates from 1 when the network is strained and becomes close to 0 for high strains. All three effects—fiber alignment, buckling, and stiffening—contribute to this strain-induced anisotropy. Inset shows E₂/E₁ vs. strain (without normalization). To see this figure in color, go online.

The stiffness ratio E₂/E₁, measuring the elastic anisotropy of the network, systematically decreases with increasing external strain (Fig. 3 C), showing that the fibrous networks become increasingly anisotropic as they are stretched. Note that this strain-induced anisotropy occurs in networks composed of all model fibers, even for networks composed of linear fibers. This indicates that strain-induced elastic anisotropy is driven by both mechanical nonlinearities of individual fibers and geometrical anisotropy such as collective fiber alignment.

In addition, we find that the data points of E₂/E₁ for all types of fibers can be approximately fitted by a master curve if plotted versus the normalized strain, ϵ/ϵ_crit (Fig. 3 C). Here, ϵ_crit is the critical strain, a characteristic parameter of the network, in which E₂/E₁ becomes smaller than 0.9, and the strain-induced elastic anisotropy is significant. The normalized strain ϵ/ϵ_crit, similar to the normalized cell contraction $\mathcal{C}/{\mathcal{C}}_{\text{crit}}$ in cell contraction networks, is another “emergent” dimensionless parameter for the fibrous network upon external uniaxial strain; it measures the degree of nonlinearity in the externally stretched network and determines the strain-induced elastic anisotropy.

Collective fiber alignment measured by nematic order parameter: A structural indicator of the network elastic anisotropy

We next aim to quantify the elastic anisotropy that develops in the fibrous network due to cell-induced strains in the circular geometry as depicted in Fig. 1 A. For this purpose, we use fiber alignment as a structural indicator of elastic anisotropy. In our model, the networks are isotropic in their undeformed state, contrary to the case of prealigned systems, and hence, fiber alignment is always coupled with external strains applied on them. Furthermore, for a given fiber model, we assume that if two different networks have the same degree of fiber alignment or nematic order parameter (NOP), they also have the same elastic anisotropy. We then approximate the elastic anisotropy near the contracting cell by that of the uniaxially stretched bulk network with the same NOP, as shown in Fig. 3 C; in other words, we measure the NOP in both the bulk uniaxial and cell contraction networks and use it as a mapping parameter to estimate the elastic anisotropy of the cell system from the measurements of the bulk system.

For rectangular networks under uniaxial strain, we measure the orientation of each fiber with respect to the direction of the applied external strain (Fig. 4 A). Before stretching, the network is isotropic, and the distribution of fiber angles is uniform without any preferred orientation. After stretching, this distribution shifts toward the direction of the applied stretch (Fig. 4 B), indicating a clear collective fiber alignment. The degree of fiber alignment can be measured by the NOP in two dimensions (24): S = $\langle \cos \left(2\theta \right)\rangle$. S ranges from −1 to 1, where a value of 0 corresponds to an isotropic network, a value of 1 corresponds to a network with fully aligned fibers along the strain direction, and a value of −1 corresponds to a network of transversely aligned fibers.

Figure 4.

Strain-induced collective alignment of fibers. (A) A schematic illustration of a uniaxially stretched network. The orientational angle θ of each fiber is defined with respect to the strain axis. (B) A histogram of the distribution of individual fiber angles. (top) Fiber angle distribution in an undeformed isotropic network. (bottom) Fiber angle distribution for a linear fiber network upon 0.52 uniaxial strain; collective fiber alignment along the strain direction is indicated with more fiber fraction toward zero angle. (C) S (i.e., NOP) of the stretched network as a function of the applied uniaxial strain ϵ₁ (inset). All fiber models follow the affine prediction S = 1/2(1 + ν)ϵ₁. (D) A schematic illustration of a cell-contracted network. The orientational angle θ of each fiber is defined with respect to the radial direction. (E) S (i.e., NOP) of the contracted network (of linear fibers) is shown as a function of $\tilde{\text{R}}$. S decays with ∼R⁻² in the far field, with a slower decay in the vicinity of the cell. S increases with cell contraction. (F) Averaged S in the near-field region as a function of cell contraction. S increases linearly with cell contraction and fits well to the affine theory (dashed black line). Error bars are standard deviations over five network realizations. To see this figure in color, go online.

The network composed of linear fibers shows a linear increase of S with strain, whereas nonlinear networks exhibit stronger alignment with strain (Fig. 4 C, inset). To understand this behavior, we use affine approximation to derive the analytical relation between alignment and external strain and obtain S = $\left(1/2\right)\left(1+\nu \right){ϵ}_1$, with ν = −ϵ₂/ϵ₁ being the Poisson ratio (Supporting Materials and Methods, Section SIII.2; note that ν = +1 corresponds to incompressible networks in two dimensions). We find that the theoretical prediction of S is in good agreement with the measured S from the bulk simulations (Fig. 4 C), despite local nonaffine deformations in our fibrous networks (Supporting Materials and Methods, Section SIII.1). Thus, a larger Poisson ratio is directly coupled to enhanced alignment. Indeed, linear fiber networks have a relatively constant Poisson ratio (ν ∼ 0.4), whereas nonlinear fiber models are characterized by a larger Poisson ratio that increases with external strain (Fig. S6). S therefore depends linearly on the applied strain only for linear networks.

To quantify fiber alignment (i.e., S) in cell contraction networks, we measure the angles relative to the radial direction (Fig. 4 D). This is in accordance with the evaluation of alignment described in recent studies (25,49). S is averaged over fibers in annular domains around the cell. Note that although undeformed networks are macroscopically isotropic, they can locally have some weak preferred fiber orientation. We thus measure the degree of alignment with respect to the undeformed state: ΔS = S_deformed − S_undeformed for each annular domain around the cell. As shown in Fig. 4 E, ΔS decays with a power law of ΔS ∼ R⁻² at distances far from the cell, independent of the degree of cell contraction. This is expected, as S is linearly proportional to strain at small strains (72), and in the far-field regime, strain decays as R⁻² (because strains are the first derivatives of displacements that decay as R⁻¹ in the far-field regime).

In the near-field regime, we observe that S increases linearly with cell contraction, and remarkably, it is almost independent of the fiber model type (Fig. 4 F), in comparison to the case of uniaxially stretched networks in rectangular geometry. To understand this better, we derive an analytical prediction for the dependence of S on cell contraction $\mathcal{C}$ in the near field, using affine displacement approximation combined with the near-field effective power-law scaling Ũ = ${\tilde{R}}^{-n}$. We obtain the relation S = Q(n, ${{\tilde{R}}^{\ast }}^{}$) $\mathcal{C}$, where n is the near-field scaling exponent and ${{\tilde{R}}^{\ast }}^{}$ is the size of the near-field region normalized by the cell radius (the derivation and exact form of Q(n, R^∗) is given in Supporting Materials and Methods, Section SIV). We find that the dependence of Q on n and R^∗ is rather weak, and Q(n, R^∗) is almost constant for all of our simulations. This analytical relation fits nicely to the simulation results (dotted curve in Fig. 4 F), which suggests that fiber alignment near the cell can be well predicted by affine theory and has robust trends independent of fiber mechanics. To conclude, we now have a full description of the network alignment in both the uniaxially stretched bulk and cell-contracted networks.

Cell-induced elastic anisotropy dictates the slow displacement decay in fibrous networks

As the cell pulls on the matrix, the network alignment in the near field increases, and the elastic anisotropy is expected to rise. For each magnitude of cell contraction, we estimate the elastic anisotropy in the near field, measured by 1 − $\sqrt{E_2/E_1}$, based on the measurements in uniaxially stretched bulk networks composed of the same model fibers and having the same NOP (Fig. 5 A, schematics). We can now plot the effective power-law exponent n of displacement transmission against the elastic anisotropy in the near-cell area. We find a universal linear relation that is similar for all network types, independent of particular fiber mechanical properties (Fig. 5 B). Note that this unified linear relation takes into account the unified master curve for n vs. normalized cell contraction $\mathcal{C}/{\mathcal{C}}_{\text{crit}}$ (Fig. 2 D). Furthermore, the obtained unified linear relation indicates that once the elastic anisotropy is set by the nonlinear parameter $\mathcal{C}/{\mathcal{C}}_{\text{crit}}$, the displacement decay will be dictated accordingly, independent of the fiber mechanical model. Therefore, the cell-induced elastic anisotropy is a “lumped” parameter that takes into account the effects of both fiber nonlinearities and fiber alignment and that governs the slow decay (n < 1) of cell-induced displacements in fibrous networks.

Figure 5.

Elastic anisotropy dictates the decay of displacements in fibrous networks. (A) A schematic illustration of the transformation from bulk to cell contraction simulations: if two different networks (both isotropic at the undeformed state) are composed of similar fiber properties and have the same NOP, they are assumed to be in the same mechanical state, i.e., have the same elastic anisotropy E₂/E₁. (B) The near-field power-law exponent n for the decay of displacements is plotted as a function of the square root of the network anisotropy$\sqrt{{\text{E}}_2/{\text{E}}_1}$. We found n ∝ $\sqrt{{\text{E}}_2/{\text{E}}_1}$ which is consistent with the theoretical prediction for an anisotropic continuum material. Error bars are standard deviations over five network realizations. To see this figure in color, go online.

Effect of network connectivity on displacement transmission

Network connectivity greatly affects the mechanics of fibrous networks. For example, collagen networks below the isostatic connectivity (four in our 2D case) are bending dominated at low strains (i.e., can deform with negligible fiber stretching) (73), whereas networks above the isostatic point are typically stretching dominated (40). The connectivity of most reconstituted biopolymer networks is reported to be between 3 and 4 (57,58). Thus, it is important to verify that our observations are valid also in low-connectivity, bending-dominated networks. We chose to compare three different connectivity values: ∼8, ∼5, and ∼3.5. To simulate deformations of networks with a low connectivity of 3.5, we include bending interactions between joint fiber segments. This interaction is negligible in higher connectivities but necessary to stabilize the networks with a connectivity lower than 4 to avoid floppy modes (2).

With connectivity 3.5, the developed strains are dramatically lower than those in networks of higher connectivity (Fig. 6). This is because fibers can deform by bending, rather by stretching, which is energetically favorable. Therefore, we find that the response of the 3.5 connectivity networks is similar for different fiber mechanical properties (with or without buckling or stiffening) because the developed strains are smaller than the critical nonlinear threshold in which stiffening and buckling initiate. We therefore only consider linear fibers when comparing networks with different connectivity numbers.

Figure 6.

Strain map created by a cell contracting to 30%, comparing different connectivity networks: (A) ∼8, (B) ∼5, and (C) ∼3.5. To see this figure in color, go online.

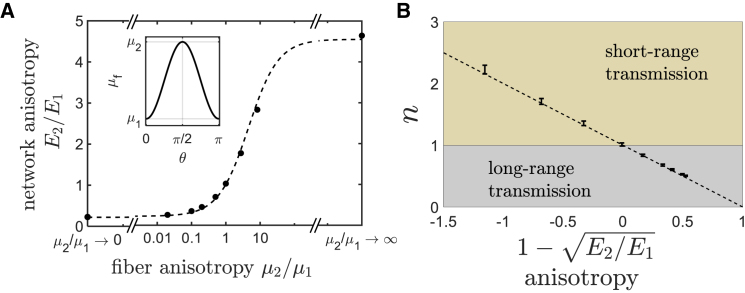
For all the connectivity numbers tested, the decay exponent (i.e., n) decreases almost linearly with cell contraction, with a substantially steeper slope for lower connectivity (Fig. 7 A). Thus, networks with lower connectivity can transmit displacements to longer ranges. The displacements in the 3.5 connectivity networks are highly nonaffine and inhomogeneous, as manifested by the large standard deviations (Fig. 7 A). We also observe that networks with lower connectivity tend to align more near the contracting cell (Fig. 7 B) and in uniaxial tension (Fig. 7 C). Furthermore, under uniaxial tension, networks with lower connectivity adopt a faster transition to an anisotropic elastic state in comparison to higher connectivity networks (Fig. 7 D). Strikingly, although networks with different connectivity values respond differently to an applied force (either cell induced or uniaxial bulk), a similar linear relationship between the decay exponent and the anisotropy is preserved (Fig. 7 E). These results indicate that the mechanism of elastic anisotropic in dictating the decay of displacements holds for networks composed of various fiber types and of different connectivity values and thus is robust and general.

Figure 7.

Behavior of networks with connectivities around 8, 5, and 3.5. (A) The decay exponent n as a function of cell contraction. (B) Fiber alignment as a function of cell contraction. (C) Fiber alignment of rectangular networks as a function of uniaxial strain. (D) Elastic moduli ratio as a function of uniaxial strain. (E) Decay exponent n as a function of the anisotropy measure 1 − $\sqrt{{\text{E}}_2/{\text{E}}_1}$. Error bars are standard deviations over five network realizations. To see this figure in color, go online.

Controlling the range of displacement transmission by modifying the intrinsic elastic anisotropy

The change of force transmission by elastic anisotropy can be seen more explicitly by looking at the decay of displacements in an intrinsically anisotropic fiber network with predefined tunable elastic anisotropy. An intrinsically anisotropic fiber network can be constructed by introducing an angle-dependent fiber modulus: for example, μ_f = μ₁cos²θ + μ₂sin²θ, where μ_f is the axial fiber modulus, θ is the fiber orientation (measured relative to the radial direction), and μ₁ and μ₂ are two given stiffnesses (Fig. 8 A, inset). Note that all the constituent fibers are linear elastic, but their moduli are orientation dependent. Moreover, in the undeformed state, the network is elastically anisotropic but geometrically isotropic, with a uniform fiber angle distribution. In this case, calculations from affine deformation predict that the ratio between the two principal stiffnesses takes the form of E₂/E₁ = (ρμ₂ + μ₁)/(μ₂ + ρμ₁), where ρ = 5.0 for uniform distribution of fiber orientation (Supporting Materials and Methods, Section SV). We carry out bulk uniaxial simulations to measure E₂/E₁ for different predefined ratios μ₂/μ₁ and obtain ρ = 4.1 by least-squares fitting (Fig. 8 A). Note that in contrast to the strain-induced anisotropy that is determined by the normalized external strain ϵ/ϵ_crit or normalized internal cell contraction $\mathcal{C}/{\mathcal{C}}_{\text{crit}}$, the elastic anisotropy in intrinsically anisotropic networks is determined by design based on predefined fiber anisotropy, μ₂/μ₁.

Figure 8.

The decay of cell-induced displacements in intrinsically anisotropic networks. (A) An intrinsically anisotropic network is constructed by introducing an orientation-dependent fiber modulus μ_f = μ₁cos²(θ) + μ₂sin²(θ) (inset). The elastic anisotropy of the network is predicted by affine theory as E₂/E₁ = (ρμ₂ + μ₁)/(ρμ₁ + μ₂) (dashed line), with ρ ≈ 4.1 (black dots, simulation data), which is close to the theoretical prediction ρ = 5.0. (B) The near-field power-law exponent, n, is plotted as a function of network anisotropy at infinitesimal cell contractions; a very good linear fitting to n = $\sqrt{{\text{E}}_2/{\text{E}}_1}$ is obtained in both regions: E₂ > E₁ (with n > 1 indicating fast displacement decay) and E₁ > E₂ (with n < 1 indicating slow displacement decay). Error bars are standard deviations over five network realizations. To see this figure in color, go online.

We then study the decay of displacements induced by a contractile cell in such intrinsically anisotropic networks. For very small cell contractions, we can consider only the effect of predefined elastic anisotropy while neglecting the effect of fiber alignment. We find that the power-law exponent shows a very good linear proportionality to the elastic anisotropy, n ∼ $\sqrt{E_2/E_1}$ for all values of n (Fig. 8 B). When the network is stiffer along the radial direction (E₂ < E₁), we obtain n < 1, i.e., the displacements decay slowly, in which case the range of cell-cell communications mediated by the matrix is considerably enhanced. In contrast, when the network is stiffer along the angular direction (E₂ > E₁), we obtain n > 1, i.e., the displacements decay faster than in linear isotropic elastic medium. In this case, the range of cell-cell communication is restricted. This indicates that the transmission of cellular forces in fibrous networks and hence the efficiency of matrix-mediated cell-cell communications can be reprogrammed by modifying the network anisotropic properties. This opens the possibility of designing biomaterials to control the range of cell-induced forces and, with that, gain control over cellular interactions.

In summary, we show that the unified mechanism of elastic anisotropy governs the long-range transmission of cell-induced displacement in networks consisting of various types of fibers with different mechanical properties. These findings show that the two effects that were previously considered separately, fiber nonlinearity (buckling or stiffening) and fiber reorientation (or alignment), are related, and both contribute to the network’s elastic anisotropy, which is a key strain-dependent “lumped” parameter that dictates the decay of the displacements. Whereas in previous works, elastic anisotropy resulted from unique mechanisms introduced by the computational models and was regarded only implicitly (22,27,74), here, we measure it explicitly. We show that the anisotropy is sensitive to the buckling, stiffening, and alignment behavior of the fibers and show its direct effect on the transmission of displacements. The validity of this unified mechanism of elastic anisotropy is shown for several cases: cells that contract strongly enough to generate a local anisotropic environment and cells that contract weakly in an existing predesigned anisotropic network. In all cases, the elastic anisotropy dictates the decay of cell-induced displacements.

In this work, we only focused on the elastic response of networks without taking into consideration dynamical remodeling of fibers by cells such as fiber degradation or secretion of new fibers, as well as viscoelasticity and plasticity of the ECM fibers and the potential feedback of cells to the change in their mechanical microenvironment (5). For simplification, our predictions and simulations are held in 2D. Based on (70), the analytical prediction for the decay of displacements in the case of an isotropic cell contraction in a three-dimensional (3D) linear anisotropic elastic continuum is:

$$n_{3\text{D}}=\frac{1}{2}\left(1+\sqrt{1+8\frac{E_2\left(1-{\nu }_{12}\right)}{E_1\left(1-{\nu }_{22}\right)}}\right),$$ (3)

where ν₁₂ and ν₂₂ are the Poisson ratios in the radial and transverse planes, respectively. This is in comparison to our 2D result, n_2D ∼ $\sqrt{E_2/E_1}$. It indicates that the dependence on the elastic anisotropy in 3D is qualitatively similar to the 2D case, although quantitatively different. Specifically, n_3D is dominated by an anisotropic term, which also includes dependence on the Poisson ratios. In principle, this anisotropic term can be determined for a deformed network using uniaxial strain simulations, similar to the ones we have described here in 2D. The anisotropy can then be mapped back to the cell contraction simulations using a 3D NOP. All these aspects of cell-cell and cell-matrix interactions should be investigated more carefully in the future by extending the continuum theory and finite element simulation presented in this work. Still, this work relates and unifies previous single effects into a general mechanism of elastic anisotropy that explains how (strongly or weakly) contracting cells can maintain long-range mechanical communications with one another. Our findings provide, to our knowledge, new insights into various biological processes that involve cell-ECM interactions and ECM-mediated cell-cell interactions and may provide new design parameters for tissue engineering scaffolds.

Author Contributions

A.L. and X.X. conceived the project. A.L. supervised the project as principal investigator. S.G. created the network geometries, and Y.K. and S.G. performed the simulations. S.G. and Y.K. analyzed the data. X.X. and S.G. developed the analytical models. All authors wrote the manuscript.

Editor: Celeste Nelson.

Supporting Citations

References (75, 76, 77, 78, 79, 80) can be found in the Supporting Material.