Abstract
In a contracting muscle, myosin cross-bridges extending from thick filaments pull the interdigitating thin (actin-containing) filaments during cyclical ATP-driven interactions toward the center of the sarcomere, the structural unit of striated muscle. Cross-bridge attachments in the sarcomere have been reported to exhibit a similar stiffness under both positive and negative forces. However, in vitro measurements on filaments with a sparse complement of heads detected a decrease of the cross-bridge stiffness at negative forces attributed to the buckling of the subfragment 2 tail portion. Here, we review some old and new data that confirm that cross-bridge stiffness is nearly linear in the muscle filament lattice. The implications of high myosin stiffness at positive and negative strains are considered in muscle fibers and in nonmuscle intracellular cargo transport.
Main Text
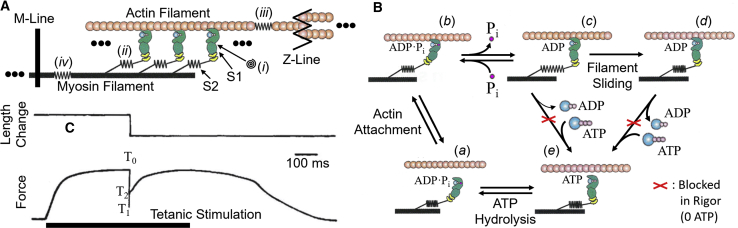
Motor proteins are mechanoenzymes able to use the free energy liberated from ATP hydrolysis to power motion in eukaryotes; among them are the many isoforms of myosin responsible either for muscle contraction and cell motility, in which they are organized into filaments, or for many other cell motility and transport processes (1). In the half sarcomere, arrays of myosin motor heads extending from the thick filament cyclically interact with the nearby actin (thin) filaments (Fig. 1 A), splitting ATP to produce steady force and filament sliding that lead to shortening of the sarcomere (2,3). Favorable control of thick filament activation matches energy utilization to the mechanical load (4). The elastic properties of the actin and myosin filaments and the myosin cross-bridges are fundamental constraints on mechanical and energetic properties of contraction. A group of mechanical and x-ray diffraction structural studies in muscles and in single muscle fibers (5, 6, 7, 8, 9, 10) determined that, when muscles are generating maximal force (T0) during isometric contractions, ∼50% of the sarcomere compliance (the reciprocal of stiffness) resides in the array of myosin cross-bridges (compliant elements i and ii in Fig. 1 A), and the other 50% is in the backbones of the thin and thick filaments (compliant elements iii and iv, respectively). The compliance of the cross-bridge is almost fully explained by flexibility within the myosin subfragment 1 (S1, the head domain), with the compliant element i represented by a coiled spring, on the basis of both x-ray diffraction data (10) and expectations from the structure. Myosin subfragment 2 (S2, the rod linking the myosin head to the filament backbone) is an α-helical coiled coil with an expected axial stiffness of 60–80 pN/nm ((11); compliant element ii), ∼30-fold greater than the cross-bridge stiffness. Both the cross-bridges and the myofilaments have usually been considered to exhibit nearly linear elasticity.
Figure 1.
Basics of muscle contraction. (A) A schematic diagram of a half sarcomere is given. The sarcomere encompasses a Z-line through the M-line to the next Z-line (not shown to the left of the diagram). Three myosin heads (S1 heavy chain green and light chains yellow) are shown extending from the myosin filament backbone through the S2 tail (zig-zags) and attached to actin. The symbols (●●●) indicate that many more myosin molecules (∼150 per myosin filament) are present in each half sarcomere. Each myosin molecule contains two heads, but in muscle, normally only one of the two heads attaches at a time. The mechanically compliant elements are indicated as (i) the hinge between the myosin motor domain and the light-chain domain, also termed the lever arm; (ii) the myosin S2 tail; (iii) the actin filament; and (iv) the myosin filament. (B) The chemomechanical scheme for transduction of ATP hydrolysis into mechanical work is shown. The myosin⋅ADP⋅Pi complex (a) attaches to actin, forming the cross-bridge (b), which triggers tilting of the lever arm, Pi release, generation of force, and strain in the compliant elements (c). If the mechanical load is not too high, the filaments will slide, keeping the strain low (d), while tilting of the lever arm progresses. ADP release from the actomyosin⋅ADP complex and ATP binding cause myosin detachment from actin (c → e and d → e). ADP release is slower during a highly loaded contraction, when the high strain prevents tilting. ADP release becomes faster at a lower load. This difference is illustrated by a thicker arrow for ADP release from state (d) than state (c). Hydrolysis of ATP in the detached head and reversal of the lever arm position (repriming, e → a) completes the cross-bridge cycle. Cross-bridge detachment is suppressed when ATP is depleted (the rigor condition), as indicated by the red X symbols (reproduced with permission from (68)). (C) Force response in a tetanic contraction of a single frog muscle fiber is shown, in which a step release (∼0.3% L0 (L0 is the fiber length)) was superimposed on the plateau force (T0) to test the mechanical stiffness and the subsequent dynamics (reprinted by permission from Nature, (14)). T0 is ∼250 kN/m2 of cross-sectional area, or ∼420 pN per myosin filament. Upon the step release, the force decreases, attaining a minimal value T1 at completion of the step, and force recovers during the next few ms to T2. At T1, the reduction in strain of the compliant elements identified in (A) with decreased force is proportional to their compliances.
The interaction between myosin and actin involves an enzymatic pathway that couples splitting of MgATP to MgADP and inorganic phosphate (Pi) with cyclic attachment, force generation, and detachment (Fig. 1 B). The structural change in the myosin head that produces force and filament sliding is a tilting motion (states b → c) of a lever arm within the head that is coupled to release of Pi from actomyosin⋅ADP⋅Pi (state b). In isometric contraction, tilting increases the force exerted by the half sarcomere, increasing the strain of all the elastic elements (represented for simplicity in Fig. 1 B by stretching of S2). When the load is low or suddenly reduced (as shown by the transition c → d), lever arm tilting results in relative filament sliding with a reduced strain in the elastic components. Chemomechanical models of the cyclic interactions of cross-bridges with the actin filament that most successfully explain the dependence of the shortening speed on the load (force-velocity relation (12)), dynamics, and energy consumption of muscle contraction are generally based on relatively linear elasticities (13, 14, 15, 16, 17, 18, 19). Acceleration of detachment when a cross-bridge becomes negatively strained, which occurs during high shortening speed, is a crucial feature for explaining mechanical and energetic features such as the increased rate of energy liberation (i.e., ATPase rate) (12,13,20,21). Accelerated detachment of negatively strained cross-bridges is attributed to an acceleration of ADP dissociation followed by rapid ATP binding (Fig. 1 B, states d → e; (22, 23, 24, 25, 26, 27)). This is also observed when the strain becomes negative for nonmuscle myosins (28, 29, 30, 31, 32, 33). This “gating” of the actomyosin mechanochemical cycle, which enables load-dependent energy transduction in muscle and synchronizes the biochemical reactions in processive myosins, is thought to arise from stress- and strain-dependent kinetics of the underlying chemical and structural transitions. Thus, the mechanical characteristics of the force-extension relation of actin-attached myosin motors are essential elements in the function of all force-generating myosin isoforms.
Recently, single-molecule force measurements on filaments containing a sparse complement of myosin heads (34) showed that cross-bridges in this geometry seem to slide well beyond the zero-force position without generating much negative stress. This almost free sliding was attributed to a large compliance rising in series with the myosin S1 at negative strain by the “buckling” of the myosin S2 tail. This result led to the conclusion that the elasticity of the cross-bridge is highly nonlinear, with stiffness decreasing ∼100-fold in the negative strain region. These results motivated a recent mathematical model proposing radical changes to the classical view of the cross-bridge kinetic cycle (35), postulating that some of the mechanical and energetic features of the cross-bridge cycle do not depend on strain-dependent acceleration of detachment. The cross-bridges might remain attached to actin for ∼80 nm, approximately twice the length of S2 in the shortening direction, without affecting the mechanical output. This model can predict the maximal power and coupling efficiency between mechanical and biochemical cycles. But none of the dynamic mechanical properties of the myosin motors that have been revealed by step perturbations in length or load (14,36, 37, 38, 39, 40) were simulated (35), so it is unclear if those features are also captured by this strain-independent model.
Whether the high compliance of negatively strained cross-bridges in the sparse head geometry of the in vitro experiment (34) applies to the normal filament lattice of a muscle fiber is not evident. In this Perspective, we review some old and new data aimed at clarifying the issue of linear or nonlinear cross-bridge elasticity in situ and implications of stress-strain curves for muscle and nonmuscle myosins.
Force-extension relation in active muscles
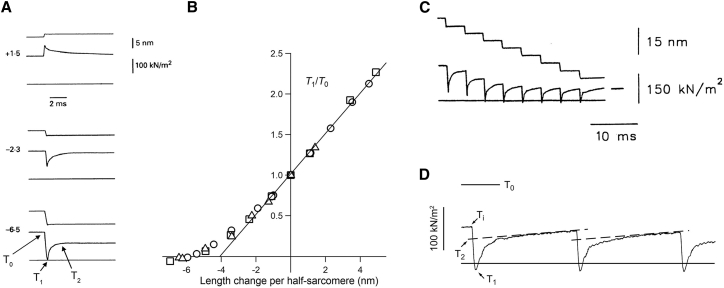
The classic test of stiffness for the cross-bridges in muscle is the mechanical force-extension relation. An intact muscle fiber is electrically stimulated at a high frequency, inducing a steady maximal force (T0) characteristic of the fused tetanus (Fig. 1 C). Sudden small length steps to alter the strain are imposed on T0, and the force T1 attained at the end of the step is measured (Fig. 1 C; (5,14,41)). T1-values recorded with step stretches and releases of different sizes (Fig. 2 A) are plotted against the step amplitude to obtain the so-called T1 relation (Fig. 2 B). Given the finite time taken to complete the step, the force responses are partially “truncated” by the subsequent force recovery that, within ∼2 ms, attains the quasisteady near-isometric force, termed T2 (Figs. 1 C and 2 A).
Figure 2.
(A) Sample records of force transients in response to step length changes of different sizes superimposed on the isometric contraction of a single frog muscle fiber. In each frame of (A), from top to bottom, traces represent sarcomere length change, force response, and resting force. Numerical values close to each record indicate the size of the step length change (nm per half sarcomere; negative values for releases). Arrows indicate the force at the corresponding phase of the transient. (Reproduced with permission from (40).) (B) The T1 relation from three different fibers as indicated by different symbols is shown. The line is the linear regression on data points for steps > −3 nm. Force values are expressed in units relative to T0. Data are from tibialis anterior muscle of Rana esculenta. (C) Tension transients elicited by a staircase of eight 3.8 nm shortening steps superimposed on the isometric tetanus plateau at 4.2 ms intervals are shown. Top trace, length change per half sarcomere; middle trace, force response; lowest trace, resting force. (D) Force response to the last three steps in (C) with vertical and horizontal scales expanded ×2.5 and ×6, respectively, is shown. The relevant parameters of the force transient are identified along the record. A single fiber from frog tibialis anterior was used (reproduced with permission from (15)).
The T1 → T2 recovery is caused by the cross-bridge working stroke synchronized by the step and is faster for larger releases (Fig. 2 A; see (14)), thereby causing a greater truncation of the T1 response and an upward curvature of the T1 relation (Fig. 2 B). This explanation of the deviation of the T1 relation from linearity is supported by experiments in which the T1 relations are obtained with steps of different durations (5). The longer the time taken by the step, the greater the upward deviation of the T1 relation, as the tension recovered during the step becomes larger.
Cross-bridges with linear elasticity should produce an instantaneous T1 relation that intersects the abscissa at a sharp angle, maintaining the same slope in the negative, compressive range of forces. Testing this with intact muscle fibers is difficult not only because of the T2 recovery but also because at zero and negative forces, the sarcomeres are not compressed because of series compliance in the tendon attachments and loss of contact with the hook of the moving shaft of the motor. In the experiment of Fig. 2, C and D (15), tendon lengths were trimmed down to 200 μm total, and attachments were very accurately aligned with the fiber axis. To minimize the quick tension recovery, a staircase of step releases was imposed during the active contraction, which causes accumulation of cross-bridges biased toward the end of their working stroke (42). Moreover, the tension before the step (Ti) and thus the size of the release and acceleration necessary to get to zero force are smaller, thereby minimizing lever detachment. During a staircase of eight releases at 4.2 ms intervals (Fig. 2 C), together with the progressive depletion of T2 recovery, negative T1-values progressively emerge as expected from nearly linear cross-bridge elasticity (Fig. 2 D). Thus, the predominant factor that causes curvature of the normal T1 relation is the quick T2 recovery.
Force-extension relation in rigor muscles
The conclusion above might be questioned on the basis of the in vitro observation with reconstituted sparse head filaments of a large reduction in stiffness at negative forces (34). That experiment was conducted in the absence of ATP, a condition that maintains steady cross-bridge attachment because ATP enters the enzymatic cycle at the step of actomyosin dissociation (see Fig. 1 B; (43)). In the zero-ATP state, termed rigor, muscle fiber stiffness is maximal because cross-bridge detachment is suppressed (red X symbols), and all of the cross-bridges are attached (44, 45, 46). An advantage of measuring the mechanical properties on muscles in rigor is that quick force recovery after the length step is suppressed, which avoids T2-based truncation as a source of nonlinearity in the active muscle fiber.
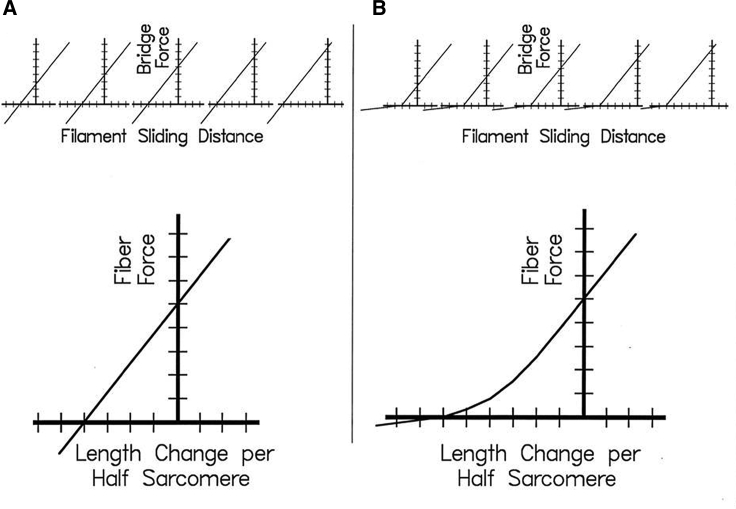
If the stiffness of cross-bridges in the negative strain region is much smaller than that under positive strain, the T1 curve would be nonlinear even at positive forces, as explained in Fig. 3 (47). Axial periodicities of the actin subunits in the thin filament (5.5 nm) and the myosin motors in the thick filament (14.3 nm) are different, and this mismatch allows asynchronous cyclic interactions of myosin motors, thereby accounting for steady shortening. Because of these mismatched periodicities, cross-bridges attach over a range of strains corresponding to variation of positions on each of their stress-strain relations. The measured T1 curve is the sum of these individual stress-strain relations. If the cross-bridge stiffness drops for negative forces (Fig. 3 B), the slope of the relation is expected to decrease progressively as the force approaches zero because of myosin heads that are shifted into the negative strain range.
Figure 3.
Hypothetical force-extension relations for the case that cross-bridges can support negative forces (A) and the case that cross-bridge stiffness decreases at negative strain (B). The distribution of strains among cross-bridges at a given sarcomere length is represented by horizontal shifts between the five cross-bridge force-extension relations in the top of (A) and (B). The bottom shows fiber force-extension relations (T1curves) resulting from the summation of cross-bridge forces. (Reproduced from (47).)
Note that these considerations are valid for a muscle in rigor, but in an active contraction, the force-generating T1 to T2 transition in the cross-bridges maintains a uniform stress, independent of the initial attachment distribution (14). This generates a unique force-extension relation for the whole population of attached cross-bridges, relatively independent of the initial strain upon attachment.
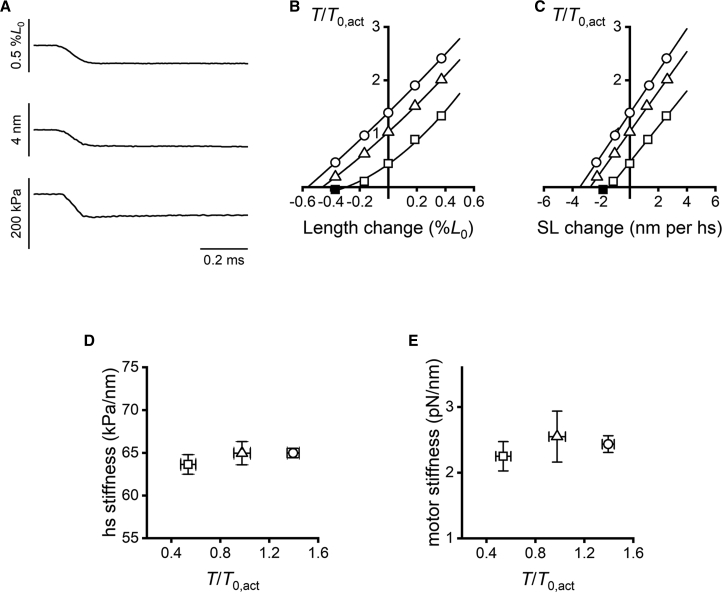
The rigor condition can be induced in an intact muscle fiber by depleting ATP with metabolic poisons (9). As shown in Fig. 4 A, the force transient elicited by a length step in rigor is almost completely characterized by the elastic phase 1 response. The T1 relations for the whole fiber (including attachments; Fig. 4 B) bend near zero forces, but this effect is unrelated to cross-bridges and filaments, as shown by the T1 relations measured in the same experiment using a striation follower device (48) to monitor the length changes of a selected population of sarcomeres (Fig. 4 C), which are quite linear, including at low forces. The difference is most evident comparing the position of the T1 point attained with the largest release imposed from the lowest steady force in plots Fig. 4, B and C (solid squares): below zero force, the sarcomeres stop shortening (Fig. 4 C) even though the motor lever continues moving (Fig. 4 B). Most importantly, even though the cross-bridge attachment positions before the step are different at the various steady forces (the symbols on the ordinate) from ∼0.5 T0 (T0 = 175 ± 13 kPa, n = 4 fibers) to ∼1.5 T0, all the T1 relations show a similar stiffness (mean ± SEM = 64.5 ± 0.4 kPa/nm per half sarcomere; Fig. 4 D). This nearly constant stiffness in rigor implies that the force-extension curve extends almost linearly into the negative strain region (Fig. 3 A).
Figure 4.
Mechanical parameters of an intact frog muscle fiber in rigor at different steady tensions. (A) Force transient (lower trace) elicited by a step release of 0.16% L0 (upper trace) is shown, corresponding to 1.2 nm per half sarcomere (middle trace), imposed at a steady force of 1.4 times the active isometric tetanic force (T0, 142 kPa/m2 in this fiber). A single fiber from frog tibialis anterior was used. (B and C) T1 relations at 0.44 T0 (squares), 1.03 T0 (triangles), and 1.39 T0 (circles) determined for the fiber (B) and for a selected population of sarcomeres (C) using the same four steps are shown. The solid square indicates the T1 point attained with the largest release imposed from 0.44 T0. (D) Half-sarcomere stiffness calculated by the slope of the T1 relations as in (C) at the three different steady forces is shown. Mean and SEM from four fibers are shown. (E) Stiffness per myosin head calculated as described in the text is shown.
The half-sarcomere compliance in rigor is (1000/64.5 =) 15.5 ± 0.1 nm/MPa. Subtracting the contribution of filament compliance (13.0 ± 0.7 nm/MPa from both x-ray diffraction and mechanical experiments (10)) from the total compliance, we estimate the cross-bridge compliance in rigor to be 2.5 ± 0.7 nm/MPa per half sarcomere, corresponding to a stiffness of 400 ± 112 kPa/nm. In frog muscle, the thick filament density, estimated from the fraction of cross-sectional area occupied by myofibrils (0.83 (49)) and the filament lattice spacing (d1,0 = 35 nm (50)), is 5.87 × 1014 thick filaments per m2. There are 294 heads per half-thick filament. The average stiffness per head is thus (400 × 103/(5.87 × 1014 × 294)) = 2.32 ± 0.65 pN/nm (Fig. 4 E; see also (10)), which is consistent with in situ and in vitro measurements at positive forces (34,51,52). Even though in rigor, the T1 relation (Fig. 4 C) shows a sharp intercept on the abscissa, this experiment illustrates the difficulties in applying significant compressive force to an intact fiber.
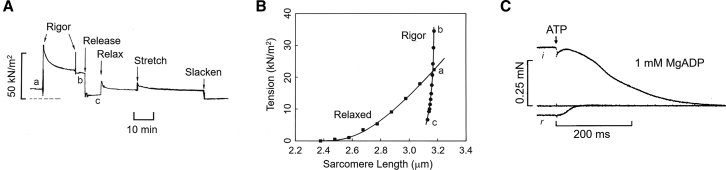
Substantial negative strain was imposed on the cross-bridges in the experiment of Fig. 5 A on a demembranated (glycerol-extracted) fiber from rabbit psoas muscle (53). While it was relaxed in the presence of MgATP, it was stretched to a sarcomere length of 3.35 μm, at which significant resting tension is present (point a) because of parallel elastic components such as titin (54). When ATP was removed from the bathing medium, the fiber went into the rigor state and generated force (b) above the resting tension. A small length release reduced tension below the resting level, thereby placing negative tension (c) on the cross-bridges. The increase of force accompanying cross-bridge detachment upon readdition of MgATP (Relax) clearly demonstrates that the cross-bridges were supporting a steady negative tension. As shown in Fig. 5 B, the rigor T1 relation in a fiber at 3.2 μm sarcomere length shows no discontinuity of slope at the intersection of the rigor and relaxed force-extension curves, indicating that the cross-bridges did not buckle under negative strain.
Figure 5.
Relaxation of glycerol-extracted single fiber from rabbit psoas from negative and positive cross-bridge strain in rigor. (A) A relaxed fiber was stretched to generate significant resting tension (point a) above zero (thin dashed line). It was then put into rigor solution (two washes (arrows) to remove residual ATP; point b). A small length release (120 μm) decreased tension to below the relaxed level (point c). Addition of MgATP (Relax, final concentration 0.7 mM) then caused tension to increase. At “Stretch,” the fiber length was increased to the prerigor length, and at “Slacken,” the zero-force level was recorded. The recording starts at a sarcomere length of 3.35 μm. (B) Force-extension curves from another fiber undergoing the same protocol are shown. a, b, and c indicate corresponding conditions in the two fibers. (Reproduced with permission from (53).) (C) Relaxation of a single fiber from isometric (i) and negatively strained (r) rigor tension by photorelease of 1 mM MgATP from caged ATP in the presence of 1 mM MgADP is shown. The top trace (i) is isometric at positive tension, sarcomere length of 3.3 μm. The center trace shows the tension of the relaxed fiber recorded 1 min later. The fiber was then put in rigor again and released by 3% L0 to apply negative cross-bridge strain. The lowest trace (r) shows relaxation of negative cross-bridge tension on photorelease of ATP. For clarity, the negative tension record (r) and its baseline were shifted vertically to superimpose the two baselines. (Reproduced with permission from (22).)
In the experiment of Fig. 5 C, positive (i) and negative (r) rigor tensions at a 3.3 μm sarcomere length generated as in Fig. 5 A were relaxed by rapid release of 1 mM ATP upon laser photolysis of caged ATP in the presence of 1 mM MgADP (22). The relaxation to the baseline resting tension was much faster from the negative tension, in part because of the faster dissociation of ADP from negatively strained cross-bridges before ATP binding (Fig. 1 B, transition d → e compared to c → e). The upward deflection of the force recording from negative strained cross-bridges implies that in the AM⋅ADP state, as well as in the nucleotide-free AM state, cross-bridges supported negative force.
Implications of negatively strained actomyosin attachments
Almost a century ago, in his basement laboratory in Cambridge, A. V. Hill and his colleagues discovered the surprising feature of muscle contraction that the rate of total energy liberation, fueled by the biochemical reactions, depended on the mechanical load and the speed of muscle shortening (12,20). This finding implied feedback from the mechanics of the contractile apparatus back to the biochemical reactions. In the brilliant and prescient model of the contraction mechanism developed by A. F. Huxley in 1957 (13), the acceleration of the enzymatic turnover of the actomyosin ATPase as the load is reduced and the shortening speed increases was explained by postulating that the cross-bridge detachment rate increases under negative strain. At moderate velocities, the pulling force of positively strained cross-bridges is higher than the drag force of cross-bridges in the negatively strained region, whereas at maximal shortening velocity, a balance between positively and negatively strained cross-bridges results in zero net force. These features of the 1957 model have been subsequently supported by studies in different muscle types, showing how the strain dependence of detachment rate contributes, along with the rate of cross-bridge attachment, to modulation of the power (force times velocity), the total rate of energy liberation (power plus rate of heat production), and the rate of ATP hydrolysis and thus efficiency of energy conversion (21,55).
More recent estimates of the cross-bridge stiffness (2–3 pN/nm (10)) are four to five times larger than those assumed in the Huxley 1957 model. To preserve the efficiency of work production during the cycle, the strain dependency of detachment rate at negative strain must be correspondingly higher, a feature directly verified in x-ray diffraction experiments, which show that the conformational dispersion of myosin cross-bridges during shortening remains quite limited (9). Those observations contradict the hypothesis that cross-bridges maintain attachment for long distances by buckling of the S2.
The predominant reaction step that controls the enzymatic turnover rate of the muscle actomyosin ATPase cycle during contraction is the rate of ADP release from AM⋅ADP (Fig. 1 B, state c), which is slow until filament sliding under a reduced load shifts the cross-bridge into the range in which it exerts low or negative forces (state d). Thus, the stiffness in the negative region is important for the modulation of the biochemical energy liberation and efficiency. The strain dependence of ADP release from AM⋅ADP has been documented in both striated and smooth muscles (22, 23, 24, 25, 26, 27).
A question about energetics, which was unresolved for decades, is the mechanism of a transient unexplained energy liberation observed during unloaded shortening (21,56). The rate of ATP utilization is unexpectedly low during rapid shortening of frog skeletal muscle, insufficient to account for the energy output, mostly heat (57,58). This was puzzling because the rate of ATP utilization was expected to increase with the shortening velocity because the rate of cross-bridge detachment (estimated from the velocity of filament sliding and the attachment distance) does increase with the shortening velocity. Moreover, during prolonged unloaded shortening, the ATP splitting continuously declines, reaching that observed during isometric contraction (1.7 s−1 per myosin head in frog muscle at 0°C). A deficit of heat production during isometric force redevelopment while ATP splitting is temporarily increased (56) balances out the energetic budget. These data indicated that unloaded shortening is accompanied by an unidentified exothermic reaction that is reversed during the subsequent isometric period.
More recently, these puzzling results found a straightforward explanation in the finding that during rapid shortening, the thick filament undergoes a structural change that switches OFF the cross-bridges’ availability for attachment to actin (4). In the ON state that characterizes loaded contractions, they are available for attachment, but in the OFF state, they lie along the thick filament surface folded toward the center of the sarcomere and are unable to attach to actin or split ATP (59,60). Accordingly, the number of attached cross-bridges continuously decreases during unloaded shortening (61). These results lead to the suggestion that the mysterious exothermic reaction occurring during rapid shortening is due to forcible detachment of negatively stressed cross-bridges before the completion of their chemical cycles (ADP release and ATP binding). These detached off-pathway cross-bridges are hypothesized to accumulate in the OFF state, from which they return when tension redevelops after the shortening, accounting for the extra ATP splitting (61). This mechanism is based on the negative stress in the cross-bridges sliding past the zero-force position. To the contrary, a nonlinear cross-bridge elasticity leading to maintained attachment because of S2 buckling would imply a lag in reaching a steady ATPase rate during rapid shortening rather than the observed extra heat output.
Mechanical control of the ATPase rate is also a prominent aspect of nonmuscle myosins. For instance, myosin V is an intracellular cargo transporter whose two myosin heads translocate for many hand-over-hand steps along actin per diffusional encounter with the filament (62,63). This property, termed processivity, is a key factor in enabling myosin V to carry cargos individually or in very small groups. The two heads of the molecule alternate in initiating a step by binding ATP, detaching from actin, hydrolyzing the ATP, rebinding to actin, and completing the enzymatic cycle on release of the hydrolysis products phosphate and ADP. This alternating (anti-) synchronization is achieved by mechanical control of ADP release from AM⋅ADP, as is observed with muscle myosin. When both heads of the molecule are attached to actin, the mechanical strain between the heads pulls the leading head backward and the trailing head forward. The trailing head, under negative stress, releases ADP more rapidly than the leading head, again very similar to the strain dependence of ADP release by muscle myosin. This gating of ADP release contributes to high directionality toward the plus end of actin because the trailing head initiates a forward step before the slower leading head (29). The positive and negative arms of the force-extension curve confer this important function for achieving high processivity and directionality.
Myosin 1s differ in properties that are tuned to facilitate their varied functions in cell biology. Myosin 1B exhibits the strongest known stress-strain-related ADP release rate, slowing ∼50-fold at 1–2 pN of resisting mechanical load (28). The motor stops moving but maintains actin attachment under such a load, suggesting that its function is a stress-dependent cellular anchor instead of a transporter. Gating of ADP release is common to myosin 1B, II, and V, but it is not universal in myosin 1s. Myosin 1C shows strain-dependent ATP binding (64), which is not prominent in the other isoforms mentioned so far.
Myosin X and VI have also been shown to exhibit gating of ADP release from AM⋅ADP (31, 32, 33). Myosin VI binds ATP relatively slowly and this step also is probably gated by mechanical strain between its heads. These examples of strain-dependent dissociation of ADP and of ATP binding rate in nonmuscle myosins (65,66) mechanistically tie muscle and nonmuscle myosins together as an evolutionary superfamily beyond their sequence homology. They emphasize the functionally crucial forces on the myosin heads in both positive and negative directions.
Conclusion
In the native filament lattice, muscle cross-bridges exhibit a similar stiffness under both positive and negative strains. The drop of the cross-bridge rigor stiffness observed in sparse-headed thick filaments in the negative strain region (34), due to the proposed buckling of the S2 portion of the myosin, seems to be limited to those in vitro measurements. Consequently, kinetic models of muscle contraction based on cross-bridge nonlinearity (35) that ignore the available and compelling evidence that cross-bridges can support negative load are not viable. The force-extension relation, its shape, and its slope, which express the stiffness of the actomyosin cross-bridges, are primary mechanical parameters that control the dynamics of energy transduction, enabling muscles to precisely and efficiently support and move the body. Stress-strain-dependent gating of biochemical rates also tunes nonmuscle myosins to efficiently perform varied tasks in many cell types.
In the half sarcomere, the emergent properties of the entire ensemble control the mechanical performance and the energetically beneficial mechanism that relates the degree of thick filament activation to the load. Motors under the negative stress experienced during rapid shortening can detach before completing the biochemical cycle, and they accumulate in the energy-sparing OFF state. In cargo transport by processive nonmuscle myosins, negative stress in the trailing head leads to acceleration of ADP release that contributes to directionality for stepping forward. Modeling performance of fully integrated physiological systems on the basis of molecular events observed with minimal in vitro geometries requires quantifying how the individual forces and motions interact and combine through the stiffness of their linkages (26,67). Defining the basis of pathology due to mutations in the motor proteins and optimizing therapeutic pharmaceuticals are potential benefits of understanding contraction and motility over the full range of structural complexity.
Author Contributions
M.L., G.P., J.A.D., Y.E.G., and V.L. designed research. M.L., G.P., J.A.D., and I.P. performed research, contributed analytic tools, and analyzed data. Y.E.G. and V.L. wrote the manuscript.
Acknowledgments
This work was supported by Fondazione Cassa di Risparmio di Firenze (Italy), National Institutes of Health (United States) grants P01-GM087253 and R35-GM118139 to Y.E.G., and the Center for Engineering MechanoBiology, National Science Foundation Science and Technology Center (United States), CMMI: 15-48571.
Editor: Brian Salzberg.
Contributor Information
Yale E. Goldman, Email: goldmany@upenn.edu.
Vincenzo Lombardi, Email: vincenzo.lombardi@unifi.it.
References
- 1.Sellers J.R. Oxford University Press; Oxford, UK: 1994. Myosins. [Google Scholar]
- 2.Huxley H., Hanson J. Changes in the cross-striations of muscle during contraction and stretch and their structural interpretation. Nature. 1954;173:973–976. doi: 10.1038/173973a0. [DOI] [PubMed] [Google Scholar]
- 3.Huxley A.F., Niedergerke R. Structural changes in muscle during contraction; interference microscopy of living muscle fibres. Nature. 1954;173:971–973. doi: 10.1038/173971a0. [DOI] [PubMed] [Google Scholar]
- 4.Linari M., Brunello E., Irving M. Force generation by skeletal muscle is controlled by mechanosensing in myosin filaments. Nature. 2015;528:276–279. doi: 10.1038/nature15727. [DOI] [PubMed] [Google Scholar]
- 5.Ford L.E., Huxley A.F., Simmons R.M. Tension responses to sudden length change in stimulated frog muscle fibres near slack length. J. Physiol. 1977;269:441–515. doi: 10.1113/jphysiol.1977.sp011911. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Huxley H.E., Stewart A., Irving T. X-ray diffraction measurements of the extensibility of actin and myosin filaments in contracting muscle. Biophys. J. 1994;67:2411–2421. doi: 10.1016/S0006-3495(94)80728-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Wakabayashi K., Sugimoto Y., Amemiya Y. X-ray diffraction evidence for the extensibility of actin and myosin filaments during muscle contraction. Biophys. J. 1994;67:2422–2435. doi: 10.1016/S0006-3495(94)80729-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Higuchi H., Yanagida T., Goldman Y.E. Compliance of thin filaments in skinned fibers of rabbit skeletal muscle. Biophys. J. 1995;69:1000–1010. doi: 10.1016/S0006-3495(95)79975-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Piazzesi G., Reconditi M., Lombardi V. Skeletal muscle performance determined by modulation of number of myosin motors rather than motor force or stroke size. Cell. 2007;131:784–795. doi: 10.1016/j.cell.2007.09.045. [DOI] [PubMed] [Google Scholar]
- 10.Brunello E., Caremani M., Reconditi M. The contributions of filaments and cross-bridges to sarcomere compliance in skeletal muscle. J. Physiol. 2014;592:3881–3899. doi: 10.1113/jphysiol.2014.276196. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Adamovic I., Mijailovich S.M., Karplus M. The elastic properties of the structurally characterized myosin II S2 subdomain: a molecular dynamics and normal mode analysis. Biophys. J. 2008;94:3779–3789. doi: 10.1529/biophysj.107.122028. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Hill A.V. The heat of shortening and the dynamic constants of muscle. Proc. R. Soc. Lond. B Biol. Sci. 1938;126:136–195. doi: 10.1098/rspb.1949.0019. [DOI] [PubMed] [Google Scholar]
- 13.Huxley A.F. Muscle structure and theories of contraction. Prog. Biophys. Biophys. Chem. 1957;7:255–318. [PubMed] [Google Scholar]
- 14.Huxley A.F., Simmons R.M. Proposed mechanism of force generation in striated muscle. Nature. 1971;233:533–538. doi: 10.1038/233533a0. [DOI] [PubMed] [Google Scholar]
- 15.Piazzesi G., Lombardi V. A cross-bridge model that is able to explain mechanical and energetic properties of shortening muscle. Biophys. J. 1995;68:1966–1979. doi: 10.1016/S0006-3495(95)80374-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Smith D.A., Geeves M.A. Strain-dependent cross-bridge cycle for muscle. Biophys. J. 1995;69:524–537. doi: 10.1016/S0006-3495(95)79926-X. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Smith D.A., Geeves M.A. Strain-dependent cross-bridge cycle for muscle. II. Steady-state behavior. Biophys. J. 1995;69:538–552. doi: 10.1016/S0006-3495(95)79927-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Smith D.A., Geeves M.A., Mijailovich S.M. Towards a unified theory of muscle contraction. I: foundations. Ann. Biomed. Eng. 2008;36:1624–1640. doi: 10.1007/s10439-008-9536-6. [DOI] [PubMed] [Google Scholar]
- 19.Mijailovich S.M., Kayser-Herold O., Geeves M.A. Three-dimensional stochastic model of actin-myosin binding in the sarcomere lattice. J. Gen. Physiol. 2016;148:459–488. doi: 10.1085/jgp.201611608. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Fenn W.O. The relation between the work performed and the energy liberated in muscular contraction. J. Physiol. 1924;58:373–395. doi: 10.1113/jphysiol.1924.sp002141. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Woledge R.C., Curtin N.A., Homsher E. Academic Press; London: 1985. Energetic Aspects of Muscle Contraction. [PubMed] [Google Scholar]
- 22.Dantzig J.A., Hibberd M.G., Goldman Y.E. Cross-bridge kinetics in the presence of MgADP investigated by photolysis of caged ATP in rabbit psoas muscle fibres. J. Physiol. 1991;432:639–680. doi: 10.1113/jphysiol.1991.sp018405. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Capitanio M., Canepari M., Pavone F.S. Ultrafast force-clamp spectroscopy of single molecules reveals load dependence of myosin working stroke. Nat. Methods. 2012;9:1013–1019. doi: 10.1038/nmeth.2152. [DOI] [PubMed] [Google Scholar]
- 24.Greenberg M.J., Shuman H., Ostap E.M. Inherent force-dependent properties of β-cardiac myosin contribute to the force-velocity relationship of cardiac muscle. Biophys. J. 2014;107:L41–L44. doi: 10.1016/j.bpj.2014.11.005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Liu C., Kawana M., Spudich J.A. Controlling load-dependent kinetics of β-cardiac myosin at the single-molecule level. Nat. Struct. Mol. Biol. 2018;25:505–514. doi: 10.1038/s41594-018-0069-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Woody M.S., Greenberg M.J., Ostap E.M. Positive cardiac inotrope omecamtiv mecarbil activates muscle despite suppressing the myosin working stroke. Nat. Commun. 2018;9:3838. doi: 10.1038/s41467-018-06193-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Veigel C., Molloy J.E., Kendrick-Jones J. Load-dependent kinetics of force production by smooth muscle myosin measured with optical tweezers. Nat. Cell Biol. 2003;5:980–986. doi: 10.1038/ncb1060. [DOI] [PubMed] [Google Scholar]
- 28.Laakso J.M., Lewis J.H., Ostap E.M. Myosin I can act as a molecular force sensor. Science. 2008;321:133–136. doi: 10.1126/science.1159419. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Veigel C., Wang F., Molloy J.E. The gated gait of the processive molecular motor, myosin V. Nat. Cell Biol. 2002;4:59–65. doi: 10.1038/ncb732. [DOI] [PubMed] [Google Scholar]
- 30.Wulf S.F., Ropars V., Schröder R.R. Force-producing ADP state of myosin bound to actin. Proc. Natl. Acad. Sci. USA. 2016;113:E1844–E1852. doi: 10.1073/pnas.1516598113. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Oguchi Y., Mikhailenko S.V., Ishiwata S. Load-dependent ADP binding to myosins V and VI: implications for subunit coordination and function. Proc. Natl. Acad. Sci. USA. 2008;105:7714–7719. doi: 10.1073/pnas.0800564105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Altman D., Sweeney H.L., Spudich J.A. The mechanism of myosin VI translocation and its load-induced anchoring. Cell. 2004;116:737–749. doi: 10.1016/s0092-8674(04)00211-9. [DOI] [PubMed] [Google Scholar]
- 33.Caporizzo M.A., Fishman C.E., Goldman Y.E. The antiparallel dimerization of myosin X imparts bundle selectivity for processive motility. Biophys. J. 2018;114:1400–1410. doi: 10.1016/j.bpj.2018.01.038. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Kaya M., Higuchi H. Nonlinear elasticity and an 8-nm working stroke of single myosin molecules in myofilaments. Science. 2010;329:686–689. doi: 10.1126/science.1191484. [DOI] [PubMed] [Google Scholar]
- 35.Månsson A., Persson M., Rassier D.E. Nonlinear actomyosin elasticity in muscle? Biophys. J. 2019;116:330–346. doi: 10.1016/j.bpj.2018.12.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Lombardi V., Piazzesi G., Linari M. Rapid regeneration of the actin-myosin power stroke in contracting muscle. Nature. 1992;355:638–641. doi: 10.1038/355638a0. [DOI] [PubMed] [Google Scholar]
- 37.Irving M., Lombardi V., Ferenczi M.A. Myosin head movements are synchronous with the elementary force-generating process in muscle. Nature. 1992;357:156–158. doi: 10.1038/357156a0. [DOI] [PubMed] [Google Scholar]
- 38.Caremani M., Melli L., Linari M. Force and number of myosin motors during muscle shortening and the coupling with the release of the ATP hydrolysis products. J. Physiol. 2015;593:3313–3332. doi: 10.1113/JP270265. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Piazzesi G., Lucii L., Lombardi V. The size and the speed of the working stroke of muscle myosin and its dependence on the force. J. Physiol. 2002;545:145–151. doi: 10.1113/jphysiol.2002.028969. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Reconditi M., Linari M., Lombardi V. The myosin motor in muscle generates a smaller and slower working stroke at higher load. Nature. 2004;428:578–581. doi: 10.1038/nature02380. [DOI] [PubMed] [Google Scholar]
- 41.Piazzesi G., Francini F., Lombardi V. Tension transients during steady lengthening of tetanized muscle fibres of the frog. J. Physiol. 1992;445:659–711. doi: 10.1113/jphysiol.1992.sp018945. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Linari M., Lombardi V., Piazzesi G. Cross-bridge kinetics studied with staircase shortening in single fibres from frog skeletal muscle. J. Muscle Res. Cell Motil. 1997;18:91–101. doi: 10.1023/a:1018637118052. [DOI] [PubMed] [Google Scholar]
- 43.Lymn R.W., Taylor E.W. Mechanism of adenosine triphosphate hydrolysis by actomyosin. Biochemistry. 1971;10:4617–4624. doi: 10.1021/bi00801a004. [DOI] [PubMed] [Google Scholar]
- 44.Cooke R., Franks K. All myosin heads form bonds with actin in rigor rabbit skeletal muscle. Biochemistry. 1980;19:2265–2269. doi: 10.1021/bi00551a042. [DOI] [PubMed] [Google Scholar]
- 45.Thomas D.D., Cooke R. Orientation of spin-labeled myosin heads in glycerinated muscle fibers. Biophys. J. 1980;32:891–906. doi: 10.1016/S0006-3495(80)85024-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Lovell S.J., Knight P.J., Harrington W.F. Fraction of myosin heads bound to thin filaments in rigor fibrils from insect flight and vertebrate muscles. Nature. 1981;293:664–666. doi: 10.1038/293664a0. [DOI] [PubMed] [Google Scholar]
- 47.Goldman Y.E. Mechano-chemistry of negatively strained cross-bridges in skeletal muscle. In: Simmons R., editor. Muscular Contraction. Cambridge University Press; 1992. pp. 219–236. [Google Scholar]
- 48.Huxley A.F., Lombardi V., Peachey L.D. A system for fast recording of longitudinal displacement of a striated muscle fibre. J. Physiol. 1981;317:12P–13P. [Google Scholar]
- 49.Mobley B.A., Eisenberg B.R. Sizes of components in frog skeletal muscle measured by methods of stereology. J. Gen. Physiol. 1975;66:31–45. doi: 10.1085/jgp.66.1.31. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Reconditi M., Brunello E., Piazzesi G. Sarcomere-length dependence of myosin filament structure in skeletal muscle fibres of the frog. J. Physiol. 2014;592:1119–1137. doi: 10.1113/jphysiol.2013.267849. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Takagi Y., Homsher E.E., Shuman H. Force generation in single conventional actomyosin complexes under high dynamic load. Biophys. J. 2006;90:1295–1307. doi: 10.1529/biophysj.105.068429. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Lewalle A., Steffen W., Sleep J. Single-molecule measurement of the stiffness of the rigor myosin head. Biophys. J. 2008;94:2160–2169. doi: 10.1529/biophysj.107.119396. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Goldman Y.E., McCray J.A., Vallette D.P. Cross-bridges in rigor fibres of rabbit psoas muscle support negative forces. J. Physiol. 1987;398:72P. [Google Scholar]
- 54.Granzier H.L., Wang K. Passive tension and stiffness of vertebrate skeletal and insect flight muscles: the contribution of weak cross-bridges and elastic filaments. Biophys. J. 1993;65:2141–2159. doi: 10.1016/S0006-3495(93)81262-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Barclay C.J. Energetics of contraction. Compr. Physiol. 2015;5:961–995. doi: 10.1002/cphy.c140038. [DOI] [PubMed] [Google Scholar]
- 56.Homsher E., Irving M., Wallner A. High-energy phosphate metabolism and energy liberation associated with rapid shortening in frog skeletal muscle. J. Physiol. 1981;321:423–436. doi: 10.1113/jphysiol.1981.sp013994. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57.Kushmerick M.J., Larson R.E., Davies R.E. The chemical energetics of muscle contraction. I. Activation heat, heat of shortening and ATP utilization for activation-relaxation processes. Proc. R. Soc. Lond. B Biol. Sci. 1969;174:293–313. doi: 10.1098/rspb.1969.0095. [DOI] [PubMed] [Google Scholar]
- 58.Rall J.A., Homsher E., Mommaerts W.F. A temporal dissociation of energy liberation and high energy phosphate splitting during shortening in frog skeletal muscles. J. Gen. Physiol. 1976;68:13–27. doi: 10.1085/jgp.68.1.13. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 59.Woodhead J.L., Zhao F.Q., Padrón R. Atomic model of a myosin filament in the relaxed state. Nature. 2005;436:1195–1199. doi: 10.1038/nature03920. [DOI] [PubMed] [Google Scholar]
- 60.Stewart M.A., Franks-Skiba K., Cooke R. Myosin ATP turnover rate is a mechanism involved in thermogenesis in resting skeletal muscle fibers. Proc. Natl. Acad. Sci. USA. 2010;107:430–435. doi: 10.1073/pnas.0909468107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 61.Fusi L., Percario V., Piazzesi G. Minimum number of myosin motors accounting for shortening velocity under zero load in skeletal muscle. J. Physiol. 2017;595:1127–1142. doi: 10.1113/JP273299. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 62.Mehta A.D., Rock R.S., Cheney R.E. Myosin-V is a processive actin-based motor. Nature. 1999;400:590–593. doi: 10.1038/23072. [DOI] [PubMed] [Google Scholar]
- 63.Hammer J.A., III, Sellers J.R. Walking to work: roles for class V myosins as cargo transporters. Nat. Rev. Mol. Cell Biol. 2011;13:13–26. doi: 10.1038/nrm3248. [DOI] [PubMed] [Google Scholar]
- 64.Greenberg M.J., Lin T., Ostap E.M. Myosin IC generates power over a range of loads via a new tension-sensing mechanism. Proc. Natl. Acad. Sci. USA. 2012;109:E2433–E2440. doi: 10.1073/pnas.1207811109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 65.De La Cruz E.M., Ostap E.M. Relating biochemistry and function in the myosin superfamily. Curr. Opin. Cell Biol. 2004;16:61–67. doi: 10.1016/j.ceb.2003.11.011. [DOI] [PubMed] [Google Scholar]
- 66.Heissler S.M., Sellers J.R. Kinetic adaptations of myosins for their diverse cellular functions. Traffic. 2016;17:839–859. doi: 10.1111/tra.12388. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 67.Pertici I., Bongini L., Bianco P. A myosin II nanomachine mimicking the striated muscle. Nat. Commun. 2018;9:3532. doi: 10.1038/s41467-018-06073-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 68.Nyitrai M., Geeves M.A. Adenosine diphosphate and strain sensitivity in myosin motors. Philos. Trans. R. Soc. Lond. B Biol. Sci. 2004;359:1867–1877. doi: 10.1098/rstb.2004.1560. [DOI] [PMC free article] [PubMed] [Google Scholar]