Thermal and Chemical Unfolding of a Monoclonal IgG1 Antibody: Application of the Multistate Zimm-Bragg Theory

Abstract

The thermal unfolding of a recombinant monoclonal antibody IgG1 (mAb) was measured with differential scanning calorimetry (DSC). The DSC thermograms reveal a pretransition at 72°C with an unfolding enthalpy of ΔH_cal ∼200–300 kcal/mol and a main transition at 85°C with an enthalpy of ∼900–1000 kcal/mol. In contrast to small single-domain proteins, mAb unfolding is a complex reaction that is analyzed with the multistate Zimm-Bragg theory. For the investigated mAb, unfolding is characterized by a cooperativity parameter σ ∼6 × 10⁻⁵ and a Gibbs free energy of unfolding of g_nu ∼100 cal/mol per amino acid. The enthalpy of unfolding provides the number of amino acid residues ν participating in the unfolding reaction. On average, ν∼220 ± 50 amino acids are involved in the pretransition and ν∼850 ± 30 in the main transition, accounting for ∼90% of all amino acids. Thermal unfolding was further studied in the presence of guanidineHCl. The chemical denaturant reduces the unfolding enthalpy ΔH_cal and lowers the midpoint temperature T_m. Both parameters depend linearly on the concentration of denaturant. The guanidineHCl concentrations needed to unfold mAb at 25°C are predicted to be 2–3 M for the pretransition and 5–7 M for the main transition, varying with pH. GuanidineHCl binds to mAb with an exothermic binding enthalpy, which partially compensates the endothermic mAb unfolding enthalpy. The number of guanidineHCl molecules bound upon unfolding is deduced from the DSC thermograms. The bound guanidineHCl-to-unfolded amino acid ratio is 0.79 for the pretransition and 0.55 for the main transition. The pretransition binds more denaturant molecules and is more sensitive to unfolding than the main transition. The current study shows the strength of the Zimm-Bragg theory for the quantitative description of unfolding events of large, therapeutic proteins, such as a monoclonal antibody.

ΔH_calSignificance

First application of the multistate Zimm-Bragg theory for the analysis and quantitative thermodynamic evaluation of heat capacity curves of an antibody.

Introduction

Thermal induced protein unfolding is commonly used to investigate the stability of proteins in different solution conditions, varying in pH, presence of cosolutes and excipients, e.g., during pharmaceutical formulation screening (1). Although different methods are applicable, differential scanning calorimetry (DSC) provides thermodynamic parameters, which can only be obtained indirectly by other methods (2,3). In most cases, improvement of the thermal stability is judged from the maximum of the heat capacity curve (i.e., the melting temperature T_m of the protein unfolding reaction). However, solely extracting T_m is not sufficient to describe thermal stability, and a number of different assays are used to evaluate protein stability (4,5). Various authors have suggested analyzing the enthalpy contribution ΔH_cal of the unfolding process (6, 7, 8). The models used to describe the heat capacity curves of the unfolding process, however, are not straightforward.

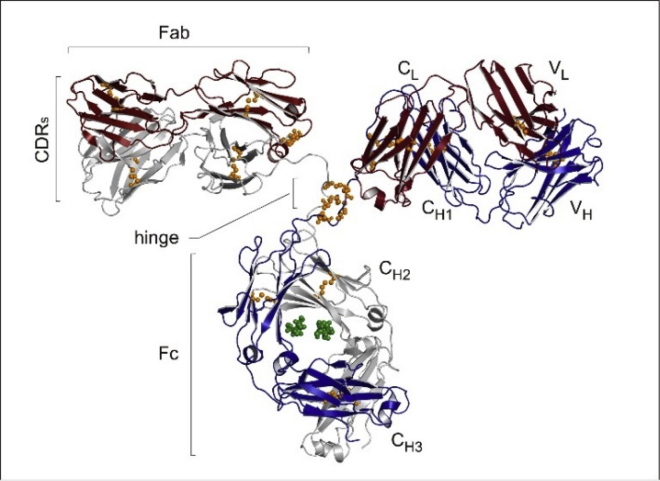
The standard unfolding model for small proteins (e.g., single-domain molecules of 10–20 kDa molecular weight) is the two-state model. Only two types of molecules exist in solution, the native protein (N) and its structural unfolded conformation (U) (all-or-none model) (9). However, “peptides that form helices in solution do not show a simple two-state equilibrium between a fully folded and a fully unfolded structure. Instead, they form a complex mixture of all helix, all coil, or, most frequently, central helices with frayed coil ends” (10). A more realistic model is provided by the multistate Zimm-Bragg theory, originally developed for the temperature-induced coil-to-α-helix transition (11,12). It has been applied successfully to describe the thermal unfolding of a variety of proteins (13,14). In fact, the Zimm-Bragg theory provides a perfect quantitative description of the thermal unfolding of proteins with predominantly α-helical structure (15, 16, 17) as well as for globular proteins with a high β-sheet content (13,14) In this study, the Zimm-Bragg theory is extended to the unfolding of a large multidomain protein (i.e., a monoclonal antibody (mAb) of molecular weight 143 kDa with the structure shown in Fig. 1).

Figure 1.

Three-dimensional structure of a complete IgG1 antibody showing the heavy (colored in blue and gray) and light (brown) chains, which together form the Fc domain and the two Fab domains. Each Fab domain is formed by one light chain (V_L and C_L domains) and the V_H and C_H1 domains of the heavy chain. The Fc domain is formed by the C_H2 and C_H3 domains of each of the two heavy chains. Glycosylation is at Asn297.

We used DSC to investigate the stability of mAb as a function of temperature, solvent pH, and guanidineHCl concentration. The denaturation parameters such as temperature T_m and enthalpy ΔH_cal depend on the molecular structure of the protein and solution conditions (5,18,19). GuanidineHCl is a commonly used chemical to induce protein unfolding. Increasing the concentration of denaturant shifts the folding equilibrium toward the unfolded state. The molecular mechanism of chemical denaturation is still discussed controversially (20). One theory postulates an indirect mechanism by which chemical denaturants change the water structure and thereby reduce the magnitude of the hydrophobic effect. The alternative view is a direct interaction of the denaturant with the protein (21,22). Strong support for this mechanism comes from isothermal titration calorimetry, which provides evidence for an exothermic binding reaction of guanidineHCl with proteins (23). Molecular dynamics simulations (24) and x-ray studies (25) also support a direct interaction mechanism.

As seen in Fig. 1, antibodies are formed of different domains, with two identical heavy chains of ∼450 amino acid (AA) residues each and two identical light chains of ∼220 AA residues each. The exact number of AA residues can vary depending on the immunoglobulin (Ig) isotypes. The chains fold into domains of ∼110 AA residues. The light chain is formed of two domains, denoted as V_L and C_L (variable (V), constant (C)) The heavy chain is composed of four Ig domains: V_H, C_H1, C_H2, and C_H3.

Fig. 1 displays the characteristic β-sheet architecture of antibodies (26). Midinfrared spectroscopic studies show that the secondary structure of antibodies is composed of ∼7–11% α-helix and 40–45% β-sheet (5). This is confirmed by circular dichroism spectroscopy and is more or less independent of the IgG subtypes (5). Biochemical digestion by papain results in two fragments of similar size, the crystallizable region fragment (Fc) and antigen-binding region fragment (Fab). The Fc fragment is composed of the two C_H2 and two C_H3 domains, whereas the Fab fragment is composed of C_H1, C_L, V_H, and V_L. The transitions, as observed in DSC, result from the denaturation of specific domains of the mAb (5,8). Several DSC studies have succeeded in identifying the thermodynamic characteristics of individual domains (8,27,28).

Antibody thermograms may display a single peak, several distinct peaks, or overlapping peaks. The investigated mAb exhibits a pretransition at low temperature and a main transition at higher temperature. These transitions are characterized by a midpoint transition temperature T_m, an unfolding enthalpy ΔH_cal, and a heat capacity increase $\Delta {\mathrm{C}}_{\mathrm{p}}^{\mathrm{0}}$. The software of commercial DSC instruments provides an empirical approach and fits the thermograms with multiple Gaussians. In contrast, this analysis uses a physical model, the multistate Zimm-Bragg theory. GuanidineHCl was added up to a concentration of 2.5 M. The chemical denaturant destabilized mAb by lowering the midpoint temperature T_m and decreasing the unfolding enthalpy ΔH_cal. The molecular mechanism behind destabilization correlates with the binding of denaturant molecules. The number of guanidineHCl molecules per AA can be deduced from the decrease of the unfolding enthalpy.

Materials and Methods

mAb sample preparation

The humanized recombinant mAb of IgG1 isotype was produced by mammalian cell culture technology and purified accordingly (29,30). The concentration of the IgG1 sample solutions were determined by ultraviolet measurement at 280 nm using an extinction coefficient of 1.32 for a 1 mg/mL solution (path length d = 1 cm) and formulated in a 10 mM succinate/220 mM sucrose buffer. Purity was determined by size exclusion chromatography. The monomer content as measured by high pressure size exclusion chromatography was >99% (5). The pH of the sample was varied by titrating HCl and respective NaOH to obtain the target pH value as described in the text. GuanidineHCl was added to the protein sample to generate a concentration range from 0 to 2.5 M. If necessary, the pH was adjusted after the addition of guanidineHCl.

Analysis of mAb DSC thermograms

Protein concentrations were typically 3 mg/mL corresponding to a concentration of ∼20 μM. Starting at 5°C, the thermal unfolding of mAb was measured by increasing the temperature to 95°C at a heating rate of 1 K/min. DSC experiments were performed with a VP-DSC instrument (MicroCal, Northampton, MA). Protein solutions were degassed, and the reference cell was filled with buffer. The cell volume was 0.51161 mL. Several authors have reported thermal unfolding of monoclonal antibodies with DSC, focusing on the midpoint temperature T_m (18,19,31, 32, 33, 34, 35, 36, 37). However, data on the enthalpy of unfolding are also available (8,36).

In a DSC thermogram, unfolding appears as an endothermic event. The temperature of the peak maximum is the midpoint temperature T_m, and the area under the peak is the enthalpy change ΔH_cal of unfolding. In addition, the post-transitional heat capacity is larger than that of the native protein by $\Delta {\mathrm{C}}_{\mathrm{p}}^{\mathrm{0}}$. The calorimetric unfolding enthalpy ΔH_cal is thus composed of the conformational enthalpy proper, $\Delta {\mathrm{H}}_{\mathrm{N}\mathrm{U}}^{\mathrm{0}}$(often called van’t Hoff enthalpy ΔH_vH) and the enthalpy increase $\Delta {\mathrm{H}}_{\Delta {\mathrm{C}}_{\mathrm{p}}^{\mathrm{0}}}^{\mathrm{0}}$, caused by the increased molar heat capacity $\Delta {\mathrm{C}}_{\mathrm{p}}^{\mathrm{0}}$ of the unfolded protein.

$$\Delta {\mathrm{H}}_{\mathrm{c}\mathrm{a}\mathrm{l}}=\Delta {\mathrm{H}}_{\mathrm{N}\mathrm{U}}^{\mathrm{0}}+\Delta {\mathrm{H}}_{\Delta {\mathrm{C}}_{\mathrm{p}}^{\mathrm{0}}}^{\mathrm{0}}.$$ (1)

Antibodies are characterized by several domains (e.g., C_H2, C_H3, Fab). Their independent unfolding generates thermograms of different complexity (8,32,37). We analyze the thermograms with the Zimm-Bragg theory, deconvoluting individual domains (13,14).

Heating rates influence midpoint temperature T_m and unfolding enthalpy ΔH_cal. A heating rate of 1 K/min was found to yield results almost identical to those obtained at 0.2 and 0.5 K/min (18). A 1 K/min heating rate is nowadays standard in almost all DSC unfolding experiments. It guarantees a dynamic thermal equilibrium during the heating process. Heating/cooling cycles of the mAb pretransition confirmed the reversibility. Thermal reversibility is maintained until antibody aggregation occurs (8). Once aggregated, antibodies cannot be refolded by cooling. All DSC experiments were performed in duplicate and were reproducible within error limits.

Theory

Thermal unfolding: multistate model (Zimm-Bragg theory)

We use N and U to denote the native and the unfolded conformation of the antibody, whereas n and u refer to a single amino acid residue. We describe protein unfolding as a multistate equilibrium between “native (n)” and “unfolded (u)” amino acid residues (discussed in detail in (13)). A quantitative analysis is possible with the Zimm-Bragg theory (11,12). The essential parameters are the protein cooperativity σ and the equilibrium parameter q(T) of the n $\rightleftarrows$ u equilibrium:

$$\mathrm{q}\left(\mathrm{T}\right)={\mathrm{e}}^{\frac{\mathrm{h}}{\mathrm{R}}\left(\frac{\mathrm{1}}{\mathrm{T}}-\frac{\mathrm{1}}{{\mathrm{T}}_{\mathrm{\infty }}}\right)}.$$ (2)

The enthalpy h of the n$\to$u unfolding reaction is endothermic and is ∼1.1 kcal/mol. α-Helix and β-sheet structures are usually assumed to require specific hydrogen bonds. Experimental studies on short alanine-based peptides contradict this classical view (38) as do free energy calculations using the CHARM potential function (39,40). Apparently, hydrogen bonds contribute little to α-helix/β-sheet stability because the major driving forces favoring structure formation are enhanced van der Waals interactions and hydrophobic effects (39). Protein unfolding can thus be characterized by an average enthalpy h = 1.1 kcal/mol per amino acid, independent of the specific protein conformation (13). This value is used in this analysis.

The cooperativity parameter σ determines the steepness of the unfolding transition. A small σ corresponds to a high cooperativity. In this study, the reference temperature T_∞ is identical with the midpoint temperature T_m. The change in Gibbs free energy per amino acid for a temperature-induced unfolding in the interval T_ini ≤ T_m ≤ T_end is as follows:

$${\mathrm{g}}_{\mathrm{n}\mathrm{u}}=-\mathrm{R}{\mathrm{T}}_{\mathrm{e}\mathrm{n}\mathrm{d}}\ln \mathrm{q}\left({\mathrm{T}}_{\mathrm{e}\mathrm{n}\mathrm{d}}\right)+\mathrm{R}{\mathrm{T}}_{\mathrm{i}\mathrm{n}\mathrm{i}}\ln \mathrm{q}\left({\mathrm{T}}_{\mathrm{i}\mathrm{n}\mathrm{i}}\right)=\mathrm{h}\frac{\Delta \mathrm{T}}{{\mathrm{T}}_{\infty }}\simeq \mathrm{h}\frac{\Delta \mathrm{T}}{{\mathrm{T}}_{\mathrm{m}}}.$$ (3)

The free energy g_nu depends on the unfolding enthalpy h, the midpoint temperature T_m, and the width of the unfolding transition ΔT = T_end − T_ini.

The central building block of the Zimm-Bragg theory is the partition function Z(T) = Z(σ,q(T)), which determines the statistical and thermodynamic properties of protein unfolding. Z(T) can be calculated with a matrix method (41):

$$\mathrm{Z}\left(\mathrm{T}\right)=\left(\begin{array}{cc}1& 0\end{array}\right){\left(\begin{array}{cc}1& \mathrm{\sigma }\mathrm{q}\left(\mathrm{T}\right)\\ 1& \mathrm{q}\left(\mathrm{T}\right)\end{array}\right)}^{\mathrm{\nu }}\left(\begin{array}{c}1\\ 1\end{array}\right),$$ (4)

where ν is the number of amino acids involved in the unfolding reaction. ν can be deduced from the unfolding enthalpy ΔH_cal according to ν $\approx$ ΔH_cal/h. The precise value of ν is not critical as long as $\mathrm{\nu }>1/\sqrt{\sigma }$. The fraction Θ_N of native protein is as follows:

$${\Theta }_{\mathrm{N}}\left(\mathrm{T}\right)=\frac{\mathrm{q}\left(\mathrm{T}\right)}{\mathrm{\nu }}\frac{\mathrm{d}\left(\ln \mathrm{Z}\left(\mathrm{T}\right)\right)}{\mathrm{d}\mathrm{T}}{\left(\frac{\mathrm{d}\mathrm{q}\left(\mathrm{T}\right)}{\mathrm{d}\mathrm{T}}\right)}^{-1}.$$ (5)

DSC

The transition from native protein (N) to the unfolded protein (U) is associated with an endothermic temperature-dependent enthalpy ΔH_NU(T):

$$\Delta {\mathrm{H}}_{\mathrm{N}\mathrm{U}}\left(\mathrm{T}\right)=\Delta {\mathrm{H}}_{\mathrm{N}\mathrm{U}}^{\mathrm{0}}+\Delta {\mathrm{C}}_{\mathrm{p}}^{\mathrm{0}}\left(\mathrm{T}-{\mathrm{T}}_{\mathrm{m}}\right).$$ (6)

$\Delta {\mathrm{H}}_{\mathrm{N}\mathrm{U}}^{\mathrm{0}}$ is the conformational enthalpy, whereas the second term defines the contribution of the heat capacity increase $\Delta {\mathrm{C}}_{\mathrm{p}}^{\mathrm{0}}$. In the thermal unfolding experiment, $\Delta {\mathrm{H}}_{\mathrm{N}\mathrm{U}}\left(\mathrm{T}\right)$ is convoluted with the extent of protein unfolding, Θ _U(T) = 1−Θ_N(T):

$${\mathrm{H}}_{\mathrm{N}\mathrm{U}}\left(\mathrm{T}\right)=\Delta {\mathrm{H}}_{\mathrm{N}\mathrm{U}}\left(\mathrm{T}\right){\Theta }_{\mathrm{U}}\left(\mathrm{T}\right).$$ (7)

DSC measures the heat capacity:

$${\mathrm{C}}_{\mathrm{p},\mathrm{N}\mathrm{U}}\left(\mathrm{T}\right)=\frac{\mathrm{d}{\mathrm{H}}_{\mathrm{N}\mathrm{U}}\left(\mathrm{T}\right)}{\mathrm{d}\mathrm{T}}=\Delta {\mathrm{H}}_{\mathrm{N}\mathrm{U}}\left(\mathrm{T}\right)\frac{\mathrm{d}{\Theta }_{\mathrm{U}}\left(\mathrm{T}\right)}{\mathrm{d}\mathrm{T}}+\Delta {\mathrm{C}}_{\mathrm{p}}^{\mathrm{0}}{\Theta }_{\mathrm{U}}\left(\mathrm{T}\right).$$ (8)

The enthalpy and entropy of unfolding are given by the following:

$$\Delta {\mathrm{H}}_{\mathrm{c}\mathrm{a}\mathrm{l}}\left(\mathrm{T}\right)=\underset{{\mathrm{T}}_{\mathrm{i}\mathrm{n}\mathrm{i}}}{\overset{\mathrm{T}}{\int }}{\mathrm{C}}_{\mathrm{p},\mathrm{N}\mathrm{U}}\left(\mathrm{T}\right)\mathrm{d}\mathrm{T},$$ (9)

$$\Delta {\mathrm{S}}_{\mathrm{c}\mathrm{a}\mathrm{l}}\left(\mathrm{T}\right)=\underset{{\mathrm{T}}_{\mathrm{i}\mathrm{n}\mathrm{i}}}{\overset{\mathrm{T}}{\int }}\frac{{\mathrm{C}}_{\mathrm{p},\mathrm{N}\mathrm{U}}\left(\mathrm{T}\right)}{\mathrm{T}}\mathrm{d}\mathrm{T}.$$ (10)

The Gibbs free energy of the N$\to$U conformational transition is as follows:

$$\Delta {\mathrm{G}}_{\mathrm{c}\mathrm{a}\mathrm{l}}\left(\mathrm{T}\right)=\Delta {\mathrm{H}}_{\mathrm{c}\mathrm{a}\mathrm{l}}\left(\mathrm{T}\right)-\mathrm{T}\Delta {\mathrm{S}}_{\mathrm{c}\mathrm{a}\mathrm{l}}.$$ (11)

Results

Thermal unfolding (DSC) of mAb in guanidineHCl solution

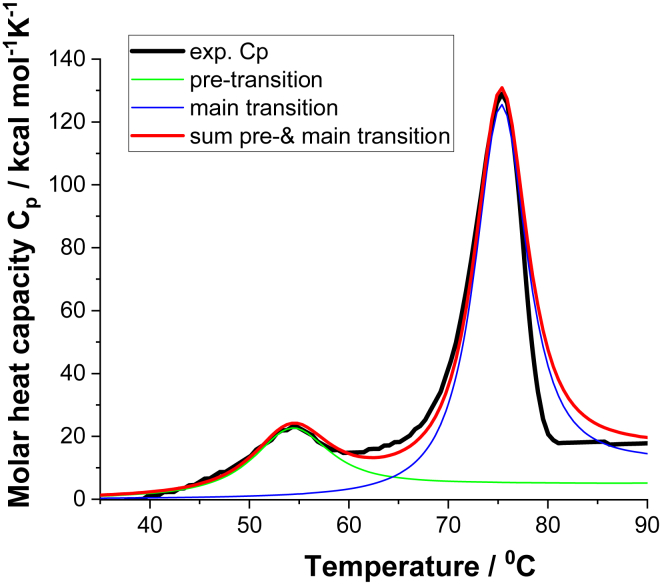
DSC is the gold standard for thermodynamic analysis of protein unfolding because thermodynamic data are directly obtained from the experiment. DSC measures the heat capacity C_p,NU(T) and, by integration, the unfolding enthalpy ΔH_cal. These mAb unfolding experiments in guanidineHCl solution were performed at pH 4.0, 6.2, and 8.0. Fig. 2 shows the DSC scan of mAb in 1.0 M guanidineHCl at pH 6.2. The thermogram displays a low-temperature pretransition and a high-temperature main transition, the general pattern of these mAb unfolding experiments. Similar DSC thermograms are presented in (8,35). Pre- and main transition are each characterized by a midpoint temperature T_m and an unfolding enthalpy ΔH_cal. As discused above, the number of amino acid residues participating in unfolding can be estimated as ν ≈ ΔH_cal/h with h = 1.1 kcal/mol. In the absence of guanidineHCl, the averages are ν = 220 ± 50 for the pretransition and 850 ± 30 for the main transition.

Figure 2.

Thermal unfolding of mAb in 1.0 M guanidineHCl at pH 6.2, measured with differential scanning calorimetry (DSC). Shown is molar heat capacity Cp(T) as a function of temperature. Black line: experimental result. Smooth lines: simulations with the multistate Zimm-Bragg theory (green: pretransition; blue: main transition; red: sum of pre- and main transition). Pretransition parameters: T_m = 54°C, ΔH_cal = 322 kcal/mol (ν = ΔH_cal/h = 293); ΔC_p =5.02 kcal/mol⋅K, σ = 1.5 × 10⁻⁴. Main transition parameters: T_m = 75.4°C, ΔH_cal = 976 kcal/mol (ν = 887); ΔC_p =12.42 kcal/mol⋅K, σ = 7 × 10⁻⁵.

The multistate Zimm-Bragg theory provides an almost perfect simulation of the DSC thermogram (Fig. 2, smooth red line). The heat capacity of the unfolded protein is $\Delta {\mathrm{C}}_{\mathrm{p}}^{\mathrm{0}}$, larger than that of the native mAb. Similar effects are well documented for thermograms of small proteins (42,43). $\Delta {\mathrm{C}}_{\mathrm{p}}^{\mathrm{0}}$ is caused by a restructuring of solvent molecules (42). The data in (42) suggest a linear relationship between $\Delta {\mathrm{C}}_{\mathrm{p}}^{\mathrm{0}}$ and ν, the number of amino acid residues involved in unfolding.

$$\Delta {\mathrm{C}}_{\mathrm{p}}^{\mathrm{0}}\left(\mathrm{c}\mathrm{a}\mathrm{l}/\mathrm{m}\mathrm{o}\mathrm{l}\mathrm{K}\right)=18.6\mathrm{\nu }-300.$$ (12)

The heat capacity changes in Fig. 2 are $\Delta {\mathrm{C}}_{\mathrm{p}}^{\mathrm{0}}$ = 5.0 kcal/mol⋅K for the pretransition and 12.4 kcal/mol⋅K for the main transition. Using Eq. 12, the numbers of amino acid residues are estimated as ν∼280 for the pretransition and 680 for the main transition, in broad agreement with the results derived from ΔH_cal with ν∼290 and 890, respectively. Similar increases in the molar heat capacity of antibodies can be found in published DSC thermograms (e.g., (31,37)).

Most DSC studies ignore the $\Delta {\mathrm{C}}_{\mathrm{p}}^{\mathrm{0}}$ effect. The change in heat capacity between native and unfolded protein is eliminated by applying a sigmoid baseline. This choice of baseline results in a reduced unfolding enthalpy (e.g., (36)). The enthalpy of this truncated heat capacity peak is the conformational enthalpy proper (also called “van’t Hoff enthalpy” in the two-state model). However, “it is clear that in considering the energetic characteristics of protein unfolding, one has to take into account all energy that is accumulated upon heating and not only the very substantial heat effect associated with gross conformational transitions, that is, all the excess heat effects must be integrated” (43).

Midpoint temperature T_m as a function of the guanidineHCl concentration

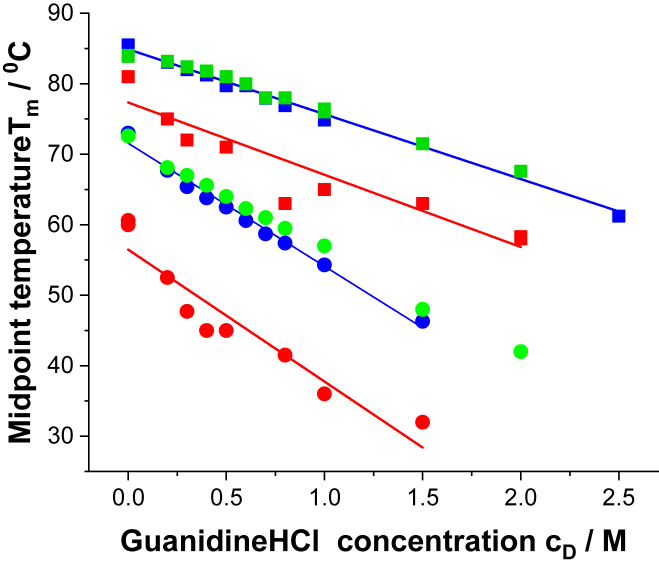
The addition of guanidineHCl lowers the midpoint temperature T_m defined by the C_p maximum (Fig. 3).

Figure 3.

Midpoint temperature T_m as a function of denaturant concentration c_D. Red squares, blue squares, and green squares represent main transitions at pH 4.0, 6.2, and 8.0, respectively. Red circles, blue circles, and green circles represent pretransitions at pH 4.0, 6.2, and 8.0, respectively.

DSC thermograms at pH 6.2 and 8.0 show almost identical transition temperatures. At pH 4.0, the antibody is destabilized, and the T_m values of pre- and main transitions are reduced by 15 and 7°C, respectively. Linear regression analysis of the data shown in Fig. 3 yields for the pretransition:

$$\begin{array}{c}\mathrm{p}\mathrm{H}4.0\\ {\mathrm{T}}_{\mathrm{m}}\left(°C\right)=-18.7{\mathrm{c}}_{\mathrm{D}}\left(\mathrm{M}\right)+56.5\\ \left({\mathrm{R}}^2=0.901\right)\end{array},$$ (13a)

$$\begin{array}{c}\mathrm{p}\mathrm{H}6.2\\ {\mathrm{T}}_{\mathrm{m}}\left(°C\right)=-17.5{\text{c}}_{\mathrm{D}}\left(\mathrm{M}\right)+71.6\\ \left({\mathrm{R}}^2=0.990\right)\end{array},$$ (13b)

$$\begin{array}{c}\text{pH}8.0\\ {\text{T}}_{\text{m}}\left(°C\right)=-15.4{\text{c}}_{\text{D}}\left(\text{M}\right)+71.9\\ \left({\text{R}}^2=0.996\right)\end{array}.$$ (13c)

The guanidineHCl concentrations (c_D: denaturant concentration) for mAb denaturation at 25°C are predicted as 1.7 M (pH 4.0), 2.7 M (pH 6.2), and 3.0 M (pH 8.0).

The results for the main transition are as follows:

$$\begin{array}{c}\text{pH}4.0\\ {\text{T}}_{\text{m}}\left(°C\right)=-10.3{\text{c}}_{\text{D}}\left(\text{M}\right)+77.3\\ \left({\text{R}}^2=0.882\right)\end{array},$$ (14a)

$$\begin{array}{c}\text{pH}6.2\\ {\text{T}}_{\text{m}}\left(°C\right)=-9.21{\text{c}}_{\text{D}}\left(\text{M}\right)+84.9\\ \left({\text{R}}^2=0.983\right)\end{array},$$ (14b)

$$\begin{array}{c}\text{pH}8.0\\ {\text{T}}_{\text{m}}\left(°C\right)=-8.69{\text{c}}_{\text{D}}\left(\text{M}\right)+84.7\\ \left({\text{R}}^2=0.994\right)\end{array}.$$ (14c)

The guanidineHCl concentrations for denaturation of the mAb main transition at 25°C are predicted as 5.1 M (pH 4.0), 6.5 M (pH 6.2), and 6.9 M (pH 8.0). The maximal solubility of guanidineHCl in water at room temperature is ∼6 M. The pretransition is twice as sensitive to guanidineHCl denaturation as the main transition.

Unfolding enthalpy ΔH_cal as a function of guanidineHCl concentration

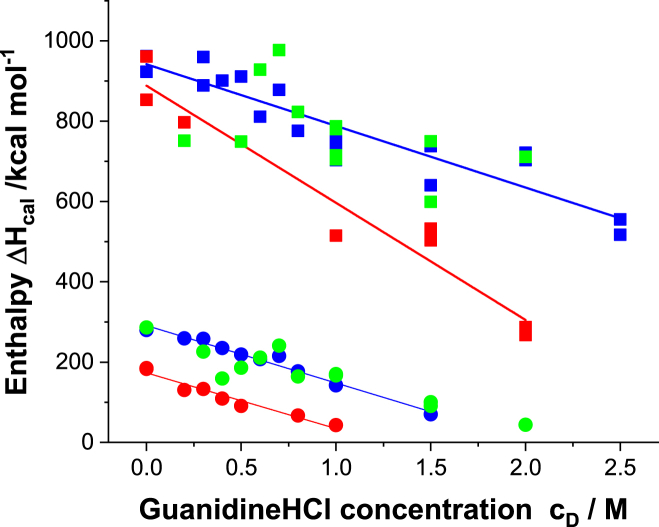
The calorimetric unfolding enthalpy, ΔH_cal, decreases with increasing denaturant concentration c_D (Fig. 4).

Figure 4.

Unfolding enthalpy ΔH_cal as a function of denaturant concentration c_D. Red squares, blue squares, and green squares represent main transitions at pH 4.0, 6.2, and 8.0, respectively. Red circles, blue circles, and green circles represent pretransitions at pH 4.0, 6.2, and 8.0, respectively.

Linear regression analysis yields for the pretransition:

$$\begin{array}{c}\text{pH}4.0\\ \Delta {\text{H}}_{\text{cal}}\left(\text{kcal}/\text{mol}\right)=-139{\text{c}}_{\text{D}}\left(\text{M}\right)+173\\ \left({\text{R}}^2=0.956\right)\end{array},$$ (15a)

$$\begin{array}{c}\text{pH}6.2\\ \Delta {\text{H}}_{\text{cal}}\left(\text{kcal}/\text{mol}\right)=-143{\text{c}}_{\text{D}}\left(\text{M}\right)+291\\ \left({\text{R}}^2=0.973\right)\end{array},$$ (15b)

$$\begin{array}{c}\text{pH}8.0\\ \Delta {\text{H}}_{\text{cal}}\left(\text{kcal}/\text{mol}\right)=-107{\text{c}}_{\text{D}}\left(\text{M}\right)+261\\ \left({\text{R}}^2=0.830\right)\end{array}.$$ (15c)

The numbers of amino acid residues involved in the unfolding transition can be estimated from ΔH_cal at c_D = 0 M according to ν = ΔH_cal/h and are 157 (pH 4.0), 265 (pH 6.2), and 237 (pH 8.0) (average: 220 ± 50).

The results for the main transition are as follows:

$$\begin{array}{c}\text{pH}4.0\\ \Delta {\text{H}}_{\text{cal}}\left(\text{kcal}/\text{mol}\right)=-292{\text{c}}_{\text{D}}\left(\text{M}\right)+884\\ \left({\text{R}}^2=0.972\right)\end{array},$$ (16a)

$$\begin{array}{c}\text{pH}6.2\\ \Delta {\text{H}}_{\text{cal}}\left(\text{kcal}/\text{mol}\right)=-153{\text{c}}_{\text{D}}\left(\text{M}\right)+941\\ \left({\text{R}}^2=0.858\right)\end{array},$$ (16b)

$$\begin{array}{c}\text{pH}8.0\\ \Delta {\text{H}}_{\text{cal}}\left(\text{kcal}/\text{mol}\right)=-174{\text{c}}_{\text{D}}\left(\text{M}\right)+971\\ \left({\text{R}}^2=0.670\right)\end{array}.$$ (16c)

The numbers of amino acid residues are ν = 808 (pH 4.0), 855 (pH 6.2), and 883 (pH 8.0). (average: 849 ± 30). Antibody chains are divided into domains consisting of around 100–120 amino acids. As discussed in detail below, the pretransition represents the reversible unfolding of two C_H2 domains, and the main transition represents the unfolding of the Fab fragment and the C_H3 domains.

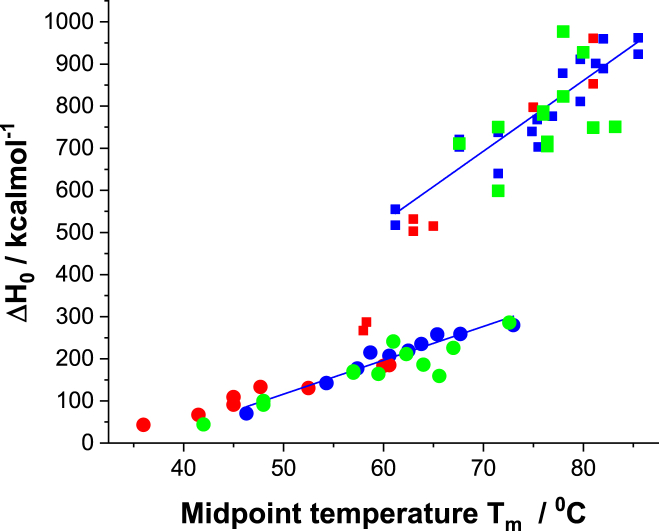
Unfolding enthalpy ΔH_cal as a function of midpoint temperature T_m

The unfolding enthalpy ΔH_cal and the midpoint temperature T_m correlate linearly with the denaturation concentration c_D. This predicts a linear correlation between ΔH_cal and T_m.

As shown in Fig. 5, the enthalpies of pre- and main transitions cluster in narrow intervals. The slopes of the ΔH_cal versus T_m plots have the dimensions of a molar heat capacity, denoted ${\text{C}}_{{\text{p,T}}_{\text{m}}}$ in the following. At present, ${\text{C}}_{{\text{p,T}}_{\text{m}}}$is an empirical parameter correlated with the number of amino acids involved. The ratio ${\text{C}}_{{\text{p,T}}_{\text{m}}}\left(\text{pre}\right)/{\text{C}}_{{\text{p,T}}_{\text{m}}}\left(\text{main}\right)=0.27$±0.3 is identical within error to ν(pre)/ν(main)= 0.30, calculated from the unfolding enthalpy. ${\text{C}}_{{\text{p,T}}_{\text{m}}}$ is ∼20% larger than $\Delta {\mathrm{C}}_{\mathrm{p}}^{\mathrm{0}}$, the increase representing molar heat capacity upon protein unfolding. $\Delta {\mathrm{C}}_{\mathrm{p}}^{\mathrm{0}}$ is often difficult to evaluate because of baseline problems, and a plot ${\text{C}}_{{\text{p,T}}_{\text{m}}}$ versus T_m could provide a more precise alternative. A similar result was found for the thermal unfolding of lysozyme (14).

Figure 5.

Unfolding enthalpy ΔH_cal as a function of midpoint temperature T_m. Red squares, blue squares, and green squares represent main transitions at pH 4.0, 6.2, and 8.0, respectively. Slope ${\text{C}}_{{\text{pT}}_{\text{0}}}$ = 16.8 ± 1.6 kcal/mol∙K. Red circles, blue circles, and green circles represent pretransitions at pH 4.0, 6.2, and 8.0, respectively. Slope ${\text{C}}_{{\text{pT}}_{\text{0}}}$ = 8.0 ± 0.5 kcal/mol∙K.

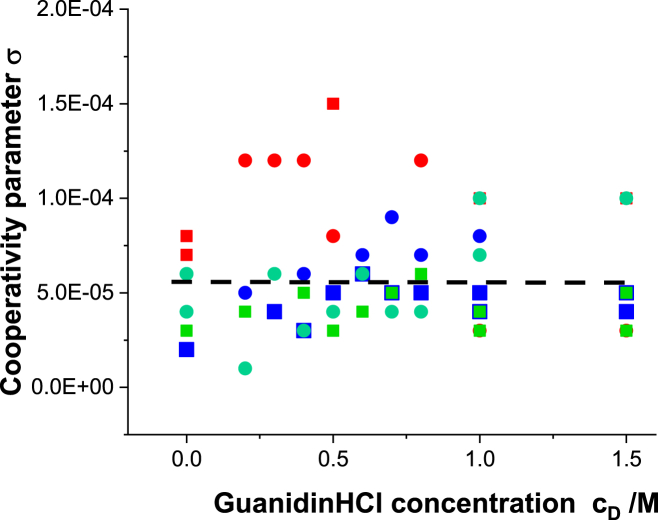
Cooperativity parameter σ

Fig. 6 summarizes the cooperativity parameters for pretransitions and main transitions. The σ parameter varies between 1.5 × 10⁻⁵ and 1.5 × 10⁻⁴ with an average of σ∼6 × 10⁻⁵. It is 10–100 times larger than σ of small proteins. The unfolding of mAb is thus distinctly less cooperative than the unfolding of small proteins such as ubiquitin or lysozyme (cf (13), Table 3). Fig. 6 further demonstrates that σ increases from pH 8.0 (green symbols) over pH 6.2 (blue symbols) to pH 4.0 (red symbols).

Figure 6.

Cooperativity parameter σ as a function of guanidineHCl concentration c_D. Red squares, blue squares, and green squares represent main transitions at pH 4.0, 6.2, and 8.0, respectively. Red circles, blue circles, and green circles represent pretransitions at pH 4.0, 6.2, and 8.0, respectively.

The cooperativity parameter σ determines the average length <1> of a folded region according to $\langle \text{l}\rangle \sim 1/\sqrt{\sigma }$. A cooperativity parameter σ = 10⁻⁴ thus predicts an average length of <1> = 100 amino acid residues, comparable to the size of an individual mAb domain. Several domains of length <1> will unfold independently and simultaneously upon heating mAb.

Discussion

Analysis of the DSC thermograms with the multistate Zimm-Bragg theory

The two-state model cannot fit the mAb pre- or main transition. In fact, it generally fails when applied to thermograms of large proteins as large unfolding enthalpies ΔH_cal generate very sharp unfolding transitions in the two-state model. In contrast, ΔH_cal has no influence on the shape of the unfolding transition calculated with the Zimm-Bragg theory. The unfolding of mAb is a multistate transition with a large number of intermediates. The cooperative Zimm-Bragg theory fits the mAb unfolding with three parameters of physical relevance: 1) the unfolding enthalpy h per amino acid residue, 2) the number ν of amino acids residues involved in the transition, and 3) the cooperativity parameter σ. The three parameters are determined independently of each other. The unfolding enthalpy h = 1.1 kcal/mol is an average value encompassing all relevant interactions and not specific for α-helix and β-sheet (see above and (13)). The number of amino acids residues ν is estimated from the unfolding enthalpy ΔH_cal and is ∼220 for the pretransition and 850 for the main transition. A precise number is not required as any $\mathrm{\nu }\gg 1/\sqrt{\sigma }$ will lead to the same result. In this study, the average σ is ∼6 × 10⁻⁵, yielding a cooperative length of ν_coop∼130 amino acid residues. Protein domains of this length will unfold independently. The variable, shape-determining factor in the C_p(T) versus T simulation is the cooperativity parameter σ. A large σ corresponds to a low protein cooperativity and a broad DSC transition. With h and ν defined as above, σ can be determined with high precision.

Antibody stability and unfolding temperature T_m

The Zimm-Bragg theory predicts segments of length 100–130 amino acids, which are in dynamic equilibrium and fold/unfold independently. This is consistent with the structure shown in Fig. 1 displaying 12 domains with 100–120 amino acids each. The factors determining domain stability are of particular interest in developing antibodies for therapeutic use and have been investigated in several studies. Ionescu et al. investigated three different humanized IgG1s by DSC and reported thermograms for the intact antibodies as well as for their Fab and Fc fragments (8). The mAb thermogram shown in Fig. 2 is almost identical to those observed for intact Mrk and Her antibodies. Mrk and Her show a pretransition at 71°C (160 kcal/mol) and a main transition at 82°C (820 kcal/mol). The Fab fragment with four domains has a single high-temperature peak at 82°C (330 kcal/mol) (5,8). In contrast, the Fc fragment has transitions at 71°C (190 kcal/mol) and 82°C (160 kcal/mol), each comprising two domains. Based on T_m data of individual domains, the pretransition of the Fc segment can be assigned to the unfolding of C_H2 domains (Table 1 in (35)). It is thus safe to conclude that the pretransition of mAb results from the unfolding of two C_H2 domains, whereas the main transition represents the unfolding of the Fab fragments (eight domains) and the two C_H3 domains of the Fc fragment.

The unfolding temperature and enthalpy depend not only on the stability of individual domains but also on additional stabilization energies of interacting domains (6,44). Various attempts have been made to correlate the unfolding temperature T_m with structural characteristics of the antibody, assigning individual antibody domains to specific transition temperatures T_m (31,32,35,37). The associated enthalpies and entropies were, however, not considered, even though they are essential in determining T_m. At the midpoint of the unfolding transition, the Gibbs free energy is ΔG_cal = ΔH_cal − T_mΔS_cal = 0, leading to the following:

$${\text{T}}_{\text{m}}=\frac{\Delta {\text{H}}_{\text{cal}}}{\Delta {\text{S}}_{\text{cal}}}.$$ (17)

The entropy of unfolding is given by ΔS_cal = ΔH_cal/T_m.

T_m is the ratio of two thermodynamic quantities. A small change in either ΔH_cal or ΔS_cal can lead to a significant change in T_m. As an example, we compare the pre- and main transition of mAb unfolding at pH 6.2 in the absence of denaturant. The pretransition is centered at 71.6°C (Eq. 13b), the main transition at 84.9°C (Eq. 14b). The corresponding enthalpies are ΔH_cal = 291 kcal/mol (Eq. 15b) and 941 kcal/mol (Eq. 16b). The entropies calculated with Eq. 17 are ΔS_cal= 0.84 and 2.63 kcal/mol∙K, respectively. The entropies normalized with the number of amino acid residues are ΔS_cal/ν = 3.19 cal/mol∙K for the pretransition and 3.07 cal/mol∙K for the main transition. The larger entropy of the pretransition explains its lower melting temperature compared to the main transition. An entropy change of 2.8–3.1 cal/mol∙K per amino acid residue was found for lysozyme (129 AA) (14). The entropy change for the helix-to-coil transition has been calculated to be 3–7 cal/mol∙K per amino acid residue (Table 3 in (39)).

Unfolding enthalpy and the number of bound guanidineHCl molecules

GuanidineHCl decreases the unfolding enthalpy ΔH_cal of the mAb pre- and main transition (Fig. 4). In parallel, the transition temperature also decreases (Fig. 3). DSC studies of small proteins, such as lysozyme (23,45,46), ribonuclease (23), ubiquitin (47), and apolipoprotein A-1 (17), report similar results. According to Eq. 17, the lower T_m is only possible if ΔS_cal changes less than ΔH_cal.

Guanidine is fully charged in the pH range of 4–8. A strong electrostatic interaction with charged peptide side chains was found (48). Recent x-ray studies of lysozyme also show that guanidine binds to the polypeptide protein backbone and side chains and replaces water from the proteins first solvent shell (5). GuanidineHCl binds to proteins with an exothermic binding enthalpy h_Gnd $\simeq$ −2.63 kcal/mol (23) compensating, in part, the endothermic unfolding enthalpy ΔH_cal. A concentration increase by Δc_D = 1 M reduces the mAb pretransition enthalpy ΔH_cal by δΔH_cal = −143 ± 5 kcal/molM (Eq. 15b). The number of bound guanidine molecules can thus be calculated as ΔN_Gnd = δΔH_cal/h_Gnd = (54 ± 2)/M. The corresponding results for the main transition are δΔH_cal = −(153 ± 10 kcal/molM) (Eq. 16b) and ΔN_Gnd = (58 ± 5)/M. Relevant for the unfolding reaction is the number of bound denaturants at complete unfolding. The pretransition is completed at ∼3.5 M, and N_Gnd = 190 guanidines are bound. The number of amino acid residues participating in the unfolding transition is N_aa = 265 (pH 6.2), leading to a stoichiometry of guanidineHCl/amino acid residues N_Gnd/N_aa = 0.72. The main transition is completed at ∼7.3 M, resulting in N_Gnd = 424, N_aa = 855 (pH 6.2), and N_Gnd/N_aa = 0.50. The pretransition binds relatively more guanidineHCl molecules than the main transition. The same analysis applied to published DSC data predicts for lysozyme (14,23) N_Gnd = 49 ± 3, N_aa = 129, N_Gnd/N_aa = 0.38; ribonuclease (23) N_Gnd = 49, N_aa =124, N_Gnd/N_aa =0.4; ubiquitin (47) N_Gnd = 15, N_aa = 76, N_Gnd/N_aa = 0.2; and apolipoprotein A-1 (17) N_Gnd = 50, N_aa = 110, N_Gnd/N_aa = 0.45. Average N_Gnd/N_aa = 0.36 ± 0.09 (0.41 ± 0.03 without ubiquitin).

Free energy of unfolding

The free energy g_nu of the n$\to$ u transition of a single residue depends on the width ΔT of the transition and the midpoint temperature T_m (Eq. 3). The width of pre- and main transition is $\Delta \text{T}\simeq 30-35°\text{C}$ with ∼95% unfolded protein at the higher temperature. The free energy is thus ${\text{g}}_{\text{nu}}\simeq 95-110\text{cal}/\text{mol}$. The free energy for the propagation of the α-helix was predicted as ∼100 cal/mol per residue with the finite difference Poisson-Boltzmann/γ(charmm) model (39,40). The same g_nu was obtained for small proteins such as lysozyme or ubiquitin (13).

A completely different line of experiments supports these results. The binding of amphipathic peptides/proteins to phospholipid membranes induces α-helix- or β-sheet structure. The Gibbs free energy change of the folding reaction was found experimentally and model independent to be −140 to −400 cal/mol per amino acid (49, 50, 51, 52, 53, 54). This result is of similar magnitude but of opposite sign than the mAb unfolding free energy g_NU. The binding of amphipathic peptides to phospholipid promotes structure formation, and the free energy change is negative. In contrast, the binding of denaturants disrupts protein structure, and the free energy change is positive. The two processes are of different signs but of equal magnitude.

The total Gibbs free energy of unfolding is ΔG_NU(T) = ΔH_NU(T) − TΔS_NU(T) (Eq. 11). As anticipated δΔG_NU(T_end) − ΔG_NU(T_ini) must be negative and is −6 to −12 kcal/mol for the pretransition and −16 to −20 kcal for the main transition, varying with the guanidineHCl concentration and pH.

Conclusions

Thermal unfolding of the mAb displays two independent folding regions composed of 2 and 10 domains, respectively. A low-temperature pretransition, centered at 72°C and containing ∼220 amino acids, corresponds to to the C_H2 domains of the Fc fragment. The main transition at 85°C with ∼850 amino acids represents the unfolding of the remaining domains. Both regions are characterized by almost identical cooperative parameters σ. Unfolding is not a two-state equilibrium between a fully folded and a fully unfolded domain but a complex reaction with many intermediates. The multistate Zimm-Bragg theory provides an excellent description of the experimental data. The analysis of the DSC thermograms yields the unfolding enthalpy, the protein cooperative parameter σ, the number of residues participating in the unfolding, and the Gibbs free energy for the unfolding of a single amino acid residue and the whole protein. The Zimm-Bragg theory provides useful parameters for protein formulation screening. The theory predicts segments of average length <1> ∼100–130 amino acid residues, which fold independently, consistent with the domain structure of mAb. The addition of guanidineHCl up to 2.5 M has only little influence on the protein cooperativity but decreases drastically the unfolding enthalpy. The binding of guanidineHCl to the polypeptide backbone and side chains is an exothermic reaction, which compensates in part the endothermic unfolding enthalpy. The decrease in the unfolding enthalpy yields the number of guanidineHCl molecules bound to each of the two domains. The stoichiometry guanidineHCl-to-amino acids is 0.72 for the small domain and 0.50 for the large domain. The small domain (C_H2) is better accessible to the denaturant and thus easier to destabilize.

Author Contributions

Antibody preparation and DSC measurements were performed by P.G., A.E., and M.B. Theoretical analysis was made by J.S.

Editor: Arne Gericke.