Abstract
Advances in imaging methods such as electron microscopy, tomography, and other modalities are enabling high-resolution reconstructions of cellular and organelle geometries. Such advances pave the way for using these geometries for biophysical and mathematical modeling once these data can be represented as a geometric mesh, which, when carefully conditioned, enables the discretization and solution of partial differential equations. In this work, we outline the steps for a naïve user to approach the Geometry-preserving Adaptive MeshER software version 2, a mesh generation code written in C++ designed to convert structural data sets to realistic geometric meshes while preserving the underlying shapes. We present two example cases: 1) mesh generation at the subcellular scale as informed by electron tomography and 2) meshing a protein with a structure from x-ray crystallography. We further demonstrate that the meshes generated by the Geometry-preserving Adaptive MeshER software are suitable for use with numerical methods. Together, this collection of libraries and tools simplifies the process of constructing realistic geometric meshes from structural biology data.
Significance
As biophysical structure determination methods improve, the rate of new structural data is increasing. New methods that allow the interpretation, analysis, and reuse of such structural information will thus take on commensurate importance. In particular, geometric meshes such as those commonly used in graphics and mathematics can enable a myriad of mathematical analysis. In this work, we describe the Geometry-preserving Adaptive MeshER software version 2 (GAMer 2), a mesh generation library designed for biological data sets. Using GAMer 2 and the associated tools PyGAMer and BlendGAMer, biologists can robustly generate computer- and algorithm-friendly geometric mesh representations informed by structural biology data. We expect that GAMer 2 will be a valuable tool to bring realistic geometries to biophysical models.
Introduction
The use of partial differential equations (PDEs) in mathematical modeling of cellular phenomena is becoming increasing common, particularly for problems that include electrostatics, reaction-diffusion systems, fluid dynamics, and continuum mechanics. Solutions to these equations using idealized geometries have provided insight into how cell shape can affect signaling (1, 2, 3, 4) and how blood flows in vessels (5).
On the other hand, to gain better insight into how cellular geometry can affect the dynamics of these mechanochemical processes, using realistic geometries is necessary. Already, freely available tools such as Virtual Cell (6) and CellOrganizer (7) have paved the way for using realistic cellular geometries in simulations. With the increasing availability of high-resolution images of the cellular ultrastructure, including the size and shape of organelles and the curvature of the various cellular membranes, there is a need for computational tools and algorithms that can enable us to use these data as the geometry or domain of interest and conduct simulations using numerical methods (8).
For most relevant geometries, it is impossible to obtain analytical solutions for PDEs; this necessitates the use of numerical methods to provide an approximate solution. These numerical methods are based on discretization (approximating the PDE with a discrete algebraic system) combined with solvers (typically iterative methods that converge to the solution to the algebraic system). The first step usually requires the generation of a geometric mesh over which the problem can be discretized using techniques such as finite difference, finite volume, finite element, or other methods to build the algebraic system that approximates the PDE. The numerical approximation to the PDE is then produced by solving the resulting linear or nonlinear algebraic equations using an appropriate fast solver. One of the computational challenges associated with generating meshes of biological data sets is the presence of highly irregular surfaces with curvatures at the nanometer or Ångstrom length scales. Although many tools from the graphics community exist to generate meshes for visualization, these poor-quality meshes, when used to solve a PDE, can both destroy the quality of the discretization as an approximation to the PDE and also produce algebraic systems that are badly conditioned and difficult to solve efficiently or accurately with iterative solvers.
Although it is possible to design discretizations of PDE problems on surfaces using the finite volume methods or other techniques, we prefer the finite element method (FEM) here for a number of reasons. To begin with, the FEM first arose in the 1960s in the engineering community as a response to the poor performance of the existing discretization techniques for PDEs involving shells and other complex physical shapes. In addition, methods such as the FEM that are built on the basis of function expansion to provide a natural framework both for treating highly nonlinear problems and for discretizing multiple PDEs that couple together to form a larger multiphysics system. Lastly, the FEM framework is quite general and can, in fact, be shown to reproduce finite volume, spectral, and other discretizations through the appropriate choices of the basis and test functions.
One challenge preventing the routine use of experimental ultrastructural data with PDE-based mathematical modeling is the difficulty associated in generating a discretization, or commonly a mesh, that accurately represents the structures of interest. Building upon existing meshing codes such as TetGen (9), NetGen (10), TetWild (11), MeshLab (12), Gmsh (13), and CGAL (14)—along with commercial codes such as ANSYS Meshing, among others—we describe the development of a meshing framework, the Geometry-preserving Adaptive MeshER software version 2 (GAMer 2), which is designed specifically for biological mesh generation. This code has been completely rewritten from version 1, which was previously described by Yu et al. (15,16) and Gao et al. (17, 18, 19). GAMer 2 features the original GAMer algorithms but with significantly improved ease of use, distributability, and maintainability. We have also developed a new Python application programming interface (API) called PyGAMer and streamlined the GAMer Blender add-on called BlendGAMer. The complete explanation of the mathematics and underlying algorithms are available in (15, 16, 17, 18, 19, 20). In what follows, we provide an overview of the GAMer mesh generation capabilities for the general biophysicist.
Methods
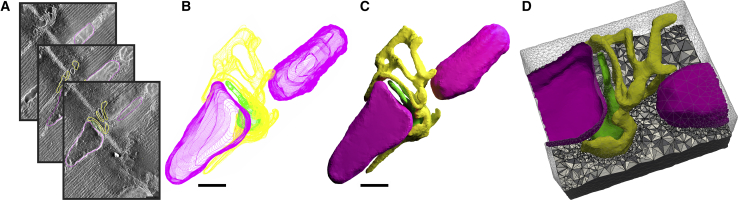
At its core, GAMer is a mesh generation and conditioning library that uses concepts from the graphics and engineering literature. It can be used to produce high-quality surface and volume meshes from several types of input: 1) Protein Data Bank (PDB)/procedure qualification record (PQR) file (Ångstrom to nanometer), 2) volumetric data set (Ångstrom to meter), or 3) initial surface mesh (Ångstrom to meter). To enable FEM-based applications, GAMer also has utilities to support boundary marking. Tetrahedral meshes of a domain can be constructed in GAMer through the use of functionality provided by TetGen (21). Surface or volume meshes can be outputted to several common formats for use with other tools such as FEniCS (22,23), ParaView (24), MCell (25), and FFEA (26), among others. We note that although GAMer is designed primarily with FEM-based applications in mind, conditioned meshes of realistic geometries can also be used for geometric analysis such as the estimation of curvatures, volumes, and surface areas (27). Conditioned meshes can also be used in other tools such as MCell (25) and three-dimensional (3D) printing. Example tutorials of using GAMer 2 to generate surface and volume meshes of a protein structure (PDB: 2JHO) and a subcellular scene of a calcium release unit (CRU) from a murine cardiac myocyte imaged using electron tomography (ET) (Cell Image Library: 3603 (28)) (Fig. 1) are provided in the documentation (https://gamer.readthedocs.io/en/latest/tutorial.html) and described in this report. Here, we will summarize the key implementation steps and refer the interested reader to (27) for technical details of the implementation.
Figure 1.
Example workflow using GAMer to construct a tetrahedral domain suitable for use with finite element simulations. (A) A segmented electron tomogram of a murine cardiac calcium release unit (CRU) from Cell Image Library: 3603 is shown here. (B) Stacks of contours from the traced model are shown here. (C) The conditioned surface mesh of the model is shown here. (D) The tetrahedralized domain that can be used for simulating cytosolic diffusion is shown here. Note that we have inverted the tetrahedralized domain to represent the free space surrounding the CRU geometry. Scale bars, 200 nm. To see this figure in color, go online.
GAMer 2 development
One of the limitations of the prior versions of GAMer is the inability to robustly represent meshes of arbitrary manifoldness and topology. This limitation prevented the safe application of GAMer to nonmanifold meshes, which often produced segmentation faults or other undefined behaviors. To ameliorate this, in GAMer 2, we replaced the underlying mesh representation to use the colored abstract simplicial complex (CASC) data structure (29). CASC keeps careful track of the mesh topology and, therefore, makes it trivial to track the manifoldness of a given mesh object. By eliminating the need for a code to handle encounters with nonmanifold elements, the code base is significantly reduced, and segmentation faults are eliminated. Another benefit of using CASC is that it can represent both surface meshes (2D simplices embedded in 3D) and volume meshes (3D simplices embedded in 3D), allowing users to interact with both the surface and volume meshes using an identical API. This simplification contributes to the long-term maintainability of the GAMer 2 code.
In the development of GAMer 2, we have also migrated to use the cross-platform CMake build toolchain and away from the previous GNU build system Autotools. Using CMake, GAMer 2 can now be compiled and run on major operating systems, including Linux, Mac OS, and Windows, which were previously unsupported. Detailed installation instructions are provided online (https://gamer.readthedocs.io/en/latest/install.html). We note that the Windows binary can be built using Microsoft Visual Studio and does not require the installation of Unix-like environments such as Cygwin. By supporting the compilation of GAMer 2 that uses native and preferred tools, this improves binary compatibility with other libraries and simplifies distribution.
Collaborative workflow
To further improve code availability and to encourage community collaboration, the GAMer code is now hosted on Github (https://github.com/ctlee/gamer). In this environment, users can file issues to report bugs or ask questions. Users are also encouraged to contribute to the code by submitting pull requests. All pull requests are subject to rigorous continuous-integration testing, using both Travis-CI (Linux and Mac OS) and Appveyor (Windows), to ensure code compatibility across a wide range of operating systems, compilers, and compiler versions before integration with the main deployment branches. Along with source control, GAMer 2 also implements git-tagging-based semantic versioning to track the software version. The compiled code can report the source version, which aids in reporting and debugging. This strict versioning introduces improved ability for both users and developers to track code provenance.
Implementation of a new PyGAMer API
In addition to the complete redesign of the core library, the corresponding Python interface, now called PyGAMer, is generated using PyBind 11 (30) instead of SWIG (31). PyBind 11 was designed to expose C++ data types to Python and vice-versa while minimizing boilerplate code by capitalizing upon the capabilities of the C++ compiler. One of the benefits of this approach is the ability to bind complex template types, which are extensively used in CASC, enabling users to develop the Python script to interact with various elements of the mesh and call C++ methods. Another benefit of using PyBind 11 is its support for embedding Python docstrings, which enable straightforward documentation of PyGAMer using popular Python tools such as Sphinx. As a result, documentation for GAMer 2 and PyGAMer is now automatically generated and hosted online (https://gamer.readthedocs.io).
Using scikit-build, which connects setup tools and CMake, installation of PyGAMer in any Python environment can be achieved using pip. Versions of pip ≥ 10.0 will automatically download and resolve build-time and runtime dependencies, compile, and install the PyGAMer Python extension module. Users of older pip versions need to install any missing build-time dependencies beforehand. Instructions on how to install these dependencies are provided in both the online documentation and demonstrated in Video S1.
BlendGAMer development
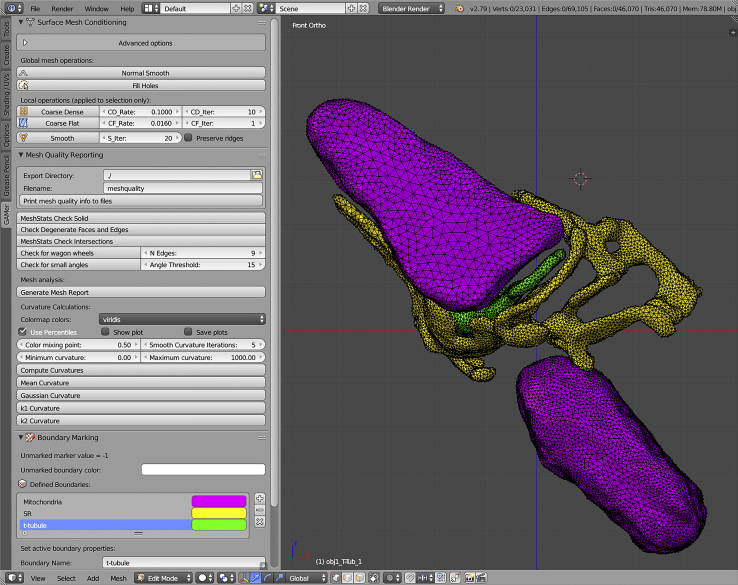
To support interactive modeling with graphical feedback, we have also developed a GAMer add-on for Blender (32) called BlendGAMer, which has also been rewritten to use PyGAMer. In addition to this update, the user interface has been redesigned to be user friendly as shown in Fig. 2. The boundary marking capability of BlendGAMer now uses Blender attribute layers instead of lists of values. Many features now have corresponding toggles in the interface, for example, the number of neighborhood rings to consider when computing the local structure tensor. Several mesh conditioning operations have also been updated to operate only upon selected vertices. This provides users with the flexibility to refine local portions of the mesh as desired. There is also a new Mesh Analysis panel that contains several helpful features for analyzing the quality of a mesh and includes curvature estimation. Based upon the newly implemented semantic versioning, BlendGAMer can now track the version of metadata that is stored in a given file. Using this information, BlendGAMer can perform automatic metadata migration from version to version as improved schemes for metadata storage are created.
Figure 2.
Screenshot of the BlendGAMer tool shelf menu in 3D modeling software Blender. The user can call GAMer mesh conditioning, analysis, boundary marking, and tetrahedralization functions by clicking buttons and adjusting settings in the tool shelf. Shown on the right is a conditioned surface mesh of the CRU model. To see this figure in color, go online.
Modeling diffusion in the CRU geometry
To demonstrate the use of the mesh generated from GAMer 2 with the FEM, we model the diffusion of a molecule with concentration u in the realistic geometry of a CRU (Fig. 3). In the volume, the dynamics of u are given by
| (1) |
| (2) |
where D is the diffusion coefficient, τ is a decay constant and represents reactions that consume u, Ω is the cytosolic domain, and t is time. We define the following boundary conditions:
| (3) |
| (4) |
| (5) |
where Jin is the inward flux on the t-tubule membrane (). No flux boundary conditions are applied to all other boundaries. The following system is solved using FEniCS (22,23) and visualized using ParaView (24). We note that the boundaries and are differentiated by markers applied using BlendGAMer.
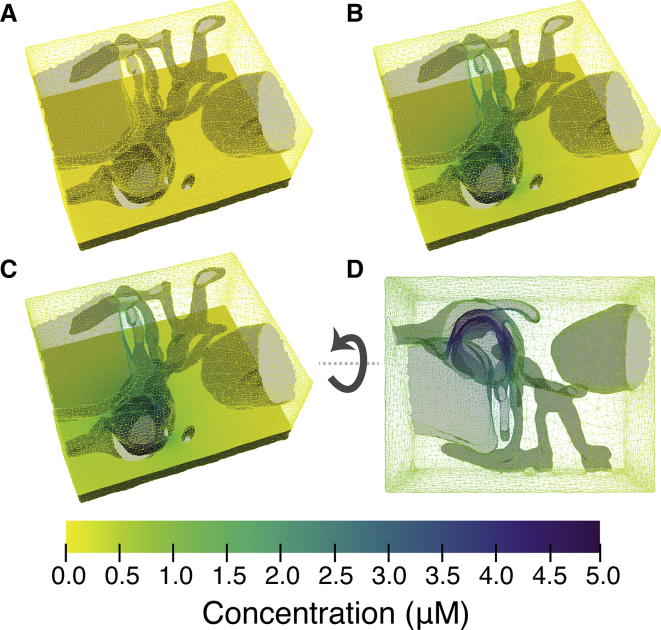
Figure 3.
Snapshots of molecular diffusion in the CRU geometry. In (A), the initial condition is shown; in (B), 200 μs is shown; in (C), 400 μs is shown; in (D), 5000 μs is shown. The molecules can be trapped in locally confined regions leading to microdomains with locally increased concentrations. To see this figure in color, go online.
Results and Discussion
We demonstrate that GAMer is capable of generating high-quality surface and volume simplex meshes of geometries as informed by structural biology data sets. The incorporated Python library (PyGAMer) and Blender add-on (BlendGAMer) enable users to prototype or interact with meshes as they are conditioned. Collectively, these tools facilitate mathematical modeling of biological systems using realistic geometries.
The GAMer workflow has been previously applied in several works (27,33, 34, 35, 36, 37, 38). Several example applications are also described in the online GAMer 2 documentation. As an example, the steps to go from ET data to simulation quality mesh are shown in Fig. 1. In this example, a segmented ET data set (Fig. 1 A) featuring a murine CRU is retrieved from the Cell Image Library as shown in Fig. 1 B. We note that this is the same starting geometry previously used by Hake et al. (36). From the model contours, we generated a preliminary mesh that was conditioned using BlendGAMer to produce Fig. 1 C. To model the cytosolic space surrounding the CRU, Blender Boolean mesh operations were used to invert the geometry followed by tetrahedralization (Fig. 1 D). The mesh is now sufficiently high-quality and suitable for use with FEM-based simulations as shown in Fig. 3.
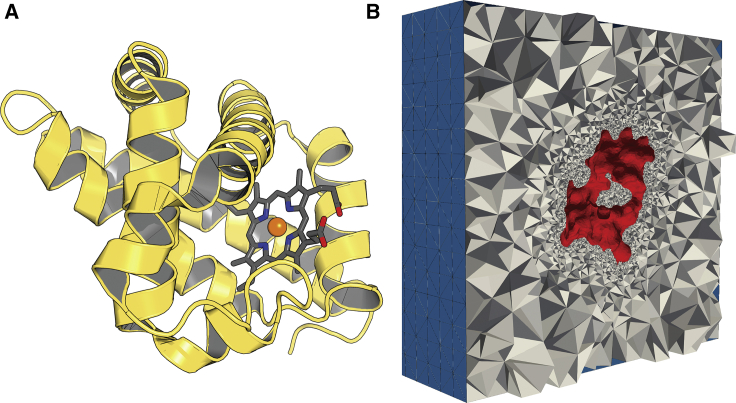
In Fig. 4, we demonstrate the mesh generation capabilities of GAMer from atomistic protein-structural data such as those available from the PDB. A volume data set representing the approximate occupied space of all atoms is generated by applying a Gaussian kernel over the atomic positions. An isosurface of the data set can then be meshed using the marching cubes algorithm (39). Although GAMer includes a basic table of atom types to assign radii, more sophisticated atomic radius assignment tools (e.g., PDB2PQR (40)) can be used and radius information passed via the PQR file format.
Figure 4.
Example demonstrating the meshing of protein myoglobin (PDB: 2JHO). In (A), the rendered cartoon representation with heme and iron shown as sticks is shown. In (B), the tetrahedralization of the space excluding the protein volume is shown. Red denotes faces marked as protein, and blue denotes faces on the boundary of the enclosing cube. To see this figure in color, go online.
Conclusions
The realism of biophysical models can be enhanced by incorporating realistic geometries from structural biology at various length scales. We have demonstrated the applicability of GAMer 2 at two different length scales and suggest that tools such as GAMer 2 brings the community closer to realizing the goal of conducting physics-based simulations in realistic cellular geometries by simplifying the mesh generation process. We believe that, moving forward, GAMer 2 can serve as an integrative platform for meshing biological mesh generation. Furthermore, our design strategies in implementing GAMer 2 encourage community collaboration, an important aspect of tool building for systems and computational biology.
Software availability
GAMer is licensed under GNU Lesser General Public License, version 2.1 or later. Full documentation and examples are available at the project home page, https://gamer.readthedocs.io/, and development is hosted on GitHub at http://github.com/ctlee/gamer. The latest release v2.0.5 is archived on Zenodo (https://doi.org/10.5281/zenodo.2340294).
Author Contributions
C.T.L., J.G.L., J.B.M., and M.J.H. developed the software. C.T.L. drafted the article. C.T.L., J.G.L., J.B.M., J.A.M., R.E.A., M.J.H., and P.R. edited the article. All authors read and approved the final article.
Acknowledgments
This work was supported by grants from the National Institutes of Health: P41-GM103426 and R01-GM31749; the National Science Foundation: DMS-CM1620366 and DMS-FRG1262982; and the Air Force Office of Scientific Research Multidisciplinary Research Program of the University Research Initiative FA9550-18-1-0051. C.T.L. also acknowledges support from the National Institutes of Health grant MBTG T32-GM008326 and a Hartwell Foundation Postdoctoral Fellowship. J.G.L. acknowledges support from a University of California, San Diego Center for Trans-scale Structural Biology and Biophysics/Visible Molecular Cell Consortium Fellowship. R.E.A. is a cofounder and scientific advisor of, and has equity interest in, Actavalon, Inc.
Editor: Ruth Baker.
Footnotes
Supporting Material can be found online at https://doi.org/10.1016/j.bpj.2019.11.3400.
Contributor Information
Christopher T. Lee, Email: ctlee@ucsd.edu.
Padmini Rangamani, Email: prangamani@ucsd.edu.
References
- 1.Rangamani P., Lipshtat A., Iyengar R. Decoding information in cell shape. Cell. 2013;154:1356–1369. doi: 10.1016/j.cell.2013.08.026. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Bell M., Bartol T., Rangamani P. Dendritic spine geometry and spine apparatus organization govern the spatiotemporal dynamics of calcium. J. Gen. Physiol. 2019;151:1017–1034. doi: 10.1085/jgp.201812261. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Cugno A., Bartol T.M., Rangamani P. Geometric principles of second messenger dynamics in dendritic spines. Sci. Rep. 2019;9:11676. doi: 10.1038/s41598-019-48028-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Ohadi D., Schmitt D.L., Rangamani P. Computational modeling reveals frequency modulation of calcium-cAMP/PKA pathway in dendritic spines. Biophys. J. 2019;117:1963–1980. doi: 10.1016/j.bpj.2019.10.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Updegrove A., Wilson N.M., Shadden S.C. SimVascular: an open source pipeline for cardiovascular simulation. Ann. Biomed. Eng. 2017;45:525–541. doi: 10.1007/s10439-016-1762-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Loew L.M., Schaff J.C. The virtual cell: a software environment for computational cell biology. Trends Biotechnol. 2001;19:401–406. doi: 10.1016/S0167-7799(01)01740-1. [DOI] [PubMed] [Google Scholar]
- 7.Murphy R.F. CellOrganizer: image-derived models of subcellular organization and protein distribution. Methods Cell Biol. 2012;110:179–193. doi: 10.1016/B978-0-12-388403-9.00007-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Xu C.S., Hayworth K.J., Hess H.F. Enhanced FIB-SEM systems for large-volume 3D imaging. eLife. 2017;6:e25916. doi: 10.7554/eLife.25916. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Si H. TetGen, a delaunay-based quality tetrahedral mesh generator. ACM Trans. Math. Softw. 2015;41:1–36. [Google Scholar]
- 10.Schöberl J. NETGEN an advancing front 2D/3D-mesh generator based on abstract rules. Comput. Vis. Sci. 1997;1:41–52. [Google Scholar]
- 11.Hu Y., Zhou Q., Panozzo D. Tetrahedral meshing in the wild. ACM Trans. Graph. 2018;37:1–14. [Google Scholar]
- 12.Cignoni P., Callieri M., Ranzuglia G. MeshLab: an open-source mesh processing tool. In: Scarano V., De Chiara R., Erra U., editors. Eurographics Italian Chapter Conference. The Eurographics Association; 2008. pp. 129–136. [Google Scholar]
- 13.Geuzaine C., Remacle J.-F. Gmsh: a 3-D finite element mesh generator with built-in pre- and post-processing facilities. Int. J. Numer. Methods Eng. 2009;79:1309–1331. [Google Scholar]
- 14.CGAL, Computational Geometry Algorithms Library. http://www.cgal.org.
- 15.Yu Z., Holst M.J., McCammon J.A. Feature-preserving adaptive mesh generation for molecular shape modeling and simulation. J. Mol. Graph. Model. 2008;26:1370–1380. doi: 10.1016/j.jmgm.2008.01.007. [DOI] [PubMed] [Google Scholar]
- 16.Yu Z., Hoist M.J., Andrew McCammon J. High-fidelity geometric modeling for biomedical applications. Finite Elem. Anal. Des. 2008;44:715–723. [Google Scholar]
- 17.Gao Z., Yu Z., Holst M. Quality tetrahedral mesh smoothing via boundary-optimized delaunay triangulation. Comput. Aided Geom. Des. 2012;29:707–721. doi: 10.1016/j.cagd.2012.07.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Gao Z., Yu Z., Holst M. Feature-preserving surface mesh smoothing via suboptimal Delaunay triangulation. Graph. Models. 2013;75:23–38. doi: 10.1016/j.gmod.2012.10.007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Chen L., Hoist M. Efficient mesh optimization schemes based on optimal delaunay triangulations. Comput. Methods Appl. Mech. Eng. 2011;200:967–984. Published online November, 16, 2010. [Google Scholar]
- 20.Lee, C.T., Moody, J.B., Laughlin, J.G., Holst, M. (2019, November 12). ctlee/gamer: Release v2.0.5 (Version v2.0.5). Zenodo. 10.5281/zenodo.3538541. [DOI]
- 21.Si H. TetGen, a delaunay-based quality tetrahedral mesh generator. ACM Trans. Math Software. 2015;41:1–36. [Google Scholar]
- 22.Logg A., Mardal K.-A., Wells G. Springer; Berlin, Germany: 2012. Automated Solution of Differential Equations by the Finite Element Method. [Google Scholar]
- 23.Alnass M.S., Blechta J., Wells G.N. The FEniCS Project Version 1.5. Archive of Numerical Software. 2015;3:100. [Google Scholar]
- 24.Ahrens J., Geveci B., Law C. Visualization Handbook. Elsevier; Amsterdam, the Netherlands: 2005. ParaView: an end-user tool for large-data visualization. [Google Scholar]
- 25.Stiles J.R., Bartol T.M. Monte Carlo methods for simulating realistic synaptic microphysiology using MCell. In: De Schutter E., editor. Computational Neuroscience: Realistic Modeling for Experimentalists. CRC Press; 2001. pp. 87–127. [Google Scholar]
- 26.Solernou A., Hanson B.S., Harris S.A. Fluctuating finite element analysis (FFEA): a continuum mechanics software tool for mesoscale simulation of biomolecules. PLoS Comput. Biol. 2018;14:e1005897. doi: 10.1371/journal.pcbi.1005897. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Lee C.T., Laughlin J.G., Rangamani P. GAMer 2: a system for 3D mesh processing of cellular electron micrographs. bioRxiv. 2019 doi: 10.1101/534479. [DOI] [Google Scholar]
- 28.Hoshijima M. CCDB:3603, MUS MUSCULUS, T-tubules, sarcoplasmic reticulum, myocyte. CIL. Dataset. 2004 [Google Scholar]
- 29.Lee C.T., Moody J.B., Holst M.J. The implementation of the colored abstract simplicial complex and its application to mesh generation. ACM Trans. Math Software. 2019;45:1–20. doi: 10.1145/3321515. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Jakob W., Rhinelander J., Moldovan D. pybindll - Seamless operability between C++11 and Python. 2017. https://github.com/pybind/pybind11
- 31.Beazley D.M. USENIX Association; 1996. SWIG: an easy to use tool for integrating scripting languages with C and C++”; p. 15. (Proceedings of the 4th Conference on USENIX Tcl/Tk Workshop, 1996 - Volume 4. TCLTK’96). [Google Scholar]
- 32.Blender Foundation. Stichting Blender Foundation; Amsterdam, the Netherlands: 2018. Blender - a 3D modelling and rendering package.http://www.blender.org [Google Scholar]
- 33.Yu Z., Holst M.J., Hoshijima M. Three-dimensional geometric modeling of membrane-bound organelles in ventricular myocytes: bridging the gap between microscopic imaging and mathematical simulation. J. Struct. Biol. 2008;164:304–313. doi: 10.1016/j.jsb.2008.09.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Cheng Y., Yu Z., Michailova A.P. Numerical analysis of Ca2+ signaling in rat ventricular myocytes with realistic transverse-axial tubular geometry and inhibited sarcoplasmic reticulum. PLoS Comput. Biol. 2010;6:el000972. doi: 10.1371/journal.pcbi.1000972. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Cheng Y., Kekenes-Huskey P., Michailova A. Multi-scale continuum modeling of biological processes: from molecular electro-diffusion to sub-cellular signaling transduction. Comput. Sci. Discov. 2012;5:015002. doi: 10.1088/1749-4699/5/1/015002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Hake J., Edwards A.G., McCulloch A.D. Modelling cardiac calcium sparks in a three-dimensional reconstruction of a calcium release unit. J. Physiol. 2012;590:4403–4422. doi: 10.1113/jphysiol.2012.227926. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Kekenes-Huskey P.M., Cheng Y., Michailova A.P. Modeling effects of L-type ca(2+) current and na(+)-ca(2+) exchanger on ca(2+) trigger flux in rabbit myocytes with realistic T-tubule geometries. Front. Physiol. 2012;3:351. doi: 10.3389/fphys.2012.00351. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Bromer C., Bartol T.M., Harris K.M. Long-term potentiation expands information content of hippocampal dentate gyrus synapses. Proc. Natl. Acad. Sci. USA. 2018;115:E2410–E2418. doi: 10.1073/pnas.1716189115. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Lorensen W.E., Cline H.E. Marching cubes: a high resolution 3D surface construction algorithm. ACM SIGGRAPH Comput. Graph. 1987;21:163–169. [Google Scholar]
- 40.Dolinsky T.J., Nielsen J.E., Baker N.A. PDB2PQR: an automated pipeline for the setup of Poisson-Boltzmann electrostatics calculations. Nucleic Acids Res. 2004;32:W665–W667. doi: 10.1093/nar/gkh381. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.