An Ensemble-based Model of PM_2.5 Concentration across the Contiguous United States with High Spatiotemporal Resolution

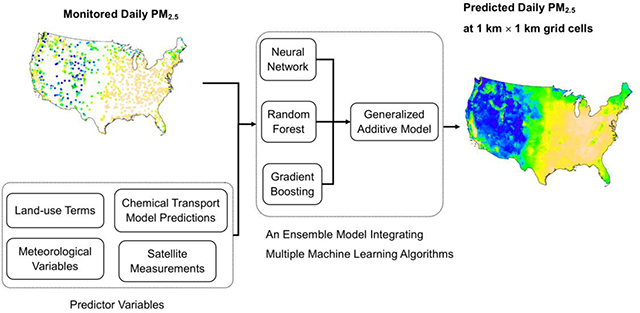
Abstract

Various approaches have been proposed to model PM_2.5 in the recent decade, with satellite-derived aerosol optical depth, land-use variables, chemical transport model predictions, and several meteorological variables as major predictor variables. Our study used an ensemble model that integrated multiple machine learning algorithms and predictor variables to estimate daily PM_2.5 at a resolution of 1 km×1 km across the contiguous United States. We used a generalized additive model that accounted for geographic difference to combine PM_2.5 estimates from neural network, random forest, and gradient boosting. The three machine learning algorithms were based on multiple predictor variables, including satellite data, meteorological variables, land-use variables, elevation, chemical transport model predictions, several reanalysis datasets, and others. The model training results from 2000 to 2015 indicated good model performance with a 10-fold cross-validated R² of 0.86 for daily PM_2.5 predictions. For annual PM_2.5 estimates, the cross-validated R² was 0.89. Our model demonstrated good performance up to 60 μg/m³. Using trained PM_2.5 model and predictor variables, we predicted daily PM_2.5 from 2000 to 2015 at every 1 km×1 km grid cell in the contiguous United States. We also used localized land-use variables within 1 km×1 km grids to downscale PM_2.5 predictions to 100 m × 100 m grid cells. To characterize uncertainty, we used meteorological variables, land-use variables, and elevation to model the monthly standard deviation of the difference between daily monitored and predicted PM_2.5 for every 1 km×1 km grid cell. This PM_2.5 prediction dataset, including the downscaled and uncertainty predictions, allows epidemiologists to accurately estimate the adverse health effect of PM_2.5. Compared with model performance of individual base learners, an ensemble model would achieve a better overall estimation. It is worth exploring other ensemble model formats to synthesize estimations from different models or from different groups to improve overall performance.

Graphical Abstract

1. Introduction

PM_2.5, or fine particulate matter, is a major public health concern (Seaton, MacNee et al. 1995, Cohen, Brauer et al. 2017), and is associated with multiple adverse health outcomes, including mortality (Di, Wang et al. 2017), morbidity (Lippmann, Ito et al. 2000), cardiovascular disease (Pope 2003), respiratory symptoms (Dominici, Peng et al. 2006), diabetes (Yang, Guo et al. 2018), and others. Both long-term and short-term PM_2.5 exposures are associated with adverse health effects (Kloog, Ridgway et al. 2013, Shi, Zanobetti et al. 2016). Recent studies suggest that PM_2.5 may penetrate blood brain barrier and enter the brain, causing various neurodegenerative diseases (Maher, Ahmed et al. 2016, de Prado Bert, Mercader et al. 2018).

Accurate estimation of PM_2.5 is a prerequisite of related epidemiological analyses. As PM_2.5 concentrations decline in the United States, there is a growing need for accurate estimation of PM_2.5 at lower levels. A variety of methods have been used to model PM_2.5, evolving from typical linear regressions to machine learning approaches. In the following, we briefly summarized major methods used for PM_2.5 modeling to pave the way for our own method.

Linear Regression and Correlational Study:

Ever since Wang et al. (2003) proposed that satellite-derived aerosol optical depth (AOD) could be used to model air quality (Wang and Christopher 2003), AOD has remained an important predictor for PM_2.5 modeling. Early studies used simple regression models and correlational studies to model PM_2.5 with AOD (Engel-Cox, Holloman et al. 2004, Koelemeijer, Homan et al. 2006). This approach soon lost popularity and almost disappeared from recent literature, since the relationship between PM_2.5 and AOD is not straightforward. Explanatory power from a simple linear model was too low to be useful.

Mixed-Effect Model:

Kloog et al. blended AOD with local land-use data and used a mixed-effect model to account for the temporally changing slope between PM_2.5 and AOD due to meteorological conditions (Kloog, Koutrakis et al. 2011). Use of a mixed-effect model partially resolves the complex relationship between AOD and PM_2.5. Mixed-effect models received wide application ever since, for its simplicity and flexibility. Chudnovsky et al. used similar methodology on AOD to predict PM_2.5 concentration within the Northeastern United States (Chudnovsky, Lee et al. 2012). Similar mixed-effect models have been re-applied with slightly different predictor variables, to different study areas, including Mid-Atlantic States in the United States (Kloog, Nordio et al. 2014), Southeastern United States (Lee, Kloog et al. 2015), Mexico City (Just, Wright et al. 2015), Israel (Kloog, Sorek-Hamer et al. 2015), Beijing, China (Xie, Wang et al. 2015), Beijing and neighboring areas of China (Zheng, Zhang et al. 2016), entire China (Ma, Hu et al. 2014), and London, United Kingdom (Beloconi, Kamarianakis et al. 2016),

Geographically Weighted Regression:

Mixed-effect models grant flexibility in the temporal dimension, and their counterparts, geographically weighted regression (GWR) models grant flexibility in the spatial dimension. Hu (2009) found a spatially inconsistent relationship between AOD and PM_2.5 across the contiguous United States, and used geographically weighted regression to account for the spatially heterogeneous relationship (Hu 2009), and later updated the model for the Southeastern United States (Hu, Waller et al. 2013). van Donkelaar et al. (2015) used AOD and simulation data to obtain high-resolution PM_2.5 estimation across the North America using geographically weighted regression (van Donkelaar, Martin et al. 2015). Similar methods have been repeated in Pearl River Delta Region (Song, Jia et al. 2014), Beijing and its neighboring areas (Zou, Pu et al. 2016), Central China (Bai, Wu et al. 2016), and entire China (You, Zang et al. 2016).

Generalized Additive Model:

Both mixed-effect models and geographically weighted regression assume a linear relationship between predictor variables and the dependent variable, although the coefficients may vary. Generalized additive models use smoothing functions to account for nonlinear relationships. Paciorek et al. (2008) used generalized additive model and found nonlinear relationships between relative humidity, planetary boundary layer height, PM_2.5 monitoring data and AOD (Paciorek, Liu et al. 2008). Using a similar method, Liu et al. (2009) applied smoothing functions on AOD and several meteorological variables, and predicted PM_2.5 for the Northeastern United States (Liu, Paciorek et al. 2009). Similar models have been applied to PM_2.5 modeling in California (Strawa, Chatfield et al. 2013), and Northern China (Liu, He et al. 2012).

Machine Learning Algorithms:

Neural networks are able to model any kind of nonlinear and interactive relationship given enough data, suitable for modeling PM_2.5, where the underlying atmospheric dynamics are elusive, and variables have complex interactions (Bishop 1995, Haykin and Network 2004). Gupta et al. (2009) used a neural network and included AOD, relative humidity, planetary boundary layer height, temperature, location, and month. The neural network was trained with monitored 1-hour averaged and 24-hour averaged PM_2.5 (Gupta and Christopher 2009). Our previous PM_2.5 model in the contiguous United States was also based on neural networks, but with a larger number of predictor variables. (Di, Kloog et al. 2016). Besides neural networks, other machine learning algorithms have been used in PM_2.5 modeling for different study areas around the world, such as random forest for a Europe-wide model (Chen, de Hoogh et al. 2018), a US-wide model (Hu, Belle et al. 2017), a regional model for China (Wu, Guo et al. 2011), and Northern China (Huang, Xiao et al. 2018), and some localized models (Brokamp, Jandarov et al. 2017), boosted regression tree (Suleiman, Tight et al. 2016); support vector machine at city level (Sotomayor-Olmedo, Aceves-Fernández et al. 2013, Weizhen, Zhengqiang et al. 2014) and at national level (de Hoogh, Héritier et al. 2018); and gradient boosting (Zhan, Luo et al. 2017).

In summary, we found the following patterns from existing studies, which motivate us to propose our own ensemble-based PM_2.5 model. First, most models used a few predictor variables, but additional variables did contribute to better modeling. Adding extra variables, even when they are intuitively less relevant to PM_2.5 modeling, improves model performance. For example, NO₂ column measurement (Zheng, Zhang et al. 2016) and other OMI (Ozone Monitoring Instrument) measurements (Strawa, Chatfield et al. 2013) were found to improve models. Penalty terms can avoid overfitting by the use of too many covariates. Second, the model performance of different algorithms seems to vary by location and concentration. For example, Chen et al. (2018) found that all machine learning algorithms performed similarly, and no method demonstrated superior external validity (Chen, de Hoogh et al. 2018). A neural network only performed slightly better than a boosting regression tree in London (Suleiman, Tight et al. 2016). Further, geographic weighted regressions indicated spatial variability in predictive performance. Thus, it is theoretically infeasible to have a single model optimally fit all regions. Consequently, there is a recent tendency to use hybrid models instead of a single model, expecting that multiple methods would “complement” each other. A hybrid model usually combines variables or fitting algorithms. Some examples include a hybrid model combining mixed-effect model with land-use regression (Kloog, Chudnovsky et al. 2014), autoregressive-moving-average model with support vector machine (Wang, Zhang et al. 2017), geographically weighted regression with gradient boosting (Zhan, Luo et al. 2017).

Therefore, in this study, we fit a nationwide PM_2.5 model using a large number of data set as predictor variables and multiple learning methods. We incorporated three machine learning algorithms: neural network, random forest, and gradient boosting. We modeled PM_2.5 separately with each algorithm and used a geographically weighted generalized additive model as an ensemble model to obtain an overall PM_2.5 prediction. Predictor variables included satellite-derived AOD, other satellite-based measurements, chemical transport model predictions, land-use variables, meteorological variables, and many others. The ensemble model was validated with 10-fold cross-validation. After model validation, we made predictions of daily PM_2.5 at 1 km × 1 km grid cells in the contiguous United States from 2000 to 2015. We also predicted the monthly standard deviation of the difference between monitored and predicted PM_2.5 to quantify the uncertainty of PM_2.5 modeling in the same 1 km × 1 km grid cells. Finally, we downscaled PM_2.5 predictions from 1 km × 1 km grid cells to 100 m × 100 m grid cells, using selected downscaling predictor variables. The high resolution PM_2.5 estimates allow epidemiologists to assess the health effects of PM_2.5 with higher accuracy, and the PM_2.5 estimates further help correct residual exposure measurement errors. The ensemble model framework is also useful to combining air pollution models from different sources for future studies.

2. Data

2.1. Study Area

The study area was constrained to the contiguous United States due to data availability, from January 1^st, 2000 to December 31^st, 2015, in total 5,844 days.

2.2. PM_2.5 Monitoring Data

Monitoring data for PM_2.5 were obtained from the Air Quality System (AQS) operated by the Environmental Protection Agency (EPA), The Interagency Monitoring of Protected Visual Environments (IMPROVE), Clean Air Status and Trends Network (CASTNET), and other regional or local monitoring data sets, with 2,156 monitoring sites in our study area from 2000 to 2015. Not all monitoring sites were operating throughout the study period, and many of them operated every 3 or 6 days. We obtained or calculated 24-hour averaged PM_2.5 and converted the unit into microgram per cubic meter (μg/m³) if needed. Monitoring sites were not equally distributed across the study area, with more sites in the Eastern United States, Western coast, and urban areas. Besides, the monitoring network does not adequately sample the full range of concentration scales, due to the limited number of monitoring sites and various monitoring siting criteria. For example, mountainous regions and rural areas had fewer sites.

The PM_2.5 distribution exhibits some degree of spatial autocorrelation. Monitoring data from nearby monitoring sites are more correlated than data from faraway sites. To leverage spatial autocorrelation and improve model performance, we incorporated spatially lagged monitored PM_2.5 into the model as predictor variables. Spatially lagged variables were weighted averages of monitored PM_2.5 from nearby monitoring sites, and weights were inversely proportional to distance and distance squared. We also incorporated one-day lagged and three-day lagged values of spatially lagged terms.

2.3. AOD Measurements and Related Satellite Data

The Moderate Resolution Imaging Spectroradiometer (MODIS) instrument aboard the Earth Observing System (EOS) satellite has been widely used to measure AOD (Salomonson, Barnes et al. 1989, King, Kaufman et al. 1992). The Multi-Angle Implementation of Atmospheric Correction (MAIAC) algorithm has been developed to retrieve AOD measurements from raw MODIS data at 1 km × 1 km resolution, especially for conditions of dark vegetated surfaces or bright backgrounds, where conventional AOD retrieval algorithms may have issues (Sayer, Hsu et al. 2013). The absorption optical depth of aerosol species varies with wavelength (Bergstrom, Pilewskie et al. 2007); thus, AOD measurements at different wavelengths are informative to account for different chemical compositions of PM_2.5 and potentially helpful to achieve accurate modeling. We therefore included AOD measurements at 470 nm and 550 nm from both the Aqua and Terra satellites. AOD measurements retrieved from the deep-blue algorithm (with 10 km resolution) were also included to provide complementary information. Similar to previous studies, AOD measurements (1) with high uncertainty, (2) over water bodies, (3) over snow coverage, and (4) above 1.5 were excluded from modeling, based on the quality assurance flags (Kloog, Koutrakis et al. 2011, Kloog, Chudnovsky et al. 2014).

Previous studies have documented the association between errors in AOD retrievals and surface characteristics (i.e., surface brightness) (Drury, Jacob et al. 2008). MAIAC algorithm, although designed to retrieve AOD from complex background conditions, is not immune to distortion from surface brightness (Lyapustin, Wang et al. 2011). Thus, we incorporated surface reflectance (MOD09A1) from MODIS measurements to control for the impact of surface brightness on AOD data quality (Vermote 2015).

PM_2.5 composition affects AOD measurements. For example, absorbing aerosols include aerosols from biomass burning, desert dust, and volcanic ash (Herman, Bhartia et al. 1997). The presence of absorbing aerosol components may lead to different AOD values compared with values for the same mass concentration of predominantly scattering components. Similarly, PM_2.5 with larger portion of black carbon leads to higher AOD values in MODIS retrievals. To address this behavior, we used the absorbing aerosol index (AAI), which measures the portion of absorbing aerosol. We used two AAI measurements at UV and visible ranges (OMAERUVd, OMAEROe) from OMI (Herman, Bhartia et al. 1997, Torres, Bhartia et al. 1998). We also incorporated other measurements from OMI, such as column NO₂ and SO₂ measurements.

In addition to satellite-derived AOD, some reanalysis datasets provide aerosol estimation, such as MERRA2 (Modern-Era Retrospective analysis for Research and Applications, Version 2). Aerosol products from MERRA2 are not measured but simulated, and prone to simulation errors, but they have almost no missing values and serve as good complement to satellite-derived AOD. We used MERRA2 variables related to aerosol concentrations, including sulfate aerosol, hydrophilic black carbon, hydrophobic black carbon, hydrophilic organic carbon, and hydrophobic organic carbon (Buchard, Randles et al. 2017).

2.4. Meteorological Conditions

Meteorological conditions were retrieved from the North American Regional Reanalysis (NOAA) data set, with more details about this data set found elsewhere (Kalnay, Kanamitsu et al. 1996). The full list of 16 meteorological variables can be found in the supplementary material (Section 1).

2.5. Chemical Transport Model

A chemical transport model (CTM) is a numerical simulation model that incorporates emission inventories and simulates the chemical formation, loss, transportation, and deposition of trace gases and particles for a 3-D Eulerian gridded domain. CTMs simulate the concentration of air pollutants at the surface level, and their vertical distribution using process-based mechanistic parameterizations. Predicted vertical profiles allow us to estimate the ground-level contribution to column aerosol concentrations. Since AOD is a column measurement of aerosols, and not the surface-level aerosol concentration, CTM predictions of PM_2.5 vertical profiles can help calibrate AOD to ground-based monitors (Liu, Park et al. 2004).

CTMs are also able to capture secondary aerosol formation due to complex gas, particle, and multiphase reactions. For example, isoprene is an important precursor of PM_2.5, but relevant reactions were not well modeled in most CTMs. Recently, GEOS-Chem, a global CTM (http://www.geos-chem.org) (Bey, Jacob et al. 2001), developed a new aqueous-phase mechanism to simulate secondary PM_2.5 coupled to a detailed gas-phase isoprene oxidation scheme (Marais, Jacob et al. 2016). We obtained daily predictions of total PM_2.5 mass and mass concentration of several PM_2.5 components from this new version of GEOS-Chem at 0.5° × 0.625° resolution, as well as from the Community Multiscale Air Quality (CMAQ, www.epa.gov/cmaq) model, a regional CTM that is commonly run with 12-km horizontal resolution over the U.S. (Appel, Napelenok et al. 2017, Kelly, Jang et al. 2018).

2.6. Land-use Variables

Land-use variables are proxies for local emissions and air pollution levels. Chemical transport models are generally unable to simulate air pollution at fine spatial scales, due to the high computational cost and the lack of availability of fine scale emission inventories. Land-use variables approximate emission of air pollutants, often at kilometer or sub-kilometer scale. Previous models often incorporated land-use variables directly, as an approximation of those localized air pollution dynamics. Land-use variables have been used for long-term (e.g., annual or seasonal) exposure assessment in local to continental (Eeftens, Beelen et al. 2012), and global scales (Larkin, Geddes et al. 2017). Recent developments included short-term predictions (e.g. hourly or daily) as well (Son, Osornio-Vargas et al. 2018).

We prepared (1) land-use coverage types, (2) road density, (3) restaurant density, (4) elevation, and (5) NDVI (Normalized difference vegetation index) at 1 km × 1 km grid cells, and also aggregated them to 10 km × 10 km grid cells, to capture the impact of emissions from neighboring areas. Details of data preparation can be found in the supplementary material (Section 2). We used both 1-km and 10-km land-use gridded variables in the model as separate predictor variables. We also aggregated land-use coverage type and elevation from its original resolution to 100 m × 100 m resolution to use as downscaling variables in the localized model.

3. Methods

3.1. Overview

We trained a neural network, random forest, and gradient boosting on all input variables, with parameters of each machine learning algorithm selected by cross-validated grid search processes. We obtained predicted PM_2.5 from each learner; and then used a geographically weighted generalized additive model as an ensemble model to combine PM_2.5 estimation. Furthermore, PM_2.5 concentration exhibits some degree of spatial and temporal autocorrelation, which can be used to improve model performance. We calculated spatially and temporally lagged PM_2.5 predictions from nearby monitoring sites and neighboring days, treated them as additional input variables, and fit the above models again alongside with existing predictor variables (Figure 1).

Figure 1.

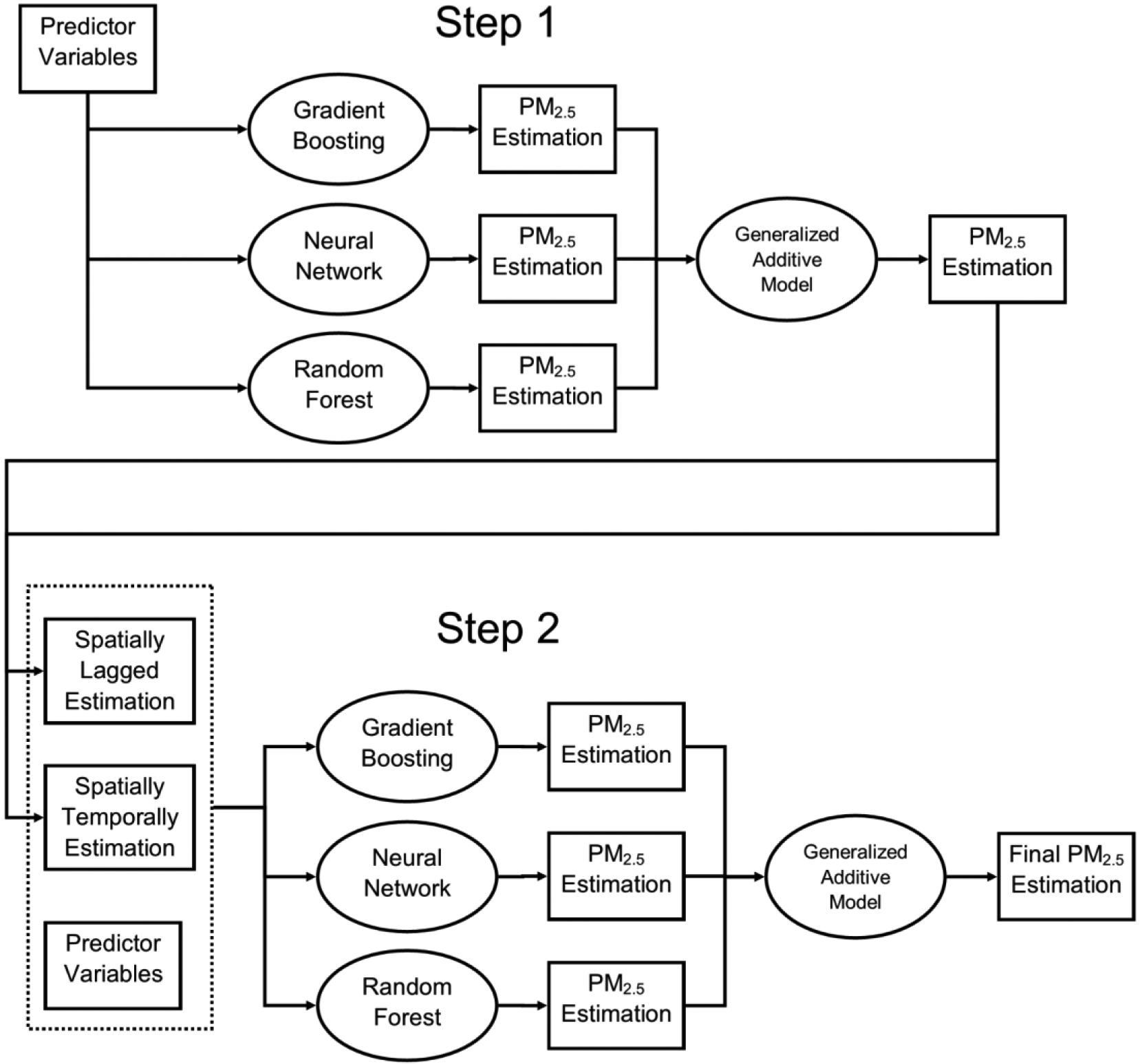
Flowchart of Model Training Process

To avoid overfitting, we validated our model with 10-fold cross-validation. After splitting all monitoring sites into 10 splits, we trained with 90% of the data and predicted PM_2.5 at the remaining 10% of monitoring sites. The same process also held for other splits. After assembling PM_2.5 predictions from all ten splits, we calculated R², spatial R², and temporal R² between predicted and monitored PM_2.5 at each monitoring site. We also reported R² by year.

3.2. Base Learners and Ensemble Model

The details of neural network, random forest and gradient boosting algorithms can be found elsewhere (Bishop 2006). A simple explanation is that all three machine learning algorithms attempt to model the complex relationship between input variables (X’s, predictor variables of PM_2.5 model) and the dependent variable (Y, or monitored PM_2.5 for this study) with different approaches. In previous studies, the three algorithms had different model performance under different conditions, probably because of different study areas. By combining the three complementary algorithms, we expect to obtain a better estimate of PM_2.5.

The performance of each learner depends on hyper parameters, such as how many trees in a random forest, depth of tree; number of layers in a neural network, number of neurons in each layer, lasso penalty, etc. We chose values of hyper parameters for each base learner in a grid search process (Table S1).

A common approach for ensemble averaging is to regress the monitor measurements against the estimates from base learners, with the regression coefficients representing the weight given to each learner. This approach assumes those weights are constant across the country, and do not depend on the pollution concentration. We relaxed these assumptions by regressing the monitored values against thin plate splines of latitude, longitude, and the predicted concentration for each learner. This allows, for example, one learner to have more weight at higher concentrations, but not at lower concentrations; or to have more weight in particular regions of the country.

3.3. Missing Values

Missing values occur among predictor variables. Sometimes missing values can be quite common. Missing values arose from different sources: (1) some predictor variables were unavailable for early years, such as OMI measurements and AOD measurements from the Aqua satellite, because the satellites were launched in 2005 and 2002, respectively. (2) Measurements were not possible over some locations and time, such as AOD over clouds or snow, or soil moisture near a waterbody. (3) Data processing removed some measurements due to high uncertainty, such as AOD measurements greater than 1.5, which were excluded. To predict PM_2.5 concentration for the entire study area and during the entire study period, some method is required to fill in the missing values.

A good method should predict what the values would have been had they not been missing, so we used variables without missing values to predict each variable with missing values. We identified all variables with no missing values and used them as predictor variables of a random forest. For example, AOD measurement at 550 nm (AOD 550) has more than 50% missing values. We used CMAQ and GEOS-Chem predictions, land-use types, and meteorological variables as predictors of a random forest, since these variables have no missing values, and trained the random forest when AOD 550 were available. Then we predicted AOD 550 when AOD 550 were missing to fill in the missing values. Again, a grid search was used to obtain the best parameter combinations.

Some land-use measurements were intermittent and unavailable over a certain period. For example, NDVI and surface reflectance measurements are available every 16 and 8 days; all land-use terms from the NLCD were available every 5 years. Since land-surface characteristics can be assumed to change gradually, we use simple linear interpolation to fill in missing values.

3.4. Model Prediction

After filling in missing values and interpolating, all input variables were available across the study area. We trained the three base learners and the ensemble model with input variables and monitored PM_2.5 as the dependent variable, and then used trained models and predictor variables at each 1 km × 1 km grid cell to predict PM_2.5.

We also downscaled the 1-km-level predictions to 100 m × 100 m grid cells. We took the difference between monitored and predicted PM_2.5 at monitoring sites, and used downscaling predictors within 100 m of the monitor as predictors in a random forest to predict the difference. The downscaling predictors include NLCD land-use cover types, road density, and elevation at 100-m level, as well as meteorological variables: air temperature, humidity, wind speed, and planetary boundary layer height. We trained the random forest at each monitoring site and predicted the within-cell variations at every 100 m × 100 m grid cell.

Finally, we estimated the spatial and temporal pattern of model uncertainty. Model performance is determined by various factors and varies by location and time. By referring to previous studies and using prior knowledge, we identified several variables that edict model performance and used them to model monthly standard deviation of the difference between daily monitored and predicted PM_2.5 at each monitoring site:

$$s{d}_{P{M}_{ij}}=f_1\left(\mathit{\text{Locatio}}{n}_i\right)+f_2\left(\mathit{\text{Locatio}}{n}_i,{\widehat{PM}}_{ij}\right)+f_3\left(\mathit{\text{elevation}}\right)+f_4\left(\mathit{\text{surface}} \mathit{\text{reflectance}}\right)+f_5\left(\mathit{\text{humidity}}\right)+f_6\left(\mathit{\text{tree}} \mathit{\text{canopy}}\right)+f_8\left(\mathit{\text{NDVI}}\right)+f_9\left(\mathit{\text{urban}}\right)+\mathit{\text{Year}}+e_{ij}$$

where $s{d}_{P{M}_{ij}}$ is the monthly standard deviation of the difference between daily monitored and predicted PM_2.5 at location i and in the month j; f₁ denotes a penalized spline for location i; f₂ denotes a thin-plate spline for an interaction between location i and predicted PM_2.5 at location i and in the month j; f₃ ~ f₉ denote splines for predictors at location i; ${\widehat{PM}}_{ij}$ is the mean predicted PM_2.5 at a location i in the month j; and e_ij is the error term.

4. Results

Table 1 presents the cross-validated R² by year. R² values ranged from 0.75 to 0.90, with an average of 0.86, indicating good model performance. The spatial R² ranged from 0.73 to 0.91, with an average of 0.89, demonstrating that our model can well capture the spatial variation of long-term PM_2.5. The average RMSE (root mean square error) was 1.26 μg/m³ spatially, and 2.53 μg/m³ temporally. There is a noticeable improvement compared with our previous model (Di, Kloog et al. 2016). Of the three machine learning algorithms, model performance of neural network and random forest was quite close, and better than gradient boosting. Overall, neural network outperformed random forest (R²: 0.855 vs. 0.854, Table 1); but random forest outperformed for some years (Table 1), some regions (Table 2), all seasons except summer (Table 3), and spatially (Table S2). The overall model performance from the ensemble model outperformed that from any single algorithm.

Table 1.

Cross-Validated R² for the Entire Study Area

	Ensemble Model						Neural Network	Random Forest	Gradient Boosting
Year	R2	RMSE	Bias	Slope	Spatial R2	Temporal R2	R2	R2	R2
2000	0.868	3.189	0.805	0.953	0.904	0.855	0.865[a]	0.863	0.836
2001	0.854	3.385	0.626	0.964	0.897	0.835	0.849[a]	0.849	0.822
2002	0.892	2.808	0.590	0.960	0.894	0.888	0.884	0.891[a]	0.860
2003	0.885	2.706	0.547	0.965	0.883	0.877	0.877	0.881[a]	0.853
2004	0.883	2.660	0.629	0.955	0.885	0.873	0.879	0.882[a]	0.854
2005	0.902	2.670	0.494	0.971	0.905	0.894	0.901	0.901[a]	0.880
2006	0.884	2.496	0.506	0.969	0.890	0.877	0.881[a]	0.876	0.855
2007	0.884	2.696	0.483	0.976	0.905	0.877	0.879	0.880[a]	0.859
2008	0.876	2.417	0.440	0.972	0.890	0.867	0.872[a]	0.865	0.834
2009	0.861	2.404	0.341	0.981	0.883	0.851	0.855[a]	0.847	0.817
2010	0.849	2.538	0.538	0.965	0.872	0.844	0.842[a]	0.835	0.809
2011	0.832	2.670	0.742	0.940	0.871	0.832	0.829[a]	0.822	0.792
2012	0.818	2.656	0.921	0.914	0.884	0.809	0.814[a]	0.805	0.744
2013	0.781	3.020	0.929	0.908	0.734	0.789	0.777[a]	0.775	0.718
2014	0.751	2.940	0.792	0.936	0.772	0.752	0.746[a]	0.734	0.701
2015	0.783	2.851	0.804	0.922	0.824	0.786	0.767	0.774[a]	0.711
Overall	0.860	2.786	0.625	0.956	0.894	0.847	0.855[a]	0.854	0.818

^[a]the learner outperformed other learners in that year.

Note: All presented R² values were based on 10-fold cross-validation from the ensemble model. We used the trained ensemble model to make prediction at 1-km level. The calculation of daily R², spatial R², and temporal R² have been described elsewhere (Kloog, Koutrakis et al. 2011). We regressed predicted PM_2.5 against monitored PM_2.5 in a linear regression model, and obtained the slope and intercept (bias in the Table).

Table 2.

Cross-Validated R² for Different Regions

	Ensemble Model						Neural Network	Random Forest	Gradient Boosting
Region	R2	RMSE	Bias	Slope	Spatial R2	Temporal R2	R2	R2	R2
East North Central	0.924	2.106	0.344	0.981	0.915	0.925	0.917	0.921[a]	0.899
East South Central	0.894	2.214	0.533	0.964	0.897	0.891	0.888	0.891[a]	0.872
Middle Atlantic	0.893	2.512	0.420	0.978	0.870	0.900	0.887[a]	0.883	0.863
Mountain	0.769	3.337	0.891	0.911	0.769	0.764	0.765	0.769[a]	0.694
New England	0.889	2.122	0.356	0.979	0.878	0.894	0.883[a]	0.875	0.852
Pacific	0.802	4.045	0.929	0.936	0.850	0.776	0.797[a]	0.797	0.750
South Atlantic	0.895	2.117	0.441	0.974	0.907	0.890	0.888	0.893[a]	0.872
West North Central	0.862	2.326	0.408	0.966	0.875	0.854	0.856[a]	0.851	0.824
West South Central	0.850	2.246	0.717	0.942	0.788	0.857	0.841[a]	0.841	0.824

^[a]the learner outperformed other learners in that location.

Note: Region division was based on U.S. Census Bureau. New England: Connecticut, Maine, Massachusetts, New Hampshire, Rhode Island, Vermont; Middle Atlantic: New Jersey, New York, Pennsylvania; East North Central: Indiana, Illinois, Michigan, Ohio, Wisconsin; West North Central: Iowa, Nebraska, Kansas, North Dakota, Minnesota, South Dakota, Missouri; South Atlantic: Delaware, District of Columbia, Florida, Georgia, Maryland, North Carolina, South Carolina, Virginia, West Virginia; East South Central: Alabama, Kentucky, Mississippi, Tennessee; West South Central: Arkansas, Louisiana, Oklahoma, Texas; Mountain: Arizona, Colorado, Idaho, New Mexico, Montana, Utah, Nevada, Wyoming; Pacific: Alaska, California, Hawaii, Oregon, Washington. Although the Pacific Region includes Alaska and Hawaii, both states were not included in our modeling.

Table 3.

Cross-Validated R² for Four Seasons

	Ensemble Model						Neural Network	Random Forest	Gradient Boosting
Season	R2	RMSE	Bias	Slope	Spatial R2	Temporal R2	R2	R2	R2
Spring	0.853	2.801	0.604	0.955	0.890	0.837	0.848	0.848[a]	0.812
Summer	0.858	2.271	0.421	0.972	0.895	0.841	0.852[a]	0.847	0.826
Autumn	0.901	2.445	0.544	0.962	0.939	0.881	0.896	0.896[a]	0.859
Winter	0.825	3.484	0.888	0.940	0.829	0.813	0.819	0.820[a]	0.777

^[a]the learner outperformed other learners in that season.

Figure 2 displays the cross-validated R² at each monitoring site, with high R² in most areas of the Eastern United States and parts of the West Coast. For mountainous regions, especially the Appalachian and Rocky Mountains, we obtained lower R², indicating that mountainous terrain has an important influence on model performance (Table 2). The spatial pattern of model performance for this study was similar to our previous model and other previous studies (Engel-Cox, Holloman et al. 2004). The predicted uncertainty demonstrated a similar spatial pattern. If examined by season, model performed well in the autumn and less unsatisfyingly in winter.

Figure 2. Cross-Validated R² at Monitoring Sites and Predicted Monthly Standard Deviation.

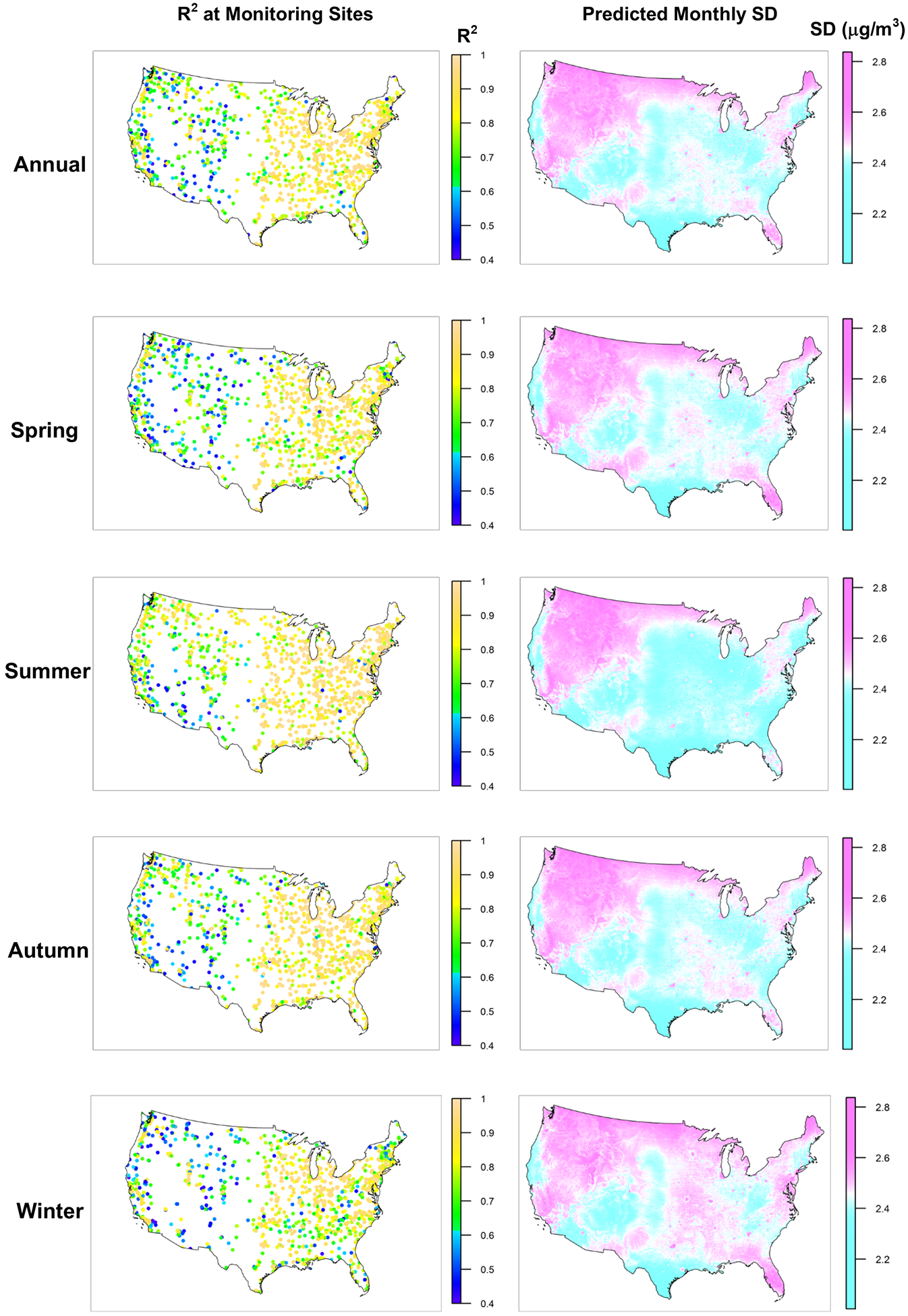
The left figures present cross-validated R² at each monitoring site; the right figures present predicted monthly standard deviation at 1 km × 1 km grid cells, averaged over the entire years and four seasons. All maps were plotted at the same color scale.

While the incremental R² from ensemble averaging compared to the best single learner was not large overall, it affected the linearity of the association between measured and predicted PM_2.5. For the ensemble, a spline fit between daily predicted and monitored PM_2.5 is almost a straight 1:1 line up to 60 μg/m³, a concentration seldom seen in the United States, demonstrating satisfying performance even at high concentration, when monitoring data were scarce (Figure 3). The performance of the individual base learners was worse than the ensemble average. The random forest overestimated at high concentrations. Overestimation was even more serious for the gradient boosting. Overall, the ensemble model improved model performance although quite close to the neural network. This pattern exemplifies the usefulness of ensemble averaging, and the use of splines on individual learners to do the averaging. The spline comparing monitored to predicted annual PM_2.5 was almost a straight 1:1 line, indicating good fit at the annual level (Figure 4).

Figure 3. Relationship between Monitored and Predicted PM_2.5 from the Ensemble Model and Three Machine Learning Algorithms.

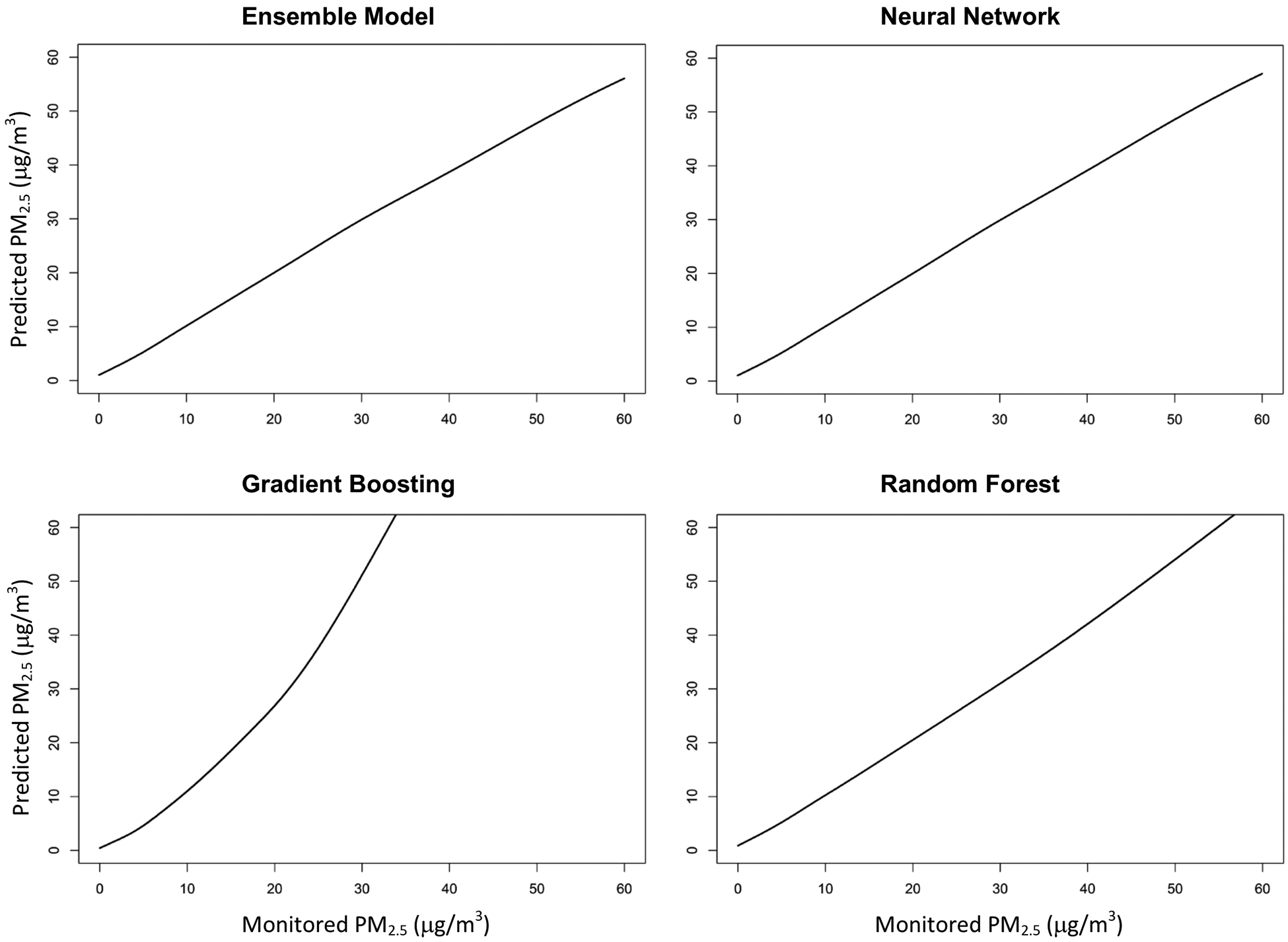
We regressed daily predicted PM_2.5 from the ensemble model, neural network, gradient boosting, and random forest against monitored PM_2.5 in a generalized additive model, with spline on the monitored PM_2.5. Dashed lines represent 95% confidence interval. All plots were truncated to 60 μg/m³, since 99.99% of daily PM_2.5 monitoring values from 2000 to 2015 were below 60 μg/m³.

Figure 4. Relationship between Monitored and Predicted PM_2.5 at Annual Level.

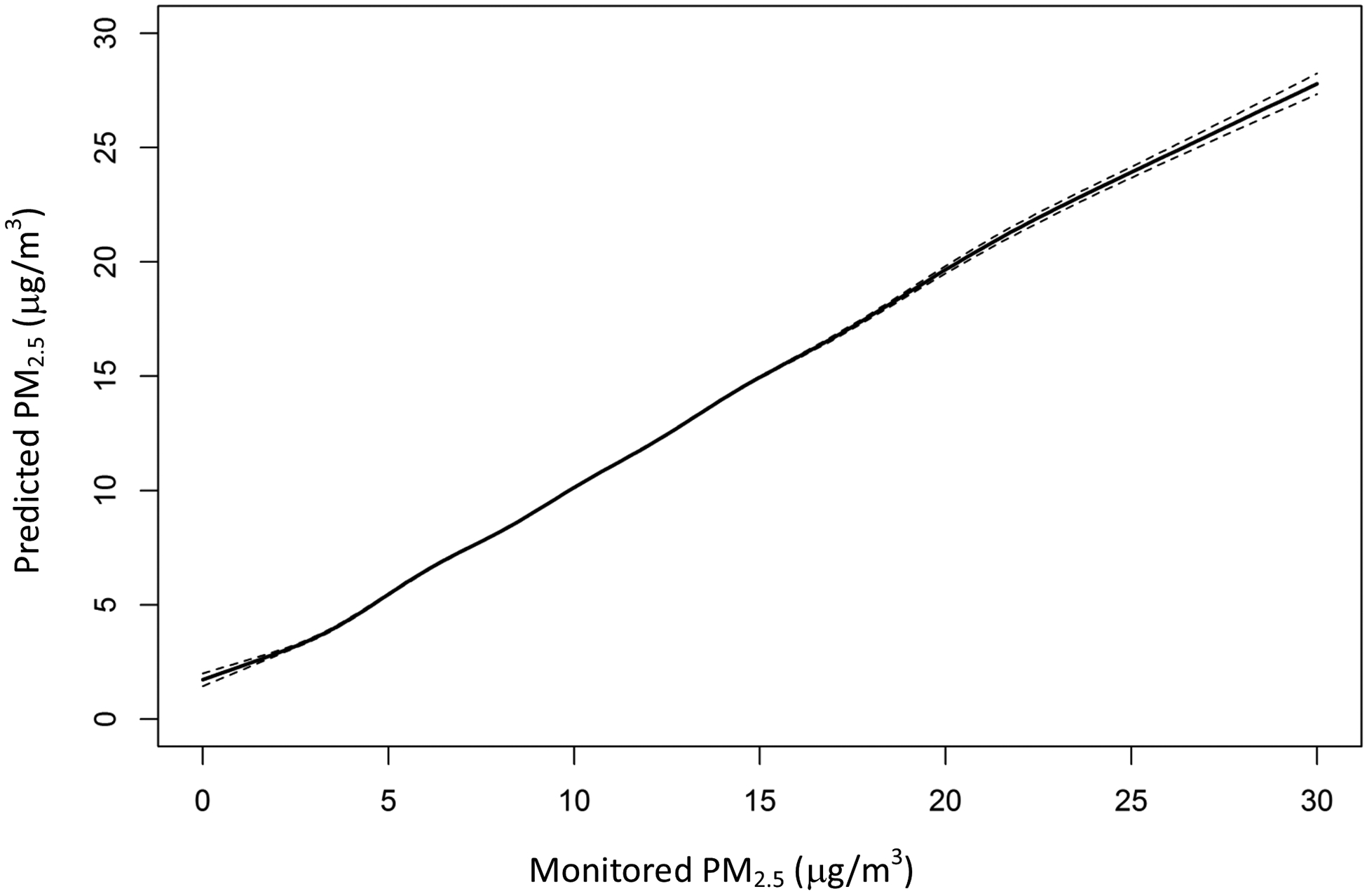
We regressed annual averaged PM_2.5 predictions from the ensemble model against annual averaged monitored PM_2.5 in a generalized additive model, with spline on the monitored PM_2.5. Dashed lines represent 95% confidence interval.

We reported the variable importance of predictor variables from three machine learning algorithms in Table 4. Spatially lagged PM_2.5 from nearby monitoring sites was clearly an important predictor. For the random forest and gradient boosting, spatially lagged PM_2.5 contributed significantly to model performance, followed by CMAQ predictions. The relative contribution of predictor variables varies by algorithms, and the contribution was spread out across more predictor variables for the neural network than random forest and gradient boosting. AOD related variables contributed the most to the neural network, along with latitude, longitude and other land-use variables.

Table 4.

Relative Contribution of Predictor Variables for Three Machine Learning Algorithms

Gradient Boosting	%	Neural Network	%	Random Forest	%
Spatially Lagged Monitored PM2.5	46.52%	AOD related variables[c]	9.25%	Spatially Lagged Monitored PM2.5	28.96%
CMAQ PM2.5	11.58%	Spatially Lagged Monitored PM2.5	2.68%	CMAQ PM2.5	16.51%
CMAQ PM2.5 Sulfate	4.89%	Road Density (All Roads)	2.10%	CMAQ PM2.5 Elemental Carbon	14.80%
Standard Deviation of Elevation	3.58%	Longitude	2.02%	CMAQ PM2.5 Organic Carbon	6.28%
NLCD Developed Area[a]	2.79%	Latitude	1.99%	CMAQ PM2.5 Sulfate	5.88%
CMAQ PM2.5 Elemental Carbon	2.74%	Standard Deviation of Elevation	1.93%	Spatially Lagged Monitored PM2.5[b]	3.29%
CMAQ PM2.5 Organic Carbon	2.65%	NLCD Planted Land Coverage[a]	1.93%	AOD related variables[c]	2.65%
Spatially Lagged Monitored PM2.5[b]	2.22%	Soil moisture	1.92%	CMAQ NO2	1.86%
Longitude	1.93%	Road Density (Pri-Secondary Road)	1.80%	Latitude	1.69%
NLCD Impervious Land Coverage[a]	1.82%	NLCD Developed Area	1.72%	NLCD Impervious Land[a]	1.40%
Standard Deviation of Elevation[a]	1.51%	NLCD Waterbody Coverage[a]	1.63%	NLCD Developed Area[a]	1.37%
Road Density (All Roads)	1.51%	NLCD Tree Canopy[a]	1.57%	Road Density (All Roads)	1.32%
AOD related variables[c]	1.50%	Standard Deviation of Elevation[a]	1.55%	Longitude	0.99%
Latitude	1.36%	Road Density (Pri-Secondary Road)[a]	1.55%	Standard Deviation of Elevation	0.91%
NLCD Planted Land Coverage[a]	1.03%	NLCD Herbaceous Land[a]	1.53%	Upward Longwave Radiation	0.59%
NLCD Tree Canopy Coverage	0.81%	NLCD Wetland Coverage[a]	1.51%	CMAQ PM2.5 Nitrate	0.59%
Road Density (Pri-Secondary Road)[a]	0.72%	NLCD Tree Canopy Coverage	1.51%	Daily Maximal Air Temperature	0.54%
NLCD Barren Land Coverage[a]	0.72%	Road Density (Primary Road)[a]	1.46%	Road Density (Pri-Secondary Roads)[a]	0.54%
MERRA2 Sulfate Aerosol	0.59%	Road Density (Primary Road)	1.45%	MODIS Daytime Surface Temperature	0.54%
OMI NO2 Column Concentration	0.57%	Spatially Lagged Monitored NO2	1.41%	NLCD shrubland[a]	0.44%

^[a]These land-use variables were averaged over 10000 m × 10000 m;

^[b]These were 1-day lagged values;

^[c]AOD related variables include: AOD at 470 nm from the Terra and Aqua satellites (both retrieved by the MAIAC algorithms), AOD at 550 nm from the Terra and Aqua satellites (both retrieved by the MAIAC algorithms), AOD at 550 nm (retrieved by the deep blue algorithm), OMI AAI (at the visible and UV spectrum), surface reflectance, and aerosol products from MERRA2 (sulfate aerosol, hydrophilic black carbon, hydrophobic black carbon, hydrophilic organic carbon, and hydrophobic organic carbon)

Note: For each learning algorithm, we ranked the importance of predictor variables and listed the first 20 of them. For random forest and gradient boosting, we calculated how much the squared error over all trees decreased after a variable was selected to split on in the tree building process. The decreased squared error was determined as the relative influence of that variable (Rifkin and Klautau 2004). For neural network, the sensitivity of output to input was used to assess variable importance (Gedeon 1997).

For spatial distribution, PM_2.5 concentrations were higher in populous places, such as Los Angeles, and the entire Eastern United States, excluding the Appalachian Mountains and some remote areas in Northern Maine and Florida. The Central Valley of California also had high concentrations. PM_2.5 concentration dropped significantly after 2008 (Figure 5). The hotspots on the 2015 map were almost indistinguishable under the same color scale (Figure 6).

Figure 5. Temporal Trend of PM_2.5.

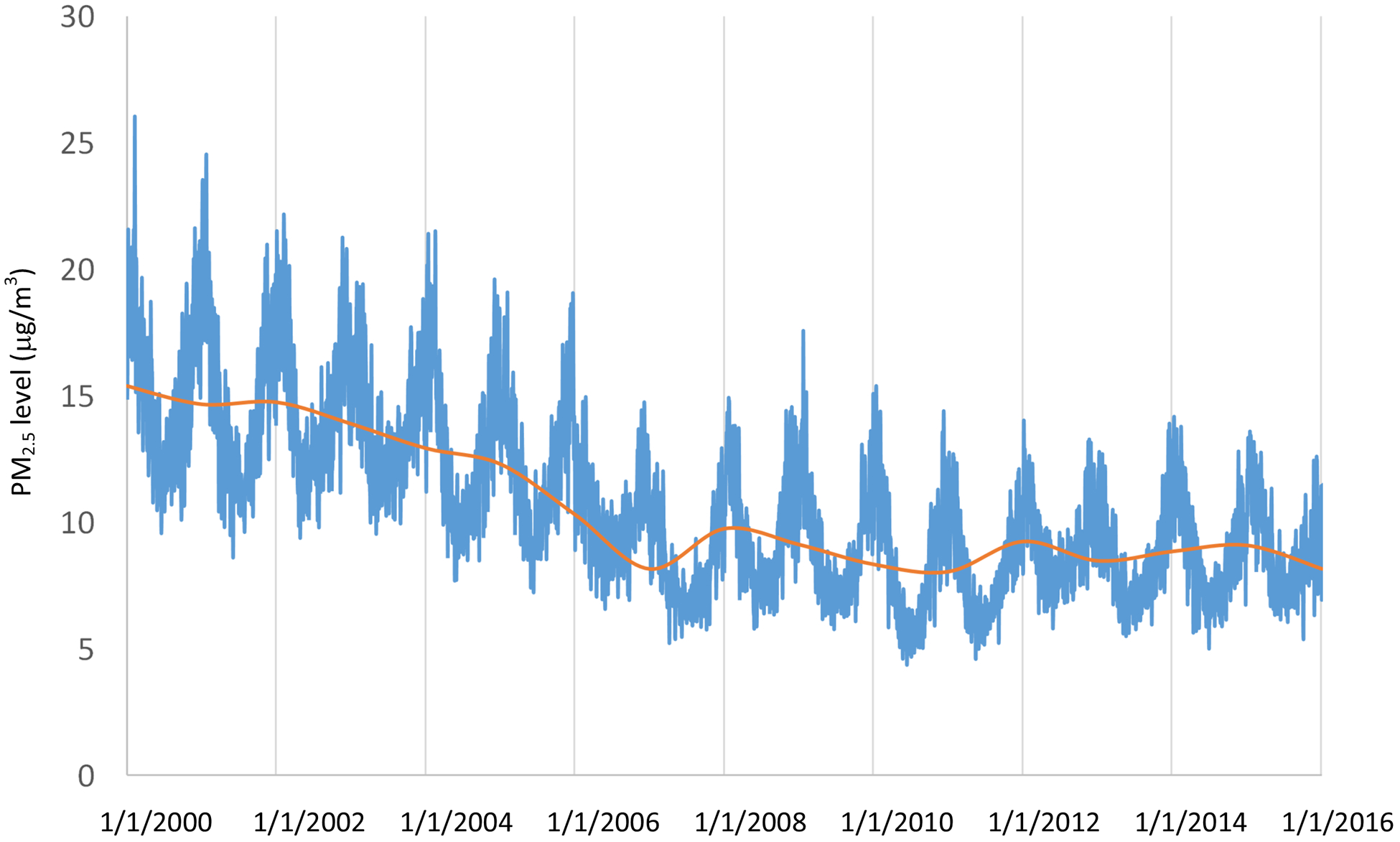
We calculated the daily nationwide averages (blue line), by averaging daily predictions at all 1 km × 1 km grid cells; then we calculated nationwide annual averages (orange line).

Figure 6. Spatial Distribution of Predicted PM_2.5.

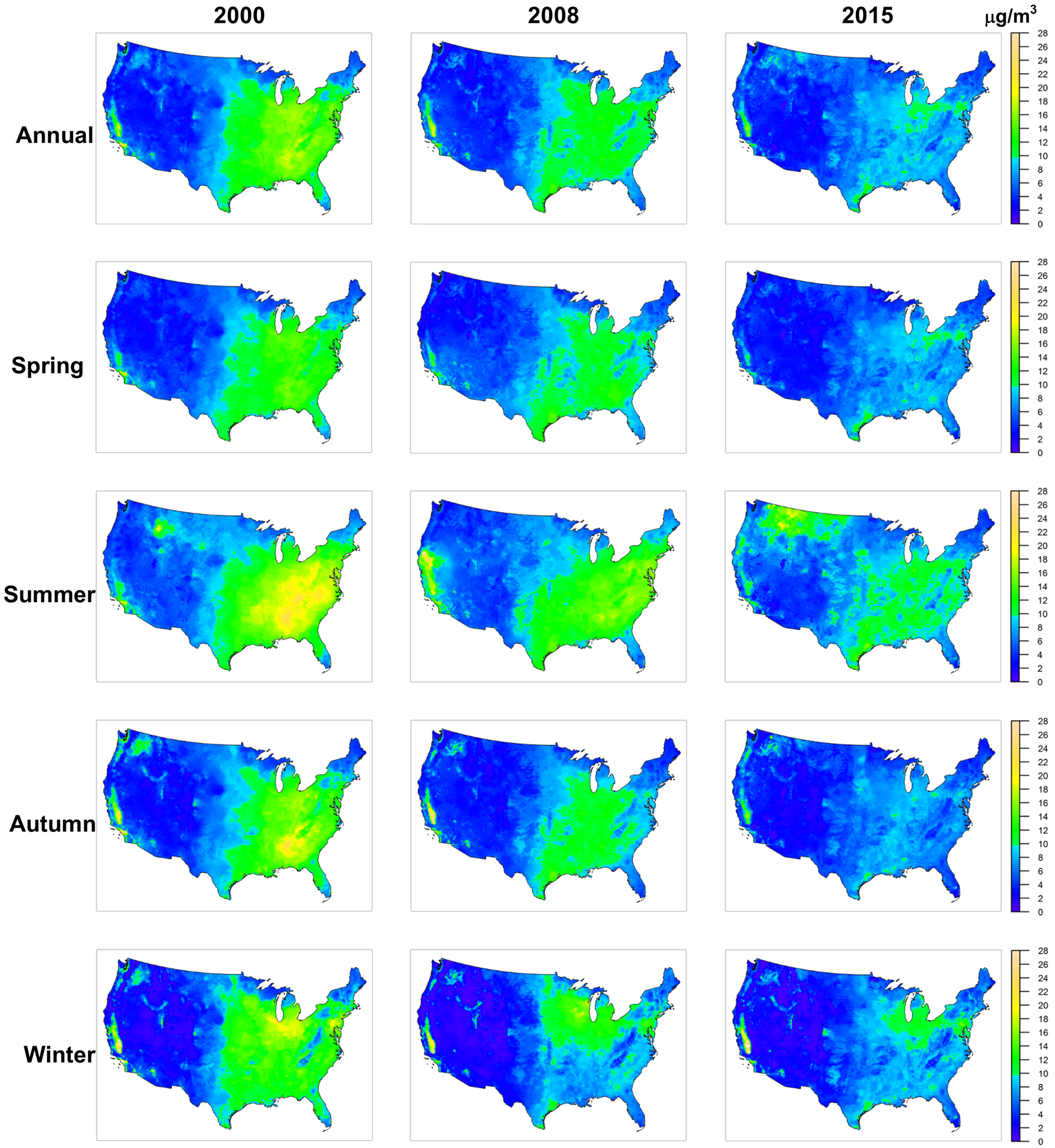
We predicted daily PM_2.5 at each 1 km × 1 km grid cell in the contiguous United States and calculated annual and seasonal averages for each grid cell. All maps were plotted at the same color scale.

The local regression predicting address-specific differences from the 1-km average was examined in the Boston metropolitan area. Figur e 7 shows the estimated concentrations on 100 m × 100 m grid.

5. Discussion

Our ensemble model incorporates PM_2.5 predictions from three machine learning algorithms, including neural network, random forest, and gradient boosting, and achieved excellent performance, with a spatial R² of 0.89 and spatial RMSE of 1.26 μg/m³. Temporal R² was also good (0.85). The three machine learning algorithms used more than 100 predictor variables, ranging from satellite data, land-use data, meteorological data, and CTM predictions, with cross-validation controlling for overfitting. A generalized additive model combined PM_2.5 estimates from machine learning algorithms and allowed the contribution of each algorithm to vary by location. With the trained model, we predicted daily PM_2.5 for the entire contiguous United States from 2000 to 2015 at every 1 km × 1 km grid cell. This high-resolution accurate estimation allows the estimation of both short-term and long-term exposures to PM_2.5. The modeled uncertainty of PM_2.5 enables to further correct exposure assessment errors in epidemiology.

Our PM_2.5 model outperforms previous models and our own previous model in the following ways. First, our model achieved high R², with better agreement between monitored PM_2.5 and predicted PM_2.5. The cross-validated R² (0.86) was higher compared with our previous model that was solely based on neural network (R² 0.84), a geographically weighted regression model with AOD as input (R² 0.67 in the east and 0.22 in the west) (Hu 2009), another a geographically weighted regression model with GEOS-Chem and AOD as inputs (R² 0.82) (van Donkelaar, Martin et al. 2015), and other studies estimating PM_2.5 for the entire contiguous United States (Liu, Park et al. 2004). Moreover, our model achieved large spatiotemporal coverage and high spatiotemporal resolution at the same time, and demonstrated a potential to downscale to 100-meter level. Previous studies either achieved large coverage or high resolution, and few of them achieve both at the same time. Finally, our model estimated the monthly uncertainty of PM_2.5 prediction for every 1 km grid cell, being the first study of this kind.

Our model outperformed previous models for the following three reasons. First, we incorporated a larger number of predictor variables, including two CTMs. Compared with our previous model, we added more detailed classification of land-use types, and new variables such as restaurant density. For different land-use types, the emission profiles and rates vary, and such differences are informative for modeling PM_2.5 at local scales. The variable importance of land-use types also proved the importance of such detailed classification (Table 4). Second, we developed an approach to fill in missing values. Missing values in satellite data, due to cloud or snow coverage, is a concern for PM_2.5 modeling, particularly since they are not missing at random. Previous studies either ignored the missing values (potentially biasing long-term averages), or used smoothing with inverse probability of missingness weights (Kloog, Koutrakis et al. 2011), or multiple imputation (Huang, Xiao et al. 2018). Our previous model used a simple interpolation to fill in missing values for some predictor variables. For this study, we developed a separate prediction model for each variable and filled in the missing values before model training and model prediction. This strategy is computationally intensive, but improves model performance, with most of the gain in spatial R², indicating better model performance at annual level. Third, the three machine learning algorithms complement each other. While the neural network and random forest had similar overall performance, they did not perform equally well in every location (Table 2). The spline plots also demonstrate that the three machine learning algorithms do not perform equally well at all concentration levels (Figure 3). The neural network was better at capturing temporal variation of PM_2.5, while the random forest modeled spatial variation better (Table S2). By non-linearly combining different base learners and allowing their contributions to vary by location and concentration, the base learner that performs better at a specific location or concentration level contributes more to the ensemble model in that instance. Therefore, the ensemble model can outperform the individual machine learning algorithms.

Our PM_2.5 model revealed spatial and temporal trends in PM_2.5 levels in the contiguous United States. Overall, there was an east-west gradient in PM_2.5 concentration, with the Eastern United States, except the Appalachian Mountains and some remote areas of Maine, having relatively higher PM_2.5 concentration than the Western United States, where most areas are either mountainous or covered by desert (Figure 6). There are some hotspots in the Western U.S., such as the Central Valley of California. At a small spatial scale, PM_2.5 concentration is primarily driven by land-use (Figure 7). As revealed by our localized modeling, PM_2.5 concentrations near highways are elevated, consistent with recent near-road PM_2.5 monitoring (DeWinter, Brown et al. 2018). In terms of temporal pattern, PM_2.5 concentrations decreased noticeably after 2008 (Figure 5). This may be due to a combination of economic recession and emission controls, particularly the cross-state air pollution rule, which reduced emissions from coal fired power plants. The time series of PM_2.5 concentration also indicate strong seasonal patterns, with peaks in the summer (Figure 5). High summer concentrations were observed particularly in the Southeastern United States, likely due to increased secondary organic aerosol associated with isoprene and monoterpene emissions from trees under conducive summer conditions (Figure 6) (Sharkey, Singsaas et al. 1996, Sharkey, Wiberley et al. 2008, Zhang, Yee et al. 2018). Relatively low regional PM_2.5 was observed in winter due to reduced photochemistry, associated with shorter daytime, lower sunlight intensity, colder temperatures, and reduced biogenic and wildfire emissions. However, elevated wintertime PM_2.5 did occur in localized areas due to increased emission from home heating in combination with reduced meteorological mixing. For example, Salt Lake City and Central Valley experienced wintertime PM_2.5 episodes due to temperature inversions trapping emission from residential wood combustion and other resources in the valley (Franchin, Fibiger et al. 2018, Kelly, Parworth et al. 2018). Elevated wintertime PM_2.5 was also observed in the Ohio River Valley, where power plants are concentrated. Model performance degraded slightly in recent years (Table 1). Although the reason for this trend is not entirely clear, it may be associated with CMAQ, an important predictor variable. Annual R² values for CMAQ sulfate predictions in the Ohio River Valley were negatively correlated with year during 2007–2015 (r = −0.74). Although the mean bias in CMAQ predictions improved over these years, the degradation in R² suggests that predicting the variability of some pollutants with CTMs may be more challenging under lower air pollution concentrations.

Figure 7. Downscaled PM_2.5 levels in the Great Boston Area.

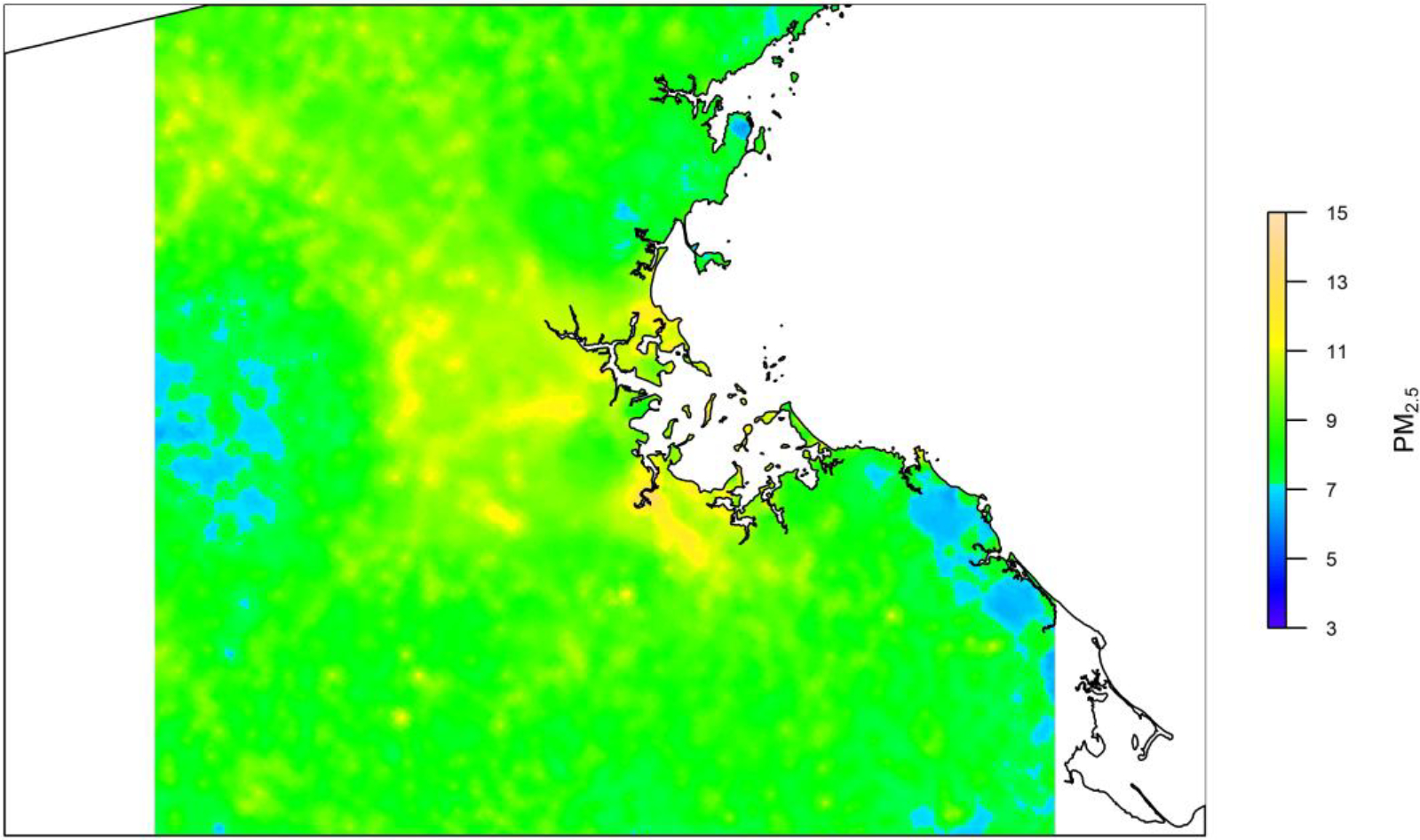
First, we made daily predictions of PM_2.5 at 1 km × 1 km grid cells in the Great Boston Area; and then we predicted residuals at 100 m × 100 m grid cells using our localized downscaling model; finally, we added residual with 1-km-level prediction to obtain 100-m-level predictions for the year of 2010. We visualized the annual averages at 100-m level for the year 2010.

The relative importance of predictor variables varied by machine learning algorithm. Gradient boosting heavily depended on the spatially lagged PM_2.5, followed by CMAQ predictions, standard deviation of elevation, and land-use terms. The random forest demonstrated a similar pattern with less contribution from spatially lagged PM_2.5. PM_2.5 distribution demonstrates a high degree of spatial and temporal autocorrelation, and that is why spatially lagged PM_2.5 could be an important predictor variable for both gradient boosting and random forest. But for the neural network, AOD variables were the primary predictor, followed by spatially lagged PM_2.5, road density, latitude, and longitude. The contribution of spatially lagged PM_2.5 was negligible for the neural network (2.68%), suggesting that the neural network may find some complex and nonlinear associations between AOD and other predictors to predict PM_2.5. For example, the AOD-PM_2.5 relationship not only relies on temperature, humidity and other meteorological conditions, but also demonstrates regional difference. The AOD-PM_2.5 relationship in the Southeastern United States, where primary source of PM_2.5 is from tree emission, is different from the Northeastern United States, where primary source is from power plants and vehicles. Also, the elevation variation in the Mountainous region imposes challenge to modeling, and simulating such complex relationship is the strength of neural network method. In comparison, without the ability of uncovering such complex relationship, gradient boosting and random forest use the superficial and obvious auto-correlation to estimate PM_2.5.

Our study suggests that the best learning algorithm varies based on context (e.g., year, season, location, concentration, etc.), and a single fitting method will not be optimal for air pollution modeling in all situations. Approaches that integrate and synthesize individual base learners could be developed to achieve a better overall estimation. Performance improvement for ensemble model in this study seems to be negligible, because the three base learners all performed relatively well and used the same predictor predictors, and there is little extra information by combining them. In practice, if combining models from different research groups or with different predictor variables, performance improvement would be more obvious. Our ensemble model demonstrates features of both geographically weighted regression and generalized additive models, showing flexibility and good performance. As more researchers explored different approaches of air pollution modeling, it is worth exploring other ensemble model formats to synthesize different models or estimation from different research groups in order to obtain an optimized overall estimation.

Our PM_2.5 model can benefit subsequent epidemiological studies in multiple ways. First, our PM_2.5 model exhibits high overall model performance. As environmental epidemiological studies are important to inform air quality standard setting and receive more scrutiny, accurate exposure assessment is both essential and critical, especially as pollution concentrations decrease. Moreover, our PM_2.5 model performs particularly well at predicting annual averages, the standard metric used to assess long-term health effects of PM_2.5. Also, the performance is good at both low and high concentrations, including daily levels up to 60 μg/m³. Finally, we have quantified model uncertainty in the PM_2.5 prediction, which will allow subsequent studies to take into account exposure measurement error (Spiegelman 2016).

Conclusion

We used an ensemble model to integrate neural network, random forest and gradient boosting to estimate daily PM_2.5 from 2000 to 2015 for the entire contiguous United States. Predictor variables included satellite measurements, chemical transport model predictions, land-use terms, meteorological variables, etc. After cross-validation, the mean R² between daily predicted and monitored PM_2.5 was 0.86, with RMSE 2.79 μg/m³. R² was 0.89 at annual level, indicating good model performance. After model training, the model produced daily PM_2.5 predictions at 1 km × 1 km grid cells. We further downscaled the 1-km-level predictions to 100 m × 100 m levels, with additional downscaling predictors. We also predicted monthly standard deviation of the difference between daily monitored and predicted PM_2.5 at 1 km × 1 km grid cells. By comparing model performance of individual machine learning algorithms, we found that a single machine learning algorithm may underperform at a particular year, season, location, pollution concentration etc., and an ensemble model incorporating estimation from these multiple machine learning algorithms can achieve a superior model performance.

Highlights.

• An ensemble model integrates three machine learning algorithms and estimates PM_2.5;

• Satellite measurements, land-use terms, and many variables were predictors;

• Model predicts daily PM_2.5 at 1 km × 1 km grid cells in the entire United States;

• Model predictions were downscaled to 100 m × 100 m level;

• Monthly uncertainty level of prediction was also estimated.