INFERENCE ABOUT CAUSALITY FROM CARDIOTOCOGRAPHY SIGNALS USING GAUSSIAN PROCESSES

Abstract

In this paper, we propose a novel and simple method for discovery of Granger causality from noisy time series using Gaussian processes. More specifically, we adopt the concept of Granger causality, but instead of using autoregressive models for establishing it, we work with Gaussian processes. We show that information about the Granger causality is encoded in the hyper-parameters of the used Gaussian processes. The proposed approach is first validated on simulated data, and then used for understanding the interaction between fetal heart rate and uterine activity in the last two hours before delivery and of interest in obstetrics. Our results indicate that uterine activity affects fetal heart rate, which agrees with recent clinical studies.

1. INTRODUCTION

The main goals of science are to understand Nature and, based on this understanding, predict how the world around us evolves. The identification of causal relationships is an important part of scientific research, since it provides us with insights about consequences for actions [1]. The gold standard for identifying causal relationships is using controlled randomized experiments. However, in many situations, these experiments are either impractical, unethical, or simply impossible [2]. The problem of inferring causal interactions from data has challenged scientists and philosophers for centuries [3] and many efforts have been made to solve it. [4].

Causal inference from time series is one important area of research in this domain, where many concepts and methods have been proposed. They include intervention causality [1, 5, 6], structural causality [7] and Granger causality [8,9] (see [10] for a detailed review). The Granger causality is probably the most prominent and most widely used concept although its usefulness is somewhat controversial [10].

In practice, when detecting Granger causality a (vector) autoregressive (AR) model is often used, and yet in reality, many causal relationships are likely to be nonlinear, this giving rise to doubts about the approach [11]. Further, it has been shown that non-linearity can be helpful in causal discovery [2]. Therefore, instead of using AR models, we adopt the use of Gaussian processes (GPs) for this purpose. They are more powerful for learning functions or mappings and moreover, they can accommodate prior knowledge and assumptions easily. A similar idea was proposed in [12], for testing Granger causality between time series using GPs. Unlike [12], instead of only relying on model evidence for casual discovery, we directly learn the mappings of possible causes and use cross-validation and model evidence for model selection. Further, we look into the hyper-parameters for causal discovery, which is more natural in the modeling sense and more robust to over-fitting.

In this paper, we are also interested in making inference about causality from cardiotocography (CTG). CTG is the most widely used technology for monitoring the well-being of fetuses during labor. CTG comprises of the fetal heart rate (FHR) and uterine activity (UA) signals, which are both recorded and visually inspected by clinicians. The interpretation of FHR recordings is a highly intricate and complex task with high inter- and intra-variable evaluations among obstetricians, notwithstanding the availability of various clinical guidelines from both the National Institute of Child Health and Human Development (NICHD) and the International Federation of Gynecology and Obstetrics (FIGO) [13–15]. In fact, the current guidelines for FHR evaluation have been criticized for simplistic interpretation [16]. The classification of CTG tracings by computerized systems remains a challenging problem [17]. For improved understanding of CTG recordings, the interactions between FHR tracings and UA is crucial, and especially establishing if there is causality between them. Interestingly, this issue has been largely overlooked in the literature of computerized analysis of CTG.

In the machine learning literature, Gaussian processes (GPs) provide data-efficient and flexible Bayesian machinery for learning functions or mappings from data. GPs have been successfully applied in both supervised and unsupervised learning tasks [18]. For example, in our previous work [19], we proposed a GP-based method that employs UA signals to recover missing samples of FHR recordings and had excellent results. This work also provided evidence that the UA signals contain information about fetal well-being. Also, there are many applications that exploit the hyper-parameters of GPs for making inference. For example, in [20, 21], the hyper-parameters are used for detecting change points, and in [22], for epilepsy detection from electroencephalograms.

In this paper, we propose a novel and simple method for discovery of Granger causality from noisy time series using GPs. Our approach to finding the possible causes and effects is based on the hyper-parameters of the GPs. Our hypothesis is that information about causality is encoded in the covariances of the GPs, and in particular in the characteristic length scales of the used features by the GPs. We use these length scales to define coefficients that reflect on the direction of causality. We tested the method based on these coefficients on simulated data and then applied it to CTG. The results indicate that the UA is a Granger cause of FHR. Our finding is consistent with recent clinical studies [23].

The paper is organized as follows. In the next section, we provide a brief background on Granger causality and GPs. In Section 3, we present the details of our model. In Section 4, we describe our experiment results. Finally, we conclude with final remarks in Section 5.

2. BACKGROUND

2.1. Granger causality

Two principles are fundamental in Granger causality: (i) the effect does not precede its cause in time; (ii) the causal series contains unique information about the series being caused that is not available otherwise. The Granger causality is usually tested using an AR model or a vector autoregressive (VAR) model. For the bivariate case, given x₁(t) and x₂(t), the AR models are

$$\begin{gathered} x_1(t)=\sum _{j=1}^p{a}_{11,j}{x}_1(t-j)+\sum _{j=1}^p{a}_{12,j}{x}_2(t-j)+e_1(t), \\ {x}_2(t)=\sum _{j=1}^p{a}_{21,j}{x}_1(t-j)+\sum _{j=1}^p{a}_{22,j}{x}_2(t-j)+e_2(t), \end{gathered}$$ (1)

where p is the order of the model, and e₁(t) and e₂(t) are perturbations. If the prediction error of x₁(t) is reduced by using x₂(t) or equivalently, the coefficients ${\left\{a_{12,j}\right\}}_{j=1}^p$ are jointly significantly different from zero, then x₂(t) is a Granger cause of x₁(t). A statistical test is often performed where the null hypothesis is that ${\left\{a_{12,j}\right\}}_{j=1}^p$ are jointly zero. Similarly, a test is performed on ${\left\{a_{21,j}\right\}}_{j=1}^p$.

2.2. Gaussian Processes

By definition, a GP is a collection of random variables such that every finite collection of those random variables has a joint Gaussian distribution. This makes GPs suitable to model distributions over functions, and infinite dimensionality becomes a bless instead of a curse given their consistency property. To be more specific, if y denotes an output and x signifies a vector of input variables, and if y = f(x), where f(x) is a real-valued function, than a GP can be seen as the distribution of the function f(x). This GP is completely specified by its mean function m(x) and covariance function k_f(x_i,x_j), which are defined by $m(\text{x})=\mathbb{E}[f(\text{x})]$ and $k_f\left({\text{x}}_i,{\text{x}}_j\right)=\mathbb{E}\left[\left(f\left({\text{x}}_i\right)-m\left({\text{x}}_i\right)\right)\left(f\left({\text{x}}_j\right)-m\left({\text{x}}_j\right)\right)\right]$. In machine learning, a GP is usually assumed to be zero mean, that is, m(x) = 0 for every x. It is also practical and common to assume the presence of observation noise i.e.,

$$y=y(\mathbf{\text{x}})=f(\mathbf{\text{x}})+ϵ,$$ (2)

where $ϵ~\mathcal{N}\left(0,{\sigma }_{ϵ}^2\right)$ is additive white Gaussian noise.

In the GP regression framework, a prior distribution of the latent function can be directly placed in the function space. With the model and the Gaussian noise assumption, one can obtain tractable posteriors of the latent function and marginal likelihoods, which makes the GPs a powerful Bayesian non-parametric machinery for learning functions or mappings. Although the function f(x) is non-parameteric, the covariance function k_f(x_i,x_j) is parameterized by its set of hyper-parameters θ.

Let $\text{X}={\left\{{\text{x}}_i\right\}}_{i=1}^N$ denote the collection of all input vectors, and K_ff the covariance matrix obtained by evaluating the covariance function for X, i.e., K_ff = k_f(X,X). Then the prior probability density function (pdf) of f given X is given by

$$p(\mathbf{\text{f}}|\mathbf{\text{X}},\mathit{\theta })=\mathcal{N}\left(\mathbf{\text{f}}|0,{\mathbf{\text{K}}}_{ff}\right).$$ (3)

The hyper-parameters θ are learned in the training stage by maximizing the marginal likelihood or model evidence,

$$\begin{gathered} \text{log\hspace{0.17em}}p(\mathbf{\text{y}}|\mathbf{\text{X}},\mathit{\theta })=\text{log\hspace{0.17em}}\mathcal{N}\left(\mathbf{\text{y}}|0,{\mathbf{\text{K}}}_{ff}+{\sigma }_{ϵ}^2\mathbf{\text{I}}\right) \\ =\text{log\hspace{0.17em}}\mathcal{N}(\mathbf{\text{y}}|0,\mathbf{\text{K}}) \\ =-\frac{1}{2}{\mathbf{\text{y}}}^T{\mathbf{\text{K}}}^{-1}\mathbf{\text{y}}-\frac{1}{2}\text{log}|\mathbf{\text{K}}|-\frac{N}{2}\text{log\hspace{0.17em}}2\pi . \end{gathered}$$ (4)

If we have test inputs X_*, the mean predictive distribution p(f_*|X_*,X,θ) will be Gaussian with a mean and covariance given by

$$E\left({\mathbf{\text{f}}}_{*}\right)=\left[{\mathbf{\text{K}}}_f\left({\mathbf{\text{X}}}_{*},\mathbf{\text{X}}\right)\right]{\mathbf{\text{K}}}^{-1}\mathbf{\text{y}},$$ (5)

$$cov\left({\mathbf{\text{f}}}_{*}\right)={\mathbf{\text{K}}}_f\left({\mathbf{\text{X}}}_{*},{\mathbf{\text{X}}}_{*}\right)-\left[{\mathbf{\text{K}}}_f\left({\mathbf{\text{X}}}_{*},\mathbf{\text{X}}\right)\right]{\mathbf{\text{K}}}^{-1}{\left[{\mathbf{\text{K}}}_f\left({\mathbf{\text{X}}}_{*},\mathbf{\text{X}}\right)\right]}^T.$$ (6)

In this work, we use the time variable as an input and we do not specify lengths of histories in the model. In other words, we model the time series simply as functions of time and do not make Markovian assumptions (as in AR processes). From (5), we see that the mean of the predictive distribution is a linear combination of all the previous observations.

2.3. Automatic Relevance Determination

The design of the covariance is of great importance, since it quantifies the distance or similarity between the inputs to the covariance between outputs. Thus, it encodes our prior knowledge or assumptions about the latent function, e.g., smoothness, periodicity, and stationarity. One of the most popular covariance functions is the radial basis function (RBF), which for the 1-D case has the form

$$k_{RBF}\left(x_i,x_j\right)={\sigma }_f^2\text{\hspace{0.17em}exp}\left(-\frac{1}{l}{\left(x_i-x_j\right)}^2\right),$$ (7)

where the characteristic length-scale l > 0 and the signal variance ${\sigma }_f^2$ are its hyper-parameters. They also have interesting meanings; ${\sigma }_f^2$ represents the variability of the function, and l affects the model complexity in that dimension. If l is small, a small change in the input distance will cause a large change in the covariance of the outputs and vice versa. This leads to another important interpretation of the characteristic length-scale, which is a measure of the importance or relevance of that dimension in the modeling. If l is small, the corresponding dimension is relevant. When x is a vector, we can compute the $r=\frac{1}{l}$ values for each dimension, where, e.g., each dimension could be a different feature, and then use them for feature selection. This is known as automatic relevance determination (ARD) [18], and is used in supervised learning and automatic dimensionality reduction in unsupervised learning [24–26].

3. MODEL DESCRIPTION

Given two time series x_t and y_t, we would like to determine their Granger causality. For each time series, as shown in Fig. 2, we can model it as a function of time and the history values of the other time series up to a certain length w, similar to the order of an AR model, i.e.,

$$x_t=f_x\left(t,y_{t-w:t-1}\right)+{ϵ}_{x,t},$$ (8)

$$y_t=f_y\left(t,x_{t-w:t-1}\right)+{ϵ}_{y,t},$$ (9)

where ${ϵ}_{x,t}~\mathcal{N}\left(0,{\sigma }_x^2\right)$ and ${ϵ}_{y,t}~\mathcal{N}\left(0,{\sigma }_y^2\right)$ are independent and additive white Gaussian noises, and the latent functions f_x and f_y are governed by two GPs, respectively, i.e.,

$$\begin{gathered} f_x~\mathcal{G}\mathcal{P}\left(0,k_x\left(\left[t,y_{t-w:t-1}\right],\left[t^{\prime },y_{t-w:t-1}^{\prime }\right]\right)\right), \\ {f}_y~\mathcal{G}\mathcal{P}\left(0,k_y\left(\left[t,x_{t-w:t-1}\right],\left[t^{\prime },x_{t-w:t-1}^{\prime }\right]\right)\right), \end{gathered}$$ (10)

where the covariance functions k_x and k_y have the same form but each has a different set of hyper-parameters, and [.,.] denotes concatenation.

Fig. 2.

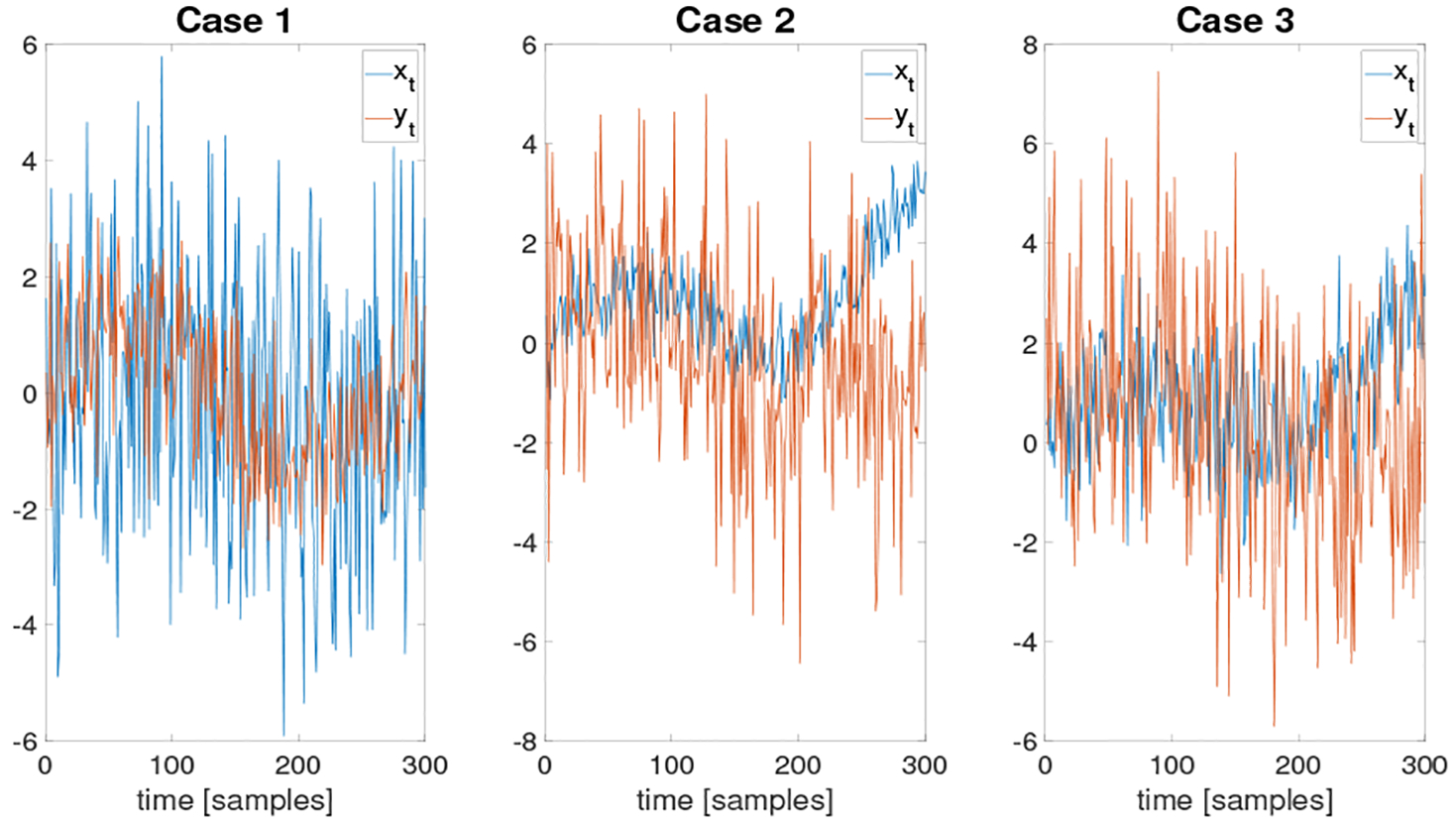
Simulated time series pairs in each simulation cases.

We propose to use the hyper-parameters of the GPs to determine Granger causality. In particular, we use the concept of relevance weights, which we define by r = 1/l. We measure the relevance of the history of y_t when modeling x_t with the maximum value of the relevance weight of the input y_t−w:t−1, i.e., $r_y^x=\text{max}\left(r_{y_{t-1}}^x,r_{y_{t-2}}^x,\dots ,r_{y_{t-w}}^x\right)$, where w is the history length, and $r_{y_{t-k}}^x$ is the relevance weight of the y sample with lag k. We denote the relevance weight of time, or equivalently x_t, by $r_x^x$. It represents the overall relevance of the history of x_t when modelling x_t. Finally, we normalize $r_x^x$ and $r_y^x$ by their sum for proper comparison, i.e.,

$$R_x^x=\frac{r_x^x}{r_x^x+r_y^x},$$ (11)

$$R_y^x=\frac{r_y^x}{r_x^x+r_y^x}.$$ (12)

Similarly, we can define $r_y^y$ and $r_x^y$, and their normalized versions $R_y^y$ and $R_x^y$. The former metric measures the percentage of relevance of the history of y_t on y_t and the latter, the percentage of relevance of a window of history of x_t on y_t. An illustration of our model is shown in Fig 1.

Fig. 1.

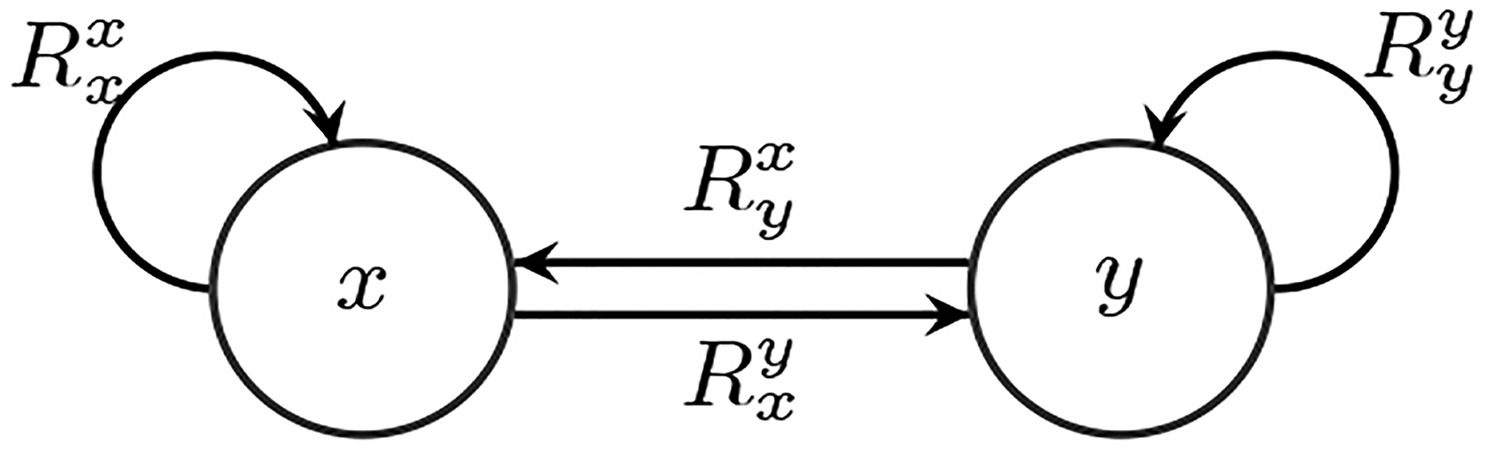
Illustration of our model, where the arrows stand for flow of information, and the normalized relevance weights indicate importance.

If the true direction of Granger causality is from x_t to y_t, then the relevance of the past values of x_t in modeling of y_t will be greater than the past values of y_t in modeling x_t. The reason is simple: the cause occurs before the effect and the change in cause entails a change in effect, and not the other way around. We note that from a machine learning perspective, the cause and effect are often viewed as a correlation only. Our interpretation of the values of $R_x^x$, $R_y^x$, $R_x^y$, and $R_y^y$ is similar to that of the VAR model, which is that the information of Granger causality is encoded in the relevance weights of the GP models. Therefore, with our approach, if the true Granger causality is from x_t to y_t, this will be indicated as $R_x^y>R_y^x$, and vice versa. Obviously, it is possible that the above analysis of the two time series can show that there is cause and effect in both directions. In principle, the determination of causality would require comparisons of the obtained normalized relevances with thresholds. Setting thresholds, however, is out of the scope of this paper.

If there is no Granger causality between the two time series, the information from the history of the other time-series will not benefit the modeling of the modeled time series. This will be encoded with small values of both $R_x^y$ and $R_y^x$. We note that since our method is based on GP regression, if we have more prior knowledge about the interaction or relationship between the time series, e.g., in forms of superpositions and/or compositions, this can be included in the used model. In that case, the hyper-parameters will encode even richer information about the possible interactions. However, then the comparisons should be made more carefully, i.e., the relevance weights should also be normalized by the importance of the corresponding explanatory variables of the model.

The above discussion is based on the assumption that we have properly selected the covariance function. If an inappropriate covariance function is used, the modeling and predictive performance will severely be deteriorated, which will most likely lead to unreliable conclusions. The choice of covariance function and window length of history w are model selection problems. Often this choice depends on how much we know about the addressed problem and the nature of the problem itself. One may use cross validation and exploit model evidence and predictive performance to select good covariance functions and window lengths. A tutorial on designing of covariance functions and model selection in GPs can be found in [18]. The window size w should not be very long, since this will increase the number of hyper-parameters in the model. Empirically, for determining Granger causality, we found that the model is robust with different choices of w.

4. EXPERIMENTS AND RESULTS

4.1. Simulations

In this section, we first provide a description of a test for our method. We simulated three pairs of time series (three cases), all shown in Fig. 2. The complexity of relationships between the time series was gradually increased as we moved from the first case to the third case. For each case, we wanted to discover the Granger causality. We used the RBF covariance function with ARD between two observed noisy time series x_t and y_t, each of length T = 300. The ground truth in the three simulations was that x_t was a Granger cause of y_t. For Case 2 and Case 3, we included nonlinear mappings and function composition to increase the complexity of the relationships. To remove bias, rather than using deterministic functions, we generated the mappings by GPs.

4.1.1. Case 1: A delayed function with additive noise

This simple simulation represents the case where we have a time series x_t, which represents a sinusoid in noise, and another time series y_t, which is generated by the same, but delayed, sinusoid. The time series y_t also contained additive noise. More precisely, we generated the time series according to the following model:

$$x_t=\text{sin}(t+0.5)+{ϵ}_{x,t},$$ (13)

$$y_t=0.5\text{\hspace{0.17em}sin}(t)+{ϵ}_{y,t},$$ (14)

where t was equally spaced in [0,2π], and where the additive Gaussian noises in x_t and y_t was white, and ${ϵ}_{x,t}~\mathcal{N}\left(0,{\sigma }_x^2\right)$ and ${ϵ}_{y,t}~\mathcal{N}\left(0,{\sigma }_y^2\right)$, respectively, with ${\sigma }_x^2=1$ and ${\sigma }_y^2=4$. The noises ϵ_x,t and ϵ_y,t were independent of each other.

4.1.2. Case 2: A noisy function with a nonlinear mapping

With the second simulation we generated more complicated relationship between the time series x_t and y_t. The time series x_t was a superposition of two deterministic signals in additive Gaussian noise. The time series y_t was composed of two parts, a function sampled from a GP that used x_t as an input and a deterministic function of time. This time series also had zero mean additive Gaussian noise which was independent from the noise of x_t. The exact generative model of the data is given by

$$x_t=\text{sin}(t/10)+{(t/50)}^2+{ϵ}_{x,t},$$ (15)

$$y_t=f(x)+\text{sinc}\left({(t/40)}^2\right)+{ϵ}_{y,t},$$ (16)

$$f(x)~\mathcal{G}\mathcal{P}\left(0,k\left(x,x^{\prime }\right)\right),$$ (17)

where the noise variances were ${\sigma }_x^2=0.25$ and ${\sigma }_y^2=4$.

4.1.3. Case 3: A delayed noisy function with two layers of function composition

In this simulation, we further complicated the previous case by introducing another layer of function composition and delay. We first generated a time series x_t as in Case 2, and we used its delayed version as the input to a GP with an RBF covariance function. A function was then sampled from this GP and used as the input to another GP. This generative model is described by

$$x_t=\text{sin}(t/10)+{(t/50)}^2+{ϵ}_{x,t},$$ (18)

$$y_t=f_2\left(f_1\left(x_{t-2.5}\right)\right)+\text{sinc}\left({(t/40)}^2\right)+{ϵ}_{y,t},$$ (19)

$$f_1(x)~\mathcal{G}\mathcal{P}\left(0,k_1\left(x,x^{\prime }\right)\right),$$ (20)

$$f_2(x)~\mathcal{G}\mathcal{P}\left(0,k_2\left(x,x^{\prime }\right)\right),$$ (21)

where k₁ and k₂ are both RBF covariance functions but with different sets of hyper-parameters. The noises, as before, were independent and zero-mean Gaussian with variances ${\sigma }_x^2=1$ and ${\sigma }_y^2=4$.

4.1.4. Results

The results of our method are summarized in Table. 1. The method correctly determined the causality in all three cases. We repeated the experiment five times, and correct decisions were made in each of them.

Table 1.

Simulation Results

	$R_x^x$	$R_y^x$	$R_y^y$	$R_x^y$	Granger causality
Case 1	0.9931	0.0069	0.1566	0.8434	xt Granger causes yt
Case 2	0.7914	0.2086	0.0008	0.9992	xt Granger causes yt
Case 3	0.4029	0.5971	0.3986	0.6014	xt Granger causes yt

4.2. Real data: CTG segment

In our experiments with real CTG data, we used data records from an open access database that were acquired at the obstetrics ward of the University Hospital in Brno, Czech Republic. A detailed description of the database can be found in [27].

We applied the method on a real CTG segment of length 491 samples, as shown in Fig. 3, which corresponds to a duration of 2.04 minutes (the sampling rate for both FHR and UA signals was 4 Hz). We used the RBF covariance function with a window size of w = 4. The results are shown in Table 2. The values of the normalized relevance weights indicate that the UA is a Granger cause of FHR. This agrees with a recent clinical study [23].

Fig. 3.

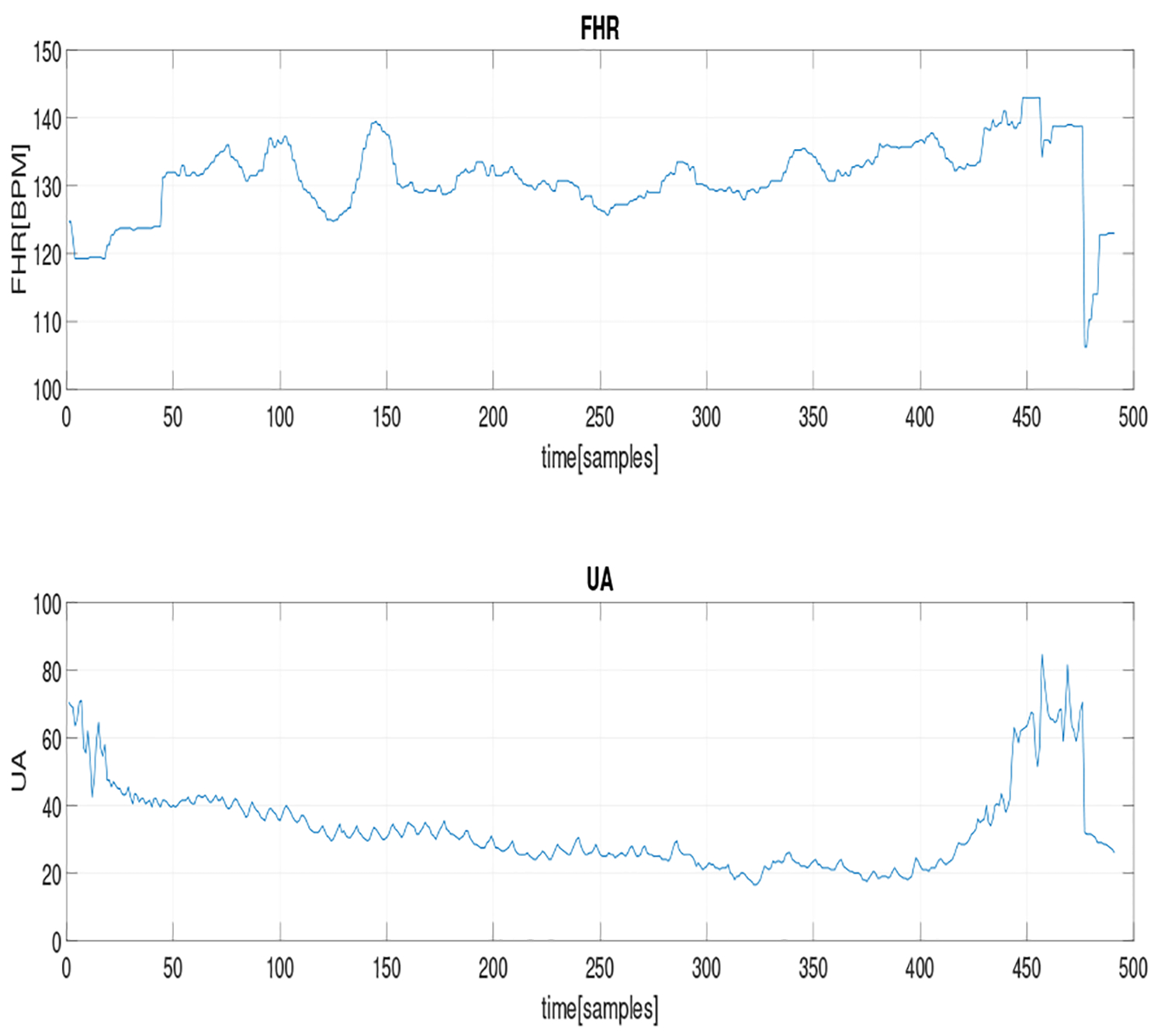
A segment of not-preprocessed (raw) FHR tracing and the corresponding UA signals.

Table 2.

Granger causality in CTG

	$R_{\text{FHR}}^{\text{FHR}}$	$R_{\text{UA}}^{\text{FHR}}$	$R_{\text{UA}}^{\text{UA}}$	$R_{\text{FHR}}^{\text{UA}}$
CTG signal	0.5090	0.4910	0.7917	0.2083

Another interpretation of the second principle of Granger causality is that if the UA Granger-causes the FHR, then past values of UA should contain information that helps in predicting future values of the FHR. With this information, the predictive performance of the method should be better than that of using information from past values of FHR alone. This is consistent with our observation in [19]. There we showed that adopting information from UA signals helps in recovering missing samples of FHR tracings.

We also used deep Gaussian processes [28] to see if FHR and UA signals have a common manifold. The results indicate that they cannot be generated from a common manifold, i.e., the FHR and UA encode different information about fetal well-being. This is also consistent with our observations in [29], where the performance of classification of FHR can be improved using features from UA.

5. CONCLUSIONS

In this paper, we proposed a Gaussian processes-based method for detecting Granger causality. We showed that the interaction or causal information can be extracted from the hyperparameters of the Gaussian processes. itemand real CTG recordings and found the results very promising. Although we used bivariate time series, this methodology can be easily extended to more than two time series. Furthermore, if we have additional prior knowledge about the time series and their interactions, it can be easily injected in the GP framework. After applying our method on real CTG recording, we found that uterine activity is a Granger cause of fetal heart rate, which agrees with recent clinical studies.