Alternative Approaches to the Assessment of the Systemic Circulation and Left Ventricular Performance: A Proof-of-Concept Study

Abstract

Background

The purpose of this article is to examine the systemic circulation and left ventricular (LV) performance by alternative, nonconventional approaches: systemic vascular conductance (G_SV) and the head-capacity relation (ie, the relation between LV pressure and cardiac output), respectively; in so doing, we aspired to present a novel and improved interpretation of integrated cardiovascular function.

Methods

In 16 open-chest, anaesthetized pigs, we measured LV pressure (P_LV), central aortic pressure (P_Ao), and central venous pressure (P_CV) and aortic flow (Q_Ao). We calculated heart rate (HR), stroke volume, cardiac index (CI = cardiac output/body weight), mean P_LV (${\overline{\text{P}}}_{\text{LV}})$, and the average arteriovenous pressure difference ($\Delta P={\overline{P}}_{\mathit{Ao}}-{\overline{P}}_{\mathit{CV}}$); G_SV = CI/(${\overline{P}}_{\mathit{Ao}}-{\overline{P}}_{\mathit{CV}}$). We studied the effects of changing loading conditions with the administration of phenylephrine (Δ${\overline{P}}_{\mathit{Ao}}$ ≥ +25 mm Hg), isoproterenol (ΔHR ∼+25%), sodium nitroprusside (Δ${\overline{P}}_{\mathit{Ao}}$ ≥ −25 mm Hg), and proximal aortic constriction (to maximize developed P_LV and minimize Q_Ao).

Results

Sodium nitroprusside and isoproterenol increased G_SV compared with phenylephrine and constriction. A maximum head-capacity curve was derived from pooled data using nonlinear regression on the maximum ${\overline{P}}_{\mathit{LV}}$ values in Q_Ao bins 12.5 mL/min/kg wide. The head-capacity relation and the plots of conductance were combined using CI as a common axis, which illustrated that CI is the output of the heart and the input of the circulation.

Conclusions

Thus, at a given CI, G_SV determines the driving pressure and, thereby, P_Ao. We also demonstrated how decreases in G_SV compensate for arterial hypotension by restoring the arteriovenous pressure difference and arterial pressure.

By using 2 rarely used concepts—systemic vascular conductance and the head-capacity principle—the goals of the present study were to reexamine 2 important areas of cardiovascular physiology, the systemic circulation and left ventricular (LV) performance, and thereby to present a novel and improved interpretation of integrated cardiovascular function.

With respect to the systemic circulation, we suggest that systemic vascular conductance (G_SV) be used. For generations, medical teaching has emphasized systemic vascular resistance (R_SV) as a hydraulic application of Ohm’s Law to the circulation. To be sure, G_SV, an alternative application of Ohm’s Law, is simply the reciprocal of R_SV, but it is superior to R_SV in certain important ways.1, 2, 3 For example, G_SV is the sum of the individual organ G’s in a parallel circulation. Basic electrophysiologists who study membranes measure conductance, not resistance. Further, Abe et al.,⁴ in seeking to optimize the regulation of the output of an artificial heart, calculated G_SV, which they then used to calculate the flow that the peripheral circulation required to establish a desired level of arterial pressure. Also, as shown next, the fact that conductances can be added (resistances cannot be added) makes the mechanism of the compensatory vascular response to hypotension more clear.

Ventricular performance has been studied intensively for many decades,5, 6, 7, 8 but although there are widely accepted means of measuring whether the performance of the LV has improved or deteriorated, the only “absolute” measures of ventricular performance are the ejection fraction (EF) and related indices such as fractional shortening or circumferential fibre shortening, which vary with preload and afterload, and therefore are sometimes difficult to interpret.9, 10 As clinicians have learned from experience, a normal LV EF may sometimes exist in the presence of abnormal cardiac function.11, 12, 13, 14 An absolute measure of ventricular performance would provide a value to describe a given LV, perhaps indexed only to the sex and age of the subject, that could be used to compare the performance of that LV to others.

We suggest that consideration of the pump function of the LV from the engineering perspective might be informative. While people have transported water from one level to another for 5000 years¹⁵ and the Archimedes screw may be thought of as a displacement pump, the first force pump was devised approximately 2000 years ago.¹⁶ The power that could be used to drive these pumps was limited to that which could be supplied by humans or animals, so the capacity (the volume of water that could be moved in unit time) was limited, as was the height (the head) to which the water could be raised. A water wheel or a series of buckets on a loop chain could be used to raise water up a certain height, but the speed at which that was done (and thus the capacity) depended on the power available; a horse (providing a horsepower) could raise water faster than a person. As the industrial revolution began in the 18th century, the need to remove water from ever deeper metal and coal mines increased. Thus, there was a need for water to be pumped in greater volumes to greater heights, and more power was needed (Fig. 1). The introduction of steam engines provided the power. What then became important for pumps was their head-capacity curve, where the head is the height to which the liquid is pumped and the capacity is the flow the pump can generate against that head. The National Fire Protection Agency of the United States established the first standard for fire-engine pumps in 1899, requiring manufacturers to supply the head-capacity curves for their pumps, as is still done today.¹⁷ Because the LV is a pump, it is natural that engineers would examine head-capacity curves of LV assist devices to determine their suitability for patients.¹⁸ We were interested in assessing the maximum pumping capability of the LV, so we examined its head-capacity curve.

Figure 1.

Head-capacity curves for 1/3 and 3 horsepower (HP) pumps. By comparing the 2 curves, the 1/3 HP pump can pump a 3 gallons per minute flow to a head of 250 feet, but to pump that flow to a head of 1200 feet requires 3 HP, 9× the HP. Also, notice that an increase in HP shifts the curve upward and to the right. The 0.002 HP curve corresponds to Figure 6. GPM, gallons per minute.

Reproduced from https://inspectapedia.com/water/WellPump Capacity.php, as visited November 30, 2018, with permission from InspectAPedia.com. Image has been provided courtesy of InspectAPedia.com. InspectAPedia.com is an independent publisher of building, environmental, and forensic inspection, diagnosis, and repair information for the public - InspectApedia.com has no business nor financial connection with any manufacturer or service provider discussed at our website.

In this study of anaesthetized open-chest pigs, we evaluated the effects of changing loading conditions (phenylephrine [PE], sodium nitroprusside [NP], and isoproterenol [ISO] administrations, and proximal aortic constriction [CONST]) on the systemic circulation and on LV pump performance.

Methods

Animal preparation

Experiments were performed on 16 male pigs (30 ± 6 [standard deviation] kg) in accordance with institutional animal-care procedures. The animals were sedated with an intramuscular injection of midazolam (0.2 mg/kg) and fentanyl citrate (2.0 μg/kg). Anaesthesia was then induced with alfaxalone (2.0 mg/kg), and the animals were intubated. After intubation, anaesthesia was maintained with fentanyl citrate (2.0 μg/kg/min), midazolam (1.1 μg/kg/min), and ketamine (14.3 μg/kg/min) at a constant infusion rate of 100 mL/h through an indwelling catheter in an ear vein. Lidocaine was administered intravenously: 3 boluses (1 mg/kg) initially and subsequently as an infusion (0.03 mg/kg/min). Isoflurane was inhaled at 1.0% to 1.5% throughout the surgery. Pigs were ventilated using a constant-volume respirator (Model 607, Harvard Apparatus Inc, Natick, MA) to maintain normal blood gases and pH. Body temperature was kept at 38°C by a circulating warm-water blanket.

Each pig was positioned supine, and a midline sternotomy was performed; the pericardium was opened with a base-to-apex incision. Catheters were inserted through the external jugular and the internal jugular veins to infuse fluid and drugs, respectively. A 7F, high-fidelity pressure catheter with a fluid-filled reference lumen (Transonic Scisense Inc, London, ON) was introduced in the LV through the right carotid artery. A 3F, micro-manometer catheter (Millar Instruments, Houston, TX) was advanced into the ascending aorta though the right brachial artery. A fluid-filled catheter was inserted in the inferior vena cava to measure central venous pressure (P_CV). Fluid-filled catheters were attached to transducers (Edwards Lifesciences [Irvine, CA] PX260) and referenced to the level of the heart. Ascending aortic flow (Q_Ao) was measured using an ultrasonic flow probe (Transonic System, Ithaca, NY). Stroke volume was calculated as the time integral of Q_Ao and multiplied by heart rate (HR) gave cardiac output (CO). An electrocardiogram was recorded throughout the experiment. After the surgical instrumentation had been completed, the pericardium was reapproximated with loose sutures. The aorta was constricted by inflating a pneumatic cuff around the ascending aorta, just distal to the flow probe.

Data were recorded at 200 Hz with data-acquisition software (Sonometrics Corp, London, ON). Data included aortic pressure (P_Ao), LV pressure (P_LV), LV end-diastolic pressure, P_CV, Q_Ao, and HR. During each intervention, data were recorded while the ventilator was turned off at end expiration for no more than 20 seconds.

Experimental protocol

In general, blood volume and afterload (PE and CONST) were manipulated to define values of ${\overline{P}}_{\mathit{LV}}$ throughout a range of cardiac index (CI) values (CI = CO/body weight), described next.

After instrumentation and the pig achieved hemodynamic stability at an LV end-diastolic pressure of 6 to 10 mm Hg, baseline recordings were taken. PE (0.025 mg/mL) was infused to increase ${\overline{P}}_{\mathit{Ao}}$ by at least 25 mm Hg. ISO (0.2 μg/mL) was infused to increase HR by approximately 25%. NP (0.2 mg/mL) was infused to reduce ${\overline{P}}_{\mathit{Ao}}$ by at least 25 mm Hg. In later experiments (ie, experiments 11-16), the aorta was constricted (CONST) to maximize developed P_LV and minimize Q_Ao. Between each intervention, enough time was allowed for hemodynamic stability to be reestablished, as ascertained by a postintervention baseline recording.

Data analysis

The systemic circulation was evaluated using G_SV. G_SV determines the flow that a vascular bed will allow for a given driving pressure (ie, the difference between ${\overline{P}}_{\mathit{Ao}}$ and ${\overline{P}}_{\mathit{CV}}$). Equation 1 defines conductance (indexed for body weight):

$$G_{\mathit{SV}}\left(I\right)=\frac{\mathit{CI}}{\left({\overline{P}}_{\mathit{Ao}}-{\overline{P}}_{\mathit{CV}}\right)}$$ Equation 1

LV performance was evaluated using the head-capacity relation. The pressure head was calculated by averaging LV pressure over 1 cycle (${\overline{P}}_{\mathit{LV}}$),¹⁹ which was plotted against CI for that beat (ie,$\frac{\mathit{SV}\times \mathit{HR}}{\mathit{body}\mathit{weight}}$). (Nomograms to calculate porcine surface area are not available, so body weight was used to reduce the variation due to different body sizes).

Statistical analysis

One-way analysis of variance was used to determine statistical significance for comparisons between conductances at baseline and during PE, ISO, and NP administration, and CONST. A P value < 0.05 was considered significant. All analyses were performed using Microsoft Excel (Microsoft Corp, Redmond, WA).

Results

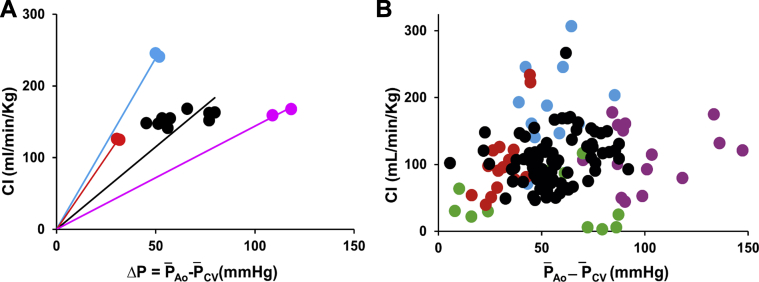
Figure 2 shows data from a representative experiment (Experiment 13), plotted as CI vs $(\Delta {\overline{P}}_{\mathit{Ao}}-{\overline{P}}_{\mathit{CV}})$. CI values for baseline observations and during each intervention were similar. However, with NP and ISO administration, the driving pressure $(\Delta {\overline{P}}_{\mathit{Ao}}-{\overline{P}}_{\mathit{CV}})$ was less than during baseline observations, and during PE administration it was greater. Lines were drawn from the origin to each group of points, the slopes of which indicate their conductances.

Figure 2.

(A) Results from a representative experiment (Experiment 13). Cardiac index (CI) is plotted against the driving pressure across the systemic circulation (${\overline{P}}_{\mathit{Ao}}$ – ${\overline{P}}_{\mathit{CV}}$). (B) Pooled data from all the experiments. Isoproterenol (ISO) data are indicated in blue, sodium nitroprusside (NP) data are indicated in red, baseline data are indicated in black, phenylephrine (PE) data are indicated in violet, and constriction (CONST) data are indicated in green.

Figure 3 shows pooled conductance data from 16 experiments during baseline observations and under the effects of each intervention. Note that during ISO and NP administration, conductance tended to be the highest, and during PE administration and CONST, conductance tended to be the least. Table 1 shows the numerical data.

Figure 3.

Conductance values for baseline measurements and each intervention. Solid lines represent mean values, and dashed lines represent upper and lower confidence intervals of the regression lines.

Table 1.

Systemic vascular conductance at baseline and with each intervention

Systemic vascular conductance
	${\overline{G}}_{\mathit{SV}}$ ± CI	vs Baseline	vs NP	vs ISO	vs CONST	vs PE
Baseline	2.19 ± 0.44	-	∗	NS	NS	NS
NP	3.28 ± 0.64	∗	-	NS	∗	†
ISO	3.21 ± 0.84	NS	NS	-	∗	†
CONST	1.65 ± 1.16	NS	∗	∗	-	NS
PE	1.16 ± 0.28	NS	†	†	NS	-

CI, confidence interval; CONST, constriction; ${\overline{G}}_{\mathit{SV}}$, mean systemic conductance, mL/min/kg/mm Hg; ISO, isoproterenol; NP, sodium nitroprusside; NS, not significant; PE, phenylephrine.

^∗P ≤ 0.05.

^†P ≤ 0.001.

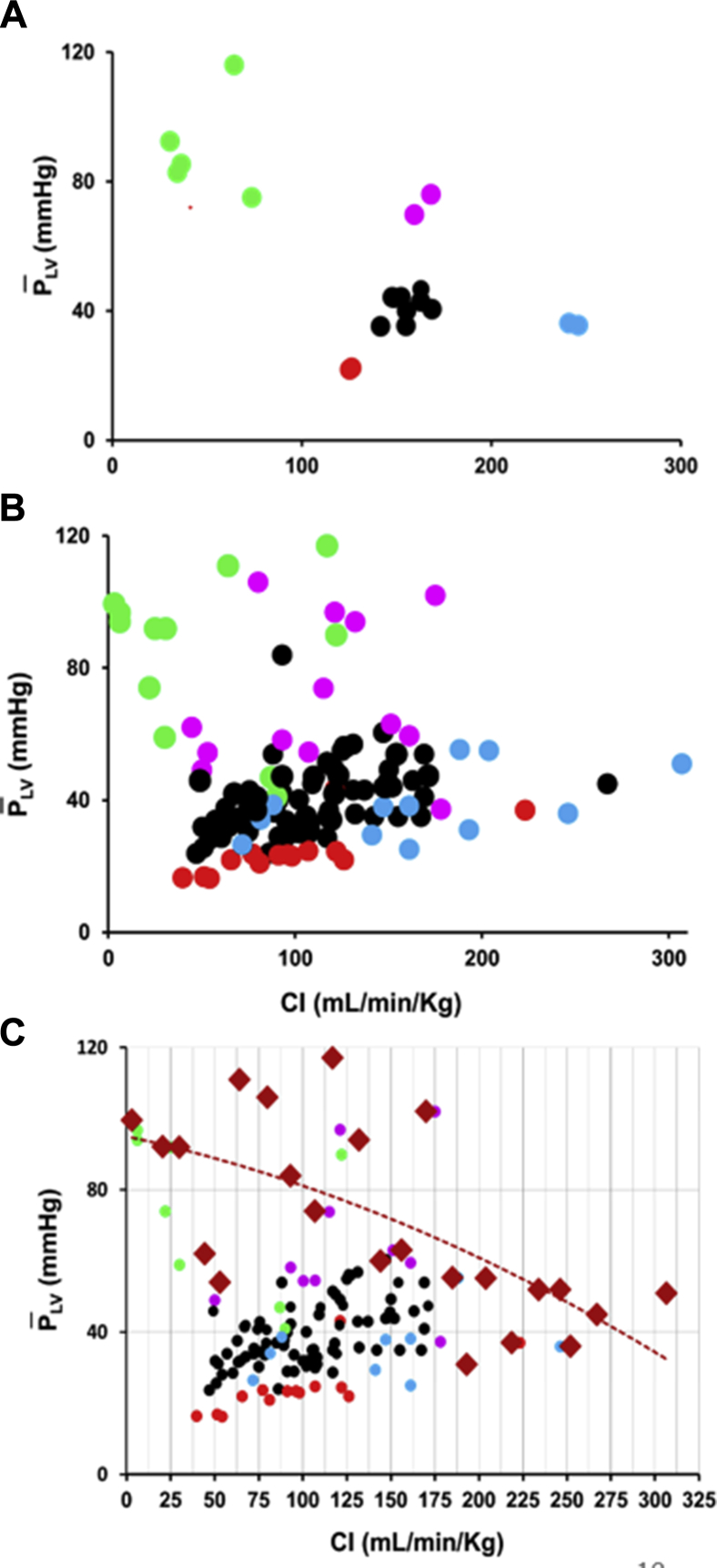
Figure 4A shows the head-capacity relation from a representative experiment (Experiment 13). Figure 4B shows the pooled data from all 16 experiments. Note that ISO (blue points) increased flow substantially but not pressure. Figure 4C illustrates how we determined the maximum head-capacity curve. Vertical CI bins 12.5 mL/min/kg wide were constructed, the maximum ${\overline{P}}_{\mathit{LV}}$ value within that bin was identified, and this value was indicated by a red diamond. These values were then fitted using a polynomial (ie, quadratic) equation.

Figure 4.

(A) Head (${\overline{P}}_{\mathit{LV}}$) – capacity (CI) relations for a representative experiment.¹³ (B) Head (${\overline{P}}_{\mathit{LV}}$) – capacity (CI) relations for pooled data. (C) Pooled data illustrating how the maximum head-capacity curve was determined. Vertical bins 12.5 mL/min/kg wide were constructed, and the maximum ${\overline{P}}_{\mathit{LV}}$ value within that bin was identified and indicated by a red diamond. These values were then fitted as a polynomial (ie, quadratic) to define the maximum head-capacity curve. Other abbreviations as in Figure 2.

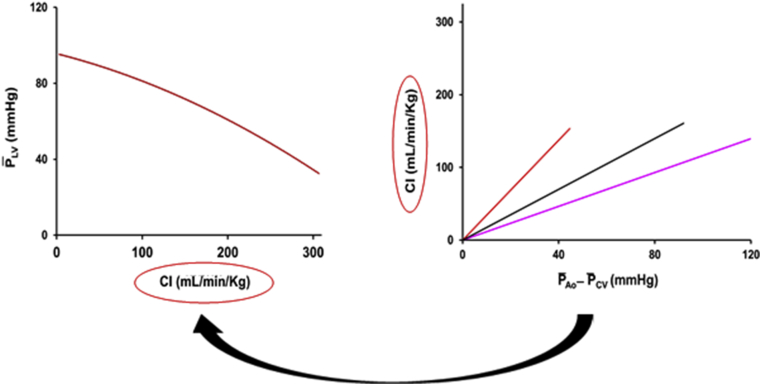
Figure 5 shows the maximum head-capacity curve (Fig. 4C) and ${\overline{G}}_{\mathit{NP}}$, ${\overline{G}}_{\mathit{Baseline}}$, and ${\overline{G}}_{\mathit{PE}}$ values (Fig. 3). Note that the 2 curves have a common axis, CI. Figure 5 shows the combination of the 2 relationships and demonstrates that whatever the value of CI, it is the G_SV that determines the driving pressure (Equation 2) and, therefore, ${\overline{P}}_{\mathit{Ao}}$ (Equation 3).

$$\frac{\mathit{CI}}{G\text{(}I\text{)}}={\overline{P}}_{\mathit{Ao}}-{\overline{P}}_{\mathit{CV}}$$ Equation 2

$$\left({\overline{P}}_{\mathit{Ao}}-{\overline{P}}_{\mathit{CV}}\right)+{\overline{P}}_{\mathit{CV}}={\overline{P}}_{\mathit{Ao}}$$ Equation 3

Figure 5.

Head-capacity curve (from Fig. 3C) and mean conductance relations (Fig. 3). Right: The red line indicates NP, black line indicates baseline, and pink line indicates PE. Note that the CI axis is common to both relationships.

Discussion

Current approaches to assessing the systemic circulation and LV performance may be limited, especially clinically. In this study, we propose using systemic vascular conductance to assess the systemic circulation and the head-capacity curve to assess LV pump performance. Our results suggest that these approaches may be clinically applicable and possibly advantageous.

Assessment of the systemic circulation

Systemic vascular conductance is the amount of blood flow that the circulation will allow per unit of driving pressure.¹ Given the parallel arrangement of the peripheral circulation, G_SV is the sum of the conductances of all the peripheral organs. In contradistinction to resistance, conductance is an “extensive” parameter that answers the question, “How much?”, and therefore can be added. (Resistance, an “intensive” parameter, can only answer the question, “To what degree?”) For example, if one is evaluating the degree of vasodilatation that results from spinal transection or the administration of a drug, we would claim that it is fundamentally more meaningful to state how much G_SV has increased than to state the degree to which R_SV has decreased.

In this study, we plotted CI vs the net driving pressure (${\overline{P}}_{\mathit{Ao}}–{\overline{P}}_{\mathit{CV}}$) to define G_SV. The data recorded during each intervention were subjected to linear regression analysis. We constrained the lines to pass through the origin because there could be no flow in the absence of a driving pressure. Although the interventions were different and each intervention was dose-dependent, it is of some interest to note that proximal CONST decreased conductance to a similar degree as PE administration (Table 1): The circulation allowed the same amount of flow even though one intervention was proximal and focal, and the other was distal and diffuse.

Assessment of LV performance

LV EF is measured clinically using widely available imaging techniques, which provide end-diastolic and end-systolic volume measurements that are generally accurate enough for most purposes. As such, the values obtained are useful to assess LV performance under baseline (resting) conditions. However, changes in LV preload or afterload can substantially affect EF, which may make interpretation difficult.²⁰

We find the head-capacity curve intuitively attractive. Like the force-velocity relation, there must be an inverse relation between the pressure a pump develops and the flow it is able to produce: Head/force must decrease as capacity/flow/velocity increases. Furthermore, it is appealing that pressure never needs to be normalized and that CO (normalized by the size of the body) is the most fundamental of circulatory parameters. Obviously, as a measure of the effectiveness of LV pump performance, the head-capacity curve depends on effective valvular action and myocardial contraction.

Accordingly, we attempted to define maximum LV pump function in this population of anaesthetized, open-chest, normal, young pigs (Fig. 4C). Vertical CI bins 12.5 mL/min/kg wide were constructed, and the maximum ${\overline{P}}_{\mathit{LV}}$ value in each bin was identified. Regression analysis was performed on these values, using a polynomial (quadratic) equation. Therefore, this function represents a measure of the maximal ${\overline{P}}_{\mathit{LV}}$ values over the range of CI values studied. We maintain that the pump performance of the LV can be evaluated if only the maximum value of ${\overline{P}}_{\mathit{LV}}$ is known throughout the range of CI.

Although this function represents maximal LV pump performance, the values below the curve should not be interpreted as indicative of inferior or impaired performance. Rather, it is simply not necessary for the heart to operate at maximal capacity under most conditions.

Our criterion for the dosage of ISO was to increase HR by at least 25%. This dosage was accompanied by an average increase in maximum dP_LV/dt from 1120 to 2710 mm Hg/s, an increase of approximately 140%. Other inotropic interventions might have different effects, but the vascular effects of ISO must not be overlooked (Fig. 4B). As demonstrated by this example, LV pump function is related to a pressure-flow product (which has the dimensions of power), and pump function may be maximal at lower pressures and higher flows. We maintain that the head-capacity curve is sufficient to assess LV performance. It is used routinely by engineers who do not know the “contractility” of the pump they are assessing.

Possible clinical applications

The results of this study could form the basis of a new approach to clinical stress testing. CI and systolic pressures might be measured noninvasively, for example, by using the Modelflow method.21, 22, 23, 24 CI could be varied by the manipulation of LV preload (eg, lower-body negative pressure or head-up tilt to pool blood peripherally and positive pressure or leg raising to mobilize peripheral blood). As limited by practical and ethical considerations, P_LV could be increased to near-maximal values using isometric hand-grip exercise or cold-pressor testing. Data might be segregated by sex and intervals of age to define LV pump-performance standards for different populations. Under a standard stress (eg, isometric hand-grip exercise), P_LV – CI data could be collected from a cohort (eg, ∼50 male participants, 20-40 years of age) of normal subjects and regression analysis performed. Given that definition of normal LV pump performance, 1 or 2 P_LV – CI data points from a test subject could be compared. If those points lie outside the confidence intervals of the normal data, the test subject might be said to have super-normal or a sub-normal LV pump performance. Effective power is the product of pressure (head) and CO (capacity). As shown in Figure 6, maximum power was developed at CO = 8 L/min: 2.13 Watts of power and 0.0029 horsepower.

Figure 6.

A plot of peak aortic systolic pressure vs cardiac output (CO) demonstrating an inverse curvilinear relationship. PE data are indicated in pink, cold-pressor data are indicated in green, baseline data are indicated in black, and upright-tilt data are indicated in gray. Data were measured using the noninvasive Modelflow technique from an individual subject in an ongoing study by Dr Raj et al. (www.clinicaltrials.gov, NCT02673996).

Among the features of this article is a renewed, focused emphasis on power, the time rate of doing work. Some decades ago, there was tremendous enthusiasm and activity around the intuitively attractive concept of “contractility.” However, even its most enthusiastic advocates had to admit that it could not be defined in terms that an engineer or physical scientist could recognize. The head-capacity curve defines the LV’s ability to develop pressure as a function of flow, each pressure-flow point on that curve defining the power developed. In this context, the ability of the LV to adapt commands attention. To produce a CO consistent with normal activity, the hypertensive person may have to increase his/her LV power by 30% to 40%. To produce the documented increases in CO while maintaining arterial pressure, the cross-country skier must increase LV power by 4- to 5-fold. Energetic constraints must be obeyed, and energy must be provided appropriately (1 mL of O₂ is approximately equivalent to 20 J²⁵ [0.0056 Watt-hours]).

The feasibility of such a clinical study is supported by the observations shown in Figure 6. Representative data from an in-progress study in a group of subjects with the postural tachycardia syndrome by Dr Raj et al. (www.clinicaltrials.gov, NCT02673996) suggest a curvilinear relation between peak systolic pressure and CO, both measured by the Modelflow method.21, 22, 23, 24 Participants were assessed at rest (supine), with a hand in ice water for 60 seconds (cold pressor test), with incremental doses of intravenous PE to increase the systolic blood pressure transiently by 25 mm Hg, and with tilt to 80° head-up (upright posture).

Figure 7 is completely consistent with the views of Levy²⁶ discussed in his 1979 article (Fig. 8). In his view, the heart generates a CO as a function of 2 intrinsic factors, HR and contractility, and 2 extrinsic factors, arterial and venous pressures. For any value of CO, the resistive elements (Vascular [B]) in the systemic circulation define the difference between arterial and venous pressures. Rather than using resistance as Levy²⁶ did, we have chosen to use conductance for a number of reasons, among them because CI is common to both the head-capacity curve and the systemic conductance relations (Figs. 5 and 7). Intuitively and obviously, CI is the output of the LV and the input of the systemic circulation. The graphical relations shown in Figure 7 clearly demonstrate that it is the systemic conductance that directly determines the arteriovenous pressure difference (Equation 2) and, after accounting for the usually minor effect of central venous pressure, arterial pressure (Equation 3).

Figure 7.

Regardless of the value of CI, it is the systemic conductance that determines the driving pressure across the circulation and, therefore, arterial pressure. Bottom: The red line indicates NP conductance, the black line indicates baseline conductance, and the pink line indicates PE conductance. (See the Results section of the text.)

Figure 8.

A block diagram of the feedback loop involved in the interaction between the cardiac and vascular portions of the circulatory system. The block labelled Vascular (B) represents the resistance/conductance elements that define the arteriovenous pressure difference at any given G_SV and $CO$. The block labelled Vascular (C) represents the capacitative elements that define the absolute values of ${\overline{P}}_{\mathit{Ao}}$ and ${\overline{P}}_{\mathit{CV}}$.

Adapted from Levy²⁶ with permission from Wolters Kluwer Health, Inc.

When CO decreases and activates the baroreceptor mechanism, it is commonly taught that one of the compensatory, sympathetically mediated responses to systemic hypotension is an increase in R_SV. We suggest that it may be more instructive to teach that the response is a decrease in G_SV. At rest, the CO is approximately 5 L/min and the R_SV is 20 mm Hg/L/min.²⁶ An R_SV of 20 mm Hg/L/min equates to a G_SV of 50 mL/min/mm Hg (Fig. 9A). Assume that the kidneys receive 20% of the CO (ie, $G_{\mathit{Renal}}$ = 10 mL/min/mm Hg) and the gut 30% (ie, $G_{\mathit{Gut}}$ = 15 mL/min/mm Hg), and assume further that because of a myocardial infarction, CO has decreased to half its normal value (ie, 2.5 L/min). Given a normal value of G_SV (ie, 50 mL/min/mm Hg), Figure 9B shows that the driving pressure across the circulation will have decreased to 50 mm Hg. However, if the circulation compensates by reducing $G_{\mathit{Renal}}$ and then $G_{\mathit{Gut}}$ to zero, the driving pressures will have been restored to 62.5 and 100 mm Hg, respectively. The profound but transient reductions in renal and gut flow that are sometimes observed during hypotension have the capacity to completely restore perfusion pressure to normal levels, thus maintaining cardiac and cerebral perfusion pressure.

Figure 9.

(A) Systemic vascular conductance of the circulation at rest.²⁶ (B) By assuming a 50% reduction in CO, (${\overline{P}}_{\mathit{Ao}}–{\overline{P}}_{\mathit{CV}}$) decreases from 100 to 50 mm Hg (red line). If renal conductance is decreased to zero, (${\overline{P}}_{\mathit{Ao}}–{\overline{P}}_{\mathit{CV}}$) increases from 50 to 62.5 mm Hg (orange line). If gut conductance is also decreased to zero, (${\overline{P}}_{\mathit{Ao}}–{\overline{P}}_{\mathit{CV}}$) increases from 62.5 to 100 mm Hg (green line). This illustrates the compensatory effects of reducing renal and then gut flow to zero.

Study limitations

As shown in Figure 4B, the degree of scatter around the (maximal) head-capacity curve is very large and prevents rigorous curve fitting that might exclude other mathematical relationships. We assumed that there was an inverse, monotonically decreasing relationship between ${\overline{P}}_{\mathit{LV}}$ and CI and used a second-degree polynomial function, merely intending to prove the concept.

Conclusions

By using systemic vascular conductance to characterize the arterial circulation and the head-capacity curve to assess maximum LV pump performance, we offer a new interpretation of integrated cardiovascular function.