A Sense of Space in Postrhinal Cortex

Abstract

A topographic representation of local space is critical for navigation and spatial memory. In humans, topographic spatial learning relies upon the parahippocampal cortex, damage to which renders patients unable to navigate their surroundings or develop novel spatial representations. Stable spatial signals have not yet been observed in its rat homolog, the postrhinal cortex. We recorded from single neurons in the rat postrhinal cortex whose firing reflects an animal’s egocentric relationship to the geometric center of the local environment, as well as the animal’s head direction in an allocentric reference frame. Combining these firing correlates revealed a population code for a stable topographic map of local space. This may form the basis for higher-order spatial maps such as those seen in the hippocampus and entorhinal cortex.

One Sentence Summary:

Single neurons in the rat postrhinal cortex provide a template for the formation of high-level topographic spatial maps.

Navigation and the encoding of spatial memory require an accurate sense of one’s location within the environment. Humans and animals form a topographic representation of space defined by local features and geometry (1–12). This representation is considered allocentric (world-centered), meaning it is independent of the observer’s perspective. However, its formation and updating are accomplished via incoming sensory information, which is egocentric (observer-centered). Thus, topographic spatial representation requires the transformation of egocentric information into an allocentric framework (13–20).

In humans, topographic spatial learning is thought to rely upon the parahippocampal cortex (PHC; 21) and damage to this area results in topographical disorientation (22). Included in this region is the parahippocampal place area (PPA), which is activated by images of scenes regardless of their contents (23) and is thought to encode spatial layouts (24). The rodent homolog of the PHC, postrhinal cortex (POR), is strongly interconnected with brain regions thought to process elements of egocentric (15–18, 25) as well as allocentric space (4–7, 26–29). Reports of egocentric encoding in areas connected with POR, including the lateral entorhinal cortex (LEC; 30), hippocampus (31), posterior parietal cortex (PPC; 32), postsubiculum (33), and dorsal striatum (34), support a potential role for POR as a hub of egocentric processing. POR is therefore well positioned to contribute to the integration of egocentric spatial information into an allocentric spatial map (35).

This integration might be carried out by single neurons encoding egocentric bearing (i.e. the angle of a reference point from an animal’s heading) and distance (i.e. the distance of a reference point from an animal’s position) of the geometric center of the local environment (13). Combining these measures with a sense of allocentric head direction, determined by the principal axis of the local environment, would provide the necessary elements for constructing a map of allocentric space as well as a set of tools for vector computations supporting navigation (13–15, 19, 20). This coding scheme would allow for representation of local space using a common coordinate system across environments with disparate geometries.

Ego- and allocentric spatial correlates in POR

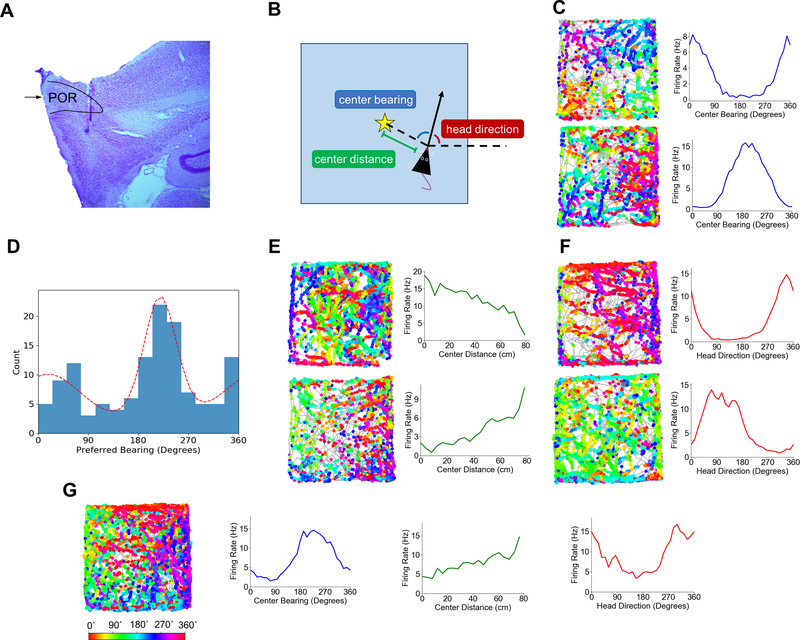
We recorded the activity of 338 putative principal neurons (N = 11 rats) in POR (Fig. 1A, S1; Table S1) as rats foraged for randomly scattered sucrose pellets in a 1.2 m square arena. We performed an exhaustive search for potential egocentric bearing reference points throughout the local environment by plotting each cell’s firing rate against the instantaneous egocentric bearings (sorted into 12˚ bins) of a 20 × 20 grid of locations evenly spaced throughout the arena. Many POR cells showed strong tuning to the geometric center of the environment, indicated by high mean vector lengths (MVL; Fig. S2). We subsequently classified POR cells (36, 37) as encoding any of three navigational variables: egocentric bearing of the environment center (‘center bearing’), egocentric distance of the environment center (‘center distance’), and allocentric head direction (Fig. 1B).

Fig. 1. Egocentric and Allocentric Spatial Correlates in POR.

(A) An example Nissl-stained sagittal section from one rat (PL61) showing the boundaries of POR. Black arrow indicates the border between dorsal and ventral subdivisions of POR. (B) Schematic top-down view of a rat in the recording arena illustrating three measures that together specify a single allocentric location in the environment. The dotted line extending rightward from the rat indicates the reference axis for allocentric head direction tuning; HD measurements increase with counterclockwise rotation of the rat, such that the rat has an allocentric head direction of 0˚ when it is facing ‘east’ (in line with the reference axis) and 90˚ when it is facing ‘north’. Center bearing is calculated as the eccentricity of the environment center from the rat’s heading. The star indicates the location of the environment center. (C) Directional spike plots (gray trace shows animal’s path, dots show spike locations colored by head direction; color bar below) and center-bearing tuning curves for two example cells that encode egocentric bearing of the environment center. (D) Histogram of the preferred bearings of all center-bearing cells recorded in POR. Dotted red line shows a bimodal von mises mixture fit to the histogram, with peaks at 30˚ and 224˚. (E) Directional spike plots and center-distance curves for two example center-distance cells recorded in POR. (F) Directional spike plots and head direction curves for two example head direction cells recorded in POR. (G) A directional spike plot and three tuning curves (center bearing in blue, head direction in red, and center distance in green) for a POR cell tuned conjunctively to head direction and center bearing with a moderate linear response to center distance. Color bar indicates head direction for directional spike plots.

Of the 338 POR cells, 132 (39%) were classified as encoding center bearing (38; Fig. 1C, S3, S8). Percentages differed by cell layer (layer II (N = 38): 5%; layer III (N = 88): 30%; layer V (N = 120): 53%; layer VI (N = 92): 45%; χ²(3) = 31.86, P = 5.60e-07), such that center-bearing cells were more prevalent in deep than superficial layers (χ²(1) = 22.80, P = 1.80e-06) and least prevalent in layer II (χ²(1) = 18.97, P = 1.33e-05) where they were largely absent (Fig. S3). Layers I and IV were not investigated here and below due to lack of sampling from those regions. There was no difference in the proportion of center-bearing cells between dorsal and ventral subdivisions of POR (χ²(1) = 1.54, P = .21). The preferred bearings of these cells covered the full spectrum of angles but were approximately distributed bimodally, with peaks at 30˚ (to the front left the animal) and 224˚ (to the back right of the animal; 39; Fig. 1D). The tuning curves of center-bearing cells tended to be broad (median MVL: .30, 95% CI: [.29, .33]) and appeared sinusoidal, with all classified cells (132/132) passing a shuffle threshold for fit by a cosine function (median fit R²: .86; Fig. S4). Center-bearing cells showed no difference in preferred bearing between the inner and outer segments of the arena (Rayleigh test, r = .86, p = 0; median shift: −1.18˚; Wilcoxon signed rank test, Z = .51, P = .70; Fig. S5), eliminating wall-hugging as a potential confounding variable. Center-bearing tuning was largely absent in both neighboring MEC (superficial layers) and parasubiculum (PaS), with only 3% (9/278) and 5% (7/137) of cells classified as encoding center bearing in these regions, respectively (Fig. S13; Table S2).

To establish a vector representation of allocentric space, signals encoding the egocentric bearing of a reference point (i.e. environment center) should be accompanied by signals representing egocentric distance of that reference point. Consistent with this framework, 59 of the 338 POR cells (17%) showed tuning to center distance (median linear R²: .72, 95% CI: [.70, .75]; 38; Fig. 1E, S3, S9). The proportion of center-distance cells differed across layers (layer II (N = 38): 5%; layer III (N = 88): 7%; layer V (N = 120): 30%; layer VI (N = 92): 16%; χ²(3) = 24.02, P = 2.47e-05), such that deep layers had more distance-tuned cells than superficial layers (χ²(1) = 15.99, P = 6.37e-05) and layer V had the most of all (χ²(1) = 18.99, P = 1.31e-05; Fig. S3). There was no difference between dorsal and ventral POR (χ²(1) = .25, P = .61). Both positive (37/59 cells; median positive slope: .038 Hz/cm, 95% CI: [.32, .59]) and negative (22/59 cells; median negative slope: −.052 Hz/cm, 95% CI: [−.082, −.032]) tuning slopes were observed, such that cells had their peak firing rates at the corners or center of the environment, respectively. As with center-bearing cells, and similar to POR layer II, center-distance cells were largely absent in MEC and PaS, accounting for only 5% (14/278) and 7% (9/137) of cells, respectively (Fig. S13; Table S2).

In addition to representing the egocentric bearing and distance of a reference point, a vector estimate of allocentric position requires a sense of allocentric head direction (13–15, 19, 20). 128 of the 338 recorded POR cells (38%) were classified as encoding allocentric head direction (12; Fig. 1F, S3, S10). Here, there were also significant differences across layers (layer II (N = 38): 5%; layer III (N = 88): 30%; layer V (N = 120): 28%; layer VI (N = 92): 72%; χ²(3) = 69.256, P = 6.16e-15), with layer VI having the largest proportion of head direction (HD) cells (χ²(1) = 59.67, P = 1.12e-14) and layer II having the smallest (χ²(1) = 17.82, P = 2.43e-05; Fig. S3). There was no difference between dorsal and ventral POR (χ²(1) = 9.34e-4, P = .98). MEC and PaS also contained sizable proportions of HD cells (12% and 35%, of cells, respectively; Fig. S13; Table S2). However, POR HD cells tended to show broad tuning curves (median MVL: .33, 95% CI: [.28, .37]; see Table S3 for other directional properties) that were significantly more sinusoidal than those in MEC/PaS (POR median fit R²: .75; MEC/PaS median fit R²: .70; Wilcoxon rank-sum test, Z = 2.49, P = .0063), and 94% of POR HD cells (120/128) passed a shuffle threshold for fit by a cosine function (Fig. S4). HD cell peak firing rates (mean: 7.01 Hz) were considerably lower than peak rates seen in other subcortical areas that contain HD cells (e.g., anterodorsal thalamus, mean: 41.1 Hz (40) and lateral mammillary nuclei, mean: 69.5 Hz (41)), but comparable to those seen in MEC (5.41 Hz; 42).

POR cells tended to show conjunctive tuning to multiple behavioral variables (Fig. 1G, S3, S9, S11, S12). 55% of center-bearing cells showed conjunctive tuning to head direction, while 36% were conjunctively tuned to center distance. Center-bearing tuning was not an artifact of conjunctive HD by 2D position tuning, as 128 of 132 originally classified center-bearing cells (97%) were still classified as center-bearing cells after correcting for 2D position encoding (43). Center-distance cells were especially conjunctive, with 81% conjunctively tuned to center bearing and 44% tuned to head direction. 57% of POR HD cells showed conjunctive tuning to center bearing, while 20% were conjunctively tuned to center distance. Overall, just over half (51%) of POR cells classified as encoding at least one of these three variables (99/196) showed conjunctive tuning to at least one other variable. Only 5 of 338 POR cells (1%) showed modulation by theta rhythm (5–11 Hz), while 48% of MEC cells and 47% of PaS cells showed theta modulation.

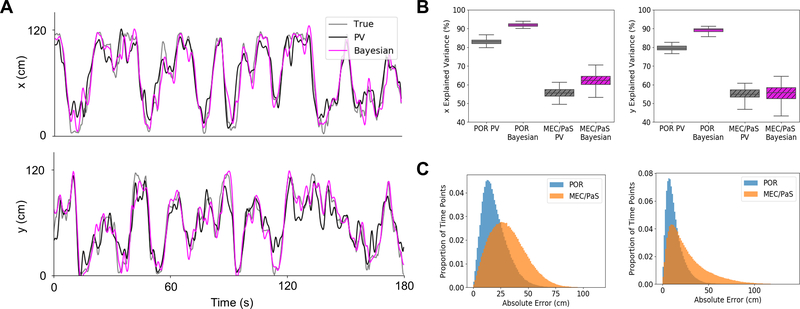
POR cells code for allocentric location

Egocentric bearing and distance information might be combined with a sense of allocentric head direction to encode allocentric location (13–15, 19, 20). We employed two decoding strategies to determine if the firing properties of POR cells could provide an accurate readout of an animal’s allocentric location: a simple population vector decoding method (PV; 44, 45), which is best suited to cells that encode angles with sinusoidal tuning curves and distances with linear curves (44–46), and a two-step Bayesian decoding algorithm (47, 48). Using spike counts from a selection of separately recorded POR cells (30, 43, 45), PV and Bayesian methods were effective in decoding center bearing (PV median R²: .94; Bayesian median R²: .95), center distance (PV median R²: .79; Bayesian median R²: .88), and head direction (PV median R²: .90; Bayesian median R²: .95). The POR decoders outperformed decoders based on pooled MEC and PaS cells across all measurements (Fig. S7). The allocentric location correlates derived from these decoded values showed strong fits to the real locational data (Fig. 2A), with the PV method explaining 83% of the variance for x location and 79% for y location, and the Bayesian algorithm explaining 92% and 89% of the variance for x and y locations, respectively (Fig. 2B). The median Euclidean decoding error was 18 cm for the PV method and 11 cm for the Bayesian algorithm (Fig. 2C). Decoding based on pooled MEC and PaS cells showed worse performance across all measurements using both PV (MEC/PaS median x fit R²: .56; Wilcoxon rank-sum test, Z = 12.22, P = 2.52e-34; MEC/PaS median y fit R²: .55; Wilcoxon rank-sum test, Z = 12.22, P = 2.52e-34; (MEC/PaS median absolute error: 30 cm; Wilcoxon rank-sum test, Z = −343.24, P = 0) and Bayesian methods (MEC/PaS median x fit R²: .62; Wilcoxon rank-sum test, Z = 12.22, P = 2.52e-34; MEC/PaS median y fit R²: .56; Wilcoxon rank-sum test, Z = 12.22, P = 2.52e-34; MEC/PaS median absolute error: 21 cm; Wilcoxon rank-sum test, Z = −344.90, P = 0).

Fig. 2. Coding for allocentric location by cells in POR.

(A) Results from an example decoding iteration showing fit of two decoding algorithms (population vector (PV) and 2-step Bayesian) to the real x- and y-positions of an animal over a 3 min period. (B) Box plots showing variance in the x- and y-positions of the animal explained by each decoder based on cells drawn from each region (POR and MEC/PaS). Center line indicates median, box limits indicate upper and lower quartiles, and whiskers indicate 1.5x interquartile range. (C) Histograms showing counts of absolute error in decoded location across all iterations of each decoder (left: population vector, right: Bayesian) for cells drawn from POR and MEC/PaS.

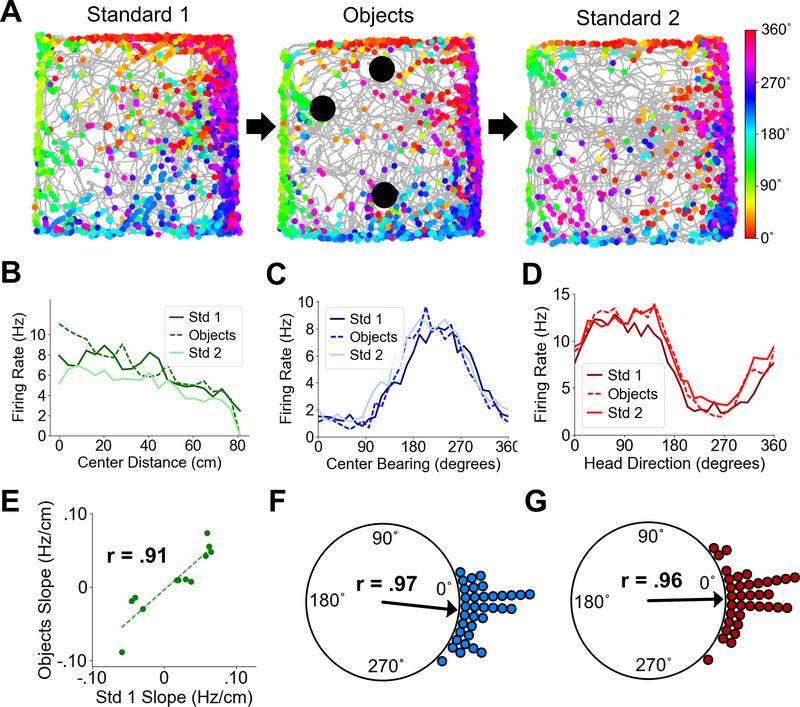
Center-bearing and center-distance cells in POR do not encode objects

If the cells recorded in POR were purely encoding the spatial layout of the local environment, they should encode elements of local space regardless of its contents (23). We therefore recorded the activity of 35 center-bearing cells, 12 center-distance cells, and 36 HD cells in POR as animals foraged in a 1.2 m box with and without objects (Fig. 3A). Center-bearing cells maintained their center-bearing preferences across the two sessions, with mean angles showing a nonuniform angular shift (Std1-Objects, Rayleigh test of uniformity, r = .97, P = 0) that was not different from zero (median shift: −2.72˚; Wilcoxon signed rank test, Z = −1.51, P = .065; Fig. 3C, F). HD cells also maintained their preferred directions across sessions (Std1-Objects, Rayleigh test, r = .96, P = 0; median shift: 1.61˚; Wilcoxon signed rank test, Z = .21, P = .58; Fig. 3D, G). The tuning slopes of center-distance cells were highly correlated across standard and object sessions (Std1-Objects, Pearson product moment correlation, t(10) = 6.99, P = 3.74e-05, r = .91) with no difference in absolute slopes between the sessions, indicating that the response gain across center-distance cells did not change (Wilcoxon signed rank test, Z = −1.32, P = .092; Fig. 3B, E).

Fig. 3. POR spatial cell types in the presence of objects.

(A) Directional spike plots for an example center-bearing by center-distance cell showing tuning stability between standard and object sessions. Color bar indicates head direction. (B) Center-distance tuning curves for an example distance-tuned cell showing stability between standard and object sessions. (C) Center-bearing tuning curves for an example bearing-tuned cell showing stability across sessions. (D) Head direction tuning curves for an example HD cell showing stability across sessions. (E) Scatter plot showing firing rate slopes of center-distance tuning curves between Standard 1 and Object sessions for all recorded POR center distance cells. (F) Polar plot showing shift in preferred center bearing between Standard 1 and Object sessions for all recorded POR center-bearing cells (each dot represents one cell). (G) Polar plot showing shift in preferred firing direction between Standard 1 and Object sessions for all recorded POR HD cells (each dot represents one cell).

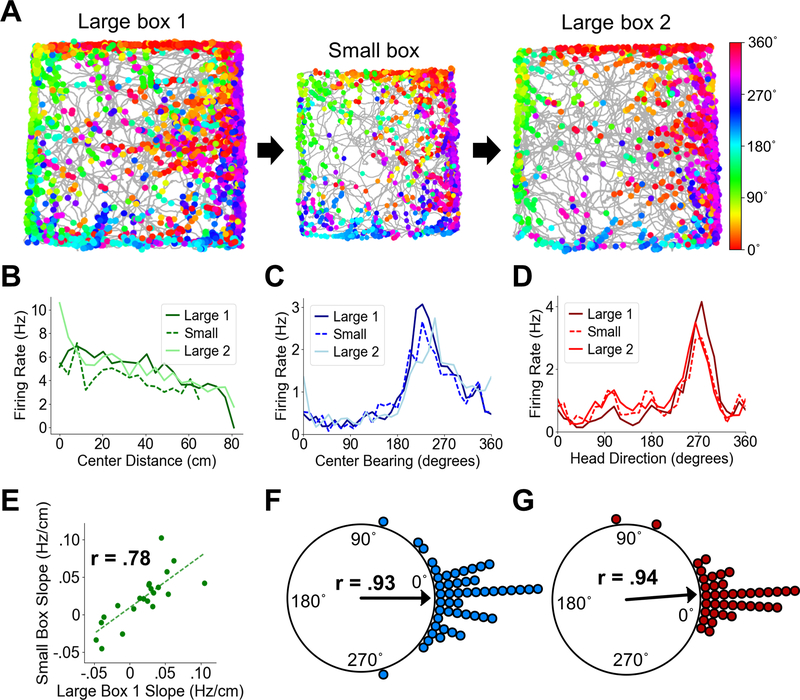
Center-distance cells in POR encode absolute distances

We next sought to determine the impact of the size of the local environment on the slopes of distance response curves for center-distance cells. If movement to a smaller box caused an increase in the slope of distance tuning, it would suggest that center-distance cells encode relative distance proportional to the size of the local environment. If the slope remained the same, however, it would suggest that cells encoded absolute distance. This latter finding would allow them to support a universal distance mechanism, such as that hypothesized to be encoded by downstream entorhinal grid cells (49). We recorded from 22 center-distance cells as animals foraged in both a 1.2 m square enclosure and a visually similar 1 m square enclosure (Fig. 4A). Distance tuning slopes were strongly correlated across the two environments (Large1-Small, Pearson product moment correlation, t(20) = 5.55, P = 1.97e-05, r = .78) and showed no significant difference in absolute slopes (Wilcoxon signed rank test, Z = .53, P = .70; Fig. 4B, E). We also recorded from 49 center-bearing cells across these two sessions, which showed no difference in preferred center bearing (Large1-Small, Rayleigh test, r = .93, P = 0; median shift: .70˚; Wilcoxon signed rank test, Z = 1.11, P = .87; Fig. 4C, F), as well as 40 HD cells, which also maintained their preferred directions (Large1-Small, Rayleigh test, r = .94, P = 0; median shift: 1.12˚; Wilcoxon signed rank test, Z = −.53, P = .29; Fig. 4D, G).

Fig. 4. POR center-distance cells encode absolute distances.

(A) Directional spike plots for an example center-bearing by center-distance cell showing tuning stability across the large box – small box – large box cycle. Color bar indicates head direction. (B) Center-distance tuning curves for an example distance-tuned cell showing highly similar tuning slopes across sessions. (C) Center bearing tuning curves for an example center-bearing cell showing stability across sessions. (D) Head direction tuning curves for an example HD cell showing stability across sessions. The curves in C and D are taken from one conjunctively tuned cell. (E) Scatter plot showing firing rate slopes for center-distance tuning curves between Large 1 and Small sessions for all recorded POR center-distance cells. (F) Polar plot showing shift in preferred center bearing between Large 1 and Small sessions for all recorded POR center-bearing cells (each dot represents one cell). (G) Polar plot showing shift in preferred firing direction between Large 1 and Small sessions for all recorded POR HD cells (each dot represents one cell).

Spatial cell firing in POR is tied to local cues

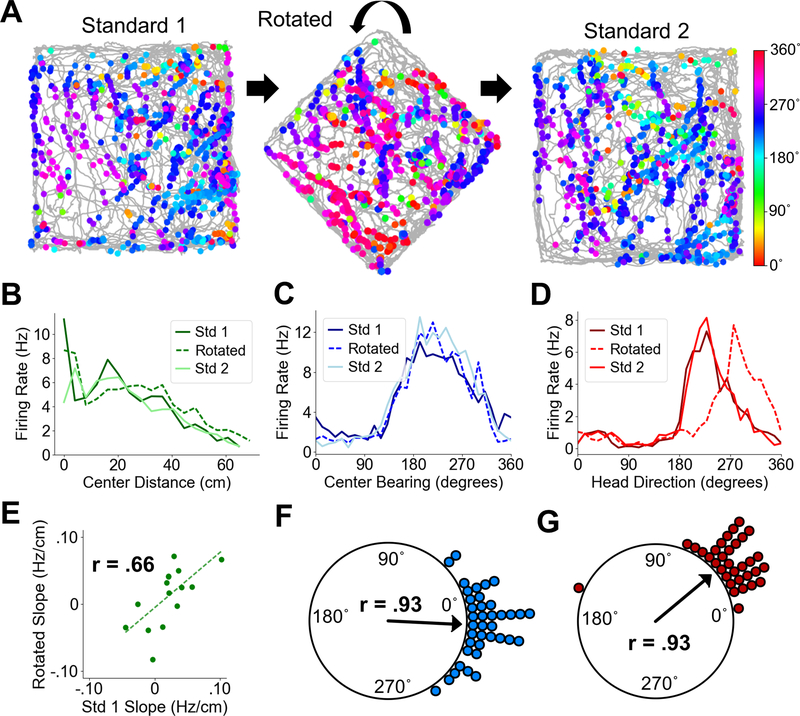
We next tested whether rotation of the local environment caused a change in the spatial tuning of POR cells. While we hypothesized that center-bearing and center-distance tuning would not change, HD cells should exhibit a rotation of their preferred firing direction if their firing is truly tied to the layout or features of the local environment. We recorded from 38 center-bearing cells, 15 center-distance cells, and 33 HD cells as animals foraged in a 1 m square box and the same box that had been rotated by 45˚ (Fig. 5A). There was no change in the preferred bearings of center-bearing cells (Std1-Rotated, Rayleigh test, r = .93, P = 0; median shift: −.51˚; Wilcoxon signed rank test, Z = .11, P = .55; Fig. 5C, F) or the tuning slopes of center-distance cells (Std1-Rotated, Pearson product moment correlation, t(13) = 3.13, P = .0079, r = .66; Wilcoxon signed rank test on absolute slopes, Z = .58, P = .72; Fig. 5B, E). In contrast, HD cells showed a significant shift in the direction of environmental rotation (Std1-Rotated, median shift: 40˚; Rayleigh test, r = .93, P = 0; Wilcoxon signed rank test, Z = 6.23, P = 2.33e-10; Fig. 5D, G).

Fig. 5. POR spatial cell types during cue rotations.

(A) Directional spike plots for an example POR HD cell showing a shift in preferred firing direction across standard and rotated sessions. Color bar indicates head direction. (B) Center distance tuning curves for an example center-distance tuned cell showing similar tuning slopes across sessions. (C) Center-bearing tuning curves for an example center-bearing tuned cell showing stability across sessions. (D) Head direction tuning curves for an example HD cell showing a shift in the direction of local environmental rotation during the rotation session. (E) Scatter plot showing firing rate slopes for center-distance tuning curves between Standard 1 and Rotated sessions for all recorded POR center-distance cells. (F) Polar plot showing shift in preferred center bearing between Standard 1 and Rotated sessions for all recorded POR center-bearing cells (each dot represents one cell). (G) Polar plot showing shift in preferred firing direction between Standard 1 and Rotated sessions for all recorded POR HD cells (each dot represents one cell).

Center-bearing and center-distance cells in POR maintain their tuning properties in darkness

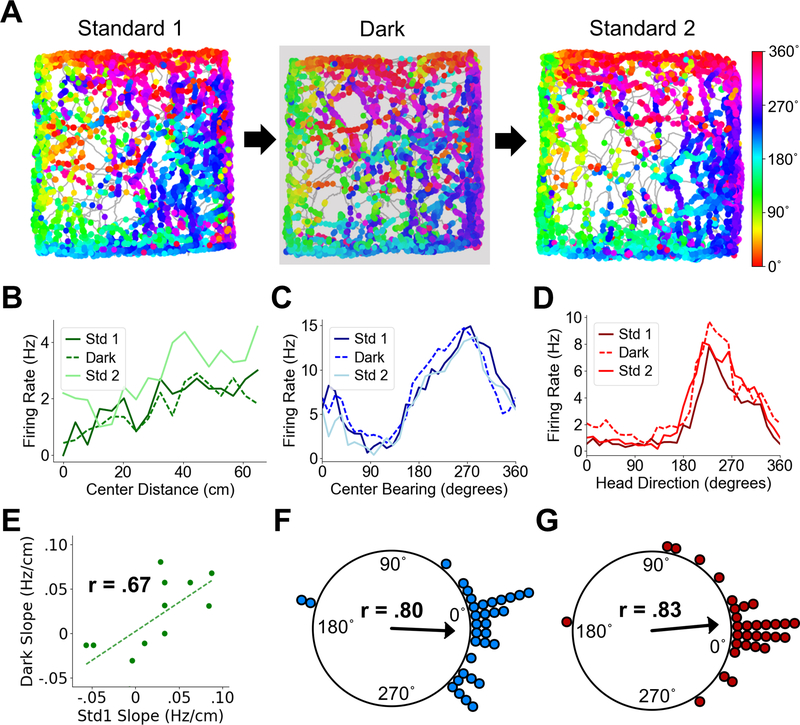
We finally determined whether POR cells can maintain their tuning properties in darkness. As POR receives heavy visual input (25), its spatial tuning properties might rely on the presence of visual cues. We recorded from 33 center-bearing cells, 12 center-distance cells, and 31 HD cells as rats foraged in a 1 m square enclosure in both light and darkness (Fig. 6A). Center-bearing cells showed no difference in preferred direction between light and dark sessions (Std1-Dark, Rayleigh test, r = .80, P = 0; median shift: 5.97˚; Wilcoxon signed rank test, Z = .86, P = .81; Fig. 6C, F), nor did HD cells (Std1-Dark, Rayleigh test, r = .83, P = 0; median shift: 1.82˚; Wilcoxon signed rank test, Z = −.39, P = .35; Fig. 6D, G). In addition, center-distance cells maintained their distance tuning slopes (Std1-Dark, Pearson product moment correlation, t(10) = 2.87, P = .017, r = .67; Wilcoxon signed rank test on absolute slopes, Z = .62, P = .73; Fig. 6B, E).

Fig. 6. POR spatial cell types in darkness.

(A) Directional spike plots for an example center-bearing cell showing tuning stability across light and dark sessions. Color bar indicates head direction. (B) Center-distance tuning curves for an example center-distance tuned cell showing similar tuning slopes across sessions. (C) Center-bearing tuning curves for an example center-bearing tuned cell showing stability across sessions. (D) Head direction tuning curves for an example HD cell showing stability across sessions. (E) Scatter plot showing firing rate slopes for center-distance tuning curves between Standard 1 and Dark sessions for all recorded POR center-distance cells. (F) Polar plot showing shift in preferred center bearing between Standard 1 and Dark sessions for all recorded POR center-bearing cells (each dot represents one cell). (G) Polar plot showing shift in preferred firing direction between Standard 1 and Dark sessions for all recorded POR HD cells (each dot represents one cell).

Discussion

Single neurons in POR encode both the egocentric bearing and distance of the geometric center of the local environment, as well as allocentric head direction. Moreover, they represent these spatial correlates with tuning curves ideally suited for a population code (44–46) from which allocentric self-location information can be decoded (Fig. 2; 13–15, 19, 20). The tuning properties of these cells were tied to local cues and remained stable in response to environmental manipulations, including darkness. They continued to encode aspects of spatial layout even in the presence of objects, suggesting that they are specifically tuned to represent local space. Thus, POR contains all the elements for constructing a stable allocentric map of local space.

The egocentric correlates found in POR could result from interactions with visuospatial areas such as retrosplenial cortex (RSC) or PPC (25), where egocentric spatial correlates have been reported (32, 50). Projections from both RSC and PPC preferentially target deep layers of POR (51, 52) where the largest proportions of center-bearing and center-distance cells were found (Fig. S3). Neurons that resemble center-bearing cells have been reported in RSC (ref. 53; ‘direction-dependent place cells’), so it is possible that POR and RSC are functionally coupled in their processing of local space. Return projections to PPC originate primarily in deep layers of POR (52). Deep layers of POR also project strongly to the dorsal striatum (54, 55) which has been implicated in egocentric spatial processing (34, 56). Head direction signals in POR might be provided by afferents from several areas including RSC (25, 53), PPC (25, 32), postsubiculum (12, 27), or the anterodorsal, lateral dorsal, and reuniens thalamus (40, 57–59).

A recent report of egocentric encoding in LEC reported a subset of cells that were responsive to external items within an egocentric reference frame, including objects and salient locations (30). The POR functional cell types investigated here encoded spatial elements of the local environment with and without objects, with no priming of salient locations, suggesting that they are preferentially involved in processing the spatial layout of a scene. Another subset of LEC cells had egocentric spatial properties reminiscent of POR center-tuning (‘bearing_boundary’ cells), including during object presentation. While POR primarily targets MEC, it also projects to LEC (28) and could be the source of the egocentric signals found there. Egocentric spatial representations originating in POR could be used by LEC to place external objects and salient locations into a common spatial reference frame that is subsequently routed to the hippocampus, and could be a unifying factor in the ‘what’ and ‘where’ pathways thought to be represented in LEC and MEC processing streams, respectively (35). Still, the combination of center-tuned cells and co-localized (or conjunctive) HD cells in POR make it uniquely fit for population coding of allocentric space.

POR is a major source of cortical input to MEC (28), and projections from POR synapse directly onto principal cells in superficial layers of MEC (29) where grid cells are most abundant (5, 26). These projections originate primarily from cells in layers II/III and V of POR (28), with an emphasis on superficial layers (29). Deep layer activity is also conveyed to MEC through intrinsic POR connections between deep and superficial layers (29). Return projections from MEC, though less strong, preferentially target layer VI of POR (28). Grid cells have been suggested to provide a distance metric for the spatial navigation system (49). Inputs from POR cells could provide support for vector computations that create or reinforce such a metric (13–15, 19, 20). That POR center-distance cells appear to encode absolute instead of relative distance supports this notion (Fig. 4). It has been hypothesized that grid cells maintain a reference to the geometric center of the local environment (60). Our observation that MEC does not contain a significant amount of center-bearing or center-distance tuning (Fig. S13, Table S2) implies that inputs from POR are heavily processed within MEC.

Spatial processing within POR has been suggested (35), though studies of single neuron activity in POR have revealed cells that either change their locational correlates between recording sessions (61), encode conjunctions of objects, locations, and rewards (62), or do not show locational correlates at all (63). Discrepancies between our study and the former two studies, as well as the fact that the second study found significant theta modulation among POR cells (62) while we did not, could be due to our more medial recording location immediately dorsal to caudal MEC, where grid cells are primarily found (5, 26). Cells in POR project to cells in MEC that are almost directly ventral to them (29); thus, it is likely that some of the cells we recorded project to the region of MEC that contains grid cells. The absence of theta modulation among our recorded POR cells could reflect a need for nonrhythmic signals to be compared with a downstream theta reference signal for the encoding of self-location (13).

The activity observed in POR parallels the activity of the homologous human PPA, which shows preferential activation in response to images of scenes, regardless of their contents (23, 24), as well as the human PHC in general. The cells investigated in this study could provide insights into the processing that takes place in these regions, as well as the severe spatial deficits that occur when the PHC is damaged (22).

Formation and updating of a spatial map require alignment of one’s current perception of the environment with a stored representation (20). One possible mechanism for this alignment could be to match the perceived boundaries of the environment with a stored representation of those boundaries, which is a fundamental process in some computational models of navigation (17, 18). However, this process quickly becomes computationally cumbersome, as one would need to establish a separate representation for every boundary configuration encountered in every new environment. A more efficient method consists of aligning the centroid and principal axis of the represented and perceived environments (20). In the case of POR, the centroid of the environment can be represented by center-bearing and center-distance cells, while the principal axis can be signaled by HD cells (13). Thus, POR may provide a computationally efficient template for mapping space in disparate environments. This template may serve as a foundation for mapping local space in the appropriate context, and it could provide a foundation for the higher-level spatial maps observed in the hippocampus and entorhinal cortex.

Materials and Methods

For additional information on the classification, artifact correction, decoding, and control procedures, please see the supplementary materials.

Subjects

Subjects were 11 female Long-Evans rats weighing 220–470 grams (median 277 grams) at the start of testing. Rats were individually housed in Plexiglas cages and maintained on a 12 h light/dark cycle. Prior to surgery, food and water were provided ad libitum. All experimental procedures involving the rats were performed in compliance with institutional standards as set forth by the National Institutes of Health Guide for the Care and Use of Laboratory Animals and approved by the Dartmouth Institutional Animal Care and Use Committee.

Electrode Construction

All animals were implanted with a moveable microdrive consisting of a bundle of four tetrodes targeting postrhinal cortex. The tetrodes were constructed by twisting together four strands of 17 μm nichrome wire. These twisted strands were subsequently threaded through a single 26-gauge stainless steel cannula, and the end of each wire was connected to a single pin of a Mill-Max connector. The two center pins of the connector were attached to the cannula, which acted as an animal ground. Three drive screws were secured around the connector using dental acrylic, making the electrode driveable in the dorsal-ventral plane.

Electrode Implantation

Animals were anesthetized with isoflurane. They were subsequently placed in a stereotaxic frame, and an incision was made in the scalp to expose the skull. A single craniotomy was drilled and the electrode was implanted .25-.45 mm anterior to the transverse sinus, 4.2–4.6 mm lateral to lambda, and 1–1.5 mm ventral to the cortical surface. Electrodes targeting superficial layers of the postrhinal cortex were positioned closer to the transverse sinus than those targeting deep layers. The electrodes were also angled 10˚ forward in the sagittal plane, such that the tetrodes were pointing anteriorly. All electrodes were secured to the skull using dental acrylic.

Recovery and Behavioral Training

Rats were allowed 7 days to recover from surgery, after which they were placed on food restriction such that their body weight reached 85–90% of its pre-surgical level. During this time, the rats were also trained to forage for randomly scattered sucrose pellets within a gray square box (120 cm x 120 cm; 50 cm in height) surrounded by a uniform black curtain. The box itself was featureless except for a white cardboard sheet placed along one inside wall. The floor was composed of gray photographic backdrop paper. Recording began when the animals’ walking paths showed uniform coverage (>80%) of the entire arena.

Recording of Neural Data

Over the course of weeks to months, tetrodes were ‘screened’ for cells as the animals foraged for sucrose pellets in the open arena. Electrical signals were pre-amplified using unity-gain operational amplifiers on an HS-18-MM headstage. Signals from each tetrode wire were then differentially referenced against a quiet channel from a separate tetrode and bandpass filtered (600 Hz to 6 kHz) using a Cheetah 32 Data Acquisition System. If signals on a given tetrode crossed a pre-defined amplitude threshold (30–50 μV), they were time-stamped and digitized at 32 kHz for 1 msec. The headstage was also equipped with red and green light-emitting diodes (LEDs) spaced ~6 cm apart over the head and back of the animal, respectively. A color video camera positioned over the arena captured video frames with a sampling rate of 30 Hz, and an automated video tracker extracted the x- and y-positions of the LEDs as well as their angle in an allocentric frame. The tracking frames were timestamped so they could be matched up to the neural data. If clearly isolated waveforms were visually apparent, a 20 min baseline recording session in the 1.2 m square box took place. Otherwise, tetrodes were advanced ~50–100 μm and screened again at least 2 h later or the next day. In a few cases, recordings were cut a few minutes short due to technical difficulties; these sessions were only included in analyses if the animal showed full sampling (>80%) of the environment.

Spike Sorting

Spike sorting was conducted offline. Spikes collected from a recording session were first automatically sorted into clusters using the automated clustering program Kilosort (64), after which manual cleanup was performed using the manual clustering program SpikeSort3D (Neuralynx). For the manual step, waveform features including peak, valley, height, width, and principal components were used to visualize the characteristics of individual spikes across multiple wires of a tetrode simultaneously as a 3D scatter plot. Cleanup of automatically sorted clusters, which was not always required, was performed by drawing a polygon around the visually apparent boundaries of each cluster. Single unit isolation was assessed using metrics such as L-ratio and isolation distance, as well as assessment of temporal autocorrelograms for the presence of a refractory period. Cross-correlograms were also analyzed in order to make sure the same cells were not recorded across different tetrodes. Despite significant advancement of the tetrodes between recording sessions, we sometimes found that the same cells were recorded multiple times on the same tetrodes across recording sessions (by analyzing waveform shape and location in cluster space); in these cases we only used the first recording of the cell. For each well-isolated cluster, we saved the timestamps for each spike and then analyzed and matched them to the tracking data.

Behavioral Testing

Object session

Following the initial baseline session in the 1.2 m square box, the rat was returned to its home cage and the floor paper of the recording arena was changed to reduce the presence of local cues from the previous session. This procedure was repeated between all subsequent sessions. Three objects (glass jars with black lids) were then placed in the arena. The locations of the objects were kept relatively constant from day to day so that any lack of object tuning could not be attributed to cue instability (65). The rat was then returned to the arena and allowed to forage for sugar pellets in the presence of the objects for a 20 min recording session.

Arena size sessions

Arena size sessions typically followed the object session. Objects were removed from the arena and the rat was then returned to the 1.2 m box for a 20 min recording session; this recording constituted the ‘large box’ session. In cases where an object session was not run first, the baseline session for the day was used as the ‘large box session.’ In either case, the 1.2 m box was then replaced with a 1 m square box (height 50 cm). The smaller box was visually similar to the large box with gray walls and a white cue card along the same inside wall. The rat was allowed to forage in the small box for a 10 min recording session (‘small box’ session). In some cases this session was followed by a second ‘large box’ session, but usually it was followed by a rotation session.

Rotation session

Following the ‘small box’ session, the small box was rotated by 45˚ and the rat was allowed to forage in the rotated box for a 10 min recording session. No attempt was made to disorient the animal before recording. This procedure ensured that any shift in the preferred firing direction of head direction cells would be due to changes in the local environment despite the perceived stability of the global environment and despite the rat’s own self-motion cues.

Dark sessions

Following the rotation session, the small box was rotated back to its standard orientation and the rat was allowed to forage in the standard small box for a 10 min recording session (lights on). A 10 min dark session (lights off) followed this session, with the rat brought into the recording room in the dark. A final standard session in the small box (lights on) then took place.

Histology

Once recordings were complete, animals were deeply anesthetized with sodium pentobarbital and small marking lesions were made at the tetrode tips by passing a small anodal current (15 μA, 15–20 sec) through two active wires from separate tetrodes. Animals were then intracardially perfused with saline followed by 10% formalin solution, after which the brains were removed from the skull and post-fixed in 10% formalin solution with 2% potassium ferrocyanide for at least 24 h. The brains were then transferred to 20% sucrose solution for at least 24 h, after which they were frozen and sliced sagitally (30 um sections) using a cryostat. Sections were mounted on glass microscope slides and stained with thionin, after which electrode tracks were examined using a light microscope. Locations of recorded cells were determined by measuring backwards from the most ventral location of the marking lesions or, if marking lesions were not visible, the electrode tracks. Delineations of parahippocampal regions were drawn mainly from refs. 26, 66, and 67.

Computation of egocentric bearing

For a given egocentric reference point (i.e. environment center) we first computed the allocentric bearing of that location from the animal (defined as the angle between the positive x axis with origin centered on the animal and a line drawn from the animal to the reference point) for each time point in the recording session, using the following equation:

$${\text{Bearing}}_{\text{allocentric}}=\text{arctan2}\left({\text{y}}_{\text{ref}}{-\text{y}}_{\text{animal}}{,\text{x}}_{\text{ref}}{-\text{x}}_{\text{animal}}\right)$$

The egocentric bearing of the reference point relative to the animal was then computed by subtracting the animal’s allocentric head direction (HD) at each time point:

$${\text{Bearing}}_{\text{egocentric}}{=\text{Bearing}}_{\text{allocentric}}{–\text{HD}}_{\text{allocentric}}$$

An egocentric bearing of 0˚ (‘egocentric north’; 20) would indicate that the reference point was in front of the animal (allocentric bearing equal to allocentric heading), while an egocentric bearing of 180˚ indicates that the reference point was behind the animal. 90˚ and 270˚ indicate bearings to the left and right of the animal, respectively.

Egocentric bearing tuning curves

Egocentric bearing tuning curves were created using 12˚ bins. For each cell, the amount of time that each bin was sampled and the number of spikes fired per bin over the course of a session were calculated, and the tuning curve was computed by dividing the number of spikes per bin by the amount of sampling time per bin. The mean vector length and mean angle were then extracted to indicate tuning strength and preferred firing direction, respectively.

For center-bearing tuning (egocentric bearing of the geometric center of the environment) a single period cosine curve was also fit to the center-bearing tuning curve, and the explained variance (R²) value of the fit was calculated as the cosine tuning strength. Units were only classified as center-bearing cells if they a) passed the classification procedure for center-bearing modulation (Supplementary Methods) b) had mean vector lengths > 95^th percentile of a shuffle distribution (discussed below), and c) had maximum firing rates >1 Hz in their center-bearing tuning curves.

Egocentric bearing mean vector length maps

As any location within the environment could constitute a potential egocentric bearing reference point, we created egocentric bearing tuning curves for a grid of possible reference locations across the entire environment, spaced 6 cm apart (20 × 20 for the 1.2 m box). The mean vector lengths of the curves were extracted and visualized as a heatmap. Locations with strong egocentric tuning for a given cell could be visually discerned as a ‘hot spot’ of high mean vector length values, such that the cell fired preferentially when that location occupied a certain angle relative to the animal’s heading. The location with the highest mean vector length for each cell was extracted as that cell’s preferred egocentric reference location (Fig. S2). Because many cells showed conjunctive tuning to allocentric head direction that skewed the location of the preferred reference, we also corrected for head direction tuning using a maximum likelihood method (Fig. S2).

Egocentric distance tuning curves

Egocentric distance is defined here as the instantaneous distance between an animal and a given reference location. Egocentric center distance was calculated as the distance between the animal and the geometric center of the environment. For tuning curve construction, 4 cm bins were used. For each cell, the number of spikes fired over the course of the session per bin was divided by the amount of time the animal spent in each bin. A regression line was fit to each curve and the R² fit of the line was calculated as the linear tuning strength. Cells were only classified as center-distance cells if they a) passed the classification procedure for center-distance modulation (Supplementary Methods), b) had linear fit values > 95^th percentile of a shuffle distribution (discussed below), and c) had maximum firing rates >1 Hz in their center-distance tuning curves.

Allocentric head direction tuning curves

Allocentric head direction tuning curves were constructed using the same procedures as egocentric bearing tuning curves but using instantaneous allocentric head direction. Cells were considered HD cells if they a) passed the classification procedure for head direction modulation (Supplementary Methods), b) had mean vector lengths > 95^th percentile of a shuffle distribution (discussed below), and c) had maximum firing rates >1 Hz in their head direction tuning curves. HD cell properties shown in Table S3 were calculated based on previous methods and analyses (see 40, 68).

Allocentric position firing rate maps

The animal’s two-dimensional location throughout the recording session was divided into 2 cm x 2 cm bins. For each cell, the number of spikes fired when the animal occupied each bin was divided by the amount of time the animal spent in that bin to calculate a firing rate for each location in the environment. The resulting firing rate heatmaps were smoothed with a gaussian filter with a standard deviation of 2 bins.

Directional spike plots

In order to visualize the directional firing of cells across space, we created directional spike plots that plot the path taken by the animal during foraging (gray trace) overlaid with dots indicating the animal’s location when a single cell fired a spike. The dots are colored (circular rainbow color palette) according to the animal’s allocentric head direction when the spike was fired; red = 0˚, green = 90˚, blue = 180˚, purple = 270˚.

Assessment of temporal and spatial stability

We employed several methods to establish that center-bearing cells showed consistent tuning over time and space. The GLM cross-validation procedure (Supplementary Methods) ensured that tuning to each specific variable was consistent across the entire recording session. Additionally, we divided each 20 min baseline session in the 1.2 m square box into four 5 min segments, and the mean angles of the center-bearing tuning curves for each segment were compared (Fig. S5). For stability across space, we divided the environment into inner and outer portions, the inner portion being a square area that had side lengths equal to one-half of a side length of the entire arena. We compared mean angles between periods when the animal occupied each region to assess spatial stability. We also split the cells into two groups: those that showed preferred center bearings in front of or behind the animal (315º - 45º, 135º - 225º), and those that showed preferred bearings to the left and right of the animal (45º - 135º, 225º - 315º). We then tested the stability of each group across inner and outer zones (Fig. S5).

Theta modulation index

Theta rhythmicity of each cell’s spike train was assessed using a theta index (69, 70). We first created a temporal autocorrelogram for each cell by tallying the number of spikes that occurred within each 5ms bin of a 1s window centered on each spike. A power spectrum was then computed by performing a Fast Fourier Transform on the autocorrelogram. The strength of theta modulation (theta index) was computed by first calculating the mean power within 1 Hz on either side of the frequency with the highest power within a 5–11 Hz (theta) range and dividing this by the mean power between 1 and 125 Hz. Only cells with a theta index >5 were considered theta-modulated.

Gridness score

Gridness scores were computed as described previously (42). Briefly, for each cell, a spatial autocorrelogram was computed for the smoothed allocentric position firing rate map which correlated the map with itself (Pearson’s r) at all possible spatial lags. If a cell was hexagonally periodic (like a grid cell) there would be a ring around the center of the autocorrelogram with six evenly spaced peaks. The ring around the center (not including the center) was then correlated with itself (Pearson’s r) at 3º offsets from 0º to 180º. A hexagonally periodic signal would cause peaks at offsets of 60º and 120º and troughs at offsets of 30º, 90º, and 150º. The gridness score was calculated as the difference between the smallest correlation value at 60º and 120º and the largest correlation value at 30º, 90º, and 150º. Cells with gridness scores > 0.4 were considered grid cells (30).

Border score

Smoothed allocentric position firing rate maps were first thresholded to only include bins higher than 20% of each cell’s maximum firing rate. Firing fields were defined as above-threshold contiguous groups of bins with size > 200 cm². We next determined the firing field with the most bins along one wall of the enclosure, and converted that number of bins into a distance along that wall, d. We then calculated the average distance of each of the bins in that firing field from the associated wall, m. The border score was then computed according to the following equation (70):

$$B=\left(d–a\right)/\left(d+a\right)$$

Cells that did not pass the gridness threshold but had border scores > 0.5 were considered border cells (30).

Shuffling procedure

Each cell’s spike train was randomly shifted between 30 sec and 30 sec less than the length of the recording session, with entries beyond the end wrapped to the beginning, in order to offset the spike data from the behavioral data without interrupting its temporal structure. Relevant tuning scores were then computed based on the shifted spike train. This procedure was repeated 100 times for each cell, and all of the shuffled measures were combined into a single shuffle distribution for each brain region. A 95^th percentile cutoff was used to determine tuning significance for individual cells.

Statistics

Statistical analyses were carried out using custom Python and R code. As several distributions appeared non-normal (e.g. center-distance slopes), medians and bootstrapped 95% confidence intervals were included in the text instead of means and standard errors. All tests were two-sided (except for GLM classifier cross-validation comparisons) and used an alpha level of 0.05.