Genome‐enable prediction for health traits using high‐density SNP panel in US Holstein cattle

Summary

The objective of this study was to compare accuracies of different Bayesian regression models in predicting molecular breeding values for health traits in Holstein cattle. The dataset was composed of 2505 records reporting the occurrence of retained fetal membranes (RFM), metritis (MET), mastitis (MAST), displaced abomasum (DA), lameness (LS), clinical endometritis (CE), respiratory disease (RD), dystocia (DYST) and subclinical ketosis (SCK) in Holstein cows, collected between 2012 and 2014 in 16 dairies located across the US. Cows were genotyped with the Illumina BovineHD (HD, 777K). The quality controls for SNP genotypes were HWE P‐value of at least 1 × 10⁻¹⁰; MAF greater than 0.01 and call rate greater than 0.95. The fimpute program was used for imputation of missing SNP markers. The effect of each SNP was estimated using the Bayesian Ridge Regression (BRR), Bayes A, Bayes B and Bayes Cπ methods. The prediction quality was assessed by the area under the curve, the prediction mean square error and the correlation between genomic breeding value and the observed phenotype, using a leave‐one‐out cross‐validation technique that avoids iterative cross‐validation. The highest accuracies of predictions achieved were: RFM [Bayes B (0.34)], MET [BRR (0.36)], MAST [Bayes B (0.55), DA [Bayes Cπ (0.26)], LS [Bayes A (0.12)], CE [Bayes A (0.32)], RD [Bayes Cπ (0.23)], DYST [Bayes A (0.35)] and SCK [Bayes Cπ (0.38)] models. Except for DA, LS and RD, the predictive abilities were similar between the methods. A strong relationship between the predictive ability and the heritability of the trait was observed, where traits with higher heritability achieved higher accuracy and lower bias when compared with those with low heritability. Overall, it has been shown that a high‐density SNP panel can be used successfully to predict genomic breeding values of health traits in Holstein cattle and that the model of choice will depend mostly on the genetic architecture of the trait.

Introduction

Maintaining cow health and productivity around parturition and during early lactation is critical for the overall welfare and profitability of dairy herds. Transition from the non‐lactating pregnant state to non‐pregnant lactating state requires a dairy cow to drastically adjust her metabolism, so that nutrients can be partitioned to support milk synthesis, a process referred to as homeorhesis (Bauman & Currie 1980). Endocrine changes at calving and drastic metabolic adjustments to support milk synthesis result in negative energy balance and immune suppression (Goff 2004; Hammon et al. 2006). Despite orchestrated homeostatic controls and homeorhetic adjustments to cope with the changes in metabolism caused by milk production, 40–70% of dairy cows across different levels of milk production, breeds and management systems develop metabolic or infectious diseases in the first month of lactation (Santos et al. 2010; Ribeiro et al. 2013). These health problems not only cause reductions in milk yield and increases in treatment costs, but also affect the reproductive performance of dairy cows, which consequently impairs the sustainability of dairy herds.

This suboptimal status in the health and wellness of dairy cattle has led to a growing interest in the use of genetic improvement as part of a comprehensive health management strategy for dairy cows. Consequently, several new methodologies for genomic selection (GS) have been proposed (Weller et al. 2017).

The prediction quality of various Bayesian models has been computed and compared in multiple genomic selection studies (Meuwissen et al. 2001; Pérez et al. 2010; Magnabosco et al. 2016). However, the performance of each model depends on the trait evaluated and its genetic architecture. For example, models that perform some sort of variable selection (e.g. Bayes B and C) might have a predictive ability advantage for traits controlled by smaller numbers of major effect QTL. On the other hand, for polygenic traits that are affected by several QTL of small effects, most of the methods have similar predictive ability, including simpler models, such as ridge regression (Daetwyler et al. 2010). As such, each application of GS requires a step of model comparison. However, computing measures of predictive ability, such as prediction accuracy, require the use of cross‐validation (CV) methods, which might be time‐consuming, depending the number of individuals and or markers analyzed.

Efficient strategies for leave‐one‐out cross‐validation (LOOCV) have been proposed and their theory fully described for GS using analytical solutions (Gianola & Schön 2016), including the importance of sampling weights in the context of Bayesian inference (Gianola & Schön 2016). Such approaches permit the estimation of CV results by running the model only once, with no need for the fully iterative implementation of LOOCV. These methods have the advantage of being computationally cost‐efficient, reducing the total amount of time to run the analysis, and avoiding the use of parallel computing. Thus, this study was carried out to assess the potential of genomic selection in Holstein cattle by investigating the accuracy of molecular breeding values for health traits. Four Bayesian specifications of genomic regression models, namely Bayesian Ridge Regression (BRR), Bayes A, Bayes B, and Bayes Cπ, were compared in terms of prediction accuracy using the “LOOCV without CV” approach.

Materials and methods

Study population, health assessment and outcomes of interest

A total of 11 733 cows calving between 2012 and 2014 on 16 dairy farms located in four US regions [northeast (four herds), midwest (six herds), southeast (one herd) and southwest (five herds)] were enrolled at parturition and monitored for health and reproductive events assessed by the research team using the same standardized protocols.

Monitoring of disease was performed on weekly visits to the study farms. Procedures included: (i) evaluation of vaginal discharge at 7 ± 3 days in milk (DIM) and 28 ± 7 DIM using a 0–5 score system – 0 = no mucus, 1 = crystalline, 2 = flecks of pus, 3 = mucopurulent <50% pus, 4 = purulent, >50% pus and 5 = watery, reddish/brownish fetid discharge; (ii) collection of blood samples at 7 ± 3 DIM for determination of serum BHBA; and (iii) lameness scoring at 35 ± 3 DIM using a 1–5 score system – 1 = normal, 2 = mildly lame (stands with flat back, but arches when walks; gait slightly abnormal), 3 = moderately lame (stands and walk with arched back), 4 = lame (arched back standing and walking, one or more limbs favored) and 5 = severely lame (arched back, refuses to bear weight in one limb, great difficulty moving from lying position).

Diseases included retained fetal membranes (RFM; membranes not expelled within 24 h after calving), metritis (MET; 7 ± 3 DIM; mucus score 5), clinical mastitis (MAST; obtained from farm records, definition consisting of udder inflammation/milk altered), left displaced abomasum (DA; farm records), lameness (LS; score >2), clinical endometritis (CE; 28 ± 3 DIM; mucus score >2), respiratory disease (RD; farm records), dystocia (DYS; calving requiring significant intervention) and subclinical ketosis (SCK; 7 ± 3 DIM; serum BHBA >1.0 mmol/l). In addition, records included milk yield tested monthly, up to 305 days after calving.

Based on phenotypic information from individual cows, a reproductive index (RI) was developed, representing a calculated predicted probability that a cow will become pregnant as a function of the explanatory variables used in a logistic model. Potential significant effects were initially tested by univariable analysis. Effects with P < 0.05 were offered to the multivariable analysis and the final model was determined through backward elimination, considering potentially significant interactions.

The final model for RI included a complement of significant fixed effects and interactions as explanatory variables influencing a pregnancy outcome: parity number; body condition score at 40 DIM; incidence of RFM; MET; resumption of ovulation by 50 DIM; region; SCK; MAST; CE; milk yield at the first milk test after calving; interaction effect of resumption of ovulation by 50 DIM × region; interaction MAST × region; and interaction milk yield at the first milk test after calving × parity number.

The RI was developed as a continuous variable, originating from the probability equation of the logistic regression model, ranging from 0 to 1, which is directly related to the probability of pregnancy: $P\left(\text{pregnancy}|\alpha ,\beta \right)={\mathrm{e}}^{\mathrm{\Sigma }{\beta }_i{Z}_i+\mu \sigma }/1+{\mathrm{e}}^{\mathrm{\Sigma }{\beta }_i{Z}_i+\mu \sigma }$, where P(pregnancy|α,β) is the probability that a cow will be pregnant given a set of fixed factors Z_i, interactions, the set of multiplicative slopes β_i and a scale parameter σ.

The selection of cows for genotyping was performed by including two groups within each farm and calving season: (i) high‐fertility individuals = diagnosed pregnant at 60 days after the first post‐partum artificial insemination and within the highest 15% RI (n = 1750); and (ii) low‐fertility individuals = cows diagnosed not pregnant on day 60 after two post‐partum artificial insemination and within the lowest 7.25% RI (n = 850).

Animals and genotyping

The initial population included 11 733 Holstein cows calving between 2012 and 2014 on 16 US farms. The dataset in analysis was composed of a subpopulation of 2505 records in cows that were determined with high and low reproductive performance based on the calculated RI. Cow records included information on the presentation of RFM, MET, MAST, DA, LS, CE, RD, DYST and SCK. Except for LS that was treated as a multicategorical variable, all other traits are dichotomous (yes or no). An exploratory analysis was performed to investigate data consistency and to evaluate the significance of environmental effects on traits. The environmental factors studied included farm (16 farms), year (2012, 2013 and 2014) and season of the calving (summer or winter), and parity (primiparous or multiparous).

A total of 2505 cows were selected based on a reproductive index (IndexP60) and genotyped using Illumina bovine hd snp chip (777 962 SNPs; Illumina, Inc.). The data‐cleaning steps removed: (i) SNPs located on sex and mitochondrial chromosomes; (ii) SNPs without map position information; (iii) SNPs with call rate less than 0.95; (iv) SNPs with MAF less than 0.01; and (v) SNPs with deviation from HWE (P < 10⁻¹⁰). After data cleaning, 603 986 SNPs were retained for analyses.

Imputation

The fimpute program version 2.2 (Sargolzaei et al. 2014) was used for imputation of missing SNP genotypes in the HD chip. This program uses deterministic methods to combine family and population information. The imputation is based on overlapping sliding windows and assumes that individuals are related to some degree. Overlapping of windows allows for consistency of haplotype phases across windows. As pedigree information was available, fimpute was run using both family‐ and population‐based algorithms, with its own default parameters.

Pedigree‐based analyses

Pedigree‐based analyses were performed using a univariate threshold animal model (logit). Such models applied belong to the class of generalized linear mixed models, which can be used to analyze data with different distributions from the exponential family (e.g. binomial). This model uses a link function relating the expected value E(y_ijkl) = μ_ijkl to the linear predictor η_ijkl. The following linear predictor was used:

$${\eta }_{\mathit{ijkl}}=\phi +{\text{YS}}_i+{\text{Parity}}_j+H_k+u_l,$$

where η_ijkl is a function of the expected phenotype, φ is an intercept, YS_i is the fixed effect of year‐season of calving (j = 1, 2, …, 5); Parity_j is the fixed effect of parity (primiparous or multiparous), H_k is a random effect for the herd of calving (k = 1, 2, …, 16) and u_l is a random effect animal (l = 1, 2, …, 11 733). The pedigree file contained the relationships of 18 610 animals.

The threshold model postulates an underlying continuous variable, liability, such that the observed binary response takes value 1 if liability exceeds a fixed threshold and 0 otherwise. The threshold and the residual variance are not identifiable, so these parameters were set equal to 0 and 1 respectively. Variance components were estimated using a generalized linear mixed model using the ai‐reml algorithm in the dmu package (Madsen & Jensen 2008).

Genomic prediction

Genomic prediction models were fit using four Bayesian specifications: BRR, Bayes A, Bayes B and Bayes Cπ. For these methods, the general statistical model is:

$$\mathit{y}=\mathbf{X}\mathit{\beta }+\sum _{j=1}^k{\mathit{m}}_j{a}_j+\mathit{e}$$

where y is an n × 1 vector of phenotypic information, β is a p × 1 vector of fixed effects, X is the incidence matrix for fixed effects, m _j is an n × 1 vector representing the genotypes of the jth SNP for all of the animals (j = 1, 2,…, k), a_j is the genetic effect of the jth SNP and $\mathit{e}\approx N\left(0,I{\sigma }_{\mathrm{e}}^2\right)$ is a vector of residuals.

In the BRR method, an independent Gaussian prior with common variance is assigned to each regression coefficient, that is, $p(a_1,a_2,\dots ,a_k|{\sigma }_a^2)=\prod _{j=1}^{k}N(a_j|0,{\sigma }_a^2)$. The variance parameter ${\sigma }_a^2$ is treated as an unknown and assigned a scaled inverse chi‐squared (χ ⁻²) prior density, $p({\sigma }_a^2)={\chi }^{-2}({\sigma }_a^2|v_a,S_a^2)$, with degrees of freedom, $v_a=2$ and scale $S_a^2$. Similarly, a χ ⁻² prior density is assumed also for the residual variance ${\sigma }_{\mathrm{e}}^2$, i.e. $p({\sigma }_{\mathrm{e}}^2)={\chi }^{-2}({\sigma }_{\mathrm{e}}^2|v_{\mathrm{e}},S_{\mathrm{e}}^2)$.

In the Bayes A model (Meuwissen et al. 2001), independent Gaussian distributions are assumed a priori for the SNP effects a_j, $a_j\approx N(0,{\sigma }_{a_j}^2)$, with zero mean and SNP‐specific dispersion parameter ${\sigma }_{a_j}^2$. The variance associated with the effect of each SNP is assigned an independent and identically distributed scaled inverse chi‐square prior to distribution, $p({\sigma }_{a_j}^2)={\chi }^{-2}({\sigma }_{a_j}^2|v_a,S_a^2)$, where $v_a$ and $S_a^2$ are known degrees of freedom and scale parameters respectively. With these specifications, the marginal prior distribution of each marker effect follows a t‐distribution, $p(a_j|v_a,S_a^2)={\int }_0^{\infty }N(a_j|0,{\sigma }_{a_j}^2){\chi }^{-2}({\sigma }_{a_j}^2|v_a,S_a^2)\mathrm{d}{\sigma }_{a_j}^2$, i.e. $p(a_j|v_a,S_a^2)=t(0,v_a,S_a^2)$ (Rosa et al. 2003).

The Bayes B model (Meuwissen et al. 2001) assumes that, a priori, an SNP has no effect at all with a probability π, or it follows a normal distribution with zero mean and an SNP‐specific variance ${\sigma }_j^2$ with a probability 1 − π. That is,

$$p(a_j|{\sigma }_{a_j}^2,\pi )=\left\{\begin{array}{cc}0& \text{with}\text{probability}\pi \\ N(0,{\sigma }_{a_j}^2)& \text{with}\text{probability}(1-\pi )\end{array}\right.$$

Again, the prior distribution of SNP variances is a scaled inverse chi‐square distribution. Thus, the marginal prior distribution of a_j, after integrating ${\sigma }_{a_j}^2$ out, is a mixture distribution, as follows:

$$p(a_j|\pi )=\left\{\begin{array}{cc}0& \text{with}\text{probability}\pi \\ t(0,v_a,S_a^2)& \text{with}\text{probability}(1-\pi )\end{array}\right.$$

The Bayes Cπ method (Habier et al. 2011) is similar to the Bayes B approach, except that a prior distribution is also assumed for the proportion π of null‐effect markers, and that a Gaussian prior with a common variance is assumed for each of the non‐null marker effects. The inclusion (or exclusion) of each marker in the model is modeled by an indicator variable δ_j, which is equal to 1 if the marker j is fitted in the model or it is zero otherwise.

Predictive ability

The predictive ability was assessed by employing the strategy called “cross‐validation without doing cross‐validation” (Gianola & Schön 2016). The model performance was assessed using the area under the curve, the mean square error of the prediction and accuracy, defined as the correlation between the phenotypic information and its predicted genomic breeding value. The LOOCV without CV was performed for the Bayesian models by weighing the marker effects by importance sampling weights (Gelfand 1992; Gianola & Schön 2016). The following steps were used to assess the predictive ability:

For the GBLUP method, the algorithm used to predict the genomic breeding value û can be described as follows:

1. Compute the GEBV using the whole dataset:

$$\widehat{u}={\mathbf{C}}^{-1}y.$$

where ${\mathbf{C}}^{-1}={(I+{\mathbf{G}}^{-1}\lambda )}^{-1}$ and $\lambda ={\sigma }_{\mathrm{e}}^2/{\sigma }_{\mathrm{g}}^2$.

1. For $i=1,2,\dots ,n$

$${\tilde{u}}_i=\frac{1}{1-c^i}({\widehat{u}}_i-c^i{y}_i),$$

where G is the genomic relationship matrix, λ is the ratio between the residual and genetic variances and cⁱ is the diagonal element of the ith individual obtained from the matrix C ⁻¹.

The LOOCV without CV can be performed for the Bayesian alphabet methods by weighting the marker effects by importance sampling weights (Gelfand 1992; Gelfand & Sahu 1999; Gianola & Schön 2016; Vehtari et al. 2017). The following steps can be used to access the prediction accuracy:

1. Once the Markov chain Monte Carlo (MCMC) iterations are completed, the importance sampling weights for the marker effects can be computed as follows:

$$w_{i,s}=\frac{\exp \left[\frac{{\left(y_i-x_i{a}_s\right)}^2}{2{\sigma }_{\mathrm{e}}^2}\right]}{{\sum }_{s=1}^s\exp \left[\frac{{\left(y_i-x_i{a}_s\right)}^2}{2{\sigma }_{\mathrm{e}}^2}\right]}$$

1. For $i=1,2,\dots ,n$,

$${\tilde{u}}_i={\mathit{m}}_i\sum _{s=1}^s{w}_{i,s}{a}_i^{(s)}$$

where w is the importance sampling weight, a is the marker effect, y is the phenotype and m _i is a vector representing the genotypes of the ith animal.

Genomic heritability

The narrow‐sense genomic heritabilities (h²) were estimated using the BRR, Bayes A, Bayes B, and Bayes Cπ models as:

$$h^2=\frac{{\sigma }_{\mathrm{g}}^2}{{\sigma }_{\mathrm{g}}^2+{\sigma }_{\mathrm{e}}^2},$$

where ${\sigma }_{\mathrm{g}}^2$ and ${\sigma }_{\mathrm{e}}^2$ are the genomic and residual variances respectively. The genomic variance was calculated as

$${\sigma }_{\mathrm{g}}^2=\sum _{i=1}^{j}2p_j(1-p_j)a_j^2.$$

Analyses and computer resources

The bglr package (de los Campos & Pérez‐Rodríguez 2014) was used to fit the BRR, Bayes A, Bayes B and Bayes Cπ models using an MCMC method. For each model, the MCMC sampling length was 100 000 iterations, with the first 80 000 excluded as the burn‐in and a thinning interval of 10. Convergence was checked by visual inspection of trace plots and the convergence tests of Brooks, Gelman, and Rubin (Gelman & Rubin 1992) and Geweke (1992). The analyses were performed using the UW–Madison Center for High Throughput Computing in the Department of Computer Sciences.

Results and discussion

One of the most significant advances in dairy cattle health and welfare in recent decades has been the shift from treatment of clinical diseases to the implementation of preventive strategies to maintain health (LeBlanc et al. 2006). Moreover, significant research efforts are now centered on exploring genetic variation associated with the ability of animals to control disease (König & May 2019).

As reported in the literature (Gagneur et al. 2011; Miar et al. 2014), with the continuous reduction of genotyping costs over time, phenotyping has become the most important component in the calibration of GS models. In addition, the identification of a model that provides the best predictive ability and captures most of the genetic variance is one of the most important steps in genomic prediction.

Unlike the Bayesian models that use a probit link function, the pedigree‐based analyses performed to estimate the heritability used a threshold model with logit as a link function. In addition to the 2505 cows used in the genomic analyses, there were more 9229 cows with valid records. The pedigree‐based heritability ranged from 0.0418 (0.0168) to 0.3849 (0.1127) for CE and RD respectively (Table 1). The SNP‐heritability ranges among models for the health traits were (Table 2): RFM, 0.13 (Bayesian Ridge Regression) and 0.19 (Bayes B); MET, 0.12 (Bayes A) and 0.16 (Bayes Cπ); MAST, 0.09 (Bayes A) and 0.14 (Bayes B); DA, 0.06 (Bayesian Ridge Regression) and 0.09 (Bayes Cπ); lameness, 0.15 (Bayes B) and 0.20 (Bayes A); CE, 0.10 (Bayesian Ridge Regression) and 0.21 (Bayes A); RD, 0.09 (Bayesian Ridge Regression) and 0.19 (Bayes Cπ); DYST, 0.10 (Bayesian Ridge Regression) and 0.22 (Bayes Cπ); and SCK, 0.12 (Bayesian Ridge Regression) and 0.19 (Bayes A). Figures S1–S9 show Manhattan plots visualizing the genetic architecture of the health disorders considered in this study. Although the models usually deliver similar predictive abilities when properly tuned, their prior assumptions, distributions and the variable selection performed by some models (i.e. Bayes B and Bayes Cπ) result in different marker effect estimates, which could explain the difference in the genomic heritabilities obtained within traits.

Table 1.

Genetic variance and heritability estimated using pedigree‐based logit mixed model.

Trait	Genetic variance (SD)	Herd variance (SD)	Heritability1
Retained placenta	0.6338 (0.2555)	0.1675 (0.0010)	0.1516 (0.0536)
Metritis	0.1920 (0.0748)	0.0589 (0.0007)	0.0538 (0.0200)
Mastitis	0.6077 (0.2329)	0.1946 (0.0005)	0.1457 (0.0490)
Displaced abomasum	1.3013 (0.5794)	0.1927 (0.0028)	0.2608 (0.0944)
Lameness	1.5849 (0.5800)	0.2045 (0.0000)	0.3027 (0.0831)
Clinical endometritis	0.1477 (0.0614)	0.0685 (0.0001)	0.0418 (0.0168)
Respiratory disease	2.3445 (0.9729)	0.1824 (0.0009)	0.3849 (0.1127)
Dystocia	1.1502 (0.4278)	0.0803 (0.0002)	0.2476 (0.0730)
Subclinical ketosis	0.7009 (0.2615)	0.3287 (0.0000)	0.1592 (0.0514)

¹Logit model: $h^2={\sigma }_{\mathrm{u}}^2+{\sigma }_{\mathrm{h}}^2+{\pi }^2/3$, where ${\sigma }_{\mathrm{u}}^2$ and ${\sigma }_{\mathrm{h}}^2$ are the estimated additive genetic and herd variances respectively.

Table 2.

Genomic heritability for retained placenta, metritis, mastitis, displaced abomasum, lameness, clinical endometritis, respiratory disease, dystocia and subclinical ketosis using the Bayesian alphabet.

Trait	Bayesian Ridge Regression	Bayes A	Bayes B	Bayes C
Retained placenta	0.1342 (0.0017)	0.1576 (0.0011)	0.1935 (0.0039)	0.1729 (0.0027)
Metritis	0.1501 (0.0077)	0.1202 (0.0006)	0.1404 (0.0036)	0.1687 (0.0029)
Mastitis	0.1299 (0.0025)	0.0995 (0.0013)	0.1428 (0.0055)	0.1016 (0.0019)
Displaced abomasum	0.0609 (0.0014)	0.0671 (0.0005)	0.0799 (0.0004)	0.0965 (0.0014)
Lameness	0.1621 (0.0042)	0.2076 (0.0018)	0.1356 (0.0027)	0.1687 (0.0105)
Clinical endometritis	0.1071 (0.0014)	0.2129 (0.0014)	0.1327 (0.0016)	0.1803 (0.0042)
Respiratory disease	0.0908 (0.0007)	0.1263 (0.0014)	0.1311 (0.0008)	0.1921 (0.0028)
Dystocia	0.1043 (0.0018)	0.2064 (0.0019)	0.1783 (0.0026)	0.2246 (0.0075)
Subclinical ketosis	0.1249 (0.0039)	0.1922 (0.0019)	0.1338 (0.0039)	0.1613 (0.0095)

Table 3 shows the results of CV analysis for the predictive ability, in which a measure of the overall fit achieved with each method was assessed by the mean square error of prediction. The Bayesian Ridge Regression had the smallest mean square error for RFM; Bayes A for DA and CE; Bayes B for MET and MAST; and Bayes Cπ for lameness, RD, DYST and SCK.

Table 3.

Predictive ability (accuracy), area under the ROC curve (AUC) and mean squared error of prediction for retained fetal membranes, metritis, mastitis, displaced abomasum, lameness, clinical endometritis, respiratory disease, dystocia and subclinical ketosis using GBLUP and four Bayesian model specifications: Bayesian Ridge Regression, Bayes A, Bayes B and Bayes C.

Trait	GBLUP	Bayesian Ridge Regression	Bayes A	Bayes B	Bayes C
	Accuracy
Retained placenta	0.2600	0.2009	0.3000	0.3401	0.3219
Metritis	0.3360	0.3629	0.2097	0.2932	0.2418
Mastitis	0.3170	0.2352	0.1984	0.5546	0.2044
Displaced abomasum	0.1710	0.0615	0.0258	0.1275	0.2572
Lameness	0.1040	0.0858	0.1160	0.0931	0.1227
Clinical endometritis	0.3100	0.2530	0.3178	0.2780	0.2671
Respiratory disease	0.2510	0.0280	0.2105	0.1122	0.2350
Dystocia	0.2590	0.1307	0.3481	0.1443	0.3156
Subclinical ketosis	0.3480	0.2316	0.3023	0.2178	0.3761
	AUC
Retained placenta	0.7750	0.6819	0.7670	0.8108	0.7881
Metritis	0.7170	0.7332	0.6320	0.6805	0.6528
Mastitis	0.7810	0.6930	0.6593	0.8870	0.6707
Displaced abomasum	0.8630	0.6111	0.5515	0.7209	0.8829
Lameness	0.5809	0.6467	0.6364	0.5656	0.6572
Clinical endometritis	0.6920	0.6488	0.6896	0.6636	0.6624
Respiratory disease	0.8140	0.5626	0.8440	0.6799	0.8957
Dystocia	0.6970	0.5947	0.7301	0.6109	0.7133
Subclinical ketosis	0.7520	0.6531	0.7016	0.6447	0.7598
	Mean square error
Retained placenta	0.8970	0.2446	0.5299	0.3414	0.3077
Metritis	0.3700	0.3996	0.2481	0.1988	0.4018
Mastitis	0.7430	0.5279	0.3446	0.0879	0.5666
Displaced abomasum	0.3130	0.1940	0.1453	0.3283	0.3299
Lameness	1.4090	1.7929	1.3596	1.1740	1.0702
Clinical endometritis	0.4490	0.2634	0.2187	0.2330	0.2630
Respiratory disease	1.7760	0.5032	0.4340	0.6731	0.0202
Dystocia	0.1530	0.1370	0.1372	0.3051	0.1279
Subclinical ketosis	0.5380	0.4337	0.3405	0.4614	0.2971

Except for DA, lameness and RD, the predictive abilities were similar across models for all other traits. Overall, these results are in accordance with results in the literature (de los Campos et al. 2013; Gianola 2013), which indicate the similarity of the Bayesian models in terms of predictive ability. The models for best predictive abilities were: RFM, Bayes B (r = 0.34 and AUC = 0.81); MET, Bayes B (r = 0.34 and AUC = 0.81); MAST, Bayes B (r = 0.55 and AUC = 0.89); DA, Bayes Cπ (r = 0.26 and AUC = 0.88); lameness, Bayes Cπ (r = 0.26 and AUC = 0.88); CE, Bayes A (r = 0.32 and AUC = 0.69); RD, Bayes Cπ (r = 0.23 and AUC = 0.91); DYST, Bayes Cπ (r = 0.23 and AUC = 0.91); and SCK, Bayes Cπ (r = 0.23 and AUC = 0.91) respectively (Table 3).

The relatively low estimates of heritability might have limited the prediction accuracies of genomic breeding values. The correlation (Fig. 1) between heritability and accuracy (across methods and traits) ranges from 0.21 (Bayes C) to 0.64 (Bayes A) and from 0.30 (MET) to 0.93 (RFM). These positive and overall high estimates of correlation show that the heritability has indeed limited the prediction accuracies, among other factors. In fact, some authors have reported superior accuracies of genomic breeding values in scenarios involving higher heritable traits as well as larger numbers of phenotypic records and genotyped animals (Bolormaa et al. 2013a,b; Neves et al. 2014; Fernandes Júnior et al. 2016).

Figure 1.

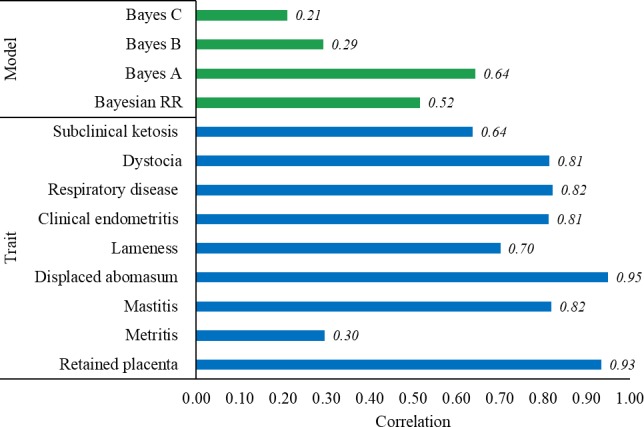
The correlation between heritability and accuracy across methods and traits.

Although four different modeling approaches were used for the genomic prediction, the correlations between phenotypes and their genomic breeding values were similar among them. However, it is important to stress that results from any specific genomic selection application cannot always be easily applied to other populations. This means that each application should involve its own model comparison exercise to maximize the predictive ability for each trait.

Conclusion

In this study, we investigated different methods for genomic prediction of breeding values of RFM, MET, MAST, DA, lameness, CE, RD, DYST and SCK. Except for DA, lameness and RD, the predictive abilities were similar between methods. Although the relatively low estimates of heritability might have limited the prediction accuracies of genomic breeding values, there was observed a strong relationship between the predictive ability and the heritability of the trait, where traits with higher heritability achieved higher accuracy and lower bias when compared with those with lower heritability. Overall, the information from high‐density SNP panel can be successfully used to predict genomic breeding values of health traits in Holstein cattle, but the model choice will most likely depend on the genetic architecture of the trait.

Conflict of interest

The authors declare that there is no conflict of interest.

Supporting information

Appendix S1 Genome‐wide association study for health traits.

Figures S1–S9 show Manhattan plots visualizing the genetic architecture of retained fetal membranes, metritis, mastitis, displaced abomasum, lameness, clinical endometritis, respiratory disease, dystocia and subclinical ketosis.

Data availability

The phenotypes and SNP datasets of this Holstein population will be made accessible upon request for reproduction of results.