Microscopic Properties of Na and Li—A First Principle Study of Metal Battery Anode Materials

Abstract

Using density functional theory, we studied the bulk and surface properties of Li and Na electrodes on an atomistic level. To get a better understanding of the initial stages of surface growth phenomena (and thus dendrite formation), various self‐diffusion mechanisms were studied. For this purpose, dedicated diffusion pathways on the surfaces of Na and Li were investigated within the terrace‐step‐kink (TSK) model utilizing nudged elastic band calculations. We were able to prove that the mere investigation of terrace self‐diffusion on the respective low‐index surfaces does not provide a possible descriptor for dendritic growth. Finally, we provide an initial view of the surface growth behavior of both alkali metals as well as provide a basis for experimental investigations and theoretical long‐scale kinetic Monte Carlo simulations.

From the atom up: Needle‐like dendrite growth may cause internal short circuits or even induce a thermal runaway in metallic Na and Li batteries. Therefore, we have investigated the fundamental diffusion and surface properties of both metals by means of first‐principle calculations. These results provide important insights into the diffusion on an atomic level that determines the overall growth phenomena.

Introduction

Li‐ion batteries (LIBs) have been the leading technology in the field of electrochemical energy storage since its commercial market launch in 1991 by Sony.1 Li is the lightest metallic element (0.59 g cm⁻³) with a low redox potential [−3.04 V vs. standard hydrogen electrode (SHE)] and an extremely high theoretical capacity of 3860 mAh g⁻¹ (2062 mAh cm⁻³).2, 3, 4 Thus, the fabrication of batteries featuring high voltage and high energy density became feasible, making LIBs the common type of secondary battery cells. Until today, almost all portable devices in the modern world are powered by rechargeable LIBs. Consequently, since 2010 the price has risen substantially owing to the world‐wide increasing demand for Li.5 Furthermore, most of the global Li resources are located in distant or politically sensitive geographical regions.6 Here, Na‐ion batteries (SIBs) are considered a promising alternative to LIBs,2, 7 as Na is inexpensive and has a high natural and uniform abundance in the earth's crust.2, 8 Cathode materials for Li‐ion‐based systems can readily be adapted to SIBs and the more expensive Cu negative current collector can be replaced by cheaper Al. However, Na‐ions have a much larger mass‐to‐electron ratio (23.00) compared to Li‐ions (6.94), which may reduce their diffusivity.9 Moreover, Na only intercalates into hard carbon but not into graphite, which would be more suitable as electrode material owing to its higher specific capacity and specific gravity.10 Hence, the use of a Na‐metal anode instead of graphitic electrodes is promising. Metallic Na batteries have a high energy density owing to the high theoretical specific capacity of 1166 mAh g⁻¹ (1131 mAh cm⁻³) and a very suitable redox potential of −2.71 V vs. SHE. As also for metallic Li batteries, major challenges and safety issues must first be tackled to enable the commercial viability of such an Na‐ion‐based energy storage system. The high reactivity of metallic Na with electrolytes leads to the formation of an inhomogeneous solid electrolyte interface (SEI). Further, low plating–stripping Coulombic efficiency (CE) is observed, resulting in a rapid capacity decrease after repeated charge/discharge cycles.11, 12 Dendritic electrochemical deposition on metallic Na electrodes raises serious safety hazards as it may cause short circuits in the cell or induce a thermal runaway.

Analogous to Li metal battery systems,13, 14 different strategies were pursued to stabilize the Na metal surface. Possible techniques involve the formation of a protective layer on the electrode to prevent direct contact between metallic Na and the electrolyte.15 Also, novel electrolyte compositions were introduced to increase the interfacial stability of metallic Na anodes.12, 16 In further works, the liquid electrolyte was replaced by a solid electrolyte to create a natural barrier against the formation of dendrites.17 However, poor reversibility and large volume change in upscaled metallic Na batteries remain an unsolved challenge. Although various strategies exist to suppress dendritic growth, its initial stages are still not fully understood on an atomistic level.

Owing to the high reactivity of metallic Na and Li, the study of microscopic surface properties is experimentally hardly accessible. As in our preliminary work on metallic Li electrodes,3 we will explore the atomistic properties of Na and Li utilizing density functional theory (DFT). First, we focused on the various bulk properties of both alkaline metals as well as the structural and energetic information of the low‐index surfaces. Afterwards, the gained information is employed to investigate well‐selected diffusion processes on perfect and imperfect surface structures. The generated data set enables us to gain a deeper understanding of the bulk and surface characteristics as well as to extract preliminary information for the formation of dendrites at a microscopic perspective.

Methodology

First‐principles DFT calculations were carried out using the Vienna Ab initio simulation package (VASP)18 within the projector‐augmented‐plane‐wave (PAW) method.19 As exchange‐correlation functional, the Perdew–Burke–Ernzerhof generalized gradient approximation (PBE‐GGA)20 functional was applied. Standard deviations were determined using the Bayesian error estimation functional with van der Waals (BEEF‐vdW) exchange‐correlation functional.21 All total energy calculations were performed using a k‐point mesh density of 0.15 Å⁻¹, according to the scheme of Monkhorst and Pack.22 For the integration of the Brillouin zone (BZ) the Methfessel–Paxton method23 with a smearing width of 0.2 eV was applied. As a result of our extensive convergence studies, the energy cut‐off for the plane‐wave expansion was set to 340 eV. The electronic self‐consistent field (SCF) cycle was considered converged when the total energy difference was less than 10⁻⁵ eV, and all forces were at least smaller than 10⁻³ eV Å⁻¹. The transition state of the minimum energy path (MEP) was identified utilizing climbing image nudged elastic band (CI‐NEB) calculations, as implemented in the transition state tools for VASP (VTST) of Henkelman and Jónsson.24 All images have been separated by a spring constant of 5.0 eV Å⁻² to guarantee continuity of the path.

The investigated surface properties were simulated within the supercell approach. A vacuum region of 20 Å along the z‐axis has been introduced to prevent the interaction between the surfaces of periodic replicas. Well‐converged symmetrical slabs with a thickness of 30–35 Å were utilized to determine the respective surface energies of the low‐index single crystal surface configurations. Here, a single atom was kept fixed in the center of the slab to avoid net translations. Asymmetrical eight‐, eight‐, and thirteen‐layer slabs were used to simulate the adsorption and diffusion properties on (100), (110), and (111) surface planes, respectively. Here, the two lowermost layers for the (100) and (110) surfaces, as well as the bottom three layers of (111) planes were kept in their corresponding bulk configuration. Whereas 2 D diffusion processes were investigated on (6×6) Na(100) and (6×6) Li(100) surface unit cells, we chose a vicinal 5(100)×(110) slab to achieve an accurate description of the 3 D diffusion properties on step‐edges.

Results and Discussion

In this section, we first discuss the bulk properties of metallic Na and Li. Subsequently, surface and adsorption properties of the low‐index surfaces are presented. Here, we calculated the standard deviation of the respective quantities utilizing the BEEF xc‐functional.21 The error estimation was done by constructing a probability distribution of functionals, represented by an ensemble of functionals. For a deeper understanding of surface growth phenomena, we will then focus on decisive self‐diffusion processes on perfect and imperfect surfaces. In the future, all these data will serve as a basis for the development and validation of a reactive force‐field as well as for further studies of nucleation and growth events on metallic Na and Li electrodes.

Bulk properties

First, we studied the properties of Li and Na in various bulk phases: body‐centered cubic (bcc), face‐centered cubic (fcc), hexagonal close‐packed (hcp), and samarium 9R (hR9). Further investigated bulk phases [(i.e., ß‐tungsten (a15), diamond (dia), and simple‐cubic (sc)] are given in the Supporting Information. For this purpose, the equation of state (EOS) for each of these crystal structures was determined through the uniform expansion and compression of the bulk unit cell. Based on the obtained results, we determined the bulk modulus B ₀ as well as the lattice constant α ₀ by an inverse third‐order polynomial fit according to the stabilized jellium equation of state (SJEOS).25, 26 As a measure of the compressibility of a given material, the bulk modulus is an important experimental benchmark and serves as an essential criterion in the optimization of a reactive force‐field. The required energy to separate individual atoms of a solid from each other and bring them to an assembly of neutral free atoms27 is known as the cohesive energy E _coh and is calculated by subtracting the energy of an isolated atom E _atom of the minimum bulk energy E _bulk divided by the number of atoms per unit cell N:

$${\displaystyle E_{\mathrm{coh}}=-\frac{1}{N}\left(E_{\mathrm{bulk}}-N•E_{\mathrm{atom}}\right)}$$ (1)

In general, the direct comparability of ground‐state electronic structure calculations (performed at T=0 K) and experimental findings is not feasible as the zero‐point phonon effects (ZPPEs), temperature effects, and zero‐point vibrational energy (ZPVE) have to be taken into account. However, we can estimate the influence of these quantities utilizing the concepts of Perdew and co‐workers.25, 26, 28 The impact of the ZPPEs on the lattice constant α ₀ can be estimated within the zero‐point anharmonic expansion (ZPAE). Utilizing the Grüneisen parameter from the Dugdale–MacDonald model29 and the Debye approximation for the mean phonon frequency, the volume change can be calculated by25, 30

$${\displaystyle \frac{\Delta a_0}{a_0}=\frac{\Delta v_0}{3v_0}=\frac{3}{16}\left(B_1-1\right)\frac{k_{\mathrm{B}}{\theta }_{\mathrm{D}}}{B_0{v}_0}}$$ (2)

For the lattice constant α ₀, the bulk modulus B ₀ and its pressure derivative B ₁, the equilibrium volume ν ₀, and the Debye temperature θ _D experimental reference values are used. Furthermore, the Debye temperature can be used to calculate the ZPVE to adapt the experimental cohesive energy.28

$${\displaystyle E_{\mathrm{Z}\mathrm{P}\mathrm{V}\mathrm{E}}=\frac{9}{8}{k}_{\mathrm{B}}{\theta }_{\mathrm{D}}}$$ (3)

An estimation for the bulk modulus can be done via

$${\displaystyle \frac{\Delta B_0}{B_0}=-\left[\frac{1}{2}\left(B_1-1\right)+\frac{2}{B_1-1}\left(\frac{2}{9}-\frac{1}{3}{B}_1-\frac{1}{2}{B}_0{B}_2\right)\right]\frac{\Delta v_0}{v_0}}$$ (4)

where B ₂ is the second derivative of the bulk modulus B ₀.

Table 1 shows the calculated and experimental lattice constants, cohesive energies, and bulk moduli for Na and Li. All values were deduced from the EOS of the different bulk phases calculated by the PBE and BEEF‐vdW functionals.

Table 1.

Calculated (PBE, BEEF‐vdW) and experimental (Expt.) physical constants for important bulk phases of Na and Li.^[a]

Material	Method	a 0 [Å]				c 0 [Å]		E coh [eV atom−1]				B 0 [GPa]
		bcc	fcc	hcp	hR9	hcp	hR9	bcc	fcc	hcp	hR9	bcc	fcc	hcp	hR9
Na	PBE	4.19	5.29	3.74	3.72	6.11	27.0	1.09	1.09	1.09	1.09	7.96	7.87	7.91	7.84
	BEEF‐vdW	4.18	5.27	3.73	3.71	6.09	27.71	1.15 (0.25)	1.14 (0.25)	1.14 (0.25)	1.14 (0.25)	8.48	8.43	8.38	8.43
	Expt.	4.21 (0.02)	–	–	–	–	–	1.13 (0.02)	–	–	–	7.73 (−0.03)	–	–	–
Li	PBE	3.443	4.333	3.063	3.07	5.003	22.33	1.613	1.613	1.613	1.61	13.923	13.863	13.873	13.97
	BEEF‐vdW	3.40	4.28	3.03	3.04	4.95	22.09	1.66 (0.16)	1.66 (0.16)	1.65 (0.16)	1.66 (0.16)	15.43	15.50	15.21	15.47
	Expt.	3.45 (0.03)	–	–	–	–	–	1.67 (0.03)	–	–	–	13.90 (−0.05)	–	–	–

[a] All experimental results were taken from Ref. 28. For BEEF‐vdW the calculated standard deviation of the cohesive energy is given in parentheses. For the experimental data of a ₀, E _coh, and B ₀ the values of Δa ₀/a ₀, zero‐point vibrational energy correction E _ZPVE, and ΔB ₀/B ₀ are given in parentheses, respectively.

Both nearly free‐electron alkali metals are crystallizing in a bcc structure under ambient conditions. Moreover, Na and Li transform into a surface‐centered phase on compression followed by a pressure‐induced symmetry lowering.31, 32 At ambient pressure conditions and at a temperature below ≈77 K, Li exhibits a martensitic transition. Barrett initially identified the low‐temperature phase as hcp.33 Later, this was resolved as the hR9 structure, which has a nine‐layer stacking sequence and seems to be the ground‐state structure.31, 34 Likewise, bcc Na undergoes a martensitic transition to a closed‐packed structure, which is assigned to be either hcp 33 or a 9R structure.35 For both alkali metals, the PBE functional reveals excellent agreement between the theoretically and experimentally obtained lattice constants and bulk moduli. However, it underestimates the cohesive energy for Na by 0.04 eV and for Li by 0.06 eV. While the BEEF‐vdW functional slightly underestimates the lattice constant and tends to overestimate the bulk modulus, the energetics of the bcc bulk phases are described very well. The computational error estimation showed standard deviations of 0.25 eV (Na) and 0.16 eV (Li) for the cohesive energies of the various bulk phases and thus exhibited a significant dependence of this quantity regarding to the chosen functional.

In the most stable phase, the cohesive energy of Li is 0.51 eV higher as the value for Na. Further, the investigation of the respective bulk moduli revealed a higher stiffness of Li relative to Na in all bulk phases.

Surface energies

The surface energy $\gamma$ of a solid is an important physical quantity that affects a wide range of phenomena such as the rate of sintering, the stress for brittle fracture, surface segregation, or the equilibrium shape of mesoscopic crystals. It is defined as the surface excess free energy per unit area and can be obtained by

$${\displaystyle \gamma =\frac{1}{2A}\left(E_{\mathrm{slab}}-N•E_{\mathrm{bulk}}\right),}$$ (5)

where E _slab is the total energy of the slab, E _bulk is the bulk energy per atom, $A$ is the surface area, and $N$ is the number of atoms per supercell.36

Table 2 summarizes the theoretical and experimental surface energies for the low‐index surfaces of Na and Li. We also estimated the computational error over an ensemble of functionals generated within the Bayesian error estimation functional framework.

Table 2.

Theoretical and experimental surface energies γ for low‐index surfaces of Na and Li.^[a]

Material	Method	Surface energy [J m−2]
		γ 100	γ 110	γ 111
Na	PBE	0.247	0.246	0.271
	BEEF‐vdW	0.282 (0.043)	0.279 (0.039)	0.304 (0.043)
	Expt.	–	0.260, 0.261	–
Li	PBE	0.4733	0.4993	0.5423
	BEEF‐vdW	0.583 (0.076)	0.619 (0.075)	0.652 (0.080)
	Expt.	–	0.522, 0.525	–

[a] For BEEF‐vdW, the calculated standard deviation of the respective surface is given in parentheses. Experimental values are from Refs. 37 and 38.

In general, the thermodynamic stability sequence (110)<(100)<(111) is observed for the low‐index bcc alkali metal surfaces. However, Li is not in‐line with the predetermined trend, revealing a more stable Li(100) surface.3, 39 Whereas the surface energies of Na(100) and Na(110) are almost degenerate, Li(100) is slightly more stable than Li(110). For both metals, the (111) surface is the least stable low‐index orientation. However, it should be noted that the energy difference for the investigated surfaces is at most 0.03 J m⁻² for Na and 0.07 J m⁻² for Li, which is in the range of the calculated standard deviation. Both DFT functionals are in good agreement with the experimental findings. As the experimental values were obtained measuring the liquid surface tension and subsequent interpolation to zero, a direct comparison of the results is difficult.

Adsorption energies

We investigated the adsorption energy E _Ad of the atomic species on the low‐index surfaces of Na and Li to determine the binding strength on various adsorption sites. The adsorption energy was calculated by the energy difference between the separated constituents (clean surface+adatom) and the interacting system

$${\displaystyle E_{\mathrm{Ad}}=E_{\mathrm{tot}}-(E_{\mathrm{slab}}+E_{\mathrm{atom}})}$$ (6)

Table 3 summarizes the calculated adsorption energies of the atomic species on the low‐index surfaces of Na and Li as well as the estimated standard deviation.

Table 3.

Calculated adsorption energies of the atomic species on the (6×6) (100), (4×6) (110), and (4×4) (111) surfaces of Na and Li.^[a]

Material	Method	Absorption energies [eV atom−1]
		(100)			(110)				(111)
		bridge	hollow	ontop	hollow	long‐bridge	short‐bridge	ontop	bridge	fcc	hcp	ontop
Na	PBE	−0.81	−0.90	−0.59	−0.81	−0.82	−0.79	−0.78	−0.88	−1.11	−0.84	−0.51
	BEEF‐vdW	−0.87 (0.26)	−0.98 (0.26)	−0.67 (0.23)	−0.89 (0.27)	−0.90 (0.25)	−0.85 (0.24)	−0.85 (0.25)	−0.95 (0.26)	−1.16 (0.25)	−0.92 (0.26)	−0.57 (0.26)
Li	PBE	−1.233	−1.273	−1.073	−1.343	−1.353	−1.353	−1.393	−1.333	−1.613	−1.223	−0.903
	BEEF‐vdW	−1.27 (0.15)	−1.32 (0.15)	−1.10 (0.13)	−1.38 (0.14)	−1.38 (0.13)	−1.38 (0.13)	−1.43 (0.14)	−1.36 (0.15)	−1.65 (0.16)	−1.26 (0.15)	−1.01 (0.12)

[a] For BEEF‐vdW, the calculated standard deviation of the adsorption energy is given in parentheses.

We find a stronger binding between the substrate and its adatom for Li compared to Na on all investigated surfaces. On Na(100) and Li(100), the four‐fold hollow‐site is the most stable adsorption position followed by the metastable bridge‐ and ontop‐positions. Whereas for Na(110) the adsorption of the atomic species on the long‐bridge‐position shows the utmost stability, on Li(110) the ontop‐position is preferred. However, the maximum energy difference between the respective adsorption sites on Na(110) and Li(110) is less than 0.05 eV atom⁻¹. For the (111) surfaces of both alkali metal, we found a very “rough” energy landscape. The energy difference between the most stable fcc‐position and the unstable ontop‐position is more than 0.6 eV atom⁻¹ for Na and Li, respectively. Both DFT functionals provide the same stability order for the different adsorption sites and deviate moderately in the calculated adsorption energies. Further, we have obtained a standard deviation of 0.25 eV atom⁻¹ and 0.15 eV atom⁻¹ for Na and Li, indicating a significant dependence of the total adsorption energy on the selected functional.

Terrace self‐diffusion

In the next step, we investigated the self‐diffusion properties on the perfect low index surfaces of Na and Li. Compared to other studies reported in literature,40, 41 we have identified critical diffusion processes that were not taken into account so far. Further, we found that extended slab configurations are necessary to obtain really converged diffusion barriers.5

Table 4 summaries the obtained self‐diffusion barriers of Na and Li on their low‐index surfaces as well as the respective standard deviations. An overview of the various investigated diffusion pathways is given in Figure 1. Further, estimated room‐temperature reaction rates are given in the Supporting Information. For both alkali metals, the fourfold hollow‐site is the preferred adsorption position on the (100) plane. On a defect‐free terrace, the adjacent sites can be accessed either by atom‐hopping via the bridge‐ and ontop‐position or by a surface exchange mechanism. Whereas Na favors the exchange mechanism [h₀↔h₂ (Ex.), $E_{\mathrm{a}}$ =0.06 eV], the dominant process for Li is the atom‐hopping via the bridge position (h₀↔h₁, $E_{\mathrm{a}}$ =0.04 eV). In both cases, the pathway across the ontop position (h₀↔h₂) is the least favored one.

Table 4.

Calculated terrace self‐diffusion barriers of Na and Li on its low‐index surfaces.

Material	Surface		$E_{\mathrm{a}}^{\mathrm{f}\mathrm{o}\mathrm{r}}$  [eV]		$E_{\mathrm{a}}^{\mathrm{r}\mathrm{e}\mathrm{v}}$  [eV]
	plane	position	PBE	BEEF‐vdW	PBE	BEEF‐vdW
Na	(100)	h0↔h1	0.09	0.11 (0.03)	0.09	0.11 (0.03)
		h0↔h2	0.31	0.31 (0.09)	0.31	0.31 (0.09)
		h0↔h2 (Ex.)	0.06	0.06 (0.03)	0.06	0.06 (0.03)
	(110)	lb0↔lb1	0.04	0.04 (0.07)	0.04	0.04 (0.07)
		lb0↔lb2	0.03	0.05 (0.04)	0.03	0.05 (0.04)
	(111)	fcc0↔fcc1 (Ex.)	0.09	0.08 (0.04)	0.09	0.08 (0.04)
		fcc0↔hcp1	0.27	0.25 (0.04)	0.00	0.01 (0.02)
		fcc1↔hcp1 (Ex.)	0.29	0.29 (0.05)	0.03	0.05 (0.05)
Li	(100)	h0↔h1	0.04	0.05 (0.04)	0.04	0.05 (0.04)
		h0↔h2	0.20	0.21 (0.07)	0.20	0.21 (0.07)
		h0↔h2 (Ex.)	0.11	0.11 (0.03)	0.11	0.11 (0.03)
	(110)	ot0↔ot1	0.05	0.05 (0.03)	0.05	0.05 (0.03)
		ot0↔ot2	0.05	0.05 (0.02)	0.05	0.05 (0.02)
	(111)	fcc0↔fcc1 (Ex.)	0.13	0.12 (0.02)	0.13	0.12 (0.02)
		fcc0↔hcp1	0.39	0.40 (0.07)	0.00	0.00 (–)
		fcc1↔hcp1 (Ex.)	0.39	0.40 (0.07)	0.00	0.00 (–)

[a] For BEEF–vdW, the calculated standard deviation of the forward (for) and reversed (rev) activation energy $E_a$ is given in parentheses. All values are reported in eV.

Figure 1.

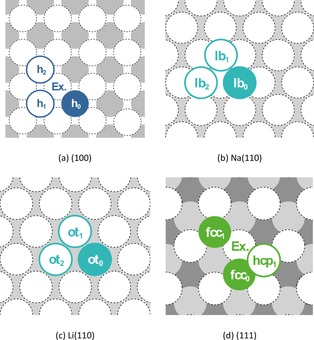
Representation of the examined self‐diffusion pathways on (a) Na(100) and Li(100), (b) Na(110), (c) Li(110), and (d) Na(111) and Li(111). For the initial positions the most stable adsorption site on the respective surface was chosen, that is, hollow (h), long‐bridge (lb), ontop (ot), and fcc. Here, a filled circle marks the initial position, whereas a framed circle indicates possible final positions of the diffusion pathway. All circles marked with Ex. symbolize atoms participating in the exchange process. The obtained activation energies are given in Table 4.

In the case of Na(110), we investigated the diffusion pathway between the adjacent long‐bridge‐positions as well as for Li(110) between the adjacent ontop‐positions. The obtained energy barriers are within the range of 0.03–0.05 eV and thus have the same order‐of‐magnitude as the preferred processes on the (100) surfaces. Our investigations of the adsorption properties on the (111) planes indicate again a “rough” energy landscape. Both hopping and exchange mechanisms for the diffusion of a single adatom from fcc to hcp exhibited increased energy barriers.

However, the exchange diffusion pathway to an adjacent fcc‐position [fcc₀↔fcc₁ (Ex.)] is only hindered by an energy barrier of 0.09 eV (Na) and 0.13 eV (Li). Consequently, we can identify terrace diffusion processes on all low‐indexed surfaces of Na and Li terraces occurring nearly barrier‐free under ambient conditions. Consequently, we were not able to verify the reported significant energy differences for terrace self‐diffusion on these both alkali metal surfaces.40, 41

Diffusion properties on Na(100) and Li(100)

In accordance with the calculated surface energies, Na(110), Na(100), and Li(100) are the most stable surface faces of both metals. In our previous work, we had already discussed the diffusion processes on perfect and imperfect Li(100) planes in great detail.3 Hence, in the following, we will mainly discuss the diffusion properties on Na(100). The values for Li(100) have been taken from Ref. 3 and are given again for comparative purposes. Further, we will discuss the results for Na(110) in the next section.

Estimated room‐temperature reaction rates for the corresponding diffusion pathways are given in the Supporting Information.

An illustration of the various investigated diffusion pathways is given in Figure 2. Here, filled circles mark the initial state of the process, whereas dashed circles illustrate possible final states of the diffusion pathways. The shape of islands (ramified vs. compact islands) is primarily determined by the mobility of the attached adatom to diffuse along the edges and kinks as well as to migrate around the corners of the island. Consequently, we have studied the self‐diffusion properties at kinks, inner‐corner, and outer‐corner systems.

Figure 2.

Representation of the investigated self‐diffusion on Na(100). Here, a filled circle marks the initial position, whereas a framed circle indicates possible final positions of the diffusion pathway. Circles labeled by Ex. mark atoms participating in the exchange process. For all illustrated processes, the characteristic values are listed in Table 5.

As observed for Li,3 the incorporation of an attached Na atom is consistently preferred against the reverse process [i.e., K₀↔K₁, K₀↔K₂, K₀↔K₄ (Ex.), IC₀↔IC₁]. The decrease in unsaturated bonds increases the stability of the atom attached to the island. This is evident for the diffusion pathway SV₀→SV₁ leading to the removal of an island atom from the step‐edge, which has the highest activation energy of all investigated processes. Considering the Na adatom OC₀ directly located at the outer corner of the island, the migration along the island (OC₀→OC₃) is favored against the detachment of the atom directly to the terrace (OC₀→OC₂) and the corner‐crossing via atom‐hopping (OC₀→OC₁). As the preferred outer‐corner pathway, we have identified the exchange process OC₀↔OC₄ (Ex.), shifting atoms around the island corners with a rather low activation barrier of only 0.04 eV. Accordingly, the adatoms can easily cross the corners of the island, resulting in the formation of compact islands.

In the case of Li, we had observed an increase of the activation energy for corner‐crossing via exchange mechanism. Here, the diffusion along the step‐edge S₀↔S₁ and the exchange process OC₀↔OC₄ (Ex.) revealed almost identical energy barriers.

Table 5 summarizes the associated activation energies of the forward and reversed diffusion processes. All energy profiles of the studied diffusion pathways can be found in the Supporting Information. The various surface configurations are abbreviated with capital letters [i.e., step‐edge (S), step‐vacancy (SV), kink (K), outer‐corner (OC), inner‐ corner (IC), dimer (D), concerted dimer (CD), trimer‐linear (TRL), trimer (TR), Ehrlich–Schwöbel–Barrier (E), Ehrlich–Schwöbel–Barrier‐dimer (ED), and upper‐step (US)]. Processes based on exchange mechanism are labeled by (Ex.).

Table 5.

Calculated forward (for) and reversed (rev) activation energies ($E_{\mathrm{a}}$ ) for the various diffusion pathways on Na(100) and Li(100).^[a]

System	Pathway	$E_{\mathrm{a}}^{\mathrm{f}\mathrm{o}\mathrm{r}}$  [eV]		$E_{\mathrm{a}}^{\mathrm{r}\mathrm{e}\mathrm{v}}$  [eV]
		Na(100)	Li(100)	Na(100)	Li(100)
step‐edge	S0↔S1	0.13	0.09	0.13	0.09
	S0↔S2	0.15	0.19	0.05	0.01
	S1a↔S2 (Ex.)	0.15	0.24	0.06	0.06
step‐vacancy	SV0↔SV1	0.32	0.47	0.06	0.00
	SV0↔SV2 (Ex.)	0.20	0.39	0.04	0.07
kink	K0↔K1	0.21	0.20	0.11	0.06
	K0↔K2	0.26	0.34	0.06	0.01
	K1↔K3	0.13	0.24	0.05	0.04
	K0↔K4 (Ex.)	0.18	0.26	0.08	0.09
inner‐corner	IC0↔IC1	0.19	0.20	0.10	0.05
	IC1↔IC2	0.18	0.25	0.08	0.04
outer‐corner	OC0↔OC1	0.19	0.21	0.09	0.02
	OC0↔OC2	0.17	0.19	0.06	0.01
	OC0↔OC3	0.13	0.06	0.12	0.07
	OC0↔OC4 (Ex.)	0.04	0.11	0.04	0.12
dimer	D0↔D1	0.21	0.21	0.07	0.01
	D0↔D2 (Ex.*)	0.20	0.26	0.06	0.06
	D0↔D3	0.18	0.14	0.04	0.00
	D0↔D4 (Ex.)	0.05	0.08	0.05	0.08
concerted dimer	CD0↔CD1	0.29	0.14	0.29	0.14
	CD0↔CD2	0.24	0.21	0.24	0.21
trimer	TRL0↔ TRL1	0.20	0.19	0.08	0.01
	TRL0↔ TRL2	0.19	0.17	0.07	0.00
	TRL0↔ TRL3 (Ex.)	0.06	0.10	0.05	0.13
	TR0↔ TR1	0.18	0.20	0.06	0.00
	TR0↔ TR2	0.13	0.03	0.13	0.03
	TR0↔ TR3	0.18	0.24	0.06	0.02
Ehrlich–Schwöbel barrier	E0↔E1	0.26	0.39	0.17	0.22
	E0↔E1 (Ex.)	0.23	0.28	0.14	0.11
Ehrlich–Schwöbel barrier (dimer)	ED0↔ED1	0.26	0.38	0.31	0.41
	ED0↔ED1 (Ex.)	0.23	0.22	0.28	0.24
upper step	US0↔US1	0.12	0.08	0.12	0.08
	US0↔US2	0.07	0.02	0.06	0.01
	US1↔US2 (Ex.)	0.06	0.06	0.05	0.05

[a] The values for Li were adapted from Ref. 3. All values have been calculated by means of DFT‐PBE.

To get a better understanding of the atomic mechanisms of thin film growth on the (100) surfaces, we have studied diffusion processes within the terrace‐step‐kink (TSK) model.42 As already discussed in the previous section, the diffusion of a single adatom on a defect‐free terrace is practically barrier‐free, which enables high surface mobility. However, high mobility does not necessarily indicate the formation of smoother surface films43 as the growth mode is qualitatively linked to the surface tension. In the initial growth phase on flat surfaces, the adatoms diffuse across the surface until they either hit and join existing clusters or defect structures (see also Figure 2) or combine with other adatoms to a possible new cluster. Thus, we will first discuss the effect of defect structures on the diffusion and subsequently address the initial stages of nucleation.

In the vicinity of a step‐edge, the self‐diffusion behavior is affected compared to the migration on a defect‐free terrace. Both the atom‐hopping (S₂→S₀) and the exchange mechanisms [S₂→S₁ (Ex.)] are possible ways to approach the step‐edge. Whereas the attachment of a single Na atom to the step‐edge via the pathways S₂→S₀ and S₂→S₁ (Ex.) only requires low activation energies of 0.05 and 0.06 eV, respectively, we can observe a three‐times higher barrier for the respective inverse processes, S₀→S₂ and S₁→S₂ (Ex.). The competing process along the step‐edge (S₀→S₁) reveals only a marginally lower barrier of 0.13 eV. Whereas sticking single Li adatoms to the step‐edge happens nearly barrier‐free as well, the diffusion along the step‐edge is favored against the detachment process. Further, the dominant mechanism to join the pre‐existing step is the atom‐hopping process.

The shape of islands (ramified islands vs. compact islands) is primarily determined by the mobility of the attached adatom to diffuse along the edges and kinks as well as to migrate around the corners of the island. Consequently, we have studied the self‐diffusion properties at kinks, inner‐corner, and outer‐corner systems.

As observed for Li,3 the incorporation of an attached Na atom is consistently preferred against the reverse process [i.e., K₀↔K₁, K₀↔K₂, K₀↔K₄ (Ex.), IC₀↔IC₁]. The decrease in unsaturated bonds increases the stability of the atom attached to the island. This is evident for the diffusion pathway SV₀→SV₁ leading to the removal of an island atom from the step‐edge, which has the highest activation energy of all investigated processes. Considering the Na adatom OC₀ directly located at the outer corner of the island, the migration along the island (OC₀→OC₃) is favored against the detachment of the atom directly to the terrace (OC₀→OC₂) and the corner‐crossing via atom‐hopping (OC₀→OC₁). As the preferred outer‐corner pathway, we have identified the exchange process OC₀↔OC₄ (Ex.), shifting atoms around the island corners with a rather low activation barrier of only 0.04 eV. Accordingly, the adatoms can easily cross the corners of the island, resulting in the formation of compact islands.

In the case of Li, we had observed an increase of the activation energy for corner‐crossing via exchange mechanism. Here, the diffusion along the step‐edge S₀↔S₁ and the exchange process OC₀↔OC₄ (Ex.) revealed almost identical energy barriers.

The aggregation of single adatoms induces the formation of metastable surface clusters. As the size of the agglomerate increases, the probability of decay back into its individual atoms decreases until the critical island size is reached. Thus, in the following, we will discuss the formation of dimer and trimer structures on the (100) surface as the initial stages of island growth.

The collision of two single Na adatoms on a flat surface produces a surface dimer. This can happen either via atom hopping processes D₁→D₀ and D₂→D₀ or via the exchange mechanism D₂→D₀ (Ex.*). We have found small activation barriers of 0.04 eV (D₁→D₀), 0.06 eV 8D₂→D₀ (Ex.*)] and 0.07 eV (D₂→D₀) for the formation of a Na dimer, which is of the same order‐of‐magnitude as the terrace diffusion of a single Na atom. Conversely, the decomposition of the dimer is inhibited by significantly higher energy barriers of 0.21 eV (D₀→D₁), 0.20 eV [D₀→D₂ (Ex.*)], and 0.18 eV (D₀→D₂), respectively. Moving the dimer vertically (CD₀↔CD₁) or horizontally (CD₀↔CD₂) along the surface plane via the concerted diffusion mechanism reveals an activation barrier of more than 0.24 eV. However, we determined a low barrier of 0.05 eV for migration of the dimer through the exchange process D₀↔D₃ (Ex.), suggesting a high degree of surface mobility.

Dimer interaction energies E _Int between the individual atoms of the dimer were calculated by subtracting the adsorption energy of a single atom $E\genfrac{}{}{0pt}{}{\mathrm{single}}{\mathrm{ad}}$ from the adsorption energy of the dimer $E\genfrac{}{}{0pt}{}{\mathrm{dimer}}{\mathrm{ad}}$

$${\displaystyle E_{\mathrm{Int}}=E_{\mathrm{ad}}^{\mathrm{dimer}}-2·E_{\mathrm{ad}}^{\mathrm{single}}}$$ (7)

Table 6 summarizes the estimated dimer interaction energies. A representation of possible dimer configurations is given in Figure 3.

Table 6.

Calculated dimer interaction energies of two adatoms on (6×6) Na(100) and (6×6) Li(100).^[a]

Dimer configuration	$E_{\mathrm{I}\mathrm{n}\mathrm{t}}$ (Na) [eV]	$E_{\mathrm{I}\mathrm{n}\mathrm{t}}$ (Li) [eV]
0↔1	−0.138	−0.194
0↔2	+0.004	−0.053
0↔3	−0.001	−0.003
0↔4	+0.002	−0.003
0↔5	±0.000	±0.000

[a] The representation of the different dimer configurations is illustrated in Figure 3.

Figure 3.

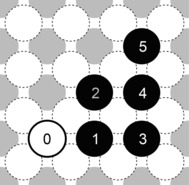
Representation of the investigated dimer configurations. Dimer interaction energies were determined between the first adatom at position 0 (black framed circle) and the possible adsorption sites 1–5 of the second adatom (black filled circles). All calculated dimer interaction energies are listed in Table 6.

Whereas we obtain an attractive interaction of −0.138 eV for the densest Na dimer configuration 0↔1, basically no interaction has been found among larger distant structures. No significant differences are evident comparing the values of Na and Li for the different adatom combinations 0↔3, 0↔4, and 0↔5. However, Li reveals attractive interactions between the two shortest separated dimer configurations (0↔1, 0↔2), which was only observable for Na at structure 0↔1. Self‐diffusion properties on the (100) surfaces may be affected by this disparity: whereas the horizontal detachment of the Li dimer (D₀→D₁) exhibits the same activation energy (E _a=0.21 eV) as for Na, we obtain a reduced energy barrier for the vertical diffusion process (D₀→D₂).

Analogous to the aggregation of the dimer, we found low activation barriers between 0.05 and 0.08 eV for the formation of the linear and right‐angled trimer structure. Likewise, the reverse processes for the detachment of an atom are inhibited by barriers ranging from 0.18 to 0.21 eV. Transformations from linear to right‐angled trimer structures and vice versa [TRL₀↔TRL₃ (Ex.)] are almost barrier‐free with $E\genfrac{}{}{0pt}{}{\mathrm{for}}{\mathrm{a}}$ =0.06 eV and $E\genfrac{}{}{0pt}{}{\mathrm{rev}}{\mathrm{a}}$ =0.05 eV. Consequently, we expect a high degree of surface mobility for the trimer structures. In contrast, the atom‐hopping of the attached adatom along the initial dimer structure (TR₀↔ TRL₂) has an activation barrier twice as high (E _a=0.13 eV) and thus the same value as the diffusion along the step‐edge (S₀↔S₁).

For Li, we have found similar diffusion barriers for the detachment of a single atom from the trimer. However, the barriers for trimer formation as well as atom migration along the initial dimer structure do not exceed a value of 0.03 eV and are thus significantly lower than for identical processes of Na.

Until now, we have only considered 2 D diffusion processes. Besides intralayer mass transport (i.e., atom diffusion on flat terraces), interlayer mass transport (i.e., atom diffusion across step‐edges) plays an important role in homoepitaxial surface growth. For this reason, we will discuss different 3 D diffusion processes along (US₀↔US₁) and away (US₀↔US₂) from upper steps as well as possible step‐crossing mechanisms [i.e., E₀↔E_1, E₀↔E₁ (Ex.)_, ED₀↔ED_1, ED₀↔ED₁ (Ex.)].

In general, an additional energy barrier E _ES, known as the Ehrlich–Schwöbel barrier (ESB), must be overcome while crossing the step‐edge. This additional energy barrier arises from the undercoordination of the adatom during diffusion across the step‐edge and can be calculated by subtracting the activation energy of the terrace migration E _T from the barrier of the step‐down diffusion process E _ESB.

$${\displaystyle E_{\mathrm{ES}}=E_{\mathrm{ESB}}-E_{\mathrm{T}}}$$ (8)

For the step‐down diffusion, we studied the atom hopping process E ₁→E ₀ as well as the push‐out mechanism E ₁→E ₀ (Ex.). Whereas in the case of Na the step‐down hopping process is hindered by an Ehrlich–Schwöbel barrier of 0.11 eV (E _a=0.17 eV), we obtain a slightly lower value of E _ES=0.08 eV (E _a=0.14 eV) for the push‐out mechanism. However, a significant increase in activation barriers of 0.14 eV [see ED₁→ED₀ and ED₁→ED₀ (Ex.)] can be observed when an additional Na atom is located in the direct vicinity of the adatom on the upper terrace. An impact of the second adatom on the upwards diffusion was not apparent. The same activation energies have been obtained for atom hopping processes (E ₀→E ₁ and ED₀→ED₁) and push‐out mechanisms [E ₀→E ₁ (Ex.) and ED₀→ED₁ (Ex.)] of 0.26 and 0.23 eV, respectively. Whereas the higher coordination of the adatom on the lower terrace leads to a thermodynamically more stable initial state E ₀ compared to the final state E ₁, the presence of the dimer at the upper step‐edge results in higher stability of the final state ED₁ relative to ED₀ and E ₀.

Competing processes to migration across the step‐edge are diffusion along (US₀↔US₁) and away from upper steps (US₀↔US₂). Here, the diffusion pathway perpendicular to the step‐edge (E _a=0.12 eV) is preferred over the parallel movement of the atom along the margin of the upper terrace (E _a=0.07 eV). Also, as a consequence of the Ehrlich–Schwöbel barrier, the atom hopping diffusion pathway US₀→US₂ and the exchange process US₁→US₂ (Ex.) exhibit lower activation energies with 0.07 and 0.06 eV, respectively, than the favored step‐down hopping process E ₁→E ₀ (Ex.).

In our previous studies for Li,3 we obtained similar results for the 3 D diffusion processes on Li(100). However, while Li possesses a more significant energy difference of 0.11 eV between the atom hopping process E ₁→E ₀ and the push‐out mechanism E ₁→E ₀ (Ex.), Na shows only a minor difference of 0.03 eV.

We have described the characteristic diffusion processes that are essential in the initial phases of homoepitaxial film growth on Na(100) and Li(100): Adatom diffusion on terraces, migration along step‐edges and the formation of step vacancies, corner structures at step‐edges (i.e., kink, inner‐corner, and outer‐corner systems) and corner‐crossing, nucleation and initial processes of island growth, adatom attachment and detachment, and interlayer mass transport.

Owing to the high diffusibility of Na adatoms, we expect their migration across the terrace via an exchange mechanism until they reach pre‐existing steps. The attached adatom diffuses along the step‐edge via atom‐hopping until it gets incorporated into a kink site structure or reaches an outer‐corner and migrates to the affiliated step‐edge via an exchange mechanism. Subsequently, we postulate a compact island growth on Na(100) by the propagation of pre‐existing steps. In the event of two colliding adatoms, a surface dimer is formed, which can expand into more massive surface clusters through the attachment of further adatoms and thus serves as a nucleus for larger island structures that are mobile on the surface.

Whereas the surface diffusion controls the smoothness of the horizontal film growth, the vertical direction is controlled by the interlayer mass transport. For Na, we obtained a low ESB of less than 0.10 eV for the push‐out mechanism, which would indicate a stable growth regime with a smooth growth front. However, the presence of further adatoms in the direct vicinity of the moving adatom at the upper terrace will lead to a significant increase in the activation energy for the step‐down process. Further, the perpendicular diffusion pathway away from the upper step margin reveals a 50 % lower activation energy as the dominant step‐down process. Hence, in addition to the ESB, 3 D growth is controlled by the interplay between deposition rate and nucleation rate. The correlation between the various processes can be well‐studied within the framework of kinetic Monte Carlo (kMC) simulations. Therefore, it is of utmost importance to consider all relevant processes to achieve a realistic description of the surface growth phenomena. As a consequence, the results of this work will be used as a training set to develop a reactive force‐field for the comprehensive description of further diffusion processes on various surface facets and structures. In the future, the force‐field will then be part of a multi‐scale approach that will enable us to perform on‐the‐fly kMC simulations to investigate the surface growth of Na and Li on a mesoscopic level.

Diffusion properties on Na(110)

Finally, we will examine the diffusion properties on the highly stable Na(110) surface. For this purpose, we studied various diffusion pathways alongside well‐defined surface configurations within the TSK model. The reaction rates for all studied diffusion pathways can be found in the Supporting Information.

The collision of two single Na‐adatoms on a terrace may lead to the formation of a surface dimer. These dimers then serve as nuclei for the growth of larger island structures, which may be formed through the attachment of further diffusing adatoms. An overview of the investigated dimer diffusion pathways is given in Figure 4 and Table 7. Our investigations of the surface dimer structures revealed that the accumulation of two adatoms (D ₀₂→D ₀₀, D ₀₃→D ₀₀, D ₁₂→D ₁₀, and D ₁₃→D ₁₀) is thermodynamically favored. To decompose a dimer into its single atoms, an activation barrier of 0.10–0.15 eV must first be overcome.

Figure 4.

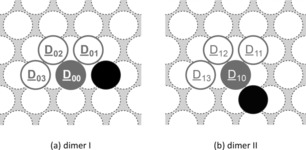
Representation of the examined self‐diffusion pathways of a dimer on Na(110). Here, a filled circle marks the initial position, whereas a framed circle indicates possible final positions of the diffusion pathway. The obtained activation energies are given in Table 7.

Table 7.

Calculated forward (for) and reversed (rev) activation energies ($E_{\mathrm{a}}$ ) for the different diffusion pathways of a surface dimer on Na(110).^[a]

Pathway	$E_{\mathrm{a}}^{\mathrm{f}\mathrm{o}\mathrm{r}}$  [eV]	$E_{\mathrm{a}}^{\mathrm{r}\mathrm{e}\mathrm{v}}$  [eV]
D 00↔D 01	0.03	0.02
D 00↔D 02	0.15	0.01
D 00↔D 03	0.13	0.00
D 10↔D 11	0.04	0.00
D 10↔D 12	0.10	0.02
D 10↔D 13	0.14	0.01

[a] All values were calculated by means of DFT‐PBE.

Furthermore, the dimer is highly mobile owing to the low energy barrier of merely 0.03 eV for migration across the surface via the atom‐hopping process D ₀₀↔D ₀₁.

Once a single adatom encounters an island structure, its self‐diffusion behavior will be significantly influenced. Thus, the nature of surface growth is strongly correlated to the diffusion properties along step‐edges and kinks as well as the ability to cross the corners of the island.

On Na(110) we investigated the diffusion properties along step‐edges with {100}‐, {110}‐ and {211}‐facets. An overview of the studied processes is given in Figure 5 and Table 8.

Figure 5.

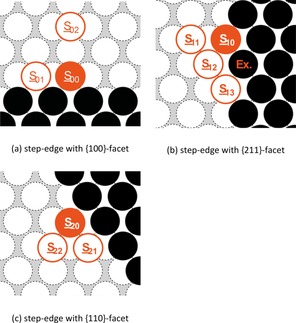
Representation of the examined self‐diffusion pathways along step‐edges with (a) {100}, (b) {211}, and (c) {110} facet. Here, a filled circle marks the initial position, whereas a framed circle indicates possible final positions of the diffusion pathway. The obtained activation energies are given in Table 8.

Table 8.

Calculated forward (for) and reverse (rev) activation energies ($E_{\mathrm{a}}$ ) for the investigated diffusion pathways alongside the different step‐edge structures on Na(110).^[a]

Pathway	$E_{\mathrm{a}}^{\mathrm{f}\mathrm{o}\mathrm{r}}$  [eV]	$E_{\mathrm{a}}^{\mathrm{r}\mathrm{e}\mathrm{v}}$  [eV]
S 00↔S 01	0.12	0.12
S 00↔S 02	0.23	0.04
S 10↔S 11	0.27	0.00
S 10↔S 12	0.16	0.01
S 10↔S 13 (Ex.)	0.08	0.08
S 20↔S 21	0.03	0.03
S 20↔S 22	0.19	0.00

[a] All values were calculated by means of DFT‐PBE.

The attachment of a single adatom onto the different step‐edge structures (S ₀₂→S ₀₀, S ₁₂→S _10, and S ₂₂→S ₂₀) requires only low activation energies of less than 0.04 eV and is thus nearly barrier‐free. Conversely, the inverse diffusion pathways reveal a more than four times higher energy barrier with activation energies of 0.19 eV (S ₂₀→S ₂₂), 0.23 eV (S ₀₀→S ₀₂), and 0.27 eV (S ₁₀→S ₁₁), respectively. Whereas the migration along the {110}‐faceted step‐edge is only hindered by 0.03 eV, we observe an increased diffusion barrier of 0.12 eV along the {100} step. In both cases, the obtained diffusion barriers are in the same order‐of‐magnitude as the respective atom‐hopping processes on the defect‐free terraces of the corresponding surfaces. In the case of migration along the {211} step, we considered both the diffusion via atom‐hopping (S ₁₀→S ₁₂→S ₁₃) and by the exchange mechanism S ₁₀↔S ₁₃ (Ex.).

It was found that the exchange process S ₁₀↔S ₁₃ (Ex.) has an activation energy of 0.08 eV, which is only half as high as the diffusion barrier of the hopping process S ₁₀→S ₁₂. One possible explanation might be the minimization of broken bonds during the exchange mechanism compared to the atom‐hopping process.

Next, we looked into the possible corner‐crossing processes of an attached adatom at inner‐corner systems with different step facets. A representation of the examined diffusion pathways and the corresponding activation energies are given in Figure 6 and Table 9, respectively.

Figure 6.

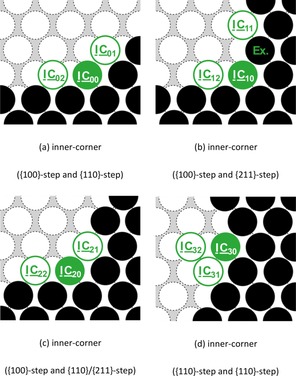
Representation of the examined self‐diffusion pathways at different inner‐corner systems on Na(110). Here, a filled circle marks the initial position, whereas a framed circle indicates possible final positions of the diffusion pathway. The obtained activation energies are given in Table 9.

Table 9.

Calculated forward (for) and reverse (rev) activation energies ($E_{\mathrm{a}}$ ) for the investigated diffusion pathways at different inner‐corner systems on Na(110).^[a]

Pathway	$E_{\mathrm{a}}^{\mathrm{f}\mathrm{o}\mathrm{r}}$  [eV]	$E_{\mathrm{a}}^{\mathrm{r}\mathrm{e}\mathrm{v}}$  [eV]
IC 00↔IC 01	0.09	0.02
IC 00↔IC 02	0.18	0.10
IC 10↔IC 11 (Ex.)	0.11	0.05
IC 10↔IC 12	0.21	0.06
IC 20↔IC 21	0.07	0.07
IC 20↔IC 22	0.19	0.10
IC 30↔IC 31	0.07	0.02
IC 30↔IC 32	0.25	0.00

[a] All values were calculated by means of DFT‐PBE.

We found that the incorporation of the diffusing adatom into the inner‐corner structures [i.e., IC ₀₁→IC ₀₀, IC ₀₂→IC ₀₀, IC ₁₁→IC ₁₀ (Ex.), IC ₁₂→IC ₁₀, IC ₂₁→IC ₂₀, IC ₂₂→IC ₂₀, and IC ₃₁→IC ₃₀] is consistently favored over the reversed detachment process along the step‐edge. Through the decreased number of unsaturated bonds, the inner‐corner positions IC ₀₀, IC ₁₀, IC ₂₀, and IC ₃₀ are thermodynamically stabilized with respect to an attached atom at the corresponding step‐edge.

For the detachment process, we observed the same trend as for the migration along the differently facetted step‐edges: The separation of the embedded adatom along the {100} step (IC ₂₀→IC ₂₂) reveals the largest activation barrier of 0.19 eV, followed by diffusion pathway along the {211} step and {110} step with diffusion barriers of 0.11 eV [IC ₁₀↔IC ₁₁ (Ex.)], 0.09 eV (IC ₀₀↔IC ₀₁), and 0.07 eV (IC ₂₀↔IC ₂₁ and IC ₃₀↔IC ₃₁), respectively. Our case study for direct diffusion from the inner‐corner position onto the terrace (IC ₃₀→IC ₃₂) revealed the highest diffusion barrier of 0.25 eV owing to the large decrease of direct neighbor atoms.

Besides the transition of an adatom between two step‐edges at inner‐corners, the ability of a diffusing adatom to cross an outer‐corner has a large influence on the shape of an island (ramified vs. compact islands).

An overview of the investigated outer‐corner diffusion pathways is given in Figure 7 and Table 10.

Figure 7.

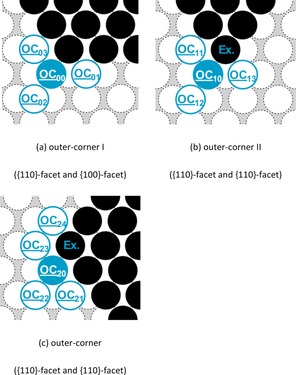
Representation of the examined self‐diffusion pathways at different outer‐corner systems on Na(110). Here, a filled circle marks the initial position, whereas a framed circle indicates possible final positions of the diffusion pathway. The obtained activation energies are given in Table 10.

Table 10.

Calculated forward (for) and reversed (rev) activation energies ($E_{\mathrm{a}}$ ) for the investigated diffusion pathways at different outer‐corner systems on Na(110).^[a]

Pathway	$E_{\mathrm{a}}^{\mathrm{f}\mathrm{o}\mathrm{r}}$  [eV]	$E_{\mathrm{a}}^{\mathrm{r}\mathrm{e}\mathrm{v}}$  [eV]
OC 00↔OC 01	0.05	0.10
OC 00↔OC 02	0.14	0.02
OC 00↔OC 03	0.05	0.12
OC 10↔OC 11	0.00	0.07
OC 10↔OC 12	0.13	0.02
OC 10↔OC 13	0.04	0.04
OC 10↔OC 13 (Ex.)	0.06	0.06
OC 20↔OC 21	0.05	0.04
OC 20↔OC 22	0.20	0.00
OC 20↔OC 23	0.11	0.01
OC 20↔OC 24 (Ex.)	0.16	0.16

[a] All values were calculated by means of DFT‐PBE.

The investigation of the various diffusion pathway at the outer‐corner systems showed that diffusion of the attached adatoms away from the outer‐corner along the different step‐edges (i.e., OC ₀₀→OC ₀₁, OC ₀→OC ₀₃ , OC ₁₀→OC ₁₁, and OC ₂₃→OC ₂₀) is always preferred. Conversely, the removal of an attached adatom from the outer‐corner onto the terrace is unlikely owing to the significantly lower diffusion barriers of the competing processes.

Moreover, the migration around the outer‐corner via atom‐hopping (OC ₂₀→OC ₂₃→OC ₂₄ and OC ₁₀→OC ₁₃) is favored against the corresponding diffusion pathway via the exchange mechanism [OC ₂₀↔OC ₂₄ (Ex.) and OC ₁₀↔OC ₁₃ (Ex.)].

Whereas for the intralayer mass transport the hitherto examined 2 D diffusion processes are of utmost importance, we still have to consider the 3 D diffusion processes to gain a better understanding of the interlayer mass transport and thus for the 3 D surface growth phenomena.

For this purpose, we have studied possible diffusion processes across the different step systems. An overview of the studied processes is given in Figure 8 and Table 11.

Figure 8.

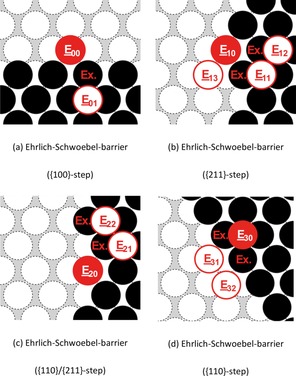
Representation of the examined self‐diffusion pathways across the steps (Ehrlich–Schwöbel barrier) on Na(110). Here, a filled circle marks the initial position, whereas a framed circle indicates possible final positions of the diffusion pathway. The obtained activation energies are given in Table 11.

Table 11.

Calculated forward (for) and reversed (rev) activation energies ($E_{\mathrm{a}}$ ) for the investigated diffusion pathways across the different steps on Na(110).^[a]

Pathway	$E_{\mathrm{a}}^{\mathrm{f}\mathrm{o}\mathrm{r}}$  [eV]	$E_{\mathrm{a}}^{\mathrm{r}\mathrm{e}\mathrm{v}}$  [eV]
E 00↔E 01	0.29	0.10
E 00↔E 01 (Ex.)	0.28	0.09
E 10↔E 11 (Ex.)	0.31	0.04
E 10↔E 12	0.36	0.09
E 10↔E 12 (Ex.)	0.37	0.10
E 13↔E 11 (Ex.)	0.19	0.08
E 20↔E 21	0.35	0.09
E 20↔E 21 (Ex.)	0.27	0.00
E 20↔E 22 (Ex.)	0.30	0.03
E 30↔E 31	0.42	0.19
E 30↔E 31 (Ex.)	0.25	0.02
E 30↔E 32 (Ex.)	0.27	0.04

[a] All values were calculated by means of DFT‐PBE.

For all investigated diffusion pathways across steps on Na(110), we have studied both the self‐diffusion via atom‐hopping and by the push‐out mechanism [labeled with (Ex.)]. We were able to identify possible diffusion pathways at all investigated step facets revealing low energy barriers of 0.09 eV [E ₀₁→E ₀₀ (Ex.), {100} step], 0.04 eV [E ₁₁→E ₁₀ (Ex.), {110} step], and 0.00 eV [E ₂₁→E ₂₀ (Ex.), {211} step] for the step‐down diffusion. In all listed cases, the push‐out mechanism proved to be the preferred diffusion mechanism.

However, for the reversed pathways, we obtained higher diffusion barriers: whereas the migration of a single adatom onto the upper terrace at a {211}‐facetted step requires an activation energy of less than 0.20 eV [E ₁₃→E ₁₁ (Ex.)], we observed increased energy barriers of 0.25 eV [E ₃₀→E ₃₁ (Ex.)] and 0.28 eV [E ₀₀→E ₀₁ (Ex.)] at steps with {110} and {100} facets, respectively. Again, the diffusion via the exchange processes revealed to be the favored diffusion mechanism.

Conclusions

We examined bulk and surface properties of metallic Na and Li at the atomistic level by means of density functional theory. Although we concentrated on model systems where the influence of the realistic battery environment (e.g., presence of electrolytes, potential solid electrolyte interface layers, or charge/discharge processes) was not treated explicitly, our studies already contributes to a better understanding of the initial stages of surface growth on Na and Li. For instance, Steiger et al.44 proved in their experimental work that the needle formation is an inherent property of Li and thus the diffusion properties are of great importance. However, the surface and diffusion properties may be influenced in the presence of an electrochemical environment.45

First, we examined the bulk properties of Na and Li in various crystal phases. We obtained an energetic degeneration between the low‐temperature phase hR9 and the ambient pressure bcc phase as well as high stability for the fcc and hcp crystal structures of both alkali metals. The comparison of the adsorption properties indicated a higher stabilization of adsorbed states on Li surfaces compared to adsorption complexes on the different facets of Na, which is also in agreement with the calculated cohesive energies. Of interest is the deviation in the most stable adsorption position on the (110) surfaces: Whereas on Na(110) the long‐bridge position proved to be the most stable adsorption site, adsorption on the ontop position of Li(110) is preferred. The dissent may be caused by the different stability of the low‐index surfaces. Whereas Li(100) is the most stable low‐index surface, we found (almost) identical surface energies for Na(110) and Na(100).

Next, self‐diffusion processes on the low‐index surfaces were investigated. Here, we were able to prove that previously postulated differences in the terrace diffusion barriers are primarily caused by critical diffusion pathways that had been omitted so far. However, exactly these exchange processes are the preferred diffusion mechanisms on Na(100), Na(111), and Li(111). On all studied surfaces reaction pathways were identified having activation energies of less than 0.09 and 0.13 eV for Na and Li, respectively.

Finally, we conducted a detailed study of well‐chosen diffusion processes on perfect and imperfect (100) surfaces to provide a preliminary assessment of the crystal growth behavior. On flat terraces of Na, the exchange mechanism proved to be the preferred diffusion mechanism, whereas for Li the atom‐hopping to the adjacent hollow side was favored. For both alkali metals, an attractive interaction between the individual adatoms was found, producing a high driving force for the formation of stable surface clusters. Moreover, we could identify diffusion pathways inducing high surface mobility of dimer and trimer structures. For both elements, the attachment of an atom to pre‐existing step‐edges is preferred against the atom detachment onto the terrace. Furthermore, the incorporation into kink sites is thermodynamically stabilized owing to the higher coordination of the adsorption site. Outer‐corner structures can be crossed easily via the exchange mechanism, resulting in a compact 2 D island growth.

The 3 D growth depends mainly on the interlayer mass transport. For Na and Li, the push‐out mechanism is the dominant step‐down process revealing low Ehrlich–Schwöbel barriers of 0.08 and 0.07 eV, respectively. A significant increase of the energy barrier can be observed as soon as additional adatoms are present in the direct vicinity of the moving atom at the upper terrace margin. However, for both metals, the perpendicular diffusion away from the ledge of the upper edge exhibit a more than 50 % lower activation energy relative to the migration on the lower terrace. To elucidate the precise interplay between deposition, nucleation, and the influence of the Ehrlich–Schwöbel barrier, further in‐depth simulations are necessary.

Next, we investigated the self‐diffusion properties on perfect and imperfect surface structures of Na(110). Our studies showed thermodynamic stabilization for the accumulation of two adatoms, forming the nucleus for further agglomerations, and revealed high surface mobility for these dimer structures. The investigations of different step‐edges (i.e., {100}, {110}, and {211} steps) indicated high mobility of the attached adatom along the {110} step (E _a=0.03 eV), whereas the {100} step revealed the highest migration barrier (E _a=0.12 eV). The transition of an adatom at outer‐ and inner‐corner structures requires rather small activation energies of 0.10 to 0.15 eV. In general, the maximization of the binding partners of the adatom led to a thermodynamic stabilization of the system.

Our investigations of the 3 D diffusion processes revealed possible diffusion pathways at all investigated step facets that result in a nearly barrier‐free step‐down diffusion. For the inverse process (diffusion onto the upper terrace), the {211} steps had the lowest activation energy (0.19 eV), followed by the {110} steps (0.25 eV) and the {100} steps (0.28 eV). In all these cases, the exchange mechanism was consistently favored over the diffusion via atom‐hopping, which further emphasizes its importance.

Finally, we believe that the investigated diffusion and surface properties will enhance our understanding of the initial stages of surface growth phenomena on Na and Li.

Conflict of interest

The authors declare no conflict of interest.

Supporting information

As a service to our authors and readers, this journal provides supporting information supplied by the authors. Such materials are peer reviewed and may be re‐organized for online delivery, but are not copy‐edited or typeset. Technical support issues arising from supporting information (other than missing files) should be addressed to the authors.

Supplementary

D. Gaissmaier, M. van den Borg, D. Fantauzzi, T. Jacob, ChemSusChem 2020, 13, 771.