Dynamic Recovery from Depression Enables Rate Encoding in Inhibitory Synapses

Summary

Parvalbumin-expressing fast-spiking interneurons (PV-INs) control network firing and the gain of cortical response to sensory stimulation. Crucial for these functions, PV-INs can sustain high-frequency firing with no accommodation. However, PV-INs also exhibit short-term depression (STD) during sustained activation, largely due to the depletion of synaptic resources (vesicles). In most synapses the rate of replenishment of depleted vesicles is constant, determining an inverse relationship between depression levels and the activation rate, which theoretically, severely limits rate-coding capabilities. We examined STD of the PV-IN to pyramidal cell synapse in the mouse visual cortex and found that in these synapses the recovery from depression is not constant but increases linearly with the frequency of use. By combining modeling, dynamic clamp, and optogenetics, we demonstrated that this recovery enables PV-INs to reduce pyramidal cell firing in a linear manner, which theoretically is crucial for controlling the gain of cortical visual responses.

Graphical Abstract

Highlights

• •Recovery rate from depression in inhibitory synapses from PV-INs is use dependent
• •Dynamic recovery from depression enables rate coding in inhibitory inputs
• •PV-IN synapses reduce pyramidal firing in a frequency-dependent manner

Biological Sciences; Neuroscience; Molecular Neuroscience; Cellular Neuroscience; Mathematical Biosciences

Introduction

In cortex, the primary mechanism that limits cortical activity is the inhibitory action of parvalbumin-expressing fast-spiking interneurons (PV-INs). Indeed, the recruitment of PV-INs controls the spiking activity of cortical pyramidal cells in a linear fashion (Atallah et al., 2012; see Tremblay et al., 2016, for a review). Concordant with this function, PV-INs can fire at high rates without attenuation and are highly interconnected with pyramidal cells. However, like most cortical synapses, synapses made by PV-INs exhibit marked short-term depression (STD) of presynaptic release (Abbott et al., 1997, Zucker and Regehr, 2002). As STD strongly limits synaptic efficacy in the temporal domain, unraveling its rules and mechanisms is crucial for understanding neural processing by PV-INs.

Experimentally, STD is typically revealed as a progressive, yet reversible, depression of synaptic release that occurs during a train of repetitive stimulation. Conceptually, STD can be understood in terms of use-dependent depletion of synaptic resources. In the simplest models synaptic depression results from the depletion of the readily releasable pool (RRP) of synaptic vesicles (Alabi and Tsien, 2012, Zucker and Regehr, 2002). Released vesicles are retrieved from the terminal surface followed by refilling with neurotransmitter via a process of “kiss-and-run” (He et al., 2006) and/or clathrin-mediated endocytosis (Granseth and Lagnado, 2008). The steady-state amplitude of synaptic depression during a stimulation train reflects the balance between vesicle release and recovery.

In cortex, both excitatory and inhibitory synapses often exhibit STD, but with different properties and consequences. In most connections between pyramidal cells STD during repetitive stimulation follows the 1/f rule. That is, at the steady state the synaptic response amplitude decreases in inverse proportion to the presynaptic firing frequency (Abbott et al., 1997, Tsodyks and Markram, 1997). According to the depletion model, a 1/f rule could result when the vesicle release probability and recovery rate are constant and independent of presynaptic activity, as reported in hippocampal synapses (Wesseling and Lo, 2002). A cardinal consequence of this 1/f rule is that increases of the presynaptic firing rate above a certain limiting frequency do not result in commensurate increases in postsynaptic firing (Abbott et al., 1997, Tsodyks and Markram, 1997). This low-pass filtering limits rate coding in these synapses but makes them more suitable for temporal coding and the detection of coincidences and synchrony (Abbott et al., 1997, Cook et al., 2003, Grande and Spain, 2005, Tsodyks and Markram, 1997).

In contrast to excitatory synapses, cortical inhibitory synapses formed by parvalbumin-expressing fast-spiking interneurons (PV-INs) do not follow the 1/f rule. Instead, in these synapses, the synaptic impact (total synaptic charge in a given interval) correlates positively with the stimulation frequency (Galarreta and Hestrin, 1998, Varela et al., 1999). The mechanisms underlying this positive relationship, and their functional consequences, remain largely unknown. By combining whole-cell recordings in connected PV-interneuron to pyramidal cell (PV→Pyr) pairs, dynamic clamp, and optogenetics, we revealed that use-dependent dynamic recovery from synaptic depression accounts for the positive correlation between frequency of presynaptic firing and synaptic impact. We also showed that this dynamic recovery enables a rate coding for the inhibitory function of PV-INs, that is, increasing the firing rate of PV-INs causes a linear reduction of firing in pyramidal cells.

Results

Use-Dependent Recovery from Depression in Inhibitory Synapses from PV-INs

In a resource depletion model of synaptic depression, the 1/f rule arises as a consequence of a constant rate of the replenishment of depleted resources. The deviation from 1/f in synapses made by PV-INs onto pyramidal cells suggests a use-dependent recovery. We examined this possibility by recording unitary inhibitory postsynaptic current (IPSCs) (uIPSCs) in pairs of connected PV→Pyr cells in the layer 2/3 of visual cortical slices from G42 mice (Gu et al., 2013), a line that expresses GFP in a subpopulation of PV-INs. Synaptic depression and recovery were quantified by evoking trains of 30 action potentials in the PV-INs at various frequencies (Figures 1A and 1B).

Figure 1.

Dynamic Synaptic Replenishment in Synapses Made by Parvalbumin Interneurons (PV-INs) onto Pyramidal Cells (Pyr)

(A) Recording from PV→Pyr pairs. Representative traces of action potentials (blue) and unitary inhibitory postsynaptic currents (black) in a connected PV→Pyr pair.

(B) Normalized amplitudes of uIPSCs evoked by 10- and 50-Hz presynaptic stimulation. Curves were fitted by the equation inset in the graph. Data are represented as mean ± SEM.

(C and D) uIPSCs depart from the 1/f rule. At the steady state (P20-P30) the uIPSC amplitude (C) decreased exponentially with the stimulation frequency, and the average synaptic charge (D) increased parabolically with the stimulation frequency.

(E) Rates of recovery from depletion, increased linearly with presynaptic frequency.

(F) Initial release probabilities were not affected by changing the presynaptic frequency.

Data points in (C–F) represent averages ± SEM from 7, 19, 10, and 21 cell pairs at 10, 20, 30, and 50 Hz, respectively, and 10 repetitions per frequency per cell pair. Goodness of fit R² and Pearson correlation p values are indicated in corresponding panels. Fitting equation: one-phase decay (black) and 1/f (red) in (C), parabola in (D), and line in (E) and (F).

First, we confirmed the departure from the 1/f rule in the PV→Pyr synapses of layer 2/3. We found that at steady-state the relationship between uIPSC amplitude and the stimulation frequency was not fitted by a 1/f function (R² = −4.01, shown in red in Figure 1C); indeed it was better fitted by a single exponential function (R² = 1.0). In addition, under a constant recovery regime, steady-state depression is proportional to the stimulation frequency. As a consequence, the total synaptic charge during a given time interval (synaptic impact) is independent of the frequency (Abbott et al., 1997, Tsodyks and Markram, 1997). In contrast, we found that this relationship was not a constant, but was well fitted by a parabola (Figure 1D). Thus, the depression of uIPSCs does not follow the 1/f rule, suggesting that the recovery rate of depleted synaptic resources depends on their use.

Next, we evaluated the rate of recovery at different stimulation frequencies by fitting the depression of uIPSCs during the stimulation train to two equations derived from Equation 1 that describes a model in which synaptic resources are depleted and replenished (Wesseling and Lo, 2002).

$$\frac{dn}{dt}=\alpha \cdot \left(N-n\right)-\beta \cdot n$$ (Equation 1)

In this model, β is the intrinsic release probability, α is the rate of replenishment of synaptic resources (vesicles), n represents the pool of the available resources, and N is the maximal capacity of the resource pool (see Transparent Methods for more details). The results indicate that at the steady state the rate of replenishment increased linearly with the stimulation frequency (Figure 1E), whereas the initial release probability remained constant (Figure 1F). These results indicated that synaptic activity dynamically regulates the replenishment of synaptic resources.

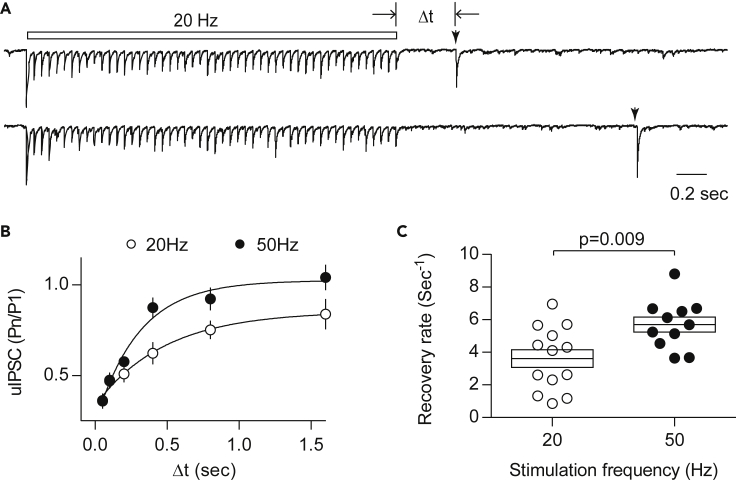
We also directly tested the use dependency of the recovery rate by conditioning with two different stimulation frequencies (50 pulses at 20 Hz or 50 Hz). Recovery was then evaluated by single test pulses delivered at varied delay intervals (Figure 2A). The temporal recovery of the test uIPSC amplitudes was well fitted by an exponential curve (Figure 2B), and it was faster in the case of conditioning with 50 Hz (Figure 2C). The recovery rates measured in this way were smaller than those estimated from the model fitting. It is likely that the recovery rate after the conditioning might have decayed at the longer intervals used. Nevertheless, these results confirmed that recovery is dynamically regulated by synaptic activity and that it is faster in more active synapses.

Figure 2.

Synaptic Recovery Is Faster after a Higher Stimulation Frequency

(A) Example uIPSCs evoked at two intervals (indicated by arrowhead) after repetitive presynaptic firing at 20 Hz.

(B) The relative magnitudes of the uIPSCs after conditioning stimuli (20 Hz: open symbols; 50 Hz: filled symbols) were fitted by a single exponential function to obtain τ. Data are represented as mean ± SEM.

(C) On average, the recovery rate (1/τ) after 50-Hz conditioning is significantly faster than that after 20-Hz conditioning.

Unpaired t test. Boxes indicate mean ± SEM. Averages are represented by the middle horizontal lines in each box. Sample size: n = 13 cells (20 Hz) and n = 11 cells (50 Hz). Data from each cell are the averages of 10–20 repetitions.

We also confirmed that the rules of depression of synaptic excitation and inhibition are different. We recorded long trains of both excitatory postsynaptic currents (EPSCs) and IPSCs in the same pyramidal cell (Figure S1) and found that the average depression at the end of a train roughly followed the 1/f rule in the case of EPSCs, whereas the relationship with stimulation frequency was better fitted with an exponential function in the case of IPSCs (Figure S1D). Similarly, the total synaptic charge (integrated between the 60^th and 80^th pulses and normalized to a single response) was constant over the 10 to 60 Hz range, in the case of EPSCs, but better fitted by a parabola in the case of IPSCs (Figure S1E). Then we evaluated the possibility that these differences relate to the distinct replenishment regimes for synaptic inhibition and excitation by modeling responses to stimulation trains in synapses with similar release probability and RRP, but with either constant or dynamic replenishment (green and black symbols in Figure S2). The response magnitudes for both types of synapses are similar at the beginning of the trains, but the ones with constant recovery became smaller as the train progressed, and more so at higher stimulation frequencies (Figures S2A and S2B). The relationship between stimulation frequency and steady-state response (Figure S2C) or total synaptic change (Figure S2D) was different for both types of synapse cases and, notably, resembles the differences between EPSCs and IPSCs (compare Figure S1D with S2C and Figure S1E with S2D). These results support the idea that the replenishment regime is an important determinant of the differences in short-term depression between IPSCs and EPSCs.

Inhibitory Inputs with Dynamic Recovery from Depression Can Reduce Pyramidal Firing in a Frequency-Dependent Manner

The constant recovery and dynamic recovery models of synaptic inhibition each have distinct consequences for the firing of action potentials in pyramidal cells. In the case of constant recovery, increasing the stimulation rate of inhibitory inputs will barely increase the total synaptic charge per time unit thus barely affecting pyramidal firing rates. In the case of dynamic recovery, increasing the stimulation rate will allow an increase in inhibitory synaptic charge per time unit leading to reduced firing rates. We first explored these ideas in an all-active biophysical neuronal model from the Allen Cell Types Database (Model ID: 497232641) based on the morphology and electrophysiology of a pyramidal cell in layer 2/3 visual cortex (Cell ID: 477127614). The neuron model was driven by three independent excitatory inputs (2.8 nS each) and three independent inhibitory inputs on the soma (2.9 nS each) (Figure 3A, see Transparent Methods for more details). These inputs were activated with Poisson trains of different frequencies (10 different Poisson trains per frequency trial), and firing rates were measured from whole trials. In the absence of inhibition, increasing the excitation frequency increased the firing rates up to a limit of about 20 Hz (Figure 3C). The recruitment of inhibition with constant or dynamic recovery had very different effects on the cell firing rates (Figures 3B–3D). When recruited at low frequencies (∼10 Hz) both types of inhibitory synapses produce a comparable and modest decrease in the firing rate to ∼85% of initial. Further increases in the inhibitory frequency up to 60 Hz minimally impacted the firing rate in the case of constant recovery, but it progressively reduced the firing to ∼30% in the case of dynamic recovery (Figures 3B–3D). The differential impact of constant and dynamic recovery on firing was also observed when the model cell fired at a higher rate of ∼60 Hz and when the Gin magnitude was varied (Figure S3).

Figure 3.

Comparison of Constant and Dynamic Recovery of Inhibition on the Firing Rates of Modeled and Actual Pyramidal Cells

(A) Example of Poisson trains (1 s) of excitatory synaptic conductance (Gex, red trace) and inhibitory synaptic conductance with either constant rate of recovery (Constant Gin, green trace) or dynamic rate of recovery (Dynamic Gin, black trace) used to activate the cells. Note that the responses of the Constant Gin and the Dynamic Gin were initially comparable and that Constant Gin responses became preferentially smaller as the train progresses.

(B–D) Changes induced in an “all-active” neuron model. (B) Example traces of membrane potential during activation of excitatory inputs only (top), or excitatory and inhibitory synapses with either constant recovery rate (middle) or dynamic recovery (bottom). The vertical lines at the bottom in (A, B, and E) indicate the activation timing of excitatory synapses (red) and inhibitory synapses (blue). (C) Firing rates elicited in the model cell by different frequencies of the excitatory input in the absence of (red triangles) or in conjunction with stimulation of inhibitory inputs with constant (green circles) or dynamic (black circles) recovery at the indicated frequencies. (D) Effects of increasing the frequency of inhibitory inputs with constant (green circles) or dynamic recovery (black circles) on the firing rate of a maximally stimulated model cell (excitation at 30 Hz).

(E–G) Changes in firing induced in actual pyramidal cells. Excitatory and inhibitory synaptic conductances were mimicked by current injection in the dynamic clamp mode. (E) Example traces of membrane potential changes. Like in the model cell, inhibitory inputs with dynamic recovery are more effective in reducing firing rates (F) and increasing their frequency reduces the firing of a maximally stimulated (excitation at 30 Hz) pyramidal neuron in a linear fashion (G).

Symbols and conventions in (E–G) are as in (B–D). Fitting curves: sigmoid in (C and F); one phase decay in (D and G). Data points in (C and D) are the averages from 10 trials; in (F and G) represent averages ± SEM from 30 cells. Goodness of fit R² and Pearson correlation p values are indicated in corresponding panels. Calibration bars in (B and E): 20 mV, 0.1 s.

We also confirmed the differential effects of these two types of inhibitory synapses in actual neurons using dynamic clamp to simulate excitatory and inhibitory currents. Current trains based on excitatory and inhibitory conductances, with the same response shape and release parameters as those used in the neuronal model of dynamic or constant recovery, were injected into layer 2/3 pyramidal cells, and the effect on the membrane potential was recorded (Figures 3E–3G). The excitatory conductance was set to 1.5 times the action potential threshold, and the inhibitory conductance was set such that inhibitory inputs (30 Hz) with constant recovery could reduce the firing induced by excitatory inputs (30 Hz) by about 30% (see Transparent Methods for details). In the absence of inhibition, increasing the excitation frequency increased the firing rate, reaching a plateau with excitation frequencies larger than 20 Hz (Figure 3F). As in the case of the model neuron, inhibitory synapses with dynamic recovery imposed graded inhibition on the firing activity of the pyramidal neuron, whereas inhibitory synapses with constant recovery had only a modest effect on firing rate, which was largely independent of the inhibitory frequency (Figure 3G). Thus, only inhibitory synapses endowed with dynamic recovery can support a frequency-dependent graded attenuation of pyramidal cell firing.

PV-IN Synapses Reduce Pyramidal Firing in a Frequency-Dependent Manner

Finally, we asked whether real inhibitory synapses have the capacity to reduce pyramidal cell firing in a frequency-dependent manner. We recorded from pyramidal cells and combined dynamic clamp (to mimic trains of excitatory conductance) with optogenetic recruitment of inhibitory cells in slices prepared from mice expressing channelrhodopsin-2 in PV-INs (see Transparent Methods for details). To validate the optogenetic approach we confirmed that upon light stimulation these PV-INs do fire up to 50 Hz (Figure S4A), and that the light-evoked IPSCs depress (Figure S4B) with steady-state amplitudes that decrease linearly with the light pulse frequency and a synaptic charge that increases in a parabolic manner (Figures S4C and S4D). Importantly, the recovery rates estimated with Equation 1 depended linearly on light frequency (Figure S4E), although the release probability was found to depend on frequency slightly (Figure S4F). These experiments were conducted at two temperatures, our standard 30°C and 35°C, more similar to actual mouse body temperature. Changing the recording temperature from 30°C to 35°C slightly shifted the steady state and synaptic charge (Figures S4C and S4D) and decreased the release probability, but not the recovery rate (Figures S4E and S4F). The reduced release probability at 35°C was somewhat surprising (but see Pyott and Rosenmund, 2002). This could be a consequence of the shortening of the action potential duration, often associated with reduced release, which occurs at higher temperatures (Buzatu, 2009, Hyun et al., 2012, Money et al., 2005, Yu et al., 2012).

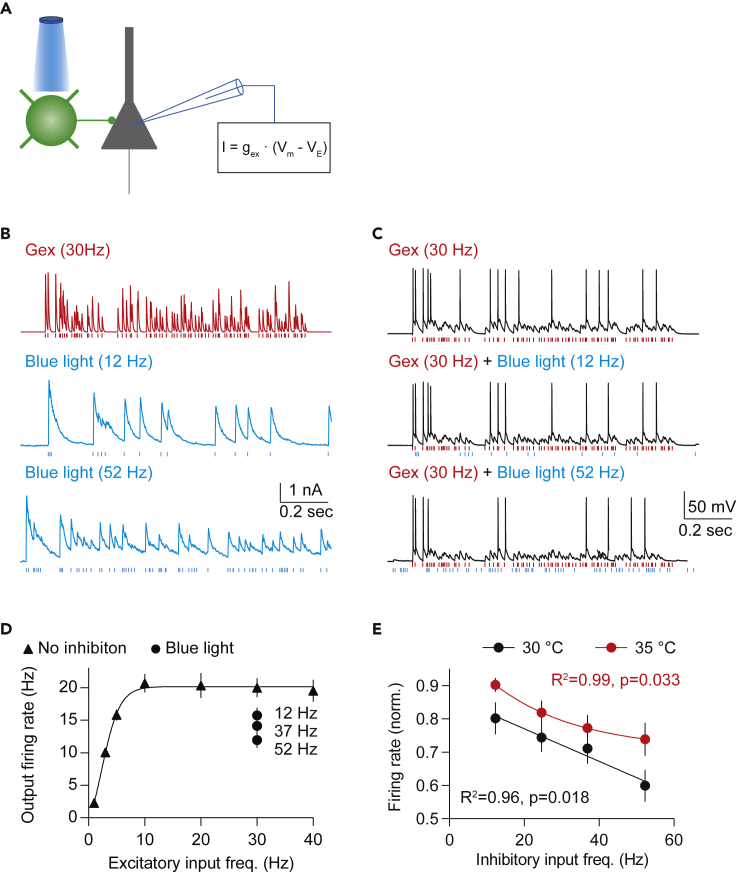
To evaluate the impact of recruiting inhibition mediated by PV-INs, we first made the pyramidal cell fire by injecting trains of excitatory currents (30 Hz, the same excitatory conductance as that in Figure 3E) in the dynamic-clamp mode while delivering a Poisson train of light pulses (Figure 4A and 4B), with the light intensity adjusted to induce IPSCs of more than 1 nA when holding at 0 mV. As shown in Figures 4C and 4D, increasing the average frequency of the light pulses increased the attenuation of the firing of the pyramidal cell. Moreover, the firing rate of the pyramidal cell was decreased linearly as a function of the frequency of the recruitment of PV-IN synapses at both recording temperatures of 30°C and 35°C (Figure 4E). These results indicate that synapses made by PV-INs, endowed with dynamic recovery, can exert a graded control of pyramidal cell spiking based on the firing rate of the PV-INs.

Figure 4.

Optogenetically Activated Inhibition Exhibits Linear Gain Control

(A) Illustration of experimental configuration. Inhibitory inputs from light-controlled parvalbumin interneurons and excitatory inputs from dynamic clamp.

(B) The top trace (red) is an example of the excitatory conductance. The bottom two traces (blue) are examples of inhibitory postsynaptic currents evoked by blue light stimulation. The vertical red lines indicate the activation timing of excitatory synapses, whereas the vertical blue lines indicate the activation timing of inhibitory synapses by blue light stimulation.

(C) Example of membrane potentials evoked by excitatory inputs only, excitatory inputs and inhibitory inputs at 12 Hz, or excitatory inputs and inhibitory inputs at 52 Hz. The vertical lines at the bottom of the membrane potential traces indicate the activation timing of excitatory synapses (red) and blue light (blue).

(D) Excitatory input versus firing output without or with inhibition (12, 37, and 52 Hz).

(E) Averaged firing rate (normalized to the firing rate evoked by 30-Hz excitation only) versus the frequency of inhibitory inputs recorded at 30°C (black) or 35°C (red) in different cells, indicating that inhibition from PV cells linearly reduced neural activity in pyramidal cells independent of the recording temperature. The frequency of excitation in E is 30 Hz. Sample size: n = 15 cells (30°C) and n = 9 cells (35°C).

Fitting equation: sigmoid and one-phase decay in (D and E), respectively. Goodness of fit R² and Pearson correlation p values are indicated in corresponding panels. Data are represented as mean ± SEM.

Discussion

The study revealed that the recovery from short-term depression in inhibitory synapses made by PV-INs onto pyramidal cells is activity dependent, such that increasing the frequency of presynaptic activity also increases recovery rates. As a result, the inhibitory output, measured as the total charge per unit time, varies linearly with the presynaptic frequency. This dynamic synaptic recovery allows these inhibitory synapses to multiplicatively reduce pyramidal cell firing rates over a wide range of frequencies.

The exact mechanisms underlying such dynamic recovery at inhibitory synapses made by PV interneurons remain unknown. One attractive possibility is the accumulation of intracellular Ca²⁺. In many synapses the replenishment of the RRP of vesicles can be accelerated by activity-induced calcium accumulation (Dittman and Regehr, 1998, Fuhrmann et al., 2004, Sakaba and Neher, 2001, Smith et al., 1998, Stevens and Wesseling, 1998, Wang and Kaczmarek, 1998). Repetitive stimulation causes calcium to accumulate in presynaptic terminals (Kreitzer et al., 2000), potentially at levels commensurate with the stimulation frequency. It must be noted that parvalbumin, being a slow calcium buffer, may contribute to the activity-dependent accumulation of Ca²⁺ at presynaptic terminals. However, in PV knockout mice the IPSCs evoked by repetitive stimulation are altered only in the early part of the train, not in the steady state, when the rate of replenishment becomes a limiting factor of the IPSC amplitude (Caillard et al., 2000, Eggermann and Jonas, 2011, Orduz et al., 2013).

The genetic ablation of downstream Ca²⁺-sensing molecules can impair the activity-dependent recovery of the vesicle pool in various synapses. These molecules include the Ca²⁺/calmodulin-Munc13-1 complex found at the calyx of Held synapses (Lipstein et al., 2013, Sakaba and Neher, 2001) as well as synaptotagmin 2 and 7 (Syt-2 and Syt-7), found at basket cell to Purkinje cell synapses and hippocampal synapses (Chen et al., 2017, Liu et al., 2014, Luo and Sudhof, 2017, Turecek et al., 2017). Of these calcium sensor molecules, a particularly attractive candidate to mediate dynamic recovery in the cortex is Syt-2, which is highly and selectively expressed in the terminals of cortical PV-INs (Sommeijer and Levelt, 2012).

Concerning the functional consequences of dynamic recovery, a widely accepted role of the network of PV-INs in sensory cortices is to control the gain of pyramidal cell responses to sensory stimulation (Atallah et al., 2012, Hofer et al., 2011, Packer and Yuste, 2011). According to this view, the high interconnectivity between PV-INs and pyramidal cells (Gu et al., 2013, Holmgren et al., 2003, Packer and Yuste, 2011) allows PV-INs to sense the activity of a population of pyramidal cells and to broadcast back a proportionate and graded inhibitory signal to multiple pyramidal cells. Relevant to this function is our finding that increasing PV-IN firing can reduce pyramidal cell firing in a linear fashion (Figure 4E), which in a model can only be accomplished by inhibitory synapses. Thus, dynamic recovery complements other unique functional specializations of PV-INs, including the expression of Kv3 channels in the soma that allows a large dynamic range of action potential firing (with rates > 200 Hz) and in the axon terminals, to allow high rates of release (Goldberg et al., 2005). In addition, PV-INs also contribute to the generation of gamma-oscillations (Bartos et al., 2007), and it is conceivable that dynamic recovery at PV synapses could be essential for maintaining these high-frequency oscillations. Besides, dynamic recovery at inhibitory synapses resulted in relativity less depression at high frequencies of activity, which tilted the balance of excitation and inhibition toward inhibition (Figure S1E) (Galarreta and Hestrin, 1998, Varela et al., 1999). This shift of excitation-inhibition balance may stabilize network activity (Varela et al., 1999). As imbalanced excitation and inhibition and altered gamma-oscillation have been linked to autism, schizophrenia, and many other neurodevelopmental disorders (Bridi et al., 2017, Hussman, 2001, Lisman, 2012, Rojas and Wilson, 2014, Rubenstein and Merzenich, 2003), it could be of interest to determine whether altered dynamic recovery of PV-IN synapses contributes to these conditions.

Limitations of the Study

The results show that a dynamic recovery from depression in inhibitory synapses is crucial for a linear control of the firing rate of pyramidal cells. How this mechanism could operate in vivo cannot be fully predicted with the available data. Such predictions would require additional information, including how fast the rate of recovery is updated in response to changes in activity and whether these parameters are affected by neuromodulators that are prevalent in vivo.

Methods

All methods can be found in the accompanying Transparent Methods supplemental file.

Published: March 27, 2020

Data and Code Availability

Raw data and code used to produce Figures 1, 2, 3, and 4 and Figures S1–S4 are available upon reasonable request to the corresponding authors.