Summary
Performance-stability contradiction of high-energy-density materials (HEDMs) is a long-standing puzzle in the field of chemistry and material science. Bridging the gap that exists between detonation performance of new HEDMs and their stability remains a formidable challenge. Achieving optimal balance between the two contradictory factors is of a significant demand for deep-well oil and gas drilling, space exploration, and other civil and defense applications. Herein, supercomputers and latest quantitative computational strategies were employed and high-throughput quantum calculations were conducted for 67 reported HEDMs. Based on statistical analysis of large amounts of physico-chemical data, in-crystal interspecies interactions were identified to be the one that provokes the performance-stability contradiction of HEDMs. To design new HEDMs with both good detonation performance and high stability, the proposed systematic and comprehensive strategies must be satisfied, which could promote the development of crystal engineering of HEDMs to an era of theory-guided rational design of materials.
Subject Areas: Computational Method in Materials Science, Density Functional Theory (DFT), Energy Materials, Materials Design
Graphical Abstract

Highlights
-
•
High-throughput quantum calculations conducted for 67 HEDMs directly on a crystal level
-
•
Main reason that provokes the performance-stability contradiction was identified
-
•
Systematic strategies for balancing performance and stability of HEDMs were proposed
Computational Method in Materials Science; Density Functional Theory (DFT); Energy Materials; Materials Design
Introduction
With the dramatic increase in the human population and concomitant depletion of available resources, exploration of oil and gas deposits in ultra-deep wells is becoming a major challenge. Since extreme temperature conditions exist in deep holes, there is a significant demand for advanced high-energy-density materials (HEDMs) that would be highly stable to accidental stimulus, corresponding to low sensitivity toward accidental initiation of detonation. These HEDMs are expected to maintain high detonation performance that corresponds to high energy density and to have high stability to mechanical impact and friction, which is out of capability of many of the presently used state-of-the-art explosives (Shukla et al., 2017). Therefore, detonation performance and stability constitute the most valued features when evaluating an energetic material. However, high performance and high stability of HEDMs are known to be inherently contradictory and an optimal balance between them is one of the ultimate goals in the field of high-energy materials (Zeman and Jungová, 2016, Sabin, 2014).
Most of the HEDMs have molecular or ionic crystals with complex geometries, and the in-crystal non-bonding and anti-bonding interactions among species endow these materials with various spatial packing compactness, crystal stability, and energy density. Therefore, comprehensive understanding of how diverse in-crystal parameters affect the balance in the performance-stability relationship is one of the key tools to the rational design of advanced HEDMs with outstanding properties.
For decades, researchers have invested significant research efforts in searching for empirical quantitative structure-property relationships (QSPRs) (Zeman and Jungová, 2016). Moreover, in order to provide an insight into the physical and chemical connotations, quantum calculations were performed by researchers to address the performance-stability contradiction issue. For example, Zhang et al. proposed that HEDMs having crystal structures packed with planar layers could efficiently buffer against external mechanical stimuli, thus reducing the sensitivity of such compounds (Zhang et al., 2008, Zhang et al., 2018). More than 10 years passed since the synthesis of HEDMs with low sensitivity was inspired by the aforementioned theoretical principle and a series of advanced HEDMs, such as hydroxylammonium salts (Zhang et al., 2015a, Zhang et al., 2015b) and ammonium 3-dinitromethanide-1,2,4-triazolone (Shreeve et al., 2018), was developed. Furthermore, a “materials genome” approach, based on the theoretical calculations of six-member aromatic and heteroaromatic rings, was recently proposed. Notably, following this approach, a novel 2,4,6-triamino-5-nitropyrimidine-1,3-dioxide compound, with very good performance and sensitivity, was successfully synthesized (Wang et al., 2018).
However, to the best of our knowledge, experimental or theoretical strategies have not been reported till date, which systematically and clearly define guidelines or rules of thumb for the selection of appropriate parameters, critical for the design of advanced HEDMs with both satisfactory performance and stability, as, for example, was done by the molecular structure guidelines that are prevalent in the field of orally active pharmaceuticals development (Lipinski's “Rule of Five”) (Lipinski et al., 2001, Lipinski, 2004). The main reasons associated with the lack of experimentally derived guidelines may be related to a significant effort required for (1) the cost-effective preparation and characterization of a wide variety of HEDMs, which are essential for the reliable data statistics and rules deduction, and (2) scaled-up syntheses of all studied HEDMs, which is highly desirable for the field testing of the actual performance of these compounds. Moreover, the main bottleneck that hinders the breakthrough in the theoretical strategies for the design of the advanced HEDMs and causes numerous problems for practical applications is the lack of suitable, reliable, and powerful numerical methods. Particularly, traditionally used numerical methods, such as thermodynamic statistical method and empirical force field method, have been known for their insufficient accuracy. Quantum method, on the other hand, is known to be of the highest accuracy. Unfortunately, the consumption of computational resources by the latter method is very high. Noteworthy, traditional quantum chemical method is mainly applicable only for individual molecules rather than for crystals, owing to the lack of a reliable approach to describe the periodic crystal structure and the in-crystal intermolecular weak interactions. Therefore, for a long time, most of the research was limited to the development of QSPR models, based on the constitutional, topological, geometric, or quantum chemical descriptions of free molecules (Shukla et al., 2017, Dearden et al., 2013, Fayet et al., 2012). With respect to the studies related to how crystal packing can affect the balance in the performance-stability relationship of HEDMs, albeit their great importance (Jain et al., 2016, Tsyshevsky et al., 2017), these studies have rarely been conducted.
In the past few decades, supercomputers underwent a tremendous development in their performance, as predicted by Gordon Moore. Cross-fusion and integration of high-throughput supercomputing and advanced quantum modeling has naturally become one of the most promising ways to address the performance-stability contradiction issue of the HEDMs. To tackle and overcome this problem, a new software was recently developed, which was found to be suitable for supercomputers-based applications. This software was specifically designed for handling issues related to the HEDMs, namely, High Accuracy atomistic Simulation package for Energetic Materials (HASEM) was developed, which in our perspective should be capable of addressing both the above-mentioned structural and energy issues (Zhang et al., 2016). Use of the HASEM software to perform high-throughput calculations on a large number of physicochemical parameters for a large number of samples allowed us to obtain sufficient and comprehensive data to extract valuable information and guidelines for achieving optimal balance between performance and crystal stability of HEDMs. This facilitated the realization of artificial intelligence-based robotic platforms, capable of safe automated synthesis and screening of the future HEDMs (Coley et al., 2019).
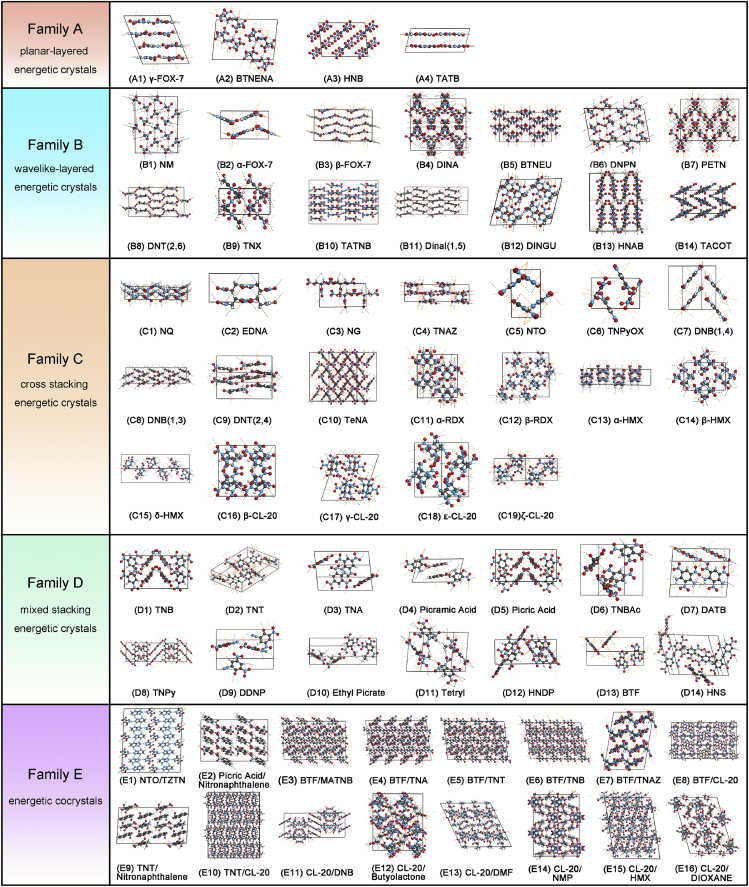
In order to search for the plausible physicochemical parameters that make the HEDMs excelling in both their performance and stability, 67 types of HEDMs were collected, wherein 25 compounds exhibited better detonation performance than 2,4,6-trinitrotoluene (TNT, detonation velocity Vd: 7.15 km s−1; detonation pressure Pd: 22.35 GPa; heat of explosion He: 1,290 kcal mol−1; and detonation temperature Td: 3017 K) and 25 compounds were found to be thermally stable at temperatures above 200°C. The crystal-stacking manner of the as-studied objects includes planar-layered (Family A), wavelike-layered (Family B), cross-stacking (Family C), and mixed stacking (Family D), as shown in Figure 1(Ma et al., 2014). Their correspondence to the common crystal terminologies of polycyclic aromatic hydrocarbons (Campbell et al., 2017) is given in Table S1. Figure S1 shows that the molecules include one-dimensional (1D) linear (12 compounds), 2D coplanar (26 aromatic compounds), and 3D non-planar or caged structures (13 compounds). The inclusion of 16 types of novel cocrystal HEDMs (Family E) further enriches our list of compounds to be more complete and reprehensive.
Figure 1.
Families of Crystal Packing Arrangement of Studied 67 HEDMs
White spheres represent hydrogen atoms, red denotes oxygen, cyan represents nitrogen, and gray denotes carbon. Black dashed lines represent interspecies hydrogen bonds, and orange dashed lines are other interspecies interactions. The corresponding molecular diagram for each compound is shown in Figure S1.
Based on our high-throughput quantum calculations, the detonation performance (including Vd, Pd, He, and Td) was predicted and crystal stability of the 67 HEDMs was studied, which were confirmed to be of high-level reliability by comparison with reported data. Numerous physicochemical parameters, including nitrogen density (ρN), oxygen balance (OB), functional group, molecular backbone, molecular weight (MW), crystal symmetry (including number of molecules per cell, space group, and crystal family), lattice lengths (a, b, and c), packing coefficient (PC), interlay distance (dlayerlayer), interspecies non-bonding interactions (hydrogen bonding and others; both amount and strength), material density (ρ), lattice energy (LE), and detonation products (both gaseous and solid), were calculated and correlated with their performance and stability. Eventually, it was successfully revealed that the interspecies interaction was the root cause in provoking the performance-stability contradiction of HEDMs. Therefore, in order to synthesize novel HEDMs, having both high performance and high stability, systematic strategy including the selection of molecular backbones, crystal packing arrangements, and the plausible ranges of a series of critical parameters was found, which is expected to provide useful guidelines for the molecular design of such compounds.
Results
Crystalline Structures: Theoretical Optimization and Experimental Validation
The crystalline characteristics of HEDMs mainly comprise the crystal family, number of molecules in each primitive cell, geometric symmetry, and geometry of the unit cell. Figure S2 exhibits that the crystals of the 67 HEDMs studied herein generally belong to monoclinic, orthorhombic, and triclinic families, with two, eight, or four molecules located in each primitive cell, respectively. Notably, most HEDMs have relatively low symmetry with the space group number (SGN) smaller than 62, with P21/c (SGN = 14) being the most popular space group.
Furthermore, the geometries of the 67 HEDMs were optimized based on the conjugate gradient method (Magnus and Stiefel, 1952), with the lattice parameters and atomic coordinates from single-crystal X-ray crystallography data as input (Crawford et al., 2007, Cai et al., 1983, Akopyan et al., 1966, Cady and Larson, 1965, Bagryanskaya and Gatilov, 1983, Meents et al., 2008, Wilkins and Small, 1982, Lind, 1970, Bracuti, 1996, Zhurova et al., 2006, Zhurova et al., 2007, Nie et al., 2001, Bryden, 1972, Adam et al., 2002, Trotter, 1960, Oyumi and Brill, 1988, Graeber and Morosin, 1974, Altmann et al., 1998, Choi, 1981, Turley, 1968, Espenbetov et al., 1984, Archibald et al., 1990, Zhurova and Pinkerton, 2001, Li et al., 2005, Abrahams, 1950, Reeve and Miller, 2002, Sarma and Nagaraju, 2000, Dickinson et al., 1966, Hakey et al., 2008, Millar et al., 2009, Millar et al., 2010, Millar et al., 2012, Cady et al., 1963, Cady et al., 1966, Cobbledick and Small, 1974; ; Ou et al., 1998, Bolotina et al., 2004, Thallapally et al., 2004, Vrcelj et al., 2003, Holden et al., 1972, Behrend and Heesche-Wagner, 1999, Bertolasi et al., 2011, Rheingold et al., 1989, Holden, 1967, Lowe-Ma et al., 1987, Gramaccioli et al., 1968, Cady, 1967, Huang et al., 2011, Gerard and Hardy, 1987, Wu et al., 2015, Hong et al., 2015, Zhang et al., 2013, Yang et al., 2012, Bolton and Matzger, 2011, Wang et al., 2014, Gao et al., 2014). The results indicated that, when the residual forces were less than 0.03 eV Å−1 and the stress components were less than 0.01 GPa, the calculated structures were considered as completely relaxed. Figure 2 demonstrates that all geometric parameters of the completely optimized calculated structures, including lattice constants a, b, and c; lattice angles α, β, and γ; and unit cell volumes, show satisfactory agreement with the experimental parameters obtained by X-ray crystallography. The linear coefficient of correlation between the calculated and experimental values of the lattice constants is R2 = 0.9993, with the standard error σ = 0.17 Å. For the comparative analysis between the calculated and experimental unit cell volumes, the statistical parameters are R2 = 0.9995 and σ = 28.37 Å3. The small discrepancies between the calculated and the experimental values present the high reliability and robustness of the currently used method in describing the crystal structures of HEDMs in a comprehensive manner.
Figure 2.
Calculated Crystal Structures of the 67 HEDMs Studied herein and their Experimental Validation
(A) Lattice constants (a, b, and c); (B) lattice angles (α, β, and γ); and (C) unit cell volumes of the 67 HEDMs studied.
Strategy for Improving Detonation Performance of High-Energy-Density Materials
Performance of Solid-State High-Energy-Density Materials: Theoretical Prediction and Experimental Validation
The detonation performance of HEDMs of concern generally includes detonation velocity Vd, detonation pressure Pd, heat of explosion He, and detonation temperature Td. Vd, which is defined as the stable velocity of the shock front, determines the power delivered by an HEDM and can be measured by Dautriche test method, high-speed photography, ion gap method, and similar methods (Cybulski et al., 1949). Pd denotes the stable pressure developed behind the shock front. It determines the shock wave energy of products and is generally measured by flyer plate method, impedance window method, detonation electric effect, etc. (Pachman et al., 2018). He provides the count of the total amount of energy released by an HEDM in the reaction and can be measured by calorimetry (Kiciński and Trzciński, 2009). Td can be measured by single-color pyrometry, multicolor pyrometry, or time-integrated optical emission spectroscopy (Ferguson et al., 2017).
The measurements of He, Vd, Pd, and Td required scaled-up synthesis of all studied HEDMs, which are usually not satisfied owing to the complex preparation or high synthesis cost reasons; therefore, many compounds do not have available experimental data for their detonation performance. In particular, the experimental data of Td in the literature are scarce because of the difficulty of its measurement. Table S2 summarizes that, among the 67 HEDMs used in this study, we found experimental data of He for 38 of them, experimental Vd for 36 HEDMs, and experimental Pd for 24 HEDMs (Dong and Zhou, 1989, Meyer et al., 2007, Keshavarz, 2005, Keshavarz, 2007, Keshavarz, 2008, Keshavarz, 2012, Rice and Hare, 2002, Wang et al., 2006a, Wang et al., 2006b, Akst, 1989, Bemm and Östmark, 1998, Rothstein and Petersen, 1979, Kamlet and Dickinson, 1968, Wang et al., 2006a, Wang et al., 2006b, Army, 1984, Keshavarz and Pouretedal, 2005, Hobbs and Baer, 1993, Gill et al., 2006, Volk and Bathelt, 1997, Politzer and Murray, 2011, Tsyshevsky et al., 2017). However, only the experimental data derived from HEDMs with dense packing (ρ > 95% ρmax, wherein ρmax is the maximum theoretical density as determined by X-ray crystallography, represented by solid scatters in Figure 3 and Table S2) could be used for comparative analysis and statistical analysis, because the measured results of He, Vd, and Pd largely depend on the density of packing of HEDMs. Consequently, experimental detonation parameters of more than half of the HEDMs are not available for comparison among different compounds, which strongly suggests an urgent request for the high-throughput quantum calculations for these HEDMs.
Figure 3.
Theoretically Predicted Performance of Solid-State HEDMs and their Experimental Validation
(A) Heat of explosion He of 38 HEDMs, (B) detonation velocity Vd of 36 HEDMs, and (C) detonation pressure Pd of 24 HEDMs studied herein. Solid scatters represent the dense packing HEDMs, whereas open circles are the HEDMs with the non-dense packing.
As a result, the detonation performance parameters were calculated, directly on a crystal structural level, for all the 67 HEDMs in this study and are summarized in Table S2. The advantages of our theoretical calculations, over the traditional type of calculations, include the simultaneous consideration of the periodic crystal structure and the weak interactions among interspecies (Zhang et al., 2019a, Zhang et al., 2019b). Therefore, the detonation performance parameters reported in this study are for the solid-state compounds instead of individual, gas phase molecules. Figure 3 shows a satisfactory agreement between the theoretically predicted performance and the experimentally measured performance of the HEDMs with dense packing (solid scatters). The linear correlation coefficient between the calculated and experimental He of the HEDMs with dense packing is R2 = 0.9492, with the standard error σ = 81.24 kcal mol−1. The statistical data are R2 = 0.9869, σ = 0.17 km s−1 for Vd, and R2 = 0.9858, σ = 1.22 GPa for Pd. The small discrepancies between the calculated and the experimental values present the high-level reliability of the currently used method in describing the detonation performance of the solid-state HEDMs.
Preferred Physicochemical Characteristics of High-Performing Energetic Crystals
Noteworthy, ρN, OB, and ρ are the main determinates of detonation performance of HEDM. First, ρN, defined as the mass of nitrogen per unit volume of an HEDM, is the most critical factor. This is attributed to the fact that the energy that is released from HEDMs is mainly derived from the average bond energy difference between the N–N bond in the reactants and the N≡N bond in the products. Second, OB describes the content to which a certain HEDM could be oxidized and it also determines the distribution of the detonation products, thereby deciding the amount of energy release during detonation. It is generally accepted that OB = 0% is conducive for HEDMs to attain the best performance. From the invention of TNT (OB = −74.0%) in the 1880s, to the synthesis of octahydro-1,3,5,7-tetranitro-1,3,5,7-tetrazocine (HMX, OB = −21.6%) during the First World War, till the synthesis of hexanitrohexaazaisowurtzitane (CL-20, OB = −11.0%) in the modern era, the development of HEDMs has always been accompanied by an increase in OB. Third, ρ determines the performance of an HEDM on a solid-state level, with Vd increasing linearly with ρ, whereas Pd increases as a cubic function of ρ. Table S3 presents that most HEDMs have parameters in the following range: 0.2 < ρN < 1.0 g cm−3, −140% < OB < 20%, and 1.5 < ρ < 2.1 g cm−3.
Preferred Molecular Backbones of High-Performing Compounds
Homocycle is by far the most commonly used molecular backbones of HEDMs. Among the 23 single-ring HEDMs investigated in this study, 19 of them have homo-cyclic backbones, such as compounds A3–A4, B8–B10, C7–C10, and D1–D11. Owing to the high proportion of carbon in the homocyclic molecules, most of these compounds have relatively low nitrogen content ρN and low detonation performance, as shown in Figures S3A–S3D. Among them, compounds A3–A4, B10, and C10 are exceptions, because most hydrogen atoms of the benzene are replaced by nitrogen-containing functional groups, which diminishes such carbon-dominated effect and thereby improves their detonation performance.
Noteworthy, introduction of nitrogen or oxygen atoms to the homocyclic backbone is an effective strategy to increase ρN and OB, both of which help to improve the performance of HEDMs. This strategy may be realized by synthesizing heterocyclic (either planar or nonplanner) or cage-like backbones. Considering homo-cyclic D2 (TNT) as the standard reference, crystals C5, C6, C11–C19, D8 all have higher ρN and OB, as well as better detonation performance (Figure S3; Supplemental Information). Table 1 presents that the molecular backbone of C5 is planar heterocyclic, and compared with crystals D2, it has an improved ρN (by 156.3%) and OB (by 66.8%) and the Vd and Pd are consequently improved by 6.2% and 20.2%, respectively. By using non-planar heterocyclic and cage-like backbones, such as crystals C11–C19, the improvement in detonation performance is more drastic. Table 1 further summarizes that, compared with crystal D2, these compounds have their Vd and Pd improved by up to 29.8% and 82.6%, respectively.
Table 1.
Effect of Different Molecular Backbones on the Performance of HEDMs
| Molecular Backbones | HEDMs | ρN (g cm−3) | OB (%) | Vd (km s−1) | Pd (GPa) | Hd(kcal kg−1) | Td (K) | |
|---|---|---|---|---|---|---|---|---|
| Planar | Homocycle | TNT (D2) | 0.32 | −74.0 | 7.15 | 22.35 | 1,290.1 | 3,016.9 |
| Heterocycle | NTO (C5) | 0.82 | −24.6 | 7.59 | 26.86 | 790.2 | 2,130.7 | |
| Non-planar | Heterocycle | β-HMX (C14) | 0.72 | −21.6 | 8.84 | 36.47 | 1,300.3 | 3,298.2 |
| Cage-like | ε-CL-20 (C18) | 0.77 | −11.0 | 9.28 | 41.61 | 1,399.5 | 3,953.7 | |
| Bridged | HNS (D14) | 0.33 | −67.5 | 7.34 | 24.12 | 1,359.3 | 4,052.6 | |
| Linear | α-FOX-7 (B2) | 0.74 | −21.6 | 8.32 | 32.80 | 951.9 | 2,464.3 | |
An alternate approach to improve ρN and OB of homocyclic compounds includes the introduction of “bridge bond” to connect the separate energetic rings into a whole. Compared with heterocyclic backbone, such bridged backbone leads to much weaker improvement of performance, approximately only half of the former, as shown in Figure S3. For example, crystal D14 is composed of two D2 molecules that are connected by a –CH = CH– bridge bond and it has slightly improved ρN (by 3.1%) and OB (by 8.8%), as well as slightly increased Vd (by 2.7%) and Pd (by 7.9%).
Figure S3 shows that, without the limitation of number of carbon atoms in the backbones, linear molecules have more flexible distribution on ρN, ranging from 0.33 (B7) to 0.98 (C1). Their OB values are generally high, distributing from −39.3% (B1) to +16.5% (A2). Moreover, their performance can be better than the monocyclic D2, with their Vd varying from 7.26 (C1) to 8.91 km s−1 (B7) and Pd from 22.28 (C1) to 36.67 GPa (B7).
Preferred Functional Groups of High-Performing Compounds
Functional groups are critical in increasing ρN and OB of HEDMs, thereby improving their detonation performance. Herein, the most seen functional groups, including –NO2, –NH2, –CH3, –OH, and –N3, were focused upon, and their effect on the performance of HEDMs was analyzed, as presented in Table 2.
Table 2.
Effect of Functional Groups including –NO2, –NH2, –CH3, –OH, and –N3 on the Performance of HEDMs
| Functional Groups |
HEDMs | ρN (g cm−3) | OB (%) | Vd (km s−1) | Pd (GPa) | Hd (kcal kg−1) | Td (K) | |
|---|---|---|---|---|---|---|---|---|
| Type | Number | |||||||
| –NO2 | 2 | DNB (C8) | 0.27 | −95.2 | 6.54 | 18.20 | 1,218.2 | 2,712.6 |
| 3 | TNB (D1) | 0.33 | −56.3 | 7.30 | 23.25 | 1,337.0 | 3,398.4 | |
| 6 | HNB (A3) | 0.48 | 0.0 | 9.28 | 41.28 | 1,654.9 | 5,418.3 | |
| –N3 | 0 | TNB (D1) | 0.36 | −56.3 | 7.30 | 23.25 | 1,337.0 | 3,398.4 |
| 3 | TATNB (B10) | 0.92 | −28.6 | 8.31 | 31.58 | 1,466.6 | 4,572.5 | |
| –NH2 | 0 | TNB (D1) | 0.33 | −56.3 | 7.30 | 23.25 | 1,337.0 | 3,398.4 |
| 1 | TNA (D3) | 0.44 | −56.1 | 7.46 | 25.10 | 1,160.1 | 2,904.0 | |
| 2 | DATB (D7) | 0.54 | −55.9 | 7.50 | 25.98 | 1,008.3 | 2,485.5 | |
| 3 | TATB (A4) | 0.64 | −55.8 | 7.68 | 28.17 | 889.4 | 2,154.5 | |
| –OH | 0 | TNB (D1) | 0.33 | −56.3 | 7.30 | 23.25 | 1,337.0 | 3,398.4 |
| 1 | Picric acid (D5) | 0.33 | −45.4 | 7.58 | 25.89 | 1,244.5 | 3,265.7 | |
| –CH3 | 0 | TNB (D1) | 0.33 | −56.3 | 7.30 | 23.25 | 1,337.0 | 3,398.4 |
| 1 | TNT (D2) | 0.32 | −74.0 | 7.15 | 22.35 | 1,290.1 | 3,016.9 | |
| 2 | TNX (B9) | 0.29 | −89.6 | 6.82 | 19.94 | 1,239.9 | 2,722.1 | |
Figures S3E–S3H exhibit that most HEDMs are negative in OB. Therefore, the inclusion of –NO2 would simultaneously increase OB and ρN of an HEDM. Table 2 presents that C8, D1, and A3 have the same molecular backbone of six-membered carbon ring; however, the number of –NO2 groups increase from 2–3 to 6. Accordingly, their OB values are improved from −95.2, −56.3% to 0%, and their ρN from 0.27, 0.33 to 0.48. Thus, their Vd increases by 41.9%, Pd increases by 126.8%, Hd increases by 35.8%, and Td increases by 99.7%. In particular, A3 has an optimal OB = 0%, making its detonation performance approaching the extreme of traditional CHNO HEDMs. Owing to the significant role of –NO2 in improving the performance of HEDMs, introduction of –NO2 has been the most used strategy for synthesizing high-performing compounds.
The functional group –N3 could lead to a significant increase in both ρN and OB, which would improve the detonation of HEDMs. For example, the inclusion of three –N3 on D1 leads to the formation of B10, with improvement in ρN by 155.6% and improvement in OB, Vd, and Pd, Hd, and Td by 49.2%, 13.8%, 35.8%, 9.7%, and 34.5%, respectively. In general, –N3 has only half of the effect of –NO2 in improving the detonation performance of HEDMs, mainly due to the high bond order in –N3, and thereby less amount of energy can be released when generating nitrogen gas products.
The inclusion of –NH2 effectively improves ρN, whereas it keeps OB almost unchanged. For example, D1, D3, D7, and A4 contain different number of –NH2 functional groups; however, the difference of their OB is within 1%. When the number of –NH2 increases from 0 to 3, the ρN increases twice as much, Vd increases by 5.2%, and Pd increases by 21.2%. However, owing to the excessive amount of H2O in the products of compound A4 compared with compound D1, an obvious decrease in their Hd (by 33.5%) and Td (by 36.6%) is observed, and this is discussed in more detail in the section Preferred Detonation Products of High-Performing Compounds.
The inclusion of –OH, on the other hand, is conducive to the improvement of OB and leads to the increase in the population of H2O and CO2 among the detonation products (by reducing the population of carbon clusters). For example, compared with D1, compound D5 shows an improved OB (by 19.4%), Vd (by 3.8%), and Pd (by 11.4%) attributed to the inclusion of an additional –OH group. The slight decrease in Hd (by 6.9%) and Td (by 3.9%) is caused by the formation of extra H2O in the products, similar to the effect of –NH2.
In contrast, the inclusion of –CH3 leads to the simultaneous decrease in OB and ρN of the compound, thereby reducing its detonation performance. Table 2 summarizes that D1, D2, and B9 have the same molecular backbone constituting 1,3,5-trinitrobenzene, but the number of methyl groups –CH3 in their molecules increases from 0, 1 to 2. Accordingly, their OB values decrease from −56.3%, −74.0%, and 89.6% and their ρN values decrease from 0.33, 0.32, and 0.29. Thus, their Vd decreases by 6.6%, Pd decreases by 14.2%, Hd decreases by 7.3%, and Td decreases by 19.9%. Notably, compared with –NO2, the effect of –CH3 is about one order of magnitude less strong.
Preferred Detonation Products of High-Performing Compounds
The energy released by an HEDM is determined by the energy difference between total energy of unreacted crystal and total energy of all detonation products. Therefore, the type and amount of various detonation products are decisive to the performance level of HEDMs. For each of the 67 HEDMs studied herein, the distribution of detonation products was determined based on the principle of minimization of their Gibbs free energy. Figure S5 exhibits that the main products are N2 (gaseous), H2O (gaseous), CO2 (gaseous), and C (solid) and their proportion among the total products was mainly determined based on the value of OB. Hydrogen is the easiest element to be oxidized (into H2O), and carbon is the second in number (into CO2). The residual of the hydrogen consumes nitrogen and changes into NH3, the residual carbon aggregates into solid clusters with a graphene structure, and the residual nitrogen atoms combine together and form N2.
Figures 4 and S6 show an obvious correlation between the product distribution of the HEDMs and their detonation performance. Generation of large amount of N2 and CO2 gas is conducive to the improvement of Vd, Pd, Hd, and Td of the HEDMs, with the effect of N2 being stronger than CO2. In contrast, the high proportion of solid carbon clusters in the products, which happens when oxygen severely lacks, would lead to a drastic decrease in the performance of HEDMs. The population of H2O in the products is not obvious in regulating Vd and Pd, as shown in Figure 4C. However, high proportion of H2O in the products leads to a decrease in Hd and Td, as shown in Figures S6J and S6N. This is attributed to the significantly higher specific heat capacity of H2O compared with those of other detonation products.
Figure 4.
Correlation between Vd and Pd of the 67 HEDMs with their Detonation Products
(A) N2, (B) CO2, (C) H2O, and (D) solid carbon clusters.
The found correlation between the product distribution of the HEDMs and their detonation performance is well consistent with our findings described in the sections Preferred Molecular Backbones of High-Performing Compounds and Preferred Functional Groups of High-Performing Compounds, both indicating high ρN and optimal OB to be the target parameters in designing high-performing HEDMs. The former ensures the abundant generation of N2 gas, whereas the latter guarantees the least generation of solid carbon clusters in the detonation products. Moreover, the performance-products correlation also indicated that, in order to synthesize high-performing HEDMs, the proportion of hydrogen in the compound should be low to promise the complete oxidation of the carbon element.
Preferred Crystal Characteristics of High-Performing Compounds
In order to extract the plausible crystalline characteristics of high-performing HEDMs, the detonation performance evolution of the 67 HEDMs with respect to each corresponding PC and ρ was plotted in Figures S4, S7, and S11. The performance of the HEDMs studied herein shows close correlation with their PC and ρ, with most of the high-performing compounds owning PC > 70% and ρ > 1.73 g cm−3.
From the perspective of manner of crystal stacking, Family A refers to planar-layered compounds, Family B is for wavelike-layered compounds, Family C incorporates cross-stacking, Family D consists of mixed stacking compounds, and Family E refers to cocrystals, as shown also in Figure 1. Family A has an obvious advantage of having high PC and high ρ, among all the HEDMs investigated in this study. In contrast, compounds belonging to Family B have relatively low values of PC and ρ. The PC and ρ of Family C compounds generally locate in between the two. Therefore, it is theoretically recommended to synthesize planar-layered and cross-stacking crystals, which would have higher probability of having high density, close packing, and high performance.
Figure S2 displays the distribution characteristics of high-performing HEDMs (better than TNT) with respect to their crystal symmetry. Clearly, no obvious preference of high-performing compounds in space group, crystal family, or number of molecules in each primitive cell is observed.
Strategy for Improving Detonation Performance of Energetic Crystals
To extract the plausible physicochemical characteristics of high-performing HEDMs, the detonation performance parameters, i.e., Vd, Pd, He, and Td, were plotted as a function of ρN, OB, and ρ for all the HEDMs studied, as presented in Figures 5 and S3.
Figure 5.
Correlation between the Detonation Performance of the 67 HEDMs and their ρN, OB, and ρ
The detonation performance of TNT is taken as reference. Related scatterplots and histograms are provided in Figures S3 and S4 of the Supplemental Information.
Figure S3 exhibits a strong dependence of Vd and Pd of the HEDMs on their ρN, OB, and ρ. Notably, Vd and Pd almost linearly increase with OB. Histograms were plotted to present the average values of detonation performance at certain ranges of the three physicochemical parameters, as shown in Figure 5, with the Vd, Pd, and Td of TNT set as the reference values (Nielsen et al., 1979, Note).
Figure 5 demonstrates that, when the HEDMs satisfy the following conditions: ρN > 0.3 g cm−3, −60% < OB < +20%, or ρ > 1.73 g cm−3, their detonation performance becomes better than that of TNT with a very high probability (>80%). Within the recommended scope, the higher the density ρ, OB, and ρN, the higher the performance achieved by the HEDMs.
Strategy for Improving Crystal Stability of High-Energy-Density Materials
Crystal stability of HEDMs refers to the extent to which the crystal can resist melting and decomposition and is therefore an important indicator of heat-resistant explosives to be applicable for drilling deep oil/gas wells, space exploration, and other industrial applications. Crystal thermostability of HEDMs is usually experimentally characterized by thermogravimetric analysis (TGA) and differential scanning calorimetry (DSC) at a constant heating rate. In order to extract the preferred in-crystal parameters of thermostable energetic crystals, the literature reports related to the experiments determining thermostability (62 compounds' data were reported among the 67 HEDMs studied) (Sun et al., 2015, Liu et al., 2016, Nielsen et al., 1979, Atkins et al., 1986, Siavosh-Haghighi and Thompson, 2006, Wright and Chute, 1952, Kwasny and Syczewski, 1980, Lange et al., 2009; Bachman and Vogt, 1958, Ling-Yun et al., 2010, Manelis et al., 2006, Boileau et al., 1985, Leemann and Grandmougin, 1908, Hervé et al., 2005, Hall and Wright, 1951, Altenburg et al., 2009, Singh et al., 2005, Schmidt and Gehlen, 1965, Boyer and Morgan, 1959, Foster, 1960, Hernández et al., 2006, Veselova, 2008, Gao et al., 2014, Kofler and Brandstätter, 1948, Šarlauskas, 2010, Spencer and Wright, 1946, Srinivasan et al., 2006, Siele and Warman, 1962, Licht and Ritter, 1988, Leonard et al., 1956, Huang et al., 2011, Ohta et al., 1963, Klapötke and Witkowski, 2016, Wu et al., 2015, Hong et al., 2015, Zhang et al., 2013, Yang et al., 2012, Bolton and Matzger, 2011, Wang et al., 2014, Millar et al., 2012) were collected and these temperatures were correlated with the main crystal packing characteristics, as shown in Figure S8.
Theoretical Indicator of Crystal Stability: Lattice Energy
Theoretically, lattice energy (LE), defined as the total energy difference between the constituent ions in the free state and the crystal, comprehensively characterizes the crystal packing force and interspecies association strength, thereby quantifying the solid-state stability from an energetics perspective. Figure 6A shows an obvious positive correlation between the measured thermostability and the calculated LE. Figure S9 also exhibits a general positive correlation between the mechanical sensitivity and the calculated LE (Zhang et al., 2019a, Zhang et al., 2019b). Therefore, it is reasonable to employ LE as a theoretical indicator of crystal stability, which reflects the thermal and mechanical sensitivity of HEDMs. Figure 6B demonstrates that most HEDMs have satisfactory thermostability, with their degenerating temperature higher than 200°C if their LE is higher than 25 kcal mol−1.
Figure 6.
Correlation between the Calculated Lattice Energy and the Reported Experimental Degeneration Temperatures of 62 HEDMs
(A) Scattered and (B) bar plots. Yellow region represents the optimal range of LE to make HEDMs stable.
Preferred Molecular Characteristics of Highly Stable Energetic Crystals
Molecular characteristics including ρN, OB, and MW were considered for further study, as presented in Table S2. Figure S8 exhibits the plot of the correlation between these parameters and the crystal stability (both experimentally determined degeneration temperature and calculated LE) to obtain the optimal ranges of these parameters that make HEDMs thermally stable.
Figures S8A–S8D show a strong correlation between the ρN and OB values of the HEDMs studied with respect to their crystal stability, whereas no obvious trend of stability is observed with respect to MW, as shown in Figures S8M and S8N. For obtaining HEDMs with thermostability higher than 200°C, the plausible ρN and OB values are in the range of 0.6–1.0 g cm−3 and −80% to 0%, respectively. For example, the well-known thermostable compound A4 (2,4,6-triamino-1,3,5-trinitobenzene (TATB)), with a decomposition temperature of 366.4°C, has an OB = −55.8%, which is in the recommended range of OB. Interestingly, all the bridge compounds (B13, B14, D12, and D14) and non-planar heterocyclic/caged compounds (from C12 to C20) fall into this region, further confirming the advantage of these molecular backbones in enhancing crystal stability.
In particular, Figure 6A clearly indicates that all the bridged compounds (such as B13, B14, D12, and D14) and non-planar heterocyclic/caged compounds (from C12 to C20) are highly stable. Therefore, bridge connected energetic rings and non-planar heterocycles/cages were referred to as stable compounds preferred molecular backbones. Noteworthy, the effectiveness of the bridge characteristics in improving thermostability of HEDMs has been confirmed by the successful synthesis of three heat-resistant compounds.
Preferred Crystalline Characteristics of Highly Stable Energetic Crystals
Crystal stacking is the factor that is mainly responsible for making solid-state HEDMs different from separate, gaseous molecules and is thereby critical in deciding the crystal stability of practical compounds. Table S2 presents that, besides LE, calculated crystal characteristics also include PC, ρ, interspecies nonbonding interactions (hydrogen bonding and others; both amount and strength), manner of crystal stacking, the closest interlayer distance (dinterlayer), as well as crystal symmetry (including number of molecules per cell, space group, and crystal family).
PC reflects the extent to which the volume of a crystal is occupied by hard spherical atoms. PC, along with ρ, exhibits a good correlation with crystal stability of the HEDMs studied herein. Figures S8E–S8H reveal that most of the heat resistant compounds locate within relatively narrow ranges of PC > 73% and ρ > 1.73 g cm−3.
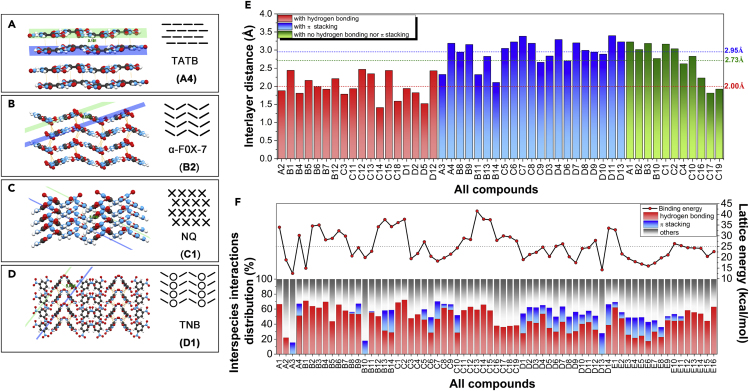
Figure 7 shows the schematic illustration of crystal stacking, grouping the studied 67 HEDMs into Family A to Family E. As discussed in the section Preferred Crystal Characteristics of High-Performing Compounds, Family A and Family C, namely, the planar-layered and cross-stacking compounds, respectively, have an obvious advantage in leading HEDMs to be of high PC and high ρ. We thereby recommend the synthesis of energetic crystals using these two packing manners, because of their higher probability to be of high stability.
Figure 7.
Crystal-Stacking Manner as well as its Influence on Crystal Stability
(A–D) Schematic illustrations of crystal-stacking manner and interlayer distance measurement for Family A–D compounds, (E) Closest interlayer distances of the 51 pristine crystals studied and their classification based on types of interlayer interaction. Red represents the interlayer HB interaction; blue represents the interlayer π-stacking interaction; green indicates that neither HB nor π stacking is present. (F) Interspecies interaction type, distribution, and lattice energy (LE) of all 67 HEDMs studied herein.
Furthermore, hydrogen bonding (HB) is an important factor that governs the reactivity of HEDM to external stimuli. Figures S8I–S8L show an obvious correlation between the HB and the crystal stability of the 67 HEDMs studied herein (Nielsen et al., 1979, Note). Noteworthy, most heat-resistant compounds have relatively high HB amount with the HB occupied area on the Hirshfeld surface of more than 90 Å. In order to figure out the advantageous characteristics of thermostable HEDMs, cluster analysis on the plot of the correlation between LE and HB amount was made as indicated in Figure S10. The results reveal that all the bridged compounds and the non-planar heterocyclic/caged compounds show higher LE than the aromatic compounds that have the identical HB amount, indicating the advantage of these molecular backbones to make HEDMs thermally stable.
In addition to large HB amount, high HB strength is also critical for making HEDMs thermally stable. For example, the HB in B1 (nitromethane, NM) and C3 (nitroglycerin, NG) is very weak, both values smaller than 5 kcal mol−1, making these compounds to be liquid under ambient conditions. Figures S8K and S8L indicate that HEDMs with good crystal stability generally have their HB to be at least higher than 2.5 kcal mol−1. Again, noteworthy, all the bridged compounds and non-planar heterocyclic/caged compounds fall into the recommended region, further confirming the advantage of these molecular backbones in enhancing crystal stability.
For each pristine crystal, the dinterlayer was measured in a way shown in Figures 7A–7D. Figure 7E summarizes the dinterlayer values, exhibiting a strong dependence on the types of interlayer interactions. The presence of HB interactions between layers leads the HEDMs to have a generally small dinterlayer with an average value of 2.00 Å. In contrast, the presence of π-stacking interaction leads to a relatively large distance with the average dinterlayer = 2.95 Å. Moreover, the compounds with neither HB nor π stacking present between the layers have their interlayer distance lying between the two, with an average dinterlayer = 2.73 Å. This crystal packing rule is well consistent with the interspecies interactions mechanism that was revealed in our previous study (Zhang et al., 2019a, Zhang et al., 2019b): HB is essentially a proton–lone pair attractive force and tends to decrease interlayer distance, whereas π-stacking interaction is lone pair–π exclusive and results in an increase in the interlayer distance. Figure 7F further confirms this mechanism and shows that HB interaction population plays a decisive role in regulating the LE of the HEDMs. For example, Figure S1 shows that A3 (hexanitrobenzene, HNB) and B10 (triazidotrinitrobenzene, TATNB) are very alike in structure with A4 (triaminotrinitrobenzene, TATB). However, the former two are hydrogen free and thereby have only about half the LE of the latter. Similarly, D13 (benzotrifuroxan, BTF) is HB free and has the most percentage of intermolecular π-stacking interactions among Family D, leading to one of the lowest LE among all the compounds. Therefore, in order to synthesize stable HEDMs, abundant interlayer HB is necessary attributed to its positive effect on improving PC, ρ, and LE of the energetic crystals.
Figure S2 clearly indicates that no obvious preference of highly stable energetic crystals in crystal symmetry is observed.
Strategy for Improving Crystal Stability of Energetic Crystals
To extract plausible physicochemical characteristics of highly stable HEDMs, the average values of LE were plotted with respect to ρN, OB, PC, ρ, HB amount, and HB strength for all the 67 HEDMs studied, as shown in Figure 8, with the LE = 25 kcal mol−1 being set as the reference.
Figure 8.
Stable HEDMs with Preferred Ranges of Physicochemical Characteristics
(A) ρN, (B) OB, (C) PC, (D) ρ, (E) HB amount, and (F) HB strength.
When the HEDMs satisfy the following conditions: LE > 25 kcal mol−1, ρN > 0.6 g cm−3, −80% < OB < 0%, PC > 73%, ρ > 1.73 g cm−3, HB area >90 Å2, and interspecies HB strength >2.5 kcal mol−1, their thermostability becomes higher than 25 kcal mol−1 (corresponding to a temperature of 200°C) at a very high probability. Moreover, the higher the density ρ, PC, and HB amount, the higher the crystal stability of the HEDMs. Noteworthy, the slight difference in the ranges derived herein and our recent study is ascribed to the use of totally different sets of sample compounds (Li et al., 2020). In the future, the range of the critical physicochemical parameters will become more converged, utilizing larger samples and machine learning methodologies.
Guidelines for Synthesizing Advanced High-Energy-Density Materials with Simultaneous High Performance and High Stability
Mutual Contradiction Factors between High Performance and High Stability of High-Energy-Density Materials
The sections Strategy for Improving Detonation Performance of High-Energy-Density Materials and Strategy for Improving Crystal Stability of High-Energy-Density Materials reveal how diverse physicochemical factors regulate the detonation performance and crystal stability of HEDMs. By plotting the probability of the HEDMs to be of high performance (better than TNT) and to be of high stability (higher than 200°C) in Figures 9 and S11, the factors that cause performance-stability contradiction of HEDMs were successfully obtained.
Figure 9.
Performance-Stability Contradiction and Theoretically Recommended Strategy
(A-F) (A) Performance-Stability Contradiction and Theoretically Recommended Strategy from the Perspectives of (B) Nitrogen Density, (C) Oxygen Balance, (D) Packing Coefficient, (E) Material density, and (F) Molecular Skeleton.
Figure 9A exhibits an obvious violation in HB amount leading to high performance and high stability of HEDMs. With the increase in the HB amount of HEDM, the probabilities to be of high performance and to be of high stability go in the opposite direction. For example, when HB proportion among the interspecies interactions increases from 0% to 50%, the probability of HEDMs to acquire high stability dramatically increases from 0% to >50%; nonetheless, the probability of HEDMs to attain high performance capability decreases by ∼40%. Such contradiction factor corresponds to the distribution characteristics of interspecies interaction, which belongs to a crystal packing characteristic. The opposite requirement of performance and stability to interspecies interaction distribution makes most of known HEDMs either high performing or highly stable; however, simultaneously meeting both the criteria is not commonly observed.
In contrast, for other crystal packing characteristics, such as PC and ρ, no performance-stability contradiction is found. Moreover, high performance and high crystal stability of HEDMs can be simultaneously satisfied at overlapping ranges, as shown in Figures 9D, 9E, S11D, and S11E. Consequently, in order to design novel HEDMs with good detonation performance (better than TNT) combined with satisfactory crystal stability (above 200°C), the recommended range is PC > 73% and ρ > 1.81 g cm−3 (the higher the better).
Also, for molecular characteristics, no contradiction was found between high performance and high crystal stability at the preferred distributions of the ρN and OB values; however, highly stable HEDMs generally require much narrower regions. In order to design advanced HEDMs with good detonation performance (better than TNT) combined with satisfactory crystal stability (above 200°C), ρN > 1.0 g cm−3 and −40% < OB < 0 should be satisfied.
Strategy for Overcoming the Performance-Stability Contradiction of High-Energy-Density Materials
Noteworthy, in order to overcome the performance-stability contradiction and synthesize advanced HEDMs with the highest probability, the following guidelines should be strictly followed: (1) molecular structure: bridged or non-planar heterocyclic/caged backbones, (2) crystal structure: planar-layered and cross-stacking manner, and (3) critical physicochemical parameters: nitrogen density >0.6 g cm−3, −40% < oxygen balance <0%, packing coefficient >73%, and material density >1.73 g cm−3.
The underlying of the selection of bridged molecular structures is as follows: bridged HEDMs maintain their ρN and OB to be almost unchanged, with improved values of PC and ρ compared with the corresponding single rings structures, which promise the detonation performance level being slightly influenced. At the same time, the HB amount of the bridged compound gets altered due to the significant increase in the molecular size. For example, D14 is formed by connecting two D1 molecules with a −CH = CH– bridge and the enlargement of the molecular size leads to the increase in the HB area on the Hirshfeld surface of each individual molecule by three times. From D1 to D14, the HB area increases from 58.3 to 154.9 Å2 and the crystal stability is also improved three times. However, the detonation performance is only slightly weakened by 3% because of the improvement in PC and ρ, and D14 is still in the range of high-performing HEDMs. Similarly, an –NH– bridge connects two D1 molecules into a D12 molecule, which increases the HB area to double the value (from 58.3 to 112.5 Å2) and also the crystal stability, but brings little influence to detonation performance.
The reason for selecting non-planar heterocyclic/caged molecular structures is that these compounds generally exhibit higher LE values compared with the single homocyclic ones, as shown in Figure S10, providing them outstanding crystal stability. At the same time, the introduction of nitrogen or oxygen atoms of the heterocyclic molecules leads to the substantial increase in the ρN and OB of HEDMs, as discussed in the section Preferred Molecular Backbones of High-Performing Compounds. Thus, the performance of these non-planar heterocyclic/caged HEDMs could be doubly improved compared with the traditional homocyclic compounds.
Finally, co-crystalizing technology, which mixes different compounds at a molecular level, could also increase the probability of HEDMs to be of high performance (by 11%) and to be of high stability (by 3%), as presented in Figure 9F. Nonetheless, the probability of meeting both high performance and high stability using this strategy is currently not so sound as introducing bridged molecular backbones or non-planar heterocyclic/caged backbones. This is mainly ascribed to the fact that the PC and ρ of the cocrystals generally distribute at relatively low regions, which are out of the optimal ranges as presented in Table 3. In order to synthesize more cocrystals with both high performance and high crystal stability, a critical issue that chemists should address is the structural compatibility of the pre-mixed molecules, so as to enhance the interspecies HB strength of the cocrystals and push their PC and ρ to the corresponding optimal ranges.
Table 3.
Synthesis Guidelines for Advanced High-Energy-Density Materials with Both High Performance and Stability
| Characteristics | Optimal Ranges |
|---|---|
| Nitrogen density ρN | >0.6 g cm−3 |
| Oxygen balance OB | −40%–0% |
| Packing coefficient PC | >73% |
| Material density ρ | >1.73 g cm−3 |
| Molecular backbone | Bridged backbones |
| Non-planar heterocyclic or cage-like backbones | |
| Crystal packing manner | Planar-layered or crossed packing |
Discussion
High-throughput quantum calculations were performed for 67 typical HEDMs directly on a crystal structural level. For each compound, detonation performance, crystal stability, and dozens of physicochemical properties were calculated and thoroughly verified by comparison with the reported data. The mechanism of how diverse physicochemical parameters of HEDMs control their detonation performance and crystal stability was proposed. The factor that provokes the performance-stability contradiction was discovered to be a crystal packing characteristic, namely, interspecies interactions. With respect to other physicochemical factors, high performance and high stability of HEDMs could be of mutual promotion at certain overlapping ranges with the latter requiring a narrower scope.
The guidelines for synthesizing both high-performing (better than TNT) and stable (>200°C) HEDMs were proposed to be as follows: (1) molecular structure: bridged or non-planar heterocyclic/caged structure, (2) crystal structure: planar-layered and cross-stacking manner, and (3) critical parameters: nitrogen density >0.6 g cm−3, −40% < oxygen balance <0%, packing coefficient >73%, and material density >1.73 g cm−3. To the best of our knowledge, this study presents the most comprehensive and systematic strategy for the design of advanced HEDMs, which is expected to provide powerful guidance for molecular and crystal design of these materials.
Limitations of the Study
Crystal stability of HEDMs refers to the extent to which the crystal can resist melting and decomposition under external stimulus. The stimuli could be of heat, mechanics, optics, electrostatics, radio-frequency, and others. In this study, we limit the crystal stability to be thermostability and mechanical stability.
In this study, we limit the high-performing HEDMs to be better than TNT and thermostable HEDMs to be above 200°C. However, the requirement for the explosive performance and crystal stability could be different in different application environments, so the recommended ranges of the key parameters may slightly shift accordingly. In addition, the rational ranges were obtained by statistical analysis of large amounts of physico-chemical data, so considering larger number of compounds would lead to more precise ranges.
Methods
All methods can be found in the accompanying Transparent Methods supplemental file.
Acknowledgment
The authors greatly acknowledge the financial support from the National Natural Science Foundation of China (Grant Nos. 11604017, 11872052, 21603172, and 21875024). L.Z. thanks Prof. C.Y. Zhang and J.G. Zhang for the helpful discussions.
Author Contributions
C.L. and H-H.Z. conducted the calculations and data analysis. H.L. estimated the experimental application value based on the theoretical results. Y.H., M.G., and C.Q.S. co-wrote the manuscript. L.Z. conceived the theory, designed the calculations, and drafted the manuscript. All authors contributed to the overall scientific interpretation.
Declaration of Interests
The authors declare no competing interests.
Published: March 27, 2020
Footnotes
Supplemental Information can be found online at https://doi.org/10.1016/j.isci.2020.100944.
Contributor Information
Yongli Huang, Email: huangyongli@xtu.edu.cn.
Michael Gozin, Email: cogozin@gmail.com.
Chang Q. Sun, Email: ecqsun@gmail.com.
Lei Zhang, Email: zhang_lei@iapcm.ac.cn.
Data and Code Availability
All the crystal geometries, in-crystal interspecies interactions, crystal energetics, and solid-state detonation performance of the 67 HEDMs were calculated based on the recently developed supercomputing software, namely, High Accuracy atomistic Simulation package for Energetic Materials (HASEM) (Chen et al., 2016, Zhang et al., 2016), which is adapted to modern supercomputers on the basis of the J parallel Adaptive Structured Mesh applications INfrastructure (JASMIN) (Mo et al., 2010).
The source data that support the plots in this article and the other findings of this study are available from the corresponding authors upon reasonable request.
Supplemental Information
References
- Abrahams S.C. The crystal structure of p-dinitrobenzene. Acta Crystallogr. 1950;3:194–196. [Google Scholar]
- Adam D., Karaghiosoff K., Klapötke T.M., Holl G., Kaiser M. Triazidotrinitro benzene: 1, 3, 5-(N3)3-2, 4, 6-(NO3)3C6. Propellants Explos. Pyrotech. 2002;27:7–11. [Google Scholar]
- Akopyan Z.A., Struchkov Y.T., Dashevskii V.G. Crystal and molecular structure of hexanitrobenzene. J. Struct. Chem. 1966;7:385–392. [Google Scholar]
- Akst I.B. Heat of detonation, the cylinder test, and performance munitions. Los Alamos Natl. Lab. 1989 LA-UR-89-1345. [Google Scholar]
- Altenburg T., Klapötke T.M., Penger A. Primary nitramines related to nitroglycerine: 1-nitramino-2, 3-dinitroxypropane and 1, 2, 3-trinitraminopropane. Cent. Eur. J. Energ. Mater. 2009;6:255–275. [Google Scholar]
- Altmann K.L., Chafin A.P., Merwin L.H., Wilson W.S., Gilardi R. Chemistry of tetraazapentalenes. J. Org. Chem. 1998;63:3352–3356. [Google Scholar]
- Archibald T.G., Gilardi R., Baum K., George C. Synthesis and X-ray crystal structure of 1, 3, 3-trinitroazetidine. J. Org. Chem. 1990;55:2920–2924. [Google Scholar]
- Army H.D.O.T. Military explosives. In: ARMY H.D.O.T., editor. Headqurters Department of the Army; 1984. [Google Scholar]
- Atkins R.L., Hollins R.A., Wilson W.S. Synthesis of polynitro compounds. Hexasubstituted benzenes. J. Org. Chem. 1986;51:3261–3266. [Google Scholar]
- Bachman G.B., Vogt C.M. The BF3· N2O4 complex as a nitrating agent. J. Am. Chem. Soc. 1958;80:2987–2991. [Google Scholar]
- Bagryanskaya I.Y., Gatilov Y.V. Crystal structure of nitromethane. J. Struct. Chem. 1983;24:150–151. [Google Scholar]
- Behrend C., Heesche-Wagner K. Formation of hydride-meisenheimer complexes of picric acid (2, 4, 6-trinitrophenol) and 2, 4-dinitrophenol during mineralization of picric acid by nocardioides sp. strain CB 22-2. Appl. Environ. Microb. 1999;65:1372–1377. doi: 10.1128/aem.65.4.1372-1377.1999. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bemm U., Östmark H. 1,1-diamino-2,2-dinitroethylene: a novel energetic material with infinite layers in two dimensions. Acta Crystallogr. 1998;54:1997–1999. [Google Scholar]
- Bertolasi V., Gilli P., Gilli G. Hydrogen bonding and electron donor−acceptor (EDA) interactions controlling the crystal packing of picric acid and its adducts with nitrogen bases. Their rationalization in terms of the pKa equalization and electron-pair saturation concepts. Cryst. Growth Des. 2011;11:2724–2735. [Google Scholar]
- Boileau J., Carail M., Wimmer E., Gallo R., Pierrot M. Dérivés nitrés acétylés du glycolurile. Propellants Explos. Pyrotech. 1985;10:118–120. [Google Scholar]
- Bolotina N.B., Hardie M.J., Speer R.L., JR., Pinkerton A.A. Energetic materials: variable-temperature crystal structures of γ-andε-HNIW polymorphs. J. Appl. Cryst. 2004;37:808–814. [Google Scholar]
- Bolton O., Matzger A.J. Improved stability and smart-material functionality realized in an energetic cocrystal. Angew. Chem. Int. Ed. 2011;50:8960–8963. doi: 10.1002/anie.201104164. [DOI] [PubMed] [Google Scholar]
- Boyer J., Morgan J.,L. Acid catalyzed reactions between carbonyl compounds and organic azides. II. Aromatic aldehydes. J. Org. Chem. 1959;24:561–562. [Google Scholar]
- Bracuti A.J. Army Armament Research Development and Engineering Center, Picatinny Arsenal; 1996. Molecular Structure of Bis (2, 2-Dinitropropyl)-Nitramine (BDNPN): Possible RDX Replacement. [Google Scholar]
- Bryden J.H. The crystal structure of 2, 4, 6-trinitro-m-xylene (TNX) Acta Crystallogr. B. 1972;28:1395–1398. [Google Scholar]
- Cady H.H. The crystal structure of N-methyl-N-2, 4, 6-tetranitroaniline (tetryl) Acta Crystallogr. 1967;23:601–609. [Google Scholar]
- Cady H.H., Larson A.C. The crystal structure of 1, 3, 5-triamino-2, 4, 6-trinitrobenzene. Acta Crystallogr. 1965;18:485–496. [Google Scholar]
- Cady H.H., Larson A.C., Cromer D.T. The crystal structure of α-HMX and a refinement of the structure of β-HMX. Acta Crystallogr. 1963;16:617–623. [Google Scholar]
- Cady H.H., Larson A.C., Cromer D.T. The crystal structure of benzotrifuroxan (hexanitrosobenzene) Acta Crystallogr. 1966;20:336–341. [Google Scholar]
- Cai X.T., Mao J.H., Zhang S.P. The Crystal structure of C_4H_4N_8O_ (14) J. Struct. Chem. 1983;2:41–45. [Google Scholar]
- Campbell J.E., Yang J., Day G.M. Predicted energy–structure–function maps for the evaluation of small molecule organic semiconductors. J. Mater. Chem. C. 2017;5:7574–7584. [Google Scholar]
- Chen J., Jiang S.-L., Zhang L., Yu Y. 1.3 ed. CAEP-SCNS; 2016. HASEM Software.http://www.caep-scns.ac.cn/ruanjian.php?id=62 [Google Scholar]
- Choi C.S. Refinement of 2-nitroguanidine by neutron powder diffraction. Acta Crystallogr. B. 1981;37:1955–1957. [Google Scholar]
- Cobbledick R.E., Small R.W.H. The crystal structure of the δ-form of 1, 3, 5, 7-tetranitro-1, 3, 5, 7-tetraazacyclooctane (δ-HMX) Acta Crystallogr. B. 1974;30:1918–1922. [Google Scholar]
- Coley C.W., Thomas D.A., Lummiss J.A.M., Jaworski J.N., Breen C.P., Schultz V., Hart T., Fishman J.S., Rogers L., Gao H. A robotic platform for flow synthesis of organic compounds informed by AI planning. Science. 2019;365:eaax1566. doi: 10.1126/science.aax1566. [DOI] [PubMed] [Google Scholar]
- Crawford M.J., Evers J., Göbel M., Klapötke T.M., Mayer P., Oehlinger G., Welch J.M. γ-FOX-7: structure of a high energy density material immediately prior to decomposition. Propellants Explos. Pyrotech. 2007;32:478–495. [Google Scholar]
- Cybulski W.B., Payman W., Woodhead D.W., Robertson R. Explosion waves and shock waves. VII. The velocity of detonation in cast TNT. Proc. Roy. Soc. Lond. Math. Phys. Sci. 1949;197:51–72. [Google Scholar]
- Dearden J.C., Rotureau P., Fayet G. QSPR prediction of physico-chemical properties for REACH. SAR QSAR Environ. Res. 2013;24:279–318. doi: 10.1080/1062936X.2013.773372. [DOI] [PubMed] [Google Scholar]
- Dickinson C., Stewart J.M., Holden J.R. A direct determination of the crystal structure of 2, 3, 4, 6-tetranitroaniline. Acta Crystallogr. 1966;21:663–670. [Google Scholar]
- Dong H.S., Zhou F.F. Science Press; 1989. High-Energy Explosives and Related Properties. [Google Scholar]
- Espenbetov A.A., Antipin M.Y., Struchkov Y.T., Philippov V.A., Tsirel'son V.G., Ozerov R.P., Svetlov B.S. Structure of 1, 2, 3-propanetriol trinitrate (β modification), C3H5N3O9. Acta Crystallogr. C. 1984;40:2096–2098. [Google Scholar]
- Fayet G., Rotureau P., Prana V., Adamo C. Global and local quantitative structure–property relationship models to predict the impact sensitivity of nitro compounds. Process. Saf. Prog. 2012;31:291. [Google Scholar]
- Ferguson J.W., Richley J.C., Sutton B.D., Price E., Ota T.A. The measured temperature and pressure of EDC37 detonation products. AIP Conf. Proc. 2017;1793:030013. [Google Scholar]
- Foster R. The absorption spectra of molecular complexes. Tetrahedron. 1960;10:96–101. [Google Scholar]
- Gao B., Wang D., Zhang J., Hu Y., Shen J., Wang J., Huang B., Qiao Z., Huang H., Nie F. Facile, continuous and large-scale synthesis of CL-20/HMX nano co-crystals with high-performance by ultrasonic spray-assisted electrostatic adsorption method. J. Mater. Chem. A. 2014;2:19969–19974. [Google Scholar]
- Gerard F., Hardy A. Crystal structure of HNS, 2, 2’, 4, 4’, 6, 6’-Hexanitrostilbene. Acta Crystallogr. A. 1987;43:C167. [Google Scholar]
- Gill R., Asaoka L., Baroody E. On underwater detonations, 1. A new method for predicting the CJ detonation pressure of explosives. J. Energ. Mater. 2006;5:287–307. [Google Scholar]
- Graeber E.J., Morosin B. The crystal structures of 2, 2', 4, 4', 6, 6'-hexanitroazobenzene (HNAB), forms I and II. Acta Crystallogr. B. 1974;30:310–317. doi: 10.1107/S0108270105000569. [DOI] [PubMed] [Google Scholar]
- Gramaccioli C.M., Destro R., Simonetta M. The structure of 2, 4, 6-trinitrophenetole. Acta Crystallogr. B. 1968;24:129–136. [Google Scholar]
- Hakey P., Ouellette W., Zubieta J., Korter T. Redetermination of cyclo-trimethylenetrinitramine. Acta Crystallogr. E. 2008;64:o1428. doi: 10.1107/S1600536808019727. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hall R.H., Wright G.F. Reaction of acetyl chloride with 1-nitro-2-nitramino-2-propoxyimidazolidine. J. Am. Chem. Soc. 1951;73:2213–2216. [Google Scholar]
- Hernández M.D., Santiago I., Padilla I.Y. International Society for Optics and Photonics; 2006. Macro-sorption of 2, 4-dinitrotoluene onto Sandy and Clay Soils. Detection and Remediation Technologies for Mines and Minelike Targets XI. [Google Scholar]
- Hervé G., Jacob G., Latypov N. The reactivity of 1, 1-diamino-2, 2-dinitroethene (FOX-7) Tetrahedron. 2005;61:6743–6748. [Google Scholar]
- Hobbs, M.L., & Baer, M.R. (1993). Calibrating the BKW-EOS with a large product species data base and measured C-J properties. 10th Symposium (International) on Detonation. Boston, Massachusetts.
- Holden J.R. The structure of 1, 3-diamino-2, 4, 6-trinitrobenzene, form I. Acta Cryst. 1967;22:545–550. [Google Scholar]
- Holden J.R., Dickinson C., Bock C.M. Crystal structure of 2, 4, 6-trinitroaniline. J. Phys. Chem. 1972;76:3597–3602. [Google Scholar]
- Hong D., Li Y., Zhu S., Zhang L., Pang C. Three insensitive energetic co-crystals of 1-nitronaphthalene, with 2, 4, 6-trinitrotoluene (TNT), 2, 4, 6-trinitrophenol (picric acid) and D-mannitol hexanitrate (MHN) Cent. Eur. J. Energ. Mater. 2015;12:47–62. [Google Scholar]
- Huang H., Zhou Z., Song J., Liang L., Wang K., Cao D., Sun W., Dong X., Xue M. Energetic salts based on dipicrylamine and its amino derivative. Chem. Eur. J. 2011;17:13593–13602. doi: 10.1002/chem.201101411. [DOI] [PubMed] [Google Scholar]
- Jain A., Shin Y., Persson K.A. Computational predictions of energy materials using density functional theory. Nat. Rev. Mater. 2016;1:15004. [Google Scholar]
- Kamlet M.J., Dickinson C. Chemistry of detonations. III. Evaluation of the simplified calculational method for chapman-jouguet detonation pressures on the basis of available experimental information. J. Chem. Phys. 1968;48:43–50. [Google Scholar]
- Keshavarz M.H. Simple procedure for determining heats of detonation. Thermochim. Acta. 2005;428:95–99. [Google Scholar]
- Keshavarz M.H. Quick estimation of heats of detonation of aromatic energetic compounds from structural parameters. J. Hazard. Mater. 2007;143:549–554. doi: 10.1016/j.jhazmat.2006.09.078. [DOI] [PubMed] [Google Scholar]
- Keshavarz M.H. Estimating heats of detonation and detonation velocities of aromatic energetic compounds. Propellants Explos. Pyrotech. 2008;33:448–453. [Google Scholar]
- Keshavarz M.H. A simple way to predict heats of detonation of energetic compounds only from their molecular structures. Propellants Explos. Pyrotech. 2012;37:93–99. [Google Scholar]
- Keshavarz M.H., Pouretedal H.R. Predicting the detonation velocity of CHNO explosives by a simple method. Propellants Explos. Pyrotech. 2005;30:105–108. [Google Scholar]
- Kiciński W., Trzciński W.A. Calorimetry studies of explosion heat of non-ideal explosives. J. Therm. Anal. Calorim. 2009;96:623–630. [Google Scholar]
- Klapötke T.M., Witkowski T.G. 5,5′-Bis(2,4,6-trinitrophenyl)-2,2′-bi(1,3,4-oxadiazole) (TKX-55): thermally stable explosive with outstanding properties. ChemPlusChem. 2016;81:357–360. doi: 10.1002/cplu.201600078. [DOI] [PubMed] [Google Scholar]
- Kofler A., Brandstätter M. Zur isomorphen vertretbarkeit von H, OH, Cl: S-trinitrobenzol, pikrinsäure, pikrylchlorid. Monatsh. Chem. Chem. Mon. 1948;78:65–70. [Google Scholar]
- Kwasny M., Syczewski M. Preparation and some physicochemical properties of compounds with trinitromethyl group. Biul. Wojsk. Akad. Tech. Im. Jaroslawa Dabrowskiego. 1980;29:165–172. [Google Scholar]
- Lange K., Koenig A., Roegler C., Seeling A., Lehmann J. NO donors. part 18: bioactive metabolites of GTN and PETN—synthesis and vasorelaxant properties. Bioorg. Med. Chem. Lett. 2009;19:3141–3144. doi: 10.1016/j.bmcl.2008.04.057. [DOI] [PubMed] [Google Scholar]
- Leemann H., Grandmougin E. Zur Kenntnis des symm. Hexanitro-azobenzols. Ber. Dtsch. Chem. Ges. 1908;41:1295–1305. [Google Scholar]
- Leonard N.J., Miller L.A., Thomas P.D. Unsaturated amines. VIII. Dehydrogenation and hydroxylation of 1-methyldecahydroquinoline by means of mercuric acetate1. J. Am. Chem. Soc. 1956;78:3463–3468. [Google Scholar]
- Li H., Zhang L., Petrutik N., Wang K., Ma Q., Shem-Tov D., Zhao F., Gozin M. Molecular and crystal features of thermostable energetic materials: guidelines for architecture of “bridged” compounds. ACS Cent. Sci. 2020;6:54–75. doi: 10.1021/acscentsci.9b01096. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li J.R., Zhao J.M., Dong H.S. Crystal structure of 2, 4, 6-trinitropyridine and its N-oxide. J. Chem. Cryst. 2005;35:943–948. [Google Scholar]
- Licht H., Ritter H. 2, 4, 6-Trinitropyridine and related compounds, synthesis and characterization. Propellants Explos. Pyrotech. 1988;13:25–29. [Google Scholar]
- Lind M.D. Crystal structure of N, N'-bis (β, β, β-trinitroethyl) urea. Acta Crystallogr. B. 1970;26:590–596. [Google Scholar]
- Ling-Yun T., Lei L., Jing L., Wan-Sheng X., Yan-Chun L., Xiao-Dong L., Yan B. Equation of state of tantalum up to 133GPa. Chin. Phys. Lett. 2010;27:016402. [Google Scholar]
- Lipinski C.A. Lead- and drug-like compounds: the rule-of-five revolution. Drug Discov. Today Technol. 2004;1:337–341. doi: 10.1016/j.ddtec.2004.11.007. [DOI] [PubMed] [Google Scholar]
- Lipinski C.A., Lombardo F., Dominy B.W., Feeney P.J. Experimental and computational approaches to estimate solubility and permeability in drug discovery and development settings. Adv. Drug Deliv. Rev. 2001;46:3–26. doi: 10.1016/s0169-409x(00)00129-0. [DOI] [PubMed] [Google Scholar]
- Liu L., Jin X., Wang P., Zhou X., Ming L.U. Synthesis improvement and thermal properties of bis( 2,2,2-trinitroethyl)-nitramine( BTNNA) Explos. Mater. 2016;45:47–50. [Google Scholar]
- Lowe-Ma C.K., Nissan R.A., Wilson W.S. Naval Weapons Center China Lake; 1987. Diazophenols-their Structure and Explosive Properties. [Google Scholar]
- Ma Y., Zhang A., Zhang C., Jiang D., Zhu Y., Zhang C. CRYSTAL packing of low-sensitivity and high-energy explosives. Cryst. Growth Des. 2014;14:4703–4713. [Google Scholar]
- Magnus R.H., Stiefel E.L. Methods of conjugate gradients for solving linear systems. J. Res. Natl. Bur. Stand. 1952;49:409–436. [Google Scholar]
- Manelis G.B., Nazin G.M., Prokudin V.G. Springer; 2006. The Additional Activation Volume of Unimolecular Reactions in the Solid phase. Doklady Physical Chemistry. [Google Scholar]
- Meents A., Dittrich B., Johnas S.K.J., Thome V., Weckert E.F. Charge-density studies of energetic materials: CL-20 and FOX-7. Acta Crystallogr. B. 2008;64:42–49. doi: 10.1107/S0108768107055292. [DOI] [PubMed] [Google Scholar]
- Meyer R., Köhler J., Homburg D.I.A. Wiley-VCH Verlag GmbH & Co. KGaA; 2007. Explosives. [Google Scholar]
- Millar D.I., Maynard-Casely H.E., Allan D.R., Cumming A.S., Lennie A.R., Mackay A.J., Oswald I.D.H., Tang C.C., Pulham C.R. Crystal engineering of energetic materials: Co-crystals of CL-20. CrystEngComm. 2012;14:3742–3749. [Google Scholar]
- Millar D.I., Maynard-Casely H.E., Kleppe A.K., Marshall W.G., Pulham C.R., Cumming A.S. Putting the squeeze on energetic materials—structural characterisation of a high-pressure phase of CL-20. CrystEngComm. 2010;12:2524–2527. [Google Scholar]
- Millar D.I., Oswald I.D.H., Francis D.J., Marshall W.G., Pulham C.R., Cumming A.S. The crystal structure of β-RDX—an elusive form of an explosive revealed. Chem. Commun. (Camb.) 2009:562–564. doi: 10.1039/b817966b. [DOI] [PubMed] [Google Scholar]
- Mo Z., Zhang A., Cao X., Liu Q., Xu X., An H., Pei W., Zhu S. JASMIN: a parallel software infrastructure for scientific computing. Front. Comput. Chin. 2010;4:480–488. [Google Scholar]
- Nie J.J., Xu D.J., Li Z.Y., Chiang M.Y. 2, 6-Dinitrotoluene. Acta Crystallogr. E. 2001;57:o827–o828. [Google Scholar]
- Nielsen A.T., Atkins R.L., Norris W.P. Oxidation of poly (nitro) anilines to poly (nitro) benzenes. Synthesis of hexanitrobenzene and pentanitrobenzene. J. Org. Chem. 1979;44:1181–1182. [Google Scholar]; Note: Herewith we quantify HB amount by the absolute occupied area of HB on the Hirshfeld surface, which divides the region of each single molecule in the crystal according to the electron density contribution of the molecules. The HB strength, on the other hand, is characterized by the integration of the crystal orbital Hamilton population (COHP) below the Fermi energy level.; Note: We note if the heat of explosion of TNT He = 1,290 kcal·kg−1 is set as a reference, as shown in Figure S4 (Supplemental Information), the high-performing HEDMs required OB would fall into a range of OB > −20%, which is too strict and narrow for practical design of HEDMs. We thereby used a relatively lower value of He = 1,200 kcal·kg−1 to screen the target HEDMs with satisfactory heat of explosion.
- Ohta A., Ogihare Y., Nei K., Shibata S. On methylphenylnaphthalenes. I. syntheses of methylphenylnaphthalenes. Chem. Pharm. Bull. 1963;11:754–758. [Google Scholar]
- Ou Y., Jia H., Chen B. Crystal structure of four polymorphs of hexanitrohexaazaisowurtzitane. J. Explos. Propellants. 1998;4:41–43. [Google Scholar]
- Oyumi Y., Brill T.B. Thermal decomposition of energetic materials XXVIII. Predictions and results for nitramines of bis-imidazolidinedione: DINGU, TNGU and TDCD. Propellants Explos. Pyrotech. 1988;13:69–73. [Google Scholar]
- Pachman J., Künzel M., Němec O., Majzlík J. A comparison of methods for detonation pressure measurement. Shock Waves. 2018;28:217–225. [Google Scholar]
- Politzer P., Murray J.S. Some perspectives on estimating detonation properties of C, H, N, O compounds. Cent. Eur. J. Energ. Mater. 2011;8:209–220. [Google Scholar]
- Reeve I.T., Miller M.G. 1, 3-Dinitrobenzene metabolism and protein binding. Chem. Res. Toxicol. 2002;15:352–360. doi: 10.1021/tx015554+. [DOI] [PubMed] [Google Scholar]
- Rheingold A.L., Baldacchini C.J., Grote C.W. The crystal and molecule structure of three 2, 4, 6-trinitrobenzene derivatives: α, α, α-trifluoro-2, 4, 6-trinitrotoluene (C7H2F3N3O6), 2, 4, 6-trinitrobenzamide (C7H4N4O7), 2, 4, 6-trinitrobenzoic acid (C7H3N3O8) J. Crystallogr. Spectrosc. Res. 1989;19:25–37. [Google Scholar]
- Rice B.M., Hare J. Predicting heats of detonation using quantum mechanical calculations. Thermochim. Acta. 2002;384:377–391. [Google Scholar]
- Rothstein L.R., Petersen R. Predicting high explosive detonation velocities from their composition and structure. Propellants Explos. Pyrotech. 1979;4:56–60. [Google Scholar]
- Sabin J.R. Academic Press; 2014. Advances in Quantum Chemistry. [Google Scholar]
- Šarlauskas J. Polynitrobenzenes containing alkoxy and alkylenedioxy groups: potential HEMs and precursors of new energetic materials. Cent. Eur. J. Energ. Mater. 2010;7:313–324. [Google Scholar]
- Sarma J.A.R.P., Nagaraju A. Solid state nuclear bromination with N-bromosuccinimide. Part 1. Experimental and theoretical studies on some substituted aniline, phenol and nitro aromatic compounds. J. Chem. Soc. Perkin Trans. 2000;2:1113–1118. [Google Scholar]
- Schmidt J., Gehlen H. PK-werte von derivaten des 1, 2, 4-triazols. Z. Chem. 1965;5:304. [Google Scholar]
- Shreeve J.M., Yin P., Yu Q., Dharavath S. Taming of tetranitroethane: a promising precursor to high performance energetic ingredients. J. Mater. Chem. A. 2018;6:15815–15820. [Google Scholar]
- Shukla M.K., Boddu V.M., Steevens J.A., Damavarapu R., Leszczynski J. Springer International Publishing; 2017. Energetic Materials: From Cradle to Grave. [Google Scholar]
- Siavosh-Haghighi A., Thompson D.L. Molecular dynamics simulations of surface-initiated melting of nitromethane. J. Chem. Phys. 2006;125:184711. doi: 10.1063/1.2370904. [DOI] [PubMed] [Google Scholar]
- Siele V., Warman M. Preparation of 1, 3-difluoro-2, 4, 6-trinitrobenzene. J. Org. Chem. 1962;27:1910–1911. [Google Scholar]
- Singh A., Sikder N., Sikder A.K. Improved synthesis of an energetic material, 1, 3, 3-trinitroazetidine (TNAZ) exploiting 2-iodoxy benzoic acid (IBX) as an oxidising agent. ChemInform. 2005;37:91. [Google Scholar]
- Spencer E.Y., Wright G.F. Preparation of picramide. Can. J. Res. 1946;24:204–207. [Google Scholar]
- Srinivasan P., Gunasekaran M., Kanagasekaran T., Gopalakrishnan R., Ramasamy P. 2, 4, 6-trinitrophenol (TNP): an organic material for nonlinear optical (NLO) applications. J. Cryst. Growth. 2006;289:639–646. [Google Scholar]
- Sun Q., Zhang Y., Xu K., Ren Z., Song J., Zhao F. Studies on thermodynamic properties of FOX-7 and its five closed-loop derivatives. J. Chem. Eng. Data. 2015;60:2057–2061. [Google Scholar]
- Thallapally P.K., Jetti R.K.R., Katz A.K., Carrell H.L., Singh K., Lahiri K., Kotha S., Boese R., Desiraju G.R. Polymorphism of 1, 3, 5-trinitrobenzene induced by a trisindane additive. Angew. Chem. Int. Ed. 2004;43:1149–1155. doi: 10.1002/anie.200352253. [DOI] [PubMed] [Google Scholar]
- Trotter J. The crystal structure of 1, 5-dinitronaphthalene. Acta Crystallogr. 1960;13:95–99. [Google Scholar]
- Tsyshevsky R., Pagoria P., Smirnov A.S., Kuklja M.M. Comprehensive end-to-end design of novel high energy density materials: II. Computational modeling and predictions. J. Phys. Chem. C. 2017;121:23865–23874. [Google Scholar]
- Turley J.W. A refinement of the crystal structure of N, N'-dinitroethylenediamine. Acta Cryst. Sect. B. 1968;24:942–946. [Google Scholar]
- Veselova, E.V. (2008). On the reaction of trinitroaromatic compounds with 4-amino-1,2,4-triazole. New trends in research of energetic materials. 11th new trends in research of energetic materials. Czech Republic.
- Volk F., Bathelt H. Influence of energetic materials on the energy-output of gun propellants. Propellants Explos. Pyrotech. 1997;22:120–124. [Google Scholar]
- Vrcelj R.M., Sherwood J.N., Kennedy A.R., Gallagher H.G., Gelbrich T. Polymorphism in 2-4-6 trinitrotoluene. Cryst. Growth Des. 2003;3:1027–1032. [Google Scholar]
- Wang G., Xiao H., Ju X., Gong X. Calculation of detonation velocity, pressure, and electric sensitivity of nitro arenes based on quantum chemistry. Propellants Explos. Pyrotech. 2006;31:361–368. [Google Scholar]
- Wang G., Xiao H., Xu X., Ju X. Detonation velocities and pressures, and their relationships with electric spark sensitivities for nitramines. Propellants Explos. Pyrotech. 2006;31:102–109. [Google Scholar]
- Wang Y., Liu Y., Song S., Yang Z., Qi X., Wang K., Liu Y., Zhang Q., Tian Y. Accelerating the discovery of insensitive high-energy-density materials by a materials genome approach. Nat. Commun. 2018;9:2444. doi: 10.1038/s41467-018-04897-z. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang Y., Yang Z., Li H., Zhou X., Zhang Q., Wang J., Liu Y. A novel cocrystal explosive of HNIW with good comprehensive properties. Propellants Explos. Pyrotech. 2014;39:590. [Google Scholar]
- Wilkins A., Small R.W.H. The polymorphs of 2, 2'-dinitroxydiethylnitramine (DINA). The structure of DINA (II) Acta Cryst. Sect. B. 1982;38:488–490. [Google Scholar]
- Wright, G.F., & Chute, W.J. (1952). Bis(nitroxyethyl)nitramine. Canada patent application.
- Wu J., Zhang J., Li T., Li Z., Zhang T. A novel cocrystal explosive NTO/TZTN with good comprehensive properties. RSC Adv. 2015;5:28354–28359. [Google Scholar]
- Yang Z., Li H., Zhou X., Zhang C., Huang H., Li J., Nie F. Characterization and properties of a novel energetic–energetic cocrystal explosive composed of HNIW and BTF. Cryst. Growth Des. 2012;12:5155–5158. [Google Scholar]
- Zeman S., Jungová M. Sensitivity and performance of energetic materials. Propellants Explos Pyrotech. 2016;41:426–451. [Google Scholar]
- Zhang C., Jiao F., Li H. Crystal engineering for creating low sensitivity and highly energetic materials. Cryst. Growth Des. 2018;18:5713–5726. [Google Scholar]
- Zhang C., Wang X., Huang H. π-Stacked interactions in explosive crystals: buffers against external mechanical stimuli. J. Am. Chem. Soc. 2008;130:8359–8365. doi: 10.1021/ja800712e. [DOI] [PubMed] [Google Scholar]
- Zhang H., Guo C., Wang X., Xu J., He X., Liu Y., Liu X., Huang H., Sun J. Five energetic cocrystals of BTF by intermolecular hydrogen bond and π-stacking interactions. Cryst. Growth Des. 2013;13:679–687. [Google Scholar]
- Zhang J., Mitchell L.A., Parrish D.A., Shreeve J.M. Enforced layer-by-layer stacking of energetic salts towards high-performance insensitive energetic materials. J. Am. Chem. Soc. 2015;137:10532–10535. doi: 10.1021/jacs.5b07852. [DOI] [PubMed] [Google Scholar]
- Zhang J., Zhang Q., Vo T.T., Parrish D.A., Shreeve J.M. Energetic salts with pi-stacking and hydrogen-bonding interactions lead the way to future energetic materials. J. Am. Chem. Soc. 2015;137:1697–1704. doi: 10.1021/ja5126275. [DOI] [PubMed] [Google Scholar]
- Zhang L., Jiang S., Yu Y., Long Y., Zhao H., Peng L., Chen J. Phase transition in octahydro-1,3,5,7-tetranitro-1,3,5,7-tetrazocine (HMX) under static compression: an application of the first-principles method specialized for CHNO solid explosives. J. Phys. Chem. B. 2016;120:11510–11522. doi: 10.1021/acs.jpcb.6b08092. [DOI] [PubMed] [Google Scholar]
- Zhang L., Jiang S.L., Yu Y., Chen J. Revealing solid properties of high-energy-density molecular cocrystals from the cooperation of hydrogen bonding and molecular polarizability. Sci. Rep. 2019;9:1257. doi: 10.1038/s41598-018-37500-y. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang L., Yu Y., Xiang M.-Z. A study of the shock sensitivity of energetic single crystals by large-scale Ab initio molecular dynamics simulations. Nanomaterials. 2019;9:1251. doi: 10.3390/nano9091251. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhurova E.A., Pinkerton A.A. Chemical bonding in energetic materials: β-NTO. Acta Cryst. Sect. B. 2001;57:359–365. doi: 10.1107/s0108768100020048. [DOI] [PubMed] [Google Scholar]
- Zhurova E.A., Stash A.I., Tsirelson V.G., Zhurov V.V., Bartashevich E.V., Potemkin V.A., Pinkerton A.A. Atoms-in-molecules study of intra-and intermolecular bonding in the pentaerythritol tetranitrate crystal. J. Am. Chem. Soc. 2006;128:14728–14734. doi: 10.1021/ja0658620. [DOI] [PubMed] [Google Scholar]
- Zhurova E.A., Zhurov V.V., Pinkerton A.A. Structure and bonding in β-HMX-characterization of a trans-annular N···N interaction. J. Am. Chem. Soc. 2007;129:13887–13893. doi: 10.1021/ja073801b. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
All the crystal geometries, in-crystal interspecies interactions, crystal energetics, and solid-state detonation performance of the 67 HEDMs were calculated based on the recently developed supercomputing software, namely, High Accuracy atomistic Simulation package for Energetic Materials (HASEM) (Chen et al., 2016, Zhang et al., 2016), which is adapted to modern supercomputers on the basis of the J parallel Adaptive Structured Mesh applications INfrastructure (JASMIN) (Mo et al., 2010).
The source data that support the plots in this article and the other findings of this study are available from the corresponding authors upon reasonable request.