Density Functional Theory Calculation on the Structural, Electronic, and Optical Properties of Fluorene-Based Azo Compounds

Abstract

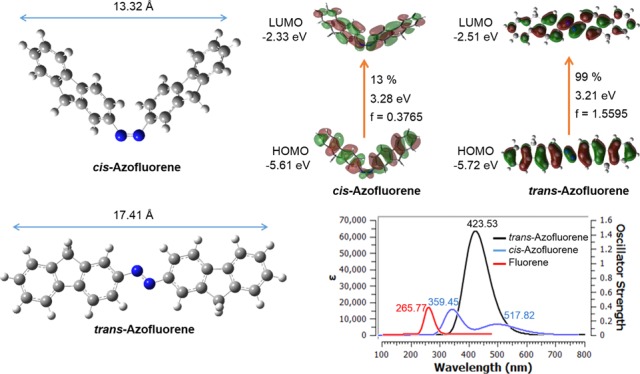
In the present work, a theoretical study was carried out to study the molecular structure, harmonic vibrational frequencies, normal force field calculations, and Raman scattering activities for fluorene π-conjugation spacer containing azo-based dye named trans- and cis-bis(9H-fluoren-2-yl)diazene (AzoFL) at density functional theory using B3LYP (Becke-3–Lee–Yang–Parr) functional and 6-31+G(d,p) basis set. The theoretical calculations have also been performed with fluorene and the trans- and cis-isomers of diazene, difluorodiazene by the same method DFT-B3LYP/6-31+G(d,p) and basis set. The present DFT calculation shows that the trans-AzoFL is more stable than the cis-AzoFL by 16.33 kcal/mol. We also report the results of new assignments of vibrational frequencies obtained on the basis of the present calculations. Time-dependent DFT (TD-DFT) and ZIndo calculations have been performed to study the UV–vis absorption behavior and frontier molecular orbitals for the above-mentioned compounds. The UV–vis spectrum from TD-DFT calculation shows the π–π* transition bands at λ_max 423.53 nm (ε_max 6.0 × 10⁴ M^–1 cm^–1) and at λ_max 359.45 nm (ε_max 1.7 × 10⁴ M^–1 cm^–1), respectively, for trans- and cis-AzoFL. Compared to parent trans-diazene (λ_max 178.97 nm), a significant variation to longer wavelength (∼245 nm) is observed due to the incorporation of the fluorene (FL) ring into the −N=N– backbone. The co-planarity of the two FL rings with the longer N=N bond length compared to the unsubstituted parent diazene indicates the effective red shift due to the extended π-conjugation in trans-AzoFL. The nonplanarity of cis-AzoFL (48.1° tilted about the C–N bond relative to the planar N=N–C bond) reflects its ∼64 nm blue shift compared to that of trans-counterpart.

1. Introduction

Azo compounds represent one of the oldest and largest class of synthesized organic compounds used not only in dye industry¹ but also in analytical chemistry as indicators in acid–base, redox, and complexometric titration.^2,3 In addition, azo compounds were reported to exhibit biological activities such as antibacterial, antifungal, pesticides, antiviral, and anti-inflammatory properties.⁴⁻¹⁰ Beyond their dyeing properties and biological activities, azo compounds exhibit interesting electronic and geometrical features relating to their application for reversible optical data storage.¹¹⁻¹⁷ The storage process makes use of the light-induced trans–cis–trans isomerization of the azo moiety, thereby utilizing the local variation of the refractive index of the medium.¹¹ Because of its ability to induce a molecular motion and a significant geometric change upon trans ⇆ cis photoisomerization, azo compounds can be utilized for the construction of light-driven molecular devices.^18,19

The light induced changes in the molecular structure and physical properties of azo moiety associated with E ⇆ Z photoisomerization have led to the incorporation of azobenzene into a wide variety of molecular architectures including polymers, dendrimers, liquid crystals, self-assembled monolayers, and biomaterials.²⁰⁻²⁵ Because trans-azobenzene shows intense π–π* absorption in the UV region, the rapid trans-to-cis isomerization can be induced by noncoherent UV light. The cis isomer has an enhanced n−π* absorption in the visible region; the cis-to-trans isomerization is triggered through visible-light irradiation.²⁰ The light-driven structural changes of the azobenzene unit incorporated into a larger compound affect the properties of azo-functionalized molecular systems.¹⁸ Emerging applications of azo compounds require the extension of π-conjugated systems of azo derivatives to design visible-light-driven switches.²⁶⁻³⁰ The increasing π-conjugated length allows for more obvious red shift of azo π → π* transition bands.²⁶ Therefore, the synthesis of azo-containing π-conjugated compounds attracts considerable attention because of the possible red shifts of azo π → π* transition bands and novel optoelectrical properties.²⁶ On the basis of these fascinating features and properties of azo-containing π-conjugated compounds, our aim in this present work is to provide a purely theoretical perspective on the optimized geometries, orbital energies (HOMO, LUMO), IR, Raman activity, and UV–vis spectra of trans and cis-bis(9H-fluoren-2-yl)diazene (AzoFL) (Figure 1).

Figure 1.

Chemical structures of trans-and cis-bis(9H-fluoren-2-yl)diazene (AzoFL).

The valuable electronic properties of fluorene-based compounds, characterized by extensive π conjugation together with their photochemical features, make them promising candidates for use in organic light-emitting diodes,^31,32 solar cells,^33,34 and field-effect transistors.^35,36 In an effort to gain a better understanding of the structure and electronic properties of difluorene-substituted diazene, in this paper we have investigated the optimized geometries and vibrational and absorption spectra of cis and trans-bis(9H-fluoren-2-yl)diazene (Figure 1) and compared them with those of fluorene, cis, and trans isomers of diazene and difluorodiazene (Figure 2) using the same method and basis set.

Figure 2.

Structures of fluorene and cis and trans isomers of diazene and difluorodiazene.

All of the calculations for the above-mentioned three pairs of azo compounds and fluorene are calculated by the same widely used density functional theory³⁷ (DFT) which has capability to produce different results with high accuracy and better consistency.^11,37−44 In spite of the vast literature on the studies of photoisomerization and other photophysical properties of azo dyes by means of various spectroscopic and photochemical methods, the chemistry of azo compounds are not well understood completely yet. This is probably due to the fact that sometimes it is difficult to isolate cis- and trans-isomers of the azo compounds in pure form possibly due to reversible cis–trans isomerization of the compounds. Thereby, the determination of the different properties of a pure isomer of azo compound is not straightforward. In this paper, our target is to investigate the different properties of the cis- and trans-isomers of azo fluorene individually and compare them with those of the parent diazene, fluorine, and difluorodiazene using the same DFT method and same basis set by theoretical aspect. The findings of this study might be important to understand the chemistry of π-conjugated azo compounds.

2. Results and Discussion

2.1. Geometrical Structures

The atom numbering of the trans- and cis-isomers of the model compound, bis(9H-fluoren-2-yl)diazene (AzoFL) is shown in Figure 1. The optimized geometries of both the cis- and trans-isomers of AzoFL calculated at the B3LYP/6-31+G(d,p) level are shown in Figure 3. The B3LYP/6-31+G(d,p) optimized molecular geometries of fluorene (FL) and cis- and trans-isomers of parent diazene (DZ) and difluorodiazene (DFDZ) are presented in Figure 4. The most relevant optimized geometric parameters of trans- and cis-AzoFL and fluorene (FL) are summarized in Table 1. The geometric parameters of other azo compounds are listed in Table 2 and shown in Figure 4.

Figure 3.

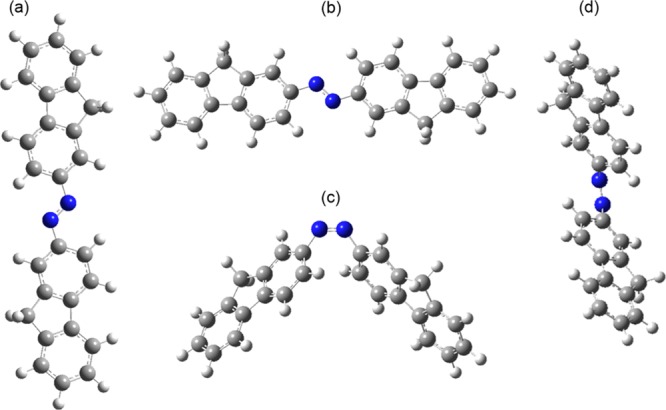
Optimized geometries of trans-AzoFL (a,b) and cis-AzoFL (c,d) calculated at B3LYP/6-31+G(d,p) method. Deep blue: N, ash: C, cyano: H.

Figure 4.

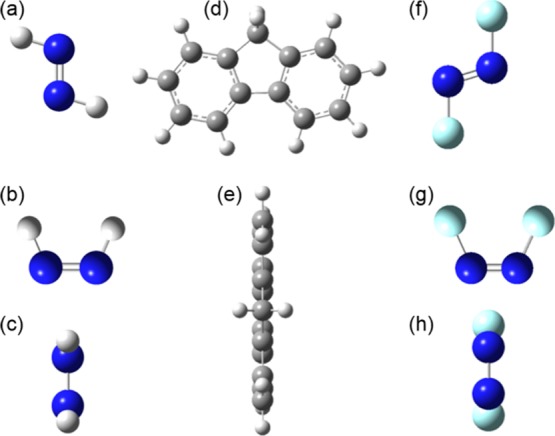
B3LYP/6-31+G(d,p) optimized geometries of (a) trans-DZ; (b,c) cis-DZ; (d,e) FL; (f) trans-DFDZ; and (g,h) cis-DFDZ,. Deep blue: N; cyano: H; ash: C; sky blue: F.

Table 1. Optimized Geometric Parameters^a of Fluorene (FL), trans-AzoFL, and cis-AzoFL in the Ground State Calculated at B3LYP/6-31+G(d,p) and AM1 Methods.

	FL		trans-AzoFL		cis-AzoFL
parametersa	AM1	DFTb	AM1	DFTb	AM1	DFTb
N=N			1.231	1.262	1.204	1.252
C–N			1.436	1.414	1.442	1.433
C1–C2	1.403	1.401	1.421	1.407	1.417	1.406
C2–C3	1.392	1.401	1.407	1.412	1.405	1.408
C3–C4	1.402	1.398	1.399	1.390	1.398	1.394
C4–C11	1.385	1.398	1.383	1.403	1.384	1.400
C5–C12	1.385	1.398	1.385	1.399	1.385	1.399
C5–C6	1.402	1.398	1.402	1.397	1.402	1.397
C6–C7	1.392	1.401	1.392	1.402	1.392	1.401
C7–C8	1.403	1.401	1.403	1.401	1.408	1.401
C8–C13	1.382	1.392	1.382	1.392	1.382	1.392
C1–C10	1.429	1.392	1.378	1.388	1.379	1.388
C11–C12	1.461	1.470	1.460	1.466	1.461	1.468
C12–C13	1.429	1.411	1.429	1.413	1.429	1.412
C9–C10	1.504	1.516	1.505	1.515	1.505	1.516
C9–C13	1.504	1.516	1.504	1.516	1.504	1.516
C10–C11	1.429	1.411	1.429	1.411	1.428	1.413
C1–H	1.099	1.087	1.100	1.086	1.101	1.087
C2–H	1.100	1.086
C3–H	1.100	1.086	1.102	1.084	1.102	1.086
C4–H	1.110	1.086	1.100	1.087	1.099	1.086
C5–H	1.110	1.086	1.099	1.086	1.099	1.086
C6–H	1.100	1.086	1.100	1.086	1.100	1.086
C7–H	1.100	1.086	1.100	1.086	1.100	1.086
C8–H	1.099	1.087	1.099	1.087	1.098	1.087
C9–H	1.119	1.098	1.120	1.098	1.119	1.098
C9–H	1.119	1.098	1.120	1.098	1.119	1.098
N1–C2–C3			124.9	124.6	122.5	123.0
C2–N1=N2			119.7	115.5	129.4	124.4
N1=N2–C2′			119.7	115.5	129.4	124.4
C2–C3–C4	120.9	120.6	121.1	120.3	121.1	120.3
C1–C2–C3	120.9	120.5	119.8	120.2	120.0	120.3
C10–C1–C2	118.7	119.1	118.7	119.3	118.6	119.1
C3–C4–C11	118.6	118.9	119.1	119.4	118.9	119.4
C4–C11–C10	120.5	120.4	120.2	120.3	120.2	120.1
C1–C10–C11	120.5	120.5	121.1	120.4	110.0	120.6
C9–C10–C11	110.5	110.0	110.0	110.0	110.0	110.0
C9–C13–C12	110.5	110.0	110.1	110.0	110.1	110.1
C10–C9–C13	103.3	102.8	103.3	102.7	103.3	102.7
C10–C11–C12	108.3	108.6	108.4	108.7	108.4	108.6
C13–C12–C11	108.3	108.6	108.3	108.5	108.3	108.5
C12–C5–C6	118.6	118.9	118.6	118.8	118.6	118.9
C5–C6–C7	120.9	120.6	120.9	120.6	120.9	120.7
C6–C7–C8	120.9	120.5	120.9	120.6	120.9	120.6
C7–C8–C13	118.7	119.1	118.7	119.0	118.7	119.0
C8–C13–C12	120.5	120.5	120.4	120.4	120.4	120.4
C13–C12–C5	120.5	120.4	120.5	120.5	120.5	120.5
C1–C2–N1			115.3	115.2	117.3	116.1
C3–C2–N1			124.9	124.6	122.5	123.0
C2N1N2C2′			179.3	–179.99	2.3	10.9
C3C2N1N2			–15.7	0.01	46.9	48.1

^aBond lengths in angstroms and bond angles and dihedral angles in degrees.

^bB3LYP/6-31+G(d,p).

Table 2. Calculated Optimized Geometric Parameters of trans-Diazene (DZ), cis-Diazene (DZ), trans-Difluoro Diazene (DFDZ), and cis-Difluoro Diazene (DFDZ).

	trans-DZ		trans-DFDZ
parametersa	AM1	DFTb	AM1	HFc	HFd	HFe	DFTb	expf
N=N	1.212	1.244	1.244	1.192	1.192	1.188	1.225	1.224
dN1–H1	1.018	1.036
dN2–H2	1.018	1.036
∠H1N1N2	112.3	106.7
∠N1N2H2	112.3	106.7
∠HNNH	180.0	180.0
dN1–F1			1.348	1.339	1.339	1.326	1.395	1.398
dN2–F2			1.348	1.339	1.339	1.326	1.395
∠F1N1N2			113.0	106.9	106.9	107.5	105.1	115.5
∠N1N2F2			113.0	106.9	106.9	107.5	105.1
∠FNNF			180.0	180.0	180.0	180.0	180.0

	cis-DZ		cis-DFDZ
parametersa	AM1	DFTb	AM1	HFc	HFd	HFe	DFTb	expf
N=N	1.197	1.242	1.220	1.193	1.193	1.190	1.217	1.209
dN–H	1.019	1.043
dN–H	1.019	1.043
∠H1N1N2	120.6	113.0
∠N1N2H2	120.6	113.0
∠HNNH	0.0	0.0
dN1–F1			1.356	1.337	1.337	1.327	1.399	1.409
dN2–F2			1.356	1.337	1.337	1.327	1.399
∠F1N1N2			124.2	114.4	114.4	114.6	114.9	114.4
∠N1N2F2			124.2	114.4	114.4	114.6	114.9
∠FNNF			0.0	0.0	0.0	0.0	0.0

^ad, bond lengths in angstroms and ∠, bond angles, and dihedral angles in degrees.

^bB3LYP/6-31+G(d,p).

^cHF/6-31+G(d,p); N=N_cis (1.19323 Å); N=N_trans (1.19208 Å); N–F_cis (1.133918 Å); N–F_trans (1.133745 Å).

^dHF/6-31++G(d,p); N=N_cis (1.19323 Å); N=N_trans (1.19208 Å).

^eHF/6-311+G(d,p); N=N_cis (1.19043 Å); N=N_trans (1.18799 Å); N–F_cis (1.132657 Å); N–F_trans (1.132601 Å).

^fPls. See lit refs (52−54).

The optimized geometry parameters (Table 1) show that the trans-AzoFL is almost planar (central CNNC dihedral angle: 179.99°) according to our DFT calculation. Complete geometry optimization for cis-AzoFL in present work resulted in nonplanarity (central CNNC dihedral angle: 10.9°) of the molecule. The fluorene (FL) rings are rotated by 48.1° about the C–N bond relative to planar N=N–C arrangement to decrease the H–H non bonded interaction in cis-AzoFL. According to our DFT calculation the energy difference shows that the trans-AzoFL in its ground state is more stable than the cis-AzoFL by 16.33 kcal/mol (Table 3).

Table 3. Calculated Energies (Hartree), Energy Differences (kcal/mol) between the Cis- and Trans-Isomers of AzoFL, DFDZ, and DZ and Their Respective Dipole Moments (Debye), Respectively.

compound	methoda	Etrans	Ecis	Ecis–transg	μ (trans)	μ (cis)
AzoFL	AM1b	0.261988	0.254685	–4.58	0.17	2.99
	DFTc	–1111.176069	–1111.150053	+16.33	0.00	3.12
DFDZ	AM1b	0.049665	0.033056	–10.4	0.00	0.66
	HFd	–307.595444	–307.593029	+1.52	0.00	0.17
	HFe	–307.595444	–307.593029	+1.52	0.00	0.17
	HFf	–307.673508	–307.670734	+1.74	0.00	0.18
	DFTc	–309.033536	–309.036420	–1.81	0.00	0.22
DZ	AM1b	0.050244	0.051651	+0.88	0.00	2.70
	HFd	–110.006960	–109.994657	+7.72	0.00	3.37
	DFTc	–110.651970	–110.641101	+6.82	0.00	3.20

^aThe symmetry of trans-DZ and DFDZ in different methods are C_2h, C_2v for cis-DZ and DFDZ; C₂ for both the trans- and cis-AzoFL.

^bSemiempirical AM1 method using predefined ZDO basis set.

^cB3LYP/6-31+G(d,p) basis set.

^d6-31+G(d,p) basis set.

^e6-31++G(d,p) basis set.

^f6-311+G(d,p) basis set.

^gThe negative values of energy difference in respective cases indicate the cis-preference over trans-isomer.

The trans-AzoFL has no dipole moment, whereas the cis-AzoFL exhibits a dipole moment of 3.12 D. However, our semiempirical AM1 calculation shows that the cis-AzoFL is more stable by 4.18 kcal/mol (Table 3) compared to that of trans-AzoFL, which possess some deviation from planarity having a bit dipole moment (0.17 D).

Our calculated geometry parameters at B3LYP/6-31+G(d,p) for trans-DZ (Table 2) (NN: 1.244 Å, NH: 1.036 Å, ∠NNH: 106.7°) is well agreed with the earlier reported experimental value (NN: 1.247 Å, NH: 1.029 Å, ∠NNH: 106.3°)⁴⁵ and theoretical work⁴⁶ (NN: 1.238 Å, NH: 1.035 Å, ∠NNH: 107°) by B3LYP/6-311++G(d,p) method. The calculated work⁴⁷ by CCSD(T)/CBS found (NN: 1.246 Å, NH: 1.029 Å, ∠NNH: 106.4°) which also has good agreement with our present work (Table 2). The geometric parameters (Table 2) for cis-diazene (NN: 1.242 Å, NH: 1.043 Å, ∠NNH: 113°) calculated by present B3LYP/6-31+G(d,p) method is also quite well agreed with the earlier reported (NN: 1.237 Å, NH: 1.041 Å), (∠NNH: 113°) by B3LYP/6-311++G(d,p) method.⁴⁸ All of the ground-state geometries were verified by vibrational frequency analysis at the same level of theory and found as true minima because negative vibrational frequencies were absent in all cases.

The calculated energies (hartree), energy differences (kcal/mol) between the cis- and trans-isomers of AzoFL, DFDZ, and DZ and their respective dipole moments (debye) are summarized in Table 3. The trans-AzoFL was found as more stable than the cis-AzoFL by the calculation at B3LYP/6-31+G(d,p). Similarly trans-DZ was also found stable as compared to cis-DZ. Back et al.⁴⁸ by near-ultraviolet absorption investigation of diazene in gas phase showed that the trans-DZ was the most stable isomer. However, the cis-DFDZ was found as more stable (Table 3) by 1.81 kcal/mol than the trans-DFDZ by B3LYP/6-31+G(d,p), which supports the preference of cis-DFDZ energetically by the earlier work.⁴⁹ The trans- and cis-isomers of AzoFL in ground state adopted the C₂ symmetry, whereas the trans-DZ and trans-DFDZ adopt the C_2h point groups. The cis-DZ, cis-DFDZ, and FL possess C_2v points group. We have made a comparative study of the N=N, N–H, H–F, C–N, C–C, and C–H bond lengths as well as C–N=N and C–C–N bond angles in DZ, FL, DFDZ, and AzoFL. As shown in Tables 1 and 2, we have found that the N=N bond lengths of trans-isomers of DZ, DFDZ, and AzoFL, are 1.244, 1.225, and 1.262 Å, respectively. The N=N bond length order among the three trans-isomers has been found as AzoFL > DZ > DFDZ by our DFT-B3LYP/6-31+G(d,p) calculation, and the same trend has been observed for the respective cis-isomers as well. Upon substitution in the parent trans-DZ molecule by two electron donor fluorene (FL) moiety causes an increase of the N=N bond distance from 1.244 to 1.262; an 0.018 Å increase of bond length is observed. This is due to the extensive π-bond conjugation of the N=N bond with the fluorene (FL) ring in trans-isomer of AzoFL. On the other hand, incorporation of the two F atoms in the parent DZ by replacing two H-atoms causes shortening of the N=N bond length from 1.244 to 1.225 Å (Table 2) in trans-DFDZ. Hence, an opposite trend, a decrease of 0.019 Å is observed in trans-DFDZ compared to that of trans-DZ. This effect is stronger in cis-DFDZ, a bit shorter of 0.025 Å N=N bond length in cis-DFDZ is found compared to cis-DZ (Table 2).

As aromatic fluorene (FL) moiety is the major structural unit of our target AzoFL, we have calculated FL for comparison even though there are detailed experimental⁵⁰ as well as some theoretical works⁴⁴ present in the literature. Our calculated structure of FL (Table 1) by B3LYP/6-31+G(d,p) is well agreed with the reported work done by Lee and Boo⁴⁴ calculated at the B3LYP/6-31G* level. There is reasonable agreement found with the reported X-ray crystal structure.⁵¹ A minor deviation was observed with the X-ray crystal structure⁵¹ of bond angles, for example, ∠C₁C₁₀C₁₁ by 1.43°.

Our DFT calculation shows that the FNN angle in the trans-DFDZ is 105.1° whereas the same angle in cis-form is 114.9°. Our HF calculation shows that the FNN angle in the trans-form is 106.9°, whereas the same angle in cis-form is 114.4°. This supports earlier work.⁴⁹ As fluorine atoms are electronegative, they have stronger electron affinity relative to the nitrogen atoms and possibility to polarize the bonds. The cis-isomer has a small dipole moment (0.22 D), whereas the trans-DFDZ has no dipole moment according to our present B3LYP/6-31+G(d,p) calculation.

The N=N bond length of cis-DFDZ is found to be shorter (Table 2) than that of the corresponding trans-DFDZ by our B3LYP-DFT/6-31+G(d,p) calculation. On the contrary, the N–F bond (1.399 Å) in cis-DFDZ is longer (0.004 Å) than its trans-counterpart (1.395 Å). It should be mentioned that the shortening of the N=N bond in conjunction with elongation of the N–F bond indicates the presence of negative hyperconjugation.^49,55 This difference in geometrical parameters leads to a higher stability of the cis-DFDZ, which is nicely reflected in our DFT-B3LYP/6-31+G(d,p) calculation. In addition, a considerable widening of ∠NNF has been observed for cis-DFDZ (Table 2) compared to that of trans-DFDZ. The reason for such type of structural change is due to repulsion of the F atom lone pairs, the electrostatic repulsion of the N–F dipolar bonds, and steric effect.⁴⁹ Such type of structural/geometrical change has also been observed by earlier work.^49,55,56 In our DFT-B3LYP/6-31+G(d,p) calculation, the two C–N bonds in cis-AzoFL is also found to be longer by (0.019 Å) compared to that of trans-AzoFL, whereas the same bond is longer by only 0.006 Å in semiempirical AM1 (Table 1).

The N=N bond of DZ, DFDZ, and AzoFL (Tables 1 and 2) is shorter in cis-isomer over trans-isomer by 0.015, 0.024, and 0.027 Å in semiempirical AM1 method. Similar behavior, that is, shorter N=N bond in DZ, DFDZ, and AzoFL by 0.002, 0.008, and 0.01 Å by DFT/6-31+G(d,p) method.

Our result from semiempirical AM1 method shows the preference of cis-isomer over trans-isomer (Table 3) by 4.58 and 10.4 kcal/mol for AzoFL and DFDZ, respectively. On the other hand, the parent trans-DZ isomer is stable by 0.88 kcal/mol over cis-DZ. The preference of cis-AzoFL over the trans-isomer by AM1 method is not clear, but the preference of cis-isomer over trans-isomer for DFDZ due to cis-effect is known in the literature for dihalodiazenes.^49,52,55,56 Different explanations were found for the cis-effect in the literature by different authors, viz., (i) the sum of the repulsive forces between the N lone pairs and between the two N–F bonds is less in cis-DFDZ compared to that of the trans-DFDZ,⁵⁷ (ii) mutual interplay of various interactions, for example, antiperiplanar interaction, Coulombic interaction, and lone pair-lone pair interaction in diazene moiety.⁴⁹ (iii) delocalization of the N lone pair over the antibonding orbital of the adjacent N–F bond along with the lone pair delocalization of F over the antibonding orbital of the N=N bond,⁵⁸ and (iv) mutual interactions between the nitrogen lone pairs and the neighboring antibonding orbital of the N–X bond (X = F, Cl, Br).⁵⁶ The shorter N=N bond length is also observed in the parent and unsubstituted cis-DZ along with longer N–H and wider NNH angle compared to that of trans-DZ. However, the parent trans-DZ isomer is stable by 0.88 kcal/mol over cis-DZ, and the cis-effect, that is, the stability of cis-DZ over trans-DZ was not observed in our both the DFT and semiempirical AM1 calculation in accordance with different previous work.^49,55 Because DZ contains no F atoms, as a consequence there are no lone pair electrons for delocalization of halogen lone pairs into the antibonding orbitals of N=N bond. This could be the inability of parent cis-DZ to get any stabilizing energy via delocalization effects and causes preference of trans-isomer.⁵⁵

An attempt were also taken to observe the cis effect by the HF method using three different basis sets, for example, 6-31+G(d,p), 6-31++G(d,p), and 6-311+G(d,p), respectively for DFDZ. The ab initio Hartree–Fock produces insignificant but somewhat longer N=N bond length by 0.00044 Å in cis-DZ (1.21530 Å) over trans-DZ (1.21486 Å) using 6-31+G(d,p) basis set. Similar insignificant longer N=N bond length is also observed in cis-DFDZ by 0.00115 and 0.00244 Å over trans-DFDZ by HF using 6-31+G(d,p) and 6-311+G(d,p) basis set, respectively. The N–F bond of cis-DFDZ is also found to be longer compared to trans-DFDZ by 0.00173 and 0.00056 Å in HF/6-31+G(d,p) and 6-311+G(d,p) basis sets. In HF both the 6-31+G(d,p) and 6-311+G(d,p) basis sets produces longer N=N bond and N–F bond. In both cases, they have larger FNN bond angles. The FNN bond angle of cis-DFDZ is 0.2° in wider by HF/6-311+G(d,p) basis set compared to HF/6-311+G(d,p) over trans-isomer. The HF calculation shows that 6-31+G(d,p) and 6-31++G(d,p) basis set produces the same geometric parameters and equal energy (Table 3). However, energetically preference of the cis-DFDZ was not found by all of the basis sets of HF methods by our present work. Earlier work by HF^49,55 with small basis set and the SS-MRCCSD/aug-cc-pVDZ⁵⁵ calculation was also unable to show the cis-effect.

2.2. Electronic Absorption Spectra

The photophysical properties of trans- and cis-AzoFL consisting of donor (fluorene ring) and acceptor (−N=N−) azo group have been investigated in gas phase by theoretical calculation. The UV–vis absorption spectra of parent trans- and cis-DZ, electron withdrawing F atom-containing difluorodiazene (DFDZ) and FL were calculated and made comparison with the model compound AzoFL. In the past decade, time-dependent DFT (TD-DFT) has become the leading method for the calculation of excitation energies and optical properties of organic molecules.⁵⁹⁻⁶² Starting from the each fully optimized ground-state structures of B3LYP/6-31+G(d,p), TD-DFT excited-state calculations with the hybrid functional B3LYP and 6-31+G(d,P) basis set were calculated on the three lowest spin allowed singlet–singlet transitions for the above-mentioned azo compounds and fluorene in the gas phase. The calculated UV–vis spectra of those compounds are shown in Figure 5. The theoretical excitation energies (E_ex), oscillator strengths (f), and absorption wavelengths (λ_max) are listed in Tables 4–6. All of the transition probabilities of the different trans- and cis-azo compounds by TD-DFT calculation are given in Tables 4 and 5, respectively.

Figure 5.

UV–vis spectrum of (a) trans- and cis-AzoFL, (b) trans- and cis-DZ, (c) trans- and cis-DFDZ (inset: UV–vis peak of cis-DFDZ: half-width at half height 0.033 eV), and (d) FL (inset: UV–vis peak of FL UV–vis peak: peak half-width at half height 0.033 eV) obtained by TD-DFT/B3LYP/6-31+G(d,p) calculation. The calculated UV–vis spectra are represented with a Gaussian UV–vis peak half-width at half height 0.333 eV.

Table 4. Comparison of Electronic Absorption Wavelengths λ_Max (nm), Excitation Energies, E_ex (eV), and Oscillator Strengths (f) Obtained by TD/DFT and ZIndo Calculation for the Model AzoFL and Other Compounds for π–π* Transition.

		trans-				cis-
method	properties	DZ	DFDZ	AzoFL	DZ	DFDZ	AzoFL	FL
TD/DFTa,b	λmax	178.97	189.32	423.53	205.43	∼190.00	359.45	265.77
	Eex	6.9277	6.5490	2.9274	6.0355	6.4312	3.4492	4.6650
	f	0.0386	0.0111	1.5595	0.0277	0.0104	0.3765	0.2862
ZIndoc,d	λmax	140.80	175.65	387.20	135.98	169.51	355.21	296.84
	Eex	8.8057	7.0586	3.2021	9.1177	7.3142	3.4905	4.1767
	f	0.4735	0.4028	1.5678	0.5269	0.3670	0.7533	0.4446

^aUsing B3LYP/6-31+G(d,p).

^bFrom initial optimized geometry of B3LYP/6-31+G(d,p).

^cUsing semi empirical ZIndo with predefined STO-3G basis set.

^dFrom initial optimized geometry of semi empirical AM1.

Table 6. Electronic Transition, Absorption Wavelengths λ_Max (nm), Excitation Energies, E_ex (eV), and Oscillator Strengths (f) Obtained by TD-DFT/B3LYP/6-31+G(d,p) Calculation for all of the cis-Azo Compounds from the Optimized Initial Geometry at B3LYP/6-31+G(d,p)^e.

compound	electronic transition	λmax	f	Ex	MOa	MOb	symc	wave functionsd
cis-DZ	S0 → S1	371.78	0.0056	3.3348	8 → 9	0.70904	B1	H → L (100%)
	S0 → S2	205.43	0.0277	6.0355	8 → 10	0.70584	B2	H → L + 1 (99%)
	S0 → S3	183.64	0.0000	6.7516	7 → 9	0.70622	A2	H – 1 → L (99%)
cis-DFDZ	S0 → S1	194.49	0.0000	6.3748	14 → 17	0.70624	A2	H – 2 → L (99%)
	S0 → S2	192.79	0.0104	6.4312	15 → 18	0.34743	B1	H – 1 → L + 1 (24%)
					16 → 17	0.61543		H → L (75%)
	S0 → S3	180.82	0.0058	6.8569	15 → 18	0.61259	B1	H – 1 → L + 1 (75%)
					16 → 17	–0.34590		H → L (23%)
cis-AzoFL	S0 → S1	517.82	0.1774	2.3944	92 → 95	–0.24158	B	H – 2 → L (11%)
					94 → 95	0.65138		H → L (84%)
	S0 → S2	359.45	0.3765	3.4492	92 → 95	0.63933	B	H – 2 → L (81%)
					94 → 95	0.25998		H → L (13%)
	S0 → S3	352.82	0.0486	3.5141	93 → 95	0.65249	A	H – 1 → L (85%)
					94 → 96	–0.23956		H → L + 1 (11%)

^aMolecular orbitals involved in the transition.

^bMolecular orbital coefficients.

^csym, orbital symmetry-singlet.

^dThe wave functions based on the eigenvectors predicted by TD-DFT. H and L are used to denote the HOMO and LUMO.

^ePercentage of contribution obtained by (100 × c × c × 2), where c is the coefficient.

Table 5. Absorption Wavelengths λ_Max (nm), Excitation Energies, E_ex (eV), and Oscillator Strengths (f) Calculated by TD/DFT-B3LYP/6-31+G(d,p) Method for all of the trans-Azo Compounds and FL From the Initial Optimized Geometry at B3LYP/6-31+G(d,p).

compound	electronic transition	λmax	f	Ex	MOa	MOb	symc	wave functionsd,e
trans-DZ	S0 → S1	387.78	0.0000	3.1972	8 → 9	0.70891	BG	H → L (100%)
	S0 → S2	184.08	0.0000	6.7354	8 → 10	0.70579	AG	H → L + 1 (99%)
	S0 → S3	178.97	0.0386	6.9277	8 → 11	0.70527	BU	H → L + 2 (99%)
trans-DFDZ	S0 → S1	227.47	0.0000	5.4505	16 → 17	0.70544	BG	H → L (99%)
	S0 → S2	189.32	0.0111	6.5490	15 → 17	0.29661	BU	H – 1 → L (17%)
					16 → 18	0.63732		H → L + 1 (81%)
	S0 → S3	179.59	0.0000	6.9033	15 → 18	0.70238	BG	H – 1 → L + 1 (98%)
trans-AzoFL	S0 → S1	489.35	0.0000	2.5336	93 → 95	0.69879	B	H – 1 → L (97%)
	S0 → S2	423.53	1.5595	2.9274	94 → 95	0.70581	B	H → L (99%)
	S0 → S3	344.48	0.0000	3.5992	92 → 95	0.68177	A	H – 2 → L (92%)
					94 → 96	–0.13547		H → L + 1 (3%)
FL	S0 → S1	276.39	0.1648	4.4858	42 → 45	0.22186	B2	H – 2 → L (9%)
					42 → 46	0.11652		H – 2→L + 1 (2%)
					44 → 45	0.48597		H → L (47%)
					44 → 46	–0.43727		H → L + 1 (38%)
	S0 → S2	265.77	0.2862	4.6650	42 → 45	–0.15521	B2	H – 2 → L (4%)
					44 → 45	0.48553		H → L (47%)
					44 → 46	0.48096		H → L + 1 (46%)
	S0 → S3	256.82	0.0072	4.8277	43 → 45	0.55822	A1	H – 1 → L (62%)
					44 → 47	–0.40501		H → L + 2 (32%)

^aMolecular orbitals involved in the transition.

^bMolecular orbital coefficients.

^csym, orbital symmetry-singlet.

^dThe wave functions based on the eigenvectors predicted by TD-DFT. H and L are used to denote the HOMO and LUMO.

^ePercentage of contribution obtained by (100 × c × c × 2), where c is the co-efficient.

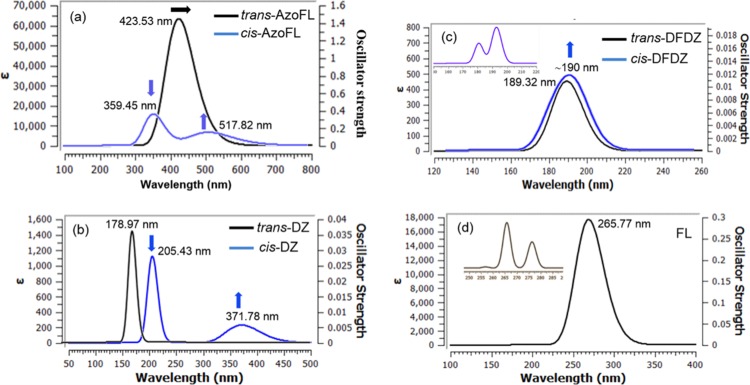
The present TD-DFT calculations show that the model trans-AzoFL afforded characteristics broad and long-waved absorption band around 300–700 nm (Figure 5a). The band at λ_max 423.53 nm is very high with a molar extinction coefficient ε_max 6.0 × 10⁴ M^–1 cm^–1, which is indicative of the π–π* transition⁶³ (S₀–S₂) in trans-AzoFL. On the other hand, the band for n−π* transition was not observed in trans-AzoFL by TD-DFT calculation. The spectra (Figure 5a) of cis-AzoFL shows the disappearance of the band at λ_max 423.53 nm, while a well resolved band at 359.45 nm (S₀–S₂) for π–π* and a second band at 517.82 nm (S₀–S₁) for n−π* transition, respectively, was observed (Figure 5a). The band at 359.45 nm (π–π*) is decreased in intensity (ε_max 1.7 × 10⁴ M^–1 cm^–1), whereas the n−π* transition band at 517 nm has strong ε_max 7.0 × 10³ M^–1 cm^–1 absorbance compared to that of other azo compounds under study. The absorption band for the π–π* transition in cis-AzoFL shifts to shorter wavelength at λ_max 359 45 nm, a 64.08 nm blue shift is observed compared to that of trans-AzoFL. The broad band at λ_max 517.82 nm (n−π*) transition for cis-AzoFL (Figure 5a) is shifted to longer wavelength compared to all other cis-azo compounds by present TD-DFT calculation.

Liu and co-workers²⁶ investigated the UV–vis spectrum of 1,2-bis(9,9-dioctyl-9H-fluoren-2-yl)diazene in 1,2-dichloroethane (concentration of the compound is 0.02 g/L) and found the experimental absorption maxima (λ_max) for π–π* transition at 394 nm and n−π* transition at 500 nm. They²⁶ also performed TD-DFT calculation at the level of ONIOM (M06-2x/6-31G*: AM1), and the calculated absorption maximum (π–π* transition) of 1,2-bis(9,9-dioctyl-9H-fluoren-2-yl)diazene was found at 345 nm. These results supports our TD-DFT calculated UV–vis spectra of trans-AzoFL (π–π* transition band at λ_max 423.53 nm) at the level of B3LYP/6-31+G(d,p) in gas phase.

Bagheri and Hashemianzadeh³⁴ employed TD-DFT calculations with B3LYP/6-311+G** basis set, based on the optimized geometries of B3LYP/6-311+G** for azo dye-containing fluorene derivative at one end and 4-carboxyphenyl group at the other end of the azo group (−N=N−). The TD-DFT calculated maximum wavelengths (π–π* transition) of the azo dye³⁴ are shown at 405.41 nm in gas phase and at 438.62 nm in THF in UV–vis absorption spectra. The steady-state UV–visible absorption spectrum of trans-azobenzene in n-hexane shows one weak band at 445 nm assigned for the n−π* transition (S₁ state) and a stronger band at 315 nm for π–π* transition (S₂ state) by Lednev et al.⁶⁴ The n−π* transition is very weaker (ε ≈ 400 M^–1 cm^–1) and is not allowed in the trans-isomer of azobenzene compounds by symmetry rules. However, the electronic transition n−π* (380–520 nm) is allowed in cis-isomer, resulting in an increase in intensity with respect to the trans-isomer in azobenzene compounds.^65,66

The present TD-DFT calculation performed by our group shows that the parent trans-DZ (Figure 5b) has λ_max 178.97 nm (ε_max 1.4 × 10³ M^–1 cm^–1) for π–π* (S₀–S₃) transition. The n−π* transition band in the parent trans-DZ was also not observed similar to trans-AzoFL. The band at 178.97 nm in cis-DZ (Figure 5b) completely disappears and instead of that two new well-separated nice bands at λ_max 205.43 nm (ε_max 1.2 × 10³ M^–1 cm^–1) for π–π* (S₀–S₂) and at λ_max 371.78 nm (ε_max 200 M^–1 cm^–1) for n−π* (S₀–S₁) transition, respectively, is found. It is also observed that in cis-DZ (Figure 5b), the λ_max at 205.43 nm (ε_max 1.2 × 10³ M^–1 cm^–1) for π–π* transition is decreased in intensity compared to that of trans-DZ λ_max 178.97 nm (ε_max 1.4 × 10³ M^–1 cm^–1) and shifts to longer wavelength.

Figure 5d shows a broad band around 200–350 nm for fluorene (FL). The three bands (Figure 5d inset, half-width at half height 0.033 eV) at 256.82 nm (S₀–S₃), 265.77 nm (S₀–S₂), and 276.39 nm (S₀–S₁) merge together at λ_max 265.77 nm (ε_max 1.6 × 10³ M^–1 cm^–1) for the π–π* transition (S₀–S₂).

It is crystal like clear that a significant variation on the absorption spectra of AzoFL occurred by incorporation of the fluorene (FL) ring into the −N=N– backbone (Figure 5). The same trend in extinction-coefficient, that is, much higher extinction-coefficient and higher oscillator strength in trans-AzoFL in comparison with that of parent trans-DZ (Figure 5) is observed.

The results show that incorporation of the FL ring into the −N=N– back bone causes bathochromic shifts of both the trans- and cis-AzoFL and higher extinction-coefficient (Figure 5a,d). A 157.76 and 93.68 nm wavelength increment is observed compared to FL in trans- and cis-AzoFL, respectively, for π–π* transition band. The weak band for n−π* (S₀–S₁) transition at λ_max 371.78 nm (ε_max 200 M^–1 cm^–1) for cis-diazene shifts to λ_max 517.82 nm (ε_max 7.0 × 10³ M^–1 cm^–1) in cis-AzoFL, a red shift of 146.04 nm is observed with higher intensity. On the other hand, the intensity of the π–π* band in both the cis-DZ and cis-AzoFL causes hypochromic effect by TD-DFT calculation compared to the corresponding trans-isomers.

In trans-AzoFL, the absorption maxima λ_max 423.53 nm of π–π* transition showed an obvious red shift of ∼245 nm increment to longer wavelength compared to that of trans-diazene (λ_max 178.97 nm). This effective red shift is attributed due to the extended π-conjugation length which reflects the longer N=N bond length of AzoFL (Table 1). Even a 154.02 nm of wavelength increment toward longer wave length is observed in cis-azoFL (λ_max 359.45 nm) compared to that of cis-diazene (λ_max 205.43 nm). Because of coplanarity of the two FL rings in trans-isomer, the π–π* transition band shifts to lower energy longer wavelength compared to that of cis-AzoFL.

Introducing two F atoms into the −N=N– backbone in DFDZ shows interesting results. The trans-DFDZ (Figure 5c) has a band at λ_max 189.32 nm (S₀–S₂) with low absorbance. The molar absorptivity was found only ε_max ≈ 420 M^–1 cm^–1 with low oscillator strength (0.0111). It is expected that π–π* transition should have high molar absorptivity usually at ε_max ≈ 10⁴ M^–1 cm^–1, but this unusual result is surprising. The π–π* transition band at λ_max 189.32 nm of trans-DFDZ causes a red shift of 10.35 nm compared to that of trans-DZ (λ_max 178.97 nm, ε_max ≈ 1.4 × 10³ M^–1 cm^–1).

In cis-DFDZ, a broad band appeared at λ_max ≈ 190 nm with low molar absorptivity (ε_max ≈ 500 M^–1 cm^–1) by Gaussian UV–vis peak half-width at half height (0.333 eV) in UV–vis spectra (Figure 5c). However, the band was found as separated bands at λ_max 180.82 nm (S₀–S₃, f = 0.0058) and λ_max 192.79 nm (S₀–S₂, f = 0.0104) (Figure 5c, inset) at UV–vis peak half-width at half height (0.033 eV). Compared to cis-DZ (λ_max 205.43 nm, ε_max 1.2 × 10³ M^–1 cm^–1), cis-DFDZ (λ_max ≈ 190 nm, ε_max ≈ 500 M^–1 cm^–1) shows a blue shift of 15.43 nm with reduced molar absorptivity. The cis-DFDZ (λ_max ≈ 190 nm, ε_max ≈ 500 M^–1 cm^–1) and trans-DFDZ (λ_max 189.32 nm, ε_max ≈ 420 M^–1 cm^–1) shows a similar type of absorption behavior (Figure 5c).

In order to examine the TD-DFT excited-state behavior of the DZ and DFDZ, a further investigation was carried out (Table S1). TD-DFT//B3LYP/6-31+G(d,p) calculations by using different initial geometries obtained from HF/6-31+G(d,p) and HF/6-31++G(d,p) basis sets were done. The two initial geometries gave the similar results by TD-DFT//B3LYP/6-31+G(d,p) calculations. In trans-DFDZ, a band appeared at λ_max ≈ 168 nm with low molar absorptivity (ε_max ≈450 M^–1 cm^–1) by Gaussian UV–vis peak half-width at half height (0.333 eV) in UV–vis spectra (Figure S1a). However, the band was found as separated bands at λ_max 161.62 nm (S₀–S₃, f = 0.0092) and λ_max 172.36 nm (S₀–S₂, f = 0.0067) (Figure S1a, inset) at UV–vis peak half-width at half height (0.233 eV). By using HF/6-31+G(d,p) as initial geometry in TD-DFT//B3LYP/6-31+G(d,p) calculation, the absorptivity is enhanced in some extent and causes a ∼17 nm red shift in cis-DFDZ (λ_max 185.82 nm, S₀–S_1,f = 0.0181, ε_max ∼750 M^–1 cm^–1) compared to trans-DFDZ (λ_max 168 nm, ε_max ≈ 450 M^–1 cm^–1).

ZIndo excited-state calculations with the predefined STO-3G basis set by using optimized geometries of semiempirical AM1 as the initial structure were also calculated on the three lowest spin allowed singlet–singlet transitions for the above-mentioned azo compounds and FL in the gas phase. The electronic transition data, for example, the theoretical excitation energies (E_ex), oscillator strengths (f), and absorption wavelengths (λ_max) are listed in the Tables 4, S2 and S3. The calculated UV–vis spectra of the three pairs of azo compounds and FL by ZIndo are shown in Figure 6.

Figure 6.

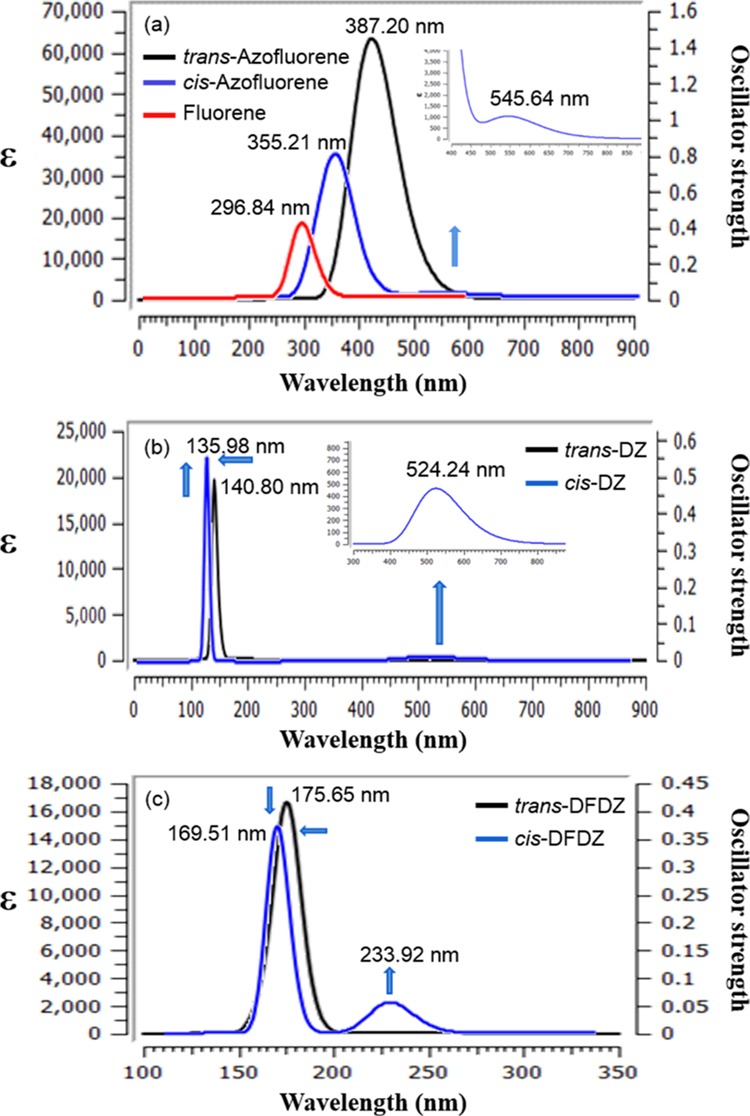
Calculated UV–vis spectra of (a) trans- and cis-AzoFL with FL (b) trans- and cis-DZ (c) trans- and cis-DFDZ by ZIndo. The calculated UV–vis spectra are represented with a Gaussian UV–vis peak half-width at half height 0.333 eV or 2685.83 cm^–1.

ZIndo produces nice bands for π–π* and n−π* transitions for the three pairs of azo compounds. The π–π* transition band of trans- and cis-AzoFL were observed at λ_max 387.20 nm and λ_max 355.21 nm, respectively, by ZIndo. As shown in (Figures 5 and 6), similar behavior and same spectral pattern were observed by introducing FL ring into the backbone of −N=N– unit. A nice bathochromic shift (Figure 6a) of π–π* transition band of trans-AzoFL (λ_max 387.20 nm, ε_max 6.0 × 10⁴ M^–1 cm^–1) and cis-AzoFL (λ_max 355.21 nm, ε_max 3.0 × 10⁴ M^–1 cm^–1) compared to that of FL (λ_max 296.84 nm, ε_max 1.85 × 10⁴ M^–1 cm^–1) were observed. A comparison of π–π* transition band of cis- and trans-AzoFL with parent trans-DZ (λ_max 140.80 nm (S₀ → S₃), ε_max 2.1 × 10⁴ M^–1 cm^–1) and cis-DZ (λ_max 135.98 (S₀ → S₃), ε_max 2.0 × 10⁴ M^–1 cm^–1) also shows that cis- and trans-AzoFL are red-shifted by ZIndo method.

The cis- and trans-DFDZ also shows some extent of red shift compared to that of corresponding isomers of DZ.

The assignment of n−π* transition band of the above-mentioned cis-compounds is straightforward. The transition bands (n−π*) are at λ_max 545.64 nm (ε_max 950 M^–1 cm^–1), λ_max 524.24 nm (ε_max 400 M^–1 cm^–1), and λ_max 233.92 nm (ε_max 2 × 10³ M^–1 cm^–1) for cis-AzoFL, cis- DZ, and cis-DFDZ respectively. The n−π*transition band of both the cis-AzoFL and cis-DFDZ is red-shifted compared to that of cis-DZ.

Though the ZIndo produces n−π* transition band in trans-AzoFL at λ_max 562.02 nm (ε_max ≈ 450, f = 0.0105, Gaussian UV–vis peak half-width at half height 0.233 eV) but the n−π* bands were not seen in trans-DFDZ and parent trans-DZ in both the DFT and ZIndo method.

Unlike the spectral pattern obtained from TD-DFT method, ZIndo produces well-separated π–π* (S₀ → S₃) and n−π* (S₀ → S₂) transition bands at λ_max 169.51 nm (ε_max 1.4 × 10⁴, f = 0.3671) and λ_max 233.92 nm (ε_max 1.4 × 10⁴, f = 0.0543), respectively, for cis-DFDZ (Figure 6c). A slight blue shift and small hypochromic effect for π–π* transition were observed for the parent DZ and DFDZ compared to that of respective trans-isomers by ZIndo method. In trans-DFDZ, the transition of (S₀ → S₃) at 163.06 nm (f = 0.0524) is underneath the π–π* transition band (S₀ → S₂) at 175.65 nm (f = 0.4028).

It is noteworthy that using DFT/6-31+G(d,p) as initial geometry in TD-DFT//B3LYP/6-31+G(d,p) calculation, there is no significant differences were observed between absorption spectra of cis and trans-DFDZ (Figure 5c). However, with different initial geometry, HF/6-31+G(d,p) was used in TD-DFT//B3LYP/6-31+G(d,p) calculation, and the π–π* transition band of trans-DFDZ was blue-shifted (∼17 nm) compared to cis-DFDZ (Figure S1a). In the case of ZIndo method, trans-DFDZ was red-shifted (∼6 nm) compared to cis-DFDZ (Figure 6c).

2.3. Frontier Molecular Orbitals

The highest occupied molecular orbital (HOMO) and the lowest-lying unoccupied molecular orbital (LUMO) are known as frontier molecular orbital (FMO). The molecular orbital is a mathematical function that describes the behavior of an electron or a pair of electrons within a molecule.⁶⁷ These functions are plotted as surfaces around the molecular structure. The HOMO represents the ability to donate an electron, on the other hand LUMO as an electron acceptor. The energy gap between the HOMO and LUMO determines not only the chemical reactivity and kinetic stability, but also optical and electrical properties of a molecule.⁶⁸

The energies of six important molecular orbitals and the 3D plots of the third HOMO [HOMO – 2], second highest [HOMO – 1], and the highest HOMO, the lowest unoccupied MO [LUMO], second lowest unoccupied MOs [LUMO + 1], and the third lowest unoccupied MOs [LUMO + 2] of the model compound AzoFL calculated using B3LYP/6-31+G(d,p) basis set at DFT level of theory are shown in Figures 7 and 8. The energy values of HOMO, LUMO, and energy gap between them, E_g (HOMO–LUMO), and dipole moments of the ground and excited states of the AzoFL, DFDZ; parent DZ and FL are listed in Table 7.

Figure 7.

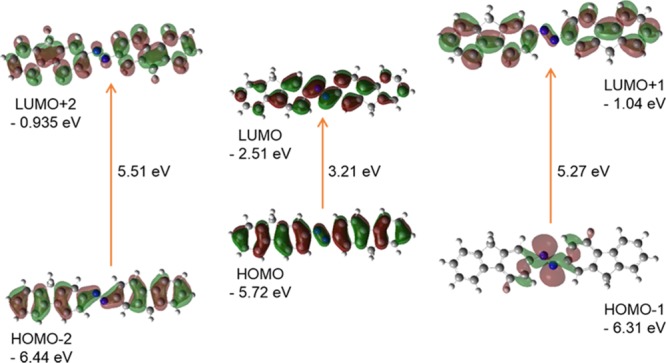
Diagram of FMO (isovalue: 0.02 [e bohr^–3]^1/2 of trans-AzoFL generated from TD/DFT calculation). Green and Maroon colors depict different phases.

Figure 8.

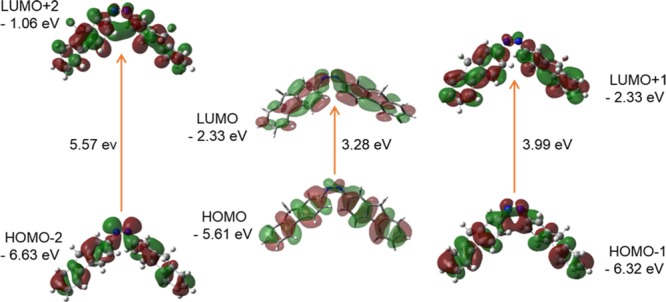
Diagram of FMO (isovalue: 0.02 [e bohr^–3]^1/2 of cis-AzoFL generated from TD/DFT calculation). Green and Maroon colors depict different phases.

Table 7. Energy Values^a of HOMO, LUMO, and Energy Gap Between Them, E_g (HOMO–LUMO), Dipole Moments^b (μ) of the AzoFL, DFDZ; Parent DZ and FL.

	DFTc			semiempiricald			dipole moment
compound	HOMO	LUMO	ΔEg	HOMO	LUMO	ΔEg	μgrounde,f	μexcitede,g
trans-AzoFL	–5.72	–2.51	3.21	–8.49	–1.02	7.46	0.00	0.00
							0.17	0.30
cis-AzoFL	–5.61	–2.33	3.28	–8.70	–0.81	7.89	3.12	3.12
							2.99	3.24
trans-DFDZ	–10.30	–3.15	7.14	–13.67	–2.21	11.42	0.00	0.00
							0.00	0.00
cis-DFDZ	–10.77	–2.93	7.84	–13.85	–2.02	11.83	0.22	0.22
							0.66	0.57
trans-DZ	–6.96	–1.99	4.98	–10.32	0.84	10.97	0.00	0.00
							0.00	0.00
cis-DZ	–7.07	–2.06	5.01	–0.86	–10.56	11.42	3.20	3.20
							2.70	3.99
FL	–6.04	–1.12	4.93	–8.71	–0.22	8.49	0.58	0.58
							0.37	0.70

^aEnergies are in electron volts (eV).

^bDipole moments are in debye.

^cDFT calculation using B3LYP/6-31+G(d,p).

^dSemiempirical ZIndo.

^eUpper value: DFT.

^fDown value: AM1.

^gDown value: ZIndo.

The model trans-AzoFL compound has a total of 610 alpha orbitals, out of which 94 are occupied and the remaining 516 are virtual orbitals. The orbital 94 represents HOMO, whereas orbital 95 represents LUMO orbitals. In our analyses, we found that the energy values of HOMO and LUMO are −5.72 and −2.51 eV, respectively, in trans-AzoFL (Figure 7, Table 7).

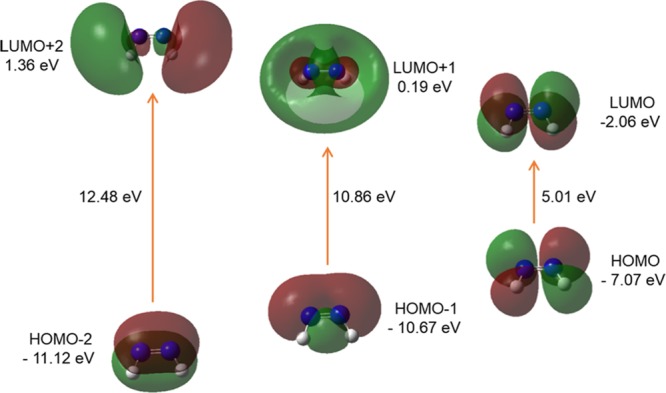
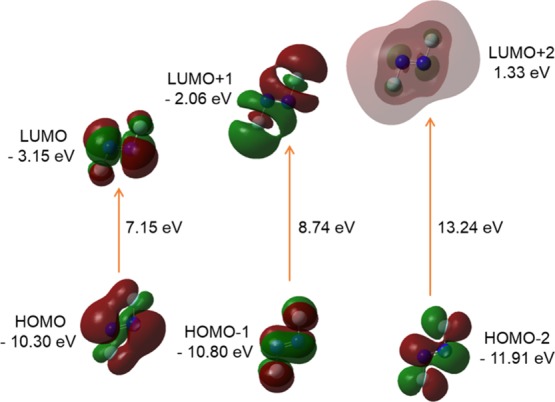
It is evident from Figures 7 and 8 that the HOMO and LUMO are localized on almost the whole molecule showing π- and π*-bonding MO, respectively. HOMO – 1 is localized on the N=N linkage, C2, C1, and C2′, C1′ atoms of the trans-AzoFL ring with almost no participation of the FL linker groups (Figure 7). The energy separation between the HOMO and the LUMO of trans-AzoFL is 3.21 eV, whereas the value is 3.28 eV for cis-AzoFL (Table 7). The HOMO (94a)–LUMO (95b) transition implies for π–π*(S₀–S₂) transition with 99% probability (Table 6).

The 3D FMOs of FL, DZ, and DFDZ are shown in Figures 9–13, respectively. Both the trans-DZ and cis-DZ has a total of 48 alpha molecular orbitals, out of which 8 are occupied and the remaining 40 are virtual orbitals. The orbital 8 represents HOMO whereas 9 represents LUMO orbitals in DZ. In trans-DZ HOMO – 1 is π-bonding MO whereas in cis-DZ HOMO – 2 is π-bonding MO. LUMO is showing π*-antibonding MO. The LUMO + 2 in both the cis- and trans-diazene are showing similar behavior.

Figure 9.

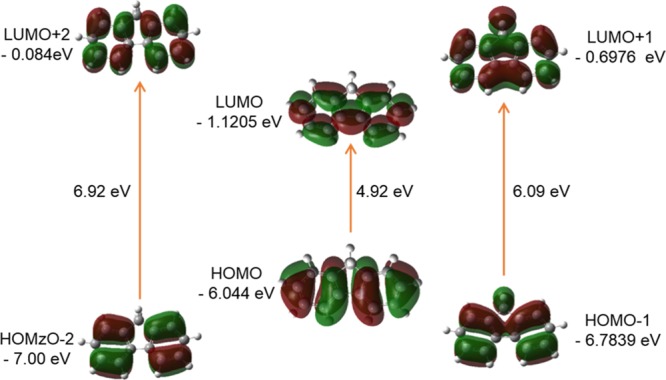
FMO orbitals (isovalue: 0.02 [e bohr^–3]^1/2 of FL generated from TD/DFT calculation). Green and Maroon colors depict different phases.

Figure 13.

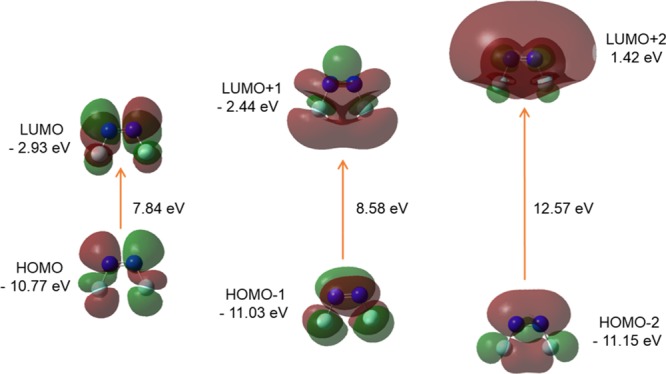
FMO orbitals (isovalue: 0.02 [e bohr^–3]^1/2 of cis-DFDZ generated from TD/DFT calculation). Green and Maroon colors depict different phases.

Figure 10.

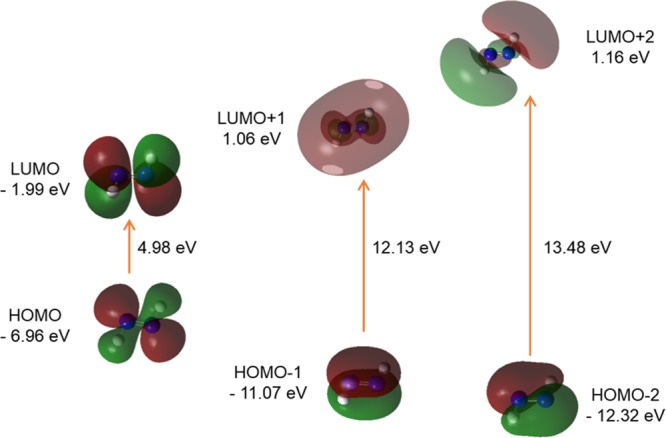
FMO orbitals (isovalue: 0.02 [e bohr^–3]^1/2 of trans-DZ generated from TD/DFT calculation). Green and Maroon colors depict different phases.

Figure 11.

FMO orbitals (isovalue: 0.02 [e bohr^–3]^1/2 of cis-DZ generated from TD/DFT calculation). Green and Maroon colors depict different phases.

The orbitals 16 and 17 represent the HOMO and LUMO, respectively, in both the cis- and trans- DFDZ. The LUMO pattern of both the trans- and cis-DFDZ looks similar, whereas HOMO is different (Figures 12 and 13). The lone pairs on the nitrogen atoms are jot out in the plane of the molecule as seen in the HOMO of trans-DFDZ (Figure 12). The HOMO–LUMO energies and gap (E_g) between the HOMO–LUMO are given in the Table 7.

Figure 12.

FMO orbitals (isovalue: 0.02 [e bohr^–3]^1/2 of trans-DFDZ generated from TD/DFT calculation). Green and Maroon colors depict different phases.

From the HOMO and LUMO energies, global reactivity descriptor properties can be calculated.⁶⁹⁻⁷² The ionization potential I and electron affinity A are equal to orbital energies of HOMO and LUMO as I = −E_HOMO and A = −E_LUMO. The ionization potential I and electron affinity A are found as 5.72 and 2.51 eV (Table 8), respectively, for trans-AzoFL. The electronegativity χ = (I + A)/2, chemical potential, μ = −χ, chemical hardness η = (I – A)/2, chemical softness, S = 1/η, electrophilicity index (ω) = μ²/2η, respectively, is calculated and tabulated in Table 8. The global reactivity descriptors of FL and trans- and cis-AzoFL, DZ, and DFDZ are summarized and given in the Table 8.

Table 8. Calculated Polarizability^a (α) and Global Reactivity Descriptors^b by B3LYP/6-31+G(d,p) Basis Set at DFT Level of Theory.

compound	α	I	A	χ	μ	η	S	ω
trans-AzoFL	430.03	5.72	2.51	4.12	–4.12	1.61	0.62	5.26
cis-AzoFL	365.23	5.61	2.33	3.97	–3.97	1.64	0.61	4.80
trans-DFDZ	21.12	10.30	3.15	6.73	–6.73	3.58	0.28	6.33
cis-DFDZ	20.69	10.77	2.93	6.85	–6.85	3.92	0.26	5.98
trans-DZ	16.34	6.96	1.99	4.48	–4.48	2.49	0.40	4.03
cis-DZ	16.72	7.07	2.06	4.57	–4.57	2.51	0.40	4.16
FL	152.05	6.04	1.12	3.58	–3.58	2.46	0.41	2.62

^aPolarizability, α in a.u.

^bI, ionization potential; A, electron affinity; χ, electronegativity; μ, chemical potential; η, chemical hardness; S, chemical softness and ω, electrophilicity index in eV.

2.4. Assignments of Vibrational Frequencies

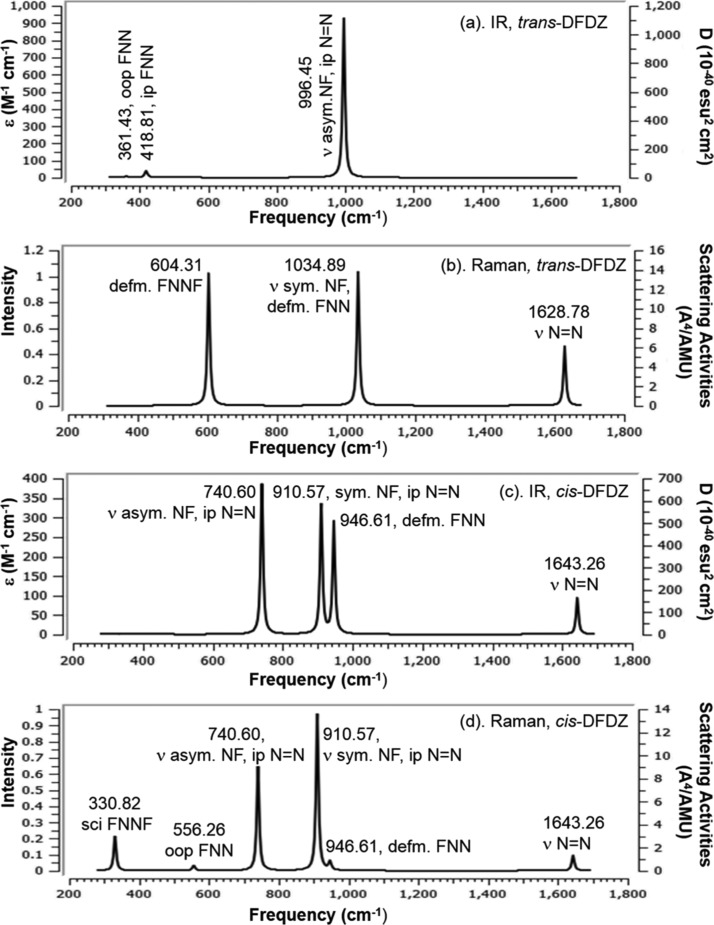
Nowadays, description of theoretical vibrational spectra has attracted much attention not only for the identification of different compounds but also for spectrochemical investigation. There have been several theoretical reports on vibrational frequencies for trans-azobenzene in the ground state at the MP2, DFT, and CASSCF levels.^11,73−77 As far as we are aware, there have been no previous reports on detailed descriptions of vibrational frequencies of azofluorene compounds. In an effort to gain a better understanding of the vibrational frequencies of both cis and trans-isomers of our studied azo compounds, we have calculated IR and Raman scattering activities at the level of DFT-B3LYP/6-31+G(d,p). As fluorene (FL) moiety and the −N=N– are the major structural unit of our target AzoFL, at first we have calculated and discussed theoretically predicted IR and Raman scattering activity spectra of the parent DZ, DFDZ, and FL for comparison even though there is experimental⁴⁹ as well as some theoretical work⁴⁴ present in the literature.

The IR and the Raman activity spectra calculated by B3LYP/6-31+G(d,p) basis set at DFT level of theory of the trans- and cis-DZ, DFDZ, respectively, are shown in Figures 14 and 15 and their vibrational assignments of the fundamental modes along with their calculated IR and Raman activity intensities, frequencies, and normal mode of vibrations along with the respective force constants are given in Tables 9 and 10. Generally, force constants help us to know the strength of the bond and molecular stability.

Figure 14.

Calculated (a) IR; (b) Raman spectra of trans-DZ; (c) IR; (d) Raman spectra of cis-DZ at B3LYP/6-31+G (d,p). The calculated harmonic frequencies are represented with a Gaussian IR peak half-width at half height 4 cm^–1.

Figure 15.

Calculated (a) IR; (b) Raman spectra of trans-DFDZ; (c) IR (d) Raman spectra of cis-DFDZ at DFT-B3LYP/6-31+G(d,p). The calculated harmonic frequencies are represented with a Gaussian IR peak half-width at half height 4 cm^–1.

Table 9. Calculated IR and Raman Activity Frequencies for trans- and cis-DZ by Present Different Methods.

		AM1			HFb				DFTc
	modea	freqd	IIRe	kf	freqd	IIRe	IRamang	kf	freqd	IIRe	IRamang	kf
trans-DZ	oop HNN	1237.39	65.74	0.9696	1466.02	109.99	0.00	1.3354	1344.41	95.85	0.00	1.1446
	ip HNN	1275.21	67.35	1.0298	1452.15	111.62	0.00	1.3610	1348.65	74.67	0.00	1.1518
	HNNH defm	1620.30	0.00	1.9728	1733.40	0.00	14.65	2.1834	1596.94	0.00	11.23	2.0720
	str N=N	2162.06	0.00	34.4968	1896.02	0.00	26.30	27.2443	1659.03	0.00	19.23	9.8621
	sym str NH	3280.27	0.00	6.7102	3592.80	0.00	239.56	8.1736	3251.63	0.00	277.76	6.6818
	asym. str NH	3312.97	6.68	6.9504	3626.00	2.54	0.00	8.3259	3280.65	21.98	0.00	6.8154
cis-DZ	oop HNN	1289.82	58.36	1.0062	1399.11	0.00	0.58	1.3724	1269.07	0.00	1.74	1.1291
	HNNH sci	1282.31	0.00	1.2137	1489.89	0.01	12.91	1.3311	1354.10	1.64	22.19	1.1166
	HNNH roc	1494.39	4.10	1.8079	1687.61	79.89	1.49	2.2188	1538.87	42.00	1.95	1.8468
	str N=N	2169.63	19.80	27.9352	1892.56	5.84	24.58	25.4603	1662.43	6.60	9.25	16.9573
	asym str. NH	3225.57	13.76	6.5184	3486.24	26.86	139.74	7.6871	3088.26	79.74	207.53	6.0310
	sym. str. NH	3261.52	13.08	6.7251	3555.23	13.23	129.71	8.0195	3185.08	51.12	163.88	6.4231

^aApproximate description of mode; defm, deformation; tor, torsion; str, stretching; sym, symmetric; asym, asymmetric; oop, out-of-plane; ip, in-plane; sci, scissoring; roc, rocking.

^bHF/6-31+G(d,p).

^cB3LYP/6-31+G(d,p).

^dVibrational frequencies in cm^–1.

^eInfrared intensities in km/mol.

^fk, force constants in mDyne/A.

^gRaman intensities in Å⁴/AMU.

Table 10. Calculated IR and Raman Scattering Activities for trans- and cis-DFDZ by Present Different Methods.

		AM1			HFb				DFTc
	modea	freqd	IIRe	kg	freqd	IIRe	IRamanf	kg	freqd	IIRe	IRamanf	kg
trans-DFDZ	ip FNN	338.64	9.70	1.0649	484.39	14.22	0.00	1.7041	418.81	11.95	0.00	1.2131
	oop FNN	345.83	0.51	1.1107	428.37	4.77	0.00	2.1789	361.41	2.82	0.00	1.6292
	defm FNNF	597.41	0.00	3.7344	707.74	0.00	12.06	5.4027	604.31	0.00	13.59	3.9914
	asym. str NF + ip N=N.	1304.92	121.86	15.8130	1205.13	309.84	0.00	13.4871	996.45	269.08	0.00	9.2159
	sym. str NF + FNN defm.	1328.96	0.00	15.7538	1261.13	0.00	23.59	13.8330	1034.89	0.00	15.11	9.2118
	str N=N	1934.25	0.00	30.8745	1969.90	0.00	17.06	32.0281	1628.78	0.00	7.72	21.8882
cis-DFDZ	sci FNNF	240.22	1.40	0.6241	409.44	2.02	1.56	1.8490	330.82	0.33	2.71	1.2097
	oop FNN	636.35	0.00	3.4565	631.98	0.00	0.97	3.4454	556.26	0.00	0.45	2.6647
	defm FNN	815.80	8.17	5.9643	901.05	62.69	6.48	7.7988	946.61	83.58	0.79	5.3934
	sym. str NF + ip N=N	1144.24	34.95	12.5026	1138.62	98.64	2.71	12.1812	910.57	96.49	13.88	7.7810
	asym str NF + ip N=N	1281.70	101.15	14.8780	1155.58	139.24	16.58	11.5335	740.60	111.95	8.91	7.5733
	str N=N	1967.24	26.35	31.9714	1963.07	25.99	8.14	31.8142	1643.26	27.42	1.65	22.2798

^aApproximate description of mode; defm, deformation; tor, torsion; str, stretching; sym, symmetric; asym, asymmetric; oop, out-of-plane; ip, in-plane; sci, scissoring.

^bHF/6-31+G(d,p).

^cB3LYP/6-31+G(d,p).

^dVibrational frequencies in cm^–1.

^eInfrared intensities in km/mol.

^fRaman intensities in Å⁴/AMU. .

^gk, force constants in mDyne/Å.

2.4.1. N–H Vibration in DZ

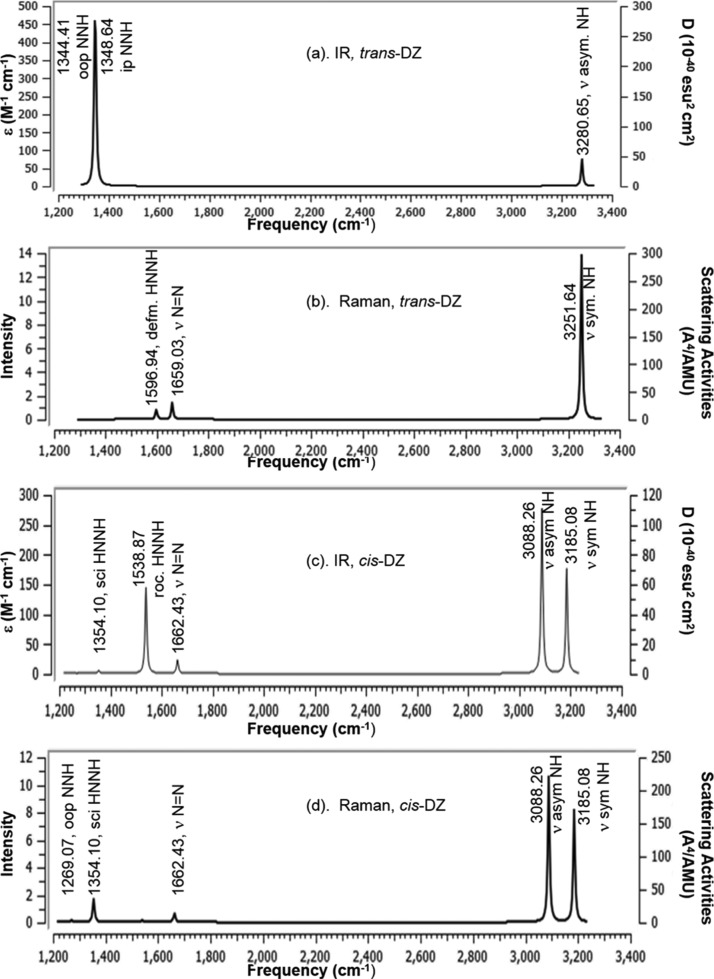
Among six vibrational modes in trans-N₂H₂ (DZ), three modes were found as IR inactive, viz., 1596.94 (Ag, ip NH), 1659.03 (Ag, str N=N), and 3251.64 (Ag, sym str NH) cm^–1 (Figure 14a) but found as Raman scattering active (Figure 14b). The asymmetric N–H stretching, in-plane and out-of-plane N–H vibrations observed at 3280.65 (Bu), 1348.64 (Bu), and 1344.41 (Au) cm^–1 were found as IR active mode, but Raman inactive mode.

In cis-DZ, among the six vibration modes, five modes are found as IR active, for example, 1354.10 (A₁), 1538.87 (B₂), 1662.43 (A₁), 3088.26 (B₂), and 3185.08 (A₁) cm^–1. The out-of-plane twist mode of NH at 1269.07 (A₂) cm^–1 is Raman active but appears as very weak peak. In cis-isomer two peaks are observed for NH stretching vibration at 3088 for asymmetric and at 3185 cm^–1 for symmetric stretching vibration in both the IR and Raman activity spectra (Figure 14c,d). The six vibrational modes of trans- and cis-DZ by DFT-B3LYP/6-31+G(d,p) calculation are shown in Figures S3 and S4.

On the other hand, in trans-DZ the asymmetric stretching of NH at 3280 cm^–1 is IR active, but NH symmetric stretching vibration at 3251.63 cm^–1 is IR inactive. Reversed trend is observed in Raman activity spectrum for trans-DZ (Table 9).

Jensen et al.⁷⁸ mentioned the different vibrational mode as 1526 (ω₁ N–N), 3154 (ω₂ N–H sym), 3197 (ω₃ N–H asym), 1663 (ω₄ N–N–H sym), 1374 (ω₅ N–N–H asym), and 1351 (ω₆ tor) cm^–1 for trans-DZ by CASSCF. Craig and Levin⁷⁹ mentioned the experimental values as 1529 (N–N), 3128 (N–H sym), 3120 (N–H asym), 1582 (N–N–H sym), 1322 (N–N–H asym), and 1286 (tor) cm^–1. On the other hand, Hwang and Mebel⁸⁰ found the values at much higher frequencies at 1525 (N–N), 3382 (N–H sym), 3353 (N–H asym), 1628 (N–N–H sym), 1360 (N–N–H asym), and 1349 (tor) cm^–1 by high-level G2M(MP2)//MP2/G-31G* calculation.

For cis-DZ, the vibrational modes are found by Jensen et al.⁷⁸ at 1535 (ω₁ N–N), 3144 (ω₂ N–H sym), 3074 (ω₃ N–H asym), 1416 (ω₄ N–N–H sym), 1616 (ω₅ N–N–H asym), and 1267 (ω₆ tor) cm^–1 by CASSCF.

The experimental values at 1558 (ω₁ N–N), 2966 (ω₂ N–H sym), 2884 (ω₃ N–H asym), 1390 (ω₄ N–N–H sym), 1439 (ω₅ N–N–H asym), and 1259 (ω₆ tor) cm^–1 by Craig and Levin⁷⁹ estimated from the approximate force field of trans-DZ. On the other hand Hwang and Mebel⁸⁰ found the values at much higher frequencies at 1562 (ω₁ N–N), 3306 (ω₂ N–H sym), 3225 (ω₃ N–H asym), 1373 (ω₄ N–N–H sym), 1567 (ω₅ N–N–H asym), and 1287 (ω₆ tor) cm^–1 by high level G2M(MP2)//MP2/G-31G* calculation. Biczysko et al.⁸¹ mentioned additional comparison for different parameters of both the trans-DZ and cis-DZ by different authors.

2.4.2. N–F Vibration in DFDZ

The different vibrational modes of trans-DFDZ at 361.43 (AU), 418.81 (BU), 604.31 (AG), 996.45 (BU), 1034.89 (AG), and 1628.78 (AG) cm^–1 of our present calculation is very close to the experimental work⁸² viz. 364 (AU), 423 (BU), 603 (AG), 991 (BU), 1018 (AG), and 1523 (AG) cm^–1. The six vibrational modes of trans- and cis-DFDZ by present DFT-B3LYP/6-31+G(d,p) calculation are shown in Figures S5 and S6.

Among six vibrational modes in trans-N₂F₂ (DFDZ), three modes were found as IR active (Figure 15a) by our B3LYP/6-31+G(d,p) calculation. The out-of-plane FNN, in-plane FNN, and asymmetric N–F stretching vibrations observed at 361.43, 418.86, and 996.20 cm^–1 were found as IR active mode, but Raman inactive. On the other hand the IR inactive modes at 604.30, 1034.48, and 1628.71 cm^–1 for FNNF torsion, symmetric stretching of NF and stretching vibration of N=N were found as Raman active mode in trans-DFDZ (Figure 15b).

The different vibrational modes of cis-DFDZ at 330.82 (A1), 556.26 (A2), 740.60 (B2), 910.57 (A1), 946.61 (B2), and 1643.26 (A1) cm^–1 are also close to the experimental work,⁸² for example, 332 (A1), 546 (A2), 731 (B2), 897 (A1), 957 (B2), and 1492 (A1) cm^–1. In cis-DFDZ, all of the vibrations were found as IR active except out-of-plane of FNN at 556.26 cm^–1, which is Raman active however appears as very weak peak (Figure 15c).

The other five peaks at 1643.27 (str N=N), 946.61 (oop N=N), 910.57(sym str NF), 740.60 (asym str NF), and 330.82 (oop FNN) cm^–1, respectively, are both the IR and Raman active (Figure 15d).

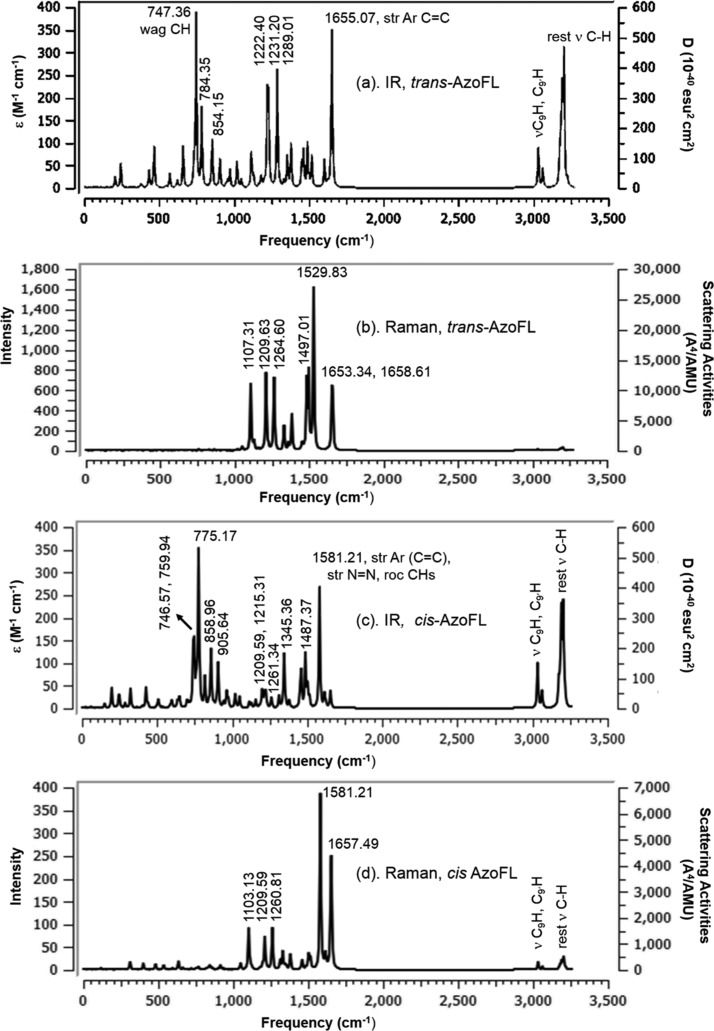
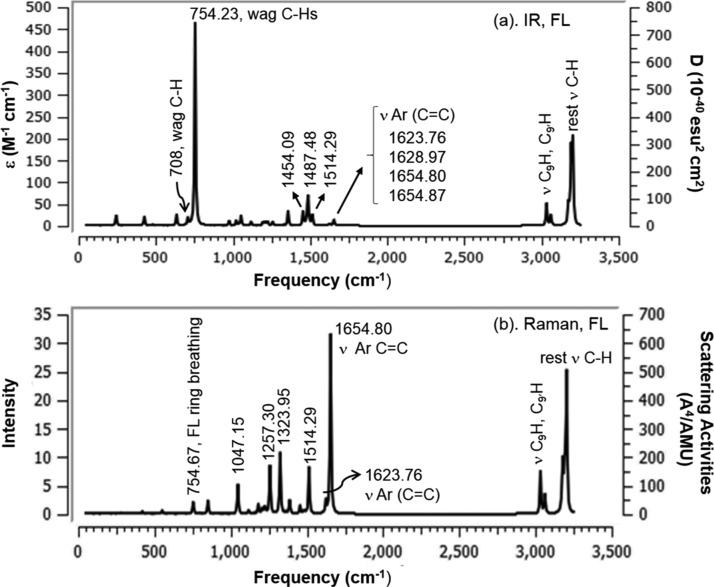
The resulting vibrational frequencies for the optimized geometries and predicted vibrational assignments of the fundamental modes of both the trans- and cis-AzoFL along with the theoretically calculated harmonic vibrational frequencies, IR intensities, Raman scattering activities, and normal mode of vibrations are given in Tables 11 and 12, respectively, using B3LYP/6-31+G(d,p) basis set at DFT level of theory. Some of the vibrational modes of both the trans- and cis-AzoFL are shown in Figures S7 and S8. In aromatic cyclic compounds, almost all of the modes are delocalized over the whole molecule;⁸³ hence, assignments of several vibrational modes are very difficult. However, the assignment of the calculated frequencies is aided by the animation option of Gauss View 6 graphical interface for Gaussian program, which gives a visual presentation of the shape of the vibrational modes.

Table 11. Calculated IR and Raman Activity Frequencies of trans-AzoFL with B3LYP/6-31+G(d,p) in the Ground State.

mode no.	syma	freqb	IIRc	IRamand	ke	approximate description of modef
1	A	15.40	0.1306	0.0000	0.0006	twist (FL1 wrt FL2)
2	A	20.19	0.1109	0.0000	0.0013	wag (FL1 wrt FL2) + wag (N=N)
3	B	35.05	0.3784	0.0000	0.0044	tor FL ring
4	B	47.18	0.0000	2.9250	0.1080	defm FL ring + oop (CH)
5	A	101.53	0.0041	0.0000	0.3050	defm FL ring + oop (CH) + oop (N=N)
6	A	122.77	0.0000	9.8997	0.0539	tor FL ring
7	B	125.22	0.0000	2.0646	0.0568	defm ring + oop (CH) + oop (N=N)
8	B	134.25	0.0000	0.0527	0.0408	defm ring + oop (CH)
9	A	137.57	0.3727	0.0000	0.0422	defm ring + oop (CH)
10	A	165.20	0.0000	2.8101	0.1067	tor ring
11	B	206.31	7.5155	0.0000	0.1305	tor ring (A, C) + (A′, C′)
12	B	240.13	0.0000	1.5216	0.1119	ring defm + twist (N=N) + oop (CH)
13	A	243.89	16.1469	0.0000	0.0805	defm ring + oop (C9H)
14	B	250.70	0.0000	1.1733	0.1230	defm ring + twist (N=N) + oop (CH)
15	A	256.87	0.0646	0.0001	0.1974	defm ring + oop (N=N) + oop (CH)
16	A	287.18	0.0000	11.3418	0.2415	sci ring (A, C) + (A′, C′) + tor (CNNC)
17	B	346.18	0.0000	8.1400	0.3737	twist ring + twist (N=N)
18	B	378.25	2.3707	0.0000	0.7009	ip (ring + N=N)
19	A	384.53	1.5695	0.0000	0.4152	wag (ring A, C) + wag (N=N) + oop (CH)
20	B	430.51	0.0000	0.3769	0.3059	twist (FL1, FL2)
21	A	433.15	11.5592	0.0000	0.3052	wag (FL1, FL 2)
22	A	445.17	0.0997	0.0000	0.3415	ring defm + rot (C9Hs)
23	B	448.40	0.0000	2.1609	0.3527	twist ring
24	B	466.63	26.6329	0.0000	0.6957	tor ring
25	A	480.19	0.0000	7.5415	0.8080	defm angle
26	B	506.58	0.0000	0.7934	0.4932	twist FL1 + twist FL2 + twist (N=N)
27	A	513.21	0.0000	5.0313	0.6578	sci FL1 + sci FL2 + ip (N=N)
28	A	524.41	0.0087	0.0000	0.5675	twist FL1 + twist FL2+ wag (N=N)
29	B	547.75	1.2942	0.0000	0.9779	tors ring + ip (N=N)
30	A	557.17	0.0000	31.4107	1.0816	tor ring
31	B	571.35	9.1429	0.0000	1.0384	sci (FL1 wrt FL2) + ip (N=N)
32	B	582.70	0.0000	0.3227	0.6431	twist (FL1 wrt FL2)
33	B	595.31	0.0467	0.0000	1.4851	CCC defm + ip (CNNC)
34	A	623.01	4.8431	0.0001	0.7032	wag (ring A + ring A′) + twist (ring C, C′)
35	A	648.30	0.0000	91.0341	1.6913	defm CCC + defm CCN
36	B	660.49	26.9341	0.0000	1.6296	defm CCC + sci (ring A, A′) + ip (N=N)
37	A	675.62	0.0000	22.4051	1.6754	defm CCC + defm CCN
38	B	708.48	0.0000	2.3301	1.0291	twist (FL1 wrt FL2)
39	A	716.97	0.1941	0.0000	0.9115	wag (ring A, ring A′) + wag (ring C, C′) + twist (ring A, C) + twist (ring A, C′)
40	B	733.72	14.7894	0.0000	1.7404	defm CCC + ip (CNN)
41	B	743.38	0.0000	0.1909	0.5322	wag (ring CH of ring C, C′) + twist (ring C, ring C′)
42	A	747.36	110.7069	0.0000	0.5334	wag (CH)
43	A	758.63	0.0000	271.7288	1.8586	breathing (FL1 + FL2)
44	B	773.10	0.9828	0.0000	1.9565	defm CCC
45	B	781.15	0.0000	18.5025	0.7666	twist (FL1 wrt FL2)
46	A	784.35	50.9480	0.0000	0.8703	wag (FL1 wrt FL2) + rot (C9H)
47	A	830.40	0.0000	150.7548	1.6810	defm CCC + ip (CNN)
48	B	837.65	1.1534	0.0000	1.9166	Defm (CCC)
49	B	850.84	0.0000	0.7253	0.6349	twist (ring A, ring A) + wag (CH of ring A, ring A′)
50	A	854.15	30.9248	0.0007	0.6399	wag (CH) + wag (ring A, A′)
51	A	864.12	0.0000	211.1922	2.7803	defm [(CNN) + (CCC)]
52	B	876.04	0.0000	0.9303	0.6194	wag (CH of ring C, C′)
53	A	876.38	0.4976	0.0000	0.6233	twist (CH of ring C, C′)
54	B	901.99	0.0000	0.2642	0.6911	twist (CH ring A, CH ring A′)
55	A	905.86	18.6493	0.0000	0.7332	Wag (CH ring A, A′)
56	B	945.51	0.0000	0.9680	0.7815	twist CH ring C + twist CH ring C′+ twist (FL1, FL2)
57	A	946.12	2.4263	0.0000	0.7810	CH Ring
58	B	957.95	4.9996	0.0000	1.6768	roc (CH ring A, CH ring A′)
59	A	962.52	0.0000	25.2250	1.9971	str (CC) + defm (CNN, ring A, ring A′)
60	B	972.04	0.0000	0.6574	0.9856	twist (ring A, C) + wag (FL1 + FL2)
61	A	972.60	11.8089	0.0000	1.0041	twist (ring A, C) + twist (A′, C′) + twist (FL1, FL2)
62	B	984.72	0.0000	1.7196	0.7933	twist (ring A + A′)
63	A	985.26	0.2813	0.0001	0.7891	twist A + twist A′
64	B	992.07	0.0000	2.3310	0.7479	twist (ring C + ring C) + twist (FL1, FL2)
65	A	992.08	0.1066	0.0000	0.7479	twist (ring C) + twist (ring C′)
66	A	1020.42	0.0000	279.0661	4.3569	ip (CCC) + ip (CC)
67	B	1020.57	17.0765	0.0000	4.3326	Ip (CCC)
68	A	1049.26	0.0000	661.2481	1.3802	ip (CHs) + ip (CCC)
69	B	1049.38	5.8000	0.0000	1.3780	Ip (CCC)
70	A	1107.31	0.0000	10612.1266	1.5274	ip (CH) + ip (CCC) + sym str C–N
71	B	1115.72	23.0272	0.0000	1.4555	ip (CHs)
72	A	1128.81	0.0000	1479.4138	1.3370	ip (CHs)
73	B	1130.87	8.1503	0.0000	1.2852	sci (CHs)
74	B	1156.71	0.0000	9.7794	0.8964	ip (C9Hs + C9′Hs)
75	A	1156.84	0.0250	0.0007	0.8968	ip (C9Hs + C9′Hs)
76	A	1159.19	0.0000	435.9443	1.0448	sci (CHs) + roc (CHs)
77	B	1165.34	1.7000	0.0000	1.0925	sci (CHs) + roc (CHs)
78	A	1181.07	0.0000	142.5714	0.9725	sci (CHs) + asym sci (FL1, FL2 CHs)
79	B	1181.39	7.2494	0.0000	0.9680	asym sci (CHs FL1, FL2)
80	A	1200.55	0.0000	104.9316	1.6617	ip (CCC) + sci (CHs C9Hs + C9′Hs)
81	B	1202.04	3.5008	0.0000	1.7514	sci (CHs C9Hs + C9′Hs) + ip (CCC)
82	A	1209.63	0.0000	12583.3187	3.1893	ip (CCC) + sci CHs + roc CHs + sym str (C–N)
83	B	1222.40	56.0718	0.0000	1.8815	ip CHs
84	A	1225.19	0.0000	745.0504	1.5251	ip CHs
85	B	1231.20	54.5108	0.0000	1.7872	sci CHs + roc CHs + breathing (FL1, FL2) + asym str C–N
86	A	1264.60	0.0000	12036.5886	2.5479	sci CHs + breathing (FL1, FL2) + sym str C–N
87	B	1289.01	75.3458	0.0000	3.1057	roc (CH) + breathing (A, A′ ring) + asym str (C–N).
88	B	1308.45	1.8658	0.0000	1.8966	roc CHs
89	A	1313.87	0.0000	7.1549	1.8008	roc CHs
90	A	1330.98	0.0000	4202.1486	1.8113	roc CHs
91	B	1332.51	4.3273	0.0000	1.9298	roc CHs
92	B	1356.62	20.1559	0.0000	7.4855	roc CHs
93	A	1360.72	0.0000	1265.4991	7.6120	str Ar (C=C) + ip CC
94	B	1381.32	28.0791	0.0000	4.9607	breathing B, B′ ring, roc CHs + sci CHs
95	A	1383.50	0.0000	6199.7816	5.3489	ip CCC
96	A	1452.84	0.0000	1222.2265	1.4355	sci C9Hs + asym CHs (FL1, FL2)
97	B	1453.11	15.7754	0.0000	1.4073	sci (C9Hs + C9′Hs)
98	A	1463.43	0.0000	328.5309	4.9904	sci CHs + ip CC
99	B	1465.09	23.0809	0.0000	5.0421	sci CHs + str Ar (C=C)
100	A	1484.09	0.0000	11663.8821	3.1207	sci (CHs FL1 wrt CHs FL2) + roc CHs
101	B	1490.76	28.1557	0.0000	3.1617	roc all CHs
102	A	1497.01	0.0000	13011.3686	4.1202	roc CHs + str N=N + sci CHs
103	B	1502.90	4.2781	0.0000	3.7202	str Ar (C=C) + roc CHs
104	A	1513.48	0.0000	521.0812	4.3967	str Ar (C=C) + str N=N + roc CHs
105	B	1520.07	20.6099	0.0000	4.3109	str Ar (C=C) + sci C9Hs + roc CHs
106	A	1529.83	0.0000	28230.3369	7.2216	str Ar (C=C) + str N=N + roc CHs
107	B	1604.96	17.9432	0.0000	10.0612	str Ar (C=C) + roc CHs
108	A	1613.87	0.0000	141.7826	11.2227	str Ar (C=C) + str N=N + roc CHs
109	B	1625.55	3.3940	0.0000	9.5645	str Ar (C=C)
110	A	1625.72	0.0000	210.1051	9.7473	str Ar (C=C)
111	B	1652.38	32.7979	0.0000	10.3799	str Ar (C=C)
112	A	1653.34	0.0000	9012.2045	10.4304	str Ar (C=C) + str (N=N)
113	B	1655.07	77.6056	0.0000	11.0443	str Ar (C=C)
114	A	1658.61	0.0000	7430.5054	11.7092	str Ar (C=C) + str (N=N)
115	B	3033.36	25.8446	0.0001	5.7475	sym str (C9Hs + C9′Hs) + asym str (C9Hs wrt C9′Hs)
116	A	3033.37	0.0000	387.4819	5.7475	sym str (C9Hs + C9′Hs) + sym str (C9Hs wrt C9′Hs)
117	B	3062.81	0.0000	176.3528	6.0918	asym str (C9Hs + C9′Hs) + sym str (C9Hs wrt C9′Hs)
118	A	3062.82	12.3280	0.0004	6.0918	asym str (C9H + C9′H) + asym str (C9Hs wrt C9′Hs)
119	B	3174.85	15.1999	0.0000	6.4524	asym str CHs
120	A	3174.87	0.0000	84.2479	6.4525	(sym + asym) str CHs
121	B	3181.31	13.2558	0.0000	6.4913	asym str (CH)
122	A	3181.32	0.0000	335.5393	6.4913	asym str CHs
123	B	3184.62	17.9921	0.0000	6.5110	asym str CHs
124	A	3184.72	0.0000	126.8227	6.5114	asym str (C4H, C4′H)
125	A	3192.56	0.0000	370.0879	6.5627	sym str (FL1, FL2 CHs)
126	B	3192.56	52.0569	0.0000	6.5627	asym str (FL1, FL2 CHs)
127	B	3194.96	5.4030	0.0000	6.5625	asym str (C1Hs, C1H)
128	A	3195.04	0.0000	138.1649	6.5632	sym str (C1H, C1H)
129	B	3204.19	82.7763	0.0000	6.6368	asym str (CH ring C, CH ring C′)
130	A	3204.26	0.0000	925.6424	6.6370	sym str (CH FL1 + CH FL2)
131	A	3226.84	0.0000	79.2692	6.6985	sym str (C3H, C3′H)
132	B	3226.98	4.7576	0.0000	6.6996	asym str (C3H, C3′H) + sym str (C4H, C4′H) + asym str (C3H, C3′H)

^asym, symmetry.

^bVibrational frequencies in cm^–1.

^cInfrared intensities in km/mol.

^dRaman scattering activities A⁴/AMU.

^ek, force constants in mDyne/A.

^fdefm, deformation; tor, torsion; str, stretching; sym, symmetric; asym, asymmetric; oop, out-of-plane bending; ip, in-plane bending; sci, scissoring; roc. rocking; wrt, with respect to.

Table 12. Calculated IR and Raman Activity Frequencies of cis-AzoFL with B3LYP/6-31+G(d,p) in the Ground State.

mode no.	syma	freqb	IIRc	IRamand	ke	approximate description of modef
1	A	16.10	0.0354	21.1321	0.0010	sci (FL1 wrt FL2) + wag (N=N)
2	B	23.20	0.9214	2.5838	0.0013	twist (FL 1 wrt FL2)
3	A	33.03	0.0118	15.8790	0.0026	twist (FL 1 wrt FL2)
4	B	57.74	1.1551	1.0155	0.0115	defm FL ring + oop (CH)
5	A	81.21	0.0049	5.9617	0.0219	twist FL1 + twist FL2 + wag (N=N)
6	A	114.28	0.3861	56.0888	0.0453	roc FL ring + oop defm + twist (N=N)
7	B	128.35	0.2046	4.2641	0.0424	twist ring + oop (CHs)
8	A	149.78	0.4114	12.4845	0.0496	twist ring + oop (CHs)
9	B	150.11	2.7730	0.1719	0.0652	twist ring + oop (CHs)
10	B	196.72	13.3724	0.6190	0.1326	wag (ring A, C) + wag (N=N) + wag (ring A′, C′)
11	A	204.52	0.1416	1.1113	0.1282	tor ring (A, C) + (A′,C′)
12	A	236.47	0.0025	28.4148	0.1555	sci (A, C) + wag (CNNC) + sci (A′, C′)
13	B	243.51	5.7391	0.9453	0.0752	defm ring + oop (C9H) + oop (CHs)
14	A	247.94	6.4319	26.3393	0.0851	defm ring + oop (CHs)
15	B	285.45	3.3517	10.0966	0.2542	defm ring + defm (CNNC)
16	A	310.85	0.2273	251.3607	0.3552	defm ring + defm (CNNC)
17	B	322.27	13.0652	0.7972	0.3900	twist ring + ip (CNNC)
18	B	366.62	0.6868	0.9933	0.5795	ip (ring + CNNC)
19	A	400.35	1.3971	202.2271	0.4316	wag (ring A, C)+ wag (N=N) + oop (CHs)
20	B	425.73	13.7947	4.7201	0.3012	wag (FL 1 + FL2)
21	A	438.84	1.0108	0.2072	0.3462	wag (A, C) + wag (FL1, FL2)
22	B	440.49	1.2049	0.8478	0.3341	defm ring + rot (C9H)
23	A	441.40	0.4384	6.0995	0.3370	twist ring + ip C9H
24	A	481.22	0.0118	190.0508	0.6275	tor ring + twist (N=N) + defm C9H
25	B	493.78	0.9959	4.4919	0.5385	defm CCC + oop (CNNC)
26	B	507.46	5.8230	0.0114	0.5664	Oop (CCC)
27	A	514.04	1.2477	6.5145	0.6680	twist FL1 + twist FL2 + oop (N=N) + defm C9Hs
28	A	535.70	0.8259	158.0208	0.7761	twist FL1 + twist FL2 + oop (N=N)
29	B	537.59	0.3535	1.7202	1.0500	ring tors + ip (N=N)
30	A	560.82	0.3996	31.3759	1.0440	ring tor + oop (CCC) + ip (CCC)
31	B	570.01	0.3014	2.2451	1.0294	defm (CCC) + ip (CNNC) + ip (C9Hs)
32	B	585.51	1.5405	13.0525	0.7889	twist (FL1 wrt FL2) + defm (CNNC)
33	A	597.31	5.4282	57.6224	1.1750	CCC defm + oop (CNNC)
34	A	634.99	5.3238	285.0074	0.9178	wag (CHs ring A + CHs ring A′) + twist (ring C + C′)
35	B	648.25	7.4542	0.0203	1.6524	defm CCC + defm CNN
36	A	664.35	0.2260	69.2317	1.5363	defm CCC + sci (ring A, A′) + twist (N=N)
37	B	699.46	4.7357	10.6299	1.2211	defm CCC + defm CNN + defm (H–C9–H)
38	A	703.54	0.0008	3.5729	1.7322	defm CCC + wag (CNNC)
39	B	711.51	2.9284	0.2414	1.3482	ip (CNNC) + mixing of ip + oop CHs
40	A	717.21	0.0938	52.0916	0.9457	tor CNNC + twist (CHs ring A, CHs ring C) + twist (CHs ring A′, CHs ring C′)
41	B	740.14	32.3067	4.5337	0.5761	wag (CHs of ring C+ CHs of ring C′) + twist (ring C wrt C′) + twist (C9Hs)
42	A	746.57	33.9975	48.0180	0.5371	wag (CHs of ring C, CHs of ring C′) + twist (C9Hs) + twist (CHs of ring A, ring A′)
43	B	759.94	14.0169	33.7320	1.3485	breathing (FL1 + FL2)
44	A	768.83	0.5835	104.4676	1.9254	defm CCC
45	B	775.17	97.4902	0.6544	0.7040	wag (CHs of A, CHs of C) + wag (CHs of A′, CHs of C′) + twist (FL 1 wrt FL2)
46	A	782.63	12.2314	19.2813	0.8340	wag (FL1 wrt FL2) + ip (C9Hs)
47	B	817.47	19.7106	55.4728	0.9403	twist (CHs of A, CHs of C) + twist (CHs of A′, CHs of C′) + oop (CNN)
48	A	834.03	0.0093	64.5449	1.7862	defm (CCC) + ip C9Hs
49	B	836.07	0.4532	16.7616	1.8038	defm CCC (FL1 + FL2) + ip (HC9H)
50	A	844.32	3.5224	147.8764	0.6390	wag (C3H, C4H) + wag (C3′H, C4′H)
51	B	858.96	37.5160	69.5819	0.8108	twist (C1H, C3H), twist (C1′H, C3′H), wag (C3H, C4H) + wag (C3′H, C4′H) + defm (CNN)
52	A	876.08	0.0805	1.1247	0.6205	oop (CH of ring C + CH of ring C′)
53	B	876.82	2.0257	4.6846	0.6344	oop (CH of ring C) + oop (CH of ring C′)
54	A	896.50	3.9054	44.8419	0.7112	wag (C1H wrt C1′H)
55	B	905.64	28.6929	11.4053	0.8903	twist (C1H, C1′H), defm (CNNC)
56	A	915.04	0.2439	159.0103	1.9629	defm CCC + sci (C1H, C9H) + sci (C1′H, C9′H) + wag (N=N)
57	B	935.55	1.2191	60.3666	1.9948	ip (C9H + C9′H) + ip (CCC + CCN + CNN)
58	A	943.50	0.4601	0.6865	0.7927	twist (CHs FL1 + CHs FL2)
59	B	944.14	3.5314	0.1416	0.7962	twist (CHs FL1) + twist (CHs FL2)
60	B	963.21	10.4801	2.5244	0.7617	twist (C3H, C4H) + twist (C3′H,C4′H)
61	A	963.32	0.2611	12.4265	0.7626	twist (C3H, C4H) + twist (C3′H, C4′H)
62	B	974.85	3.0234	1.2928	1.0137	twist (CHs FL1 + CHs FL2)
63	A	974.89	2.5418	8.6102	1.0040	twist (CHs FL1 + twist CHs)
64	B	991.63	0.1159	0.3457	0.7476	twist (CHs ring C + CHs ring C′)
65	A	991.65	0.0290	1.2768	0.7476	twist (CHs ring A) + twist (CHs ring A′)
66	A	1020.15	0.8340	28.3434	4.2962	ip (CCC) + ip (CC)
67	B	1020.18	8.3474	0.2482	4.3072	ip (CCC) + ip (CC) ip CH)
68	A	1049.36	5.1414	207.8673	1.3839	ip (CHs) + ip (CCCC)
69	B	1049.46	2.5014	26.8516	1.3826	ip (CCCC) + CHs ip
70	A	1103.13	0.0056	1454.4185	1.4552	sci (C1H, C3H) + sci (C1′H, C3′H) + ip (CCC)
71	B	1113.52	4.1562	176.5421	1.5513	sci (C1H, C3H) + sci (C1′H, C3′H)
72	A	1126.01	0.9559	45.0660	1.3721	ip (CHs FL1 + CHs FL2)
73	B	1128.52	2.6721	22.3835	1.3585	ip (CHs)
74	B	1155.73	4.1544	0.8568	1.1050	ip (C9Hs + C9′Hs)
75	A	1156.95	0.2232	7.4892	0.9379	ip (C9Hs + C9′Hs) + sci (C3H, C4H) + sci (C3′H, C4′H)
76	B	1158.02	0.8281	1.5203	0.9553	sci (CHs) + roc (CHs)
77	A	1159.84	0.7999	2.2940	1.1079	sci (C3H, C4H) + sci (C3H, C4H) + rot (C9Hs, C9′Hs)
78	A	1180.51	0.1856	60.0919	0.9888	sci (CHs ring C + C′+ C9H+ C9′H)
79	B	1180.70	1.1577	9.0697	0.9804	ip (CHs ring C + C′)
80	A	1197.11	0.9682	166.3222	1.5546	ip (CHs ring C + C′) + ip (C9Hs + C9′Hs)
81	B	1198.66	10.8312	0.0735	1.6174	ip (CHs ring C + C′) + ip (C9Hs + C9′Hs)
82	A	1209.59	2.2357	1118.7989	2.4233	defm (CCC) + ip CHs + sym str CN
83	B	1215.31	8.1421	185.1219	2.3385	ip CCC + ip CHs + asym str CN
84	B	1224.42	8.8441	11.8070	1.5404	ip CHs
85	A	1224.43	1.3426	35.1919	1.5615	ip CHs
86	A	1260.81	0.5616	1171.3536	2.3165	ip CHs + breathing (FL1, FL2) + sym str CN
87	B	1261.34	6.3533	368.2336	2.4705	ip (CHs) + breathing (FL1, FL2 ring) + asym str CN
88	B	1311.72	8.2546	94.3526	1.8547	ip CHs
89	A	1313.53	0.0144	270.3249	1.7991	ip CHs
90	B	1330.04	1.1844	153.2975	1.7712	roc (CHs ring C + C′) + ip (CHs + CCC)
91	A	1330.52	0.0032	536.8398	1.7683	ip CHs
92	B	1345.36	33.9201	100.7305	6.3844	str Ar (C=C)
93	A	1351.73	5.0802	163.4050	7.3540	str Ar (C=C) + ip (C9H + C9′H)
94	B	1378.91	4.1174	94.8485	4.7393	str Ar (C=C), (breathing B, B′) + ip CHs
95	A	1380.86	1.1511	530.3869	4.8915	str Ar (C=C), (breathing B, B′) + ip CHs
96	B	1452.45	9.4167	12.3591	1.5043	sci (C9Hs + C9′Hs)
97	A	1452.55	0.9079	42.8585	1.5021	sci (C9Hs + C9′Hs)
98	B	1459.31	12.2895	23.2562	3.9503	sci CHs + ip CC
99	A	1459.79	10.1687	345.8181	3.7889	sci CHs + str C=C
100	A	1486.39	3.2886	101.6084	3.0486	sci (CHs FL1 wrt CHs FL2) +roc CHs
101	B	1487.37	31.3337	2.0133	3.0645	roc all CHs
102	B	1501.64	7.8461	125.2425	3.5549	roc CHs + sci CHs
103	A	1502.81	6.7233	490.6604	3.6339	str Ar (C=C) + roc CHs
104	A	1514.83	0.9425	170.6483	4.0351	str Ar (C=C) + roc CHs
105	B	1515.05	5.6894	283.2436	4.0391	str Ar (C=C) + sci C9Hs + roc CHs
106	A	1581.21	77.5397	6875.2755	4.6318	str Ar (C=C) + str N=N + roc CHs
107	B	1601.91	0.4325	130.5009	9.6223	str Ar (C=C) + roc CHs
108	A	1614.82	9.2285	598.8006	10.9474	str Ar (C=C) + str N=N + roc CHs
109	B	1625.92	2.1664	26.2751	9.5054	str Ar (C=C)
110	A	1626.08	0.3527	79.5832	9.6688	str Ar (C=C)
111	B	1651.10	1.4909	2076.4003	10.6608	str Ar (C=C)
112	A	1653.75	1.6761	2460.3547	10.5096	str Ar (C=C), str N=N, ip CH, defm CCC
113	B	1654.53	8.4589	98.6487	10.7875	Ar (C=C), ip CH, defm CCC
114	A	1657.49	0.6588	981.3998	11.8993	str Ar (C=C), str N=N, ip CH, defm CCC
115	B	3033.87	21.7959	64.7313	5.7495	sym str (C9Hs, + C9′H) + asym str (C9H wrt C9′Hs)
116	A	3033.89	7.3265	388.4236	5.7496	sym str (C9Hs, + C9′H) + sym (C9Hs wrt C9′H)
117	A	3063.31	3.2802	136.3858	6.0937	asym str (C9Hs, + C9′Hs) + asym str (C9Hs wrt C9′Hs)
118	B	3063.31	7.8622	56.9552	6.0937	asym str (C9Hs, + C9′Hs) + sym str (C9Hs wrt C9′Hs)
119	B	3174.81	14.7400	40.7724	6.4521	str CHs ring C + str CHs ring C′
120	A	3174.83	0.2286	51.5632	6.4522	str CHs ring C + str CHs ring C′
121	B	3181.12	2.5596	68.7996	6.4898	str CHs ring C + str CHs ring C′
122	A	3181.12	4.9886	184.4987	6.4898	str CHs ring (C + C′)
123	B	3186.67	6.7277	12.6357	6.5170	asym str (C4H, C4′H)
124	A	3186.82	4.5728	22.0377	6.5177	str (CHs)
125	B	3190.95	5.9328	78.6016	6.5459	asym str (C1H, C1′H)
126	A	3190.97	6.0211	138.6614	6.5461	sym str (C1H, C1′H)
127	B	3192.37	42.6610	108.7342	6.5613	asym str (CHs ring C, C′)
128	A	3192.40	2.5487	184.9013	6.5612	asym str (CH ring C + CH ring C′)
129	B	3204.14	32.2569	178.3448	6.6365	sym str (CHs ring C + CHs ring C′) + asym str (CHs ring C, CHs ring C′)
130	A	3204.20	30.1293	552.0913	6.6367	sym str (CH ring C + CH ring C′)
131	A	3215.99	0.0045	116.4154	6.6591	sym str (C3H, C4H) + sym (C3′H, C4′H) + sym str (C3H, wrt C3′H)
132	B	3216.10	8.9671	1.6723	6.6601	sym str (C3H, C4H), sym str (C3′H, C4′H) + asym str (C3H, wrt C3′H)

^asym, symmetry.

^bVibrational frequencies in cm^–1.

^cInfrared intensities in km/mol.

^dRaman scattering activities in A⁴/AMU.

^ek, force constants in mDyne/A.

^fdefm, deformation; tor, torsion; str, stretching; sym, symmetric; asym, asymmetric; oop, out-of-plane bending; ip, in-plane bending; sci, scissoring; roc, rocking; wag, waging; wrt, with respect to.

The model compound AzoFL has 46 atoms; hence, there are 138 motions, 3 of which are translational, 3 of which are rotational, and 132 (τ_3N-6′) of which are vibrational modes. The azo compound AzoFL belongs to C₂ point group symmetry. Sixty-six vibrational modes are IR active and 66 modes are IR inactive. All of the IR inactive modes are found as Raman active modes.

The theoretically predicted IR and Raman scattering activity spectra by using B3LYP/6-31+G(d,p) basis set at DFT level of theory for both the trans- and cis-AzoFL with the FL are shown in Figures 16 and 17 by using B3LYP/6-31+G(d,p) basis set at DFT level of theory.

Figure 16.

Calculated (a) IR (b) Raman spectra of trans-AzoFL (c) IR (d) Raman spectra of cis-AzoFL at B3LYP/6-31+G (d,p). The calculated harmonic frequencies are represented with a Gaussian IR peak half-width at half height 4 cm^–1.

Figure 17.

Calculated (a) IR and (b) Raman scattering activity spectra of FL at DFT-B3LYP/6-31+G(d,p). The calculated harmonic frequencies are represented with a Gaussian IR peak half-width at half height 4 cm^–1.

2.4.3. N=N Vibration

The stretching vibrations of azo N=N unit is usually observed^11,73 around at 1556–1420 cm^–1. The nature of the compound is very important in analyzing spectra of azo compounds. The stretching vibration of N=N is found to vary for the different-nitrogen containing compounds. The N=N stretching vibration of a symmetrical trans-azo compound is forbidden in the IR due to no change in the dipole moment. Thus, the identification of this vibration and to distinguish between the cis- and trans-isomers is somewhat problematic due to its weakness or absence in the IR. Hence, the IR spectrum alone is not straightforward to analyze for such type of compounds. The trans-DZ at 1659 cm^–1 for N=N stretching vibration shows zero intensity in IR but is Raman scattering active. However, the cis-azo (N=N) compounds due to nonzero dipole moment is expected to show active IR bands. The calculated N=N stretching vibrations at 1658.61, 1653.34, 1613.87, 1529.83, 1513.48, and 1497.01 cm^–1 is found with zero intensity for the trans-AzoFL in the present work but are Raman scattering active. Conjugation with FL ring lowers the frequency of the N=N double bond in AzoFL. At the present study, the same N=N stretching vibration was found at 1657.49, 1653.75, 1614.82, and 1581.21 cm^–1, respectively, for the cis-AzoFL. The parent cis-DZ due to its isolated and stronger N=N double bond character shows IR band at higher frequency at 1662 cm^–1, which reflects the 0.01 Å shorter bond length of cis-DZ compared to cis-AzoFL. Minisini et al.⁸⁴ found N=N stretching vibration at 1591 and 1544 cm^–1 for cis-4-hydoxyazobenzene and trans-4-hydoxyazobenzene, respectively, by DFT calculation.

The N=N stretching frequency of cis-DFDZ at 1643.26 cm^–1 shifted at 1628.78 cm^–1 in trans-DFDZ, a 14.48 cm^–1 shift to lower frequency is observed by Raman activity spectrum. The N=N stretching frequency of cis-DZ at 1662.43 cm^–1 shifted at 1659.03 cm^–1 in trans-DZ, a 3.40 cm^–1 shift to lower frequency is observed by Raman activity spectrum. It should be noted that though the cis-DZ has higher N=N stretching vibration (1662.43 cm^–1) compared to that of cis-DFDZ (1643.26 cm^–1), the force constant is considerably lower (16.96 vs 22.28 mDyne/Å) in cis-DZ (Tables 9 and 10). Similarly, even though the trans-DZ has higher N=N stretching frequency (1659.03 cm^–1) compared to that of cis-and trans-DFDZ, its force constant was found as lower value (9.86 mDyne/Å) by our B3LYP/6-31+G(d,p) calculation (Tables 9 and 10). Normally, bonds with stronger force constants have higher vibrational frequencies; however, in this case, we have observed the anomalies.

The in-plane vibration of N=N was observed at 322.27, 366.62, and 537.59 cm^–1 as rocking mode with weak intensity band in cis-AzoFL. The CNNC angle deformation was found at 905.64 cm^–1 as moderate weak band. The out-of-plane vibration of N=N appeared at low frequency at 16.10, 196.72, and 915.04 cm^–1 as wagging vibration mode, whereas the 114.28, 481.22, 535.70, and 664.35 cm^–1 bands appeared as twisting mode in cis-AzoFL.

The in-plane vibration of N=N appeared at 571.35 and 660.49 with moderate strong band but zero intensity in Raman activity scattering spectrum for trans-AzoFL.

2.4.4. C–N Vibration

The C–N stretching bands generally appear around at 1000–1300 cm^–1.^65,85 The identification of this vibration is somewhat difficult due to the mixing of vibrations in this region. In trans-AzoFL, the asymmetric C–N vibrations were found at 1231.20 and 1289.01 cm^–1 as strong band in IR which is Raman inactive, whereas the symmetric stretching of C–N at 1264.60 cm^–1 with zero intensity is Raman scattering active.

Our calculated C–N vibration mode in cis-AzoFL appeared at 1209.59, 1215.31, 1260.81, and 1261.34 cm^–1 as mixing mode with in-plane CH vibration and CCC deformation. All of the modes are IR and Raman active. The in-plane and out-of-plane bending vibrations assigned for AzoFL are also presented in Tables 11 and 12.

2.4.5. Aromatic C=C Vibrations

Ar_(C=C) stretching vibrations usually found at 1625–1430 cm^–1.^65,85 For the model trans-AzoFL, the calculated Ar_(C=C) stretching vibration appears at 1502.90, 1513.48, 1520.07, 1604.96, 1613.87, and 1529.83 cm^–1 together with other modes. The vibrations at 1652.38 and 1655.07 cm^–1 appear as a strong peak for Ar_(C=C) stretching vibration. The stretching vibration at 1625.72, 1653.34, and 1658.61 cm^–1 for Ar_(C=C) appears as zero intensity in IR spectra but as strong peak in Raman activity spectrum. The in-plane vibration of Ar_(C=C) was observed at 513.35 and 547.75 cm^–1 with zero intensity in IR spectrum.

For the model cis-AzoFL, the calculated Ar_(C=C) stretching vibration appears at 1502.81, 1514.83, 1515.05, 1601.91, and 1614.82, cm^–1 together with the other mode. The vibrations at 1625.92 and 1626.08 and 1651.10 cm^–1 appear as a strong peak for only Ar_(C=C) stretching vibration.

For the parent fluorene (FL), the calculated Ar_(C=C) stretching vibration appears at 1623.76, 1628.97, 16.54.80, and 1654.87 cm^–1. The calculated IR spectra of FL at B3LYP/6-31+G(d,p) are shown in Figure 17. The frequencies of different bonds, their IR intensities, Raman scattering activities, and force constants are listed in Table S4.

2.4.6. C–H Vibrations

The aromatic C–H stretching typically exhibits^65,85 several weak-to-moderate bands above 3000 cm^–1. In trans-AzoFL, the four C–H bonds from C₉Hs and C_9′Hs are stretches at 3033.36, 3033.37, 3062.81, and 3062.82 cm^–1 as moderate strong band. The two C–H bonds at C₉ position stretches both symmetrically and asymmetrically among themselves and with respect to other fluorene ring C_9′Hs as well. Among the two symmetric modes for the two C–H bonds at C₉ position, one is asymmetric at 3033.36 cm^–1 with respect to other ring found as IR active. However, the other one at 3033.37 cm^–1 that is symmetric with respect to other ring is found as IR inactive but Raman active. The same trend is observed for the asymmetric stretching vibration of the two C₉–H bonds. The stretching vibration of rest aromatic 14 C–H bonds from two fluorenyl ring appeared together at 3174.85, 3174.87, 3181.31, 3181.32, 3184.62, 3184.72, 3192.56, 3194.96, 3195.04, 3204.19, 3204.26, 3226.84, and 3226.98 cm^–1. Among those seven modes are IR inactive but Raman active, while seven IR active modes are Raman inactive. A similar spectral pattern was observed for the aromatic C–H absorption band region. The entire vibration modes in this region are found as both IR and Raman active with low intensity. The two C–H bonds in C₉ of fluorene appears at 3032.08 and 3060.75 cm^–1 as doublet, one symmetric and the other for asymmetric stretching, respectively. The calculated harmonic frequencies for the AzoFL molecule are related to the gaseous phase, but the reported values from experimental works are done in the solid phase. Hence, a slight disagreement between the present calculated and reported experimental frequencies can be expected. Aromatic C–H in-plane bending vibrations usually occur in the region of 1390–990 cm^–1 and are very useful for characterization and identification of aromatic compounds, whereas C–H out-of-plane deformations generally appears at 1000–700 cm^–1.^65,85 Both the in-plane and out-of-plane bending vibrations within the fluorene ring and between the two fluorene ring in different pattern for 18 C–H groups as scissoring, rocking, twisting, and wagging mode were observed. The out–of plane wagging vibration for aromatic ring C–H appeared at 754.23 cm^–1 as a strong band together with fluorene ring breathing at 754.67 cm^–1 in parent FL. The same wagging mode in trans-AzoFL shifted to 747.35 and at 775.17 cm^–1 in cis-AzoFL as strong band. Though the C–H bonds in both the FL ring of cis-AzoFL vibrate in wagging mode, they twist as a net result with respect to one another ring.

In cis-AzoFL, the four C–H bonds from C₉Hs and C_9′Hs are stretches at 3033.87, 3033.89, 3063.31, and 3063.31 cm^–1 as moderate strong band. The stretching vibration of rest aromatic 14 C–H bonds from two fluorenyl ring appeared together at 3174.81, 3174.83, 3181.12, 3181.12, 3186.67, 3186.82, 3190.95, 3190.97, 3192.37, 3192.40, 3204.14, 3204.20, 3215.99, and 3216.10 cm^–1. The C–H bonds at different positions stretch both symmetrically and asymmetrically among themselves within the ring and with respect to other fluorene ring as well. Unlike the trans-AzoFl, the vibrational frequencies of C–H bonds of cis-AzoFl are found as both the IR and Raman scattering active. All of the vibrational modes of cis-AzoFL for the different C–H bonds, their IR intensities, Raman scattering activities, and force constants are listed in Table 12. All of the frequencies were found to be well matched within the characteristics region and the details are presented in Tables 11 and 12 for both the isomers.

In FL, the two C–H bonds from C₉Hs stretch symmetrically and asymmetrically at 3032.08 and 3060.75 cm^–1 as moderate strong band, respectively. The stretching vibrations from other C–H bonds are observed at 3173.37, 3173.71, 3179.55, 3181.13, 3190.85, 3192.06, 3203.15, and 3203.80 cm^–1, respectively.

2.4.7. Ring Vibration

The fluorenyl ring breathing vibration at 759.94 cm^–1 in cis-AzoFL matches nicely with the literature value.⁸⁶ The breathing mode at 758.63 cm^–1 in trans-AzoFL is IR inactive but Raman scattering active mode. The breathing mode in parent fluorene ring appears at 754.67 cm^–1 (Figure 17) as a very weak peak in our present work.

Overall, the present computations show that both the trans- and cis-isomers possess different vibrational frequencies for the same structural −N=N– unit; hence, both the isomers were characterized and distinguished. The isolated N=N stretching vibration of trans-diazene appears at 1659.03 cm^–1 in Raman scattering spectra whereas the same vibration mode appears at 1662.43 cm^–1 for cis-diazene in both the IR and Raman scattering spectra. The N=N group in both the trans and cis-DFDZ vibrates at ∼30 and ∼19 cm^–1 lower frequency at 1628.71 and 1643.27 cm^–1, respectively, compared to that of respective DZ. We can safely conclude that the isolated N=N stretching vibration in the presence of substituents shifts toward the shorter wavelength in symmetrically disubstituted azo compounds. For cis-diazene, both the asymmetric and symmetric stretching vibration bands at 3088.26 and 3185.08 cm^–1 were observed for the two N–H groups in IR and Raman scattering spectra, whereas for trans-isomer only one, the asymmetric stretching vibration band at 3313 cm^–1 was found as IR active and the other one, symmetric vibration at 3280 cm^–1 was Raman scattering active. The same trend was observed for difluorodiazene, for example, two absorption bands of the two N–F groups, asymmetric and symmetric absorption bands at 740.60 and 910.57 cm^–1, were observed both in the IR and Raman scattering spectra for cis-DFDZ. The asymmetric stretching vibration band of N–F bonds at 996.45 cm^–1 was found as IR active and on the other hand, symmetric vibration at 1034.89 cm^–1 was found as Raman scattering active for trans-DFDZ. Similar patterns were observed for the model compound trans- and cis-AzoFL. Among different bands of stretching vibration, the two asymmetric stretching vibrations at 1289.01 and 1231.20 cm^–1 for C–N bond are IR active, whereas the band is found as inactive mode in Raman scattering spectra. The IR inactive mode of symmetric stretching vibration at 1264 and 1209.63 cm^–1 for the same C–N bond are found as Raman active mode.

3. Conclusions

In order to gain insight into the azo −N=N– backbone, studies on the molecular geometry, vibrational frequencies, infrared intensities, force constants, and Raman scattering activities were carried out at the DFT with B3LYP functional using 6-31+G(d,p) basis set for trans- and cis-bis(9H-fluoren-2-yl)diazene (AzoFL). The work has been extended with the π-conjugation spacer fluorene, the parent trans-/cis-diazene and difluorodiazene by the same method (DFT) and same basis set 6-31+G(d,p). The influences of substituents on the azo −N=N– backbone of parent trans- and cis-diazene by using (i) electron rich π-bonded aromatic fluorene rings and (ii) electron-rich lone pairs of F atoms having electron withdrawing nature, for example, in model AzoFL and difluorodiazene were observed. Introducing fluorene ring into the −N=N– backbone causes an increase of the N=N bond length due to the extensive π-bond conjugation in AzoFL. The longer bond length reflects on the stretching vibration of AzoFl. Both the trans- and cis-AzoFL vibrates at a much lower frequency compared to that of parent trans- and cis-diazene. A reverse trend (shorter −N=N– bond length) is observed by introducing F atoms into the −N=N– backbone. Though it is expected that compounds having shorter bond length should vibrate at higher frequency but unexpectedly both the trans- and cis-difluorodiazene vibrates at lower frequency compared to that of parent diazene. It should be noted that though the trans-AzoFL is stable by 16.33 kcal/mol than the cis-AzoFL, the trans-DFDZ is less stable than its cis-counterpart.

To study the electronic properties, viz. UV–vis spectra, excitation energies and the maximum absorption wavelength, oscillator strength, energies of HOMO, LUMO, and energy difference between them, E_g (HOMO–LUMO), electronic transitions, and transition probabilities for the model trans- and cis-AzoFL by TD-DFT calculation using B3LYP/6-31+G(d,p) starting from the initial optimized geometry by DFT-B3LYP/6-31+G(d,p) in gas phase were performed. Both the UV–vis spectral and vibrational analyses show a substantial influence on the −N=N– backbone and a significant variation were observed. Critical comparisons were carried out with the above-mentioned compounds using TD-DFT and ZIndo method.

Compared to parent trans-diazene (λ_max 178.97 nm), a significant variation to longer wavelength (∼245 nm) is observed due to incorporation of the fluorene (FL) ring into the −N=N– backbone. The co-planarity of the two FL ring with the longer N=N bond length compared to the unsubstituted parent diazene indicates the effective red shift due to the extended π-conjugation in trans-AzoFL. The nonplanarity of cis-AzoFL (48.1° tilted about the C–N bond relative to the planar N=N–C bond) reflects its ∼64 nm blue shift compared to that of trans-counterpart. However, two F atoms into the backbone of −N=N– causes only ∼10 nm red shift in trans-DFDZ but ∼15 nm opposite blue shift in cis-DFDZ respectively for π–π* transition band compared to that of trans- and cis-diazene.

The same trend is observed for n−π* transition as well, that is, the n−π* band shifts to longer wavelength (λ_max 517.82 nm) in cis-AzoFL, on the other hand the same band shifts to shorter wavelength (λ_max ≈ 190 nm) in cis-DFDZ compared to that of parent cis-diazene (λ_max 371.78 nm). Present calculation shows that the ZIndo method is reasonably good to explain the absorption behavior of the cis-/trans-isomers of studied azo compounds.

These findings can provide the basic understanding on the electronic properties of geometric cis–trans azo isomers. The opposite absorption behavior between AzoFL and DFDZ clearly imply that the aromatic fluorene (FL) ring and fluorine atoms (F) as substituents on the azo −N=N– backbone play a vital role among the different pair of cis–trans azo compounds under study. Because all of the calculations were performed in the same platform, it allowed us to compare and investigate the behaviors of the azo compounds more accurately. Isac and co-workers⁸⁷ observed charge-transfer transitions in azobenzene when substituted with maleimide functional group. Compared to azobenzene, our model azofluorene compounds have extended π-conjugation framework and thus might have the possibility to play a potential role in such type of charge transfer transitions. We believe that the findings of the present work are of substantial interest in the field of optoelectronic properties of π-conjugated azo polymers.

4. Computational Methods

The ground-state geometries of six azo compounds, viz., trans- and cis-isomers of diazene (DZ), difluorodiazene (DFDZ), our model compound bis(9H-fluoren-2-yl)diazene (AzoFL) respectively, and the π-conjugation spacer, fluorene (FL) were calculated at the DFT level of theory. The B3LYP hybrid functional^88,89 using 6-31+G(d,p) basis set was employed to perform the calculations in gas phase for all of the above-mentioned compounds in neutral state. The geometries for all of the DFT calculations were initially optimized at the semi-empirical AM1⁹⁰ level. The resulting geometry is then employed as starting geometry for optimization at the DFT/B3LYP level of theory for better description. Geometry optimization by ab initio Hartree–Fock calculations were also performed using HF/6-31+G(d,p), HF/6-31++G(d,p), and HF/6-311+G(d,p) basis set for DZ and DFDZ. Bernys optimization algorithm⁹¹ was used to run the complete geometry optimization for both the trans- and cis-AzoFL and all other above-mentioned compounds. The optimized structural parameters of DFT calculations and all other calculations at the same level of theory and basis set were used in the vibrational frequency calculations. Vibrational frequency calculations were performed with high degree of accuracy, and no imaginary frequencies were found. Hence, true minimum on the potential energy surface were obtained in each case. The unscaled calculated harmonic frequencies, force constants, infrared intensities, and Raman scattering activities were obtained from the output result of the frequency calculations.

The GaussView program⁹² which is a graphical user interface designed to be used with Gaussian,⁹³ has been used to predict the vibrational modes, intensities, and spectra by visual animation for the verification of the normal mode assignments. The defined coordinates form a complete set and match quite well with the motions observed using the gauss view 6.0.16 program. Density functional time-dependent, TD/DFT⁹⁴⁻⁹⁷ excited-state calculations with the B3LYP/6-31+G(d,p) basis set based on the optimized geometries of B3LYP/6-31+G(d,p) were carried out on the three lowest spin allowed singlet–singlet transitions for the model compound AzoFL, other mentioned azo compounds and FL in the gas phase to get the excitation energies, UV–vis absorption maximum wavelengths (λ_max), oscillator strength (f) and UV–vis absorption spectra, HOMO, LUMO energies, and the FMO orbitals. Based on the optimized geometry from AM1, ZIndo⁹⁸⁻¹⁰⁰ calculations were performed in similar fashion. All of the calculations mentioned above were performed by Gaussian 16⁹³ and Gauss View 6.0.16⁹² program package by intel core i3-6006U CPU@2.00 GHz, 1.99 GHz on note book computer by windows version 10.

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acsomega.9b03839.

• Additional material with computational results which includes (Figures and Tables) ZIndo calculation, TD-DFT//B3LYP/6-31+G(d,p) calculation with different initial geometry HF/6-31+G(d,p) methods, excitation energies, electronic transitions, transition probabilities, and different modes of vibrational frequencies of different compounds (PDF)

Author Contributions

The manuscript was written through contributions of both authors. Both the authors have given approval to the final version of the manuscript.

The present work is carried out by personal expenses of the authors.

The authors declare no competing financial interest.