Abstract
Accurate prediction of the absolute or relative protein–ligand binding affinity is one of the major tasks in computer-aided drug design projects, especially in the stage of lead optimization. In principle, the alchemical free energy (AFE) methods such as thermodynamic integration (TI) or free-energy perturbation (FEP) can fulfill this task, but in practice, a lot of hurdles prevent them from being routinely applied in daily drug design projects, such as the demanding computing resources, slow computing processes, unavailable or inaccurate force field parameters, and difficult and unfriendly setting up and post-analysis procedures. In this study, we have exploited practical protocols of applying the CPU (central processing unit)-TI and newly developed GPU (graphic processing unit)-TI modules and other tools in the AMBER software package, combined with ff14SB/GAFF1.8 force fields, to conduct efficient and accurate AFE calculations on protein–ligand binding free energies. We have tested 134 protein–ligand complexes in total for four target proteins (BACE, CDK2, MCL1, and PTP1B) and obtained overall comparable performance with the commercial Schrodinger FEP+ program (Wanget al. J. Am. Chem. Soc. 2015, 137, 2695−2703). The achieved accuracy fits within the requirements for computations to generate effective guidance for experimental work in drug lead optimization, and the needed wall time is short enough for practical application. Our verified protocol provides a practical solution for routine AFE calculations in real drug design projects.
1. Introduction
On average, the cost of bringing a medicine from research and development (R&D) to the market has been estimated to be $2.6 billion according to a survey study published in 2016,1 and the process takes at least 10 years. In order to improve the efficiency of drug design and development and reduce the time and cost arising from expensive and tedious experiments in the trial-and-error procedures, tremendous amounts of efforts have been poured into computational methods, especially in the early stages (from hit to lead) of drug development, with the hope of shortening and saving iterative steps of synthesis and tests of large number of compounds to search for better compound potency and biopharmaceutical properties.2−9 Since a drug molecule needs to bind, usually the stronger the better, to its target receptor (usually a protein), the measurement of the magnitude of the protein–ligand binding interaction is underpinning all drug design projects, and correspondingly, the quantitative estimation of the protein–ligand binding affinities becomes a primary task of computer-aided drug design (CADD) projects. Various methods have been developed during the past three decades, which were claimed practically promising. They have led to different levels of successes and disappointments at the same time and brought hopes and frustrations to the drug discovery community. For instance, the docking and scoring methods have been proven to be suitable for high-throughput screening of potentially bioactive ligands from reservoirs of huge amount of candidate compounds3,10 and achieve generally reliable predictions of most likely ligand binding modes (i.e., conformation and orientation) at the binding sites of receptor proteins;8,11 however, they are poor at correctly ranking the docked compounds according to their predicted binding affinities.11−13 This is due to their inherent limitations, for example, not considering the flexibility of the receptor in the calculation. Physics-based endpoint approximation methods, such as LIE (linear interaction energy) and MM-PBSA (molecular mechanics Poisson–Boltzmann surface area), adopt the molecular dynamics (MD) or Monte Carlo simulations to sample the conformational space of both protein and ligands in aqueous solutions and use energy functional terms to estimate the binding free energy.7,14−20 Their accuracies are usually higher than empirical scoring methods, and the correlation between estimated and experimentally obtained binding free energies vary from system to system. Overall, their performance is effective enough to further narrow down the screened pool of compounds but not accurate enough for reliably guiding lead optimization in silico, in which a series of congeneric compounds with minor substitution difference need to be properly ranked by their binding affinities. Although moderate accuracy like with a root-mean-square error (RMSE) of ∼2 kcal/mol can produce efficiency gains in wet-lab screening,21 a stricter criterion, about 5-fold binding affinity that corresponds to ∼1 kcal/mol, is preferred to efficiently search for an ideal candidate ligand in the lead optimization stage22 because the range of experimental values of small modification compounds are usually spanning only 3–4 kcal/mol or less.
Alchemical free energy (AFE) calculations, such as free-energy perturbation (FEP), thermodynamic integration (TI) methods, λ dynamics, and so on,21−26 which are theoretically rigorous and are in principle more accurate than the endpoint methods (such as MM-PBSA), can meet the above requirement. AFE-based methods incorporate the statistical mechanical effects (such as contributions from entropy change and discrete nature of solvent) and chemical effects (such as protonation states and tautomer distributions), which are often neglected or roughly approximated in aforementioned docking methods or endpoint approximation methods. However, several factors hurdled the routine usage of AFE calculations in real CADD projects: (1) the enormous demand of computing resources and time needed for adequate sampling of simulation and convergence of calculation, (2) often unavailable or inaccurate force field parameters for possibly encountered ligand compounds in the huge chemical space, and (3) tedious and troublesome procedures of system setting up, simulation running, and data analyzing. In 2015, researchers from Schrodinger Inc. reported that their newly developed AFE module (called FEP+) combined with their newly developed OPLS2 force field, could obtain an RMSE of 0.93–1.41 kcal/mol after a large-scale validation of 8 proteins and 200 ligands in total.22 Nowadays, Schrodinger’s FEP+ program has become the de facto standard in the pharmaceutical industry. Whilst such an excellent commercial program is available for users, it is also of great importance and need to have an academic program and force field as an alternative solution that can achieve similar performance and convenience.
In this study, we report our exploitation of practical and reliable protocols with the popular academic AMBER program and AMBER force fields. Some of us have been working on the implementation of fast TI calculation with the affordable graphic processing units (GPU) in AMBER program.27,28 Some of us have been working on the development, expansion, and improvement of the general AMBER force fields (GAFF) and related tools29−31 for arbitrary organic compounds, which may be encountered in drug discovery projects. Together, we here report feasible solutions for routine usage of fast and accurate TI calculations of relative protein–ligand binding free energies. Our goal is to get the simulation and calculation work done as quickly as possible (e.g., simplifying the procedures and reducing the wall time) and get an accuracy under a threshold of ∼1 kcal/mol for the mean of unsigned error (MUE) and RMSE. The accomplishment of such a goal could pave the road for AFE methods to be routinely used in practice in real drug discovery R&D. We have explored various computational protocols that determine the accuracy and efficiency of AFE calculations, including the setting up of systems, the schedules of λ windows and integration, and the impact of simulation time and number of repeated individual runs, using four different protein systems32−35 that have 134 ligands in total. These four protein data sets were reported as more difficult, leading to higher MUE and RMSE among the eight retrospective data sets calculated by Schrodinger’s FEP+.22 The structures of investigated ligands span a diverse range of chemical space of pharmaceutically relevant compounds. In this study, the performance of the central processing unit (CPU) version of TI (CPU-TI) and GPU version of TI (GPU-TI) in AMBER was also evaluated. We hope that the established computational protocols not only enable us to achieve the aforementioned 1 kcal/mol threshold but also provide us overall guidance on conducting AFE-guided lead optimization for other drug design projects.
2. Methods
2.1. Data Set Preparation
The same crystallographic structures for each of four protein receptors (BACE, CDK2, MCL1, and PTP1B) as taken by the Schrodinger FEP+ study22 were adopted in this study. The experimental data of binding affinity and corresponding structures of ligands were taken from the same references32−35 used in the Schrodinger FEP+ study (ref (22)). For each protein system, we compared the ligands reported in ref (22) and the ligands in the original experimental study, identified which tables in the experimental reference contain the ligands covered by the Schrodinger FEP+ study, and then included all of the ligands with specific Ki or IC50 values in these tables in our study. As a consequence, our study not only included all the ligands reported in ref (22) but also included more ligands (Table 2 in the Results section and Figures S2 and S4–S6 in the Supporting Information), which were omitted by ref (22). The perturbation pathways of the four protein systems are shown in the Supporting Information. They were designed according to the following strategies: (1) set perturbations from the same ligand A to as many ligand Bs as possible and (2) set a pathway to every ligand from the common reference ligand as short as possible, except for the BACE system in which we exploited the effects of different paths to some query ligands.
Table 2. Overall Performance of AMBER GPU-TI on Four Protein Systems Comparing with the Performance of Schrodinger FEP+ Whose Data Are Taken from ref (22).
| systems | BACE32 |
CDK233 |
MCL134 |
PTB1B35 |
||||
|---|---|---|---|---|---|---|---|---|
| protocols | FEP+ | GPU-TI | FEP+ | GPU-TI | FEP+ | GPU-TI | FEP+ | GPU-TI |
| #compounds | 36 | 41 | 16 | 22 | 42 | 44 | 23 | 27 |
| ΔΔG MUE (kcal/mol) | 0.84 | 0.93 | 0.91 | 0.94 | 1.16 | 0.82 | 0.89 | 0.71 |
| ΔΔG RMSE (kcal/mol) | 1.03 | 1.22 | 1.11 | 1.16 | 1.41 | 1.01 | 1.22 | 0.91 |
| Pearson’s R for ΔG | 0.78 | 0.61 | 0.48 | 0.64 | 0.77 | 0.65 | 0.80 | 0.75 |
2.2. TI Method
The principle of the TI method has been well described in many references.8,36,37 The calculation of relative protein–ligand binding free energy relies on the thermodynamic cycle, which has also been well explained in literature.5,7,36,37
2.3. Force Fields and Preparation of Systems
The setup for all TI simulations has been carried out with the help of the tool FESetup (version 1.2.1),38 which was modified by us to allow specific functions, including assigning the RESP charges39 to ligand molecules from the output files of quantum chemistry HF/6-31G* calculations with the Gaussian16 package.40 Proteins, ligands, and water were represented by ff14SB,41 GAFF1.8,29 and TIP3P models,42 respectively. Atom types and parameters of GAFF1.8 for all ligand molecules were obtained by Antechamber31 and Parmchk2 in the Amber16 tool set.43 All complex systems and solution systems were solvated in rectangular water boxes with at least 12 Å distances between the edges of the box and any atom of ligands or protein–ligand complexes.
2.4. Simulation Protocols
TI simulations in both complex and solution environments were conducted for each mutation pair as normal TI methods based on the thermodynamic cycle.36 The unique atoms in both ligands of a mutation pair were put in the softcore region for both van der Waals and electrostatic interactions. Periodic boundary condition and the NPT ensemble were adopted in all simulations, including both the equilibration and production runs. The temperature was kept at 298 K using Langevin dynamics with the collision frequency gamma_ln being set to 2.0. The pressure was kept at 1.01325 bar with Monte Carlo barostat and a pressure relaxation time of 2.0 ps. The bond constraint SHAKE algorithm is disabled for TI mutations in AMBER GPU-TI module pmemdGTI,27 and therefore a time step of 1 fs was used for all MD simulations. The energy information was saved every 0.5 ps for post-analysis. Other important settings in the simulation control files are the same as the default values from FESetup1.2.1 and AMBER16/18 packages43,44 except for specific λ values. Various schedules of λ windows for TI simulations have been tested in this study (Table 1). After setting up of systems, initial equilibrations were conducted at λ = 0.5 with CPU-TI for 100–200 ps before switching to GPU-TI runs because AMBER CPU-TI has more tolerance for changes in the size of the simulation box than AMBER GPU-TI in NPT ensemble simulations. Five snapshots were extracted at even intervals from the last 100 ps trajectory of CPU-TI equilibration as starting configurations of five individual TI runs at λ = 0.5 with GPU-TI (Figure S1 in the Supporting Information). A 5 ns simulation was performed for each individual TI run at λ = 0.5, and a snapshot at the end of 3 ns was used as the starting configuration at two neighboring λ windows (0.4 and 0.6 in λ schedules 1 and 2, 0.33787 and 0.66213 in λ schedule 3; see Table 1 and Figure S1). The snapshots after 3 ns TI runs at these two neighboring λ windows were used as starting configurations of their neighboring λ windows toward two endpoints (Figure S1). The beginning 1 ns of each 5 ns individual simulation was considered as a further equilibration step at the corresponding λ window and therefore was skipped for post-analysis of dU/dλ. For five replicas of each mutation pair, five relative binding free energy ΔΔG values were separately calculated from corresponding replicas (run1 to run5) at all λ windows and then the arithmetic average was used to calculate the final absolute binding free energy ΔG for each ligand.
Table 1. Schedules of λ Windows for TI Tested in This Study.
| schedules | # of λs | specific λ values | integration method |
|---|---|---|---|
| schedule 1 | 13 | 0.0, 0.05, 0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, 0.9, 0.95, 1.0 | trapezoidal rule |
| schedule 2 | 13 | 0.001, 0.05, 0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, 0.9, 0.95, 1.0 | extrapolation and trapezoidal rule |
| schedule 3 | 9 | 0.01592, 0.08198, 0.19331, 0.33787, 0.5, 0.66213, 0.80669, 0.91802, 0.98408 | gaussian quadrature |
3. Results
First of all, it is worth noting that all reported absolute binding free energies (ΔG) in this manuscript are the raw data directly calculated from a single experimental value of a common reference ligand for each protein system plus all calculated relative binding free energies ΔΔG along the alchemical transformation path from the same reference ligand to each individual query ligand, as described in the Supporting Information. We did not adopt the offset ways like “cycle closure ΔΔG values”22,36 or “centered RMSE”,45 in which “all of the ligands’ experimental values were used as a reference and the sum of the predicted ΔG values was set to be equal to the sum of the experimental ΔG values”36 to make the mean signed error zero, even though they can “artificially improve the overall results”36 and make calculated MUE and RMSE for ΔG lower. We avoided applying these procedures of processing data to mimic scenarios of real drug design projects, in which most of calculated ligands have not been synthesized and experimentally measured, and most probably, only one of them has experimental data available beforehand.
3.1. Performance of AMBER CPU-TI with λ Schedule 1 on the PTP1B System
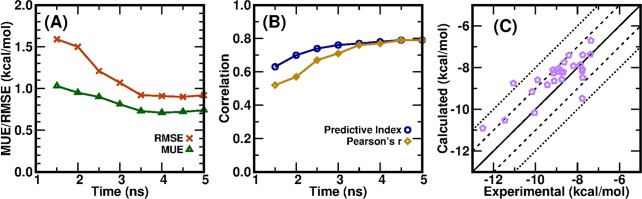
We first tested various simulation protocols on the protein tyrosine phosphatase 1B (PTP1B) system with 27 congeneric ligands,35 among which 23 ligands were calculated and reported in the Schrodinger FEP+ paper.22 The setting up of the systems and simulations, the adopted force fields, and the alchemical transformation paths, and so on are described in the Methods section and Supporting Information. We first carried out calculations with the CPU-TI implemented in the AMBER16 package43 for a series of 13 λ windows (λ schedule 1 in Table 1). As shown in Figure 1a, MUE and RMSE for ΔG decrease as the simulation time t for each λ window increases and reach a plateau at t > ∼4 ns. The predictive index (PI)8,37 and Pearson’s correlation coefficient r (PR) increase as the simulation time t for each λ window increases and also reach plateaus at t > ∼4 ns (Figure 1b). At t = 5 ns, the MUE and RMSE for this series of 27 ligands are 0.75 kcal/mol and 0.92 kcal/mol, respectively.
Figure 1.
Results for a series of PTP1B–ligand complexes calculated with AMBER16 CPU-TI and λ schedule 1. (a) Mean unsigned error and root-mean-square error for ΔG and (b) predictive index and Pearson’s correlation coefficient r for this series as a function of simulation time for each λ window. (c) Calculated binding free energies at t = 5 ns versus experimental values.
3.2. AMBER CPU-TI versus GPU-TI with λ Schedule 1 on the PTP1B System
The computing demand for TI calculations is high and the speed is slow, even with parallel CPU clusters. This is one of the biggest hurdles preventing the extensive use of TI calculations in practice. The GPU version of the AMBER TI method has been developed recently and implemented in the AMBER18 package.27,28,44 According to our test on the PTP1B system, the speed on a single Nvidia GeForce GTX1080 GPU card is ∼100 folds faster for the protein–ligand complexes (∼48,240 atoms) and ∼40 folds faster for the ligand solutions (∼4070 atoms) than the speed on a single core of an Intel Xeon Gold 6126 Skylake processor (2.60 GHz). This speedup agrees with the benchmarks on other protein systems.27 With one Nvidia GTX1080 card, a 1 ns TI simulation of a PTP1B–ligand complex can be done in ∼0.65 h (wall time) and a 1 ns TI simulation of ligand solution can be done in ∼0.17 h.
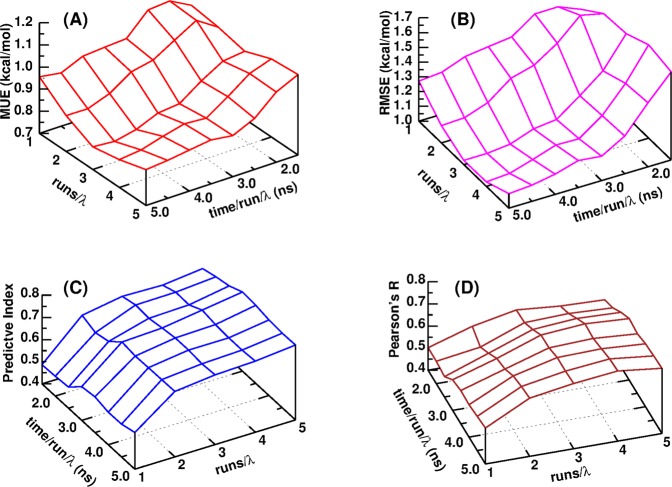
Due to the intrinsic limitation of applying GPUs in MD simulations and TI calculations27 and the fact that AMBER18 GPU-TI calculation is already fast enough, it is recommended to carry out several runs for each λ window, either from different starting configurations or from the same starting configuration but with different initial velocities of atoms, which could be randomly generated from a Maxwell–Boltzmann distribution according to the simulation temperature, and take averages from repeated runs to get more precise and accurate results. As to the GPU-TI calculation of the tested PTP1B system,35 the MUE for ΔG decreases as the number of repeated runs (Nrun) at each λ window and the simulation time (t) for each run increase and approaches a plateau of ∼0.75 kcal/mol at the region of Nrun ≥ 4 and t > ∼4 ns (Figure 2a), and this plateau value of MUE for ΔG is the same as that from CPU-TI calculation. The RMSE for ΔG has a very similar behavior pattern (Figure 2b) and reaches its plateau at the same region. Meanwhile, the rank coefficient PI and correlation coefficient PR are more affected by Nrun than t. They both increase as Nrun increases (Figure 2c,d) and approach plateaus in the same region of Nrun ≥ 4 and t > ∼4 ns. Such patterns suggest that in order to save the computing resource and wall time as much as possible when performing AMBER GPU-TI calculations, a strategy of adopting Nrun as less as 4 and t as less as 4 ns would lead to close results as conducting more repeated runs and longer simulations. In the following sessions of this manuscript, all reported results of GPU-TI were taken from Nrun = 5 and t = 5.0 ns.
Figure 2.
(a) MUE for ΔG, (b) RMSE for ΔG, (c) predictive index, and (d) Pearson’s R for a series of 27 PTP1B–ligand complexes calculated with AMBER18 GPU-TI and λ schedule 1 as functions of the number of repeated runs for each λ window and the simulation time per run per λ window.
3.3. AMBER GPU-TI with Different λ Schedules on the PTP1B System
It is well known that TI calculations can suffer from instabilities during the creation or annihilation of particles, which correspond to the states of λ of 0 or 1, according to the convention of TI setting up. In this study, the state of λ = 0 corresponds to the smaller ligand and the state of λ = 1 corresponds to the bigger one. For instance, in the alchemical transformation of ligand 9 → ligand 17 in the PTP1B system35 (Figure S2 in the Supporting Information), the root-mean-squared (RMS) fluctuations of ∂U/∂λ (marked as “DV/DL” in AMBER output files) is ∼2000 kcal/mol at λ = 0, ∼500 kcal/mol at λ = 0.001, ∼40 kcal/mol at λ = 0.01592, and ∼10 kcal/mol at λ > 0.1. Therefore, it is a common practice to avoid direct simulation at the endpoint window (λ = 0 in this study) where particles appear/disappear. Instead, the ∂U/∂λ value at endpoint λ is either fitted from other close λ windows by an extrapolation method or just simply neglected in practice. In our λ schedule 2 (Table 1), TI simulations at λ = 0.001were carried out and used to fit ∂U/∂λ at λ = 0 for all GPU-TI calculations for the PTP1B system. It turned out that MUE and RMSE reduced by ∼0.09 kcal compared to those using λ schedule 1 and PR increased by ∼0.04, although PI decreased slightly from 0.74 by λ schedule 1 to 0.72 (Figure S3), which is understandable since even small changes in the computed free energies can lead to a different ranking of the ligands with similar affinities.45 We have also tested a 9 λ window schedule of Gaussian quadrature integration (schedule 3 in Table 1 of this manuscript, eq 21.2 and Table 21.1 in the AMBER18 manual44) and found that all merit metrics (MUE, RMSE, PI, and PR) are improved or very similar compared to schedules 1 and 2 (Figure S3). Considering that schedule 3 saves calculations of four λ windows compared to schedule 1/schedule 2 and it can still obtain a very similar or better performance in the benchmark on the PTP1B system, it has been adopted for GPU-TI calculations for three other protein systems (BACE,32 CDK2,33 and MCL134), which have also been calculated by Schrodinger FEP+.22
3.4. Overall Performance of AMBER GPU-TI on the Tested Four Protein Systems
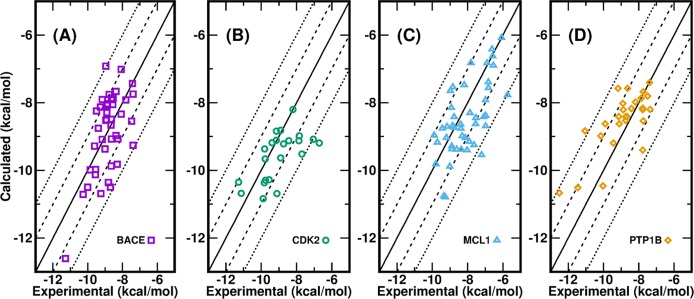
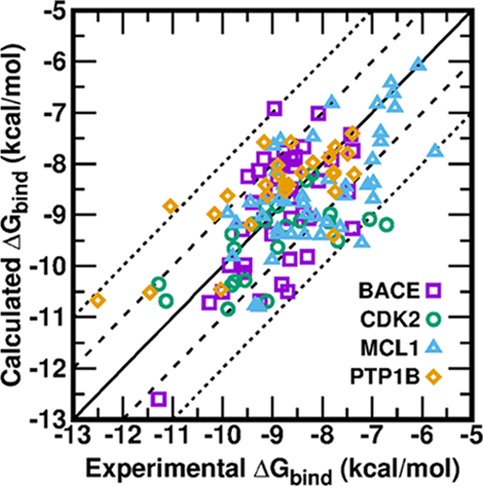
The calculated ΔGbind of all ligands of four protein systems compared to experiment by AMBER18 GPU-TI are presented in Figure 3. Of the 134 data points in total, all unsigned errors for ΔG (ΔG UEs) are <2.5 kcal/mol, three ΔG UEs (2.3%) are >2.1 kcal/mol, three ΔG UEs (2.3%) are between 2.0 and 2.1 kcal/mol, 34 ΔG UEs (25.6%) are between 1.0 and 2.0 kcal/mol, and 93 ΔG UEs (69.9%) are smaller than 1.0 kcal/mol. The ΔG MUEs are 0.77 kcal/mol for BACE, 0.80 kcal/mol for CDK2, 0.81 kcal/mol for MCL1, and 0.71 kcal/mol for PTP1B. The ΔG RMSEs are 0.93, 1.04, 0.98, and 0.91 kcal/mol for BACE, CDK2, MCL1, and PTP1B, respectively. All ΔG MUEs and ΔG RMSEs are lower than the aforementioned threshold of 1 kcal/mol except for the ΔG RMSE of CDK2 (1.04 kcal/mol). Note that the offset ways like “cycle closure ΔΔG values”22,36 or “centered RMSE”45 were not adopted in the calculations of ΔG for all ligands from ΔΔG of perturbation pairs, even though they could artificially reduce the appeared ΔG MUEs and ΔG RMSEs. We only used one experimental ΔG value of a common reference compound in each protein system. While it is true that all calculated ΔG values are more or less dependent on the chosen common reference compound, we chose the compound in each protein system with either the simplest structure or the most connections in the graph of the perturbation pathway (Figures S2 and S4–S6 in the Supporting Information). Such a scenario is close to real situations encountered in real drug design projects.
Figure 3.
Calculated binding free energies for 134 ligands of four protein systems versus their experimental values: (a) BACE, (b) CDK2, (c) MCL1, and (d) PTP1B.
As to the MUEs and RMSEs for relative ΔΔG of mutation pairs, Table 2 shows that for the four protein systems, AMBER GPU-TI leads to ΔΔG MUEs between 0.71 and 0.94 kcal/mol and ΔΔG RMSE between 0.91 and 1.22 kcal/mol compared to the ΔΔG MUEs between 0.84 and 1.16 kcal/mol and ΔΔG RMSEs between 1.03 and 1.41 kcal/mol achieved by Schrodinger FEP+.22 As to the correlation coefficient PR for ΔG, GPU-TI leads to slightly higher PR for CDK2 (0.64 vs 0.48), slightly lower values (by −0.12 to −0.17) for other three protein systems, and comparable PR ranges in general (0.61–0.75 for GPU-TI vs 0.48–0.80 for Schrodinger FEP+22).
4. Discussion
As described above, we investigated the ability of AMBER CPU-TI and newly implemented GPU-TI on the prediction of binding free energies on data sets of four protein systems that were originally tested by Schrodinger Inc. with their GPU free-energy code FEP+, OPLS2.1 force field, and REST2 replica exchange sampling method.22 We adopted the ff14SB force field41 for protein receptors, the general AMBER force field (GAFF, version 1.8)29 for ligand compounds, and TIP3P model42 for water molecules. By using the 9 λ window protocol (Table 1), our calculated results not only obtained ΔΔG MUE and ΔΔG RMSE overall slightly lower than those by Schrodinger FEP+ but also approached the threshold of ΔG MUE/RMSE ≈ 1 kcal/mol, which are necessary for effectively guiding the lead optimization in drug design projects. Recently, Song et al. carried out calculations with the same AMBER GPU-TI program and the same ff14SB/GAFF1.8 force fields on the same protein systems.36 However, their computed results had larger average errors than the FEP+ results.36 For the same number of ligands as in the FEP+ study, Song et al. got ΔΔG MUE of 1.20, 0.97, 1.52, and 1.06 kcal/mol for BACE, CDK2, MCL1, and PTP1B, respectively, and ΔΔG RMSE of 1.47, 1.13, 1.83, and 1.40 kcal/mol for BACE, CDK2, MCL1, and PTP1B, respectively.36 Here, we point out several differences in our calculations from their calculations that might contribute to the discrepancy in the calculated results.
First of all, different water models were used in two studies although the same protein and general force fields were applied. In our calculations, we adopted the TIP3P water model,42 whereas Song et al.36 adopted the SPC/E water model.46 Usually, each biomolecular or soft-matter force field is bound to a specific water model, and the force field parameters are adjusted and validated based on that specific water model. While mixed usage of noncompatible force fields for macromolecules and small molecules can lead to large computational errors, the substitution of the default water model is also not recommended. Both ff14SB and GAFF were developed based on the TIP3P water model, as described in their corresponding references.29,41 Therefore, the TIP3P water model should always be adopted with ff14SB and GAFF, and the substitution of TIP3P to another water model is not recommended. After all, the calculation of the protein–ligand binding free energy deeply involves the interactions between protein–ligand and the surrounding environment, which is the aqueous solution. Especially, the thermodynamic cycle, which is used in binding free energy calculations, specifically includes the simulation of the ligand in water.5,7,36,37 In order to test the effect of switching water models, we performed extra TI calculations of seven ligand pairs in the PTP1B system (ligand 3 → ligand 8, ligand 8 → ligand 11, ligand 8 → ligand 12, ligand 8 → ligand 13, ligand 8 → ligand 14, ligand 8 → ligand 15, and ligand 8 → ligand 16) with the same settings in our GPU-TI protocol (ff14sb for protein, GAFF for ligands, 12 Å thickness of the water shell for complexes and solutions, λ schedule 3, and five independent runs) except that the SPC/E water model was adopted instead of TIP3P. Compared to the TIP3P water model, the SPC/E water model led to ΔΔG MUE of these seven mutation pairs that is increased by 0.44 kcal/mol and ΔΔG RMSE that is increased by 0.48 kcal/mol (Table S1 in the Supporting Information).
Second, although both studies solved the complex and the ligand in rectangular simulation cells, different values were used for the minimum distance between the edge of the cell and the solute atoms of the protein and ligand systems. While we used 12 Å as the minimum thickness of the water shell for both protein and ligand systems, Song et al. applied 5 and 10 Å for the protein and ligand systems, respectively.36 The 10 Å thickness of the water shell for the ligand system might be acceptable in most cases, but we are concerned about the only 5 Å thickness of the water shell for the protein system. Although the number of solvent particles and the corresponding computing burden can be greatly reduced with such a thin water shell, the density of the protein–ligand complex would be very high compared to real biological systems, which makes the complex and surrounding water molecules cannot fully relax and reorganize as they are supposed to. We also performed extra TI simulations on the aforementioned seven mutation pairs in the PTP1B system with the same setting as our GPU-TI protocol except that 5 and 12 Å thickness of the water shell was used for the protein system and the ligand only system, respectively. As shown in Table S1 in the Supporting Information, decreased simulation boxes led to ΔΔG MUE of these seven mutation pairs that is increased by 0.26 kcal/mol and ΔΔG RMSE that is increased by 0.22 kcal/mol.
Third, while we carried out five independent runs at each λ point from different initial conformations extracted from equilibrium runs at this λ point or from the product runs at neighbor λ points (Figure S1 in the Supporting Information), Song et al. performed only one run for each λ point.36 As demonstrated in Figure 2, we found that repeating runs at each λ point help improve the merit metrics (MUE and RMSE for ΔG decrease and PI and PR for ΔG increase). This is understandable that a single simulation within a limited time cannot sample all important potential binding modes.47,48 On the other hand, a single long-time simulation is supposed to be able to sample all important binding modes, but in reality, the simulated systems might drift away from correct binding modes due to an inaccurate force field. A practical solution would be individual runs from different initial conformations with an appropriate length of simulation time. Although extra simulations are needed in such protocol, it is affordable and tolerable with GPU computing, and the gained improvement in precision and accuracy is worth the extra investment if four or five repeated runs could be achieved, as this study demonstrated. Other researchers also suggested adopting such an ensemble of independent simulations (termed as “replicas”) to reduce the uncertainty and improve quantification in AFE calculations.49−51 For instance, no less than 25 and 5 replicas were suggested to be run for the “ESMACS (enhanced sampling of molecular dynamics with approximation of continuum solvent)” and “TIES (thermodynamic integration with enhanced sampling)” methods, respectively, with the length of each replica being 4 ns.51
Next, the λ window processing protocols adopted in both studies share similarities and have differences. A conservative strategy of processing λ states is to start from one end (either λ = 0 or λ = 1), which has a crystallographic structure from experiment, equilibrate and run at this λ end, then move to the neighboring λ point, equilibrate and run, and so on, gradually moving to the other λ end step by step. Such a conservative procedure unavoidably causes idle waiting periods and does not fit the expectation of shortening wall time in real drug development work. By coincidence, both we and Song et al.36 chose to do the initial equilibration process after system setting up at λ = 0.5, but the rest of the procedures are different. Song et al. sent the initially equilibrated conformation at λ = 0.5 to 12 λ windows (0.00922, 0.04794, 0.11505, 0.20634, 0.31608, 0.43738, 0.56262, 0.68392, 0.79366, 0.88495, 0.95206, 0.99078) simultaneously as their starting structures.36 Such a process is quite aggressive compared to the aforementioned conservative step-by-step strategy. Another minor disadvantage is that these λ windows do not include λ = 0.5, where initial equilibration is done, causing somehow waste. Our strategy is in the intermediate between the conservative step-by-step procedure and the aggressive one by Song et al. Our tested λ schedules (Table 1) start from the state at λ = 0.5, where initial equilibration is performed, then propagate sequentially and separately to both ends. Taking the λ schedule 3 as an example (Figure S1), the TI simulation jobs at λ = 0.33787 and λ = 0.66213 can get started immediately after the system is well equilibrated at λ = 0.5 (no need to wait for the production run at λ = 0.5 to be done). The TI job at λ = 0.19331 can start immediately once the equilibration run at λ = 0.33787 is done, and the TI job at λ = 0.80669 can start immediately once the equilibration run at λ = 0.66213 is done (again, no need to wait until their production runs are done). The jobs at the rest of the λ windows are performed in a similar way. This strategy is a trade-off considering both efficiency and accuracy.
Still other differences between the protocols in our study and in that of Song et al.36 exist, but the influence on the calculated results are expected to be minor. For instance, the NPT ensemble is applied for production runs in our study, whereas the NVT ensemble is applied by Song et al.36
In TI calculations, two computational protocols are widely adopted to transform from ligand A to ligand B, that is, the one-step protocol and the three-step protocol.36,52 For the former, the vanishing of ligand A and the emergence of ligand B occur simultaneously; whereas, for the latter, the whole transformation is divided into three phases, namely, removing charges of ligand A, changing van der Waals and bonded terms of ligand A to those of ligand B, and adding charges back for ligand B. Each of these three processes needs to be simulated at a set of individual λ windows. Both Song et al. and we adopted the one-step protocol instead of the three-step protocol for the following reasons. First, for the three-step protocol, the net charge of the system may change during the discharging/charging steps, which may affect the long-range electrostatic interactions in AMBER.36 Second, the one-step protocol takes significantly less amounts of simulations. When the overall accuracies of different protocols are comparable, the faster and more efficient one is often preferred in real drug development because the time also matters.
5. Conclusions
In this study, we carried out simulations and calculations of a data set of protein–ligand binding free energies covering four protein targets and 134 ligands using the alchemical thermodynamic integration (TI) method implemented in the AMBER16 CPU module (PMEMD) and AMBER18 GPU code (PMEMD.GTI) with ff14SB/GAFF1.8/TIP3P force field combination for proteins, ligands, and water solvent, respectively. We explored the effects of protocols of different transformation scheme, λ schedule, number of parallel runs, simulation time, and so on on the overall merit metrics such as mean of unsigned errors (MUEs), root-mean-square errors (RMSEs), predictive index (PI), and Pearson’s correlation coefficient r (PR). We found that with AMBER18 GPU-TI code, the aforementioned force field combination, a 9 λ window schedule of Gaussian quadrature integration with an appropriate equilibration/production procedure along λ windows, appropriate number of repeated runs and length of simulation time, we can efficiently achieve MUEs and RMSEs for binding free energies (ΔG) not only lower than 1 kcal/mol, which is a threshold criterion for effectively guiding real drug lead optimization research, but also comparable MUEs and RMSEs for ΔΔG of mutation pairs obtained by the Schrodinger FEP+ program, which is currently the de facto standard in pharmaceutical industry. As the AMBER code developers and force field developers, we hope that our proposed protocol may serve as a cost-efficient solution for daily routine usage of rigorous alchemical free energy calculations in real drug research and development projects to broad communities, especially the academic research labs.
Acknowledgments
The authors gratefully acknowledge the funding support from the National Institutes of Health (NIH) to J.W. (R01GM079383, P30DA035778 and R21GM097617), and to D.M.Y (R01GM107485). The authors also thank the computing resources provided by the Center for Research Computing (CRC) at University of Pittsburgh, the Extreme Science and Engineering Discovery Environment (XSEDE, grant no. CHE090098), and the Pittsburgh Supercomputing Center (PSC, grant nos. CHE180028P and MCB180045P).
Supporting Information Available
The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acsomega.9b04233.
Figures of the transformation paths of ligands for four protein systems, performance of AMBER GPU-TI on the PTP1B system with three different λ schedules, and procedures of equilibration/production runs and λ propagation (PDF)
Calculated relative binding free energies for each pair of alchemical transformation using AMBER GPU-TI with the λ schedule 3 and five repeated runs of 5 ns simulation at each λ window, derived absolute binding free energies and corresponding experimental values for each ligand, and resulting MUE, RMSE, PI, and PR for each protein system. (XLSX)
The authors declare no competing financial interest.
Supplementary Material
References
- DiMasi J. A.; Grabowski H. G.; Hansen R. W. Innovation in the pharmaceutical industry: New estimates of R&D costs. J. Health Econ. 2016, 47, 20–33. 10.1016/j.jhealeco.2016.01.012. [DOI] [PubMed] [Google Scholar]
- Beveridge D. L.; DiCapua F. M. Free energy via molecular simulation: applications to chemical and biomolecular systems. Annu. Rev. Biophys. Biophys. Chem. 1989, 18, 431–492. 10.1146/annurev.bb.18.060189.002243. [DOI] [PubMed] [Google Scholar]
- Gilson M. K.; Zhou H. X. Calculation of protein-ligand binding affinities. Annu. Rev. Biophys. Biomol. Struct. 2007, 36, 21–42. 10.1146/annurev.biophys.36.040306.132550. [DOI] [PubMed] [Google Scholar]
- Deng Y.; Roux B. Computations of standard binding free energies with molecular dynamics simulations. J. Phys. Chem. B 2009, 113, 2234–2246. 10.1021/jp807701h. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jorgensen W. L. The many roles of computation in drug discovery. Science 2004, 303, 1813–1818. 10.1126/science.1096361. [DOI] [PubMed] [Google Scholar]
- Jorgensen W. L. Efficient drug lead discovery and optimization. Acc. Chem. Res. 2009, 42, 724–733. 10.1021/ar800236t. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Åqvist J.; Luzhkov V. B.; Brandsdal B. O. Ligand binding affinities from MD simulations. Acc. Chem. Res. 2002, 35, 358–365. 10.1021/ar010014p. [DOI] [PubMed] [Google Scholar]
- Michel J.; Verdonk M. L.; Essex J. W. Protein-ligand binding affinity predictions by implicit solvent simulations: a tool for lead optimization?. J. Med. Chem. 2006, 49, 7427–7439. 10.1021/jm061021s. [DOI] [PubMed] [Google Scholar]
- Huang S. Y.; Zou X. Advances and challenges in protein-ligand docking. Int. J. Mol. Sci. 2010, 11, 3016–3034. 10.3390/ijms11083016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hawkins P. C. D.; Skillman A. G.; Nicholls A. Comparison of shape-matching and docking as virtual screening tools. J. Med. Chem. 2007, 50, 74–82. 10.1021/jm0603365. [DOI] [PubMed] [Google Scholar]
- Warren G. L.; Andrews C. W.; Capelli A. M.; Clarke B.; LaLonde J.; Lambert M. H.; Lindvall M.; Nevins N.; Semus S. F.; Senger S.; Tedesco G.; Wall I. D.; Woolven J. M.; Peishoff C. E.; Head M. S. A critical assessment of docking programs and scoring functions. J. Med. Chem. 2006, 49, 5912–5931. 10.1021/jm050362n. [DOI] [PubMed] [Google Scholar]
- Plewczynski D.; Łaźniewski M.; Augustyniak R.; Ginalski K. Can We Trust Docking Results? Evaluation of Seven Commonly Used Programs on PDBbind Database. J. Comput. Chem. 2011, 32, 742–755. 10.1002/jcc.21643. [DOI] [PubMed] [Google Scholar]
- Ferreira L. G.; dos Santos R. N.; Oliva G.; Andricopulo A. D. Molecular Docking and Structure-Based Drug Design Strategies. Molecules 2015, 20, 13384–13421. 10.3390/molecules200713384. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hansson T.; Marelius J.; Åqvist J. Ligand binding affinity prediction by linear interaction energy methods. J. Comput.-Aided Mol. Des. 1998, 12, 27–35. 10.1023/A:1007930623000. [DOI] [PubMed] [Google Scholar]
- Zhou R.; Friesner R. A.; Ghosh A.; Rizzo R. C.; Jorgensen W. L.; Levy R. M. New linear interaction method for binding affinity calculations using a continuum solvent model. J. Phys. Chem. B 2001, 105, 10388–10397. 10.1021/jp011480z. [DOI] [Google Scholar]
- He X.; Man V. H.; Ji B.; Xie X.-Q.; Wang J. Calculate protein-ligand binding affinities with the extended linear interaction energy method: application on the Cathepsin S set in the D3R Grand Challenge 3. J. Comput.-Aided Mol. Des. 2019, 33, 105–117. 10.1007/s10822-018-0162-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Massova I.; Kollman P. A. Combined molecular mechanical and continuum solvent approach (MM-PBSA/GBSA) to predict ligand binding. Perspect. Drug Discovery Des. 2000, 18, 113–135. 10.1023/A:1008763014207. [DOI] [Google Scholar]
- Genheden S.; Ryde U. The MM/PBSA and MM/GBSA methods to estimate ligand-binding affinities. Expert Opin. Drug Discovery 2015, 10, 449–461. 10.1517/17460441.2015.1032936. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang C.; Greene D. A.; Xiao L.; Qi R.; Luo R. Recent Developments and Applications of the MMPBSA Method. Front. Mol. Biosci. 2018, 4, 87. 10.3389/fmolb.2017.00087. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang E.; Sun H.; Wang J.; Wang Z.; Liu H.; Zhang J. Z. H.; Hou T. End-Point Binding Free Energy Calculation with MM/PBSA and MM/GBSA: Strategies and Applications in Drug Design. Chem. Rev. 2019, 119, 9478–9508. 10.1021/acs.chemrev.9b00055. [DOI] [PubMed] [Google Scholar]
- Chodera J. D.; Mobley D. L.; Shirts M. R.; Dixon R. W.; Branson K.; Pande V. S. Alchemical free energy methods for drug discovery: progress and challenges. Curr. Opin. Struct. Biol. 2011, 21, 150–160. 10.1016/j.sbi.2011.01.011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang L.; Wu Y.; Deng Y.; Kim B.; Pierce L.; Krilov G.; Lupyan D.; Robinson S.; Dahlgren M. K.; Greenwood J.; Romero D. L.; Masse C.; Knight J. L.; Steinbrecher T.; Beuming T.; Damm W.; Harder E.; Sherman W.; Brewer M.; Wester R.; Murcko M.; Frye L.; Farid R.; Lin T.; Mobley D. L.; Jorgensen W. L.; Berne B. J.; Friesner R. A.; Abel R. Accurate and Reliable Prediction of Relative Ligand Binding Potency in Prospective Drug Discovery by Way of a Modern Free-Energy Calculation Protocol and Force Field. J. Am. Chem. Soc. 2015, 137, 2695–2703. 10.1021/ja512751q. [DOI] [PubMed] [Google Scholar]
- Knight J. L.; Brooks C. L. III λ-Dynamics Free Energy Simulation Methods. J. Comput. Chem. 2009, 30, 1692–1700. 10.1002/jcc.21295. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zheng L.; Chen M.; Yang W. Random walk in orthogonal space to achieve efficient free-energy simulation of complex systems. Proc. Natl. Acad. Sci. U. S. A. 2008, 105, 20227–20232. 10.1073/pnas.0810631106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gallicchio E.; Levy R. M. Advances in all atom sampling methods for modeling protein-ligand binding affinities. Curr. Opin. Struct. Biol. 2011, 21, 161–166. 10.1016/j.sbi.2011.01.010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hansen N.; van Gunsteren W. F. Practical Aspects of Free-Energy Calculations: A Review. J. Chem. Theory Comput. 2014, 10, 2632–2647. 10.1021/ct500161f. [DOI] [PubMed] [Google Scholar]
- Lee T. S.; Hu Y.; Sherborne B.; Guo Z.; York D. M. Toward Fast and Accurate Binding Affinity Prediction with pmemdGTI: An Efficient Implementation of GPU-Accelerated Thermodynamic Integration. J. Chem. Theory Comput. 2017, 13, 3077–3084. 10.1021/acs.jctc.7b00102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lee T. S.; Cerutti D. S.; Mermelstein D.; Lin C.; LeGrand S.; Giese T. J.; Roitberg A.; Case D. A.; Walker R. C.; York D. M. GPU-Accelerated Molecular Dynamics and Free Energy Methods in Amber18: Performance Enhancements and New Features. J. Chem. Inf. Model. 2018, 58, 2043–2050. 10.1021/acs.jcim.8b00462. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang J.; Wolf R. M.; Caldwell J. W.; Kollman P. A.; Case D. A. Development and testing of a general amber force field. J. Comput. Chem. 2004, 25, 1157–1174. 10.1002/jcc.20035. [DOI] [PubMed] [Google Scholar]
- Wang J.; Wolf R. M.; Caldwell J. W.; Kollman P. A.; Case D. A. Erratum: Development and testing of a general amber force field (vol 25, pg 1157, 2004). J. Comput. Chem. 2005, 26, 114–114. 10.1002/jcc.20145. [DOI] [PubMed] [Google Scholar]
- Wang J.; Wang W.; Kollman P. A.; Case D. A. Automatic atom type and bond type perception in molecular mechanical calculations. J. Mol. Graphics Modell. 2006, 25, 247–260. 10.1016/j.jmgm.2005.12.005. [DOI] [PubMed] [Google Scholar]
- Cumming J. N.; Smith E. M.; Wang L.; Misiaszek J.; Durkin J.; Pan J.; Iserloh U.; Wu Y.; Zhu Z.; Strickland C.; Voigt J.; Chen X.; Kennedy M. E.; Kuvelkar R.; Hyde L. A.; Cox K.; Favreau L.; Czarniecki M. F.; Greenlee W. J.; McKittrick B. A.; Parker E. M.; Stamford A. W. Structure based design of iminohydantoin BACE1 inhibitors: identification of an orally available, centrally active BACE1 inhibitor. Bioorg. Med. Chem. Lett. 2012, 22, 2444–2449. 10.1016/j.bmcl.2012.02.013. [DOI] [PubMed] [Google Scholar]
- Hardcastle I. R.; Arris C. E.; Bentley J.; Boyle F. T.; Chen Y.; Curtin N. J.; Endicott J. A.; Gibson A. E.; Golding B. T.; Griffin R. J.; Jewsbury P.; Menyerol J.; Mesguiche V.; Newell D. R.; Noble M. E. M.; Pratt D. J.; Wang L.-Z.; Whitfield H. J. N2-substituted O6-cyclohexylmethylguanine derivatives: potent inhibitors of cyclin-dependent kinases 1 and 2. J. Med. Chem. 2004, 47, 3710–3722. 10.1021/jm0311442. [DOI] [PubMed] [Google Scholar]
- Friberg A.; Vigil D.; Zhao B.; Daniels R. N.; Burke J. P.; Garcia-Barrantes P. M.; Camper D.; Chauder B. A.; Lee T.; Olejniczak E. T.; Fesik S. W. Discovery of Potent Myeloid Cell Leukemia 1 (Mcl-1) Inhibitors Using Fragment-Based Methods and Structure-Based Design. J. Med. Chem. 2013, 56, 15–30. 10.1021/jm301448p. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wilson D. P.; Wan Z. K.; Xu W. X.; Kirincich S. J.; Follows B. C.; Joseph-McCarthy D.; Foreman K.; Moretto A.; Wu J.; Zhu M.; Binnun E.; Zhang Y. L.; Tam M.; Erbe D. V.; Tobin J.; Xu X.; Leung L.; Shilling A.; Tam S. Y.; Mansour T. S.; Lee J. Structure-based optimization of protein tyrosine phosphatase 1B inhibitors: From the active site to the second phosphotyrosine binding site. J. Med. Chem. 2007, 50, 4681–4698. 10.1021/jm0702478. [DOI] [PubMed] [Google Scholar]
- Song L. F.; Lee T.-S.; Zhu C.; York D. M.; Merz K. M. Jr. Using AMBER18 for Relative Free Energy Calculations. J. Chem. Inf. Model. 2019, 59, 3128–3135. 10.1021/acs.jcim.9b00105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pearlman D. A.; Charifson P. S. Are free energy calculations useful in practice? A comparison with rapid scoring functions for the p38 MAP kinase protein system. J. Med. Chem. 2001, 44, 3417–3423. 10.1021/jm0100279. [DOI] [PubMed] [Google Scholar]
- Loeffler H. H.; Michel J.; Woods C. FESetup: Automating Setup for Alchemical Free Energy Simulations. J. Chem. Inf. Model. 2015, 55, 2485–2490. 10.1021/acs.jcim.5b00368. [DOI] [PubMed] [Google Scholar]
- Bayly C. I.; Cieplak P.; Cornell W.; Kollman P. A. A Well-Behaved Electrostatic Potential Based Method Using Charge Restraints for Deriving Atomic Charges - the Resp Model. J. Phys. Chem. 1993, 97, 10269–10280. 10.1021/j100142a004. [DOI] [Google Scholar]
- Frisch M. J.; Trucks G. W.; Schlegel H. B.; Scuseria G. E.; Robb M. A.; Cheeseman J. R.; Scalmani G.; Barone V.; Petersson G. A.; Nakatsuji H.; Li X.; Caricato M.; Marenich A. V.; Bloino J.; Janesko B. G.; Gomperts R.; Mennucci B.; Hratchian H. P.; Ortiz J. V.; Izmaylov A. F.; Sonnenberg J. L.; Williams-Young D.; Ding F.; Lipparini F.; Egidi F.; Goings J.; Peng B.; Petrone A.; Henderson T.; Ranasinghe D.; Zakrzewski V. G.; Gao J.; Rega N.; Zheng G.; Liang W.; Hada M.; Ehara M.; Toyota K.; Fukuda R.; Hasegawa J.; Ishida M.; Nakajima T.; Honda Y.; Kitao O.; Nakai H.; Vreven T.; Throssell K.; Montgomery J. A. Jr.; Peralta J. E.; Ogliaro F.; Bearpark M. J.; Heyd J. J.; Brothers E. N.; Kudin K. N.; Staroverov V. N.; Keith T. A.; Kobayashi R.; Normand J.; Raghavachari K.; Rendell A. P.; Burant J. C.; Iyengar S. S.; Tomasi J.; Cossi M.; Millam J. M.; Klene M.; Adamo C.; Cammi R.; Ochterski J. W.; Martin R. L.; Morokuma K.; Farkas O.; Foresman J. B.; Fox D. J.. Gaussian 16; Revision C.01. Gaussian, Inc.: Wallingford CT, 2016. [Google Scholar]
- Maier J. A.; Martinez C.; Kasavajhala K.; Wickstrom L.; Hauser K. E.; Simmerling C. ff14SB: Improving the Accuracy of Protein Side Chain and Backbone Parameters from ff99SB. J. Chem. Theory Comput. 2015, 11, 3696–3713. 10.1021/acs.jctc.5b00255. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jorgensen W. L.; Chandrasekhar J.; Madura J. D.; Impey R. W.; Klein M. L. Comparison of Simple Potential Functions for Simulating Liquid Water. J. Chem. Phys. 1983, 79, 926–935. 10.1063/1.445869. [DOI] [Google Scholar]
- Case D. A.; Cerutti D. S.; Cheatham T. E. III; Darden T. A.; Duke R. E.; Giese T. J.; Gohlke H.; Goetz A. W.; Izadi S.; Janowski P.; Kaus J.; Kovalenko A.; Lee T. S.; LeGrand S.; Li C.; Lin T. L., Luo R.; Madej B.; Mermelstein D.; Merz K. M.; Monard G.; Nguyen H.; Nguyen I.; Omelyan A. O., Roe D. R.; Roitberg A.; Sagui C.; Simmerling C. L.; Botello-Smith W. M.; Swails J.; Walker J. W., Wolf R. M.; Wu X.; Xiao L.; Kollman P. A.. AMBER 2016; University of California: San Francisco, 2016
- Case D. A.; Ben-Shalom I. Y.; Brozell S. R.; Cerutti D. S.; Cheatham T. E. III; Cruzeiro V. W. D.; Darden T. A.; Duke D. G.; Gilson M. K.; Gohlke H.; Goetz A. W.; Greene D.; Harris R.; Homeyer N.; Huang Y.; Izadi S.; Kurtzman A. K. T.; Lee T. S.; LeGrand S.; Li P.; Lin C.; Liu J.; Luchko T.; Luo D. J.; Mermelstein K. M. M.; Miao Y.; Monard G.; Nguyen C.; Nguyen H.; Omelyan I.; Onufriev A.; Pan R.; Qi D. R. R.; Roitberg A.; Sagui C.; Schott-Verdugo S.; Shen J.; Simmerling C. L.; Smith J.; Salomon Ferrer R.; Swails J.; Walker R. C.; Wang J.; Wei H.; Wolf R. M.; Wu X.; Xiao L.; York D. M.; Kollman P. A.. AMBER 2018. University of California: San Francisco, 2018.
- Gathiaka S.; Liu S.; Chiu M.; Yang H.; Stuckey J. A.; Kang Y. N.; Delproposto J.; Kubish G.; Dunbar J. B. Jr.; Carlson H. A.; Burley S. K.; Walters W. P.; Amaro R. E.; Feher V. A.; Gilson M. K. D3R grand challenge 2015: Evaluation of protein-ligand pose and affinity predictions. J. Comput.-Aided Mol. Des. 2016, 30, 651–668. 10.1007/s10822-016-9946-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Berendsen H. J. C.; Grigera J. R.; Straatsma T. P. The Missing Term in Effective Pair Potentials. J. Phys. Chem. 1987, 91, 6269–6271. 10.1021/j100308a038. [DOI] [Google Scholar]
- Boyce S. E.; Mobley D. L.; Rocklin G. J.; Graves A. P.; Dill K. A.; Shoichet B. K. Predicting Ligand Binding Affinity with Alchemical Free Energy Methods in a Polar Model Binding Site. J. Mol. Biol. 2009, 394, 747–763. 10.1016/j.jmb.2009.09.049. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Coveney P. V.; Wan S. On the calculation of equilibrium thermodynamic properties from molecular dynamics. Phys. Chem. Chem. Phys. 2016, 18, 30236–30240. 10.1039/c6cp02349e. [DOI] [PubMed] [Google Scholar]
- Lawrenz M.; Baron R.; McCammon J. A. Independent trajectories thermodynamic-integration free-energy changes for biomolecular systems: Determinants of H5N1 avian influenza virus neuraminidase inhibition by peramivir. J. Chem. Theory Comput. 2009, 5, 1106–1116. 10.1021/ct800559d. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bhati A. P.; Wan S.; Wright D. W.; Coveney P. V. Rapid, accurate, precise, and reliable relative free energy prediction using ensemble based thermodynamic integration. J. Chem. Theory Comput. 2017, 13, 210–222. 10.1021/acs.jctc.6b00979. [DOI] [PubMed] [Google Scholar]
- Bhati A. P.; Wan S.; Hu Y.; Sherborne B.; Coveney P. V. Uncertainty Quantification in Alchemical Free Energy Methods. J. Chem. Theory Comput. 2018, 14, 2867–2880. 10.1021/acs.jctc.7b01143. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Loeffler H. H.; Bosisio S.; Matos G. D. R.; Suh D.; Roux B.; Mobley D. L.; Michel J. Reproducibility of Free Energy Calculations across Different Molecular Simulation Software Packages. J. Chem. Theory Comput. 2018, 14, 5567–5582. 10.1021/acs.jctc.8b00544. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.