 Explaining most known double perovskite electronic structures and predicting new ones using Linear Combination of Atomic Orbitals analysis.
Explaining most known double perovskite electronic structures and predicting new ones using Linear Combination of Atomic Orbitals analysis.
Abstract
Halide double perovskites are an important emerging alternative to lead-halide perovskites in a variety of optoelectronic applications. Compared to ABX3 single perovskites (A = monovalent cation, X = halide), A2BB′X6 double perovskites exhibit a wider array of compositions and electronic structures, promising finer control over physical and electronic properties through synthetic design. However, a clear understanding of how chemical composition dictates the electronic structures of this large family of materials is still lacking. Herein, we develop a qualitative Linear Combination of Atomic Orbitals (LCAO) model that describes the full range of band structures for double perovskites. Our simple model allows for a direct connection between the inherently local bonding between atoms in the double perovskite and the resulting delocalized bands of the solid. In particular, we show how bands in halide double perovskites originate from the molecular orbitals of metal–hexahalide coordination complexes and describe how these molecular orbitals vary within a band. Our results provide both an enhanced understanding of known perovskite compositions and predictive power for identifying new compositions with targeted properties. We present a table, which permits the position of the conduction band minimum and valence band maximum in most double perovskites to be immediately determined from the frontier atomic orbitals of the B-site metals. Using purely qualitative arguments based on orbital symmetries and their relative energies, the direct/indirect nature of the bandgap of almost all halide double perovskites can thus be correctly predicted. We hope that this theory provides an intuitive understanding of halide double perovskite band structures and enables lessons from molecular chemistry to be applied to these extended solids.
1. Introduction
Perovskites encompass a vast structural and compositional diversity featuring 0-, 1-, 2-, and 3-dimensional lattices incorporating s-, p-, d-, and f-block metals. This diversity is reflected in the widely varying properties of perovskites, which have been studied as superconductors,1 catalysts,2 rare-earth phosphor hosts,3 and conductors for lithium ions,4 oxide ions,5 and protons.6 The most-studied perovskites are oxides. However, halide perovskites have recently attracted a resurgence of interest. This is largely due to the outstanding photovoltaic performance of the lead-halide 3D perovskites (Fig. 1A), which have afforded solar cells with power conversion efficiencies exceeding 24% 7 only 10 years since their initial demonstration.8 However, the inherent instability, high toxicity, and environmental mobility of these water-soluble Pb2+ salts9,10 have instigated a large effort to identify other compositions that possess similar electronic properties.
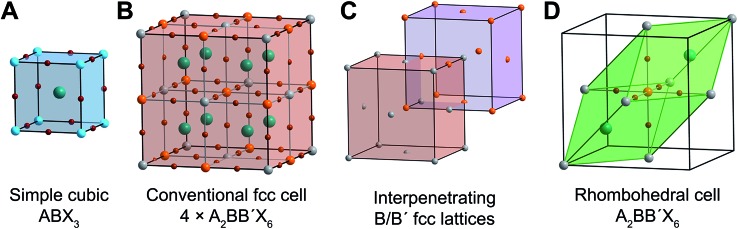
Fig. 1. Ball-and-stick representations of (A) the unit cell of the cubic single perovskite CsPbIIBr3 and (B) the conventional (four formula units) face-centered-cubic (fcc) cell of the double perovskite Cs2AgIBiIIIBr6. (C) Depiction of the interpenetrating B/B′ fcc lattices present in rock-salt-ordered double perovskites such as Cs2AgBiBr6. (D) The rhombohedral (one formula unit) unit cell of Cs2AgBiBr6. Turquoise, orange, silver, green, and brown spheres represent Pb, Bi, Ag, Cs, and Br atoms, respectively.
The recent revival of interest in halide double perovskites (elpasolites),11–13 which have been known since the 1880s,14 has been primarily motivated by the desire to replicate the electronic structures of the lead-halide perovskites15 in alternative compositions. We have been deeply invested in this effort, primarily through the introduction of double perovskites as potential solar absorbers11 and the synthesis of targeted new compositions for obtaining suitable bandgaps for sunlight absorption.16,17 The AI2BB′X6 double perovskites (A = monovalent cation, X = halide; Fig. 1B) have the same connectivity as the ABIIX3 single perovskites but divide the formally 2+ charge at the octahedral site (the B site) unevenly over two sites, allowing for the incorporation of metals with oxidation states from +1 to +4. This uneven division is advantageous because almost every element has a stable oxidation state between +1 and +4 allowing a wider variety of metals to be incorporated. The compositional flexibility of double perovskites leads to an incredible degree of complexity and diversity in their electronic structures. In these materials, a single metal substitution can drastically modify the band edges, leading to the observation of direct-allowed, direct-forbidden, and indirect bandgaps, both large and small in magnitude, all within the same structural family.11–13,17–21 It is increasingly evident that double perovskites afford a highly tunable electronic platform; however, in order to realize their true potential, we must first understand the origins of their electronic diversity.
With computing time now quite cheap, electronic structures are determined almost exclusively through density functional theory (DFT) calculations. Many such studies have been performed for halide perovskites, providing important insights to their optoelectronic properties.12,13,17–26 These methods and the band diagrams they produce, however, are specific to the perovskite under study and not necessarily generalizable. Additionally, typical band structure diagrams often obscure the local chemical information contained in the electronic structure. For instance, the atomic composition of the bands, the directionality (σ and π character) and symmetry (bonding, antibonding, nonbonding nature) of the interactions between the orbitals that compose the bands, and the variation of these parameters within a band, are often not readily available from the final band structure.
In this contribution, we develop a simple theory, complementary to the existing DFT paradigm, which bridges our chemical understanding of metal–halide coordination complexes and halide perovskite band structure. In particular, we flesh out the perovskite band structure with atomistic detail, emphasizing the local molecular interactions that ultimately dictate the bandgap and band dispersion. We construct the band diagrams using arguments founded on the symmetries and relative energies of atomic orbitals—methods that are intuitive to both molecular and solid-state chemists and that have a long history of correctly predicting material properties from simple starting points.
We will show that a linear combination of atomic orbitals (LCAO) approach,27,28 in particular the qualitative analysis demonstrated by Hoffmann and others,29 accurately reproduces the electronic band structure of halide double perovskites near their high-symmetry k points. For the lead–halide perovskites, a similar qualitative approach was recently reported,30 and a handful of quantitative (but closely related) tight-binding models have been developed.31,32 Additionally, tight-binding models for some oxide perovskites are also available.33–35 However, to our knowledge, this is the first report of LCAO analysis on halide double perovskites. We hope that this work will develop a general, intuitive picture of double perovskite electronic structure, provide a simple check for theoretical investigations of electronic structure, and serve as a useful starting point for exploratory syntheses of new double perovskites.
The paper is organized as follows: in Section 2, we present our LCAO method for constructing extended electronic states, which is a modification of prior approaches (Fig. 2).29,30 In Section 3, we apply the LCAO method to two case studies demonstrating its utility for understanding the electronic structure of known halide double perovskites. We also derive general rules for predicting band extrema in halide double perovskites. In Section 4, we condense our results to a simple table (Table 1), where knowledge (based on measurement or chemical intuition) of the frontier atomic orbitals of a given perovskite composition enables immediate determination of the conduction band minimum (CBM) and valence band maximum (VBM) for the vast majority of double perovskites. We compare our predictions against DFT results for many known halide double perovskites and show overwhelming agreement. We conclude by discussing the limitations and possible extensions of the method.
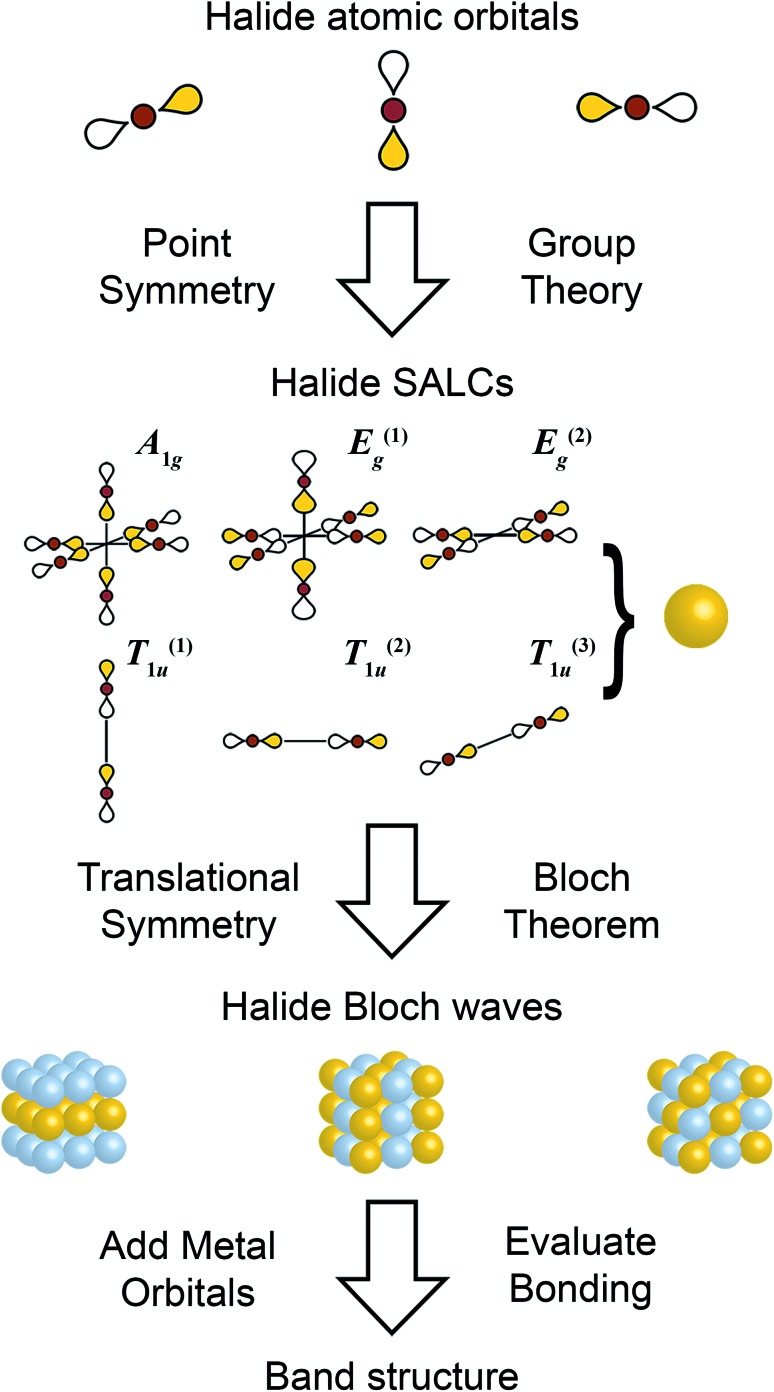
Fig. 2. Schematic showing the steps of the Linear Combination of Atomic Orbitals (LCAO) method. Halide p orbitals are used to form symmetry adapted linear combinations (SALCs), which are propagated through three-dimensions to form halide-only Bloch waves. Metal orbitals are then introduced to evaluate band dispersion. Only σ bonds are considered here. See ESI† for consideration of π bonds.
Table 1. Expected k points of the conduction band minimum (CBM) and valence band maximum (VBM) for all possible combinations of B and B′ orbitals. Note that the VBM and CBM must be evaluated separately for a given perovskite.
| Orbitals |
Prediction |
||
| B | B′ | VBM | CBM |
| σ-Bonding states a | |||
| s | s | Γ | Γ |
| p | p | Γ | Γ |
| dx2–y2/dz2 | dx2–y2/dz2 | Γ & X | Γ & X |
| s | p | L | L |
| s | dx2–y2/dz2 | X | X |
| p | dx2–y2/dz2 | — | — |
| s | Null | X | Γ |
| p | Null | L | L |
| dx2–y2/dz2 | Null | Γ & X | X |
| Null | Null | Γ & X | — |
| π-Bonding states a | |||
| dxy/yz/xz | dxy/yz/xz | Γ & X | Γ & X |
| dxy/yz/xz | Null | X | Γ & X |
| Null | Null | Γ b | — |
aπ- and σ-bonding states involve orthogonal orbitals and cannot interact (see ESI).
bThe σ-bonding halide-only states have more 90° X–X interactions than the π-bonding ones and will often form the band extrema (see ESI).
2. Methods
For a general overview of the LCAO method, we refer the reader to one of several excellent texts;29,36,37 a brief primer is also provided in the ESI.† Our approach deviates from prior LCAO schemes, which typically apply translational symmetry to the molecular metal–ligand complex in order to build the extended solid.29,30 In order to generalize to all halide double perovskites (with any combination of B-site metals), here we apply translational symmetry to just the octahedrally arranged ligands and introduce metal–ligand interactions only after the extended electronic states have been constructed (Fig. 2).
The DFT calculations used to check our results were performed using the PBEsol exchange–correlation approximation as implemented in the VASP program code, including spin–orbit coupling (SOC) self-consistently (see ESI† for computational details).
2.1. The double perovskite crystal structure and unit cell
The ABX3 perovskite structure (Fig. 1A) consists of a 3D lattice of corner-sharing halide octahedra, with the (typically divalent) B-site metal occupying the center of the octahedra. The (typically monovalent) A-site cation occupies the cuboctahedral cavities defined by eight corner-sharing metal–halide octahedra. The A-site cation (e.g., Cs+, CH3NH3+) generally does not interact electronically with the B–X sublattice and does not contribute meaningfully to the electronic structure near the band edges. Consequently, we will neglect it going forward.
Double perovskites contain two crystallographically distinct B sites. Most commonly, two distinct metal cations (differing in identity or oxidation state) occupy the B sites, alternating in all three directions (Fig. 1B). This ordering generates two interpenetrating face-centered-cubic (fcc) sublattices that are shifted by half a unit cell (in all three directions) from one another, similar to the NaCl rock-salt structure (Fig. 1C). Therefore, while cubic ABX3 perovskites have a primitive cubic lattice, the broken B-site symmetry gives A2BB′X6 double perovskites a face-centered-cubic (fcc) lattice, placing them in the Fm3[combining macron]m space group. The conventional double perovskite fcc cell contains four formula units and, thus, is actually a supercell of the double perovskite lattice. The unit cell containing a single formula unit is a rhombohedral cell, which is the primitive unit cell of one of the fcc lattices (Fig. 1D). Unlike the cubic conventional cell, which has 90° angles between its axes, the angle between the rhombohedral cell axes (a1, a2, and a3) is 60°. Geometric transformations between primitive and conventional fcc cells are provided in Fig. S2.†
2.2. Constructing symmetry-adapted linear combinations (SALCs) of halide orbitals
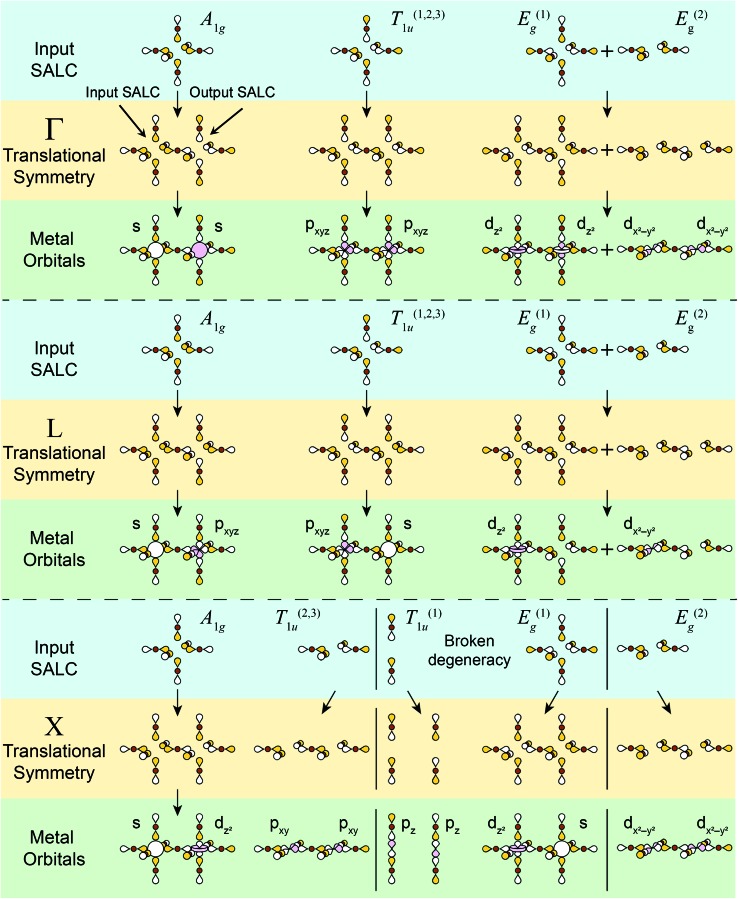
As the first step in the LCAO theory, we will consider only the halides and use group theory to find their symmetry-adapted linear combinations (SALCs). Here, we consider the 6 halides arranged in an octahedral geometry around the B site in the rhombohedral unit cell (Fig. 1D). Each halide contributes three orthogonal p orbitals: one σ-bonding orbital and two π-bonding orbitals. We will initially neglect the two π-bonding p orbitals. When only main group or d10 cations are in the B site, this simplification is valid as the band edges will consist of only σ-bonding states (see Fig. S1†). When a d0–d9 or a lanthanide cation is present at one or both B sites, the π interactions must be considered (shown in the ESI†). Due to the rock-salt ordering of the B and B′ cations, the rhombohedral double-perovskite unit cell has D3d point symmetry. However, because we initially neglect the metals and only consider the halides, we can treat the point symmetry as Oh (and account for D3d symmetry when applying translational symmetry). Using group theory, we generate the symmetry adapted linear combinations (SALCs) of the 6 halide orbitals: A1g, E(1),(2)g, and T(1),(2),(3)1u (Fig. 2, see Fig. S4† for full analysis) as expected for a molecular octahedral complex with σ bonding.
2.3. Applying translational symmetry
To move from a molecular picture to that of an extended solid, we must propagate our halide SALCs using the translational symmetry of the double perovskite lattice. Translational symmetry is described mathematically by the Bloch theorem:ψ(r + R) = eik·Rψ(r)where ψ(r) represents the wavefunction of a single unit cell (here a halide SALC) at the origin, the vector R describes the position of a second unit cell with respect to the origin, and the vector k describes how the phase of the wavefunction (the SALC) changes upon translation. Thus, the Bloch theorem states that the wavefunction in a crystalline solid may only change by a phase factor (the exponential factor) upon translating from one unit cell to the next (Fig. 3). The degree of that phase change is described by the translational quantum number k. For three dimensional materials, k is a vector with coordinates derived from the three lattice vectors of the unit cell. We will focus our analysis on the high-symmetry k points, where the coordinates of k adopt values of either 0 or π/a (a = unit-cell length). A coordinate of 0 denotes symmetric translation of the wavefunction along the corresponding direction (ψ(r)ei·0·a = ψ(r)) whereas a coordinate of π/a denotes antisymmetric translation (ψ(r)ei·(π/a)·a = –ψ(r)). At lower-symmetry k points, k holds an intermediate value, resulting in some unit cells having wavefunctions with less than the maximal amplitude. For example, a coordinate of π/2a results in every unit cell being out of phase with its second-nearest neighbours and in phase with its fourth-nearest neighbours, while the first- and third-nearest neighbours are nodes with zero amplitude. The Bloch theorem thus produces periodic patterns of in-phase and/or out-of-phase SALCs, termed Bloch waves. High-symmetry k points produce Bloch waves where the wavefunction of every unit cell has maximal amplitude, allowing for strong bonding and antibonding interactions. Thus, band extrema (the most bonding or antibonding states within a band) typically occur at high-symmetry k points.
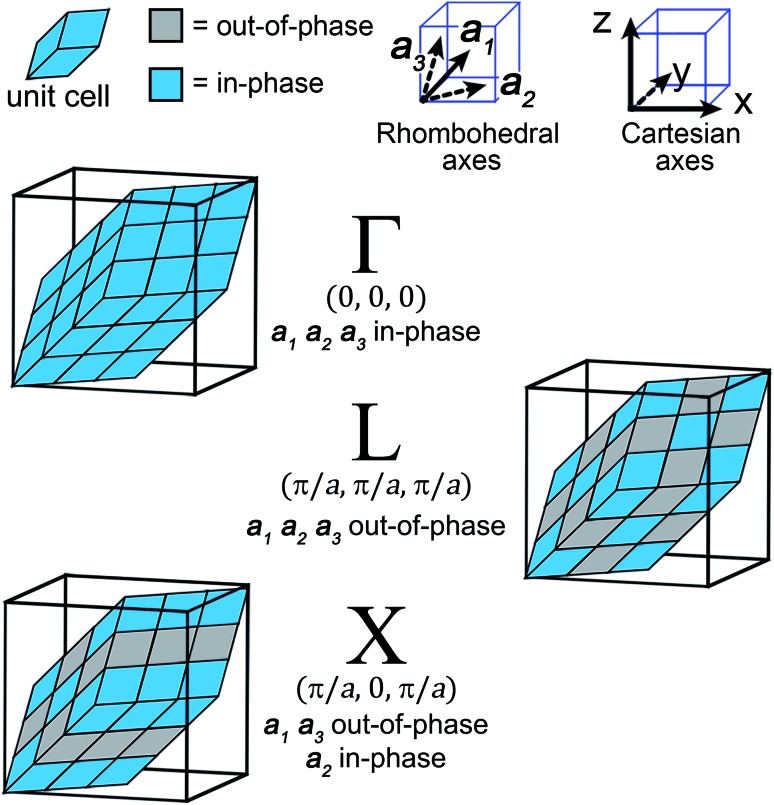
Fig. 3. The translational symmetry, in real space, of the high-symmetry k points (Γ, L & X) for the double-perovskite structure.
For our analysis, we will consider the three highest-symmetry k points of the fcc lattice: Γ: (0,0,0), L: (π/a,π/a,π/a), and X: (π/a,0,π/a). Here, Γ corresponds to in-phase SALCs along each axis, L to out-of-phase SALCs along each axis, and X to out-of-phase SALCs along the a1 and a3 axes and in-phase SALCs along the a2 axis (see Fig. 3). These axes are defined with respect to the rhombohedral unit cell and point at 60° angles with respect to one another. Visualizing translations along these non-orthogonal rhombohedral lattice vectors is rather difficult, so we use a geometric trick to transform the three rhombohedral vectors into two orthogonal vectors that lie within a Cartesian plane (see Fig. S2†).
We now apply translational symmetry to the SALCs to construct halide-based Bloch waves (Fig. 4). We arbitrarily pick one unit cell as the origin and place a halide SALC around the B (or B′) site. Note that for ease of visualization, the unit-cell origin in Fig. 4 has been shifted from that in Fig. 1D. We then translate the SALC along one of the two orthogonal vectors to the adjacent unit cell. Depending on the coordinate of k for our chosen direction, the phases of the orbitals in the new unit cell will either be in-phase or out-of-phase with respect to the SALC at the origin. We continue to propagate the Bloch wave by translating to additional unit cells, making use of both orthogonal vectors. This yields a Bloch wave propagated along two dimensions (x and z in Fig. 4). Different combinations of the rhombohedral vectors allow for propagation of the Bloch wave along the xy (or yz) plane. Note that the translational symmetry at some k points results in Bloch waves that lift the degeneracies of formerly degenerate SALCs (the two Eg and three T1u SALCS). In particular, while Γ and L are isotropic (ka1 = ka2 = ka3) X is anisotropic (ka1 = ka3 ≠ ka2), leading to splitting of both the Eg and T1u SALCs at X. Overall, this procedure generates 11 high-symmetry non-degenerate Bloch waves, 3 each at Γ and L and 5 at X (see Fig. 5).
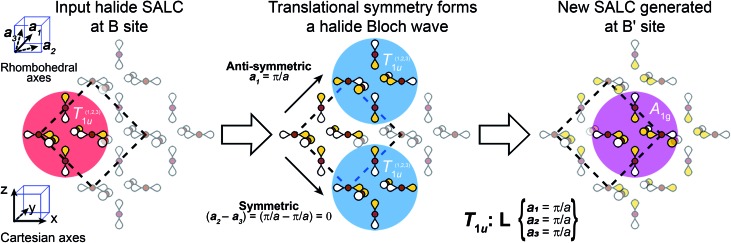
Fig. 4. An example of how to obtain the halide-based Bloch waves at one of the high-symmetry k points of the double-perovskite lattice. The SALC we place at the B site (the “input SALC” highlighted in red, in this example T1u) is propagated along the unit-cell axes using the translational symmetry of the k point (in this example L). Here, translational symmetry generates a SALC at the B′ site that exhibits A1g symmetry (the “output SALC”, highlighted in pink). Yellow and white lobes represent positive and negative phases, respectively.
Fig. 5. Summary of all possible Bloch waves for the σ-bonding halide SALCs at the high-symmetry k points Γ, L, and X and their interactions with metal-centered orbitals. The “input SALC” is shown on the left side and the “output SALC”, which is generated by translational symmetry (see Fig. 4 for further explanation), is shown on the right side. Here, only one unit cell is shown, but all other unit cells will have the same symmetry. Colored and empty lobes represent positive and negative phases respectively. For ease of visualization, the three degenerate T1u SALCs (T(1)1u, T(2)1u, T(3)1u) and their associated Bloch waves are shown together whereas the two degenerate Eg SALCs (E(1)g, E(2)g) and their associated Bloch waves are shown separately. Both degenerate sets (Eg and T1u) split at X with the new non-degenerate SALCs and associated Bloch waves separated by solid black lines. Metal orbitals are assigned by inspecting the symmetry around the B and B′ sites.
At high-symmetry k points, the SALCs around every B site in the lattice will be identical (although the phases may be flipped), and likewise, every B′ site will be identical. Note that this is not true for lower-symmetry k points. Thus, it is sufficient to represent each Bloch wave at high-symmetry k points by showing the SALCs around just one B and one B′ site. Fig. 5 depicts this for all eleven Bloch waves. Complete pictures of the 11 nondegenerate Bloch waves are given in Fig. S5–S17.†
There are several important observations we can make at this point. Inspection of Fig. 5 shows that, although the local symmetry at the B site is set by our initial choice of SALC, the environment around the B′ site is generated entirely by the translational symmetry of the double perovskite lattice at the various k points. Additionally, many of the SALCs that surround the B and B′ sites appear to be a combination of two of the original SALCs (A1g, T1u, Eg). Note that, due to the application of translational symmetry, the Bloch waves do not necessarily maintain the degeneracy of their parent SALC (i.e., an Eg SALC does not form a doubly degenerate Bloch wave at all k points). However, to make the connection between the original input SALC and the Bloch wave derived from it explicit, we refer to Bloch waves as “X-derived”, where X is one of the original three SALCs (A1g, Eg, T1u). For example, Fig. 4 shows a T1u-derived Bloch wave.
2.4. Adding the metals and evaluating bonding interactions
Thus far, we have focused on symmetry and neglected any energetic considerations. Now we consider how the halide-only Bloch waves we have constructed interact with the B-site metal atomic orbitals and use this to rank all the possible Bloch waves on a relative energy scale. Although this approach will work for any set of orbitals, because we are primarily concerned with the valence band maximum (VBM) and conduction band minimum (CBM), we can limit our discussion to the frontier atomic orbitals of the B and B′ elements. This is because, when metal contributions are present, the highest occupied and lowest unoccupied molecular orbitals (HOMO and LUMO, respectively) will give rise to the highest-energy valence and lowest-energy conduction bands, respectively.
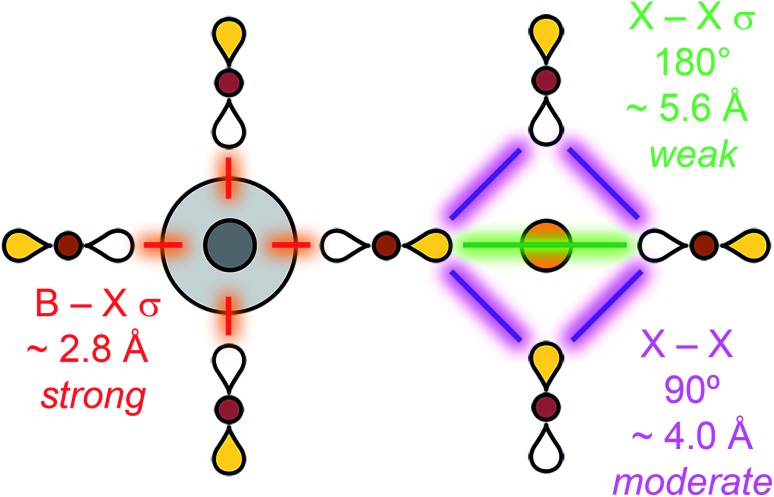
Intuitively, the energy of a given Bloch wave is proportional to the sum of all the bonding and anti-bonding interactions it generates throughout the material. The large number of atoms in the unit cell and complex geometry of the structure makes this sum difficult to evaluate fully. Instead, we must decide which interactions have the largest effect on the overall energy and are the most important to consider. Fig. 6 summarizes our key assumptions. The B–X nearest-neighbour interactions (σ bonds) are, by far, the largest contributors to the overall energy. This statement can be justified by observing that B–X bonds are the shortest bonds in the perovskite structure and, therefore, large orbital overlap and strong energy-level splitting are expected. The next strongest interactions, although much weaker than B–X bonds, are the 90° X–X interactions and the 180° X–X σ bonds that occur between the halides surrounding the B site. Whereas the 90° X–X interaction occurs over a shorter distance, the 180° X–X σ bond might be expected to have better overlap due to the head-to-head orientation of the p orbitals. However, empirically we find that, for chlorides, bromides, and iodides, treating the 90° X–X interaction as the stronger of the two interactions gives the correct results (see Section 3.2). This may differ for fluorides or oxides, which have smaller p orbitals and lattice spacings. Evaluating the energy of each Bloch wave considering just these B–X and 90° X–X interactions leads to correct predictions of the CBM and VBM of the vast majority of double perovskite band structures. This approach is the qualitative equivalent of a tight-binding model, which includes both nearest-neighbour and second-nearest-neighbour interactions.
Fig. 6. Hierarchy of bonding interactions in a halide perovskite lattice. Distances are given for Cs2AgBiBr6.10 B = metal, X = Cl, Br or I.
3. Results
To demonstrate our methodology, we now present two case studies of known perovskites. These studies represent cases where the material's band extrema are determined by B–X interactions only, X–X interactions only, or a combination of B–X and X–X interactions. These three situations cover all possibilities for cubic double perovskites and the rules we develop for them can be generalized to predict the extrema of double perovskites with any combination of B-site cations. We then evaluate the success of our LCAO theory against a large number of known perovskites.
3.1. Case study 1: perovskites where both B-site frontier orbitals participate in the band
Summary: in perovskites where both the B- and B′-site metal orbitals contribute to a band, the conduction band minimum or valence band maximum occurs at the k point where the symmetry of the halide SALCs around the B and B′ sites match the symmetry of the metal frontier orbitals at both sites.
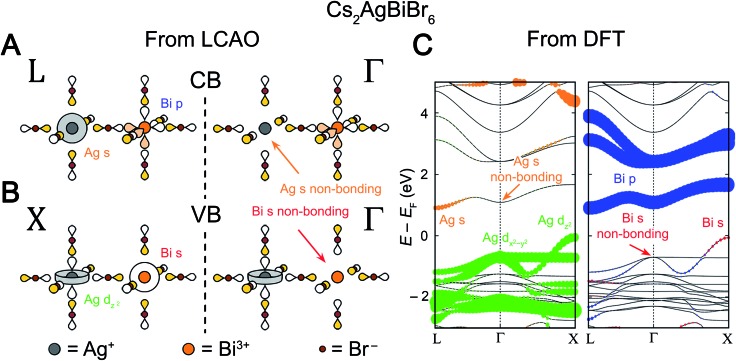
When both the B and B′ elements have orbitals that participate in a band, our assumption that B–X interactions largely determine the relative energies of the Bloch waves at the high-symmetry k points is valid. It is instructive to use Cs2AgBiBr6 as an example of this case. The indirect bandgap of this perovskite has been experimentally and theoretically verified by several different groups.11–13 Using our analysis we can understand the atomistic origins of this indirect transition.
We will begin by examining the valence band. We know that the VBM will occur at one of the high-symmetry k points, so our task is to determine which of these points has the highest energy. We postulate that the frontier orbitals of both metals (Ag+ 4dz2/4dx2–y2 and Bi3+ 6s) have sufficiently similar energies to contribute to the valence band (Section 3.2 will address perovskites where this is not the case). For cations with the valence electron configuration of 4d105s0 (Ag+) or 6s26p0 (Bi3+), a simple octahedral MO diagram (Fig. S1†) indicates that the HOMO (and therefore the VBM) will have antibonding character. Therefore, to find the highest-energy k point of the valence band, we simply need to find which of the Bloch waves in Fig. 5 maximizes the number of antibonding interactions between the halide SALCs and the metal orbitals. A metal orbital will form bonding or antibonding interactions with a halide SALC that matches its symmetry and a nonbonding interaction with a SALC that does not. Since both filled Bi3+ 6s and Ag+ 4d orbitals participate in the valence band, the Bloch wave with maximal antibonding interactions should involve SALCs that match the symmetry of the s and dz2/dx2–y2 orbitals. Inspection of Fig. 5 shows that two Bloch waves, both at X, simultaneously match the symmetry of the Bi3+ 6s and the Ag+ 4dz2 orbitals implying that the VBM will be at X (Fig. 7B). Due to the splitting of the Eg-derived Bloch waves at X, the Ag+ 4dx2–y2 orbital forms a separate band that has fewer overall antibonding interactions and is, therefore, not the VBM.
Fig. 7. LCAO representations of (A) the conduction band (CB) at L and Γ and (B) the valence band (VB) at X and Γ for Cs2AgBiBr6, obtained using the LCAO theory illustrated in Fig. 5. Net nonbonding interactions between the halide SALCs and the metal s orbitals explain the missing Ag 5s0 (orange arrow) and Bi 6s2 (red arrow) orbital contributions at Γ at the CB and VB, respectively. Colored and empty lobes represent positive and negative phases, respectively. (C) Band structure of the double perovskite Cs2AgBiBr6 computed using DFT, showing an indirect gap from X to L. The band structure is shown in duplicate and the orbital contributions of the B-site atoms (Ag and Bi) are given in color with the dot size proportional to the size of the orbital contribution. Bromide contributions are present but not shown. Note that Ag 5s character is absent at the Γ point in the CB and that Bi 6s character is absent at the Γ point in the VB (denoted by orange and red arrows, respectively), in agreement with the LCAO analysis.
A similar analysis is possible for the CBM. Again, we assume that the B and B′ frontier orbitals (empty Bi3+ 6p and Ag+ 5s orbitals) both participate in the band. We know from the simple octahedral MO diagram (Fig. S1†) that the LUMO is antibonding, meaning that the conduction band will be antibonding overall. We are seeking the lowest-energy k point for the CBM; therefore, we should maximize bonding interactions while maintaining an overall antibonding character to the band. Because both metals contribute to the CBM, the lowest-energy net-antibonding state is one where one metal is bonding and the other is anti-bonding with the halides. As long as the antibonding metal contributes more to the electronic state, the band will remain net antibonding. Importantly, we do not need to know which metal is antibonding and which is bonding with the halides in order to correctly predict the CBM since both bonding and antibonding interactions require a symmetry match between the metal orbital and SALC. As for the VBM, we simply need to determine which Bloch wave has SALCs that match the orbital symmetry of both metals. In this case, the symmetry of the Bi3+ 6p and Ag+ 5s orbitals are matched by two Bloch waves, which both occur at L, indicating that the CBM is at L (Fig. 7A).
We can check our results against the band structure of Cs2AgBiBr6 computed through DFT (Fig. 7C). Consistent with our model's predictions, the VBM lies at X and the CBM at L, yielding the experimentally observed indirect gap. The band structure can be deconstructed with atomic detail by projecting the electronic states from the DFT calculation onto spherical harmonics centered at each metal ion (plotted in color in Fig. 7C). We can view each individual band as arising from a root metal–hexahalide (BX6n–) molecular orbital at the B site, whose energy is perturbed by the additional metal–halide interactions around the B′ site (or vice versa). For the two highest-energy valence bands, Fig. 7C shows Ag d character present at all values of k. This means that the MOs formed from an antibonding combination of Ag 4dz2 or 4dx2–y2 atomic orbitals with the Eg SALCs can be considered as the root MOs that form these bands. One of these MOs will be a component of every electronic state in the upper two valence bands. Reading down the Eg column in Fig. 5 gives the Bloch waves for these bands at Γ, L, and X (Fig. 7B; L not shown). From Fig. 5, the dz2 and dx2–y2 bands are degenerate at Γ and split at X, which is reproduced in the band structure. In both bands, the SALC around the Ag site remains constant, while the SALC around the Bi site changes with k. For example, in the Ag dz2 band along the Γ to X direction, the Bi-centered SALC gradually transitions from Eg symmetry to A1g symmetry and its interaction with the Bi 6s orbital changes from non-bonding at Γ to antibonding at X (Fig. 5). This increased antibonding character pushes the energy at X above that at Γ to form the VBM at X. Consistent with this prediction, Fig. 7C shows Bi s character only near X, coincident with an upturn in the Ag dz2 band's energy. In contrast, the Ag dx2–y2 band remains nonbonding with the Bi 6s orbital from Γ to X and is energetically flat. According to Fig. 5, the two bands should be degenerate at L, but they are split in the DFT band structure due to spin–orbit coupling (see Fig. S3 and discussion in the ESI†).
We can perform a similar analysis for the conduction bands. Here the presence of Bi p character at all k points in Fig. 7A indicates that these bands' root MOs are the antibonding combinations of the three Bi 6p orbitals with the T1u symmetry halide SALCs, leading to the observation of Bi p character at all k points in Fig. 7C. From the T1u column of Fig. 5, we find that, moving from Γ to L, the symmetry of the SALC at the Ag site gradually changes from T1u symmetry to A1g symmetry (Fig. 7A). As the symmetry of the SALC approaches A1g, the bonding interaction between the SALC and the Ag 5s orbital becomes more significant, lowering the energy of the band at L relative to that at Γ and forming the CBM at L. Notice again that while the band is derived from a Bi-centered MO, the dispersion (the variation of a band's energy with k) is determined by changes in the bonding around the Ag site. The three conduction bands in Fig. 7C (derived from mixtures of px, py, and pz orbitals) are not degenerate at Γ and L although they are expected to be from Fig. 5. As in the valence band, this is due to spin–orbit coupling (see Fig. S3 and discussion in the ESI†).
DFT provided information about which orbital was present at all k points within a given band (and therefore was the root MO) and which was present at only one, enabling us to develop a detailed and intuitive description of band dispersion in Cs2AgBiBr6. However, we were able to correctly predict the VBM/CBM without utilizing DFT, relying on qualitative arguments alone. In general, if both orbitals participate in the band edges, determining the VBM/CBM only requires knowledge of the frontier orbitals. The results, for every possible combination of B and B′ orbitals, are summarized in Table 1. Here, the conduction band and the valence band should be evaluated independently. For example, using Table 1 for Cs2AgBiBr6, the filled Ag and Bi frontier orbitals that form the valence band are d and s orbitals, respectively, affording a maximum at X. Similarly, empty Ag s and Bi p orbitals compose the conduction band, generating a minimum at L.
3.2. Case study 2: perovskites where at least one B-site frontier orbital does not participate in the band
Summary: in perovskites where only one metal contributes to the band, the conduction band minimum or valence band maximum is set by the 90° interactions of the halides surrounding the other (nonparticipating) metal site.
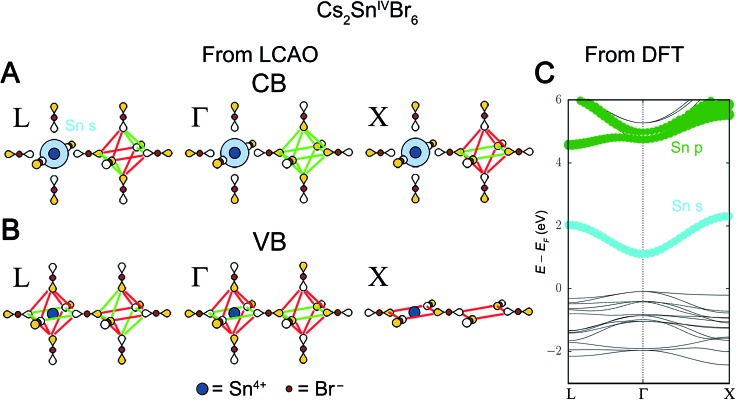
The analysis in Section 3.1 requires both B-site atoms to have orbitals that participate in the bands near the bandgap. However, there are several examples of double perovskites where one of the B sites is empty, as in A2BIV□X6 (□ = vacancy),38–42 or where the orbitals of one or both of the B-site HOMOs/LUMOs are of incorrect energy to be near the bandgap (for example the valence band of Cs2AgTlX6).17 We use the example of Cs2SnIV□Br6 to illustrate how to use weaker X–X interactions to obtain the correct band structure in these cases.
The Sn4+ LUMO is the 5s orbital and, from Fig. S1,† we expect it to be a major component of the lowest-energy Cs2SnIV□Br6 conduction band. To match the Sn 5s orbital symmetry, the Bloch waves of this conduction band must be derived from the A1g SALC. Reading down the A1g column in Fig. 5 gives the Bloch waves for the Cs2SnIV□Br6 conduction band at Γ, L, and X (Fig. 8A). Because the SALC around the Sn site is the same in all three of these Bloch waves, each has the same number of B–X antibonding interactions. In fact, the three Bloch waves only differ in what SALC is generated around the vacant B′ site where B–X interactions are not possible. Therefore, to understand the dispersion of this band and energetically distinguish the three k points, we must consider how the weaker X–X interactions affect the energy of each Bloch wave.
Fig. 8. LCAO representations of (A) the conduction band (CB) and (B) valence band (VB) of Cs2SnIV□Br6 obtained from Fig. 5. Colored lobes represent positive phases and empty lobes represent negative phases. Green and red lines show the 90° X–X bonding and antibonding interactions, respectively, between the bromide p orbitals. (C) DFT band structure of the double perovskite Cs2SnIV□Br6. The orbital contributions of the Sn atom are given in color with dot size proportional to the size of orbital contribution. Bromide contributions are present but not shown.
There are two possible X–X interactions that may be significant: the 180° X–X σ interaction and the 90° X–X interaction (Fig. 6). We will consider three limiting scenarios. First, that only the 180° interactions are important, second that only the 90° X–X interactions are important, and third that both the 180° and 90° interactions are equally important. The relative energies of the three SALCs surrounding the vacant site in Fig. 8A can be evaluated based on the number of bonding and antibonding interactions they produce under each of these assumptions (Fig. S18†). For a stronger 180° X–X σ interaction, the conduction band Bloch waves at the high-symmetry k points are ranked from lowest to highest energy as follows: Γ = X < L. Assuming a stronger 90° X–X interaction gives: Γ < L < X. If both interactions are equally significant, the ordering becomes Γ < X < L. To distinguish between these scenarios, we use information from DFT.
The DFT band structure of Cs2SnIV□Br6 is shown in Fig. 8C with the Sn contributions shown in color. As expected, the Sn 5s orbital is present at all k points in the conduction band. The relative energies of the conduction band Bloch waves in Fig. 8C (Γ < L < X) is consistent with the 90° X–X interaction being stronger than the 180° X–X interaction. In fact, every reported A2BIV□X6 perovskite electronic structure (BIV = Sn4+, Pd4+, Hf4+, Te4+, Ti4+)38–42 supports the conclusion that the 90° X–X interaction is, after B–X interactions, the most important.
In some double perovskites, no metal orbital has the correct energy to be present near the valence band maximum and the band is composed of pure halide orbitals that are non-bonding with respect to the B-site metals. The valence band of Cs2SnIV□Br6 is one such case. The Sn4+ HOMO, a 4d orbital, has a binding energy of 23–27 eV below vacuum, as determined by X-ray photoelectron spectroscopy,43 too low in energy to participate in bonding. Thus, the bandgap transition is a pure ligand-to-metal charge transfer (LMCT). Although there are no B–X interactions in the Cs2SnIV□Br6 valence band, the 90° X–X interactions are still present, and these alone will determine the VBM. Fig. 8B shows the Bloch waves from Fig. 5 with the most X–X antibonding character at L, Γ, and X. These Bloch waves correspond to the highest-energy occupied states at each high-symmetry k point in the valence band. The Bloch wave at L shows 4 net-antibonding interactions, whereas both Γ and X show 8 net-antibonding interactions. The Eg-derived Bloch waves at Γ and X, thus produce the VBM. While the valence band Bloch waves at Γ and X have the same number of net antibonding interactions, in the DFT band structure of Cs2SnIV□I6, X lies slightly below Γ. This can be justified by noting that antibonding interactions are slightly more destabilizing than their corresponding bonding interactions are stabilizing. This should push Γ slightly higher than X as it has more antibonding interactions overall. However, this phenomenon does not appear to be general; other compounds with halide-only valence bands (Cs2HfIV□I6, Cs2PdIV□Br6, Cs2TiIV□I6) show a much closer match between Γ and X.40–42 We collect predictions for all possible perovskite compositions where only one B-site orbital or no B-site orbitals participate in the band edges in Table 1.
Finally, we note that the diagrams we construct in Fig. 8A and B contain additional information beyond the relative energies of the high-symmetry k points. For example, Cs2SnIV□Br6 is isostructural and isoelectronic with Cs2SnIV□I6, which is known to possess a parity-forbidden bandgap.39 Parity-forbidden bandgaps have been identified in several other double perovskites,17,44 and are an emerging topic of interest. While treating this problem exhaustively is beyond the scope of our current work, we can see from Fig. 8 how the parity-forbidden bandgap arises in Cs2SnIV□I6. Inspection of Fig. 8A and B at Γ show that, around both the B and B′ site, the CBM consists of A1g symmetry SALCs and the VBM consists of Eg symmetry SALCs. The gerade symmetry of both the VBM and CBM states means that an optical transition between them is parity (or Laporte) forbidden.
4. Discussion
4.1. Rules for determining band extrema
We have now treated all possible scenarios involving perovskites with σ-bonding orbitals at their band edges (main group and d10 cations). A similar analysis for perovskites with π-bonding orbitals at their band edges (d0–d9 cations) is given in the ESI.† It is worth pausing at this point to summarize our results and benchmark them to literature DFT reports of double perovskites (Section 4.2). From the case studies, we have developed three rules for determining band extrema:
1. If both B and B′ metal orbitals contribute substantially to the band, the band extremum will be at the k point where the halide SALCs around each site match the symmetry of the B and B′ HOMOs (for the VBM) or LUMOs (for the CBM).
2. If only one B-site metal orbital is significantly involved in a band, the VBM will be at the k point with SALCs that match the symmetry of the HOMO around the participating metal and maximize the 90° X–X antibonding interactions around the non-participating metal site. Similarly, the CBM will be at the k point with SALCs that match the symmetry of the LUMO around the participating metal and maximize the 90° X–X bonding interactions around the non-participating metal site.
3. If no B-site metal orbitals participate in the valence band, the VBM will occur at the k point that maximizes the number of 90° X–X antibonding interactions around both sites. This will always be at the Γ and X points.
Following these rules allows for predictions of band extrema for all possible combinations of orbitals. These predictions are summarized in Table 1.
4.2. Comparison of the theory to experiment and calculations
For the LCAO theory to be successful, it must accurately predict the k point of both the VBM and CBM for the full range of double perovskites. In Table 2, we compare the predictions contained in Table 1 to predictions determined by DFT-based methods for a wide range of known cubic double perovskites. To ensure consistency in making this comparison, we use the computed density of states to determine the orbital composition of the valence and conduction bands of each compound. In many cases, this additional information is unnecessary as determining the orbital composition of these bands from chemical reasoning or experimental measurement of orbital energies results in the correct answer. The LCAO theory is remarkably successful, showing full agreement with DFT results for all synthesized double perovskite compositions of which we are aware, except for one. The exception is the valence band of Cs2AgYCl6. Here, the reported density of states shows predominantly Ag orbital character in the VBM and a band maximum at L, instead of a maximum at Γ or X as our model predicts for a pure Ag d band. Nevertheless, the overwhelming agreement between our predictions and computational methods instils confidence in the validity of our approach.
Table 2. Comparison of the band extrema predicted in Table 1 to those predicted by DFT calculations for a wide range of cubic double perovskites. The B and B′ orbitals that contribute to a band were determined from DFT density-of-states calculations but, in principle, could come from chemical reasoning or experimental information. For a given perovskite, the k points corresponding to band extrema that are calculated to be within 0.1 eV of each other are listed together.
| Compound | Valence band maximum |
Conduction band minimum |
Bandgap | Reference | ||||||
| B | B′ | Pred. | Calc. | B | B′ | Pred. | Calc. | |||
| Cs2AgBiBr6 a | Ag 4dz2 | Bi 6s | X | X | Ag 5s | Bi 6p | L | L | Indirect | 12 |
| Cs2AgInCl6 | Ag 4dz2 b | Null | Γ | Γ | Ag 5s | In 5s | Γ | Γ | Direct | 18 |
| Cs2AgSbBr6 a | Ag 4dz2 | Sb 5s | X | X | Ag 5s | Sb 5p | L | L | Indirect | 46 |
| Cs2AgTlBr6 a | Ag 4dz2 b | Null | Γ | Γ | Ag 5s | Tl 6s | Γ | Γ | Direct | 17 |
| Cs2AgYCl6 | Ag 4dz2 b | Null | Γ & X | L | Ag 5s | Null c | Γ | Γ | Indirect | 47 |
| Cs2KBiCl6 | K 3p | Bi 6s | L | L | K 4p d | Bi 6p | Γ | Γ & L | Direct | See ESI |
| Cs2KYCl6 | Null | Null | Γ & X | Γ & X | Null | Y 4dxy e | Γ | Γ | Direct | 44 |
| Cs2NaBiCl6 | Null | Bi 6s | X | X | Na 3p d | Bi 6p | Γ | Γ & L | Indirect | See ESI |
| Cs2NaInBr6 a , f | Null | Null | Γ & X | Γ & X | Null | In 5s | Γ | Γ | Direct | 48 and 49 |
| (MA)2TlBiBr6 g | Tl 6s | Bi 6s | Γ | Γ | Tl 6p | Bi 6p | Γ | Γ | Direct | 19 |
| Cs2TlTlCl6 h | Tl 6s | Null | X | X | Tl 6p | Tl 6s | L | L | Indirect | 50 |
| Cs2HfIV□Cl6 a | Null | Null | Γ & X | Γ & X | Hf 5dxy e | Null | Γ & X | Γ & X | Indirect | 41 |
| Cs2PdIV□Br6 | Null | Null | Γ & X | Γ & X | Pd 4dz2 | Null | X | X | Direct | 40 |
| Cs2SnIV□I6 a | Null | Null | Γ & X | Γ | Sn 5s | Null | Γ | Γ | Direct | 38 |
| Cs2TeIV□I6 | Te 6s | Null | X | X | Te 6p | Null | L | L | Indirect | 39 |
| Cs2TiIV□I6 a | Null | Null | Γ & X | Γ | Ti 3dxy e | Null | Γ & X | Γ & X | Indirect | 42 |
aIsostructural compounds with other halides are known. These compounds are also well-described by the LCAO model.
bThe dz2 orbital is degenerate with the dx2–y2 orbital.
cBands originating from the Y 4dxy orbitals π-bonding with the halides are also present near the CBM but are at slightly higher energies and don't interact with the σ-bonding Ag 5s states (see ESI).
dSee ESI for extended discussion of the appearance of alkali p character in the conduction band of these materials.
eThe dxy orbital is degenerate with dxz and dyz orbitals.
fThe calculated density of states is only available for the bromide, which has not been synthesized experimentally. The isostructural Cs2NaInCl6 has been synthesized.
g“MA” corresponds to CH3NH3+.
hThe reported density of states does not distinguish between Tl+ and Tl3+ contributions. These were determined based on chemical reasoning.
4.3. Limitations of the theory
The major limitation of the LCAO approach is that prior knowledge of the orbital compositions of the bands is necessary to obtain accurate results. In our construction of Table 2, we used the calculated wavefunction projections to determine the orbital composition of the bands, but ideally, the theory would require no computational inputs. In fact, for many double perovskites, an experienced chemist can accurately guess the orbital compositions of the band, and therefore the band extrema using the three rules presented here, using chemical reasoning alone (considering the electronic configuration of the metals). We consider this a primary advantage of the LCAO approach as one can often rapidly obtain the most salient aspects of the band structure from nothing more than the chemical formula and Table 1. In more ambiguous cases, it is possible to use experimental orbital energies (determined from photoelectron spectroscopy)45 to identify the correct band composition. We used this approach in Section 3.2 to determine that the Sn 4d orbitals are not involved in the Cs2Sn□Br6 valence band. However, for many orbitals (particularly the metal LUMOs), photoelectron data are not available. To remedy this, we are currently compiling a database of frontier orbital energies for a variety of metal cations, which will be presented in a future publication.
We also must caution the reader against applying this LCAO theory too aggressively in compounds that lack dispersive bands. Flatter bands imply weaker B–X and X–X interactions either due to greater energetic mismatch between B and X orbitals or reduced X–X overlap resulting from smaller X anions (e.g., F– replacing I–). To construct Table 1, we have focused only on B–X and the 90° X–X interactions and neglected other effects (for example the 180° X–X interactions). If the B–X and 90° X–X interactions are weak, then these neglected effects may indeed influence the band extrema. Additionally, flatter bands imply that the absolute energetic differences between different k points are small, making distinguishing between them more difficult and less meaningful.
It is also important to recognize that our theory is a nonrelativistic one and does not account for the effects of spin–orbit coupling (SOC) on the band structure. Despite this, we obtain remarkable correspondence between our predictions and DFT calculations, which include SOC, even in compounds with heavy elements where relativistic effects are known to be significant. In general, SOC can be viewed as a relatively small perturbation to the overall energy of the electronic states. The primary effects of this perturbation are additional splitting of nominally degenerate bands derived from p and d orbitals. The relative dispersion of each band is also affected to a lesser extent.
In all of the double perovskites examined here, SOC does not change the position of the VBM or CBM. Nevertheless, in Section 3.1, we noted two examples in which SOC leads to subtle variations in band structure, providing a reminder that it is important to consider potential effects of SOC when applying this theory.
4.4. Extensions of the theory
In this work, we have focused exclusively on double perovskites that adopt the undistorted cubic Fm3[combining macron]m structure, accounting for most known halide double perovskite compositions. However, this excludes a number of double perovskites that show tilting between octahedra (for example, Rb2SnIV□I6)51 or contain metals that exhibit Jahn–Teller distortions, which lower the local symmetry from octahedral point symmetry (e.g., Cs2AuIAuIIICl6).52 The theory can be adapted to these cases as well, and we will provide a detailed analysis in future work.
We also see opportunities in extending the LCAO theory to address more complicated situations. In particular, there have been many recent reports of complex, non-stochiometric mixtures of B-site cations16,21,39,46,49,53 which, due to their disorder and low concentrations of dopants, are difficult to model computationally. We expect that our LCAO theory can accurately describe several limiting cases in these alloyed systems, potentially allowing for rapid identification of interesting and useful double perovskite alloys.
5. Conclusions
We demonstrate a qualitative approach for determining band structures of double perovskites with a high level of accuracy. Beginning from the double perovskite crystal structure and using basic LCAO methodologies, we explicitly determine all possible halide wavefunctions at the high-symmetry k points Γ, X, and L. By examining how these wavefunctions interact with the B-site metal frontier orbitals as well as the halide–halide interactions within the wavefunctions themselves, we are able to accurately predict the band extrema for almost all experimentally known halide double perovskites. In many cases, the direct/indirect nature of the bandgap of a halide double perovskite can be estimated immediately from the material's atomic composition. Our results show that double perovskite band structures are dominated by the match or mismatch of symmetry between the frontier orbitals of the B- and B′-site metals. We also highlight the important role that halide–halide interactions, specifically those between halides oriented 90° from one another, have in determining band dispersion when there is no contribution to the band from a B-site orbital. Importantly, we find that when the B and B′ cations are isoelectronic and participate in the band edges, a direct bandgap at Γ is expected, whereas other cases can produce indirect or direct bandgaps (Tables 1 and 2). We hope that this theory will provide a platform for developing an intuitive understanding of double perovskite band structures and that Table 1 serves as a useful guide for identifying new and interesting double perovskite compositions.
Conflicts of interest
There are no conflicts to declare.
Note added after first publication
This article replaces the version published on 30 Sep 2019, which contained an error in the first equation in section 2.3.
Supplementary Material
Acknowledgments
This work was supported by the Department of Energy, Office of Basic Energy Sciences, Division of Materials Sciences and Engineering, under contract DE-AC02-76SF00515. B. A. C. is supported by an NSF graduate fellowship (DGE-114747). L. L. acknowledges support by the Bavarian State Ministry of Science, Research, and the Arts through the grant “Solar Technologies go Hybrid (SolTech)”, the Elite Network Bavaria, and computational resources provided by the Bavarian Polymer Institute and the German Research Foundation (DFG) through SFB840.
Footnotes
†Electronic supplementary information (ESI) available: Computation methods, supplementary figures, detailed group theoretical analysis, and analysis of π-bonding bands. See DOI: 10.1039/c9sc03219c
References
- Bednorz J. G., Müller K. A. Z. Phys. B: Condens. Matter. 1986;64:189. [Google Scholar]
- Royer S., Duprez D., Can F., Courtois X., Batiot-Dupeyrat C., Laassiri S., Alamdari H. Chem. Rev. 2014;114:10292. doi: 10.1021/cr500032a. [DOI] [PubMed] [Google Scholar]
- Combes C. M., Dorenbos P., van Eijk C. W. E., Krämer K. W., Güdel H. U. J. Lumin. 1999;82:299. [Google Scholar]
- Li Y., Zhou W., Xin S., Li S., Zhu J., Lü X., Cui Z., Jia Q., Zhou J., Zhao Y., Goodenough J. B. Angew. Chem., Int. Ed. 2016;55:9965. doi: 10.1002/anie.201604554. [DOI] [PubMed] [Google Scholar]
- Li M., Pietrowski M. J., De Souza R. A., Zhang H., Reaney I. M., Cook S. N., Kilner J. A., Sinclair D. C. Nat. Mater. 2014;13:31. doi: 10.1038/nmat3782. [DOI] [PubMed] [Google Scholar]
- Zhou Y., Guan X., Zhou H., Ramadoss K., Adam S., Liu H., Lee S., Shi J., Tsuchiya M., Fong D. D., Ramanathan S. Nature. 2016;534:231. doi: 10.1038/nature17653. [DOI] [PubMed] [Google Scholar]
- NREL record efficiency chart. <https://www.nrel.gov/pv/assets/pdfs/best-research-cell-efficiencies-190416.pdf> Accessed June 12, 2019. This plot is courtesy of the National Renewable Energy Laboratory.
- Kojima A., Teshima K., Shirai Y., Miyasaka T. J. Am. Chem. Soc. 2009;131:6050. doi: 10.1021/ja809598r. [DOI] [PubMed] [Google Scholar]
- Babayigit A., Ethirajan A., Muller M., Conings B. Nat. Mater. 2016;15:247. doi: 10.1038/nmat4572. [DOI] [PubMed] [Google Scholar]
- Slavney A. H., Smaha R. W., Smith I. C., Jaffe A., Umeyama D., Karunadasa H. I. Inorg. Chem. 2017;56:46. doi: 10.1021/acs.inorgchem.6b01336. [DOI] [PubMed] [Google Scholar]
- Slavney A. H., Hu T., Lindenberg A. M., Karunadasa H. I. J. Am. Chem. Soc. 2016;138:2138. doi: 10.1021/jacs.5b13294. [DOI] [PubMed] [Google Scholar]
- McClure E. T., Ball M. R., Windl W., Woodward P. M. Chem. Mater. 2016;28:1348. [Google Scholar]
- Volonakis G., Filip M. R., Haghighirad A. A., Sakai N., Wenger B., Snaith H. J., Giustino F. J. Phys. Chem. Lett. 2016;7:1254. doi: 10.1021/acs.jpclett.6b00376. [DOI] [PubMed] [Google Scholar]
- Cross C. W., Hillebrand W. F. Am. J. Sci. 1883;26:271. [Google Scholar]
- Huang J., Yuan Y., Shao Y., Yan Y. Nat. Rev. Mater. 2017;2:17042. [Google Scholar]
- Slavney A. H., Leppert L., Bartesaghi D., Gold-Parker A., Toney M. F., Savenije T. J., Neaton J. B., Karunadasa H. I. J. Am. Chem. Soc. 2017;139:5015. doi: 10.1021/jacs.7b01629. [DOI] [PubMed] [Google Scholar]
- Slavney A. H., Leppert L., Saldivar Valdes A., Bartesaghi D., Savenije T. J., Neaton J. B., Karunadasa H. I. Angew. Chem., Int. Ed. 2018;57:12765. doi: 10.1002/anie.201807421. [DOI] [PubMed] [Google Scholar]
- Volonakis G., Haghighirad A. A., Milot R. L., Sio W. H., Filip M. R., Wenger B., Johnston M. B., Herz L. M., Snaith H. J., Giustino F. J. Phys. Chem. Lett. 2017;8:772. doi: 10.1021/acs.jpclett.6b02682. [DOI] [PubMed] [Google Scholar]
- Deng Z., Wei F., Sun S., Kieslich G., Cheetham A. K., Bristowe P. D. J. Mater. Chem. A. 2016;4:12025. [Google Scholar]
- Wei F., Deng Z., Sun S., Xie F., Kieslich G., Evans D. M., Carpenter M. A., Bristowe P. D., Cheetham A. K. Mater. Horiz. 2016;3:328. [Google Scholar]
- Tran T. T., Panella J. R., Chamorro J. R., Morey J. R., McQueen T. M. Mater. Horiz. 2017;4:688. [Google Scholar]
- Filip M. R., Giustino F. J. Phys. Chem. C. 2016;120:166. [Google Scholar]
- Cai Y., Xie W., Ding H., Chen Y., Thirumal K., H. Wong L., Mathews N., Mhaisalkar S. G., Sherburne M., Asta M. Chem. Mater. 2017;29:7740. [Google Scholar]
- Zhao X.-G., Yang D., Sun Y., Li T., Zhang L., Yu L., Zunger A. J. Am. Chem. Soc. 2017;139:6718. doi: 10.1021/jacs.7b02120. [DOI] [PubMed] [Google Scholar]
- Körbel S., Marques M. A. L., Botti S. J. Mater. Chem. C. 2016;4:3157. [Google Scholar]
- Faber F. A., Lindmaa A., von Lilienfeld O. A., Armiento R. Phys. Rev. Lett. 2016;117:135502. doi: 10.1103/PhysRevLett.117.135502. [DOI] [PubMed] [Google Scholar]
- Bloch F. Z. Phys. 1929;52:555. [Google Scholar]
- Slater J. C., Koster G. F. Phys. Rev. 1954;94:1498. [Google Scholar]
- Hoffmann R., Solids and Surfaces: A Chemist's View of Bonding in Extended Structures, Wiley-VCH, 1988. [Google Scholar]
- Goesten M. G., Hoffmann R. J. Am. Chem. Soc. 2018;140:12996. doi: 10.1021/jacs.8b08038. [DOI] [PubMed] [Google Scholar]
- Boyer-Richard S., Katan C., Traoré B., Scholz R., Jancu J.-M., Even J. J. Phys. Chem. Lett. 2016;7:3833. doi: 10.1021/acs.jpclett.6b01749. [DOI] [PubMed] [Google Scholar]
- Kim M., Im J., Freeman A. J., Ihm J., Jin H. Proc. Natl. Acad. Sci. U. S. A. 2014;111:6900. doi: 10.1073/pnas.1405780111. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wolfram T. and Ellialtıoğlu S., Electronic and Optical Properties of d-Band Perovskites, Cambridge University Press, 2006. [Google Scholar]
- Honig J. M., Dimmock J. O., Kleiner W. H. J. Chem. Phys. 1969;50:5232. [Google Scholar]
- Kahn A. H., Leyendecker A. J. Phys. Rev. 1964;135:A1321. [Google Scholar]
- Ashcroft N. W. and Mermin N. D., Solid State Physics, Holt, Rinehart, and Winston, 1976. [Google Scholar]
- Harrison W. A., Electronic Structure and the Properties of Solids, W. H. Freeman, 1980. [Google Scholar]
- Lee B., Stoumpos C. C., Zhou N., Hao F., Malliakas C., Yeh C.-Y., Marks T. J., Kanatzidis M. G., Chang R. P. H. J. Am. Chem. Soc. 2014;136:15379. doi: 10.1021/ja508464w. [DOI] [PubMed] [Google Scholar]
- Maughan A. E., Ganose A. M., Bordelon M. M., Miller E. M., Scanlon D. O., Neilson J. R. J. Am. Chem. Soc. 2016;138:8453. doi: 10.1021/jacs.6b03207. [DOI] [PubMed] [Google Scholar]
- Sakai N., Haghighirad A. A., Filip M. R., Nayak P. K., Nayak S., Ramadan A., Wang Z., Giustino F., Snaith H. J. J. Am. Chem. Soc. 2017;139:6030. doi: 10.1021/jacs.6b13258. [DOI] [PubMed] [Google Scholar]
- Kang B., Biswas K. J. Phys. Chem. C. 2016;120:12187. [Google Scholar]
- Ju M.-G., Chen M., Zhou Y., Garces H. F., Dai J., Ma L., Padture N. P., Zeng X. C. ACS Energy Lett. 2018;3:297. [Google Scholar]
- Grutsch P. A., Zeller M. V., Fehlner T. P. Inorg. Chem. 1973;12:1431. [Google Scholar]
- Meng W., Wang X., Xiao Z., Wang J., Mitzi D. B., Yan Y. J. Phys. Chem. Lett. 2017;8:2999. doi: 10.1021/acs.jpclett.7b01042. [DOI] [PubMed] [Google Scholar]
- NIST X-ray Photoelectron Spectroscopy Database, National Institute of Standards and Technology, Gaithersburg, MD, https://srdata.nist.gov/xps/.
- Du K., Meng W., Wang X., Yan Y., Mitzi D. B. Angew. Chem., Int. Ed. 2017;56:8158. doi: 10.1002/anie.201703970. [DOI] [PubMed] [Google Scholar]
- Du M.-H., Biswas K. J. Lumin. 2013;143:710. [Google Scholar]
- Shi H., Du M.-H. Phys. Rev. Appl. 2015;3:054005. [Google Scholar]
- Luo J., Wang X., Li S., Liu J., Guo Y., Niu G., Yao L., Fu Y., Gao L., Dong Q., Zhao C., Leng M., Ma F., Liang W., Wang L., Jin S., Han J., Zhang L., Etheridge J., Wang J., Yan Y., Sargent E. H., Tang J. Nature. 2018;563:541. doi: 10.1038/s41586-018-0691-0. [DOI] [PubMed] [Google Scholar]
- Retuerto M., Yin Z., Emge T. J., Stephens P. W., Li M.-R., Sarkar T., Croft M. C., Ignatov A., Yuan Z., Zhang S. J., Jin C., Paria Sena R., Hadermann J., Kotliar G., Greenblatt M. Inorg. Chem. 2015;54:1066. doi: 10.1021/ic502400d. [DOI] [PubMed] [Google Scholar]
- Maughan A. E., Ganose A. M., Almaker M. A., Scanlon D. O., Neilson J. R. Chem. Mater. 2018;30:3909. [Google Scholar]
- Elliott N., Pauling L. J. Am. Chem. Soc. 1938;60:1846. [Google Scholar]
- Lindquist K. P., Mack S. A., Slavney A. H., Leppert L., Gold-Parker A., Stebbins J. F., Salleo A., Toney M. F., Neaton J. B., Karunadasa H. I. Chem. Sci. 2019 doi: 10.1039/C9SC02581B. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.