Modelling variable proton relative biological effectiveness for treatment planning

Abstract

Dose in proton radiotherapy is generally prescribed by scaling the physical proton dose by a constant value of 1.1. Relative biological effectiveness (RBE) is defined as the ratio of doses required by two radiation modalities to cause the same level of biological effect. The adoption of an RBE of 1.1. assumes that the biological efficacy of protons is similar to photons, allowing decades of clinical dose prescriptions from photon treatments and protocols to be utilized in proton therapy. There is, however, emerging experimental evidence that indicates that proton RBE varies based on technical, tissue and patient factors. The notion that a single scaling factor may be used to equate the effects of photons and protons across all biological endpoints and doses is too simplistic and raises concern for treatment planning decisions. Here, we review the models that have been developed to better predict RBE variations in tissue based on experimental data as well as using a mechanistic approach.

Introduction

Proton beam therapy (PBT) has expanded rapidly in the last decade as a treatment for cancer. For many treatment sites, the physical characteristics of protons make PBT dosimetrically superior to photon radiotherapy. However, protons are believed to be only slightly more effective than photons at inducing biological damage for the same physical dose.¹ This is reflected by the universal adoption of a constant relative biological effectiveness (RBE) of 1.1 in both tumour and normal tissues. An increasing body of experimental data, however, strongly suggests that the RBE is not spatially invariant and depends on a multitude of parameters, both biological and physical.^2,3 The use of a constant RBE has led to concern for end-of-range effects, which may influence treatment planning decisions for beam configurations with sites bordering on sensitive organs.³ Since many other sources of uncertainty already exist, an RBE value of 1.1 as a conservative estimate might actually be satisfactory.⁴ However, as sources of error in delivery techniques are reduced and more patient treatment response data are collected, the clinical evidence of RBE variability may become more evident and therefore important for optimizing treatment.

The use of a constant RBE of 1.1 was based on measured RBE values in vivo from some of the very first proton studies.^5,6 There is substantial evidence that numerous factors influence proton RBE, including physical parameters of the beam (proton energy, scanning technique, number of treatment fields), dose, cell type, oxygenation, intrinsic radiosensitivity, and the biological or clinical endpoint of interest (local tumour control or treatment complication).^2,6 The majority of studies investigating the dependency of RBE on various parameters for local tumour control assess in vitro clonogenic cell survival, using mostly Chinese hamster cell lines for doses between ~1 and 10 Gy⁷. There is a paucity of data on RBE variation in human tumours and even more so in healthy human tissue.² Despite decades of research, we still do not fully understand which underlying biological mechanisms contribute to RBE variations. This is a major limitation in our understanding of RBE and the potential to optimize PBT by identifying patients with tumours particularly sensitive to protons and to curtail serious toxicities in healthy tissue.

Investigating and developing accurate proton RBE models is a very active area of research. Despite the development of numerous models, none are currently used in clinical treatment planning because the uncertainties in the published RBE values are still too large to sufficiently allow clinically precise RBE predictions.⁴ However, RBE end-of-range effects are generally indirectly considered in clinical decisions by trying to avoid placing the distal edge close to sensitive organs.⁸ To implement a proton RBE model in the clinic would require accurate predictions of the radiation-induced biological response with both simplicity and robustness. Currently, RBE models are either phenomenological, fitting a radiobiological model to empirical data, or biophysical and based on a mechanistic approach.

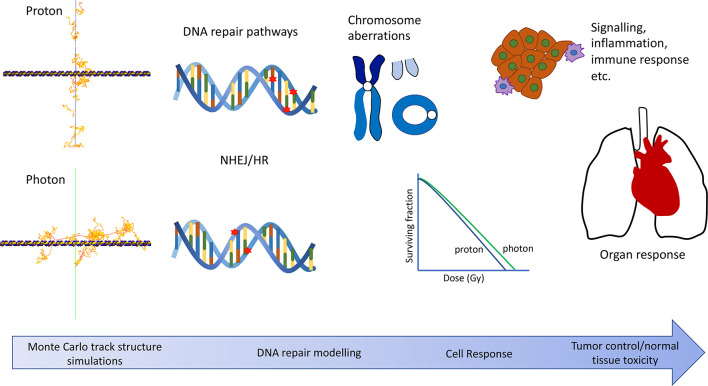
A mechanistic approach aims to accurately predict biological damage induced by both physical and chemical interactions of radiation within the cell (e.g., DNA strand breaks) and the subsequent biological processes (e.g., cell repair) to quantify lethal cell damage. Damage to DNA by ionizing radiation may be caused by direct effects, an ionization or excitation event produced by primary or secondary particles within the DNA molecule itself. Or by indirect effects, DNA damage resulting from interactions from the chemical species formed from the dissociation of water molecules. Although the total number of double strand breaks (DSBs) for photon or proton irradiation of a cell for the same dose may not be different, especially at low proton LET, small differences in the distribution or complexity of the breaks may initiate a different biological repair pathway and subsequently an overall different biological response.⁹ Protons induce slightly more clustered damage than photon irradiation. Accurate mechanistic approaches are challenging since so few of the biological pathways involved are well understood. Furthermore, linking the distribution of nanoscopic energy depositions to the cell response is already a complex task but to then connect this to a macroscopic clinical quantity, such as the tumour response or toxicity in an organ, is an especially difficult multiscale problem.¹⁰ Mechanistic models do currently exist but vastly approximate the overall process.

In this article, we review both the empirical and biophysical models available to predict and understand variable proton RBE in tissues. We also review limitations of the models and suggest approaches to aid in the development of a comprehensive mechanistic model for the prediction of proton RBE at multiple scales.

Proton RBE models

Phenomenological RBE models

Numerous proton RBE models have been developed to predict the variation of RBE with both physical and biological factors. The majority of the models are phenomenological, based on the well-established linear-quadratic (LQ) model, and use mostly empirical data of clonogenic cell survival for fitting. The LQ model relates the surviving fraction of cells to the dose, taking into account the radiosensitivity of the cells.¹¹ It should be noted that the LQ model has been used to predict other endpoints, including chromosome aberrations and the onset of oncogenesis, which also seem to correlate with a quadratic dose–response curve for clinical doses.

Table 1 presents a comparison of 10 phenomenological RBE models, all based on the LQ model, fitted to different experimental datasets of clonogenic cell survival. These models all predict that the proton RBE is dependent on the dose averaged LET (LET_d), the proton dose per fraction (D_p) and cell specific parameters ($\alpha ,\beta$) for the reference photon radiation and is based on the following LQ formulism:

Table 1.

Summary of phenomenological RBE proton models based on a similar formalism of the LQ model (equation 1)^{12 13}

Model	Cell lines (size)	RBEmax	RBEmin	Parameter values
				p0	p1	p2	p3
Carabe14	V79 (44)	${\displaystyle p_0+p_1\frac{LE{T}_d}{{\left(\alpha /\beta \right)}_x}}$	${\displaystyle p_2+p_3\frac{LE{T}_d}{{\left(\alpha /\beta \right)}_x}}$	0.843	0.413644	1.09	0.01612
Chen15	V79 (14)	${\displaystyle \frac{p_0}{{\alpha }_x}+\frac{1-e^{-p_{1}LE{T}_d^2}}{{\alpha }_x{p}_{2}LE{T}_d}}$	1.0	0.1	0.0013	0.045	--
McNamara16	Multiple (285)	${\displaystyle p_0+p_1\frac{LE{T}_d}{{\left(\alpha /\beta \right)}_x}}$	${\displaystyle p_2+p_3\sqrt{{\left(\alpha /\beta \right)}_x}LE{T}_d}$	0.99064	0.35605	1.1012	−0.0039
Peeler17	Multiple (48)	${\displaystyle p_0+p_1\frac{LE{T}_d^3}{{\left(\alpha /\beta \right)}_x}}$	${\displaystyle p_2+p_3{\left(\alpha /\beta \right)}_{x}LE{T}_d^3}$	0.75	0.00143	1.24	0.00074
Tilly18	Multiple (11)	${\displaystyle 1+p_1\frac{LE{T}_d}{{\left(\alpha /\beta \right)}_x}}$	1.0	0.309* or 0.550964	--	--	--
Rørvik12	Multiple (85)	${\displaystyle p_0+p_1\frac{LE{T}_d}{{\left(\alpha /\beta \right)}_x}}$	1.0	1.0	0.645	--	--
Wilkens19	V79 (19)	${\displaystyle \frac{p_0+p_{1}LE{T}_d}{{\alpha }_x}}$	1.0	0.1	0.02	--	--
Wedenberg20	V79 (19)	${\displaystyle p_0+p_1\frac{LE{T}_d}{{\left(\alpha /\beta \right)}_x}}$	1.0	1.0	0.434	--	--
Model	Cell lines (size)		RBEmin	Other
Belli21	V79 (6)	${\displaystyle \frac{1}{0.13}{\int }_0^{\mathrm{\infty }}\alpha \left(E\right)d\left(E\right)dE}$	${\displaystyle \frac{1}{0.214}\sqrt{{\int }_0^{\mathrm{\infty }}\beta \left(E\right)d\left(E\right)dE}}$	$\alpha \left(E\right)$and $\beta \left(E\right)$ are biological weighting functions
Jones22	Multiple (28)	${\displaystyle 1+\frac{LE{T}_d-0.22}{30.28}\times }$ ${\displaystyle \left(\frac{{\alpha }_u}{{\alpha }_x}-1\right)}$	${\displaystyle \sqrt{1+\frac{LE{T}_d-0.22}{30.28}\left(\frac{{\beta }_u}{{\beta }_x}-1\right)}}$	${\alpha }_u=2.696\left(1-e^{-3.92{\alpha }_x}\right)$ ${\beta }_u=0.06\left(1-e^{-50{\beta }_x}\right)$

RBE, relative biological effectiveness.

The definition of the RBE_min and RBE_max functions for each model differs as shown, and the fit parameters (p₀, p₁, p₂ and p₃) are summarized were applicable. The type of in vitro data and size of each dataset used in the fitting is indicated. The last two models have been separated from the table since the formulations differ. Only the linear fit of the Rørvik et al¹³ is shown here for simplicity. *For low and high (α/β)_x, respectively.

$$\begin{gathered} {\displaystyle RBE\left[D_p,{\left(\frac{\alpha }{\beta }\right)}_x,LE{T}_d\right] \\ =\frac{1}{2D_p}\left(\sqrt{{\left(\frac{\alpha }{\beta }\right)}_x^2+4D_p{\left(\frac{\alpha }{\beta }\right)}_{x}RB{E}_{max}+4D_p^{2}RB{E}_{min}^2}-{\left(\frac{\alpha }{\beta }\right)}_x\right).} \end{gathered}$$ (1)

RBE_min and RBE_max correspond to the asymptotic values of the RBE at dose 0 and $\infty$, respectively.²³ The models in Table 1 only differ in how RBE_min and RBE_max terms are defined. The majority of the models assume that RBE_max is dependent on LET_d. Some of the models assume that the RBE_min term also has a dependency with LET_d, but the majority set this term to 1.

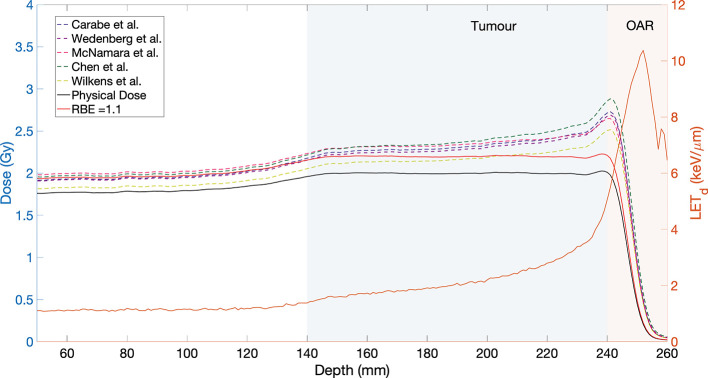
A recent comparison of 11 phenomenological proton RBE models, showed that the data sets used to fit the models have large variations in both the range of ${\left(\alpha /\beta \right)}_x$ values as well as the LET_d.¹² These models are summarized in Table 1 with the exception of the model by Mairani et al²⁴ which was originally designed for He ions. In a comparison between models for patient cases, Rørvik et al¹² found that the average RBE calculated for the PTV was in the range of 1.09–1.2,¹² which is a reasonable estimate for the tumour volume and is aligned with the goal of selecting a conservative value of 1.1 for the target. The greatest variation between models appeared in tissue with a low ${\left(\alpha /\beta \right)}_x$ (~2.0–3.1 Gy) at the end-of-range LET elevation. This would correlate to late responding organs at risk (OARs) distal to the target. Figure 1 illustrates this particular case, by showing the predicted biological dose for a spread-out Bragg peak (SOBP) for five representative models, for the case of a low ${\left(\alpha /\beta \right)}_x$ value of 2 Gy. Each of the empirical models predict an increase of the biological dose with increasing LET_d, at the distal edge of the SOBP. This could be problematic for an OAR distal to the treated tumour, as indicated by the shaded regions. In general, the available data predicts an increase of RBE with LET_d,⁷ however, there is some evidence that the dependence of RBE on LET_d might not be linear.^25–27

Figure 1.

Biological dose (left hand scale) for five representative phenomenological RBE models for a simulated SOBP with modulation width and range of 100 mm and 250 mm, respectively, for a dose of 2 Gy. The physical dose is shown by the black solid curve, while the physical dose scaled by an RBE of 1.1 is shown by the red curve. The ${\left(\alpha /\beta \right)}_x$ ratio was 2 Gy. The corresponding LET_d distribution is also shown (orange solid curve, right hand scale). The case of an OAR distal to the target tumour volume is indicated by the shaded regions. LET, linear energy transfer; OAR, organ at risk; SOBP, spread-out Bragg peak; RBE, relative biological effectiveness.

Proton RBE models based on the LQ model are appealing since the implementation into treatment planning systems could be done.²⁸ Empirical models connect to clinical endpoints (e.g. tumour control or normal tissue complication) by scaling the dose in each CT voxel with an RBE correction. However, the Achilles’ heel of these models is the experimental data used for fitting. The cell line data for proton RBE studies from the published literature, summarized in Paganetti,⁷ is shown in Figure 2. The available data shows an astoundingly large spread for the same reported cell line and LET_d (e.g. V79), possibly due to inconsistencies in experimental design amongst different labs as well as large uncertainties in the dosimetry.²⁹ The histogram in Figure 2 (right panel) shows the classification of cell lines used in the experiments. Table 2 lists the cell lines with numbers corresponding to the histogram. Non-human cell lines comprise the majority of the data (mostly Chinese hamster lung fibroblasts V79 or CHO Chinese hamster ovary cells). Fewer studies have used human cancer cell lines and the least amount of data exists for human normal tissue. These discrepancies as well as lack of human samples in the data question the accuracy of the models, particularly for clinical cases. Furthermore, the validity of cell survival as the biological endpoint for defining clinical RBE is not indisputably justified. It can be argued that cell survival is most relevant for tumour control. However, the relevancy of the available in vitro data for human tumours, given the considerable genomic heterogeneity across cancers even for the same type and histology, remains an unanswered question.² The rationality of using in vitro data for predicting in vivo responses is disputable. Although, Kellard et al³⁰ found that the in vivo response of irradiated human cervix carcinomas followed the trends of in vitro data, this may not be the case for all organs. In vitro data not only fails to account for tissue and tumour heterogeneity in a single individual but would also fail to capture some non-targeted effects, such as those mediated by interactions between cells and their microenvironment as well as neglects the role of the immune system. Lastly, models based on the LQ model may not accurately capture the full cellular response, since there is evidence of the model failing at very low and high doses.^31–33 To meticulously assess the variability of RBE for the clinic, data from both in vivo studies as well as clinical outcomes are necessary.

Figure 2.

Cell line data used for proton RBE in vitro studies.⁷ The left panel (a) shows the spread in the available data as a function of the reported ${\left(\alpha /\beta \right)}_x$ and the LET_d. The right panel shows a histogram of the cell line data, with classifications shown for human cancer and healthy tissue cell lines as well as non-human cell lines. The majority of the data is for Chinese hamster fibroblasts (V79) and ovary cells (CHO). Data for normal human cell lines are derived mostly from skin fibroblasts (AGO1522) while cancer lines are derived from HSG. See Table 2 for the corresponding names to the cell line plot numbers. HSG, human salivary glands; LET, linear energy transfer; RBE, relative biological effectiveness.

Table 2.

Summary of the cell lines from Figure 2 for the experimental proton RBE studies

Human cancer cell lines		Human healthy tissue cell lines		Non-human cell lines
1	HeLa cervix cancer	22	NB1RGB skin fibroblast	29	V79 Chinese hamster lung fibroblasts
2	HMV melanoma	23	AG01522 fibroblast	30	V79/753B
3	SQ20B laryngeal squamous cell carcinoma	24	HFIB2/HFIB15/HFIB30 fibroblasts pelvic region	31	V79-379A
4	HEp-2 larynx carcinoma	25	HF19 lung fibroblast	32	V79-WNRE
5	SCC61 tongue squamous cell carcinoma	26	M/10 epithelium	33	V79-4
6	SCC25 tongue squamous cell carcinoma	27	EUE embryonic human epithelium	34	CHO Chinese hamster ovary cells
7	HSG tumour	28	HFFF2 foetal foreskin fibroblasts	35	CHO-AA8
8	CAL4 melanoma metastatic			36	CH clone 431
9	HTB140 melanoma			37	Chinese hamster B11
10	LS-174T colorectal carcinoma			38	C1-1 Chinese hamster embryonic lung
11	DLD1 colorectal adenocarcinoma			39	B14 Chinese hamster fibroblasts
12	HCT116 colorectal carcinoma			40	H4 rat hepatoma
13	DU-145 prostate cancer			41	C3Hf mouse fibrosarcoma
14	A549 NSCLC			42	NFSa-mice lung fibrosarcoma
15	H460 NSCLC			43	HD1 rat-mouse hybrid
16	U87 glioma			44	PDV mouse skin cancer
17	ONS76 medulloblastoma			45	PDV57 mouse skin cancer
18	HT1080 fibrosarcoma			46	C3H10T1/2 mouse fibroblast (sarcoma)
19	MOLT4 lymphoblast, acute leukaemia			47	FRTL-5 Fisher rat normal thyroid
20	59M ovarian carcinoma			48	Mouse squamous carcinoma (epithelial cells) in vivo
21	U-138MG glioblastoma

HSG, human salivary gland; NSCLC, non-small cell lung cancer.

Mechanistic models

The effect of radiation on living cells depends on a complex sequence of physical, biochemical and biological processes. The goal of mechanistic models is to understand the radiation response of tissue using a ground-up approach.³⁴ It is based on the premise that the distribution of energy depositions, pertaining to the incident particle track structure, on a subcellular level is the key driver for the variability of the RBE. A true mechanistic approach would be multitiered, combining several mathematical models to cover the initiated response from the molecular scale to an organ scale (Figure 3). Modelling would ideally start by generating the nanoscopic physical and chemical interactions in the cell, to calculate a distribution of biological damages, e.g. DNA lesions. This damage distribution could be used in the next stage of modelling to predict the subsequent biological processes (e.g. DNA repair) to generate a cellular response (e.g. apoptosis). Other than the induction of DNA damage, radiation can have secondary effects such as the activation of the immune system and may also modify the tumour phenotype or microenvironment.³⁵ DNA-mediated effects such as apoptosis, senescence or mitotic catastrophe are better understood, and thus currently more modellable, than the non-targeted effects. However, to arrive at the end goal of mechanistic models, that is connecting the nanoscopic distribution of energy depositions to a clinical outcome (e.g. tumour control, healthy tissue complications), requires a better understanding of these non-targeted effects. This is a complex multiscale problem and each modelling step requires a comprehensive understanding of the physical, chemical and biological processes occurring. A large amount of effort has been put into the development of track structure modelling with accurate model representations of DNA geometry, and other biological targets, to predict damage distributions.³⁶ DNA damage predictions can be combined with repair models to predict the cellular response. On the opposite side of the modelling scale, normal tissue complication probability (NTCP) and tumour control probability (TCP) models are commonly used to assess the outcomes of radiotherapy. Presently, the missing link in true mechanistic modelling, is the ability to combine these two scales. This requires more knowledge on the intracellular radiation responses (e.g. inflammation response) and the role of the immune system.³⁷

Figure 3.

Illustration of a full mechanistic modelling approach capturing the effects of radiation on multiple scales.

Mechanistic models that are truly capable of modelling the radiation response from the molecular to organ level do not currently exist, but a few mechanism-inspired models for proton RBE have been developed.

Modelling of DNA radiation-induced damage

Monte Carlo (MC) track structure algorithms are commonly used to determine the induction of radiation damage in cellular components, predominantly the nuclear DNA. In the early codes, track structure modelling was limited to electrons in water vapour.³⁸ Over the last few decades, modelling has expanded to include other particle interactions within both liquid water and some nucleic acid materials, as well as modelling of the physicochemistry stage, within accurate representations of nuclear DNA target models.³⁹ The physical stage of track structure simulations model the clustering of energy depositions (i.e. individual ionization and excitation events) along the particle track, down to very low energies (~few eV). When tracks are modelled within target volumes, e.g. a DNA double helix, an estimation of the number of single or double strand breaks can be calculated.⁴⁰ In addition, some track structure simulations include the physicochemical stage occurring one ps after irradiation, where ionized and excited water molecules (H₂O⁺, e_eq-, H₂O*) produced in the physics stage decay, producing hydrolysis chemical species (•OH, H• , •O• , H₃O+, H₂, e_aq^_).^38,41 The primary chemical species, *OH causes the most significant damage to the DNA. However, the other species may interact with each other forming highly reactive species such as H₂, OH^- and H₂O₂, which may diffuse and also interact with biological targets to initiate damage.^42,43

Mechanistic-inspired models

In addition to the LQ model there are numerous mechanistic-inspired dose–response models. Many of these models were developed for predicting RBE in heavy ion therapy, however, some are relevant for proton therapy applications. Here we summarize the models applicable to proton RBE, other reviews provide a more comprehensive overview of the models.^44,45 Mechanistic models are based on the premise that cell fate post-irradiation will be determined by the repair of the initial DNA damage distribution. Very early radiation response models, such as the lethal–potentially lethal (LPL) model or dual action model,⁴⁶ were successful at predicting the basic features of the experimental radiation dose response curve. These models have been extended to be more mechanistic in order to better understand the contribution of the underlying physics and biology to cell inactivation.

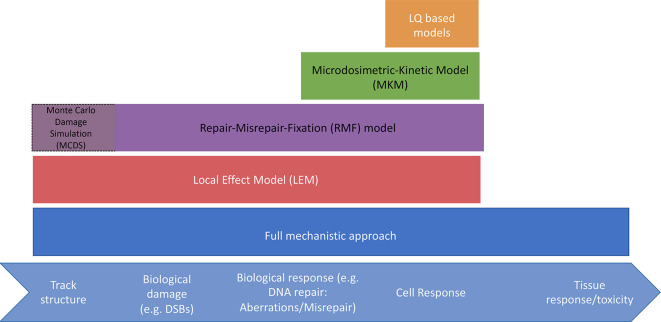
The LPL model⁴⁶ is based on the assumption of repairable or non-repairable damage. Non-repairable lesions are responsible for the linear part of the dose–response curve, while repairable lesions include repair and binary misrepair. Furthermore, lesions are categorized into slow and fast repairing. At low doses, the model converges to the LQ formulation. Even though such models are capable of parameterizing RBE, they were not specifically designed for describing the difference between radiation modalities. Three examples of biophysical or mechanistic-inspired models that have been developed to calculate proton RBE are the Microdosimetric-Kinetic Model (MKM),⁴⁷ the Repair-Misrepair-Fixation (RMF) model⁴⁸ and a recent version of the Local Effect Model (LEM).⁴⁹ All three models aim at understanding the dependency of the cell response on the physical particle characteristics of the incidence beam using the induction and biological processing of damage, i.e. repair of DNA double strand breaks (DSBs), to predict lethal damage such as chromosome aberrations. The models differ in the assumptions made about the damage induction mechanisms and in the way subcellular target volumes (size and interaction between volumes) are handled. For example, in the MKM both individual and pairs of DSB repair events are the primary contributors to lethal damage, while in the RMF model it is assumed that misrepair or fixation of DSBs and chromosome damage, is the mechanism of importance for RBE variations. Although the RMF model itself does not predict DSB induction, it is frequently combined with the Monte Carlo Damage Simulation (MCDS) algorithm which provides the initial DSB distribution within the cell.⁵⁰ Figure 4 shows a schematic of the models.

Figure 4.

Schematic of current biophysical models and the areas covered mechanistically.

LEM makes use of the concept of local dose and assumes that the same amount of “local dose” will initiate an equivalent biological response, independent of the type of radiation. The particle effectiveness is determined from the microscopic dose distribution within the nucleus. This local dose is calculated from an amorphous track structure representation of the energy deposition as a function of the radial distance to the particle path. The LEM has several implementations based on this general concept. Later implementations of LEM assume that the final biological response of the irradiated cell is dependent on the initial DNA damage spatial distribution rather than just the local dose distribution.

While all three models use a microdosimetric approach, the MKM and LEM combine this approach with biological response data from X-ray irradiation to predict the RBE for high-LET particles. The nature of the models allowed both the MKM and LEM to be used clinically to calculate RBE weighted doses for carbon ion therapy. All three models have been implemented into research treatment planning systems as well as other RBE platforms.⁵¹ This shows the potential of semi-mechanistic models to support clinical decisions. As with empirical models, expected tumour control and normal tissue complication differences between photons and protons are predicted by scaling the dose in each CT voxel by a calculated RBE value.

Towards full mechanistic modelling

Differences in the local complexity of DNA damage as well as the initiation of different DNA repair pathways determine the biological effect. DNA repair mechanisms are highly efficient in most cells, with only a small fraction of DSBs leading to cell death.⁵² The complexity and the yield of clustered damage within DNA increases with the ionization density of the primary particle.⁴⁰ More complex damage may lead to less efficient repair and lethality, through either repair failures or misrepair events, which may lead to serious chromosomal abnormalities.⁵³ Slightly dissimilar distributions and complexities of DNA damage as well as the differences in the subsequent repair mechanisms initiated in response to the radiation may explain the higher observed cell killing of protons to photons, which is the subject of active research.

Cells repair radiation induced DSBs using two main pathways, non-homologous end joining (NHEJ) and homologous recombination (HR). These two pathways are cell-cycle dependent but also differ biochemically with different substrate requirements. NHEJ is the main pathway of ionizing radiation-induced DSB repair in G1- and early S-phase cells, while both HR and NHEJ contribute to DSB repair in late S-/G2-phase cells. Although only a few studies have attempted to investigate the repair pathways instigated by protons or high-LET charged particles, there is evidence indicating that NHEJ is less capable of removing clustered DSBs induced by high-LET radiations as compared to low-LET radiations.⁵⁴ Experimental measurements indicate that NHEJ is the major repair pathway for DSBs induced by photon radiation.⁵⁵ Furthermore, accumulating evidence suggests that proton induced DSBs rely more heavily on the HR pathway for repair, supporting the notion that tumours with defects in HR may be more susceptible to protons than to photons.⁵⁶ Proton RBE variations due to alternations in HR and associated repair pathways have been reported, suggesting some cancers might be more sensitive to protons.^57,58 The majority of current published data support the idea that differential DNA repair capabilities between tumour and surrounding normal tissues could be exploited to improve regimens of PBT. However, these experiments have been limited to a few in vitro studies and further evidence in vivo and in clinical outcome data is required.²

Although the development of a true multiscale mechanistic model is currently beyond our ability, our capacity to model endpoints on cellular and subcellular scales is improving. MC track structure algorithms offer a powerful method of predicting the distribution of energy depositions on the subcellular level step-by-step.⁵⁹ Simulations are capable of modelling the interaction of physical, physicochemical and chemical processes within biological structures to predict damage induction. MC toolkits, such as Geant4-DNA⁶⁰ (TOPAS-nBio⁶¹) and PARTRAC³⁹ are continuously improving by expanding the physics process modelling in both water and biological materials, developing the chemistry processes for water radiolysis, optimizing simulation run-time and improving biological geometric models. Even though a wide range of models already exist for predicting the yield and distribution of DNA damage, the variation of the predictions is still significantly large. This is mostly in part due to different modelling assumptions because of the large uncertainties in the biological parameters and the difficulty in refining experimental measurements of DNA damage. This includes parameters such as the modelled DNA structure and hierarchy, the DNA break threshold energy as well as the likelihood of free radical species to interact with the DNA and cause damage. Recently, a new data standard for reporting on DNA damage has been proposed to facilitate efficient comparisons between models.⁶²

To connect MC models with biological response, several DNA repair models have been developed in order to better understand what types of clustered DNA damage may lead to lethality.⁶³ These models generally focus on the repair of DSBs and consider proximity effects as the primary cause of misrepair, with dense clusters of damage having a high probability of leading to deleterious misrepair. The models are capable of inputting clustering distributions predicted from MC simulations to predict the yield of mutations and chromosome aberrations, which can be used to predict cell death and be experimentally tested. The models are, however, vastly limited as they do not yet include the full biochemistry of the pathways and are primarily focused on the NHEJ pathway.⁶⁴ In a similar vein to DNA clustered damage modelling, the biological parameter space is extensive for modelling DNA repair with large uncertainties, making it difficult to refine and validate the models.

To date, radiation-induced damage in DNA has been the focus of radiobiology and all current mechanistic models are based on initial damage to the DNA, but the cell may contain other radiation targets (e.g. mitochondria, cell membranes) that may induce other significant biological responses. Damage to other cellular components may be important for determining toxicity effects in healthy tissue (e.g. dendrite morphological changes leading to cognitive dysfunction).

Connecting RBE to organ effects

Both tumour control and toxicity are the endpoints of importance in the clinic and both are likely related to DNA damage. It is however not clear how an endpoint would be affected by both the amount and the distribution of DNA damage within an organ or tumour. Cell killing is the most relevant effect for TCP models. However, other endpoints may be more relevant for NTCP models and may not directly correlate with cell survival and hence RBE. NTCP models generally depend on somewhat complex dose distributions in an organ. The current mechanistic-based models do not consider the effects from organ dose distributions, fractionation effects or multiorgan interplay (e.g. heart and lung) effects. In addition to this shortcoming, there is a lack of clinical evidence of patient under- or overdosing.^65,66 This could in part be due to the conservative and safe application of radiation therapy and particularly patient variability in radiosensitivity.

Recently, studies have investigated alternative endpoints for normal tissue injury in retrospective patient data and did find a correlation between patient image changes (e.g. lung density changes) after proton therapy with proton dose and LET.⁶⁷ However, other studies that have investigated the correlation of high LET regions with toxicity, e.g. incidence of CNS injury, have found no significant correlation and found the incidence of injury to be similar to that reported for photon therapy.⁶⁵ Data are scarce for proton RBE in non-lethal injuries and such retrospective studies using clinical data are important for investigating the RBE for different biological endpoints.

The lack of biological input parameters makes the prediction of a variable RBE in all tissues for treatment planning challenging. Despite the large uncertainty in RBE, all the existing data strongly suggest that RBE increases with LET up to a given value, then decreases. For this reason, LET optimization has been proposed as a method of optimizing proton treatment planning.^68,69

The need for more experimental data

For local tumour control, the most relevant cellular endpoint is clonogenic cell survival, which is also the most studied endpoint for proton RBE. In vitro studies offer valuable information to study the basic biological responses to proton and photon radiation. Challenges, however, remain on how to standardize the in vitro measurements,⁷⁰ to allow inter-institutional comparison and to limit the large uncertainties in the current data. Standardization techniques have been outlined in a recent report by Paganetti et al.⁷¹ More genomically characterized human cancer cell lines and normal human tissue would be valuable. There is considerable RBE heterogeneity between cell lines, which may be due to defective DNA repair pathways. In both human and CHO cells, it has been shown that defective HR increases the RBE for low-LET proton radiation. Patient variability and genomic heterogeneity may thus also affect the proton RBE. It is however clear that in vivo proton RBE studies are necessary. This is especially the case when considering alternative endpoints to cell survival which are likely to be important for normal tissue complications.

The relevance to human clinical endpoints, cost as well as ethics of animal in vivo studies makes it less desirable than in vitro studies, however it would be helpful in validating proton RBE models. Human tumour responses could be determined in vivo using measurements such as TCD50 (the dose for 50% local control of the tumour) using human tumour cells implanted in immune-deficient animals.

In healthy tissue especially, retrospective patient studies investigating toxicity (e.g. lung fibrosis, bone fractures) are currently limited by the number of patients, but as more data are collected, they could become a statistically viable technique of estimating proton RBE using alternative endpoints. Robust biomarkers could be used to identify individual patients with proton-susceptible tumours and thus identify information on patient radiosensitivity. Since interpatient variability in tumour and OAR radiosensitivity may have an impact on proton RBE, it would be important to identify these patients for any clinical studies.

Prospective, randomized controlled trials will remain the gold-standard for gathering clinical evidence in radiation oncology, and the results from photon vs proton trials would allow a direct comparison of the response of tumours to the two modalities. It has been suggested that using a model-based trial would help to select a subpopulation of patients expected to experience a clinically significant benefit from protons over photons and could improve the trial design allowing differences to be better investigated.^72,73 Even with reliable clinical data, RBE extraction from the sigmoid-shaped curves for tissue response will still be challenging.

Conclusion

Knowledge of RBE in proton therapy is required to utilize our existing knowledge and experience of photon therapy. However, despite decades of research, RBE remains poorly understood and a constant dose scaling factor of 1.1 has been adopted in the clinic. In an attempt to better predict variable RBE, especially to account for end-of-range effects, several biophysical models have been developed.

Empirical models are based mostly on clonogenic cell survival and the applicability of these data for patients is questionable, particularly since some normal tissue toxicity endpoints may not be related to cell survival alone. Furthermore, phenomenological models may be able to predict RBE trends (e.g. RBE increasing with LET) but are unlikely to provide an in-depth understanding of the underlying physical and biological processes responsible. Ultimately, optimized PBT requires a multiscale understanding of RBE, incorporating the physical and chemical processes occurring on the subcellular scale with the initiated biological processes on both the cellular and intracellular (organ) scale.

Although a true mechanistic modelling approach does not yet exist, a few mechanistic-inspired models have been developed for proton therapy. Linking the distribution of energy depositions on a nanoscopic level to an RBE outcome in the clinic is still a challenging problem. Currently, there is still an inadequate amount of data on the clinical dose–response of human tissues on which to reliably derive RBE model parameters.