Myths and realities of range uncertainty

Abstract

Range uncertainty is a much discussed topic in proton therapy. Although a very real aspect of proton therapy, its magnitude and consequences are sometimes misunderstood or overestimated. In this article, the sources and consequences of range uncertainty are reviewed, a number of myths associated with the effect discussed with the aim of putting range uncertainty into clinical context and attempting to de-bunk some of the more exaggerated claims made as to its consequences.

Introduction

Simply put, protons stop. On penetrating through matter, they gradually interact with orbiting electrons, losing a tiny amount of energy in each collision, eventually resulting in the well-known Bragg peak (Figure 1). It is due to this simple effect that proton therapy can, by using modern delivery technologies such as pencil beam scanning (PBS)¹ and intensity modulated proton therapy (IMPT),² lead to such dramatic and impressive dose distributions (Figure 2). At least on the computer screen.

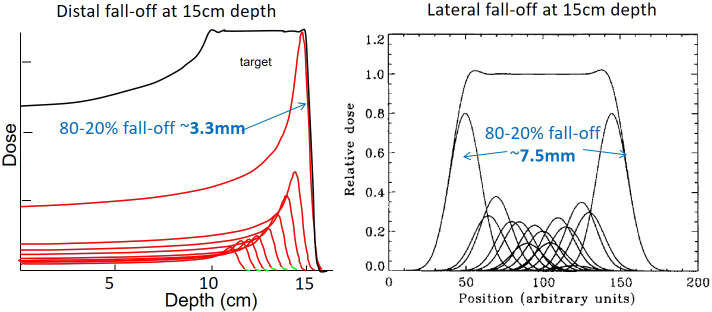
Figure 1.

A comparison of distal and lateral fall-offs for PBS proton therapy in water. Both are for a Bragg peak depth of 15 cm in water. PBS,pencil beam scanning.

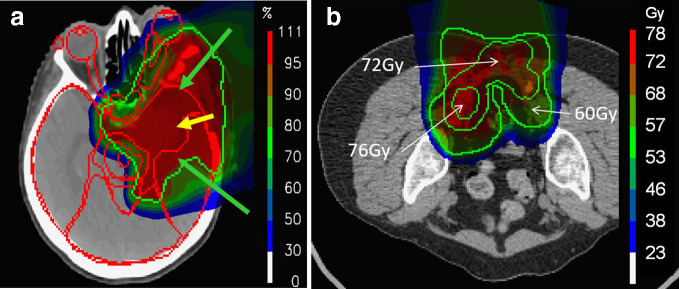
Figure 2.

Example clinical dose distributions delivered at our institute using PBS proton therapy, showing the large volumes of normal tissue spared by the stopping characteristcis of protons. (a) A large meningioma treated using 3-fields. (b) A sacral chordoma treated with two posterior-oblique fields. PBS, pencil beam scanning.

What possibly could go wrong with this? Well, many things according to many authors (including the author of this paper). The problem is, the sharper the gradient, such as on the distal side of the proton Bragg peak (Figure 1), the more dependent we are on it being positioned in exactly the position we want it to be to achieve the planned dose distribution. By the very nature of sharp gradients however, any small shifts in their position cause drastic, if localized, changes in dose. Indeed, this is the paradox of conformal radiotherapy of any form. Being conformal means constructing sharp gradients around the target volume, and sharp gradients are fundamentally unrobust. For proton therapy, this simple truism leads naturally to the concept of "range uncertainty"—i.e uncertainty in the exact position of Bragg peaks in the patient, translating directly into concerns of the "robustness" of the planned dose distribution.

It is this concept of range uncertainty, and its consequences on plan robustness, that is discussed in this paper. As such, an unconventional format has been adopted. In the first section, the sources and potential consequences of range uncertainty will be discussed (The reality), whilst in the second section, we will move on to discuss, and hopefully "debunk," some of the more exaggerated claims made on the consequences of such uncertainties (The myths). In the final section (Clinical possibilities and outcomes), the clinical benefits of proton therapy, despite the reality of range uncertainty, will be outlined. The aim is to revisit the issues of range uncertainty from a critical, but also balanced and pragmatic viewpoint, attempting to put range uncertainty into clinical context.

The reality

Sources of range uncertainty

Let’s be clear—range uncertainty is a reality. Even in the simplest geometries and media like water, proton range is inevitably uncertain. For instance, there will always be measurement limitations involved in measuring the Bragg peak (because of the sharp gradient), as well as possible fluctuations in the energy of the beam. However, both are small and lead to submillimeter uncertainties only. Clinically, these are irrelevant.

Range uncertainty, however, certainly increases when it comes to predicting range in the patient. Patients are not water, and accurate range prediction needs an accurate model of the patient, or more precisely, an accurate model of the relative stopping power of different tissues in the patient. The current state-of-the-art to determine these is by X-ray tomography (CT) imaging. Given that this provides information on attenuation of the tissues to X-rays however, proton stopping power must then be deduced using a calibration procedure.³ Current estimates on the range uncertainty from this procedure, including inherent limitations of the modality including, e.g. beam hardening, is of the order of 3-%, although this can be reduced with the use of dual-energy CT.^4,5 Thus, the best-case range uncertainty for a Bragg peak at 10 cm water equivalent range in the patient is of the order of 1.5–3.5 mm.

This is what would be expected for a good quality CT and unchanging patient. By good quality, we mean a CT with high spatial resolution, low noise and minimal reconstruction artefacts due to high-density materials. This is not always the case, and for CT data sets with diminished quality (e.g. due to metal implants), range errors, at least locally, can be up to the centimeter range when irradiating through major reconstruction artefacts created by dense (e.g. metal) implants. Although new CT acquisitions and reconstruction techniques (e.g. dual-energy and iterative reconstruction techniques) can help, this remains a major source of range uncertainty for some patients. In addition, even with a perfect CT, additional, but small range uncertainties may remain due to limitations in the accuracy of the dose calculation.⁶

However, many patients also change during the course of fractionated therapy, leading to additional changes in in-vivo range. As a result of daily misalignments of the patient, range will change due to changes in the relative position of density heterogeneities, and the patient surface, in relation to the treatment beam. Indeed, both rigid translations and rotations of the patient will affect range, even though current approaches to evaluate the effect of such uncertainties, and attempts to mitigate them during the optimization process, typically only consider translations.^7–9 On the other hand, as daily positional misalignments can be considered to be random in nature (at least if daily imaging and correction protocols are adopted to reduce systematic errors), the dosimetric effects of these will be significantly reduced over the course of the treatment.

More worrying problems are deformable (e.g. non-rigid changes such as shoulder movements¹⁰) and/or anatomical changes to the patient. The former are problematic for all treatment sites outside of the upper cranium, whilst the latter are, to a greater or lesser extent, present in all treatment sites. Range uncertainties due to deformable changes are extremely difficult to predict or correct, and for this reason, are also typically ignored in robustness evaluation or optimization. However, the magnitude of changes due to these effects, at least locally, can be large. Even worse are changes in the anatomy of the patient, such as weight changes or varying filling of internal cavities. For instance, in a study performed at our institute,¹¹ local range changes of over a centimeter were found simply due to an additional layer of fat resulting from a weight gain of only 1.5 kg in a pediatric patient. Indeed, anatomical changes of the patient are, by magnitude, likely the largest source of range uncertainty, and procedures for mitigating their effect need to be adopted wherever possible.^12–14

Consequences of range uncertainty

Uncertain range, resulting from any of the sources discussed above, can have consequences on a number of aspects of a treatment, including target coverage, dose conformation, dose homogeneity and critical organ doses, each of which will be briefly discussed in the following.

As the primary aim of proton therapy is tumour control, a major clinical consequence of range uncertainty is potential under dosage of regions of the tumour due to under shoot (i.e. the delivered range in the patient is less than planned). In principle, due to the sharp distal fall-off of the Bragg peak, even relatively small under shoots can lead to extreme under dosage of the tumour. For instance, in water, the distal 80–20% fall-off for a Bragg peak with a range of 15 cm is of the order of 4 mm. Consequently, a 4 mm range could change the dose at the distal end of the distribution by up to 60%! Scary indeed. To mitigate this in practice, either the target volume needs to be extended at the distal, and (to a lesser extent) proximal, border [the so-called range adapted planning target volume (PTV) approach], or the effects of range uncertainty incorporated into the optimization process (robust optimization), both of which lead to deliberate over shoot of the target in the nominal plan. Inevitably, this leads to a loss of dose conformation at the distal end, thus mitigating, at least to a certain extent, the primary advantage of proton therapy (see above). More subtly, and particularly for IMPT plans, range uncertainty can also affect dose homogeneity within the tumour volume. As a highly modulated IMPT plan may patch many field-internal dose gradients, both orthogonal to and along the beam direction, the relative positions of these gradients may change due to range changes, leading to unplanned hot and cold regions of dose.¹⁵ Note, that these dose changes occur within the gross tumour volume/clinical target volume (GTV/CTV) area, and cannot therefore be corrected by simply extending the PTV margin.

Finally, the consequences of range uncertainties are not restricted to tumour dose. If under shoot equates to potential under dosage of the tumour, then over shoot can just as importantly result in over doseage of critical structures that lie at, or beyond, the distal edge of the volume. Thus, range uncertainty (together with the fear of potentially enhanced biological effects in the Bragg peak) is typically considered the main obstacle to the use of the distal fall-off for organ sparing.

The myths

So much for the very real realities of range uncertainty. In this section, we will now turn our attention instead to some of the "myths" often associated to range and its uncertainty, four of which will be considered.

Myth 1: range uncertainty substantially mitigates the advantage of protons

This is a common myth, often raised to question the effectiveness of protons. And to a certain extent it is correct, at least for the "water" Bragg peak. Uncertainties in range will lead to uncertainties in dose, and additional measures may need to be taken to account for them, for instance "deliberate overshoot" (see above). Inevitably therefore, their advantage will be mitigated somewhat when range uncertainty is present or considered. The question, however, is not whether the advantage is mitigated, but by how much. To put this in context, consider Figure 3.

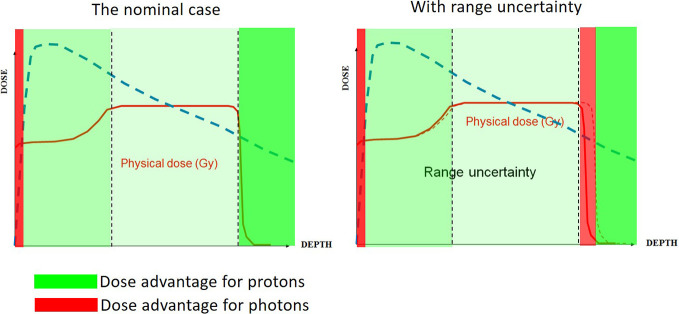
Figure 3.

A schematic comparison of the dosimetric advantage of protons versus photons. (a) The nominal case (i.e. with perfectly accurate range), with the regions of dosimetric advantage of protons indicated in green. (b) The same comparison with an un-planned overshoot of the field.

Figure 3a shows a comparison of depth–dose curves for photons and a proton Spread-Out-Bragg-Peak (SOBP) in water. The green shaded areas indicate, in the ideal case, the regions where protons have an advantage, and red where photons have an advantage. For protons, there are advantages at all depths, with the largest beyond the distal fall-off, whereas for photons, there is an advantage only in the first few millimeters, due to the skin sparing effect. Figure 3b shows a similar comparison, now including an unplanned over shoot. This leads to an additional region where photons have an advantage (at and around the distal edge of the SOBP) which is however small. At the vast majority of depths, the advantage of protons remains. Thus, even with range uncertainty, protons bring many advantages in reducing dose to normal tissue. This is not to say that the additional red region is not important—it could be, if that is where a small critical structure is—just that the effect should be kept in context of the clinical big picture.

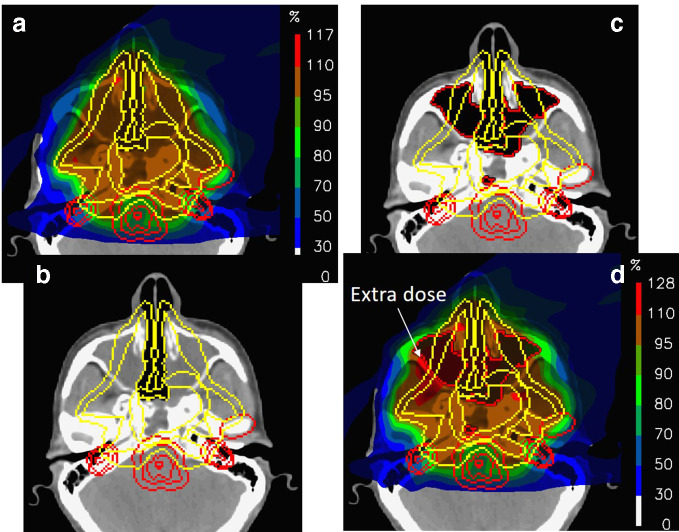
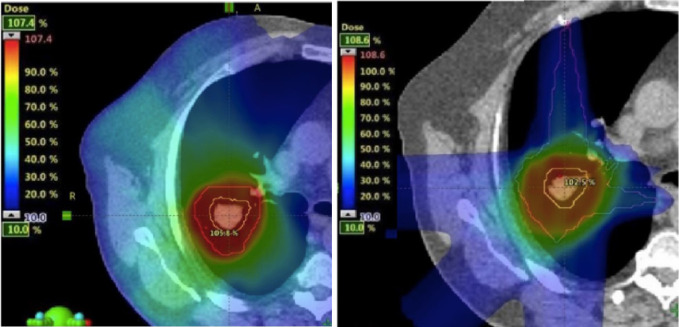
A clinical demonstration of this is shown in Figure 4. Figure 4a shows a three-field IMPT plan to a large, skull-base chordoma, planned on the CT in Figure 4b, for which the CTV/PTV totally encompasses both nasal cavities. Despite the large target volume, protons allow for excellent high dose conformation, reduced dose to the brain stem and almost complete sparing of the posterior portion of the brain. On starting treatment however, a new CT was acquired (Figure 4c) for which the changes in the nasal cavity could not be more dramatic. Indeed, this is one of the most extreme cases of anatomical changes we have observed, and one which will naturally lead to range changes in the centimeter range for all fields. The dose distribution recalculated on this new CT is shown in Figure 4d.

Figure 4.

The dosimetric consequences of major changes in the filling of nasal cavities for a large chordoma in the paranasal region. (a) The nominal plan planned on the CT shown in (b). (c) New CT acquired on the first treatment day and the corresponding recalculated dose (d).

The differences are surprisingly small. Although there is some inevitable dose "leakage" into the normal tissues anterior to the target volume (as indicated in the figure), all the most important organs at risk are spared as well as in the original plan. In addition, the target volume remains well covered. As such, due to the incident beam angles used for this plan, the clinical effects of even the huge range changes in this case were surprisingly minimal. This is not to say that this situation is acceptable for the whole treatment (indeed, complete replanning was performed immediately after this was observed), or the effects would necessarily be minimal for other cases or field arrangements. It just shows that even dramatic anatomical changes do not need to substantially reduce the advantage of protons. Indeed, similar robustness to anatomical changes have been found by a number of authors through a similarly careful selection of beam angles,^16,17 the use of robust optimizaton¹⁸ or through reduced in-field modulation of plans.¹⁹

Myth 2: the Bragg peak is the sharpest gradient

The distal fall-off of a Bragg peak in water is indeed sharp, as seen in Figures 1 and 3. Indeed, for a SOBP with a range of 15 cm in water, corresponding to a maximum energy of about 150 MeV, the distal 80–20% fall-off is 4.5 mm (Figure 1). For comparison, the best-case lateral fall-off (at the Bragg peak) of a single proton pencil beam at the same depth is about 7.5 mm.^20,21 The distal fall-off therefore is the sharpest peak, at least in water. The reality in the patient can be quite different however.

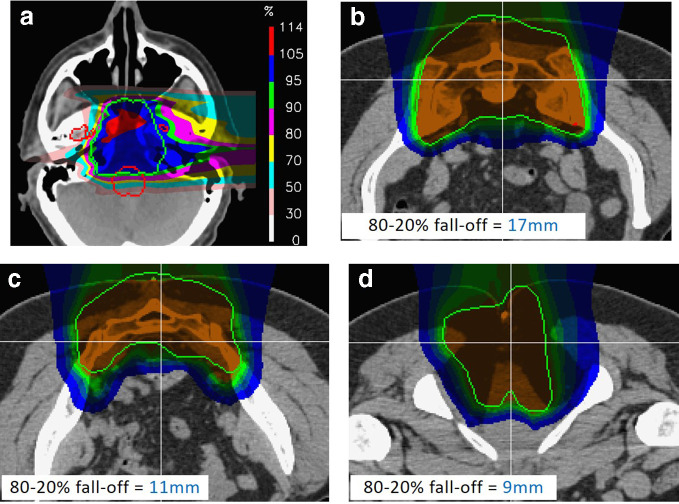
Figure 5a shows a single PBS field to a skull base chordoma, planned using a single field coming from the right. This has been optimized in order to maximize homogeneity and conformality of dose across, and to the tumour. Although the maximum dose is quite high (114% in this case), there is nevertheless an impressive conformation to the target at the 95% dose level (the blue colour-wash region).

Figure 5.

Realistic, in-vivo distal fall-offs for proton therapy. (a) For a single lateral field to a skull base chordoma. Note the extreme degradation of fall-off at the distal end due to density heterogeneities in the patient. (b–d). Example distal fall-offs to through different slices of the same sacral chordoma case. Note, all fall-offs are considerably larger than the distal fall-off shown in Figure 1.

However, where is the sharp distal fall-off in this field? The answer is, there isn’t one. Although the dose drops beyond the distal end of the target, this fall-off is in no way sharp. The problem is that, particularly in this part of the human anatomy, the patient is anything but a homogenous water phantom, and the typical pristine Bragg peak of Figure 1 is literally torn apart by the density heterogeneities through which it must pass, drastically blurring the distal end. Indeed, for this field, the lateral fall-off is visibly sharper than the distal.

Although the example of Figure 5 may be considered an extreme example (but nevertheless a field which would be perfectly acceptable as part of a multifield PBS plan), then also consider the dose distributions shown in Figure 5b–d. These show distributions through different levels of a 2-field IMPT treatment to a sacral chordoma, together with the calculated 80–20% distal fall-offs of the dose distribution along the lines indicated. These vary from 9 to 17 mm, at least twice the fall-off of the Bragg peak shown in Figure 1 and are once again not appreciably sharper than the lateral fall-offs of the same plan. Indeed, these distal fall-offs are for fields with relatively shallow maximum depths (just a few centimeters). The distal fall-off will be even less sharp for deeper fields as may be used for the treatment of prostate cancer, where distal fall-off will be further degraded due to range straggling.

In summary, the "sharpest gradient" of proton therapy is often not as sharp in the patient as we may believe when looking at Bragg peaks in water, which will inevitably reduce sensitivity of treatments to range uncertainty. This should not come as a surprise if the reader is familiar with the excellent (and largely under read) paper by Urie et al²² on the degradation of distal fall-offs due to density heterogeneities. Despite this, myth two persists in much of the proton community, maybe because little has been published on this important topic in the literature, particularly in respect of comparing distal to lateral fall-offs in clinical conditions. Additional studies therefore would be welcome to refute (or confirm) this myth.

Myth 3: photon therapy robust, proton therapy unrobust

The concept of plan robustness is something that the proton community can be proud of. In contrast, rarely is the robustness of a photon plan ever questioned. Does this mean that proton therapy is inherently less robust than photons? Well, only partially. Certainly, due to their finite range, protons are fundamentally less robust than photons at the distal end of the field, but only because there is no distal end of a photon field! However, as discussed above, robustness is strongly correlated (inversely) to dose gradients, with any radiotherapy technique with high dose gradients therefore being less robust than a technique with shallow gradients (see, e.g. the classic paper on margin calculations by van Herk²³ where sharper dose penumbras lead to larger margins!). Interestingly, as the lateral penumbra for protons is typically shallower than that for photons,²⁰ protons will therefore often be more robust to positional misalignments orthogonal to the beam direction than photons.

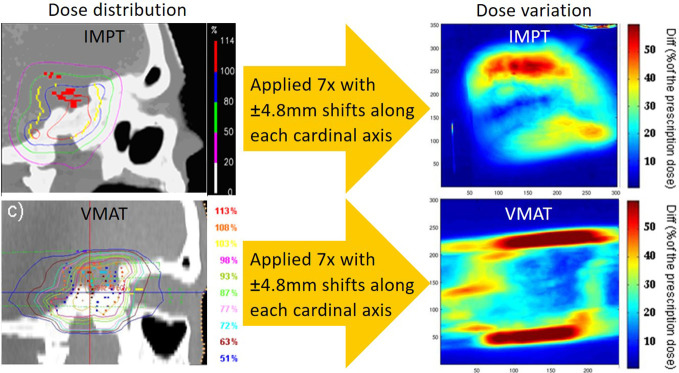
To demonstrate this, Figure 6 shows an experimental comparison of the robustness of IMPT and volumetric-modulated arc therapy (VMAT) plans to the same target volume applied to the same anthropomorphic phantom. It is important to note that neither plan was robustly optimised. Both plans were delivered multiple times to the phantom, each time with a deliberate misalignment of the phantom along one of its cardinal axes (L-R, A-P, S-I). For each, film dosimetry was performed, and point-to-point differences between the maximum and minimum doses over all films calculated, effectively providing the dose uncertainty at any point. Although the spatial distributions of dose uncertainty are quite different between the plans (partially due to the different field arrangements used), there are clear regions of uncertainty for the VMAT plan where the magnitude is substantially higher than any of the measured proton uncertainties. It is also interesting to note that, for the proton deliveries, these results inherently include all additional range uncertainties induced, e.g. by CT calibration and phantom misalignments etc.

Figure 6.

An experimental evaluation of plan robustness to set-up errors for VMAT and PBS proton therapy in an anthropomorphic phantom. Interestingly, the largest dose uncertainties are found at the lateral aspects of the VMAT plan even though this analysis inevitably includes the additional effects of set-up error induced range uncertainties for the proton plan. PBS,pencil beam scanning; VMAT, volumetric-modulated arc therapy.

Myth 4: the Bragg peak is not used in proton therapy

This could not be further from the truth. Every proton therapy plan exploits the Bragg peak, even if it is badly degraded (see Myth 2), allowing proton therapy to deliver the types of treatments shown in Figures 2, 4 and 5. That protons stop somewhere, even if not as sharply as in water and/or with some uncertainty, still allows for the sparing of large volumes of normal tissue (cf. Figure 3). Rather, what this myth really implies is that current proton therapy does not exploit the "sharp" distal fall-off of the Bragg peak. As such, it is strongly related to Myth 2, and whether a misnomer or a distinct myth, it clearly needs to be "debunked". The Bragg peak has been, and is, exploited in every proton therapy treatment, allowing to substantially reduce dose to large volumes of normal tissue, even when range is uncertain and the distal fall-off degraded.

Clinical possibilities and outcomes

In this final section, some of the possible and real clinical advantages of the range-uncertain and degraded Bragg peak will be discussed and highlighted.

Theoretical advantages

Despite Bragg peak blurring and range uncertainty, the most striking advantage of proton therapy remains—its ability to substantially reduce the so-called dose bath outside of the target volume (the green regions in Figure 3). Clinically, this could have two main consequences—the reduction of radiation induced tumours, and side-effects in organs that have a strong volume effect. By this, we mean organs whose risk of complication is associated more with the mean dose they receive, as opposed to small volumes of high dose.

Perhaps, the most obvious of these is secondary tumour induction. Radiation is a well-documented carcinogenic agent, and any reduction of dose to uninvolved healthy tissues should, theoretically, reduce the risk of radiation induced second cancers. Quite sophisticated models have been developed to predict risk based on three-dimensional dose distributions,^24–27 most of which consistently predict reductions in secondary cancer rates through the use of PBS proton therapy by about a factor of two, even when taking into account secondary neutron dose. Interestingly, this figure is also roughly the average reduction in non-target integral dose found when moving from highly conformal photon therapy (e.g. IMRT, VMAT) to PBS proton therapy.²⁸

Let’s move now to the reduction of side-effects. The volume effect in many human organs is one of the great unknowns of radiotherapy. Although models and parameters for the prediction of normal tissue complication probabilities (NTCP) have been around for 30 years or so,²⁹ organ-specific parameters for these are still very uncertain. Nevertheless, organs such as the lung, liver and pancreas are considered to have strong volume effects, and thus a reduction of the dose-bath delivered to these organs could have a significant impact on treatment-related toxicity. Indeed, given the typical volume of the liver and pancreas, degraded and uncertain Bragg peaks will have little impact on the amount of normal tissue spared, and thus advantages from proton therapy would be expected in these anatomical regions.³⁰ That an advantage remains in the lung is perhaps not so obvious, given that with the low stopping power of lung tissue, even small uncertainties in range could have a large impact on the volume of irradiated lung. Nevertheless, potential advantages can remain.

Figure 7 compares VMAT and 2-field proton plans to a Grade 1, non-small cell lung cancer. For VMAT, a typical internal target volume has been used, taking into account all positions of the tumour during the breathing cycle, as determined from four-dimensional CT. In contrast, range adapted internal target volume’s (one per field) have been used for the proton plan in order to compensate for the large potential motion induced range changes in the lung region. Despite this, there is nevertheless a clear reduction of the dose-wash in the involved lung compared to the VMAT plan, a reduction which translates into a reduction in NTCP from 3 to 1.5%.³¹

Figure 7.

A comparison between VMAT and PBS proton therapy to a Grade 1 NSCLC tumour. For the proton plan, field-specific range adapted PTV’s have been used in order to take into account range induced range changes. Even though such an approach somewhat mitigates the advantage of proton therapy, there is still a clear reduction of integral dose to the ipsi-lateral lung using protons. NSCLC,non-small-cell lung carcinoma; PBS, pencil beam scanning; PTV, planning targetvolume; VMAT, volumetric-modulated arc therapy.

The lung is a classic case of an organ with a large volume effect, but are there others? Interestingly, some pre-clinical data in mice would suggest that the spinal cord is as well.³² If such results are also indicative of the response of these organs for humans, the reduction of the dose-bath by protons could have many more advantages than previously thought. This could also be compounded by observations that organs are not independent of each other in their response to dose. For example, modern NTCP models for dysphaygia in head and neck cancer patients are based on the mean dose to two, spatially separated structures [e.g. the pharyngeal constrictor muscles and Supraglottic larynx], whilst lung and heart toxicity may also be dependent on the dose to both organs, rather than the dose received individually.^33,34

Clinical advantages

As shown by the studies discussed above, although there is a potential clinical advantage of reduced dose-bath to the human patient, it is as yet unclear whether these translate into real clinical advantages. Nevertheless, there are an increasing number of studies indicating that this may be the case.

Take for instance the study by Chung et al.³⁵ In this, a roughly two times reduction in secondary cancer induction was reported between matched populations of proton and photon pediatric patients, in close agreement to differences predicted by planning and modeling studies. In other studies comparing matched patient populations, improvements in quality of life after irradiation³⁶ and impressive reductions of 1.4–6.8 times in the incidence of side-effects such as hypothyroidism, sex hormone deficiency and the need for endocrine replacement therapy after paediatric cranial–spinal irradiation have been reported for proton therapy.³⁷ In addition, Schneider et al³⁸ reported on outcomes of 31 patients treated with high dose (72 Gy) PBS proton therapy to large mesenchymal tumours, in which minimal bowel toxicity was reported, despite the fact patients were typically irradiated using predominantly posterior fields, which partially overlapped with, and ranged out in, the bowel. Note, all these clinical results have been achieved using the fundamentally range-uncertain and degraded Bragg peaks that are inevitable in clinical practice.

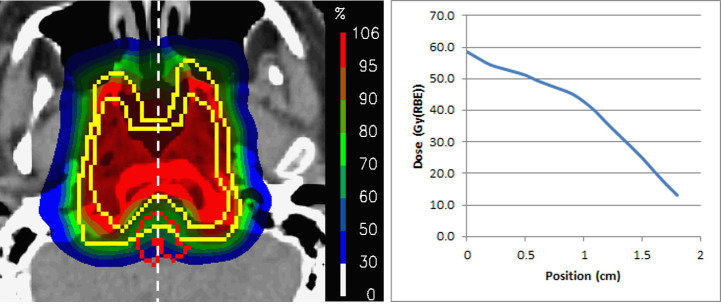
Next, is there any evidence that the fascinating preclinical results of a strong volume effect in the spinal cord translate to human patients? The answer is no. However, a publication from our own group, reporting on clinical results of 222 skull base chordoma/chondrosarcoma patients, opens up a fascinating possibility. In this study, despite taking the brainstem surface to 64 Gy, not one patient presented with a brain stem toxicity,³⁹ a remarkable result considering the maximum doses received by the brainstem (and the inevitable presence of range uncertainty!). Although the reasons for this low incidence is unclear, one possibility is that, for nearly all plans, dose gradients were applied across the brainstem, such that it’s posterior surface (the portion furthest from the target volume) received doses of 20 Gy or less (Figure 8). It is interesting to compare this with the results found in cross-sectional irradiations of rat spinal cords, where a reduction of the dose-bath across the cord allowed for substantially higher maximum doses to be applied before significant side-effects were observed.³²

Figure 8.

An example dose distribution to one of the 222 skull base chordomas reported by Weber et al.³³ On the right is the dose profile along the white line from the anterior to posterior surface of the brainstem. Note the well-defined dose gradient across the organ, with the posterior surface receiving well under 20 Gy.

To finish, it is important to mention one of the most successful applications of proton therapy and the uncertain Bragg peak. This is the treatment of ocular tumours such as uveal melanomas. This is one of the rare cases of proton therapy where treatments are always delivered using a single field, and is also one of the relatively rare indications where the Bragg peak maintains its sharpness. Despite the resulting very sharp distal gradient, and the inevitable presence of clinical range uncertainties, outcomes for this treatment are amongst the best in radiotherapy, with tumour control rates at 5 years of well over 90%^40–43—a clear indication that the Bragg peak can be clinically sharp even if somewhat uncertain.

Summary

The paradox of proton therapy is that its main advantage, a finite range, is more often than not represented as a disadvantage. However, even though the Bragg peak may be blunted and blurred by uncertainty, the considerable clinical benefits of proton therapy can, and will, remain.